Noise Effects and Perfect Controlled Remote State Preparation

Abstract

We investigate how the efficiency is affected on the noise environments in the controlled remote state preparation protocol, where the several realistic scenarios, i.e., a part or all of the qubits are subjected to the same or different types of noise, are considered. We find that more noise or less entanglement of qubits environment lead to more efficiency in terms of average fidelity. We show that it is better way to subject the qubits in different noise channels in order to increase the fidelity of the controlled remote state preparation protocol. By using a non-maximally three-qubit pure entangled state as quantum channel, furthermore, we could realize a perfect controlled remote state preparation by choosing the right noisy environments and adjusting their relations in terms of noisy rates.

1 Introduction

Transmission of quantum states is a central task in realistic quantum communication. If a sender (Alice) wants to transmit an unknown quantum state to a receiver (Bob), they can use quantum teleportation (QT) [1,2,3]. If the sender Alice knows the quantum state and can use another quantum communication way to transmit it, which is known as a remote state preparation (RSP). It is known that RSP can be carried out with less classical communication costs and simpler measurements than QT [4,5,6,7]. Due to its interesting properties, RSP has been widely investigated both theoretically [8,9,10,11,12,13,14,15,16] and experimentally [17,18,19,20,21,22,23,24,25] in recent years.

In conventional RSP protocols, there is one sender who knows the amplitude information and the phase information of the quantum state to be transmitted and one receiver who has no any information about the state. In order to satisfy the requirements of different communication scenarios, two kinds of RSP have been proposed including joint remote state preparation (JRSP) [26,27,28,29,30] and controlled remote state preparation (CRSP) [31,32,33,34,35]. In JRSP, several senders share the amplitude information and phase information of quantum state, with each sender only having partial information about the state. In CRSP, there is a controller who does not know the information of state, but the state cannot be faithfully prepared without the controller’s permission. The combination of these two variants of RSP protocols was called controlled joint remote state preparation (CJRSP) [36,37,38], and can involve in multiple senders and controllers.

As ones know, one of the key factors in the perfect controlled RSP is to use an entangled pure quantum channel [33,34,35]. In any realistic RSP protocol, unfortunately, a quantum system interacts irreversibly with its reservoir [39,40,41]. Such an effect of noise or decoherence is to turn a pure state into a mixed one, and perfect controlled RSP is not possible since, instead of entangled pure states, noise or decoherent effects force us to deal with the mixed states. It has been shown that, under a complex scheme of both classical communication and local operations perfect controlled RSP with the mixed states, it is impossible in both theoretically [42] and experimentally [24] and therefore, one of the current major challenges in accomplishing perfect controlled RSP is to overcome the limitations imposed by noise.

An increasing interest is to study the environment-assisted quantum processes [43,44,45,46,47]. The results show that noise or decoherence can enhance the efficiency of quantum communication protocols. Our goals is to study the mechanism how we increase the efficiency of the controlled RSP in the presence of noise. And we want to beat the decrease in the efficiency of the protocol due to noise with noise.

In this work, we investigate how the efficiency is affected on the noisy environments in the controlled RSP protocol, where all possible types of noise or decoherence effects are considered, where the several realistic scenarios are considered, i.e., a part or all of the qubits are subjected to the same or different types of noise. We find several scenarios in which more noise, less entanglement, or different noise acting on different qubits can increase the efficiency of the controlled RSP protocol. We show that the average fidelity can reach one, i.e., perfect controlled RSP can be achieved by adjusting the initial angle of the quantum channel and controlling the noise rate and choosing the types of noisy environments. At the same time, the controller Bob only needs to perform a single-particle measurement in the diagonal basis $\mid \pm \Big\rangle =\left(|0\Big\rangle \pm |1\Big\rangle \right)/\sqrt{2}$. Thus it is possible to conquer the decrease of efficiency in the protocol due to the noise interacting with another noise.

2 Controlled Remote State Preparation Protocol

Suppose that two participants, the sender Alice and the controller Bob, help for the remote receiver Charlie to prepare an arbitrary single-qubit state ∣ψ〉 =  ∣ α‖0〉 +  ∣ β ∣ e^iδ ∣ 1〉, where |α|² + |β|² = 1 with the absolute values ∣α∣ and ∣β∣ of the constant coefficients α and β and the relative phase δ, and δ = 2πj(j = 0, 1). The sender Alice has the complete messages about the state ∣ψ〉 including the amplitude information ∣α∣ and ∣β∣ and the phase information δ. The controller Bob and the receiver Charlie know nothing information of the state.

Here, Charlie prepares a three-qubit state ∣Φ^θ〉₁₂₃ = cos θ ∣ 000〉₁₂₃ + sin θ ∣ 111〉₁₂₃, where the qubit 1 belongs to Alice, qubit 2 belongs to Bob and qubit 3 belongs to Charlie, respectively. It is obvious that such three-qubit state is a three qubits GHZ state when θ = π/4, i.e., a maximally entangled pure state, where the initial angle 0 ≤ θ ≤ π/2 under a quantum entangled channel will be taken as a free parameter in order to fit the maximum efficiency of noisy controlled RSP protocol.

Next, it is necessary to define two orthogonal states in order to project the qubit onto Alice with her,

$$ \mid {A}_1\left\rangle {}_1=\mid \alpha \right\Vert 0\left\rangle +\mid \beta \mid {e}^{- i\delta}\mid 1\right\rangle, \mid {A}_2\left\rangle {}_1=\mid \beta \mid {e}^{- i\delta}\mid 0\right\rangle -\mid \alpha \left\Vert 1\right\rangle, $$

(1)

where the Bob’s measurement basis vectors are given by

$$ \mid {B}_1^{\varphi}\left\rangle {}_2=\cos \varphi \mid 0\right\rangle +\sin \varphi \mid 1\left\rangle, \mid {B}_2^{\varphi}\right\rangle {}_2=\sin \varphi \mid 0\left\rangle -\cos \varphi \mid 1\right\rangle, $$

(2)

in the region 0 ≤ φ ≤ π/2. When φ = π/4, the two single-qubit projective states are $\mid \pm \Big\rangle =\left(|0\Big\rangle \pm |1\Big\rangle \right)/\sqrt{2}$. Under the noisy environment, the controllable free parameter φ will be adjusted to optimize the efficiency of controlled RSP. In terms of Alice’s and Bob’s measurement basis vectors, the quantum channel can be rewritten as

$$ {\displaystyle \begin{array}{c}\mid {\varPhi}^{\theta}\left\rangle {}_{123}=\mid {A}_1\right\rangle {}_1\mid {B}_1^{\varphi}\Big\rangle {}_2{\left(|\alpha |\cos \theta \cos \varphi |0\Big\rangle +|\beta |{e}^{i\delta}\sin \theta \sin \varphi |1\Big\rangle \right)}_3\\ {}+\mid {A}_1\left\rangle {}_1\mid {B}_2^{\varphi}\right\rangle {}_2{\sigma}_3^z{\left(|\alpha |\cos \theta \sin \varphi |0\Big\rangle +|\beta |{e}^{i\delta}\sin \theta \cos \varphi |1\Big\rangle \right)}_3\\ {}+\mid {A}_2\left\rangle {}_1\mid {B}_1^{\varphi}\right\rangle {}_2{\sigma}_3^z{\sigma}_3^x{\left(|\alpha |\sin \theta \sin \varphi |0\Big\rangle +|\beta |{e}^{i\delta}\cos \theta \cos \varphi |1\Big\rangle \right)}_3\\ {}+\mid {A}_2\left\rangle {}_1\mid {B}_2^{\varphi}\right\rangle {}_2{\sigma}_3^x{\left(|\alpha |\sin \theta \cos \varphi |0\Big\rangle +|\beta |{e}^{i\delta}\cos \theta \sin \varphi |1\Big\rangle \right)}_3.\end{array}} $$

(3)

To achieve the controlled RSP, Alice and Bob perform a single-qubit measurement on own qubit, respectively. Alice’s and Bob’s outcomes may be one of $\mid {A}_1\left\rangle {}_1\mid {B}_1^{\varphi}\right\rangle {}_2$or $\mid {A}_1\left\rangle {}_1\mid {B}_2^{\varphi}\right\rangle {}_2,\mid {A}_2\left\rangle {}_1\mid {B}_1^{\varphi}\right\rangle {}_2$ and $\mid {A}_2\left\rangle {}_1\mid {B}_2^{\varphi}\right\rangle {}_2$. Next Alice and Bob inform Charlie about their measured results by using a classical channel. In terms of Alice’s and Bob’s measured results, Charlie can recover the desired state as shown in Eq. (3) by using a suitable unitary operation.

In order to simplify our equations, we will take a discrete variable j = 1, 2, 3 and 4 (i.e., $j=\mid {A}_1\left\rangle {}_1\mid {B}_1^{\varphi}\right\rangle {}_2,\mid {A}_1\left\rangle {}_1\mid {B}_2^{\varphi}\right\rangle {}_2,\mid {A}_2\left\rangle {}_1\mid {B}_1^{\varphi}\right\rangle {}_2,$and $\mid {A}_2\left\rangle {}_1\mid {B}_2^{\varphi}\right\rangle {}_2$) in the following, with each j representing one of the above four possible joint measurement result, respectively. Thus the successful probabilities Q_j{j = 1, 2, 3, 4} can be obtained by

$$ {Q}_1={\left|\alpha \right|}^2{\cos}^2\theta {\cos}^2\varphi +{\left|\beta \right|}^2{\sin}^2\theta {\sin}^2\varphi, $$

(4)

$$ {Q}_2={\left|\alpha \right|}^2{\cos}^2\theta {\sin}^2\varphi +{\left|\beta \right|}^2{\sin}^2\theta {\cos}^2\varphi, $$

(5)

$$ {Q}_3={\left|\alpha \right|}^2{\sin}^2\theta {\sin}^2\varphi +{\left|\beta \right|}^2{\cos}^2\theta {\cos}^2\varphi, $$

(6)

$$ {Q}_4={\left|\alpha \right|}^2{\sin}^2\theta {\cos}^2\varphi +{\left|\beta \right|}^2{\cos}^2\theta {\sin}^2\varphi . $$

(7)

It is convenient to quantify the protocol efficiency in terms of the fidelity [48]. Since the benchmark state is an initially pure one, the fidelity F_j{j = 1, 2, 3, 4} can be written as

$$ {F}_1=\frac{{\left|\alpha \right|}^4{\cos}^2\theta {\cos}^2\varphi +{\left|\beta \right|}^4{\sin}^2\theta {\sin}^2\varphi +2{\left|\alpha \right|}^2{\left|\beta \right|}^2\cos \theta \cos \varphi \sin \theta \sin \varphi }{{\left|\alpha \right|}^2{\cos}^2\theta {\cos}^2\varphi +{\left|\beta \right|}^2{\sin}^2\theta {\sin}^2\varphi }, $$

(8)

$$ {F}_2=\frac{{\left|\alpha \right|}^4{\cos}^2\theta {\sin}^2\varphi +{\left|\beta \right|}^4{\sin}^2\theta {\cos}^2\varphi +2{\left|\alpha \right|}^2{\left|\beta \right|}^2\cos \theta \cos \varphi \sin \theta \sin \varphi }{{\left|\alpha \right|}^2{\cos}^2\theta {\sin}^2\varphi +{\left|\beta \right|}^2{\sin}^2\theta {\cos}^2\varphi }, $$

(9)

$$ {F}_3=\frac{{\left|\alpha \right|}^4{\sin}^2\theta {\sin}^2\varphi +{\left|\beta \right|}^4{\cos}^2\theta {\cos}^2\varphi +2{\left|\alpha \right|}^2{\left|\beta \right|}^2\cos \theta \cos \varphi \sin \theta \sin \varphi }{{\left|\alpha \right|}^2{\sin}^2\theta {\sin}^2\varphi +{\left|\beta \right|}^2{\cos}^2\theta {\cos}^2\varphi }, $$

(10)

$$ {F}_4=\frac{{\left|\alpha \right|}^4{\sin}^2\theta {\cos}^2\varphi +{\left|\beta \right|}^4{\cos}^2\theta {\sin}^2\varphi +2{\left|\alpha \right|}^2{\left|\beta \right|}^2\cos \theta \cos \varphi \sin \theta \sin \varphi }{{\left|\alpha \right|}^2{\sin}^2\theta {\cos}^2\varphi +{\left|\beta \right|}^2{\cos}^2\theta {\sin}^2\varphi }. $$

(11)

Consider a controlled RSP protocol occurred in each state in terms of the different probabilities, we define the average fidelity as $\overline{F}=\sum \limits_{j=1}^4{Q}_j{F}_j$, with Q_jis a successful probability of the Charlie state, i.e., any qubit is equally probable to be picked as an original state in the controlled RSP protocol. Thus we have

$$ \overline{F}={\left|\alpha \right|}^4+{\left|\beta \right|}^4+2{\left|\alpha \right|}^2{\left|\beta \right|}^2\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(12)

where $\overline{F}$ depends on the original state and the initial angle φ. The average value $\left\langle \overline{F}\right\rangle =\frac{1}{2\pi }{\int}_0^{2\pi }{\int}_0^1\overline{F}\left({\left|\alpha \right|}^2,\delta \right)d{\left|\alpha \right|}^2 d\delta,$and therefore the quantity

$$ \left\langle \overline{F}\right\rangle =\frac{2}{3}+\frac{1}{3}\sin \left(2\theta \right)\sin \left(2\varphi \right) $$

(13)

is the efficiency of the controlled RSP protocol. Under the condition of θ = φ = π/4, $\left\langle \overline{F}\right\rangle =1$. The result implies that we recover the perfect controlled RSP protocol with Q₁ = Q₂ = Q₃ = Q₄ = 1/4 in terms of a maximally three-qubit pure entangled channel. Under the other situations, especially for the noises interacting with the quantum channel, Q_j{j = 1, 2, 3, 4} depends on the desired state and an averaging over the other possible degrees of freedom in the controlled RSP protocol.

3 Noisy Controlled RSP Protocol

The interaction of between a noisy environment and a qubit can be described by the quantum operators. In the operator-sum representation formalism, the trace-preserving Kraus operators E_k{k = 1, 2, ⋯, n} can represent such a noise and satisfy the complete condition,

$$ \sum \limits_{k=1}^n{E}_k^{\dagger }{E}_k=I, $$

(14)

where I is an identity operator acting on the qubit’s Hilbert space. Under the noisy environment, the density matrix ρ_j of the qubit j becomes

$$ {\rho}_j\to {\varepsilon}_j=\sum \limits_{k=1}^n{E}_k^{\dagger }{\rho}_j{E}_k. $$

(15)

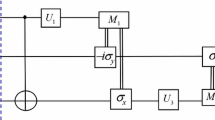
In the following, we will discuss all possible types of noise from the realistic noisy environment as shown in Fig. 1, where one, two, or all three qubits of the quantum entangled pure channel in the controlled RSP protocol are affected by such a noise in a different way. And all possible types of noise are given in the Appendix.

Fig. 1

(Color online) A schematic picture of the controlled RSP protocol. Three-qubit pure entangled channel ∣Φ^θ〉₁₂₃ refers to a source producing states in terms of Eq. (3), where SQM is a single-qubit measurement. The noise before the SQM makes the ∣Φ^θ〉₁₂₃ mixed while the noise in the last step of the protocol allows one to obtain the desired state

Under case of that each qubit is independently subjected to the noisy environments, the initial density matrix will evolve in terms of all possible types of noise.

From Eq. (15) with the three sources of noise, the density matrix including the noise effects is given by

$$ \varepsilon =\sum \limits_{i=1}^{n_1}\sum \limits_{j=1}^{n_2}\sum \limits_{k=1}^{n_3}{E}_{ijk}\left({p}_1,{p}_2,{p}_3\right)\mid \varPhi \left\rangle \right\langle \varPhi \mid {E}_{ijk}^{\dagger}\left({p}_1,{p}_2,{p}_3\right), $$

(16)

where E_ijk(p₁, p₂, p₃) = M_i(p₁) ⊗ N_j(p₂) ⊗ L_k(p₃), with M_i(p₁) = M_i(p₁) ⊗ I ⊗ I, N_j(p₂) = I ⊗ N_j(p₂) ⊗ I and L_k(p₃) = I ⊗ I ⊗ L_k(p₃). It is obvious that each Kraus operator associates with one kind of the noise interacting on the desired qubit. Generally, the different noises can act during different times with different probabilities, which can be distinguished by the decay rates p₁, p₂ and p₃. Inserting Eq. (16) into Eqs. (3)–(13), we could get the relevant physical quantities to analyze the perfect controlled RSP protocol under the noise environments. Under the limit of p₁ = p₂ = p₃ = 0, on the other hand, we can recover the noiseless case, i.e., the pure entangled state.

4 Discussions and Results

4.1 Noise in Alice’s Qubit

In order to make it clear which qubits are subjected to the noise, we introduce the notation $\left\langle {\overline{F}}_{X,\varnothing, Y}\right\rangle$ in terms of the optimal efficiency of the protocol, where the first subindex represents the qubit 1 interacting with the noise X, the second one denotes that Bob’s qubit of the quantum channel without any noise, and the third subindex is Charlie’s qubit interacting with the noise Y. Here X and Y can be any one of the four kinds of noise described in the appendix.

At the initial time, suppose that the qubits 2 and 3 of quantum channel are not affected from the noise, i.e., p₂ = p₃ = 0, and the qubit 1 lies in a noisy environment (p₁ ≠ 0). The efficiency, for each type of noise as described in Sec. 3, can be obtained by

$$ \left\langle {\overline{F}}_{BF,\varnothing, \varnothing}\right\rangle =\frac{2}{3}\left[1-\frac{p_1}{2}+\frac{1}{2}\sin \left(2\theta \right)\sin \left(2\varphi \right)\right], $$

(17)

$$ \left\langle {\overline{F}}_{AD,\varnothing, \varnothing}\right\rangle =\frac{2}{3}\left[1-\frac{p_1}{2}{\sin}^2\theta +\frac{{\sqrt{1-p}}_1}{2}\sin \left(2\theta \right)\sin \left(2\varphi \right)\right], $$

(18)

$$ \left\langle {\overline{F}}_{PhF,\varnothing, \varnothing}\right\rangle =\frac{2}{3}\left[1+\frac{\mid 1-2{p}_1\mid }{2}\sin \left(2\theta \right)\sin \left(2\varphi \right)\right], $$

(19)

$$ \left\langle {\overline{F}}_{D,\varnothing, \varnothing}\right\rangle =\frac{2}{3}\left[1-\frac{p_1}{4}+\frac{1-{p}_1}{2}\sin \left(2\theta \right)\sin \left(2\varphi \right)\right]. $$

(20)

In Eqs. (17)–(20), the subscripts on the left-hand side are the particular type of noise, i.e., BF→ bit-flip, AD→ amplitude-damping, PhF→ phase-flip, and D→ depolarizing.

From Eqs. (17)–(20), we see that the optimal efficiency is a function of p₁, the initial angle θ of the quantum channel, and the initial angle φ of the Bob’s measurement basis vectors. The maximum efficiencies are occurred at φ = π/4 due to the conditions 0 ≤ sin(2θ) sin(2φ) ≤ 1 and 1 − p₁ ≥ 0. In Fig. 2, we plot the numerical results of Eqs. (17)–(20), where 0 ≤ p₁ ≤ 1, 0 ≤ θ ≤ π/2, and φ = π/4.

Fig. 2

(Color online) Efficiency of the controlled RSP protocol when the desired qubit is only affected by a noisy environment, with the decay ratep₁ from the noise interacting with the qubit 1, and the initial angle θ of the quantum channel

According to Fig. 2, the maximum efficiencies $\left\langle {\overline{F}}_{BF,\varnothing, \varnothing}\right\rangle =\left\langle {\overline{F}}_{AD,\varnothing, \varnothing}\right\rangle =\left\langle {\overline{F}}_{D,\varnothing, \varnothing}\right\rangle =1$ occur at p₁ = 0 and θ = π/4, i.e., the qubit 1 is not affected from the noise. It is surprised that the efficiency $\left\langle {\overline{F}}_{PhF,\varnothing, \varnothing}\right\rangle$ is separated into two the two regions, which is resulted from the relations ∣1 − 2p₁ ∣  ≥ 0 and sin(2θ) sin(2φ) = 1. In Eq. (19), sin(2θ) sin(2φ)is multiplied by ∣1 − 2p₁∣ and therefore$\left\langle {\overline{F}}_{PhF,\varnothing, \varnothing}\right\rangle$ changes sign at p₁ = 1/2. In the range 0 ≤ p₁ ≤ 1/2, the average fidelity decreases and increases in the range of 1/2 ≤ p₁ ≤ 1. Thus the maximum efficiency $\left\langle {\overline{F}}_{PhF,\varnothing, \varnothing}\right\rangle =1$ occur at p₁ = 0 or p₁ = 1 for θ = π/4. In the two cases of p₁ = 0 and p₁ = 1, therefore, the phase flip does not affect on the physical system. The results give out an approach to control the RSP protocol under the environment of phase flip. For high values of p₁, the phase-flip noise give the greatest efficiency in the case of θ = φ = π/4.

Next, let us investigate a more real situation. We firstly study that the qubit 1 is always subjected to the bit-flip noise and Charlie’s qubit lies in one of the four different types of noisy environments given in Sec. 3. The optimal efficiencies are given by

$$ \left\langle {\overline{F}}_{BF,\varnothing, BF}\right\rangle =\frac{2}{3}-\frac{1}{3}\left({p}_1+{p}_3-2{p}_1{p}_3\right)+\frac{1}{3}\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(21)

$$ \left\langle {\overline{F}}_{BF,\varnothing, AD}\right\rangle =\frac{2}{3}-\frac{p_1}{3}-\frac{p_3}{3}\left(1-2{p}_1\right){\sin}^2\theta +\frac{\sqrt{1-{p}_3}}{3}\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(22)

$$ \left\langle {\overline{F}}_{BF,\varnothing, PhF}\right\rangle =\frac{2}{3}-\frac{1}{3}{p}_1+\frac{\mid 1-2{p}_3\mid }{3}\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(23)

$$ \left\langle {\overline{F}}_{BF,\varnothing, D}\right\rangle =\frac{2}{3}-\frac{p_3}{6}-\frac{p_1}{3}+\frac{p_1{p}_3}{3}+\frac{1}{3}\left(1-{p}_3\right)\sin \left(2\theta \right)\sin \left(2\varphi \right). $$

(24)

From Eqs. (21)–(24), we see the efficiencies depend on noisy rates p₁ and p₃ for the optimal efficiencies with θ = φ = π/4, where the coupling terms between the noisy rates p₁ andp₃emerge in Eqs. (21)–(24). Such coupling terms imply the entanglement of noisy environments. Therefore, there exists a possible approach to obtain the maximum efficiencies by adjusting the values of the parameters p₁ and p₃ in the efficiencies $\left\langle {\overline{F}}_{BF,\varnothing, BF}\right\rangle$, $\left\langle {\overline{F}}_{BF,\varnothing, AD}\right\rangle$, $\left\langle {\overline{F}}_{BF,\varnothing, PhF}\right\rangle$ and $\left\langle {\overline{F}}_{BF,\varnothing, D}\right\rangle$. In Fig. 3, thus, we firstly plot the efficiencies for different values of the noisy rate p₁ and p₃ in terms of Eqs. (21)–(24).

Fig. 3

(Color online) Efficiency of the controlled RSP protocol when both Alice’s qubit (p₁) and Charlie’s qubit (p₃) are affected by the different environments, where the qubit 1 is always subjected to the bit-flip (BF) noise while Charlie’s qubit may suffer from several types of noise

Forp₁ < 0.5, we find that $\left\langle {\overline{F}}_{BF,\varnothing, BF}\right\rangle, \left\langle {\overline{F}}_{BF,\varnothing, PhF}\right\rangle$ and $\left\langle {\overline{F}}_{BF,\varnothing, D}\right\rangle$ reduce with increasing of the noisy rate p₃. The results imply that the average fidelities decrease with increasing of noisy rate. Differently from $\left\langle {\overline{F}}_{BF,\varnothing, AD}\right\rangle$ and $\left\langle {\overline{F}}_{BF,\varnothing, D}\right\rangle, \left\langle {\overline{F}}_{BF,\varnothing, PhF}\right\rangle$ is divided into two regions, where $\left\langle {\overline{F}}_{BF,\varnothing, PhF}\right\rangle$ raises for p₃ > 0.5 and reduces for p₃ < 0.5.

Under the situations of p₁ > 0.5, the average fidelity $\left\langle {\overline{F}}_{BF,\varnothing, BF}\right\rangle$ becomes bigger with increasing of noisy rate p₃. The results show that more noise means higher efficiency in the cases. By putting Charlie’s qubit in a noisy environment described by the bit-flip map, thus, we can raise the efficiency of the protocol beyond the classical limit with the value 2/3 for p₁ > 0.5.

In addition, we find that $\left\langle {\overline{F}}_{BF,\varnothing, BF}\right\rangle =1$ for p₁ = p₃ = 0 or p₁ = p₃ = 1 with θ = φ = π/4, $\left\langle {\overline{F}}_{BF,\varnothing, PhF}\right\rangle =1$ for p₃ = 0 or p₃ = 1 with θ = φ = π/4 and p₁ = 0, and $\left\langle {\overline{F}}_{BF,\varnothing, AD}\right\rangle =\left\langle {\overline{F}}_{BF,\varnothing, D}\right\rangle =1$ for p₁ = p₃ = 0 with θ = φ = π/4 as shown in Fig. 3.

In order to find a perfect controlled RSP by using a non-maximally three-qubit pure entangled state under the noisy environments in terms of the noisy rates, we set $\left\langle {\overline{F}}_{BF,\varnothing, AD}\right\rangle =1$ with φ = π/4 in Eq. (22). Thus we have

$$ {\displaystyle \begin{array}{c}{p}_3=\frac{1}{2\sin^2\theta {\left(1-2{p}_1\right)}^2}\Big\{2{\sin}^2\theta {p}_1-2{\sin}^2\theta -{\sin}^2\left(2\theta \right)+4{\sin}^2\theta {p}_1^2\\ {}+\sin \left(2\theta \right)\sqrt{4\sin^2\theta +4{\sin}^4\theta +{\sin}^2\left(2\theta \right)-4{\sin}^2\theta {p}_1-16{\sin}^2\left(2\theta \right){p}_1-8{\sin}^2\theta {p}_1^2+16{\sin}^4\theta {p}_1^2}\Big\}.\end{array}} $$

(25)

For 0 ≤ p₁ ≤ 1, 0 ≤ θ ≤ π/2 in Eq. (25), if p₃exist in the range 0 ≤ p₃ ≤ 1, we can recover the perfect controlled RSP protocol, otherwise, we cannot realize the perfect controlled RSP. We plot the numerical results of Eq. (25), where 0 ≤ p₁ ≤ 1 and 0 ≤ θ ≤ π/2. Fortunately, one can obtain $\left\langle {\overline{F}}_{BF,\varnothing, AD}\right\rangle =1$ for 0.5 < p₁ ≤ 0.6, 0 ≤ p₃ < 0.3, and 0 < θ ≤ 1[rad] as shown in Fig. 4.

Fig. 4

(Color online) The relations of realizing the perfect controlled RSP between the noisy rates and measured angle, where the qubit 1 is subjected to the bit-flip (BF) noise while Charlie’s qubit may suffer from amplitude-damping (AD) noise:0.5 < p₁ ≤ 0.6, 0 ≤ p₃ < 0.3, 0 < θ ≤ 1[rad], and $\left\langle {\overline{F}}_{BF,\varnothing, AD}\right\rangle =1$

The results show that one can implement the perfect controlled RSP by using a non-maximally three-qubit pure entangled state under the noise environment in terms of Eq. (22). For the other environments, unfortunately, we cannot find a way to implement the perfect controlled RSP in terms of Eq. (21) and Eqs.(23)–(24).

Let us consider another case of qubit 1 interacting with the amplitude-damping noise, while Charlie’s qubit can suffer any one of the four kinds of noise as shown in the appendix. The optimal efficiencies are now given by

$$ \left\langle {\overline{F}}_{AD,\varnothing, BF}\right\rangle =\frac{2}{3}-\frac{p_3}{3}-\frac{p_1}{3}-\frac{p_1{p}_3}{6}+\frac{p_1}{6}\left(1+{p}_3\right){\sin}^2\theta +\frac{\sqrt{1-{p}_1}}{3}\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(26)

$$ \left\langle {\overline{F}}_{AD,\varnothing, AD}\right\rangle =\frac{2}{3}-\frac{1}{3}\left({p}_1+{p}_3-2{p}_1{p}_3\right){\sin}^2\theta +\frac{\sqrt{\left(1-{p}_1\right)\left(1-{p}_3\right)}}{3}\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(27)

$$ \left\langle {\overline{F}}_{AD,\varnothing, PhF}\right\rangle =\frac{2}{3}-\frac{p_1}{3}+\frac{p_1}{3}{\sin}^2\theta +\frac{\mid 1-2{p}_3\mid \sqrt{1-{p}_1}}{3}\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(28)

$$ \left\langle {\overline{F}}_{AD,\varnothing, D}\right\rangle =\frac{2}{3}-\frac{p_3}{6}-\frac{p_1}{3}+\frac{p_1{p}_3}{12}+\frac{p_1}{6}\left(2+{p}_3\right){\sin}^2\theta +\frac{\left(1-{p}_3\right)\sqrt{1-{p}_1}}{3}\sin \left(2\theta \right)\sin \left(2\varphi \right). $$

(29)

From Eqs. (26)–(29), we see that the efficiencies depend on the parameters p₁, p₃, θ and φ, where the optimal efficiencies are occurred at θ = φ = π/4. In Fig. 5, we plot the optimal efficiencies for different values of the noisy rate p₁ and p₃ in terms of Eqs. (26)–(29), where 0 ≤ p₁ ≤ 1, 0 ≤ p₃ ≤ 1, and θ = φ = π/4.

Fig. 5

(Color online) Optimal efficiency of the controlled RSP protocol when both Alice’s qubit (p₁) and Charlie’s qubit (p₃) are affected by the different environments, where the qubit 1 is always subjected to the amplitude-damping (AD) noise while Charlie’s qubit may suffer from several types of noise

In Fig. 5, we find that $\left\langle {\overline{F}}_{AD,\varnothing, AD}\right\rangle =\left\langle {\overline{F}}_{AD,\varnothing, PhF}\right\rangle =\left\langle {\overline{F}}_{AD,\varnothing, D}\right\rangle =1$ for p₁ = p₃ = 0 and θ = φ = π/4, $\left\langle {\overline{F}}_{BF,\varnothing, PhF}\right\rangle =1$ for p₃ = 0 or p₃ = 1 with θ = φ = π/4 and p₁ = 0.

From Eqs. (26)–(29), we see that the efficiencies depend on the coupling terms between the two noisy rates. In the other words, such efficiencies are relative to the entanglement of environments. It is happens again when Charlie’s qubit interacts with the bit-flip noise [Eq. (26)], for the optimal θ is not π/4, the less entanglement of environments leads to a better performance for the controlled RSP protocol.

Similarly, in order to implement the perfect controlled RSP by using a non-maximally three-qubit pure entangled state under the noise environments in this case, we set $\left\langle {\overline{F}}_{AD,\varnothing, BF}\right\rangle =1$ with φ = π/4 in Eq. (26). Thus we have

$$ {p}_3=\frac{2-{\sin}^2\theta +2{p}_1-2\sin \left(2\theta \right)\sqrt{1-{p}_1}}{\sin^2\theta -2-{p}_1}. $$

(30)

The numerical results p₃ of Eq. (30) is shown in Fig. 6. We see that one can obtain $\left\langle {\overline{F}}_{AD,\varnothing, BF}\right\rangle =1$ for 0 ≤ p₁ ≤ 0.15, 0 < p₃ < 0.45, 0.75 ≤ θ ≤ 1.08[rad]. For the other environments, we cannot find an approach to realize such a perfect controlled RSP in terms of Eqs.(27)–(29).

Fig. 6

(Color online) The relations of realizing the perfect controlled RSP between the noisy rates and measured angle, where the qubit 1 is subjected to the amplitude-damping (AD) noise while Charlie’s qubit may suffer from bit-flip (BF) noise: 0 ≤ p₁ ≤ 0.15, 0 < p₃ < 0.45, 0.75 ≤ θ ≤ 1.08[rad], and $\left\langle {\overline{F}}_{AD,\varnothing, BF}\right\rangle =1$

When the qubit 1 is subjected to the phase-flip noise and Charlie’s qubit is subjected to the four different types of noise as shown in the appendix, the optimal efficiencies are

$$ \left\langle {\overline{F}}_{PhF,\varnothing, BF}\right\rangle =\frac{2}{3}-\frac{p_3}{3}+\frac{1}{3}\mid 1-2{p}_1\mid \sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(31)

$$ \left\langle {\overline{F}}_{PhF,\varnothing, AD}\right\rangle =\frac{2}{3}-\frac{p_3}{3}{\sin}^2\theta +\frac{1}{3}\mid 1-2{p}_1\mid \sqrt{1-{p}_3}\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(32)

$$ \left\langle {\overline{F}}_{PhF,\varnothing, PhF}\right\rangle =\frac{2}{3}+\frac{1}{3}\mid \left(1-2{p}_1\right)\left(1-2{p}_3\right)\mid \sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(33)

$$ \left\langle {\overline{F}}_{PhF,\varnothing, D}\right\rangle =\frac{2}{3}-\frac{p_3}{6}+\frac{1}{3}\mid 1-2{p}_1\mid \left(1-{p}_3\right)\sin \left(2\theta \right)\sin \left(2\varphi \right). $$

(34)

In Eqs. (31)–(34), the optimal efficiencies are occurred at θ = φ = π/4. In Fig. 7, we plot the maximum efficiencies for different values of the noisy rate p₁ and p₃ in terms of Eqs. (31)–(34), where 0 ≤ p₁ ≤ 1, 0 ≤ p₃ ≤ 1, and θ = φ = π/4.

Fig. 7

(Color online) Optimal efficiency of the controlled RSP protocol when both Alice’s qubit (p₁) and Charlie’s qubit (p₃) are affected by the different environments, where the qubit 1 is always subjected to the phase-flip (PhF) noise while Charlie’s qubit may suffer from several types of noise

For p₁ < 0.5, we find that $\left\langle {\overline{F}}_{PhF,\varnothing, BF}\right\rangle$ and $\left\langle {\overline{F}}_{PhF,\varnothing, D}\right\rangle$ reduce with increasing of the noisy rate p₃. The results imply that the average fidelities decrease with increasing of noisy rate. Differently from $\left\langle {\overline{F}}_{PhF,\varnothing, PhF}\right\rangle$, $\left\langle {\overline{F}}_{PhF,\varnothing, BF}\right\rangle$ and $\left\langle {\overline{F}}_{PhF,\varnothing, D}\right\rangle$ are divided into two regions, which raise for p₃ > 0.5 and reduce for p₃ < 0.5.

It is interesting that $\left\langle {\overline{F}}_{PhF,\varnothing, PhF}\right\rangle$ is divided into four regions, which is reduces for p₃ < 0.5 and p₁ < 0.5 and raises for p₃ > 0.5 and p₁ > 0.5. It is surprised that under the situations of p₃ > 0.5 and p₁ > 0.5due to the entanglement of environments as shown in Eq. (33), the average fidelity $\left\langle {\overline{F}}_{PhF,\varnothing, PhF}\right\rangle$ becomes bigger with increasing of noisy rate p₃. The results show that more noise means more efficiency in the case. By putting Charlie’s qubit in a noisy environments described by the phase-flip map, thus, we can raise the efficiency of the protocol beyond the classical limit with the value 2/3 [49].

Next, we discuss the optimal efficiencies under case of the qubit 1 with the depolarizing noise. Under this situation, the optimal efficiencies can be expressed as

$$ \left\langle {\overline{F}}_{D,\varnothing, BF}\right\rangle =\frac{2}{3}-\frac{p_1}{6}-\frac{p_3}{3}+\frac{p_1{p}_3}{3}+\frac{1}{3}\left(1-{p}_1\right)\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(35)

$$ \left\langle {\overline{F}}_{D,\varnothing, AD}\right\rangle =\frac{2}{3}-\frac{p_1}{6}-\frac{p_3}{3}\left(1-{p}_1\right){\sin}^2\theta +\frac{1}{3}\left(1-{p}_1\right)\sqrt{1-{p}_3}\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(36)

$$ \left\langle {\overline{F}}_{D,\varnothing, PhF}\right\rangle =\frac{2}{3}-\frac{p_1}{6}+\frac{1}{3}\left(1-{p}_1\right)\mid 1-2{p}_3\mid \sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(37)

$$ \left\langle {\overline{F}}_{D,\varnothing, D}\right\rangle =\frac{2}{3}-\frac{p_1}{6}-\frac{p_3}{6}+\frac{p_1{p}_3}{6}+\frac{1}{3}\left(1-{p}_1\right)\left(1-{p}_3\right)\sin \left(2\theta \right)\sin \left(2\varphi \right). $$

(38)

From Eqs. (35)–(38), the optimal efficiencies are occurred at θ = φ = π/4. In this case, the environments are all entangled. In Fig. 8, we plot the maximum efficiencies for different values of the noisy rate p₁ and p₃ in terms of Eqs. (35)–(38), where 0 ≤ p₁ ≤ 1, 0 ≤ p₃ ≤ 1, and θ = φ = π/4.

Fig. 8

(Color online) Optimal efficiency of the controlled RSP protocol when both Alice’s qubit (p₁) and Charlie’s qubit (p₃) are affected by the different environments, where the qubit 1 is always subjected to the depolarizing (D) noise while Charlie’s qubit may suffer from several types of noise

In Fig. 8, with increasing the noisy rate p₁, $\left\langle {\overline{F}}_{D,\varnothing, AD}\right\rangle, \left\langle {\overline{F}}_{D,\varnothing, D}\right\rangle$ and $\left\langle {\overline{F}}_{D,\varnothing, BF}\right\rangle$ decrease beside the $\left\langle {\overline{F}}_{D,\varnothing, PhF}\right\rangle,$ where $\left\langle {\overline{F}}_{D,\varnothing, PhF}\right\rangle$ is divided into two regions. In the case of p₃ < 0.5, $\left\langle {\overline{F}}_{D,\varnothing, PhF}\right\rangle$ reduces and increases for p₃ > 0.5. For values p₁ greater than ≈0.7 we see that any values of average fidelities are below the classical 2/3 limit. In this situation, the RSP protocol is not possible. Therefore, it is necessary to controlling the noisy rate p₁ and p₃ < 0.5 in processing of the protocol.

In above two cases of $\left\langle {\overline{F}}_{PhF,\varnothing, \varnothing}\right\rangle$ and $\left\langle {\overline{F}}_{PhF,\varnothing, \varnothing}\right\rangle$, such a perfect controlled RSP is not possible by using a non-maximally three-qubit pure entangled state in terms of Eqs.(31)–(38).

4.2 Noise in Bob’s Qubit

Let us discuss the qubit 2 interacting with the amplitude damping noise, while Charlie’s qubit can suffer any one of the four kinds of noise as shown in the appendix. The optimal efficiencies are given by

$$ \left\langle {\overline{F}}_{\varnothing, AD, BF}\right\rangle =\frac{2}{3}-\frac{p_2}{3}-\frac{p_3}{3}+\frac{p_2{p}_3}{6}+\left(\frac{2{p}_2}{3}-\frac{p_2{p}_3}{3}\right){\sin}^2\theta +\frac{\sqrt{1-{p}_2}}{3}\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(39)

$$ \left\langle {\overline{F}}_{\varnothing, AD, AD}\right\rangle =\frac{2}{3}-\frac{p_3}{6}\left[1-\cos \left(2\theta \right)\right]+\frac{1}{3}\sqrt{\left(1-{p}_2\right)\left(1-{p}_3\right)}\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(40)

$$ \left\langle {\overline{F}}_{\varnothing, AD, PhF}\right\rangle =\frac{2}{3}-\frac{p_2}{3}+\frac{2{p}_2}{3}{\sin}^2\theta +\frac{\sqrt{1-{p}_2}}{3}\mid 1-2{p}_3\mid \sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(41)

$$ \left\langle {\overline{F}}_{\varnothing, AD,D}\right\rangle =\frac{2}{3}-\frac{p_3}{6}-\frac{p_2}{3}+\frac{1}{12}{p}_2{p}_3+\left(\frac{2}{3}-\frac{p_3}{6}\right){p}_2{\sin}^2\theta +\frac{\sqrt{1-{p}_2}}{3}\left(1-{p}_3\right)\sin \left(2\theta \right)\sin \left(2\varphi \right). $$

(42)

In Eqs. (39)–(42), the optimal efficiencies are occurred at θ = φ = π/4, where the coupling terms of environments are emerged in all cases. In Fig. 9, we plot the maximum efficiencies for different values of the noisy rate p₂ and p₃ in terms of Eqs. (39)–(42), where 0 ≤ p₂ ≤ 1, 0 ≤ p₃ ≤ 1, and θ = φ = π/4.

Fig. 9

(Color online) Optimal efficiency of the controlled RSP protocol when both Bob’s qubit (p₂) and Charlie’s qubit (p₃) are affected by the different environments, where the qubit 2 is always subjected to the amplitude-damping (AD) noise while Charlie’s qubit may suffer from several types of noise

In Fig. 9, with increasing the noisy rate p₂, $\left\langle {\overline{F}}_{\varnothing, AD, BF}\right\rangle,$$\left\langle {\overline{F}}_{\varnothing, AD, AD}\right\rangle$ and $\left\langle {\overline{F}}_{\varnothing, AD,D}\right\rangle$ decrease beside the $\left\langle {\overline{F}}_{\varnothing, AD, PhF}\right\rangle$, where $\left\langle {\overline{F}}_{\varnothing, AD, PhF}\right\rangle$ is divided into two regions. In the case of p₃ < 0.5, $\left\langle {\overline{F}}_{\varnothing, AD, PhF}\right\rangle$ reduces and increases for p₃ > 0.5.

We find $\left\langle {\overline{F}}_{\varnothing, AD, BF}\right\rangle =\left\langle {\overline{F}}_{\varnothing, AD, AD}\right\rangle =\left\langle {\overline{F}}_{\varnothing, AD, PhF}\right\rangle =\left\langle {\overline{F}}_{\varnothing, AD,D}\right\rangle =1$ for p₂ = p₃ = 0 with θ = φ = π/4. In addition, $\left\langle {\overline{F}}_{\varnothing, AD, PhF}\right\rangle =1$ for p₂ = 0, p₃ = 1 and θ = φ = π/4.

If Bob’s qubit 2 is subjected to the depolarizing noise and Charlie’s qubit that lies in one of the four different types of noisy environments as shown in the appendix. We have the following optimal efficiencies,

$$ \left\langle {\overline{F}}_{\varnothing, D, BF}\right\rangle =\frac{2}{3}-\frac{p_3}{3}+\frac{1}{3}\left(1-{p}_2\right)\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(43)

$$ \left\langle {\overline{F}}_{\varnothing, D, AD}\right\rangle =\frac{2}{3}-\frac{p_3}{6}\left[1-\cos \left(2\theta \right)\right]+\frac{1}{3}\left(1-{p}_2\right)\sqrt{1-{p}_3}\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(44)

$$ \left\langle {\overline{F}}_{\varnothing, D, PhF}\right\rangle =\frac{2}{3}+\frac{1}{3}\left(1-{p}_2\right)\mid 1-2{p}_3\mid \sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(45)

$$ \left\langle {\overline{F}}_{\varnothing, D,D}\right\rangle =\frac{2}{3}-\frac{p_3}{6}+\frac{1}{3}\left(1-{p}_2\right)\left(1-{p}_3\right)\sin \left(2\theta \right)\sin \left(2\varphi \right). $$

(46)

In Eqs. (43)–(46), the optimal efficiencies are occurred at θ = φ = π/4. In Fig. 10, we plot the maximum efficiencies for different values of the noisy rates p₂ and p₃ in terms of Eqs. (43)–(46), where 0 ≤ p₂ ≤ 1, 0 ≤ p₃ ≤ 1, and θ = φ = π/4.

Fig. 10

(Color online) Optimal efficiency of the controlled RSP protocol when both Bob’s qubit (p₂) and Charlie’s qubit (p₃) are affected by the different environments, where the qubit 2 is always subjected to the depolarizing (D) noise while Charlie’s qubit may suffer from several types of noise

In Fig. 10, with increasing the noisy rate p₂, $\left\langle {\overline{F}}_{\varnothing, D, BF}\right\rangle,$$\left\langle {\overline{F}}_{\varnothing, D, AD}\right\rangle$and $\left\langle {\overline{F}}_{\varnothing, D,D}\right\rangle$ decrease beside the $\left\langle {\overline{F}}_{\varnothing, D, PhF}\right\rangle$, where $\left\langle {\overline{F}}_{\varnothing, D, PhF}\right\rangle$ is divided into two regions. In the case of p₃ < 0.5, $\left\langle {\overline{F}}_{\varnothing, D, PhF}\right\rangle$ reduces and increases for p₃ > 0.5. By putting Charlie’s qubit in a noisy environments described by the phase-flip map, thus, we can raise the efficiency of the protocol beyond the classical limit with the value 2/3.

When the qubit 2 is subjected either to the bit-flip noise or to the phase-flip noise, we find that the qualitative behavior of $\left\langle {\overline{F}}_{\varnothing, BF,Y}\right\rangle, \left(Y=\varnothing, BF, PhF,D, AD\right)$ is similar to Fig. 8. A direct calculation shows $\left\langle {\overline{F}}_{\varnothing, PhF,Y}\right\rangle =\left\langle {\overline{F}}_{PhF,\varnothing, Y}\right\rangle$. In other words, the qualitative behavior of $\left\langle {\overline{F}}_{\varnothing, PhF,Y}\right\rangle$ is the same as Fig. 7.

In the above four cases, we do not find an approach to improve the overall efficiency by adjusting the noise rate from Bob’s qubit and one could not implement the perfect controlled RSP by using a non-maximally three-qubit pure entangled state. When Bob’s qubit is subjected to the bit-flip noise and amplitude-damping noise, however, we can perform such a protocol in the higher efficiency for low values of p₂. For the higher values of p₂, on the other hand, the phase-flip channel may be a better choose to perform the protocol.

4.3 Noise in Alice’s and Bob’s Qubits

Next, we further investigate the scenario that the qubits 1 and 2 are subjected to the same type of noises. This scenario is useful in the controlled RSP protocol since the entangled channel is employed by Charlie for the quantum communication tasks, suppose thatp₁ = p₂ = p, but Charlie’s qubit may suffer a different type of noise.

For the qubits 1 and 2 interacting with the bit-flip noise, we have the following optimal efficiencies,

$$ \left\langle {\overline{F}}_{BF, BF, BF}\right\rangle =\frac{2}{3}-\frac{4}{3}p+{p}^2-\frac{1}{3}{p}_3+\frac{2}{3}p{p}_3+\frac{1}{3}\left(1-2p+2{p}^2\right)\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(47)

$$ {\displaystyle \begin{array}{c}\left\langle {\overline{F}}_{BF, BF, AD}\right\rangle =\frac{2}{3}-\frac{4}{3}p+{p}^2-\frac{p_3}{6}\left(1-2p+2{p}^2\right)\left[1-\cos \left(2\theta \right)\right]\\ {}+\frac{1}{3}\left(1-2p+2{p}^2\right)\sqrt{1-{p}_3}\sin \left(2\theta \right)\sin \left(2\varphi \right),\end{array}} $$

(48)

$$ \left\langle {\overline{F}}_{BF, BF, PhF}\right\rangle =\frac{2}{3}-\frac{4}{3}p+{p}^2+\frac{1}{3}\mid 1-2{p}_3\mid \left(1-2p+2{p}^2\right)\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(49)

$$ \left\langle {\overline{F}}_{BF, BF,D}\right\rangle =\frac{2}{3}-\frac{4}{3}p+{p}^2-\frac{p_3}{6}+\frac{1}{3}p{p}_3+\frac{1}{3}\left(1-2p+2{p}^2\right)\left(1-{p}_3\right)\sin \left(2\theta \right)\sin \left(2\varphi \right). $$

(50)

From Eqs. (47)–(50), the optimal efficiencies depend on the parameters p, p₃, θ and φ. And the optimal efficiencies are occurred at θ = φ = π/4. In Fig. 11, we plot the maximum efficiencies different values of the noisy rate p and p₃ in terms of Eqs. (47)–(50), where 0 ≤ p ≤ 1, 0 ≤ p₃ ≤ 1, and θ = φ = π/4.

Fig. 11

(Color online) Optimal efficiency of the controlled RSP protocol when the qubits 1 and 2 (p) and Charlie’s qubit (p₃) are affected by the different environments, where the qubits 1 and 2 is always subjected to the bit-flip (BF) noise while Charlie’s qubit may suffer from several types of noise

Figure 11 shows the dynamic behaviors of Eqs. (43)–(46) for the different noisy rates p and p₃. In the region of p > 0.9, we see that more noise means more efficiency. By adding more noise to Charlie’s qubit in a noisy environment of the bit-flip map, we can increase the efficiency of protocol, where the following optimal efficiency increases with increasing the noisy rate p₃ > 0.5 above the classical limit.

Under the case of qubits 1 and 2 interacting with the amplitude-damping noise, the optimal efficiencies are

$$ \left\langle {\overline{F}}_{AD, AD, BF}\right\rangle =\frac{1}{6}\left(2-{p}_3\right)\left(2-2p+{p}^2\right)+\frac{1}{3}{p}^2\left(1+{p}_3\right){\sin}^2\theta +\frac{1}{3}\left(1-p\right)\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(51)

$$ \left\langle {\overline{F}}_{AD, AD, AD}\right\rangle =\frac{2}{3}-\frac{1}{3}\left(4p-3{p}^2+{p}_3-2p{p}_3\right){\sin}^2\theta +\frac{1}{3}\left(1-p\right)\sqrt{1-{p}_3}\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(52)

$$ \left\langle {\overline{F}}_{AD, AD, PhF}\right\rangle =\frac{2}{3}-\frac{2}{3}p+\frac{1}{3}{p}^2+\frac{1}{3}{p}^2{\sin}^2\theta +\frac{1}{3}\left(1-p\right)\mid 1-2{p}_3\mid \sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(53)

$$ \left\langle {\overline{F}}_{AD, AD,D}\right\rangle =\frac{1}{12}\left(4-{p}_3\right)\left(2-2p+{p}^2\right)+\frac{1}{6}{p}^2\left(2+{p}_3\right){\sin}^2\theta +\frac{1}{3}\left(1-p\right)\left(1-{p}_3\right)\sin \left(2\theta \right)\sin \left(2\varphi \right). $$

(54)

From Eqs. (51)–(54), we see the optimal efficiencies depend on the parameters p, p₃, θ and φ. And the optimal efficiencies are occurred at θ = φ = π/4. In Fig. 12, we plot the optimal efficiencies at the different values of the noisy rates p and p₃ in terms of Eqs. (51)–(54), where 0 ≤ p ≤ 1, 0 ≤ p₃ ≤ 1, and θ = φ = π/4.

Fig. 12

(Color online) Optimal efficiency of the controlled RSP protocol when the qubits 1 and 2 (p) and Charlie’s qubit (p₃) are affected by the different environments, where the qubits 1 and 2 is always subjected to amplitude-damping (AD) noise while Charlie’s qubit may suffer from several types of noise

In Fig. 12, with increasing the noisy rate p, $\left\langle {\overline{F}}_{AD, AD, BF}\right\rangle,$$\left\langle {\overline{F}}_{AD, AD, AD}\right\rangle$ and $\left\langle {\overline{F}}_{AD, AD,D}\right\rangle$ decrease beside the $\left\langle {\overline{F}}_{AD, AD, PhF}\right\rangle$, where $\left\langle {\overline{F}}_{AD, AD, PhF}\right\rangle$ is divided into two regions. In the case of p₃ < 0.5, $\left\langle {\overline{F}}_{AD, AD, PhF}\right\rangle$ reduces and increases for p₃ > 0.5.

When the qubits 1 and 2 are subjected to the phase-flip noise and Charlie’s qubit suffer any one of the four kinds of noise given in Sec. 3. The optimal efficiencies become

$$ \left\langle {\overline{F}}_{PhF, PhF, BF}\right\rangle =\frac{1}{3}\left(2-{p}_3\right)\left(1-2p+2{p}^2\right)+\frac{1}{3}\left(1-2p+2{p}^2\right)\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(55)

$$ {\displaystyle \begin{array}{c}\left\langle {\overline{F}}_{PhF, PhF, AD}\right\rangle =\frac{2}{3}\left(1-2p+2{p}^2\right)-\frac{p_3}{6}\left[1-\cos \left(2\theta \right)\right]\\ {}+\frac{1}{3}\left(1-2p+2{p}^2\right)\sqrt{1-{p}_3}\sin \left(2\theta \right)\sin \left(2\varphi \right),\end{array}} $$

(56)

$$ \left\langle {\overline{F}}_{PhF, PhF, PhF}\right\rangle =\frac{2}{3}\left(1-2p+2{p}^2\right)+\frac{1}{3}\left(1-2p+2{p}^2\right)\mid 1-2{P}_3\mid \sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(57)

$$ \left\langle {\overline{F}}_{PhF, PhF,D}\right\rangle =\frac{1}{6}\left(4-{p}_3\right)\left(1-2p+2{p}^2\right)+\frac{1}{3}\left(1-{p}_3\right)\left(1-2p+2{p}^2\right)\sin \left(2\theta \right)\sin \left(2\varphi \right). $$

(58)

From Eqs. (55)–(58), the optimal efficiencies are occurred at θ = φ = π/4. In Fig. 13, we plot the maximum efficiencies at the different values of noisy rates p and p₃ in terms of Eqs. (55)–(58), where 0 ≤ p ≤ 1, 0 ≤ p₃ ≤ 1, and θ = φ = π/4.

Fig. 13

(Color online) Optimal efficiency of the controlled RSP protocol when the qubits 1 and 2 (p) and Charlie’s qubit (p₃) are affected by the different environments, where the qubits 1 and 2 is always subjected to the phase-flip (PhF) noise while Charlie’s qubit may suffer from several types of noise

Figure 13 shows the dynamic behaviors for the different noisy rates p and p₃. Here $\left\langle {\overline{F}}_{PhF, PhF, BF}\right\rangle$ is divided into four regions, which is reduces for p₃ < 0.5 and p < 0.5 and raises for p₃ > 0.5 and p > 0.5. It is surprised that under the situations of p₃ > 0.5 and p > 0.5, the average fidelity $\left\langle {\overline{F}}_{PhF, PhF, BF}\right\rangle$ becomes bigger with increasing of noisy rate p₃. The results show that more noise means more efficiency in this case. By putting Charlie’s qubit in a noisy environment described by the phase-flip map, thus, we can raise the efficiency of the protocol beyond the classical limit with the value 2/3.

Assuming that the qubits 1 and 2 are subjected to the depolarizing noise and Charlie’s qubit is subjected to the four different types of noise, the optimal efficiencies are

$$ \left\langle {\overline{F}}_{D,D, BF}\right\rangle =\frac{2}{3}-p+\frac{11}{24}{p}^2+\frac{1}{2}p{p}_3-\frac{1}{3}{p}_3-\frac{1}{6}{p}^2{p}_3+\left(\frac{1}{3}-\frac{1}{2}p+\frac{1}{4}{p}^2\right)\sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(59)

$$ {\displaystyle \begin{array}{c}\left\langle {\overline{F}}_{D,D, AD}\right\rangle =\frac{2}{3}-p+\frac{11}{24}{p}^2-\frac{1}{6}\left(2{p}_3-3p{p}_3+{p}^2{p}_3\right)\left[1-\cos \left(2\theta \right)\right]\\ {}+\frac{1}{3}\left(1-\frac{3}{2}p+\frac{3}{4}{p}^2\right)\sqrt{1-{p}_3}\sin \left(2\theta \right)\sin \left(2\varphi \right),\end{array}} $$

(60)

$$ \left\langle {\overline{F}}_{D,D, PhF}\right\rangle =\frac{2}{3}-p+\frac{11}{24}{p}^2+\left(\frac{1}{3}-\frac{1}{2}p+\frac{1}{4}{p}^2\right)\mid 1-2{p}_3\mid \sin \left(2\theta \right)\sin \left(2\varphi \right), $$

(61)

$$ {\displaystyle \begin{array}{c}\left\langle {\overline{F}}_{D,D,D}\right\rangle =\frac{2}{3}-p+\frac{11}{24}{p}^2+\frac{1}{4}p{p}_3-\frac{1}{6}{p}_3-\frac{1}{12}{p}^2{p}_3\\ {}+\left(\frac{1}{3}-\frac{1}{2}p+\frac{1}{4}{p}^2\right)\left(1-{p}_3\right)\sin \left(2\theta \right)\sin \left(2\varphi \right).\end{array}} $$

(62)

From Eqs. (59)–(62), we see the optimal efficiencies depend on the parameters p, p₃, θ and φ. And the optimal efficiencies are occurred at θ = φ = π/4. In Fig. 14, we plot the optimal efficiencies at the different values of noisy rates p and p₃ in terms of Eqs. (59)–(62), where 0 ≤ p ≤ 1, 0 ≤ p₃ ≤ 1, and θ = φ = π/4.

Fig. 14

(Color online) Optimal efficiency of the controlled RSP protocol when the qubits 1 and 2 (p) and Charlie’s qubit (p₃) are affected by the different environments, where the qubits 1 and 2 is always subjected to the depolarizing (D) noise while Charlie’s qubit may suffer from several types of noise

The results show that by putting Charlie’s qubit in a noisy environment given in Sec. 3, thus, we cannot raise the efficiency of the protocol.

In these four cases in terms of Eqs.(47)–(62) for a non-maximally three-qubit pure entangled state as quantum channel, we do not find an approach to implement the perfect controlled RSP under the noisy effects environments. By adjusting the relations among the noisy rates and initial entangled angles or choosing an adapted noisy environment, however, we can improve the optimal efficiency of the controlled RSP protocol.

5 Conclusions

In summary, we investigated how the efficiency of the controlled RSP protocol is affected by all possible noisy environments, i.e., the bit-flip noise, amplitude-damping noise, phase-flip noise, and depolarizing noise channels, where the several realistic scenarios, i.e., a part and all of the qubits are subjected to the same or different types of noise, are considered. We show how to beat the decrease in the efficiency of the protocol due to noise with noise.

At first, we find that less entanglement means more efficiency when the qubit 1 lies in the bit-flip noise and at the same time Charlie’s qubit lies in the amplitude damping noise. And the similar result is also observed when the channel qubit 1 is subjected to the amplitude-damping noise and at the same time Charlie’s qubit lies in the bit-flip noise. For other noise scenarios with the same initial entanglement state, we could not find this behavior. In the limit of pure quantum channels, more entanglement leads to more efficiency.

Secondly, we show a scenario that more noise leads to more efficiency. This fact occurred when the qubit 1 lies in the bit-flip noise (or phase-flip noise) and Charlie’s qubit is also affected by this same noise, the efficiency is considerably greater in comparison with the situation of only the qubit 1 in this type of noise. Such a behavior was also observed in Ref. [45] when the channel qubits are subjected to the amplitude-damping noise.

Under an unavoidable noisy environment, thirdly, we find that Charlie should keep his qubit in a noisy environments described by the phase-flip map in order to get the best performance for the protocol. Furthermore, in many scenarios we can raise the efficiency of the protocol beyond the classical limit with the value 2/3.

By using a non-maximally three-qubit pure entangled state as quantum channel in a noisy environment, especially, it is surprise that the average fidelity can reach one, i.e., perfect controlled RSP can be achieved by adjusting the initial angle of the quantum channel and controlling the noise rate and choosing the types of noisy environments. In this case, the controller Bob only needs to perform a single-particle measurement in the diagonal basis $\mid \pm \Big\rangle =\left(|0\Big\rangle \pm |1\Big\rangle \right)/\sqrt{2}$. Thus it is possible to conquer the decrease of efficiency in the protocol due to the noise with another noise.

Finally, we find that the optimal combination in the noisy environments can lead to the greatest efficiencies by choosing the kinds of noise interacting with the qubits. In many situations, Alice, Bob and Charlie should subject their qubits to the same noise in order to get the better scheme to perform the controlled RSP protocol. A potentially feasible approach to the optimal efficiency is obtained by putting one of the qubits that are sent to different kinds of noise for a longer time than the other one.

Appendix

1.1 Bit-flip noise

The bit-flip noise changes a qubit state from ∣0〉 to ∣1〉 or from ∣1〉 to ∣0〉 with a probability p and is frequently used in the theory of quantum-error correction. The associated Kraus operators are given by

$$ {E}_1=\left(\begin{array}{cc}\sqrt{1-p}& 0\\ {}0& \sqrt{1-p}\end{array}\right),{E}_2=\left(\begin{array}{cc}0& \sqrt{p}\\ {}\sqrt{p}& 0\end{array}\right). $$

(63)

1.2 Amplitude-damping noise

The amplitude-damping noise channel allows us to describe the decay of a two-level system due to spontaneous emission of a phonon. This process is accompanied with the loss of energy and can be described by the Kraus operators,

$$ {E}_1=\left(\begin{array}{cc}1& 0\\ {}0& \sqrt{1-p}\end{array}\right),{E}_2=\left(\begin{array}{cc}0& \sqrt{p}\\ {}0& 0\end{array}\right). $$

(64)

The quantity p is regarded as a decay probability from the excited to the ground state for a two-level system.

1.3 Phase-flip noise

The phase-flip noise channel has no classical analog because it describes the loss of quantum information without loss of energy. The quantum information corresponding to the ability of a system to produce quantum interferences hence is described by the off-diagonal elements of a density matrix. Phase-flip map can be occurred in the phase kicks or scattering processes. Such a channel can be modeled by the following Kraus operators,

$$ {E}_1=\left(\begin{array}{cc}\sqrt{1-p}& 0\\ {}0& \sqrt{1-p}\end{array}\right),{E}_2=\left(\begin{array}{cc}\sqrt{p}& 0\\ {}0& -\sqrt{p}\end{array}\right). $$

(65)

1.4 Depolarizing noise

The depolarizing noise channel is a decoherent model. The Kraus operators including all possible decay ways for the depolarizing channel are given by

$$ {\displaystyle \begin{array}{l}{E}_1=\left(\begin{array}{cc}\sqrt{1-3p/4}& 0\\ {}0& \sqrt{1-3p/4}\end{array}\right),{E}_2=\left(\begin{array}{cc}0& \sqrt{p/4}\\ {}\sqrt{p/4}& 0\end{array}\right){\sigma}_x,{E}_3=\left(\begin{array}{cc}0& -i\sqrt{p/4}\\ {}i\sqrt{p/4}& 0\end{array}\right),\\ {}{E}_4=\left(\begin{array}{cc}\sqrt{p/4}& 0\\ {}0& -\sqrt{p/4}\end{array}\right).\end{array}} $$

(66)