1 Introduction

Developing quantum information science have exhibited unusual potentiality [1, 2]. Much of the fascination with quantum information processing derives from the properties of entanglement [3]. On the one hand, quantum entanglement can give rise to nonlocal correlations that defy explanation in terms of local, realistic theories [4]. On the other hand, it is a crucial resource to implement various quantum information processing tasks such as quantum teleportation [5–10], quantum dense coding [11], quantum state preparation [12–15], quantum information concentration [16, 17], and so on. A new kind of entangled state, named as a cluster state, was first introduced by Briegel and Raussendorf, which can be generated efficiently in any system with an Ising-type interaction [18]. Owing to their distinct advantages, e.g., their robustness against decoherence, they have been applied for many quantum information processing, such as single-qubit measurement [19], teleportation [8, 9], quantum information concentration [16] and dense coding [20]. Recently, Su et al. [21] presented experimental achievements on producing the eight-partite linear and two-diamond shape cluster states. Moreover, the eight-qubit cluster state has been experimentally prepared by Yao et al. [22] and applied for quantum information splitting [23]. Muralidharan et al. [24] further provided a number of quantum state sharing schemes for splitting an arbitrary two-qubit state among k parties using a N-qubit linear cluster state as a quantum channel.

Using shared entanglement between two parties, Bennett et al. [5] first proposed quantum teleportation by which an unknown single-qubit state can be transmitted to a distant node without sending any physical particles but with local operations and classical communication. Quantum state teleportation can be linked directly to various interrelated principles of quantum information processing, such as the impossibility of superluminal communication, the nonincrease in entanglement under local operations and classical communication [3], and the no-cloning theorem [5]. Subsequently, quantum state sharing was presented by Hillery, Bužek and Berthiaume[25]. In original quantum teleportation, there are only one sender and one receiver, while in quantum state sharing, the receiver is generalized to multi sharers. Moreover, in the former, no special security demand is needed, while in the latter, a specific security against any inside sharer’s cheating or outsider’ attack is required. As a modification of quantum teleportation, quantum remote control was proposed by Huelga et al. in 2001 [26] through bidirectional quantum teleportation method to perform an arbitrary unitary operation upon a distant quantum system. Further, the tripartite scheme of bidirectional controlled teleportation was proposed by Zha et al. [27] by utilizing a five-qubit cluster state as quantum channel, which generalized the scheme of bidirectional quantum teleportation and improved the communication security. Since then, many schemes for bidirectional controlled teleportation have been reported using different quantum entangled states like five-qubit entangled state [28], six-qubit cluster state [29] and seven-qubit entangled state [30], etc. In addition, another interesting modified teleportation, called remote state preparation, was presented by Lo [31], which also utilizes a prior shared entanglement and some classical communication to transmit a pure quantum state. As was designed, remote state preparation includes only one sender so all the information about the state to be prepared is disclosed to him/her. To avoid such full leakage of information, joint remote state preparation schemes were put forward [12–15]. In joint remote state preparation, there are two or more senders located in different place, and the information of the to-be-prepared state is secretly split among the senders in such a way that neither an individual sender nor a subgroup of them can infer the state. This feature is highly needed in secret communication between agencies.

In this paper, we propose the concept of bidirectional controlled joint remote state preparation (BCJRSP) which is essentially a fusion of the ideas of bidirectional controlled teleportation and joint remote state preparation. The aim of our protocol is as follows. The senders Alice and Charlie want to remotely prepare a single-qubit state at Bob’s site; meanwhile, the senders Bob and David wish to prepare another single-qubit state at distant Alice’s site under the control of the supervisor Fred. For security reasons, we devise a physical procedure to realize this task in such a way that the original states can only be recreated if and only if the participants Charlie, David and Fred can cooperate. We first employ eight-qubit cluster state as quantum channel for implementing BCJRSP task, then generalize it to the case in which two multi-qubit GHZ-type states are used as quantum channel, and to the multidirectional controlled joint remote state preparation via multi GHZ-type states of multi-qubit.

The rest of this paper is organized as follows. In Sect. 2, we present a five-party BCJRSP via eight-qubit cluster state as quantum channel. In Sect. 3, Based on analyzing eight-qubit cluster state, we discuss the generalization of the five-party BCJRSP. Finally, discussions and summary are given in Sect.  4.

2 BCJRSP with eight-qubit cluster state as quantum channel

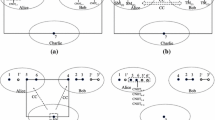
In this section, we present a five-party BCJRSP protocol which is applicable for arbitrary single-qubit states. As we see, this protocol is simple fusion of bidirectional controlled teleportation [27] and joint remote state preparation [12–15]. The specific aim of the BCJRSP protocol is as follows. Suppose that in our scheme, there are five legitimate participants, say, Alice, Bob, Charlie, David and Fred, located at five spatially separated nodes, respectively. The quantum channel linking Alice, Bob, Charlie, David and Fred is an eight-qubit cluster state, which has the form

$$\begin{aligned} |\mathcal {C}_8\rangle _{12345678}=\frac{1}{2}(|00000000\rangle +|00001111\rangle +|11110000\rangle +|11111111\rangle )_{12345678},\nonumber \\ \end{aligned}$$
(1)

where Alice holds the qubit pair (1, 8), Bob possesses the qubit pair (4, 5), Charlie owns the qubit 2, David has the qubit 6 and the remaining qubit pair (3, 7) belongs to Fred.

Assume that the senders Alice and Charlie want to help the receiver Bob remotely prepare a single-qubit state written as

$$\begin{aligned} |\tau \rangle =a|0\rangle +be^{i\alpha }|1\rangle , \end{aligned}$$
(2)

where the real numbers \(a\ge 0, b\ge 0\) and \(\alpha \in [0,2\pi ]\) with the normalization condition \(a^2+b^2=1\), and that senders Bob and David wish to help the receiver Alice remotely prepare a single-qubit state

$$\begin{aligned} |\tau '\rangle =x|0\rangle +ye^{i\beta }|1\rangle , \end{aligned}$$
(3)

where the real parameters \(x\ge 0\), \(y\ge 0\) and \(\beta \in [0,2\pi ]\) with the normalization condition \(x^2+y^2=1\). The full information in state \(|\tau \rangle \) in Eq. (2) is \(S=\{a,b,\alpha \}\), which can be somehow divided into \(S_1=\{a,b\}\) and \(S_2=\{\alpha \}\) in such a way that S cannot be inferred from either \(S_1\) or \(S_2\), but can be from both. Herein, the set S is known partially to Alice and Charlie, and we also assume that \(S_1\) is given only to Alice, \(S_2\) only to Charlie, but no information to Bob, David and Fred. Similarly, Bob only knows \(\{x,y\}\), David only knows \(\beta \), but Alice, Charlie and Fred do not know the information of state \(|\tau '\rangle \) in Eq. (3). Clearly, no participant alone can help the receiver to reconstruct the original state. Our protocol is composed of three sequential steps.

In the first step, Alice chooses the basis \(\{|\xi _m\rangle _1: m=0,1\}\) which is related to the computation basis \(\{|0\rangle _1, |1\rangle _1\}\) as

$$\begin{aligned} \left( \begin{array}{c} |\xi _0\rangle _1 \\ |\xi _1\rangle _1 \\ \end{array} \right) = \left( \begin{array}{cc} a &{} b \\ b &{} -a \\ \end{array} \right) \left( \begin{array}{c} |0\rangle _1 \\ |1\rangle _1 \\ \end{array} \right) . \end{aligned}$$
(4)

Since Alice knows \(S_1=\{a,b\}\), she is able to perform a projective measurement on her particle 1 in the basis \(\{|\xi _m\rangle _1: m=0,1\}\). When carrying out the single particle measurement, Alice obtains a state \(|\xi _m\rangle _1\) randomly (i.e., with an equal probability of 1 / 2), and then tells the result m to Bob and Charlie by classical communication. After that, Charlie needs to measure his particle 2 in a delicately chosen basis which is important to achieve unit success probability without adding the local operations. Namely, Charlie not only utilizes \(\alpha \), which was given to him a priori, but also should take into account Alice’s measurement outcome in terms of m. Explicitly, the basis \(\{|\eta ^{(m)}_n\rangle _2: n=0,1\}\) (\(m=0,1\)) for Charlie’s measurement on qubit 2 is determined by \(\{m,\alpha \}\) as follows:

$$\begin{aligned} \left( \begin{array}{c} |\eta ^{(m)}_0\rangle _2 \\ |\eta ^{(m)}_1\rangle _2 \\ \end{array} \right) =\frac{1}{\sqrt{2}}U^{(m)}(\alpha ) \left( \begin{array}{c} |0\rangle _2 \\ |1\rangle _2 \\ \end{array} \right) \end{aligned}$$
(5)

with

$$\begin{aligned} U^{(0)}(\alpha ) =\left( \begin{array}{cc} 1 &{} e^{-i\alpha } \\ 1 &{} -e^{-i\alpha } \\ \end{array} \right) \end{aligned}$$
(6)

and

$$\begin{aligned} U^{(1)}(\alpha ) =\left( \begin{array}{cc} e^{-i\alpha } &{} 1 \\ e^{-i\alpha } &{} -1 \\ \end{array} \right) . \end{aligned}$$
(7)

For each specific m, the states \(\{|\eta ^{(m)}_n\rangle _2: n=0,1\}\) comprise an orthonormal complete set in a two-dimensional Hilbert space. After doing this operation, Charlie gets a state \(|\eta ^{(m)}_n\rangle _2\) with an equal probability of 1 / 2, and tells Bob of his result n via classical communication.

Similarly, Bob measures his particle 5 in the basis \(\{|\mu _s\rangle _5: s=0,1\}\) determined by \(\{x,y\}\) as

$$\begin{aligned} \left( \begin{array}{c} |\mu _0\rangle _5 \\ |\mu _1\rangle _5 \\ \end{array} \right) = \left( \begin{array}{cc} x &{} y \\ y &{} -x \\ \end{array} \right) \left( \begin{array}{c} |0\rangle _5 \\ |1\rangle _5 \\ \end{array} \right) , \end{aligned}$$
(8)

gets a state \(|\mu _s\rangle _5\) with the probability of 1 / 2, and announces the result s to Alice and David via classical communication. Then, David makes a single particle measurement on his particle 6 with the basis \(\{|\nu ^{(s)}_t\rangle _6: t=0,1\}\) (\(s=0,1\)) determined by \(\{s,\beta \}\) as

$$\begin{aligned} \left( \begin{array}{c} |\nu ^{(s)}_0\rangle _6 \\ |\nu ^{(s)}_1\rangle _6 \\ \end{array} \right) =\frac{1}{\sqrt{2}}V^{(s)}(\beta ) \left( \begin{array}{c} |0\rangle _6 \\ |1\rangle _6 \\ \end{array} \right) \end{aligned}$$
(9)

with

$$\begin{aligned} V^{(0)}(\beta ) =\left( \begin{array}{cc} 1 &{} e^{-i\beta } \\ 1 &{} -e^{-i\beta } \\ \end{array} \right) ,~~~ V^{(1)}(\beta ) =\left( \begin{array}{cc} e^{-i\beta } &{} 1 \\ e^{-i\beta } &{} -1 \\ \end{array} \right) . \end{aligned}$$
(10)

After that, he obtains the a state \(|\nu ^{(s)}_t\rangle _6\) with an equal probability of 1 / 2, and announces t to Alice via classical communication.

In terms of the basis states \(|\xi _m\rangle _1\), \(|\eta ^{(m)}_n\rangle _2\), \(|\mu _s\rangle _5\) and \(|\nu ^{(s)}_t\rangle _6\), the whole quantum system \(|\mathcal {C}_8\rangle _{12345678}\) consisting of the eight particles can be expressed as

$$\begin{aligned} |\mathcal {C}_8\rangle _{12345678}=\frac{1}{4}\sum ^1_{m,n,s,t=0}|\xi _m\rangle _1|\eta ^{(m)}_n\rangle _2|\mu _s\rangle _5|\nu ^{(s)}_t\rangle _6 |Q_{mnst}\rangle _{3478}, \end{aligned}$$
(11)

where

$$\begin{aligned} \begin{aligned} |Q_{mnst}\rangle _{3478}&=[(-1)^{\max (m-n,0)}a|m,m\rangle +(-1)^{\max (n-m,0)}be^{i\alpha }|1-m,1-m\rangle ]_{34}&\\&~~~\otimes [(-1)^{\max (s-t,0)}x|s,s\rangle +(-1)^{\max (t-s,0)}ye^{i\beta }|1-s,1-s\rangle ]_{78}.&\quad \end{aligned} \end{aligned}$$
(12)

After their measurements, Charlie needs to know the outcome m, David needs to know the outcome s, and Alice and Bob need to know the outcomes mnst. What is interesting is that it is not necessary for them to send secret massages. Instead, they just need to broadcast their outcomes via any public media since these outcomes in fact mean nothing to any outside parties. From Eq. (11), one can get one of the 16 kinds of possible measured results with equal probability, and the remaining qubits 3, 4, 7 and 8 may collapse into one of the 16 kinds of possible states contained in a unified form \(|Q_{mnst}\rangle _{3478}\) [see Eq. (12)].

It is worth noting that in first step Charlie and David utilized the adaptive measurement strategy, that is to say, the choice of bases for measuring particles 2 and 6 depends essentially on the outcomes of prior measurements on particles 1 and 5, respectively. Obviously from Eq. (11), if the outcomes of Alice’s, Bob’s, Charlie’s and David’s measurements are msnt, then the four unmeasured particles 3, 4, 7 and 8 are projected onto the state \(|Q_{mnst}\rangle _{3478}\) [see Eq. (12)] with an equal probability of 1 / 16. Note also that at this stage Alice and Bob are still unable to complete the task without Fred’s participation since their particle 8 and 4 are still entangled with particles 7 and 3, respectively. The role of the controller Fred will be seen in the next step.

In the second step, let \(|\varepsilon _l\rangle =\frac{1}{\sqrt{2}}\sum ^1_{j=0}(-1)^{\max (j+l-1, 0)}|j\rangle \) (\(l=0, 1\)) be a single state. Clearly, \(|\varepsilon _0\rangle \) \(=\frac{1}{\sqrt{2}}(|0\rangle +|1\rangle )=|+\rangle , |\varepsilon _1\rangle =\frac{1}{\sqrt{2}}(|0\rangle -|1\rangle )=|-\rangle \), and so \(\{|\varepsilon _0\rangle , |\varepsilon _1\rangle \}\) is usual standard orthogonal basis \(\{|+\rangle , |-\rangle \}\) in a two-dimensional Hilbert space. Using the basis set \(\{|\varepsilon _0\rangle , |\varepsilon _1\rangle \}\), we can write

$$\begin{aligned} |l\rangle =\frac{1}{\sqrt{2}}(|\varepsilon _0\rangle +(-1)^l|\varepsilon _1\rangle )~~(l=0, 1), \end{aligned}$$
(13)

and using (13) we can express the collapsed state \(|Q_{mnst}\rangle _{3478}\) shared by the receivers and controller as follows:

$$\begin{aligned} \begin{aligned}&|Q_{mnst}\rangle _{3478}\\&\quad =\frac{1}{2}\left\{ \left[ (-1)^{\max (m-n,0)}a|m\rangle _4+(-1)^{\max (n-m,0)}be^{i\alpha }|1-m\rangle _4\right] |\varepsilon _0\rangle _3\right.&\\&\left. \qquad +\left[ (-1)^{\max (m-n,0)+m}a|m\rangle _4 +(-1)^{\max (n-m,0)+1-m}be^{i\alpha }|1-m\rangle _4\right] |\varepsilon _1\rangle _3\right\}&\\&\quad \otimes \left\{ \left[ (-1)^{\max (s-t,0)}x|s\rangle _8+(-1)^{\max (t-s,0)}ye^{i\beta }|1-s\rangle _8\right] |\varepsilon _0\rangle _7\right.&\\&\left. \qquad +\left[ (-1)^{\max (s-t,0)+s}x|m\rangle _8+(-1)^{\max (t-s,0)+1-s}ye^{i\beta }|1-s\rangle _8\right] |\varepsilon _1\rangle _7\right\} .&\end{aligned} \end{aligned}$$
(14)

Now Fred makes two single particle measurements on his own particle 3 and 7 in basis sets \(\{|l\rangle _3: l=0,1\}\) and \(\{|l'\rangle _7: l'=0,1\}\), and communicates the results l and \(l'\) to Bob and Alice, respectively. Depending on the outcomes \(msntll'\) of all the measurements described above, the state of particles 4 and 8, with an equal probability of 1 / 64, collapses into one of the following forms:

$$\begin{aligned}&\begin{aligned}&\left[ (-1)^{\max (m-n,0)}a|m\rangle _4+(-1)^{\max (n-m,0)}be^{i\alpha }|1-m\rangle _4\right]&\\&\otimes \left[ (-1)^{\max (s-t,0)}x|s\rangle _8+(-1)^{\max (t-s,0)}ye^{i\beta }|1-s\rangle _8\right] ,~~~~~~~~~~~&\end{aligned} \end{aligned}$$
(15)
$$\begin{aligned}&\begin{aligned}&\left[ (-1)^{\max (m-n,0)}a|m\rangle _4+(-1)^{\max (n-m,0)}be^{i\alpha }|1-m\rangle _4\right]&\\&\otimes \left[ (-1)^{\max (s-t,0)+s}x|m\rangle _8+(-1)^{\max (t-s,0)+1-s}ye^{i\beta }|1-s\rangle _8\right] ,~&\end{aligned} \end{aligned}$$
(16)
$$\begin{aligned}&\begin{aligned}&\left[ (-1)^{\max (m-n,0)+m}a|m\rangle _4+(-1)^{\max (n-m,0)+1-m}be^{i\alpha }|1-m\rangle _4\right]&\\&\otimes \left[ (-1)^{\max (s-t,0)}x|s\rangle _8+(-1)^{\max (t-s,0)}ye^{i\beta }|1-s\rangle _8\right]&\end{aligned} \end{aligned}$$
(17)

and

$$\begin{aligned} \begin{aligned}&\left[ (-1)^{\max (m-n,0)+m}a|m\rangle _4+(-1)^{\max (n-m,0)+1-m}be^{i\alpha }|1-m\rangle _4\right]&\\&\otimes \left[ (-1)^{\max (s-t,0)+s}x|m\rangle _8+(-1)^{\max (t-s,0)+1-s}ye^{i\beta }|1-s\rangle _8\right] .&\end{aligned}\end{aligned}$$
(18)

As is evident form Eqs. (15–18), for any possible collection \(msntll'\) of outcomes, the corresponding collapsed state turns out to be a product state, but it is not yet readily in the desired form \(|\tau \rangle _4\otimes |\tau '\rangle _8\). Thus, a find step, the third step, is needed for Alice and Bob to locally reconstruct the target state.

In the third step, Alice and Bob should apply the proper unitary operators \(R^A_{stl'}\) and \(R^B_{mnl}\), if they exist, on particles 8 and 4 to transform the collapsed state corresponding the outcomes \(msntll'\) to \(|\tau '\rangle _8\) and \(|\tau \rangle _4\), respectively. That is, to be successful, Alice (Bob) needs to know not only the outcomes of Bob’s (Alice’s) and David’s (Charlie’s) measurements in the first step, but also the outcome \(l'\) (l) of Fred’s measurement in the second step, certifying the controller’s role in our scheme. Should Fred, by some important reasons, decline to carry out the measurements or to disclose the measurement outcomes, the task remains unfulfilled. Carefully analyzing the data in Eqs. (15–18), we have, for any possible outcomes \(msntll'\), come up with the general formulae for \(R^A_{stl'}\) and \(R^B_{mnl}\) as

$$\begin{aligned} R^A_{stl'}=\sigma ^s_x\sigma ^{s\oplus t\oplus l'}_z \end{aligned}$$
(19)

and

$$\begin{aligned} R^B_{mnl}=\sigma ^m_x\sigma ^{m\oplus n\oplus l}_z, \end{aligned}$$
(20)

where \(\sigma ^0_x=\sigma ^0_z=I\) is an identical operator, \(\sigma _x\) and \(\sigma _z\) are the X- and Z-Pauli operators, respectively, and \(\oplus \) is an addition mod 2. Since Alice and Bob are always able to reconstruct the desired state by the operators \(R^A_{stl'}\) and \(R^B_{mnl}\) defined above, our bidirectional controlled joint remote state preparation protocol is deterministic, i.e., the success probability is one.

The classical message plays an important role in remote state preparation process. How many bits of classical information are required in our scheme? Now we calculate classical information of our scheme using the method proposed by Dai et al. [32–35]. For the outcomes \(msntll'\), the classical information of bidirectional joint prepared process can be divided into two single bidirectional prepared processes. One is the classical information of the prepared process from the senders Alice and Charlie to the receiver Bob, which Alice performs a projective measurement on qubit 1 and informs Bob, Charlie and Fred of her measurement result, and one which Charlie makes a projective measurement on qubit 2 and informs Bob and Fred of his measurement result as well as one which Fred measures the qubit 3 and informs Bob of his measurement result. The other is the classical information of the prepared process from the senders Bob and David to the receiver Alice. That is, it includes the classical information which Bob implements a projective measurement on qubit 5 and informs Alice, David and Fred of his measurement result, and one which David performs a projective measurement on qubit 6 and informs Alice and Fred of his measurement result as well as one which Fred makes a projective measurement on qubit 7 and informs Alice of his outcome.

We first consider the former case. After projective measurement on qubit 1, Alice obtains outcome m with the probability 1 / 2, so the amount of the classical information sent from Alice to Bob is \(S_\mathrm{AB}=-\frac{1}{2}\log _2 \frac{1}{2}=0.5\) bits. The amount of the classical information from Alice to Charlie and from Charlie to Bob is \(S_\mathrm{ACB}=-\frac{1}{4}\log _2 \frac{1}{4}=0.5\) bits. The amount of the classical information from Alice to Fred and from Fred to Bob is \(S_\mathrm{AFB}=-\frac{1}{4}\log _2 \frac{1}{4}=0.5\) bits. The amount of the classical information required in this process from Alice to Fred, from Charlie to Fred and from Fred to Bob is \(S_\mathrm{ACFB}=-\frac{1}{8}\log _2 \frac{1}{8}=0.375\) bits. Therefore, the total classical communication cost required in this case is \(S_1=S_\mathrm{AB}+S_\mathrm{ACB}+S_\mathrm{AFB}+S_\mathrm{ACFB}=1.875\) bits.

Similarly, for the latter case, the total classical communication cost is also \(S_2=1.875\) bits. Thus the classical communication cost for the outcomes \(msntll'\) is \(S=S_1+S_2=3.75\) bits. Obviously, there are 64 kinds of possible measurement results, and every measurement result has the same classical communication cost in the schemes, so the total classical information needed in our scheme is \(3.75\times 64=240\) bits.

Remark

Our scheme can be modified into a four-party BCJRSP protocol: there are four legitimate participants, they have the qubit pairs (1, 8), (4, 5), (3, 7) and (2, 6), respectively, and these qubits are derive from the eight-qubit cluster state \(|\mathcal {C}_8\rangle _{12345678}\) in Eq. (1). If a participant plays the roles of Charlie and David, the other participants act, respectively, as Alice, Bob and Fred in the above protocol, then this scheme can also be achieved with unit success probability.

If the ideas of bidirectional quantum teleportation, quantum state sharing and joint remote state preparation are fused, then we have the following modified versions of the our original protocol:

(a) In the second step of our original protocol, if Alice and Bob measure, respectively, the particles 8 and 4 with the basis \(\{|\varepsilon _0\rangle , |\varepsilon _1\rangle \}\) getting the outcomes \(ll'\), and communicates all measurement results \(msntll'\) to Fred, then Fred can reconstruct two states \(|\tau \rangle \) and \(|\tau '\rangle \) by using the unitary operations \(\sigma ^m_x\sigma ^{m\oplus n\oplus l}_z\) and \(\sigma ^s_x\sigma ^{s\oplus t\oplus l'}_z\) on particles 3 and 7, respectively. Clearly, the successful probability is also one. Here, each of Alice and Bob essentially plays the roles of the controller and the sender.

(b) In the second step of our original protocol, if Alice and Fred measure, respectively, the particles 8 and 3 with the basis \(\{|\varepsilon _0\rangle , |\varepsilon _1\rangle \}\) getting the outcomes \(ll'\), and communicate the measurement results l and \(l'\) to Fred and Bob, respectively, and the outcomes st to Fred; then, Bob and Fred can obtain \(|\tau \rangle \) and \(|\tau '\rangle \) (with unit success probability) by using the unitary operations \(\sigma ^m_x\sigma ^{m\oplus n\oplus l}_z\) and \(\sigma ^s_x\sigma ^{s\oplus t\oplus l'}_z\) on particles 4 and 7, respectively. Obviously, Alice plays the sender’s and the controller’s roles, and Fred plays the controller’s and receiver’s roles. For Bob plays the sender’s and the controller’s roles and Fred plays the controller’s and receiver’s roles, the conclusion is similar because of symmetry of \(|\mathcal {C}_8\rangle _{12345678}\) in Eq. (1).

For the four-party BCJRSP protocol mentioned above, we can discuss it like the cases (a) and (b).

3 BCJRSP with two \((M+N+2)\)-qubit GHZ-type states as quantum channel

Before presenting our scheme in detail, let us elaborate on the quantum channel in the above section. In Sect. 2, the quantum channel is an eight-particle cluster state (1) which can be written as

$$\begin{aligned} |\mathcal {C}_8\rangle _{12345678}=|\mathrm{GHZ}\rangle _{1234}\otimes |\mathrm{GHZ}\rangle _{5678}, \end{aligned}$$
(21)

where \(|\mathrm{GHZ}\rangle =\frac{1}{\sqrt{2}}(|0000\rangle +|1111\rangle )\) is the four-qubit GHZ-type state. Essentially two parts \(|\mathrm{GHZ}\rangle _{1234}\) and \(|\mathrm{GHZ}\rangle _{5678}\) can be, respectively, regarded as two systems of usual controlled joint remote state preparation. Thus, the above BCJRSP task can be always accomplished successfully. This idea stimulates us to generalize the scheme described in the above section to a more general case that the \((M+N)\) senders Alice\(_1\), Alice\(_2\), \(\cdots \), Alice\(_M\), Charlie\(_1\), Charlie\(_2\), \(\cdots \), Charlie\(_N\) share the classical information of the original state \(|\tau \rangle \) in Eq. (2) in such a way that Alice\(_m\) (\(m=1, 2, \cdots , M\)) knows only the real number pair \((a_m, b_m)\), and Charlie\(_n\) (\(n=1,2,\cdots , N\)) knows only the real number \(\alpha _n\), with \(\Pi ^M_{m=1}a_m=a\), \(\Pi ^M_{m=1}a_m=b\) and \(\Sigma ^N_{n=1}\alpha _n=\alpha \). Similarly, the \((M+N)\) senders Bob\(_1\), Bob\(_2\), \(\cdots \), Bob\(_M\), David\(_1\), David\(_2\), \(\cdots \), David\(_N\) share the classical information of the original state \(|\tau '\rangle \) in Eq. (3) in such a way that Bob\(_s\) (\(s=1, 2, \cdots , M\)) knows only the real number pair \((x_s, y_s)\), and David\(_t\) (\(t=1,2,\cdots , N\)) knows only the real number \(\beta _t\), with \(\Pi ^M_{s=1}x_s=x\), \(\Pi ^M_{s=1}y_s=y\) and \(\Sigma ^N_{t=1}\beta _t=\beta \).

Suppose that the senders Alice\(_m\) (\(m=1, 2, \cdots , M\)), Bob\(_s\) (\(s=1, 2, \cdots , M\)), Charlie\(_n\) (\(n=1,2,\cdots , N\)), David\(_t\) (\(t=1,2,\cdots , N\)) and the controller Fred have shared two \((M+N+2)\)-qubit GHZ-type states in the following form:

$$\begin{aligned} \begin{aligned}&|\mathrm{GHZ}\rangle _{12\cdots (M+N+1)B}=\frac{1}{\sqrt{2}}(|00\cdots 0\rangle +|11\cdots 1\rangle )_{12\cdots (M+N+1)B},&\\&|\mathrm{GHZ}\rangle _{1'2'\cdots (M+N+1)'A}=\frac{1}{\sqrt{2}}(|00\cdots 0\rangle +|11\cdots 1\rangle )_{1'2'\cdots (M+N+1)'A},&\end{aligned} \end{aligned}$$
(22)

where the qubit pair (1, A) belongs to Alice\(_1\), \((1',B)\) to Bob\(_1\), \((M+N+1,(M+N+1)')\) to Fred, Alice\(_m\) (\(2\le m\le M\)) possesses qubit m, Charlie\(_n\) (\(1\le n\le N\)) holds qubit \((M+n)\), Bob\(_s\) (\(2\le s\le M\)) owns qubit \(s'\) and David\(_t\) (\(1\le t\le N\)) has qubit \((M+t)'\), respectively.

Now the senders Alice\(_m\) (\(m=1, 2, \cdots , M\)) and Charlie\(_n\) (\(n=1,2,\cdots , N\)) wish to help the receiver Bob\(_1\) remotely prepare a single-qubit state \(|\tau \rangle \) in Eq. (2); meanwhile, the sender Bob\(_s\) (\(s=1, 2, \cdots , M\)) and David\(_t\) (\(t=1,2,\cdots , N\) want to help the receiver Alice\(_1\) prepare the state \(|\tau '\rangle \) in Eq. (3). The initial system of the total qubits can be written as

$$\begin{aligned} |T\rangle =|\mathrm{GHZ}\rangle _{12\cdots (M+N+1)B}\otimes |\mathrm{GHZ}\rangle _{1'2'\cdots (M+N+1)'A}. \end{aligned}$$
(23)

To realize this quantum task, each sender carries out a single-qubit projective measurement on his/her own qubit, respectively. First, each Alice\(_m\) (\(m=1,2,\cdots ,M\)) chooses the basis \(\{|\xi _{mk}\rangle _m: k=0,1\}\) which is related to the computational basis \(\{|0\rangle _m, |1\rangle _m\}\) as

$$\begin{aligned} \left( \begin{array}{c} |\xi _{m0}\rangle _m \\ |\xi _{m1}\rangle _m \\ \end{array} \right) =\lambda _m\left( \begin{array}{cc} a_m &{} b_m \\ b_m &{} -a_m \\ \end{array} \right) \left( \begin{array}{c} |0\rangle _m \\ |1\rangle _m \\ \end{array} \right) , \end{aligned}$$
(24)

where \(\lambda _m=1/\sqrt{a^2_m+b^2_m}\) is the normalize factor, then measures her qubit m in this basis and tells the outcome \(|\xi _{mk}\rangle \) to Bob\(_1\) and each Charlie\(_n\) (\(n=1,2,\cdots ,N\)) with \((N+1)\) cbits of communication cost, 1 cbit to Bob\(_1\), and 1 cbit to each Charlie\(_n\). Next, each Bob\(_s\) (\(s=1, 2, \cdots , M\)) measures his qubit \(s'\) in the basis \(\{|\mu _{sj}\rangle _{s'}:j=0,1\}\) determined by \(\{x_s, y_s\}\) as

$$\begin{aligned} \left( \begin{array}{c} |\mu _{s0}\rangle _{s'} \\ |\mu _{s1}\rangle _{s'} \\ \end{array} \right) =\kappa _s\left( \begin{array}{cc} x_s &{} y_s \\ y_s &{} -x_s \\ \end{array} \right) \left( \begin{array}{c} |0\rangle _{s'} \\ |1\rangle _{s'} \\ \end{array} \right) , \end{aligned}$$
(25)

where \(\kappa _s=1/\sqrt{x^2_s+y^2_s}\) is also the normalize factor, and transmits his measurement result \(|\mu _{sj}\rangle \) to Alice\(_1\) and each David\(_t\) (\(t=1,2,\cdots , N\)) with \((N+1)\) cbits, 1 cbit to Alice\(_1\), and 1 cbit to each David\(_t\). Only when the joint outcome is one of \(|\xi _{1k}\rangle |\xi _{2k}\rangle \cdots |\xi _{Mk}\rangle |\mu _{1j}\rangle |\mu _{2j}\rangle \cdots |\mu _{Mj}\rangle \), \(k,j=0,1,\) the original states \(|\tau \rangle \) and \(|\tau '\rangle \) may be reconstructed, and the \(|T\rangle \) will collapse, respectively, into the following forms:

$$\begin{aligned}&\begin{aligned}&\frac{1}{2}\prod ^M_{m=1}\lambda _m\kappa _m\left[ \prod ^M_{m=1}a_m|00\cdots 0\rangle +\prod ^M_{m=1}b_m|11\cdots 1\rangle \right] _{(M+1)\cdots (M+N+1)B}&\\&\otimes \left[ \prod ^M_{s=1}x_s|00\cdots 0\rangle +\prod ^M_{s=1}y_s|11\cdots 1\rangle \right] _{(M+1)'\cdots (M+N+1)'A},&\end{aligned} \end{aligned}$$
(26)
$$\begin{aligned}&\begin{aligned}&\frac{1}{2}\prod ^M_{m=1}\lambda _m\kappa _m\left[ \prod ^M_{m=1}a_m|00\cdots 0\rangle +\prod ^M_{m=1}b_m|11\cdots 1\rangle \right] _{(M+1)\cdots (M+N+1)B}&\\&\otimes \left[ \prod ^M_{s=1}y_s|00\cdots 0\rangle +(-1)^M\prod ^M_{s=1}x_s|11\cdots 1\rangle \right] _{(M+1)'\cdots (M+N+1)'A},&\end{aligned} \end{aligned}$$
(27)
$$\begin{aligned}&\begin{aligned}&\frac{1}{2}\prod ^M_{m=1}\lambda _m\kappa _m\left[ \prod ^M_{m=1}b_m|00\cdots 0\rangle +(-1)^M\prod ^M_{m=1}a_m|11\cdots 1\rangle \right] _{(M+1)\cdots (M+N+1)B}&\\&\otimes \left[ \prod ^M_{s=1}x_s|00\cdots 0\rangle +\prod ^M_{s=1}y_s|11\cdots 1\rangle \right] _{(M+1)'\cdots (M+N+1)'A},&\qquad \end{aligned}\end{aligned}$$
(28)

and

$$\begin{aligned} \begin{aligned}&\frac{1}{2}\prod ^M_{m=1}\lambda _m\kappa _m\left[ \prod ^M_{m=1}b_m|00\cdots 0\rangle +(-1)^m\prod ^M_{m=1}a_m|11\cdots 1\rangle \right] _{(M+1)\cdots (M+N+1)B}&\\&\otimes \left[ \prod ^M_{s=1}y_s|00\cdots 0\rangle +(-1)^M\prod ^M_{s=1}x_s|11\cdots 1\rangle \right] _{(M+1)'\cdots (M+N+1)'A}.&\end{aligned}\end{aligned}$$
(29)

Otherwise, \(|T\rangle \) will collapse into the state like

$$\begin{aligned} \begin{aligned}&\frac{1}{2}\prod ^M_{m=1}\lambda _m\kappa _m\left[ b_M\prod ^{M-1}_{m=1}a_m|00\cdots 0\rangle -a_M\prod ^{M-1}_{m=1}b_m|11\cdots 1\rangle \right] _{(M+1)\cdots (M+N+1)B}&\\&\otimes \left[ y_s\prod ^M_{j\ne s}x_j|00\cdots 0\rangle -x_s\prod ^M_{j\ne s}y_j|11\cdots 1\rangle \right] _{(M+1)'\cdots (M+N+1)'A},&\end{aligned}\end{aligned}$$
(30)

which cannot be converted into the product of two original states. Therefore, Alice\(_1\) and Bob\(_1\) only need to consider the cases (26), (27), (28) and (29). Hearing the classical messages from all Alice\(_m\) (\(m=1,2,\cdots ,M\)), each Charlie\(_n\) (\(n=1,2,\cdots ,N\)) measures his qubit \(M+n\) in delicately chosen basis and publicly broadcasts his outcome to Bob\(_1\). That is to say, Charlie\(_n\) not only use the real number \(\alpha _n\), but should also take into account all Alice\(_m\)’s measurement outcomes \(|\xi _{1k}\rangle |\xi _{2k}\rangle \cdots |\xi _{Mk}\), \(k=0,1\). Explicitly, the basis \(\{|\eta ^{(k)}_{ln}\rangle _{M+n}:l=0,1\}\) (\(k=0,1\)) for Charlie\(_n\)’s measurement is given by

$$\begin{aligned} \left( \begin{array}{c} |\eta ^{(k)}_{0n}\rangle _{M+n} \\ |\eta ^{(k)}_{1n}\rangle _{M+n} \\ \end{array} \right) =\frac{1}{\sqrt{2}}U^{(k)}(\alpha _n) \left( \begin{array}{c} |0\rangle _{M+n} \\ |1\rangle _{M+n} \\ \end{array} \right) \end{aligned}$$
(31)

with

$$\begin{aligned} U^{(0)}(\alpha _n) =\left( \begin{array}{cc} 1 &{} e^{-i\alpha _n} \\ 1 &{} -e^{-i\alpha _n} \\ \end{array} \right) ,~~~ U^{(1)}(\alpha _n) =\left( \begin{array}{cc} e^{-i\alpha _n} &{} 1 \\ e^{-i\alpha _n} &{} -1 \\ \end{array} \right) . \end{aligned}$$
(32)

For each specific k, \(\{|\eta ^{(k)}_{ln}\rangle _{M+n}:l=0,1\}\) comprise an orthonormal complete set in a two-dimension Hilbert space. Similarly, according to the outcomes \(|\mu _{1j}\rangle |\mu _{2j}\rangle \cdots |\mu _{Mj}\rangle \) (\(j=0,1\)) of all Bob\(_s\), each David\(_t\) (\(t=1,2, \cdots , N\)) measures his qubit \((M+t)'\) in the basis \(\{|\nu ^{(j)}_{pt}\rangle _{(M+t)'}: p=0,1\}\) determined by \(\{j, \beta _t\}\) as

$$\begin{aligned} \left( \begin{array}{c} |\nu ^{(j)}_{0t}\rangle _{(M+t)'} \\ |\nu ^{(j)}_{1t}\rangle _{(M+t)'} \\ \end{array} \right) =\frac{1}{\sqrt{2}}V^{(j)}(\beta _t) \left( \begin{array}{c} |0\rangle _{(M+t)'} \\ |1\rangle _{(M+t)'} \\ \end{array} \right) \end{aligned}$$
(33)

with

$$\begin{aligned} V^{(0)}(\beta _t) =\left( \begin{array}{cc} 1 &{} e^{-i\beta _t} \\ 1 &{} -e^{-i\beta _t} \\ \end{array} \right) ,~~~ V^{(1)}(\beta _t) =\left( \begin{array}{cc} e^{-i\beta _t} &{} 1 \\ e^{-i\beta _t} &{} -1 \\ \end{array} \right) , \end{aligned}$$
(34)

and publicly broadcasts his outcome to Alice\(_1\) with 1 cbit of communication cost. After implementing measurements by all Charlie\(_n\) and all David\(_t\), the state of qubits \(M+N+1\), \((M+N+1)'\), A and B will collapse into one of the following states:

$$\begin{aligned} \begin{aligned}&(a|00\rangle \pm be^{i\alpha }|11\rangle )_{(M+N+1)B}\otimes (x|00\rangle \pm ye^{i\beta }|11\rangle )_{(M+N+1)'A},\\&(a|00\rangle \pm be^{i\alpha }|11\rangle )_{(M+N+1)B}\otimes (x|11\rangle \pm ye^{i\beta }|00\rangle )_{(M+N+1)'A},\\&(a|11\rangle \pm be^{i\alpha }|00\rangle )_{(M+N+1)B}\otimes (x|00\rangle \pm ye^{i\beta }|11\rangle )_{(M+N+1)'A},\\&(a|11\rangle \pm be^{i\alpha }|00\rangle )_{(M+N+1)B}\otimes (x|11\rangle \pm ye^{i\beta }|00\rangle )_{(M+N+1)'A}. \end{aligned}\end{aligned}$$
(35)

Whether it is possible for Alice\(_1\) and Bob\(_1\) to reconstruct the original state with local operation to the state is dependent on Fred. If Fred allows Alice\(_1\) and Bob\(_1\) to reconstruct the initial state, then he needs to carry out two single-qubit measurements in the basis of \(\{|\varepsilon _0\rangle , |\varepsilon _1\rangle \}\) on qubits \(N+M+1\) and \((N+M+1)'\), and tells the outcomes \(|\varepsilon _l\rangle _{N+M+1}\) and \(|\varepsilon _{l'}\rangle _{(N+M+1)'}\) to Bob\(_1\) and Alice\(_1\), respectively. After doing those measurements, the qubits B and A will collapse into one of the following 16 states:

$$\begin{aligned} \begin{aligned}&(a|0\rangle \pm be^{i\alpha }|1\rangle )_B\otimes (x|0\rangle \pm ye^{i\beta }|1\rangle )_A,\\&(a|0\rangle \pm be^{i\alpha }|1\rangle )_B\otimes (x|1\rangle \pm ye^{i\beta }|0\rangle )_A,\\&(a|1\rangle \pm be^{i\alpha }|0\rangle )_B\otimes (x|0\rangle \pm ye^{i\beta }|1\rangle )_A,\\&(a|1\rangle \pm be^{i\alpha }|0\rangle )_B\otimes (x|1\rangle \pm ye^{i\beta }|0\rangle )_A. \end{aligned}\end{aligned}$$
(36)

By combining information from some senders and Fred, Bob\(_1\) and Alice\(_1\) can reconstruct the original state by making an appropriate unitary transformation U on the qubits B and A according to the Eq. (36), where \(U\in \{I\otimes I, I\otimes \sigma _z, \sigma _z\otimes I, \sigma _z\otimes \sigma _z, I\otimes \sigma _x, \sigma _z\otimes \sigma _x, I\otimes i\sigma _y, \sigma _z\otimes i\sigma _y, \sigma _x\otimes I, i\sigma _y\otimes I, \sigma _x\otimes \sigma _z, i\sigma _y\otimes \sigma _z, \sigma _x\otimes \sigma _x, i\sigma _y\otimes \sigma _z, \sigma _x\otimes i\sigma _y, i\sigma _y\otimes i\sigma _y\}\). It is demonstrated that the original states \(|\tau \rangle \) in Eq. (2) and \(|\tau '\rangle \) in Eq. (3) can always be reconstructed at Bob\(_1\)’s and Alice\(_1\)’s site, respectively, no matter what kind of the four joint measurement outcomes \(|\xi _{1k}\rangle |\xi _{2k}\rangle \cdots |\xi _{Mk}\rangle |\mu _{1j}\rangle |\mu _{2j}\rangle \cdots |\mu _{Mj}\rangle \), \(k,j=0,1\). So, the successful probability of our protocol is \(4\times (\frac{1}{2}\prod ^M_{m=1}\lambda _m\kappa _m)^2=\prod ^M_{m=1}(\lambda _m\kappa _m)^2\).

Now we discuss classical communication of the scheme about multi-partite case. Similar method as in the former section. At first, we consider the single direction from Alice\(_1\) to Bob\(_1\). In the process, without loss of generality, there exists a classical information transmitted sequence:Alice\(_1\),Alice\(_{i_1}\), Alice\(_{i_2}\),...,Alice\(_{i_s}\),Charlie\(_{j_1}\),...,Charlie\(_{j_t}\), Fred\(_k\), Bob\(_1\). According to the former ,we know the probability obtained \(|\xi _{mk}\rangle \) by Alice\(_i\) is \(\lambda _i\), the probability obtained \(|\eta _{ln}^{(k)}\rangle \) by Charlie\(_j\) is \(\frac{1}{2}\) and the probability obtained \(|\varepsilon _{l}\rangle \) is also \(\frac{1}{2}\). The corresponding probability of the sequence is \(p(s,t,k)=\lambda _1\lambda _{i_1}\cdots \lambda _{i_s}(\frac{1}{2})^{t+k}\), where \(s=0,1,...,M-1;t=0,1,...,N,k=0,1\) and \(s=0,t=0\) and \(k=0\) means that Alice\(_i\), Charlie\(_j\) and Fred are disappeared in the sequence, respectively, \(1< i \le M-1, 1\le j\le N\). Therefore, the amount of classical information in the former sequence is \(-p(s,t,k)\log _2 p(s,t,k)\). So the total classical information of single direction from Alice\(_1\) to Bob\(_1\) is \(-\sum \limits _{k=0}^{1}\sum \limits _{s=0}^{M-1}\sum \limits _{t=0}^{N}p(s,t,k)\log _2 p(s,t,k)\). Similarly, the total classical information of single direction from Bob\(_1\) to Alice\(_1\) is \(-\sum \limits _{k=0}^{1}\sum \limits _{s=0}^{M-1}\sum \limits _{t=0}^{N}p'(s,t,k)\log _2 p'(s,t,k)\), where \(p'(s,t,k)=\kappa _1\kappa _{i_1}\cdots \kappa _{i_s}(\frac{1}{2})^{t+k}\). Therefore, the number of bits of total classical communication cost in this scheme is

$$\begin{aligned} -4\sum \limits _{k=0}^{1}\sum \limits _{s=0}^{M-1}\sum \limits _{t=0}^{N}[p(s,t,k)\log _2 p(s,t,k)+p'(s,t,k)\log _2 p'(s,t,k)]. \end{aligned}$$
(37)

According to the above equation, we know the classical communication cost is decided by the number of the senders (M, N) and the coefficients x, y, a, b. When the coefficients a, b, x, y are deterministic, the larger the number \(M+N\) is, the larger the classical communication cost is. It is consistent with the physical facts.

Remark

If \(M=1\), then the successful probability of our scheme is \(\prod ^M_{m=1}(\lambda _m\kappa _m)^2=\frac{1}{(a^2+b^2)(x^2+y^2)}=1\), i.e., our scheme is deterministic. Similar to the remark in Sect. 2, we can obtain some modified versions about BCJRSP with two \((M+N+2)\)-qubit GHZ-type states as quantum channel.

4 Discussion and conclusion

Obviously, the scheme in Sect. 2 has been generalized in Sect. 3. In fact, when \(M=N=1\) in Sect. 3, the protocol described in Sect. 3 is same as that one in Sect. 2. In Sect. 3, the number of senders sharing the state \(|\tau \rangle \) in Eq. (2) equals to that of senders sharing the state \(|\tau '\rangle \) in Eq. (3). Indeed, the numbers of a part of senders sharing the information about the modulus of the coefficients of two original states need not be the same. Likewise, the numbers of the other part of senders sharing the information for arguments of the coefficients of two original states also do not have to be equal. Further, The number of the controllers can be more than one. In this situation, we can employ two multi-qubit GHZ-type states as follows

$$\begin{aligned} \begin{aligned}&|\mathrm{GHZ}\rangle _{12\cdots (M+N+S)B}=\frac{1}{\sqrt{2}}(|00\cdots 0\rangle +|11\cdots 1\rangle )_{12\cdots (M+N+S)B},&\\&|\mathrm{GHZ}\rangle _{1'2'\cdots (K+L+S)'A}=\frac{1}{\sqrt{2}}(|00\cdots 0\rangle +|11\cdots 1\rangle )_{1'2'\cdots (K+L+S)'A},&\end{aligned}\end{aligned}$$
(38)

where there are M senders sharing the real number pair (a, b) and a part of the N senders share the real number \(\alpha \). Similarly, another part of the K senders and the other part of the L senders share the real number pair (x, y) and \(\beta \), respectively, and there are S controllers in this situation. Similar to the method in Sect. 3, Alice\(_1\) and Bob\(_1\) can, respectively, reconstruct the original states \(|\tau '\rangle \) in Eq. (3) and \(|\tau \rangle \) in Eq. (2) with successful probability of \(\prod ^M_{m=1}\lambda ^2_m\prod ^K_{j=1}\kappa ^2_j\) under the control of the S controllers.

In addition, we can easily generalize our protocols to the circumstance that p-directional controlled joint state preparation by employing p multi-qubit GHZ-type states \(|\mathrm{GHZ}\rangle _k\):

$$\begin{aligned} |\mathrm{GHZ}\rangle _k=\frac{1}{\sqrt{2}}(|00\cdots 0\rangle +|11\cdots 1\rangle )_{1_k\cdots (M^{(k)}+N^{(k)}+2)_k}, k=1,\cdots , p \end{aligned}$$
(39)

are used as quantum channel

$$\begin{aligned} |T'\rangle =\otimes ^p_{k=1}|\mathrm{GHZ}\rangle _k. \end{aligned}$$
(40)

where \(p\ge 2\). Similar to the above method, every sender performs a single-qubit measurement on his/her particle using delicately chosen basis in two-dimension Hilbert space and publicly announces the outcome, then the controller makes several single-qubit measurements with the basis \(\{|+\rangle , |-\rangle \}\) and tells his/her outcomes to the receivers. The receivers can reconstruct the desired original state with certain probability by using local operations.

In summary, by integrating the ideas of bidirectional controlled teleportation and joint remote state preparation, we have studied the bidirectional controlled joint state preparation (BCJRSP) in this paper. Firstly, by employing eight-qubit cluster state as quantum channel for implementing BCJRSP, two senders can simultaneously exchange their quantum states securely, deterministically, with the cooperation of the other senders and under the control of the controller using only local operations and classical communication. However, if one agent does not cooperate, the receiver cannot recover the original state of each qubit. Fusing the ideas of bidirectional quantum teleportation, quantum state sharing and joint remote state preparation, we have discussed some modified BCJRSP schemes. Secondly, in the intending quantum networks, more users may participate to solve some common quantum tasks due to some special demands, such as multiparty BCJRSP. So we have generalized the four sharers in BCJRSP to multi sharers, and proposed two generalized schemes for performing multiparty BCJRSP via two multi-qubit GHZ-type states as quantum channel. Finally, in order to realize authentically controlled joint remote preparation from the multiparty to the multiparty, we have further generalized the BCJRSP to multidirectional controlled joint state preparation by using multi GHZ-type states of multi-qubit. We would like to emphasize that the total success probability is not only determined by the normalization factors of the senders’ projective measurement basis vectors which depend on the coefficients of the two original states, but also depends on the adaptive measurement strategy, where chosen adaptive measurement strategy is that in order to construct a measurement operator, the sender not only utilize his/her own shared information for argument of the original state, but should also take into account the measurement outcomes of the former part of senders who share the information about the modulus of the coefficients of the original state. In all schemes, it is necessary for single-qubit measurement and local operation as well as classical communication. Moreover, with the development of research on the multi-partite entangled state, there are several experimental schemes for the generation of the eight-partite entangled state[22–24]. On the other hand, the two-qubit controlled-NOT gate and the single-qubit gates regarding photon qubits, of which arbitrary multi-qubit unitary operation can be expressed as composition, have been realized by using optical element [36]. Therefore, our scheme with five party might be realizable with current techniques.