1 Introduction

Quantum communication, a novel method of transmitting information safely and rapidly, has attracted much attention in the field of quantum information. In quantum communication process, quantum entanglement plays a fundamental and key role. By far, great progress has been made on quantum communication, and there are many branches of quantum communication requiring entanglement, such as quantum key distribution [1–4], quantum teleportation (QT) [5–7], controlled teleportation [8–12], remote state preparation (RSP) [13–18], controlled remote state preparation [19–22], quantum secret sharing [23–26], quantum state sharing [27–29], quantum dense coding [30, 31], quantum secure direction communication [32–34]. Furthermore, entanglement is also an essential resource for entanglement purification [35–39], entanglement concentration [40, 41], and several quantum computing schemes [42–45].

As we know, QT and RSP are two typical protocols of quantum communication. Teleportation enables the sender to transfer an unknown quantum state to a remote receiver, while in RSP a known quantum state is transferred from the sender to the receiver. Due to knowing the initial state to be teleported in advance, it is possible in RSP to have a trade-off between entanglement cost and classical communication cost. Until now, RSP has been extensively investigated both in theory and in experiment [13–22]. Subsequently, a new generalization of remote state preparation called joint remote state preparation (JRSP) [46, 47] has been proposed. Different from standard RSP [13–15], in the JRSP protocols each sender shares partial information of the initial state, and only if all the senders cooperate with each other, the initial state can be remotely prepared at the side of the receiver [46, 47]. Recently, researchers have presented various JRSP protocols, such as JRSP with higher success probability [48], joint remote preparation of a multipartite state [49, 50], probabilistic joint remote preparation of a high-dimensional equatorial quantum state [51–53], joint remote preparation of cluster-type states [54–56], deterministic JRSP [57–61].

Note that the above-mentioned RSP protocols are implemented in ideal conditions, namely the RSP protocols were not taken into account any environmental noises. In general, an actual quantum system inevitably interacts with its surrounding environment, which leads to the loss of the system’s coherent property. Thus, how to efficiently transmit quantum information and to overcome the influence of noises are significant problems for realistic quantum communication network. In recent years, much attention has been paid on the noise effects on the quantum state transmission including QT and RSP [62–65]. For example, Oh et al. [62] investigated QT through noisy quantum channels by solving analytically a master equation in the Lindblad form. Jung et al. [63] analyzed the effect of the noises on the process of QT via the noisy GHZ and W channels and discussed the capacity of the quantum channel to resist the influence of the noisy environment. Liang et al. [65] examined the remote preparation of a qubit state and an entangled state in noisy environments, respectively.

Generally, in JRSP protocols several senders locate in different nodes of quantum network and the priorly shared entanglement resource needs to be distributed through different paths. Moreover, each sender needs to implement proper unitary operators and to transfer some classical information. Thus, the noise effects on the JRSP protocols is relatively complex when compared to previous RSP protocols, and more factors affecting the JRSP process should be taken into account. On the other hand, GHZ-class state is a useful quantum resource for information processing. By means of GHZ-class states as entangled resource, many protocols of quantum communication were studied [12, 45, 46, 49, 64, 65]. And the experimental implementation of GHZ states has been reported in some physical systems including optical systems [66–68], trapped ions [69], superconducting circuit [70], and nuclear magnetic resonance system [71]. Recently, by using two tripartite GHZ states as quantum channel, Chen et al. [72] examined the deterministic joint remote preparation of an arbitrary two-qubit state in the presence of Pauli noises. To our knowledge, seldom studies [72] have involved with JRSP via noisy quantum channels. In this paper, we study the joint remote preparation of a qubit state via a noisy GHZ-class state. The influence of various types of Pauli noises on the fidelity and the average fidelity of the JRSP protocol is discussed in detail. Furthermore, we analyze the difference between the maximally entangled GHZ channel and partially entangled GHZ-class channel for their ability to resist the influence of the Pauli noises. In addition, we devote to finding something new for the Pauli noise affecting the JRSP process and shedding light on quantum state transmission for enhancing the ability to resist the influence of environmental noises.

This paper is arranged as follows. In Sect. 2, we first briefly describe the joint remote preparation of a qubit state via a GHZ-class state in close quantum system. Then, the influence of four types of Pauli noises on the fidelity of the JRSP protocol is analyzed in detail in Sect. 3. Finally, we give a brief discussion and conclusions.

2 JRSP via an ideal GHZ-class channel

Firstly, we briefly describe the protocol of the joint remote preparation of a qubit state via the GHZ-class quantum channel in ideal condition [46, 47]. Suppose that the tripartite GHZ-class state shared by the two senders (Alice and Bob) and the receiver (Charlie) takes the form

$$\begin{aligned} \left| \mathrm{GHZ} \right\rangle _{\mathrm{ABC}} =\alpha \left| {000} \right\rangle _{\mathrm{ABC}} +\beta \left| {111} \right\rangle _{\mathrm{ABC}}, \end{aligned}$$
(1)

in which particles A, B, and C belong to Alice, Bob, and Charlie, respectively, and \(\alpha \) and \(\beta \) are assumed to be real which satisfy \(\alpha ^{2}+\beta ^{2}=1\) and \(\alpha ^{2}\ge \beta ^{2}>0\). When \(\alpha =\beta =\frac{1}{\sqrt{2}}\) and \(\alpha ^{2}>\beta ^{2}>0\), the state \(\left| \mathrm{GHZ} \right\rangle _{\mathrm{ABC}} \) corresponds to the maximally entangled state and the partially entangled one, respectively.

The initial state to be jointly prepared is assumed to take the form

$$\begin{aligned} \left| q \right\rangle =\cos \frac{\theta }{2}\left| 0 \right\rangle +\sin \frac{\theta }{2}e^{i\phi }\left| 1 \right\rangle ,\quad \left( \theta \in [0,\pi ],\phi \in [0,2\pi )\right) , \end{aligned}$$
(2)

where \(\theta \) and \(\phi \) are the polar and azimuthal angles of the initial state, respectively. In this paper, we assume

$$\begin{aligned} \cos \frac{\theta }{2}=a\cdot c, \quad \sin \frac{\theta }{2}=b\cdot d,\hbox { and }\phi =\gamma +\delta , \end{aligned}$$
(3)

where \(a, c, b, d, \gamma \), and \(\delta \) are real. The complete classical information of the state \(\left| q \right\rangle \) is independently shared between Alice and Bob through the following method: The coefficients \(a, b, \gamma \) are only known to Alice and \(c, d, \delta \) are only known to Bob.

To jointly prepare the state for Charlie, Alice performs a von Neumann measurement (vNM) on qubit A with the basis \(\left\{ {\left| \varphi \right\rangle _\mathrm{A},\left| {\varphi _\bot } \right\rangle _\mathrm{A} } \right\} \)

$$\begin{aligned} \left| \varphi \right\rangle _\mathrm{A} =\frac{a\left| 0 \right\rangle +be^{i\gamma }\left| 1 \right\rangle }{ \sqrt{a^{2}+b^{2}}}, \quad \left| {\varphi _{_\bot } } \right\rangle _\mathrm{A} =\frac{be^{-i \gamma }\left| 0 \right\rangle -a\left| 1 \right\rangle }{\sqrt{a^{2}+b^{2}}}. \end{aligned}$$
(4)

Then, Bob performs a vNM on qubit B with the basis \(\left\{ {\left| \varphi \right\rangle _\mathrm{B},\left| {\varphi _\bot } \right\rangle _\mathrm{B} } \right\} \)

$$\begin{aligned} \left| \varphi \right\rangle _\mathrm{B} =\frac{c\left| 0 \right\rangle +de^{i\delta }\left| 1 \right\rangle }{ \sqrt{c^{2}+d^{2}}}, \quad \left| {\varphi _{_\bot } } \right\rangle _\mathrm{B} =\frac{de^{-i\delta } \left| 0 \right\rangle -c\left| 1 \right\rangle }{\sqrt{c^{2}+ d^{2}}}. \end{aligned}$$
(5)

So the GHZ-class channel can be rewritten as

$$\begin{aligned} \left| \mathrm{GHZ} \right\rangle _{\mathrm{ABC}}= & {} \frac{1}{\sqrt{a^{2}+ b^{2}}\sqrt{c^{2}+d^{2}}}\cdot \left[ \left| \varphi \right\rangle _\mathrm{A} \left| \varphi \right\rangle _\mathrm{B} \left( ac\alpha \left| 0 \right\rangle + bde^{-i\gamma }e^{-i\delta }\beta \left| 1 \right\rangle \right) _\mathrm{C} \right. \nonumber \\&+\, \left| \varphi \right\rangle _\mathrm{A} \left| {\varphi _\bot } \right\rangle _\mathrm{B} \left( ade^{i\delta }\alpha \left| 0 \right\rangle -bce^{-i\gamma }\beta \left| 1 \right\rangle \right) _\mathrm{C}\nonumber \\&+\,\left| {\varphi _\bot } \right\rangle _\mathrm{A} \left| \varphi \right\rangle _\mathrm{B} \left( bce^{i\gamma }\alpha \left| 0 \right\rangle - ade^{-i\delta }\beta \left| 1 \right\rangle \right) _\mathrm{C}\nonumber \\&\left. +\, \left| {\varphi _\bot } \right\rangle _\mathrm{A} \left| {\varphi _\bot } \right\rangle _\mathrm{B} \left( bde^{i\gamma }e^{i\delta }\alpha \left| 0 \right\rangle +ac\beta \left| 1 \right\rangle \right) _\mathrm{C} \right] . \end{aligned}$$
(6)

After measuring the GHZ-class state with the operator \(M_\mathrm{AB} =\left| {\varphi _\bot } \right\rangle _\mathrm{A} \left\langle {\varphi _\bot } \right| \otimes \left| {\varphi _\bot } \right\rangle _\mathrm{B} \left\langle {\varphi _\bot } \right| \) and calculating the partial trace over particles A and B, particle C is collapsed to

$$\begin{aligned} \left| \psi \right\rangle _\mathrm{C} =bde^{i(\gamma +\delta )} \alpha \left| 0 \right\rangle +ac\beta \left| 1 \right\rangle = bde^{i\phi }\alpha \left| 0 \right\rangle +ac\beta \left| 1 \right\rangle , \end{aligned}$$
(7)

the corresponding success probability is \(\frac{\alpha ^{2}b^{2}d^{2}+\beta ^{2}a^{2}c^{2}}{\left( {a^{2}+b^{2}} \right) \left( {c^{2}+d^{2}} \right) }\). If \(\alpha =\beta =\frac{1}{\sqrt{2}}\), the success probability reduces to \(\frac{1}{2\left( {a^{2}+b^{2}} \right) \left( {c^{2}+d^{2}} \right) }\).

In order to retrieve the initial state from the state \(\left| \psi \right\rangle _\mathrm{C} \), Charlie introduces an auxiliary particle D with the state \(\left| 0 \right\rangle _\mathrm{D} \). In this case, the total state at Charlie’s side can be expressed as

$$\begin{aligned} \left| \psi \right\rangle _\mathrm{CD} =bde^{i\phi }\alpha \left| {00} \right\rangle _\mathrm{CD} +ac\beta \left| {10} \right\rangle _\mathrm{CD}. \end{aligned}$$
(8)

Then, Charlie makes a unitary transformation \(U_\mathrm{CD} \) on the state \(\left| \psi \right\rangle _\mathrm{CD} \) which reads

$$\begin{aligned} U_\mathrm{CD} \left| \psi \right\rangle _\mathrm{CD} =\beta \left( {bde^{i\phi }\left| 0 \right\rangle _\mathrm{C} + ac\left| 1 \right\rangle _\mathrm{C} } \right) \left| 0 \right\rangle _\mathrm{D} + \sqrt{\alpha ^{2}-\beta ^{2}}bd\left| 0 \right\rangle _\mathrm{C} \left| 1 \right\rangle _\mathrm{D}, \end{aligned}$$
(9)

where the normalization constant \(\frac{1}{\sqrt{\alpha ^{2}b^{2}d^{2}+\beta ^{2}a^{2}c^{2}}}\) is omitted, and \(U_\mathrm{CD} \) is given by

$$\begin{aligned} U_\mathrm{CD}= & {} \frac{\beta }{\alpha }\left| {00} \right\rangle \left\langle {00} \right| -\sqrt{1-\frac{\beta ^{2}}{\alpha ^{2}}}\left| { 00} \right\rangle \left\langle {01} \right| +\sqrt{1-\frac{\beta ^{ 2}}{\alpha ^{2}}}\left| {01} \right\rangle \left\langle {00} \right| \nonumber \\&+\,\frac{\beta }{\alpha }\left| {01} \right\rangle \left\langle {01} \right| +\left| {10} \right\rangle \left\langle {10} \right| +\left| {11} \right\rangle \left\langle {11} \right| . \end{aligned}$$
(10)

Charlie then measures the state of the auxiliary particle D with the projective measurement \(\left\{ \left| 0 \right\rangle ,\left| 1 \right\rangle \right\} \). When he obtains the result \(\left| 0 \right\rangle _\mathrm{D} \), the particle C will be collapsed to the state

$$\begin{aligned} \left| {{\psi }'} \right\rangle _\mathrm{C} =bde^{i\phi }\left| 0 \right\rangle _\mathrm{C} +ac\left| 1 \right\rangle _\mathrm{C}, \end{aligned}$$
(11)

and the corresponding success probability is \(\frac{\beta ^{2}}{\alpha ^{2}b^{2}d^{2}+\beta ^{2}a^{2}c^{2}}\). After performing \(\sigma _x \) on the particle C, the state \(\left| {{\psi }'} \right\rangle _\mathrm{C} \) can be changed into the desired state, i.e.,

$$\begin{aligned} \left| \psi \right\rangle _\mathrm{out} =\sigma _x \left| {{\psi }'} \right\rangle _\mathrm{C} =\sigma _x \left( {bde^{i\phi }\left| 0 \right\rangle _\mathrm{C} + ac\left| 1 \right\rangle _\mathrm{C} } \right) =\cos \frac{\theta }{2} \left| 0 \right\rangle +\sin \frac{\theta }{2}e^{i\phi } \left| 1 \right\rangle . \end{aligned}$$
(12)

Thus, the total success probability for the JRSP via the ideal GHZ-class channel is \(\frac{\alpha ^{2}b^{2}d^{2}+\beta ^{2}a^{2}c^{2}}{\left( {a^{2}+b^{2}} \right) \left( {c^{2}+d^{2}} \right) }\cdot \frac{\beta ^{2}}{\alpha ^{2}b^{2}d^{2}+\beta ^{2}a^{2}c^{2}}=\frac{\beta ^{2}}{\left( {a^{2}+b^{2}} \right) \left( {c^{2}+d^{2}} \right) }\). Based on the above calculations, the output state at Charlie’s side for the JRSP process can be expressed as

$$\begin{aligned} \rho _\mathrm{out} =\sigma _x tr_\mathrm{D} \left\{ M_\mathrm{D} U_\mathrm{CD} \left[ tr_\mathrm{AB} \left( M_\mathrm{AB} \rho _\mathrm{GHZ} M_\mathrm{AB}^{\dagger } \right) \otimes \left( \left| 0 \right\rangle _\mathrm{D} \left\langle 0 \right| \right) \right] U_\mathrm{CD}^{\dagger } M_\mathrm{D}^{\dagger } \right\} \sigma _x^{\dagger }, \end{aligned}$$
(13)

where \(\rho _\mathrm{GHZ} =\left| \mathrm{GHZ} \right\rangle _{\mathrm{ABC}} \left\langle \mathrm{GHZ} \right| \) and \(M_\mathrm{D} =\left| 0 \right\rangle _\mathrm{D} \left\langle 0 \right| \). Here \(M_\mathrm{D} \) is the projective measurement on the auxiliary particle D.

3 JRSP via a GHZ-class channel subject to Pauli noise

Now we investigate the above JRSP process through noisy channel. It is well known that the time evolution of an open quantum system in Markovian environment can be described by a master equation in Lindblad form [73]

$$\begin{aligned} \frac{\partial \rho }{\partial t}=\sum _{j,\alpha } {\left( {L_{j,\alpha } \rho L_{j,\alpha }^{\dagger } - \frac{1}{2}L_{j,\alpha }^{\dagger } L_{j,\alpha } \rho - \frac{1}{2}\rho L_{j,\alpha }^{\dagger } L_{j,\alpha } } \right) }, \end{aligned}$$
(14)

where the Lindblad operator \(L_{j,\alpha } =\sqrt{k_{j,\alpha } }\sigma _\alpha ^j \) describes the coupling of the system to its environment with \(\sigma _\alpha ^j \ (\alpha =x,y,z)\) denoting the Pauli operator of the j-th qubit, and \(k_{j,\alpha } \) being the strength of decoherence rates acting on the j-th qubit (here \(j = 1\), 2, 3). For simplicity, we assume that the Pauli noise acting in the same direction (say \(\sigma _x, \sigma _y \), and \(\sigma _z\)) has the identical strength.

Because the GHZ-class quantum channel is influenced by noises, Eq. (13) should be rewritten as

$$\begin{aligned} \rho _\mathrm{out} =\sigma _x tr_\mathrm{D} \left\{ M_\mathrm{D} U_\mathrm{CD} \left[ tr_\mathrm{AB} \left( M_\mathrm{AB} \rho _\mathrm{GHZ}^\mathrm{evo} M_\mathrm{AB}^{\dagger } \right) \otimes \left( \left| 0 \right\rangle _\mathrm{D} \left\langle 0 \right| \right) \right] U_\mathrm{CD}^{\dagger } M_\mathrm{D}^{\dagger } \right\} \sigma _x^{\dagger }, \end{aligned}$$
(15)

where \(\rho _\mathrm{GHZ}^\mathrm{evo} \) is the time evolution of density matrix of the GHZ-class channel. In terms of the fact that Alice, Bob, and Charlie are in different nodes in the JRSP process, we assume that the Pauli noises affecting the quantum channel take the following four cases: Only particle A is affected by Pauli noises, only particle B is affected by Pauli noises, only particle C is affected by Pauli noises, and particles A, B, and C are all affected by Pauli noises.

3.1 Only particle A is affected by Pauli noises

Firstly, we assume that only particle A of the GHZ-class state \(\left| \mathrm{GHZ} \right\rangle _{\mathrm{ABC}} \) is affected by Pauli noises. In this case, the Lindblad operators can be written as \(L_{1,x} =\sqrt{k_1 }\sigma _x, L_{1,y} =\sqrt{k_2 }\sigma _y \), and \(L_{1,z} =\sqrt{k_3 }\sigma _z \). According to Eqs. (1) and (14), the density matrix of the time evolution of the GHZ-class quantum channel can be calculated as

$$\begin{aligned} \rho _{11}^\mathrm{evo}= & {} \frac{1}{2}\alpha ^{2}\left[ {1+e^{-2(k_1 +k_2 )t}} \right] , \nonumber \\ \rho _{44}^\mathrm{evo}= & {} \frac{1}{2}\beta ^{2}\left[ {1-e^{-2(k_1 +k_2 )t}} \right] ,\nonumber \\ \rho _{55}^\mathrm{evo}= & {} \frac{1}{2}\alpha ^{2}\left[ {1-e^{-2(k_1 + k_2 )t}} \right] ,\nonumber \\ \rho _{88}^\mathrm{evo}= & {} \frac{1}{2}\beta ^{2}\left[ {1+e^{-2(k_1 + k_2 )t}} \right] ,\nonumber \\ \rho _{18}^\mathrm{evo}= & {} \rho _{81}^\mathrm{evo} =\frac{1}{2}\alpha \beta \left[ e^{-2(k_1 +k_3 )t}+e^{-2(k_2 +k_3 )t}\right] ,\nonumber \\ \rho _{45}^\mathrm{evo}= & {} \rho _{54}^\mathrm{evo} =\frac{1}{2}\alpha \beta \left[ -e^{-2(k_1 +k_3 )t}+e^{-2(k_2 +k_3 )t}\right] ,\nonumber \\ \rho _{m,n}^\mathrm{evo}= & {} 0\quad \hbox {for other values of }m,n. \end{aligned}$$
(16)

In terms of Eqs. (15) and (16), the output state obtained by Charlie is given by

$$\begin{aligned} \frac{\rho _\mathrm{out,1} }{C_{N,1} }= & {} \frac{1}{2}\left\{ {\cos ^{2} \frac{\theta }{2}\left[ {1+e^{-2(k_1 +k_2 )t}} \right] + \frac{b^{2}}{a^{2}}\cos ^{2}\frac{\theta }{2}\left[ {1-e^{-2(k_1 + k_2 )t}} \right] } \right\} \left| 0 \right\rangle _3 \left\langle 0 \right| \nonumber \\&+\,\frac{1}{4}\sin \theta e^{-i\delta } \left\{ e^{i\gamma } \left[ {-e^{-2(k_1 +k_3 )t}+e^{-2(k_2 +k_3 )t}} \right] \right. \nonumber \\&\left. +\, e^{-i\gamma }\left[ {e^{-2(k_1 +k_3 )t}+e^{-2(k_2 +k_3 )t}} \right] \right\} \left| 0 \right\rangle _3 \left\langle 1 \right| \nonumber \\&+\,\frac{1}{4}\sin \theta e^{i\delta }\left\{ e^{-i\gamma } \left[ {-e^{-2(k_1 +k_3 )t}+e^{-2(k_2 +k_3 )t}} \right] \right. \nonumber \\&\left. +\,e^{i\gamma }\left[ {e^{-2(k_1 +k_3 )t}+e^{-2(k_2 +k_3 )t}} \right] \right\} \left| 1 \right\rangle _3 \left\langle 0 \right| \nonumber \\&+\,\frac{1}{2}\left\{ \frac{a^{2}}{b^{2}}\sin ^{2}\frac{\theta }{2} \left[ {1-e^{-2(k_1 +k_2 )t}} \right] \right. \nonumber \\&\left. +\,\sin ^{2} \frac{\theta }{2}\left[ {1+e^{-2(k_1 +k_2 )t}} \right] \right\} \left| 1 \right\rangle _3 \left\langle 1 \right| , \end{aligned}$$
(17)

where \(\frac{1}{C_{N,1} }=\frac{1}{2}\left[ {1+e^{-2(k_1 +k_2 )t}} \right] +\frac{1}{2}\left( {\frac{a^{2}}{b^{2}}\sin ^{2}\frac{\theta }{2}+\frac{b^{2}}{a^{2}}\cos ^{2}\frac{\theta }{2}} \right) \left[ {1-e^{-2(k_1 +k_2 )t}} \right] \).

From Eq. (17), we find that the final state Charlie obtained is independent of the parameters of quantum channel (say, \(\alpha \) and \(\beta \)). In order to measure the quality of JRSP via the noisy channel, we need to calculate the fidelity between the output and initial states. Generally, fidelity is defined as

$$\begin{aligned} F\equiv \left\langle q \right| \rho _\mathrm{out} \left| q \right\rangle . \end{aligned}$$
(18)

Here we only consider the case for successful JRSP process. If the JRSP is failure, i.e., Alice does not find \(\left| {\varphi _\bot } \right\rangle _\mathrm{A} \) or Bob does not find \(\left| {\varphi _\bot } \right\rangle _\mathrm{B} \) after Alice performs a vNM on qubit A with the basis \(\left\{ {\left| \varphi \right\rangle _\mathrm{A},\left| {\varphi _\bot } \right\rangle _\mathrm{A} } \right\} \) and Bob on qubit B with the basis\(\left\{ {\left| \varphi \right\rangle _\mathrm{B},\left| {\varphi _\bot } \right\rangle _\mathrm{B} } \right\} \), we then give up the quantum state transmission and try once more until it is successful.

According to Eqs. (2), (17), and (18), through some direct calculations, the fidelity can be obtained as

$$\begin{aligned} \frac{F_1 }{C_{N,1} }= & {} \frac{1}{2}\left( {1-\frac{1}{2}\sin ^{2} \theta } \right) \left[ {1+e^{-2(k_1 +k_2 )t}} \right] \nonumber \\&+\, \frac{1}{2}\left( {\frac{a^{2}}{b^{2}}\sin ^{4}\frac{\theta }{2}+ \frac{b^{2}}{a^{2}}\cos ^{4}\frac{\theta }{2}} \right) \left[ {1-e^{-2(k_1 +k_2 )t}} \right] \nonumber \\&+\,\frac{1}{4}\sin ^{2}\theta \left[ {e^{-2(k_1 +k_3 )t}+ e^{-2(k_2 +k_3 )t}} \right] \nonumber \\&+\,\frac{1}{4}\sin ^{2}\theta \cos 2\gamma \left[ {-e^{-2(k_1 +k_3 )t}+e^{-2(k_2 +k_3 )t}} \right] . \end{aligned}$$
(19)

From above expression, we can see that the fidelity \(F_1 \) is a function of \(\theta , \frac{b}{a}, \gamma \) (say, \(\gamma \) is only known to Alice), and independent of \(\phi \) and \(\delta \) (\(\delta \) is only known to Bob). When \(\theta =0\) or \(\pi \), i.e., the initial state to be jointly prepared is \(\left| q \right\rangle =\left| 0 \right\rangle \) or \(\left| 1 \right\rangle \), the fidelity \(F_1 \) will be 1.

In order to measure how much quantum information can be transferred through the JRSP process, we need to calculate the average fidelity. Commonly, average fidelity is defined as

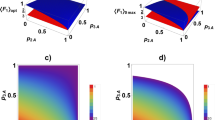
$$\begin{aligned} F_\mathrm{av} \equiv \frac{1}{4\pi }\int _0^{2\pi } {d\phi } \int _0^\pi {d\theta \sin \theta F(\theta ,\phi )}. \end{aligned}$$
(20)

Figure 1 depicts the average fidelity as the functions of \(\frac{b}{a}\) and \(\gamma \) with \(kt=0.1\) in the presence of Pauli noises. From Fig. 1a, particle A is subject to bit flip noise (\(k_1 =k\) and \(k_2 =k_3 =0\)), and three peaks can be observed. When \(\frac{b}{a}={1}\) and \(\gamma =0, \pi \) or \(2\pi \), the average fidelity \(F_{1\mathrm{av},a\max } \) equals 1. In Fig. 2b, particle A is affected by the bit-phase flip noise (\(k_2 =k\) and \(k_1 =k_3 =0)\), and two peaks can be observed. When \(\frac{b}{a}={1}\) and \(\gamma =\frac{\pi }{2}\) or \(\frac{3}{2}\pi \), the average fidelity \(F_{1\mathrm{av},b\max } \) is equal to 1. Average fidelity being 1 means that the qubit can be accurately transmitted in those special circumstances. The situation \(\frac{b}{a}={1}\) indicates that Bob shares the complete information of the polar angle of initial state to be remotely prepared. When \(\frac{b}{a}\) and \(\gamma \) deviates from the above special values (\(\frac{b}{a}=1\) and \(\gamma =0, \pi \), or \(2\pi \) for bit flip noise, \(\frac{b}{a}=1\) and \(\gamma =\frac{\pi }{2}\) or \(\frac{3}{2}\pi \) for bit-phase flip noise), the average fidelity decreases from 1. Figure 1c indicates that the average fidelity remains a steady value \(F_{1\mathrm{av},c} =0.9396\) under the phase flip noise (\(k_3 =k\) and \(k_1 =k_2 =0\)) when \(kt=0.1\). In this case, the average fidelity is independent of \(\frac{b}{a}\) and \(\gamma \). From Fig. 1d, where particle A is affected by the isotropic noises (\(k_1 =k_2 =k_3 =\frac{1}{3}k\)), we can see that the average fidelity is only the function of \(\frac{b}{a}\) and independent of \(\gamma \). When \(\frac{b}{a}=1, F_{1\mathrm{av},d\max } \) becomes 0.9584. It should be pointed out that it is invalid for too small or too large value of \(\frac{b}{a}\) in the JRSP process due to its small success probability.

Fig. 1
figure 1

(Color online) Average fidelity as the functions of \(\frac{b}{a}\) and \(\gamma \) with \(kt=0.1\) for different noise types, where a \(k_1 =k\) and \(k_2 =k_3 =0\), b \(k_2 =k\) and \(k_1 =k_3 =0\), c \(k_3 =k\) and \(k_1 =k_2 =0\), and d \(k_1 =k_2 =k_3 =\frac{1}{3}k\)

Full size image
Fig. 2
figure 2

(Color online) Average fidelity versus \(\frac{b}{a}\) and kt with \(\gamma =\frac{\pi }{3}\) for different noise types, where a \(k_1 =k\) and \(k_2 =k_3 =0\), b \(k_2 =k\) and \(k_1 =k_3 =0\), c \(k_3 =k\) and \(k_1 =k_2 =0\), and d \(k_1 =k_2 =k_3 =\frac{1}{3}k\)

Full size image

Next, we study the average fidelity varying with the decoherence time kt. Figure 2 plots the average fidelity versus \(\frac{b}{a}\) and kt with \(\gamma =\frac{\pi }{3}\). From the figure, it can be seen that the average fidelity \(F_{1\mathrm{av}} =1\) when \(kt=0\). Thus, the JRSP process has not been affected by the noises in the initial time. Comparing Fig. 2a, b, d, the quantum channel is influenced by bit flip noise, bit-phase noise, and isotropic noise, and we can see that the influence of bit-phase flip noise on the average fidelity is the weakest and that of isotropic noise is the strongest. Figure 2c shows that when the JRSP process is influenced by the phase flip noise, the average fidelity \(F_{1\mathrm{av},c} \) is independent of \(\frac{b}{a}\) and decreases monotonically with kt. From Fig. 2a, b, d, the average fidelity has a strong dependence on \(\frac{b}{a}\). When \(\frac{b}{a}=1\), Bob has the polar angle information of quantum state to be transmitted, and the average fidelity reaches the maximal value. But the fidelity decays if \(\frac{b}{a}\) deviates from 1.

When \(\gamma \ne \frac{\pi }{3}\), we can find the similar character for the average fidelity varying with \(\frac{b}{a}\) and kt except that the strength of noise is different. For example, when \(\gamma =\frac{\pi }{4}, F_{1\mathrm{av},a} \) is equal to \(F_{1\mathrm{av},b} \) for the same condition, indicating that the bit flip noise has the same strength as the bit-phase flip noise. When \(\gamma =\frac{\pi }{6}\), the average fidelity \(F_{1\mathrm{av},a} \ge F_{1\mathrm{av},b} \), indicating the strength of the bit-phase flip noise is stronger than that of the bit flip noise, this is different from the case when \(\gamma =\frac{\pi }{3}\). In case we are asked which noise is stronger between the bit flip noise and bit-phase flip noise in the process of JRSP, the answer will be that sometimes bit flip noise is stronger, and sometimes bit-phase flip noise is stronger. Thus, the parameter \(\gamma \) (or \(\delta \)) may affect which noise is stronger; i.e., how the two senders share the phase information in the JRSP process may affect which noise is stronger between the bit-phase flip noise and bit flip noise.

3.2 Only particle 2 is affected by Pauli noises

In this situation, only particle 2 of the GHZ-class quantum channel is affected by Pauli noises; i.e., the Lindblad operators can be expressed as \(L_{2,x} =\sqrt{k_1 }\sigma _x, L_{2,y} =\sqrt{k_2 }\sigma _y \), and \(L_{2,z} =\sqrt{k_3 }\sigma _z \). According to Eqs. (1) and (14), we can obtain the time evolution of the density matrix for the GHZ-class channel

$$\begin{aligned} \rho _{11}^\mathrm{evo}= & {} \frac{1}{2}\alpha ^{2}\left[ {1+e^{-2(k_1 +k_2 )t}} \right] ,\nonumber \\ \rho _{33}^\mathrm{evo}= & {} \frac{1}{2}\alpha ^{2}\left[ {1-e^{-2(k_1 +k_2 )t}} \right] ,\nonumber \\ \rho _{66}^\mathrm{evo}= & {} \frac{1}{2}\beta ^{2}\left[ {1-e^{-2(k_1 +k_2 )t}} \right] ,\nonumber \\ \rho _{88}^\mathrm{evo}= & {} \frac{1}{2}\beta ^{2}\left[ {1+e^{-2(k_1 +k_2 )t}} \right] ,\nonumber \\ \rho _{18}^\mathrm{evo}= & {} \rho _{81}^\mathrm{evo} =\frac{1}{2}\alpha \beta \left[ {e^{-2(k_1 +k_3 )t}+e^{-2(k_2 +k_3 )t}} \right] ,\nonumber \\ \rho _{36}^\mathrm{evo}= & {} \rho _{36}^\mathrm{evo} =\frac{1}{2}\alpha \beta \left[ {-e^{-2(k_1 +k_3 )t}+e^{-2(k_2 +k_3 )t}} \right] ,\nonumber \\ \rho _{m,n}^\mathrm{evo}= & {} 0\quad \hbox { for the other values of }m, n. \end{aligned}$$
(21)

Similarly, the output state at Charlie’s side can be calculated as

$$\begin{aligned} \frac{\rho _\mathrm{out,2} }{C_{N,2} }= & {} \frac{1}{2}\left\{ {\cos ^{2}\frac{\theta }{2}\left[ {1+e^{-2(k_1 +k_2 )t}} \right] +\frac{a^{2}}{b^{2}} \sin ^{2}\frac{\theta }{2}\left[ {1-e^{-2(k_1 +k_2 )t}} \right] } \right\} \left| 0 \right\rangle _3 \left\langle 0 \right| \nonumber \\&+\,\frac{\sin \theta }{4}\left\{ e^{i(-\gamma -\delta )} \left[ {e^{-2(k_1 +k_3 )t}+e^{-2(k_2 +k_3 )t}} \right] \right. \nonumber \\&\left. +\, e^{i(-\gamma +\delta )}\left[ -e^{-2(k_1 +k_3 )t} + e^{-2(k_2 +k_3 )t} \right] \right\} \left| 0 \right\rangle _3 \left\langle 1 \right| \nonumber \\&+\,\frac{\sin \theta }{4}\left\{ e^{i(\gamma +\delta )} \left[ {e^{-2(k_1 +k_3 )t}+e^{-2(k_2 +k_3 )t}} \right] \right. \nonumber \\&\left. +\, e^{i(\gamma -\delta )}\left[ {-e^{-2(k_1 +k_3 )t}+ e^{-2(k_2 +k_3 )t}} \right] \right\} \left| 1 \right\rangle _3 \left\langle 0 \right| \nonumber \\&+\,\frac{1}{2}\left\{ {\sin ^{2}\frac{\theta }{2} \left[ {1+e^{-2(k_1 +k_2 )t}} \right] +\frac{b^{2}}{a^{2}} \cos ^{2}\frac{\theta }{2}\left[ {1-e^{-2(k_1 +k_2 )t}} \right] } \right\} \left| 1 \right\rangle _3 \left\langle 1 \right| ,\nonumber \\ \end{aligned}$$
(22)

where \(\frac{1}{C_{N,2} }=\frac{1}{2}\left[ {1+e^{-2(k_1 +k_2 )t}} \right] +\frac{1}{2}\left( {\frac{a^{2}}{b^{2}}\sin ^{2}\frac{\theta }{2}+\frac{b^{2}}{a^{2}}\cos ^{2}\frac{\theta }{2}} \right) \left[ {1-e^{-2(k_1 +k_2 )t}} \right] \), or \(\frac{1}{C_{N,2} }=\frac{1}{2}\left[ {1+e^{-2(k_1 +k_2 )t}} \right] +\frac{1}{2}\left( {\frac{c^{2}}{d^{2}}\sin ^{2}\frac{\theta }{2}+\frac{d^{2}}{c^{2}}\cos ^{2}\frac{\theta }{2}} \right) \left[ {1-e^{-2(k_1 +k_2 )t}} \right] \).

When only particle 2 is subject to noises, with similar method, the fidelity can be calculated as

$$\begin{aligned} \frac{F_2 }{C_{N,2} }= & {} \frac{1}{2}\left( {1-\frac{1}{2}\sin ^{2} \theta } \right) \left[ {1+e^{-2(k_1 +k_2 )t}} \right] \nonumber \\&+\, \frac{1}{8}\sin ^{2}\theta \left( {\frac{a^{2}}{b^{2}}+ \frac{b^{2}}{a^{2}}} \right) \left[ {1-e^{-2(k_1 +k_2 )t}} \right] \nonumber \\&+\,\frac{1}{4}\sin ^{2}\theta \left[ {e^{-2(k_1 +k_3 )t}+ e^{-2(k_2 +k_3 )t}} \right] \nonumber \\&+\,\frac{1}{4}\sin ^{2}\theta \cos 2 \delta \left[ {-e^{-2(k_1 +k_3 )t}+e^{-2(k_2 +k_3 )t}} \right] , \end{aligned}$$
(23a)

or

$$\begin{aligned} \frac{F_2 }{C_{N,2} }= & {} \frac{1}{2}\left( {1-\frac{1}{2}\sin ^{2} \theta } \right) \left[ {1+e^{-2(k_1 +k_2 )t}} \right] \nonumber \\&+\, \frac{1}{2}\left( {\frac{c^{2}}{d^{2}}\sin ^{4}\frac{\theta }{2}+ \frac{d^{2}}{c^{2}}\cos ^{4}\frac{\theta }{2}} \right) \left[ {1-e^{-2(k_1 +k_2 )t}} \right] \nonumber \\&+\,\frac{1}{4}\sin ^{2}\theta \left[ {e^{-2(k_1 +k_3 )t}+ e^{-2(k_2 +k_3 )t}} \right] \nonumber \\&+\,\frac{1}{4}\sin ^{2}\theta \cos 2\delta \left[ {-e^{-2(k_1 +k_3 )t}+e^{-2(k_2 +k_3 )t}} \right] . \end{aligned}$$
(23b)

Because Bob has the same situation as Alice in the JRSP protocol, as we expected, we can find that Eq. (23b) is similar to Eq. (19). Therefore, the variance tendency of fidelity \(F_2 \) is similar to that of \(F_1 \).

3.3 Only particle 3 is affected by Pauli noises

Next, we study the case when only particle 3 of the GHZ-class quantum channel is affected by Pauli noises. In this case, the Lindblad operators can be expressed as \(L_{3,x} =\sqrt{k_1 }\sigma _x, L_{3,y} =\sqrt{k_2 }\sigma _y \), and \(L_{3,z} =\sqrt{k_3 }\sigma _z \). In the beginning of the JRSP, the GHZ-class channel is expressed as Eq. (1). By solving the master equation, we obtain

$$\begin{aligned} \rho _{11}^\mathrm{evo}= & {} \frac{1}{2}\alpha ^{2}\left[ {1+e^{-2(k_1 +k_2 )t}} \right] ,\nonumber \\ \rho _{22}^\mathrm{evo}= & {} \frac{1}{2}\alpha ^{2}\left[ {1-e^{-2(k_1 + k_2 )t}} \right] ,\nonumber \\ \rho _{77}^\mathrm{evo}= & {} \frac{1}{2}\beta ^{2}\left[ {1-e^{-2(k_1 +k_2 )t}} \right] ,\nonumber \\ \rho _{88}^\mathrm{evo}= & {} \frac{1}{2}\beta ^{2}\left[ {1+e^{-2(k_1 +k_2 )t}} \right] ,\nonumber \\ \rho _{18}^\mathrm{evo}= & {} \rho _{81}^\mathrm{evo} =\frac{1}{2}\alpha \beta \left[ {e^{-2(k_1 +k_3 )t}+e^{-2(k_2 +k_3 )t}} \right] ,\nonumber \\ \rho _{27}^\mathrm{evo}= & {} \rho _{72}^\mathrm{evo} =\frac{1}{2}\alpha \beta \left[ {-e^{-2(k_1 +k_3 )t}+e^{-2(k_2 +k_3 )t}} \right] ,\nonumber \\ \rho _{m,n}^\mathrm{evo}= & {} 0\quad \hbox { for the other values of }m, n. \end{aligned}$$
(24)

Similarly, we can calculate the final output state at Charlie’s side

$$\begin{aligned} \frac{\rho _{\mathrm{out},3} }{C_{N,3} }= & {} \frac{1}{\beta ^{2}}\left( {\cos ^{2}\frac{\theta }{2} \rho _{88}^\mathrm{evo} +\sin ^{2}\frac{\theta }{2}\rho _{22}^\mathrm{evo} } \right) \left| 0 \right\rangle _3 \left\langle 0 \right| \nonumber \\&+\, \frac{1}{2\alpha \beta }\sin \theta \left( {e^{-i\phi }\rho _{81}^\mathrm{evo} + e^{i\phi }\rho _{27}^\mathrm{evo} } \right) \left| 0 \right\rangle _3 \left\langle 1 \right| \nonumber \\&+\,\frac{1}{2\alpha \beta }\sin \theta \left( {e^{i\phi } \rho _{18}^\mathrm{evo} +e^{-i\phi }\rho _{72}^\mathrm{evo} } \right) \left| 1 \right\rangle _3 \left\langle 0 \right| \nonumber \\&+\, \frac{1}{\alpha ^{2}}\left( {\sin ^{2}\frac{\theta }{2}\rho _{11}^\mathrm{evo} + \cos ^{2}\frac{\theta }{2}\rho _{77}^\mathrm{evo} } \right) \left| 1 \right\rangle _3 \left\langle 1 \right| , \end{aligned}$$
(25)

where \(\frac{1}{C_{N,3} }=\frac{1}{2}\left[ {1+e^{-2(k_1 +k_2 )t}} \right] +\frac{1}{2}\left( {\frac{\alpha ^{2}}{\beta ^{2}}\sin ^{2}\frac{\theta }{2}+\frac{\beta ^{2}}{\alpha ^{2}}\cos ^{2}\frac{\theta }{2}} \right) \left[ {1-e^{-2(k_1 +k_2 )t}} \right] \). By applying the analogous method, the fidelity can be calculated as

$$\begin{aligned} \frac{F_3 }{C_{N,3} }= & {} \frac{1}{2}\left( {1-\frac{1}{2}\sin ^{2} \theta } \right) \left[ {1+e^{-2(k_1 +k_2 )t}} \right] \nonumber \\&+\,\frac{ 1}{8}\sin ^{2}\theta \left( {\frac{\alpha ^{2}}{\beta ^{2}}+ \frac{\beta ^{2}}{\alpha ^{2}}} \right) \left[ {1-e^{-2(k_1 +k_2 )t}} \right] \nonumber \\&+\,\frac{1}{4}\sin ^{2}\theta \left[ {e^{-2(k_1 +k_3 )t}+ e^{-2(k_2 +k_3 )t}} \right] \nonumber \\&+\,\frac{1}{4}\sin ^{2}\theta \cos 2\phi \left[ {-e^{-2(k_1 +k_3 )t}+e^{-2(k_2 +k_3 )t}} \right] . \end{aligned}$$
(26)

From above expression, we can find that the fidelity is the function of \(\theta , \phi , \alpha \) (or \(\beta \)), and t. Because particles A and B are not disturbed by those noises, the fidelity is independent of \(\frac{a}{b}\) (or \(\frac{c}{d}\)) and \(\gamma \) (or \(\delta \)). In the following, we turn our attention to analyzing the average fidelities decaying with the decoherence time kt in the JRSP process.

Figure 3 plots the average fidelity versus \(\beta \) and kt under the influence of different Pauli noises. Figure 3c shows that the average fidelity decreases monotonically with the increase of kt and does not depend on \(\beta \) when the quantum channel is influenced by the phase flip noise. From Fig. 3a, b, d, we find that when the quantum channel is subjected to the bit flip noise, the bit-phase flip noise, and the isotropic noise, respectively, the average fidelities decrease monotonically with the increase in kt when \(\beta \) is a given value. On the other hand, if kt is set to be a fixed value, the average fidelities increase monotonically as \(\beta \) goes from 0 to \(\frac{\sqrt{2}}{2}\) for the bit flip noise, the bit-phase flip noise, and the isotropic noise, while the average fidelity remains invariable for the phase flip noise. Comparing Fig. 3a, b, we find that the average fidelity affected by the bit flip noise decays with the same speed as that affected by the bit-phase flip noise. When \(kt=0, F_{3\mathrm{av}} =1\) indicating that the quantum channel is not affected by the noisy environment in the initial time. When \(kt\rightarrow \infty \) and \(\alpha =\beta =\frac{1}{\sqrt{2}}, F_{3\mathrm{av},a}, F_{3\mathrm{av},b} \), and \(F_{3\mathrm{av},d} \) will approach to \(\frac{2}{3}, \frac{2}{3}\), and \(\frac{{1}}{2}\), respectively. Moreover, when \(kt\rightarrow \infty , F_{3\mathrm{av},c} \) is close to \(\frac{2}{3}\). Therefore, the influence of the phase flip noise on the average fidelity is the weakest, while that of the isotropic noise is the strongest. Besides, to some extent the maximally entangled quantum channel has the strongest ability to resist the influence of Pauli noises.

Fig. 3
figure 3

(Color online) Average fidelity as the functions of \(\beta \) and kt via the noisy GHZ-class channel, where a \(k_1 =k\) and \(k_2 =k_3 =0\), b \(k_2 =k\) and \(k_1 =k_3 =0\), c \(k_3 =k\) and \(k_1 =k_2 =0\), and d \(k_1 =k_2 =k_3 =\frac{1}{3}k\)

Full size image

3.4 Particles 1, 2, and 3 are all affected by Pauli noises

In this section, we assume that particles 1, 2, and 3 of the GHZ-class state are all subject to Pauli noises at the same time, and the strength of Pauli noises acting on the same direction is identical. Therefore, the Lindblad operators are given by \(L_{1,x} =\sqrt{k_1 }\sigma _x, L_{1,y} =\sqrt{k_2 }\sigma _y , L_{1,z} =\sqrt{k_3 }\sigma _z , L_{2,x} =\sqrt{k_1 }\sigma _x , L_{2,y} =\sqrt{k_2 }\sigma _y , L_{2,z} =\sqrt{k_3 }\sigma _z , L_{3,x} =\sqrt{k_1 }\sigma _x , L_{3,y} =\sqrt{k_2 }\sigma _y \), and \(L_{3,z} =\sqrt{k_3 }\sigma _z \). By solving the master equation, the time evolution of the GHZ-class channel can be expressed as

$$\begin{aligned} \rho _{11}^\mathrm{evo}= & {} \frac{1}{8}+\frac{3}{8}\left( {\alpha ^{2}-\beta ^{2}} \right) e^{-2(k_1 +k_2 )t}+\frac{3}{8}e^{-4(k_1 +k_2 )t}+ \frac{1}{8}\left( {\alpha ^{2}-\beta ^{2}} \right) e^{-6(k_1 +k_2 )t},\nonumber \\ \rho _{22}^\mathrm{evo}= & {} \rho _{33}^\mathrm{evo} =\rho _{55}^\mathrm{evo} = \frac{1}{8}+\frac{1}{8}\left( {\alpha ^{2}-\beta ^{2}} \right) e^{-2(k_1 +k_2 )t}-\frac{1}{8}e^{-4(k_1 +k_2 )t}\nonumber \\&-\, \frac{1}{8}\left( {\alpha ^{2}-\beta ^{2}} \right) e^{-6(k_1 +k_2 )t},\nonumber \\ \rho _{44}^\mathrm{evo}= & {} \rho _{66}^\mathrm{evo} =\rho _{77}^\mathrm{evo} =\frac{1}{8}- \frac{1}{8}\left( {\alpha ^{2}-\beta ^{2}} \right) e^{-2(k_1 +k_2 )t}-\frac{1}{8}e^{-4(k_1 +k_2 )t}\nonumber \\&+\, \frac{1}{8}\left( {\alpha ^{2}-\beta ^{2}} \right) e^{-6(k_1 +k_2 )t},\nonumber \\ \rho _{88}^\mathrm{evo}= & {} \frac{1}{8}-\frac{3}{8}\left( {\alpha ^{2}- \beta ^{2}} \right) e^{-2(k_1 +k_2 )t}+\frac{3}{8}e^{-4(k_1 +k_2 )t}- \frac{1}{8}\left( {\alpha ^{2}-\beta ^{2}} \right) e^{-6(k_1 +k_2 )t},\nonumber \\ \rho _{18}^\mathrm{evo}= & {} \rho _{81}^\mathrm{evo} =\frac{1}{4}\alpha \beta \left( {e^{-6k_2 t-6k_3 t}+3e^{-4k_1 t-2k_2 t-6k_3 t}} \right) ,\nonumber \\ \rho _{27}^\mathrm{evo}= & {} \rho _{36}^\mathrm{evo} =\rho _{45}^\mathrm{evo} =\rho _{54}^\mathrm{evo} = \rho _{63}^\mathrm{evo} =\rho _{72}^\mathrm{evo} \nonumber \\= & {} \frac{1}{4}\alpha \beta \left( {e^{-6k_2 t-6k_3 t}-e^{-4k_1 t-2k_2 t-6k_3 t}} \right) ,\nonumber \\ \rho _{m,n}^\mathrm{evo}= & {} 0\quad \hbox { for the other values of }m, n. \end{aligned}$$
(27)

By using the same method for calculations, we obtain

$$\begin{aligned} \frac{\rho _{\mathrm{out},4} }{C_{N,4} }= & {} \frac{1}{\beta ^{2}}\left( {\cos ^{2}\frac{\theta }{2}\rho _{88}^\mathrm{evo} +\frac{a^{2}}{b^{2}} \sin ^{2}\frac{\theta }{2}\rho _{66}^\mathrm{evo} +\frac{b^{2}}{a^{2}}\cos ^{2}\frac{\theta }{2}\rho _{44}^\mathrm{evo} + \sin ^{2}\frac{\theta }{2}\rho _{22}^\mathrm{evo} } \right) \left| 0 \right\rangle \left\langle 0 \right| \nonumber \\&+\,\frac{\sin \theta }{2\alpha \beta }\left[ {e^{-i(\gamma +\delta )} \rho _{81}^\mathrm{evo} +e^{i(\gamma +\delta )}\rho _{27}^\mathrm{evo} + e^{i(\gamma -\delta )}\rho _{45}^\mathrm{evo} +e^{i(-\gamma +\delta )} \rho _{63}^\mathrm{evo} } \right] \left| 0 \right\rangle \left\langle 1 \right| \nonumber \\&+\,\frac{\sin \theta }{2\alpha \beta }\left[ {e^{-i(\gamma + \delta )}\rho _{72}^\mathrm{evo} +e^{i(\gamma +\delta )}\rho _{18}^\mathrm{evo} + e^{i(\gamma -\delta )}\rho _{36}^\mathrm{evo} +e^{i(-\gamma +\delta )} \rho _{54}^\mathrm{evo} } \right] \left| 1 \right\rangle \left\langle 0 \right| \nonumber \\&+\,\frac{1}{\alpha ^{2}}\left( {\cos ^{2}\frac{\theta }{2} \rho _{77}^\mathrm{evo} \!+\!\frac{a^{2}}{b^{2}}\sin ^{2}\frac{\theta }{2} \rho _{55}^\mathrm{evo} \!+\!\frac{b^{2}}{a^{2}}\cos ^{2}\frac{\theta }{2} \rho _{33}^\mathrm{evo} \!+\!\sin ^{2}\frac{\theta }{2}\rho _{11}^\mathrm{evo} } \right) \left| 1 \right\rangle \left\langle 1 \right| ,\nonumber \\ \end{aligned}$$
(28)

where

$$\begin{aligned} \frac{1}{C_{N,4} }= & {} \frac{1}{\beta ^{2}}\left( {\cos ^{2}\frac{\theta }{2}\rho _{88}^\mathrm{evo} +\frac{a^{2}}{b^{2}}\sin ^{2} \frac{\theta }{2}\rho _{66}^\mathrm{evo} +\frac{b^{2}}{a^{2}}\cos ^{2} \frac{\theta }{2}\rho _{44}^\mathrm{evo} +\sin ^{2}\frac{\theta }{2} \rho _{22}^\mathrm{evo} } \right) \nonumber \\&+\,\frac{1}{\alpha ^{2}}\left( {\cos ^{2}\frac{\theta }{2} \rho _{77}^\mathrm{evo} +\frac{a^{2}}{b^{2}}\sin ^{2}\frac{\theta }{2}\rho _{55}^\mathrm{evo} +\frac{b^{2}}{a^{2}}\cos ^{2} \frac{\theta }{2}\rho _{33}^\mathrm{evo} +\sin ^{2}\frac{\theta }{2} \rho _{11}^\mathrm{evo} } \right) . \end{aligned}$$

Following the preceding procedures, we are able to calculate the fidelity as

$$\begin{aligned} \frac{F_4 }{C_{N,4} }= & {} \frac{\sin ^{2}\frac{\theta }{2}}{\alpha ^{2}} \left[ {\cos ^{2}\frac{\theta }{2}\rho _{77}^\mathrm{evo} + \left( {\frac{a^{2}}{b^{2}}\sin ^{2}\frac{\theta }{2}+ \frac{b^{2}}{a^{2}}\cos ^{2}\frac{\theta }{2}} \right) \rho _{33}^\mathrm{evo} + \sin ^{2}\frac{\theta }{2}\rho _{11}^\mathrm{evo} } \right] \nonumber \\&+\,\frac{\cos ^{2}\frac{\theta }{2}}{\beta ^{2}}\left[ {\cos ^{2} \frac{\theta }{2}\rho _{88}^\mathrm{evo} +\left( {\frac{a^{2}}{b^{2}} \sin ^{2}\frac{\theta }{2}+\frac{b^{2}}{a^{2}}\cos ^{2} \frac{\theta }{2}} \right) \rho _{44}^\mathrm{evo} +\sin ^{2}\frac{\theta }{2} \rho _{22}^\mathrm{evo} } \right] \nonumber \\&+\,\frac{\sin ^{2}\theta }{2\alpha \beta }\left[ {\rho _{18}^\mathrm{evo} + \cos 2\phi \rho _{63}^\mathrm{evo} +\cos 2\left( {\phi -\gamma } \right) \rho _{63}^\mathrm{evo} +\cos 2\gamma \rho _{63}^\mathrm{evo} } \right] . \end{aligned}$$
(29)

According to Eqs. (27) and (29), clearly the fidelity \(F_4 \) is the function of parameters \(\beta \) (or \(\alpha ), \frac{b}{a}, \theta , \phi \), and \(\lambda \)(or \(\delta \)). Next we turn to analyze the variation behavior of both the fidelity \(F_4 \) and the average fidelity \(F_{4\mathrm{av}} \).

When the GHZ-class channel is maximally entangled (\(\alpha =\beta =\frac{\sqrt{2}}{2})\), Eq. (29) can be simplified as

$$\begin{aligned} \frac{F_4 }{C_{N,4} }= & {} \frac{1}{8}+\frac{3}{8}e^{-4(k_1 +k_2 )t}- \frac{1}{4}\sin ^{2}\theta \cdot e^{-4(k_1 +k_2 )t}\nonumber \\&+\, \frac{1}{8}\left( {\frac{b^{2}}{a^{2}}\cos ^{2}\frac{\theta }{2}+ \frac{a^{2}}{b^{2}}\sin ^{2}\frac{\theta }{2}} \right) \left[ {1-e^{-4(k_1 +k_2 )t}} \right] \nonumber \\&+\,\frac{1}{16}\sin ^{2}\theta \left[ {e^{-6(k_2 +k_3 )t}+ 3e^{-(4k_1 +2k_2 +6k_3 )t}} \right] \nonumber \\&+\,\frac{1}{16}\sin ^{2}\theta \left[ {\cos 2(\phi -\gamma )+ \cos 2\gamma +\cos 2\phi } \right] \nonumber \\&\quad \cdot \,\left[ {e^{-6(k_2 +k_3 )t}- e^{-(4k_1 +2k_2 +6k_3 )t}} \right] , \end{aligned}$$
(30a)

or

$$\begin{aligned} \frac{F_4 }{C_{N,4} }= & {} \frac{1}{8}+\frac{3}{8}e^{-4(k_1 +k_2 )t}- \frac{1}{4}\sin ^{2}\theta \cdot e^{-4(k_1 +k_2 )t}\nonumber \\&+\,\frac{1}{8} \left( {\frac{c^{2}}{d^{2}}\sin ^{2}\frac{\theta }{2}+ \frac{d^{2}}{c^{2}}\cos ^{2}\frac{\theta }{2}} \right) \left[ {1-e^{-4(k_1 +k_2 )t}} \right] \nonumber \\&+\,\frac{1}{16}\sin ^{2}\theta \left[ {e^{-6(k_2 +k_3 )t}+ 3e^{-(4k_1 +2k_2 +6k_3 )t}} \right] \nonumber \\&+\,\frac{1}{16}\sin ^{2}\theta \left[ {\cos 2(\phi -\delta )+ \cos 2\delta +\cos 2\phi } \right] \nonumber \\&\quad \cdot \,\left[ {e^{-6(k_2 +k_3 )t}- e^{-(4k_1 +2k_2 +6k_3 )t}} \right] , \end{aligned}$$
(30b)

where \(C_{N,4} \) is the normalization constant given by

$$\begin{aligned} \frac{1}{C_{N,4} }=\frac{1}{4}+\frac{1}{4}e^{-4(k_1 +k_2 )t}+ \frac{1}{4}\left( {\frac{b^{2}}{a^{2}}\cos ^{2}\frac{\theta }{2}+\frac{a^{2}}{b^{2}}\sin ^{2}\frac{\theta }{2}} \right) \left[ {1-e^{-4(k_1 +k_2 )t}} \right] , \end{aligned}$$

or

$$\begin{aligned} \frac{1}{C_{N,4} }=\frac{1}{4}+\frac{1}{4}e^{-4(k_1 +k_2 )t}+ \frac{1}{4}\left( {\frac{c^{2}}{d^{2}}\sin ^{2}\frac{\theta }{2}+ \frac{d^{2}}{c^{2}}\cos ^{2}\frac{\theta }{2}} \right) \left[ {1-e^{- 4(k_1 +k_2 )t}} \right] . \end{aligned}$$

When the JRSP process is influenced by the isotropic noise, we can find from Eq. (30) that \(F_4 \) is close to 0.5 if \(kt\rightarrow \infty \).

In terms of Eqs. (20) and (30), Fig. 4 exhibits the average fidelity of the JRSP protocol via the maximally entangled channel against \(\frac{b}{a}\) and \(\gamma \) with \(kt=0.1\). When particles A, B, and C are all subject to noises simultaneously, it can be seen that Fig. 4 reveals the similar character as Fig. 1 except that the value of average fidelity \(F_{4\mathrm{av}} \) is correspondingly smaller than \(F_{1\mathrm{av}} \) in Fig. 1. First, from Fig. 4a, all three particles are subject to bit flip noise (\(k_1 =k\) and \(k_2 =k_3 =0\)). There exists three peaks in the case that \(\frac{b}{a}={1}\) and \(\gamma =0, \pi \), or \(2\pi \), and the average fidelity reaches its maximum \(F_{4\mathrm{av},a\max } =0.8901\). Then, all particles are affected by the bit-phase flip noise (\(k_2 =k\) and \(k_1 =k_3 =0\)) from Fig. 4b. There exists two peaks in the case that \(\frac{b}{a}={1}\) and \(\gamma =\frac{\pi }{2}\) or \(\frac{3\pi }{2}\), and the average fidelity reaches its maximum \(F_{4\mathrm{av},b\max } =0.8846\). It can be seen from Fig. 4c that the average fidelity does not vary with \(\frac{b}{a}\) and \(\gamma \) under the phase flip noise (\(k_3 =k\) and \(k_1 =k_2 =0\)); i.e., the fidelity is only the function of kt but independent of \(\frac{b}{a}\) and \(\gamma \). When \(kt=0.1, F_{4\mathrm{av},c} \) equals 0.8497. Finally, from Fig. 4d, all three particles are affected by the isotropic noises (\(k_1 =k_2 =k_3 =\frac{1}{3}k\)), the average fidelity is only the function of \(\frac{b}{a}\) and independent of \(\gamma \). When \(\frac{b}{a}=1\), the average fidelity reaches its maximum \(F_{4\mathrm{av},d\max } =0.8511\). Because Eq. (30a) with respect to \(\frac{b}{a}\) and \(\gamma \) as well as Eq. (30b) with respect to \(\frac{d}{c}\) and \(\delta \) are the identical, thus the character of average fidelity varying with \(\frac{d}{c}\) and \(\delta \) have also the similar results.

When the quantum channel is partially entangled (e.g., \(\beta =0.6\) and \(\alpha =0.8)\), according to Eq. (29), we can find some similar properties of the fidelity and the average fidelity as the case when the quantum channel is maximally entangled, except that the corresponding value of the average fidelity is different.

Now we analyze the average fidelity versus kt and \(\beta \) with \(\gamma =\frac{\pi }{3}\) and \(\frac{b}{a}=1\), which is plotted in Fig. 5. It can be seen that Fig. 5 exhibits similar behaviors as Fig. 3, and the average fidelity do not depend on \(\beta \) when the quantum channel is influenced by the phase flip noise (see Figs. 3c, 5c). Moreover, when kt is given and the quantum channel is maximally entangled, the average fidelity reaches its maximal value for the bit flip channel, the bit-phase flip channel, and the isotropic noisy channel. Besides, when \(kt\rightarrow \infty \) and \(\alpha =\beta =\frac{1}{\sqrt{2}}, {F}'_{4\mathrm{av},a} , {F}'_{4\mathrm{av},b} , {F}'_{4\mathrm{av},c} \), and \({F}'_{4\mathrm{av},d} \) are approximate to 0.5416, 0.5000, 0.6667, and 0.5000, respectively.

Fig. 4
figure 4

(Color online) Average fidelity versus \(\frac{b}{a}\) and \(\gamma \) with \(kt=0.1\) for different noise types, where a \(k_1 =k\) and \(k_2 =k_3 =0\), b \(k_2 =k\) and \(k_1 =k_3 =0\), c \(k_3 =k\) and \(k_1 =k_2 =0\), and d \(k_1 =k_2 =k_3 =\frac{1}{3}k\)

Full size image
Fig. 5
figure 5

(Color online) Average fidelity as the functions of \(\beta \) and kt with \(\gamma =\frac{\pi }{3}\) and \(\frac{b}{a}=1\), where a \(k_1 =k\) and \(k_2 =k_3 =0\), b \(k_2 =k\) and \(k_1 =k_3 =0\), c \(k_3 =k\) and \(k_1 =k_2 =0\), and d \(k_1 =k_2 =k_3 =\frac{1}{3}k\)

Full size image

4 Conclusions

In summary, we have investigated the effects of Pauli noises on the joint remote preparation of a qubit state via a GHZ-class quantum channel. By solving the master equation in the Lindblad form, we obtain the time evolution of the GHZ-class quantum channel infected by the bit flip noise, the phase flip noise, the bit-phase flip noise, and the isotropic noise corresponding to the case that each particle A, B, C, or all three particles are noisy, respectively. Then, the fidelity and the corresponding average fidelity of the JRSP process have been analytically or numerically calculated. Our results show that the fidelity depends on the types of noises, the GHZ-class state, the initial state to be remotely prepared, the decoherence rate, and the manner of the initial state information sharing by the senders. By comparing with the traditional RSP, we find the characteristics of noises for the JRSP are more complex, and the fidelities in the JRSP process exhibit some new features in Pauli noise environments: (1) Fidelity and average fidelity decay with the decoherence time kt with various speeds, and \(\frac{b}{a}\) is an important factor for the JRSP protocol. When \(\frac{b}{a}\) is close to 1, meaning that one sender almost has the whole polar angle information of the initial state, the fidelity and the average fidelity approach to the maximal values. Thus, to some extent the initial state information sharing in the JRSP process may reduce the ability to resist the influence of Pauli noises. (2) The influence of the bit-phase flip noise on the average fidelity is sometimes stronger than that of the bit flip noise and sometimes weaker. How the two senders share the phase information of the initial state can affect which noise is stronger between the bit-phase flip noise and the bit flip noise. (3) The fidelity of the JRSP process through the maximally entangled channel is larger than that through the partially entangled channel. Therefore, maximally entangled channel not only provides more success probability for the JRSP protocol, but also has a relatively stronger ability to resist the influence of Pauli noises. This result is similar to that achieved in traditional RSP protocols [65]. Different from the JRSP protocol of Ref. [72], here we have only adopted one GHZ-class state to achieve the probabilistic JRSP process and have introduced an auxiliary qubit to retrieve the initial state to be remotely prepared at Charlie’s side. Moreover, in the present paper, we have mainly focused the relationship between the fidelity and the senders’ information sharing manner, and the ability of the entanglement amount of the GHZ-class channel to resist the influence of the Pauli noises.

From the above analysis, we find that to enhance the fidelity of our JRSP protocol, one of the two senders owning the whole polar angle information of the state to be transferred and using the maximally entangled GHZ state as quantum channel are two good choices. Thus, we had better applied the maximally entangled state as the entangled resource. It deserves mentioning that to overcome the influence of the collective noises in quantum state transmission, researchers put forward some good techniques such as with decoherence-free subspaces [74], the addition of ancillary qubits [75], and with quantum error rejection and correction [76, 77]. Here we concentrated on the influence of the Pauli noises and the initial state sharing manner on the fidelity of the JRSP process. In addition, the Pauli noises acting on the respective particles of the GHZ-class state examined in our paper are different and can thus be regarded as independent noises, not the collective noises. We hope that our results might be helpful to design some JRSP protocols for improving their ability to resist the influence of noises.