Deterministic controlled remote state preparation using partially entangled quantum channel

Abstract

In this paper, we propose a novel scheme for deterministic controlled remote state preparation (CRSP) of arbitrary two-qubit states. Suitably chosen partially entangled state is used as the quantum channel. With proper projective measurements carried out by the sender and controller, the receiver can reconstruct the target state by means of appropriate unitary operation. Unit success probability can be achieved for arbitrary two-qubit states. Different from some previous CRSP schemes utilizing partially entangled channels, auxiliary qubit is not required in our scheme. We also show that the success probability is independent of the parameters of the partially entangled quantum channel.

1 Introduction

Applying quantum mechanics in the realm of computer science and information theory has motivated an emerging research area, quantum computation and quantum information [1]. Transmitting a quantum state that carries secret information provides a new method for quantum information processing beyond the capabilities of its classical counterparts. A landmark protocol for states transmission is quantum teleportation, put forward by Bennett et al. [2], allowing the teleportation of an unknown quantum state via a prior shared Einstein–Podolsky–Rosen (EPR) pair and two bits of classical communication. Later, a new protocol referred to as remote state preparation (RSP) [3–5] was introduced, in which a known state can be remotely prepared using the same quantum channel as in quantum teleportation but with reduced classical communication cost. Due to its pronounced advantages in quantum states transmission, RSP has attracted extensive scientific attention in both theoretical [6–10] and experimental [11–16] studies.

In conventional RSP protocols, there is one sender who has the complete knowledge about the state to be prepared (generally referred to as the target state) and one receiver who knows nothing about the target state. As a matter of fact, it often appears necessary to introduce a controller to supervise the completion of a global task in a quantum way. Wang et al. [17] first put forward a controlled RSP (CRSP) scheme where quantum key distribution is utilized for remotely preparing a single-qubit state with probability 50 %. In the same year, a scheme employing non-maximally entangled GHZ state was proposed for multiparty-controlled remote preparation of a two-qubit state [18], whose success probability can reach 50 % if and only if the maximally entangled channel is used. Later, various CRSP schemes for two-qubit states were proposed via different quantum channels [19–21]. Generally, in CRSP schemes, the optimal success probability can be achieved when the maximally entangled quantum channel is used. However, due to the unavoidable interaction between the quantum channel and its ambient environment, it is challenging to generate and maintain the maximally entanglement. Taking this into consideration, up to now, tremendous efforts have been dedicated to the investigation of CRSP via non-maximally entangled channel [22–25]. Very recently, Wang et al. [26] proposed two CRSP protocols using partially entangled quantum channels. However, the success probability is 25 % for arbitrary two-qubit states.

In order to improve the success probability of CRSP, in this paper, we propose a novel scheme for CRSP of arbitrary two-qubit states using partially entangled channel. The sender and the controller carry out proper projective measurements under elaborate measurement bases, according to their measurement results; the receiver can reestablish the target state with appropriate unitary operation. Unit success probability can always be achieved irrespective of the parameters of the quantum channel. Different from some previous CRSP schemes employing partially entangled channels, auxiliary resources are not required in our scheme.

This paper is organized as follows. In the next section, we detail the deterministic CRSP scheme for arbitrary two-qubit states and the corresponding quantum logic circuit is designed. In Sect. 3, we make a discussion and give a brief summary.

2 CRSP of an arbitrary two-qubit state

Inspired by some ideas in Ref. [26, 27], the following four-particle partially entangled state is utilized throughout this paper,

$$\begin{aligned} {\left| {QC} \right\rangle _{1234}} = \frac{1}{{\sqrt{2} }}{\left( {\left| {0000} \right\rangle + l\left| {1111} \right\rangle + k\left| {1101} \right\rangle } \right) _{1234}}. \end{aligned}$$

(1)

This state is characterized by real parameters l and k satisfying ${l^2} + {k^2} = 1$. Obviously, when $l = 0$, ${\left| {QC} \right\rangle _{1234}} = \frac{1}{{\sqrt{2} }}{\left( {\left| {000} \right\rangle + \left| {111} \right\rangle } \right) _{124}} \otimes {\left| 0 \right\rangle _3}$, this is a product state of particle 3 with a maximally entangled GHZ state of particles 1, 2 and 4. When $l = 1$, ${\left| {QC} \right\rangle _{1234}} = \frac{1}{{\sqrt{2} }}{\left( {\left| {0000} \right\rangle + \left| {1111} \right\rangle } \right) _{1234}}$ is a four-particle maximally entangled GHZ state. Considering the controller’s power [28], in this paper we are interested in $0 < l < 1$ for which ${\left| {QC} \right\rangle _{1234}}$ is partially entangled with the entanglement degree ${C_{124|3}} = l$ quantified by the concurrence [29].

We now turn our attention to detail the deterministic CRSP of an arbitrary two-qubit pure state. Suppose that under the control of Charlie, the sender Alice intend to help the remote receiver Bob prepare an arbitrary two-qubit state reads

$$\begin{aligned} {\left| \chi \right\rangle } = {a_0}\left| {00} \right\rangle + {a_1}{e^{i{\theta _1}}}\left| {01} \right\rangle + {a_2}{e^{i{\theta _2}}}\left| {10} \right\rangle + {a_3}{e^{i{\theta _3}}}\left| {11} \right\rangle , \end{aligned}$$

(2)

where the real coefficients ${\theta _j} \in \left[ {0,2\pi } \right] \,\left( {j = 1,2,3} \right)$ and ${a_i} \ge 0{} \,\left( {i = 0,1,2,3} \right)$ satisfying the normalization condition $\sum \limits _{i = 0}^3 {{{\left( {{a_i}} \right) }^2}} = 1$. The sender Alice has the complete knowledge about the target state, including the amplitude information ${a_i}{} \,\left( {i = 0,1,2,3} \right)$ and the phase information ${\theta _j}\,\left( {j = 1,2,3} \right)$. The controller Charlie and the receiver Bob know nothing about ${\left| \chi \right\rangle }$.

To accomplish the task of CRSP, Alice, Bob and Charlie previously share the quantum channel consisting of two four-particle partially entangled states given by

$$\begin{aligned}&{\left| {QC} \right\rangle _{{A_1}{A_3}{C_1}{B_1}}} \otimes {\left| {QC} \right\rangle _{{A_2}{A_4}{C_2}{B_2}}} \nonumber \\&\quad = \frac{1}{{\sqrt{2} }}{\left( {\left| {0000} \right\rangle + {l_1}\left| {1111} \right\rangle + {k_1}\left| {1101} \right\rangle } \right) _{{A_1}{A_3}{C_1}{B_1}}} \nonumber \\&\quad \quad \otimes \frac{1}{{\sqrt{2} }}{\left( {\left| {0000} \right\rangle + {l_2}\left| {1111} \right\rangle + {k_2}\left| {1101} \right\rangle } \right) _{{A_2}{A_4}{C_2}{B_2}}}. \end{aligned}$$

(3)

Among these eight particles, $A_1$, $A_2$, $A_3$, $A_4$ belong to Alice, Charlie controls particles $C_1$, $C_2$, Bob is in possession of particles $B_1$, $B_2$.

Fig. 1

Schematic quantum circuit for deterministic CRSP of an arbitrary two-qubit state via ${\left| {QC} \right\rangle _{{A_1}{A_3}{C_1}{B_1}}} \otimes {\left| {QC} \right\rangle _{{A_2}{A_4}{C_2}{B_2}}}$

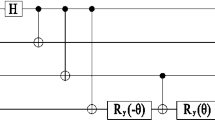
The necessary projective measurements and unitary operations should be carried out in sequence, as shown in Fig. 1. Concretely, our protocol begins with Alice performing a joint projective measurement on her particles $A_1$ and $A_2$ (denoted as $PM_A^1$). Based on her knowledge about the amplitude information $\left\{ {{a_0},{a_1},{a_2},{a_3}} \right\}$, Alice chooses a set of complete orthonormal basis $\left\{ {\left| {{\psi _1}} \right\rangle ,\left| {{\psi _2}} \right\rangle ,\left| {{\psi _3}} \right\rangle ,\left| {{\psi _4}} \right\rangle } \right\}$, reads

$$\begin{aligned} \left| {{\psi _1}} \right\rangle= & {} {a_0}\left| {00} \right\rangle + {a_1}\left| {01} \right\rangle + {a_2}\left| {10} \right\rangle + {a_3}\left| {11} \right\rangle , \nonumber \\ \left| {{\psi _2}} \right\rangle= & {} {a_0}\left| {01} \right\rangle - {a_1}\left| {00} \right\rangle + {a_2}\left| {11} \right\rangle - {a_3}\left| {10} \right\rangle , \nonumber \\ \left| {{\psi _3}} \right\rangle= & {} {a_0}\left| {10} \right\rangle - {a_1}\left| {11} \right\rangle - {a_2}\left| {00} \right\rangle + {a_3}\left| {01} \right\rangle , \nonumber \\ \left| {{\psi _4}} \right\rangle= & {} {a_0}\left| {11} \right\rangle + {a_1}\left| {10} \right\rangle - {a_2}\left| {01} \right\rangle - {a_3}\left| {00} \right\rangle . \end{aligned}$$

(4)

According to the measurement postulate of quantum mechanics, the whole quantum system consisting of eight particles can be expressed as

$$\begin{aligned}&{\left| {QC} \right\rangle _{{A_1}{A_3}{C_1}{B_1}}} \otimes {\left| {QC} \right\rangle _{{A_2}{A_4}{C_2}{B_2}}} \nonumber \\&\quad = \frac{1}{2}\left( {{{\left| {{\psi _1}} \right\rangle }_{{A_1}{A_2}}} \otimes {{\left| {{\Psi _1}} \right\rangle }_{{A_3}{A_4}{C_1}{C_2}{B_1}{B_2}}} + {{\left| {{\psi _2}} \right\rangle }_{{A_1}{A_2}}} \otimes {{\left| {{\Psi _2}} \right\rangle }_{{A_3}{A_4}{C_1}{C_2}{B_1}{B_2}}}} \right. \nonumber \\&\quad \quad \left. { +\, {{\left| {{\psi _3}} \right\rangle }_{{A_1}{A_2}}} \otimes {{\left| {{\Psi _3}} \right\rangle }_{{A_3}{A_4}{C_1}{C_2}{B_1}{B_2}}} + {{\left| {{\psi _4}} \right\rangle }_{{A_1}{A_2}}} \otimes {{\left| {{\Psi _4}} \right\rangle }_{{A_3}{A_4}{C_1}{C_2}{B_1}{B_2}}}} \right) , \end{aligned}$$

(5)

where

$$\begin{aligned}&{\left| {{\Psi _1}} \right\rangle _{{A_3}{A_4}{C_1}{C_2}{B_1}{B_2}}} \nonumber \\&\quad = {a_0}{\left| {00} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {00} \right\rangle _{{B_1}{B_2}}} + {a_1}{l_2}{\left| {01} \right\rangle _{{A_3}{A_4}}}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {a_1}{k_2}{\left| {01} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} + {a_2}{l_1}{\left| {10} \right\rangle _{{A_3}{A_4}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {a_3}{l_1}{l_2}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {11} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} + {a_3}{l_1}{k_2}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {a_2}{k_1}{\left| {10} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} + {a_3}{l_2}{k_1}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {a_3}{k_1}{k_2}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}}, \end{aligned}$$

(6)

$$\begin{aligned}&{\left| {{\Psi _2}} \right\rangle _{{A_3}{A_4}{C_1}{C_2}{B_1}{B_2}}} \nonumber \\&\quad = - {a_1}{\left| {00} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {00} \right\rangle _{{B_1}{B_2}}} + {a_0}{l_2}{\left| {01} \right\rangle _{{A_3}{A_4}}}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {a_0}{k_2}{\left| {01} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} - {a_3}{l_1}{\left| {10} \right\rangle _{{A_3}{A_4}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {a_2}{l_1}{l_2}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {11} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} + {a_2}{l_1}{k_2}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad -\, {a_3}{k_1}{\left| {10} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} + {a_2}{l_2}{k_1}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {a_2}{k_1}{k_2}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}},\end{aligned}$$

(7)

$$\begin{aligned}&{\left| {{\Psi _3}} \right\rangle _{{A_3}{A_4}{C_1}{C_2}{B_1}{B_2}}} \nonumber \\&\quad = - {a_2}{\left| {00} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {00} \right\rangle _{{B_1}{B_2}}} + {a_3}{l_2}{\left| {01} \right\rangle _{{A_3}{A_4}}}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {a_3}{k_2}{\left| {01} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} + {a_0}{l_1}{\left| {10} \right\rangle _{{A_3}{A_4}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad -\, {a_1}{l_1}{l_2}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {11} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} - {a_1}{l_1}{k_2}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {a_0}{k_1}{\left| {10} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} - {a_1}{l_2}{k_1}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad -\, {a_1}{k_1}{k_2}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}},\end{aligned}$$

(8)

$$\begin{aligned}&{\left| {{\Psi _4}} \right\rangle _{{A_3}{A_4}{C_1}{C_2}{B_1}{B_2}}} \nonumber \\&\quad = - {a_3}{\left| {00} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {00} \right\rangle _{{B_1}{B_2}}} - {a_2}{l_2}{\left| {01} \right\rangle _{{A_3}{A_4}}}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad -\, {a_2}{k_2}{\left| {01} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} + {a_1}{l_1}{\left| {10} \right\rangle _{{A_3}{A_4}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {a_0}{l_1}{l_2}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {11} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} + {a_0}{l_1}{k_2}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {a_1}{k_1}{\left| {10} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} + {a_0}{l_2}{k_1}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {a_0}{k_1}{k_2}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}}. \end{aligned}$$

(9)

Alice’s projective measurement $PM_A^1$ will project the joint state of particles $A_3$, $A_4$, $C_1$, $C_2$, $B_1$, $B_2$ onto one of the four possible states $\left\{ {\left| {{\Psi _1}} \right\rangle ,\left| {{\Psi _2}} \right\rangle ,\left| {{\Psi _3}} \right\rangle ,\left| {{\Psi _4}} \right\rangle } \right\}$ with equal probability of ${P_{R_A^1}} = 1/4$, as shown in Eq. (5). After her projective measurement, Alice informs Bob of her measurement result $R_A^1$ via a classical channel, meanwhile, according to the result $R_A^1$, she selects suitable unitary operations (denoted as ${U_A}$) to perform on her particles $A_3$ and $A_4$. Various situations involving Alice’s $PM_A^1$ results and her unitary operations are listed out in Table 1.

Table 1 Relations between Alice’s $PM_A^1$ results and her unitary operations

Without loss of generality, here we consider the case that Alice’s $PM_A^1$ result is ${\left| {{\psi _2}} \right\rangle _{{A_1}{A_2}}}$. Correspondingly, she performs the unitary operation ${U_A} = I \otimes {\sigma _x}$ on her particles $A_3$ and $A_4$. Afterward, she will perform a projective measurement on $A_3$ and $A_4$ (denoted as $PM_A^2$) with the following complete orthonormal basis,

$$\begin{aligned} \left| {{\phi _1}} \right\rangle= & {} \frac{1}{2}\left( {\left| {00} \right\rangle + {e^{ - i{\theta _1}}}\left| {01} \right\rangle + {e^{ - i{\theta _2}}}\left| {10} \right\rangle + {e^{ - i{\theta _3}}}\left| {11} \right\rangle } \right) , \nonumber \\ \left| {{\phi _2}} \right\rangle= & {} \frac{1}{2}\left( {\left| {00} \right\rangle - {e^{ - i{\theta _1}}}\left| {01} \right\rangle + {e^{ - i{\theta _2}}}\left| {10} \right\rangle - {e^{ - i{\theta _3}}}\left| {11} \right\rangle } \right) , \nonumber \\ \left| {{\phi _3}} \right\rangle= & {} \frac{1}{2}\left( {\left| {00} \right\rangle + {e^{ - i{\theta _1}}}\left| {01} \right\rangle - {e^{ - i{\theta _2}}}\left| {10} \right\rangle - {e^{ - i{\theta _3}}}\left| {11} \right\rangle } \right) , \nonumber \\ \left| {{\phi _4}} \right\rangle= & {} \frac{1}{2}\left( {\left| {00} \right\rangle - {e^{ - i{\theta _1}}}\left| {01} \right\rangle - {e^{ - i{\theta _2}}}\left| {10} \right\rangle + {e^{ - i{\theta _3}}}\left| {11} \right\rangle } \right) . \nonumber \\ \end{aligned}$$

(10)

Above operations can be expressed analytically as follows,

$$\begin{aligned}&{\left| {{\Psi _2}} \right\rangle _{{A_3}{A_4}{C_1}{C_2}{B_1}{B_2}}}\xrightarrow [{on\;particles\;{A_3}\;and\;{A_4}}]{{{U_A} = I \otimes {\sigma _x}}} \nonumber \\&\quad \quad -\, {a_1}{\left| {01} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {00} \right\rangle _{{B_1}{B_2}}} + {a_0}{l_2}{\left| {00} \right\rangle _{{A_3}{A_4}}}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {a_0}{k_2}{\left| {00} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} - {a_3}{l_1}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {a_2}{l_1}{l_2}{\left| {10} \right\rangle _{{A_3}{A_4}}}{\left| {11} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} + {a_2}{l_1}{k_2}{\left| {10} \right\rangle _{{A_3}{A_4}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad -\, {a_3}{k_1}{\left| {11} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} + {a_2}{l_2}{k_1}{\left| {10} \right\rangle _{{A_3}{A_4}}}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {a_2}{k_1}{k_2}{\left| {10} \right\rangle _{{A_3}{A_4}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad =\frac{1}{2}\left( {{{\left| {{\phi _1}} \right\rangle }_{{A_3}{A_4}}} \otimes {{\left| {{\Phi _1}} \right\rangle }_{{C_1}{C_2}{B_1}{B_2}}} + {{\left| {{\phi _2}} \right\rangle }_{{A_3}{A_4}}} \otimes {{\left| {{\Phi _2}} \right\rangle }_{{C_1}{C_2}{B_1}{B_2}}}} \right. \nonumber \\&\quad \quad \left. { +\, {{\left| {{\phi _3}} \right\rangle }_{{A_3}{A_4}}} \otimes {{\left| {{\Phi _3}} \right\rangle }_{{C_1}{C_2}{B_1}{B_2}}} + {{\left| {{\phi _4}} \right\rangle }_{{A_3}{A_4}}} \otimes {{\left| {{\Phi _4}} \right\rangle }_{{C_1}{C_2}{B_1}{B_2}}}} \right) , \end{aligned}$$

(11)

where

$$\begin{aligned}&{\left| {{\Phi _1}} \right\rangle _{{C_1}{C_2}{B_1}{B_2}}} \nonumber \\&\quad \quad = - {a_1}{e^{i{\theta _1}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {00} \right\rangle _{{B_1}{B_2}}} + {l_2}{a_0}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {k_2}{a_0}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} - {l_1}{a_3}{e^{i{\theta _3}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {l_1}{l_2}{a_2}{e^{i{\theta _2}}}{\left| {11} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} + {l_1}{k_2}{a_2}{e^{i{\theta _2}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad -\, {k_1}{a_3}{e^{i{\theta _3}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} + {l_2}{k_1}{a_2}{e^{i{\theta _2}}}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {k_1}{k_2}{a_2}{e^{i{\theta _2}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}}, \end{aligned}$$

(12)

$$\begin{aligned}&{\left| {{\Phi _2}} \right\rangle _{{C_1}{C_2}{B_1}{B_2}}} \nonumber \\&\quad = {a_1}{e^{i{\theta _1}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {00} \right\rangle _{{B_1}{B_2}}} + {l_2}{a_0}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {k_2}{a_0}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} + {l_1}{a_3}{e^{i{\theta _3}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {l_1}{l_2}{a_2}{e^{i{\theta _2}}}{\left| {11} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} + {l_1}{k_2}{a_2}{e^{i{\theta _2}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {k_1}{a_3}{e^{i{\theta _3}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} + {l_2}{k_1}{a_2}{e^{i{\theta _2}}}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {k_1}{k_2}{a_2}{e^{i{\theta _2}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}}, \end{aligned}$$

(13)

$$\begin{aligned}&{\left| {{\Phi _3}} \right\rangle _{{C_1}{C_2}{B_1}{B_2}}} \nonumber \\&\quad = - {a_1}{e^{i{\theta _1}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {00} \right\rangle _{{B_1}{B_2}}} + {l_2}{a_0}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {k_2}{a_0}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} + {l_1}{a_3}{e^{i{\theta _3}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad -\, {l_1}{l_2}{a_2}{e^{i{\theta _2}}}{\left| {11} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} - {l_1}{k_2}{a_2}{e^{i{\theta _2}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {k_1}{a_3}{e^{i{\theta _3}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} - {l_2}{k_1}{a_2}{e^{i{\theta _2}}}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad -\, {k_1}{k_2}{a_2}{e^{i{\theta _2}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}}, \end{aligned}$$

(14)

$$\begin{aligned}&{\left| {{\Phi _4}} \right\rangle _{{C_1}{C_2}{B_1}{B_2}}} \nonumber \\&\quad = {a_1}{e^{i{\theta _1}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {00} \right\rangle _{{B_1}{B_2}}} + {l_2}{a_0}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad +\, {k_2}{a_0}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {01} \right\rangle _{{B_1}{B_2}}} - {l_1}{a_3}{e^{i{\theta _3}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad -\, {l_1}{l_2}{a_2}{e^{i{\theta _2}}}{\left| {11} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} - {l_1}{k_2}{a_2}{e^{i{\theta _2}}}{\left| {10} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad -\, {k_1}{a_3}{e^{i{\theta _3}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {10} \right\rangle _{{B_1}{B_2}}} - {l_2}{k_1}{a_2}{e^{i{\theta _2}}}{\left| {01} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}} \nonumber \\&\quad \quad -\, {k_1}{k_2}{a_2}{e^{i{\theta _2}}}{\left| {00} \right\rangle _{{C_1}{C_2}}}{\left| {11} \right\rangle _{{B_1}{B_2}}}. \end{aligned}$$

(15)

From Eq. (11) it is obvious that after the projective measurement $PM_A^2$, with an equal conditional probability ${P_{R_A^2|R_A^1}} = 1/4$, Alice will obtain one of the four possible states ${\left\{ {\left| {{\phi _1}} \right\rangle ,\left| {{\phi _2}} \right\rangle ,\left| {{\phi _3}} \right\rangle ,\left| {{\phi _4}} \right\rangle } \right\} _{{A_3}{A_4}}}$ which she needs to inform Bob via a classical channel.

The deciding role is now played by the controller Charlie, who should carefully review the felicity condition for the CRSP task. If there are any unfavorable problems, he decides to stop or postpone the task by doing nothing. Otherwise, if everything is favorable, he decides to proceed by performing two single-qubit projective measurements on $C_1$ and $C_2$ simultaneously (denoted as $PM_C^1$ and $PM_C^2$ respectively) under the following basis,

$$\begin{aligned} {\left| {{\varphi _1}} \right\rangle _{{C_1}}}= & {} \frac{1}{{\sqrt{l_1^2 + {{\left( {1 + {k_1}} \right) }^2}} }}\left[ {\left( {1 + {k_1}} \right) {{\left| 0 \right\rangle }_{{C_1}}} + {l_1}{{\left| 1 \right\rangle }_{{C_1}}}} \right] ,\nonumber \\ {\left| {{\varphi _2}} \right\rangle _{{C_1}}}= & {} \frac{1}{{\sqrt{l_1^2 + {{\left( {1 - {k_1}} \right) }^2}} }}\left[ {\left( {1 - {k_1}} \right) {{\left| 0 \right\rangle }_{{C_1}}} - {l_1}{{\left| 1 \right\rangle }_{{C_1}}}} \right] , \end{aligned}$$

(16)

$$\begin{aligned} {\left| {{\varphi _1}} \right\rangle _{{C_2}}}= & {} \frac{1}{{\sqrt{l_2^2 + {{\left( {1 + {k_2}} \right) }^2}} }}\left[ {\left( {1 + {k_2}} \right) {{\left| 0 \right\rangle }_{{C_2}}} + {l_2}{{\left| 1 \right\rangle }_{{C_2}}}} \right] ,\nonumber \\ {\left| {{\varphi _2}} \right\rangle _{{C_2}}}= & {} \frac{1}{{\sqrt{l_2^2 + {{\left( {1 - {k_2}} \right) }^2}} }}\left[ {\left( {1 - {k_2}} \right) {{\left| 0 \right\rangle }_{{C_2}}} - {l_2}{{\left| 1 \right\rangle }_{{C_2}}}} \right] . \end{aligned}$$

(17)

After finishing the measurement, Charlie informs Bob of his measurement result by virtue of classical media. Finally, in the light of Alice and Charlie’s measurement results, Bob’s job is simply to perform an appropriate unitary operation (denoted as ${U_B}$) on particles $B_1$ and $B_2$ to reconstruct the target state ${\left| \chi \right\rangle }$. Various situations are listed out in Table 2.

As an example, we might as well consider the situation that Alice’s $PM_A^2$ result is ${\left| {{\phi _2}} \right\rangle _{{A_3}{A_4}}}$, based on Eq. (11), the state of particles $C_1$, $C_2$, $B_1$ and $B_2$ evolves as

(18)

where

$$\begin{aligned} \sqrt{{p_1}}= & {} \frac{1}{4}\sqrt{l_1^2 + {{\left( {1 + {k_1}} \right) }^2}} \sqrt{l_2^2 + {{\left( {1 + {k_2}} \right) }^2}} , \nonumber \\ \sqrt{{p_2}}= & {} \frac{1}{4}\sqrt{l_1^2 + {{\left( {1 + {k_1}} \right) }^2}} \sqrt{l_2^2 + {{\left( {1 - {k_2}} \right) }^2}} , \nonumber \\ \sqrt{{p_3}}= & {} \frac{1}{4}\sqrt{l_1^2 + {{\left( {1 - {k_1}} \right) }^2}} \sqrt{l_2^2 + {{\left( {1 + {k_2}} \right) }^2}} , \nonumber \\ \sqrt{{p_4}}= & {} \frac{1}{4}\sqrt{l_1^2 + {{\left( {1 - {k_1}} \right) }^2}} \sqrt{l_2^2 + {{\left( {1 - {k_2}} \right) }^2}} . \end{aligned}$$

(19)

Note that after Charlie’s $PM_C^1$ and $PM_C^2$, the state of particles $B_1$ and $B_2$ is perfectly correlated to the target state ${\left| \chi \right\rangle }$, as expressed in Eq. (18). According to Alice and Charlie’s measurement results, Bob can easily recover the target state ${\left| \chi \right\rangle }$ by appropriate local unitary operations. In our discussion here, Alice’s measurement results are ${\left| {{\psi _2}} \right\rangle _{{A_1}{A_2}}}{\left| {{\phi _2}} \right\rangle _{{A_3}{A_4}}}$, if Charlie’s measurement results are ${\left| {{\varphi _1}} \right\rangle _{{C_1}}}{\left| {{\varphi _1}} \right\rangle _{{C_2}}}$ with the conditional probability ${P_{{R_C^1R_C^2}|R_A^2R_A^1}} = \frac{1}{{16}}\left[ {l_1^2 + {{\left( {1 + {k_1}} \right) }^2}} \right] \left[ {l_2^2 + {{\left( {1 + {k_2}} \right) }^2}} \right]$, then ${U_B} = I \otimes {\sigma _x}$ is required to perform on particles $B_1$ and $B_2$, the target state ${\left| \chi \right\rangle }$ can be readily reestablished, as shown in Table 2.

As a supplement, when it comes to the other three cases corresponding to Alice’s $PM_A^1$ results ${\left| {{\psi _1}} \right\rangle _{{A_1}{A_2}}}$, ${\left| {{\psi _3}} \right\rangle _{{A_1}{A_2}}}$ and ${\left| {{\psi _4}} \right\rangle _{{A_1}{A_2}}}$, there will be a similar analysis process. For simplicity, we no longer depict them one by one here. According to Table 2, it is easily found that, for all the possible measurement results of Alice and Charlie, the receiver Bob is always able to reconstruct the target state ${\left| \chi \right\rangle }$ by performing appropriate unitary operation ${U_B}$ on particles $B_1$ and $B_2$. Thus, our CRSP scheme is deterministic. Mathematically, the total success probability reads

$$\begin{aligned} {P_{suc}}= & {} \sum \limits _{R_A^1} {\sum \limits _{R_A^2} {\sum \limits _{R_C^1R_C^2} {{P_{R_A^1}}{P_{R_A^2|R_A^1}}{P_{R_C^1R_C^2|R_A^2R_A^1}}} } } \nonumber \\= & {} 16 \times \frac{1}{4} \times \frac{1}{4} \times \left( {{p_1} + {p_2} + {p_3} + {p_4}} \right) \nonumber \\= & {} 1. \end{aligned}$$

(20)

Table 2 Bob’s recovery unitary operator ${U_B}$ conditioned on Alice’s $R_A^1$, $R_A^2$ and Charlie’s ${R_C^1}$, ${R_C^2}$, where I is the identity operator and ${\sigma _x}$, $i{\sigma _y}$ and ${\sigma _z}$ are Pauli matrices

3 Discussions and conclusions

In summary, we have proposed a deterministic CRSP scheme for arbitrary two-qubit state via suitably chosen partially entangled state $\left| {QC} \right\rangle$, expressed as Eq. (1). Without introducing auxiliary qubits, the success probability of our scheme is always 100 %, independent of parameters of the quantum channel.

It deserves emphasizing that, although partially entangled quantum channel is utilized, the unit success probability of our scheme is the same as that of some CRSP schemes utilizing maximally entangled channels. In this paper, unit success probability can always be achieved, independent of the entanglement degree of the quantum channel. This is due to the fact that partially entangled state $\left| {QC} \right\rangle$ is utilized as the quantum channel. $\left| {QC} \right\rangle$ has an interesting character that if the controller performed a projective measurement under the basis like Eq. (16), no matter what results he obtains, the state shared between the sender and the receiver collapsed into a maximally entangled GHZ state.

Compared with some previous CRSP protocols using partially entangled channels, our scheme has several notable advantages as follows. (i) The assistance of auxiliary qubit is not required, whereas in some earlier schemes [18–21], the controllers generally introduce auxiliary qubits to remove the channel’s parameters. (ii) Our CRSP scheme succeeds with unit probability, irrespective of parameters of the quantum channel. This is a higher success probability than that of some CRSP protocols [18, 20, 21, 26]. (iii) The proposed scheme can be easily extended to the deterministic CRSP of arbitrary N-qubit states, N four-particle partially entangled quantum channels are needed, incidentally the success probability is still 100 % by means of the projective measurements $PM_A^1$, $PM_A^2$, $PM_C$ and the unitary operations $U_A$, $U_B$. This is superior to the scheme in Ref. [26], where the success probability is merely $1 /2^{N}$ when it is generalized to prepare arbitrary N-qubit states.

Here, we have to point out that the implementation of our scheme was conditioned on the cooperation of all participants. The receiver selects his recovery unitary operation $U_B$ according to the sender and the controller’s measurement results. In the CRSP scheme involving one sender and one receiver, maybe it is considered that the receiver can take on the controller’s job concurrently. However, when we generalized our scheme to a CRSP network involving multiple sender-receivers, the controller’s role is highlighted. The controller equipped with projective measurement units can function as a central node serving multiple sender-receivers, he sends measurement results to corresponding receivers, who need only to carry out appropriate local unitary operations to reconstruct the target states without performing projective measurements. Hence, it is not necessary to equip every receiver with projective measurement units, thereby economizing the overall expenses dramatically. This point might be of importance to prospective CRSP networks.