1 Introduction

Entanglement has been exploited as a quantum resource to carry out different types of quantum information processing such as quantum teleportation [1], quantum dense coding [2], quantum state sharing [3–5], quantum geometric computation [6]. Teleportation of an arbitrary single-qubit state was first proposed by using a Bell state between the sender Alice and receiver Bob [1]. Over the past years, various teleportation protocols have been demonstrated with the help of different types of multipartite entangled [7–9]. In 2013, Zha et al. [10] demonstrated that the five-qubit cluster state can be used for bidirectional quantum controlled teleportation. Some different schemes for bidirectional controlled teleportation have been devised using different kinds of entangled states [11–17].

It is known that the n-particle (n>3) cluster state is maximally connected with the better persistency than the GHZ state [18, 19]. Also the cluster states are robust against decoherence [20]. The four-particle cluster state has some preferences for quantum error correction [21] and quantum computation [22–24]. In Ref. [25], it was demonstrated that a four-particle cluster state may be useful in quantum information splitting (QIS) of a single-qubit state and an entangled two-qubit state, and argued it is impossible to split an arbitrary two-qubit state by using a four-particle cluster state. Recently, Nie et al. [26] demonstrated that two four-qubit cluster states can be used to realize the deterministic QIS of an arbitrary three-qubit state by performing only the Bell-state measurements. It is worth mentioning that the six-qubit cluster state has been created in laboratory conditions [27]. Many striking applications of six-qubit cluster state have been found, such as quantum teleportation, quantum dense coding and quantum information splitting [28].

In this work, we present a protocol for implementing asymmetric bidirectional controlled teleportation by using a six-qubit cluster state as quantum channel. Suppose that Alice has two qubits A and B in an unknown state, she wants to transmit an arbitrary two-qubit entangled state of qubits A and B to Bob; at the same time, Bob has a qubit C in an unknown state, he wants to transmit the state of qubit C to Alice. The asymmetric bidirectional controlled teleportation task is completed following the typical procedure that, the receiver applies an appropriate unitary transformation to his qubit, after receiving the measurement results of both the sender Alice (Bob) and the controller Charlie on their separate qubits.

2 Asymmetric Bidirectional Controlled Teleportation

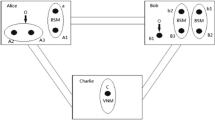
Now let us present our asymmetric bidirectional controlled teleportation scheme in detail. The schematic demonstration is illustrated in Fig. 1. Our scheme can be described as follows. Suppose Alice has an arbitrary two-qubit entangled state, which is given by

$$ \left|\Psi \right\rangle_{AB} =a_{0} \left|00 \right\rangle +a_{1} \left| 11\right\rangle , $$
(1)

and at the same time Bob has a qubit C in an unknown state,

$$ \left| \Psi\right\rangle_{C} =b_{0} \left|0 \right\rangle +b_{1} \left|1 \right\rangle , $$
(2)

where |a 0|2+|a 1|2=|b 0|2+|b 1|2=1.

Fig. 1
figure 1

A asymmetric bidirectional controlled teleportation protocol is shown for exchanging secret quantum information, where a solid circle represents a qubit and the solid line an entanglement between qubits, where a Alice holds a 2-qubit state \(\left | \psi \right \rangle _{AB} \), and Bob holds a 1-qubit state |ψ〉 C . In addition, she shares a six-qubit cluster state with Bob and Charlie, b after Alice’s and Bob’s Bell-state measurements with outcomes (A, 1) and (C, 6), and Alice’s single-qubit measurement on the qubit B, then the qubits 2, 3, 4 and 5 compound system become entangling states and c after Charlie measures his qubit 5, Alice (Bob) may preserve all information of Bob’s (Alice’s) original secret qubit state

Full size image

Now Alice wants to transmit the state of qubits A and B to Bob and Bob wants to transmit the state of qubit C to Alice. Assume that Alice, Bob and Charlie share a six-qubit cluster state, which has the form

$$ \left|C_{6}\right\rangle_{123456}=\frac{1}{2}\left( \left|000000\right\rangle +\left|000111\right\rangle+\left|111000\right\rangle-\left|111111\right\rangle\right)_{123456}, $$
(3)

where the qubits 1 and 4 belong to Alice, qubit 5 belongs to Charlie and qubits 2, 3 and 6 belong to Bob, respectively. The initial state of the total system can be shown as

$$\begin{array}{@{}rcl@{}} \left|{\Psi}\right\rangle_{123456ABC} &=&\left| C_{6}\right\rangle_{123456} \otimes \left| \psi\right\rangle_{AB} \otimes \left| \psi\right\rangle_{C}\\ &=&\frac{1}{4}\left[{\left| {\Phi}^{+}\right\rangle_{A1}\left|{\Phi}^{+}\right\rangle_{C6}}\right. \left( a_{0} b_{0} \left|00000\right\rangle +a_{1} b_{0} \left| 11100\right\rangle +a_{0} b_{1} \left| 00011\right\rangle \right.\\&&\qquad\qquad\qquad\qquad\qquad\left. -a_{1}b_{1} \left|11111\right\rangle\right)_{B2345}\\ &&\qquad+\left| {\Phi}^{-}\right\rangle_{A1} \left| {\Phi}^{+}\right\rangle_{C6} \left( a_{0} b_{0} \left|00000\right\rangle -a_{1} b_{0} \left| 11100\right\rangle +a_{0} b_{1} \left| 00011\right\rangle\right.\\&&\qquad\qquad\qquad\qquad\qquad\left. +a_{1} b_{1} \left|11111\right\rangle\right)_{B2345}\\ &&\qquad+\left| {\Phi}^{+}\right\rangle_{A1} \left| {\Phi}^{-}\right\rangle_{C6} \left( a_{0} b_{0} \left| 00000\right\rangle +a_{1} b_{0} \left|11100\right\rangle -a_{0} b_{1} \left| 00011\right\rangle\right.\\&&\qquad\qquad\qquad\qquad\qquad\left. +a_{1} b_{1} \left|11111\right\rangle \right)_{B2345}\\ &&\qquad+\left|{\Phi}^{-} \right\rangle_{A1} \left| {\Phi}^{-}\right\rangle_{C6} \left( a_{0} b_{0} \left| 00000\right\rangle -a_{1} b_{0} \left| 11100\right\rangle -a_{0} b_{1} \left| 00011\right\rangle\right.\\&&\qquad\qquad\qquad\qquad\qquad\left. -a_{1} b_{1} \left|11111\right\rangle \right)_{B2345}\\ &&\qquad+\left|{\Phi}^{+} \right\rangle_{A1} \left| {\Psi}^{+}\right\rangle_{C6} \left( a_{0} b_{0} \left| 00011\right\rangle -a_{1} b_{0} \left|11111 \right\rangle +a_{0} b_{1} \left| 00000\right\rangle\right.\\&&\qquad\qquad\qquad\qquad\qquad\left. +a_{1} b_{1} \left|11100\right\rangle \right)_{B2345}\\ &&\qquad+\left| {\Phi}^{-}\right\rangle_{A1} \left| {\Psi}^{+}\right\rangle_{C6} \left( a_{0} b_{0} \left| 00011\right\rangle +a_{1} b_{0} \left| 11111\right\rangle +a_{0} b_{1} \left| 00000\right\rangle\right.\\&&\qquad\qquad\qquad\qquad\qquad\left. -a_{1} b_{1} \left|11100\right\rangle \right)_{B2345}\\ &&\qquad+\left|{\Phi}^{+} \right\rangle_{A1} \left| {\Psi}^{-}\right\rangle_{C6} \left( a_{0} b_{0} \left| 00011\right\rangle -a_{1} b_{0} \left|11111\right\rangle -a_{0} b_{1} \left|00000\right\rangle\right.\\&&\qquad\qquad\qquad\qquad\qquad\left. -a_{1} b_{1} \left|11100\right\rangle \right)_{B2345}\\ &&\qquad+\left| {\Phi}^{-}\right\rangle_{A1} \left| {\Psi}^{-}\right\rangle_{C6} \left( a_{0} b_{0} \left| 00011\right\rangle +a_{1} b_{0} \left| 11111\right\rangle -a_{0} b_{1} \left| 00000\right\rangle\right.\\&&\qquad\qquad\qquad\qquad\qquad\left. +a_{1} b_{1} \left|11100\right\rangle \right)_{B2345}\\ &&\qquad+\left|{\Psi}^{+} \right\rangle_{A1} \left| {\Phi}^{+}\right\rangle_{C6} \left( a_{0} b_{0} \left| 11100\right\rangle +a_{1} b_{0} \left| 00000\right\rangle -a_{0} b_{1} \left| 11111\right\rangle\right.\\&&\qquad\qquad\qquad\qquad\qquad\left. +a_{1} b_{1} \left|00011\right\rangle \right)_{B2345}\\ &&\qquad+\left|{\Psi}^{-}\right\rangle_{A1} \left| {\Phi}^{+}\right\rangle_{C6} \left( a_{0} b_{0} \left|11100\right\rangle -a_{1} b_{0} \left|00000 \right\rangle -a_{0} b_{1} \left| 11111\right\rangle\right.\\&&\qquad\qquad\qquad\qquad\qquad\left. -a_{1} b_{1} \left|00011 \right\rangle \right)_{B2345}\\ &&\qquad+\left|{\Psi}^{+}\right\rangle_{A1} \left| {\Phi}^{-}\right\rangle_{C6} \left( a_{0} b_{0} \left| 11100\right\rangle +a_{1} b_{0} \left| 00000\right\rangle +a_{0} b_{1} \left| 11111\right\rangle\right.\\&&\qquad\qquad\qquad\qquad\qquad\left. -a_{1} b_{1} \left|00011\right\rangle \right)_{B2345}\\ &&\qquad+\left|{\Psi}^{-}\right\rangle_{A1} \left| {\Phi}^{-}\right\rangle_{C6} \left( a_{0} b_{0} \left|11100 \right\rangle -a_{1} b_{0} \left| 00000\right\rangle +a_{0} b_{1} \left| 11111\right\rangle\right.\\&&\qquad\qquad\qquad\qquad\qquad\left. +a_{1} b_{1} \left|00011\right\rangle \right)_{B2345}\\ &&\qquad+\left|{\Psi}^{+} \right\rangle_{A1} \left| {\Psi}^{-}\right\rangle_{C6} \left( -a_{0} b_{0} \left|11111 \right\rangle +a_{1} b_{0} \left| 00011\right\rangle +a_{0} b_{1} \left| 11100\right\rangle\right.\\&&\qquad\qquad\qquad\qquad\qquad\left. +a_{1} b_{1} \left|00000 \right\rangle \right)_{B2345}\\ &&\qquad+\left|{\Psi}^{-} \right\rangle_{A1} \left| {\Psi}^{+}\right\rangle_{C6} \left( -a_{0} b_{0} \left|11111 \right\rangle -a_{1} b_{0} \left| 00011\right\rangle +a_{0} b_{1} \left| 11100\right\rangle\right.\\&&\qquad\qquad\qquad\qquad\qquad\left. -a_{1} b_{1} \left|00000 \right\rangle \right)_{B2345}\\ &&\qquad+\left| {\Psi}^{+}\right\rangle_{A1} \left| {\Psi}^{-}\right\rangle_{C6} \left( -a_{0} b_{0} \left|11111 \right\rangle +a_{1} b_{0} \left| 00011\right\rangle -a_{0} b_{1} \left| 11100\right\rangle\right.\\&&\qquad\qquad\qquad\qquad\qquad\left. -a_{1} b_{1} \left|00000 \right\rangle \right)_{B2345}\\ && \qquad+\left| {\Psi}^{-}\right\rangle_{A1}\left| {\Psi}^{-}\right\rangle_{C6} \left( -a_{0} b_{0} \left| 11111\right\rangle -a_{1} b_{0} \left|00011\right\rangle\right.\\ &&\qquad\qquad\qquad\qquad\left.\left. \quad\hspace*{5pt}-a_{0} b_{1} \left| 11100\right\rangle +a_{1} b_{1} \left|00000\right\rangle\right)_{B2345}\right], \end{array} $$
(4)

where \(\left |{\Phi }^{\pm }\right \rangle =\frac {1}{\sqrt {2}}(\left |00\right \rangle \pm \left |11\right \rangle )\) and \(\left |{\Psi }^{\pm }\right \rangle =\frac {1}{\sqrt {2}}(\left |01\right \rangle \pm \left |10\right \rangle )\).

To achieve the purpose of bidirectional controlled teleportation task, Alice and Bob firstly perform a Bell-state measurement on qubit pairs (A, 1) and (C, 6), respectively. Then they announce their results to each other via classical channel. Suppose, Alice’s measurement result is |Φ+〉 A1 and at the same time Bob’s measurement result is |Φ+〉 C6, the corresponding collapse state of qubits B, 2 , 3, 4, 5 are given as

$$\begin{array}{@{}rcl@{}} \left|\varphi \right\rangle_{B2345} &=&a_{0} b_{0} \left| 00000\right\rangle +a_{0} b_{1} \left| 00011\right\rangle +a_{1} b_{0} \left| 11100\right\rangle -a_{1} b_{1} \left|11111\right\rangle. \end{array} $$
(5)

Then Alice takes single-qubit measurement in the basis of \(\left \{ {{\left | \pm \right \rangle =\left ({\left | 0 \right \rangle \pm \left | 1\right \rangle } \right )}\left /{\sqrt 2 }\right .} \right \}\) on qubit B and conveys her result to Bob. If Alice’s measurement result is |+〉 B , the state of the remaining qubits 2, 3, 4, 5 collapse into the state as

$$ \left| \varphi^{\prime}\right\rangle_{2345} =a_{0} b_{0} \left| 0000\right\rangle +a_{0} b_{1} \left| 0011\right\rangle +a_{1} b_{0} \left| 1100\right\rangle -a_{1} b_{1} \left|1111\right\rangle . $$
(6)

And Alice and Bob can co-operate and make a quantum controlled phase gate (QCPG) operation on the qubits 2 (set as a target qubit) and 4 (set as a control qubit). The action of this operation may be described as follow equations:

$$ \left| 00\right\rangle_{24} \to \left| 00\right\rangle_{24} , \left| 01\right\rangle_{24} \to \left| 01\right\rangle_{24} , \left| 10\right\rangle_{24} \to \left| 10\right\rangle_{24} , \left| 11\right\rangle_{24} \to -\left| 11\right\rangle_{24} , $$
(7)

then the state |φ ′〉2345 will become the following state,

$$ \left| \varphi^{\prime\prime}\right\rangle_{2345} =a_{0} b_{0} \left| 0000\right\rangle +a_{0} b_{1} \left| 0011\right\rangle +a_{1} b_{0} \left|1100 \right\rangle +a_{1} b_{1} \left|1111 \right\rangle . $$
(8)

If Charlie allows Bob and Alice to reconstruct the initial unknown state, he needs to carry out single qubit measurement in the basis of \(\left \{{{\left |\pm \right \rangle =\left ({\left | 0\right \rangle \pm \left | 1\right \rangle }\right )} \left / {\sqrt 2 }\right .} \right \}\) on qubit 5 and tells the receivers his result. If Charlie’s measured result is |+〉5 or |−〉5, then the state of the remaining qubits 2, 3, 4 collapse into the state as

$$\begin{array}{@{}rcl@{}} \left| \phi\right\rangle_{234} &=&a_{0} b_{0} \left| 000\right\rangle +a_{0} b_{1} \left| 001\right\rangle +a_{1} b_{0} \left|110\right\rangle +a_{1} b_{1} \left|111\right\rangle \\ &=&\left( {a_{0} \left| 00\right\rangle +a_{1} \left| 11\right\rangle } \right)_{23} \otimes \left( {b_{0} \left|0 \right\rangle +b_{1} \left|1\right\rangle } \right)_{4} , \end{array} $$
(9)

or

$$\begin{array}{@{}rcl@{}} \left| \phi^{\prime}\right\rangle_{234} &=&a_{0} b_{0} \left| 000\right\rangle -a_{0} b_{1} \left| 001\right\rangle +a_{1} b_{0} \left|110 \right\rangle -a_{1} b_{1} \left|111\right\rangle \\ &=&\left( {a_{0} \left| 00\right\rangle +a_{1} \left|11 \right\rangle } \right)_{23} \otimes \left( {b_{0} \left|0 \right\rangle -b_{1} \left|1\right\rangle } \right)_{4} , \end{array} $$
(10)

then Bob and Alice need to apply the local unitary operation I 2⊗I 3⊗I 4 or \(I_{2} \otimes I_{3} \otimes {{\sigma _{4}^{z}}} \). After doing those operations, Bob and Alice can successfully reconstruct the original state. Thus the asymmetric bidirectional quantum controlled teleportation is successfully realized.

Similarly, if Alice and Bob got any other measuring results, with the agreement of Charlie, both Alice and Bob can also effectively recover the original state. According to all the measurement results informed by the others, the appropriate operations which Alice and Bob perform in the last step to gain the quantum information are shown in the Appendix.

3 Discussion and Conclusion

Now let’s us briefly consider the feasibility of this scheme in experiment. It is found that the necessary local unitary operation in the protocol contains QCPG and single-qubit operations, the employed measurement includes Bell-state measurements and single-qubit measurement. It is well known that Bell-state measurements can be decomposed into an ordering combination of a single-qubit Hadmard operation and a two-qubit CNOT operation as well as two single-qubit measurements. Up to now, the progress of Bell-state measurement and the single-qubit unitary operation in experiment in various quantum systems [29–32] has been reported. In addition, the six-qubit cluster state in our scheme has been reported in experiment [27].

In this paper, we have demonstrated that a six-qubit cluster state can be used as the quantum channel to realize the deterministic asymmetric bidirectional quantum controlled teleportation of a single and two qubit states. In the scheme, Alice may transmit an arbitrary two-qubit entangled state of qubits A and B to Bob and at same time Bob may transmit an arbitrary single qubit state of qubit C to Alice via the control of the supervisor Charlie. We hope that such an asymmetric bidirectional quantum controlled teleportation scheme can be realized experimentally in the future.