1 Introduction

Quantum teleportation is a technique of transmitting an unknown state from the sender to the receiver. Since the first theoretical teleportation protocol was proposed by using an entangled pair of two particles in 1993 [1], many protocols of quantum teleportation are devised [2–7]. And some of these protocols have already been realized in experiment. As a new field of quantum teleportation, bidirectional quantum teleportation has received a great attention. In 2013, the first bidirectional quantum teleportation protocol was reported by applying cluster state as a quantum channel [8], up to now, some bidirectional quantum teleportation protocols have been investigated by using multi-qubit state as quantum channel [9–15].

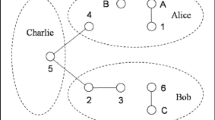
In this work, we propose a protocol for implementing bidirectional quantum teleportation by using a five-qubit cluster state as quantum channel. Suppose that Alice has two qubits A and B in an unknown state, she wants to transmit an arbitrary two-qubit entangled state of qubits A and B to Bob; at the same time, Bob has a qubit C in an unknown state, he wants to transmit the state of qubit C to Alice.

2 Bidirectional Quantum Teleportation

Our scheme can be described as follows. Suppose Alice has an arbitrary two-qubit entangled state, which is given by

$$ \left|{\varPsi}\right.\rangle_{AB} =a_{0} \left|00 \right.\rangle +a_{1} \left| 11\right.\rangle, $$
(1)

and at the same time Bob has qubit C in an unknown state,

$$ \left| {\Psi}\right.\rangle_{C} =b_{0} \left| 0\right.\rangle +b_{1} \left| 1\right.\rangle . $$
(2)

Now Alice wants to transmit the state of qubits A and B to Bob and Bob wants to transmit the state of qubit C to Alice. Assume that Alice and Bob share a five-qubit cluster state, which has the form

$$ {\left|C_{5} \right.\rangle}_{12345}=\frac{1}{2}{\left( \left|00000\right.\rangle+\left|00111\right.\rangle+\left|11101\right.\rangle+\left|11010\right.\rangle\right)}_{12345}, $$
(3)

in which the qubits 1 and 5 belong to Alice and qubits 2, 3 and 4 belong to Bob, respectively. The initial state of the total system can be shown as

$$\begin{array}{@{}rcl@{}} {\left| {\Psi}\right\rangle}_{12345 ~ABC} &=&{\left| \varPsi\right\rangle}_{AB} \otimes {\left| \varPsi\right\rangle}_{C} \otimes {\left|C_{5} \right\rangle}_{12345}\\ &=&\frac{1}{4}\left[ {\left|{\Phi}^{\pm} \right\rangle}_{A1}{\left|{\Phi}^{\pm}\right\rangle}_{C4} {\left| \eta^{1}\right\rangle}_{B235} +{\left| {\Phi}^{\pm}\right\rangle}_{A1} {\left| {\Psi}^{\pm}\right\rangle}_{C4} {\left| \eta^{2}\right\rangle}_{B235}\right.\\ &&\left.+{\left|{\Psi}^{\pm}\right\rangle}_{A1}{\left|{\Phi}^{\pm}\right\rangle}_{C4}{\left|\eta^{3}\right\rangle}_{B235}+{\left|{\Psi}^{\pm}\right\rangle}_{A1}{\left|{\Psi}^{\pm}\right\rangle}_{C4}{\left|\eta^{4}\right\rangle}_{B235}\right], \end{array} $$
(4)

where

$$\begin{array}{@{}rcl@{}} {\left|\eta^{1}\right\rangle}_{B235}&=&\left( a_{0}b_{0}{\left|0000\right.\rangle}\pm_{1}a_{1}b_{0}{\left|1111\right.\rangle}\pm_{2}a_{0}b_{1}{\left|0011\right.\rangle}\pm_{1}\pm_{2}a_{1}b_{1}{\left|1100\right.\rangle}\right), \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} {\left|\eta^{2}\right\rangle}_{B235}&=&\left( a_{0}b_{0}{\left|0011\right.\rangle}\pm_{1}a_{1}b_{0}{\left|1100\right.\rangle}\pm_{2}a_{0}b_{1}{\left|0000\right.\rangle}\pm_{1}\pm_{2}a_{1}b_{1}{\left|1111\right.\rangle}\right), \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} {\left|\eta^{3}\right\rangle}_{B235}&=&\left( a_{0}b_{0}{\left|1111\right.\rangle}\pm_{1}a_{1}b_{0}{\left|0000\right.\rangle}\pm_{2}a_{0}b_{1}{\left|1100\right.\rangle}\pm_{1}\pm_{2}a_{1}b_{1}{\left|0011\right.\rangle}\right), \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} {\left|\eta^{4}\right\rangle}_{B235}&=&\left( a_{0}b_{0}{\left|1100\right.\rangle}\pm_{1}a_{1}b_{0}{\left|0011\right.\rangle}\pm_{2}a_{0}b_{1}{\left|1111\right.\rangle}\pm_{1}\pm_{2}a_{1}b_{1}{\left|0000\right.\rangle}\right), \end{array} $$
(8)

with \({\left | {\Phi }^{\pm }\right \rangle }=\frac {1}{\sqrt {2}}\left ({\left |00\right .\rangle }\pm {\left |11\right .\rangle }\right )\) and \({\left | {\Psi }^{\pm }\right \rangle }=\frac {1}{\sqrt {2}}\left ({\left |01\right .\rangle }\pm {\left |10\right .\rangle }\right )\). In the above equations, the notes “ ±1” or “ ±2” correspond to the Bell-state measurements on her atoms (A, 1) and (C, 4) in the basis of {|Φ±〉,|Ψ±〉}, respectively, and they mean multiplication of ± signs.

To achieve the purpose of bidirectional quantum teleportation task, Alice and Bob firstly perform a Bell-state measurement on qubit pairs (A, 1) and (C, 4), respectively. Then they announce their results to each other via classical channel. Suppose, Alice’s measurement result is |Φ+〉 A1 and at the same time Bob’s measurement result is |Φ+〉 C4, the corresponding collapse state of qubits B, 2 , 3, 5 are given as

$$ \left| \varphi\right.\rangle_{B235} =a_{0} b_{0} \left|0000 \right.\rangle +a_{0} b_{1} \left|0011 \right.\rangle +a_{1} b_{0} \left|1111 \right.\rangle +a_{1} b_{1} \left| 1100\right.\rangle . $$
(9)

Also, Alice takes X-basis measurement on qubit B and conveys her result to Bob. If Alice’s measurement result is |+〉 B , then the state of the remaining qubits 2, 3, 5 collapse into the state as

$$ {\left| \varphi^{\prime}\right.\rangle}_{235} =a_{0} b_{0} \left| 000\right.\rangle +a_{0} b_{1} \left|011 \right.\rangle +a_{1} b_{0} \left|111 \right.\rangle +a_{1} b_{1} \left| 100\right.\rangle . $$
(10)

Then Alice needs to carry out a controlled-NOT operation on his qubits with qubit 2 as controlled qubit and qubit 5 as target qubit, then the state |φ ′〉235 becomes the following state,

$$ {\left|\phi \right.\rangle}_{235} =a_{0} b_{0} \left|000 \right.\rangle +a_{0} b_{1} \left| 011\right.\rangle +a_{1} b_{0} \left| 110\right.\rangle +a_{1} b_{1} \left| 101\right.\rangle . $$
(11)

And then Alice performs another controlled-NOT operation on his qubits with qubit 5 as controlled qubit and qubit 3 as target qubit, then the state |ϕ〉235 would become

$$\begin{array}{@{}rcl@{}} {\left| \phi^{\prime}\right\rangle}_{235} &=&a_{0} b_{0} \left| 000\right.\rangle +a_{0} b_{1} \left|001 \right.\rangle +a_{1} b_{0} \left| 110\right.\rangle +a_{1} b_{1} \left| 111\right.\rangle\\ &=&\left( {a_{0} \left| 00\right.\rangle +a_{1} \left| 11\right.\rangle } \right)_{23} \otimes \left( {b_{0} \left|0\right.\rangle +b_{1} \left| 1\right.\rangle } \right)_{5} . \end{array} $$
(12)

Thus the asymmetric bidirectional quantum teleportation is successfully realized.

3 Conclusions

In this paper, we have demonstrated that the five-qubit cluster state can be used as the quantum channel to realize the deterministic bidirectional quantum teleportation of single and two qubit states. In the scheme, Alice may transmit an arbitrary two-qubit entangled state of qubits A and B to Bob and at same time Bob may transmit an arbitrary single qubit state of qubit C to Alice. We hope that such a bidirectional quantum teleportation scheme can be realized experimentally in the future.