A class of well-behaved generalized charged analogues of Vaidya-Tikekar type fluid sphere in general relativity

Abstract

In this paper first ever we have developed a class of well behaved charged fluid spheres expressed by a space time with its hypersurfaces $t = \operatorname {const}$. as spheroid for the case 0<K<1 with surface density 2×10¹⁴ gm/cm³. The same utilized to construct a superdense star and seen that star satisfies all well behaved condition for 0<K≤0.038. The maximum mass occupied and the corresponding radius are found to be 4.830982M _Θ and 20.7612 km respectively. The redshift at the center and on the surface is given z ₀=0.425367 and z _a =0.240901.

1 Introduction

Since the inception of Reissner-Nordstrom metric, research workers have been busy in deriving interior regular charged perfect fluid solutions such as Tiwari et al. (1991), Tiwari and Ray (1991a, 1991b, 1993) and many more. Some of the workers, charged the well-known uncharged perfect fluid solutions e.g. Kuchowicz (1968) solutions by Nduka (1977), Adler (1974), Wyman (1949) solution by Nduka (1976) and so on a good account of the above can be had from the work of Ivanov (2002). The relevance of the study of charged fluid distributions is connected with the following interesting facts such as: (i) Charge dust (CD) (pressure free distribution) may be realized in the slight ionization of neutral hydrogen. (ii) CD may possess arbitrary mass and radius, can attain very large redshifts, their exteriors can be made arbitrarily near to the exterior of an extreme charged black hole. (iii) A classical model of an electron is likely to be represented by CD if many of its characteristics remain finite and non-trivial while the junction radius shrinks to zero. (iv) Besides many other speciality, the charge in the fluid distribution helps in countering the gravitational collapse by means of the Coulombian repulsion together with the pressure gradient. Although one can reach this goal with non perfect fluids, a perfect fluid solution of the type mentioned was recently found (Gupta and Kumar, 2005a) but with the presence of an electric charge. In the presence of electric charge the gravitational collapse of a spherically symmetric distribution of matter to a point singularity may be avoided as the gravitational attraction is counter balanced by the repulsive Coulombian force in addition to the negative pressure gradient due to the matter. Also presence of the charge, remove the gravitational collapse, which absorbs much of the fine tuning necessary in the uncharged case (Ivanov, 2002). After the model is charged thorough a specific electric intensity (Charge function) it starts possessing the negative density gradient which is necessary for a physically valid model. Vaidya and Tikekar (1982) coined a space-time involving a parameter K whose hypersurfaces t=constant were spheroids for K<1. They also obtained a perfect fluid distribution (for K=−2) which was utilized to describe a superdense star model. In fact the above space-time owes its origin to Buchdahl (1959) with a passage of time perfect fluid models were obtained for all K except for 0<K<1 by Gupta and Jasim (2003). Then the fluid spheres so obtained were electrified by means of a particular electric field (Gupta and Kumar, 2005a, 2005b; Sharma et al., 2001). It is observed that the case 0<K<1 fails to yield negative gradient of energy density for an uncharged case. Also Gupta and Kumar (2005c) has obtained most general class of charged fluid spheres described by space-time with hypersurfaces ‘$t =\operatorname {const}$’ as spheroids or hyperboloids considering the electric field intensity that has positive gradient. Recently, Gupta et al. (2010, 2011) discussed new closed form solutions for spheroid and hyperboloid, respectively considering a special form of charge profile satisfying ultra relativistic and non-relativistic conditions. Recently Naveen Bijalwan and Gupta (2011, 2012) have obtained perfect fluid charged analogues models for all K except for 0<K<1 using different electric intensity and Kumar and Gupta (2013) also obtained the Buchdhal’s type fluid with generalized charged intensity for 0<K≤0.05 which satisfies the reality conditions except casualty condition.

In this paper we have obtained a class of well-behaved charged fluid spheres satisfying the reality as well as casualty conditions and expressed by space time metric with its hypersurfaces $t = \operatorname {const}$. as spheroid for the case 0<K<1. The charged fluid spheres so obtained are utilized to construct super-dense star models with surface density 2×10¹⁴ gm/cm³. In this process we come across various astrophysical objects like white dwarf, quark and neutron stars. A neutron star has mass between 1.35 and about 2.1 solar mass with a corresponding radius of about 12 km. It is shown by Chanderasekhar that no stable White Dwarf can be more massive than 1.42 solar mass. However 2 to 3 solar mass correspond to quark star.

2 Field equations

Let us take the static spherically symmetric space-time with $t =\operatorname {const}$ hypersurfaces as spheroids or hyperboloids as

$$ ds^{2} = - \frac{K ( 1 + Cr^{2} )}{ ( K + Cr^{2} )}dr^{2} - r^{2} \bigl( d\theta^{2} + \sin^{2}\theta d \phi^{2} \bigr) + y^{2} ( r )dt^{2} $$

(2.1)

where C and K are constant parameters.

If the metric (2.1) describes charged fluid distribution then the metric has to satisfy the Einstein-Maxwell equations

$$\begin{aligned} R_{j}^{i} - \frac{1}{2}R \delta_{j}^{i} =& - \kappa \biggl[ \bigl( c^{2}\rho+ p \bigr)v^{i}v_{j} - p\delta_{j}^{i} + \frac{1}{4\pi} \biggl( - F^{im}F_{jm} \\ &{} + \frac{1}{4} \delta_{j}^{i}F_{mn}F^{mn} \biggr) \biggr], \end{aligned}$$

(2.2)

where $\kappa= \frac{8\pi G}{c^{4}}$, ρ, p and v ⁱ denote matter density, fluid pressure and the unit time-like flow vector of the fluid respectively and F _ik being the skew symmetric electromagnetic field tensor satisfying the Maxwell equations

$$\begin{aligned} &{F_{ik; j} + F_{kj;i} + F_{ji; k} = 0, } \end{aligned}$$

(2.3)

$$\begin{aligned} &{\frac{\partial}{\partial x^{k}} \bigl( \sqrt{ - g} F^{ik} \bigr) = - 4\pi \sqrt{ - g} j^{i}, } \end{aligned}$$

(2.4)

where j ⁱ=σv ⁱ represents the four-current vector of charged fluid while the charge density is denoted by σ.

The field equations (2.2) with respect to (2.1) reduce to (Dionysiou 1982)

$$\begin{aligned} &{\frac{ ( K + Cr^{2} )}{K ( 1 + Cr^{2} )} \biggl[ \frac { - 2y'}{ry} + \frac{C ( K - 1 )}{K + Cr^{2}} \biggr] } \end{aligned}$$

(2.5)

$$\begin{aligned} &{\quad = - \kappa p + \frac{q^{2}}{r^{4}} - \biggl[ \frac{y''}{y} + \frac{y'}{ry} - \frac{C ( K - 1 )ry'}{ ( K + Cr^{2} ) ( 1 + Cr^{2} )y} } \\ &{\qquad{} - \frac{C ( K - 1 )}{ ( K + Cr^{2} ) ( 1 + Cr^{2} )} \biggr] \frac{ ( K + Cr^{2} )}{K ( 1 + Cr^{2} )}} \\ &{\quad = - \kappa p - \frac{q^{2}}{r^{4}} } \end{aligned}$$

(2.6)

$$\begin{aligned} &{\frac{C ( K - 1 ) ( 3 + Cr^{2} )}{K ( 1 + Cr^{2} )^{2}} = \kappa c^{2}\rho+ \frac{q^{2}}{r^{4}} } \end{aligned}$$

(2.7)

where

$$ q(r) = 4\pi\int_{0}^{r} \sigma r^{2}e^{\lambda/2}dr = r^{2}\sqrt{ - F_{14}F^{14}} = r^{2}F^{41}e^{ ( \lambda+ \upsilon )/2} $$

(2.8)

represents the total charge contained with in the sphere of radius ‘r’. Equation (2.4) reduces to

$$ \frac{\partial}{\partial r} \bigl(e^{ ( \lambda+ \upsilon )/2}r^{2}F^{41} \bigr) = - 4\pi e^{ ( \lambda+ \upsilon )/2}r^{2}j^{4} $$

(2.9)

Beyond the pressure free interface ‘r=a’ the charged fluid sphere is expected to join with the Reissner-Nordström metric:

$$\begin{aligned} ds^{2} =& - \biggl( 1 - \frac{2M}{r} + \frac{e^{2}}{r^{2}} \biggr)^{ - 1}dr^{2} - r^{2} \bigl( d \theta^{2} + \sin^{2}\theta d\phi^{2} \bigr) \\ &{} + \biggl( 1 - \frac{2M}{r} + \frac{e^{2}}{r^{2}} \biggr)dt^{2} \end{aligned}$$

(2.10)

where M is the gravitational mass of the distribution such that

$$M = \mu ( a ) + \varepsilon ( a ) $$

while

$$\begin{aligned} &{\mu(a) = \frac{\kappa}{2}\int_{0}^{a} \rho r^{2}dr, } \\ &{\varepsilon(a) = \frac{\kappa}{2}\int_{0}^{a} r\sigma qe^{\lambda/2}dr,\quad e = q ( a ) } \end{aligned}$$

(2.11)

ε(a) is the mass equivalence of the electromagnetic energy of distribution while μ(a) is the mass and e is the total charge inside the sphere (Florides 1983).

For the given expression of q, the expressions for the pressure and energy density can be had from (2.5) and (2.7) subject to the consistency of (2.6), which requires elimination of p.

$$ \frac{ ( K + Cr^{2} )}{K ( 1 + Cr^{2} )} \biggl[ \frac{y''}{y} + \frac{y'}{ry} - \frac{C ( K - 1 )r ( Cr - \frac{y'}{y} )}{ ( K + Cr^{2} ) ( 1 + Cr^{2} )} \biggr] = \frac{2q^{2}}{r^{4}} $$

(2.12)

If we let

$$ X = \sqrt{\frac{K}{1 - K}} \sqrt{1 + \frac{C r^{2}}{K}}, $$

(2.13)

then (2.12) transforms to a simple form

$$ \bigl( 1 + X^{2} \bigr)\frac{d^{2}y}{dX^{2}} - X \frac{dy}{dX} - \alpha y = 0 $$

(2.14)

where

$$\alpha= 1 - K + 2Kq^{2}\frac{ ( Cr^{2} + 1 )^{2}}{C^{2}r^{6}} $$

In order to obtained closed form solution of (2.14), when 0<K<1, then we get

$$ y = \bigl( 1 + X^{2} \bigr)^{1/4}\cdot v $$

(2.15)

Now put (2.15) into (2.14), we get

$$ \frac{d^{2}v}{dX^{2}} + Sv = 0 $$

(2.16)

where

$$S = - \frac{\alpha}{ ( 1 + X^{2} )} + \frac{ ( 2 - 3X^{2} )}{4 ( 1 + X^{2} )^{2}} $$

The electric intensity can be explicitly determined as

$$\begin{aligned} \frac{q^{2}}{r^{4}} =& \frac{C^{2}r^{2}}{2 ( Cr^{2} + 1 )^{2}} \biggl[ \frac{5 ( 1 - K )}{4K ( 1 + Cr^{2} )} \\ &{} - \frac{S ( 1 + Cr^{2} )}{K ( 1 - K )} + 1 - \frac{7}{4K} \biggr] \end{aligned}$$

(2.17)

The expressions for density and pressure are given as

$$\begin{aligned} &{ \begin{aligned}[b] \kappa c^{2}\rho&= \frac{C ( K - 1 )}{K}\frac{ ( 3 + Cr^{2} )}{ ( 1 + Cr^{2} )^{2}} - \frac{C^{2}r^{2}}{2 ( 1 + Cr^{2} )^{2}}\\ &\quad{}\times \biggl[ \frac{5 ( 1 - K )}{4K ( 1 + Cr^{2} )} - \frac{S ( 1 + Cr^{2} )}{K ( 1 - K )} + 1 - \frac{7}{4K} \biggr]\end{aligned} }\\ \end{aligned}$$

(2.18)

$$\begin{aligned} &{ \begin{aligned}[b] \kappa p &= \frac{2y'}{ry} \frac{ ( K + Cr^{2} )}{K ( 1 + Cr^{2} )} - \frac{C ( K - 1 )}{K ( 1 + Cr^{2} )} + \frac{C^{2}r^{2}}{2 ( 1 + Cr^{2} )^{2}}\\ &\quad{}\times \biggl[ \frac{5 ( 1 - K )}{4K ( 1 + Cr^{2} )} - \frac{S ( 1 + Cr^{2} )}{K ( 1 - K )} + 1 - \frac{7}{4K} \biggr] \end{aligned} } \end{aligned}$$

(2.19)

The expression for velocity of sound can be written as

$$ \frac{dp}{c^{2}d\rho} = \frac{dp / dr}{c^{2}d\rho/ dr} $$

(2.20)

Now we can solve (2.16) easily if we let,

$$ S = D \quad \mathrm{or}\quad S = \frac{D}{X^{2}} $$

(2.21)

The expression for the pressure can be derived as follows:

Case (a)::

$S = \frac{D}{X^{2}} = \frac{\beta}{X^{2}}$, $\beta<\frac{1}{4}$

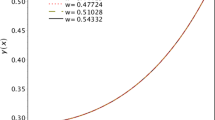
$$ y ( X ) = \bigl( 1 + X^{2} \bigr)^{1/4} \bigl[ AX^{m_{1}} + BX^{m_{2}} \bigr] $$

(2.22)

where

$$m_{1} = \frac{1 + \sqrt{1 - 4\beta}}{2} \quad \mathrm{and}\quad m_{2} = \frac{1 - \sqrt{1 - 4\beta}}{2} $$

The expression of the pressure is given as

$$\begin{aligned} \kappa p =& - \frac{2X^{2}}{KQ} \bigl[ \beta Q \bigl( Am_{1}X^{m_{1} - 1} + Bm_{2}X^{m_{2} - 1} \bigr) \\ &{} + 0.5X \bigl( AX^{m_{1}} + BX^{m_{2}}\bigr) \bigr] \bigl[Q \bigl( AX^{m_{1}} + BX^{m_{2}}\bigr)\bigr]^{-1} \\ &\times\frac{C}{ ( 1 - K )X} + \frac{C}{X^{2}} + \frac{C^{2}r^{2} ( 1 - K )^{2}}{2Q^{2}} \\ &{}\times \biggl[ \frac{5}{4KQ} - \frac{\beta Q}{KX^{2}} + 1 - \frac{7}{4K} \biggr] \end{aligned}$$

(2.23)

where

$$Q = \frac{1 + Cr^{2}}{1 - K} $$

For numerically investigation of the models here we are taking following symbols throughout the article

$$D = \frac{8\pi G}{c^{2}}a^{2}\rho,\qquad P = \frac{8\pi G}{c^{4}}a^{2}p, $$

c=2.997×10¹⁰ cm/s, G=6.673×10⁻⁸ cm³/gs², M _Θ =1.475 km.

Case (b)::

$S = \frac{D}{X^{2}} = \frac{\beta}{X^{2}}$, $\beta=\frac{1}{4}$

$$ y ( X ) = X^{1/2} \bigl( 1 + X^{2} \bigr)^{1/4} [ A + B\log X ] $$

(2.24)

The expression of the pressure is given as

$$\begin{aligned} \kappa p =& - \frac{2X^{2}}{KQ} \\ &{} \times \biggl[ \frac{\frac{BQ^{1/4}}{AX} + \frac{1}{2} ( 1 + \frac{B}{A}\log X ) ( Q^{ - 3/4}X^{3} + \frac{Q^{1/4}}{X} )}{QX ( 1 + \frac{B}{A}\log X )} \biggr] \\ &{}\times\frac{C}{ ( 1 - K )X} + \frac{C}{X^{2}} + \frac{C^{2}r^{2} ( 1 - K )^{2}}{2Q^{2}} \\ &{}\times \biggl[ \frac{5}{4KQ} - \frac{Q}{4KX^{2}} + 1 - \frac{7}{4K} \biggr] \end{aligned}$$

(2.25)

where

$$Q = \frac{1 + Cr^{2}}{1 - K} $$

Case (c)::

$S = \frac{D}{X^{2}} = \frac{\beta}{X^{2}}$, $\beta> \frac{1}{4}$

$$\begin{aligned} y ( X ) =& X^{1/2} \bigl( 1 + X^{2} \bigr)^{1/4} \bigl[ A\cos ( m_{1}\log X ) \\ &{} + B\sin ( m_{1}\log X ) \bigr] \end{aligned}$$

(2.26)

where $m_{1} = \frac{\sqrt{4\beta- 1}}{2}$.

The expression of the pressure is given as

$$\begin{aligned} \kappa p =& - \frac{2X^{2}}{KQ}\biggl[ \biggl[ \frac{m_{1}Q^{1/4}}{X} \biggl\{ - \sin ( m_{1}\log X ) \\ &{} + \frac{B}{A}\cos ( m_{1}\log X ) \biggr\} + 0.5 \biggl\{ \cos ( m_{1}\log X ) \\ &{} + \frac{B}{A}\sin ( m_{1}\log X ) \biggr\} \bigl\{ Q^{- 3/4}X^{3} + Q^{1/4}X^{ - 1}\bigr\} \biggr] \\ &{}\times \biggl[{QX \biggl\{ \cos ( m_{1}\log X ) + \frac{B}{A}\sin ( m_{1}\log X ) \biggr\} } \biggr]\biggr]^{-1} \\ &{}\times\frac {C}{ ( 1 - K )X} + \frac{C}{X^{2}} + \frac{C^{2}r^{2} ( 1 - K )^{2}}{2Q^{2}} \\ &{}\times \biggl[ \frac{5}{4KQ} - \frac{\beta Q}{KX^{2}} + 1 - \frac{7}{4K} \biggr] \end{aligned}$$

where

$$Q = \frac{1 + Cr^{2}}{1 - K} $$

3 Well behaved conditions to be satisfied

The physical validity of the charged fluid sphere (CFS) depends upon the following conditions (called reality conditions or energy conditions) inside and on the sphere r=a such that

• (i) ρ>0, 0≤r≤a,

• (ii) p>0, r<a,

• (iii) p=0, r=a,

• (iv) dp/dr<0,dρ/dr<0,0<r<a.

• (v) c ² ρ≥p weak energy condition (WEC) or c ² ρ≥3p strong energy condition (SEC) 0≤r≤a.

• (vi) The velocity of sound (dp/dρ)^1/2 should be less than that of light throughout the CFS (0≤r≤a).

• (vii) $\frac{d}{dr} ( \frac{p}{c^{2}\rho} ) < 0$.

• (viii) $\frac{d}{dr} ( \frac{dp}{c^{2}d\rho} ) < 0$.

• (ix) The adiabatic constant $\gamma=(( \frac{c^{2}\rho+ p}{p} ) ( \frac{dp}{c^{2}d\rho} ) ) > 1$.

• (x) Red Shift red as (e ^−ν/2−1) or $(\frac{1}{\vert y ( r ) \vert } - 1)$

Beside the above the smooth joining with the Reissner-Nordström metric, requires the continuity of e ^λ, e ^υ and q across the pressure free interface r=a and we get,

$$\begin{aligned} &{\frac{K ( 1 + Ca^{2} )}{ ( K + Ca^{2} )} = 1 - \frac{2m ( a )}{a} + \frac{e^{2}}{a^{2}} } \end{aligned}$$

(3.1)

$$\begin{aligned} &{y^{2} ( a ) = 1 - \frac{2m ( a )}{a} + \frac{e^{2}}{a^{2}} } \end{aligned}$$

(3.2)

$$\begin{aligned} &{q(a) = e } \end{aligned}$$

(3.3)

$$\begin{aligned} &{p_{(r = a)} = 0 } \end{aligned}$$

(3.4)

The conditions (3.1) and (3.3) are automatically satisfied due to the preposition (2.11) however (3.2) and (3.4) can provide the unique values of arbitrary constants A and B.

4 Conclusion

In this paper the fluid spheres is electrified in a particular way which leads to a second order differential equation in normal form with g ₄₄=(1+X ²)^1/2 v ² and $\frac{d^{2}v}{dr^{2}} + Sv = 0$. The later is solved for three cases, but only one case i.e. $S = \frac{\beta}{X^{2}}$, $( \beta< \frac{1}{4} )$ could yield the charged fluid spheres satisfying all the well behaved conditions for 0<K≤0.038 and depict the models for super dense star with the maximum mass and the corresponding radius as 4.830982M _Θ and 20.7612 km respectively for K=0.02 with red shifts at the center and on the surface are given by z ₀=0.425367 and z _a =0.240901 respectively (where surface density is taken to be 2×10¹⁴ g/cm³). The star models are seen to satisfy Chandrasekhar limit. In this article we come across various astrophysical objects like white dwarf, quark and neutron stars with the masses 1.342129M, 4.830982M _Θ and 1.584497M _Θ respectively and the corresponding radius are 14.29049 km, 20.7612 km and 15.03099 km respectively. Also in the cases (b) and (c) from the numerical Tables 5, 6, 7, 8 we have concluded that due to positive density gradient for all numerical values of K, Ca ² and β, all the mentioned cases are unphysical. Finally through the numerically as well as graphically investigations we have concluded that only the case (a) is satisfied the well behaved conditions of the charged fluid sphere. Here we have constructed the graphs only for well behaved case (Tables 1, 2, 3, 4).

Table 1 −0.0055≤Ca ²≤−0.001 and −0.04≤β≤−.0.01

Table 2 −0.0115≤Ca ²≤−0.001 and −0.04≤β≤−.0.03

Table 3 −0.088≤Ca ²≤−0.001 and β=−0.04

Table 4 −0.0101≤Ca ²≤−0.001 and β=−0.04

Table 5 Numerical table for the various values of the parameter K

Table 6 Numerical table for the various values of the parameter K

Table 7 Numerical table for the various values of the parameter K

Table 8 Numerical table for the various values of the parameter K

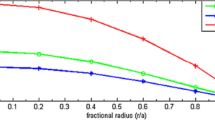
Figure 1 shown that the pressure (P) is monotonically decreasing with respect to radius for the various values of the parameter K.

Fig. 1

Behaviour of pressure versus radius

Figure 2 shown that the density (D) is monotonically decreasing with respect to radius for the various values of the parameter K.

Fig. 2

Behaviour of density versus radius

Figure 3 shown that the charge (q) is monotonically increasing with respect to radius for the various values of the parameter K.

Fig. 3

Behaviour of density versus radius

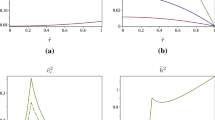
Figure 4 shown that the velocity of sound is monotonically decreasing with respect to radius for the various values of the parameter K.

Fig. 4

Behavior of density versus radius

Figure 5 shows that the ratio (P/D) of pressure and density is monotonically decreasing with respect to radius for the various values of the parameter K.

Fig. 5

Behavior of ration (P/D) versus radius