Introduction

In recent years, integer ambiguity resolution (IAR) has been developed to shorten the initialization time of precise point positioning (PPP, Zumberge et al. 1997) and thereby improve its accuracy (Ge et al. 2008; Geng et al. 2009). Such methods estimate the fractional cycle bias (FCB) or further merge it with satellite clock products and PPP users can then apply these products to float PPP for ambiguity fixing. Although great achievements have been reported, Geng et al. (2011) showed that PPP-IAR still suffer from a long initial fix time (IFT) of more than 30 min.

With the full operation of GLONASS and BeiDou Navigation Satellite System (BDS) regional service, the PPP-IAR performance can be improved compared with GPS-only solutions, if a combination of these satellite systems is used. Geng and Shi (2017b) analyzed the contribution of adding GLONASS to GPS-only PPP-IAR, and the results show that the fixing percentage with observation duration of 10 min can be improved from 39.81 to 87.50%. Liu et al. (2017b) showed that the fixing percentage in kinematic PPP is only 46.8% within 10 min for the GPS only, and improves to 95.8% upon adding GLONASS. For GPS + BDS, Liu et al. (2017a) showed that the fixing percentage in GPS-only kinematic PPP is 17.6% within 10 min, and improves to 42.8% upon adding inclined geosynchronous satellite orbit (IGSO) and medium earth orbit (MEO) satellites of the BDS. However, because geostationary earth orbit (GEO) satellites maintain almost stationary with respect to the earth, their orbit accuracy is very poor, the fixing percentage within 10 min is reduced to only 23.2% if GEO satellites are further included.

There has been extensive research into BDS precise orbit determination (POD) using GNSS observations. Shi et al. (2012) studied the data quality and POD accuracy for GEO and IGSO satellites, and the results show that overlapping radial accuracy can be a few decimeters. Ge et al. (2012b) showed that the three-dimensional (3D) overlapping accuracy for GEO and IGSO satellites are 3.3 and 0.51 m, respectively. Steigenberger et al. (2013a) achieved an orbit consistency of sub-meter and better than 20 cm for GEO and IGSO satellites, respectively. Based on the BeiDou Experimental Test Service (BETS) network, Zhao et al. (2013) performed POD for the entire BDS constellation, and the results show 3D root mean square (RMS) values of 35.5, 33.8 and 174.1 cm for MEO, IGSO and GEO satellites, respectively. Lou et al. (2016) later used a combined BETS and Multi-GNSS Experiment (MGEX) (Steigenberger et al. 2013b; Montenbruck et al. 2013, 2017) network established by the Internal GNSS Service (IGS) (Dow et al. 2005, 2009; Beutler et al. 2009) for BDS POD. The results show the 3D RMS of the BDS orbit error at 10.6, 20.2, and 130.9 cm for MEO, IGSO, and GEO satellites, respectively.

Guo et al. (2010a, b) proposed using combined L-band pseudorange and C-band ranging to determine high-accuracy orbit and clock corrections for GEO satellites simultaneously. The results show that meter-level accuracy is achievable using data collected for a Chinese GEO satellite with three C-band transfer ranging stations and four L-band pseudorange tracking stations. Satellite laser ranging (SLR) has a high accuracy of centimeter level and can also be used for POD. Simulation studies by Urschl et al. (2007) revealed that the overlap accuracy can be improved by 20% for GPS and 50% for GLONASS if there are evenly distributed SLR data covering the entire orbital arc. However, Thaller et al. (2011) pointed out that, such SLR observations are not currently available, and joint adjustments with actual GPS and SLR observations did not show strong improvement of orbit accuracy. Qing et al. (2017) considered the systematic bias between GNSS and SLR observations in a combined POD for BDS (GEO and IGSO) satellites and found that the improvement of orbit accuracy is very limited by adding SLR observations, owing to the lack of SLR tracking stations and observations for BDS.

To remove the effect of low-accuracy GEO orbits, we estimated the narrow-lane FCB and orbit error simultaneously and corrected the satellite orbit with the estimated orbit error. We also estimated a systematic bias in the clock product to compensate its effect on the code observation, making full use of multi-GNSS data. Data recorded at intervals of 15 s over a week by 45 stations were then processed to assess the contribution of the proposed strategy.

Methods

The GNSS code and carrier phase observations at a frequency \(g{\text{ }}(g=1,2)\) at a particular epoch for receiver \(i\) and satellite \(k\) can be written as

$$\begin{gathered} P_{{g,i}}^{k}=\rho _{i}^{k}+dt_{i}^{{}} - dt_{{}}^{k}+\mu _{i}^{k}/f_{g}^{{k2}}+b_{{g,i}}^{k} - b_{g}^{k}+e_{{g,i}}^{k} \hfill \\ L_{{g,i}}^{k}=\rho _{i}^{k}+dt_{i}^{{}} - dt_{{}}^{k} - \mu _{i}^{k}/f_{g}^{{k2}} - CPB_{{g,i}}^{{}}+B_{{g,i}}^{k} - B_{g}^{k}+\lambda _{g}^{k}N_{{g,i}}^{k}+\varepsilon _{{g,i}}^{k} \hfill \\ \end{gathered}$$
(1)

where \(P_{{g,i}}^{k}\) and \(L_{{g,i}}^{k}\) are code and carrier phase observations corresponding to wavelength \(\lambda _{g}^{k}\) and frequency \(f_{g}^{k}\). \(\rho _{i}^{k}\) is the non-dispersive delay that includes the geometric delay, tropospheric delay, and any other delay that affects all observations identically. \(dt_{i}^{{}}\) and \(dt_{{}}^{k}\) are the receiver and satellite clock biases, respectively. The quotient \(\mu _{i}^{k}/f_{g}^{{k2}}\) denotes the ionospheric delay. \(N_{{g,i}}^{k}\) denotes an integer ambiguity. \(b_{{g,i}}^{k}\) and \(B_{{g,i}}^{k}\) represent receiver code and carrier phase hardware biases for satellite \(k\), whereas \(b_{g}^{k}\) and \(B_{g}^{k}\) are the satellite hardware biases. \({\text{CPB}}_{{g,i}}^{{}}\) is the code-phase bias (CPB) (Sleewaegen et al. 2012), which must be corrected for ambiguity fixing. Phase center offset and variation, phase windup, tidal loading, earth rotation, and relativistic effects should be corrected in modeling (Kouba 2009). The CPB can be calculated with the carrier phase inter-frequency bias (IFB) given in, e.g., Wanninger (2012), Sleewaegen et al. (2012), and Liu et al. (2017b). For some stations, the CPB may differ appreciably from the model, and it is, therefore, best to estimate a CPB correction for each station (Geng et al. 2017a). For this, we can refer to Tian et al. (2015) and Liu et al. (2016).

Multi-GNSS FCB estimation

Unlike GPS and BDS, there are different code hardware biases in the GLONASS receiving channels (Kozlov et al. 2000; Yamada et al. 2010; Chuang et al. 2013), which can differ between satellites up to several meters. This introduces a difficulty in wide-lane FCB estimation, such that we cannot separate the receiver FCB from the satellite FCB (Liu et al. 2017b). The GLONASS receiver code hardware biases can be written as a sum of an average term and satellite-dependent term:

$${\text{ }}b_{{g,i}}^{k}=b_{{g,i}}^{R}+\Delta b_{{g,i}}^{k}$$
(2)

where \(\Delta b_{{g,i}}^{k}\) is also called the code IFB in some publications. Although there is no general correction model for the code IFB, if we use a network of receivers with identical hardware configurations, the code IFB can be assumed identical for all receivers and can be grouped with the satellite code hardware bias (Liu et al. 2017b, c). In this way, the code IFB will not affect the wide-lane FCB estimation.

BDS satellites are affected by the satellite-induced code bias (SICB). Wanninger and Beer (2015) generated an individual correction model for IGSO and MEO satellites. Lou et al. (2017) found that GEO satellites can be corrected with the same model used for IGSO satellites. We, therefore, used the same model of IGSO satellites for GEO satellites. Because a zero-mean condition was added to all correction values in Wanninger and Beer (2015), the correction model can thus be expressed as:

$$b_{g}^{s}={\text{SICB}}_{g}^{s}(e)+C_{g}^{s}$$
(3)

where \(s\) represents the satellite type (GEO, IGSO, or MEO) and \(e\) is the satellite elevation angle. \({\text{SICB}}\) is the correction model, and \(C\) is the offset induced by the zero-mean condition.

Considering the previous discussion, the combined GPS + GLONASS + BDS observation model can be expressed as:

$$\begin{gathered} G\left\{ \begin{gathered} P_{{g,i}}^{l}=\rho _{i}^{l}+dt_{i}^{G} - dt_{{}}^{l}+\mu _{i}^{l}/f_{g}^{{G2}}+b_{{g,i}}^{G} - b_{g}^{l}+e_{{g,i}}^{l} \hfill \\ L_{{g,i}}^{l}=\rho _{i}^{l}+dt_{i}^{G} - dt_{{}}^{l} - \mu _{i}^{l}/f_{g}^{{G2}}+B_{{g,i}}^{G} - B_{g}^{l}+\lambda _{g}^{G}\tilde {N}_{{g,i}}^{l}+\varepsilon _{{g,i}}^{l} \hfill \\ \end{gathered} \right. \hfill \\ R\left\{ \begin{gathered} P_{{g,i}}^{m}=\rho _{i}^{m}+dt_{i}^{R} - dt_{{}}^{m}+\mu _{i}^{m}/f_{g}^{{m2}}+b_{{g,i}}^{R} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{b} _{g}^{m}+e_{{g,i}}^{m} \hfill \\ L_{{g,i}}^{m}=\rho _{i}^{m}+dt_{i}^{R} - dt_{{}}^{m} - \mu _{i}^{m}/f_{g}^{{m2}}+B_{{g,i}}^{R} - B_{g}^{m}+\lambda _{g}^{m}N_{{g,i}}^{m}+\varepsilon _{{g,i}}^{m} \hfill \\ \end{gathered} \right. \hfill \\ C\left\{ \begin{gathered} P_{{g,i}}^{n}=\rho _{i}^{n}+dt_{i}^{C} - dt_{{}}^{n}+\mu _{i}^{n}/f_{g}^{{C2}}+b_{{g,i}}^{C} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{b} _{g}^{n}+e_{{g,i}}^{n} \hfill \\ L_{{g,i}}^{n}=\rho _{i}^{n}+dt_{i}^{C} - dt_{{}}^{n} - \mu _{i}^{n}/f_{g}^{{C2}}+B_{{g,i}}^{C} - B_{g}^{n}+\lambda _{g}^{C}\tilde {N}_{{g,i}}^{n}+\varepsilon _{{g,i}}^{n} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$
(4)

where G, R, and C refer to the GPS, GLONASS, and BDS systems, respectively, and \(l\), \(m\), and \(n\) indicate one satellite for each corresponding system. The GLONASS satellite code hardware bias is \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{b} _{g}^{m}=b_{g}^{m} - \Delta b_{{g,i}}^{m}\), which has absorbed the satellite-dependent bias from the receiver. Note that the hardware delay is the same for each receiver, and the subscript \(i\) is thus dropped for \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{b} _{g}^{m}\). We neglect the satellite-dependent part in the GLONASS phase hardware bias (Sleewaegen et al. 2012) and write the phase hardware bias as \(B_{{g,i}}^{R}\). \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{b} _{g}^{n}\) is the BDS satellite hardware delay, which has been corrected by the Wanninger and Beer (2015) model, and we note that the constant bias \(C_{g}^{s}\) is absorbed into \(\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{b} _{g}^{n}\). The ambiguity has absorbed \({\text{CPB}}_{{g,i}}^{{}}\), which is denoted by \(\lambda _{g}^{G}\tilde {N}_{{g,i}}^{l}\) and \(\lambda _{g}^{C}\tilde {N}_{{g,i}}^{n}\).

Equation (4) is the basis of the multi-GNSS PPP-IAR in the present study. The undifferenced wide- and narrow-lane FCB can be estimated by the strategy proposed in Laurichesse et al. (2009). Because of the inter-system hardware and time bias, individual wide- or narrow-lane receiver FCBs should be estimated for each system. To achieve consistency with FCB products, PPP users should use receivers with the same hardware configuration as the reference stations. The same BDS satellite SICB correction model, which is consistent with the wide-lane FCB products, should also be used.

GEO satellite orbit error estimation

The large orbit error of GEO satellites must be accounted for, or it will severely affect the narrow-lane FCB estimation and ambiguity fixing (Liu et al. 2017a). Taking satellite orbit error into account and denoting the orbit error vector as \((dx_{{}}^{k},dy_{{}}^{k},dz_{{}}^{k})\), the ionospheric-free (IF) observations can be rewritten as:

$$\begin{gathered} P_{{c,i}}^{k}=\rho _{i}^{k}+dt_{i}^{{}} - dt_{{}}^{k}+d\rho _{r}^{k} \hfill \\ L_{{c,i}}^{k}=\rho _{i}^{k}+dt_{i}^{{}} - dt_{{}}^{k}+d\rho _{r}^{k}+N_{{c,i}}^{k} \hfill \\ \end{gathered}$$
(5)

where \(d\rho _{r}^{k}=(l_{r}^{k},m_{r}^{k},n_{r}^{k}) \cdot (dx_{{}}^{k},dy_{{}}^{k},dz_{{}}^{k})=\cos \phi \cdot |(dx_{{}}^{k},dy_{{}}^{k},dz_{{}}^{k})|\) is the orbit error, \((l_{r}^{k},m_{r}^{k},n_{r}^{k})\) is the direct cosine unit vector of the satellite, \(\phi\) is the included angle of the related vectors, and \(\left| \cdot \right|\) represents the modulus of a vector. We call \(|(dx_{{}}^{k},dy_{{}}^{k},dz_{{}}^{k})|\) the 3D orbit error and \(\cos \phi\) the mapping coefficient.

Figure 1 shows that for two ground stations A and B that tracked satellite K, we can write the difference in mapping coefficient between A and B as

Fig. 1
figure 1

Effect of orbit error on two tracking stations A and B. \(K\) represents the actual satellite position and K′ the biased position. \({K^{''}}\) is the projection of K′ onto the plane A–B–K. \(\alpha\) is \(\angle K^{\prime}KK^{\prime\prime}\), \(\beta\) is \(\angle AKK^{\prime\prime}\), \(\theta\) is \(\angle AKB\), \({\phi _1}\) is \(\angle K^{\prime}KA\), and \({\phi _2}\) is \(\angle K^{\prime}KB\)

Full size image
$$\Delta {\text{map}}_{{AB}}^{k}=\cos \alpha \cdot \left| {\cos \beta - \cos (\beta - \theta )} \right|$$
(6)

where \(\alpha \in [0,90]\) and \(\beta \in [0,180]\). To analyze the numerical range of (6), we can reformulate the equation as

$$\Delta {\text{map}}_{{AB}}^{k}=2 \cdot \cos \alpha \cdot \left| {\sin \frac{\theta }{2}} \right| \cdot \left| {\sin \frac{{2\beta - \theta }}{2}} \right| \leq 2 \cdot \left| {\sin \frac{\theta }{2}} \right|$$
(7)

The network used in Fig. 2, see section on data and processing strategy below, covers an area with a radius 350 km; we can, therefore, calculate the maximum \(\theta\) as 1.86° for MEO satellites and 1.13° for GEO and IGSO satellites. We thus obtain the maximum value of the expression in (6) as 0.0325 for MEO satellites and 0.0197 for GEO and IGSO satellites. Taking the 3D orbit error given by Lou et al. (2014), we can attain the maximum difference in orbit error for the narrow-lane ambiguity (with a wavelength of about 10 cm) as 0.034, 0.040, and 0.256 cycles for the MEO, IGSO, and GEO satellites, respectively. The effect of orbit error of MEO and IGSO satellites on narrow-lane FCB estimation can thus be neglected, whereas the orbit error of GEO satellites must be accounted for.

Fig. 2
figure 2

Distribution of stations used in China. Red points denote reference stations and blue the rover stations

Full size image

In PPP analysis for estimating satellite FCBs, because the receiver and satellite coordinates, as well as the satellite clock, have been fixed (Ge et al. 2008; Geng and Shi 2017b), the only estimated parameters are the receiver clock parameter, zenith tropospheric delay (ZTD) parameter, and float IF ambiguities. The satellite orbit error is correlated with these parameters. We can assign much less weight, i.e., by a factor of 50 in the present work, to the GEO observations, such that its orbit error will not affect the receiver clock and ZTD estimation. We can thus assume that the orbit error of GEO satellites will be absorbed entirely by the corresponding IF ambiguities. Thus, if the wide-lane ambiguity can be fixed with the Hatch–Melbourne–Wübbena (HMW) combination (Hatch 1982; Melbourne 1985; Wübbena 1985), which is unaffected by orbit error, the associated narrow-lane ambiguity is actually (Li et al. 2016)

$$\tilde {N}_{{n,r}}^{k}=N_{{n,r}}^{k}+\phi _{{n,r}}^{k} - \phi _{n}^{k}+\frac{{l_{r}^{k}}}{{\lambda _{n}^{k}}}dx_{{}}^{k}+\frac{{m_{r}^{k}}}{{\lambda _{n}^{k}}}dy_{{}}^{k}+\frac{{n_{r}^{k}}}{{\lambda _{n}^{k}}}dz_{{}}^{k}$$
(8)

With a tracking network, and after fixing all the integer ambiguities in (8), the narrow-lane FCBs and satellite orbit errors can be estimated together using the least squares adjustment method (LSQ). As revealed by (7), we cannot estimate true orbit errors but the part that affects the narrow-lane FCB estimation over the area that the reference network covers. Equation (7) shows that the maximum difference in the mapping coefficient depends on the angle \(\theta\). With the revolution of the satellite, when its elevation angle is very low, \(\theta\) may be nearly zero, which means that the coefficient of the orbit error parameter in (8) will be nearly identical for all tracking stations. This will cause a singularity in the LSQ estimation using (8), and we, therefore, add an initial constraint on all orbit parameters:

$$(dx_{{}}^{k},dy_{{}}^{k},dz_{{}}^{k})=(0,0,0),{\text{ }}{\sigma ^k}$$
(9)

where \({\sigma ^k}\) is the variance of the constraint, which was set to \(\sigma =10\,{\text{m}}\) in our study. The orbit error is then used to correct the satellite orbit product. Finally, the FCB products together with the satellite orbit and clock products are broadcast to users for PPP ambiguity fixing.

Satellite clock bias estimation

In satellite clock estimation, the satellite code hardware bias is absorbed into the constant offset of each clock (Ge et al. 2012a). Because the analysis centers used a network of mixed receivers to estimate GLONASS satellite clock, the accuracy of the daily constant offset estimates will be poor (Song et al. 2014). Moreover, they do not use the same type of GLONASS receivers or the same SICB correction model for BDS as used in the present study, so the satellite code hardware bias that is absorbed into the satellite clock will not be the same as the bias shown in (4), which will cause a constant bias in the GLONASS and BDS clock. We, therefore, need to estimate the satellite clock bias of the clock used.

Assuming the station coordinates and satellite orbits are known and fixed in the satellite clock bias estimation, after applying the satellite clock corrections, the IF carrier phase and code observations can be expressed as:

$$\begin{gathered} G\left\{ \begin{gathered} P_{{c,i}}^{l}=\rho _{i}^{l}+dt_{i}^{G} - {\text{SY}}{{\text{S}}^l} \hfill \\ L_{{c,i}}^{l}=\rho _{i}^{l}+dt_{i}^{G} - {\text{SY}}{{\text{S}}^l}+\tilde {N}_{{c,i}}^{l} \hfill \\ \end{gathered} \right. \hfill \\ R\left\{ \begin{gathered} P_{{c,i}}^{m}=\rho _{i}^{m}+dt_{i}^{R} - {\text{SY}}{{\text{S}}^m} \hfill \\ L_{{c,i}}^{m}=\rho _{i}^{m}+dt_{i}^{R} - {\text{SY}}{{\text{S}}^m}+\tilde {N}_{{c,i}}^{m} \hfill \\ \end{gathered} \right. \hfill \\ C\left\{ \begin{gathered} P_{{c,i}}^{n}=\rho _{i}^{n}+dt_{i}^{C} - {\text{SY}}{{\text{S}}^n} \hfill \\ L_{{c,i}}^{n}=\rho _{i}^{n}+dt_{i}^{C} - {\text{SY}}{{\text{S}}^n}+\tilde {N}_{{c,i}}^{n} \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$$
(10)

where \({\text{SYS}}\) represents the constant bias for each satellite in the clock products. The satellite clock bias is estimated as a daily constant, and other parameters are estimated with the commonly used strategy in satellite clock estimation (Ge et al. 2012a).

The receiver clock bias and satellite clock bias in (10) are linearly dependent. To separate them, we add the constraints

$$\begin{gathered} \sum {{\text{SY}}{{\text{S}}^l}} =0 \hfill \\ \sum {{\text{SY}}{{\text{S}}^m}} =0 \hfill \\ \sum {{\text{SY}}{{\text{S}}^n}} =0 \hfill \\ \end{gathered}$$
(11)

Using this approach, we can estimate the daily satellite clock bias, which will be used to correct the satellite clock of each epoch.

PPP ambiguity resolution

The float estimate of the wide-lane ambiguity can be obtained by averaging the HMW combination over a few epochs. After applying the satellite wide-lane FCB, we still need to remove the receiver counterpart, which can be estimated by averaging the fractional parts of the related ambiguities (Liu et al. 2017a, b). We can then subtract the receiver wide-lane FCB from all the wide-lane ambiguity estimates to retrieve their integer nature:

$$\begin{gathered} N_{w}^{l}=\hat {L}_{w}^{l} - \phi _{w}^{G} \hfill \\ N_{w}^{m}=\hat {L}_{w}^{m} - \phi _{w}^{R} \hfill \\ N_{w}^{n}=\hat {L}_{w}^{n} - \phi _{w}^{c} \hfill \\ \end{gathered}$$
(12)

Then, the rounding decisions for WL ambiguity fixing can be made according to the probability calculated by either Dong and Bock (1989) or Blewitt (1989).

The LAMBDA method was used to search the narrow-lane ambiguities (Teunissen 1995), and the ratio test was used for validation (Han 1997). Before applying LAMBDA, we must separate the receiver FCB and receiver clock from the narrow-lane ambiguities (Ye et al. 2016). This can be done by fixing the ambiguity \({N_I}\) with the highest satellite elevation to its nearest integer \({N_0}\) as the reference, which can be expressed as an artificial observation:

$$\begin{gathered} N_{I}^{G}=N_{0}^{G},P_{0}^{G} \in \infty \hfill \\ N_{I}^{R}=N_{0}^{R},P_{0}^{R} \in \infty \hfill \\ N_{I}^{C}=N_{0}^{C},P_{0}^{C} \in \infty \hfill \\ \end{gathered}$$
(13)

where \({P_0}\) is the weight of this artificial observation; in practice, it can be set to \(10_{{}}^{6}\), for example. The reference ambiguity may be biased, but its effect can be absorbed into the receiver clock parameter and will not affect the integer ambiguity resolution or position results; for further details refer to Liu et al. (2017b).

Data and processing strategy

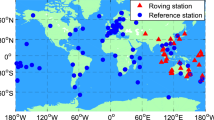
One week (DOY 8–14, 2014) of observation data sampled at 15 s from 45 stations were processed. Twenty stations were used as reference stations to generate the FCB products, while the remaining 25 stations were used as rover stations to perform PPP-IAR. All stations are equipped with Trimble NetR9 receivers with the same firmware version and antenna type. The station distribution is shown in Fig. 2.

The Positioning and Navigation Data Analyst (PANDA) software (Liu and Ge 2003) was modified to process the data. Final orbit and clock products generated at Wuhan University were used. We applied the absolute satellite and receiver phase center corrections (Schmid et al. 2007), phase windup effects (Wu et al. 1993), and station displacement models according to IERS 2010 conventions (Petit et al. 2010). The elevation cutoff angle was set to 7° for each system and the measurements were weighted using an elevation-dependent weighting strategy (Parkinson and Spilker 1996). To avoid high noise levels and large biases, the ambiguity was not fixed for satellites below 10° elevation. We computed the RMS values for each system at different elevation angle and visualized it in Fig. 3. This figure shows that after applying the clock bias correction, the code residuals of BDS declined to the same level as those of GPS. For GLONASS, the code residual also decreased but was slightly larger than those for GPS or BDS. The carrier phase measurements, which are the primary observables for PPP, appeared to be of similar quality for each system. We, therefore, set equal weights for the carrier phase observations of each system but reduced the weight of GLONASS code observations by a factor of 1.5 as compared with the GPS.

Fig. 3
figure 3

Elevation dependence of IF code and carrier phase residuals. It is seen that after clock bias correction, the code and carrier phase have comparable accuracy for each system

Full size image

Respective receiver clocks were estimated for each system, and a common tropospheric zenith wet delay estimated as a piece-wise constant every 60 min using the global mapping function (Boehm et al. 2006). The ambiguity parameters and static position parameters were modeled as constant, while the kinematic position parameters were considered white noise. In FCB estimation, the station coordinates are fixed to the weekly estimates. Because there is no accurate differential code bias (DCB) product for GLONASS satellites (Zhang et al. 2017), we used C1 and P2 code observations for GLONASS, instead of using mixed C1 and P1 observations. Each daily observation was split into 24 hourly datasets to perform PPP-IAR. Thus, if there is no loss of data, there are 168 hourly solutions for one station and 4200 for all stations. We assumed that we could fix the integer ambiguity correctly in daily PPP-IAR, thereby obtaining a “truth” with which to assess the correctness of the hourly PPP-IAR. The IFT of each hourly solution was recorded, and we calculated the cumulative distribution of the IFT and obtained the fixing percentage at different observation durations.

Experimental results and validation

In this section, we first analyze the contribution of the proposed strategy to narrow-lane FCB estimation. Then, PPP-IAR based on the improved orbit and FCB products is conducted.

FCB and orbit error estimation results

The wide- and narrow-lane FCB products are critical for PPP ambiguity resolution. In FCB estimation, the float wide- and narrow-lane ambiguities are taken as the observations, and the integer ambiguities, the receiver- and satellite-FCB and the orbit errors are the estimated parameters. After fixing the integer ambiguities, the FCBs and orbit errors can be estimated with LSQ method, and we can get the a posteriori residuals of the float wide- and narrow-lane ambiguities. The residuals are actually the fractional parts of the float ambiguity after removal of the estimated FCBs and orbit errors and can be used to evaluate the quality of the FCB estimation.

A statistical histogram of the residuals of the daily wide-lane float ambiguity is shown in Fig. 4. For GPS, IGSO, and MEO satellites, more than 95% of all wide-lane residuals are within ± 0.15 cycles, and more than 99% are within ± 0.25 cycles. For GLONASS satellites, the residuals are slightly larger, with only 75.7% within ± 0.15 cycle and 92.9% within ± 0.25 cycles. While for GEO satellites, only 65.1 and 84.4% of residuals are within ± 0.15 and ± 0.25 cycles, respectively. However, upon excluding satellites C04 and C05, which have low elevation angles, we can have 94.5 and 99.2% of the residuals within ± 0.15 and ± 0.25 cycles, respectively.

Fig. 4
figure 4

Distribution of a posteriori residuals of daily wide-lane ambiguities. Excluding C04 and C05 with low elevation, more than 98% of residuals are within 0.25 cycles for GPS, GEO IGSO, and MEO satellites, and 92% for GLONASS satellites

Full size image

Figure 5 shows the time series of narrow-lane residuals for GEO satellites obtained by the traditional FCB estimation method. Because the orbit error is small, the narrow-lane residuals of C01 and C03 are within ± 0.2 cycles, which barely meets the requirement of narrow-lane FCB estimation. For C02, C04, and C05, the respective residuals are within ± 0.4, ± 0.5, and ± 0.5 cycles, because the orbit error is large. Such large residuals mean that the estimated FCB has poor accuracy and cannot be used for PPP ambiguity resolution in the area.

Fig. 5
figure 5

A posteriori residuals of GEO narrow-lane ambiguities on DOY 09, 2014 obtained using the traditional method, with different colors representing different stations. Because of large orbit error, residuals for C04 and C05 are in the range of (− 0.5, 0.5)

Full size image

Figure 6 portrays the corresponding narrow-lane residuals of GEO satellites obtained by the method considering orbit errors. Compared with Fig. 5, the effect of orbit error on narrow-lane FCB estimation is eliminated upon using the proposed method; more than 98% of residuals are within ± 0.1 cycles for C01, C02, and C03. For C04 and C05, because the mean satellite elevation is respectively about 20° and 28°, the residuals are slightly larger, but within ± 0.2 cycles except for some outliers.

Fig. 6
figure 6

A posteriori residuals of GEO narrow-lane ambiguities on DOY 09, 2014 obtained using the new method, with different colors representing different stations. After considering orbit error, residuals are within ± 0.1 cycles for C01, C02, and C03, and within ± 0.2 cycles for C04 and C05

Full size image

Figure 7 depicts the corresponding estimated orbit errors for GEO satellites. The figure shows that the 3D orbit errors of C01 and C03 are within 1.3 and 2.3 m, respectively, whereas those of C02, C04, and C05 are about 3–4 m. This explains why a better result was obtained for C01 and C03 using the traditional method. Furthermore, the orbit error is stable over a short period and can be updated at intervals of 5 or 10 min.

Fig. 7
figure 7

Estimated GEO orbit errors on DOY 9, 2014, obtained using the new method. The large orbit error explains why the residuals are very large in traditional narrow-lane FCB estimation

Full size image

Figure 8 shows the distribution of the residuals in the estimates of the narrow-lane FCBs. More than 98% of the residuals are within 0.1 cycles for GPS, GLONASS, IGSO, and MEO satellites. Although the residuals are slightly larger for GEO satellites, of which only 96.8% are within 0.1 cycles, if we exclude C04 and C05 with low elevation angles, the percentage improves to 99.4%. In contrast, the distribution of the residuals without considering orbit error is more discrete: only 93.6% are within 0.2 cycles, even excluding C04 and C05.

Fig. 8
figure 8

Distribution of a posteriori residuals of narrow-lane ambiguities. Red bars represent residuals without considering orbit error. In this case, only 93.6% of the residuals are within 0.2 cycles, even excluding C04 and C05 that have low elevations

Full size image

To further validate that the estimated orbit error is actually orbit related, we also estimated orbit error for GPS satellites, which have a high orbit accuracy of about 2.5 cm (RMS). If the proposed method is effective and unaltered by other effects, the estimated orbit error should be near zero. That estimated error is shown in Fig. 9. It is seen that except for two satellites, orbit error in the X-direction exceeded 5 cm at low elevations. The errors of all the other satellites are within 2 cm in the X-, Y-, and Z-directions. Considering the above, we believe that the estimated orbit error in the present study is indeed orbit related.

Fig. 9
figure 9

Estimated orbit errors for GPS satellites on DOY 9, 2014. Because GPS satellites have a high orbit accuracy of about 2.5 cm (RMS), the estimated orbit errors are nearly zero

Full size image

Improvements to PPP-IAR performance

We calculated the fixing percentage in kinematic PPP for various observation durations (Fig. 10). Adding GLONASS or BDS can greatly improve the fixing percentage. If the GPS + GLONASS + BDS model is used, the fixing percentage further improves for an observation duration of 10 min. However, for the GPS + GLONASS + BDS solution, if GEO satellites are used without considering orbit error, the fixing percentage decreases to even much smaller than that of GPS-only solutions.

Fig. 10
figure 10

Fixing percentage (%) for different observation periods in kinematic PPP. Fixing percentages for GPS + GLONASS + BDS without considering GEO orbit error are much smaller than that of the GPS-only solution

Full size image

Table 1 gives the fixing percentages at typical observation durations of 6, 8, 10, and 15 min. Within 6 min, the fixing percentage for the GPS-only solution is only 14.7%. That percentage improves to 77.3% by adding GLONASS and to 88.4% by adding BDS. In contrast, if the GPS + GLONASS + BDS model is used, the fixing percentage reached 96.9% for a duration of 6 min and 99.0% for 8 min. However, if we do not consider the orbit error, the fixing percentage of GPS + GLONASS + BDS is only 17.3% for 15 min. This confirms that in performing GPS + GLONASS + BDS PPP-IAR, we must consider the GEO orbit errors.

Table 1 Fixing percentage (%) for typical observation periods in kinematic PPP
Full size table

The fixing percentages for different observation periods in the case of the static model are given in Fig. 11, and typical values are shown in Table 2. Compared with the case for kinematic PPP, the fixing percentage for the GPS alone within 6 min improved to 27.9%; while the percentage improves very little for combined GNSS solutions. It was also revealed that for the GPS + GLONASS + BDS static solution, if GEO orbit error is not considered, the fixing percentage also considerably declines, being only 19.5% for a 15-min observation period.

Fig. 11
figure 11

Fixing percentages (%) for different observation periods in static PPP. Fixing percentages for GPS + GLONASS + BDS without considering GEO orbit error are much lower than that of the GPS-only solution

Full size image
Table 2 Fixing percentage (%) for typical observation periods in static PPP
Full size table

Figure 12 shows the fixing percentage in kinematic and static PPP within 10 min for each station. For the kinematic solution, the fixing percentage of the GPS alone varies considerably from 15.5 to 51.4%. The percentage improves to 71.0–98.5% when using GPS + GLONASS and 84.7–99.2% when using GPS + BDS. When using GPS + GLONASS + BDS, the percentages exceed 98% except for only one station (with an average of 99.51%). When using the static solution, the minimum fixing percentage improves to 34.7% for the GPS alone, whereas it is 82.6% for GPS + GLONASS and 87.6% for GPS + BDS. However, if we do not consider GEO orbit errors, the fixing percentages for all stations are < 18.1% in the kinematic model and < 21.0% in the static model.

Fig. 12
figure 12

Fixing percentages of kinematic (top) and static (bottom) PPP within 10 min for each station. Fixing percentages for GPS + GLONASS + BDS without considering GEO orbit error are smaller than that of GPS-only solution for each station

Full size image

We calculated the RMS of position error in kinematic PPP-IAR at different times after the first fixed epoch, as shown in Fig. 13. For each solution type, the accuracy in the north and east directions remain constant with increasing observation duration. On average, the RMS in the north direction is 7.38, 4.94, 4.83 and 3.66 mm for GPS only, GPS + GLONASS, GPS + BDS and GPS + GLONASS + BDS, respectively, and 6.34, 4.64, 4.54 and 3.58 mm in the east direction.

Fig. 13
figure 13

Positioning RMS in kinematic PPP-IAR with different observation durations after the first fixed epoch. Because of its dependency on the zenith tropospheric parameter, accuracy of the upward direction showed major improvement with observation duration

Full size image

Regarding accuracy of the upward direction, there was a substantial improvement with observation duration. At the first epoch, the ambiguity was fixed, and RMS was 27.91, 28.95, 31.04, and 25.32 mm for the four solution types. When the duration was prolonged to 40 min, the RMS degraded considerably, to 19.37, 17.63, 18.81 and 15.12 mm. We believe that the upward direction is strongly correlated with the zenith tropospheric delay parameter, even if the ambiguity is fixed. Thus, the estimation relies on the accumulation of observations with different satellite geometry to separate them and thereby obtain a better estimate.

Conclusions

In the present work, we estimated the orbit error of GEO satellites together with the narrow-lane FCBs, and the orbit error was used to refine the orbit. It was demonstrated that after considering GEO orbit errors, more than 98% of the narrow-lane a posteriori residual were within ±0.1 cycles for each satellite type. Within 6 min, the fixing percentage for the GPS-only solution was only 14.7%; that percentage improved to 77.3% for GPS + GLONASS and 88.4% for GPS + BDS. However, if we used GPS + GLONASS + BDS without considering GEO orbit error correction, the fixing percentage greatly decreased, to 7.5% and 9.7% for 6 min and 8 min, respectively. In contrast, if the GEO orbit error was considered, the fixing percentage improved substantially, to 96.9% for a duration of 6 min, and 99.0% for 8 min. With the proposed strategy, the effect of GEO orbit error can be eliminated, achieving reliable and nearly instantaneous PPP-IAR using GPS + GLONASS + BDS data.

Although homogeneous receivers are used for GLONASS PPP-IAR, this will not affect the realization and validation of the proposed method. For GLONASS PPP-IAR with heterogeneous receivers, one can refer to Yi et al. (2016), Geng and Shi (2017) and Liu et al. (2017b, 2018). In our work, the FCB estimation and PPP-IAR were conducted in simulated real time, so the performance needs to be further validated in real time in future work.