1 Introduction

Beside GPS, the Russian GLONASS is currently another Global Navigation Satellite System (GNSS) with full operational capability that provides global positioning, navigation and timing services. Precise orbit determination (POD) is the prerequisite for high accuracy GNSS applications. From 1998, the GLONASS precise orbit products were developed with the International GLONASS Experiment (IGEX) (Willis et al. 1999). From 2001, the International GNSS Service (IGS) (Dow et al. 2009) established the International GLONASS Service Pilot Project (IGLOS-PP) (Slater et al. 2004). Through these efforts POD of GLONASS constellation has been gradually improved (Ineichen et al. 2001; Kuang et al. 2001; Romero et al. 2002; Weber et al. 2005) and its orbit precision reaches centimeter level recently. However, the GLONASS orbits precision could hardly reach that of GPS, both in terms of consistency among individual IGS analysis centers and discontinuity at overlapping day boundaries (Griffiths and Ray 2009; Fritsche et al. 2014; Jean and Dach 2015; Li et al. 2015). One of the major reasons is that the GPS POD solution is significantly enhanced due to its successful ambiguity resolution (Blewitt 1989; Dong and Bock 1989; Mervart 1995; Ge et al. 2005, 2006), whereas the GLONASS ambiguity resolution is rather difficult, especially for long baselines up to several thousand kilometers.

Since GPS adopts the code division multiple access (CDMA) and all GPS satellites transmit signals on the same frequency for each carrier band, the biases are similar for the same type of observables and can be eliminated by forming differences between satellites. The frequency division multiple access (FDMA) adopted in present GLONASS (ICD 2008) introduces inter-frequency bias (IFB) at the receiver-end in both code and phase observables, and the biases cannot be eliminated by differences between satellites (Pratt et al. 1998; Wanninger and Wallstab-Freitag 2007; Zinoviev et al. 2009; Schaer et al. 2010; Sleewagen et al. 2012). This prevents current ambiguity resolution methods for GPS long baselines being applied to GLONASS, in which the double-differenced (DD) wide-lane ambiguities derived from the Melbourne–Wübbena (MW) combination (Melbourne 1985; Wübbena 1985) and the narrow-lane ambiguities derived from the adjustment are sequentially fixed to integers. Besides the IFBs, another challenge in GLONASS ambiguity resolution is that unlike the GPS DD-ambiguities, the wavelength of the two GLONASS inter-station single-differenced (SD) ambiguities is different, which needs to be handled properly to recover the integer feature of the DD-ambiguities. In GLONASS modernization, new signals will adopt CDMA as in GPS (Revnivykh 2010). However, in the next few years, mainly FDMA signals are available for GLONASS. Moreover, it is definitely important to enhance the contribution of GLONASS historical data by implementing reliable ambiguity resolution for long baselines.

In order to increase the strength of the GLONASS solution, a number of studies have been carried out for GLONASS integer ambiguity resolution, which are mainly for Real-Time Kinematic (RTK) positioning. A variety of mathematical and stochastic modeling methodologies and specific ambiguity resolution strategies for GLONASS were systematically investigated in Wang et al. (2001). To address the different wavelengths of the two SD-ambiguities that form the DD-ambiguities, several studies express the phase observations in the unit of cycles instead of length and directly recover the integer feature of the DD-ambiguities. However, in this case receiver clock biases cannot be eliminated due to the different wavelength and must be estimated (Leick 1998; Pratt et al. 1998; Han et al. 1999). Another method is to directly estimate the SD-ambiguities and then transform the SD-ambiguities and their covariance matrix to that of DD-ambiguities for integer ambiguity resolution (Leick 1998; Wang 2000; Takasu and Yasuda 2009). These two types of mathematical modeling are demonstrated to have similar performance in GPS/GLONASS RTK from comparative studies (Li and Wang 2011; Al-Shaery 2012).

In the following review, we first investigate the properties of IFB and then its calibration. As for the properties of GLONASS receiver phase IFB, Pratt et al. (1998) and Wanninger and Wallstab-Freitag (2007) showed that it is linearly correlated to the frequency number, and thus can be represented by a constant offset and IFB rate with respect to the frequency number. Sleewagen et al. (2012) further demonstrated that the dominant linear correlation between phase IFB and the frequency number is caused in the digital signal process of the receivers according to the linear relationship. Wanninger (2012) showed that the phase IFBs in L1 and L2 are similar in unit of length and receivers from the same manufacturer show similar values. It was also demonstrated that the phase IFBs are very stable and do not change considerably even over a 6-month period, with differences smaller than 2 mm for 92 % of the receivers. As for the properties of the GLONASS receiver code IFB, Kozlov et al. (2000) demonstrated that it has no obvious pattern of magnitude with frequency numbers. Reußner and Wanninger (2011) showed that the code IFB is mainly frequency dependent, but cannot be modeled with a simple modeling function. Large differences exist even between receivers of the same type. Shi et al. (2013) demonstrated that code IFBs are stable over time and are receiver firmware individual and antenna individual. Also the code IFBs cannot be precisely modeled by a simple linear or quadratic function and thus should be addressed for individual satellites, as they may vary even on the same frequency. There is no evident proof that the code IFBs in L1 and L2 have similar values.

Banville et al. (2013) proposed an effective approach to fix GLONASS ambiguity in short baselines without external IFB calibration. However, the mandatory condition is that two GLONASS satellites with adjacent frequency numbers are observed simultaneously and the solution is weaker compared to those using external calibration. As for the calibration of GLONASS receiver phase IFB, it is shown that the phase IFB can be precisely estimated for baselines shorter than 15 km (Zhang et al. 2011; Al-Shaery et al. 2013; Tian et al. 2015) and for baselines of several hundred km (Wanninger 2012). It should be mentioned that for short baselines the atmospheric delay between two stations can be eliminated in between-station differences, while for baselines of several hundred kilometers the atmospheric delay correlation between two stations, especially the ionosphere delay correlation, can be utilized for ambiguity resolution (Schaffrin et al. 1988). However, this atmospheric delay correlation becomes weaker and weaker when the baselines length increases. Among the calibration methods for phase IFB, Tian et al. (2015) developed a method using particle filter with likelihood function derived from the fixing RATIO (Teunissen 1995; Teunissen and Verhagen 2009), based on the fact that the closer the IFB rate value is to its true value, the larger the fixing RATIO will be. It was demonstrated that using this method, the phase IFB rate can be precisely estimated just with GLONASS data of a few epochs. As for the calibration of the GLONASS receiver code IFB, Reußner and Wanninger (2012) showed that the code IFB is much more difficult to handle. Therefore, for precise point positioning (PPP) (Zumberge et al. 1997) integer ambiguity resolution (Collins 2008; Ge et al. 2008; Laurichesse et al. 2009; Bertiger et al. 2010; Geng et al. 2010, 2012) using GLONASS observations, instead of using WM combination, wide-lane ambiguity resolution using the pure phase combination is recommended. Yi (2015) showed that for GLONASS PPP integer ambiguity resolution, the code IFB can be calibrated using MW combination; however, for some receivers it cannot be estimated precisely and thus can hardly be used in the wide-lane ambiguity resolution. To avoid the code IFB calibration and the wide-lane ambiguity resolution using MW combination, the ionosphere-free ambiguities are transformed into a combination with a wavelength of about 5.3 cm (Dai 200; Roßbach 2000), so that the ambiguity resolution can be directly carried out without the code IFB calibration. Using this kind of combination ambiguity and applying the phase IFB correction from Wanninger (2012), a GLONASS integer ambiguity resolution with the fixing-rate of about 57 % can be realized for regional kinematic PPP.

As for the GLONASS ambiguity resolution for long baselines, it is well known that through the calibration of phase IFB and usage of IGS ionospheric grid models (global ionospheric maps-GIM), single-differenced (SD) GLONASS ambiguity resolution for baselines of several hundred kilometers can be achieved (Wanninger 2012). In the IGS data processing at CODE (Center for Orbit Determination in Europe), for baselines shorter than 200 km, GLONASS ambiguity resolution is enabled for all satellites, whereas for longer baselines but not longer than 2000 km only ambiguities of the same frequency numbers are considered in order to improve the orbit quality (Dach et al. 2012). However, most of the IGS analysis centers have not yet implemented the GLONASS ambiguity resolution most likely due to its complexity and limited benefit.

Based on the above investigations on the GLONASS mathematical modeling, the characteristics of code and phase IFBs and their calibration methods, a new ambiguity resolution approach is developed for GLONASS POD, in which the defined double-differenced ionosphere-free linear combination ambiguities for baselines up to several thousand kilometers are fixed to integers after accurately calibrating the phase IFB using particle filter. It is demonstrated that the approach can achieve a fixing-rate of about 85.6 % even for baselines longer than 2000 km. After ambiguity resolution, the GLONASS orbits are substantially improved in terms of reduction of the discontinuity at overlapping day boundaries.

This article is organized as follows: Sect. 2 presents the GLONASS mathematical model and the new ambiguity resolution approach. Section 3 describes the validation experiment and Sect. 4 analyses the performance of the approach and the improvements in the GLONASS orbits after ambiguity resolution. Conclusions are given in Sect. 5.

2 The new method

We first introduce the mathematical model of the GLONASS POD data processing and then present the new ambiguity resolution approach. Afterwards the proposed phase IFB calibration procedure and ambiguity resolution strategy are discussed in detail.

2.1 Basic observation equations

The observation equations for GLONASS code and phase observations can be expressed as

$$\begin{aligned} P_{a,n}^i&=\rho _a^i -c( {dt^i-dt_a})+I_{a,n}^i+T_a^i+\delta _{a,n}^i +\xi _{a,n}^i\end{aligned}$$
(1a)
$$\begin{aligned} L_{a,n}^i&=\lambda _n^i \phi _{a,n}^i =\rho _a^i -c( {dt^i-dt_a })-I_{a,n}^i+T_a^i \nonumber \\&\quad +\lambda _n^i B_{a,n}^i +\gamma _{a,n}^i +\varepsilon _{a,n}^i \end{aligned}$$
(1b)

with P,L as the code and phase measurement in unit of length, respectively; \(\lambda \) is the wavelength; \(\phi \)is the phase measurement in unit of cycle; i and a are the index for satellites and receivers, respectively; \(n=1, 2\) for the frequency bands of L1 and L2; \(\rho \) is the geometric distance between the satellite and receiver antenna phase centers; c is the speed of light in vacuum; \(dt^i\) and \(dt_a \) are the satellite and receiver clock offset, respectively; I and T are the ionospheric and tropospheric delays; \(\delta _n \)is the IFB for code; \(B_n \) is the unknown phase ambiguity; \(\gamma _n \) is the IFB for phase; \(\xi \) and \(\varepsilon \) are the measurement noise for range and phase, respectively.

In general, we assume that the undifferenced ionosphere-free code \(P_{c}\)and phase \(L_{c}\)observations are used in POD data processing (Zumberge et al. 1997), and the observation equations are

$$\begin{aligned}&P_{a,n}^i=\rho _a^i -c( {dt^i-dt_a})+T_a^i+\delta _{a,c}^i +\xi _{a,c}^i\end{aligned}$$
(2a)
$$\begin{aligned}&L_{a,c}^i =\rho _a^i -c( {dt^i-dt_a })+T_a^i +\lambda _1^i B_{a,c}^i +\gamma _{a,c}^i +\varepsilon _{a,c}^i\nonumber \\ \end{aligned}$$
(2b)

with \(\delta _c \)the IFB for \(P_{c} \); \(B_c \) the ionosphere-free phase ambiguity; \(\gamma _c \) the IFB for \(L_{c} \).

For ambiguity resolution, the ionosphere-free ambiguity \(B_{a,c}^i \) is usually expressed by the wide-lane ambiguities \(B_{a,w}^i \) and narrow-lane ambiguities \(B_{a,1}^i \) (Dong and Bock 1989; Ge et al. 2008) as following, where \(B_{a,w}^i =B_{a,1}^i -B_{a,2}^i \)

$$\begin{aligned} B_{a,c}^i =\frac{f_1^i f_2^i }{f_1^{i2} -f_2^{i2} }B_{a,w}^i +\frac{f_1^i }{f_1^i +f_2^i }B_{a,1}^i \end{aligned}$$
(3)

   Usually in GPS ambiguity resolution for long baseline, wide-lane ambiguities are first fixed based on the MW combination, whereas narrow-lane ambiguities are derived based on the fixed wide-lane and the estimated ionosphere-free ambiguities and then are fixed accordingly.

2.2 Ionosphere-free ambiguity resolution

Both \(B_{a,w}^i \) and \(B_{a,n}^i \) include integer ambiguity and uncalibrated phase delay (UPD) at the receiver and satellite (Blewitt 1989; Ge et al. 2008). Assume that the phase IFB has been precisely calibrated and corrected, and then the wide-lane and narrow-lane ambiguities can be expressed as follows with N for the integer ambiguity and \(\Delta \emptyset \) for the UPD at the receiver and satellite,

$$\begin{aligned}&B_{a,w}^i =N_{a,w}^i +\Delta \emptyset _{a,w} +\Delta \emptyset _w^i\end{aligned}$$
(4a)
$$\begin{aligned}&B_{a,1}^i =N_{a,1}^i +\Delta \emptyset _{a,1} +\Delta \emptyset _1^i \end{aligned}$$
(4b)

Equation (3) can be transformed to

$$\begin{aligned} \frac{f_1^i +f_2^i }{f_1^i }B_{a,c}^i =\frac{f_2^i }{f_1^i -f_2^i }B_{a,w}^i +B_{a,1}^i \end{aligned}$$
(5)

For GLONASS satellite i, the frequency in L1 and L2 is \(f_1^i =( {1602+0.5625*K(i)})\) MHz, \(f_2^i =( 1246\,+\,0.4375* K(i))\) MHz (ICD 2008), where K(i) is the frequency number. For any GLONASS satellite i, the ratio of the frequency in L1 and L2 is \(f_1^i :f_2^i =9:7\), and we can get \(\frac{f_1^i +f_2^i }{f_1^i }=\frac{16}{9}\) and \(\frac{f_2^i }{f_1^i -f_2^i }=3.5\) . Substitute the corresponding terms in Eq. (5) and multiply both sides of the equation by 2, we get

$$\begin{aligned} \frac{32}{9}B_{a,c}^i =7B_{a,w}^i +2B_{a,1}^i \end{aligned}$$
(6)

Define \(B_{a,e}^i =\frac{32}{9}B_{a,c}^i \) and insert Eq. (4a, 4b) into Eq. (6), we get

$$\begin{aligned} B_{a,e}^i \equiv \frac{32}{9}B_{a,c}^i =7( {N_{a,w}^i +\Delta \emptyset _{a,w} +\Delta \emptyset _w^i })+2(N_{a,1}^i +\Delta \emptyset _{a,1} +\Delta \emptyset _1^i ) \end{aligned}$$
(7)

Replace \(B_{a,c}^i \) with \(B_{a,e}^i \) in the ionosphere-free ambiguity term of Eq. (2b), we can get \(\lambda _1^i B_{a,c}^i =\frac{9}{32}\lambda _1^i B_{a,e}^i \). The wavelength of \(B_{a,e}^i \) is about 5.3 cm according to the following equation,

$$\begin{aligned} \lambda _e^i =\frac{\lambda _1^i \lambda _w^i }{7\lambda _1^i +2\lambda _w^i }=\frac{9}{32}\lambda _1^i \end{aligned}$$
(8)

where \(\lambda _w^i \), \(\lambda _1^i \) denotes wide-lane wavelength (\(\sim \)84 cm) and L1 wavelength (\(\sim \)19 cm), respectively.

According to Eq. (7), for DD-ambiguity between satellite i, j and station a, b, we can get the following equation, where the wide-lane and narrow-lane UPD terms at the receiver and satellite are eliminated

$$\begin{aligned} \Delta \nabla B_{ab,e}^{ij} =7\Delta \nabla N_{ab,w}^{ij} +2\Delta \nabla N_{ab,1}^{ij} \end{aligned}$$
(9)

We can see in Eq. (9) that the DD-ambiguity \(\Delta \nabla B_{ab,e}^{ij} \) must have integer feature since both wide-lane and narrow-lane DD-ambiguity are integer. More important is that from the definition of \(B_{a,e}^i \) in Eq. (7), it is the scaled ionosphere-free ambiguity. That means the ionosphere-free ambiguities can be transformed and the related DD-ambiguities can be fixed into integer.

\(\text{ B }_{a,e}^i \) is called extra-narrow-lane in Yi (2015). Actually this kind of ambiguity can be interpreted as the original or natural ionosphere-free linear combination ambiguity (Dai 200; Roßbach 2000). From Eq. (9), if the integer wide-lane can be estimated correctly, its wavelength is exactly that of the standard narrow-lane of about 10.5 cm. Otherwise, it still has integer feature but with a wavelength of half of the standard narrow-lane, i.e., approximately 5.3 cm, which then can also be interpreted as a new kind of ionosphere-free narrow-lane. According to the previous definition (Dai 200; Roßbach 2000), we call \(\text{ B }_{a,e}^i \) the ionosphere-free linear combination ambiguity in the following text.

Therefore, for GLONASS we can avoid the commonly used two-step ambiguity resolution for long baselines, where the wide-lane ambiguities are first fixed to integers and then the narrow-lane. We can directly compute \(\Delta \nabla B_{ab,e}^{ij} \) and its corresponding standard deviation \(\sigma \) and try to fix it to integer according to the probability function as follows Dong and Bock (1989)

$$\begin{aligned} P= & {} 1-\mathop \sum \limits _{n=1}^\infty \left[ \mathrm{erfc}\left( {\frac{n-( {\Delta \nabla B_{ab,e}^{ij} -I})}{\sqrt{2} \sigma }}\right) \nonumber \right. \\&\left. -\mathrm{erfc}\left( \frac{n+( {\Delta \nabla B_{ab,e}^{ij} -I})}{\sqrt{2} \sigma }\right) \right] \end{aligned}$$
(10a)
$$\begin{aligned}&\mathrm{erfc} ( x)=\frac{2}{\sqrt{\pi }}\mathop \smallint \nolimits _x^\infty e^{-t^2}\mathrm{d}t \end{aligned}$$
(10b)

where I is the nearest integer candidate for \(\Delta \nabla B_{ab,e}^{ij} \) to be tested. Taking the confidence level \(\alpha \) of the ambiguity resolution as 0.1 %, if the fixing probability P is bigger than \(1-\alpha \), then \(\Delta \nabla B_{ab,e}^{ij} \) be confidently fixed to the integer I, otherwise we leave it as its estimated real value. After successful ambiguity resolution, we can apply the fixed DD-ambiguity as tight constraint to the normal equation in the undifferenced processing and achieve the ambiguity fixed POD solution (Ge et al. 2005).

It is worth to point out that the new approach is suitable for post-processing of long-time observations, such as the IGS data processing. In such data processing, the DD-ambiguities are usually estimated based on long continuous observations and the observations are also accurately modeled, so that bias and STD of the ambiguity estimates are rather small and consequently they can be fixed to integer reliably even the wavelength is rather short. For its application to real-time and short period observations, further validation must be undertaken.

2.3 IFB rate estimation and calibration

From Eq. (2), in order to obtain DD-ambiguities with integer characteristic, the phase IFB should first be precisely calibrated and corrected. Be aware that code IFBs do not affect the integer feature of \(\Delta \nabla \text{ B }_{ab,e}^{ij} \). The code IFBs can be estimated for each receiver and satellite pair. Although phase IFBs are given by Wanninger (2012) for individual receiver manufacturers, we noticed that the IFBs of receivers from the same manufacturer could have differences of several mm and phase IFBs may change slightly over time. Therefore, we have to estimate and calibrate the IFBs with actual observations for ambiguity resolution. In the following, IFB always means receiver phase inter-frequency bias.

The IFBs for L1 and L2 have the similar value in units of length (Sleewagen et al. 2012; Wanninger 2012), thus the IFB term \(\gamma _c \) in Eq. (2b) in the ionosphere-free combination can be modeled as one parameter, which has the same value as in L1 and L2. According to the linear relationship between IFBs and the frequency numbers, the IFB term for the SD-ambiguity between satellite i and station \(\text{ a }\), b can be expressed as

$$\begin{aligned} \gamma _{ab}^i =K(i)\Delta \gamma _{ab}, \end{aligned}$$
(11)

where \(\gamma _{{ab}}^{{ i}} \) is the IFB term for the SD-ambiguity; \(\text{ K(i) }\) is the satellite frequency number; \({\Delta \gamma }_{{ab}} \) is the differenced IFB rate between the two receivers, i.e., the difference between the IFB for the two receivers on adjacent GLONASS frequencies (Wanninger 2012). Once \({\Delta \gamma }_{{ ab}} \) is known, the corresponding terms can be corrected and then the DD-ambiguity resolution can be performed.

Usually the closer the differenced IFB rate \({\Delta \gamma }_{{ ab}} \) is to its true value, the larger the fixing RATIO will be. Tian et al. (2015) demonstrated that a limited number of samples of \({\Delta \gamma }_{{ab}} \) can be defined and introduced one by one into the processing for integer ambiguity resolution. The best estimate of the IFB rate can be reliably found out according to the likelihood function derived from the resulted RATIO values with the rigorous estimation using the particle filter (Gordon et al. 1993; Kitagawa 1996; Doucet et al. 2001; Gustafsson et al. 2002).

Fig. 1
figure 1

Graphical distribution of the 140 IGS tracking stations used in the experiment, denoted by blue triangles

Full size image

In this study, we first apply the a priori phase IFB correction provided by Wanninger (2012) for each receiver according to the manufacturers, and then use the particle filter method (Tian et al. 2015) to estimate the remaining differenced IFB rate \({\Delta \gamma }_{{ab}} \) for each baseline. As demonstrated in Wanninger (2012), the phase IFB variations over a 6-month period are smaller than 2 mm for 92 % of the receivers. We can reasonably infer that the remaining \({\Delta \gamma }_{{ab}} \) is within the interval of [\(-2, 2\)] in unit of cm per frequency number (cm/FN). The samples of \({\Delta \gamma }_{{ab}} \) are defined to be uniformly distributed in the interval with the increment step of 0.5 mm/FN. After introducing the \({\Delta \gamma }_{{ab}} \) samples one by one and making the corresponding correction in Eq. (11), the ambiguity resolution for all selected DD-ambiguities \(\Delta \nabla B_{ab,e}^{xy}\) of the baseline can be performed using the LAMBDA method and get the fixing performance statistical parameter RATIO defined as (Teunissen 1995; Teunissen and Verhagen 2009)

$$\begin{aligned} \text{ RATIO }=\frac{\check{\sigma }^{'2}}{\check{\sigma }^2}=\frac{\Vert \hat{\varvec{b}} -\check{\varvec{b}^{\prime }}\Vert ^2{\varvec{Q}}_{\hat{\varvec{b}}}}{\Vert \hat{\varvec{b}}-\check{\varvec{b}}\Vert ^2{\varvec{Q}}_{\hat{\varvec{b}}}}, \end{aligned}$$
(12)

where \(\check{\sigma }^2\)and \(\check{\sigma }^{'2}\) are the weighted squared norm of the ambiguity residuals for the best integer ambiguity candidate \(\check{\varvec{b}}\) and the second best one \(\check{\varvec{b}}'\), respectively. Vector \(\hat{\varvec{b}}\) contains the float ambiguities and \({{\varvec{Q}}}_{\hat{\varvec{b}}} \) is the associated variance-covariance matrix, \(\Vert \cdot \Vert ^2{{\varvec{Q}}} \) is the weighted squared norm. For each independent baseline, we can get a time series of RATIO in all the daily POD solutions. As soon as the estimated IFB rate for a baseline has converged in the particle filter, for example its STD is smaller than a threshold, it can be fixed for ambiguity resolution.

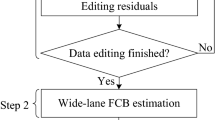
2.4 Data processing scheme of the new method

Based on the above discussion, the proposed data processing scheme is given in five steps.

  1. 1.

    Process data using the ionosphere-free code and phase observations as usual with the float ambiguities and repeat the data cleaning until no more data is removed and no new cycle slip is detected.

  2. 2.

    Transform the Normal Equation (NEQ) from the ionosphere-free ambiguities to the defined ionosphere-free linear combination ambiguities. In this step, before the transformation, the a priori phase IFB correction by Wanninger (2012) can be applied to the ionosphere-free ambiguities.

  3. 3.

    For each baseline, the related NEQ is retrieved from the network NEQ with the defined ionosphere-free linear combination ambiguities. Then, the IFB rate is estimated using the particle filter as described by Tian et al. (2015) for the baseline, and the converged estimate of the IFB rate of the last epoch is taken as known value for the IFB correction for the subsequent ambiguity resolution. The integer ambiguities corresponding to the estimated IFB rate are accepted as fixed DD-ambiguities of the baseline.

  4. 4.

    An independent set of the fixed DD-ambiguities is selected from the results in step 3. In step 3, the IFB rate estimation can be carried out for all possible baselines shorter than a certain length, for example 3000 km in this study, or just for a set of independent baselines. For the former one, an independent set of fixed ambiguities can be selected from all the fixed ambiguities, whereas for the latter one we can simply take all the fixed ambiguities. The former one will give more fixed constraints than the latter one but is rather time consuming.

  5. 5.

    Implementing all the independent fixed ambiguities as constraints to the network NEQ to get the fixed solution (Ge et al. 2005). In this way, the strength of the solution can be increased and consequently the orbit quality can be improved.

3 Experimental validation

In order to validate the proposed ambiguity resolution method and its impact on the products of GLONASS POD, an experiment was carried out using well distributed IGS stations with daily observations. Observations of 140 IGS stations from the day 270 to 300, 2013 were used in GLONASS POD. Figure 1 shows the geographical distribution of the selected stations with GLONASS tracking capability.

The Positioning And Navigation Data Analyst (PANDA) software (Liu and Ge 2003; Shi et al. 2008) was adapted for the GLONASS ambiguity resolution for POD processing in this study. All GLONASS observation segments shorter than 40 min were deleted. Ambiguity resolution for baselines shorter than 3000 km was carried out for GLONASS using the proposed method, as very few DD-ambiguities could be defined beyond this baseline length. The selection of independent baselines was carried out in accordance with that by Ge et al. (2005) without any restrictions on receiver types, i.e., baselines with mixed receiver types were also allowed. The DD-ambiguities fixing decision was made according to Eq. (10) (Dong and Bock 1989). The DD-ambiguity candidates can be arranged on baseline level and network level by their fixing probabilities for the independency check if all possible baselines are involved (Ge et al. 2005). The POD solution was carried out in accordance with the routine processing at the GFZ (German Research Center for Geosciences) IGS analysis center (Gendt et al. 2012). The important options of the processing strategy about observations and force models in the experiment are listed in Table 1.

Table 1 Observation and force models in the GLONASS precise orbit determination
Full size table
Fig. 2
figure 2

The estimated IFB rate and its STD for the baselines DYNG-SOFI (\(\sim \)500 km) (a), ALIC-TOW2 (\(\sim \)1500 km) (b), NKLG-STHL (\(\sim \)2500 km) (c). The estimates are with respect to the initial values by Wanninger (2012).

Full size image

4 Results

We first analyzed the stability of the estimated phase IFB rate. Then the ambiguity resolution effectiveness was investigated for all independent baselines in terms of the decimal fractional distribution of the DD-ambiguities and the fixing-rate. Afterwards, GLONASS orbits with and without the ambiguity resolution were compared with the IGS final orbit products. Finally, the overlapping RMS of the solution on the day boundaries and the satellite laser ranging (SLR) residuals were assessed to confirm the improvements of the GLONASS orbit quality.

4.1 Phase IFB rate stability

After applying the a priori phase IFB correction from Wanninger (2012), for each independent baseline the remaining IFB rate was estimated using the particle filter (Tian et al. 2015). As soon as the estimate has converged it can be fixed for ambiguity resolution. The IFB rate estimate was considered as converged when its STD was smaller than an empirical threshold of 0.2 mm/FN in the experiment. The IFB rate estimate converged for all the independent baselines, with the value ranging from about \(-\)4 to 3 mm/FN. As for the stability, most of the IFB rates had variations within 0.5 mm/FN for the experiment period, which is quite stable and agrees well with the results from Wanninger (2012). To show the stability of the estimated IFB rate, in Fig. 2 the results of the daily solutions are plotted for three baselines, of which the length is about 500, 1500, 2500 km, respectively.

Fig. 3
figure 3

The distribution of the fractional part of the DD ambiguities over baselines of various lengths: a below 1000 km, b from 1000 to 2000 km, c above 2000 km, and d all the baselines.

Full size image

For baseline (a), stations DYNG and SOFI were equipped with a Trimble NetR9 and a Leica GRX1200GGPRO receiver, respectively. For baseline (b), both stations were equipped with Leica GRX1200GGPRO. For baseline (c), stations NKLG and STHL were equipped with a Trimble NetR9 and a TPS NET-G3A receiver, respectively. The IFB rate estimate can be carried out regardless of the receivers of the same type or of mixed types. It can be seen that the time series of the IFB rate was relatively stable with variations within the range defined by the STD, and the IFB rate estimate could be introduced as known value for the ambiguity resolution.

4.2 Ambiguity resolution performance

Figure 3 shows the decimal fractional distribution of all the DD-ambiguities for the experiment period grouped according to the baseline length. The average RMS of the decimal fraction was about 0.133 cycles for all baselines and 0.126, 0.134, and 0.173 cycles for the baselines of length below 1000 km, between 1000 and 2000 km, and above 2000 km, respectively. The RMS of the decimal fraction distribution has positive correlation with the baseline length, which indicates that the geometrical error is the major factor that influences the ambiguity resolution performance. With the overall RMS of 0.133 cycles, the ambiguity resolution can be carried out for most of the DD-ambiguities.

Table 2 shows the number of independent DD-ambiguities and the percentage of fixed DD-ambiguities in daily solutions averaged for the experiment period. Overall the method has fixed 91.4 % of the independent ambiguities, which is slightly lower than that of GPS with the fixed percentage of more than 97 % (Ge et al. 2005). The fixing-rate is also correlated with the baseline length as indicated in the fractional distribution. For baselines longer than 2000 km, a fixing-rate of 85.6 % can be achieved.

Table 2 Averaged number of independent DD-ambiguities and fixing-rate in daily solutions
Full size table
Fig. 4
figure 4

Orbit comparison with IGS final orbit products with and without ambiguity resolution for the experiment period

Full size image

4.3 Orbit comparison with IGS final products

The GLONASS satellite orbits with and without ambiguity resolution were compared with the IGS final orbit products. After a seven-parameter Helmert transformation for removing possible systematic differences, the averaged RMS for the experimental period is shown in Fig. 4. The RMS of all the GLONASS satellites was almost the same of about 36 mm for the two POD solutions. We can also see that for several GLONASS satellites, the RMS got even larger with ambiguity resolution. One possible explanation could be that IGS final products could not be used to assess the GLONASS orbit improvement by the ambiguity resolution because it is mainly a combination of AC’s float solutions, although they are of high quality.

CODE is the first IGS AC that started to perform GLONASS ambiguity resolution as part of the IGS analysis and achieved a considerable number of fixed GLONASS ambiguities (Dach et al. 2012). The ambiguity-fixed GLONASS orbits in the experiment should be more consistent with the CODE orbits. In the following, the GLONASS satellite orbits with and without ambiguity resolution in the experiment were compared with the CODE final orbit products. Shown in Fig. 5, the overall RMS was reduced from about 44 mm for the float solutions to about 33 mm for the fixed solution, with the reduction percentage of about 25 %. The results match what we expect and indicate the practical applicability of the presented ambiguity resolution method.

Fig. 5
figure 5

Orbit comparison with CODE final orbit products with and without ambiguity resolution for the experiment period

Full size image

4.4 Orbit discontinuity at overlapping day boundaries

In order to evaluate more objectively the precision of IGS orbits, the discontinuity at day boundaries was adopted as a measure (Griffiths and Ray 2009), which is a more realistic indicator for orbit quality assessment. Similarly, we also assessed the quality of the estimated GLONASS orbits using the vector misclosures of the satellite positions at the overlapping day boundaries. Since the day-boundary misclosures are computed from orbits of two consecutive days, the inferred orbit precision for a single day should be small by about sqrt(2). The overlapping orbit RMS of the GLONASS satellites with and without ambiguity resolution is shown in Fig. 6.

Fig. 6
figure 6

Overlapping orbit comparison with and without ambiguity resolution for the experiment period

Full size image

The averaged RMS of the overlapping orbits for all the GLONASS satellites was improved by about 21.4 %, reduced from about 70 mm to about 55 mm after ambiguity resolution, and for individual satellites the largest improvement was by about 37.2 %. For comparison, the averaged RMS for all the GPS satellites was improved by about 32.4 % after ambiguity resolution for the experiment period. We can see that although the improvement for GLONASS is not as good as for GPS, the proposed ambiguity resolution method can already significantly improve the orbit quality.

4.4.1 Satellite laser ranging validation

Satellite laser ranging (SLR) observations are usually employed as external data resources to assess GNSS satellite orbit quality. The SLR range residuals, i.e., the differences between the SLR observation and the distance computed from microwave-based satellite positions, mainly reflect the orbit accuracy in the radial direction, as the maximum angle of incidence of a laser observation is about 14\(^{\circ }\) for the GLONASS satellites. The GLONASS satellites are equipped with laser retroreflector arrays (LRAs) and were observed by the SLR stations coordinated by the International Laser Ranging Service (ILRS) (Pearlman et al. 2002) for the experimental data set. The SLR station coordinates were fixed to the a priori reference frame SLRF2008. The station displacement models were applied consistently with the microwave-based solutions. The troposphere delays, relativistic effects, and the offset of the LRAs with respect to the satellites’ centers of mass were corrected in the SLR observations. There were 7932 normal points available after removal of outliers for the experimental data set. The mean offset, STD, and RMS of the residuals for the orbits with and without ambiguity resolution are given in Table 3. It is clear that both the bias and the STD were reduced by the ambiguity resolution, although the reduction is not as significant as in the overlapping RMS. Nevertheless, it also confirms the improvement of the orbit quality through the proposed ambiguity resolution method.

Table 3 Mean offset, STD, and RMS of the residuals with and without ambiguity resolution (AR)
Full size table

5 Conclusions

Due to the existence of IFB in both code and phase observations, the GLONASS integer ambiguity resolution for long baselines is hardly available, which prevents GLONASS to provide precise products, such as orbits and clocks, of the comparable quality as GPS. In this study, we developed a new ambiguity resolution approach especially for GLONASS global networks. The ionosphere-free ambiguities are directly transformed into the defined ionosphere-free linear combination ambiguities instead of wide-lane and narrow-lane ones, so that the related IFB rate can be estimated using the particle filter. Furthermore, after applying the estimated phase IFB correction, the defined double-differenced ionosphere-free linear combination ambiguities for baselines up to several thousand kilometers were fixed to integers.

The new approach was evaluated for GLONASS POD with one-month observations from 140 IGS stations. The results show that the phase IFB rate could be estimated precisely and was very stable with a variation of about 0.5 mm per frequency number. Applying the estimated phase IFB rate, overall 91.4 % of the independent ambiguities could be fixed, although the wavelength of the defined ionosphere-free linear combination ambiguity is only about 5.3 cm. Finally, the fixed solutions were achieved by introducing the fixed constraints into the float solutions.

From the comparison of the overlapping orbit differences with and without ambiguity resolution, the RMS of the overlapping orbits was reduced by about 21.4 % from 70 to 55 mm with the proposed ambiguity resolution method. The orbit validation with SLR observations also confirmed that the orbits were improved by ambiguity resolution, as the RMS of the SLR residuals was reduced.

Finally, the new integer ambiguity resolution approach can be applied to the IGS data reprocessing to enhance the strength of GLONASS solutions. Consequently, combined solutions of GPS and GLONASS could be improved for providing products of higher quality.