1 Introduction

In recent years, PPP-RTK, integer ambiguity resolution-enabled precise point positioning (PPP) (Teunissen and Khodabandeh 2015) has been developed to reduce the time to first fix (TTFF) and subsequently improve the positioning accuracy. The most crucial requirement is to recover the integer property of the un-differenced phase ambiguities which is corrupted by the existence of fractional cycle biases (FCBs). This in turn requires the determination of FCBs with as high precision as possible, so that FCBs can be removed from the phase ambiguity estimates. FCBs are attributed to signal delays in both receiver and satellite hardware and thus presumed to be hardware-dependent (Geng et al. 2010). The temporal property of the FCBs has been investigated since 1999 (Gabor and Nerem 1999). Li et al. (2014b) reported that the FCBs on either GPS frequency could change up to 0.2 cycles within 2 h. Ge et al. (2008) and Zhang and Li (2013), the wide-lane (WL) FCBs were modeled as a daily constant whereas the narrow-lane (NL) FCBs were modeled by a piece-wise constant within 10–15 min.

Table 1 summary of RMS values of various kinds of real-time orbits (Li et al. 2015b)
Full size table

Several PPP-RTK implementations have been proposed, by Ge et al. (2008), Laurichesse et al. (2009), Collins (2008), and Teunissen et al. (2010) with slight differences in the corrections applied and/or in the estimation employed (Shi and Gao 2014). The common strategy of correction estimation goes through the following sequential steps. First, the WL FCBs are estimated with the Hatch–Melbourne–Wübbena’ (HMW) combinations (Hatch 1982; Melbourne 1985; Wübbena 1985) and the WL ambiguities are fixed to integers. These integer WL ambiguities are then introduced into ionosphere-free (IF) combinations so that the IF ambiguities can be reduced to NL ambiguities. The NL ambiguities, FCBs or integer/ decoupled (Laurichesse et al. 2009; Collins 2008) satellite and receiver clocks, zenith tropospheric delay (ZTD) parameters are then estimated with satellite orbits and receiver coordinates fixed.

However, all these PPP-RTK implementations assume the ignorance of orbit errors, which could probably affect the precision of FCB or integer/decoupled satellite clocks. A variety of precise orbit products are available from different organizations with varying qualities. For example, the IGS rapid (IGR) and final orbit accuracy for post-mission applications is reported with a RMS of 2.5 cm. On the other hand, the IGS real-time service (RTS) orbit product (officially available on April 1, 2013) is accurate to 5 cm for GPS and 13 cm for GLONASS compared to IGS final orbit products (Hadas and Bosy 2015). Li et al. (2015b) generated 6-h predicted orbits for BeiDou and Galileo as alternative real-time orbits to implement real-time multi-constellation PPP. The statistical analysis showed that the radial and cross orbit RMS values are smaller than 10 cm for BeiDou and Galileo satellites while the along RMS values were larger than 10 cm. The specific summary of various real-time orbit products are listed in Table 1. Li et al. (2015a) also demonstrated the PPP ambiguity correct fixing rate decreases from 84.7 to 65.9 % when the RMS of GPS orbit errors increased from 6.6 to 12.8 cm. When these real-time orbits, especially Beidou and Galileo, are used, the estimated satellite FCB corrections will suffer from larger biases compared to post-processing orbit products. Hence the real-time orbit errors should be carefully considered otherwise ambiguity resolution and positioning performance will be significantly affected.

Though the minimization of the orbital errors on FCB estimates were proposed by Wang (2014) and verified by Li et al. (2014a), their method estimated each satellite orbit error by three additional parameters together with all station-specific ambiguities and tropospheric parameters. Thus the estimation strength as well as the estimation precision was weakened due to the increased parameterization burden. As a result, long convergence time up to several hours was required to obtain reliable estimates on FCB corrections. In this contribution, a cascaded method is proposed to effectively reduce the effect of the orbital errors on FCB estimates in three steps. First, the satellite and receiver clocks, float ionosphere-free ambiguities and tropospheric delays are estimated with station coordinates and satellite orbits fixed. Second, all WL and NL ambiguities at the reference stations are fixed by using the satellite FCBs without considering the orbit errors. The NL ambiguity bias caused by orbit errors is computed based on the real data and then used as a criterion of successful ambiguity fixing. Third, observational residuals in the first step are used to estimate the orbit errors. The improved FCBs considering the orbit errors are broadcast to users for PPP ambiguity resolution. The performance of the proposed methodology is validated with IGR and RTS orbits using two-scaler networks to consider the possible impact of inter-station distance on NL FCBs. To further investigate the potential feasibility of applying this method to improve the quality of satellite FCBs for emerging constellations, the predicted GPS orbits with RMS of more than 10 cm are simulated to process the aforementioned two networks.

The rest of the paper is organized as follows. Section 2 describes the method of improved NL FCB determination by cascadedly separating the orbit errors from original FCBs. Section 3 details the GPS measurements, satellite products, correction models, processing strategies used and experimental implementation in this study. Section 4 presents the performance of the proposed satellite NL FCB method compared to the original one form the perspective of recovering integer property of ambiguities and positioning accuracy. The investigation about potential feasibility of the COES method applying in other GNSS systems based on simulated results is also presented. Finally, conclusions are given in Sect. 5.

2 Methodology

PPP data processing for ambiguity resolution and FCB estimation at reference station is first introduced in this section. Then the impact of orbit errors on NL ambiguity resolution and FCB estimation after estimated satellite clock compensation is investigated. Finally, the NL FCB estimates with considering the orbit errors are elaborated.

2.1 PPP data processing for ambiguity resolution at reference station

Un-differenced GNSS code and phase observations after correcting the satellite and receiver phase center, site displacement effects, phase windup and relativistic effects (Kouba 2009) are denoted as

$$\begin{aligned} P_{r,j}= & {} \rho +d_\mathrm{orb} +e_m ( {dt^r+b_{P_j }^r })+g\tau +\mu _j \iota \nonumber \\&-\,dt^s-b_{P_j }^s +\varepsilon _{P_j } \nonumber \\ L_{r,j}= & {} \rho +d_\mathrm{orb} +e_m (dt^r+b_{L_j }^r )+g\tau \nonumber \\&-\,\mu _j \iota -\lambda _j N_{r,j} -dt^s-b_{L_j }^s +\varepsilon _{L_j } \end{aligned}$$
(1)

where the subscripts r denotes the receiver; \(j = 1,2\) denotes the L1 and L2 frequencies, respectively. Assuming that m \(\psi \) satellites are simultaneously tracked, \(P_{r,j} \) and \(L_{r,j} \) are the un-differenced code and phase observation vector; \(\rho \) is the vector of geometric distances between satellites and a receiver; \(dt^r\) is the receiver clock; \(dt^s\) is the satellite clock vector; \(d_\mathrm{orb} \) is the satellite orbit error; \(\tau \)is the Zenith Tropospheric Delays (ZTD) with its mapping matrix g; \(\iota \)is the first-order ionospheric delay on frequency \(L_{1}\) with \(\mu _j = f_1^2 /f_j^2 \); \(\lambda _j \) is the carrier phase wavelength; f is frequency; \(N_{r,i} \) is the integer ambiguity vector (cycle); \(e_m = \left[ {1\ldots 1} \right] ^T\); \(b_{P_j }^r \) is the receiver code biases and \(b_{P_j }^s \)is satellite code bias vector; \(b_{L_j }^r \) is the receiver FCB and \(b_{L_j }^s \)is the satellite FCB vector; \(\varepsilon _{P_j } \)and \(\varepsilon _{L_j } \) are the code and phase observation errors including multipath and noises.

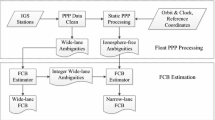
The purpose of processing network data is to generate the satellite FCBs, which are needed for users to recover the integer ambiguities of un-differenced observations. The network PPP data processing procedure is described as following.

Ambiguity resolution is conducted first for wide-lane, and then narrow-lane ambiguities. The float WL ambiguities \(B_{r,\mathrm{WL}} \) can be calculated simply by taking the time average of the HMW combination of the dual-frequency phase and code observations. \(B_{r,\mathrm{WL}} \) can be expressed as follows

$$\begin{aligned} B_{r,\mathrm{WL}} = N_{r,\mathrm{WL}} -{( {e_m b_\mathrm{WL}^r -b_\mathrm{WL}^s })} \big / {\lambda _\mathrm{WL} } \end{aligned}$$
(2)

where \(b_\mathrm{WL}^s \), \(b_\mathrm{WL}^r \)are the WL satellite FCB vector and the WL receiver FCB; \(\lambda _\mathrm{WL} \) and \(N_{r,\mathrm{WL}} \)are the WL wavelength and the ambiguity vector.

Assuming that station coordinates and satellite orbits are precisely known and fixed, satellite clocks \(dt_{P_\mathrm{IF} }^s \), receiver clock \(d_{P_\mathrm{IF} }^r \), float ionosphere-free ambiguities \(B_{r,\mathrm{IF}} \) and zenith tropospheric delay (ZTD) \(\tau \) can be estimated based on float-ambiguity PPP solution using IF phase and code combinations as follows

$$\begin{aligned} L_{r,\mathrm{IF}} -\rho= & {} \alpha _\mathrm{IF} L_{r,1} -\beta _\mathrm{IF} L_{r,2} -\rho = e_m dt_{P_\mathrm{IF}}^r -dt_{P_\mathrm{IF} }^s \nonumber \\&+g\tau -\lambda _\mathrm{IF} B_{r,\mathrm{IF}}+\varepsilon _{L_\mathrm{IF}} \nonumber \\ P_{r,\mathrm{IF}} -\rho= & {} \alpha _\mathrm{IF} P_{r,1} -\beta _\mathrm{IF} P_{r,2} -\rho = e_m dt_{P_\mathrm{IF}}^r\nonumber \\&-dt_{P_\mathrm{IF} }^s +g\tau +\varepsilon _{P_\mathrm{IF}} \end{aligned}$$
(3)

where \(P_{r,\mathrm{IF}}\, { \mathrm and }\, L_{r,\mathrm{IF}} \) are the code and phase IF combination; \(\alpha _\mathrm{IF} = f_1^2 /( {f_1^2 -f_2^2 }); \beta _\mathrm{IF} = f_2^2 /( {f_1^2 -f_2^2 });\lambda _\mathrm{IF} \) is the IF wavelength; \(B_{r,\mathrm{IF}} \) is the float IF ambiguity vector.

Then the float NL ambiguities \(B_\mathrm{NL} \)can be derived with the fixed WL ambiguity and the float ionosphere-free ambiguity as follows

$$\begin{aligned} \lambda _\mathrm{IF} B_{r,\mathrm{IF}}= & {} \alpha _\mathrm{IF} \lambda _1 B_{r,1} -\beta _\mathrm{IF} \lambda _2 B_{r,2}\nonumber \\= & {} \lambda _\mathrm{NL} B_{r,\mathrm{NL}} +\beta _\mathrm{IF} \lambda _2 N_{r,\mathrm{WL}} \end{aligned}$$
(4)
$$\begin{aligned} B_{r,\mathrm{NL}}= & {} ( {\lambda _\mathrm{IF} B_{r,\mathrm{IF}} -\beta _\mathrm{IF} \lambda _2 N_{r,\mathrm{WL}})} / {\lambda _\mathrm{NL} }\nonumber \\= & {} N_{r,1} -{( {e_m b_\mathrm{NL}^r -b_\mathrm{NL}^s })}/ {\lambda _\mathrm{NL} } \end{aligned}$$
(5)

where \(B_{r,\mathrm{NL}} \) is the float NL ambiguity vector; \(\lambda _\mathrm{NL} \) is the NL wavelength. \(b_\mathrm{NL}^r \) is the receiver FCB and \(b_\mathrm{NL}^s \)is the satellite FCB vector;

Second, the satellite WL and NL FCBs (\(b_\mathrm{WL}^s,b_\mathrm{NL}^s )\) are determined using the corresponding float ambiguities estimated from the network.

Let us assume that we have a network of n stations tracking m satellites. The float un-differenced ambiguities at each station are estimated as \(B_{i}\). For all the float ambiguity, we have an observation as follows (Li et al. 2012)

$$\begin{aligned} \left[ {{\begin{array}{l} {B_1 }\\ {B_2 }\\ \vdots \\ \vdots \\ {B_n }\\ \end{array} }} \right] = \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} I &{} &{} &{} &{} &{} {R_1 } &{} {S_1 } \\ &{} I &{} &{} 0 &{} &{} {R_2 } &{} {S_2 } \\ &{} &{} I &{} &{} &{} \vdots &{} \vdots \\ &{} 0 &{} &{} I &{} &{} \vdots &{} \vdots \\ &{} &{} &{} &{} I &{} {R_n } &{} {S_n } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {n_1 } \\ {n_2 } \\ \vdots \\ {n_n } \\ {b^r} \\ {b^s} \\ \end{array} }} \right] \end{aligned}$$
(6)

where \(R_{i }\) and \(S_{i }\) are the coefficient matrices of receiver and satellite FCBs. In matrix \(R_{i}\), all elements of the column corresponding to station i are \(-\)1/\(\lambda \) and the elements of the other columns are zero. For matrix \(S_{i}\), each line has one element of 1/\(\lambda \), the other entries are zero. \(N_{i}\) is the un-differenced integer ambiguity vector for station i.

Under the condition that all the integer ambiguities are known and that the receiver FCB at the reference station is fixed to zero, the satellite and receiver FCBs can be estimated by means of a least square from the following observation

$$\begin{aligned} \left[ {{\begin{array}{*{20}c} {B_1 -n_1 } \\ {B_2 -n_2 } \\ \vdots \\ \vdots \\ {B_n -n_n } \\ \end{array} }} \right] = \left[ {{\begin{array}{*{20}c} {R_1 } &{}\quad {S_1 } \\ {R_2 } &{}\quad {S_2 } \\ \vdots &{}\quad \vdots \\ \vdots &{}\quad \vdots \\ {R_n } &{}\quad {S_n } \\ \end{array} }} \right] \left[ {{\begin{array}{*{20}c} {b^r} \\ {b^s} \\ \end{array} }} \right] \end{aligned}$$
(7)

The specific data processing procedure is as follows. The receiver FCB at the reference station is assumed as zero. Then the nearest integers of the ambiguities at this station are the integer ambiguities, and the fractional parts are estimates of the corresponding satellite FCBs. When applying these satellite FCBs to the common satellites of the next station, the corrected ambiguities should have a very similar fractional part. The mean fractional parts of all the common satellites attribute to the receiver FCB. With this receiver FCB, FCBs of the newly appearing satellites at the station can be estimated. Repeating this procedure for all stations, we can obtain the approximate FCBs for all receivers and satellites.

After correcting the ambiguities with the FCBs, the integer property of ambiguity can be recovered, thus ambiguity-fixing can be attempted. Replacing the ambiguity parameters with their fixed values, the remaining parameters can be estimated. The FCB estimates are improved and will in turn help to resolve more integer ambiguities. The above procedure can be done iteratively until no more integer ambiguities can be fixed.

The approach described above is first applied to all the float un-differenced WL ambiguities to estimate the WL FCBs and integer WL ambiguities. With the integer WL ambiguities estimated, the float NL ambiguities are derived from the ionosphere-free ambiguities. Afterwards, the same approach is used to estimate the NL FCBs from the float NL ambiguities. For more details about ambiguity fixing, we recommend the reader to take a look at Laurichesse et al. (2009) or Li et al. (2012). For distinguishing with the proposed unbiased satellite NL FCBs with considering the orbit errors, the NL satellite FCB vector without considering orbit errors are denoted as \(b_{\mathrm{NL}, 0}^s \) in the later discussion.

2.2 Impact of orbit errors on NL ambiguity resolution

In Sect. 2.1, the NL ambiguities at the reference network are directly fixed without considering orbit errors. These fixed ambiguities can be used for further processing only if they are fixed to correct integer. To guarantee the correctness of ambiguity fixing, the impact of orbit errors in NL ambiguity resolution should be numerically analyzed, and used for establishing a criterion of successfully ambiguity resolution.

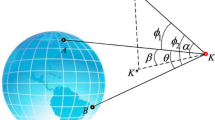
The satellite clocks, calculated with specific precise orbits are capable of compensating at least 96 % of the radial orbit errors, due to the fact that the maximum nadir angle at any satellite to any receiver visible on earth is about 15\(^\circ \) (Dousa 2010). The receiver clocks, which are common to the observations of all the satellites, are not able to compensate the errors in individual orbits. Ambiguity is considered to assimilate the remaining orbit error not compensated by the satellite clocks. The orbit errors are usually assessed using the user-range-error (URE) indicator, which provides the average range error in the line-of-sight (LOS) direction in a global scale. The URE for satellite k can be determined using the following approximate formula (Hauschild and Montenbruck 2009)

$$\begin{aligned} \mathrm{URE}^k = \sqrt{( {\mathrm{aRMS}_R^k })^2+b( {( {\mathrm{RMS}_A^k })^2+( {\mathrm{RMS}_C^k })^2})} \end{aligned}$$
(8)

The RMS contributions of along, cross and radial orbit errors to the URE are denoted as RMS\(_{A}\), RMS\(_{C}\) and RMS\(_{R.} a\) and b are scale factors. For GPS, \(a = \)0.98, \(b =\) 1/49. For GLONASS, \(a =\) 0.98, \(b =\) 1/45. For Galileo, \(a =\) 0.98, \(b =\) 1/61. For Beidou GEO/IGSO, \(a =\) 0.99, \(b =\) 1/126; for MEO, \(a =\) 0.98, \(b =\) 1/54 (Montenbruck et al. 2015).

Considering at least 96 % of the radial orbit errors are compensated by estimated satellite clock, and ignoring the partial along and cross errors compensated by satellite clock, the compensated effects of tropospheric correction and receiver clock, the maximum biases of NL ambiguities \(\delta N_{r,1}^k \) caused by orbit error can be computed as follows

$$\begin{aligned} \delta N_{r,1}^k = {\sqrt{( {(a-0.96)RMS_R^k })^2+b( {( {RMS_A^k })^2+( {RMS_C^k })^2})} } {/} {\lambda _\mathrm{NL}}\nonumber \\ \end{aligned}$$
(9)

Table 1 shows the maximum bias of NL ambiguity caused by various kinds of orbit errors calculated using Eq. (9). These biases achieve 0.06, 0.09–0.19, 0.14, 0.17, 0.13 and 0.78 cycles for GPS, GLONASS, Galileo, Beidou MEO/IGSO/GEO satellites. The calculated maximum biases of NL ambiguities are not significant enough to result in incorrect ambiguity except for Beidou GEO satellites. Hence, we can preliminarily say that most of the NL ambiguities can be reliably fixed even without considering the orbit errors. However, if the orbit errors are not completely separated from satellite FCBs, the satellite FCBs which mix with orbit error would affect the ambiguity fixing time and positioning accuracy at user stations. Hence, it is necessary to make further efforts to separate the orbit errors from satellite FCBs based on analysis in this section.

Fig. 1
figure 1

Distribution of the global network with 80 stations and the regional network with 38 stations located in North America

Full size image

2.3 Satellite NL FCB model considering orbit errors

Substituting the estimated satellite, receiver NL FCBs and NL integer ambiguities to Eq. (5), Eq. (5) can be rewritten as

$$\begin{aligned} l_{r,\mathrm{NL}} = d_{\mathrm{orb},r} -\delta b_{\mathrm{NL},0}^s -g\delta \tau \end{aligned}$$
(10)

where \(l_{r,\mathrm{NL}} = \lambda _\mathrm{NL} B_{r,\mathrm{NL}} -\lambda _\mathrm{NL} N_{r,1} +e_n b_\mathrm{NL}^r -b_{\mathrm{NL},0}^s \) is the observation-minus-correction (omc) term; \(\delta b_{\mathrm{NL},0}^s \) is the satellite directional-independent bias correction with respect to \(b_{\mathrm{NL},0}^s \); \(\delta \tau \) is the bias vector compensated by tropospheric correction.

The orbit error from satellite k to receiver r can be expressed as the function of directional cosines and orbit error in three components in Earth-Centered-Earth-Fixed (ECEF) frame.

$$\begin{aligned} d_{\mathrm{orb},r}^k = a_{1,r}^k \delta O_X^k +a_{2,r}^k \delta O_Y^k +a_{3,r}^k \delta O_Z^k \end{aligned}$$
(11)

where \(a_{1,r}^k \), \(a_{2,r}^k \), \(a_{3,r}^k \) are directional-dependent coefficients from satellite k to receiver r; we let \(b_{\mathrm{NL},1}^s = \left[ {\delta O_X^1,\ldots ,\delta O_X^m } \right] ^T,b_{\mathrm{NL},2}^s = \left[ {\delta O_Y^1,\ldots ,\delta O_Y^m } \right] ^T,b_{\mathrm{NL},3}^s = \left[ {\delta O_Z^1,\ldots ,\delta O_Z^m } \right] ^T;b_{\mathrm{NL},1}^s \), \(b_{\mathrm{NL},2}^s \), \(b_{\mathrm{NL},3}^s \) are the directional-dependent biases. At each epoch, un-differenced measurements for all observed satellites at all reference stations are stacked on the normal equation. Hence, the final normal equation after the accumulation of all measurements reads

$$\begin{aligned} \left[ {{\begin{array}{ll} {D_{11} } &{} {D_{12} } \\ {D_{21} } &{} {D_{22} } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {\hat{\delta }_{b_{_\mathrm{NL} }^s } } \\ {\hat{\delta }_\tau } \\ \end{array} }} \right] = \left[ {{\begin{array}{l} {w_1 } \\ {w_2 } \\ \end{array} }} \right] \end{aligned}$$
(12)

where \(\hat{\delta } _{b_{\mathrm{NL}}^s } = \left[ {{\begin{array}{llll} {\delta b_{\mathrm{NL},0}^s } &{} {b_{\mathrm{NL},1}^s } &{} {{\begin{array}{ll} {b_{\mathrm{NL},2}^s } &{} {b_{\mathrm{NL},3}^s } \\ \end{array} }} \\ \end{array} }} \right] \) is the satellite bias correction vector; \(\hat{\delta }_\tau \) is the tropospheric compensation vector; \(D_{11} = \sum \nolimits _{r = 1}^{r = n} {A_r^T Q_s^{-1} A_r } \), \(D_{12} = \sum \nolimits _{r = 1}^{r = n} {A_r^T Q_s^{-1} C_r } \), \(D_{21} = \sum \nolimits _{r = 1}^{r = n} {C_r^T Q_s^{-1} A_r } \), \(D_{22} = \sum \nolimits _{r = 1}^{r = n} {C_r^T Q_s^{-1} C_r } \), \(w_1 = \sum \nolimits _{r = 1}^{r = n} {A_r^T Q_s^{-1} l_{r,\mathrm{NL}} } \), \(w_2 = \sum \nolimits _{r = 1}^{r = n} {C_r^T Q_s^{-1} l_{r,\mathrm{NL}} } \); \(A_r\) is the design matrix for satellite biases correction vector; \(C_r \) is the design matrix corresponding to the biases compensated by tropospheric correction; \(Q_s \) is the satellite elevation-dependent cofactor matrix of the m un-differenced observations, which can be expressed as (Gendt et al. 2003)

$$\begin{aligned} {Q_s}= & {} diag\left( {\begin{array}{*{20}{c}} {q_s^1}&\ldots&{q_s^m} \end{array}} \right) \nonumber \\&\times \left\{ {\begin{array}{*{20}{l}} {q_s^i = 1}&{}\quad {\theta \ge {{30}^{\circ }}}\\ {{{q_s^i = 1} / {(2\sin \theta )}}}&{}\quad {\theta < {{30}^{\circ }}} \end{array}} \right. , \; i = 1 \ldots m \end{aligned}$$
(13)

where \(\theta \) is the satellite elevation; \(q_s^i \) is the cofactor of the un-differenced observations. Finally, by inverting the normal matrix of Eq. (12), we obtain the estimated directional-dependent biases and tropospheric compensation

$$\begin{aligned} \left[ {{\begin{array}{*{20}c} {\hat{\delta }_{b_{L_\mathrm{NL} }^s } } \\ {\hat{\delta }_\tau } \\ \end{array} }} \right] = \left[ {{\begin{array}{*{20}c} {Q_{11} } &{}\quad {Q_{12} } \\ {Q_{21} } &{}\quad {Q_{22} } \\ \end{array} }} \right] \left[ {{\begin{array}{*{20}c} {w_1 } \\ {w_2 } \\ \end{array} }} \right] \end{aligned}$$
(14)

where the second matrix is the variance–covariance matrix. The directional-dependent component \(\delta b_{\mathrm{NL,} 0}^s \) is used to correct the biased FCB while the three directional-dependent components are used to assimilate the orbit errors. The satellite NL FCB corrections with considering orbit errors at the user station \(b_{L_{u,\mathrm{NL}} }^s \) can be written as

$$\begin{aligned} b_{u,\mathrm{NL}}^s = b_{\mathrm{NL},0}^s +\delta b_{\mathrm{NL},0}^s +a_{1,u} b_{\mathrm{NL},1}^s +a_{2,u} b_{\mathrm{NL},2}^s +a_{3,u} b_{\mathrm{NL},3}^s \end{aligned}$$
(15)

The proposed NL FCB method represents not only the actual satellite NL FCBs but also the corresponding orbit errors. Hence the performances at both server and client rover side can be improved using this method.

Fig. 2
figure 2

IGS RTS GPS orbit RMS on 2014 doy 103

Full size image

3 Data and model

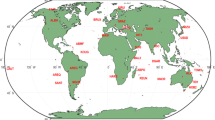
In order to demonstrate the performance of the proposed methodology, the regional and global networks shown in Fig. 1 were used for experiments and numerical analyses. In the regional network, 24-h GPS data with 30-s observation intervals at 38 stations in North America were collected on DOY 103, 2014. 28 stations denoted by red triangles were selected to estimate satellite FCBs. The remaining 10 stations denoted by green triangles were treated as user stations to assess PPP AR. For the global network, 24 h GPS data with 30 s observation intervals at 80 stations around the world were collected whereas 60 stations denoted by red circles were selected to estimate satellite FCBs. The remaining 20 stations denoted by green circles as user stations. The IGS RTS orbit products were downloaded from IGS03 stream by using the NTRIP Client software BNC provided by BKG (2013) while the IGS final products were used as reference for assessing the IGS RTS products accuracy.

For the measurement modeling, we applied the absolute phase center offset model (Schmid et al. 2007), the phase-wind up effects (Wu et al. 1993) and the models for site displacement effects proposed by the International Earth Rotation and Reference Systems Service conventions 2010 (Petit and Luzum 2010). The elevation cut-off angle was 10\(^\circ \) and an elevation-dependent weighting strategy was applied to the measurements.

The regional and global networks were used to estimate satellite clocks and FCBs by fixing the IGS RTS and IGR orbits. The station ‘bake’ shown as blue triangle was selected as the reference station in the regional network while the stations ‘urum’, ‘algo’, ‘karr’ and ‘unsa’ shown as blue circles were selected in the global network. The NL FCBs were estimated with and without considering the orbit errors. We processed the GPS data at all the stations in PPP mode and fixed the integer ambiguities. For brevity, the NL FCBs estimated without considering the orbit errors were named as “original” FCBs, and those estimated with considering the orbit errors were named as “improved” FCBs.

Table 2 RMS of IGS RT orbits in and out of eclipses (cm)
Full size table
Fig. 3
figure 3

Maximum biases of NL ambiguity caused by RTS GPS orbit errors

Full size image
Fig. 4
figure 4

Original NL FCBs for all satellites estimated with different orbits and networks

Full size image

4 Results and discussion

In this section, the performance of COES method was demonstrated with following aspects: (1) the accuracy of RTS GPS orbit products in and out of the eclipse durations and its impact on NL ambiguity resolution was evaluated. (2) The impact of the orbit errors on the quality of estimated original FCBs was analyzed by using RTS and IGR products with regional and global networks. (3) The improvement in recovering integer property of ambiguity based on the improved FCBs was demonstrated. (4) The position accuracy improvement based on the improved FCBs was demonstrated. (5) The simulation investigation was used to prove potential performance of the proposed method when satellite orbits with lower quality were fixed.

Fig. 5
figure 5

Estimated directional FCBs (satellite orbit errors) of RTS and IGR products

Full size image

4.1 Accuracy assessment of RTS orbits and its impact on NL ambiguities

In order to assess the accuracy of the RTS products, the orbit comparisons were made every 15 min, according to the interval of IGS final products. Figure 2 shows the RMS values of the RTS GPS orbits for each satellite while the summative results for the satellites in and out of eclipse are presented in Table 2. PRN 24, 27 are included in the RTS products while PRN 6, 10 and 30 are excluded from computation due to the long period of data loss. The non-eclipsing data subset does not contain the eclipsing periods, whereas the eclipsing data subset contains only epochs previously excluded. Based on the results shown in Table 2, the radial component is determined with accuracy of 2.2 cm for all GPS satellites. The accuracy of the cross-track component is 4.0 cm on average and two times worse for the along-track component. The along-track component is slightly less accurate during the eclipsing periods. The 3D orbit accuracy for GPS is 5.3 cm. During the eclipsing periods, the accuracy of the products becomes slightly worse.

Figure 3 presents the maximum biases of NL ambiguities for all satellites caused by RTS GPS orbits. It can be seen the 68\(\mathrm{th}\) percentile of ambiguity biases caused by orbit errors using (8) is around 0.05 cycles for satellites out of eclipse while 95\(\mathrm{th}\) percentile of those are about 0.1 cycles. For satellites in eclipse, both of those two values slight increase. Even though, the 95\(\mathrm{th}\) percentiles of ambiguity biases are smaller than 0.15 cycles at most time. Therefore, most of NL ambiguities can be finally correctly fixed without considering the orbit errors. In this study, the critical value of the biases caused by orbit errors is set to 0.15 cycles. Only when the biases are smaller than 0.15 cycles, the corresponding ambiguities are used to compute the improved FCBs.

Fig. 6
figure 6

Histogram of the NL ambiguity fractions applying the original FCBs estimated with regional and global network

Full size image
Table 3 Distances between reference station and the other stations in networks
Full size table
Table 4 RMS (cycle) and distribution of NL ambiguity fractions applying original and improved FCBs
Full size table

4.2 Impact of orbit errors on the estimated NL FCBs

The original FCBs for all satellites estimated from regional and global networks with ambiguity resolution by fixing RTS and IGR orbits are presented in Fig. 4. It can be seen that the magnitudes of all the original FCBs are overall consistent. Compared to the original FCBs with the IGR orbits, the original FCBs with RTS orbits presents much larger variations. Similarly, the variations of original FCBs estimated from the global network are larger than those from the regional network. One possible explanation for the larger variations is that the satellite FCBs are actually contaminated by the orbit errors. Besides, the impact of orbit errors on FCBs is affected by the scale of the network.

Table 5 RMS of position errors with float and fixed solutions applying the original and improved FCBs (cm)
Full size table
Fig. 7
figure 7

Position errors with float and fixed solutions based on original and improved FCBs

Full size image

The orbit errors for each satellite in LOS direction vary with stations and their variation increases with distances between stations. It is well established that the original FCBs are smoothed (roughly averaged) results of the data from multiple stations, which only assimilate the average part of LOS orbit errors in network. Thus, the original FCBs cannot fully describe the instantaneous variation of these orbit errors. On the other hand, the improved approach estimates separate orbit error components so that LOS orbit errors can be recovered at different stations. The estimated directional FCBs (satellite orbit errors) for RTS and IGR GPS products are shown in Fig. 5. The estimated RTS orbit errors are significantly larger than the IGR orbit errors so that the RTS orbit errors have much more impact on satellite FCBs. This result is consistent with a larger variation of FCBs with a global network and RTS orbits.

Fig. 8
figure 8

GSRT orbit RMS on doy 103, 2014

Full size image

4.3 Improvement in recovering integer property of ambiguities

To evaluate the quality of the satellite FCBs, the NL float ambiguity fractions corrected by the FCBs were computed. Three kinds of satellite FCBs including original FCBs, improved FCBs with RTS orbits and original FCBs with IGR orbits were used to derive the ambiguity fractions. Figure 6 illustrates the histograms of these NL ambiguity fractions corrected by the FCBs estimated from the regional and global networks. Table 3 lists the distances between the reference stations used for FCB estimation and the other stations. In the regional network, the average distance from the reference station to the other stations is 1990 km. 74.1 and 87.5 % of the NL ambiguity fractions corrected by original FCBs with RTS orbits are smaller than 0.15 and 0.25 cycles. These values increase to 81.6 and 93.3 % when the original FCBs with IGR orbits are applied to the float NL ambiguities. Moreover, 81.9 and 93.5 % of the NL ambiguity fractions are smaller than 0.15 and 0.25 cycles when the improved FCBs with RTS orbits are applied. As shown in Table 4, RMS of NL ambiguity fractions corrected by original FCBs with the IGR orbits instead of the RTS ones is improved by 20.1 % from 0.16 to 0.13 cycles. With the improved FCBs estimated with RTS orbits, the NL ambiguity fractions also have a similar RMS of 0.13 cycles.

Table 6 RMS values of GSRT orbits in and out of eclipses on doy 103, 2014 (cm)
Full size table
Fig. 9
figure 9

Histogram of the NL ambiguity fractions applying the original and improved FCBs with regional and global network

Full size image

In the global network, the average distances from the reference stations to the other stations are from 2876 to 4771 km, which are roughly two times longer than those in the regional network. With original FCBs, only 68.6 and 85.1 % of the NL ambiguity fractions with RTS orbits are smaller than 0.15 and 0.25 cycles. The percentages increase to 78.3 and 89.6 % with IGR orbits. However, these values can further increase to 81.9 and 93.5 % when the improved FCBs are applied to the float NL ambiguities. As shown in Table 4, the RMS of the NL ambiguity residuals after applying the improved FCBs decrease from 0.17 to 0.12 cycles, which indicates a 29.5 % improvement. Even compared to original FCBs with IGR orbits, the RMS value of NL ambiguity fractions also degrades by 20.0 %. These results show that the improved FCBs can effectively improve the integer property of ambiguity by fully separating orbit errors from the original FCBs.

Table 7 RMS, distribution of NL ambiguity fractions applying original and improved FCBs and position RMS
Full size table

4.4 Comparison of positioning accuracy based on original and improved FCBs

The kinematic positioning accuracy is significantly improved after the narrow-lane ambiguity resolution. In Table 5, the RMS statistics against the ground truth position for the north, east and up components are reduced on average by 55.8, 62.7 and 69.0 % from 6.8, 6.7 and 13.3 cm based on float ambiguities to 3.0, 2.5 and 4.1 cm based on fixed ambiguity with the original FCBs. Compared to the positioning RMS statistics with original FCBs, the ambiguity-fixed solutions based on the improved FCBs clearly have smaller RMS of position errors, 2.1, 1.7 and 3.2 cm which are further improved by 30.0, 32.0 and 22.0 % on average. Figure 7 shows the position errors based on the float ambiguity solutions (green), the fixed ambiguity solutions with the original (blue) and the improved FCBs (red). Most red dots are more highly concentrated to zero. This indicates that smaller position errors can be achieved when employing the improved rather than the original FCBs. Based on these statistics, we can confirm that the ambiguity-fixed positions based on the improved FCBs outperform those based on the original FCBs.

4.5 Simulated experiment for satellite FCB estimation using GSRT orbits

To validate the potential effectiveness with other constellations whose orbit quality is not as good as GPS, GPS-based simulated real-time (GSRT) orbits were simulated as follows: (1) the hybrid orbits were generated using four consecutive 18–24 h predicted parts of GPS IGU orbits; (2) to avoid sudden jumps every 6 h, the GSRT orbits were then generated by fitting the hybrid orbits. For more details about the orbit fitting, one can refer to Li et al. (2015a).

Figure 8 shows the individual GSRT orbit RMS values while Table 6 presents RMS values of all the GSRT orbits in and out of eclipses on DOY 103, 2014. It can be seen that the RMS values in radial, along and cross directions are 2.9, 11.4 and 6.4 cm, respectively, which are at the same level as real-time Beidou MEO and Galileo orbits generated by GFZ shown in Table 1. Figure 9 shows the histograms of the NL ambiguity fractions applying the original and improved FCBs with the regional and global networks. For regional network, with the original FCBs, 71.8 and 86.5 % of the NL ambiguities are smaller than 0.15 and 0.25 cycles, respectively. While these values increase to 82.7 and 94.3 % when the improved FCBs are applied to the float NL ambiguities. As shown in Table 7, the RMS of the NL ambiguity fractions after applying the improved FCBs decreases from 0.16 to 0.13 cycles, which indicates a 20.0 % improvement in retaining the integer ambiguity feature. Similarly, the percentages of the NL ambiguity fractions within 0.15 and 0.25 cycles increase from 65.4 and 82.9 % to 79.7 and 92.2 %. Meanwhile the RMS value of the NL ambiguity residuals decreases from 0.18 to 0.13 cycles.

Figure 10a, b present distribution of 3D static position RMS based on the original and improved FCBs with GSRT orbits. Compared to position RMS values based on the original FCBs which range between 1.9 and 2.6 cm for regional network and 2.0–3.1 cm for global network, position RMS values based on the improved FCBs are significantly smaller, which range between 1.5 and 2.1 cm for regional network and 1.4–2.0 cm for global network. The original FCBs achieve higher position accuracy with regional network compared to global network. No significant differences can be observed between the position results with regional and global network when the improved FCBs are used.

Fig. 10
figure 10

a Distribution of position RMS based on the original FCBs with GSRT orbits for all stations. b Distribution of 3D position RMS based on the improved FCBs with GSRT orbits for all stations

Full size image

5 Conclusions

In this study, we propose a cascaded method of estimating satellite NL FCBs as one directional-independent term and three directional-dependent terms. In this manner, the orbit errors can be assimilated by the directional-dependent terms of NL FCBs so that the NL FCB and position accuracy can be improved. Furthermore, no additional time is required for the improved satellite FCBs since they can be determined instantaneously after the reliable original FCBs are obtained.

Compared to the original FCB, the improved FCB estimation can fully describe the variation of the FCBs caused by the satellite orbit errors. With the improved FCBs, 81.9 and 82.5 % of the NL ambiguity fraction values are smaller than 0.15 cycles with regional and global networks, respectively, which are improved by 9.5 and 16.8 % over the original FCBs. The results demonstrate that more NL ambiguities can be reliably fixed with the improved FCBs. Furthermore, the improved FCBs outperform the original FCBs by leading to more accurate ambiguity-fixed PPP solutions. The position RMSs in north, east and up directions are reduced by 30.0, 32.0 and 22.0 % on average with the improved FCBs compared to the original FCBs.

Finally, potential benefits of COES method in new emerging GNSS systems with lower quality of orbits is investigated with simulated experiment. The results show that COES method improves the FCB quality and subsequently improve the 3D position accuracy by 24.5 and 33.9 % with regional and global network.