Introduction

Precise point positioning (PPP) uses undifferenced observations combined with precise satellite orbit and clock corrections to provide accurate positioning on a global scale (Zumberge et al. 1997; Kouba and Héroux 2001). However, the long initialization time required is a major limitation of PPP for real-time positioning (Bisnath and Gao 2009). Integer ambiguity resolution (IAR) provides an opportunity for shortening the initialization time and improving PPP accuracy (Gabor and Nerem 1999; Ge et al. 2008; Collins et al. 2008; Laurichesse et al. 2009; Li and Zhang 2012).

There are two principal PPP–IAR methods. The first is the fractional cycle bias (FCB) estimation method (Ge et al. 2008). It uses a reference network to estimate both wide-lane (WL) and narrow-lane (NL) FCBs that are applied to recover the integer nature of the PPP ambiguities. The second is the integer-recovery clock method, which was presented by Laurichesse and Mercier (2007), Laurichesse et al. (2009) and by Collins et al. (2008). It uses a reference network to estimate undifferenced WL FCBs and clock corrections that contain separate code and carrier clocks. The NL FCBs are not estimated but are assimilated into the clock estimates, which can be used to recover the integer nature of the ambiguities directly. Geng et al. (2010a), Shi and Gao (2014), and Teunissen and Khodabandeh (2014) all compared these PPP–IAR methods, and none of them found significant differences.

Although great advances have been made with GPS PPP–IAR, the time to first fix (TTFF) still requires over 30 min (Geng et al. 2010b, 2011). Jokinen et al. (2013) added GLONASS observations to shorten the TTFF of GPS PPP–IAR and their results showed that the TTFF could be improved by approximately 5%. Li and Zhang (2014) performed a similar analysis and they found that the average TTFF could be shortened by 42.0% from 34.4 to 20.0 min in kinematic mode. However, these two previous studies only fixed GPS ambiguities. Geng and Shi (2017) and Liu et al. (2017) further fix GPS and GLONASS ambiguity simultaneously and found that the fixing rate within 10 min could be improved from 39.8 to 87.5% and from 46.8 to 95.8%, respectively. Liu et al. (2016a) integrated GPS and BDS for PPP–IAR and they found that the fixing rate within 10 min could be improved from 17.6 to 42.8% by adding BDS satellites (IGSO and MEO). However, adding GEO satellites degraded the results because of the low orbital precision.

The above illustrates that most recent PPP–IAR research has focused on GPS. With the full operation of the BDS in the Asia–Pacific region, and the full global operation of GLONASS with 24 satellites, there are currently, on average, 23 satellites always visible across the Asia–Pacific region. Therefore, it is important to investigate the contribution to PPP–IAR of combining GPS, GLONASS, and BDS. In this contribution, a GPS + GLONASS + BDS combined PPP–IAR strategy is proposed. We adopted an undifferenced method for FCB estimation, and we proposed an undifferenced PPP–IAR strategy to perform a GPS + GLONASS + BDS combined solution. We used one week’s data collected at 20 stations to generate the undifferenced WL and NL FCBs. Then, we performed undifferenced PPP ambiguity resolution at each station to assess the contribution of using multi-GNSSs.

Methods

The method by Ge et al. (2008) was adopted in this study with the difference that both FCB estimation and PPP ambiguity resolution were realized in an undifferenced way.

GNSS observation model

The ionospheric-free combination is usually used in PPP to eliminate the first-order ionospheric effect. For a GNSS satellite s observed by receiver r, the ionospheric-free pseudorange and carrier phase observations can be expressed as:

$$\begin{array}{*{20}l} {P_{\text{IF,r}}^{s} = \rho_{\text{r}}^{s} + c\left( {dt_{\text{r}} - dt^{s} } \right) + m_{\text{r}}^{s} T_{\text{r}} + c\left( {B_{\text{IF,r}} - B_{\text{IF}}^{s} } \right)} \hfill \\ {L_{\text{IF,r}}^{s} = \rho_{\text{r}}^{s} + c\left( {dt_{\text{r}} - dt^{s} } \right) + m_{\text{r}}^{s} T_{\text{r}} - \lambda_{\text{IF}}^{s} N_{\text{IF,r}}^{s} + c\left( {b_{\text{IF,r}} - b_{\text{IF}}^{s} } \right)} \hfill \\ \end{array}$$
(1)

where \(P_{\text{IF,r}}^{s}\) and \(L_{\text{IF,r}}^{s}\) are the ionospheric-free pseudorange and carrier phase observations, respectively, \(\rho_{\text{r}}^{s}\) is the geometric distance between the satellite and the receiver, c represents the speed of light in a vacuum, \(dt_{\text{r}}\) and \(dt^{s}\) represent the receiver and satellite clocks, respectively, \(T_{\text{r}}\) is the zenith tropospheric delay, \(m_{\text{r}}^{s}\) is the corresponding mapping function, \(N_{\text{IF,r}}^{s}\) is the ionospheric-free ambiguity for the corresponding wavelength \(\lambda_{\text{IF}}^{s}\), \(B_{\text{IF,r}}\) and \(b_{\text{IF,r}}\) are the receiver hardware biases for the pseudorange and carrier phase, respectively, and \(B_{\text{IF}}^{s}\) and \(b_{\text{IF}}^{s}\) are the satellite hardware biases. The multipath effect and noise are ignored for clarity, while the phase center offsets and variations, the earth tides, the phase wind-up, and the relativistic delays must be corrected.

Because of the ambiguity parameter in the carrier phase observation, the absolute datum of both the satellite clock and the receiver clock can only be determined by the pseudorange observation in (1). Therefore, the IGS precise satellite clock will absorb the satellite pseudorange hardware bias \(B_{\text{IF}}^{s}\), while the receiver pseudorange hardware bias will be absorbed by the receiver clock. Thus, after applying the precise satellite clock, Eq. (1) can be rewritten as:

$$\begin{array}{*{20}l} {P_{\text{IF,r}}^{s} = \rho_{\text{r}}^{s} + cd\tilde{t}_{\text{r}} + m_{\text{r}}^{s} T_{\text{r}} } \hfill \\ {L_{\text{IF,r}}^{s} = \rho_{\text{r}}^{s} + cd\tilde{t}_{\text{r}} + m_{\text{r}}^{s} T_{\text{r}} - \lambda_{\text{IF}}^{s} \tilde{N}_{\text{IF,r}}^{s} } \hfill \\ \end{array}$$
(2)

with

$$\begin{array}{*{20}l} {d\tilde{t}_{\text{r}} = dt_{\text{r}} + B_{\text{IF,r}} } \hfill \\ {\lambda_{\text{IF}}^{s} \tilde{N}_{\text{IF,r}}^{s} = \lambda_{\text{IF}}^{s} N_{\text{IF,r}}^{s} + c\left( {b_{\text{IF,r}} - B_{\text{IF,r}} - b_{\text{IF}}^{s} + B_{\text{IF}}^{s} } \right)} \hfill \\ \end{array}$$
(3)

It can be seen from the second line of (3) that the integer nature of the undifferenced ambiguity is destroyed by the receiver and satellite hardware delays.

For a multi-constellation case, the combined GPS + GLONASS + BDS observation model can be expressed as:

$$\left\{ {\begin{array}{*{20}l} {P_{\text{IF,r}}^{a} = \rho_{\text{r}}^{a} + cd\tilde{t}_{\text{r}}^{G} + m_{\text{r}}^{a} T_{\text{r}} } \hfill \\ {P_{\text{IF,r}}^{b} = \rho_{\text{r}}^{b} + cd\tilde{t}_{\text{r}}^{R} + m_{\text{r}}^{b} T_{\text{r}} } \hfill \\ {P_{\text{IF,r}}^{c} = \rho_{\text{r}}^{c} + cd\tilde{t}_{\text{r}}^{C} + m_{\text{r}}^{c} T_{\text{r}} } \hfill \\ {L_{\text{IF,r}}^{a} = \rho_{\text{r}}^{a} + cd\tilde{t}_{\text{r}}^{G} + m_{\text{r}}^{a} T_{\text{r}} - \lambda_{\text{IF}}^{a} \tilde{N}_{\text{IF,r}}^{a} } \hfill \\ {L_{\text{IF,r}}^{b} = \rho_{\text{r}}^{b} + cd\tilde{t}_{\text{r}}^{R} + m_{\text{r}}^{b} T_{\text{r}} - \lambda_{\text{IF}}^{b} \tilde{N}_{\text{IF,r}}^{b} } \hfill \\ {L_{\text{IF,r}}^{c} = \rho_{\text{r}}^{c} + cd\tilde{t}_{\text{r}}^{C} + m_{\text{r}}^{c} T_{\text{r}} - \lambda_{\text{IF}}^{c} \tilde{N}_{\text{IF,r}}^{c} } \hfill \\ \end{array} } \right.$$
(4)

where superscripts a, b, and c represent a GPS, GLONASS, and BDS satellite, respectively, and superscripts G, R, and C stand for the GPS, GLONASS, and BDS systems, respectively. The estimated parameters include three coordinate parameters, three receiver clock offsets, a zenith tropospheric delay, and real-value ambiguity parameters.

Generally, the ionospheric-free ambiguities are decomposed into WL and NL ambiguities for fixing. In PPP data processing, because of the existence of the receiver and satellite hardware delay, see Eq. (3), the decomposition has the following form:

$$\tilde{N}_{\text{IF,r}}^{s} = \frac{{f_{1}^{s} f_{2}^{s} }}{{f_{1}^{s2} - f_{2}^{s2} }}\left( {N_{{{\text{w}},i}}^{s} + \phi_{\text{w}}^{s} - \phi_{{{\text{w}},i}} } \right) + \frac{{f_{1}^{s} }}{{f_{1}^{s} + f_{2}^{s} }}\left( {N_{n,i}^{s} + \phi_{n}^{s} - \phi_{n,i} } \right)$$
(5)

where \(N_{{{\text{w}},i}}^{k}\) and \(N_{n,i}^{s}\) are the WL and NL ambiguities, respectively, \(\phi_{\text{w}}^{s}\) and \(\phi_{{{\text{w}},i}}\) are the satellite and receiver WL hardware delays, while \(\phi_{n}^{s}\) and \(\phi_{n,i}\) are the NL hardware delays. It can be seen that the WL and NL hardware delays destroy the integer nature of the WL and NL ambiguities. It is difficult to separate the hardware delay and the integer ambiguity directly; however, only their FCB is critical for ambiguity fixing. Thus, if we can determine the satellite FCBs beforehand using a network, PPP can use the FCBs to recover the integer nature of the ambiguity and fix them to integers.

FCB estimation strategy

Since WL ambiguities have a long wavelength of about 0.86, 0.84, and 0.84 m for GPS, GLONASS, and BDS, respectively, they can be fixed easily by averaging the Hatch–Melbourne–Wübbena (HMW) combination (Hatch 1982; Melbourne 1985; Wübbena 1985) over epochs:

$$< {\text{HMW}}_{\text{r}}^{s} > = < \left( {\frac{{L_{{1,{\text{r}}}}^{s} }}{{\lambda_{1} }} - \frac{{L_{{2,{\text{r}}}}^{s} }}{{\lambda_{2} }}} \right) - \left( {\frac{{\lambda_{2} }}{{\lambda_{1} + \lambda_{2} }}P_{{1,{\text{r}}}}^{s} + \frac{{\lambda_{1} }}{{\lambda_{1} + \lambda_{2} }}P_{{2,{\text{r}}}}^{s} } \right) > \text{ } = N_{\text{w,r}}^{s} + \phi_{\text{w}}^{s} - \phi_{\text{w,r}} ,$$
(6)

where \(< \cdot >\) represents the averaging over epochs, λ is the carrier phase wavelength, \(N_{\text{w,r}}^{s}\) is the integer WL ambiguity, and \(\phi_{\text{w}}^{s}\) and \(\phi_{\text{w,r}}\) are the satellite and receiver WL FCBs, respectively. It can be seen from (6) that the HMW combination is affected directly by any systematic bias in the observations.

GLONASS uses frequency division multiple access modulation, which causes inter-frequency bias (IFB) between different satellites for both pseudorange and carrier phase observations (Pratt et al. 1998; Yamada et al. 2010; Reussner and Wanninger 2011;Wanninger 2012). Because of the IFB, the FCB estimation and PPP ambiguity resolution will be undermined (Reussner and Wanninger 2011; Chuang et al. 2013; Liu et al. 2016b). However, in this study, we used receivers with the same hardware configuration (i.e., same manufacturer, receiver type, firmware version, and antenna type); therefore, the WL and NL receiver IFBs can be absorbed into the satellite FCBs (Liu et al. 2016b). Thus, GLONASS FCB estimation and PPP ambiguity fixing can be undertaken in a straightforward manner.

For BDS pseudorange observations, there exist large multipath errors generated at the satellite, which affect the WL FCB estimation. Based on the multipath combination (Estey and Meertens 1999), a correction model for IGSO and MEO satellites was generated by Wanninger and Beer (2015). To obtain an absolute value, a zero-mean constraint on the estimated correction values was added, which causes the estimated WL FCBs to be biased. Therefore, in PPP ambiguity resolution, the same satellite multipath corrections as applied in WL FCB estimation should be used, which guarantees the consistency of the WL FCBs to recover the integer nature of the WL ambiguities (Wanninger and Beer 2015, Liu et al. 2016a).

Reference stations are processed in the PPP model to generate the ionospheric-free ambiguity. After fixing the WL ambiguity, the float NL ambiguity can be obtained with the float ionospheric-free ambiguity as:

$$\tilde{N}_{{n,{\text{r}}}}^{s} = \frac{{\lambda_{1} + \lambda_{2} }}{{\lambda_{2} }}N_{\text{IF,r}}^{s} + \frac{{\lambda_{1} }}{{\lambda_{1} - \lambda_{2} }}N_{\text{w,r}}^{s} = N_{{n,{\text{r}}}}^{s} + \phi_{n}^{s} - \phi_{{n,{\text{r}}}}$$
(7)

where \(\tilde{N}_{{n,{\text{r}}}}^{s}\) and \(N_{{n,{\text{r}}}}^{s}\) represent the float and integer NL ambiguity, respectively, and \(\phi_{n}^{s}\) and \(\phi_{{n,{\text{r}}}}\) are the satellite and receiver NL FCBs, respectively. Note only the fixed integer WL ambiguity is used in (7) and therefore, the precision of the WL FCB will not affect the estimation of the NL ambiguity (Ge et al. 2008).

The WL and NL FCB estimation can be performed using (6) and (7). Because GLONASS satellites have distinct wavelengths, differencing between GLONASS satellites should be avoided, because it would make ambiguity fixing rather complicated (Wang et al. 2001; Al-Shaery et al. 2013). The undifferenced WL and NL FCB estimation strategy proposed by Laurichesse et al. (2009) was adopted in this study. Because of inter-system hardware and time biases, individual receiver WL and NL FCBs should be estimated for GPS, GLONASS, and BDS.

PPP ambiguity resolution

Multi-GNSS PPP can be performed with (4), obtaining the float ionospheric-free ambiguity. Then, WL and NL ambiguity resolution can be undertaken sequentially. The satellite WL FCB can be removed by applying satellite WL FCB corrections, while the receiver WL FCB must be estimated to further correct the WL ambiguity estimates to retrieve their integer properties. Then, rounding decisions can be made to fix the WL ambiguities. The LAMBDA method was applied to search the NL ambiguities (Teunissen 1994), and the ratio test was used for ambiguity validation (Euler and Schaffrin 1991; Verhagen and Teunissen 2013; Leick et al. 2015). The ratio value is generally defined as the ratio of the second minimum of the quadratic form of the residuals to the minimum. It is used to discriminate between the second set of optimum integer candidates and the optimum one. Before applying the LAMBDA method, the receiver FCB and receiver clock must be separated from the NL ambiguities. This can be done by fixing the ambiguity with the highest satellite elevation to its nearest integer as reference. Further details can be found in Liu et al. (2017).

Data and processing strategy

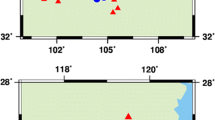
The Positioning And Navigation Data Analyst (PANDA) software, developed at Wuhan University (China), was modified to perform multi-GNSS PPP ambiguity resolution. Observations made on DOY 74–80, 2015 were used. This study used 20 stations with the same receiver hardware configuration (Trimble NetR9 receiver with antenna type “TRM59900.00 SCIS”) to conduct FCB estimation and PPP ambiguity resolution. Figure 1 shows the distribution of the 20 stations. We used C1 and P2 pseudorange observations for each system at all stations, and the details of the processing strategies are summarized in Table 1.

Fig. 1
figure 1

Distribution of the 20 stations used in this study

Full size image
Table 1 Multi-GNSS measurement model and parameter estimation strategy
Full size table

To assess the contribution of multi-GNSS, we conducted PPP–IAR on all the stations for seven days. Both kinematic and static solutions are performed with Kalman filter epoch by epoch, except that the position parameters are modeled as white noise in kinematic solution and as constant in static solution. The daily observations were divided into 24 hourly data sets; hence, there were generally 168 hourly solutions for each station and 3360 in all, if there was no data loss. The TTFF in each hourly session was recorded and analyzed. We further calculated the cumulative distribution of the TTFF, and we obtained the fixing rate for different lengths of observation time. For example, the fixing rate for 10-min observation time represents the rate of all PPP cases with 10-min observation that can achieve an ambiguity-fixed solution. We assumed that the ambiguities could be fixed correctly with daily observations, and then the hourly ambiguities were compared with the daily “truth” to verify their correctness. We define the ratio of epoch number with correctly fixed ambiguities to the number of all fixed epochs as the correct fixing rate (CFR). Because we considered partial ambiguity fixing for a given epoch, if the number of fixed ambiguities was less than six or the PDOP of the satellites corresponding to the fixed ambiguities was too poor, it was not accepted as a fixed solution.

Experiment results and discussion

In this section, the quality of the FCBs is first assessed by checking the a posteriori residuals of float ambiguities. Then, kinematic and static PPP–IAR is conducted to analyze the performance improvement by using multi-GNSS.

Assessment of FCB estimation quality

To evaluate the quality of the FCBs, the upper panels of Fig. 2 show the distribution of a posteriori residuals of all the daily WL float ambiguities. It can be seen that 98.4 and 97.2% of the WL residuals are within 0.15 cycles for GPS and BDS, respectively; over 99% are within 0.25 cycles for both. This indicates a high consistency of the fractional parts of the float WL ambiguities for GPS and BDS. Although only 77.7% are within 0.15 cycles for GLONASS, 91.5% are within 0.25 cycles, which can satisfy GLONASS PPP ambiguity resolution.

Fig. 2
figure 2

Distribution of a posteriori residuals of the daily WL (upper) and NL (lower) float ambiguities for GPS, GLONASS, and BDS (left to right)

Full size image

The lower panels of Fig. 2 show the distribution of a posteriori residuals of the NL float ambiguities with the WL ambiguity fixed. It can be seen that over 93% of the residuals are within 0.1 cycles for GPS, GLONASS, and BDS; and that over 96% are within 0.15 cycles. Although the WL residuals of GLONASS are larger than GPS and BDS, the NL residuals have the same precision as GPS and BDS. Note the residuals of BDS are a little smaller than GPS and GLONASS, which is because the BDS IGSO satellites have longer continuous tracking times and the float ambiguities converge better.

Contribution of multi-GNSS to float PPP

Figure 3 shows the distribution of the number of satellites and the PDOP for different system combinations. It can be seen that the average number of GPS satellites is 9.4 and the average PDOP is 1.9. When using GPS + GLONASS, these two values are 17.1 and 1.3, respectively, which are better than GPS + BDS. If all three systems are used, the average satellite number is 22.1 and the average PDOP is 1.1. Considering this, we expect great improvements in the performance of both float and ambiguity-fixed PPP solutions when using multi-GNSS.

Fig. 3
figure 3

Distributions of number of satellites (upper) and PDOP value (lower) for system combinations G, G + R, G + C, and G + R + C (left to right)

Full size image

We calculated the positioning RMS for different lengths of observation time from all the hourly solutions (Fig. 4). It is evident that the position accuracy of kinematic PPP can be improved significantly by adding GLONASS and BDS. Taking the 20-min observation length as an example, the position RMS for GPS-only is 19.2, 28.7, and 46.2 cm for the north, east, and up directions, respectively. When adding GLONASS, it improves to 3.7, 11.8, and 9.6 cm, respectively, and when adding both GLONASS and BDS, it improves to 2.7, 9.2, and 7.4 cm, respectively. When using the static model, the position RMS for GPS-only in the north, east, and up directions is improved significantly to 3.9 12.3, and 13.2 cm, respectively; however, the improvement by the further addition of another GNSS system is relatively low, i.e., only to 2.1, 5.9, and 6.0 cm, respectively, for GPS + GLONASS + BDS solution. We believe this is because the model is sufficiently strong for static GPS-only PPP, such that the addition of GLONASS and BDS contributes little to the model strength.

Fig. 4
figure 4

Position RMS for float kinematic (upper) and static (lower) PPP for different observation time lengths; we have about 3360 specimens to get each RMS value

Full size image

Contribution of multi-GNSS to ambiguity-fixed PPP

In this subsection, we first analyzed the contribution of multi-GNSS to kinematic PPP and then static PPP.

Kinematic PPP solution

The important issue in ambiguity validation is the selection of the criteria. Larger criteria will produce a more reliable fixing result, but many potentially correct solutions will be rejected. Therefore, as long as the fixing reliability is acceptable, the criteria should be as small as possible. Table 2 shows the CFR with different ratio criteria for kinematic PPP solutions. The CFR for GPS-only is only 51.7% when the value of the ratio criteria is set to 2.0, which is very low for industrial applications. The CFR increases with an increasing value of the ratio criteria; however, it is only 86.2% when the value of the ratio criteria is large (i.e., 6.0). The CFR with a value of the ratio criteria of 2.0 improves significantly to 93.8 and 91.0% for GPS + GLONASS and GPS + BDS, respectively, and it improves to 98.3% for GPS + GLONASS + BDS, which would satisfy industrial requirements. In the following analysis, we consider the value of the ratio criteria of 2.0 for all PPP strategies.

Table 2 Correct fixing rate (%) using different ratio criteria for kinematic PPP
Full size table

Figure 5 shows the distribution of the TTFF for different system combinations, and the fixing rate is summarized in Table 3. It can be seen, for GPS-only, that the fixing rate is only 16.2 and 42.6% at 10 and 20 min, respectively. Even when the observation time length is increased to 60 min, the fixing rate is only 86.0%. When adding GLONASS, the fixing rate is improved significantly to 75.9, 93.3, and 99.4% for observation time lengths of 10, 20, and 60 min, respectively. The fixing rate of GPS + BDS is less than GPS + GLONASS, which is because the number of satellites and the PDOP for the former are not as good as the latter. When using GPS + GLONASS + BDS, the fixing rate improves further to 90.0 and 97.6% at 10 and 20 min, respectively, which might satisfy the requirement of real-time applications.

Fig. 5
figure 5

Distribution of the TTFF of kinematic PPP. We processed 3360 hourly solutions and the TTFF of all solutions analyzed

Full size image
Table 3 Fixing rate (%) at different observation time lengths of kinematic PPP
Full size table

To avoid the effects of incorrectly fixed ambiguity on the positioning results of successive epochs, it is preferable to perform ambiguity fixing at each epoch independently. We calculated the rate of fixed epochs after the first fixed epoch, as shown in Fig. 6. It can be seen that only 95.4% of all epochs can be fixed after the first fixed epoch. When using multi-GNSS, this rate improves to 99.3, 99.1, and 99.6% for GPS + GLONASS, GPS + BDS, and GPS + GLONASS + BDS, respectively.

Fig. 6
figure 6

Rate of ambiguity fixed epochs after achieving the first fixed epoch. In practice, it is preferred to try ambiguity fixing at each epoch independently

Full size image

Figure 7 shows the position RMS of each fixed epoch. The position RMS is 0.97, 0.81, and 3.25 cm for GPS-only in the north, east, and up directions, respectively, whereas it is 0.75, 0.68, and 2.81 cm for GPS + GLONASS, representing improvement of 23.6, 16.4, and 13.5%, respectively. Because of the fewer satellites and the larger PDOP, the improvement of GPS + BDS is slightly less than GPS + GLONASS. When using GPS + GLONASS + BDS, the position RMS improves to 0.72, 0.66, and 2.68 cm in the north, east, and up directions, representing improvement of 25.6, 18.4, and 17.3%), respectively, in comparison with GPS-only.

Fig. 7
figure 7

Position RMS for ambiguity-fixed kinematic PPP solutions

Full size image

Static PPP solution

Table 4 shows the CFR with different ratio criteria for static PPP solutions. When using the static model, the model strength is improved, and the CFR can be improved for each solution type. Because the model strength for the GPS-only, GPS + GLONASS, and GPS + GLONASS + BDS solutions increases from left to right, the percentage improvement in CFR decreases with the corresponding solution.

Table 4 Correct fixing rate (%) using different ratio criteria for static PPP
Full size table

Using kinematic PPP as the benchmark, it is evident that using the static model and adding another GNSS system can both improve the CFR. Here, we compare the improvements offered by these two factors, and the results are shown in Fig. 8. For the GPS-only solution, the maximum improvement is 14.5% when using the static model, while it is as large as 42.1% by adding GLONASS. As for GPS + GLONASS, the maximum improvement is 2.4 and 4.5% when using the static model and by adding BDS, respectively. For GPS + GLONASS + BDS, the model strength is adequate and the CFR is high; therefore, the improvement is only 0.2% when using the static model. It is noted that the CFR improvement by adding another GNSS is about twice that of using the static model. Therefore, we expect that adding another GNSS (i.e., Galileo) would improve the CFR further for GPS + GLONASS + BDS (by 0.4%), reaching 99% for kinematic PPP with the value of the ratio criteria set to 2.0.

Fig. 8
figure 8

Comparisons of the improvements to CFR by using the static model and by adding another GNSS system. In each panel, the kinematic PPP solution is used as reference

Full size image

The distribution of the TTFF is shown in Fig. 9, and the fixing rate for different observation time lengths is summarized in Table 5. As expected, the fixing rate is improved for each solution type. The improvement is greatest for GPS-only PPP because its model strength is weakest. The model strength for GPS + GLONASS and GPS + GLONASS + BDS is much stronger; thus, the improvement is only slight when using the static model (i.e., less than 9.2 and 6.8%, respectively).

Fig. 9
figure 9

Distribution of the TTTF of static PPP. We processed 3360 hourly solutions and the TTFF of all solutions analyzed

Full size image
Table 5 Fixing rate (%) at different observation time lengths of static PPP
Full size table

We also used kinematic PPP as the benchmark and compared the improvements in fixing rate by using the static model and by adding another GNSS system (Fig. 10). For GPS-only solution, the maximum improvement is 30.3% when using the static model, but it is as large as 50.7% by adding GLONASS. For the GPS + GLONASS solution, the maximum improvement is 9.2% when using the static model, but it is as large as 29.8% when adding BDS satellites. For GPS + GLONASS + BDS, the model strength is adequate, and the fixing rate is high; therefore, the improvement is only 6.8% when using the static model. It is also noted that the fixing rate improvement by adding another GNSS is about twice that when using the static model. Therefore, we expect that adding another GNSS (i.e., Galileo) would further the fixing rate further for GPS + GLONASS + BDS (by 13%), reaching 73.8% for kinematic PPP with an observation time length of 5 min.

Fig. 10
figure 10

Comparisons of the improvements to fixing rate when using the static model and by adding another GNSS system. In each panel, the kinematic PPP solution is used as reference

Full size image

We also performed PPP ambiguity fixing with station coordinates fixed to well-known values from the weekly solutions. Figure 11 shows the fixing rate within 6 min. It can be seen that for GPS-only, the fixing rate is only 92.9% in 6 min. However, when using multi-GNSS, the fixing rate in 6 min improves to 99.7, 99.5, and 99.8% for GPS + GLONASS, GPS + BDS, and GPS + GLONASS + BDS, respectively.

Fig. 11
figure 11

Fixing rate with observation time length of 6 min using fixed station coordinates from weekly solutions

Full size image

Figure 12 shows the position RMS for one-hourly static ambiguity-fixed PPP. On average, the position RMS is 0.62, 0.59, and 2.45 cm for GPS-only in the north, east, and up directions, respectively, while it is 0.51, 0.45, and 2.08 cm for GPS + GLONASS, representing an improvement of 17.7, 23.7, and 15.1%, respectively. When adding BDS, the precision in the north direction is degraded slightly, which might be caused by the lower precision in the BDS orbit and clock products.

Fig. 12
figure 12

Position RMS for one-hourly static ambiguity-fixed PPP solutions

Full size image

Factors contributing to the improvement of PPP–IAR using multi-GNSS

From the above analysis, we know that using multi-GNSS can significantly improve the correct fixing rate and fixing rate. The addition of multi-GNSS introduces more satellites, providing more pseudorange and phase observations, which causes two effects: more precise float solutions and more ambiguity to be fixed. Thus, it was interesting to determine which would make the greatest contribution to the improvements of multi-GNSS.

To investigate this, we conducted PPP ambiguity resolution for five situations: GPS-only (A), and four GPS + GLONASS + BDS solutions fixing only GPS ambiguities (B), fixing only GPS + GLONASS ambiguities (C), fixing only GPS + BDS ambiguities (D), and fixing ambiguities of all satellites (E). The upper and lower panels of Fig. 13 show the CFR of each situation for kinematic and static solutions, respectively. When comparing the CFR for cases A and B, it can be seen that increasing the accuracy of float PPP (using multi-GNSS) can significantly improve the CFR. When comparing the CFR for situations B–E, it can be seen that for the same precision of float solution, if more ambiguities are fixed, the more significant the CFR improvement. It can also be seen that the greater the number of satellites used, the higher the CFR.

Fig. 13
figure 13

Correct fixing rate (CFR) using different ratio criteria for kinematic (upper) and static (lower) PPP. We have processed PPP ambiguity fixing for five situations to compare the contribution by improving the precision of float PPP and by fixing more ambiguities

Full size image

Figure 14 shows the fixing rate of each case. Comparing the fixing rate for cases A and B, it can be seen that increasing the accuracy of float PPP (using multi-GNSS) has very limited improvement on the fixing rate within a short observation time. However, when comparing the fixing rates for situations B–E, it can be seen that for the same precision of float solution, if more ambiguities are fixed, the fixing rate can be improved significantly for short observation times (i.e., 5–20 min). Therefore, fixing more ambiguities would contribute more to the improvement of fixing rate within a short observation period. With increasing observation time length (i.e., >10 min), increasing the accuracy of float PPP would play a more important role. When the observation time is >40 min, the fixing rate is so high that fixing additional ambiguities would contribute very little.

Fig. 14
figure 14

Fixing rate (%) at different observation time lengths of kinematic (upper) and static (lower) PPP. We have processed PPP ambiguity fixing for five situations to compare the contribution by improving the precision of float PPP and by fixing more ambiguities

Full size image

From the above analysis, it can be seen that increasing the accuracy of float PPP and fixing more ambiguities can improve both the CFR and the fixing rate. For the CFR, these two factors have comparable contributions for each different ratio criteria. Figure 14 shows that for a short observation time length, the additions of GLONASS and BDS to the GPS-only solution, when fixing GPS-only, have very limited contributions to the fixing rate. However, when fixing GPS, GLONASS, and BDS at the same time, the contribution is very significant. For longer observation time lengths, the fixing rate of “G + R + C, fixing G + R + C” is not much greater than “G + R + C, fixing G”. Thus, fixing more ambiguities plays a major role for short observation time lengths, while increasing the accuracy of float PPP becomes dominant when the observation time length is >30 min.

Conclusions

This study presented a mathematical model for GPS + GLONASS + BDS (IGSO, MEO) PPP–IAR. One week of data from a network of 20 stations was processed to generate multi-GNSS FCBs and to perform PPP ambiguity resolution. The contributions of multi-GNSS to both the CFR and the fixing rate were analyzed in detail.

Generally, over 99% (91.5%) of a posteriori residuals of the WL ambiguities were within ±0.25 cycles for GPS and BDS (GLONASS), whereas over 96% of the NL residuals were within ±0.15 cycles for GPS, GLONASS, and BDS. We analyzed the improvements to the CFR with different ratio criteria when using multi-GNSS. The CFR for GPS-only was only 51.7% with the value of the ratio criteria set to 2.0, increasing to 86.2% for a value of the ratio criteria set to 6.0, i.e., very low for industrial applications. The CFR with the value of the ratio criteria set to 2.0 improved significantly to 93.8 and 91.0% when adding GLONASS and BDS, respectively. When using GPS + GLONASS + BDS, the CFR was as high as 98.3% with the value of the ratio criteria set to 2.0.

For kinematic PPP, the fixing rate within 10 min for the GPS-only model was only 16.2%. When adding GLONASS, the percentage improved significantly to 75.9%. The fixing rate of GPS + BDS was lower than GPS + GLONASS (i.e., only 56.9%), which was because the number of satellites and the PDOP were not as good. When using GPS + GLONASS + BDS, the fixing rate improved further to 90.0 and 97.6% for observation time lengths of 10 and 20 min, respectively, which might satisfy the requirements of real-time applications. We compared the improvements of the fixing rate when using the static model and when adding another GNSS system. The results showed that the improvements to the CFR and the fixing rate when adding another GNSS were about twice that when using the static model. It was also revealed that adding additional satellites, i.e., Galileo, could improve the performance further in comparison with GPS + GLONASS + BDS. We compared the contributions to the improvements of the CFR and the fixing rate resulting from increasing the accuracy of float PPP and fixing more ambiguities. For the CFR, it was found that the two factors have nearly the same contribution for each different ratio criteria. Regarding the fixing rate, the results showed that fixing more ambiguities played the major role for short observation time lengths while increasing the accuracy of float PPP became dominant when the observation time length was .30 min.

Homogeneous receiver types were used in this study for both FCB estimation and PPP ambiguity resolution. In the future work, we will focus on calibrating GLONASS code IFB, such that PPP ambiguity could be performed with heterogeneous receiver types.