Introduction

Precise point positioning (PPP) is an important technology for users to get a wide-area centimeter-level positioning service. Ambiguity resolution (AR) is the key to get a fast convergence time and a high-precision solution for PPP. In general, the undifferenced ambiguity does not have integer property as it includes satellite and receiver hardware biases. The satellite fractional cycle bias (FCB) should be corrected with sufficient precision to recover the ambiguity integer property for PPP. Researchers developed the integer-recovery clock method (Laurichesse et al. 2009), the decoupled-clock method (Collins et al. 2008), and the FCB estimation method (Ge et al. 2008) to solve this problem.

For a long time, only GPS PPP AR could be implemented with GPS FCB products from CNES or the School of Geodesy and Geomatics at Wuhan University (SGG-WHU). CNES generates the precise clock products based on the integer-recovery clock method, in which the wide-lane (WL) FCBs are given in the header of the product, while the narrow-lane (NL) FCBs are assimilated into the satellite clock estimates (Loyer et al. 2012). These products are available since 2015. Users can use the WL FCBs to resolve the integer WL ambiguity, and the integer L1 ambiguity can be estimated directly when precise clock products from CNES are used. SGG has been involved in the development of PPP technology since 2002. In order to meet the need of PPP users to get an ambiguity-fixed solution, GPS WL and NL FCB products have been routinely generated for PPP users from January 1, 2015 (Li et al. 2016). These FCB products are associated with different Analyze Centers (ACs). Users who use precise products from a certain AC can use the FCB product with a naming suffix of this AC to get an ambiguity-fixed solution. The daily WL FCBs and 15-min-sessions of NL FCBs are provided in units of cycles. The service of SGG has gone through extensive testing and has been successfully used in academic researches and practical applications (Wang et al. 2019; Xiao et al. 2018; Zhou et al. 2018; Chen et al. 2017).

Multi-GNSS observations have been demonstrated to have significant improvements in PPP performance with float solutions. With the development of emerging GNSS, higher precision and better availability can be achieved with dual- or multi-GNSS. Studies showed that time to first fix (TTFF) and fixing rate of GPS AR can be improved while adding observations of other GNSS. PPP AR with integrated observations based on the standard ionospheric-free model or raw observations have also been investigated (Liu et al. 2016; Li et al. 2017; Li and Zhang 2014). Practical applications such as precise orbit determination, GNSS meteorology and geodynamics can also benefit from PPP AR which leads to more precise estimates (Chen 2004; Bisnath et al. 2001; Gendt et al. 1998; Li et al. 2015). In many studies, only GPS PPP AR is realized. In order to make full use of the integer property of ambiguities to shorten the convergence time further and to improve the estimation accuracy of parameters, the implementation of multi-GNSS PPP AR is still of great significance. The urgent need for higher accuracy and shorter convergence time is an important impetus for the improvement of the FCB at the server.

With the development and modernization of GNSS, GNSS community needs continuous multi-GNSS FCBs for multi-GNSS ambiguity-fixed PPP. For this reason, CNES has been generating precise products that contain FCBs of GPS and Galileo since the end of 2018. Users can realize PPP AR with GPS and Galileo using products from CNES. But it is still a great challenge for users who want to fix the ambiguities of BDS and QZSS as well as users who want to use precise products of other ACs.

Therefore, it is necessary to routinely generate FCB products that contain GPS, BDS, Galileo and QZSS for users who expect a faster convergence, a more precise solution and high applicability. For this reason, over the past few years, SGG has made significant improvements in the FCB service system proposed by Li et al. (2016), and implemented a new system which is capable of generating FCBs of multi-GNSS constellations. SGG has been providing GPS, BDS, Galileo and QZSS FCBs associated with precise products from GFZ, CNES and CODE since April 2019. The file format and file name convention are nearly unchanged. BDS-2 FCBs are generated, while the BDS-3 FCBs are not provided, because the only AC of WUH is generating precise products of BDS-3 with observations on B1 and B3 signals, which are incompatible with the commonly used B1 and B2 signals in BDS-2. The GLONASS FCBs are not generated because of its Frequency-Division Multiple Access (FDMA) strategy. The new FCB products are currently available at: https://github.com/FCB-SGG/FCB-FILES.

This study focuses on the introduction of improved strategies and the update of the server system. In addition, the estimated quality of GPS, Galileo, BDS-2 and QZSS FCB and the positioning performance of multi-GNSS PPP AR is fully assessed. We give detailed description of the improved strategies for multi-GNSS FCB estimation as well as the new property of SGG FCB products. Then, the temporal and spatial characteristics of the FCBs are analyzed and evaluated for each system. Some ambiguity-fixed results are given, and finally, conclusions and perspectives are provided.

Method

We start with the Ionospheric-Free (IF) combination observational equations to give a detailed description of our PPP AR and FCB estimation. Then, the overall update and improvement of our computation system is presented.

Observational equations and PPP float solution

The IF combination is one of the most commonly used models in PPP because the IF model can eliminate the first-order ionospheric delays in the pseudorange and carrier phase measurements. In our study, the IF combination is formed with L1 and L2 for GPS, B1 and B2 for BDS, E1 and E5a for Galileo, and L1 and L2 for QZSS, which keeps consistency with the ACs. The corresponding IF carrier phase \(L_{{r,{\text{IF}}}}^{s}\) and pseudorange \(P_{{r,{\text{IF}}}}^{s}\) observables for satellite s and receiver r can be formulated as:

$$ \left\{ \begin{array}{l} P_{{r,{\text{IF}}}}^{s} = \rho_{r}^{s} + c({\text{d}}t_{r} - {\text{d}}t^{s} ) + T_{r}^{s} + b_{{r,{\text{IF}}}} - b_{{{\text{IF}}}}^{s} + e_{{r,{\text{IF}}}}^{s} \hfill \\ L_{{r,{\text{IF}}}}^{s} = \rho_{r}^{s} + c({\text{d}}t_{r} - {\text{d}}t^{s} ) + T_{r}^{s} + \lambda_{{{\text{IF}}}} (N_{{r,{\text{IF}}}}^{s} + B_{{r,{\text{IF}}}} - B_{{{\text{IF}}}}^{s} ) + \varepsilon_{{r,{\text{IF}}}}^{s} \hfill \\ \end{array} \right. $$
(1)

where \(\rho_{r}^{s}\) denotes the geometric distance between satellite and receiver in m, c is the speed of light, \({\text{d}}t_{r}\) and \({\text{d}}t^{s}\) are the clock offsets of receiver and satellite in s; \(T_{r}^{s}\) is the slant troposphere delay in m, and \(\lambda_{{{\text{IF}}}}\) is the wavelength of the IF combination observation. \(B_{{r,{\text{IF}}}}\) and \(B_{{{\text{IF}}}}^{s}\) are the receiver-dependent and satellite-dependent FCB, which are grouped into the ambiguity parameters in PPP float solution due to the linearly dependency between the ambiguity and the phase hardware delay parameters (Defraigne and Bruyninx 2007). \(b_{{r,{\text{IF}}}}\) is the code hardware delay from receiver antenna to the signal correlator in the receiver; it varies with GNSS constellations for the same receiver and will be absorbed in the receiver clock estimate. \(b_{{{\text{IF}}}}^{s}\) is the code hardware delay from the satellite signal generator to satellite antenna; it will be assimilated into the satellite clock offset when the GNSS precise orbit and clock products generated by the ACs are applied. \(e_{{r,{\text{IF}}}}^{s}\) and \(\varepsilon_{{r,{\text{IF}}}}^{s}\) are the measurement noise of the IF combination pseudorange and carrier phase, respectively. Other error items such as the phase center offsets (PCOs) and phase variations (PCVs) (Schmid et al. 2005), phase windup (Wu et al. 1993), BDS satellite-induced code bias (Wanninger and Beer 2015), tidal loading and relativistic effect can be corrected according to the existing models (Kouba 2009).

When precise products are used and error items are corrected, the rewritten version of (1) becomes

$$ \left\{ \begin{array}{l} P_{{r,{\text{IF}}}}^{s} = \rho_{r}^{s} + c{\text{d}}\overline{t}_{r} + T_{r}^{s} + e_{{r,{\text{IF}}}}^{s} \hfill \\ L_{{r,{\text{IF}}}}^{s} = \rho_{r}^{s} + c{\text{d}}\overline{t}_{r} + T_{r}^{s} + \lambda_{{{\text{IF}}}} \overline{N}_{{r,{\text{IF}}}}^{s} + \varepsilon_{{r,{\text{IF}}}}^{s} \hfill \\ \end{array} \right. $$
(2)

where \({\overline{\text{d}}}t_{r}\) and \(\overline{N}_{{r,{\text{IF}}}}^{s}\) are reparameterized receiver clock and ambiguity as:

$$ c{\text{d}}\overline{t}_{r} = c{\text{d}}t_{r} + b_{{r,{\text{IF}}}} $$
(3)
$$ \overline{N}_{{r,{\text{IF}}}}^{s} { = }N_{{r,{\text{IF}}}}^{s} + d_{{r,{\text{IF}}}} - d_{{{\text{IF}}}}^{s} $$
(4)
$$ d_{{r,{\text{IF}}}} = B_{{r,{\text{IF}}}} - b_{{r,{\text{IF}}}} /\lambda_{{{\text{IF}}}} $$
(5)
$$ d_{{{\text{IF}}}}^{s} = B_{{{\text{IF}}}}^{s} - b_{{{\text{IF}}}}^{s} /\lambda_{{{\text{IF}}}} $$
(6)

Equations (4)–(6) show that the ambiguity parameter consists of a combination of the integer ambiguity, and code and phase hardware delay at both receiver and satellite. Thus, the IF ambiguity parameter in the PPP float solution has lost its integer property and is estimated as a real-value constant.

In our PPP float solution processing procedure, the receiver clock, zenith wet delay (ZWD), and carrier phase ambiguities are estimated by the least square method. For multi-constellation, the receiver clocks are estimated as white noises. The ZWD is estimated as a piecewise linear parameter instead of a piecewise constant parameter that is used in the previous system. Accurate and reliable FCB estimates require high-precision estimated parameters, so we fix the station coordinates to the IGS weekly solution.

FCB estimation

The real-value IF ambiguity can be decomposed into a combination of integer WL and NL ambiguities,

$$ \overline{N}_{{r,{\text{IF}}}}^{s} = \left( {\frac{{cf_{2} }}{{f_{1}^{2} - f_{2}^{2} }}\overline{N}_{{r,{\text{WL}}}}^{s} + \frac{c}{{f_{1} + f_{2} }}\overline{N}_{{r,{\text{NL}}}}^{s} } \right)/\lambda_{{{\text{IF}}}} $$
(7)

The WL ambiguity can be resolved with the Hatch–Melbourne–Wübbena (HMW) combination observation (Hatch 1982; Melbourne 1985; Wübbena 1985),

$$ \overline{N}_{{r,{\text{WL}}}}^{s} = \left( {\frac{{f_{1} L_{r,1}^{s} - f_{2} L_{r,2}^{s} }}{{f_{1} - f_{2} }} - \frac{{f_{1} P_{r,1}^{s} + f_{2} P_{r,2}^{s} }}{{f_{1} + f_{2} }}} \right)/\lambda_{{{\text{WL}}}} = N_{{r,{\text{WL}}}}^{s} + d_{{r,{\text{WL}}}} - d_{{{\text{WL}}}}^{s} $$
(8)

where \(d_{{r,{\text{WL}}}}\) and \(d_{{{\text{WL}}}}^{s}\) consist of a combination of receiver and satellite code and phase delays. We can see that once the WL ambiguity is fixed based on (8), the NL ambiguity can be obtained through (7) with the precisely estimated IF ambiguity,

$$ \overline{N}_{{r,{\text{NL}}}}^{s} = \frac{{\lambda_{{{\text{IF}}}} (f_{1} + f_{2} )\overline{N}_{{r,{\text{IF}}}}^{s} }}{c} - \frac{{f_{2} N_{{r,{\text{WL}}}}^{s} }}{{f_{1} - f_{2} }} = N_{r,1}^{s} + d_{{r,{\text{NL}}}} - d_{{{\text{NL}}}}^{s} $$
(9)

Note that the WL ambiguity and NL ambiguity can be written in the same format. We make WL FCB estimation for example, and the method is also applicable to NL FCB estimation. For the GECJ constellation, the detailed WL ambiguities of the four systems can be written as:

$$ \left\{ \begin{array}{l} \overline{N}_{r}^{s,G} = N_{r}^{s,G} { + }d_{r,G} - d^{s,G} \hfill \\ \overline{N}_{r}^{s,E} = N_{r}^{s,E} { + }d_{r,E} - d^{s,E} \hfill \\ \overline{N}_{r}^{s,C} = N_{r}^{s,C} { + }d_{r,C} - d^{s,C} \hfill \\ \overline{N}_{r}^{s,J} = N_{r}^{s,J} { + }d_{r,J} - d^{s,J} \hfill \\ \end{array} \right. $$
(10)

where \(\overline{N}_{r}^{s}\) denotes the float ambiguity and \(N_{r}^{s}\) denotes the integer part of \(\overline{N}_{r}^{s}\). \(d_{r}\) and \(d^{s}\) are the FCB values at the receiver and satellite, respectively.

Assuming there are \(m\) satellites for every constellation observed by a network consists of \(n\) stations, the observable equation for multi-GNSS FCB estimation can be formulated as:

$$ \left[ \begin{array}{l} \overline{N}_{1}^{1,G} - N_{1}^{1,G} \\ \vdots \\ \overline{N}_{1}^{m,G} - N_{1}^{m,G} \\ \overline{N}_{n}^{1,G} - N_{n}^{1,G} \\ \vdots \\ \overline{N}_{n}^{m,G} - N_{n}^{m,G} \\ \vdots \\ \overline{N}_{1}^{1,J} - N_{1}^{1,J} \\ \vdots \\ \overline{N}_{1}^{m,J} - N_{1}^{m,J} \\ \overline{N}_{n}^{1,J} - N_{n}^{1,J} \\ \vdots \\ \overline{N}_{n}^{m,J} - N_{n}^{m,J} \\ \end{array} \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} \begin{array}{l} \left. \begin{array}{l} - {}_{m}{\mathbf{I}}_{m} \\ \vdots \\ - {}_{m}{\mathbf{I}}_{m} \\ \end{array} \right\}n{\kern 1pt} \\ \\ \vdots \\ \\ \vdots \\ \\ \vdots \\ \\ \vdots \\ {\mathbf{O}} \\ \end{array} & \begin{array}{l} \cdots \\ \\ \\ \left. \begin{array}{l} - {}_{m}{\mathbf{I}}_{m} \\ \vdots \\ - {}_{m}{\mathbf{I}}_{m} \\ \end{array} \right\}n \\ \\ \\ \\ {\mathbf{O}} \\ \\ \cdots \\ \end{array} & \begin{array}{l} \cdots \\ \\ {\mathbf{O}} \\ \\ \\ \\ \left. \begin{array}{l} - {}_{m}{\mathbf{I}}_{m} \\ \vdots \\ - {}_{m}{\mathbf{I}}_{m} \\ \end{array} \right\}n \\ \\ \\ \cdots \\ \end{array} & \begin{array}{l} {\mathbf{O}} \\ \vdots \\ \\ \vdots \\ \\ \vdots \\ \\ \vdots \\ \\ \left. \begin{array}{l} - {}_{m}{\mathbf{I}}_{m} \\ \vdots \\ - {}_{m}{\mathbf{I}}_{m} \\ \end{array} \right\}n \\ \end{array} \\ \end{array} } & {{}_{4mn}{\mathbf{S}}_{m} } \\ \end{array} } \right] \cdot \left[ \begin{array}{l} d^{1,G} \\ \vdots \\ d^{m,G} \\ \vdots \\ d^{1,J} \\ \vdots \\ d^{m,J} \\ d_{1,G} \\ \vdots \\ d_{n,G} \\ \vdots \\ d_{1,J} \\ \vdots \\ d_{n,J} \\ \end{array} \right] $$
(11)

where \({}_{m}{\mathbf{I}}_{m}\) is an identity matrix, \({\mathbf{O}}\) is a zero matrix, \({}_{4mn}{\mathbf{S}}_{n}\) is a matrix of 4mn rows and \(n\) columns. In the matrix \({}_{4mn}{\mathbf{S}}_{n}\), all elements of the diagonal are \({}_{m}{\mathbf{A}}_{1}\) and all the other entries are zero,

$$ {}_{4mn}{\mathbf{S}}_{n} = \left[ \begin{array}{l} \begin{array}{*{20}c} {{}_{m}{\mathbf{A}}_{1} } & \ldots & \ldots & {{}_{{}}{\mathbf{O}}_{{}} } \\ \end{array} \\ \begin{array}{*{20}c} \vdots & {{}_{m}{\mathbf{A}}_{1} } & {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } & \vdots \\ \end{array} \\ \begin{array}{*{20}c} \vdots & {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } & { \ddots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} } & \vdots \\ \end{array} \\ \begin{array}{*{20}c} {{}_{{}}{\mathbf{O}}_{{}} } & \ldots & \ldots & {{}_{m}{\mathbf{A}}_{1} } \\ \end{array} \\ \end{array} \right] $$
(12)
$$ {}_{m}{\mathbf{A}}_{1} = \left[ {\begin{array}{*{20}c} 1 & 1 & \cdots & 1 \\ \end{array} } \right]^{T} $$
(13)

Considering the linear dependency between receiver FCBs and satellite FCBs, we set the sum of satellite FCBs of each constellation to zero to solve the problem of rank deficiency in (11). This differs from the datum we used before for which one satellite FCB was chosen to be zero (Li et al. 2016). The same steps can be used in the estimation of NL FCB. Once the WL and NL FCBs are precisely estimated, the PPP AR can be realized.

System design

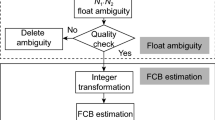
The steps at the server can be divided into two major modules: one is the float PPP module, and the other is the FCB estimation module. Detailed steps are described below.

First, all available data needed for GNSS FCB estimation are downloaded, including the observation data from the Multi-GNSS Experiment (MGEX), broadcast ephemeris, multi-GNSS precise orbits and clock products from the ACs, differential code biases (DCB) products, earth rotation parameters, and weekly station solution files. Up to now, as is shown in Table 1, the ACs are committed to providing multi-GNSS products such as precise satellite orbits and clocks. We downloaded the precise multi-GNSS products from their websites to generate satellite FCBs associated with different ACs.

Table 1 Overview of the MGEX precise orbit and clock products as of January 2019
Full size table

Observation data whose quality is not good will be excluded from the float PPP solution; and after the quality check, the “clean” data are obtained. Then, the WL ambiguities can be formed through the HMW combination and IF ambiguities can be precisely estimated by static PPP. In the float PPP processing, the amb_arc files, which contain the transmitting satellite name, phase arc start time, phase arc stop time, the WL ambiguities, estimated IF ambiguities, and the standard deviation (STD) corresponding to WL and IF ambiguities are generated.

Third, all the float WL and IF ambiguities are used to generate the WL and NL satellite FCB products. Note that in the FCB estimation procedure, we apply a system-by-system adjustment for GPS, Galileo, BDS and QZSS. For BDS-2, the satellite-induced code bias is corrected according to the model by Wanninger and Beer (2015), and only the IGSO and MEO FCBs are generated. The WL FCBs are given per day as a result of the high stability, while NL FCBs are given every 15 min due to the short wavelength which is easily affected by model inaccuracies (Ge et al. 2008).

Finally, the estimated WL and NL FCBs are written in a self-defined format and saved in a single file on the Github, which is a hosting platform for open source and private software projects and documents. Users who wish to do ambiguity-fixed multi-GNSS PPP can get free access to the website and download the FCB files corresponding to different ACs.

Strategy improvement

Significant improvements have been made in the FCB service at SGG since the initial proposal of this system.

  1. 1.

    Since July 2017, the sum of satellite FCBs is chosen as the constraint to eliminate rank deficiency in the FCB estimation procedure instead of the previous strategy. In the previous strategy, one special satellite FCB is set to zero, which may cause a jump in the estimated satellite FCB time series when the reference satellite is changed. Though the single-differenced FCBs are still stable and there is no effect for PPP AR, it is not convenient for users to analyze the time-varying characteristics of FCBs. The time series of FCB estimates are continuous and stable after applying the new strategy.

  2. 2.

    Since January 2019, more than 300 stations have been used for FCB estimations, where at least two of the GPS, Galileo, BDS and QZSS constellations can be observed. The larger number of stations indicates more reliable FCB results.

  3. 3.

    It takes an average of 21 s to complete GPS static PPP with the old system at a single station, while 56 s is required to conduct GECJ PPP with the new system. About 2 h is needed to generate GPS FCB products of one day corresponding to one AC for the old system, while about 3.5 h is needed to generate GECJ FCB products for the new system due to the increased numbers of station and satellite system.

  4. 4.

    The most important improvement is the generation of Galileo, BDS and QZSS FCBs since April 2019. Note that the FCBs are corresponding to P1 and P2 for GPS and QZSS, so that the C1 code can be used after applying the P1C1 DCB corrections. P1/P2 code should be used as it is, i.e., no P1P2 DCB corrections are needed. Pseudorange observations from B1I, B2I of BDS-2 and L1X, L5X (L1C, L5Q) for Galileo are used to generate FCB products, which is consistent with ACs, so that DCB corrections are not needed for the two systems.

Products evaluation and PPP AR experiment

The precision of the inner consistency of FCBs, as well as the PPP AR solution with GPS, Galileo, BDS and QZSS, is evaluated to demonstrate the quality of FCB products.

Quality of FCB products

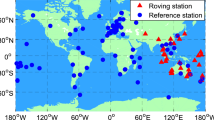
The observations from 324 globally distributed IGS or MGEX network stations are used for GECJ FCB estimation. As shown in Fig. 1, the yellow, green, blue and red dots denote stations where the GPS, Galileo, BDS and QZSS satellites can be observed. Note that the GLONASS satellites are involved in the float PPP procedure to evaluate the best positioning performance achievable when adding GPS, Galileo, BDS and QZSS in the PPP AR solution.

Fig. 1
figure 1

Distribution of global reference network stations which are used for FCB estimation

Full size image

First, the time stability of monthly WL and daily NL GECJ FCBs corresponding to CODE are evaluated, and the results are shown in Figs. 2 and 3. We select reference satellites for each system to form satellite single-differenced FCB series to remove the changes of benchmarks. We randomly select some GPS and Galileo satellites to present the time series for convenience because of the large number of satellites, while for BDS and QZSS, the results of all the satellites are given. Satellite G04 is usually abnormal, and therefore it is not shown.

Fig. 2
figure 2

Time series of the WL GECJ FCBs corresponding to CODE from day of year (DOY) 001 to 031 in 2019. a–d denote G, E, C and J, respectively. The reference satellites are G01, E01, C06 and J01

Full size image
Fig. 3
figure 3

Time series of the NL GECJ FCBs corresponding to CODE on DOY 003 in 2019. a–d denote G, E, C and J, respectively. The reference satellites are G01, E01, C06 and J01

Full size image

It can be found that the WL FCBs of Galileo are the most stable, while those of GPS are less stable; all the FCBs are stable within 0.05 cycles for a month. Satellite G18 presents the largest range of 0.15 cycles and the standard deviation (STD) is 0.05 cycles. The mean STD of WL FCBs is 0.019, 0.005, 0.015 and 0.008 cycles for G, E, C and J, respectively. For the 15-min NL FCB solution, the stability and continuity of GPS, Galileo and QZSS are better than those of BDS. For most GPS, Galileo and QZSS satellites, the NL FCBs vary within 0.15 cycles in a day. For BDS, the stability is relatively poorer, and satellite C12 is invisible at some epochs. The variation of satellite C14 is the largest and can reach 0.3 cycles, while it is within 0.2 cycles for others. Overall, the NL FCB stability of BDS is the worst among the four systems. The limited amount of satellites and non-globally distributed tracking stations may account for this. The mean STD of NL FCBs is 0.021, 0.021, 0.057 and 0.010 cycles for G, E, C and J, respectively. We can find that the quality of NL FCBs is a little worse than that of WL FCBs. This is attributable to the fact that the NL FCB estimates are easily affected by unmodeled errors.

Second, the percentage of valid float ambiguities employed to estimate FCBs, which is also called usage rate, is given to indicate the consistency of FCBs. Table 2 shows the usage rate of WL and NL float ambiguities calculated with precise products provided by CODE on DOY 001, 2019, as a typical example. It is worth noting that the NL usage rate is the rate of the 77th session on DOY 001. We can find that the usage rate of Galileo is the highest and the rate of BDS is the lowest.

Table 2 Usage rate of WL and NL float ambiguities
Full size table

Then, the quality of the FCB estimates is evaluated by examining the residuals of ambiguity observations. The histograms of the residuals of WL and NL ambiguities corresponding to GPS, Galileo, BDS and QZSS are shown in Fig. 4. The total numbers of the input WL float ambiguities are 17,959, 7660, 2852 and 484 for GPS, Galileo, BDS and QZSS, while those of NL ones are 2889, 1514, 725 and 153. We can find that the residuals are approximately obeying normal distribution subjected to zero mean. The absolute values of all residuals are less than 0.3 cycles. 98.7, 98.6, 96.6 and 98.6% of the GPS, Galileo, BDS and QZSS WL residuals are within 0.2 cycles, and for NL residuals, the percentages are 99.9, 99.9, 98.5 and 100%. This indicates a high consistency between all observations and estimates.

Fig. 4
figure 4

Histogram of a posteriori residuals of daily WL (top row) and NL (bottom row) float ambiguities. The time span for WL FCBs is DOY 001 in 2019; and the 77th session on DOY 001 in 2019 for NL FCBs

Full size image

Furthermore, we compared our FCB estimates with the FCB corrections from CNES GRG precise products, in which the GPS and Galileo WL FCBs are given in the header of the multi-GNSS precise clock files and the NL FCBs are absorbed in the satellite clocks. Thus, the single-differenced NL FCBs we estimate should be near to zero after correcting the constant bias of 0.47 cycles caused by the 1-cycle WL bias (Loyer et al. 2012). At the same time, we can compare the WL FCBs by analyzing the differences between the single-differenced WL FCB series. The histogram of the FCB difference between SGG and CNES is shown in Fig. 5. In total, 93.0% of the GPS WL and 91.3% of the Galileo WL biases are within 0.05 cycles, and 96.5% and 94.7% of them are within 0.075 cycles, while 97.6% of the GPS NL and 92.8% of the Galileo NL biases are within 0.05 cycles, and 99.6% and 99.0% of them are within 0.075 cycles. This indicates that our FCB products agree well with those from CNES.

Fig. 5
figure 5

Histogram of the difference of single-differenced GPS (left column) and Galileo (right column) WL (top row) and NL (bottom row) FCBs between SGG and CNES. The time span for WL FCBs is 31 days, from DOY 001 to 031 in 2019; and DOY 003 in 2019 for NL FCBs

Full size image

SGG has been providing GECJ FCB products corresponding to the precise products from GFZ, CODE and CNES. Table 3 gives STDs of G, E, C and J FCBs which can reflect the quality of FCB products for different ACs. The results show that the stability of GPS and Galileo FCBs are at the same level for the three ACs, while the quality of BDS FCBs corresponding to GFZ is relatively worse than that corresponding to CODE. The QZSS FCBs of CODE are the most stable, with STDs of 0.008 cycles for WL FCBS and 0.010 cycles for NL FCBs.

Table 3 STDs of GPS, Galileo, BDS and QZSS monthly WL and daily NL FCBs corresponding to GFZ, CODE and CNES (unit: cycles)
Full size table

PPP AR solution

At user, the single-differenced ambiguities are formed to be fixed to integers in a PPP AR procedure. For each navigation system, satellite with the highest elevation angle is selected as the reference satellite while forming between-satellite differencing ambiguities. These ambiguities are fixed system by system. PPP AR performance in terms of positioning accuracy, TTFF and fixing rate, as well as convergence time in float PPP, is compared and analyzed. In this study, the positioning accuracy is evaluated through the comparison between the position solutions and the station coordinates given in the IGS weekly solution files. For simulated kinematic PPP, the positioning error after convergence time is taken for purposes of accuracy analysis. The convergence time is defined as the time required to attain a three-dimensional positioning error less than 10 cm and keep at least for 10 epochs, and the TTFF is defined as the time taken for the ambiguity-fixed solution to be successfully achieved for at least 5 epochs (Feng and Wang. 2008; Gao et al. 2015). The fixing rate is defined as the ratio of the number of fixed epochs to the number of total epochs after TTFF. Observation data from 31 MGEX stations during DOY 001–010 in 2019 are processed in both static and kinematic PPP models, and the results are analyzed. As shown in Fig. 6, most stations are in the Asian-Pacific region in order to get the four systems covered.

Fig. 6
figure 6

User stations used to evaluate static and kinematic PPP results

Full size image

For static PPP, the position performance of hourly data separated from daily MGEX observations is analyzed, and the root mean square (RMS) values of the positioning errors in east (E), north (N) and up (U) components for different combinations of GNSS constellations, as well as the convergence time and TTFF, are given. Figure 7 gives a representative result of static PPP ambiguity-fixed solution and number of visible satellites of GECJ at station MRO1 on DOY 001, 2019. It is worth noting that the daily observation data are divided into six four-hour arcs for convenience. The blue lines are the RMS values of positioning errors in E, N and U components of float PPP, and the red lines denote the ambiguity-fixed PPP solutions. We can note that once the ambiguities are fixed to correct integers, the position accuracy improves significantly, especially for east and up components.

Fig. 7
figure 7

Static PPP AR solutions and number of visible satellites of GECJ at station MRO1 on DOY 001, 2019. All the parameters are initialized every 4 h

Full size image

The statistical results are given in Fig. 8 and Table 4. The average number of fixed satellites is 7.3, 5.5, 4.9, and 2.0 for GPS, Galileo, BDS and QZSS, respectively. We can find that the convergence time and TTFF of dual-system static PPP are shortened compared with single system, with a percentage of 14.3 and 3.1% for GC and 17.1 and 13.3% for GE. When the other two constellations are involved in the solution, the convergence time is shortened by 27.3% from 17.6 to 12.8 min compared with GPS static PPP, and the TTFF is shortened for 29.4% from 23.1 to 16.3 min. In addition, we can notice that the positioning accuracy can be significantly improved compared to float PPP. But for different combinations of GNSS, the positioning accuracy of ambiguity-fixed static PPP is almost at the same level, since after a long time of convergence and correctly fixed ambiguities, the unmodeled errors have less influence on the estimated precision of parameters. In the case of float PPP, the multi-GNSS observations can improve the accuracy of estimated float ambiguity parameters, so that the positioning accuracy of GECJ float PPP also improves compared to GPS float PPP.

Fig. 8
figure 8

Average convergence time (CT) and TTFF of single-system (G), dual-system (GE, GC) and four-system (GECJ) static PPP for 31 MGEX stations from DOY 001 to 010, 2019

Full size image
Table 4 Statistical results of hourly single-system (G), dual-system (GE, GC) and four-system (GECJ) static PPP for 31 MGEX stations from DOY 001 to 010, 2019
Full size table

For kinematic PPP, a random walk process is used to model the dynamics of the vehicle in the Kalman filter. In this study, we use simulated dynamic observations, in which the spectral density values of position coordinates are set to 104 m2/s to evaluate the kinematic PPP. It is worth noting that in actual kinematic applications, multipath changes from site to site, and users need to adjust the thresholds in PPP AR procedure in different situations. Figure 9 shows a typical convergence for GECJ PPP in kinematic mode, taking the results at station PERT on DOY 001, 2019, as an example. The ambiguity-fixed PPP solution is more stable than the float PPP. Even if there is a significant vibration in float PPP, the ambiguity-fixed PPP can still maintain a high-precision positioning performance when the correctly fixed ambiguities are held.

Fig. 9
figure 9

Kinematic PPP AR solutions and number of visible satellites of GECJ at station PERT on DOY 001, 2019. All the parameters are initialized every 4 h

Full size image

The kinematic PPP accuracy information, which is represented by average RMS values of epoch-wise positioning errors after convergence, together with the convergence time, TTFF and fixing rate, is shown in Fig. 10 and Table 5. The average number of fixed satellites is 6.6, 4.9, 4.7 and 2.2 for GPS, Galileo, BDS and QZSS, respectively. The convergence time and TTFF of GECJ PPP AR are the fastest, with an improvement of 42.6 and 51.9% compared with GPS-only kinematic PPP AR. At the same time, the fixing rate, as well as the positioning accuracy, also improves with multi-GNSS PPP AR. For GPS PPP AR, the RMS of position errors is 1.8, 1.3 and 4.0 cm in E, N and U directions, while the RMS of dual-system PPP AR can be reduced by 22.2, 15.4 and 7.5% for GE and 16.7, 15.4 and 7.5% for GC. The GECJ PPP AR reaches the highest positioning accuracy, with a reduction of 22.2, 15.4 and 10.0%, respectively.

Fig. 10
figure 10

Average convergence time and TTFF of single-system (G), dual-system (GE, GC) and four-system (GECJ) kinematic PPP for 31 MGEX stations from DOY 001 to DOY 010, 2019

Full size image
Table 5 Statistical results of daily single-system (G), dual-system (GE, GC) and four-system (GECJ) kinematic PPP for 31 MGEX stations from DOY 001 to 010, 2019
Full size table

Conclusion and remarks

Since April 1, 2019, the SGG-WHU has routinely generated GECJ WL and NL FCBs for users (https://github.com/FCB-SGG/FCB-FILES).

The multi-GNSS FCB estimation procedure is described in detail, and the estimated GECJ FCB products are evaluated. The WL FCBs of the four systems show a high stability within a month, and the NL FCBs remain relatively stable within one day. The mean STD of WL FCBs is 0.019, 0.005, 0.015 and 0.008 cycles, while the mean STD of NL FCBs is 0.021, 0.021, 0.057 and 0.010 cycles for G, E, C and J, respectively. When comparing the difference between our FCB products with FCBs given by CNES, results show that 93.0% of the GPS WL and 91.3% of the Galileo WL biases are within 0.05 cycles, and 96.5% and 94.7% of them are within 0.075 cycles. Also, 97.6% of the GPS NL and 92.8% of the Galileo NL biases are within 0.05 cycles, and 99.6% and 99.0% of them are within 0.075 cycles. This indicates that our products corresponding to CNES maintain high conformity with GRG precise products.

GPS + Galileo + BDS + QZSS data collected from 31 MGEX stations during the period of DOY 001 to 010, 2019, are used to demonstrate the performance of four-system PPP AR. The result of both static and simulated kinematic PPP AR indicates that the four-system PPP AR can significantly shorten the convergence time and TTFF compared with dual-system and single-system PPP AR. The convergence time and TTFF can be reduced by 27.3 and 29.4% in static PPP AR, while the reductions are 42.6 and 51.9% in kinematic PPP AR. In addition, the positioning accuracy can also be improved with multi-GNSS PPP AR. These results also highlight the necessity and importance of releasing GECJ FCB products.

Furthermore, we are preparing to generate FCB products corresponding to other ACs such as WUM, TUM and ESM soon. On the other hand, we are planning to store FCBs in the Sinex-Bias standard format in the future.

As GNSS have already begun to broadcast triple- and multi-frequency signals, studies based on multi-system and multi-frequency attract the attention of many scholars. PPP AR with the additional frequency is expected to improve the results obtained, and FCB products that are applicable to undifferenced and uncombined PPP in order to make full use of multi-frequency may also be generated.