1 Introduction

In recent times, solar energy is one of the most suitable clean energy and an excellent alternative for conventional energy (Farshad et al. 2019; Ebrahimpour et al. 2021; Kumar et al. 2021a, b). For most solar power plants, the heat transfer enhancement should be maximum in order to achieve higher exergetic efficiency (Huang and Hsu 2019; Krishna et al. 2019; Selimefendigil and Oztop 2019; Sureshkumar Raju et al. 2019; Alblawi et al. 2020). Therefore, researchers used many active and passive techniques to improve the heat transfer rate in the past decades. The use of wavy wall, nanofluids, porous media are some common examples of passive techniques, while the application of magnetic and electric field are the examples of active technique (Huang and Hsu 2019; Krishna et al. 2019; Selimefendigil and Oztop 2019; Sureshkumar Raju et al. 2019; Alblawi et al. 2020; Shyam et al. 2020, 2021; Mondal and Wongwises 2020; Tyagi et al. 2020; Kumar and Mondal 2022).

It may be mentioned here that for solar plants, natural convection is a suitable means of heat transfer (Ma et al. 2020). A number of investigations have been reported to improve the natural convective heat transfer rate by using active and passive techniques. Recently, hybrid nanofluid has been used for better heat transfer rate instead of a single component of nanofluid. The hybrid nanofluid gives improved thermal characteristics. Some of the examples of hybrid nanofluids are Ag-MgO-water nanofluid (Ghalambaz et al. 2020; Goudarzi et al. 2020), Al2O3-Cu-water nanofluid (Mansour et al. 2018; Tayebi and Chamkha 2021; Roy 2022), MWCNT (multi-walled carbon nanotubes)-Fe3O4-water nanofluid (Sundar et al. 2014; Brusly Solomon et al. 2017a, b; Izadi et al. 2018, 2019; Sajjadi et al. 2019; Mourad et al. 2021). Goudarzi et al. (2020) investigated the effect of thermophoresis and Brownian motion of Ag-MgO-Water hybrid nanofluid on the natural convective transport of heat. It is found that the thermophoresis migration causes more accumulation of nano-particle near the cold wall. Ghalambaz et al. (2020) reported the effect of Ag–MgO-water hybrid nanofluid on natural convection inside a square cavity. It is found that the average Nusselt number enhances with volume fraction for smaller Rayleigh number, while the effect of nano-particle volume fraction is opposite at the higher values of Rayleigh number. Sheikholeslami et al. (2019) numerically investigated the natural convective heat transfer characteristics inside a circular cavity filled with MWCNT-Fe3O4-water nanofluid imposing the variable magnetic forces and found that the addition of hybrid nanofluid enhances the heat transfer rate compared to the base fluid case. Moreover, a number of similar investigations have been done using the MWCNT-Fe3O4-water nanofluid inside porous corrugated enclosure, square porous cavity, and inverted T-shaped cavity (Izadi et al. 2018; Sajjadi et al. 2019; Mourad et al. 2021). It is found that MWCNT-Fe3O4-water nanofluid is a suitable hybrid nanofluid for heat transfer enhancement as the mild change in volume fraction from 0 to 0.3% augmented the thermal conductivity up to 13.89% (Sundar et al. 2014).

The use of wavy wall instead of plane wall for the heat transfer interface is one of the effective methods for heat transfer augmentation (Pati et al. 2017; Mehta and Pati 2019, 2020, 2021; Mehta et al. 2021a, 2022). Barman and Rao (2021) and Rao and Barman (2021) investigated the natural convection inside a wavy porous cavity with partial heat source. It is found that increase in amplitude and number of waves of wavy wall decreases the maximum temperature for the range of aspect ratio 0.2–5. Hamzah et al. (2021) studied the natural convection inside a porous wavy cavity filled with Al2O3-water nanofluid imposing a transverse magnetic source and reported that average Nusselt number decreases with amplitude of the wavy wall. Ma et al. (2020) investigated the natural convective heat transfer characteristic for the corrugated solar plant filled with Al2O3-water nanofluid. It is found that corrugation configuration 2 has a higher heat transfer rate among all considered configurations. Recently, a number of studies focusing on the natural convective heat transfer characteristics have been investigated using the wavy wall for the magnetohydrodynamic flow of ferrofluid, magnetohydrodynamic flow of Al2O3-Cu-water nanofluid, Cu-water nanofluid flow with magnetic field, and Al2O3- water nanofluid flow inside a crowned cavity (Ashorynejad and Shahriari 2018; Abdulkadhim et al. 2021; Afsana et al. 2021; Dogonchi et al. 2021; Hamzah et al. 2021).

We know that heat exchanging devices are associated with the loss in available energy (Kaushik et al. 2016; Gaikwad et al. 2017a; Sarma et al. 2017a). Therefore, the entropy generation should be minimum for such systems (Bhowmick et al. 2020a, b). Note that the entropy generation analysis for many thermo-fluidic devices has been done from micro to macro length scales (Chen et al. 2020; See and Leong 2020; Torabi et al. 2020; Amit et al. 2021; Avellaneda et al. 2021; Lisboa et al. 2021; Mondal 2014; Mondal and Dholey 2015; Goswami et al. 2016; Gaikwad et al. 2017b, 2019; Mondal and Wongwises 2017, 2018; Sarma et al. 2017b, 2018, 2022; Mondal et al. 2017; Sarma and Mondal 2018; Kumar et al. 2021a, b). Afsana et al. (2021) investigated the entropy generation characteristics for MHD natural convective flow of ferrofluid inside a wavy cavity. It is found that for no-magnetic field case, the thermal and viscous entropy generation decreases with increase in nano-particle volume fraction. Dogonchi et al. (2021) studied the entropy generation characteristics for the natural convective flow inside a wavy-crowned cavity filled with Al2O3- water nanofluid. It is found that the increase in curvature of the cavity augmented the total entropy generation.

From an extensive review of literature, it is found that the MWCNT-Fe3O4-water nanofluid is suitable for heat transfer application and presence of the wavy surface enhances the heat transfer rates for natural convective flow. To the best of our knowledge, it is found that the effect of MWCNT-Fe3O4-water nanofluid on natural heat transfer and entropy generation characteristics inside a wavy solar plant is yet to be investigated. Considering this lacuna in the referred literature, we here consider the aforementioned aspect as the objective of the present work as discussed in detail in the subsequent sections.

2 Theoretical formulation

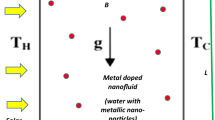
The simplified setup and the physical domain of wavy solar power plant based on natural convection mechanism filled with MWCNT-Fe3O4-water nanofluid is depicted in Fig. 1a, b, respectively. Noted that the natural convection mechanism based solar collectors are already manufactured and broadly used (Phiraphat et al. 2017; Chen and Zhang 2014). The bottom wavy wall is heated by the solar reflector and maintained at a constant temperature, \(T_{{\text{H}}}\), and top walls are acting as cooler and temperature is maintained at \(T_{{\text{C}}}\). The equation of the bottom wavy wall can be written as:

$$s\left( x \right) = A\sin \left( {\frac{{2\pi \left( {x - 0.1L} \right)}}{{L_{{\text{W}}} }}} \right)$$
(1)
Fig. 1
figure 1

a Simplified setup for solar power plant, b Computational domain of the solar power plant

Full size image

Using the length scale \(L\), the normalized form of Eq. (1) can be written as:

$$S\left( X \right) = \alpha \sin \left( {\frac{{2\pi \left( {X - 0.1} \right)}}{{{{L_{{\text{W}}} } \mathord{\left/ {\vphantom {{L_{{\text{W}}} } L}} \right. \kern-\nulldelimiterspace} L}}}} \right)$$
(2)

Here, \(S\left( X \right) = {{s\left( x \right)} \mathord{\left/ {\vphantom {{s\left( x \right)} L}} \right. \kern-\nulldelimiterspace} L}\), \(X = {x \mathord{\left/ {\vphantom {x L}} \right. \kern-\nulldelimiterspace} L}\), \(\alpha = {A \mathord{\left/ {\vphantom {A L}} \right. \kern-\nulldelimiterspace} L}\), and normalized wavelength, \({{L_{{\text{W}}} } \mathord{\left/ {\vphantom {{L_{{\text{W}}} } L}} \right. \kern-\nulldelimiterspace} L}\) is taken as 0.2 to generate the total number of waves equal to four.

We assume that the nanofluid flow through solar power plant is laminar, steady, incompressible and two-dimensional. The nanofluid distribution is considered uniform in the domain, and fluid rheology is Newtonian. Moreover, the thermo-physical properties are considered as constant except density in the body force term, where Boussinesq approximation is used. Note that the maximum temperature difference (ΔT) is achieved as ~ 7 K for the considered value of Rayleigh number (Ra = 105), L = 0.25 m and nanofluid volume fraction 0.3%. Following the criteria by Gray and Giorgini (1976), the Boussinesq approximation is valid when L/ΔT \(\le\) 9.9 \(\times\) 102 m/K for water. For the present anlysis L/ΔT is obtained as 0.0357 m/K for ΔT = 7 K and zero volume fraction. This order of magnitude analysis underlines for the validity of the Boussinesq approximation pertaining to this application. Further, the effects due to radiation and viscous dissipation are neglected for the chosen range of physical parameters as considered in this analysis.

Further, by using the following reference scales as \(U = {u \mathord{\left/ {\vphantom {u {u_{{{\text{ref}}}} }}} \right. \kern-\nulldelimiterspace} {u_{{{\text{ref}}}} }}\), \(V = {v \mathord{\left/ {\vphantom {v {u_{{{\text{ref}}}} }}} \right. \kern-\nulldelimiterspace} {u_{{{\text{ref}}}} }}\), \(u_{{{\text{ref}}}} = {{\gamma_{{\text{f}}} } \mathord{\left/ {\vphantom {{\gamma_{{\text{f}}} } L}} \right. \kern-\nulldelimiterspace} L}\), \(\gamma_{{\text{f}}} = {{k_{{\text{f}}} } \mathord{\left/ {\vphantom {{k_{{\text{f}}} } {\left( {\rho_{{\text{f}}} c_{{\text{p,f}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\rho_{{\text{f}}} c_{{\text{p,f}}} } \right)}}\), \(\gamma_{{{\text{nf}}}} = {{k_{{{\text{nf}}}} } \mathord{\left/ {\vphantom {{k_{{{\text{nf}}}} } {\left( {\rho_{{{\text{nf}}}} c_{{\text{p,nf}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\rho_{{{\text{nf}}}} c_{{\text{p,nf}}} } \right)}}\), \(P = {{\left( {pL^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {pL^{2} } \right)} {\left( {\rho_{{\text{f}}} \gamma_{{\text{f}}}^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\rho_{{\text{f}}} \gamma_{{\text{f}}}^{2} } \right)}}\), \(\Pr = {{\mu_{{\text{f}}} c_{{\text{p,f}}} } \mathord{\left/ {\vphantom {{\mu_{{\text{f}}} c_{{\text{p,f}}} } {k_{f} }}} \right. \kern-\nulldelimiterspace} {k_{f} }}\), \({\text{Ra}} = {{\left( {\beta_{{\text{f}}} gL^{3} \rho_{{\text{f}}} \left( {T_{{\text{H}}} - T_{{\text{C}}} } \right)} \right)} \mathord{\left/ {\vphantom {{\left( {\beta_{{\text{f}}} gL^{3} \rho_{{\text{f}}} \left( {T_{{\text{H}}} - T_{{\text{C}}} } \right)} \right)} {\mu_{{\text{f}}} \gamma_{{\text{f}}} }}} \right. \kern-\nulldelimiterspace} {\mu_{{\text{f}}} \gamma_{{\text{f}}} }}\), and \(\theta = {{\left( {T - T_{{\text{C}}} } \right)} \mathord{\left/ {\vphantom {{\left( {T - T_{{\text{C}}} } \right)} {\left( {T_{{\text{H}}} - T_{{\text{C}}} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {T_{{\text{H}}} - T_{{\text{C}}} } \right)}}\), the dimensionless transport equations can be written as:

$$\frac{\partial U}{{\partial X}} + \frac{\partial V}{{\partial Y}} = 0$$
(3)
$$\frac{{\rho_{{{\text{nf}}}} }}{{\rho_{{\text{f}}} }}\left( {U\frac{\partial U}{{\partial X}} + V\frac{\partial U}{{\partial Y}}} \right) = - \frac{\partial P}{{\partial X}} + \Pr \frac{{\mu_{{{\text{nf}}}} }}{{\mu_{{\text{f}}} }}\left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right)$$
(4)
$$\frac{{\rho_{{{\text{nf}}}} }}{{\rho_{{\text{f}}} }}\left( {U\frac{\partial V}{{\partial X}} + V\frac{\partial V}{{\partial Y}}} \right) = - \frac{\partial P}{{\partial Y}} + \Pr \frac{{\mu_{{{\text{nf}}}} }}{{\mu_{{\text{f}}} }}\left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right) + {\text{Ra}}\Pr \frac{{\beta_{{{\text{nf}}}} }}{{\beta_{{\text{f}}} }}\theta$$
(5)
$$\left( {U\frac{\partial \theta }{{\partial X}} + V\frac{\partial \theta }{{\partial Y}}} \right) = \frac{{\gamma_{{{\text{nf}}}} }}{{\gamma_{{\text{f}}} }}\left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right)$$
(6)

It is noted that the thermo-physical properties of MWCNT-Fe3O4-water nanofluid are taken directly from the experimentally measured value as reported in the literature and listed in Table 1 (Sundar et al. 2014). It is worth adding here that the value of thermal expansion coefficient \(\left( \beta \right)\) (DasGupta et al. (2014)) of MWCNT-Fe3O4/H2O nanofluid is not available in the reported literature. Therefore, pertaining to the present analysis, we have used the following correlation to calculate it (Sheikholeslami et al. 2019):

$$\rho_{{{\text{nf}}}} \beta_{{{\text{nf}}}} = \left( {1 - \phi } \right)\left( {\rho \beta } \right)_{{\text{f}}} + \phi \left( {\rho \beta } \right)_{{{\text{np}}}}$$
(7a)
$$\beta_{{{\text{np}}}} = \frac{{\beta_{{{\text{MWCNT}}}} \phi_{{{\text{MWCNT}}}} + \beta_{{{\text{Fe}}_{3} O_{4} }} \phi_{{{\text{Fe}}_{3} O_{4} }} }}{{\phi_{{{\text{MWCNT}}}} + \phi_{{{\text{Fe}}_{3} O_{4} }} }}$$
(7b)
Table 1 Thermo-physical properties of MWCNT-Fe3O4-water hybrid nanofluid (Sundar et al. 2014)
Full size table

Here, \(\beta_{{{\text{Fe}}_{3} O_{4} }}\), \(\beta_{{{\text{MWCNT}}}}\) and \(\beta_{{\text{f}}}\) are taken as 1.3 \(\times 10^{ - 5} \;{\text{K}}^{ - 1}\), 4.2 \(\times 10^{ - 5} \;{\text{K}}^{ - 1}\), and 2.1 \(\times 10^{ - 4} \;{\text{K}}^{ - 1}\), respectively (Dutta et al. 2019; Sheikholeslami et al. 2019). The following boundary conditions are employed to solve the aforementioned transport equations:

Top wall

$$U = V = 0,\,\,\theta = 0$$
(8a)

Bottom wavy wall

$$U = V = 0,\,\,\theta = 1$$
(8b)

Bottom flat wall

$$U = V = 0,\,\,{{\partial \theta } \mathord{\left/ {\vphantom {{\partial \theta } {\partial Y}}} \right. \kern-\nulldelimiterspace} {\partial Y}} = 0$$
(8c)

Being the dominant mode of heat transfer, the convective heat transfer rate is represented by a dimensionless number called local Nusselt number \(\left( {Nu} \right)\) and represented as (Dutta et al. 2019):

$$Nu = \left( {{{k_{{{\text{nf}}}} } \mathord{\left/ {\vphantom {{k_{{{\text{nf}}}} } {k_{{\text{f}}} }}} \right. \kern-\nulldelimiterspace} {k_{{\text{f}}} }}} \right)\left( {{{\partial \theta } \mathord{\left/ {\vphantom {{\partial \theta } {\partial N}}} \right. \kern-\nulldelimiterspace} {\partial N}}} \right)$$
(9)

Here, \(N\) is the dimensionless normal along the wavy wall.

The total heat transfer rate over the heat transfer surface is represented by average Nusselt number \(\left( {\overline{Nu} } \right)\) and mathematically represented as (Wang and Chen 2002):

$$\overline{Nu} = {{\int\limits_{X = 0.1}^{X = 0.9} {Nu{\text{d}} S} } \mathord{\left/ {\vphantom {{\int\limits_{X = 0.1}^{X = 0.9} {Nu{\text{d}} S} } {\int\limits_{X = 0.1}^{X = 0.9} {{\text{d}} S} }}} \right. \kern-\nulldelimiterspace} {\int\limits_{X = 0.1}^{X = 0.9} {{\text{d}} S} }}$$
(10)

It is noted that all the fluid flow and associated transport of heat always causes destruction in available energy. Therefore, effort should be taken to keep this loss minimum to the extent possible for any heat exchanging devices/systems. Generally, the available energy loss can be represented in terms of an increase in entropy generation function. The entropy generation function pertaining to the present analysis has two components viz., thermal entropy generation and viscous entropy generation, respectively. The dimensionless form of total entropy generation \(\left( {S^{\prime\prime\prime}_{{{\text{Total}}}} } \right)\) can be written as (Dutta et al. 2019):

$$S^{\prime\prime\prime}_{{{\text{Total}}}} = \frac{{k_{{{\text{nf}}}} }}{{k_{{\text{f}}} }}\left( {\left( {\frac{\partial \theta }{{\partial X}}} \right)^{2} + \left( {\frac{\partial \theta }{{\partial Y}}} \right)^{2} } \right) + \varphi \frac{{\mu_{{{\text{nf}}}} }}{{\mu_{{\text{f}}} }}\left( {2\left( {\frac{\partial U}{{\partial X}}} \right)^{2} + 2\left( {\frac{\partial V}{{\partial Y}}} \right)^{2} + \left( {\frac{\partial U}{{\partial Y}} + \frac{\partial V}{{\partial X}}} \right)^{2} } \right)$$
(11)

Here, \(\varphi = \frac{{\mu_{{\text{f}}} \left( {{{T_{{\text{H}}} + T_{{\text{C}}} } \mathord{\left/ {\vphantom {{T_{{\text{H}}} + T_{{\text{C}}} } 2}} \right. \kern-\nulldelimiterspace} 2}} \right)}}{{k_{{\text{f}}} }}\left( {{{\gamma_{{\text{f}}} } \mathord{\left/ {\vphantom {{\gamma_{{\text{f}}} } {L\left( {T_{{\text{H}}} - T_{{\text{C}}} } \right)}}} \right. \kern-\nulldelimiterspace} {L\left( {T_{{\text{H}}} - T_{{\text{C}}} } \right)}}} \right)^{2}\) and \(S^{\prime\prime\prime}_{{}} = {{\left( {s^{\prime\prime\prime}L^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {s^{\prime\prime\prime}L^{2} } \right)} {k_{{\text{f}}} }}} \right. \kern-\nulldelimiterspace} {k_{{\text{f}}} }}\).

The averaged entropy generation in the domain can be written as (Dutta et al. 2019):

$$S_{{{\text{Total}}}} = \frac{{\int {S^{\prime\prime\prime}_{{{\text{Total}}}} {\text{d}} \Omega } }}{{\int {{\text{d}} \Omega } }}$$
(12)

Here, \(d\Omega\) is the elemental area of the domain.

Now, in order to know the fractional contribution of thermal entropy generation, we define the Bejan number \(\left( {Be} \right)\) and given as (Dutta et al. 2019):

$$Be = \frac{{S^{\prime\prime\prime}_{{{\text{Thermal}}}} }}{{S^{\prime\prime\prime}_{{{\text{Thermal}}}} + S^{\prime\prime\prime}_{{{\text{Viscous}}}} }}$$
(13)

The average value of Bejan number in the domain can be expressed as (Dutta et al. 2019):

$$Be_{{{\text{avg}}}} = \frac{{\int {Be{\text{d}} \Omega } }}{{\int {{\text{d}} \Omega } }}$$
(14)

Also, we have solved the stream function to know the recirculation strength of the vortices being formed in the flow path. The dimensionless form of stream function \(\left( \Psi \right)\) can be written as:

$$\frac{{\partial^{2} \Psi }}{{\partial X^{2} }} + \frac{{\partial^{2} \Psi }}{{\partial Y^{2} }} = \left( {\frac{\partial U}{{\partial X}} - \frac{\partial V}{{\partial Y}}} \right)$$
(15)

Equation (15) is solved by using the computed flow field and implementing boundary condition, \(\Psi\) = 0 at the walls (Bhowmick et al. 2020a).

3 Numerical methodology and model benchmarking

We have solved the transport equations numerically using the commercial software COMSOL Multiphysics® v5.2 [www.comsol.com] consistent with finite element method. We here briefly discuss the numerical method employed here for the sake of completeness in the presentation. The Galerkin weighted method is implemented to convert the governing differential equations into the integral equation. First, the computational domain is sub-divided into small domain called an element. The non-uniform triangular mesh is considered, and it is denser near the walls. Further, transport variables are approximated (basis set, \(\{ \varphi_{{\text{e}}} \}_{e = 1}^{N}\)) using the following interpolation functions (Bhowmick et al. 2020b):

$$\begin{aligned} U &= \sum\limits_{e = 1}^{{N^{U} }} {\xi_{{\text{e}}}^{U,V} U_{{\text{e}}} } \left( {X,Y} \right)\;,\;V = \sum\limits_{e = 1}^{{N^{V} }} {\xi_{{\text{e}}}^{U,V} V_{{\text{e}}} } \left( {X,Y} \right),\nonumber\\ P & = \sum\limits_{e = 1}^{{N^{P} }} {\xi_{{\text{e}}}^{P} P_{{\text{e}}} \left( {X,Y} \right)} \;,\;\theta = \sum\limits_{e = 1}^{{N^{\theta } }} {\xi_{{\text{e}}}^{\theta } \theta_{{\text{e}}} } \left( {X,Y} \right)\end{aligned}$$
(16)

Here, \(\xi_{{\text{e}}}^{U,V}\), \(\xi_{{\text{e}}}^{P}\) and \(\xi_{{\text{e}}}^{\theta }\) are the shape functions for velocity components, pressure and temperature, respectively, at the nodes of the element. It is noted that the “P2 + P1” type discretization is used in COMSOL Multiphysics® (Finlayson 2012), which means the quadratic shape functions are used for the velocity components and the linear shape functions are used for the pressure. Whereas the quartic shape functions are used for the temperature. After substituting the approximated values of transport variables in the original differential equation, the residual, R is achieved, and using the method of weighted residuals, we can write:

$$\int\limits_{\Omega } R \;W_{{\text{e}}} \left( {X,Y} \right)d\Omega = 0$$
(17)

Here, \(W_{{\text{e}}} \left( {X,Y} \right)\) is the weight function and \(\Omega\) represents the domain. Therefore, the system of finite element equations are computed in close form and are non-linear in nature (Bhowmick et al. 2020b), and iteratively solved until satisfying the criteria, \({{\left| {\varphi^{i + 1} - \varphi^{i} } \right|} \mathord{\left/ {\vphantom {{\left| {\varphi^{i + 1} - \varphi^{i} } \right|} {\varphi^{i} }}} \right. \kern-\nulldelimiterspace} {\varphi^{i} }} \le 10^{ - 6}\). Here, \(\varphi\) and i represent transport variable and integration, respectively (Mehta et al. 2021b). In addition, the grid independence test has been conducted by calculating the average Nusselt number for the different mesh types (M) as depicted in Table 2. We have selected mesh type, M3 as it gives grid unbiased result compared to the next level fine mesh type, M4.

Table 2 Grid independency test for the different mesh system by calculating average Nusselt number \(\left( {\overline{Nu} } \right)\) when \(\phi\) = 0.3% and \(\alpha\) = 0.05
Full size table

Also, we have done extensive validation of the present numerical model essentially to establish the credibility of the proposed analysis and associated results as discussed in subsequent sections. First, as depicted in Fig. 2, the dimensionless transverse velocity component is compared with the result of Deng and Tang (2002) for natural convection inside a square cavity when Prandtl number (Pr) is 0.71with the limiting case \(\phi\) = 0% and \(\alpha\) = 0. A fairly accurate match between the present and publishes results as seen in Fig. 2 justifies the accurateness of the present modeling framework. Second, the average Nusselt number at the heated wall is compared in Table 3 with the result of Deng and Tang (2002) as well as Costa (1997) for natural convection inside a square cavity, when Pr = 0.71, \(\phi\) = 0% and \(\alpha\) = 0. From both the comparison, we have a good match with the published works (Costa 1997; Deng and Tang 2002). Following this model benchmarking analysis, we now proceed with the discussion of the results at hand in the forthcoming sections.

Fig. 2
figure 2

Comparison of normalized y-velocity component at the horizontal line in the middle section for different Ra with the result of Deng and Tang (2002) when Pr = 0.71 and limiting case \(\phi\) = 0% and \(\alpha\) = 0

Full size image
Table 3 Comparison of average Nusselt number \(\left( {\overline{Nu} } \right)\) with the results of Deng and Tang (2002) and Costa (1997) when Pr = 0.71, and limiting case \(\phi\) = 0% and \(\alpha\) = 0
Full size table

4 Results and discussion

In the present work, we have investigated the natural convective heat transfer and entropy generation characteristic inside a wavy solar power plant filled with MWCNT-Fe3O4-water nanofluid. The streamline contour, isotherm contour, local Nusselt number \(\left( {Nu} \right)\), average Nusselt number \(\left( {\overline{Nu} } \right)\), dimensionless total entropy generation \(\left( {S^{\prime\prime\prime}_{{{\text{Total}}}} } \right)\), and dimensionless average total entropy generation \(\left( {S_{{{\text{Total}}}} } \right)\) have been studied by varying the dimensionless amplitude of the wavy wall \(\left( \alpha \right)\) and nano-particle volume fraction \(\left( \phi \right)\) in the range of \(0 \le \alpha \le 0.05\) and \(0 \le \phi \le 0.3\%\), respectively. The value of \(Ra\) and \(\varphi\) are taken as 10–5 and 10–2, respectively (Dutta et al. 2019; Sheikholeslami et al. 2019; Swain et al. 2022).

Figure 3 depicts the streamline contour for the plane and wavy solar power plant at \(\phi\) = 0% and 0.3%. It is observed that two vortices with clock-wise and contour-clock-wise circulation are generated, attributed primarily to the presence of heated wall and density difference. Further, the symmetric vortices are found for the plane wall case, while the two different vortices are predicted for the wavy wall case. It is because of the uneven distribution of the wavy wall divided by the middle vertical section. The left side wavy wall starts with a convex surface, while the right side wavy wall ends with a concave surface. Therefore, the higher flow resistance provided by the extreme right concave wall on right side circulation causes its smaller strength. We found that the recirculation strength of vertices for wavy wall case is smaller compared to the plane wall case. It is because the flow resistance provided by the wavy wall reduces the flow strength and decreases the recirculation strength for this case as well. Furthermore, the recirculation strength for the nanofluid case (\(\phi\) = 0.3%) is smaller compared to the base fluid case (\(\phi\) = 0%). This observation is attributed to the augmentation in viscosity by nanofluid compared to the base fluid case, which enhances the flow resistance and results in a reduction in the recirculation strength.

Fig. 3
figure 3

Streamline contours for plane and wavy cavity (\(\alpha\) = 0.05) for different \(\phi\) at \({\text{Ra}} = 10^{5}\)

Full size image

Figure 4 depicts the isotherm contours for the plane and wavy solar power plant at \(\phi\) = 0% and 0.3%. It is noted that the heating effect is higher near the wall and in the intermediate vertical region of the domain. It is attributed to the flow of hot fluid from heated wall by counter-clock-wise vortex from the left side, and clock-wise vortex from the right side accumulates the heated fluid in the vertical intermediate region. Further, it is noted from Fig. 4 that the heating effect in the vertical intermediate region is smaller for the case of nanofluid. We can see that the isotherm level ‘0.55’ grown in the intermediate vertical region is smaller for \(\phi\) = 0.3% compared to \(\phi\) = 0%. We attribute this observation to the stronger vortex strength for \(\phi\) = 0% (see Fig. 3) that causes transport of heated fluid up to higher vertical height in the intermediate region. Moreover, as seen in Fig. 4, the presence of wavy wall causes formation of thinner and thicker thermal boundary layer at the convex and concave surface, respectively. Important to mention, the accelerated and deaccelerated flow rendered by the convex and concave surfaces, respectively results in such a demarcation in the configuration of the boundary layer.

Fig. 4
figure 4

Isotherm contours for plane and wavy cavity (\(\alpha\) = 0.05) for different \(\phi\) at \({\text{Ra}} = 10^{5}\)

Full size image

Figure 5 depicts the variation of local Nusselt number \(\left( {Nu} \right)\) for both plane and wavy wall cases, obtained at \(\phi\) = 0.3% and \({\text{Ra}} = 10^{5}\). It is found that the local maxima and minima of \(Nu\) is predicted at the convex and concave surfaces, due to the thinner and thicker thermal boundary layer near the heated wall, respectively (see Fig. 4). We observe that the value of local maxima is smaller in the intermediate region, attributed primarily to the presence of more heated fluid in that region (see Fig. 4) reduced the heat transfer rate. It is important to mention that the all local maxima of \(Nu\) for wavy wall are higher compared to the plane wall. Contrarily, the local minima of \(Nu\) as seen for wavy wall is smaller compared to the plane wall, which is mainly due to the formation of thicker thermal boundary layer triggered by the concave wavy surface (see Fig. 4).

Fig. 5
figure 5

Variation of local Nusselt number for plane and wavy case when \(\phi\) = 0.3% and \({\text{Ra}} = 10^{5}\)

Full size image

The overall heat transfer enhancement in wavy solar plant is represented by average Nusselt number \(\left( {\overline{Nu} } \right)\) and its variation with dimensionless amplitude \(\left( \alpha \right)\) is depicted in Fig. 6. The other parameters considered are \(\phi\) = 0 and 0.3% when \({\text{Ra}} = 10^{5}\). It is found that the \(\overline{Nu}\) becomes higher with an increase in the amplitude of the wavy wall, signifying the combined effect of increase in heat transfer area compared to plane wall and the presence of higher maxima of \(Nu\) at the convex region (see Fig. 5). Further, an increase in the nano-particle volume fraction from 0 to 0.3% enhances the value of \(\overline{Nu}\). It is because of the augmentation in effective thermal conductivity of the nanofluid compared to the base fluid case, which improves the total heat transfer rate. It is noted that the percentage enhancement in heat transfer rate are obtained as 63.52 and 66.10% for a change in \(\phi\) = 0 to 0.3%, respectively, with the change in \(\alpha\) from 0 to 0.05. On the other hand, the change in nanofluid volume fraction from 0 to 0.3% enhances the heat transfer rate up to 5.97% for \(\alpha\) = 0.05.

Fig. 6
figure 6

Variation of average Nusselt number with dimensionless amplitude for wavy case at \(\phi\) = 0 and 0.3% when \({\text{Ra}} = 10^{5}\)

Full size image

As we already know, the total entropy generation of any thermo-fluidic system should be minimum to maximize efficiency according to the second law of thermodynamics By doing this, we can maximize the available energy of the system (Bejan 2013). Henceforward, focus is given on the entropy generation analysis as discussed in the forthcoming paragraphs. First, to know the fractional contribution of thermal entropy generation on the total entropy generation (thermal and viscous) in the domain, the variation of average Bejan number \(\left( {Be_{{{\text{avg}}}} } \right)\) is depicted in Fig. 7. The plots are obtained for \(\alpha\), \(\phi\) = 0, 0.3% and \({\text{Ra}} = 10^{5}\). It is found from Fig. 7 that \(Be_{avg}\) <  < 0.5 for all the values of \(\phi\) considered. This observation signifies that the entropy generation due to viscous dissipation is dominating over the thermal entropy generation in the domain. It may be mentioned here that the higher value of \({\text{Ra}}\left( { = 10^{5} } \right)\) leads to the development of stronger flow field and resulting in higher contribution of viscous dissipation dominated entropy generation (Dutta et al. 2019). We find that the value of \(Be_{{{\text{avg}}}}\) enhances with an increase in the wave amplitude. It is based on the fact that the contribution of viscous entropy generation reduces with an increase in amplitude and is explained as follows. The increase in the sharpness of diverging wavy surface with an increase in amplitude decreases the flow field strength to satisfy the mass conservation in the field, and it reduces the velocity gradient with amplitude. Therefore, the reduction in velocity gradient and accordingly viscous entropy generation with an increase in amplitude near the diverging walls increases the value of \(Be_{{{\text{avg}}}}\). Moreover, the value of \(Be_{{{\text{avg}}}}\) enhances with \(\phi\). It is due to the fact that a decrease in recirculation strength for the nanofluid case as compared to the base fluid case (see Fig. 3) leads to a decreases in the velocity gradient at the interfaces of two opposite streams of the flow (clock-wise and counter-clock-wise) and near the wall with \(\phi\). Therefore, a decrease in entropy generation due to viscous dissipation for the nanofluid case leads to an increases the value of \(Be_{{{\text{avg}}}}\) with \(\phi\) as witnessed in Fig. 7.

Fig. 7
figure 7

Variation of average Bejan number with dimensionless amplitude for wavy case at \(\phi\) = 0 and 0.3% when \({\text{Ra}} = 10^{5}\)

Full size image

Figure 8 depicts the contour of the dimensionless total entropy generation \(\left( {S^{\prime\prime\prime}_{{{\text{Total}}}} } \right)\) for both the plane and wavy solar power plant, obtained at \(\phi\) = 0 and 0.3%. The distribution of \(S^{\prime\prime\prime}_{{{\text{Total}}}}\) can be explained from the variation of velocity gradient in the domain as the entropy generation due to viscous dissipation is dominating one (see Fig. 7). It is noted that the intensity of \(S^{\prime\prime\prime}_{{{\text{Total}}}}\) is higher at the attachment region of vortices, i.e., at the top and bottom walls and in the region of attachment and detachment of two vortices. The combined effects like the generation of higher velocity gradient near the walls and the interaction of two opposite stream of vortices at the attachment and detachment region give rise to higher viscous entropy generation and \(S^{\prime\prime\prime}_{{{\text{Total}}}}\). Further, the presence of wavy wall decreases the intensity of \(S^{\prime\prime\prime}_{{{\text{Total}}}}\) near the bottom wall. It is attributed to the presence of concave surface that decreases the velocity gradient and results in a decrease of the viscous dissipation modulated entropy generation compared to the plane wall. Also, the decrease in recirculation strength with \(\phi\) decreases the viscous dissipation modulated entropy generation and the intensity of \(S^{\prime\prime\prime}_{{{\text{Total}}}}\).

Fig. 8
figure 8

Dimensionless total entropy generation contours for plane and wavy cavity (\(\alpha\) = 0.05) for different \(\phi\) at \({\text{Ra}} = 10^{5}\)

Full size image

The overall entropy generation in domain represented by dimensionless averaged total entropy generation \(\left( {S_{{{\text{Total}}}} } \right)\) and corresponding variation with dimensionless amplitude \(\left( \alpha \right)\) is depicted in Fig. 9. The other parameters chosen for plotting the figure are \(\phi\) = 0 and 0.3%, \({\text{Ra}} = 10^{5}\). It is noted that the value of \(S_{{{\text{Total}}}}\) decreases with \(\alpha\) and \(\phi\), attributed primarily to the decrease in total entropy generation intensity by the wavy wall compared to the plane wall and the decrease in the same by nanofluid compared to the base fluid case (see Fig. 8). It is noted that the percentage decrement in \(S_{{{\text{Total}}}}\) are obtained as 23.03% and 29.77% for \(\phi\) = 0 to 0.3%, respectively, with the change in \(\alpha\) from 0 to 0.05. On the other hand, the change in nanofluid volume fraction from 0 to 0.3% enhances the heat transfer rate up to 40.01% for \(\alpha\) = 0.05.

Fig. 9
figure 9

Variation of average dimensionless total entropy generation with dimensionless amplitude for wavy case at \(\phi\) = 0 and 0.3% when \({\text{Ra}} = 10^{5}\)

Full size image

5 Conclusion

We have investigated the natural convective heat transfer and entropy generation characteristic inside a wavy solar power plant filled with MWCNT-Fe3O4-water nanofluid numerically consistent with the finite element method. The streamline contour, isotherm contour, local Nusselt number \(\left( {Nu} \right)\), average Nusselt number \(\left( {\overline{Nu} } \right)\), dimensionless total entropy generation \(\left( {S^{\prime\prime\prime}_{{{\text{Total}}}} } \right)\), and dimensionless average total entropy generation \(\left( {S_{Total} } \right)\) have been studied by varying the dimensionless amplitude of the wavy wall \(\left( \alpha \right)\) and nano-particle volume fraction \(\left( \phi \right)\). It is found that the presence of wavy wall and addition of nano-particle in base fluid decreases the recirculation strength appreciably. The increase in amplitude of wavy wall and nano-particle volume fraction enhances the average Nusselt number significantly. Moreover, the viscous entropy generation is seen to be the dominating mode towards bringing irreversibility into the system for the chosen value of \({\text{Ra}}\). The increase in wave amplitude and nano-particle volume fraction reduces the average entropy generation. We found 40.01% reduction in average value of total entropy generation rate for a change in nano-particle volume fraction from 0 to 0.3% when \(\alpha\) = 0.05. The findings from the present work are found to be of importance in designing an efficient solar power plant.