Numerical investigation on the effect of magnetic field on natural convection heat transfer from a pair of embedded cylinders within a porous enclosure

Abstract

The present work examines the influence of magnetohydrodynamic field on natural convection phenomena inside a porous square enclosure with a pair of embedded hot circular cylinders. Numerical investigations are performed to understand the effects of interspacing distance between the embedded cylinders, Hartmann number, Rayleigh number and Darcy number on the thermal transport process and the total irreversibility generation. It is observed that the isotherm distribution is strongly affected by the presence of magnetic field although the distribution of streamlines remains independent of the strength of magnetic field. This underlines the fact that magnetic field strongly influences the heat transfer process and entropy generation characteristics. It reveals that the natural convection is suppressed in the presence of a higher magnetic field as evident from the reduction in Nusselt number. It is observed that an increase in the spacing between the cylinders increases the heat transfer rate, and moreover, the effect of the magnetic field on heat transfer is more pronounced at higher interspacing distance between the embedded cylinders. The heat transfer rate increases significantly with the increase in the permeability of the medium. The entropy generation rate is independent of the strength of applied magnetic field. Further, the contribution of the entropy generation owing to friction is found to be negligible in total irreversibility obtained at lower values of Rayleigh number irrespective of Darcy number. However, the contribution of irreversibility owing to heat transfer is found to be minimal at higher values of Rayleigh number.

Introduction

The evolution of technology leads to the intensification of heat generation in many engineering applications which include the manufacturing process, transportation, microelectronics devices and thermal power plants. As a concequence, efficient coolants are required for proper heat dissipation [1,2,3,4,5]. In general, active and passive methods of heat transfer are adopted for these systems to obtain maximum heat transfer and energy efficiency [6,7,8,9,10,11]. This has motivated the scientific community to strive in search of ways to intensify the heat transfer without the application of external power source. This leads to more emphasis on studies concerning natural convection. In past few decades, the buoyancy-induced natural convection is one of the extensively investigated research topics owing to its wide range of applications in several areas which include the design of buildings and furnaces [12,13,14,15,16,17,18,19,20,21,22,23], nuclear reactor cooling systems [14], energy storage devices [15] and thermoelectric generator [16]. It is well known that the convection mechanism is strongly affected by the geometrical configuration of the enclosure, presence of the embedded objects, flow parameters like Rayleigh number and imposed external field like a magnetic field. In this context, most of the works have employed the square/rectangular enclosure for investigations as it involves the complicated flow pattern arising due to the boundary layer which bounds the inviscid core because of four walls of the enclosure. Moreover, the geometrical configuration of the embedded object, presence of thermal radiation and internal heat generation also affects the heat transfer phenomena inside the enclosure. Recently, investigators have worked on different discrete heat source, the aspect ratio of enclosure, porous enclosure and the different thermal boundary condition on the walls of the enclosure. Investigators have also considered an electrically conducting fluid within an enclosure which generates the resisting effect of Lorentz force under the influence of the magnetic field. The presence of this external field creates the flow physics more complicated. The researchers put an effort to explore the magnetohydrodynamic effect on thermal characteristics on natural convection phenomena. The exact mechanism by which the convection phenomena are affected in the presence of embedded objects, external magnetic field is not understood so far and remains overlooked.

The presence of embedded objects within the enclosure affects the natural convection phenomenon inside the enclosure [17,18,19,20,21,22] depending on its position, geometrical configurations and the number of embedded objects. In this context, Lee et al. [17] and Kim et al. [18] reported the interplay between the Rayleigh number and position of embedded cylinders on convection heat transfer within an enclosure. They pointed out the fact that the spacing between the embedded cylinders [17] and the geometrical configuration of the cylinders [18] dictates the thermo-hydraulic characteristics. Park et al. [19] investigated the natural convection phenomena due to the temperature difference between the hot embedded cylinders and the cold walls of the enclosure. Further, they discussed about the influence of cylinder location on natural convection mechanism. Thereafter, Siavashi et al. [20] studied the effect of the angular speed of an embedded cylinder on heat transfer characteristics in a porous enclosure. They reported that the improvement in heat transfer is strongly influenced by the direction of the angular velocity of the rotating cylinder, Darcy number and thermal conductivity ratio. Mina [21] investigated the augmentation of heat transfer rate for different configurations of the enclosure’s geometry. He worked on an oval and rectangular-shaped enclosure and stated that the Nusselt number is relatively higher in case of oval-shaped enclosure. In the similar aspect of heat transfer augmentation, Dogonchi et al. [22] considered a triangular cavity with a semicircular bottom wall. They showed that heat transfer is enhanced significantly by decreasing the radius of the semicircle.

In the recent past, researchers have employed various thermal boundary conditions on the enclosure walls to gain an insight into the complex behaviour of convection mechanism [23,24,25,26,27]. For an instance, Mahapatra et al. [23] discussed the effect of an adiabatic and an isothermal block on heat transfer augmentation within a square enclosure. They observed that the isothermal block is thermodynamically more efficient than an adiabatic block. Later on, Kolsi et al. [24] have performed a similar type of investigation by considering two adiabatic blocks in the presence of aluminium oxide–water nano-fluid. Their study reveals the fact that the size of the adiabatic blocks and volume fraction of nano-fluid are the two key parameters for maximization of heat transfer rate and minimization of total irreversibility produced within the system. In the recent past, Rashidi et al. [25] showed the asymmetric behaviour of heat transfer and entropy generation characteristics at higher values of Rayleigh number within an enclosure which is under heterogeneous heat flux condition. Shuja et al. [26] concluded that the location of the exit port has a significant effect on energy consumption and entropy generation inside a square cavity. Bhowmick et al. [27] studied the effect of sinusoidal heating and the shape of the embedded object on natural convection phenomena inside a square cavity. They found that the embedded object with circular shape at the higher wavelength of the non-uniform temperature provides a maximum heat transfer rate with minimum entropy generation.

Some of the notable studies on the thermo-fluidic characteristics within a porous enclosure include the work of Nield and Bejan [28], Vafai [29], Bejan et al. [30] and Ingham and Pop [31]. Numerous studies have been carried out on the buoyancy-driven convection within a porous enclosure by considering different shapes of enclosure geometries such as trapezoidal, triangular, conventional square one or even more complex geometries [32,33,34]. Ramakrishna et al. [32] showed that different imposed boundary conditions and thermal aspect ratio monitor the fluid flow and heat transfer characteristics inside a square porous enclosure. Further, they observed that heat transfer is conduction dominated at lower values of Darcy number. Later on, Wu et al. [33] investigated the effect of non-uniform temperature distribution on thermal characteristics inside a porous enclosure. They concluded that the Nusselt number enhances significantly when a non-uniform temperature distribution is imposed. Also, they reported that the effect of the phase difference of non-uniform temperature distribution is not significant on heat transfer enhancement. Zargartalebi et al. [34] investigated unsteady conjugate natural convection within a porous cavity. They observed that the thickness of the solid wall and thermal conductivity ratio between the solid wall and the investigating fluid alter the heat transfer characteristics. Motlagh et al. [35] discussed about the effect of different physical parameters of a porous medium, altering the heat transfer characteristics within a tilted porous enclosure. They observed that higher heat transfer occurs by reducing the porosity of the medium at higher Rayleigh number whereas, at low Rayleigh number, the opposite trend is observed.

There are some notable works that have focused on entropy generation inside the porous enclosure [36,37,38,39,40,41]. In the recent past, Bhardwaj et al. [42] worked on natural convection within a triangular porous cavity to attain maximum thermal performance and minimum thermodynamic irreversibilities by employing a non-isothermal temperature distribution at the surface of the porous cavity. Further, Meshram et al. [43] studied the effects of Darcy number and angle of inclination on free convection phenomena inside a cavity. They pointed out the fact that Darcy number has a significant effect on heat transfer and entropy generation characteristics. Later on, Datta et al. [44] investigated the influence of an adiabatic object on entropy generation within a porous cavity. They reported the formation of different regimes depending upon the value of the Rayleigh number and the position of the object. Dutta et al. [36] employed non-uniform heating conditions at the wall of a porous enclosure to achieve minimum thermodynamic irreversibilities and maximum heat transfer rate. In another study, Dutta et al. [37] discussed the convective heat transfer phenomena along with total entropy generation within a quadrantal porous enclosure. They established a relation between the buoyancy force and the Forchheimer drag force to achieve a maximum heat transfer rate in lieu of minimal entropy generation within the thermal system. Pal et al. [38] showed the effect of interspacing distance between the embedded cylinders inside a porous enclosure on entropy generation characteristics. They concluded that the thermal irreversibility has a major contribution on total entropy generation at a lower value of Darcy number.

Numerous studies have been carried out to establish the merit of MHD natural convection within an enclosure. In this context, Sheremet et al. [39] performed a numerical analysis to visualize the effect of Hartman number and the orientation angle of magnetic field on thermal transport phenomena. They pointed out that the convective flow is suppressed when the value of Hartmann number increases thereby reducing the heat transfer rate. However, Lorentz force dominates the buoyancy force when the inclination angle of the magnetic field has shifted from 0 to ${\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}$. While further increment in the orientation angle, the convective flow gets intensified. The influence of the magnetic field on heat transfer and entropy generation characteristics in a corrugated shaped cavity was studied by Chao et al. [40]. They discussed the interplay between Rayleigh number, Hartmann number and the amplitude of the wavy surface on heat transfer characteristics. In addition to this, the thermal entropy generation dominates the total entropy generation rate at a higher value of Hartmann number. Further, Bondareva et al. [41] established a relationship between the geometrical configuration of a wavy porous cavity and the magnetic field on heat transfer characteristics. Sheikholeslami and Shehzad [45] performed a numerical study on MHD free convection in a nano-fluid saturated porous enclosure. It can be concluded from their observation that enhancement of heat transfer is inconsistent with the increment of Rayleigh number, whereas the opposite trend is observed for higher values of Hartmann number and lower value of Darcy number. Dutta et al. [46] studied the effects of Hartmann number on fluid flow, heat transfer and entropy generation characteristics within a rhombic porous enclosure. They concluded that the heat transfer rate significantly decreases with the Hartmann number for the higher value of the Rayleigh number (Ra > 10⁵). Moreover, the thermal entropy generation dominates the other parameters controlling the total entropy generation. In another study, Tayeb and Chamkha [47] have performed an investigation on total irreversibility produced within a cavity that embraces a conducting cylinder due to the presence of the magnetic field. They stated that the presence of cylinder affects the flow physics, heat transfer and also entropy generation characteristics. Muthukumar et al. [48] analysed the combined effects of MHD convection and thermal radiation within a nano-fluid filled porous cavity. They observed that the heat transfer rate increases significantly in the presence of thermal radiation. However, an increase in the strength of magnetic field suppresses the effect of thermal radiation resulting in a decrement in Nusselt number variation. Li et al. [49] worked on the influence of MHD natural convection inside a sinusoidal annulus in the presence of thermal radiation. They concluded that the heat transfer rate decreases with an increase in Hartman number and number of undulations although the thermal radiation results in enhancement of heat transfer. In another study, Biswas and Manna [50] studied the Marangoni convection under the presence of an external magnetic field and argued that the order and nature of thermal mixing are strongly dependent upon Hartmann number and Marangoni number.

In spite of numerous investigations on buoyancy-driven heat transfer from a pair of embedded cylinders within a cavity, the combined effect of the magnetic field in presence of porous media with embedded cylinders in an enclosure has not been explored so far. An in-depth investigations into the flow physics and heat transfer characteristics for natural convection from a pair of embedded hot cylinders saturated with porous medium need to be executed. Accordingly, the aim of the present work is to numerically analyse the influence of Hartmann number, Darcy number and interspatial distance between embedded hot cylinders on the heat transfer and entropy generation characteristics within a square cavity in presence of the porous medium.

Physical model and mathematical formulation

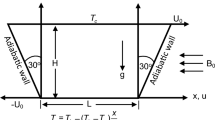
Figure 1 represents the schematic of the physical model considered for the present investigation. A pair of embedded cylinders within a square enclosure of length L is considered in our study. The width of the enclosure serves as the characteristic length scale on which Rayleigh number can be defined. The pair of embedded cylinders are situated at the vertical mid-plane of the square enclosure with an interspacing distance of s. The enclosure is saturated with porous media. Further, the walls of the enclosure are maintained at a constant temperature of T_c whereas the surfaces of the embedded cylinders are kept in a temperature of T_h (> T_c). The enclosure is filled with air which is permeated by a horizontally applied magnetic field B₀. To establish a relation between density variations due to temperature change and so as to relate the temperature field and the flow field, the Boussinesq approximation is considered. Heat transfer due to radiation, compressibility effect and viscous dissipation are neglected. Moreover, the effects of displacement current induced in an applied magnetic field and Joule heating are also ignored for the present investigation.

Fig. 1

Schematic diagram of the physical model

Governing equations

A constant thermo-physical fluid model is assumed with the exemption of density in the body force of the y-momentum equation to solve the fluid flow, heat transfer and thermodynamic irreversibilities. The flow inside the enclosure is unsteady, incompressible, two-dimensional and laminar, and the working fluid is Newtonian one. The non-dimensional form of governing equations can be expressed as:

• Continuity equation

  $$\frac{{\partial U^{*} }}{{\partial X^{*} }} + \frac{{\partial V^{*} }}{{\partial Y^{*} }} = 0$$

  (1)

• Transport of momentum

  $$\frac{{\partial U^{*} }}{{\partial \tau^{*} }} + U^{*} \frac{{\partial U^{*} }}{{\partial X^{*} }} + V^{*} \frac{{\partial U^{*} }}{{\partial Y^{*} }} = - \frac{{\partial P^{*} }}{{\partial X^{*} }} + Pr \left( {\frac{{\partial^{2} U^{*} }}{{\partial X^{{*^{2} }} }} + \frac{{\partial^{2} U^{*} }}{{\partial Y^{{*^{2} }} }}} \right) - \frac{{Pr} }{{\text{Da}}}U^{*}$$

  (2)
  $$\frac{{\partial V^{*} }}{{\partial \tau^{*} }} + U^{*} \frac{{\partial V^{*} }}{{\partial X^{*} }} + V^{*} \frac{{\partial V^{*} }}{{\partial Y^{*} }} = - \frac{{\partial P^{*} }}{{\partial Y^{*} }} + Pr \left( {\frac{{\partial^{2} V^{*} }}{{\partial X^{{*^{2} }} }} + \frac{{\partial^{2} V^{*} }}{{\partial Y^{{*^{2} }} }}} \right) - \frac{Pr }{{\text{Da}}}V^{*} + \text{Ra} \text{Pr} \theta^{*} - \text{Ha}^{2} Pr V^{*}$$

  (3)

• Transport of energy

  $$\frac{{\partial \theta^{*} }}{{\partial \tau^{*} }} + U^{*} \frac{{\partial \theta^{*} }}{{\partial X^{*} }} + V^{*} \frac{{\partial \theta^{*} }}{{\partial Y^{*} }} = \left( {\frac{{\partial^{2} \theta^{*} }}{{\partial X^{{*^{2} }} }} + \frac{{\partial^{2} \theta^{*} }}{{\partial Y^{{*^{2} }} }}} \right)$$

  (4)

The non-dimensional parameters and variables for the above-declined equations are

$$ \begin{aligned} \left( {X^{*} ,Y^{*} } \right) & = \frac{x}{L}, \, \frac{y}{L}, \, \tau = \frac{\alpha t}{{L^{2} }}, \, \left( {U^{*} ,V^{*} } \right) = \frac{uL}{\alpha }, \, \frac{vL}{\alpha }, \, \theta^{*} = \frac{{T - T_{\text{c}} }}{{T_{\text{h}} - T_{\text{c}} }}, \\ P^{*} & = \frac{{pL^{2} }}{{\rho \alpha^{2} }},\;\text{Ra} = \frac{{g\beta \left( {T_{\text{h}} - T_{\text{c}} } \right)L^{3} Pr }}{{\upsilon^{2} }},\;\text{Da} = \frac{\kappa }{{L^{2} }}, \, \text{Ha} = {B_{0}\text{L}}\sqrt {\frac{\sigma }{\mu }} \\ \end{aligned}$$

(5)

Boundary conditions

To solve the governing Eqs. (1)–(4), the following boundary conditions are employed:

Hydrodynamic boundary conditions:

All components of the velocity have been considered as zero along the wall of the enclosure as well as at the wall of the embedded cylinders.

$$U^{*} = \, V^{*} = 0.$$

(6)

Thermal boundary conditions:

A uniform lower temperature has been considered along the walls of the enclosure:

$$\theta^{*} = 0.$$

(7)

The surface of the embedded cylinders are maintained a high uniform temperature, i.e.

$$\theta^{*} = 1.$$

(8)

Stream function and Nusselt number formulation

The fluid motion within the square enclosure can be displayed with the help of stream function $\left( {\psi^{*} } \right)$ which can be evaluated from the velocity components. The relationship between the stream function and velocity components for a two-dimensional, laminar and incompressible flow is as follows:

$$U^{*} = \frac{{\partial \psi^{*} }}{{\partial Y^{*} }}\;{\text{and}}\;V^{*} = - \frac{{\partial \psi^{*} }}{{\partial X^{*} }}$$

(9)

Equation (9) reduces to the following single equation for stream function

$$\frac{{\partial^{2} \psi^{*} }}{{\partial X^{{*^{2} }} }} + \frac{{\partial^{2} \psi^{*} }}{{\partial Y^{{*^{2} }} }} = \frac{{\partial U^{*} }}{{\partial Y^{*} }} - \frac{{\partial V^{*} }}{{\partial X^{*} }}$$

(10)

A positive sign for stream function $\left( {\psi^{*} } \right)$ denotes the counterclockwise circulation of fluid, whereas the negative sign denotes the clockwise circulation. In addition to this, no-slip boundary condition has been imposed on all the walls of the enclosure and the embedded cylinders. Hence, $\psi^{*} = 0$ is applied in all the boundaries of the enclosure and the embedded cylinders.

The temperature field is obtained by solving the governing Eqs. (1)–(4) with the help of boundary conditions [refer to Eqs. (6)–(8)].

To quantify the convective heat transfer over the conduction one, local Nusselt number is calculated around the periphery of the embedded cylinders as:

$$\text{Nu}_{{\varphi }} = \frac{{h_{\varphi} d}}{k} = - \left. {\frac{{\partial \theta^{*} }}{{\partial n^{*} }}} \right|_{{{\text{ surface}}\;{\text{of}}\;{\text{the}}\;{\text{cylinder}}}} .$$

(11)

where $h_{\varphi}$ is the local surface convective heat transfer coefficient on the embedded cylinders walls and n^* indicates the direction normal to the cylinder surface. The surface average Nusselt number is calculated by integrating the local Nusselt number along the periphery of the cylinder as follows:

$${\overline{\text{Nu}}} = \left( {\frac{1}{\text{Per}}} \right)\int\limits_{0}^{\text{Per}} {{\text{Nu}}_{{\varphi }} {\text{d}}\varphi } .$$

(12)

Here ‘Per’ indicates the periphery of the embedded cylinders.

The time-averaged Nusselt number is calculated over a period over time which can be expressed as follows:

$${\overline{{\text{Nu}_{\text{t}} }}} = \frac{1}{T}\int\limits_{\rm t}^{t + T} {\overline{{\text{Nu}}} \, \text{d}t}$$

(13)

It is important to mention that the irreversibility present in the problem comprises of the irreversibility owing to temperature gradient within the square enclosure, the transformation of mechanical energy into inter-molecular energy by means of fluid-friction (viscous effect) and presence of the magnetic field. The local entropy generation in non-dimensional form can be expressed as;

$$N = N_{\uptheta} + N_{\psi} + N_{{\text{mf}}}$$

(14)

where $N_{\uptheta}$, $N_{\psi}$ and $N_{{\text{mf}}}$ denotes the local entropy generation or the irreversibility arises due to heat transfer, fluid friction, and magnetic field, respectively. The expression for thermal, viscous and magnetic field entropy generation in non-dimensional form can be expressed as:

$$N_{\theta} = \left[ {\left( {\frac{{\partial \theta^{*} }}{{\partial X^{*} }}} \right)^{2} + \left( {\frac{{\partial \theta^{*} }}{{\partial Y^{*} }}} \right)^{2} } \right]$$

(15)

$$N_{\psi} = \zeta \left[ {\left( {U^{{*^{2} }} + V^{{*^{2} }} } \right) + {\text{Da}}\left\{ {2\left\{ {\left( {\frac{{\partial U^{*} }}{{\partial X^{*} }}} \right)^{2} + \left( {\frac{{\partial V^{*} }}{{\partial Y^{*} }}} \right)^{2} } \right\} + \left( {\frac{{\partial U^{*} }}{{\partial Y^{*} }} + \frac{{\partial V^{*} }}{{\partial X^{*} }}} \right)^{2} } \right\}} \right]$$

(16)

$$N_{\text{mf}} = \zeta {\text{Ha}}^{2} V^{{*^{2} }}$$

(17)

Here, term ‘$\zeta$’ denotes the irreversibility distribution ratio which can be defined as:

$$\zeta = \frac{{\mu T_{0} }}{k}\left( {\frac{\alpha }{L\Delta T}} \right)^{2}$$

(18)

It may be noted that the value of $\zeta$ is fixed to 10⁻². The global entropy generation can be expressed as:

$$N_{\text{Total}} = N_{{\theta,{\text{T}}}} + N_{{\psi,{\text{T}}}} + N_{{{\text{mf}},{\text{T}}}}$$

(19)

where $N_{{\theta,{\text{T}}}}$, $N_{{\psi,{\text{T}}}}$ and $N_{{{ \text{mf}},{ \text{T}}}}$ represent the volumetric entropy generation due to heat transfer, fluid friction and magnetic field, respectively, which can be given as:

$$N_{{ \theta,{\text{T}}}} = \int\limits_{ \Omega } {N_{ \theta} { \text{d}} \Omega }$$

(20)

$$N_{{ \psi,{\text{T}}}} = \int\limits_{ \Omega } {N_{ \psi} { \text{d}} \Omega }$$

(21)

$$N_{{{ \text{mf}},{ \text{T}}}} = \int\limits_{\varOmega } {N_{ \text{mf}} { \text{d}} \Omega }$$

(22)

The distribution of irreversibility can be quantified using Bejan number which is formulated as follows:

$${ \text{Be}} = \frac{{N_{ \theta} }}{{N_{ \theta} + N_{ \psi} + N_{{ \text{mf}}} }}$$

(23)

The relative volumetric irreversibility distribution can be obtained by means of the average Bejan number which can be calculated as:

$$\overline{ \text{Be}} = \frac{{N_{{ \theta,{ \text{T}}}} }}{{N_{{ \theta,{ \text{T}}}} + N_{{ \psi,{\text{T}}}} + N_{{{ \text{mf}}, \text{T}}} }}$$

(24)

It may be noted that a value of $\overline{ \text{Be}} > 0.5$ indicates the dominance of thermal entropy generation, whereas $\overline{ \text{Be}} < 0.5$ implies the dominance of entropy generation due to the combined effect of fluid friction and magnetic field.

Numerical solution methodology and model validation

The finite element method has been employed to solve the governing differential equations along with boundary conditions. The computational domain is divided into a number of sub-domains which are also known as elements. Within each of these sub-domains, all the flow variables are approximated by using proper interpolation functions resulting in the finite element equations which are evaluated in a closed form and have nonlinear characteristics. The Galerkin weighted residual technique is employed to convert the partial differential governing equations into a set of integral equations. The integration of these equations is performed by using Gauss’s quadrature method. The iterative technique is used to solve these equations. This iterative technique performs the successive iterations until it satisfies residual criteria (or convergence criteria) of $\left| {\frac{{\varepsilon^{\rm{n} + 1} - \varepsilon^{\rm{n}} }}{{\varepsilon^{\rm{n}} }}} \right| \le 10^{ - 6}$ for the temperature and velocity field within the computational domain where the term $^{\prime } \varepsilon^{\prime }$ denotes any transport variable.

An extensive grid sensitivity test has been performed for different interspacing distances between the embedded hot cylinders. For mesh independence study, we have considered, Ra = 10⁶, Da = 10⁻³, S = 0.1, 0.3 and 0.5 for a range of Hartmann number (Ha = 0 – 100). Table 1 shows the time-averaged Nusselt number $\left( { \overline{{{\text{Nu}}_{\rm t} }} } \right)$ for the grid systems chosen at a various interspacing distance. It can be observed that $\left( {\overline{{{ \text{Nu}}_{\rm t} }} } \right)$ is invariant when the number of elements is increased from 9291 to 24,736 for S = 0.1. Similarly, the deviation in $\left( {\overline{{{ \text{Nu}}_{\rm t} }} } \right)$ is not significant when the number of elements is increased from 8310 and 8062 to 20,446 and 19,866 for S = 0.3 and S = 0.5, respectively. This result indicates that the grid systems with 9291, 8310, and 8062 elements are sufficient to capture the flow physics and accordingly, these number of elements are chosen for the simulations throughout the study.

Table 1 Comparison of surface time-averaged Nusselt number for different grid sizes and interspacing distance for Ra = 10⁶ and Da = 10⁻³ for the circular embedded cylinder

Prior proceed to the analysis of present numerical investigation, we first ascertain the correctness of numerical code, used to solve the governing equations. To do that, the natural convection heat transfer inside the enclosure with pair of embedded objects for S = 0.3 and 0.5 for Ra = 10³ and 10⁶ at Da = 10⁻³ is considered for the validation following the work of Pal et al. [38]. The temporal variation of the surface-averaged Nusselt number is plotted as shown in Fig. 2 and compared with the results of Pal et al. [38]. It can be seen that the temporal variation of the surface-averaged Nusselt number is in good agreement which ascertains the correctness of our results presented herein. Furthermore, a separate validation study is carried out wherein the variation of local Nusselt number along the bottom wall of the square enclosure is plotted for Ra = 10⁵ and Ha = 50 and compared with the results of Sathiyamoorthy and Chamkha [51]. The close agreement as shown in Fig. 2c reconfirms the validity of the solver.

Fig. 2

Model validation: a comparison of temporal variation of surface-averaged Nusselt number at S = 0.3, b comparison of temporal variation of surface-averaged Nusselt number at S = 0.5, c comparison of local Nusselt number with the distance of the bottom horizontal wall

Results and discussions

The primal aim of the present study is to investigate the effect of the magnetic field on buoyancy-driven convective heat transfer and entropy generation characteristics inside a cold porous enclosure with two embedded hot cylinders. Investigations are carried out for a range of Hartmann number (Ha = 0–100), Darcy number (Da = 10⁻³ and 10⁻²), Rayleigh number (Ra = 10³ and 10⁶) and three different values of interspacing distances between the embedded cylinders (S = 0.1, 0.3 and 0.5). Three competing forces, namely buoyancy force due to the applied temperature difference between the hot embedded cylinders and walls of the enclosure, Lorentz force due to the applied magnetic field and viscous resistance forces are influenced the flow physics and transport characteristics. The effect of these three forces on the heat transfer and entropy generation characteristics can be visualized by the distribution of streamlines and isotherms contours, the variation of surface-averaged Nusselt number, time-averaged Nusselt number, total entropy generation rate and average Bejan number as presented in the subsequent section.

Streamline and isotherm

The combined influences of S, Ha, and Da on the fluid flow and heat transfer characteristics can be clearly visualized from streamlines and isotherms contours plots as depicted in Figs. 3, 4 for Da = 10⁻³ and Da = 10⁻² at Ra = 10⁶. Intuitively, the fluid in the vicinity of the heated cylinders gets rarefied and starts uprising. Thereafter, the heated plumes strike the cold wall and descend towards the bottom of the enclosure and develop cells in between the heated cylinders and walls of the enclosure. It can be observed from Fig. 3 that two primary vortices are formed around the heated cylinders irrespective of any Ha at S = 0.1. One of these primary vortices is circulating in the counterclockwise direction and another one in the clockwise direction. Moreover, these two vortices are symmetrical along the vertical mid-plane of the enclosure. The commencement of breakup of the nuclei of the rotating vortices is observed when the interspacing distance between two embedded cylinders increases from S = 0.1 to S = 0.3. Moreover, two primary vortices are squished towards the vertical cold side walls and two secondary vortices are formed to fill the vacant space between two embedded cylinders when the cylinders are situated at the farthest distance (S = 0.5) from each other. It is quite evident that the effect of high Rayleigh number is not imminent when the fluidity of the porous medium is much lesser, i.e. Da = 10⁻³.

Fig. 3

Streamline distribution for different interspacing distance of cylinders and Hartmann number at $\tau = 1$, Ra = 10⁶ and Da = 10⁻³

Fig. 4

Streamline distribution for different interspacing distance of cylinders and Hartmann number at $\tau = 1$, Ra = 10⁶ and Da = 10⁻²

The effect of Hartmann number on the fluid flow characteristics in low permeable porous medium, i.e. Da = 10⁻³ is depicted in Fig. 3. When the magnetic field is applied along the horizontal direction of the enclosure, the velocity field is suppressed due to the retarding effect of Lorentz force irrespective of S. For instance, it can be observed from Fig. 3 that the maximum value of stream function is reduced from 10.88 to 4 when the value of Hartmann number increases from 0 to 100 for S = 0.1. This is basically owing to the higher strength of the magnetic field which suppresses the convective strength. The effect of the magnetic field on natural convection phenomena is more prominent with the increase in interspacing distance and attains a maximum impact for S = 0.5. Moreover, the primary and the secondary vortices are getting stretched for S = 0.3 and 0.5 when Ha = 75. An interesting observation can be seen at S = 0.5 and Ha = 100 where two small tertiary vortices are seen in the vicinity of the embedded cylinders. It can be observed from Fig. 4 that the convection current becomes more prominent at Ra = 10⁶ when the permeability of the porous medium increases (Da = 10⁻²) for different interspacing distances. The enhanced permeability helps to increase the fluid circulation within the enclosure. As a result, the strength of the primary and secondary vortices increases when the permeability of the medium is higher irrespective of Ha and S. As mentioned earlier, the onset of secondary vortices is observed for S = 0.3 onwards and similar observation can be seen for Da = 10⁻² also.

It can be observed that the area of the secondary vortices grows and attains a maximum size for S = 0.5. On the contrary, the strength of both primary and secondary vortices reduces with increasing the interspacing distance from S = 0.1 to 0.5 irrespective of Ha and Da. The combined influences of Hartmann number and Darcy number on the fluid flow characteristics are clearly reflected in Figs. 3 and 4 for buoyancy-induced convective flow. It can be seen that lowering the permeability of the porous medium reduces the strength of primary and secondary vortices. However, both the primary and secondary vortices are squeezed in between the embedded cylinders and the walls of the enclosure at Da = 10⁻². The higher value of Ha leads to a decrement in the strength of the vortices, whereas the high permeability medium (Da = 10⁻²) tends to enhance the convective strength and size of the vortices.

In order to have a clear understanding of the interplay between interspacing distance, Hartmann number and Darcy number on the temperature distribution within the square enclosure, the distribution of isotherms needs to be analysed and accordingly, the distribution of isotherms for three different values of interspacing distance (S = 0.1, 0.3 and 0.5) and a range of Hartmann number (Ha = 0, 25, 50, 75 and 100) are presented in Figs. 5 and 6 for Da = 10⁻³ and 10⁻², respectively, for a particular value of Rayleigh number (Ra = 10⁶). It can be seen from Fig. 5 that the values of isotherms are maximum in the vicinity of the embedded hot cylinders. However, with a progressive increment of Ha, the maximum value of isotherms tends to shift towards the upper cold walls. Furthermore, the isotherms are found to be non-uniformly distributed in the absence of a magnetic field. On the contrary, the presence of the magnetic field distributes the isotherms uniformly within the enclosure. This reflects the relative dominance of Lorentz force over the buoyancy forces whenever a magnetic force is applied. With an increase in interspacing distance, the density of the isotherms increases around the embedded cylinders. As a consequence, the thermal boundary layer thickness reduces leading to augmentation in heat transfer rate. The rate of fluid penetration from the top wall into the region between two cylinders is maximum for S = 0.3 without any presence of a magnetic field. Interestingly, the penetration depth becomes least for S = 0.5 due to the lower value of Da.

Fig. 5

Distribution of isotherms at $\tau = 1$ for different interspacing distance of cylinders and Hartmann number at Ra = 10⁶ and Da = 10⁻³

Fig. 6

Distribution of isotherms for different interspacing distance of cylinders and Hartmann number at $\tau = 1$, Ra = 10⁶ and Da = 10⁻²

Figure 6 shows the distribution of isotherms for a highly permeable porous medium (Da = 10⁻²). It can be observed that the enhanced permeability reduces the opposing force against fluidity and the convective heat transfer is dominated by buoyancy force. Moreover, the velocity boundary layers covering the embedded cylinders become thinner which induces a steep temperature gradient that leads to enhanced heat transfer from the cylinder surface. It is interesting to observe that an increase in the fluidity of the medium distorts the uniformity of the isotherms particularly in the vicinity of the wall of cylinders and enclosure. Similarly, the non-uniform distribution of isotherms is clearly visible in the absence of the magnetic field (Ha = 0). Further, the non-uniformity in distribution of the isotherms reduces with an increase in Ha as shown in Fig. 6.

The combined effects of S, Ha and Da on the isotherms distribution are clearly observed from Figs. 5 and 6, respectively. The penetration of fluid from the top of the wall towards the embedded cylinders is more for Ha = 0 irrespective of interspacing distance. An onset of fluid penetration starts for S = 0.3, and the length of fluid penetration is minimum when the embedded cylinders are situated at the farthest distance from each other (S = 0.5). Furthermore, the isotherms are distributed in the vicinity of the embedded cylinders tend to shift towards the walls of the enclosure for Da = 10⁻² for S = 0.3. It is observed that the isotherms are clustered around the vertical mid-plane of the enclosure when the permeability of the medium reduces. This phenomenon indicates that the flow resistance due to the presence of porous medium decreases for Da = 10⁻² and buoyancy-driven convection comes into play.

Nusselt number

It is imperative to study the temporal variation of Nusselt number in order to analyse the combined influences of Hartmann number, Darcy number, Rayleigh number and interspacing distance between the embedded cylinders on the unsteady thermal transport phenomena. Accordingly, the surface-averaged Nusselt number $\left( {\overline{ \text{Nu}} } \right)$ is calculated over the surface of the embedded cylinders and the variation of $\left( {\overline{ \text{Nu}} } \right)$ with respect to time is presented in Figs. 7 and 8 for a range of S, Da and Ha at Ra = 10³ and 10⁶, respectively. In general, it can be observed that the value of $\left( {\overline{ \text{Nu}} } \right)$ rises initially and attains a constant value after an initial transitional time period. The position of the embedded cylinders has a strong influence on the steady-state value of the surface-averaged Nusselt number for a given Darcy number, Rayleigh number and Hartmann number. Increasing the interspacing distance, the steady-state value of $\left( {\overline{\text{Nu}} } \right)$ significantly increases for Ra = 10³. A similar observation can be seen from Fig. 8 for Ra = 10⁶. It is important to reiterate that the thickness of the thermal boundary layers reduces with increasing the interspacing distance between the cylinders as enumerated in the previous section. As a consequence, there is an augmentation of heat transfer for S = 0.5. It is further observed from Figs. 7 and 8 that Hartmann number and Darcy number play an important role in the augmentation of heat transfer. It can be seen from Fig. 7a that the steady-state value of $\left( {\overline{\text{Nu}} } \right)$ increases expressively with Da. The augmentation of $\left( {\overline{\text{Nu}} } \right)$ is more prominent when there is no magnetic field applied irrespective of S. Increasing the Darcy number reduces the flow resistance and thereby fluid can flow easily through the pores and this leads to enhanced heat transfer rate for a lower value of Rayleigh number (Ra = 10³). The trends revealed in these time traces are completely consistent with the patterns established by streamlines and isotherms distribution which have been discussed in the preceding section.

Fig. 7

Temporal variation of surface-averaged Nusselt number $\left( {\overline{\text{Nu}} } \right)$ with dimensionless time $\left( \tau \right)$ for: a Ha = 0, b Ha = 25, c Ha = 50, d Ha = 75 and e Ha = 100 at Ra = 10³

Fig. 8

Temporal variation of surface-averaged Nusselt number $\left( {\overline{\text{Nu}} } \right)$ with dimensionless time $\left( \tau \right)$ for: a Ha = 0, b Ha = 25, c Ha = 50, d Ha = 75 and e Ha = 100 at Ra = 10⁶

The interplay between Hartmann number and Darcy number on the variation of surface-averaged Nusselt number is also reflected in Fig. 7. It can be observed from Fig. 7a that there is a significant enhancement of heat transfer rate for Da = 10⁻² in the absence of a magnetic field. However, when the magnetic field is applied, the difference of $\left( {\overline{ \text{Nu}} } \right)$ for Da = 10⁻² and 10⁻³ reduces monotonically (refer to Fig. 7b), indicating the dominating effect of Lorentz force together with the buoyancy force on heat transfer augmentation. Further, increasing the value of Hartmann number (Ha = 50 and 75), the variation of $\left( {\overline{ \text{Nu}} } \right)$ is nearly the same for Da = 10⁻³ and 10⁻² (refer to Fig. 7c). It can be seen in Fig. 7d that the difference in $\left( {\overline{ \text{Nu}} } \right)$ between Da = 10⁻² and 10⁻³ is minimal when a high magnetic field (Ha = 100) is applied. It is observed that the strength of vortices significantly reduces by the application of the higher magnetic field (Ha = 100). In addition to this, thicker thermal boundary layers are observed for Ha = 100 which results in a decrement in steady-state value of surface-averaged Nusselt number. Moreover, certain fluctuations in the variation of $\left( {\overline{ \text{Nu}} } \right)$ are observed for S = 0.1 and 0.3 due to relatively low damping of the convective current when the permeability of the medium is high.

Figure 8 represents the variation of $\left( {\overline{ \text{Nu}} } \right)$ with respect to time for different combinations of Da, Ha and S. It is observed that $\left( {\overline{ \text{Nu}} } \right)$ increases significantly due to the higher strength of buoyancy force overcoming the viscous resistance force and Lorentz force at a higher value of Rayleigh number (Ra = 10⁶). It can be seen from Fig. 8a that the values of $\left( {\overline{ \text{Nu}} } \right)$ for a highly permeable porous medium are significantly higher than the lower one in the absence of a magnetic field. However, when a magnetic field applied the difference between the values of $\left( {\overline{ \text{Nu}} } \right)$ for Da = 10⁻³ and 10⁻² reduces (refer to Fig. 8b). Moreover, this difference is significantly decreased with an increase in the value of Hartmann number and the minimal difference is observed for Ha = 100 irrespective of interspacing distance. The results shown in Figs. 7 and 8 clearly point out the fact that the decrement in $\left( {\overline{ \text{Nu}} } \right)$ increases with an increase in Hartmann number particularly at the higher value of Ra (= 10⁶).

Figure 9 depicts the variation of time-averaged Nusselt number $\left( {\overline{{{ \text{Nu}}_{\rm t} }} } \right)$ with Hartmann number for different values of Darcy number, Rayleigh number and interspacing distance under consideration. In Fig. 9a the variation of $\left( {\overline{{{ \text{Nu}}_{\rm t} }} } \right)$ with respect to Ha is presented for Ra = 10³. It can be seen from Fig. 9a that $\left( {\overline{{{ \text{Nu}}_{\rm t} }} } \right)$ increases with the interspacing distance. It is mentioned earlier that the thickness of the thermal boundary layer decreases with increasing in the interspacing distance which leads to the steeper temperature gradient at the surface of the embedded cylinders. Consequently, the heat transfer is maximum for S = 0.5 and minimum for S = 0.1 for all Da and Ha. Similar observation is found in the temporal variation of surface-averaged Nusselt number. In absence of the magnetic field, $\left( {\overline{{{ \text{Nu}}_{\rm t} }} } \right)$ is higher for Da = 10⁻². However, the variation of $\left( {\overline{{{ \text{Nu}}_{\rm t} }} } \right)$ is minimal when the magnetic field is relatively weak (Ha = 25). There is no substantial improvement in the heat transfer rate with further increment in Ha for Da = 10⁻³ and 10⁻². This phenomenon indicates that at higher Ha, Lorentz force is the main reason behind the heat transfer augmentation which dominates the buoyancy force (which is insignificant for Ra = 10³) as well as the Forchheimer drag force (due to presence of porous media) for Ra = 10³. However, the variation of time-averaged Nusselt number is not similar at higher values of Rayleigh number (Ra = 10⁶). It can be observed in Fig. 9b that maximum separation distance provides maximum heat transfer rate irrespective of Da and Ha, which is in line with the variation of $\left( {\overline{{{ \text{Nu}}_{\rm t} }} } \right)$ for Ra = 10³. In addition to this, the variation in $\left( {\overline{{{ \text{Nu}}_{\rm t} }} } \right)$ with Hartmann number is more prominent for higher Rayleigh number indicating that the effect of Lorentz force is quite significant when the buoyancy force begins to operate. The value of $\left( {\overline{{{ \text{Nu}}_{\rm t} }} } \right)$ reaches maximum for Ha = 0 whereas the minimum one for Ha = 100 irrespective of S and Da. This phenomenon indicates the fact that the presence of a magnetic field considerably suppresses the flow and the thermal field. Moreover, it is also reflected from Fig. 9b that the heat transfer rate is considerably enhanced with an increment in the permeability of the medium (Da = 10⁻²). The fluid flow is subjected to lesser resistance as the permeability increases facilitating its motion thereby increasing the buoyancy-induced convection.

Fig. 9

Variation of time-averaged Nusselt number with Hartmann number for different Darcy number and interspacing distance of cylinders for: a Ra = 10³ and b Ra = 10⁶

Entropy generation

One of the primary objectives of the present investigation is to analyse the irreversibility that occurs inside the square cavity embraces with two heated cylinders, for a range of Hartmann number and interspacing distance between the embedded cylinders. It is well known that the total irreversibility for the present work comprises of the irreversibility due to heat transfer, fluid friction and magnetic field. It is important to analyse the individual contribution of different components of entropy generation for efficient designing of the thermal system. Accordingly, the contours plots for entropy generation due to thermal, fluid friction and magnetic field are presented in Figs. 10–12, respectively. It can be observed from Fig. 10 that the maximum thermal entropy generation mainly occurs in the vicinity of the solid boundary of the embedded cylinders due to the presence of the steep temperature gradients at the surface. The temperature gradient further increases with the increase in dimensionless separation distance (S) as a consequence the maximum value for thermal entropy generation also increases. The effect of Hartmann number on the thermal entropy generation is also shown in Fig. 10. The maximum value of thermal entropy generation decreases with Ha. The value of thermal entropy generation is maximum when no magnetic field is imposed. Whereas, the least value is obtained at Ha = 100 due to the denser thermal boundary layer along the wall of the embedded cylinders irrespective of S.

Fig. 10

Distribution of local entropy generation due to heat transfer for different interspacing distances of embedded cylinders and Hartmann number at $\tau = 1$, Ra = 10⁶ and Da = 10⁻³

The influence of interspacing distance between the cylinders on the viscous entropy generation is quite opposite to the one observed in thermal entropy generation (refer to Fig. 11). It is observed that the velocity gradient reduces with an increment in dimensionless separation distance reducing the viscous entropy generation. It is interesting to mention that the thermal entropy generation is maximum and viscous entropy generation is minimum for S = 0.5 in the absence of a magnetic field. In this particular separation distance, a steeper temperature gradient is observed leading to a higher heat transfer rate as well as maximum thermal entropy generation. Figure 12 shows the local variation of magnetic field entropy generation. The maximum value for irreversibility due to the magnetic field is obtained at a higher Hartmann number. This phenomenon is quite obvious because the Lorentz force within the square enclosure increases as the strength of the magnetic field increases. The effect of interspacing distance is not prominent on the generation of irreversibility due to the magnetic field.

Fig. 11

Distribution of local entropy generation due to fluid friction for different interspacing distances of embedded cylinders and Hartmann number at $\tau = 1$, Ra = 10⁶ and Da = 10⁻³

Fig. 12

Distribution of local entropy generation due to the magnetic field for different interspacing distances of embedded cylinders and Hartmann number at $\tau = 1$, Ra = 10⁶ and Da = 10⁻³

To identify the major source of entropy generation, total entropy generation $\left( {N_{ \text{T}} } \right)$ in conjunction with average Bejan number $\left( {\overline{ \text{Be}} } \right)$ is evaluated for a range of Hartmann number, Darcy number, Rayleigh number and different interspacing distances between the embedded cylinders (refer Tables 2 and 3). The values of $N_{ \text{T}}$ indicate a decreasing trend with Hartmann number due to the presence of a strong magnetic field irrespective of Da, Ra and S which ultimately affects the total entropy generation. However, $N_{ \text{T}}$ decreases at a rapid rate specially at higher values of Darcy number since it offers lesser resistance against the fluid motion due to the highly permeable medium. It can be seen that heat transfer is the main source of irreversibility at lower values of Darcy number and Rayleigh number. As such observation can be inferred from the study of the streamlines distribution where the nominal influence of Hartmann number at low Darcy number has been emphasized. It can be seen that the average Bejan number is less than half $\left( {\overline{ \text{Be}} < 0.5} \right)$ when Ha increases from 0 to 75 for S = 0.1 at higher values of Darcy number (Da = 10⁻²). Also, the penetration of fluid in between the embedded cylinders increases for a highly permeable porous medium. This leads to increase the fluid friction irreversibility gradually. Moreover, the effect of thermal entropy generation on $\overline{ \text{Be}}$ becomes more prominent with an increase in separation distance independent of the value of Ra, Da and Ha. It can be seen from Table 3 that $N_{ \text{T}}$ increases significantly for Ra = 10⁶, irrespective of Ha and Da. Moreover, it is observed that the value of $\overline{ \text{Be}}$ is found to be less than 0.5 independent of the Hartmann number and Darcy number. It is seen that the advection rate indicating the flow-induced velocity increases with an increase in the value of the Rayleigh number. Hence, the values of average Bejan number are much less than half $\overline{ \text{Be}} < 0.5$ for Ra = 10⁶.

Table 2 Comparative assessment of total entropy generation (N_T) and average Bejan number for Ra = 10³ and $\tau = 1$

Table 3 Comparative assessment of total entropy generation (N_T) and average Bejan number for Ra = 10⁶ and $\tau = 1$

Conclusions

The present study investigates the combined effect of Hartmann number and interspacing distance between the embedded cylinders on thermal transport and entropy generation characteristics inside a cold porous enclosure. The fluid flow and heat transfer characteristics are examined by varying the interspacing distance between the embedded cylinders (S = 0.1, 0.3 and 0.5) for a range of Hartmann number (Ha = 0–100), Darcy number (Da = 10⁻³ and 10⁻²) and Rayleigh number (Ra = 10³ and 10⁶). The major conclusions are as follows:

• For Ra = 10⁶, the distribution of streamlines is almost invariant irrespective of Hartmann number and Darcy number when the interspacing distance is the least. However, the strength of cells decreases with increasing the dimensionless separation distance for any particular Ha. Further, the strength of primary and secondary vortices increases with increasing the permeability of the porous medium (Da = 10⁻²). This effect is more pronounced in the absence of the magnetic field.

• In general, the isotherms are found to be much denser around the solid walls of the embedded cylinders at a higher interspacing distance (S = 0.5) thus leading to the steeper temperature gradient and consequently the higher heat transfer rate.

• The presence of the magnetic field considerably suppresses the fluid flow and the thermal field resulting in lower heat transfer from the hot embedded cylinders. As a result, the distribution of isotherms is found to be relatively more uniform as the intensity of applied magnetic field increases. Further, the isotherms contours are non-uniformly distributed in the absence of the magnetic field illustrating the domination of buoyancy-induced convection.

• The heat transfer is conduction dominated mainly for a medium with low permeability (Da = 10⁻³) although the heat transfer by convection remains dominant at higher permeability (Da = 10⁻²).

• Thermal entropy generation has a major contribution to total irreversibility at lower values of Rayleigh number irrespective of all interspacing distance and Darcy number. However, the contribution of entropy generation owing to the viscous and magnetic field forms a major part of total entropy generation particularly at higher values of the Rayleigh number.

• The present investigation can be further extended by considering the effect of Prandtl number, asymmetric permeability of the porous medium and different boundary conditions on the walls of the enclosure and the surface of the cylinders.