Natural convection of hybrid nanofluids inside a partitioned porous cavity for application in solar power plants

Abstract

The present article deals with the CFD simulation of natural convection heat transfer of a hybrid nanofluid in an inverted T-shaped cavity partitioned and saturated by two different types of porous media. Suspensions of organic and inorganic nanoparticles, i.e., MWCNTs and Fe₃O₄, in water were selected as the working fluid. The macroscopic conservation equations for the flow field and heat transfer were modeled via volume averaging the microscopic equations inside porous media over a representative elementary volume. The effects of many parameters were investigated. The parameters included the Rayleigh number (Ra = 103–106), porosity coefficient ratio of two porous media (ε_r = 0.5–1.8), volume fraction of the dispersed nanoparticles ($\varphi$ = 0–0.003), Richardson number (Ri = 0.1–20), Darcy number ratio of two porous media (Dar = 0.01, 1, 100) and thermal conductivity ratio of two porous media (k_r = 0.2, 0.4, 1, 5). The results showed that, with an increase in the Rayleigh number, porosity ratio and Darcy number ratio and decrease in the thermal conductivity ratio, the averaged Nusselt number increased.

Graphical abstract

Introduction

The idea of adding solid particles to conventional liquids can be traced to the eighteenth century and became more practical with the emergence of nanotechnology. Nanofluid, a term introduced by Choi in 1995 [1], is used for mixtures of nanoscale (in the range of 1–100 nm) solid particles including metals (Cu, Fe, Al and Ag) and metal oxides (CuO, TiO₂, Al₂O₃ and SiO₂), nonmetals (carbon nanotubes and graphite), and carbides (SiC) and nitrides (AlN, SiN) in a base fluid. Such fluids have appreciably greater thermal conductivity compared with common liquids, being especially used in engineering systems for cooling electronic devices, and might be able to satisfy the rising demands for an efficient rate of heat transfer.

In the last decade, researchers have paid special attention to finding optimal solutions to reduce energy consumption, which would consequently help reduce global warming. Using both porous media and nanofluids in thermal systems such as solar power plants, active nuclear waste disposal systems and so on would be a practical approach to ameliorating the thermal efficiency of such systems through heat transfer enhancement. Heat transfer enhancement is mainly created by thermal conductivity advancement of working fluid [2, 3] and the consequent decrease in boundary layer thickness as well as increase in the heat transfer contact surface, which is provided by the porous media [4]. Using nanofluid could enhance natural [5,6,7,8,9,10,11,12] and forced convection [13,14,15,16,17,18].

Over the past several years, many studies have been done on nanofluids and natural convection inside cavities fully or partially filled with porous media [12, 19,20,21,22,23,24,25,26,27]. In preliminary studies, Beckerman et al. [28] used the Brinkman-Forchheimer extended Darcy model to simulate the effects of the porous region on natural convection inside a vertical cavity. The researchers found that the porous layer would greatly affect the patterns of natural convection in the cavity by changing the value of the Darcy number. Baytas et al. [29] examined the problem of conduction and convection heat transfer in a porous cavity. Their findings indicated that the strength of the flow inside the cavity was thoroughly related to the ratio of solid and fluid thermal conductivity. Considering the effects of Brownian diffusion and thermophoresis, Nield and Kuznetsov [30] conducted an analytical study on the phenomenon of natural convection in a porous domain saturated by nanofluids. Chamkha and Ismael [31] examined the nanofluid natural convection in a porous cavity for different Ra numbers. It was found that nanofluid enhanced the heat transfer rate. Also, at low Rayleigh number values, a significant increase in heat transfer inside the porous cavity with concentration was detected. Bourantas et al. [32] conducted a study on natural convection heat transfer inside a porous cavity. The cavity was equipped with a heat source on the bottom wall of the cavity and filled with a nanofluid. They found that nanofluid can increase the heat transfer rate.

Hajipour and Dehkordi [33] carried out a numerical study on nanofluid mixed convection flow in a vertical rectangular cavity that was in part packed with porous metal foam. The researchers found that, with a 0.3% nanoparticle concentration dispersed in the base fluid, a 20% increase in heat transfer could be achieved.

Nguyen et al. [34] examined natural convection heat transfer of nanofluids inside a porous cavity under variable heatings. Their results showed that the value of the Rayleigh number and nanoparticle volume fraction influenced the process of heat transfer. The heat transfer of TiO₂/water nanofluid in a cavity composed of a vertical porous layer was simulated by Al-Zamily [35]. The results showed that when the heat source was placed on the bottom half of the left wall, a higher rate of heat transfer could be obtained. The results also demonstrated that the average Nu decreases as the value of the Darcy number or the thickness of the porous layer increases. Sheikholeslami and Shamlooei [36] simulated the convective flow of nanofluids inside a lid-driven cavity saturated with porous media. The researchers found that the heat transfer process improved as the Darcy and Reynolds number values increased, while the process deteriorated as the Hartmann number value increased. Sheikholeslami [37] reported impacts of the electro-hydrodynamics on coupled radiative-natural convective heat transfer of a nanofluid in a porous cavity numerically and found that Nu enhances with the permeability of porous media. Recently, Hoghoughi et al. [23] used Buongiorno’s model to examine natural convection of a nanofluid inside a porous wavy wall cavity. Effects of some passive parameters have been extensively considered using a local thermal nonequilibrium model. The researchers reported that Nu declines as heat inside the enclosure increases.

Based on the authors' best knowledge, no work on the investigation of natural convection of nanofluid flow in a partitioned porous cavity has been reported so far. Therefore, the present study aims to fill this gap by studying the natural convection of a hybrid nanofluid (MWCNT–Fe₃O₄/water) inside an inverted T-shaped cavity filled with two different porous media. The effect of the Rayleigh number, nanoparticle volume fraction, porosity coefficient ratio, Darcy number ratio and thermal conductivity ratio of two porous media on the hydrodynamic and thermal characteristics was investigated. The results of this study can be applied to the design of solar power plants or thermal storage systems.

Mathematics of the problem

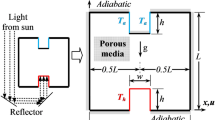
The geometry of the problem is shown in Fig. 1. The geometry is an inverted T-shaped enclosure by height $L^{*}$, length $W^{*}$ ($L^{*} = W^{*}$), width $W_{1}^{*}$ and $L_{1}^{*}$ and cavity aspect ratio $L_{1}^{*} /L^{*} = 0.2$ filled by a hybrid nanofluid. Two discrete porous media fill the cavity by different properties so that they affect the thermal and flow field of the hybrid nanofluid. It is assumed that nanofluid is homogeneous, there is no sedimentation in porous media, and the size of nanoparticles is much bigger than that of the porous holes. The macroscopic equations of an incompressible flow in a porous medium were calculated by volume averaging the microscopic conservation equations using the REV [38]:

Fig. 1

Schematic of the problem

$$\frac{{\partial u^{*} }}{{\partial x^{*} }} + \frac{{\partial v^{*} }}{{\partial y^{*} }} = 0$$

(1)

$$\begin{aligned} & \frac{{\rho_{\text{nf}} }}{{\varepsilon_{\text{i}}^{2} }}\left( {u^{*} \frac{{\partial u^{*} }}{{\partial x^{*} }} + v^{*} \frac{{\partial u^{*} }}{{\partial y^{*} }}} \right) = - \frac{{\partial p^{*} }}{{\partial x^{*} }} + \frac{{\mu_{\text{nf}} }}{{\varepsilon_{\text{i}} }}\left( {\frac{{\partial^{2} u^{*} }}{{\partial x^{*2} }} + \frac{{\partial^{2} u^{*} }}{{\partial y^{*2} }}} \right) - \frac{{\mu_{\text{nf}} }}{{K_{\text{i}} }}u^{*} \\ & - \frac{1.75}{{\sqrt {150} }}\frac{{\rho_{\text{nf}} }}{{\sqrt {K_{\text{i}} } }}\frac{{\sqrt {u^{*2} + v^{*2} } }}{{\varepsilon_{\text{i}}^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} }}u^{*} \\ \end{aligned}$$

(2)

$$\begin{aligned} & \frac{{\rho_{\text{nf}} }}{{\varepsilon_{\text{i}}^{2} }}\left( {u^{*} \frac{{\partial v^{*} }}{{\partial x^{*} }} + v^{*} \frac{{\partial v^{*} }}{{\partial y^{*} }}} \right) = - \frac{{\partial p^{*} }}{{\partial y^{*} }} + \frac{{\mu_{\text{nf}} }}{{\varepsilon_{\text{i}} }}\left( {\frac{{\partial^{2} v^{*} }}{{\partial x^{*2} }} + \frac{{\partial^{2} v^{*} }}{{\partial y^{*2} }}} \right) - \frac{{\mu_{\text{nf}} }}{{K_{\text{i}} }}v^{*} \\ & - \frac{1.75}{{\sqrt {150} }}\frac{{\rho_{\text{nf}} }}{{\sqrt {K_{\text{i}} } }}\frac{{\sqrt {u^{*2} + v^{*2} } }}{{\varepsilon_{\text{i}}^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} }}v^{*} + \rho_{\text{nf}} g\beta_{\text{nf}} \left( {T_{\text{nf}}^{*} - T_{\text{c}}^{*} } \right) \\ \end{aligned}$$

(3)

$$\left( {\rho c_{\text{p}} } \right)_{\text{nf}} \left( {u^{*} \frac{{\partial T_{\text{nf}}^{*} }}{{\partial x^{*} }} + v^{*} \frac{{\partial T_{\text{nf}}^{*} }}{{\partial y^{*} }}u} \right) = k_{{{\text{nf,m}}_{\text{i}} }} \left( {\frac{{\partial^{2} T_{\text{nf}}^{*} }}{{\partial x^{*2} }} + \frac{{\partial^{2} T_{\text{nf}}^{*} }}{{\partial y^{*2} }}} \right)$$

(4)

$$k_{{{\text{nf,m}}_{\text{i}} }} = \varepsilon_{\text{i}} k_{\text{nf}} + \left( {1 - \varepsilon_{\text{i}} } \right)k_{\text{s,i}}$$

(5)

The star superscript signifies the dimensional variables. Also, the i index shows the properties of the two porous layers defined by subscripts 1 and 2.

The boundary conditions in the dimensional $x^{*}$ and $y^{*}$ coordinates are

$${\text{At}}\quad {\text{AB,}}\;{\text{BC,}}\;{\text{DE,}}\;{\text{EF}}\quad T^{*} = T_{\text{c}}^{\text{*}} \quad u^{*} = v^{*} = 0$$

(6)

$${\text{At}}\quad {\text{HG}}\quad T^{*} = T_{\text{h}}^{\text{*}} \quad u^{*} = v^{*} = 0$$

(7)

$${\text{At}}\quad {\text{CD,}}\;{\text{AH,}}\;{\text{FG}}\quad \frac{{\partial T^{\text{*}} }}{{\partial y^{\text{*}} }} = 0$$

(8)

At the interface of the two different porous layers, the continuity of mass and heat flux was held on their interface.

$$\begin{aligned} & u_{\text{porous1}}^{*} = u_{\text{porous2}}^{*} ,\quad v_{\text{porous1}}^{*} = v_{\text{porous2}}^{*} \\ & \left. {\mu_{\text{nf, eff}} \frac{{\partial u^{*} }}{{\partial n^{*} }}} \right|_{\text{porous1}} = \left. {\mu_{{{\text{nf,}}\,{\text{ eff}}}} \frac{{\partial u^{*} }}{{\partial n^{*} }}} \right|_{\text{porous2}} ,\quad \left. {\mu_{\text{n,eff}} \frac{{\partial v^{*} }}{{\partial n^{*} }}} \right|_{\text{porous1}} = \left. {\mu_{\text{nf,eff}} \frac{{\partial v^{*} }}{{\partial n^{*} }}} \right|_{\text{porous2}} \\ & \left. {T_{\text{nf}}^{*} } \right|_{\text{porous1}} = \left. {T_{\text{nf}}^{*} } \right|_{\text{porous2}} \\ & \left. {k_{\text{nf,m}} \frac{{\partial T_{\text{nf}}^{*} }}{{\partial n^{*} }}} \right|_{\text{porous1}} = \left. {k_{\text{nf,m}} \frac{{\partial T_{\text{nf}}^{*} }}{{\partial n^{*} }}} \right|_{\text{porous2}} \\ \end{aligned}$$

(9)

where $k_{\text{nf,m}} = \varepsilon k_{\text{nf}} + \left( {1 - \varepsilon } \right)k_{\text{s}} ,\mu_{\text{nf, eff}} = \frac{{\mu_{\text{nf}} }}{\varepsilon }$.

To analyze the parametric dimensionless, the following parameters were employed to obtain the dimensionless forms for the equations modeled above:

$$\begin{aligned} & x = x^{*} /L^{*} ,\quad \, y = y^{*} /L^{*} ,\quad \, n = n^{*} /L^{*} ,\quad \, {\rm T}_{\text{nf}} = \frac{{\left( {T_{\text{nf}}^{*} - T_{\text{c}}^{*} } \right)}}{{\left( {T_{\text{h}}^{*} - T_{\text{c}}^{*} } \right)}},\quad \, u = \frac{{u^{*} }}{{{{\alpha_{\text{bf}} } \mathord{\left/ {\vphantom {{\alpha_{\text{bf}} } {L^{*} }}} \right. \kern-0pt} {L^{*} }}}}, \\ & v = \frac{{v^{*} }}{{{{\alpha_{\text{bf}} } \mathord{\left/ {\vphantom {{\alpha_{\text{bf}} } {L^{*} }}} \right. \kern-0pt} {L^{*} }}}}\quad {\text{and}}\quad p = \frac{{p^{*} }}{{\rho_{\text{bf}} \left( {{{\alpha_{\text{bf}} } \mathord{\left/ {\vphantom {{\alpha_{\text{bf}} } {L^{*} }}} \right. \kern-0pt} {L^{*} }}} \right)^{2} }} \\ \end{aligned}$$

(10)

Hence, we have the following:

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$$

(11)

$$\begin{aligned} & \frac{1}{{\varepsilon_{\text{i}}^{2} }}\left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right) = - \rho_{\text{r}} \frac{\partial p}{\partial x} + \frac{Pr}{{\varepsilon_{\text{i}} }}\mu_{\text{r}} \rho_{\text{r}} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) - \frac{Pr}{{Da_{\text{i}} }}\mu_{\text{r}} \rho_{\text{r}} u \\ & - \frac{1.75}{{\sqrt {150} }}\frac{{\sqrt {u^{2} + v^{2} } }}{{\sqrt {Da_{\text{i}} } \cdot \varepsilon_{\text{i}}^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} }}u \\ \end{aligned}$$

(12)

$$\begin{aligned} & \frac{1}{{\varepsilon_{\text{i}}^{2} }}\left( {u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}} \right) = - \rho_{\text{r}} \frac{\partial p}{\partial y} + \frac{Pr}{{\varepsilon_{\text{i}} }}\mu_{\text{r}} \rho_{\text{r}} \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - \frac{Pr}{{Da_{\text{i}} }}\mu_{\text{r}} \rho_{\text{r}} v \\ & - \frac{1.75}{{\sqrt {150} }}\frac{{\sqrt {u^{2} + v^{2} } }}{{\sqrt {Da_{\text{i}} } \cdot \varepsilon_{E}^{{{\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} }}v + RaPr\beta_{\text{r}} T_{\text{nf}} \\ \end{aligned}$$

(13)

$$u\frac{{\partial T_{\text{nf}} }}{\partial x} + v\frac{{\partial T_{\text{nf}} }}{\partial y} = \alpha_{\text{r}} \left( {\frac{{\partial^{2} T_{\text{nf}} }}{{\partial x^{2} }} + \frac{{\partial^{2} T_{\text{nf}} }}{{\partial y^{2} }}} \right)$$

(14)

$$\alpha_{\text{r}} = \frac{{\alpha_{\text{nf,m}} }}{{\alpha_{\text{bf}} }},\quad \alpha_{\text{nf,m}} = \frac{{k_{\text{nf,m}} }}{{\left( {\rho c_{\text{p}} } \right)_{\text{nf}} }}$$

(15)

Ra, Pr and Da of the above equations, respectively, are

$$Ra = \frac{{g\rho_{\text{bf}} \beta_{\text{bf}} \left( {T_{\text{h}}^{*} - T_{\text{c}}^{*} } \right)L^{{*^{3} }} }}{{\alpha_{\text{bf}} \nu_{\text{bf}} }},\quad \, Da_{\text{i}} = \frac{{K_{\text{i}} }}{{L^{{*^{2} }} }},\quad \, Pr = \frac{{\nu_{\text{bf}} }}{{\alpha_{\text{bf}} }}$$

(16)

The boundary conditions subjected to the bounds are:

$$\begin{aligned} & u_{\text{porous1}} = u_{\text{porous2}} ,\quad v_{\text{porous1}} = v_{\text{porous2}} \\ & \frac{1}{\varepsilon }\,\left. {\frac{\partial u}{\partial n}} \right|_{\text{porous1}} = \left. {\frac{1}{\varepsilon }\frac{\partial u}{\partial n}} \right|_{\text{porous2}} ,\quad \left. {\frac{\partial v}{\partial n}} \right|_{\text{porous1}} = \left. {\frac{1}{\varepsilon }\frac{\partial v}{\partial n}} \right|_{\text{porous2}} \\ & \left. {T_{\text{nf}} } \right|_{\text{porous1}} = \left. {T_{\text{nf}} } \right|_{\text{porous2}} \\ & \left. {\frac{{\partial T_{\text{nf}} }}{\partial n}} \right|_{\text{porous1}} = \left( {\frac{{k_{{{\text{nf,m}}_{2} }} }}{{k_{{{\text{nf,m}}_{ 1} }} }}} \right)\left. {\frac{{\partial T_{\text{nf}} }}{\partial n}} \right|_{\text{porous2}} \\ \end{aligned}$$

(17)

The rate of local heat transfer over the hot wall is calculated through the following equation:

$$Nu_{\text{x}} = - \frac{{k_{\text{nf,m}} }}{{k_{\text{bf}} }}\left( {\frac{\partial T}{\partial y}} \right)_{{{\text{x}} = 0}}$$

(18)

The integration of the above equations gives the total heat transfer rate:

$$Nu_{\text{avg}} = \int\limits_{0}^{1} {Nu_{\text{x}} } \,{\text{d}}x$$

(19)

Thermophysical properties of the nanofluid

A review of hybrid nanofluids showed that there is no established relation for calculating the thermophysical properties of these new types of suspensions. Hence, the current study employs the experimental data of MWCNT–Fe₃O₄ hybrid nanofluid for calculating properties as depicted in Table 1. In addition, Table 2 illustrates the thermophysical properties of Fe₃O₄ and the MWCNT nanoparticles. Other thermophysical properties of the hybrid nanofluid can be calculated using the relations given below:

$$\rho_{\text{nf}} = \left( {1 - \varphi } \right)\rho_{\text{bf}} + \varphi \rho_{\text{np}}$$

(20)

$$\rho_{\text{nf}} \beta_{\text{nf}} = (1 - \varphi )(\rho \beta )_{\text{bf}} + \varphi (\rho \beta )_{\text{np}} \,$$

(21)

$$\, \beta_{\text{np}} = \frac{{\beta_{\text{MWCNT}} w_{\text{MWCNT}} + \beta_{{{\text{Fe}}_{3} {\text{O}}_{4} }} w_{{{\text{Fe}}_{3} {\text{O}}_{4} }} }}{{w_{\text{MWCNT}} + w_{{{\text{Fe}}_{3} {\text{O}}_{4} }} }}$$

(22)

$$\alpha_{\text{nf}} = \frac{{k_{\text{nf}} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} }}$$

(23)

where $\varphi$ represents the value of volume fraction for dispersed nanoparticles.

Table 1 The thermophysical properties of carbon nanotube–Fe₃O₄ hybrid nanofluid for different volume fractions and temperatures [39]

Table 2 Thermophysical properties of Fe₃O₄ and MWCNT [8]

Grid independency and code validation

Grid independency study is performed using several different grids. The study shows that the mesh size of 8775 is optimal (see Table 3). The accuracy of the numerical procedure was checked and validated against the available results in the literature. As shown in Table 4, Figs. 2 and 3, the present numerical procedure is in good agreement with the published results.

Table 3 Grid study: Ra = 1e4, ε_r = 1, ε₁ = 0.5, k_s,1 = 5, k_s,r = 1, Da₁ = 1e−2, Da_r = 1, $\varphi_{\text{hnf}}$ = 0. 3%

Table 4 Average Nusselt number in a porous triangular-shaped enclosure occupied by Cu–water nanofluid

Fig. 2

Streamlines and isotherm lines of a the current study and b Esfe et al. [42] (reprinted with permission from Elsevier)

Fig. 3

Variation of Nu_avg according to the volume fraction of nanoparticles for the different values of Ra resulting from Kahveci [43] and the present study

Results and discussion

The present study deals with the free convective heat transfer of a MWCNT–Fe₃O₄/water hybrid nanofluid within a contrariwise T-shaped cavity saturated by two different porous medium. The results are presented for various Rayleigh number values, the porosity ratio of porous media (ε_r = ε₁/ε₂), nanoparticle volume fraction, Richardson number, Darcy number ratio (Da_r = Da₁/Da₂) and thermal conductivity ratio of the solid phases of two porous media (k_s,r = k_s,1/k_s,2).

The effect of the presence of nanoparticles on streamlines for low and high values of the Rayleigh number (Ra) in the porous medium at different porosity ratios is illustrated in Fig. 4 for ε₁ = 0.5, k_s,1 = 5, k_s,r = 1, Da₁ = 1e−2, Da_r = 1 and $\varphi_{\text{hnf}}$ = 0.3%. As seen, in a fixed porosity ratio, two symmetrical convective cells (clockwise circulation in the right and counterclockwise circulation in the left) are shaped inside the cavity at low Rayleigh number values. This is caused by the buoyancy forces effected by the difference in fluid temperature and motivates the fluid to ascend in the middle and come down on the sides of the cavity. Increasing the Ra leads to the increment of the buoyancy force, which increases the strength of the main vortices and occupies the whole of enclosure. The formation of two secondary recirculation zones in the vicinity of the side walls is due to domination of the convection heat transfer. Also, at a fixed Ra number, when the ε_r parameter increases, the power of the circulation over the porous layers is decreased.

Fig. 4

Variation of streamlines with the porosity coefficient of two porous media and Rayleigh number at ε₁ = 0.5, k_s,1 = 5, k_s,r = 1, Da₁ = 1e−2, Da_r = 1, $\varphi_{\text{hnf}}$ = 0. 3%

Figure 5 presents the isotherm lines for the nanofluid at different values of the Rayleigh number and porosity coefficient for ε₁ = 0.5, k_s,1 = 5, k_s,r = 1, Da₁ = 1e−2, Da_r = 1 and $\varphi_{\text{hnf}}$ = 0.3%. Symmetrical temperature patterns are observed inside the enclosure. Although isotherm lines would not significantly change for different porosity ratio values, an intensive change in the shape of isotherm lines occurred at Ra = 10⁶ for an increment in the porosity ratio.

Fig. 5

Variation of isotherm lines with the porosity coefficient of two porous media and Rayleigh number at ε₁ = 0.5, k_s,1 = 5, k_s,r = 1, Da₁ = 1e−2, Da_r = 1, $\varphi_{\text{hnf}}$ = 0. 3%

The bottom porous layer is heated from below. Interaction of the hot-temperature wave from porous layer 1 and cold-temperature wave from the cold besides the walls occurred inside porous layer 2. As expected, the penetration of the hot regime throughout the upper porous media increases by decreasing the porosity ratio, so that this rate is noticeable in high Ra numbers. Moreover, for the higher values of the Ra number, the layers of the thermal boundary close to the bottom walls become thinner.

The effects of the Darcy number ratio of two porous media and the Rayleigh number at ε₁ = 0.5, ε_r = 1, k_s,1 = 5, k_s,r = 1, Da₁ = 1e−3 and $\varphi_{\text{hnf}}$ = 0. 3% on streamlines and isotherm lines are shown in Figs. 6 and 7. As shown in Fig. 6, a decrease in Da_r is related to the extension observed in the permeability of the layer on the bottom porous medium through the upper porous medium by increasing the vortex strength. This moves the center the of main elliptical shape vortices from the bottom part of the cavity toward the center of the enclosure. Also, two weak secondary vortices are generated apart from the main vortices at Ra = 10⁶. The vortices with the lowest strength would, respectively, occur on the top and bottom sides in the centerline of the cavity. An overview of the isotherm lines is shown in Fig. 7, which reveals that there is no significant difference between the patterns of the temperature field when the parameters Da_r and Ra increase. In addition, while the temperature gradient in the neighborhood of the cold vertical boundary in the upper porous medium is low, the gradient is high in the vicinity of the hot horizontal wall in the lower porous medium.

Fig. 6

Variation of streamlines with the Darcy number ratio of two porous media and Rayleigh number at ε₁ = 0.5, ε_r = 1, k_s,1 = 5, k_s,r = 1, Da₁ = 1e−3, $\varphi_{\text{hnf}}$ = 0. 3%

Fig. 7

Variation of isotherm lines with the Darcy number ratio of two porous media and Rayleigh number at ε₁ = 0.5, ε_r = 1, k_s,1 = 5, k_s,r = 1, Da₁ = 1e−3, $\varphi_{\text{hnf}}$ = 0. 3%

Figures 8 and 9 show the effects of the thermal conductivity ratio of two porous media and the Rayleigh number at ε₁ = 0.5, ε_r = 1, k_s,1 = 5, Da₁ = 10⁻², Da_r = 1, $\varphi_{\text{hnf}}$ = 0.3% on streamlines and isotherm lines, respectively. An increase in the thermal conductivity ratio creates longer and stronger vortices in the cavity (see Fig. 8) and pushes the hot plume fluid to the upper section of the cavity (see Fig. 9) at a constant Ra number. This phenomenon leads to the increase in heat exchange between the two porous media. At k_s,r = 5 and Ra = 10⁶, a large penetration of flow within porous layer 2 occurs, and the strong circulation leads to dancer streamlines. It is obvious that the isotherm lines are more concentrated in the lower than upper part of the cavity, which leads to a strong temperature gradient in these regions.

Fig. 8

Variation of streamlines with the thermal conductivity ratio of two porous media and Rayleigh number at ε₁ = 0.5, ε_r = 1, k_s,1 = 5, Da₁ = 1e−2, Da_r = 1, $\varphi_{\text{hnf}}$ = 0. 3%

Fig. 9

Variation of isotherm lines with the thermal conductivity ratio of two porous media and Rayleigh number at ε₁ = 0.5, ε_r = 1, k_s,1 = 5, Da₁ = 1e−2, Da_r = 1, $\varphi_{\text{hnf}}$ = 0. 3%

The graphs illustrated in Fig. 10a, b show the variation trend in the values of the local Nusselt number over the bottom hot wall in the x-direction and average Nu number-based Ra and ε_r.

Fig. 10

a Local variation of the Nusselt number on the hot wall and b surface variation of Nu_avg with Ra and ε_r at $\varphi_{\text{hnf}}$ = 0. 3%

The other parameters are selected equally as k_s,1 = 5, Da₁ = 1e−2, Da_r = 1 and $\varphi_{\text{hnf}}$ = 0.3%. The drastic reduction in the local Nusselt number at the center of the cavity is observed for Ra = 10⁴. The thick thermal boundary layer in this region has the highest thermal resistance against heat transfer, so the minimum heat transfer rate occurs locally at the center part of the hot wall. Also, the vortices remove the heat from the hot boundary at the center of the enclosure and transmits it to the cold walls (see Figs. 4 and 5) so the rate of the local Nu number has the minimum value at x = 0 for the mentioned Ra number. Furthermore, the reduction in local Nu number along the cavity length becomes less at higher porosity ratio values (as shown in Fig. 5).

Different trends occur for Ra = 10⁶ at fixed ε_r; this implies that the heat transfer rate increases along the x-direction and reaches a maximum value at x = 0.3 (similar position on the right side of the cavity, i.e., x = 0.7). The reason for the increase in heat transfer could be easily deduced from the formation of secondary flow and its movement toward the main vortex in the opposite direction so that the thermal boundary layer becomes thinner. In the mentioned position, ε_r = 0.5 shows the maximum heat transfer rate. Anyway, from x = 0.3 to 0.5, a sharp reduction in the local Nu number occurs in the enclosure, especially at low ε_r values, because of better circulation of fluid flow in the upper part of the cavity and production of less crowded isotherm contours because of the thicker thermal boundary layer on the lower wall of the cavity.

According to Fig. 10b, with increasing Ra number at a constant ε_r, the magnitude of the buoyant force increases, which causes an increase in flow strength and in turn a heat transfer increment. At higher ε_r, Nu slightly increases by an increment of Ra. At a low porosity ratio value, the fluid flow is strong because of low flow resistance, which can be boosted at a high Ra number. This improves the ventilation and makes a bigger difference for Nu_avg from 10³ to 10⁶.

The local variation of the Nusselt number on the hot wall and surface variation of Nu_avg with Ra and Da_r are shown in Fig. 11a and b, respectively. Figure 11a shows that the enhancement of the local Nu number at a fixed Da_r starts from the beginning at Ra = 10⁶ and increases with a mild slope until x = 0.3 (because of the confrontation of two vortices with each other, as seen in Fig. 6). After that, this rising trend reduces precipitously until the middle section of the enclosure, and after this value the mentioned trends repeat reversely. By increasing the Da_r in low Ra numbers, there is no difference in the rate of heat transfer. According to Fig. 11b, at a high Ra number, the heat transfer increases with an increasing Da_r  parameter. With increasing Da_r, the rate of fluid flow through porous region 2 decreases (see Fig. 6); therefore, the temperature in porous medium 1 increases and the convection heat transfer increases. At low Ra values, the value of Nu_avg does not change significantly with Da_r.

Fig. 11

a Local variation of the Nusselt number on the hot wall and b surface variation of Nu_avg with Ra and Da_r

Finally, Fig. 12 [cases (a) and (b)] shows the impact of the thermal conductivity ratio in the porous medium on the local and average Nu number at different Ra numbers. As shown in Fig. 12a, when k_s,r increases, the local Nu number decreases totally, but at Ra = 10⁶, the heat transfer rate increases slowly until the point approaching the main vortices in the cavity, which leads to a temperature rise near the wall. Also, according to Fig. 12b, at a fixed Ra number, as the thermal conductivity ratio of porous media increases, an obvious decrease in the value of the average Nusselt number is observed. The reduction rates are equal to 7.36% and 3.049% at Ra = 10³ and 10⁶, respectively. Such behavior points to the fact that an increase in the value of the k_s,r leads to a rise in the thermal conductivity ratio for porous medium 1 compared with that of porous medium 2.

Fig. 12

a Local variation of the Nusselt number on the hot wall and b surface variation of Nu_avg with Ra and k_s,r

Conclusions

The natural convective flow and heat transfer of MWCNT–Fe₃O₄/water hybrid nanofluid in a partitioned cavity consisting of multilayer porous media were studied numerically. The effects of different parameters such as the Ra, porosity coefficient ratio, Darcy number ratio and thermal conductivity ratio on streamlines, isotherm lines and the local and averaged Nu number were investigated. The main findings are listed:

• At a given Ra number, by the increment of ε_r, the circulation power inside the porous layers decreases.

• The penetration of the hot regime throughout the upper porous media increases by decreasing the porosity ratio.

• An increase in the thermal conductivity ratio creates longer and stronger vortices in the cavity (see Fig. 7) and pushes the hot plume fluid to the upper section of the cavity (see Fig. 8) at a constant Ra number.

• Nu_ave at Ra = 10⁶ is 6.23 times larger than Nu_ave at Ra = 10³ for ε_r = 0.5, while Nu_ave at Ra = 10⁶ is 0.63 times larger than Nu_ave at Ra = 10³ for ε_r = 1.8.

• At a fixed Ra number, when the thermal conductivity ratio of the porous media goes up, an obvious decrease in the average Nusselt number is observed.