Introduction

Natural convection is a physical phenomenon of considerable interest that occurs in natural systems such as thermal atmospheres and oceans, and also in engineering such as the building design (heating, cooling and insulation), the cooling systems of electronic components and the systems for collecting solar energy.

In the past few years, the domain of nanofluidics has grown considerably due to its extremely important position in diverse technological areas such as solar thermal conversion processes to converting solar radiation into thermal energy, thermal building design, thermal exchangers, thermal storage equipment, and cooling of electronic systems, thermal engines and nuclear reactors [1,2,3,4,5,6,7,8].

Hybrid or combined nanoliquid is an innovative class of engineering liquid developed by a mixture of two kinds of nanometer-sized particles dispersed in a usual liquid. Actually, this new idea has been introduced as a new technique to improve thermal transmission performance in the thermal equipment. It is extremely important to correctly choose these two types of nanoparticle materials. Metallic nanoparticles such as Ag, Cu and Al, are known for their great thermal conductivity; however, its use alone in the manufacture of nanofluids has demonstrated its limitations and deficiencies. Therefore, the addition of metallic oxide nanoparticles may have a positive effect on getting more effective nanofluids in terms of stability and thermal performance [9,10,11,12,13,14]. In addition, the nanofluids are not only promising for heat transfer applications, but also useful for other applications. For instance, the diamond nanoparticles are very good for electrical insulation, while the silver nanoparticles show antibacterial agents. Hence, a hybrid nanofluid can benefit from the advantages of two or three types of nanoparticles.

Numerous investigations have been monitored to explore the possibility of enhancing heat transfer using hybrid nanoliquids in various thermophysical systems with different forms and boundary conditions. Labib et al. [15] examined forced convection of carbon nanotube (CNT) and aluminum oxides (Al2O3) nanoparticles dispersed in a regular liquid (H2O/EG) utilizing the multiphase method. Their results indicated a significant intensification in the heat transfer coefficient. In the investigation of Balla et al. [16], the cupric oxide–copper-based combined nanoliquid is considered to study forced convective heat transfer in a circular tube. The results of the study showed a clear improvement in the rate of heat transfer by 30–35% compared to the based ordinary fluid. Takabi and Salehi [17] have numerically studied the performance of utilizing a hybrid nanoliquid on the enhancement of free convection in a waved enclosure. They noted that employing alumina–copper/water-based hybrid nanofluid raises the rate of heat transfer compared to the similar conventional nanoliquid with alumina nanoparticles alone. Takabi et al. [18] conducted a numerical study to examine laminar forced convective flow in a uniformly heated pipe considering traditional nanoliquid and combined water-based nanoliquid in different volumic concentrations. Their results revealed that using combined water-based nanoliquid is more effective than traditional nanoliquid in heat transfer coefficient enhancement. Results of numerical studies on natural convection of hybrid nanoliquids using the single-phase approach in different bidimensional cavities are reported by Tayebi and Chamkha [9,10,11] and Tayebi and Oztop [14]. Rashad et al. [19] analyzed numerically thermohydrodynamic behavior of MHD natural convection in a triangular enclosure filled with a hybrid nanoliquid in the presence of a constant heat flux element. They observed an important influence of the addition of hybrid particles when the natural convection is weak. Steady three-dimensional forced convection behavior of a hybrid nanoliquid flowing in the laminar regime within a uniformly heated horizontal pipe considering various nanoparticle forms: Spherical, cylindrical, platelets and blades have been examined by Benkhedda et al. [20]. Moghadassi et al. [21] compared the water-based Al2O3 nanoliquid with that of Cu–Al2O3/H2O-based hybrid nanoliquid and reported far higher convective heat transfer coefficient for the hybrid nanoliquid. Sundar et al. [22] experimentally investigated the impacts of temperature (20–60 °C) and volumic concentration (up to 3%) on hybrid nanoliquid consisting of multiwalled carbon nanotube and iron oxide nanoparticles and water-based liquid.

Equipping thermal systems with solid objects in various forms may lead to control of heat exchange and fluid flow within them. Alsabery et al. [23] used Buongiorno’s approach to examine the thermohydrodynamic performance of nanofluid-filled enclosure and equipped with a solid block in different configurations. It was observed that the highest heat exchange rate is reached by enlarging the body size and Richardson. Sheremet et al. [24] have examined the natural convection of copper–water nanofluid-filled square cavity located having a hot centered block. It has been reported that the inclusion of copper nanoparticles makes the heat transfer rate improve and reduces the flow intensity. Rahman et al. [25] perused a numerical study of the effect of introducing a heat-conducting square solid at the center of a lid-driven enclosure on the flow and thermal behavior with the presence of magnetic field and Joule heating. A numerical assessment of inserting adiabatic objects on the natural convection in a square enclosure is considered by Mahapatra et al. [26]. Impacts of inserting a solid conducting block on MHD natural convection in a porous region are evaluated by Sivaraj and Sheremet [27]. Very recently, Tayebi and Chamkha [28, 29] have conducted a numerical study of magnetohydrodynamic free convection and entropy generation within a hybrid nanofluid-filled square domain by including conducting hollow cylinder [28] and conducting wavy cylinder [29].

According to the above literature review, little attention has been devoted to the natural convection in a hybrid nanofluid-filled cavity having conductive bodies. The main goal of this numerical study is to evaluate the various geometrical configurations of an inserted wavy conductive block within a square domain filled with Al2O3–Cu water-based hybrid nanofluid on the MHD natural convection. This configuration can be found in many heat transfer fluid systems, namely solar heat devices, heating and cooling buildings, chemical processing apparatus, nuclear systems cooling, energy storage applications and particularly in the cooling of electronic components. Coupled conservation equations are resolved via the finite volume technique. The effect of volumic fraction, Hartmann and Rayleigh numbers, fluid/solid heat conductivity ratio, number of undulations and their amplitudes of the inserted corrugated circular body are scrutinized.

Mathematical formulation

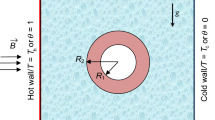
Figure 1 represents a descriptive schema concerns the problem of MHD buoyancy-driven of hybrid nanoliquid inside a domain containing a centered corrugated circular conductive cylinder. To activate the buoyancy flow within the system, a difference thermal gradient was produced between the side walls. The flow is affected by a horizontal magnetic field. The hybrid nanofluid is engineered by blending an equal concentration of copper and alumina spherical nanoparticles in the water. The Boussinesq approximation is operated. This model shows the hollow body of an electrical transformer where one side of the enclosure is exposed to the solar heat and absorbs the heat (hot wall), while the other side of the enclosure does not receive the solar energy and is at a cold temperature (cold wall). The metal insert (the wavy cylinder) is the mechanical support to hold the structure of the transformer. The hybrid nanofluid is the coolant, and the cylinder affects the thermal behavior of the hybrid nanofluid and natural convection structure in the cavities. The magnetic field is the result of the power transformation in the transformer.

Fig. 1
figure 1

A schematic view of the considered domain

Full size image

The wavy wall of the centered object is described by the following relation:

$$r\left( \eta \right) = A \times \cos \left( {N\eta } \right) + r_{\text{i}}$$
(1)

Here A is in the range of 0.1–0.4, N is in the range of 3–8.

The block cylinder size is kept constant corresponding H/L = 2.

Nanofluid property relations

Material properties of water and nanoparticles are exhibited in Table 1 [28, 29].

Table 1 Material properties [28, 29]
Full size table

Thermophysical properties of the hybrid nanoliquids are determined in the followings [9,10,11]:

$$\rho_{\text{hnf}} = \rho_{\text{Cu}} \phi_{\text{Cu}} + \rho_{{{\text{Al}}_{2} {\text{O}}_{3} }} \phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \left( {1 - \phi_{\text{Cu}} - \phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} } \right)\rho_{\text{f}}$$
(2)
$$\left( {\rho C_{\text{p}} } \right)_{\text{hnf}} = \left( {\rho C_{\text{p}} } \right)_{\text{Cu}} \phi_{\text{Cu}} + \left( {\rho C_{\text{p}} } \right)_{{{\text{Al}}_{2} {\text{O}}_{3} }} \phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \left( {1 - \phi_{\text{Cu}} - \phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} } \right)\left( {\rho C_{\text{p}} } \right)_{\text{f}}$$
(3)
$$\left( {\rho \beta } \right)_{\text{hnf}} = \left( {\rho \beta } \right)_{\text{Cu}} \phi_{\text{Cu}} + \left( {\rho \beta } \right)_{{{\text{Al}}_{2} {\text{O}}_{3} }} \phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \left( {1 - \phi_{\text{Cu}} - \phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} } \right)\left( {\rho \beta } \right)_{\text{f}}$$
(4)

The effective heat conductivity and viscosity are estimated by Eqs. (5) and (6) utilizing Corcione correlations [30] when the Brownian motion is taken into account:

$$k_{{\text {hnf}}} /k_{{\text {f}}} = \left( {1 + 4.4 {(\text{Re})}^{0.4} {(\text{Pr})}{^{0.66}} \left( {k_{{\text{f}}} } \right)^{-0.03} \left( {T/T_{{\text{fr}}} } \right)^{10}((k_{{{{\text{Al}}}_{2} {{\text{O}}}_{3} }})^{0.33}(\phi_{{{{\text{Al}}}_{2} {{\text{O}}}_{3} }})^{0.66}}+(k_{{\text{Cu}}} )^{0.33}(\phi_{{\text{Cu}}})^{0.66})\right)$$
(5)
$$\mu_{\text{hnf}} /\mu_{\text{f}} = 1/\left( { - 34.87\left( {d_{\text{p}} /d_{\text{f}} } \right)^{ - 0.3} (\phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \phi_{\text{Cu}} )^{1.03} + 1} \right)$$
(6)
$$\text{Re} = 2T\rho_{\text{f}} k_{\text{b}} /\pi d_{\text{p}} \mu_{\text{f}}^{2}$$

The mixture electrical conductivity is estimated using Maxwell relation [31]:

$$\sigma_{\text{hnf}} = \left( {\phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \phi_{\text{Cu}} } \right)\left( {1 + 3\left( {\frac{{\sigma_{\text{hp}} }}{{\sigma_{\text{f}} }} - 1} \right)\sigma_{\text{f}} /\left( {\phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \phi_{\text{Cu}} } \right)\left( {\frac{{\sigma_{\text{hp}} }}{{\sigma_{\text{f}} }} + 2} \right) - \left( {\frac{{\sigma_{\text{hp}} }}{{\sigma_{\text{f}} }} - 1} \right)} \right)$$
(7)

Here \(\sigma_{\text{hp}} = \phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} \sigma_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \phi_{\text{Cu}} \sigma_{\text{Cu}} /\left( {\phi_{{{\text{Al}}_{2} {\text{O}}_{3} }} + \phi_{\text{Cu}} } \right) .\)

It is noteworthy that the stability of nanofluids/hybrid nanofluids is an important issue in long-term applications. However, the deterioration of nanofluids is a slow process, which takes place in days and weeks. This is while the timescale of the natural convection heat transfer in the enclosure is within minutes. Hence, at any stage, the temporal thermophysical properties of the nanofluid could be used to estimate the thermal performance of the nanofluid. The time-dependent variation of thermophysical properties of nanofluids and instability problems are useful for long-term applications.

Basic equations

The transport equations for 2D steady, laminar and incompressible magnetohydrodynamic buoyancy-driven flow of hybrid nanoliquid can be established as follows.

Continuity

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$$
(8)

Momentum

$$u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = \frac{{\mu_{\text{hnf}} }}{{\rho_{\text{hnf}} }}\left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) - \frac{1}{{\rho_{\text{hnf}} }}\frac{\partial p}{\partial x}$$
(9a)
$$u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} = \frac{{\mu_{\text{hnf}} }}{{\rho_{\text{hnf}} }}\left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) - \frac{1}{{\rho_{\text{hnf}} }}\frac{\partial p}{\partial y} + \frac{{\left( {\rho \beta } \right)_{\text{hnf}} }}{{\rho_{\text{hnf}} }}g\left( {T - T_{\text{c}} } \right) - \frac{{\sigma_{\text{hnf}} }}{{\rho_{\text{hnf}} }}B_{0}^{2} v$$
(9b)

Heat equation for hybrid nanofluid domain

$$u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha_{\text{hnf}} \left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right)$$
(10a)

Heat equation for the solid domain

$$k_{\text{s}} \frac{{\partial^{2} T}}{{\partial x^{2} }} + k_{\text{s}} \frac{{\partial^{2} T}}{{\partial y^{2} }} = 0$$
(10b)

To transform the equations into their dimensionless form, we introduced the following dimensionless parameters:

$$X = \frac{x}{H},\quad Y = \frac{y}{H},\quad P = \frac{{pH^{2} }}{{\rho_{\text{f}} \alpha_{\text{f}}^{2} }},\quad U = \frac{H}{{\alpha_{\text{f}} }}u,\quad V = \frac{H}{{\alpha_{\text{f}} }}v,\quad \theta = \frac{{T - T_{\text{c}} }}{{T_{\text{h}} - T_{\text{c}} }},\quad k^{*} = \frac{{k_{\text{f}} }}{{k_{\text{s}} }}$$

The non-dimensional conservation equations are:

$$\frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0$$
(11)
$$U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y} = \frac{{\mu_{\text{hnf}} }}{{\alpha_{\text{f}} \rho_{\text{hnf}} }}\left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right) - \frac{{\rho_{\text{f}} }}{{\rho_{\text{nf}} }}\frac{\partial P}{\partial X}$$
(12a)
$$U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y} = \frac{{\mu_{\text{hnf}} }}{{\alpha_{\text{f}} \rho_{\text{hnf}} }}\left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right) + {\text{Ra}}\Pr \theta \frac{{\left( {\rho \beta } \right)_{\text{hnf}} }}{{\rho_{\text{hnf}} \beta_{\text{f}} }} - \frac{{\rho_{\text{f}} }}{{\rho_{\text{nf}} }}\frac{\partial P}{\partial Y} - {\text{Ha}}^{2} \Pr V\frac{{\rho_{\text{f}} }}{{\rho_{\text{nf}} }}\frac{{\sigma_{\text{hnf}} }}{{\sigma_{\text{f}} }}$$
(12b)
$$U\frac{\partial \theta }{\partial X} + V\frac{\partial \theta }{\partial Y} = \frac{{\alpha_{\text{hnf}} }}{{\alpha_{\text{f}} }}\left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right)$$
(13)
$$k^{*} \frac{{\partial^{2} \theta }}{{\partial X^{2} }} + k^{*} \frac{{\partial^{2} \theta }}{{\partial Y^{2} }} = 0$$
(14)
$$U = \frac{\partial \psi }{\partial Y} ,\quad V = - \frac{\partial \psi }{\partial X}$$
(15)

where

$$\Pr = \frac{{\upsilon_{\text{f}} }}{{a_{\text{f}} }},\quad {\text{Ra}} = \frac{{g\left( {T_{\text{h}} - T_{\text{c}} } \right)\beta_{\text{f}} H^{3} }}{{\upsilon_{\text{f}} \alpha_{\text{f}} }}\quad {\text{and}}\quad {\text{Ha}} = HB_{0} \sqrt {\sigma_{\text{f}} /\mu_{\text{f}} }$$

Dimensionless boundary conditions

$$\left\{ {\begin{array}{*{20}l} {U = V = \psi = 0,\quad \theta = 1\;{\text{for}}\;{\text{the}}\;{\text{left}}\;{\text{wall}}} \hfill \\ {U = V = \psi = 0,\quad \theta = 0\;{\text{for}}\;{\text{the}}\;{\text{right}}\;{\text{wall}}} \hfill \\ {U = V = \psi = 0,\quad \frac{\partial \theta }{\partial Y} = 0\;{\text{for}}\;{\text{the}}\;{\text{horizontal}}\;{\text{adiabatic}}\;{\text{walls}}} \hfill \\ {U = V = \psi = 0,\quad \theta_{\text{hnf}} = \theta_{\text{s}} ,\;\left( {k_{\text{hnf}} \frac{\partial \theta }{\partial n}} \right)_{\text{hnf}} = \left( {k_{\text{s}} \frac{\partial \theta }{\partial n}} \right)_{\text{s}} \;{\text{for}}\;{\text{solid-nanofluid}}\;{\text{interfaces}}} \hfill \\ \end{array} } \right.$$

The local and overall heat transfer rates are determined from the local and average Nusselt numbers which are defined in Eqs. (17) and (18), respectively, as follows:

$${\text{Nu}} = \left( { - \frac{{k_{\text{hnf}} }}{{k_{\text{f}} }}} \right)\left. {\frac{\partial \theta }{\partial X}} \right|_{{{\text{X}} = 0}}$$
(17)
$${\text{Nu}}_{\text{avg}} = \mathop \int \limits_{0}^{1} {\text{Nu}}\;{\text{d}}Y$$
(18)

Numerical methodology

The finite volume technique (FVM) is implemented to discretize the transport equations [32]. For the simulation analysis, an irregular grid system is used and mesh independence of the numerical solutions is assured. Table 2 shows the mesh independence test results for various grid sizes for the case of k* = 0.1, A = 0.2, N = 6, Ha = 25, Ra = 105 and ϕ = 0.06. Validation of the present code is shown in Figs. 2, 3, and Table 3 [33].

Table 2 Mean Nusselt number on the heat wall for different grids: A = 0.2, N = 6, Ra = 105, Ha = 25, ϕ = 0.06 and k* = 0.1
Full size table
Fig. 2
figure 2

Comparison of isotherms and streamlines with House et al. [33] for k* = 5 and Ra = 105

Full size image
Fig. 3
figure 3

Comparison of isotherms and streamlines with House et al. [33] for k* = 0.2 and Ra = 105

Full size image
Table 3 Comparison of the average Nusselt number of the present study with the results of House et al. [33] at Ra = 105
Full size table

Results and discussion

The present simulation work has been performed to explore the impact of various parameters, namely volumetric concentration of nanoparticles (ϕ), Rayleigh number (Ra), fluid/solid ratio of heat conductivities (k*), Hartmann number (Ha), wave number (N) and wave amplitude (A) on MHD natural convection in an enclosure with the wavy conducting block are considered.

The fluid circulation inside the cavity is shown by the maps of current function isolines which are represented in Fig. 4 for various values of Rayleigh and Hartman at N = 6, A = 0.2, ϕ = 0.06 and k* = 0.1. It is found that the flow is monocellular with a rotating vortex (primary vortex) in the clockwise direction encompassing the conducting wavy block. In fact, the fluid near to the hot wall receives heat becomes more buoyant and ascends due to buoyancy forces. Near the cold wall, the fluid cools and becomes heavier (less buoyant) and descends along this wall. It is this behavior that implements the rotational aspect of the flow within the cavity. As the value of the Rayleigh number increases, the buoyancy forces increase, and therefore, the maximum absolute values of the current function, \(\left| {\psi_{ \hbox{max} } } \right|\) increase, indicating that the flow intensity within the system increases. In contrast, streamline contours show that the increase in the magnetic forces reduces the flow intensity within the system. Thus, it can be state that the convection flow strength is obtained for the smallest value of Hartmann and the largest value of Rayleigh. In addition, it can be seen that the streamlines become tighter near the sidewalls and the crest of the waves, which shows that the flow is accelerated in these areas. It is also seen that by raising Ra and reducing Ha, the main vortex elongates horizontally and the fluid pulls away from the center where the conducting cylinder is located indicating a powerful convective flow inside the cavity and maximum heat transmission between the active walls. Figure 5 portrays that as the flow circulation increases the isotherms deform following the flow direction. This creates a large thermal gradient on the vertical active surfaces particularly at the top of the cold wall and the lower of hot wall, respectively. This leads to a high rate of local heat transmission in these areas. Furthermore, it is clear that the temperature isolines within the conductive cylinder are parallel which signifies that the heat is plainly transferred by conduction. It is noted that the heat transmission by conduction inside the solid is done horizontally from left to right (since the isotherms are vertical lines) when the convection is weak within the cavity. As the intensity of the convection increases within the cavity, the heat transmission by conduction inside the solid is done vertically from top to bottom (since the isotherms are horizontal lines).

Fig. 4
figure 4

Streamline contours for various values of Ra and Ha at A = 0.2, N = 6, ϕ = 0.06 and k* = 0.1

Full size image
Fig. 5
figure 5

Isotherm contours for various values of Ra and at A = 0.2, N = 6, ϕ = 0.06 and k* = 0.1

Full size image

In Fig. 6, isotherms and streamlines for various fluid/solid heat conductivity ratios at given values of Ra = 105, Ha = 25, ϕ = 6% N = 6 and A = 0.2 are compared when convection is predominant. As ks of the corrugated conductive cylinder increases (the heat conductivity ratio, k* decreases), the flow intensity is gradually increased and the temperature isolines within the solid are spaced from each other. This reflects an increase in the amount of the heat coming out of the heated surface via the solid cylinder to the cold surface, thus increasing the buoyancy-driven flow throughout the cavity.

Fig. 6
figure 6

Streamline and isotherm contours for various values of k* at A = 0.2, N = 6, Ra = 105, Ha = 25 and ϕ = 0.06

Full size image

The influences of the undulation amplitude and wave number on the dynamic and thermal contours at Ra = 105, k* = 0.1 and Ha = 25 are shown in Figs. 7 and 8, respectively. It is shown that by raising A and N the strength of the buoyancy flow reduces. At a fixed value of N, the more the amplitude of the waves increases, more the nanoliquid moves away from the external surface of the block (the waves pushes the fluid away from the wall) allowing less heat portion to pass through the block. Furthermore, by raising A, the streamlines will be very tight at the summit of the waves, leading to an acceleration of the nanofluid in these areas. On the other hand, at a fixed value of A, the presence of corrugations on the solid impedes the fluid flow, and as N increases, the fluid will be blocked repeatedly.

Fig. 7
figure 7

Streamline and isotherm contours for various values of wave amplitude, A at N = 6, Ra = 105, Ha = 25 and k* = 0.1

Full size image
Fig. 8
figure 8

Streamline and isotherm contours for various values of wave number, N at A = 0.2, Ra = 105, Ha = 25 and k* = 0.1

Full size image

Figures 9 and 10 show the profile of the average Nusselt number on the hot wall as a function of the number of corrugations (N) and their amplitudes (A) for various values of k* when ϕ = 0.06 and Ha = 25 when (a): Ra = 103, (b): Ra = 105. The first noticeable detail is that, when conduction is predominant, at a small Rayleigh number, the average Nusselt number augments with the augmentation of ks (diminution of k*). In contrast of that, the increase in ks leads to rising the average Nusselt number when convection is becoming predominated. This may be because when the convection is weak, the increase in the corrugated solid cylinder heat conductivity enables to pass a big portion of the heat horizontally to the opposite cold part of the cavity. But the fluid dissipates this heat to the bottom across the cylinder when the convective flow is strong. These figures also show that, at a given k*, the mean Nusselt number is a decreasing with of the undulation number and amplitude; the more the number of corrugations on the solid block and their amplitude increases, the more the rate of heat transfer decreases, except for a large ks (k* = 0.1) when the convection is weak.

Fig. 9
figure 9

Nuavg versus N for various values of k* at ϕ = 0.06, A = 0.2 and Ha = 25 when a Ra = 103, b Ra = 105

Full size image
Fig. 10
figure 10

Nuavg versus A for various values of k* at ϕ = 0.06, N = 6 and Ha = 25 when a Ra = 103, b Ra = 105

Full size image

In order to evaluate the influence of the combined nanoparticle’s volumic concentration on the rate of heat transmission, in Fig. 11 we display the progression of the mean Nusselt number with ϕ for various values of k* at Ra = 103 and 105 separately when A = 0.2, N = 6 and Ha = 25. As previously stated, at a specific value of ϕ and small Ra (103), any improvement in k* (diminishing in ks) causes the mean Nusselt to decrease (see Fig. 11a) and to increase at a high Ra (105) (see Fig. 11b). Furthermore, it is seen that the addition of both Cu and Al2O3 nanoparticles in the liquid enhances the rate of heat transmission especially at a higher Ra when the effects of viscous forces are dominated by buoyancy forces. The inverse is remarked at low Ra when the buoyancy forces are dominated by viscous forces because the nanoparticles contribute also to increase the viscosity of the mixture.

Fig. 11
figure 11

Nuavg versus ϕ for various values of k* at A = 0.2, N = 6 and Ha = 25 when a Ra = 103, b Ra = 105

Full size image

To understand how the Hartmann number affects the overall rate of heat transmission, we display, in Fig. 12 the evolution of the mean Nusselt with the volumic fraction for different Hartmann. It is clear that the existence of the horizontal magnetic field causes a decrease in the convection intensity in the cavity. So, to cool this system, it is preferable to apply a magnetic field. It is worth noting that when the convection is weak, a combination of a magnetic field and nanoparticle addition leads the rate of heat transfer to decreases very progressive (see Fig. 12a).

Fig. 12
figure 12

Nuavg versus ϕ for various values of Ha at A = 0.2, N = 6 and k* = 0.1 when a Ra = 103, b Ra = 105

Full size image

Figure 13 indicates that the presence of the magnetic field is more influential on the heat transfer rate at higher Rayleigh.

Fig. 13
figure 13

Nuavg versus Ha for various values of k* at A = 0.2, N = 6 and ϕ = 0.06 when a Ra = 103, b Ra = 105

Full size image

Conclusions

In the current numerical study, natural convection of Al2O3–Cu/water hybrid nanoliquid in a cavity with a centered corrugated conducting cylinder under constant horizontal magnetic field is examined. The finite volume technique (FVM) is applied to discretize the transport equations. The Corcione correlations to estimate the overall thermal conductivity and the overall viscosity of the hybrid nanoliquid taking into account the Brownian motion are used. The investigation has been executed considering the pertinent quantities: Rayleigh number (Ra), Hartmann number (Ha), volumic concentration of the hybrid nanoliquid (ϕ), fluid/solid heat conductivity ratio (k*), wave number of the corrugated block and their amplitudes. Principle results can be summarized as follows:

  • Natural convective flow circulation was found to increase with increasing Rayleigh and heat conductivity of the wavy solid cylinder, while it decreases with increasing Hartmann, undulation number and undulation amplitude.

  • The heat exchange rate boosts with the increase in the Ra and the decrease in the Ha.

  • When the convection is strong, at lower Ha and higher Ra, the maximum heat transfer rate was obtained for lower values of ks, N and A and higher values of ϕ.

  • When conduction mode is predominant, raising ks boosts the heat exchange rate. The opposite is true when the convection is predominant.

  • The presence of the magnetic field is more influential on the heat transfer rate at higher Ra.

  • It has also been found that enhancing the free convective flow within this configuration by suspended copper and alumina nanoparticles in water is more effective during the domination of the convection mechanism.

In the present study, it was assumed that the hybrid nanofluid is fresh and homogeneous. However, the thermophysical properties of the hybrid nanofluid will slowly change by time. Hence, the heat transfer analysis of hybrid nanofluids for long-term applications is an essential task. Such analysis demands theoretical models and experimental data to predict the variation of the dynamic viscosity and the thermal conductivity with time. At present, there are scarce data on the long-time behavior of hybrid nanofluids. Thus, future investigations could focus on the models for prediction of long-term behavior of hybrid nanofluids and analysis of long-term thermal performance of these novel liquids.