Introduction

One branch of microfluidics shows prodigious promise for potential applications in cooling in microscale thermal management systems/devices, in particular, in the micro-electromechanical system (MEMS). With the advancement of technology, several effective ways of cooling of the microdevices/systems have been proposed by the researchers in recent years [1,2,3,4,5,6]. One of the available methods relies on the use of nanoparticles in the base fluid as a coolant [5,6,7,8,9,10,11,12]. These small particles have high-thermal conductivity and consequently, increase the heat transfer rate in the associated process [8, 11, 13, 14]. It is important to mention here that the addition of nanoparticles to the base fluid makes it inhomogeneous, which at times alters the underlying thermo-hydrodynamics non-trivially [12, 15, 16]. It is needless to mention that the higher thermodynamic irreversibility generated in the underlying process destroys the exergetic efficiency of the system [17]. The analysis of entropy generation therefore appears to be a convenient tool to assess the intrinsic irreversibilities associated with a microfluidic system and to determine the optimized operating conditions leading to minimum dissipation.

Albeit intuitive, we would like to mention here that several inevitable factors involved with the underlying thermo-electro-hydrodynamics like heat transfer due to finite temperature difference, dissipative effect, and Joule heating effect invite thermodynamic irreversibility in the process and results in irreversible losses of the available energy [18,19,20,21,22]. In the paradigm of microscale transport, flow actuation by applied pressure gradients many a time encounters difficulties owing to miniaturization of the platform, and at times, the dissipative effects become significant on account of significant frictional losses [2, 22,23,24,25,26]. On the contrary, manipulation of flows in a microfluidic channel using an external electric field has gained humongous popularity owing to a few important encouraging characters like noise-free operation, ease in manipulation, finer controllability, etc. [27, 28]. However, it is important to note that the inevitable Joule heating effect associated with the purely electrically actuated transport leads to entropy generation appreciably. It deteriorates the exergetic efficiency by destroying the available work in the process [3, 4, 29]. Taking a note on these aspects, researchers have considered the combined effects of applied pressure gradient and electrokinetic influence to manipulate flows in the microfluidic environment, essentially to keep the Joule heating and dissipation effects within a manageable limit [3, 30, 31].

It may be mentioned here that several issues associated with the underlying thermo-hydrodynamics as well as thermo-electro-hydrodynamics of nanofluids (nanoparticles mixed with a base fluid) in microscale thermal management systems/devices have been reported by numerous researchers [5,6,7, 22, 23, 32,33,34,35,36,37]. In these published works, researchers have shown the promising potential of nanofluids in recovering higher heat as compared to the other coolants. Note that all the systems/devices used for convective transport of heat even in the miniaturized platform have a finite thickness. The conductive transport of heat through bounding surfaces becomes, many times, indispensable to be taken into account on the underlying microscale thermo-hydrodynamics. Simultaneous effects of heat conduction through the bounding surfaces in tandem with the convection of heat through the fluid layer (often called as conjugate heat transfer) bear a significant impact on the thermodynamic efficiency of the microsystems/devices [2, 31, 38, 39]. Paying attention to all these aspects, efforts have been directed at the minimization of system entropy generation towards the optimization of design parameters (both geometric as well as thermophysical) for which thermodynamic performance becomes maximum [21, 39,40,41,42,43,44]. To the best of authors’ knowledge, this aspect has not been explored in the literature to date.

Here, we investigate the transport of a nanofluid through an asymmetrically heated microfluidic channel having finite wall thickness. We consider the combined influences of applied pressure gradient and applied electric field strength for the transportation of the nanofluid through the channel. Considering the effects of viscous dissipation, Joule heating, and conjugate transport of heat, we focus on the entropy generation minimization of this system. Through this analysis, we have shown that the global entropy generation rate of the system displays minimum values when explored as a function of the design parameters, viz. channel wall thickness ratio, Biot number, wall to fluid thermal conductivity ratio, and Peclet number. Thus, there exist specific conditions for the geometrical and thermophysical parameters which must be taken care of in the design of heat transfer devices for their optimum performance. These parameters determine the optimal working conditions in the sense that the intrinsic irreversibilities become minimum consistent with the physical restrictions of the system and leads to the maximum exergetic efficiency of the system.

Mathematical formulation

Problem description

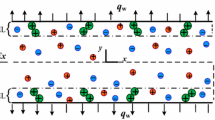
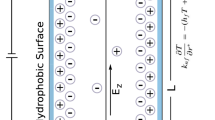
We consider here, the combined pressure and electroosmotically driven thermofluidic transport of a nanofluid comprising of alumina (\( {\text{Al}}_{2} {\text{O}}_{3} \)) as the nanoparticle and ionic aqueous solution (aqueous electrolyte) as the base fluid. This steady, unidirectional flow \( u = \left( {u\left( y \right),0,0} \right) \), is taking place through a microfluidic channel formed between two parallel plates. The length, width, and height of the channel are \( L \), \( W \) and \( 2H \), respectively, such that \( L \gg W > 2H \) as shown in Fig. 1. This assumption ensures a unidirectional flow under the applied external forcings. The underlying transport process is considered to be fully developed, both thermally and hydro dynamically. Taking a note on the practical relevance of this study, we consider different but finite thickness for each plate: \( d_{1} \) for the bottom plate and \( d_{2} \) for the top one. In this transport process, since an ionic solution is exposed to the solid plates, the surface of each plate becomes charged following an electrostatic interaction between the charged surface and electrolytic solution, and thus, a thin layer of counter ions forms in the interfacial region. This layer is referred to as the electrical double layer (EDL) [45,46,47]. In this study, we consider the EDLs to be thin and non-overlapping. However, the effect of the Joule heating, invariably present with the EOF of colloidal suspensions, is considered for the current thermofluidic transport process.

Fig. 1
figure 1

Schematic depicting the combined pressure driven and electroosmotically actuated thermofluidic transport of a nanofluid through a microchannel formed between two asymmetrically cooled parallel plates, for which L is the length, W is the width, and 2H is the height of the channel

Full size image

Thermophysical properties of nanofluid

We here make an effort to discuss the effective thermophysical properties of nanofluids. Several studies reported in the literature have attempted to discuss the mechanism of enhanced transport of nanoscale colloidal suspensions from the perspective of continuum-based formulation of the thermophysical properties of nanofluids [9]. To be precise, most of the studies have reported that factors like particle clustering, Brownian motion of the particles, and molecular layering at the fluid-particle interface enhance transport, accounting alteration of the effective thermophysical properties of nanofluid [8, 10]. In addition to these factors, there are several other issues like complex hydrodynamic interactions at small scale and the interparticle interactions, which need to be put in perspective for calculating the effective rheological behaviour and thermophysical properties of nanofluids. These factors stimulate the aggregation of nanoparticles suspended in the base fluid and allow the cluster formation. In this study, we calculate the effective properties of nanofluids from the perspective of continuum-based approach, where the effective viscosity and density of the nanofluid are given by the following relations as written below [16,17,18]. Also, for the expression of effective density and heat capacitance, we are using the model [32] which can be expressed as:

$$ (\rho C_{\text{p}} )_{\text{nf}} = \left( {1 - \phi } \right)\left( {\rho C_{\text{p}} } \right){}_{\text{f}} + \phi \left( {\rho C_{\text{p}} } \right)_{\text{np}} $$
(1)

where \( \rho \) is the density (\( \text{kg} {\kern 1pt} m^{ - 3} \)), \( C_{\text{p}} \) is the specific heat at constant pressure (\( \text{kJ} \,kg^{ - 1} K^{ - 1} \)), and \( \phi \) is the nanoparticle volume fraction. To describe the effective viscosity of the nanofluid, we consider the Brinkman model [11] and following which, the effective dynamic viscosity can be written as:

$$ \mu_{\text{nf}} = \mu_{\text{f}} \left( {1 - \phi } \right)^{{ - {5 \mathord{\left/ {\vphantom {5 2}} \right. \kern-0pt} 2}}} $$
(2)

where \( \mu_{\text{nf}} \) is the viscosity of nanofluid, \( \mu_{\text{f}} \) is the viscosity of the base fluid, and \( \phi \) is the volume fraction. The effective thermal conductivity of the nanofluid is approximated by the Maxwell–Garnett’s model and given by [21]:

$$ \frac{{k_{\text{nf}} }}{{k_{\text{f}} }} = \frac{{\left( {k_{\text{np}} + 2k_{\text{f}} } \right) - 2\phi \left( {k_{\text{f}} - k_{\text{np}} } \right)}}{{\left( {k_{\text{np}} + 2k_{\text{f}} } \right) + \phi \left( {k_{\text{f}} - k_{\text{np}} } \right)}} $$
(3)

These thermophysical properties are assumed to remain invariant of temperature in this analysis.

Governing equations for electro-hydrodynamics

For the problem under present consideration, the governing transport equations are the continuity equation, Navier–Stokes equation for the velocity field, and the Poisson-Boltzmann equation for the electrostatic charge distribution [38, 48, 49].

Continuity equation:

$$ \frac{{{\text{d}}u}}{{{\text{d}}x}} = 0 $$
(4)

Momentum equation:

Considering the assumptions pertaining to this analysis, the momentum transport equation can be written in the following form:

$$ - \frac{{{\text{d}}p}}{{{\text{d}}x}} + \mu_{\text{eff}} \frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }} + \rho_{\text{e}} E_{\text{x}} = 0 $$
(5)

where \( \rho_{\text{e}} \) is the total ionic charge density inside the electric double layer (EDL) [45] and \( E_{\text{x}} \) is the applied electric field [29, 45, 50]. The EDL charge density \( \rho_{\text{e}} \) can be obtained from the Poisson-Boltzmann equation [45] as:

$$ \rho_{\text{e}} = - \varepsilon \frac{{{\text{d}}^{2} \psi }}{{{\text{d}}y^{2} }} $$
(6)

where \( \psi \) is the electrostatic potential within the EDL and \( \varepsilon \) is the dielectric constant of electrolyte. Now, for a z:z symmetric electrolyte, the net ionic charge density is given by [45]

$$ \rho_{\text{e}} = ze\left( {n^{ + } - n^{ - } } \right) $$
(7)

here \( n^{ + } \) and \( n^{ - } \) are the densities of positive and negative ions, respectively. For the low Reynolds number flow, we can neglect the convection of ions in the microchannel. In this case, we appeal to the Boltzmann distribution to obtain ionic densities for both positive and negative ions, given by [45, 51,52,53,54]:

$$ n^{ \pm } = n_{\infty } \exp \left[ { \mp \left( {ze\psi } \right)/k_{\text{B}} T} \right] $$
(8)

where \( n_{\infty } \) is the bulk concentration of ions, \( z \) is the ionic valence, \( e \) is the electric charge, \( T \) is the absolute temperature of the system, and \( k_{\text{B}} \) is the Boltzmann constant. The following two assumptions are now considered for this analysis: (a) the zeta potential is temperature independent and (b) the value of zeta potential is less than 25 mV [45, 55,56,57]. On the basis of the abovementioned assumptions, we can now apply the Debye–Hückel approximation [38, 58], which linearizes the exponential form of the Boltzmann distribution. Thus, Eq. (6) now takes the form:

$$ \frac{{{\text{d}}^{2} \psi }}{{{\text{d}}y^{2} }} = \left( {\frac{1}{{\lambda_{D} }}} \right)^{2} \psi = \kappa^{2} \psi $$
(9)

where \( \lambda_{\text{D}} \) is the EDL thickness and \( \kappa \left( { = {1 \mathord{\left/ {\vphantom {1 {\lambda_{\text{D}} }}} \right. \kern-0pt} {\lambda_{\text{D}} }}} \right) \) is the Debye–Hückel parameter. It may be mentioned in this context that the magnitude of electroosmotic body force for a given magnitude of applied electric field acting on the fluid mass will depend upon \( \kappa \) [45]. Below we write the boundary conditions employed in this analysis to solve the transport Eqs. (5) and (9).

  • For the velocity field

    $$ \left. \begin{aligned} {\text{No}}\,{\text{slip}}\,{\text{condition}}\,{\text{at}}\,{\text{the}}\,{\text{walls}}:\quad \left. u \right|_{{{\text{y}} = \pm {\text{H}}}} = 0 \hfill \\ {\text{Symmetry}} \,{\text{at}}\,{\text{the}}\,{\text{centre}}\,{\text{line}}:\quad \left. {{{{\text{d}}u} \mathord{\left/ {\vphantom {{{\text{d}}u} {{\text{d}}y}}} \right. \kern-0pt} {{\text{d}}y}}} \right|_{{{\text{y}} = 0}} = 0 \hfill \\ \end{aligned} \right\} $$
    (10)

  • For the electric potential

    $$ \left. \begin{aligned} \text{At} \,{\text{the}}\,{\text{symmetric}}\,{\text{plane}}:\quad \left. {{{{\text{d}}\psi } \mathord{\left/ {\vphantom {{{\text{d}}\psi } {{\text{d}}y}}} \right. \kern-0pt} {{\text{d}}y}}} \right|_{{{\text{y}} = 0}} = 0 \hfill \\ \text{Specified} \,{\text{potential}}\,{\text{at}}\,{\text{wall}}:\quad \left. \psi \right|_{{{\text{y}} = \pm {\text{H}}}} = \psi_{\text{w}} \hfill \\ \end{aligned} \right\} $$
    (11)

After imposing the boundary condition as delineated in Eq. (11) on Eq. (9) and considering the ionic charge density from Eq. (8), we can rewrite the Eq. (5) as:

$$ - \frac{{{\text{d}}p}}{{{\text{d}}x}} + \mu_{{{\text{eff}}}} \frac{{{\text{d}}^{2} u}}{{{\text{d}}y^{2} }} - \left( {\varepsilon E_{\text{x}} \psi_{\text{w}} \kappa^{2} } \right)\frac{{\cosh \left( {\kappa y} \right)}}{{\cosh \left( {\kappa H} \right)}} = 0. $$
(12)

Nondimensionalization of momentum equation

Equation (12) can be non-dimensionalized using the following dimensionless parameters: \( \bar{y} = {y \mathord{\left/ {\vphantom {y H}} \right. \kern-0pt} H} \), \( \bar{u} = {u \mathord{\left/ {\vphantom {u {U_{\text{HS}} }}} \right. \kern-0pt} {U_{\text{HS}} }} \), and \( \bar{\kappa } = \kappa H\left( { = {H \mathord{\left/ {\vphantom {H {\lambda_{\text{D}} }}} \right. \kern-0pt} {\lambda_{\text{D}} }}} \right) \). Note that \( U_{\text{HS}} \) is the Helmholtz-Smoluchowski velocity and is expressed as \( U_{\text{HS}} \left( {{{ = - \varepsilon E_{\text{x}} \psi_{\text{w}} } \mathord{\left/ {\vphantom {{ = - \varepsilon E_{\text{x}} \psi_{\text{w}} } {\mu_{\text{f}} }}} \right. \kern-0pt} {\mu_{\text{f}} }}} \right) \). \( \bar{\kappa } \) is the non-dimensional Debye–Hückel parameter. Also, we define a parameter that relates the relative strength of the applied pressure gradient to the electroosmotic excitation strength as \( p_{\text{x}} = - {{H^{2} \left( {{{{\text{d}}p} \mathord{\left/ {\vphantom {{{\text{d}}p} {{\text{d}}x}}} \right. \kern-0pt} {{\text{d}}x}}} \right)} \mathord{\left/ {\vphantom {{H^{2} \left( {{{{\text{d}}p} \mathord{\left/ {\vphantom {{{\text{d}}p} {{\text{d}}x}}} \right. \kern-0pt} {{\text{d}}x}}} \right)} {\mu_{\text{f}} U_{\text{HS}} }}} \right. \kern-0pt} {\mu_{\text{f}} U_{\text{HS}} }} \). Using these non-dimensional parameters, the dimensionless transport equation reads as:

$$ \frac{{{\text{d}}^{2} \bar{u}}}{{{\text{d}}\bar{y}^{2} }} + \left( {\frac{{\bar{\kappa }}}{{\sqrt {{{\mu_{\text{eff}} } \mathord{\left/ {\vphantom {{\mu_{\text{eff}} } {\mu_{\text{f}} }}} \right. \kern-0pt} {\mu_{\text{f}} }}} }}} \right)^{2} \frac{{\cosh \left( {\bar{\kappa }\bar{y}} \right)}}{{\cosh \left( {\bar{\kappa }} \right)}} + \bar{p}_{\text{x}} = 0 $$
(13)

where \( \bar{\mu } = {{\mu_{\text{eff}} } \mathord{\left/ {\vphantom {{\mu_{\text{eff}} } {\mu_{\text{f}} }}} \right. \kern-0pt} {\mu_{\text{f}} }} \) is the fluid viscosity ratio or relative viscosity of nanofluid and carrier fluid [24], and \( \bar{p}_{\text{x}} = {{p_{\text{x}} \mu_{\text{f}} } \mathord{\left/ {\vphantom {{p_{\text{x}} \mu_{\text{f}} } {\left( {\mu_{\text{eff}} } \right)}}} \right. \kern-0pt} {\left( {\mu_{\text{eff}} } \right)}} \) is the modified pressure gradient parameter.

The boundary condition for velocity in dimensionless form

$$ {\text{No}}\,{\text{slip}}\,{\text{boundary}}\,{\text{condition}}\,{\text{at}}\,{\text{the}}\,{\text{channel}}\,{\text{walls}}:\quad \left. {\bar{u}} \right|_{{{\bar{\text{y}}} = \pm 1}} = 0 $$
(14)
$$ \text{Maximum} \,{\text{velocity}}\,{\text{at}}\,{\text{the}}\,{\text{centre}}\,{\text{line}}\,{\text{due}}\,{\text{to}}\,{\text{symmetry}}:\quad \left. {{{{\text{d}}\bar{u}} \mathord{\left/ {\vphantom {{{\text{d}}\bar{u}} {{\text{d}}\bar{y}}}} \right. \kern-0pt} {{\text{d}}\bar{y}}}} \right|_{{{\bar{\text{y}}} = 0}} = 0 $$
(15)

Utilizing the boundary conditions given in Eqs. (14)–(15), we can find the non-dimensional velocity profile solving Eq. (13). The expression for dimensionless flow velocity reads:

$$ \bar{u} = \frac{1}{{\bar{\mu }}}\left[ {1 - \frac{{\cosh \left( {\bar{\kappa }\bar{y}} \right)}}{{\cosh \left( {\bar{\kappa }} \right)}}} \right] + \frac{{\bar{p}_{\text{x}} }}{2}\left( {1 - \bar{y}^{2} } \right) $$
(16)

For the brevity in presentation, we recast Eq. (16) in the following form:

$$ \bar{u} = g_{1} \cosh \left( {\bar{\kappa }\bar{y}} \right) + g_{2} \bar{y}^{2} + g_{3} $$
(17)

where \( g_{1} = \left( { - \text{sech} {{\left( {\bar{\kappa }} \right)} \mathord{\left/ {\vphantom {{\left( {\bar{\kappa }} \right)} {\bar{\mu }}}} \right. \kern-0pt} {\bar{\mu }}}} \right) \), \( g_{2} = \left( {{{ - \bar{p}_{\text{x}} } \mathord{\left/ {\vphantom {{ - \bar{p}_{\text{x}} } 2}} \right. \kern-0pt} 2}} \right) \) and \( g_{3} = \left[ {\left( {{1 \mathord{\left/ {\vphantom {1 {\bar{\mu }}}} \right. \kern-0pt} {\bar{\mu }}}} \right) + \left( {{{\bar{p}_{\text{x}} } \mathord{\left/ {\vphantom {{\bar{p}_{\text{x}} } 2}} \right. \kern-0pt} 2}} \right)} \right] \).

Governing equation for temperature distribution

The governing equation describing the thermal energy transport associated with the flow of nanofluid inside the microchannel (considering axial conduction, viscous dissipation, and volumetric heat generation terms) can be expressed as:

$$ \left( {\rho C_{\text{p}} } \right)_{\text{nf}} u\frac{\partial T}{\partial x} = k_{\text{eff}} \left( {\frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) + \mu_{\text{eff}} \left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} + \sigma E_{\text{x}}^{2} $$
(18)

where \( \rho_{\text{nf}} \) is the density of nanofluid, \( E_{\text{x}} \) is the applied electric field, and \( \sigma \) is the charge density. Note that, the second and third terms on the right-hand side of Eq. (18) take into account the viscous dissipation and Joule heating effects, respectively. Furthermore, to take the effect of conjugate heat transfer into the underlying analysis, we consider the following energy equation for both the walls of the channel:

$$ \frac{{{\text{d}}^{2} T_{\text{si}} }}{{{\text{d}}y^{2} }} = 0 $$
(19)

where \( T_{\text{si}} \) is the wall temperature \( (i = 1,2 \) indicate the lower and upper walls, respectively). To solve the energy transport equations in the solid walls as well as in the flow field, we consider the following set of boundary conditions [31]:Temperature continuity at the fluid-wall interface:

$$ \left. \begin{aligned} \left. T \right|_{{{\text{y}} = - {\text{H}}}} = T_{\text{s1}} \hfill \\ \left. T \right|_{{{\text{y}} = + {\text{H}}}} = T_{\text{s2}} \hfill \\ \end{aligned} \right\} $$
(20)

Heat flux continuity at the fluid–wall interface:

$$ \left. \begin{aligned} \left. {k_{\text{eff}} \left( {{{{\text{d}}T} \mathord{\left/ {\vphantom {{{\text{d}}T} {{\text{d}}y}}} \right. \kern-0pt} {{\text{d}}y}}} \right)} \right|_{{{\text{y}} = - {\text{H}}}} = k_{\text{s1}} \left( {{{{\text{d}}T_{\text{s1}} } \mathord{\left/ {\vphantom {{{\text{d}}T_{\text{s1}} } {{\text{d}}y}}} \right. \kern-0pt} {{\text{d}}y}}} \right) \hfill \\ \left. {k_{\text{eff}} \left( {{{{\text{d}}T} \mathord{\left/ {\vphantom {{{\text{d}}T} {{\text{d}}y}}} \right. \kern-0pt} {{\text{d}}y}}} \right)} \right|_{{{\text{y}} = + {\text{H}}}} = k_{\text{s2}} \left( {{{{\text{d}}T_{s2} } \mathord{\left/ {\vphantom {{{\text{d}}T_{s2} } {{\text{d}}y}}} \right. \kern-0pt} {{\text{d}}y}}} \right) \hfill \\ \end{aligned} \right\} $$
(21)

where \( k_{\text{s1}} \) and \( k_{\text{s2}} \) are the thermal conductivities of the lower and upper walls, respectively.

Convective boundary conditions at the outer surface of upper and lower walls:

$$ \left. \begin{aligned} \hfill \left. {k_{s1} \left( {{{{\text{d}}T_{\text{s1}} } \mathord{\left/ {\vphantom {{{\text{d}}T_{\text{s1}} } {{\text{d}}y}}} \right. \kern-0pt} {{\text{d}}y}}} \right)} \right|_{{{\text{y}} = - \left( {{\text{H}} + {\text{d}}_{1} } \right)}} = h_{\,1} \left( {T_{\text{s1}} - T_{\text{a}} } \right) \\ \hfill \left. {k_{\text{s2}} \left( {{{{\text{d}}T_{\text{s2}} } \mathord{\left/ {\vphantom {{{\text{d}}T_{\text{s2}} } {{\text{d}}y}}} \right. \kern-0pt} {{\text{d}}y}}} \right)} \right|_{{{\text{y}} = + \left( {{\text{H}} + {\text{d}}_{2} } \right)}} = h_{\,2} \left( {T_{\text{s2}} - T_{\text{a}} } \right) \\ \end{aligned} \right\} $$
(22)

where \( h_{\,1} \) and \( h_{\,2} \) are the heat transfer coefficient of the ambient fluid at the lower and upper wall of the microchannel, respectively.

Non-dimensionalisation of energy equations

To non-dimensionalize the energy Eqs. (18) and (19), we consider the following dimensionless parameters: \( \bar{x} = {x \mathord{\left/ {\vphantom {x H}} \right. \kern-0pt} H}, \) \( \bar{y} = {y \mathord{\left/ {\vphantom {y {H,}}} \right. \kern-0pt} {H,}} \) \( \bar{u} = {u \mathord{\left/ {\vphantom {u {U_{\text{HS}} ,}}} \right. \kern-0pt} {U_{\text{HS}} ,}} \) \( \varTheta_{\text{si}} = {{\left( {T - T_{\text{a}} } \right)} \mathord{\left/ {\vphantom {{\left( {T - T_{\text{a}} } \right)} {\Delta T_{j} ,}}} \right. \kern-0pt} {\Delta T_{j} ,}} \) \( \varTheta_{\text{a}} = {{T_{\text{a}} } \mathord{\left/ {\vphantom {{T_{\text{a}} } {\Delta T_{\text{j}} }}} \right. \kern-0pt} {\Delta T_{\text{j}} }} \), \( \delta_{1} = {{d_{1} } \mathord{\left/ {\vphantom {{d_{1} } H}} \right. \kern-0pt} H} \), and \( \delta_{2} = {{d_{2} } \mathord{\left/ {\vphantom {{d_{2} } H}} \right. \kern-0pt} H} \), where \( \Delta T_{\text{j}} = \left( {{{\sigma E_{\text{x}}^{2} H^{2} } \mathord{\left/ {\vphantom {{\sigma E_{\text{x}}^{2} H^{2} } {k_{\text{eff}} }}} \right. \kern-0pt} {k_{\text{eff}} }}} \right) \) is the characteristics change in temperature due to Joule heating effect. \( \varTheta \) is the dimensionless fluid temperature, \( \varTheta_{\text{si}} \,\left( {i = 1,2} \right) \) is the dimensionless wall temperature, and \( \varTheta_{\text{a}} \) is the dimensionless ambient temperature. Substituting these dimensionless parameters into Eqs. (18) and (19), we get the dimensionless energy equation in the flow field as [38]:

$$ \overline{\text{Pe}} \;\bar{u}\frac{\partial \varTheta }{{\partial\bar{x}}} = \frac{{\partial^{2} \varTheta }}{{\partial \bar{y}^{2} }} + \overline{\text{Br}} \left( {\frac{{{\text{d}}\bar{u}}}{{{\text{d}}\bar{y}}}} \right)^{2} + \bar{J} $$
(23)

To mention, the dimensionless energy equation in solid walls reads as [38]:

$$ \frac{{{\text{d}}^{2} \varTheta_{\text{si}} }}{{{\text{d}}\bar{y}^{2} }} = 0 $$
(24)

A few dimensionless parameters appearing in Eq. (23) are described as follows: The Peclet number: \( {{{\text{Pe}} = \left( {HU_{\text{HS}} \left( {\rho C_{\text{p}} } \right)_{\text{f}} } \right)} \mathord{\left/ {\vphantom {{{\text{Pe}} = \left( {HU_{\text{HS}} \left( {\rho C_{\text{p}} } \right)_{\text{f}} } \right)} {k_{\text{f}} }}} \right. \kern-0pt} {k_{\text{f}} }} \), Brinkman number: \( {\text{Br}} = \left( {{{\mu_{\text{f}} U^{2}_{\text{HS}} } \mathord{\left/ {\vphantom {{\mu_{\text{f}} U^{2}_{\text{HS}} } {k_{\text{f}} \Delta T_{\text{j}} }}} \right. \kern-0pt} {k_{\text{f}} \Delta T_{\text{j}} }}} \right) \), Joule heating parameter: \( {{J = \left( {\sigma H^{2} E_{\text{x}}^{2} } \right)} \mathord{\left/ {\vphantom {{J = \left( {\sigma H^{2} E_{\text{x}}^{2} } \right)} {k_{\text{f}} \Delta T_{\text{j}} }}} \right. \kern-0pt} {k_{\text{f}} \Delta T_{\text{j}} }} \) and \( \bar{k} = {{k_{\text{eff}} } \mathord{\left/ {\vphantom {{k_{\text{eff}} } {k_{\text{f}} }}} \right. \kern-0pt} {k_{\text{f}} }} \) is the thermal conductivity ratio. Also, we define the following modified parameters pertinent to this analysis as: \( \overline{\text{Pe}} = {{{\text{Pe}}\left( {\rho C_{\text{p}} } \right)_{\text{nf}} } \mathord{\left/ {\vphantom {{{\text{Pe}}\left( {\rho C_{\text{p}} } \right)_{\text{nf}} } {\bar{k}}}} \right. \kern-0pt} {\bar{k}}}\left( {\rho C_{\text{p}} } \right)_{\text{f}} \) is the modified Peclet number, \( \overline{\text{Br}} = {{\text{Br}} \mathord{\left/ {\vphantom {{\text{Br}} {\left( {{{\bar{k}} \mathord{\left/ {\vphantom {{\bar{k}} {\bar{\mu }}}} \right. \kern-0pt} {\bar{\mu }}}} \right)}}} \right. \kern-0pt} {\left( {{{\bar{k}} \mathord{\left/ {\vphantom {{\bar{k}} {\bar{\mu }}}} \right. \kern-0pt} {\bar{\mu }}}} \right)}} \) is the modified Brinkman number, and \( \bar{J} = {J \mathord{\left/ {\vphantom {J {\bar{k}}}} \right. \kern-0pt} {\bar{k}}} \) is the modified Joule heating parameter. The dimensionless counterpart of the boundary conditions delineated in Eqs. (20)–(22) can be written in the following form:

Temperature continuity at the fluid–wall interface:

$$ \begin{aligned}\left. {\varTheta } \right|_{{\bar{y} = - 1}} = \varTheta_{s1} \\ \left. \varTheta \right|_{{\bar{y} = + 1}} = \varTheta_{s2} \end{aligned}$$
(25)

Heat flux continuity at the fluid–wall interface:

$$ \left. \begin{aligned} \left. {\left( {{{{\text{d}}\varTheta } \mathord{\left/ {\vphantom {{{\text{d}}\varTheta } {{\text{d}}\bar{y}}}} \right. \kern-0pt} {{\text{d}}\bar{y}}}} \right)} \right|_{y = - 1} = \gamma_{1} \left( {{{{\text{d}}\varTheta_{s1} } \mathord{\left/ {\vphantom {{{\text{d}}\varTheta_{s1} } {{\text{d}}\bar{y}}}} \right. \kern-0pt} {{\text{d}}\bar{y}}}} \right) \hfill \\ \left. {\left( {{{{\text{d}}\varTheta } \mathord{\left/ {\vphantom {{{\text{d}}\varTheta } {{\text{d}}\bar{y}}}} \right. \kern-0pt} {{\text{d}}\bar{y}}}} \right)} \right|_{y = + 1} = \gamma_{2} \left( {{{{\text{d}}\varTheta_{s2} } \mathord{\left/ {\vphantom {{{\text{d}}\varTheta_{s2} } {{\text{d}}\bar{y}}}} \right. \kern-0pt} {{\text{d}}\bar{y}}}} \right) \hfill \\ \end{aligned} \right\} $$
(26)

where the wall thermal conductivity ratio \( \gamma_{\text{i}} = \left( {{{k_{\text{si}} } \mathord{\left/ {\vphantom {{k_{\text{si}} } {k_{\text{eff}} }}} \right. \kern-0pt} {k_{\text{eff}} }}} \right) \) is the ratio between the thermal conductivities of wall and nanofluid, (here \( i = 1,2 \) stands for the lower and upper wall, respectively).

Convective boundary conditions at the outer surface of the channel walls

$$ \left. \begin{aligned} \hfill \left. {\left( {{{{\text{d}}\varTheta_{\text{s1}} } \mathord{\left/ {\vphantom {{{\text{d}}\varTheta_{\text{s1}} } {{\text{d}}\bar{y}}}} \right. \kern-0pt} {{\text{d}}\bar{y}}}} \right)} \right|_{{{\bar{\text{y}}} = - \left( {1 +\updelta_{1} } \right)}} = {\text{Bi}}_{1} \left( {\varTheta_{\text{s1}} - \varTheta_{\text{a}} } \right) \\ \hfill \left. {\left( {{{{\text{d}}\varTheta_{\text{s2}} } \mathord{\left/ {\vphantom {{{\text{d}}\varTheta_{\text{s2}} } {{\text{d}}\bar{y}}}} \right. \kern-0pt} {{\text{d}}\bar{y}}}} \right)} \right|_{{{\bar{\text{y}}} = + \left( {1 +\updelta_{2} } \right)}} = {\text{Bi}}_{2} \left( {\varTheta_{\text{s2}} - \varTheta_{\text{a}} } \right) \\ \end{aligned} \right\} $$
(27)

Note that \( {\text{Bi}}_{\text{i}} \left( { = {{h_{\text{i}} {\kern 1pt} H} \mathord{\left/ {\vphantom {{h_{\text{i}} {\kern 1pt} H} {k_{\text{si}} }}} \right. \kern-0pt} {k_{\text{si}} }}} \right) \) in Eq. (27) is the Biot number and signifies the ratio of heat convection at the surface of the microchannel to heat conduction in the walls of the channel. As mentioned earlier, our attention in this investigation is centered on the thermally fully developed transport under steady but unequal heat flux boundary conditions. Considering this aspect, we can compose the dimensionless temperature in the accompanying forms [59]:

$$ \varTheta = G\bar{x} + \theta \left( {\bar{y}} \right) $$
(28)

It is important to mention here that \( G \) in Eq. (28) signifies the axial temperature gradient and considered to remain constant in this analysis. Now, solving the energy transport Eq. (23) using the temperature profile given in Eq. (28), we get the temperature distribution in the flow field. Below we write the dimensionless temperature distribution in the flow field as:

$$ \theta = g_{4} \cosh \left( {\bar{\kappa }\bar{y}} \right) - g_{5} \cosh \left( {2\bar{\kappa }\bar{y}} \right) + g_{6} \bar{y}^{4} + g_{7} \bar{y}^{2} - g_{8} \bar{y}\sinh \left( {\bar{\kappa }\bar{y}} \right) + C_{1} \bar{y} + C_{2} $$
(29)

where \( C_{1} \) and \( C_{2} \) are the constants yet to be determined. The mathematical expressions for the coefficients \( g_{4} - g_{8} \) appearing in Eq. (29) are written below for the sake of completeness.

$$ g_{4} = \left[ {\left( {{{\overline{\text{Pe}} {\kern 1pt} {\kern 1pt} G{\kern 1pt} g_{1} } \mathord{\left/ {\vphantom {{\overline{\text{Pe}} {\kern 1pt} {\kern 1pt} G{\kern 1pt} g_{1} } {\bar{\kappa }^{2} }}} \right. \kern-0pt} {\bar{\kappa }^{2} }}} \right) + \left( {{{2\overline{\text{Br}} X_{3} } \mathord{\left/ {\vphantom {{2\overline{\text{Br}} X_{3} } {\bar{\kappa }^{3} }}} \right. \kern-0pt} {\bar{\kappa }^{3} }}} \right)} \right] $$
$$ g_{5} = \left( {{{\overline{\text{Br}} X_{1} } \mathord{\left/ {\vphantom {{\overline{\text{Br}} X_{1} } {8\bar{\kappa }^{2} }}} \right. \kern-0pt} {8\bar{\kappa }^{2} }}} \right) $$
$$ g_{6} = \left[ {\left( {{{\overline{\text{Pe}} {\kern 1pt} {\kern 1pt} Gg_{2} } \mathord{\left/ {\vphantom {{\overline{\text{Pe}} {\kern 1pt} {\kern 1pt} Gg_{2} } {12}}} \right. \kern-0pt} {12}}} \right) - \left( {{{\overline{\text{Br}} X_{2} } \mathord{\left/ {\vphantom {{\overline{\text{Br}} X_{2} } {12}}} \right. \kern-0pt} {12}}} \right)} \right] $$

\( g_{7} = \left[ {\left( {{{\overline{\text{Pe}} {\kern 1pt} {\kern 1pt} G{\kern 1pt} g_{3} } \mathord{\left/ {\vphantom {{\overline{\text{Pe}} {\kern 1pt} {\kern 1pt} G{\kern 1pt} g_{3} } 2}} \right. \kern-0pt} 2}} \right) + \left( {{{\overline{\text{Br}} X_{1} } \mathord{\left/ {\vphantom {{\overline{\text{Br}} X_{1} } 4}} \right. \kern-0pt} 4}} \right) - \left( {{{\bar{J}} \mathord{\left/ {\vphantom {{\bar{J}} 2}} \right. \kern-0pt} 2}} \right)} \right] \);

$$ g_{8} = \left( {{{\overline{\text{Br}} X_{3} } \mathord{\left/ {\vphantom {{\overline{\text{Br}} X_{3} } {\bar{\kappa }^{2} }}} \right. \kern-0pt} {\bar{\kappa }^{2} }}} \right) $$
$$ X_{1} = \left( {g_{1} \bar{\kappa }} \right)^{2} $$
$$ X_{2} = \left( {2g_{2} } \right)^{2} $$
$$ X_{3} = \left( {4g_{1} g_{2} \bar{\kappa }} \right) $$

Now, solving Eq. (24), for the wall temperatures, we get

$$ \left. \begin{aligned} \varTheta_{{\text{s}}1} = C_{3} \bar{y} + C_{4} \hfill \\ \varTheta_{{\text{s}}2} = C_{5} \bar{y} + C_{6} \hfill \\ \end{aligned} \right\} $$
(30)

where \( C_{3} - C_{6} \) are the constants. Using the boundary conditions mentioned in Eqs. (26)–(28), we evaluate the constants \( C_{1} - C_{6} \) appearing in Eqs. (29), (30) as follows:

$$ C_{1} = \frac{{X_{4} \left[ {\gamma_{2} {\text{Bi}}_{2} \left( {1 + \delta_{1} {\text{Bi}}_{1} } \right) - \gamma_{1} {\text{Bi}}_{1} \left( {1 + \delta_{2} {\text{Bi}}_{2} } \right)} \right]}}{{\left( {4\gamma_{1} \gamma_{2} {\text{Bi}}_{1} {\text{Bi}}_{2} } \right) + 2\gamma_{2} {\text{Bi}}_{2} \left( {1 + \delta_{1} {\text{Bi}}_{1} } \right) + 2\gamma_{1} {\text{Bi}}_{1} \left( {1 + \delta_{2} {\text{Bi}}_{2} } \right)}} $$
$$ C_{3} = \frac{{\left( { - X_{4} {\text{Bi}}_{1} } \right)\left( {1 + \gamma_{2} {\text{Bi}}_{2} + \delta_{2} {\text{Bi}}_{2} } \right)}}{{\left( {2\gamma_{1} \gamma_{2} {\text{Bi}}_{1} {\text{Bi}}_{2} } \right) + \gamma_{2} {\text{Bi}}_{2} \left( {1 + \delta_{1} {\text{Bi}}_{1} } \right) + \gamma_{1} {\text{Bi}}_{1} \left( {1 + \delta_{2} {\text{Bi}}_{2} } \right)}} $$
$$ C_{4} = \frac{{ - X_{4} \left( {1 + \gamma_{2} {\text{Bi}}_{2} + \delta_{2} {\text{Bi}}_{2} } \right)\left( {1 + {\text{Bi}}_{1} + \delta_{1} {\text{Bi}}_{1} } \right)}}{{\left( {2\gamma_{1} \gamma_{2} {\text{Bi}}_{1} {\text{Bi}}_{2} } \right) + \gamma_{1} {\text{Bi}}_{1} \left( {1 + \delta_{2} {\text{Bi}}_{2} } \right) + \gamma_{2} {\text{Bi}}_{2} \left( {1 + \delta_{1} {\text{Bi}}_{1} } \right)}} + \theta_{\text{a}} $$
$$ C_{5} = \frac{{X_{4} {\text{Bi}}_{2} \left( {1 + \delta_{1} {\text{Bi}}_{1} + \gamma_{1} {\text{Bi}}_{1} } \right)}}{{\left( {2\gamma_{1} \gamma_{2} {\text{Bi}}_{1} {\text{Bi}}_{2} } \right) + \gamma_{1} {\text{Bi}}_{1} \left( {1 + \delta_{2} {\text{Bi}}_{2} } \right) + \gamma_{2} {\text{Bi}}_{2} \left( {1 + \delta_{1} {\text{Bi}}_{1} } \right)}} $$
$$ C_{6} = \frac{{ - X_{4} \left( {1 + \delta_{1} {\text{Bi}}_{1} + \gamma_{1} {\text{Bi}}_{1} } \right)\left( {1 + {\text{Bi}}_{2} + \delta_{2} {\text{Bi}}_{2} } \right)}}{{\left( {2\gamma_{1} \gamma_{2} {\text{Bi}}_{1} {\text{Bi}}_{2} } \right) + \gamma_{1} {\text{Bi}}_{1} \left( {1 + \delta_{2} {\text{Bi}}_{2} } \right) + \gamma_{2} {\text{Bi}}_{2} \left( {1 + \delta_{1} {\text{Bi}}_{1} } \right)}} + \theta_{a} $$
$$ C_{2} = C_{1} - C_{3} + C_{4} + X_{5} $$

where

$$ \left. \begin{aligned} X_{4} = 2\bar{\kappa }g_{4} \sinh \left( {\bar{\kappa }} \right) - 4\bar{\kappa }g_{5} \sinh \left( {2\bar{\kappa }} \right) + 8g_{6} + 4g_{7} - 2g_{9} \left[ {\bar{\kappa }\cosh \left( {\bar{\kappa }} \right) + \sinh \left( {\bar{\kappa }} \right)} \right] \hfill \\ X_{5} = g_{4} \cosh \left( {\bar{\kappa }} \right) - g_{5} \cosh \left( {2\bar{\kappa }} \right) + g_{6} + g_{7} - g_{8} \sinh \left( {\bar{\kappa }} \right) \hfill \\ \end{aligned} \right\} $$
(31)

The aforementioned constants are used to obtain the temperature distribution for this conjugate heat transfer problem.

The entropy generation rate of the system

Entropy generation of a system is calculated by measuring its thermodynamic irreversibilities. Note that the thermal systems/devices encounter thermodynamic irreversibility largely stemming from the momentum and energy exchange phenomena involved with the underlying thermo-fluidic transport. For any thermodynamic framework, the minimization of the entropy generation is essential for obtaining the best exergetic efficiency. To mention, for the problem under the present consideration, the irreversible losses emerge from the following three sources, to be specific, heat transfer because of the finite temperature difference, inevitable Joule heating effect due to electroosmotic effect and the viscous dissipation [20]. The general articulation for the volumetric entropy generation rate [19] in the dimensional structure can be composed as [18, 40, 49, 60,61,62,63,64]:

$$ S_{\text{g}} = \frac{{k_{\text{eff}} }}{{T^{2} }}\left[ {\left( {\frac{\partial T}{\partial x}} \right)^{2} + \left( {\frac{\partial T}{\partial y}} \right)^{2} } \right] + \frac{{k_{\text{s1}} }}{{T_{\text{s1}}^{2} }}\left( {\frac{{\partial T_{\text{s1}} }}{\partial y}} \right)^{2} + \frac{{k_{\text{s2}} }}{{T_{\text{s2}}^{2} }}\left( {\frac{{\partial T_{\text{s2}} }}{\partial y}} \right)^{2} + \frac{{\mu_{\text{eff}} }}{T}\left( {\frac{{{\text{d}}u}}{{{\text{d}}y}}} \right)^{2} + \frac{{\sigma E_{\text{x}}^{2} }}{T} $$
(32)

In this expression, it can be seen that four different factors are responsible for entropy generation in the present problem. The first-term in the above equation brings up the temperature gradient in the nanofluid. In contrast, the second and third terms are also showing the effect of temperature gradient but in the lower and upper walls of the microchannel, respectively. The fourth term in Eq. (32) represents the volumetric viscous dissipation in the microchannel, while the final term takes care of the irreversibility associated with the Joule heating effect. Below we write the dimensionless form of Eq. (32) that reads as:

$$ \dot{S} = \frac{1}{{\varTheta^{2} }}\left[ {\left( {\frac{\partial \varTheta }{{\partial \bar{x}}}} \right)^{2} + \left( {\frac{\partial \varTheta }{{\partial \bar{y}}}} \right)^{2} } \right] + \frac{{\gamma_{1} }}{{\varTheta_{\text{s1}}^{2} }}\left( {\frac{{\partial \varTheta_{\text{s1}} }}{{\partial \bar{y}}}} \right)^{2} + \frac{{\gamma_{2} }}{{\varTheta_{\text{s2}}^{2} }}\left( {\frac{{\partial \varTheta_{\text{s2}} }}{{\partial \bar{y}}}} \right)^{2} + \frac{{\overline{\text{Br}} }}{\varTheta }\left( {\frac{{{\text{d}}\bar{u}}}{{{\text{d}}\bar{y}}}} \right)^{2} + \frac{{\bar{J}}}{\varTheta } $$
(33)

here \( \dot{S} = {{S_{\text{g}} H^{2} } \mathord{\left/ {\vphantom {{S_{\text{g}} H^{2} } {k_{\text{eff}} }}} \right. \kern-0pt} {k_{\text{eff}} }} \) is the non-dimensional volumetric entropy generation rate. For the evaluation of the optimum value of system parameters, which is the prime objective of this study, the overall entropy generation rate in the system is required. Accordingly, we have made an effort in this analysis to achieve the overall entropy generation rate per unit length in the axial direction, i.e. \( \left\langle {\dot{S}} \right\rangle \). In doing so, we perform numerical integration of the expression, delineated in Eq. (33), within the system volume.

Model Validation

In this section, we make an effort to validate our theoretical model by comparing the results with the experimental results of electroosmotic transport in a microfluidic channel. In doing so, we show in Fig. 2, the velocity distribution in the transverse direction of the channel. Note that the results obtained from our theoretical analysis (shown by a solid line) are compared with the reported experimental results (indicated by ‘o’ marker) of Hsieh and Yang [65]. Having a closer look at Fig. 2, it can be inferred that our analytical results match well with the experimental results reported by Hsieh and Yang [65]. This supports the efficacy of our theoretical model uses in this analysis. Note that the other parameters considered for plotting Fig. 2 confirm to those as reported in Ref. [65]. Also, we show in Fig. 2b, the variation of flow velocity for four different values of \( \bar{\kappa }\left( { = 15,20,25\;\text{and} \;35} \right) \). As seen in Fig. 2b, the flow velocity as well as its gradient increases inside the EDL with an increasing value of \( \bar{\kappa } \). With increasing \( \bar{\kappa } \), the EDL becomes thinner, and this layer squeezes more number of counter ions (ionic density in the EDL becomes higher). Upon interacting with the external electric field, these ions experience relatively stronger electroosmotic body force. Thus, the electroosmotic body force, which is acting on the fluid mass in the EDL, becomes higher for a higher value of \( \bar{\kappa } \), leading to an enhancement in flow velocity, as seen from Fig. 2b.

Fig. 2
figure 2

a Validation: plot showing the variation of axial velocity in the transverse direction of the channel. The plot shown by the solid line is obtained from the present theoretical analysis, while the variation indicated by marker ‘o’ indicates the results reported by Hsieh and Yang [65]. The other parameters considered for this plotting are: \( E_{\text{x}} = 15\,\text{KV} \,m^{ - 1} \), \( \kappa = 1.06\,\text{nm}^{ - 1} \), \( \varepsilon = 644.47 \times 10^{ - 12} \,\text{Fm}^{ - 1} \), \( \mu_{\text{f}} = 803.4 \times 10^{ - 6} \,\text{Pa} \,{\text{s}} \), and \( H = 100{\kern 1pt} \,{{\mu m}} \); b plot of velocity distribution in the channel, obtained for four different values of \( \bar{\kappa } \). The other parameters considered for this plotting are: \( \phi = 1\% \), \( \bar{\mu } = 1.025 \), \( p_{\text{x}} = 0 \). With the increasing value of \( \bar{\kappa } \), both the flow velocity and its gradient becomes higher in the EDL

Full size image

Results and discussion

Selection of parameters

In this section, we analyze the consequences of conjugate transport of heat, Joule heating effect, and viscous dissipation on the entropy generation rate associated with the field-driven transport of nanofluid in a microfluidic channel. As such, to get insights about the entropy generation rate in the system considered in the present analysis, we depict some parametric variations which include the thermophysical as well as geometrical parameters such as Peclet number (\( \overline{Pe} \)), lower wall thermal conductivity ratio (\( \gamma_{1} \)), lower wall thickness ratio (\( \delta_{1} \)), and lower wall Biot number (\( {\text{Bi}}_{1} \)). In this analysis, since the interfacial electro-chemistry enacts a crucial role in the underlying transport, we aspire for the variation for different values of Debye–Hückel parameter (\( \bar{\kappa } \)), the volume fraction of nanoparticle (\( \phi \)), and Joule heating parameter (\( J \)), respectively. Complying with the prime focus of this analysis, we look at the optimum value of the aforementioned parameters (both geometrical and thermophysical) to ensure a minimum entropy generation rate in the system. Also, unless specified otherwise, we have considered the following set of parameters in this analysis as follows: \( \varTheta_{a} = 5 \) (dimensionless ambient temperature), \( \delta_{1} = \delta_{2} = 0.1 \), \( p_{\text{x}} = 1 \), \( {\text{Br}} = 0.1 \), \( J = 1 \), \( {\text{Bi}}_{1} = 1 \), \( {\text{Bi}}_{2} = 5 \), \( {\text{Pe}} = 0.1 \), \( \gamma_{1} = 1 \), \( \gamma_{2} = 1 \), and \( G = 1 \) (axial temperature gradient). Note that the considered value of the aforementioned parameters is typical to microscale transport and has been reported in the literature [65].

Entropy generation

Effect of lower wall thickness ratio \( (\delta_{1} ) \) on the system irreversibility

In Fig. 3a, b, we depict the variation of normalized global entropy generation \( \left. {{{\left\langle {\dot{S}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {\dot{S}} \right\rangle } {\left\langle {\dot{S}} \right\rangle }}} \right. \kern-0pt} {\left\langle {\dot{S}} \right\rangle }}} \right|_{{\updelta_{1} = 0}} \) against lower wall thickness ratio \( (\delta_{1} ) \), obtained for two different parameters, viz. the Debye–Hückel parameter \( (\bar{\kappa }) \) and volume fraction of nanofluid \( (\phi ) \), respectively. For the variation depicted in Fig. 3a, we have considered three different values of \( \bar{\kappa } \) keeping nanoparticle volume fraction \( \left( \phi \right) \) constant, while for Fig. 3b nanoparticle volume fraction is varied for a given \( \bar{\kappa } \). The other parameters have been mentioned in the caption.

Fig. 3
figure 3

Disparity of the normalized global entropy generation rate as a function of dimensionless lower wall thickness ratio \( (\delta_{1} ) \) for a \( \phi = 3\% \) and different value of \( \bar{\kappa } \), b \( \bar{\kappa } = 20 \) and different value of \( \phi \). Other parameters are considered as \( p_{\text{x}} = 1 \), \( \delta_{2} = 0.1 \), \( {\text{Br}} = 0.1 \), \( J = 1 \), \( {\text{Bi}}_{1} = 1 \), \( {\text{Bi}}_{2} = 5 \), \( {\text{Pe}} = 0.1 \), and \( \gamma_{1} = \gamma_{2} = 1 \). The CPU time for \( \bar{\kappa } = (15,20,25) \) and \( \phi = (1,3,5) \) are (166.86, 172.2, 181.18) s and (177.92, 172.08, 169.44) s, respectively

Full size image

Figure 3a depicts the effect of \( \bar{\kappa } \) on the entropy generation rate of the system. Before going to discuss the variation at hand, we would like to mention here that with an increase in \( \bar{\kappa } \) the EDL becomes thinner. Thinner the EDL, higher will be the electroosmotic body force being applied on the fluid mass in EDL. Now, experiencing a relatively higher magnitude of electroosmotic body force for higher \( \bar{\kappa } \), the flow velocity will increase in the region close to the walls (which is EDL) as confirmed in Fig. 2b. To mention, this phenomenon will lead to an increase in both the magnitude of velocity as well as its gradient inside the EDL (see Fig. 2b). As a result, the viscous dissipation, which is directly proportional to the velocity gradient, will increase near the wall. Notably, this higher dissipation will lead to an increment in the temperature of the system through viscous heating. However, the increment in temperature of the system lowers the irreversibility associated with viscous dissipation effects due to its inverse relationship with the fluid temperature (see Eq. 33). Having a closer look at Fig. 3a, b, one can find that entropy generation behaviour follows a trend as discussed next. Entropy generation rate shows an initial decreasing trend with wall thickness and leaving a minimum value; it increases further as wall thickness increases further. Initial decrement of the global entropy generation rate with increasing \( \delta_{1} \left( {0 < \delta_{1} \le \delta_{{ 1 , {\text{opt}}}} } \right) \) can be explained as follows: with increasing \( \delta_{1} \) in the range of \( 0 < \delta_{1} \le \delta_{1,{\text{opt}}} \), the conductive transport of heat from the lower plate decreases and results in a simultaneous rise in fluid temperature and drop in entropy generation rate. However, with a further increasing \( \delta_{1} \) in the range of \( \delta_{1} > \delta_{{ 1 , {\text{opt}}}} \), a rise in temperature aggravates the transport of heat through the upper wall and stimulates the system entropy generation rate as can be seen from Fig. 3a. This typical variation leads to an optimum wall thickness for which system entropy generation becomes minimum. From the previous discussion, it can be inferred that the effect of heat conduction through lower wall together with the other auxiliary effects like viscous dissipation and Joule heating take a dominating role for the system entropy generation for \( \delta_{1} \le \delta_{{ 1 , {\text{opt}}}} \). On the other hand, cumulative effects to upper wall heat conduction and convection of heat from therein become the dominating factor in dictating the system entropy generation rate as the Joule heating and viscous dissipation effects are remaining almost unaffected. The definitive outcome of this effect eventually diminishes the net entropy generation rate of the system for higher values of \( \bar{\kappa } \). A critical look at Fig. 3a further restores that with an increase in \( \bar{\kappa } \), the global entropy generation decreases and the value of \( \delta_{{ 1 , {\text{opt}}}} \) also gets increased. As mentioned, higher \( \bar{\kappa } \) indicates thinner EDL, and consequently for this higher value of \( \bar{\kappa } \), the velocity gradient will increase in the EDL. The higher velocity gradient stimulates the dissipative heat, which in turn, will lower the fluid viscosity. For the relatively higher value of \( \bar{\kappa } \), thermodynamic irreversibility associated with the viscous dissipation of the present system becomes important as realized by a decrement in global entropy generation in Fig. 4. We attribute this decrement to a drop in fluid viscosity. A little increment in \( \delta_{{ 1 , {\text{opt}}}} \) with the increasing value of \( \bar{\kappa } \) as seen from Fig. 3a as well as to offset the enormous decline in entropy generation associated with viscous dissipation (with increasing \( \bar{\kappa } \), drop in fluid temperature results in a decrease in dissipation effect appreciably) with increase in the same in the present scenario.

Fig. 4
figure 4

Disparity of normalized global entropy generation rate of the individual terms associated with Eq. (33) as a function of dimensionless lower wall thickness ratio \( \left( {\delta_{1} } \right) \); other parameters: \( p_{\text{x}} = 1 \), \( \delta_{2} = 0.1 \), \( {\text{Br}} = 0.1 \), \( J = 1 \), \( {\text{Bi}}_{1} = 1 \), \( {\text{Bi}}_{2} = 5 \), \( {\text{Pe}} = 0.1 \), and \( \gamma_{1} = \gamma_{2} = 1 \)

Full size image

Figure 3b describes the effect of nanoparticle volume fraction \( (\phi ) \) on the entropy generation rate of the system. It can be noted that with increasing \( \phi \), albeit convective transport of heat increases, the entropy generation of the system increases for every value of \( \delta_{1} \). Note that with an increasing value of the nanoparticle volume fraction, the effective value of \( k_{\text{eff}} \;{\text{and}}\;\mu_{\text{eff}} \) increases. This increment in effective thermo-physical properties leads to an enhancement in the entropy generation rate of the system following augmented convective heat transport and the viscous dissipation effect. In Fig. 3b, it has been noted that \( \left. {{{\left\langle {\dot{S}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {\dot{S}} \right\rangle } {\left\langle {\dot{S}} \right\rangle }}} \right. \kern-0pt} {\left\langle {\dot{S}} \right\rangle }}} \right|_{{\updelta_{1} = 0}} \) first decreases up to \( \delta_{{ 1 , {\text{opt}}}} \), attain the lowest value and then increases further as \( \delta_{1} \) increases beyond \( \delta_{{ 1 , {\text{opt}}}} \). This observation holds good for all the values of \( \phi \) under consideration. We here make an effort to figure out the physical reasoning behind this observation as follows: with the increasing magnitude of \( \delta_{1} \), the temperature of the fluid and its gradient gets redesigned due to the increased resistance to the conductive transport of heat through the lower wall. In particular, this effect leads to a decrease in the entropy generation rate related to heat transfer through the lower wall. Regardless, an increase in temperature of the liquid and its gradient builds the heat transfer rate between the liquid and upper wall hence increasing \( \left\langle {\dot{S}} \right\rangle \) is the consequential effect, as seen from Fig. 3b. Up to a specific value of \( \delta_{1} \left( { \sim \delta_{{ 1 , {\text{opt}}}} } \right) \), the decreasing rate of entropy generation dominates over the expansion of \( \left\langle {\dot{S}} \right\rangle \) due to the augmented transport of heat in the fluid and upper wall. This results in a net decrease in entropy generation of the structure up to a point \( \delta_{{ 1 , {\text{opt}}}} \), after which \( \left\langle {\dot{S}} \right\rangle \) increases on account of the increase in the irreversibility related to the heat transfer through the liquid and upper wall.

From Eq. (33), it is seen that the global entropy generation of the present system depends upon several factors, viz. convective heat transfer, conductive transport through walls, viscous dissipation, and the Joule heating effects. Now to establish their effects through a quantitative manner, we depict Fig. 4, which shows the contribution of individual effect on the global entropy generation rate. Figure 4 shows that with the increasing value of \( \delta_{1} \), the entropy generation of the system related to the convective heat transfer through the liquid \( \left( {\left\langle {\dot{S}} \right\rangle_{{{\text{Convec}} .}} } \right) \) and conductive heat transfer through the upper wall \( \left( { < \dot{S} >_{w2} } \right) \) increases, while entropy generation related to the conductive heat transfer through the lower wall \( \left( {\left\langle {\dot{S}} \right\rangle_{\text{w1}} } \right) \) decreases. With the increasing value of \( \delta_{1} \), the temperature of the fluid and its gradient becomes higher due to the reduction in the entropy generation related to the heat transfer through the lower wall. In any case, an increase in temperature of the fluid and its gradient builds the convective heat transfer rate through the fluid and upper wall, as confirmed in Fig. 4. Also, a reduction in heat conduction through the lower wall promotes the conductive transport of heat through the upper wall, as witnessed in Fig. 4. Henceforth, we can presume that in the range \( 0 < \delta_{1} < \delta_{{ 1 , {\text{opt}}}} \), the fluid temperature controls the entropy generation rate of the system, while for the range \( \delta_{1} > \delta_{{ 1 , {\text{opt}}}} \), the temperature gradient plays a significant role in deciding the net entropy generation of the present system.

Effect of thermal conductivity ratio \( \left( {\gamma_{1} } \right) \) on the system irreversibility

In Fig. 5a, b, we illustrate the variation of normalized global entropy generation \( \left. {{{\left\langle {\dot{S}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {\dot{S}} \right\rangle } {\left\langle {\dot{S}} \right\rangle }}} \right. \kern-0pt} {\left\langle {\dot{S}} \right\rangle }}} \right|_{{\upgamma_{1} = 0}} \) versus the lower wall to nanofluid thermal conductivity ratio \( (\gamma_{1} ) \) for three distinct parameters, viz. the Debye–Hückel parameter \( (\bar{\kappa }) \) and volume fraction of nanofluid \( (\phi ) \). Figure 6 portrays the contribution of different terms on the global entropy generation with increasing value of \( \delta_{1} \). The other parameters considered for plotting the figures have been mentioned in the caption. Next, we discuss the underlying physical reasoning behind the variations as observed from Fig. 5a. Also, to support our argument in explaining the trend, as seen in Fig. 5a, b through quantitative assessment, we appeal to the variation delineated in Fig. 6.

Fig. 5
figure 5

Disparity of the normalized global entropy generation rate as a function of dimensionless thermal conductivity ratio for lower wall \( \left( {\gamma_{1} } \right) \); a for \( \phi = 3\% \) and different value of \( \bar{\kappa } \); b for \( \bar{\kappa } = 20 \) and different value of \( \phi \); and others data are \( p_{\text{x}} = 1 \), \( \gamma_{2} = 5 \), \( {\text{Br}} = 0.1 \), \( J = 1 \), \( {\text{Pe}} = 0.1 \), \( {\text{Bi}}_{1} = {\text{Bi}}_{2} = 1 \), and \( \delta_{1} = \delta_{2} = 0.1 \). The CPU time for \( \bar{\kappa } = (15,20,25) \) and \( \phi = (1,3,5) \) are (153.87, 166.27, 176.9) s and (171.35, 166.3, 161.45) s respectively

Full size image
Fig. 6
figure 6

Disparity of normalized global entropy generation rate of the individual terms associated with Eq. (33) as a function of \( \gamma_{1} \); other parameters: \( p_{\text{x}} = 1 \), \( \gamma_{2} = 5 \), \( {\text{Br}} = 0.1 \), \( J = 1 \), \( {\text{Pe}} = 0.1 \), \( {\text{Bi}}_{1} = {\text{Bi}}_{2} = 1 \), and \( \delta_{1} = \delta_{2} = 0.1 \)

Full size image

Figure 5a demonstrates the effect of \( \bar{\kappa } \) on the global entropy generation rate of the present system. Here, also, the variation of net entropy generation shows a decreasing-increasing pattern with \( \gamma_{1} \). With an increase in \( \gamma_{1} \), the entropy generation due to heat conduction through lower wall increases as confirmed by the increase in irreversibility \( \left\langle {\dot{S}} \right\rangle_{\text{w1}} \) with \( \gamma_{1} \) in Fig. 6. An increase in conductive transport of heat with increasing \( \gamma_{1} \) results in a reduction in heat transfer associated with the fluid (convective transport) and the upper wall (conductive transport) as witnessed by the decreasing trend of \( \left\langle {\dot{S}} \right\rangle_{{{\text{convec}} .}} \;\text{and} \;\left\langle {\dot{S}} \right\rangle_{\text{w2}} \) in Fig. 6. Important to mention, in the regime of \( 0 < \gamma_{1} \le \gamma_{{ 1 , {\text{opt}}}} \), the combined influences of convective heat transport through fluid and conductive transport through the upper wall take a lead role in dictating the global entropy generation in the system as witnessed by the decreasing trend of \( {{\left\langle {\dot{S}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {\dot{S}} \right\rangle } {\left. {\left\langle {\dot{S}} \right\rangle } \right|_{{\upgamma_{1} = 0}} }}} \right. \kern-0pt} {\left. {\left\langle {\dot{S}} \right\rangle } \right|_{{\upgamma_{1} = 0}} }} \) in Fig. 5a, b. However, in the range of \( \gamma_{1} > \gamma_{{ 1 , {\text{opt}}}} \), a significant increment in conductive transport of heat through lower wall \( \left( {\left\langle {\dot{S}} \right\rangle_{\text{w1}} } \right) \) together with the favourable effects of nanoparticle driven alteration in viscous dissipation effect and Joule heating (increasing trend of \( \left\langle {\dot{S}} \right\rangle_{{{\text{v}} . {\text{d}} .}} \) and \( \left\langle {\dot{S}} \right\rangle_{\text{J}} \) in Fig. 6) leads to a rise in the system entropy generation rate. This observation is realized by an increasing trend of \( {{\left\langle {\dot{S}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {\dot{S}} \right\rangle } {\left. {\left\langle {\dot{S}} \right\rangle } \right|_{{\upgamma_{1} = 0}} }}} \right. \kern-0pt} {\left. {\left\langle {\dot{S}} \right\rangle } \right|_{{\upgamma_{1} = 0}} }} \) in Fig. 5a, b). Thus, we can conclude that in this regime of \( \gamma_{1} > \gamma_{{ 1 , {\text{opt}}}} \), conductive transport of heat becomes crucial in dictating the system entropy generation rate. Because of this typical phenomenon of system entropy generation as governed by several influencing factors in different regimes of \( \gamma_{1} \), we observe a decreasing-increasing trend of global entropy generation rate in Fig. 5a, b. It is worth adding here that this decreasing-increasing trend yields an optimum value of \( \gamma_{1} \left( {\gamma_{{ 1 , {\text{opt}}}} } \right) \) as seen from Fig. 5a, b.

From Fig. 5a, it can be noticed that with increasing \( \bar{\kappa } \), the global entropy generation of the system becomes lesser for all values of \( \gamma_{1} \). Note that with increasing \( \bar{\kappa } \), the electroosmotic body force acting on the fluid mass increases, leading to a rise in velocity gradient in the flow field. This higher velocity gradient increases the dissipative heating and results in a reduction in the temperature gradient between the fluid and walls of the microchannel. The overall phenomenon leads to a reduction in conductive transport of heat, and consequently, the system irreversibility reduces. As discussed before, an increase in \( \phi \) is responsible for an increase in both effective thermal conductivity and effective viscosity of nanofluid. Thus, for a higher volume fraction of nanoparticle \( \left( \phi \right) \), the dissipative heat, as well as Joule heating produced becomes higher and results in an increment in fluid temperature. Note that this higher fluid temperature weakens the temperature gradient between the fluid and the walls of the channel. Precisely, a decrease in temperature gradient reduces the heat transfer through the walls and culminating in a reduction in system entropy generation rate, as seen in Fig. 5b. A closer look at Fig. 5b further reveals that with increasing the magnitude of \( \phi \), the optimum value of \( \gamma_{1} \left( {\gamma_{{ 1 , {\text{opt}}}} } \right) \) increases. This is because of the fact that for higher values of \( \phi \), the enhancement in viscous dissipation and heat transfer irreversibility at the lower wall counterbalances the reduction in \( < \dot{S} > \) associated with heat transfer associated irreversibility through the fluid (convective transport) and the upper wall (conductive transport) for a relatively lower value of \( \gamma_{1} \).

Effect of modified Peclet number \( \left( {\overline{\text{Pe}} } \right) \) on the system irreversibility

We show in Fig. 7a, b, the variation of normalized global entropy generation \( \left( {\left. {{{\left\langle {\dot{S}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {\dot{S}} \right\rangle } {\left\langle {\dot{S}} \right\rangle }}} \right. \kern-0pt} {\left\langle {\dot{S}} \right\rangle }}} \right|_{{\overline{\text{Pe}} = 0}} } \right) \)(normalized with its value when \( \overline{\text{Pe}} \) = 0) rate versus modified Peclet number \( \left( {\overline{\text{Pe}} } \right) \) for two distinct parameters, viz. the Debye–Hückel parameter \( (\bar{\kappa }) \) and volume fraction of nanoparticle \( (\phi ) \). Note that to obtain the plots depicted in Fig. 7a, we have considered three different \( \bar{\kappa }\left( { = 15,25\;\text{and} \;35} \right) \). From the Fig. 7a, b, we observe that with an increase in \( \overline{\text{Pe}} \) from 0 to 1.5, the variation of entropy generation shows a decreasing-increasing trend irrespective of the value of \( \bar{\kappa } \) and \( \phi \) considered. As such, this typical variation indicates the existence of optimum \( \overline{\text{Pe}} \) for all the cases at which the system entropy generation reaches a minimum value.

Fig. 7
figure 7

Disparity of the normalized global entropy generation rate as a function of dimensionless Peclet number of nanofluid \( \left( {\overline{\text{Pe}} } \right) \); a for \( \phi = 3\% \) and different value of \( \bar{\kappa } \); b for \( \bar{\kappa } = 20 \) and different value of \( \phi \). Other parameters are: \( p_{\text{x}} = 1 \), \( {\text{Br}} = 0.1 \), \( J = 1 \), \( {\text{Bi}}_{1} = 2 \), \( {\text{Bi}}_{2} = 15 \), \( \gamma_{1} = 10 \), \( \delta_{1} = \delta_{2} = 0.1 \), and \( \gamma_{2} = 15 \). The CPU time for \( \bar{\kappa } = (15,25,35) \) and \( \phi = (1,3,5) \) are (154.91, 188.65, 227.5) s and (181.35, 177.74, 167.01) s, respectively

Full size image

Also, to figure out the contribution of each term in Eq. (33) on the net entropy generation rate of the system as obtained with a change in \( \overline{\text{Pe}} \), is depicted in Fig. 8.

Fig. 8
figure 8

Disparity of normalized global entropy generation rate of the individual terms associated with Eq. (33) as a function of \( \overline{\text{Pe}} \). Other parameters are: \( p_{\text{x}} = 1 \), \( {\text{Br}} = 0.1 \), \( J = 1 \), \( {\text{Bi}}_{1} = 2 \), \( {\text{Bi}}_{2} = 15 \), \( \gamma_{1} = 10 \), \( \delta_{1} = \delta_{2} = 0.1 \), and \( \gamma_{2} = 15 \)

Full size image

Before we started discussing the variation of global entropy generation in the system as seen in Fig. 7a, b, we would like to recall the physical significance of the Peclet numbers defined in this analysis. Note that the Peclet number signifies the proportion between the convective heat transfer and diffusive heat transfer rates. Accordingly, an increase in the magnitude of \( \overline{\text{Pe}} \) signifies either an increment in the convective transport of heat or decrement in the conductive heat transfer through the fluid. With an increasing value of the \( \overline{\text{Pe}} \) in the range \( 0 < \overline{\text{Pe}} < \overline{\text{Pe}}_{\text{opt}} \), the convective heat transport through the fluid will increase, and fluid temperature will decrease. Because of this decrease in the fluid temperature, heat conduction through the walls of the channel will decrease, and the overall effect will results in a reduction in system entropy generation as confirmed by the decreasing trend of \( \left( {\left. {{{\left\langle {\dot{S}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {\dot{S}} \right\rangle } {\left\langle {\dot{S}} \right\rangle }}} \right. \kern-0pt} {\left\langle {\dot{S}} \right\rangle }}} \right|_{{\overline{\text{Pe}} = 0}} } \right) \) in Fig. 7a, b for \( 0 < \overline{\text{Pe}} < \overline{\text{Pe}}_{\text{opt}} \). Also, a reduction in \( \left\langle {\dot{S}} \right\rangle_{\text{w1}} \) and \( \left\langle {\dot{S}} \right\rangle_{\text{w2}} \) in this regime of \( 0 < \overline{\text{Pe}} < \overline{\text{Pe}}_{\text{opt}} \) is confirmed in Fig. 8. However, as the Peclet number increases beyond its optimum value \( \left( {\overline{\text{Pe}} > \overline{\text{Pe}}_{\text{opt}} } \right) \), a significant enhancement in convective transport of heat through the fluid governs the system entropy generation as realized by a further increasing trend in this regime of \( \overline{\text{Pe}} \) \( \left( {\overline{\text{Pe}} > \overline{\text{Pe}}_{\text{opt}} } \right) \). From the above discussion, it can be conjectured that the conduction through the walls takes a dominating role in dictating the system entropy generation for \( 0 < \overline{\text{Pe}} < \overline{\text{Pe}}_{\text{opt}} \), while nanoparticle driven enhancement in convective transport of heat as supported by the viscous dissipation and Joule heating effects becomes the leading character in dictating the system entropy generation for \( \overline{\text{Pe}} > \overline{\text{Pe}}_{\text{opt}} \). As such, our argument is confirmed by the contribution of each term on the net entropy generation in the system as portrayed in Fig. 8 with increasing \( \overline{\text{Pe}} \).

Figure 7b describes the effect of nanoparticle volume fraction \( (\phi ) \) on the entropy generation rate of the system. It can be observed from Fig. 7b that with increasing \( \phi \), entropy generation in the system increases for all the value of \( \overline{\text{Pe}} \). As mentioned, with an increase in \( \phi \), both the effective thermal conductivity and effective viscosity of nanofluid increases. Enhancement of convective heat transfer with increasing effective thermal conductivity of the nanofluid strongly affects the total irreversibility of the system. As a consequence, with increasing \( \phi \) the global entropy generation rate increases, as seen in Fig. 7b. Also, with increasing \( \phi \), the optimum \( \overline{\text{Pe}} \)\( \left( {\overline{\text{Pe}}_{\text{opt}} } \right) \) for which system entropy generation becomes the minimum becomes slightly higher.

Effect of Biot number (lower wall) on the system irreversibility

In Fig. 9a, b, we show the variation of normalized global entropy generation \( \left. {{{\left\langle {\dot{S}} \right\rangle } \mathord{\left/ {\vphantom {{\left\langle {\dot{S}} \right\rangle } {\left\langle {\dot{S}} \right\rangle }}} \right. \kern-0pt} {\left\langle {\dot{S}} \right\rangle }}} \right|_{{{\text{Bi}}_{1} = 0}} \)(normalized with its value when \( {\text{Bi}}_{1} \) = 0) versus lower wall Biot number \( \left( {{\text{Bi}}_{1} } \right) \). The other parameters used in plotting the figures have been mentioned in the caption. While Fig. 9a shows the variation for different values of the Debye–Hückel parameter \( (\bar{\kappa }) \), the effect of nanoparticle volume fraction \( (\phi ) \) on the entropy generation rate is demonstrated in Fig. 9b. It may be mentioned here that to explain the variation depicted in Fig. 9a, b, we have depicted the contribution of each term on the system entropy generation rate in Fig. 10. Note that the Biot number is defined as the ratio of the convective heat transfer to the conductive heat transfer in a body. An increase in the magnitude of the Biot number indicates a reduction in the resistance to the surface heat transfer as the properties of the channel wall is remaining fixed. Along these lines, it may be mentioned here that increasing \( {\text{Bi}}_{1} \) in the range \( {\text{Bi}}_{1} > {\text{Bi}}_{{ 1 , {\text{opt}}}} \) stimulates the heat transfer enhancement through the lower wall, leading to an enhancement in system entropy generation rate as seen in Fig. 9a, b. Notably, this phenomenon in the process reduces the fluid temperature and its gradient inside the system. Thus, with the increase in \( {\text{Bi}}_{1} \), the entropy generation rate related with the heat transfer through the lower wall (\( \left\langle {\dot{S}} \right\rangle_{\text{w1}} \)) increases, while entropy generation because of the convective heat transfer (\( \left\langle {\dot{S}} \right\rangle_{{{\text{convec}} .}} \)) through the fluid gets reduced. These two observations are clearly reflected in Fig. 10, where it is seen that with increasing \( {\text{Bi}}_{1} \), \( \left\langle {\dot{S}} \right\rangle_{{{\text{convec}} .}} \) decreases continuously and \( \left\langle {\dot{S}} \right\rangle_{\text{w1}} \) shows an increasing trend. Also, with a change in \( {\text{Bi}}_{1} \) in the range \( 0 < {\text{Bi}}_{1} \le {\text{Bi}}_{{ 1 , {\text{opt}}}} \), a reduction in fluid temperature and its gradient leads to a decrement in heat transfer between the fluid and upper wall, and overall effect results in a slight reduction in the system entropy generation rate. This complex change of system irreversibility modulated by several factors, as mentioned in Eq. (33) brings about a decreasing-increasing trend of the system entropy generation with a change in \( {\text{Bi}}_{1} \) as seen in Fig. 9a, b. From the above discussion, it can be concluded that for \( 0 < {\text{Bi}}_{1} \le {\text{Bi}}_{{ 1 , {\text{opt}}}} \), heat transfer through the fluid and upper wall takes a lead role in predicting the system entropy generation rate, while for \( {\text{Bi}}_{1} > {\text{Bi}}_{{ 1 , {\text{opt}}}} \) conductive heat transfer through lower wall becomes the indicative character for the net thermodynamic irreversibility of the system.

Fig. 9
figure 9

Disparity of the normalized global entropy generation rate as a function of dimensionless Biot number for the lower wall \( \left( {{\text{Bi}}_{1} } \right) \); a for \( \phi = 3\% \) and different value of \( \bar{\kappa } \); b for \( \bar{\kappa } = 20 \) and different value of \( \phi \). Other parameters: \( p_{\text{x}} = 1 \), \( {\text{Br}} = 0.1 \), \( J = 1 \), \( \delta_{1} = \delta_{2} = 0.1 \), \( {\text{Bi}}_{2} = 1 \), \( {\text{Pe}} = 0.1 \), and \( \gamma_{1} = \gamma_{2} = 1 \). The CPU time for \( \bar{\kappa } = (15,20,25) \) and \( \phi = (1,3,5) \) are (137.86, 140.54, 144.72) s and (143.24, 139.46, 135.54) s, respectively

Full size image
Fig. 10
figure 10

Disparity of normalized global entropy generation rate of the individual terms associated with Eq. (33) as a function of \( {\text{Bi}}_{1} \); Other parameters: \( p_{\text{x}} = 1 \), \( {\text{Br}} = 0.1 \), \( J = 1 \), \( \delta_{1} = \delta_{2} = 0.1 \), \( {\text{Bi}}_{2} = 1 \), \( {\text{Pe}} = 0.1 \), and \( \gamma_{1} = \gamma_{2} = 1 \)

Full size image

A relative increment in system entropy generation with increasing value of \( \bar{\kappa } \) as seen in Fig. 9a is attributed effect of viscous dissipation dominated irreversibility of system, largely stemming from electrical force modulated enhancement in the flow velocity and its gradient inside the EDL (see Fig. 2b for flow velocity with \( \bar{\kappa } \)). Figure 9b shows the impact of the volume fraction of nanoparticle in carrier fluid \( (\phi ) \) on the entropy generation rate. The volume fraction of nanoparticle affects the convective heat transfer by modulating the thermal conductivity. Also, an increment in \( \phi \) will stimulate the viscous dissipation effect following the enhancement in the effective viscosity of the fluid. For this case, as clearly seen from Fig. 10, irreversibility due to viscous heating that too becomes severe with increasing \( \phi \) surpasses the irreversibility that is stemming from the convective transport of heat (which becomes stronger with increasing \( \phi \) as well). Thus, a rise in fluid temperature with increasing \( \phi \) (due to higher viscous dissipation) will lead to a reduction in the conductive transport of heat through the lower wall, which is the influencing factor in dictating the system irreversibility. Because of this phenomenon, with the increasing \( \phi \), the entropy generation rate in the system reduces (relatively), as seen in Fig. 9b with a slight shift in \( {\text{Bi}}_{{ 1 , {\text{opt}}}} \) towards its higher value.

Conclusions

We have investigated the entropy generation characteristics for a conjugate heat transfer problem, wherein, a nanofluid, driven under the combined influence of an externally imposed pressure gradient and electroosmosis, is subjected to an asymmetric cooling at the channel walls. For this thermo-fluidic transport process, taking accounts of the viscous dissipation and Joule heating effects, we have established that the net entropy generation rate of the system is an outcome of the intricate interplay between the irreversibilities associated with heat transfer, viscous dissipation, and Joule heating. It is found that such an interplay among these irreversibilities gives rise to an optimum value of the geometrical parameter, viz. the channel wall thickness (\( \delta \)), and the thermophysical parameters viz., the thermal conductivity of the wall \( (\gamma ) \), Biot number \( (Bi) \), and the modified Peclet number (\( \overline{Pe} \)), leading to the minimum entropy generation rate of the system. This study further reveals that changes in the electroosmotic parameter \( \bar{\kappa } \) (representative of the EDL thickness) or the composition of the fluid (\( \phi \), the volume fraction of nanoparticles agglomerates) can non trivially alter the optimum values of these parameters. We believe such an analysis will be helpful in optimum design of the thermal systems/devices typically used in microscale thermal management such as micro-heat exchangers, micro-reactors, and micro heat pipes.