1 Introduction

Mixed convection in a square lid-driven has taken a great interest and possible applications in engineering and technology fields including cooling of electronic devices Louaraychi et al. (2019), oil extraction, solar collectors, nuclear reactors, crystal growth (Muthtamilselvan et al. 2010), food and float glass processing (Pilkington 1969) and dynamics of lakes, reservoirs and cooling pond (Imberger and Hamblin 1982). The effect of porous medium and the presence of heat generation lead to change the heat and fluid flow movement inside the cavity. The study on mixed convection frequently presented in previous work. Meanwhile, the heat and fluid flow studies in a porous medium with the presence of heat generation has less attention in recent years.

Lid-driven cavities flow have been studied and reported in many works of literature. The effects of the Prandtl number on the flow and heat transfer in a square lid-driven cavity was investigated by Moallemi and Jang (1992). They solved numerically by using the control volume approach with the power-law and SIMPLER scheme. Iwatsu et al. (1993) investigated numerically mixed convection in a lid-driven cavity with a stable vertical temperature gradient. Abu-Nada and Chamkha (2010) investigated on mixed convection flow in a lid-driven inclined square cavity filled with a nanofluid and solved numerically by a second-order accurate finite-volume method. While, the effects of magnetic field in a lid-driven square cavity has studied by Muthtamilselvan and Doh (2014).

The study on mixed convection in an enclosures cavity filled with porous medium has received attention among researchers. The first study on mixed convection flow in a lid-driven filled with porous medium was investigated by Khanafer and Chamkha (1999) by considered the effect of internal heat generation. The work has been solved numerically using the finite-volume approach with Alternating Direct Implicit (ADI) procedure. Al-Amiri (2000) extended the work on the laminar transport processes in a lid-driven square cavity filled with a water-saturated porous medium. Besides that, Khanafer and Vafai (2002) extended on double-diffusive mixed convection heat and mass transport in a lid-driven square cavity by considering a non-Darcian fluid-saturated porous medium. Later on, Vishnuvardhanarao and Das (2008) studied on laminar mixed convection in a parallel two-sided lid-driven differential heated square cavity filled with a fluid-saturated porous medium and solved numerically by the finite volume approach with third order accurate upwind scheme. While, Basak et al. (2010) considered mixed convection flows in a lid-driven square cavity filled with porous medium and solved numerically using penalty finite element analysis. The flow simulation and mixed convection in a lid-driven square cavity with saturated porous media has been investigated by Nayak et al. (2014). Recently, Pekmen and Tezer-Sezgin (2014) investigated the effect of a magnetic field on mixed convection flow in a lid-driven square cavity filled with a porous medium. They found that the presences of a porous medium within the cavity caused a force opposite to the flow direction that tends to resist the flow. Thus, the fluid flow move fast due the increasing of the permeability of porous medium.

There has been considerable interest in convective heat transfer in the presence of heat generation. Hydromagnetic natural convection heat transfer in an inclined porous square enclosure in the presence of heat generation is studied numerically by Khanafer and Chamkha (1998). Later on, Das and Sahoo (1999) investigated an effect of heat generation on natural convection in a porous square enclosure. The study on mixed convection in cavity enclosure in the presence of heat generation was reported by Chamkha (2002) with considering the presence of magnetic field. A temperature-dependent heat source is assumed to exist within the cavity. Later on, Saha et al. (2010) studied the effect of inclination of a lid-driven square cavity with internal heat generation and absorption. They found that the heat transfer from the bottom wall increased for internal heat absorption case than internal heat generation case. Mahapatra et al. (2013) studied the influence of thermal radiation and heat generation mixed convection in an inclined enclosure under magnetic field. The mixed convection flow in a two-sided lid-driven cavity filled with the heat-generating porous medium has been investigated by Muthtamilselvan et al. (2010) numerically by finite volume method with the SIMPLE algorithm.

There are many studies on mixed convection in cavities enclosure with considered non-uniformly temperature distribution on their walls but less with considered both cases uniform and non-uniform temperature distribution. The study on non-uniform heating boundary conditions was performed by Sivasankaran et al. (2010) on mixed convection in a lid-driven cavity enclosure. It was observed that the heat transfer increases as the non-uniform heating increases thus, the heat transfer rate for non-uniform heating of both walls is higher than non-uniform heating of one wall. While, Arani et al. (2012) numerically study on mixed convection flow of nanofluid in a lid-driven square cavity with sinusoidal heating on side walls. Later, Kefayati (2014) analyzed on laminar mixed convection of non-Newtonian nanofluids in a square lid-driven cavity with a sinusoidal heating at the right side wall.

Basak et al. (2009) presented an analysis of mixed convection flows within a square cavity where the bottom wall of the cavity maintained at a uniform or non-uniform heating. The results show that the heat transfer rate is very high at the edges of the bottom wall and it decreases at the center for the uniform heating that is contrast to lower heat transfer rate for the non-uniform heating of the bottom wall. Meanwhile, the similar conditions as previous work on the effect of heat generation on mixed convection in a lid-driven square cavity filled with nanofluid were investigated by Muthtamilselvan and Doh (2014). It is found that a sinusoidal type of the local heat transfer rate produced by the non-uniform heating.

Elsherbiny and Ismail (2015) analyzed the laminar natural convection of air in an inclined rectangular cavities with two localized heat sources. D’Orazio et al. (2015) investigated the mixed convection in an inclined lid-driven cavity with heat flux boundary condition. Kefayati (2015) analyzed the laminar mixed convection of non-Newtonian nanofluid subjected to a vertical magnetic field in a lid-driven square cavity. Bettaibi et al. (2016) studied the double-diffusive mixed convection in a rectangular enclosure by incorporating an insulated moving lid. While the study about inclined porous cavity subjected to magnetic field was studied numerically by Zainuddin et al. (2018) and found that the inclination angle, magnetic field and Darcy number affect significantly the streamline and isotherm patterns in the flow. There are some works which can be applicable for researcher in this field (Bhatti and Abbas 2016; Bhatti et al. 2016, 2017, 2019; Kumar et al. 2019; Adesanya et al. 2019; Akermi et al. 2019; Kahshan et al. 2019).

In the current work, the sidewalls of the cavity are adiabatic and impermeable to mass transfer while the bottom wall is maintained at a cold or high temperature. The top wall is subjected to a sinusoidal temperature and meanwhile it moves in the + x direction to mimic the lid motion. The present work is indeed an extension of the previous studies performed by Moallemi and Jang (1992), Muthtamilselvan et al. (2010) and Zainuddin et al. (2018). In addition, the present study intends to study the effect of heat generation on the mixed convection in a porous cavity as well. The problem will be solved numerically by using the finite-volume based SIMPLE algorithm.

2 Formulation of problem

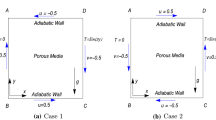
The physical model of an unsteady two-dimensional square porous cavity of height and length, H in the presence of heat generation is shown in Fig. 1. Both side walls of the cavity are kept insulated while the top lid is moving from left to right at a uniform speed, Us with a non-uniform temperature, \( T = T_{c} + (T_{h} - T_{c} ){ \sin }\pi (x/H) \) where \( T_{h} > T_{c} \). Meanwhile, two cases of thermal boundary conditions for the bottom wall are considered where the temperature is maintained at hot temperature, \( T_{h} \) or cold temperature, \( T_{c} \). The flow is assumed to be laminar and the fluid is Newtonian and incompressible. The governing equations of the problem under above assumptions for conservation of mass, momentum and energy can be written in the dimensional form

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 $$
(1)
$$ \frac{\partial u}{\partial \tau } + u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y} = - \frac{1}{{\rho_{0} }}\frac{\partial p}{\partial x} + \upsilon \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial y^{2} }}} \right) - \frac{\mu u}{\rho \kappa } $$
(2)
$$ \frac{\partial v}{\partial \tau } + u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y} = - \frac{1}{{\rho_{0} }}\frac{\partial p}{\partial y} + \upsilon \left( {\frac{{\partial^{2} v}}{{\partial x^{2} }} + \frac{{\partial^{2} v}}{{\partial y^{2} }}} \right) + g\beta \left( {T - T_{c} } \right) - \frac{\mu v}{\rho \kappa } $$
(3)
$$ \frac{\partial T}{\partial \tau } + u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \frac{K}{{\rho C_{p} }}\left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }}} \right) - \frac{{Q_{0} }}{{\rho C_{p} }}\left( {T - T_{C} } \right) $$
(4)

where the \( u \) and \( v \) are the velocity components in the \( x \) and \( y \) directions, respectively, \( g \) is the gravitational acceleration acting downward, \( \beta \) is the coefficient of thermal expansion. \( K \) is the thermal conductivity, \( \nu \) is the reference kinematic viscosity, \( \kappa \) is the permeability of the porous medium, \( \rho \) is the fluid density, \( C_{p} \) is the specific heat of constant pressure, \( \mu \) is fluid density and \( p \) is the fluid pressure. Equations (2) and (3) do not include the porosity term or porous medium inertia effect which have been shown by Nield and Bejan (1998). According to Khanafer and Chamkha (1999) and Lage (1992) the porosity have very little effect on heat transfer.

Fig. 1
figure 1

Schematic diagram of the physical model

Full size image

The governing Eqs. (2)–(4) are need to be solved subject to the initial and boundary conditions as follows:

$$ \begin{array}{*{20}c} {\tau = 0} & {u = v = 0} & {T = 0} & {{\text{on all boundaries}},} \\ {\tau \ge 0} & {u = v = 0} & {\frac{\partial T}{\partial x} = 0} & {on\;x = 0,H,} \\ {} & {u = v = 0} & {T = T_{h} \;or\;T = T_{c} } & {on\;y = 0,} \\ {} & {u = v = 0} & {T = T_{c} + \left( {T_{h} - T_{c} } \right)\sin \pi \frac{x}{H}} & {on\;y = H.} \\ \end{array} $$
(5)

The following dimensionless variables are introduced to convert the governing equations in dimensionless form:

$$ X = \frac{x}{H},\;Y = \frac{y}{H},\;U = \frac{u}{{U_{s} }},\;V = \frac{v}{{U_{s} }},\;t = \frac{{\tau U_{s} }}{H},\;\theta = \frac{{T - T_{c} }}{{T_{h} - T_{c} }},\;P = \frac{p}{{\rho U_{s}^{2} }}. $$
(6)

Using (6), the dimensionless forms of the governing Eqs. (1–4) are:

$$ \frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0, $$
(7)
$$ \frac{\partial U}{\partial t} + U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y} = - \frac{\partial P}{\partial X} + \frac{1}{\text{Re}}\left( {\frac{{\partial^{2} U}}{{\partial X^{2} }} + \frac{{\partial^{2} U}}{{\partial Y^{2} }}} \right) - \frac{U}{{Da\text{Re} }}, $$
(8)
$$ \frac{\partial V}{\partial t} + u\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial X} = - \frac{\partial P}{\partial Y} + \frac{1}{\text{Re}}\left( {\frac{{\partial^{2} V}}{{\partial X^{2} }} + \frac{{\partial^{2} V}}{{\partial Y^{2} }}} \right) + \frac{Gr}{{\text{Re}^{2} }}\theta - \frac{V}{{Da\text{Re} }}, $$
(9)
$$ \frac{\partial \theta }{\partial T} + U\frac{\partial \theta }{\partial X} + V\frac{\partial \theta }{\partial Y} = \frac{1}{{\Pr \text{Re} }}\left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right) + \frac{Q}{{\text{Re} \Pr }}\theta , $$
(10)

where \( Q = Q_{0} H^{2} /\alpha \rho C_{p} \) while, the Grashof number (\( Gr \)), Reynolds number (\( \text{Re} \)), Darcy number (\( Da \)) and the Prandtl number (\( \Pr \)), respectively are defined as

$$ Gr = g\beta \frac{{T_{h} - T_{c} }}{{\upsilon^{2} }}H^{3} ,\;\text{Re} = \frac{{U_{s} H}}{\upsilon },\;Da = \frac{\kappa }{{H^{2} }},\;\Pr = \frac{\upsilon }{\alpha }, $$
(11)

where \( \nu = \mu /\rho \) and \( \alpha = K/\rho C_{p} \) are the kinematic viscosity and the thermal diffusivity, respectively. The dimensionless initial and boundary conditions (5) are as follows

$$ \begin{array}{llll} {t = 0} &\quad {U = V = 0} &\quad {\theta = 0} &\quad {{\text{on all boundaries}},} \\ {t \ge 0} &\quad {U = V = 0,} &\quad {\frac{{\partial \theta }}{{\partial X}} = 0} &\quad {{\text{on}}\;X = 0,\;1,} \\ &\quad {U = V = 0,} &\quad {\theta = 1\;{\text{or}}\;\theta = 0} &\quad {{\text{on}}\;Y = 0,} \\ &\quad {U = V = 0,} &\quad {\theta = {\text{sin}}\pi X} &\quad {{\text{on}}\;Y = 1.} \\ \end{array} $$
(12)

The average Nusselt number, \( \overline{Nu} \) at the top wall is obtained by integrating the local Nusselt number, \( Nu_{x} \) along the top wall and could be written in dimensionless forms:

$$ \overline{Nu} = \frac{1}{H}\int\limits_{0}^{H} {Nu_{x} \;dX} , $$
(13)

where, the local Nusselt number, \( Nu_{x} \) is defined as

$$ Nu_{x} = - \left. {\frac{\partial \theta }{\partial Y}} \right|_{Y = 1} . $$
(14)

The stream function is calculated from its definition

$$ U = \frac{\partial \psi }{\partial Y},\;V = - \frac{\partial \psi }{\partial X}. $$
(15)

3 Numerical procedure

The finite volume method is used to solve the governing Eqs. (7–10) subject to their corresponding initial and boundary conditions (12). While, the coupling system of the governing equations is solved using the SIMPLE algorithm with approach the power law scheme as discussed by Patankar (1980), and a program code in Fortran is developed.

In order to check the grid independency of the solution, the numerical experiment has been conducted for different grid resolutions. The grid independence test is performed using selected non-uniform grid in both \( X \) and \( Y \) direction. The grid size are tested from 40 × 40; 60 × 60; 80 × 80; 100 × 100, 120 × 120, 140 × 140, 160 × 160 and 180 × 180 with the chosen values of \( \text{Re} \)  = 1000; \( Gr \)  = 100; \( Q \)  = 3; \( Da \)  = 0:1 and \( \Pr \)  = 0:71 as demonstrated in Fig. 2. Based on the figure, the results is observed that an 100 × 100 grid is enough accurate to require all computations in the present work. In order to check the validation of the present numerical procedure, the horizontal and vertical velocity profiles was compared to the work by Muthtamilselvan et al. (2010) and Moallemi and Jang (1992) in the presence of porous medium for both \( \text{Re} \)  = 100 and \( \text{Re} \)  = 400 as shown in Table 1 and it is observed that the minimum and maximum values of the velocity profiles results are in good agreement with both previous results.

Fig. 2
figure 2

Temperature profiles for various grids at \( X = 0.5 \) with \( Q \)  = 3 and \( Da \)  = 0.1

Full size image
Table 1 Comparisons of the maximum and minimum values of the horizontal and vertical velocities at the mid-sections of the cavity between the present solution and previous works
Full size table

4 Results and discussion

The effects of porous medium, heat generation or absorption with sinusoidal heated top wall on mixed convection square lid-driven flow and heat transfer for two cases either uniformly heated or cooled on the bottom wall of the cavity are investigated. The numerical solutions are obtained for \( Da = 10^{ - 4} \), \( 10^{ - 3} \); \( 10^{ - 2} \) and \( 10^{ - 1} \), \( Q = - 3,\; - 1, \)\( 0,\;1 \) and \( 3 \), \( \Pr = 0.71 \), \( \text{Re} = 10^{3} \) and \( Gr = 10^{2} \). The characteristics of flow, streamline distribution and isotherm with the effect of porous medium and heat generation or absorption has been demonstrated in graph inside the square cavity.

The effect of \( Da \) on the streamlines and isotherms in the presence of heat generation at \( Q \)  = 3 with \( \text{Re} \) = 100; \( Gr \) = 100 and \( \Pr \) = 0:71 have been plotted in 2D-contours inside the square enclosure for first case (hot bottom wall) as shown in Fig. 3a, b respectively. It can be seen from the Fig. 3a that as \( Da \) increases, the maximum value streamline is increase from 0:0064 at \( Da = 10^{ - 4} \), followed by 0:00183 at \( Da \)  =  \( 10^{ - 3} \), later 0:0427 at \( Da \)  =  \( 5.5 \times 10^{ - 2} \) and finally 0:0827 at \( Da \)  =  \( 10^{ - 2} \). The maximum value is kept constant or nothing changes as \( Da \) is increased to \( 10^{ - 1} \) with the maximum value 0:0827. It is observed that the circulations strength of streamlines increases as \( Da \) increase due to the increase in the permeability of porous medium. There is no resistance to flow caused by large \( Da \). Thus, the flow inside the cavity become fast. In contrast as \( Da \) approaches to zero, the circulations are seen to very weak where the permeability of the porous medium approaches to zero causes the flow move slowly. Non-uniform grid point have been applied in this computation. The grid point is finer closed to the four boundaries of the cavity compared to the middle region of the cavity. Regarding the streamlines from bottom to the top of Fig. 3, as the Darcy number (the effect of the porous medium) decreases the flow circulation is inhibited except at the region close to the top surface. This shows the flow is retarded by the effect of low porosity. Thus the permeability of the medium approaches zero causing the flow is more dominantly at the portion close to the sliding top wall due to the movement of the lid of the cavity. The corresponding isotherms are shown in Fig. 3b. It can be seen that at small \( Da \) which is \( Da = 10^{ - 4} \), the isotherms are almost parallel to the horizontal walls and symmetrical about \( x \) axis. The maximum value of the temperature is 0:4030 shows that the strength of circulation is weak. The temperature lines are compressed towards the middle of the cavity as \( Da \) increased to \( Da \)  =  \( 10^{ - 3} \) where the maximum value increase to 0:6419. The formation of primary circulation cell and thermal boundary layer start to appear at \( Da \)  =  \( 5.5 \times 10^{ - 2} \) and can be seen clearly at \( Da \)  =  \( 10^{ - 2} \) with the maximum value 0:7274 and 0:7538 respectively. Even at the large \( Da \) = \( 10^{ - 1} \), the maximum value of the temperature and the situation remains same. It is interesting to observe the formation of circulation in isotherms as the \( Da \) increase that indicates the dominance of convection.

Fig. 3
figure 3

Streamline (a) and isotherm (b) for first case (hot bottom wall) with different Darcy number at \( \Pr \)  = 0.71, \( \text{Re} \)  = 1000 and \( Gr \)  = 100

Full size image

Figure 4a shows the temperature profiles along the horizontal mid-plane at \( Y \)  = 0:5 for various \( Da \) at \( \text{Re} \)  = 1000, \( \Pr \)  = 0.71 and \( Q \)  = 3. The temperature profiles increase with an increase in \( Da \). There are not much difference between \( Da \)  =  \( 10^{ - 2} \) and \( 10^{ - 1} \) due to the effect of the high temperature on the bottom and top walls which lead the temperature profiles had reached its maximum value. Other than that, the effect of \( Da \) on the local Nusselt number along the bottom wall is shown in Fig. 5a. It is noted that \( Nu \) is high for small \( Da \) because of the small permeability of porous medium where at small \( Da \) would eventually cease the fluid flow in a bulk of the cavity. Therefore, the effect of hot temperature at the bottom wall is overwhelmed the temperature near the region. While, for large \( Da \), the fluid flows faster due to the large porosity causes the buoyancy effect increase. \( Nu \) distribution decrease because of the non-uniform heating from the top wall is overwhelmed. The effect of heat generation and absorption on the temperature profiles at mid-sections of the vertical cavity for \( \text{Re} \)  = 1000, \( \Pr \)  = 0.71 and \( Da \)  = 0.1, is shown in Fig. 4b. It is observed that as \( Q \) increased, the temperature is increased. However, Fig. 5b shows that \( Nu \) distribution is decreased as \( Q \) increased.

Fig. 4
figure 4

Temperature profiles at mid-sections of the cavity for various Darcy number (a) and Heat generation or absorption coefficient (b) for first case

Full size image
Fig. 5
figure 5

Effect of Darcy number and heat generation or absorption coefficient on the local Nusselt number at bottom wall for first case

Full size image

Figure 6a, b represent the streamline and temperature in contours within the square enclosure for the second case (cold bottom wall) at \( Q \)  = 3; \( \Pr \)  = 0:71; \( \text{Re} \)  = 1000 and \( Gr \)  = 100 with different \( Da \). Figure 6a shows that the strength of circulations for \( Da = 10^{ - 4} \) is seen to very weak as the maximum value of streamline of circulation is found to be 0.0064 where the permeability of the medium at this \( Da \) approaches to zero. Similar to the streamline at \( Da \)  =  \( 10^{ - 3} \), the circulation is seen moved to the right of the top wall due to drag force created by the movement of the upper lid. As the \( Da \) increases to \( Da \)  =  \( 10^{ - 2} \), the circulations strength increases and drag to the right side at the top wall with the maximum value of Streamline is 0.0527. As \( Da \) increases to \( Da \)  =  \( 10^{ - 1} \), the maximum value streamline increase by 0.0809. There are no much different compared to the first case. Same goes to the isotherm graph for the second case as shown in Fig. 6b. As \( Da \) increases, the isotherms are significant changes. It can be seen clearly that there are stronger circulation and also the formation of thermal boundary layers inside the cavity.

Fig. 6
figure 6

Streamline (a) and isotherm (b) for second case (cold bottom wall) with different Darcy number at \( \Pr \)  = 0.71, \( \text{Re} \)  = 1000 and \( Gr \)  = 100

Full size image

However, the effect of \( Da \) and \( Q \) on temperature profiles for the second case as shown in Fig. 7a, b are slightly different than Fig. 4a, b. At large \( Da \), the effect of bottom wall temperature is more dominant due to the high buoyancy force. Hence, the temperature profiles decrease from \( Da \) = \( 10^{ - 2} \) to \( Da \)  =  \( 10^{ - 1} \). Moreover, the \( Nu \) distribution decreases as \( Da \) increase. It is noted that the mechanical effect of the sliding lid is overwhelmed the buoyancy effect inside the cavity and the temperature gradients are very high near the bottom wall. The effect of \( Q \) on temperature profiles and Nu have been shown in Fig. 8a, b, respectively. The temperature profiles increased as \( Q \) increase while, as expected \( Nu \) distribution is also increased as \( Q \) increased. Compared to the first case, the maximum value for the temperature profiles in Fig. 4b was higher than the second case. It is show that the heating on the bottom wall is greatly affected to the flow.

Fig. 7
figure 7

Temperature profiles at mid-sections of the cavity for various Darcy number (a) and heat generation or absorption coefficient (b) for second case

Full size image
Fig. 8
figure 8

Effect of Darcy number and heat generation or absorption coefficient on the local Nusselt number at bottom wall for second case

Full size image

The presence of \( Q \) has the tendency to increase the movement of the fluid flow inside the cavity. At large \( Da \), the effect of \( Q \) on the isotherm for the first case and the second case have been illustrated in Fig. 9a, b, respectively. It is clearly shown that the circulation cells are found to be formed towards the middle of the cavity. Besides that, the maximum value of the isotherms is increases as \( Q \) increased for both cases. However, the value for the first case was higher compared to the second case.

Fig. 9
figure 9

Isotherm for first case (a) and second case (b) with different heat generation or absorption coefficient, \( Q \) at \( Da \)  = 0.1, \( \Pr \)  = 0.71, \( \text{Re} \)  = 1000 and \( Gr \)  = 100

Full size image

5 Conclusions

The study on the effect of heat generation on mixed convection in the porous cavity with sinusoidal heated moving lid and uniformly heated and cooled bottom walls was solved numerically by finite volume method with employed the SIMPLE algorithm. Comparisons with previously published work on special cases of the problem are in good agreement. The effect of the Darcy number with the presence of heat generation on both stream function and isotherms, temperature profiles and Nusselt number were presented and discussed. It was found that the presence of a porous medium has significant influence on the heat transfer and flow characteristic inside the cavity. While, the effect of heat generation and absorption coefficient by increasing of \( Q \) causes the temperature to increase. Furthermore, the local Nusselt number distribution along the bottom wall for first and second case have different results showing that the heating on the bottom wall would affects the flow. With the increase in \( Da \), the local Nusselt number signifies the convection is dominant.