1 Introduction

Neural networks have attracted the attention of many researchers of different areas since they have been fruitfully applied in signal and image processing, associative memories, combinatorial optimization, automatic control, and so on [1–4]. In 1983, Cohen and Grossberg [5] proposed competitive neural networks (CNNs). Recently, Meyer-Bäse et al. [6–8] proposed the so called CNNs with different time scales, which can be seen as the extension of Hopfield neural networks [9], cellular networks [10], Cohen and Grossberg’s CNNs [5], and Amari’s model for primitive neuronal competition [11]. In the CNNs model, there are two types state variables: the short-term memory variables (STM) describing the fast neural activity and the long-term memory variables (LTM) describing the slow unsupervised synaptic modifications. Global exponential stability of CNNs with or without delays was investigated in [6–8, 12–15].

In the past decades, since the concept of drive-response synchronization for coupled chaotic systems was proposed in [16], much attention has been drawn to control and chaos synchronization [17] due to its potential applications such as secure communication, biological systems, information science, etc., [18]. In [16], a chaotic system, called the driver (or master), generates a signal sent over a channel to a responder (or slave), which uses this signal to synchronize itself with the driver. In other words, in the drive-response (or master-slave) systems, the response (or slave) system is influenced by the behavior of the drive (or master) system, but the drive (or master) system is independent of the response (or slave) one. The principle of using chaos to secure communication is this: the useful signal information with chaos signal is transmitted from driver to responder, then the useful signal information is recovered when synchronization between the states of driver to responder is realized. It was found in [19] that some delayed neural networks can exhibit chaotic dynamics. In [20], Lou and Cui studied the exponential synchronization for a class of CNNs with time-varying delays by instantaneous state feedback control scheme. The synchronization criteria were given by linear matrix inequality (LMI). By combining adaptive control scheme with LMI approach, Gu [21] investigated synchronization for CNNs with stochastic perturbations. However, authors of [20] and [21] did not consider distributed delays.

Since neural networks usually have a spatial extent due to the presence of an amount of parallel pathways with a variety of axon size and lengths [22], it is more practical to model them by introducing distributed delays. The unbounded distributed delay implies that the distant past has less influence compared to the recent behavior of the state [22], while bounded distributed delay means that there is a distribution of propagation delays only over a period of time [25–28]. We note that most existing results on stability or synchronization of neural networks with bounded distributed delays obtained by using LMI approach can not be directly extended to those with unbounded distributed delays (see Remark 3). Although there were some results on the exponential stability or synchronization of neural networks with unbounded distributed delays, they were all obtained by algebra approach [2, 15, 29]. As is well known, compared with LMI result, algebraic one is more conservative, and criteria in terms of LMI can be easily checked by using the powerful Matlab LMI toolbox. This motivates us to investigate the exponential synchronization of CNNs with unbounded distributed delays based on LMI approach. At the same time, the LMI approach of this paper is applicable to exponential synchronization of CNNs with bounded distributed delays.

Switched systems have attracted much research attention in control theory field during recent years. A switched system is composed of several dynamical subsystems and a switching law that specifies the active subsystem at each instant of time. Switched systems have numerous applications in communication systems, control of mechanical systems, automotive industry, aircraft and air traffic control, electric power systems [30–33], and many other fields. In [30, 31, 33], asymptotic synchronization of switched systems and application in communication is investigated. In this paper, we shall investigate exponential synchronization of switched competitive neural networks with both interval time-varying delays and distributed delays. In order to guarantee exponential synchronization, switches are required not to happen too frequently [34, 35]. The concept of average dwell time [34] is then introduced in this paper to describe this phenomenon. Inspired by multiple Lyapunov function in [36], a new multiple Lyapunov-Krasovskii functional will be designed to cope with the switching problem.

Recently, the research on stochastic models has received considerable interest, since stochastic perturbations have come to play an important role in many real systems [4, 21, 23, 24, 29, 37, 38]. However, to the best of our knowledge, no published paper concerning exponential synchronization of stochastic competitive neural networks (SCNNs) with both interval time-varying delays and distributed delays is reported in the literature. Since CNNs are extensions of neural networks, we further study SCNNs.

Based on the above discussions, in this paper, we aim to investigate exponential synchronization of SSCNNs with interval time-varying delays and distributed delays. Both unbounded and bounded distributed delays are considered. The switching rule is described by introducing the concept of average dwell time. By constructing new Lyapunov-Krasovskii functionals and employing a combination of the free-weighing matrix method, Newton-Leibniz formulation, and inequality technique, controller is designed to achieve exponential synchronization of the considered systems. The provided conditions are expressed in terms of LMIs, which are dependent on not only both lower and upper bounds of the interval time-varying delays but also delay kernel for unbounded distributed delays or upper bounds for bounded distributed delays and can be easily checked by the effective LMI toolbox in Matlab. Some restrictions are imposed on control gains and average dwell time for the practical application in engineering and secure communication. Some useful lemmas can be easily obtained from our results, and some existing results are extended and improved. Numerical simulations are given to demonstrate the effectiveness of the new results.

The rest of this paper is organized as follows. In Sect. 2, models of considered SSCNNs are presented. Some necessary assumptions, definitions, and lemmas are also given in this section. Our main results and their rigorous proofs are described in Sect. 3. In Sect. 4, one example with numerical simulations is offered to show the effectiveness of our results. In Sect. 5, conclusions are given. At last, acknowledgments.

2 Preliminaries

The CNNs with time-varying delays and unbounded distributed delays is described as:

$$ \left\{\begin{array}{ll} \begin{aligned} {\rm STM}: \varepsilon\dot{x}_{i}(t)&=-c_{i}x_{i}(t) +\sum_{j=1}^{n}a_{ij}f^{j}(x_{j}(t))\\ &\quad +\sum_{j=1}^{n}b_{ij}f^{j}(x_{j}(t-\tau(t)))\\ &\quad-\sum_{j=1}^{n}d_{ij}\int\limits_{-\infty}^{t}k(t-s)f^{j}(x_{j}(s)) \,{\rm d}s \\ &\quad +E^{i}\sum_{l=1}^{p}m_{il}(t)w_{l}, \quad i=1,2,\ldots,n,\\ {\rm LTM}: \dot{m}_{il}(t)&=-\alpha_{i}m_{il}(t)+\beta_{i}w_{l}f^{i}(x_{i}(t)),\quad l=1,2,\ldots,p, \end{aligned} \end{array} \right. $$
(1)

where \({x(t)=(x_{1}(t),\ldots,x_{n}(t))^{T}\in\mathbb{R}^{n}}\) is the state vector of the CNNs; \(f(x(t))=(f^{1}(x_{1}(t)),\ldots,f^{n}(x_{n}(t)))^{T}\) denotes the neuron activation function; M(t) = (m il ) n×p is the synaptic efficiency; \(\Upxi={\rm diag}(\alpha_{1},\alpha_{2},\ldots,\alpha_{n})\) and \(\Upupsilon={\rm diag}(\beta_{1},\beta_{2},\ldots,\beta_{n})\) denote disposable scaling constants with \(\alpha_{i}>0; C={\rm diag}(c_{1},c_{2},\ldots,c_{n})^{T}\) with c i  > 0 represents the time constant of the neuron; A = (a ij ) n×n , B = (b ij ) n×n , and D = (d ij ) n×n are the connection weight matrix, time-delayed weight matrix, and the distributively time-delayed weight matrix, respectively; \(w=(w_{1},w_{2},\ldots,w_{p})^{T}\) is the constant external stimulus; \(E={\rm diag}(E^{1},E^{2},\ldots,E^{n})\) is the strength of the external stimulus. \(\varepsilon\) is the time scale of STM state. Here, τ(t) denotes the time-varying delay of the CNNs. \(k(\cdot)\) is the delay kernel.

Let \(S(t)=(S_{1}(t),S_{2}(t),\ldots,S_{n}(t))^{T}\) and \(S_{i}(t)=\sum_{l=1}^{p}m_{il}(t)w_{l}=m_{i}^{T}(t)w, i=1,2,\ldots,n. \) Then the CNNs (5) can be rewritten in the following form:

$$ \left\{ \begin{array}{l} \begin{aligned} {\rm STM}: \varepsilon\dot{x}_{i}(t)&=-c_{i}x_{i}(t) +\sum_{j=1}^{n}a_{ij}f^{j}(x_{j}(t))\\ &\quad +\sum_{j=1}^{n}b_{ij}f^{j}(x_{j}(t-\tau(t)))\\ &\quad-\sum_{j=1}^{n}d_{ij}\int\limits_{-\infty}^{t}k(t-s)f^{j}(x_{j}(s)) \,{\rm d}s+E^{i}S_{i}(t),\\ {\rm LTM}: \dot{S}_{i}(t)&=-\alpha_{i}S_{i}(t)+\beta_{i}|w|^{2}f^{i}(x_{i}(t)),\quad i=1,2,\ldots,n, \end{aligned} \end{array} \right. $$
(2)

where \(|w|^{2}=w_{1}^{2}+w_{2}^{2}+\cdots+w_{p}^{2}\) is a constant. Without loss of generality, the input stimulus vector w is assumed to be normalized with unit magnitude, i.e., |w|2 = 1, and the fast time-scale parameter \(\varepsilon\) is also assumed to be unit. Then the system (2) turns out to the following networks:

$$ \left\{ \begin{array}{ll} \begin{aligned} {\rm STM}:\dot{x}_{i}(t)&=-c_{i}x_{i}(t)+\sum_{j=1}^{n}a_{ij}f^{j}(x_{j}(t))\\&\quad+\sum_{j=1}^{n}b_{ij}f^{j}(x_{j}(t-\tau(t)))\\&\quad-\sum_{j=1}^{n}d_{ij}\int\limits_{-\infty}^{t}f^{j}(x_{j}(s))\,{\rm d}s+E^{i}S_{i}(t),\\ {\rm LTM}:\dot{S}_{i}(t)&=-\alpha_{i}S_{i}(t)+\beta_{i}f_{i}(x_{i}(t)),\quad i=1,2,\ldots,n, \end{aligned}\end{array} \right. $$
(3)

or

$$ \left\{\begin{aligned} {\rm STM}:\dot{x}(t)=&-C x(t)+A f(x(t))+Bf(x(t-\tau(t)))\\ &-D\int\limits_{-\infty}^{t}k(t-s)f(x(s))\,\text{d}s+ES(t), \\ {\rm LTM}: \dot{S}(t)=&-\Upxi S(t)+\Upupsilon f(x(t)).\end{aligned} \right. $$
(4)

By introducing switching signal into the system (4), one can obtain the following switched CNNs:

$$ \left\{\begin{array}{l}\begin{aligned} {\rm STM}: \dot{x}(t)&=-C_{\sigma}x(t)+A_{\sigma} f_{\sigma}(x(t))+B_{\sigma}f_{\sigma}(x(t-\tau_{\sigma}(t))) \\&\quad -D_{\sigma}\int\limits_{-\infty}^{t}k_{\sigma}(t-s)f_{\sigma}(x(s))\,{\rm d}s+E_{\sigma}S(t)\\{\rm LTM}: \dot{S}(t)&=-\Upxi_{\sigma} R(t) +\Upupsilon_{\sigma}f_{\sigma}(x(t)),\end{aligned}\end{array} \right. $$
(5)

A switching signal is simply a piecewise constant signal taking values on index set. In model (5), the \(\sigma:[0,+\infty)\rightarrow\mathcal{M}=\{1,2,\ldots,m\}\) is a switching signal. Then \(\{C_{\sigma},A_{\sigma},B_{\sigma},D_{\sigma},E_{\sigma},\Upxi_{\sigma},\Upupsilon_{\sigma},f_{\sigma}(\cdot),\tau_{\sigma}(\cdot),k_{\sigma}(\cdot)\}\) is a family of matrices, activation functions, time-varying delays, and delay kernels parametrized by index set \(\mathcal{M}. \) We always assume that the values of σ is unknown, but its instantaneous value is available in real time.

Based on the concept of drive-response synchronization, we design the following response CNNs:

$$ \left\{\begin{aligned} {\rm STM}: \hbox{d}y(t)=&\left[\vphantom{\int\limits_{-\infty}^{t}}-C_{\sigma}y(t)+A_{\sigma} f_{\sigma}(y(t))+B_{\sigma}f_{\sigma}(y(t-\tau_{\sigma}(t)))\right.\\&\left.-D_{\sigma}\int\limits_{-\infty}^{t}k_{\sigma}(t-s)f_{\sigma}(y(s))\,{\rm d}s +E_{\sigma}R(t)+U_{\sigma}\vphantom{\int\limits_{-\infty}^{t}}\right]\hbox{d}t\\ &+ h_{\sigma}(t,e(t),e(t-\tau_{\sigma}(t)))\,{\rm d}\omega(t),\\ {\rm LTM}:\hbox{d}R(t)=& [-\Upxi_{\sigma} R(t) +\Upupsilon_{\sigma}f_{\sigma}(y(t))]\,{\rm d}t, \end{aligned}\right. $$
(6)

where U σ is the state feedback controller given to achieve the exponential synchronization between drive and response systems, which is of the form (we assume that the information on the sizes of τσ(t) are available):

$$ U_{\sigma}=-K_{\sigma,1}e(t)-K_{\sigma,2}e(t-\tau_{\sigma}(t)). $$
(7)

Here, K σ,1 and K σ,2 are feedback gain parameters to be scheduled. Moreover, \(\omega(t)=(\omega_{1}(t),\ldots,\omega_{n}(t))^{T}\) is a n-dimensional Brown motion defined on a complete probability space \((\Upomega,\mathcal{F},\mathcal{P})\) with a natural filtration \({\{\mathcal{F}_{t}\}_{t\geq0}}\) generated by {ω(s): 0 ≤ s ≤ t}. Here, the white noise \(\mathrm{d}\omega_{i}(t)\) is independent of \(\mathrm{d}\omega_{j}(t)\) for i ≠ j, and \({h_{\sigma}:\mathbb{R}^{+}\times\mathbb{R}^{n}\times\mathbb{R}^{n}\rightarrow\mathbb{R}^{n\times n}}\) is called the noise intensity function matrix. This type of stochastic perturbation can be regarded as a result from the occurrence of random uncertainties during the process of transmission. We assume that the output signals of (5) can be received by (6).

Throughout this paper, we make the following assumptions:

  • (H1) There exist constants τσ,1, τσ,2, and μσ such that \(0\leq\tau_{\sigma,1}\leq\tau_{\sigma}(t)\leq\tau_{\sigma,2}, \dot{\tau}_{\sigma}(t)\leq\mu_{\sigma}.\)

  • (H2) The delay kernel \(k_{\sigma}:[0,+\infty)\rightarrow[0,+\infty)\) is real-valued non-negative continuous function that satisfies

    1. (1)

      there exists positive number \(\varsigma_{\sigma}\) such that \(\int_{0}^{+\infty}k_{\sigma}(s)\,{\rm d}s=\varsigma_{\sigma}, \)

    2. (2)

      there exist positive numbers a and H σ such that \(\int_{0}^{+\infty}e^{as}k_{\sigma}(s)\,{\rm d}s\leq H_{\sigma}. \)

  • (H3) There exist constants f i σ and \(F^{i}_{\sigma}, i=1,2,\ldots,n,\) such that

    $$ f^{i}_{\sigma}\leq\frac{f^{i}_{\sigma}(x)-f^{i}_{\sigma}(y)}{x-y}\leq F^{i}_{\sigma},\quad \forall x,y\in {\mathbb{R}},x\neq y. $$

  • (H4) h(t, 0, 0) = 0 and there exist symmetric positive-definite matrices J σ,1 and J σ,2 such that

    $$ \begin{aligned} &{\rm trace}(h_{\sigma}^{T}(t,e(t),e(t-\tau_{\sigma}(t))) h_{\sigma}(t,e(t),e(t-\tau_{\sigma}(t))))\\ &\quad\leq e^{T}(t)J_{\sigma,1}e(t)+e^{T}(t-\tau_{\sigma}(t)) J_{\sigma,2}e(t-\tau_{\sigma}(t)). \end{aligned} $$

In order to investigate the problem of exponential synchronization between (5) and (6), we define the error state e(t) = y(t) − x(t) and z = R(t) − S(t). Subtracting (5) from (6) yields the following switched error system:

$$ \left\{\begin{aligned} {\rm STM}:\hbox{d}e(t)=&\left[\vphantom{\int\limits_{-\infty}^{t}}-(C_{\sigma}+K_{\sigma,1})e(t)-K_{\sigma,2}e(t-\tau_{\sigma}(t))\right.\\&\left. + A_{\sigma}g_{\sigma}(e(t))+ B_{\sigma}g_{\sigma}(e(t-\tau_{\sigma}(t)))\right.\\&\left.-D_{\sigma}\int\limits_{-\infty}^{t}k_{\sigma}(t-s)g_{\sigma}(e(s))\,{\rm d}s+E_{\sigma}z(t)\right]\hbox{d}t\\& +h_{\sigma}(t,e(t),e(t-\tau_{\sigma}(t)))\,{\rm d}\omega(t),\\ {\rm LTM}: \hbox{d}z(t)=&[-\Upxi_{\sigma} z(t)+\Upupsilon_{\sigma}g_{\sigma}(e(t))]\,{\rm d}t. \end{aligned} \right. $$
(8)

where g σ(e(t)) = f σ(y(t)) − f σ(x(t)), g σ(e(t − τσ(t))) = f σ(y(t − τσ(t))) − f σ(x(t − τσ(t))).

The initial condition associated with the switched error system (8) is given in the following form:

$$ e(s)=\varphi(s),\quad z(s)=\phi(s),\quad s\leq0, $$

for any \({\varphi,\phi\in L_{\mathcal{F}_{0}}^{2}((-\infty,0],\mathbb{R}^{n}), }\) where \({L_{\mathcal{F}_{0}}^{2}((-\infty,0],\mathbb{R}^{n})}\) is the family of all \(\mathcal{F}_{0}\)-measurable \({\wp((-\infty,0],\mathbb{R}^{n})}\)-valued random variables satisfying \({\sup_{s\leq0}\mathbb{E}\|\varphi(s)\|^{2}<+\infty}\) and \({\sup_{s\leq0}\mathbb{E}\|\phi(s)\|^{2}<+\infty, }\) and \({\wp((-\infty,0],\mathbb{R}^{n})}\) denotes the family of all continuous \({\mathbb{R}^{n}}\)-valued functions \(\varphi(s),\phi(s)\) on \((-\infty,0]\) with the norm \(\|\varphi(s)\|=\max_{1\leq i\leq n}\sup_{s\leq0}|\varphi_{i}(s)|\) and \(\|\phi(s)\|=\max_{1\leq i\leq n}\sup_{s\leq0}|\phi_{i}(s)|.\)

Definition 1

[34] A switching signal σ is said to have average dwell time T a if there exist two positive constants N 0 and T a such that

$$ N_{\sigma}(T,t)\leq N_{0}+\frac{T-t}{T_{a}},\quad \forall T\geq t\geq0, $$
(9)

where N σ(T, t) denotes the number of discontinuities of a switching signal σ on the interval (t, T).

Definition 2

The zero solution of (8) is said to be exponentially stable in mean square if for any initial condition (e T(t 0), z T(t 0))T, there exist some positive constants M 0 and η such that \({\mathbb{E}(\|e(t)\|^{2}+\|z(t)\|^{2})\leq M_{0}e^{-\eta(t-t_{0})}.}\)

Lemma 1

[39]. (Schur Complement). The linear matrix inequality (LMI)

$$ S=\left(\begin{array}{cc} S_{11}&S_{12}\\ S_{12}^{T}&S_{22} \end{array}\right)<0 $$

is equivalent to any one of the following two conditions:

$$ (\hbox{L}_1) \quad S_{11}<0,\ \ S_{22}-S_{12}^{T}S_{11}^{-1}S_{12}<0, \quad ({\rm L}_{2}) \quad S_{22}<0,\ \ S_{11}-S_{12}S_{22}^{-1}S_{12}^{T}<0, $$

where S 11 = S T11 , S 22 = S T22 .

According to assumptions \((\mathrm{H}_{3})\) and \((\mathrm{H}_{4}),\) the system (8) admits a trivial solution. Obviously, if the trivial solution of (8) is exponentially stable in mean square for any given initial condition, then the global exponential synchronization between SSCNN (5) and (6) is achieved.

3 Main results

For any t > 0, let \(t_{i} (i=0,1,2,\ldots,k)\) be the switching points of σ over the interval (0, t) satisfying \(0=t_{0}<t_{1}<t_{2}<\cdots<t_{k}<t. \) Suppose system (8) with the σ(t i )th = lth subsystem is activated when \(t\in[t_{i},t_{i+1})\) for \(i=0,1,2,\ldots,k, \) where \(l\in\mathcal{M}=\{1,2,\ldots,m\}. \) Then, for \(t\in[t_{i},t_{i+1}), \) we get

$$ \left\{\begin{array}{l} \begin{aligned} \hbox{STM}:\hbox{d}e(t)=&\left[\vphantom{\int\limits_{-\infty}^{t}}-(C_{l}+K_{l,1})e(t)-K_{l,2}e(t-\tau_{l}(t))\right.\\&+A_{l}g_{l}(e(t))+ B_{l} g_{l}(e(t-\tau_{l}(t)))\\&\left.-D_{l}\int\limits_{-\infty}^{t}k_{l}(t-s)g_{l}(e(s))\,\rm {d}s +E_{l}z(t)\right]\hbox{d}t\\&+h_{l}(t,e(t),e(t-\tau_{l}(t)))\,\rm {d}\omega(t),\\ \hbox{LTM}: \hbox{d}z(t)=&[-\Upxi_{l}z(t)+\Upupsilon_{l} g_{l}(e(t))]\,{\rm d}t. \end{aligned}\end{array}\right. $$
(10)

For simplicity, we denote

$$ \begin{aligned}G_{l}(t)&=-(C_{l}+K_{l,1})e(t)-K_{l,2}e(t-\tau_{l}(t))+A_{l}g_{l}(e(t))\\&\quad+B_{l} g_{l}(e(t-\tau_{l}(t)))\\&\quad-D_{l}\int\limits_{-\infty}^{t}k_{l}(t-s)g_{l}(e(s))\,\text{d}s+E_{l}z(t), \end{aligned} $$
(11)
$$ h_{l}(t)=h_{l}(t,e(t),e(t-\tau_{l}(t))). $$
(12)

Then system (10) can be rewritten as

$$ \left\{ \begin{array}{l} {\rm STM}: \hbox{d}e(t)=G_{l}(t)\hbox{d}t +h_{l}(t)\,{\rm d}\omega(t),\\ {\rm LTM}: \hbox{d}z(t)=[-\Upxi_{l} z(t)+\Upupsilon_{l} g_{l}(e(t))] \,{\rm d}t. \end{array} \right. $$
(13)

The following theorem is the main result of this paper, which states the exponential mean square stabilization conditions for the error system (8).

Theorem 1

Suppose that the assumptions (H 1)–(H 4) hold, σ is a switching signal with average dwell time T a . Then the trivial solution of system (8) is exponentially stable in mean square, if, for a given scalar a, there exist symmetric positive-definite matrices R l,i , i = 1, 2, P l,j , j = 1, 2, 3, 4, Q l,k , k = 1, 2, 3, positive-definite diagonal matrices \(\Upphi_{l}, \Uppsi_{l}, \) matrices N l,i , S l,i , M l,i , Y l,i , i = 1, 2, an invertible matrix O l , positive scalars ρ l and θ, for each \(l\in\mathcal{M}\) such that the following LMIs hold,

$$ \left(\begin{array}{cc} \Uppi_{l}&\Updelta_{l}\\ \ast& -\Upomega_{l}\end{array} \right)<0, $$
(14)
$$ R_{l,i}\leq\theta R_{\tilde{l},i},\quad P_{l,j}\leq\theta P_{\tilde{l},j},\quad Q_{l,k}\leq\theta Q_{\tilde{l},k}, \quad \forall l,\tilde{l}\in{\mathcal{M}}, $$
(15)
$$ a-\frac{1}{T_{a}}\ln \theta>0, $$
(16)
$$ R_{l,1}\leq\rho_{l}I, $$
(17)

further more, the convergence rate can be estimated as \(a-\frac{1}{T_{a}}\ln \theta, \) where \(\Updelta_{l}=(H_{l,21}S_{l},H_{l,20}N_{l},H_{l,21}M_{l},H_{l}\widehat{O}_{l} D_{l}), S_{l}^{T}=(S^{T}_{l,1},0,S^{T}_{l,2},0,0,0,0,0), M_{l}^{T}=(M^{T}_{l,1},0,M^{T}_{l,2},0,0,0,0,0), N_{l}^{T}=(N^{T}_{l,1},0,N^{T}_{l,2},0,0,0,0,0), \widehat{O}_{l}^{T}=(O^{T}_{l},0,0,0,0,O^{T}_{l},0,0), H_{l,21}=\frac{e^{a\tau_{l,2}}-e^{a\tau_{l,1}}}{a}, H_{l,20}=\frac{e^{a\tau_{l,2}}-1}{a}, \int_{0}^{+\infty}e^{as}k_{l}(s)\,{\rm d}s\leq H_{l}, \tau_{l,21}=\tau_{l,2}-\tau_{l,1}, \overline{F}_{l}={\rm diag}(F^{1}_{l}f^{1}_{l},F^{2}_{l}f^{2}_{l},\ldots,F^{n}_{l}f^{n}_{l}),\, \overline{f}_{l}={\rm diag}(\frac{1}{2}(F^{1}_{l}+f^{1}_{l}),\frac{1}{2}(F^{2}_{l}+f^{2}_{l}),\ldots,\frac{1}{2}(F^{n}_{l}+f^{n}_{l})),\)

$$ \begin{aligned} \Uppi_{l}&=\left( \begin{array}{cccccccc} \Uppi_{l,1}& O_{l}E_{l}& \Uppi_{l,2}&M_{l,1}&-S_{l,1}&\Uppi_{l,3}&O_{l}A_{l}+\overline{f}_{l}\Upphi_{l}&O_{l}B_{l}\\ \ast& \Uppi_{l,4}&0&0&0&E_{l}^{T}O_{l}^{T}&R_{l,2}\Upupsilon_{l}&0\\ \ast&\ast&\Uppi_{l,5}&M_{l,2}&-S_{l,2}&0&0&\overline{f}_{l}\Uppsi_{l}\\ \ast&\ast&\ast&-e^{-a\tau_{l,1}}P_{l,3}&0&0&0&0\\ \ast&\ast&\ast&\ast&-e^{-a\tau_{l,2}}P_{l,4}&0&0&0\\ \ast&\ast&\ast&\ast&\ast&\Uppi_{l,6}&O_{l}A_{l}&O_{l}B_{l}\\ \ast&\ast&\ast&\ast&\ast&\ast&\Uppi_{l,7}&0\\ \ast&\ast&\ast&\ast&\ast&\ast&\ast&\Uppi_{l,8} \end{array}\right),\\ \Uppi_{l,1}&=\rho_{l}J_{l,1}+aR_{l,1}+P_{l,1}+P_{l,3}+P_{l,4}+N_{l,1}+N_{l,1}^{T}-\overline{F}_{l}\Upphi_{l} -O_{l}C_{l}-C_{l}O_{l}^{T}-Y_{l,1}-Y_{l,1}^{T},\\ \Uppi_{l,2}&=-N_{l,1}+N_{l,2}^{T}+S_{l,1}-M_{l,1}-Y_{l,2},\quad \Uppi_{l,3}=R_{l,1}-O_{l}-C_{l}O_{l}^{T}-Y_{l,1}^{T},\\ \Uppi_{l,4}&=-R_{l,2}\Upxi_{l}-\Upxi_{l}R_{l,2}+aR_{l,2}, \quad \Uppi_{l,6}=\tau_{l,2}Q_{l,1}+\tau_{l,21}Q_{l,2}-O_{l}-O_{l}^{T},\\ \Uppi_{l,5}&=\rho_{l}J_{l,2}-\overline{F}_{l}\Uppsi_{l}-(1-\mu_{l}) e^{-a\tau_{l,2}}P_{l,1}-N_{l,2}-N_{l,2}^{T}+S_{l,2} +S_{l,2}^{T}-M_{l,2}-M_{l,2}^{T},\\ \Uppi_{l,7}&=-\Upphi_{l}+P_{l,2}+\varsigma_{l}Q_{l,3},\quad \Uppi_{l,8}=-\Uppsi_{l}-(1-\mu_{l})e^{-a\tau_{l,2}}P_{l,2},\\ \Upomega_{l}&=\left( \begin{array}{cccc} H_{l,21}(Q_{l,1}+Q_{l,2})&0&0&0\\ 0& H_{l,20}Q_{l,1}&0&0\\ 0&0&H_{l,21}Q_{l,2}&0\\ 0&0&0&H_{l}Q_{l,3} \end{array} \right). \end{aligned} $$

Moreover, the estimation of the control gains is K l,i  = O −1 l Y l,i , i = 1, 2.

Proof

Consider the following multiple Lyapunov-Krasovskii functional candidate:

$$ V(l,e(t))=\sum_{i=1}^{4}V_{i}(l,e(t)), $$
(18)

where

$$ \begin{aligned}V_{1}(l,e(t))& =e^{T}(t)R_{l,1}e(t)+z^{T}(t)R_{l,2}z(t),\\V_{2}(l,e(t))& =\int\limits_{t-\tau_{l}(t)}^{t}e^{a(s-t)}[e^{T}(s)P_{l,1}e(s)\\ & \quad +g^{T}_{l}(e(s))P_{l,2}g_{l}(e(s))]\,\text{d}s+\int\limits_{t-\tau_{l,1}}^{t}e^{T}(s)e^{a(s-t)}P_{l,3}e(s)\,\text{d}s\\ & \quad+\int\limits_{t-\tau_{l,2}}^{t}e^{T}(s)e^{a(s-t)}P_{l,4}e(s)\,\text{d}s\\V_{3}(l,e(t))& =\int\limits_{-\tau_{l,2}}^{0}\int\limits_{t+\nu}^{t}G_{l}^{T}(s)e^{a(s-t)}Q_{l,1}G_{l}(s)\,\text{d}s\,{\rm d}\nu\\ & \quad +\int\limits_{-\tau_{l,2}}^{-\tau_{l,1}}\int\limits_{t+\nu}^{t}G_{l}^{T}(s)e^{a(s-t)}Q_{l,2}G_{l}(s)\,\text{d}s\,{\rm d}\nu,\\V_{4}(l,e(t))& =\int\limits_{-\infty}^{0}\int\limits_{t+\nu}^{t}k_{l}(-\nu)g_{l}^{T}(e(s))e^{a(s-t)}Q_{l,3}g_{l}(e(s))\,\text{d}s\,{\rm d}\nu \end{aligned} $$

Calculating the time derivative of V(l, e(t)) along the trajectory of system (13) by using Itô’s differential formula, one can obtain that

$$ \,{\rm d}V(l,e(t))=\sum_{i=1}^{4}{\mathcal{L}}V_{i}(l,e(t)) \,{\rm d}t+2e^{T}(t)R_{l,1}h_{l}(t)\,{\rm d}\omega(t), $$
(19)

where

$$ \begin{aligned}{\mathcal{L}}V_{1}(l,e(t))=&\,2e^{T}(t)R_{l,1}G_{l}(t)+2z^{T}(t)R_{l,2} [-\Upxi_{l}z(t)+\Upupsilon_{l} g_{l}(e(t))]\\& +{\rm trace}(h^{T}_{l}(t)R_{l,1}h_{l}(t))\\\leq &\, 2e^{T}(t)R_{l,1}G_{l}(t)+2z^{T}(t)R_{l,2}[-\Upxi_{l}z(t)+\Upupsilon_{l} g_{l}(e(t))]\\& +\rho_{l}[e^{T}(t)J_{l,1}e(t)\\& +e^{T}(t-\tau_{l}(t))J_{l,2}e(t-\tau_{l}(t))]+ae^{T}(t)R_{l,1}e(t)\\& +az^{T}(t)R_{l,2}z(t)-aV_{1}(l,e(t)),\end{aligned} $$
(20)
$$ \begin{aligned}{\mathcal{L}}V_{2}(l,e(t))& =e^{T}(t)(P_{l,1}+P_{l,3}+P_{l,4})e(t)+g^{T}_{l}(e(t))P_{l,2}g_{l}(e(t))\\& \quad-(1-\dot{\tau}_{l}(t))e^{T}(t-\tau_{l}(t))e^{-a\tau_{l}(t)}P_{l,1}e(t-\tau_{l}(t))\\& \quad-(1-\dot{\tau}_{l}(t))g^{T}_{l}(e(t-\tau_{l}(t)))e^{-a\tau_{l}(t)}P_{l,2}g_{l}(e(t-\tau_{l}(t)))\\& \quad-\sum_{i=3}^{4}e^{T}(t-\tau_{l}^{i})e^{-a\tau_{l}^{i}}P_{l,i}e(t-\tau_{l}^{i})-aV_{2}(l,e(t))\\& \leq{e}^{T}(t)(P_{l,1}+P_{l,3}+P_{l,4})e(t)+g^{T}_{l}(e(t))P_{l,2}g_{l}(e(t))\\& \quad-(1-\mu_{l})e^{T}(t-\tau_{l}(t))e^{-a\tau_{l,2}}P_{l,1}e(t-\tau_{l}(t))\\& \quad-(1-\mu_{l})g^{T}_{l}(e(t-\tau_{l}(t)))e^{-a\tau_{l,2}}P_{l,2}g_{l}(e(t-\tau_{l}(t)))\\& \quad-e^{T}(t-\tau_{l,1})e^{-a\tau_{l,1}}P_{l,3}e(t-\tau_{l,1})\\& \quad-e^{T}(t-\tau_{l,2})e^{-a\tau_{l,2}}P_{l,4}e(t-\tau_{l,2})-aV_{2}(l,e(t)),\\\end{aligned} $$
(21)
$$ \begin{aligned} {\mathcal{L}}V_{3}(l,e(t))&=\tau_{l,2}G_{l}^{T}(t)Q_{l,1}G_{l}(t) -\int\limits_{t-\tau_{l,2}}^{t}G_{l}^{T}(s)e^{a(s-t)}Q_{l,1}G_{l}(s)\,{\rm d}s-aV_{3}(l,e(t))\\ &\quad+(\tau_{l,2}-\tau_{l,1})G_{l}^{T}(t)Q_{l,2}G_{l}(t) -\int\limits_{t-\tau_{l,2}}^{t-\tau_{l,1}}G_{l}^{T}(s)e^{a(s-t)}Q_{l,2}G_{l}(s)\,{\rm d}s\\ &=G_{l}^{T}(t)(\tau_{l,2}Q_{l,1}+\tau_{l,21}Q_{l,2})G_{l}(t) -\int\limits_{t-\tau_{l,2}}^{t-\tau_{l}(t)}G_{l}^{T}(s)e^{a(s-t)}(Q_{l,1}+Q_{l,2})G_{l}(s)\,{\rm d}s\\ &\quad-\int\limits_{t-\tau_{l}(t)}^{t}G_{l}^{T}(s)e^{a(s-t)}Q_{l,1}G_{l}(s)\,{\rm d}s -\int\limits_{t-\tau_{l}(t)}^{t-\tau_{l,1}}G_{l}^{T}(s)e^{a(s-t)}Q_{l,2}G_{l}(s)\,{\rm d}s -aV_{3}(l,e(t)), \end{aligned} $$
(22)
$$ \begin{aligned} {\mathcal{L}}V_{4}(l,e(t))&=\int\limits_{-\infty}^{0}k_{l}(-\nu)g_{l}^{T}(e(t))Q_{l,3}g_{l}(e(t))\,{\rm d}\nu -\int\limits_{-\infty}^{0}k_{l}(-\nu)g_{l}^{T}(e(t+\nu))e^{a\nu}Q_{l,3}g_{l}(e(t+\nu))\,{\rm d}\nu -aV_{4}(l,e(t))\\ &=\varsigma_{l}g_{l}^{T}(e(t))Q_{l,3}g_{l}(e(t)) -\int\limits_{-\infty}^{t}k_{l}(t-s)g_{l}^{T}(e(s))e^{a(s-t)}Q_{l,3}g_{l} (e(s))\,{\rm d}s-aV_{4}(l,e(t)). \end{aligned} $$
(23)

Now define new vector ξ l (t) as

$$ \xi_{l}^{T}(t)=(e^{T}(t),z^{T}(t),e^{T}(t-\tau_{l}(t)),e^{T}(t-\tau_{l,1}),e^{T}(t-\tau_{l,2}),G_{l}^{T}(t),g_{l}^{T}(e(t)), g_{l}^{T}(e(t-\tau_{l}(t)))). $$

For any matrices N l,i , S l,i , M l,i , i = 1, 2, and any invertible matrix O l with appropriate dimensions, from Newton-Leibniz formulation and (11)–(13), we have

$$ 2[e^{T}(t)N_{l,1}+e^{T}(t-\tau_{l}(t))N_{l,2}] [e(t)-e(t-\tau_{l}(t))-\int\limits_{t-\tau_{l}(t)}^{t}G_{l}(s) \,{\rm d}s-\int\limits_{t-\tau_{l}(t)}^{t}h_{l}(s)\,{\rm d}\omega(s)]=0, $$
(24)
$$ 2[e^{T}(t)S_{l,1}+e^{T}(t-\tau_{l}(t))S_{l,2}][e(t-\tau_{l}(t)) -e(t-\tau_{l,2}) -\int\limits_{t-\tau_{l,2}}^{t-\tau_{l}(t)}G_{l}(s)\,{\rm d}s -\int\limits_{t-\tau_{l,2}}^{t-\tau_{l}(t)}h_{l}(s)\,{\rm d}\omega(s)]=0, $$
(25)
$$ 2[e^{T}(t)M_{l,1}+e^{T}(t-\tau_{l}(t))M_{l,2}][e(t-\tau_{l,1}) -e(t-\tau_{l}(t)) -\int\limits_{t-\tau_{l}(t)}^{t-\tau_{l,1}}G_{l}(s)\,{\rm d}s -\int\limits_{t-\tau_{l}(t)}^{t-\tau_{l,1}}h_{l}(s)\,{\rm d}\omega(s)]=0, $$
(26)
$$ 2[e^{T}(t)+G_{l}^{T}(t)]O_{l}[-(C_{l}+K_{l,1})e(t)-K_{l,2} e(t-\tau_{l}(t))+ A_{l}g_{l}(e(t)) +B_{l} g_{l}(e(t-\tau_{l}(t))) -D_{l}\int\limits_{-\infty}^{t}k_{l}(t-s)g_{l}(e(s))\,{\rm d}s+E_{l}z(t) -G_{l}(t)]=0. $$
(27)

On the other hand, one can derive the following inequality:

$$ \begin{aligned}&-\int\limits_{t-\tau_{l,2}}^{t-\tau_{l}(t)}G_{l}^{T}(s)e^{a(s-t)}(Q_{l,1}+Q_{l,2})G_{l}(s)\,{\rm d}s-2\xi_{l}^{T}S_{l}\int\limits_{t-\tau_{l,2}}^{t-\tau_{l}(t)}G_{l}(s)\,{\rm d}s\\& \quad=-\int\limits_{t-\tau_{l,2}}^{t-\tau_{l}(t)}\widetilde{S}^{T}\left(e^{a(s-t)}(Q_{l,1}+Q_{l,2})\right)^{-1}\widetilde{S}\,{\rm d}s\\&\quad+\xi_{l}^{T}S_{l}(Q_{l,1}+Q_{l,2})^{-1}S_{l}^{T}\xi_{l}\int\limits_{t-\tau_{l,2}}^{t-\tau_{l}(t)}e^{-a(s-t)}\,{\rm d}s\\& \quad\leq-\int\limits_{t-\tau_{l,2}}^{t-\tau_{l}(t)}\widetilde{S}^{T}\left(e^{a(s-t)}(Q_{l,1}+Q_{l,2})\right)^{-1}\widetilde{S}\,{\rm d}s\\&\quad+H_{l,21}\xi_{l}^{T}S_{l}(Q_{l,1}+Q_{l,2})^{-1}S_{l}^{T}\xi_{l},\end{aligned} $$
(28)

where \(\widetilde{S}^{T}_{l}=\xi_{l}^{T}S_{l}+G_{l}^{T}(s)e^{a(s-t)}(Q_{l,1}+Q_{l,2}).\) Similarly, one has

$$ \begin{aligned} &-\int\limits_{t-\tau_{l}(t)}^{t}G_{l}^{T}(s)e^{a(s-t)}Q_{l,1}G_{l}(s) \,{\rm d}s-2\xi_{l}^{T}N_{l}\int\limits_{t-\tau_{l}(t)}^{t}G_{l}(s)\,{\rm d}s\\ &\quad\leq-\int\limits_{t-\tau_{l}(t)}^{t}\widetilde{N}^{T} \left(e^{a(s-t)}Q_{l,1}\right)^{-1}\widetilde{N}\,{\rm d}s +H_{l,20}\xi_{l}^{T}N_{l}Q_{l,1}^{-1}N_{l}^{T}\xi_{l},\\ \end{aligned} $$
(29)
$$ \begin{aligned} &-\int\limits_{t-\tau_{l}(t)}^{t-\tau_{l,1}}G_{l}^{T}(s) e^{a(s-t)}Q_{l,2}G_{l}(s)\,{\rm d}s-2\xi_{l}^{T}M_{l} \int\limits_{t-\tau_{l}(t)}^{t-\tau_{l,1}}G_{l}(s)\,{\rm d}s\\ &\quad\leq-\int\limits_{t-\tau_{l}(t)}^{t-\tau_{l,1}}\widetilde{M}^{T} \left(e^{a(s-t)}Q_{l,2}\right)^{-1}\widetilde{M}\,{\rm d}s +H_{l,21}\xi_{l}^{T}M_{l}Q_{l,2}^{-1}M_{l}^{T}\xi_{l}, \end{aligned} $$
(30)
$$ \begin{aligned}& -\int\limits_{-\infty}^{t}k_{l}(t-s)g_{l}^{T}(e(s))e^{a(s-t)}Q_{l,3}g_{l}(e(s))\,{\rm d}s-2\xi_{l}^{T} \widehat{O}_{l}D_{l}\int\limits_{-\infty}^{t}k_{l}(t-s)g_{l}(e(s))\,{\rm d}s\\& \quad=-\int\limits_{-\infty}^{t}\widetilde{O}_{l}^{T}\left(e^{a(s-t)}k_{l}^{-1}(t-s)Q_{l,3}\right)^{-1}\widetilde{O}_{l}\,{\rm d}s\\& \qquad +\xi_{l}^{T}\widehat{O}_{l} D_{l}Q_{l,3}^{-1}D_{l}^{T}\widehat{O}_{l}^{T}\xi_{l}\int\limits_{-\infty}^{t}e^{-a(s-t)}k_{l}(t-s)\,\text{d}s\\ & \quad\leq-\int\limits_{-\infty}^{t}\widetilde{O}_{l}^{T}\left(e^{a(s-t)}k_{l}^{-1}(t-s)Q_{l,3}\right)^{-1}\widetilde{O}_{l}\,{\rm d}s\\& \qquad +H_{l}\xi_{l}^{T}\widehat{O}_{l}D_{l}Q_{l,3}^{-1}D_{l}^{T}\widehat{O}_{l}^{T}\xi_{l}, \end{aligned}$$
(31)

where \(\widetilde{N}^{T}_{l}=\xi_{l}^{T}N_{l}+G_{l}^{T}(s)e^{a(s-t)}Q_{l,1}, \widetilde{M}^{T}_{l}=\xi_{l}^{T}M_{l}+G_{l}^{T}(s)e^{a(s-t)}Q_{l,2}, \widetilde{O}^{T}_{l}=\xi_{l}^{T}\widehat{O}_{l} D_{l}+g_{l}^{T}(e(s))e^{a(s-t)}Q_{l,3}.\)

In view of assumption \((\mathrm{H}_{3}),\) for any positive diagonal matrices \(\Upphi_{l}={\rm diag}(\phi^{1}_{l},\phi^{2}_{l},\ldots,\phi^{n}_{l})\) and \(\Uppsi_{l}={\rm diag}(\psi^{1}_{l},\psi^{2}_{l},\ldots,\psi^{n}_{l}),\) the following two inequalities hold [40]:

$$ 0\leq\left(\begin{array}{c} e(t)\\ g_{l}(e(t)) \end{array}\right)^{T}\left( \begin{array}{cc} -\overline{F}_{l}\Upphi_{l}&\overline{f}_{l}\Upphi_{l}\\ \overline{f}_{l}\Upphi_{l}& -\Upphi_{l} \end{array} \right) \left(\begin{array}{c} e(t)\\ g_{l}(e(t)) \end{array}\right), $$
(32)
$$ 0\leq\left( \begin{array}{c} e(t-\tau_{l}(t))\\ g_{l}(e(t-\tau_{l}(t))) \end{array} \right)^{T} \left(\begin{array}{cc} -\overline{F}_{l}\Uppsi_{l}&\overline{f}_{l}\Uppsi_{l}\\ \overline{f}_{l}\Uppsi_{l}&-\Uppsi_{l}\end{array}\right) \left(\begin{array}{c} e(t-\tau_{l}(t))\\ g_{l}(e(t-\tau_{l}(t))) \end{array} \right). $$
(33)

Substituting (20)–(23) into (19), adding (24)–(33) to the right side of (19) and letting Y l,i  = O l K l,i produce that

$$ \mathrm{d}V(l,e(t))\leq[\xi_{l}^{T}(t)\Uptheta_{l}\xi_{l}(t) -aV(l,e(t))-\Upsigma_{l}]\mathrm{d}t+\Uplambda(\mathrm{d}\omega(t)), $$
(34)

where

$$ \begin{aligned} \Uptheta_{l}&=\Uppi_{l}+H_{l,21}S_{l}(Q_{l,1}+Q_{l,2})^{-1}S_{l}^{T}+H_{l,20}N_{l}Q_{l,1}^{-1}N_{l}^{T} +H_{l,21}M_{l}Q_{l,2}^{-1}M_{l}^{T} +H_{l}\widehat{O}_{l} D_{l}Q_{l,3}^{-1}D_{l}^{T}\widehat{O}_{l}^{T},\\ \Upsigma_{l}&=\int\limits_{t-\tau_{l}^{2}}^{t-\tau_{l}(t)} \widetilde{S}^{T}\left(e^{a(s-t)}(Q_{l,1}+Q_{l,2})\right)^{-1} \widetilde{S}\,{\rm d}s +\int\limits_{t-\tau_{l}(t)}^{t}\widetilde{N}^{T}\left(e^{a(s-t)}Q_{l,1}\right)^{-1}\widetilde{N}\,{\rm d}s\\ &\quad+\int\limits_{t-\tau_{l}(t)}^{t-\tau_{l,1}}\widetilde{M}^{T}\left(e^{a(s-t)}Q_{l,2}\right)^{-1}\widetilde{M}\,{\rm d}s +\int\limits_{-\infty}^{t}\widetilde{O}_{l}^{T}\left(e^{a(s-t)}k_{l}^{-1}(t-s)Q_{l,3}\right)^{-1}\widetilde{O}_{l}\,{\rm d}s,\\ \Uplambda(\,{\rm d}\omega(t))&=2e^{T}(t)R_{l,1}h_{l}(t)\,{\rm d}\omega(t)-2\xi_{l}^{T}N_{l}\int\limits_{t-\tau_{l}(t)}^{t}h_{l}(s)\,{\rm d}\omega(s)- 2\xi_{l}^{T}S_{l}\int\limits_{t-\tau_{l}^{2}}^{t-\tau_{l}(t)}h_{l}(s)\,{\rm d}\omega(s)\\ &\quad-2\xi_{l}^{T}M_{l}\int\limits_{t-\tau_{l}(t)}^{t-\tau_{l}^{1}}h_{l}(s)\,{\rm d}\omega(s). \end{aligned} $$

From e a(s-t) Q l,i  > 0, i = 1, 2, 3 and k −1 l (t − s) ≥ 0, we get \(\Upsigma_{l}>0. \) By virtue of Lemma 1, (14) is equivalent to \(\Uptheta_{l}<0. \) Therefore, by integrating both sides of (34) from t 0 to t (t 0 < t) and taking expectation, one can obtain that

$$ {\mathbb{E}}V(l,e(t))\leq e^{-a(t-t_{0})}{\mathbb{E}}V(l,e(t_{0})). $$
(35)

Particularly, when \(t\in[t_{k},t_{k+1}), \) it follows from (35) that

$$ {\mathbb{E}}V(\sigma(t),e(t))\leq e^{-a(t-t_{k})}{\mathbb{E}}V(\sigma(t_{k}),e(t_{k})). $$
(36)

By (15), at the switching instant t k , one gets

$$ {\mathbb{E}}V(\sigma(t_{k}),e(t_{k}))\leq \theta {\mathbb{E}}V(\sigma(t_{k}^{-}),e(t_{k}^{-})), $$
(37)

where t − k is the left limitation of t k .

According to Definition 1, there exist positive constant N 0 such that the number k of discontinuities of the switching signal σ on the interval (0, t) satisfies \(k=N_{\sigma}(t,0)\leq N_{0}+\frac{t}{T_{a}}. \) By induction, it follows from (36) to (37) that

$$ \begin{aligned} {\mathbb{E}}V(\sigma(t),e(t))& \leq e^{-a(t-t_{k})}\theta{\mathbb{E}}V(\sigma(t_{k}^{-}),e(t_{k}^{-}))\\&\leq e^{-a(t-t_{k-1})}\theta^{2}{\mathbb{E}}V(\sigma(t_{k-1}^{-}),e(t_{k-1}^{-}))\\& \cdots \\ & \leq e^{-at}\theta^{k}{\mathbb{E}}V(\sigma(0),e(0))\\& = e^{-at}e^{k\ln\theta}{\mathbb{E}}V(\sigma(0),e(0))\\ & \leq e^{-at}e^{(N_{0}+\frac{t}{T_{a}})\ln\theta}{\mathbb{E}}V(\sigma(0),e(0))\\& = e^{N_{0}\ln\theta}{\mathbb{E}}V(\sigma(0),e(0))e^{-(a-\frac{1}{T_{a}}\ln\theta)t}. \end{aligned} $$
(38)

Let \(\lambda=\min_{l\in\mathcal{M}}\{\lambda_{\min}R_{l,1},\lambda_{\min}R_{l,2}\}.\) One has from (18) that

$$ \lambda{\mathbb{E}}(\|e(t)\|^{2}+\|z(t)\|^{2})\leq {\mathbb{E}}V(\sigma(t),e(t)). $$
(39)

It follows from (38) to (39) that

$$ {\mathbb{E}}(\|e(t)\|^{2}+\|z(t)\|^{2})\leq \frac{1}{\lambda}e^{N_{0}\ln \theta}{\mathbb{E}}V(\sigma(0),e(0))e^{-(a-\frac{1}{T_{a}}\ln \theta)t}. $$

Since \(a-\frac{1}{T_{a}}\ln \theta>0, \) in view of Definition 2, the trivial solution of system (8) is exponentially stable in mean square. This completes the proof. \(\square\)

Next we shall consider synchronization of drive-response SSCNNs with time-varying delays and bounded distributed delays, which are described as:

$$ \left\{\begin{array}{l} \begin{aligned} {\rm STM}: \dot{x}(t)&=-C_{\sigma}x(t)+A_{\sigma}f_{\sigma}(x(t))+B_{\sigma} f_{\sigma}(x(t-\tau_{\sigma}(t)))\\ &\quad-D_{\sigma}\int\limits_{t-\vartheta_{\sigma}(t)}^{t}f_{\sigma}(x(s))\,{\rm d}s+E_{\sigma}S(t),\\ {\rm LTM}:\dot{S}(t)&=-\Upxi_{\sigma}S(t)+\Upupsilon_{\sigma}f_{\sigma}(x(t)), \end{aligned} \end{array} \right. $$
(40)
$$ \left\{ \begin{array}{l} \begin{aligned} {\rm STM}:\hbox{d}y(t)& =\left[\vphantom{\int\limits_{-\infty}^{t}}-C_{\sigma}y(t)+A_{\sigma}f_{\sigma}(y(t))+B_{\sigma} f_{\sigma}(y(t-\tau_{\sigma}(t)))\right.\\&\quad-D_{\sigma}\int\limits_{t-\vartheta_{\sigma}(t)}^{t}f_{\sigma}(y(s))\,{\rm d}s\\& \left.\quad +E_{\sigma}R(t)+U_{\sigma}\vphantom{\int\limits_{-\infty}^{t}}\right]\hbox{d}t\\&\quad +h_{\sigma}(t,e(t),e(t-\tau_{\sigma}(t)))\,{\rm d}\omega(t),\\ {\rm LTM}:\hbox{d}R(t)& =[-\Upxi_{\sigma} R(t)+\Upupsilon_{\sigma}f_{\sigma}(y(t))]\,{\rm d}t, \end{aligned} \end{array}\right. $$
(41)

where (40) is the drive system and (41) is the response system, 0 < ϑσ(t) ≤ ϑσ, ϑσ is positive constant, U σ has the same form as (7).

By the same method as that used in the proof of Theorem 1, we can also derive sufficient conditions under which (41) exponentially synchronize with (40).

Subtracting (40) from (41) yields

$$ \left\{ \begin{aligned} {\rm STM}:\hbox{d}e(t)& =\left[\vphantom{\int\limits_{-\infty}^{t}}-(C_{\sigma}+K_{\sigma,1})e(t)-K_{\sigma,2}e(t-\tau_{\sigma}(t))\right.\\&\quad + A_{\sigma}g_{\sigma}(e(t)) +B_{\sigma} g_{\sigma}(e(t-\tau_{\sigma}(t)))\\& \quad\left.-D_{\sigma}\int\limits_{t-\vartheta_{\sigma}(t)}^{t}g_{\sigma}(e(s))\,{\rm d}s+E_{\sigma}z(t)\vphantom{\int\limits_{-\infty}^{t}}\right]\hbox{d}t\\&\quad+h_{\sigma}(t,e(t), e(t-\tau_{\sigma}(t)))\,{\rm d}\omega(t),\\ {\rm LTM}: \hbox{d}z(t)& =[-\Upxi_{\sigma} z(t)+\Upupsilon_{\sigma}g_{\sigma}(e(t))]\,{\rm d}t. \end{aligned} \right. $$
(42)

Similarly, we get the following error system when \(t\in[t_{i},t_{i+1})\) for \(i=0,1,2,\ldots,k, \) and the lth subsystem is activated:

$$ \left\{\begin{array}{l} \begin{aligned} {\rm STM}:\hbox{d}e(t)& =\left[\vphantom{\int\limits_{-\infty}^{t}}-(C_{l}+K_{l,1})e(t)-K_{l,2}e(t-\tau_{l}(t))\right.\\& \quad+ A_{l}g_{l}(e(t))+ B_{l}g_{l}(e(t-\tau_{l}(t)))\\& \quad\left.-D_{l}\int\limits_{t-\vartheta_{l}(t)}^{t}g_{l}(e(s))\,\hbox{d}s+E_{l}z(t)\vphantom{\int\limits_{-\infty}^{t}}\right]\hbox{d}t\\& \quad+h_{l}(t,e(t),e(t-\tau_{l}(t))) \,{\rm d}\omega(t),\\ {\rm LTM}:\hbox{d}z(t)& =[-\xi_{l} z(t)+\upsilon_{l} g_{l}(e(t))]\,{\rm d}t. \end{aligned} \end{array} \right. $$
(43)

For simplicity, we also denote

$$ \begin{aligned} G_{l}(t)&=-(C_{l}+K_{l,1})e(t)-K_{l,2}e(t-\tau_{l}(t)) + A_{l}g_{l}(e(t))+B_{l} g_{l}(e(t-\tau_{l}(t)))\\ &\quad -D_{l}\int\limits_{t-\vartheta_{l}(t)}^{t}g_{l}(e(s))\,{\rm d}s+E_{l}z(t),\\ \end{aligned} $$
(44)
$$ h_{l}(t)=h_{l}(t,e(t),e(t-\tau_{l}(t))). $$
(45)

Then system (43) can be rewritten as

$$ \left\{\begin{array}{l} {\rm STM}: \hbox{d}e(t)=G_{l}(t)\hbox{d}t +h_{l}(t)\,{\rm d}\omega(t),\\ {\rm LTM}: \hbox{d}z(t)=[-\Upxi_{l} z(t)+\Upupsilon_{l} g_{l}(e(t))]\,{\rm d}t. \end{array} \right. $$
(46)

Theorem 2

Suppose that the assumptions \((\mathrm{H}_{1}), (\mathrm{H}_{3})\), and \((\mathrm{H}_{4})\) hold, σ is a switching signal with average dwell time T a . The trivial solution of error system (42) is exponentially stable in mean square, if, for a given scalar a, there exist symmetric positive-definite matrices R l,i , i = 1, 2, P l,j , j = 1, 2, 3, 4, Q l,k , k = 1, 2, 3, positive-definite diagonal matrices \(\Upphi_{l}, \Uppsi_{l}, \) matrices N l,i , S l,i , M l,i , Y l,i , i = 1, 2, , an invertible matrix O l , positive scalars ρ l and θ, for each \(l\in\mathcal{M}\) such that the following LMIs hold,

$$ \left(\begin{array}{cc} \Uppi_{l}&\Updelta_{l}\\ \ast& -\Upomega_{l} \end{array}\right)<0, $$
(47)
$$ R_{l,i}\leq\theta R_{\tilde{l},i},\quad P_{l,j}\leq\theta P_{\tilde{l},j},\quad Q_{l,k}\leq\theta Q_{\tilde{l},k}, \quad \forall l,\tilde{l}\in{\mathcal{M}}, \\ $$
(48)
$$ a-\frac{1}{T_{a}}\ln \theta>0, $$
(49)
$$ R_{l,1}\leq\rho_{l}I, $$
(50)

further more, the convergence rate can be estimated as \(a-\frac{1}{T_{a}}\ln \theta, \) where \(\Updelta_{l}=(H_{l,21}S_{l},H_{l,20}N_{l},H_{l,21}M_{l},H_{l}\widehat{O}_{l} D_{l}), S_{l}^{T}=(S^{T}_{l,1},0,S^{T}_{l,2},0,0,0,0,0), M_{l}^{T}=(M^{T}_{l,1},0,M^{T}_{l,2},0,0,0,0,0), N_{l}^{T}=(N^{T}_{l,1},0,N^{T}_{l,2},0,0,0,0,0), \widehat{O}_{l}^{T}=(O^{T}_{l},0,0,0,0,O^{T}_{l},0,0), H_{l,21}=\frac{e^{a\tau_{l,2}}-e^{a\tau_{l,1}}}{a}, H_{l,20}=\frac{e^{a\tau_{l,2}}-1}{a}, \overline{H}_{l}=\frac{e^{a \vartheta}-1}{a}, \tau_{l,21}=\tau_{l,2}-\tau_{l,1}, \overline{F}_{l}={\rm diag}(F^{1}_{l}f^{1}_{l},F^{2}_{l}f^{2}_{l},\ldots,F^{n}_{l}f^{n}_{l}), \overline{f}_{l}={\rm diag}(\frac{1}{2}(F^{1}_{l}+f^{1}_{l}),\frac{1}{2}(F^{2}_{l}+f^{2}_{l}),\ldots,\frac{1}{2}(F^{n}_{l}+f^{n}_{l})),\)

$$ \begin{aligned} \Uppi_{l}&=\left( \begin{array}{cccccccc}\Uppi_{l,1} & O_{l}E_{l}&\Uppi_{l,2}&M_{l,1}&-S_{l,1}&\Uppi_{l,3}&O_{l}A_{l}+\overline{f}_{l}\phi_{l}&O_{l}B_{l}\\\ast&\Uppi_{l,4}&0&0&0&E_{l}^{T}O_{l}^{T}&R_{l,2}\Upupsilon_{l}&0\\\ast&\ast&\Uppi_{l,5}&M_{l,2}&-S_{l,2}&0&0&\overline{f}_{l}\psi_{l}\\\ast&\ast&\ast&-e^{-a\tau_{l,1}}P_{l,3}&0&0&0&0\\\ast&\ast&\ast&\ast&-e^{-a\tau_{l,2}}P_{l,4}&0&0&0\\\ast&\ast&\ast&\ast&\ast&\Uppi_{l,6}&O_{l}A_{l}&O_{l}B_{l}\\\ast&\ast&\ast&\ast&\ast&\ast&\Uppi_{l,7}&0\\\ast&\ast&\ast&\ast&\ast&\ast&\ast&\Uppi_{l,8}\end{array}\right),\\\Uppi_{l,1}&=\rho_{l}J_{l,1}+aR_{l,1}+P_{l,1}+P_{l,3}+P_{l,4}+N_{l,1}+N_{l,1}^{T}-\overline{F}_{l}\phi_{l}-O_{l}C_{l}-C_{l}O_{l}^{T}-Y_{l,1}-Y_{l,1}^{T},\\\Uppi_{l,2}&=-N_{l,1}+N_{l,2}^{T}+S_{l,1}-M_{l,1}-Y_{l,2},\quad\Uppi_{l,3}=R_{l,1}-O_{l}-C_{l}O_{l}^{T}-Y_{l,1}^{T},\\\Uppi_{l,4}&=-R_{l,2}\Upxi_{l}-\Upxi_{l}R_{l,2}+aR_{l,2},\quad\Uppi_{l,6}=\tau_{l,2}Q_{l,1}+\tau_{l,21}Q_{l,2}-O_{l}-O_{l}^{T},\\\Uppi_{l,5}&=\rho_{l}J_{l,2}-\overline{F}_{l}\psi_{l}-(1-\mu_{l})e^{-a\tau_{l,2}}P_{l,1}-N_{l,2}-N_{l,2}^{T}+S_{l,2}+S_{l,2}^{T}-M_{l,2}-M_{l,2}^{T},\\\Uppi_{l,7}&=-\phi_{l}+P_{l,2}+\vartheta_{l}Q_{l,3},\quad\Uppi_{l,8}=-\psi_{l}-(1-\mu_{l})e^{-a\tau_{l,2}}P_{l,2},\\\Upomega_{l}&=\left( \begin{array}{cccc}H_{l,21}(Q_{l,1}+Q_{l,2})&0&0&0\\ 0&H_{l,20}Q_{l,1}&0&0\\ 0&0&Q_{l,2}&0\\0&0&0&\overline{H}_{l}Q_{l,3} \end{array}\right).\end{aligned} $$

Moreover, the estimation of the control gains is K l,i  = O −1 l Y l,i , i = 1, 2.

Proof

Consider another multiple Lyapunov-Krasovskii functional candidate as:

$$ \overline{V}(l,e(t))=\sum_{i=1}^{3}V_{i}(l,e(t))+\overline{V}_{4}(l,e(t)), $$

where V i (l, e(t)), i = 1, 2, 3, are defined as those in the proof of Theorem 1, while

$$ \overline{V}_{4}(l,e(t))=\int\limits_{-\vartheta}^{0}\int\limits_{t+\nu}^{t}g_{l}^{T}(e(s))e^{a(s-t)}Q_{l,3}g_{l}(e(s))\,{\rm d}s\,{\rm d}\nu $$

Calculating the time derivative of \(\overline{V}(l,e(t))\) along the trajectory of system (46) by using Itô’s differential formula derives that

$$ \,{\rm d}\overline{V}(l,e(t))=\sum_{i=1}^{3} {\mathcal{L}}V_{i}(l,e(t))\,{\rm d}t+{\mathcal{L}} \overline{V}_{4}(l,e(t))\,{\rm d}t+2e^{T}(t)R_{l,1}h_{l}(t) \,{\rm d}\omega(t), $$

where

$$ \begin{aligned} {\mathcal{L}}\overline{V}_{4}(l,e(t))& =\vartheta g_{l}^{T}(e(t))Q_{l,3} g_{l}(e(t))\\ &\quad -\int\limits_{-\vartheta}^{0}g_{l}^{T}(e(t+\nu))e^{a\nu}Q_{l,3} g_{l}(e(t+\nu))\,{\rm d}\nu\\ &\quad -a\overline{V}_{4}(l,e(t))\\ & \leq\vartheta_{l}g_{l}^{T}(e(t))Q_{l,3}g_{l}(e(t))\\ &\quad -\int\limits_{t-\vartheta_{l}(t)}^{t}g_{l}^{T}(e(s))e^{a(s-t)} Q_{l,3}g_{l}(e(s))\,{\rm d}s\\ &\quad -a\overline{V}_{4}(l,e(t)). \end{aligned} $$

From Newton-Leibniz formulation and (44), one has

$$ 2[e^{T}(t)+G_{l}^{T}(t)]O_{l}[-(C_{l}+K_{l,1})e(t)-K_{l,2}e(t-\tau_{l}(t))+ A_{l}g_{l}(e(t)) +B_{l} g_{l}(e(t-\tau_{l}(t)))-D_{l}\int\limits_{t-\vartheta_{l}(t)}^{t}k_{l}(t-s)g_{l}(e(s))\,{\rm d}s+E_{l}z(t)-G_{l}(t)]=0. $$

Similar to (31), it is obvious that

$$ \begin{aligned}& -\int\limits_{t-\vartheta_{l}(t)}^{t}g_{l}^{T}(e(s))e^{a(s-t)}Q_{l,3}g_{l}(e(s))\,\text{d}s\\& \qquad-2\xi_{l}^{T}\widehat{O}_{l}D_{l}\int\limits_{t-\vartheta_{l}(t)}^{t}g_{l}(e(s))\,\text{d}s\\& \quad=-\int\limits_{t-\vartheta_{l}(t)}^{t}\widetilde{O}_{l}^{T}\left(e^{a(s-t)}Q_{l,3}\right)^{-1}\widetilde{O}_{l}\,\text{d}s \\& \qquad+\xi_{l}^{T}\widehat{O}_{l}D_{l}Q_{l,3}^{-1}D_{l}^{T}\widehat{O}_{l}^{T}\xi_{l}\int\limits_{t-\vartheta_{l}(t)}^{t}e^{-a(s-t)}\,\text{d}s\\& \quad\leq-\int\limits_{t-\vartheta_{l}(t)}^{t}\widetilde{O}_{l}^{T}\left(e^{a(s-t)}Q_{l,3}\right)^{-1}\widetilde{O}_{l}\,\text{d}s \\& \qquad+\overline{H}_{l}\xi_{l}^{T}\widehat{O}_{l}D_{l}Q_{l,3}^{-1}D_{l}^{T}\widehat{O}_{l}^{T}\xi_{l}. \end{aligned}$$

The other part of the proof is same as that in the proof of Theorem 1. This completes the proof. \(\square\)

Note that, for a given a > 0, sometimes the feasible solution obtained by using LMI toolbox in Matlab is not applicable in practice, for example, the magnitude of feedback gains \(K_{l,i},i=1,2, l\in\mathcal{M}\) may be too large to operation, the scalar θ may be very large such that the average dwell time T a is also large. From a point of view of the engineering application, magnitude of feedback gains \(K_{l,i},i=1,2, l\in\mathcal{M}\) should not be very large. From a point of view of the secure communication, if T a is too large, which means the system switched to one subsystem and stay for too long, it is possible for an intruder to recover the digital binary signal [30]. Therefore, it is necessary to impose restrictions on the magnitude of feedback gains K l,1, K l,2, and θ (or T a ). Since \(K_{l,i}=O^{-1}_{l}Y_{l,i},i=1,2, l\in\mathcal{M}, \) restricting the magnitude of feedback gains K l,i is equivalent to restricting the norms of O l −1 and Y l,i , i.e. [41]:

$$ \|O^{-1}_{l}\|<\delta_{l},\quad \|Y_{l,i}\|<\lambda_{l,i},\quad i=1,2, l\in{\mathcal{M}}, $$
(51)

where δ l , λ l,i are positive scalars. According to Lemma 1, (51) is equivalent to

$$ \left( \begin{array}{cc} -\delta_{l}O_{l}&I\\ I&-\delta_{l}O_{l}\\ \end{array}\right)<0,\quad A_{1}= \left( \begin{array}{cc} -\lambda_{l,i}I&Y_{l,i}^{T}\\ Y_{l,i}&-\lambda_{l,i}I \end{array} \right)<0,\quad i=1,2, l\in{\mathcal{M}}. $$
(52)

It is easy to see that if θ < ω, then \(\frac{\ln \theta}{a}<\frac{\ln \omega}{a}.\) From (16) to (49), we know T θ a  < T ω a , where T θ a and T ω a are minimum values of average dwell time corresponding to θ and ω, respectively.

Remark 1

If the following inequalities hold

$$ \lambda_{max}(R_{l,i})\leq\theta \lambda_{min}(R_{\tilde{l},i}),\quad \lambda_{max}(P_{l,j})\leq\theta \lambda_{min}(P_{\tilde{l},j}),\quad \lambda_{max}(Q_{l,k})\leq\theta \lambda_{min}(Q_{\tilde{l},k}), \quad \forall l,\tilde{l}\in{\mathcal{M}}. $$

then (15) and (48) hold. Hence, the θ in (15) and (48) can be replaced by

$$ \theta=\max\{\theta_{i},\hat{\theta}_{j}, \tilde{\theta}_{k},i=1,2,j=1,2,3,4,k=1,2,3\}, $$

where

$$ \begin{aligned}&\lambda^{i}_{max}=\max_{l\in{\mathcal{M}}}\{\lambda_{max}(R_{l,i})\},\quad\lambda^{i}_{min}=\min_{l\in{\mathcal{M}}}\{\lambda_{min}(R_{l,i})\},\hfill \\&\theta_{i}=\frac{\lambda^{i}_{max}}{\lambda^{i}_{min}},\quad i=1,2,\hfill \\&\hat{\lambda}^{j}_{max}=\max_{l\in{\mathcal{M}}}\{\lambda_{max}(P_{l,j})\},\quad\hat{\lambda}^{j}_{min}=\min_{l\in{\mathcal{M}}}\{\lambda_{min}(P_{l,j})\},\hfill \\&\hat{\theta}_{j}=\frac{\hat{\lambda}^{j}_{max}}{\hat{\lambda}^{j}_{min}},\quad j=1,2,3,4, \hfill \\&\tilde{\lambda}^{k}_{max}=\max_{l\in{\mathcal{M}}}\{\lambda_{max}(Q_{l,k})\},\quad\tilde{\lambda}^{k}_{min}=\min_{l\in{\mathcal{M}}}\{\lambda_{min}(Q_{l,k})\},\hfill \\&\tilde{\theta}_{k}=\frac{\tilde{\lambda}^{k}_{max}}{\tilde{\lambda}^{k}_{min}},\quad k=1,2,3. \end{aligned} $$

Remark 2

In this paper, the upper bound of the derivative of time-varying delays μσ is not necessarily less than 1. Both of the lower and upper bounds of the time-varying delays are considered in the delay-dependent LMIs, which are less conservative than those (see [26, 27, 42]) only include upper bounds of the time-varying delays when the delays are interval ones. Moreover, the main results of [42] are special case of our Theorem 1 when m = 1 and S(t) = 0. Furthermore, if τσ(t) is non-derivable, then by letting P l,1 = P l,2 = 0, Theorem 1 and Theorem 2 still hold.

Remark 3

When m = 1, the models of this paper become competitive neural networks with time-varying delays and distributed delays, and the results of this paper are also new. When replace c i x i (t) by α i (x i ), and assume \((\mathrm{H}1)\) in [20] holds, our results still hold when some changes are made accordingly. In addition, assumption \((\mathrm{H}_{3}),\) which was first proposed in [40], is weaker than the assumptions \((\mathrm{H}2)\) and \((\mathrm{H}2^{*})\) in [20]. Furthermore, the conditions \((\mathrm{H}3)\) and \((\mathrm{H}3^{*})\) in [20] that the time-varying delay is differentiable are necessary, however, as pointed out in Remark 2, these conditions can be removed from our results. It is worth mentioning that, in this paper, the distributed delays are also considered and the LMIs are related to lower and upper bounds of the time-varying delays. Hence, our model is more general and the synchronization criteria are less conservative than those in [20]. Summarizing the above analysis, results of this paper extend and improve those in [20].

Remark 4

If θ = 1, then \(R_{l,i}= R_{i},i=1,2,P_{l,j}=P_{j},j=1,2,3,4,Q_{l,k}=Q_{k},k=1,2,3, \forall l\in\mathcal{M}.\) Hence, there is one common Lyapunov-Krasovskii functional for (13) or (46), which implies that the global exponential synchronization between SSCNNs (5) and (6) or (40) and (41) can be achieved under arbitrary switching.

Remark 5

When m = 1 and S(t) = 0, (5), and (40) turn out to general stochastic neural networks with time-varying and distributed delays. Our LMI conditions are also applicable to exponential synchronization of stochastic neural networks with unbounded or bounded distributed delays. In [25–28], synchronization of neural networks with mixed delays was investigated by LMI approach, and the following lemma is indispensable:

Lemma

[43]. For any constant matrix \({D\in \mathbb{R}^{n\times n}, D^{T}=D>0,}\) scalar τ > 0 and vector function \({\omega:[t-\tau,t]\rightarrow\mathbb{R}^{n},}\) one has

$$ \sigma\int\limits_{0}^{\sigma}\omega^{T}(s)D\omega(s) \,{\rm d}s\geq\left(\int\limits_{0}^{\sigma}\omega(s) \,{\rm d}s\right)^{T}D\int\limits_{0}^{\sigma}\omega(s)\,{\rm d}s $$

provided that the integrals are all well defined, where T denotes transpose and D > 0 denotes that D is positive definite matrix.

One can see that the above lemma does not necessarily hold when \(\sigma\rightarrow\infty.\) Therefore, results of this paper can not be derived by simply extending results in [25–28] by replacing bounded distributed delays with unbounded distributed delays. On the other hand, in addition to time-varying and unbounded distributed delays, one can consider impulsive effects and get exponential synchronization criteria in terms of LMIs, which is also less conservative than algebraic criteria in [2]. Hence, results of this paper extend and improve those in [25–28] and [2].

Remark 6

In this paper, exponential synchronization of SSCNNs with time-varying delays, unbounded or bounded distributed delays are studied, two theorems are obtained formulated by LMIs. Moreover, several lemmas can be easily obtained from our results. For example, (1) from Remark 1 to Remark 5, one can gets some useful lemmas by taking some special parameters; (2) if a = 0,θ = 1 in Theorems 1 and 2, then globally asymptotic synchronization between SSCNNs (5) and (6) or (40) and (41) can be achieved under arbitrary switching, respectively. To the best of our knowledge, similar problem is seldom considered in the literature. Therefore, to some extent, the results of this paper are new.

4 A numerical example

In this section, we provide one example with its simulations to show that our theoretical results obtained above are effective and practical.

Consider the switched competitive neural networks with two switched subsystems as follows:

$$ \left\{ \begin{array}{l} \begin{aligned} {\rm STM}: \dot{x}(t)&=-C_{\sigma}x(t) +A_{\sigma} f_{\sigma}(x(t))+B_{\sigma} f_{\sigma} (x(t-\tau_{\sigma}(t)))\\ &\quad-D_{\sigma}\int\limits_{-5}^{t}k_{\sigma}(t-s)f_{\sigma}(x(s)) \,{\rm d}s+E_{\sigma}S(t),\\ {\rm LTM}: \dot{S}(t)&=-\Upxi_{\sigma}S(t)+\Upupsilon_{\sigma} f_{\sigma}(x(t)), \end{aligned} \end{array}\right. $$
(53)

where \(x(t)=(x_{1}(t),x_{2}(t))^{T}, S(t)=(S_{1}(t),S_{2}(t))^{T}, \sigma:[0,+\infty)\rightarrow\mathcal{M}=\{1,2\}, k_{1}(\nu)=k_{2}(\nu)=e^{-2\nu}, f_{1}(x)=f_{2}(x)=(\tanh(x_{1}),\tanh(x_{2}))^{T}, \tau_{1}(t)=\tau_{2}(t)=1.5-|\sin t|,\)

$$ \begin{aligned} {\rm subsystem}&\quad 1 \left\{ \begin{array}{l} C_{1}=\left(\begin{array}{cc} 1.2&0\\ 0&1 \end{array} \right), A_{1}= \left( \begin{array}{cc} 3&-3\\ 8&5\\ \end{array} \right), B_{1}=\left( \begin{array}{cc} -1.4&0.1\\ 0.3&-8 \end{array} \right),D_{1}=\left( \begin{array}{cc} 1.2&0.1\\ 2&2 \end{array}\right),\\ E_{1}=\left( \begin{array}{cc} 0.5&0\\ 0&1.5 \end{array} \right),\Upxi_{1}=\left( \begin{array}{cc} 1&0\\ 0&1.5 \end{array} \right), \Upupsilon_{1}=\left( \begin{array}{cc} 0.5&0\\ 0&0.3 \end{array} \right), \end{array}\right.\\ {\rm subsystem}&\quad 2\left\{ \begin{array}{l} C_{2}=\left(\begin{array}{cc} 1&0\\ 0&1 \end{array} \right), A_{2}=\left( \begin{array}{cc} 3&-3\\ 3.5&5 \end{array} \right), B_{2}=\left( \begin{array}{cc} -1.4&-0.1\\ 0.3&-4 \end{array} \right),D_{2}=\left( \begin{array}{cc} 1.2&-0.5\\ -1&2 \end{array} \right),\\ E_{2}=\left( \begin{array}{cc} 0.5&0\\ 0&1.3 \end{array} \right),\Upxi_{2}=\left( \begin{array}{cc} 1.5&0\\ 0&1.5 \end{array} \right), \Upupsilon_{2}=\left( \begin{array}{cc} 0.5&0\\ 0&0.3 \end{array} \right). \end{array} \right. \end{aligned} $$

In the case that initial values are chosen as \(x(t)=(5,2)^{T}, S(t)=(1.5,0.5)^{T}, \forall t\in[5, 0],\) and x(t) = 0, S(t) = 0 for t < −5, chaotic-like trajectories of subsystems 1 and 2 are depicted in Figs. 1 and 2, respectively.

Fig. 1
figure 1

Phase trajectories x(t) and S(t) of subsystem 1

Full size image
Fig. 2
figure 2

Phase trajectories x(t) and S(t) of subsystem 2

Full size image

Let system (53) be the driver network and design the response SSCNNs with the same two switched subsystems as

$$ \left\{\begin{array}{l} \begin{aligned} {\rm STM}:\hbox{d}y(t)& =\left[\vphantom{\int\limits_{-5}^{t}}-C_{\sigma}y(t)+A_{\sigma}f_{\sigma}(y(t))+B_{\sigma} f_{\sigma}(y(t-\tau_{\sigma}(t)))\right.\\& \quad-D_{\sigma}\int\limits_{-5}^{t}k_{\sigma}(t-s)f_{\sigma}(y(s))\,{\rm d}s\\& \quad\left. +E_{\sigma}R(t)+U_{\sigma}\vphantom{\int\limits_{-5}^{t}}\right]\hbox{d}t\\& \quad+h_{\sigma}(t,e(t),e(t-\tau_{\sigma}(t)))\,{\rm d}\omega(t),\\ {\rm LTM}:\hbox{d}R(t)& =[-\Upxi_{\sigma} R(t)+\Upupsilon_{\sigma}f_{\sigma}(y(t))]\,{\rm d}t, \end{aligned} \end{array}\right. $$
(54)

where e(t) = y(t) − x(t), z(t) = R(t) − S(t), 

$$ h_{\sigma}(t,e(t),e(t-\tau_{\sigma}(t)))=0.5\left( \begin{array}{cc} e_{1}(t)0\\ 0&e_{2}(t) \end{array}\right) +0.5\left( \begin{array}{cc} e_{1}(t-\tau_{\sigma}(t))&0\\ 0&e_{2}(t-\tau_{\sigma}(t)) \end{array}\right). $$

It is easily to see \(\tau_{l,1}=0.5, \tau_{l,2}=1.5, \tau_{l,21}=1, \varsigma_{l}=0.5, J_{l,i}={\rm diag}(0.5,0.5), f^{i}_{l}=0, F^{i}_{l}=1, i,l=1,2.\)

It is obvious that τ1(t) and τ2(t) are interval and non-derivable, \(\overline{F}_{l}=0, \overline{f}_{l}={\rm diag}(0.5,0.5), l=1,2. \) Given a = 0.5, we have H l,21 = 1.6659, H l,20 = 2.2340, H l  = 0.6667. By letting P l,1 = P l,2 = 0, l = 1, 2, and solving LMIs (14), (15), (17) by using the Matlab LMI toolbox, we get the following feasible solutions

$$ \begin{aligned}& R_{1,1}=\left( \begin{array}{cc}860.5318&-0.5529\\ -0.5529&895.6303 \end{array} \right),R_{1,2}=\left( \begin{array}{cc} 187.4976&6.6653\\6.6653&162.4821 \end{array} \right),\\& P_{1,3}=\left(\begin{array}{cc} 200.9815&0.4022\\ 0.4022&173.8762\end{array}\right), P_{1,4}=\left( \begin{array}{cc}223.5511&0.4221\\ 0.4221&191.0878 \end{array}\right),\\& Q_{1,1}=\left( \begin{array}{cc} 6.1066&-0.3539\\-0.3539&1.2111\end{array} \right),Q_{1,2}=\left(\begin{array}{cc} 6.1860&-0.3568\\ -0.3568&1.2513\end{array} \right), \hfill \\& Q_{1,3}=\left( \begin{array}{cc}224.7438&31.4419\\ 31.4419&160.8311 \end{array} \right),\\& O_{1}=\left( \begin{array}{cc} 16.8087&-0.6138\\-0.6138&2.6952\end{array} \right),Y_{1,1}=\left(\begin{array}{cc} 874.0922&10.5085\\ 10.5085&900.7125\end{array} \right), \hfill \\& Y_{1,2}=\left( \begin{array}{cc}512.4160&0.3382\\ 0.3382&490.8519 \end{array} \right),\\& R_{2,1}=\left( \begin{array}{cc} 21.8414&-0.0022\\-0.0022&21.9478\end{array} \right), R_{2,2}=\left(\begin{array}{cc} 3.9417&0.0553\\ 0.0553&4.3805 \end{array}\right),\\& P_{2,3}=\left( \begin{array}{cc} 5.1576&0.0067\\0.0067&5.0747 \end{array}\right),P_{2,4}=\left(\begin{array}{cc} 5.6072&-0.0011\\ -0.0011&5.5143\end{array}\right),\\& Q_{2,1}=\left( \begin{array}{cc} 0.1752&0.0342\\0.0342&0.0692 \end{array} \right),Q_{2,2}=\left(\begin{array}{cc} 0.1793&0.0361\\ 0.0361&0.0676 \end{array}\right), \hfill \\& Q_{2,3}=\left( \begin{array}{cc}4.9956&0.5147\\ 0.5147&4.7656 \end{array} \right),\\& O_{2}=\left( \begin{array}{cc} 0.3489&0.0567\\ 0.0567&0.1541\end{array} \right),Y_{2,1}=\left( \begin{array}{cc}22.2930&0.0732\\ 0.0732&22.2804 \end{array} \right), \hfill\\& Y_{2,2}=\left( \begin{array}{cc} 12.7930&0.1741\\0.1741&12.6815 \end{array} \right), \end{aligned} $$

θ = 7.5514. Therefore, the average dwell time should satisfies \(T_{a}>\frac{\ln7.5514}{0.5}=4.0435,\) and the feedback gains are

$$ \begin{aligned} K_{1,1}&=\left( \begin{array}{cc} 52.582012.9366\\ 15.8741&337.1340 \end{array} \right), K_{1,2}=\left( \begin{array}{cc} 30.7454&6.7266\\ 7.1275&183.6508 \end{array} \right)\\ K_{2,1}&=\left( \begin{array}{cc} 67.8665&-24.7466\\ -24.4790&153.6421 \end{array} \right), K_{2,2}= \left(\begin{array}{cc} 38.7977&-13.6816\\ -13.1362&87.3013 \end{array}\right) \end{aligned} $$

The largest norm of control gains is 337.8669, and the average dwell time should satisfies T a  > 4.0435. They seem to be large to implement in practice. Hence, we can impose restrictions on feedback gains K i,j , i, j = 1, 2 and θ to get ideal feasible solutions. Letting P l,1 = P l,2 = 0, l = 1, 2, and solving LMIs (14), (15), (17), and (52) with δ1 = δ2 = λ1,1 = λ1,2 = λ2,1 = λ2,2 = 20 and θ < ω = 2.5, by using the Matlab LMI toolbox, we get the following ideal feasible solutions

$$ \begin{aligned} R_{1,1}&=\left( \begin{array}{cc} 9.3442&-0.3089\\ -0.3089&9.4606 \end{array} \right), R_{1,2}=\left( \begin{array}{cc} 6.4123&0.5667\\ 0.5667&22.7185 \end{array}\right),\\ P_{1,3}&=\left( \begin{array}{cc} 0.9066&-0.0446\\ -0.0446&0.7358 \end{array} \right), P_{1,4}=\left( \begin{array}{cc} 0.8988&-0.0435\\ -0.0435&0.7325 \end{array} \right),\\ Q_{1,1}&=\left( \begin{array}{cc} 0.0844&-0.0036\\ -0.0036&0.0410 \end{array} \right),Q_{1,2}=\left( \begin{array}{cc} 0.0872&-0.0034\\ -0.0034&0.0460 \end{array} \right), \hfill \\ Q_{1,3}=\left( \begin{array}{cc} 3.5597&0.4873\\ 0.4873&2.1763 \end{array} \right),\\ O_{1}&=\left( \begin{array}{cc} 0.3557&-0.0026\\ -0.0026&0.1129 \end{array}\right),Y_{1,1}=\left( \begin{array}{cc} 9.5691&0.0878\\ 0.0878&9.6528 \end{array} \right), \hfill \\ Y_{1,2}=\left( \begin{array}{cc} 6.4450&0.0112\\ 0.0112&6.4718 \end{array} \right),\\ R_{2,1}&=\left( \begin{array}{cc} 9.2648&-0.2696\\ -0.2696&9.1310 \end{array} \right), R_{2,2}=\left( \begin{array}{cc} 10.8471&1.7716\\ 1.7716&31.1135 \end{array} \right),\\ P_{2,3}&=\left( \begin{array}{cc} 0.94880.0763\\ 0.0763&0.9342 \end{array} \right),P_{2,4}= \left(\begin{array}{cc} 0.9420&0.0724\\ 0.0724&0.9294 \end{array}\right),\\ Q_{2,1}&=\left( \begin{array}{cc} 0.11990.0259\\ 0.0259&0.0761 \end{array} \right),Q_{2,2}=\left( \begin{array}{cc} 0.1269&0.0240\\ 0.0240&0.0870 \end{array} \right), \hfill \\ Q_{2,3}=\left( \begin{array}{cc} 2.8961&-0.0456\\ -0.0456&3.0642 \end{array}\right),\\ O_{2}&=\left( \begin{array}{cc} 0.38780.1055\\ 0.1055&0.2091 \end{array} \right),Y_{2,1}=\left( \begin{array}{cc} 9.5680&0.0061\\ 0.0061&9.6016 \end{array} \right), \hfill \\ Y_{2,2}=\left( \begin{array}{cc} 6.4412&-0.0166\\ -0.0166&6.4252 \end{array} \right), \end{aligned} $$

θ = 2.4231. Therefore, the average dwell time only needs to meet the \(T_{a}>\frac{\ln2.4231}{0.5}=1.7701, \) and the feedback gains are

$$ K_{1,1}=\left( \begin{array}{cc} 26.912&20.8743\\ 1.3998&85.5373\\ \end{array} \right), K_{1,2}=\left( \begin{array}{cc} 18.1228&0.4522\\ 0.5182&57.3462 \end{array} \right), $$
(55)
$$ K_{2,1}=\left( \begin{array}{cc} 28.5814&-14.4500\\ -14.3837&53.1991\\ \end{array} \right), K_{2,2}=\left(\begin{array}{cc} 19.2724&-9.7314\\ -9.7979&35.6310 \end{array} \right). $$
(56)

The largest norm of control gains is 85.56, which is much smaller than 337.1340.

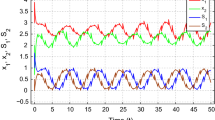
Let T a  = 2, (55) and (56) are control gains of subsystem 1 and 2, respectively, the subsystem 1 is activated at t = 0. By virtue of Theorem 1, (53) and (54) can be exponentially synchronized with the estimated exponential synchronization rate index \(0.5-\frac{\ln 2.4231}{2}=0.0575. \) The initial conditions of the numerical simulations are taken as: \(x(t)=(5,2)^{T}, S(t)=(1.5,0.5)^{T}, y(t)=(-2,-1)^{T}, R(t)=(-2.5,-5)^{T}, \forall t\in[5, 0].\) Figure 3 shows the phase trajectory of response system (54). Figure 4 presents state trajectories of the error system between (53) and (54).

Fig. 3
figure 3

Phase trajectories of y(t) and R(t) for the response system (54)

Full size image
Fig. 4
figure 4

State trajectories of the error system between (53) and (54)

Full size image

5 Conclusions

In this paper, exponential synchronization of SSCNNs with both interval time-varying delays and distributed delays is studied. Especially, the distributed delays can be unbounded. Multi-dimensional Brownian motion stochastic perturbation is included. New multiple Lyapunov-Krasovkii functionals are designed to get new sufficient conditions guaranteeing the exponential synchronization. The derived conditions are expressed in terms of LMIs, which are less conservative than algebraic results and easy to be solved by using Matlab LMI toolbox. Some useful lemmas can be easily deduced from the new results, and some existing results are extended and improved. Moreover, some restrictions are imposed on control gains and average dwell time such that obtained feasible solutions are applicable in practice. Finally, numerical simulations show the effectiveness of the theoretical results.