1 Introduction

In recent years, functionally graded material (FGM) [1,2,3,4] has received widespread attention in various engineering fields due to their high strength, excellent toughness and lightweight properties. The vibration of stationary plate-shell structures manifests as standing waves, and scholars have conducted extensive research on the wave propagation properties [5,6,7]. Considering Coriolis force induced by rotation, vibrations of rotating shells are in the form of traveling wave [8,9,10,11,12]. Conical shells are widely used in various engineering fields due to their easy processing and good mechanical load-bearing capacity. Rotating shells exhibit more complex dynamic behaviors in working conditions. Undesirable vibrations not only reduce the performance of the structure but also affect its integrity and reliability. Therefore, it is of practical importance to investigate the traveling wave vibration control of rotating FGM conical shells.

Vibration control of conical shell has attracted the attention of many scholars. Active vibration control is currently the preferred and effective method for vibration suppression. Feedback control is achieved by leveraging the characteristics of smart materials such as piezoelectric and magnetostrictive materials [13, 14]. Li et al. [15] studied the active control of axial, lateral and transverse vibrations of conical shells with clamped-free boundary using distributed piezoelectric actuators. Li et al. [16] investigated the active control of forced vibration of conical shells using negative velocity feedback, while also examining the optimal placement of actuator segments. Sun et al. [17] proposed an independent modal fuzzy sliding mode controller to suppress the vibration of conical shells. Jamshidi and Jafari [18, 19] explored the impact of geometric parameters on the modal actuator force under three different piezoelectric element layouts. Magnetostrictive actuators were used to control the vibration of simply supported conical shells by Mohammadrezazadeh and Jafari [20]. By comparing the controlled and uncontrolled free and forced vibration responses of conical shells with four different piezoelectric plate layouts, Jamshidi and Jafari [21] evaluated the vibration control effect of conical shells with distributed piezoelectric sensors/actuator patches. With the widespread application of composite materials, some scholars turned their research interests to the vibration control of composite conical shells. Shah and Ray [22] studied the vibration and acoustic active control of laminate composite truncated conical shells. Hajmohammad et al. [23] explored the intelligent control of sandwich truncated conical shells. Moghaddam and Ahmadi [24] studied the active vibration control of FGM truncated conical shells using piezoelectric smart materials. Hao et al. [25] investigated the active damping control of truncated conical shells made of porous metal foam.

The aforementioned research primarily focuses on stationary conical shells. With the increasing emphasis on the reliability of key components in rotating machinery, the study of the dynamics and control of high-speed rotating conical shells has become a recent hotspot. The study on the traveling wave vibration of rotating conical shell [26,27,28,29,30] reveals that the Coriolis force induces natural frequency of rotating conical shell bifurcation, resulting in the generation of forward and backward traveling waves. This distinctive vibration behavior, different from that of stationary conical shells, has prompted scholars to study the vibration control of rotating conical shells. Kumar and Ray [31] investigated the active vibration control of a laminated composite conical shell rotating at a specific speed using an active constraint layer damping treatment. Mohammadrezazadeh and Jafari [32] utilized magnetostrictive plates as actuators to control the vibration of rotating laminated composite conical shells under simply supported boundaries. Niasar et al. [33] optimized the position of FGM piezoelectric sensors and actuators to improve the vibration behavior of rotating simply supported FGM conical shells. Only a single mode was considered in the corresponding calculations.

To sum up, there are relatively fewer investigations on the vibration control of rotating conical shells, compared to stationary shells. From these studies, the following shortcomings can be identified. First, the electromechanical coupling model used for vibration control is specific to certain boundary conditions, such as simply supported-simply supported and clamped-free, and the model applicable to arbitrary boundary conditions should be developed. Second, the controllers designed in previous studies mainly focus on individual modes, and few articles consider multiple vibration modes. In addition, a specific rotational speed is considered during the controller design in previous investigations, indicating the need for further research to assess its applicability over a range of speeds.

In light of the mentioned shortcomings in previous studies, this paper addresses the traveling wave vibration control of rotating functionally graded material (FGM) conical shells via piezoelectric actuator and sensor pairs. The main contributions of this paper are as follows: (1) An electromechanical coupling model for rotating FGM conical shells, covered with surface-bonded piezoelectric sensors/actuators, is established considering circumferential initial stresses and Coriolis forces induced by rotation, as well as arbitrary boundary conditions. (2) An LQR (linear–quadratic regulator) controller is designed for traveling wave vibration control of rotating FGM conical shells over a range of speeds, considering the participation of multi-vibration modes in the dynamic responses. (3) Free and forced vibrations of rotating FGM conical shells with different rotational speeds, material compositions and excitation positions are shown to evaluate the performance of the controller. (4) The optimization of piezoelectric patch layout is carried out by analyzing the performance of the controller for rotating FGM conical shells with typical piezoelectric sensors/actuators distributions.

2 Theoretical formulation

2.1 Model description

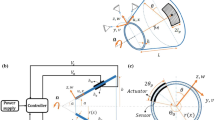
As shown in Fig. 1, the FGM conical shell with four sets of piezoelectric sensors and actuators attached to the shell’s inner and outer surfaces rotates around the symmetry axis at an angular velocity \(\Omega\). In the figure, α is the semi-vertex angle, L is the meridional length, r is the radius, h is the thickness of the conical shell. An orthogonal curvilinear coordinate system (x, \(\theta\), z) is fixed on the middle surface of the conical shell, and the displacements are denoted by u, v and w in meridional (x), circumferential (\(\theta\)) and radial (z) directions, respectively. Five sets of continuously uniformly distributed artificial springs are introduced at the boundary of the conical shell to simulate different boundary conditions, including three sets of translational springs ku, kv, kw, and two sets of rotational springs kx, kθ. In the figure, the black dashed lines at the boundaries of the conical shell represent uniformly distributed artificial springs. By adjusting the spring stiffness, it is possible to simulate various boundary conditions.

Fig. 1
figure 1

Rotating FGM conical shell with piezoelectric sensors/actuators and elastic constraints

Full size image

The FGM conical shell is composed of ceramics and metals, and the material properties vary along the thickness direction. According to the power-law function, the volume fractions of different material components can be expressed as can be written as follows [1]:

$$V_{{{\text{c1}}}} = \left( {\frac{2z + h}{{2h}}} \right)^{p} ,\;V_{{{\text{c2}}}} = 1 - \left( {\frac{2z + h}{{2h}}} \right)^{p} ,$$
(1)

where p is the volume fraction index, and the subscripts “c1” and “c2” represent metal and ceramic materials, respectively. The effective material properties P (z) of FGM at specific temperatures, such as Young’s modulus, density and Poisson’s ration, can be expressed as:

$$P\left( z \right) = \left( {P_{{{\text{c1}}}} - P_{{{\text{c2}}}} } \right)V_{{{\text{c1}}}} + P_{{{\text{c2}}}} {.}$$
(2)

According to the above equation, the Young’s modulus E, density \(\rho\) and Poisson's ratio \(\mu\) of FGM conical shell are written as:

$$\begin{gathered} E\left( z \right) = E_{{{\text{c2}}}} + \left( {E_{{{\text{c1}}}} - E_{{{\text{c2}}}} } \right)\left( {\frac{2z + h}{h}} \right)^{p} ,\;\; \hfill \\ \mu \left( z \right) = \mu_{{{\text{c2}}}} + \left( {\mu_{{{\text{c1}}}} - \mu_{{{\text{c2}}}} } \right)\left( {\frac{2z + h}{h}} \right)^{p} , \hfill \\ \rho \left( z \right) = \rho_{{{\text{c2}}}} + \left( {\rho_{{{\text{c1}}}} - \rho_{{{\text{c2}}}} } \right)\left( {\frac{2z + h}{h}} \right)^{p} . \hfill \\ \end{gathered}$$
(3)

2.2 Energy functions of rotating conical shell

According to the first-order shear deformation shell theory, the conical shell’s displacement fields can be written as [25]

$$\left\{ {\begin{array}{*{20}l} {u\left( {x,\theta ,z,t} \right) = u_{0} \left( {x,\theta ,t} \right) + z\phi_{x} \left( {x,\theta ,t} \right)} \hfill \\ {v\left( {x,\theta ,z,t} \right) = v_{0} \left( {x,\theta ,t} \right) + z\phi_{\theta } \left( {x,\theta ,t} \right)} \hfill \\ {w\left( {x,\theta ,z,t} \right) = w_{0} \left( {x,\theta ,t} \right)} \hfill \\ \end{array} } \right.,$$
(4)

where u0, v0 and w0 are, respectively, the displacements of the points on the middle surface in x, θ and z directions. \(\phi_{x}\) and \(\phi_{\theta }\) are, respectively, rotations of the transverse normal about θ and x axes.

The kinetic energy of the rotating FGM conical shell is given by

$$T_{c} = \frac{1}{2}\int_{0}^{2\pi } {\int_{0}^{L} {\int_{{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {\rho (z)\left[ {\left( {\dot{u} - \Omega v\sin \alpha } \right)^{2} + \left( {\dot{w} - \Omega v\cos \alpha } \right)^{2} + \left( {\dot{v} + \Omega u\sin \alpha + \Omega w\cos \alpha } \right)^{2} } \right]r(x){\text{d}}z{\text{d}}x{\text{d}}\theta } } } ,$$
(5)

where \(r(x) = r + x\sin \alpha\).

The stress–strain relationship of the rotating FGM conical shell is

$$\left\{ \begin{gathered} \sigma_{x} \hfill \\ \sigma_{\theta } \hfill \\ \tau_{x\theta } \hfill \\ \tau_{xz} \hfill \\ \tau_{\theta z} \hfill \\ \end{gathered} \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{12} } & {Q_{22} } & 0 & 0 & 0 \\ 0 & 0 & {Q_{66} } & 0 & 0 \\ 0 & 0 & 0 & {Q_{55} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{44} } \\ \end{array} } \right]\left\{ \begin{gathered} \varepsilon_{x} \hfill \\ \varepsilon_{\theta } \hfill \\ \gamma_{x\theta } \hfill \\ \gamma_{xz} \hfill \\ \gamma_{\theta z} \hfill \\ \end{gathered} \right\},$$
(6)

in which

$$Q_{11} { = }\frac{{E_{11} (z)}}{{1 - \mu_{12} \mu_{21} }},\;Q_{22} { = }\frac{{E_{22} (z)}}{{1 - \mu_{12} \mu_{21} }},\;Q_{12} { = }\frac{{\mu_{21} E_{11} (z)}}{{1 - \mu_{12} \mu_{21} }},\;Q_{44} = G_{23} ,\;Q_{55} = G_{13} ,\;Q_{66} = G_{12} ,$$
(7)

Here, G23, G13, G12 are the shear moduli of material.

The strain components at an arbitrary point of the FGM conical shell are given by

$$\left\{ \begin{gathered} \varepsilon_{x} \hfill \\ \varepsilon_{\theta } \hfill \\ \gamma_{x\theta } \hfill \\ \gamma_{xz} \hfill \\ \gamma_{\theta z} \hfill \\ \end{gathered} \right\} = \left\{ \begin{gathered} \varepsilon_{x,0} \hfill \\ \varepsilon_{\theta ,0} \hfill \\ \gamma_{x\theta ,0} \hfill \\ \gamma_{xz,0} \hfill \\ \gamma_{\theta z,0} \hfill \\ \end{gathered} \right\} + z\left\{ \begin{gathered} \kappa_{x} \hfill \\ \kappa_{\theta } \hfill \\ \kappa_{x\theta } \hfill \\ \kappa_{xz} \hfill \\ \kappa_{\theta z} \hfill \\ \end{gathered} \right\}$$
(8)

where \(\left\{ {\begin{array}{*{20}c} {\varepsilon_{x,0} } & {\varepsilon_{\theta ,0} } & {\gamma_{x\theta ,0} } & {\gamma_{xz,0} } & {\gamma_{\theta z,0} } \\ \end{array} } \right\}^{{\text{T}}}\) and \(\left\{ {\begin{array}{*{20}c} {\kappa_{x} } & {\kappa_{\theta } } & {\kappa_{x\theta } } & {\kappa_{xz} } & {\kappa_{\theta z} } \\ \end{array} } \right\}^{{\text{T}}}\) are the strain components and curvature components of the middle surface, respectively. According to the geometric deformation relationship, they are expressed as

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{x,0} } \\ {\varepsilon_{\theta ,0} } \\ {\gamma_{x\theta ,0} } \\ {\gamma_{xz,0} } \\ {\gamma_{\theta z,0} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial u_{0} }}{\partial x}} \\ {\frac{1}{r(x)}\frac{{\partial v_{0} }}{\partial \theta } + \frac{{w_{0} \cos \alpha }}{r(x)} + \frac{{u_{0} \sin \alpha }}{r(x)}} \\ {\frac{{\partial v_{0} }}{\partial x} + \frac{1}{r(x)}\frac{{\partial u_{0} }}{\partial \theta } - \frac{{v_{0} \sin \alpha }}{r(x)}} \\ {\varphi_{x} + \frac{{\partial w_{0} }}{\partial x}} \\ {\varphi_{\theta } + \frac{1}{r(x)}\frac{{\partial w_{0} }}{\partial \theta } - \frac{{v_{0} \cos \alpha }}{r(x)}} \\ \end{array} } \right\},\;\left\{ {\begin{array}{*{20}c} {\kappa_{x} } \\ {\kappa_{\theta } } \\ {\kappa_{x\theta } } \\ {\kappa_{xz} } \\ {\kappa_{\theta z} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\frac{{\partial \phi_{x} }}{\partial x}} \\ {\frac{1}{r(x)}\frac{{\partial \phi_{\theta } }}{\partial \theta } + \frac{{\phi_{x} \sin \alpha }}{r(x)}} \\ {\frac{1}{r(x)}\frac{{\partial \phi_{x} }}{\partial \theta } + \frac{{\partial \phi_{\theta } }}{\partial x} - \frac{{\phi_{\theta } \sin \alpha }}{r(x)}} \\ 0 \\ 0 \\ \end{array} } \right\}.$$
(9)

The elastic strain energy of the FGM conical shell is written as

$$U_{\varepsilon } = \frac{1}{2}\int_{0}^{2\pi } {\int_{0}^{L} {\int_{{ - {h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}}^{{{h \mathord{\left/ {\vphantom {h 2}} \right. \kern-0pt} 2}}} {\left[ {\sigma_{x} \varepsilon_{x} + \sigma_{\theta } \varepsilon_{\theta } + \tau_{x\theta } \gamma_{x\theta } + K_{x} \tau_{xz} \gamma_{xz} + K_{\theta } \tau_{\theta z} \gamma_{\theta z} } \right]r(x){\text{d}}z{\text{d}}x{\text{d}}\theta } } } ,$$
(10)

where Kx and Kθ are the shear correction factors and the typical value is 3/4 or 5/6.

The strain energy of the rotating FGM conical shell due to the initial hoop tension is given by

$$U_{r} = \frac{1}{2}\int_{0}^{L} {\int_{0}^{2\pi } {\int_{{ - \frac{h}{2}}}^{\frac{h}{2}} {\rho (z)\Omega^{2} } } } \left[ {\left( {\frac{\partial u}{{\partial \theta }} - v\sin \alpha } \right)^{2} + \left( {\frac{\partial v}{{\partial \theta }} + u\sin \alpha + w\cos \alpha } \right)^{2} + \left( {v\cos \alpha - \frac{\partial w}{{\partial \theta }}} \right)^{2} } \right]r(x){\text{d}}x{\text{d}}\theta .$$
(11)

The potential energy generated by the spring sets at the boundaries is obtained by

$$U_{s} = \frac{1}{2}\int_{0}^{2\pi } {r\left. {\left( {k_{u} u_{0}^{2} + k_{v} v_{0}^{2} + k_{w} w_{0}^{2} + k_{x} \phi_{x}^{2} + k_{\theta } \phi_{\theta }^{2} } \right)} \right|_{x = 0} + R\left. {\left( {k_{u} u_{0}^{2} + k_{v} v_{0}^{2} + k_{w} w_{0}^{2} + k_{x} \phi_{x}^{2} + k_{\theta } \phi_{\theta }^{2} } \right)} \right|_{x = L} } {\text{d}}\theta .$$
(12)

Generally, the value of ku, kv, kw, kx and kθ can be determined through experiments. For classical boundary conditions, the corresponding values are listed in Table 1.

Table 1 Values of spring stiffness under three classical boundary conditions
Full size table

2.3 Energy functions of piezoelectric sensor/actuator pairs

Based on Loves’ shell theory, the displacement fields of piezoelectric sensors and actuators can be written as

$$\left\{ \begin{gathered} u^{\lambda } \left( {x,\theta ,z_{\lambda } ,t} \right) = u_{{0}}^{\lambda } \left( {x,\theta ,t} \right) - z_{\lambda } \frac{{\partial w_{{0}}^{\lambda } }}{\partial x} \hfill \\ v^{\lambda } \left( {x,\theta ,z_{\lambda } ,t} \right) = v_{{0}}^{\lambda } \left( {x,\theta ,t} \right) + \frac{{z_{\lambda } }}{{r_{\lambda } (x)}}\left( {v_{{0}}^{\lambda } \cos \alpha - \frac{{\partial w_{{0}}^{\lambda } }}{\partial \theta }} \right) \hfill \\ w^{\lambda } \left( {x,\theta ,z_{\lambda } ,t} \right) = w_{{0}}^{\lambda } \left( {x,\theta ,t} \right) \hfill \\ \end{gathered} \right..\;\left( {\lambda { = }a,\;s} \right)$$
(13)

where “a” and “s” represent actuators and sensors, respectively.

According to the deformation relationship shown in Fig. 2, the displacement continuity condition between the piezoelectric sensor/actuator and the conical shell is

$$\quad \left\{ {\begin{array}{*{20}l} {\left. {u\left( {x,\theta ,z,t} \right)} \right|_{z = - h/2} = \left. {u^{s} \left( {x,\theta ,z_{s} ,t} \right)} \right|_{{z_{s} = h_{s} /2}} } \hfill \\ {\left. {v\left( {x,\theta ,z,t} \right)} \right|_{z = - h/2} = \left. {v^{s} \left( {x,\theta ,z_{s} ,t} \right)} \right|_{{z_{s} = h_{s} /2}} } \hfill \\ {\left. {w\left( {x,\theta ,z,t} \right)} \right|_{z = - h/2} = \left. {w^{s} \left( {x,\theta ,z_{s} ,t} \right)} \right|_{{z_{s} = h_{s} /2}} } \hfill \\ \end{array} } \right.,\;\left\{ {\begin{array}{*{20}l} {\left. {u\left( {x,\theta ,z,t} \right)} \right|_{z = h/2} = \left. {u^{a} \left( {x,\theta ,z_{a} ,t} \right)} \right|_{{z_{a} = - h_{a} /2}} } \hfill \\ {\left. {v\left( {x,\theta ,z,t} \right)} \right|_{z = h/2} = \left. {v^{a} \left( {x,\theta ,z_{a} ,t} \right)} \right|_{{z_{a} = - h_{a} /2}} } \hfill \\ {\left. {w\left( {x,\theta ,z,t} \right)} \right|_{z = h/2} = \left. {w^{a} \left( {x,\theta ,z_{a} ,t} \right)} \right|_{{z_{a} = - h_{a} /2}} } \hfill \\ \end{array} } \right.,$$
(14)

where hs and ha, respectively, represent the thickness of the sensor and actuator.

Fig. 2
figure 2

Deformation relationship between piezoelectric patches and core

Full size image

Substituting expressions (4) and (13) into (14) yields

$$\left\{ {\begin{array}{*{20}l} {u_{0}^{s} \left( {x,\theta ,t} \right) = u_{0} \left( {x,\theta ,t} \right) - \frac{h}{2}\phi_{x} \left( {x,\theta ,t} \right) + \frac{{h_{s} }}{2}\frac{{\partial w_{0}^{{}} }}{\partial x}} \hfill \\ {v_{0}^{s} \left( {x,\theta ,t} \right) = v_{0} \left( {x,\theta ,t} \right) - \frac{h}{2}\phi_{\theta } \left( {x,\theta ,t} \right) + \frac{{h_{s} }}{{2r_{s} (x)}}\frac{{\partial w_{0}^{{}} }}{\partial \theta }} \hfill \\ {w_{0}^{s} \left( {x,\theta ,t} \right) = w_{0} \left( {x,\theta ,t} \right)} \hfill \\ \end{array} } \right.,\;\left\{ {\begin{array}{*{20}l} {u_{0}^{a} \left( {x,\theta ,t} \right) = u_{0} \left( {x,\theta ,t} \right) + \frac{h}{2}\phi_{x} \left( {x,\theta ,t} \right) - \frac{{h_{a} }}{2}\frac{{\partial w_{0}^{{}} }}{\partial x}} \hfill \\ {v_{0}^{a} \left( {x,\theta ,t} \right) = v_{0} \left( {x,\theta ,t} \right) + \frac{h}{2}\phi_{\theta } \left( {x,\theta ,t} \right) - \frac{{h_{a} }}{{2r_{a} (x)}}\frac{{\partial w_{0}^{{}} }}{\partial \theta }} \hfill \\ {w_{0}^{a} \left( {x,\theta ,t} \right) = w_{0} \left( {x,\theta ,t} \right)} \hfill \\ \end{array} } \right..$$
(15)

Assuming that piezoelectric material is isotropic, the constitutive equation of piezoelectric materials is expressed as [34]

$$\begin{gathered} {{\varvec{\upsigma}}}^{\lambda } = \left\{ {\begin{array}{*{20}c} {\sigma_{x}^{\lambda } } \\ {\sigma_{\theta }^{\lambda } } \\ {\tau_{x\theta }^{\lambda } } \\ \end{array} } \right\} = {\mathbf{Q}}^{\lambda } {{\varvec{\upvarepsilon}}}^{\lambda } - {\mathbf{e}}^{T} {\mathbf{\rm E}}^{\lambda } = \left[ {\begin{array}{*{20}c} {C_{11} } & {C_{12} } & 0 \\ {C_{12} } & {C_{22} } & 0 \\ 0 & 0 & {C_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{\lambda } } \\ {\varepsilon_{\theta }^{\lambda } } \\ {\gamma_{x\theta }^{\lambda } } \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ {e_{31} } & {e_{32} } & 0 \\ \end{array} } \right]^{T} \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ {{{V_{0} \left( t \right)} \mathord{\left/ {\vphantom {{V_{0} \left( t \right)} {h_{\lambda } }}} \right. \kern-0pt} {h_{\lambda } }}} \\ \end{array} } \right\}, \hfill \\ {\mathbf{D}}^{\lambda } = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ {D_{z} } \\ \end{array} } \right\} = \varepsilon \varepsilon^{\lambda } + {\mathbf{\Xi E}}^{\lambda } = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ {e_{31} } & {e_{32} } & 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\sigma_{x}^{\lambda } } \\ {\sigma_{\theta }^{\lambda } } \\ {\tau_{x\theta }^{\lambda } } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {\Xi_{11} } & {} & {} \\ {} & {\Xi_{22} } & {} \\ {} & {} & {\Xi_{33} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ {{{V_{0} \left( t \right)} \mathord{\left/ {\vphantom {{V_{0} \left( t \right)} {h_{\lambda } }}} \right. \kern-0pt} {h_{\lambda } }}} \\ \end{array} } \right\}. \hfill \\ \end{gathered}$$
(16)

where \({{\varvec{\upsigma}}}^{\lambda }\) and \({{\varvec{\upvarepsilon}}}^{\lambda }\), respectively, denote stress and strain vector, \({\mathbf{D}}^{\lambda }\) is the electric displacement vector, e is equivalent piezoelectric coefficient matrix, \({{\varvec{\Xi}}}\) is the equivalent dielectric coefficient matrix, \({\mathbf{E}}^{\lambda }\) is the electric field intensity vector where V0(t) is the external voltage, and \({\mathbf{Q}}^{\lambda }\) is the stiffness coefficient matrix where elastic stiffness coefficient can be substituted by

$$C_{11} { = }C_{22} = \frac{{E_{\lambda } }}{{1 - \mu_{\lambda }^{2} }},\;\;C_{12} { = }\frac{{\mu_{\lambda } E_{\lambda } }}{{1 - \mu_{\lambda }^{2} }},\;\;C_{66} { = }\frac{{E_{\lambda } }}{{2\left( {1 + \mu_{\lambda } } \right)}},$$
(17)

in which, \(E_{\lambda }\) and \(\mu_{\lambda }\) are the Young’s modulus and Poisson’s ratio of piezoelectric materials, respectively.

The strain components at arbitrary point of the piezoelectric sensor/actuator pairs are given by

$$\left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{\lambda } } \\ {\varepsilon_{\theta }^{\lambda } } \\ {\gamma_{x\theta }^{\lambda } } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{x,0}^{\lambda } } \\ {\varepsilon_{\theta ,0}^{\lambda } } \\ {\gamma_{x\theta ,0}^{\lambda } } \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {\kappa_{x,0}^{\lambda } } \\ {\kappa_{\theta ,0}^{\lambda } } \\ {\kappa_{x\theta ,0}^{\lambda } } \\ \end{array} } \right\}.$$
(18)

\(\left\{ {\begin{array}{*{20}c} {\varepsilon_{x,0}^{\lambda } } & {\varepsilon_{\theta ,0}^{\lambda } } & {\gamma_{x\theta ,0}^{\lambda } } \\ \end{array} } \right\}^{{\text{T}}}\) and \(\left\{ {\begin{array}{*{20}c} {\kappa_{x,0}^{\lambda } } & {\kappa_{\theta ,0}^{\lambda } } & {\kappa_{x\theta ,0}^{\lambda } } \\ \end{array} } \right\}^{{\text{T}}}\) are the strain components and curvature components, respectively, which are expressed as

$$\begin{gathered} \varepsilon_{x,0}^{\lambda } = \frac{{\partial u_{0}^{\lambda } }}{\partial x} \hfill \\ \varepsilon_{\theta ,0}^{\lambda } = \frac{1}{{r_{\lambda } (x)}}\frac{{\partial v_{0}^{\lambda } }}{\partial \theta } + \frac{\sin \alpha }{{r_{\lambda } (x)}}u_{0}^{\lambda } + \frac{\cos \alpha }{{r_{\lambda } (x)}}w_{0}^{\lambda } \hfill \\ \gamma_{x\theta ,0}^{\lambda } = \frac{{\partial v_{0}^{\lambda } }}{\partial x} + \frac{1}{{r_{\lambda } (x)}}\frac{{\partial u_{0}^{\lambda } }}{\partial \theta } - \frac{\sin \alpha }{{r_{\lambda } (x)}}v_{0}^{\lambda } \hfill \\ \kappa_{x,0}^{\lambda } = - \frac{{\partial^{2} w_{0}^{\lambda } }}{{\partial x^{2} }} \hfill \\ \kappa_{\theta ,0}^{\lambda } = - \frac{\sin \alpha }{{r_{\lambda } (x)}}\frac{{\partial w_{0}^{\lambda } }}{\partial x} - \frac{1}{{r_{\lambda }^{2} (x)}}\frac{{\partial^{2} w_{0}^{\lambda } }}{{\partial \theta^{2} }} + \frac{\cos \alpha }{{r_{\lambda }^{2} (x)}}\frac{{\partial v_{0}^{\lambda } }}{\partial \theta } \hfill \\ \kappa_{x\theta ,0}^{\lambda } = 2\left( {\frac{\sin \alpha }{{r_{\lambda }^{2} (x)}}\frac{{\partial w_{0}^{\lambda } }}{\partial \theta } - \frac{1}{{r_{\lambda } (x)}}\frac{{\partial^{2} w_{0}^{\lambda } }}{\partial x\partial \theta } + \frac{\cos \alpha }{{r_{\lambda } (x)}}\frac{{\partial v_{0}^{\lambda } }}{\partial x} - \frac{\sin \alpha \cos \alpha }{{r_{\lambda }^{2} (x)}}v_{0}^{\lambda } } \right), \hfill \\ \end{gathered}$$
(19)

The kinetic energy of the piezoelectric sensor/actuator pairs is expressed as

$$T_{\lambda } = \frac{1}{2}\sum\limits_{i = 1}^{np} {\int_{{V_{ai} }} {\rho_{a} \left[ {\left( {\dot{u}^{a} } \right)^{2} + \left( {\dot{v}^{a} } \right)^{2} + \left( {\dot{w}^{a} } \right)^{2} } \right]dV} } + \frac{1}{2}\sum\limits_{i = 1}^{np} {\int_{{V_{si} }} {\rho_{s} \left[ {\left( {\dot{u}^{s} } \right)^{2} + \left( {\dot{v}^{s} } \right)^{2} + \left( {\dot{w}^{s} } \right)^{2} } \right]{\text{d}}V} } ,$$
(20)

where np represents the number of piezoelectric sensor/actuator pairs.

The strain energy of the piezoelectric sensor/actuator pairs is given by

$$U_{\lambda } = \frac{1}{2}\sum\limits_{i = 1}^{np} {\int_{{V_{ai} + V_{si} }} {\left( {\varepsilon^{\lambda } } \right)^{{\text{T}}} {{\varvec{\upsigma}}}^{\lambda } {\text{d}}V} } - \frac{1}{2}\sum\limits_{i = 1}^{np} {\int_{{V_{ai} }} {\left( {{\mathbf{D}}^{\lambda } } \right)^{{\text{T}}} {\mathbf{E}}^{\lambda } {\text{d}}V} } .$$
(21)

2.4 The displacement field

It is assumed that the displacement functions of the rotating FGM conical shell are expressed as

$$\left\{ \begin{gathered} u_{0} \left( {x,\theta ,t} \right)\; = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 0}^{\infty } {\left[ {u_{c,mn}^{{}} \left( t \right)U_{c,m} \left( x \right)\cos n\theta + u_{s,mn}^{{}} \left( t \right)U_{s,m} \left( x \right)\sin n\theta } \right]} } \; = {\mathbf{U}}\left( {x,\theta } \right){\mathbf{q}}_{u} \left( t \right) \hfill \\ v_{0} \left( {x,\theta ,t} \right)\; = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 0}^{\infty } {\left[ {v_{c,mn}^{{}} \left( t \right)V_{c,m} \left( x \right)\cos n\theta + v_{s,mn}^{{}} \left( t \right)V_{s,m} \left( x \right)\sin n\theta } \right]} } \; = {\mathbf{V}}\left( {x,\theta } \right){\mathbf{q}}_{v} \left( t \right) \hfill \\ w_{0} \left( {x,\theta ,t} \right)\; = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 0}^{\infty } {\left[ {w_{c,mn}^{{}} \left( t \right)W_{c,m} \left( x \right)\cos n\theta + w_{s,mn}^{{}} \left( t \right)W_{s,m} \left( x \right)\sin n\theta } \right]} } \; = {\mathbf{W}}\left( {x,\theta } \right){\mathbf{q}}_{w} \left( t \right) \hfill \\ \phi_{x} \left( {x,\theta ,t} \right) = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 0}^{\infty } {\left[ {\varphi_{c,mn}^{{}} \left( t \right)\Phi_{c,m} \left( x \right)\cos n\theta + \varphi_{s,mn}^{{}} \left( t \right)\Phi_{s,m} \left( x \right)\sin n\theta } \right]} } \; = {{\varvec{\Phi}}}\left( {x,\theta } \right){\mathbf{q}}_{x} \left( t \right) \hfill \\ \phi_{\theta } \left( {x,\theta ,t} \right) = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 0}^{\infty } {\left[ {\psi_{c,mn}^{{}} \left( t \right)\Psi_{c,m} \left( x \right)\cos n\theta + \psi_{s,mn}^{{}} \left( t \right)\Psi_{s,m} \left( x \right)\sin n\theta } \right]} } \; = {{\varvec{\Psi}}}\left( {x,\theta } \right){\mathbf{q}}_{\theta } \left( t \right) \hfill \\ \end{gathered} \right.,$$
(22)

where m and n are half axial wave numbers and circumferential wave numbers in x and θ directions, respectively. qu(t), qv(t), qw(t), qx(t) and qθ(t) are the generalized coordinates that are unknown functions of time t. U(x, θ), V(x, θ), W(x, θ), \({\varvec{\Phi}}\)(x, θ) and \({\varvec{\Psi}}\)(x, θ) are the vibration mode functions of the rotating conical shell, which can be obtained by the Rayleigh–Ritz method [11, 27].

2.5 Governing equations

Assuming that external excitation is a concentrated force in the radial direction, the virtual work done by the external force is expressed as

$$W = \left. {F_{0} \cos (\omega_{{\text{d}}} t)w(x,\theta ,t)} \right|_{{x = x_{0} ,\;\theta = \theta_{0} }} ,$$
(23)

where F0 is the amplitude of the concentrated force,\(\omega_{d}\) is the excitation frequency and (x0, θ0) denotes the excitation position on the shell.

The governing equations of the rotating FGM conical shells with piezoelectric sensor/actuator pairs can be derived using Lagrange equations,

$$({\mathbf{M}}_{c} + {\mathbf{M}}_{a} + {\mathbf{M}}_{s} ){{\ddot{q}}}(t) + \left( {{\mathbf{G}} + {\mathbf{C}}} \right){\dot{\mathbf{q}}}(t) + \left( {{\mathbf{K}}_{\varepsilon } + {\mathbf{K}}_{r} + {\mathbf{K}}_{a} + {\mathbf{K}}_{s} } \right){\mathbf{q}}(t) + {\mathbf{K}}_{e} {\mathbf{V}}_{a} (t) = {\mathbf{F}}(t).$$
(24)

Here \({\mathbf{q}}(t) = \left\{ {\begin{array}{*{20}c} {{\mathbf{q}}_{u} (t)^{{\text{T}}} ,} & {{\mathbf{q}}_{u} (t)^{{\text{T}}} ,} & {{\mathbf{q}}_{u} (t)^{{\text{T}}} ,} & {{\mathbf{q}}_{u} (t)^{{\text{T}}} ,} & {{\mathbf{q}}_{u} (t)^{{\text{T}}} } \\ \end{array} } \right\}^{{\text{T}}}\) is the generalized coordinate vector, Mc, G, C, \({\mathbf{K}}_{\varepsilon }\) and Kr are the mass matrix, gyroscopic matrix, damping matrix, initial stress stiffness matrix and centrifugal stiffness matrix of the rotating FGM conical shell, respectively. Ma and Ka are the mass and stiffness matrix of the piezoelectric actuator, respectively. Ms and Ks are the mass and stiffness matrix of the piezoelectric sensor. Ke is the electromechanical coupling matrix and Va(t) is the external voltage vector. F(t) is the force vector. Here, proportional damping is considered, and the damping matrix C is derived from

$${\mathbf{P}}^{{\text{T}}} {\mathbf{CP}} = \left[ {\begin{array}{*{20}c} {2\xi_{1} \omega_{1} } & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & {2\xi_{N} \omega_{N} } \\ \end{array} } \right]$$
(25)

where \(\omega_{j}\)(j = 1, 2, …, N) is natural frequency, \(\xi_{j}\)(j = 1, 2, …, N) is the corresponding modal damping ratios of each generalized coordinate and N is the number of generalized coordinates considered. P is the modal matrix. The expressions for the other matrix mentioned above are provided in the Appendix.

3 Control loop design

According to the positive piezoelectric effect of piezoelectric materials, piezoelectric sensors can deform under external forces, causing changes in charge. The value of charge generated by the ith piezoelectric sensor can be expressed as [34]

$$Q_{si} (t) = \int_{{A_{si} }} {D_{z} {\text{d}}A} = \int_{{A_{si} }} {e_{31} \varepsilon_{xx} + e_{32} \varepsilon_{\theta \theta } {\text{d}}A} = {\hat{\mathbf{\Gamma }}}_{si} {\mathbf{q}}(t),$$
(26)

where Asi is the surface area of the ith sensor. The induced voltage Vsi(t) of the ith sensor can be expressed by:

$$V_{i}^{s} (t) = \frac{{h_{p} }}{{\Xi_{33i} A_{si} }}Q_{si} (t) = \frac{{h_{p} }}{{\Xi_{33i} A_{si} }}\hat{\user2{\Gamma }}_{si} {\mathbf{q}}(t) ={\varvec{\Gamma}}_{si} {\mathbf{q}}(t)$$
(27)

The sensor voltage generated by the entire control system can be written as

$${\mathbf{V}}_{s} (t) = {{\varvec{\Gamma}}}_{s} {\mathbf{q}}(t).$$
(28)

The LQR method is used to design the controller. Based on the equation of motion (27), the standard state-space model used for controller design and numerical simulation can be expressed as:

$$\begin{gathered} {\dot{\mathbf{Z}}} = {\mathbf{AZ}} + {\mathbf{B}}_{v} {\mathbf{U}} + {\mathbf{B}}_{f} {\mathbf{F}}, \hfill \\ {\mathbf{Y}} = {\mathbf{CZ}} \hfill \\ \end{gathered}$$
(29)

where

$$\begin{gathered} {\mathbf{Z}} = \left\{ {\begin{array}{*{20}c} {{\mathbf{q}}^{{\text{T}}} } & {{\dot{\mathbf{q}}}^{{\text{T}}} } \\ \end{array} } \right\}^{{\text{T}}} ,\;{\mathbf{C}} = \left[ {\begin{array}{*{20}c} {{{\varvec{\Gamma}}}_{s} } & {\mathbf{0}} \\ \end{array} } \right],\;{\mathbf{U}} = {\mathbf{V}}_{a} , \hfill \\ {\mathbf{A}} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{I}} \\ { - ({\mathbf{M}}_{c} + {\mathbf{M}}_{a} + {\mathbf{M}}_{s} )^{ - 1} ({\mathbf{K}}_{\varepsilon } + {\mathbf{K}}_{r} + {\mathbf{K}}_{a} + {\mathbf{K}}_{s} )} & { - ({\mathbf{M}}_{c} + {\mathbf{M}}_{a} + {\mathbf{M}}_{s} )^{ - 1} ({\mathbf{G}} + {\mathbf{C}})} \\ \end{array} } \right], \hfill \\ {\mathbf{B}}_{v} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} \\ { - ({\mathbf{M}}_{c} + {\mathbf{M}}_{a} + {\mathbf{M}}_{s} )^{ - 1} {\mathbf{K}}_{e} } \\ \end{array} } \right], \hfill \\ {\mathbf{B}}_{f} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} \\ {({\mathbf{M}}_{c} + {\mathbf{M}}_{a} + {\mathbf{M}}_{s} )^{ - 1} } \\ \end{array} } \right]. \hfill \\ \end{gathered}$$
(30)

In Eq., Z is the state variable, Y is the sensor output, A is the state matrix, Bv and Bf are the control matrix and disturbance matrix, respectively. The optimal input U of the system satisfies the objective minimum cost function, which is written as

$$J = \int_{0}^{\infty } {\left[ {{\mathbf{Z}}^{{\text{T}}} {\mathbf{QZ}} + {\mathbf{U}}^{{\text{T}}} {\mathbf{RU}}} \right]} {\text{d}}t,$$
(31)

where Q is the state weight matrix and R is the control weight matrix. The voltage can be calculated by the following equation

$${\mathbf{U}} = - {\mathbf{G}}_{l} {\mathbf{Z}},$$
(32)

where Gl is the feedback control gain matrix, which is written as:

$${\mathbf{G}}_{l} = {\mathbf{R}}^{ - 1} {\mathbf{B}}^{{\text{T}}} {\mathbf{H}},$$
(33)

in which H is calculated from algebraic Riccati equation:

$${\mathbf{HA + A}}^{{\text{T}}} {\mathbf{H - HBR}}^{ - 1} {\mathbf{B}}^{{\text{T}}} {\mathbf{H + Q}} = {\mathbf{0}}.$$
(34)

4 Numerical results and discussions

4.1 Model validation

To assess the validity of the present solution procedure, comparison studies are carried out. Firstly, the natural frequencies of non-rotating FGM cylindrical shell under simply supported boundary conditions are calculated and compared with the results form Loy et al. [1]. As shown in Table 2, the current results exhibit slight differences from the data reported previously, which is attributable to differences in shell theory. Next, the comparative verification is conducted on the frequencies of rotating conical shell under clamped–clamped boundary conditions. As shown in Table 3, the calculated results of the forward and backward wave frequencies of a rotating conical shell are compared with those reported by Afshari [26]. It is apparent to discover that the current calculation results are almost consistent with the compared literature data. These comparisons listed in Tables 2 and 3 indicate that the theoretical formulation and numerical calculation in the paper are correct.

Table 2 Comparison of the natural frequencies (Hz) for non-rotating FGM cylindrical shell \((\alpha = 0^{ \circ } ,\;m = 1,\;{h \mathord{\left/ {\vphantom {h r}} \right. \kern-0pt} r} = 0.05,\;{L \mathord{\left/ {\vphantom {L r}} \right. \kern-0pt} r} = 20)\)
Full size table
Table 3 Comparison of the natural frequencies (Hz) for rotating FGM conical shell \((\alpha = 20^{ \circ } ,\;r = 0.5,\;{h \mathord{\left/ {\vphantom {h r}} \right. \kern-0pt} r} = 0.1,\;{L \mathord{\left/ {\vphantom {L r}} \right. \kern-0pt} r} = 4,\;\Omega = 79.6\;{{\text{rps}}}\)
Full size table

4.2 Vibration analysis

The FGM conical shell is composed of Ti–6Al–4V and ZrO2, and the relevant material parameters are listed as follows:

$$\begin{gathered} E_{c1} = 105.749{\text{Gpa}},\;\rho_{c1} = 4420{\text{kg/m}}^{{3}} ,\;\mu_{c1} = 0.2984, \hfill \\ E_{c2} = 116.380{\text{Gpa}},\;\rho_{c2} = 3657{\text{kg/m}}^{{3}} ,\;\mu_{c2} = 0.3330. \hfill \\ \end{gathered}$$
(35)

The geometric parameters of the conical shell are: α = 30°, h = 0.01m, L = 0.45m, r = 0.2m. The modal damping ratios \(\xi_{j}\) are assumed to be 0.001. Unless otherwise specified, the volume fraction index and angular velocities of the FGM conical shell are p = 1 and \(\Omega = 50{\text{rps}}\), respectively. The material of the piezoelectric sensor and actuator is PZT-G1195N, and the physical parameters are shown in Table 4. The layout of piezoelectric pairs is shown in Fig. 1, with four groups of piezoelectric pairs uniformly distributed in the circumferential direction, and each piezoelectric pair has a circumferential coverage angle of 45° and an axial coverage length of L. The amplitude of the concentrated force F0 is 2000N. Taking the clamped conical shell at both ends as an example, the traveling wave vibration control of a rotating FGM conical shell is investigated in this section.

Table 4 Geometric and material parameters of the piezoelectric pairs
Full size table

Figure 3 displays the Campbell diagram and mode shapes of the rotating FGM conical shell. As shown in the figure, with the increase in rotational speed, the natural frequency of vibration mode with specific (n, m) combinations bifurcates, and backward and forward wave frequencies appear due to the effects of centrifugal and Coriolis effects. The natural frequency of backward wave is higher than that of forward wave at each rotational speed. The study primarily focuses on the control effect of FGM conical shells having angular velocity within the range 0–100 rps. Within the research scope, the fundamental frequency of the conical shell is 916 Hz and six sets of vibration modes can be observed. The corresponding mode shapes are shown in Fig. 3. The above analysis lays the foundation for subsequent research.

Fig. 3
figure 3

Campbell diagram and mode shapes of rotating FGM conical shell

Full size image

The modal convergence of the rotating FGM conical shell is investigated utilizing the mode superposition method in Fig. 4. As shown in the figure, the amplitude–frequency characteristic curves of forced vibration and the displacement time–history curves of free vibration are considered for four different values of m and n. Whether for forced vibration or free vibration, the vibration response curves of conical shells are almost superposed in three cases except for n = 1–7, m = 1–3. Consequently, traveling vibration modes with m = 1–3 and n = 1–8 are considered in the following calculation.

Fig. 4
figure 4

Convergence analysis of dynamic responses considering different number of vibration modes (x0 = L/2, θ0 = 0) a free vibration responses; b forced vibration responses

Full size image

Figure 5 presents the traveling wave vibration control effect of rotating FGM conical shells under different values of Q/R. As shown in the figure, the amplitude–frequency characteristic curves and the corresponding maximum voltage for the rotating conical shell are provided for three different values of Q/R. Clearly, the LQR controller effectively suppresses the traveling wave vibration of the rotating FGM conical shell. It is noteworthy that there are significant differences in the control effectiveness and maximum control voltage under different gains. As the value of Q/R increases, the vibration suppression effect becomes more pronounced, but the provided voltage also increases accordingly. Therefore, considering Fig. 5a, b comprehensively, Q/R = 100 is chosen to ensure both significant control effect and reasonable control voltage.

Fig. 5
figure 5

Effect of weighting ratio Q/R on the forced vibration responses (x0 = L/2, θ0 = 0) a forced vibration response; b maximum voltage of actuators required

Full size image

In Fig. 6, the control effect of free vibration of rotating conical shells is depicted under the selected value of Q/R mentioned above. The displacement time–history curve of controlled and uncontrolled free vibration is described in Fig. 6a. It can be observed that, compared to the uncontrolled free vibration response of the conical shell, the controlled free vibration exhibits a significantly reduced amplitude and the vibration response converges quickly. Figure 6b displays the maximum voltage of four actuators required. Notably, the maximum control voltage is less than 300 V each until the free vibration is controlled. These conclusions prove the rationality of the current value of Q/R, which can be used for subsequent calculations and discussions.

Fig. 6
figure 6

Free vibration responses with and without control (x0 = L/2, θ0 = 0) a free vibration responses; b maximum voltage of actuators required

Full size image

The vibration suppression effects of free and forced vibration under different volume fraction indices and rotational speeds are shown in Figs. 7 and 8, respectively. Figure 7 displays the displacement time–history curves of free vibration and amplitude–frequency characteristic curves of forced vibration under the two conditions of p = 5 and p = 10. The comparison results indicate the current control method still produces good control efficiency under different volume fraction indices. As shown in Fig. 8, the control efficiency of forced and free vibration of rotating conical shells at two different speeds, namely 80rps and 100rps, is considered. By describing the vibration response at different speeds, it is demonstrated that the current control method can effectively suppress vibration over a range of rotational speeds and there is no significant difference in the control efficiency at each speed under the selected value of Q/R above.

Fig. 7
figure 7

Control efficiency of the free and forced vibration responses for different volume fraction indices (x0 = L/2, θ0 = 0)

Full size image
Fig. 8
figure 8

Control efficiency of the free and forced vibration responses for rotating FGM conical shells with different rotational speeds (x0 = L/2, θ0 = 0)

Full size image

Figure 9 demonstrates the control effects of free vibration and forced vibration at various positions in the meridian direction. In Fig. 9, the two positions (L/3, 0) and (L/6, 0) are mainly selected. According to the controlled and uncontrolled displacement time–history curves and amplitude–frequency characteristic curves in Fig. 9, it can be concluded that the current control method effectively controls the free vibration and forced vibration of the conical shell at different positions. Additionally, changes in the positions of the action and measurement points in the meridional direction have a noticeable impact on the dynamic behavior of the conical shell. Specifically, when these points are closer to the boundary, the amplitude of the conical shell is reduced.

Fig. 9
figure 9

Control efficiency of the free and forced vibration responses for rotating FGM conical shells at different positions in the meridional direction

Full size image

Figure 10 shows five classic layouts of piezoelectric sensors/actuators. The effect of piezoelectric patch layout on the control effectiveness of traveling wave vibration is investigated. As shown in Fig. 10, the circumferential coverage angle for each piezoelectric patch remains constant in the first three layouts, and four, eight and twelve piezoelectric patches are used in Cases 1, Case 2 and Case 3, respectively. For the last two layouts, the meridional coverage length of each piezoelectric patch is consistent, and Case 4 and Case 5 use eight and twelve piezoelectric patches, respectively. It is worth noting that the optimization of piezoelectric layout studied in this article is conducted for the typical layouts proposed. Piezoelectric sensors and actuators for all these five cases have the same location and total area of piezoelectric patches.

Fig. 10
figure 10

Five cases of layouts of piezoelectric patches

Full size image

The control efficiency of rotating FGM conical shells under the five types of piezoelectric distribution mentioned above is discussed. Figures 11 and 12, respectively, explore the effects of variations in the number of meridional and circumferential piezoelectric patches on control efficiency. As shown in Fig. 11, the control effectiveness of Case1 consistently surpasses that of Case2 and Case3, and the control effect of Case2 shows only a slight improvement compared to that of Case3. Therefore, fewer piezoelectric patches arranged in the meridional direction can yield more effective vibration control. Figure 12 shows that Case 1, Case 4 and Case 5 exhibit various advantages and disadvantages in different frequency ranges. Figure 13 illustrates the uncontrolled and controlled forced vibration response with the same number of piezoelectric sensors/actuators in different layouts. It is found that the vibration suppression effect in Case 4 is superior to Case 2, suggesting that arranging more piezoelectric patches in the circumferential direction yields better control effectiveness than placing more piezoelectric patches in the meridional direction when the number of piezoelectric patches remains constant.

Fig. 11
figure 11

Control efficiency of the forced vibration responses for shells with different numbers of piezoelectric patches arranged in meridional direction (x0 = L/2, θ0 = 0)

Full size image
Fig. 12
figure 12

Control efficiency of the forced vibration responses for shells with different numbers of piezoelectric patches arranged in circumferential direction (x0 = L/2, θ0 = 0)

Full size image
Fig. 13
figure 13

Control efficiency of the forced vibration responses for shells with different meridional and circumferential layouts of piezoelectric patches (x0 = L/2, θ0 = 0)

Full size image

5 Conclusion

The paper conducts traveling wave vibration control of rotating FGM shells using piezoelectric sensors and actuators. Considering circumferential initial stresses and Coriolis forces induced by rotation, as well as arbitrary boundary conditions, the electromechanically coupled governing equations of the rotating FGM conical shell with piezoelectric patches are established. To suppress vibrations of rotating FGM conical shells within a certain rotational speed range, an LQR controller is designed and the effectiveness of the controller is evaluated by the dynamic response. Furthermore, the optimization of piezoelectric patch layout is carried out by analyzing the performance of the controller for rotating FGM conical shells with typical piezoelectric sensors/actuators distributions.

The main findings are summarized as follows: (1) The electromechanical coupling equations established in this paper are applicable to the traveling wave vibration analysis and control of rotating FGM conical shells under arbitrary boundary conditions. (2) The LQR controller is highly effective in suppressing the traveling wave vibrations of rotating FGM conical shells over a speed range. (3) As long as the Q/R ratio is well-optimized, variations in rotational speed, material composition and excitation force position are not significantly impact the control effectiveness. (4) The arrangement of piezoelectric patches plays a crucial role in influencing the efficiency of active control. Specifically, with the total area and position of the piezoelectric patches held constant, a higher control efficiency is achieved with fewer patches in meridional direction.