1 Introduction

Since they were invented by Iijima in 1991, carbon nanotubes (CNTs) have become a potential nanostructured material owing to their distinct mechanical and thermal properties and good electrical conductivity. Studies of their mechanical response have attracted the attention of many scientists [1,2,3,4]. Functionally graded carbon-nanotube-reinforced (CNTR) composite (FG-CNTRC) materials provide new advantages for composite materials. In FG-CNTRC, CNTs are designed to grade with specific rules along with desired directions within an isotropic matrix to enhance the mechanical properties of the structures. The addition of CNTs improves the mechanical, electrical, and thermal properties of the structures. In addition, the integration of laminated composites with piezoelectric materials provides structures with superior mechanical properties of composite materials and the capability to sense and adapt their static and dynamic responses. It can control the shape, size, vibration, and stability of these structures because of their direct and converse piezoelectric effects.

In the past few years, many analytical and numerical methods have been proposed for analysing the mechanical behaviours of FG-CNTRC structures. Using the element-free improved moving least-squares (IMLS)-Ritz method, Zhang et al. investigated the nonlinear bending response [5,6,7,8], vibration response [9,10,11,12,13], and dynamic response [14, 15] of FG-CNTRC plates and shells. Using the first-order shear deformation theory (FSDT) and kp-Ritz method, Lei et al. presented static, large deflection, and free vibration analysis of laminated FG-CNT plates [16, 17]. Based on a refined simplified two-variable n-th-higher-order plate theory, Bouazza and Zenkour [18] presented an exact closed-form formulation for free vibration analysis of composite plates reinforced with single-walled CNTs. The mechanical analysis of bulk CNTR nanocomposites and FG-CNTRC structures can be found in a review by Liew et al. [19].

FG-CNTRC materials are often combined with smart materials, such as magnetostrictive materials, piezoelectric materials, electrostrictive materials, and shape memory alloys, to make intelligent structures.

The mechanical response of smart structures embedded with magnetostrictive layers has been discussed frequently [20,21,22,23,24]. Embedded piezoelectric actuators or sensors can be used to monitor the health of the structure and the structural integrity to adjust the shapes and focal points of space antennas and the contours of aircraft and spacecraft. In addition, the mechanical behaviours of FG-CNTRC structures integrated with piezoelectric patches or layers (PFG-CNTRC) have also been studied by several researchers. Using the three-dimensional theory of elasticity, Alibeigloo investigated the static vibration responses of PFG-CNTRC plates and cylindrical panels under mechanical uniform pressure, thermal load, and applied voltage field [25,26,27,28,29]. Rafiee et al. [30] analysed the nonlinear dynamic stability of PFG-CNTRC plates with initial geometric imperfections subjected to thermal and electrical loadings. Rafiee et al. [31] also investigated the large-amplitude free vibration of immovable simply supported PFG-CNTRC plates based on FSDT and von Kármán geometrical nonlinearity. Wu and Chang [32] investigated the 3D buckling problem of FG-CNTRC plates integrated with piezoelectric sensors and actuators. Mohsen Nasihatgozar et al. [33] investigated the effects of the volume fraction of CNTs, geometrical characteristics, and two axial and biaxial loading types on the buckling load of piezoelectric FG-CNTRC cylindrical panels based on the Donnell theory. Applying the Ritz energy approach, Ansari et al. [34] presented an analytical solution procedure for the nonlinear postbuckling analysis of PFG-CNTRC cylindrical shells subjected to combine electrothermal loading, axial compression, and lateral loads. Using Chebyshev polynomials in the Ritz method, Kiani [35] investigated the free vibration behaviour of FG-CNTRC plates with various mechanical and electrical boundary conditions. It was found that the natural frequency of a plate with a closed circuit is always lower than that of a plate with open-circuit boundary conditions. Kolahchi et al. [36] used the refined piezoelasticity zigzag theory and Hamilton's principle to discretise the governing equations for wave propagation in PFG-CNTRC plates. They found that the wave propagation of the system can be controlled effectively by the voltage applied to the actuator and the magnetic field exerted on the core. Setoodeh et al. [37] developed a model based on higher-order shear deformation theory and the differential quadrature method for the free vibration analysis of a PFG-CNTRC quadrilateral spherical panel. Using the formulation based on nonuniform rational B-spline basis functions, Nguyen-Quang et al. [38] proposed an extension of the isogeometric approach for the dynamic response of laminated PFG-CNTRC plates. Selim et al. [39] performed an impact analysis of PFG-CNTRC plates using the element-free IMLS-Ritz model with Reddy's higher-order shear deformation theory. By optimising the voltage distribution for the open-loop control and the displacement feedback control gain for the closed-loop control, Zhang et al. [40] presented an optimal shape control of FG-CNTRC plates with piezoelectric patches bonded at the top and bottom surfaces acting as actuators and sensors. Tran et al. [41, 42] developed a new four-variable shear deformation refined plate theory for the static and free vibration analysis of PFG-CNTRC plates.

There have been a limited number of studies regarding the active vibration control of FG-CNTRC structures with integrated piezoelectric actuators and sensors. Based on Reddy's higher-order shear deformation theory, Song et al. [43] presented the active vibration control of FG-CNTRC plates with surface-bonded piezoelectric actuators and sensors. Song et al. [44] also studied the active vibration control of an FG-CNTRC cylindrical shell with outer and inner surfaces with bonded piezoelectric patches acting as the actuator and sensor. Sharma et al. [45] implemented a finite-element model with a nonlinear fuzzy logic controller to perform active vibration control of FG-CNTRC plates. Zhang et al. [46] presented a solution based on Reddy’s third-order shear deformation theory for active flutter control of CNTRC cylindrical panels in supersonic airflow. Selim et al. [47] presented a novel element-free IMLS-Ritz model based on Reddy's higher-order shear deformation theory for the active vibration control of FG-CNTRC plates with two positions of piezoelectric sensor and actuator layers.

Reviewing the literature reveals that various computational methods have been used to investigate the dynamic characteristics of FG-CNTRC structures integrated with a piezoelectric layer; however, there is no work available on the free vibration behaviour and active vibration control of PFG-CNTRC spherical shell panels. Therefore, in this study, a finite-element model based on the four-variable shear deformation refined theory for active vibration control of an FG-CNTRC spherical panel with an integrated actuator and sensor was developed. The extended rule of the mixture was used to estimate the material properties of the CNT-reinforced composite panel, and the electric potential was assumed to be a linear function through the thickness of each piezoelectric layer. The domain was discretised by a four-node nonconforming rectangular element with eight mechanical and two electrical degrees of freedom per node. A feedback control algorithm was used to achieve the mechanism of active control of the panel, and the Newmark method was employed to calculate the dynamic response of the hybrid spherical shell panels. The influence of material and geometry parameters, type of load, and feedback control gains on the dynamic response of the hybrid spherical panel were also investigated and are discussed in detail.

2 Formulations

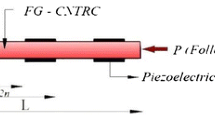
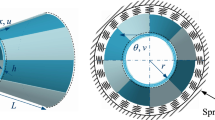
Figure 1 shows a smart piezoelectric spherical panel of a rectangular planform with constant principal radii of curvature R. The panel has three parts: the substrate, the piezoelectric layer at the top acting as an actuator, and the piezoelectric layer at the bottom acting as a sensor. The thickness of the substrate is h, and the thickness of each piezoelectric layer is \(h_{p}\). The panel is discretised into a mesh of an m × n four-node flat shell element (rectangular elements) using the surface equation of the spherical panel \(z = \frac{1}{2R}\left[ {\left( {x - \frac{a}{2}} \right)^{2} + \left( {y - \frac{a}{2}} \right)^{2} } \right]\).

Fig. 1
figure 1

Schematic of the smart piezoelectric FG-CNTRC spherical shell panel

Full size image

2.1 Effective material properties of FG-CNTRC layer

In this research, the laminated substrate of the panel was made of perfectly bonded FG-CNT layers.

As shown in Fig. 2, five types of distribution of CNTs—UD, FG-O, FG-A, FG-V, and FG-X—are considered using the rule of mixture [48, 49]. Thus, the effective material properties of CNTRC can be written as [50]

$$ E_{11} (z) = \eta_{1} V_{{{\text{CNT}}}} (z)E_{11}^{{{\text{CNT}}}} + V_{m} (z)E^{m} , $$
(1)
$$ \frac{{\eta_{2} }}{{E_{22} (z)}} = \frac{{V_{{{\text{CNT}}}} (z)}}{{E_{22}^{{{\text{CNT}}}} }} + \frac{{V_{m} (z)}}{{E^{m} }}, \, $$
(2)
$$ \frac{{\eta_{3} }}{{G_{12} (z)}} = \frac{{V_{{{\text{CNT}}}} (z)}}{{G_{12}^{{{\text{CNT}}}} }} + \frac{{V_{m} (z)}}{{G^{m} }}, $$
(3)
$$ \rho (z) = V_{{{\text{CNT}}}} (z)\rho^{{{\text{CNT}}}} + V_{m} (z)\rho^{m} , $$
(4)
$$ \nu_{12} = V_{{{\text{CNT}}}}^{*} \nu_{12}^{{{\text{CNT}}}} + V_{m} (z)\nu^{m} . $$
(5)
Fig. 2
figure 2

Types of CNT distribution

Full size image

where \(E_{11}^{{{\text{CNT}}}}\) and \(E_{22}^{{{\text{CNT}}}}\) are Young's moduli of the SWCNTs; \(G_{12}^{{{\text{CNT}}}}\) is the shear modulus of the same; \(E^{m}\) and \(G^{m}\) represent the corresponding properties of the isotropic matrix; \(\eta_{1} ,\eta_{2}\), and \(\eta_{3}\) are the CNT/matrix efficiency parameters; \(\nu_{12}^{{{\text{CNT}}}}\) and \(\nu^{m}\) are the Poisson's ratios of CNT and matrix, respectively; \(V_{m} \left( z \right)\) is the volume fraction of the matrix; and \(V_{{{\text{CNT}}}} (z)\) is the volume fraction of the CNT, which is assumed to be as follows [37]:

$$ {\text{UD:}}\;{\text{V}}_{{{\text{CNT}}}} (z) = V_{{{\text{CNT}}}}^{*} , $$
(6)
$$ {\text{FG-X:}}\;V_{{{\text{CNT}}}} (z) = 2V_{{{\text{CNT}}}}^{*} \left( {\frac{{\left| {2z - z_{k} - z_{k + 1} } \right|}}{{z_{k + 1} - z_{k} }}} \right), $$
(7)
$$ {\text{FG-V:}}\;V_{{{\text{CNT}}}} (z) = 2V_{{{\text{CNT}}}}^{*} \frac{{z - z_{k} }}{{z_{k + 1} - z_{k} }}, $$
(8)
$$ {\text{FG-A:}}\;V_{{{\text{CNT}}}} (z) = 2V_{{{\text{CNT}}}}^{*} \frac{{z_{k + 1} - z}}{{z_{k + 1} - z_{k} }}, $$
(9)
$$ {\text{FG-O:}}\;V_{{{\text{CNT}}}} (z) = 2V_{{{\text{CNT}}}}^{*} \left( {1 - \frac{{\left| {2z - z_{k} - z_{k + 1} } \right|}}{{z_{k + 1} - z_{k} }}} \right). $$
(10)

Here, \(z_{k}\) and \(z_{k + 1}\) are the coordinates of the k-th layer from the reference plane (z = 0), and \(V_{{{\text{CNT}}}}^{*}\) is the given volume fraction of the CNT,

$$ V_{{{\text{CNT}}}}^{*} = \frac{{w_{{{\text{CNT}}}} }}{{w_{{{\text{CNT}}}} + \left( {\rho^{{{\text{CNT}}}} /\rho^{m} } \right) - \left( {\rho^{{{\text{CNT}}}} /\rho^{m} } \right)w_{{{\text{CNT}}}} }}, $$
(11)

where \(w_{{{\text{CNT}}}}\) is the mass fraction of the CNT, and \(\rho^{{{\text{CNT}}}}\) and \(\rho^{m}\) are the densities of the CNT and the matrix, respectively.

2.2 Approximation of the mechanical displacement

According to the four-variable shear deformation refined plate theory [42, 51], the displacement components u, v, and w of the flat shell element in the x-, y-, and z-directions of the local coordinate are expressed as

$$ \begin{aligned} u\left( {x,y,z,t} \right) & = u_{0} (x,y,t) - z\frac{{\partial w_{b} (x,y,t)}}{\partial x} - f\left( z \right)\frac{{\partial w_{s} (x,y,t)}}{\partial x}; \, \\ v\left( {x,y,z,t} \right) & = v_{0} (x,y,t) - z\frac{{\partial w_{b} (x,y,t)}}{\partial y} - f\left( z \right)\frac{{\partial w_{s} (x,y,t)}}{\partial y}; \\ w\left( {x,y,z,t} \right) & = w_{b} (x,y,t) + w_{s} (x,y,t) \\ \end{aligned} $$
(12)

where \(u_{0}\) and \(v_{0}\) are the in-plane displacements in the x- and y-directions, respectively, \(w_{b}\) and \(w_{s}\) are the bending and shear components of the transverse displacement, respectively, and \(f(z) = z\left[ { - \frac{1}{8} + \frac{3}{2}\left( \frac{z}{h} \right)^{2} } \right]\) [42] is the shape function of the distribution of the transverse shear strain and stress along with the structural thickness. Equation (12) can be written in matrix form as

$$ \left\{ d \right\} = \left[ H \right]\left\{ {\overline{d}} \right\} $$
(13)

where

$$ \left\{ d \right\} = \left\{ {\begin{array}{*{20}c} u & v & w \\ \end{array} } \right\}^{T}, $$
(14)
$$ \left[ H \right] = \left[ {\begin{array}{*{20}l} 1 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad { - z} \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad { - f(z)} \hfill & \quad 0 \hfill \\ 0 \hfill & \quad 1 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad { - z} \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad { - f(z)} \hfill \\ 0 \hfill & \quad 0 \hfill & \quad 1 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 1 \hfill & \quad 0 \hfill & \quad 0 \hfill \\ \end{array} } \right], $$
(15)
$$ \left\{ {\overline{d}} \right\} = \left\{ {\begin{array}{*{20}l} {u_{0} } \hfill & \quad {v_{0} } \hfill & \quad {w_{b} } \hfill & \quad {w_{b,x} } \hfill & \quad {w_{b,y} } \hfill & \quad {w_{s} } \hfill & \quad {w_{s,x} } \hfill & \quad {w_{s,y} } \hfill \\ \end{array} } \right\}^{T} $$
(16)

where \(\left\{ {\overline{d}} \right\}\) is the nodal degree of freedom. In this study, a rectangular nonconforming bending element was used. The generalised displacements \(u_{0}\) and \(v_{0}\) are \(C^{0}\) interpolated over an element as

$$ \begin{aligned} u_{0} \left( {x,y,t} \right) & = \sum\limits_{i = 1}^{4} {u_{oi} \left( t \right)\psi_{i} \left( {\xi ,\eta } \right)}, \\ v_{0} \left( {x,y,t} \right) & = \sum\limits_{i = 1}^{4} {v_{oi} \left( t \right)\psi_{i} \left( {\xi ,\eta } \right)} \\ \end{aligned} $$
(17)

where \(\psi_{i}\) are linear interpolation functions:

$$ \psi_{i} = \frac{1}{4}\left( {1 + \xi \xi_{i} } \right)\left( {1 + \eta \eta_{i} } \right),\quad \left( {i = 1,2,3,4} \right). $$
(18)

Two components of the transverse displacement, \(w_{b}\) and \(w_{s}\), are \(C^{1}\) interpolated by the following expression:

$$ \begin{aligned} w_{b} \left( {x,y,t} \right) & = \sum\limits_{i = 1}^{4} {\left[ {w_{b} g_{i1} \left( {\xi ,\eta } \right) + w_{b,x} g_{i2} \left( {\xi ,\eta } \right) + w_{b,y} g_{i3} \left( {\xi ,\eta } \right)} \right]}, \\ w_{s} \left( {x,y,t} \right) & = \sum\limits_{i = 1}^{4} {\left[ {w_{s} g_{i1} \left( {\xi ,\eta } \right) + w_{s,x} g_{i2} \left( {\xi ,\eta } \right) + w_{s,y} g_{i3} \left( {\xi ,\eta } \right)} \right]} \\ \end{aligned} $$
(19)

where \(g_{ij} \;\left( {j = 1,2,3} \right)\) are nonconforming Hermite cubic interpolation functions:

$$ \begin{aligned} g_{i1} & = \frac{1}{8}\left( {1 + \xi_{i} \xi } \right)\left( {1 + \eta_{i} \eta } \right)\left( {2 + \xi_{i} \xi + \eta_{i} \eta - \xi^{2} - \eta^{2} } \right), \\ g_{i2} & = \frac{1}{8}\xi_{i} \left( {\xi_{i} \xi - 1} \right)\left( {1 + \eta_{i} \eta } \right)\left( {1 + \xi_{i}^{2} \xi^{2} } \right), \\ g_{i3} & = \frac{1}{8}\eta_{i} \left( {1 + \xi_{i} \xi } \right)\left( {\eta_{i} \eta - 1} \right)\left( {1 + \eta_{i}^{2} \eta^{2} } \right). \\ \end{aligned} $$
(20)

By using Eqs. (17) and (19), Eq. (13) can be rewritten as

$$ \left\{ d \right\} = \left[ H \right]\left[ {N_{m} } \right]\left\{ {d^{e} } \right\} $$
(21)

where

$$ \left[ {N_{m} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {N_{m1} } \right]} & {\left[ {N_{m2} } \right]} & {\left[ {N_{m3} } \right]} & {\left[ {N_{m4} } \right]} \\ \end{array} } \right], $$
(22)
$$ \left[ {N_{mi} } \right] = \left[ {\begin{array}{*{20}l} {\psi_{i} } \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill \\ 0 \hfill & \quad {\psi_{i} } \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill \\ 0 \hfill & \quad 0 \hfill & \quad {g_{i1} } \hfill & \quad {g_{i2} } \hfill & \quad {g_{i3} } \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill \\ 0 \hfill & \quad 0 \hfill & \quad {g_{i1,x} } \hfill & \quad {g_{i2,x} } \hfill & \quad {g_{i3,x} } \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill \\ 0 \hfill & \quad 0 \hfill & \quad {g_{i1,y} } \hfill & \quad {g_{i2,y} } \hfill & \quad {g_{i3,y} } \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill \\ 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad {g_{i1} } \hfill & \quad {g_{i2} } \hfill & \quad {g_{i3} } \hfill \\ 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad {g_{i1,x} } \hfill & \quad {g_{i2,x} } \hfill & \quad {g_{i3,x} } \hfill \\ 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad {g_{i1,y} } \hfill & \quad {g_{i2,y} } \hfill & \quad {g_{i3,y} } \hfill \\ \end{array} } \right]. $$
(23)

The strains associated with the displacements are

$$ \begin{aligned} \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ \end{array} } \right\} & = \left\{ {\begin{array}{*{20}c} {u_{0,x} } \\ {v_{0,y} } \\ {u_{0,y} + v_{0,x} } \\ \end{array} } \right\} - z\left\{ {\begin{array}{*{20}c} {w_{b,xx} } \\ {w_{b,yy} } \\ {w_{b,xy} } \\ \end{array} } \right\} - f(z)\left\{ {\begin{array}{*{20}c} {w_{s,xx} } \\ {w_{s,yy} } \\ {w_{s,xy} } \\ \end{array} } \right\}, \\ \left\{ {\begin{array}{*{20}c} {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \right\} & = g(z)\left\{ {\begin{array}{*{20}c} {w_{s,x} } \\ {w_{s,y} } \\ \end{array} } \right\} \\ \end{aligned} $$
(24)

or in vector form

$$ \begin{aligned} \left\{ \varepsilon \right\} & = \left\{ {\varepsilon^{0} } \right\} - z\left\{ {\varepsilon^{b} } \right\} - f(z)\left\{ {\varepsilon^{s} } \right\}, \\ \left\{ \gamma \right\} & = g(z)\left\{ {\gamma^{s} } \right\}. \\ \end{aligned} $$
(25)

Substituting Eq. (21) into Eq. (25) yields

$$ \begin{aligned} \left\{ \varepsilon \right\} & = \left[ {B_{m}^{b} } \right]\left\{ {d^{e} } \right\}, \\ \left\{ \gamma \right\} & = \left[ {B_{m}^{s} } \right]\left\{ {d^{e} } \right\} \\ \end{aligned} $$
(26)

where

$$ \left[ {B_{m}^{b} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {B_{m1}^{b} } \right]} & {\left[ {B_{m2}^{b} } \right]} & {\left[ {B_{m3}^{b} } \right]} & {\left[ {B_{m4}^{b} } \right]} \\ \end{array} } \right] = \left[ {A_{m}^{b} } \right] - z\left[ {C_{m}^{b} } \right] - f(z)\left[ {D_{m}^{b} } \right], $$
(27)
$$ \left[ {B_{m}^{s} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {B_{m1}^{s} } \right]} & {\left[ {B_{m2}^{s} } \right]} & {\left[ {B_{m3}^{s} } \right]} & {\left[ {B_{m4}^{s} } \right]} \\ \end{array} } \right] = g(z)\left[ {A_{m}^{s} } \right] $$
(28)

in which

$$ \left[ {A_{mi}^{b} } \right] = \left[ {\begin{array}{*{20}l} {\psi_{i,x} } \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill \\ 0 \hfill & \quad {\psi_{i,y} } \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill \\ {\psi_{i,y} } \hfill & \quad {\psi_{i,x} } \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill \\ \end{array} } \right], $$
(29)
$$ \left[ {C_{mi}^{b} } \right] = \left[ {\begin{array}{*{20}l} 0 \hfill & \quad 0 \hfill & \quad {g_{i1,xx} } \hfill & \quad {g_{i2,xx} } \hfill & \quad {g_{i3,xx} } \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill \\ 0 \hfill & \quad 0 \hfill & \quad {g_{i1,yy} } \hfill & \quad {g_{i2,yy} } \hfill & \quad {g_{i3,yy} } \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill \\ 0 \hfill & \quad 0 \hfill & \quad {g_{i1,xy} } \hfill & \quad {g_{i2,xy} } \hfill & \quad {g_{i3,xy} } \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill \\ \end{array} } \right], $$
(30)
$$ \left[ {D_{mi}^{b} } \right] = \left[ {\begin{array}{*{20}l} 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad {g_{i1,xx} } \hfill & \quad {g_{i2,xx} } \hfill & \quad {g_{i3,xx} } \hfill \\ 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad {g_{i1,yy} } \hfill & \quad {g_{i2,yy} } \hfill & \quad {g_{i3,yy} } \hfill \\ 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad {g_{i1,xy} } \hfill & \quad {g_{i3,xy} } \hfill & \quad {g_{i3,xy} } \hfill \\ \end{array} } \right], $$
(31)
$$ \left[ {A_{mi}^{s} } \right] = \left[ {\begin{array}{*{20}l} 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad {g_{i1,y} } \hfill & \quad {g_{i2,y} } \hfill & \quad {g_{i3,y} } \hfill \\ 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad {g_{i1,x} } \hfill & \quad {g_{i2,x} } \hfill & \quad {g_{i3,x} } \hfill \\ \end{array} } \right]. $$
(32)

2.3 Approximation of the electric potentials

In this study, the approximation of the electric potential field of each piezoelectric layer is considered as a linear function through the thickness coordinate. Therefore, for the top and bottom surfaces of the panel, the electric potential functions are [52,53,54]

$$ \Phi^{t} (x,y,z,t) = \frac{2z - h}{{2h_{p} }}\phi^{t} (x,y,t) = Z_{p}^{t} \phi^{t} (x,y,t)\quad \frac{h}{2} \le \, z \, \le \frac{h}{2} + \, h_{p}, $$
(33)
$$ \Phi^{b} (x,y,z,t) = - \frac{2z + h}{{2h_{p} }}\phi^{b} (x,y,t) = Z_{p}^{b} \phi^{b} (x,y,t)\quad - \frac{h}{2} - h_{p} \le \, z \, \le - \frac{h}{2}. $$
(34)

It can be written in matrix form as

$$ \left\{ \Phi \right\} = \left[ {Z_{p} } \right]\left\{ \phi \right\} $$
(35)

where

$$ \left\{ \Phi \right\} = \left\{ {\begin{array}{*{20}c} {\Phi^{t} } & {\Phi^{b} } \\ \end{array} } \right\}^{T} ,\quad \left[ {Z_{p} } \right] = \left[ {\begin{array}{*{20}l} {Z_{p}^{t} } \hfill & 0 \hfill \\ 0 \hfill & {Z_{p}^{b} } \hfill \\ \end{array} } \right],\quad \left\{ \phi \right\} = \left\{ {\begin{array}{*{20}c} {\phi^{t} } & {\phi^{b} } \\ \end{array} } \right\}^{T}. $$
(36)

The electric potential is also interpolated by \(C^{0}\) interpolation:

$$ \left\{ \Phi \right\} = \left[ {Z_{p} } \right]\left[ {N_{\phi } } \right]\left\{ {\phi^{e} } \right\}. $$
(37)

The electric field \(E\) is derived from the electric potential:

$$ \left\{ {E_{i} } \right\} = \left\{ {\Phi_{,i} } \right\}\quad \left( {i = x,y,z} \right). $$
(38)

Using Eqs. (34), (35), and (37), Eq. (38) can be rewritten as

$$ \left\{ E \right\} = \left[ {B_{\phi } } \right]\left\{ {\phi^{e} } \right\} \, $$
(39)

where

$$ \left\{ E \right\} = \left\{ {\begin{array}{*{20}l} {E_{x}^{t} } \hfill & {E_{y}^{t} } \hfill & {E_{z}^{t} } \hfill & {E_{x}^{b} } \hfill & {E_{y}^{b} } \hfill & {E_{z}^{b} } \hfill \\ \end{array} } \right\}^{T}, $$
(40)
$$ \left[ {B_{\phi } } \right] = \left[ {\begin{array}{*{20}c} {B_{\phi 1} } & {B_{\phi 2} } & {B_{\phi 3} } & {B_{\phi 4} } \\ \end{array} } \right] $$
(41)

where

$$ \left[ {B_{\phi i} } \right] = \left[ {\begin{array}{*{20}l} {Z_{p,x}^{t} } \hfill & \quad {Z_{p,y}^{t} } \hfill & \quad {Z_{p,z}^{t} } \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad 0 \hfill \\ 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad {Z_{p,x}^{b} } \hfill & \quad {Z_{p,y}^{b} } \hfill & \quad {Z_{p,z}^{b} } \hfill \\ \end{array} } \right]^{T}. $$
(42)

2.4 Constitutive equations

The linear constitutive relations for a single FG-CNTRC layer can be written as

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{x}^{k} } \\ {\sigma_{y}^{k} } \\ {\tau_{xy}^{k} } \\ {\tau_{yz}^{k} } \\ {\tau_{xz}^{k} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}l} {\overline{Q}_{11}^{k} (z)} \hfill & \quad {\overline{Q}_{12}^{k} (z)} \hfill & \quad {\overline{Q}_{16}^{k} (z)} \hfill & \quad 0 \hfill & \quad 0 \hfill \\ {\overline{Q}_{12}^{k} (z)} \hfill & \quad {\overline{Q}_{22}^{k} (z)} \hfill & \quad {\overline{Q}_{26}^{k} (z)} \hfill & \quad 0 \hfill & \quad 0 \hfill \\ {\overline{Q}_{16}^{k} (z)} \hfill & \quad {\overline{Q}_{26}^{k} (z)} \hfill & \quad {\overline{Q}_{66}^{k} (z)} \hfill & \quad 0 \hfill & \quad 0 \hfill \\ 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad {\overline{Q}_{44}^{k} (z)} \hfill & \quad {\overline{Q}_{45}^{k} (z)} \hfill \\ 0 \hfill & \quad 0 \hfill & \quad 0 \hfill & \quad {\overline{Q}_{45}^{k} (z)} \hfill & \quad {\overline{Q}_{55}^{k} (z)} \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \right\} $$
(43)

where \(\overline{Q}_{{{\text{ij}}}}^{{}}\) are the transformed material constants expressed in terms of material constants [55]:

$$ \begin{aligned} \overline{Q}_{11}^{k} (z) & = Q_{11}^{C} (z)\cos^{4} \theta^{k} + 2\left[ {Q_{12}^{C} (z) + 2Q_{66}^{C} (z)} \right]\sin^{2} \theta^{k} \cos^{2} \theta^{k} + Q_{22}^{C} (z)\sin^{4} \theta^{k}, \\ \overline{Q}_{12}^{k} (z) & = \left[ {Q_{11}^{C} (z) + Q_{22}^{C} (z) - 4Q_{66}^{C} (z)} \right]\sin^{2} \theta^{k} \cos^{2} \theta^{k} + Q_{12}^{C} (z)\left( {\sin^{4} \theta^{k} + \cos^{4} \theta^{k} } \right), \\ \overline{Q}_{22}^{k} (z) &= Q_{11}^{C} (z)\sin^{4} \theta^{k} + 2\left[ {Q_{12}^{C} (z) + 2Q_{66}^{C} (z)} \right]\sin^{2} \theta^{k} \cos^{2} \theta^{k} + Q_{22}^{C} (z)\cos^{4} \theta^{k}, \\ \overline{Q}_{16}^{k} (z) & = \left[ {Q_{11}^{C} (z) - Q_{12}^{C} (z) - 2Q_{66}^{C} (z)} \right]\sin \theta^{k} \cos^{3} \theta^{k} \\ & \quad + \left[ {Q_{12}^{C} (z) - Q_{22}^{C} (z) + 2Q_{66}^{C} (z)} \right]\sin^{3} \theta^{k} \cos \theta^{k}, \\ \overline{Q}_{26}^{k} (z) & = \left[ {Q_{11}^{C} (z) - Q_{12}^{C} (z) - 2Q_{66}^{C} (z)} \right]\sin^{3} \theta^{k} \cos \theta^{k} \\ & \quad + \left[ {Q_{12}^{C} (z) - Q_{22}^{C} (z) + 2Q_{66}^{C} (z)} \right]\sin \theta^{k} \cos^{3} \theta^{k}, \\ \overline{Q}_{66}^{k} (z) & = \left[ {Q_{11}^{C} (z) + Q_{22}^{C} (z) - 2Q_{12}^{C} (z) - 2Q_{66}^{C} (z)} \right]\sin^{2} \theta^{k} \cos^{2} \theta^{k} \\ & \quad + Q_{66}^{C} (z)\left( {\sin^{4} \theta^{k} + \cos^{4} \theta^{k} } \right), \\ \overline{Q}_{44}^{k} (z) & = Q_{44}^{C} (z)\cos^{2} \theta^{k} + Q_{55}^{C} (z)\sin^{2} \theta^{k}, \\ \overline{Q}_{45}^{k} (z) & = \left[ {Q_{55}^{C} (z) - Q_{44}^{C} (z)} \right]\cos \theta^{k} \sin \theta^{k}, \\ \overline{Q}_{55}^{k} (z) &= Q_{55}^{C} (z)\cos^{2} \theta^{k} + Q_{44}^{C} (z)\sin^{2} \theta^{k} \\ \end{aligned} $$
(44)

where \(Q_{ij}^{C} (z)\) are the plane stress-reduced stiffness values, which are defined in terms of the engineering constants in the layer material axes. For each CNT layer,

$$ \begin{aligned} Q_{11}^{C} \left( z \right) & = \frac{{E_{11} \left( z \right)}}{{1 - \nu_{12} \nu_{21} }};\quad Q_{12}^{C} \left( z \right) = \frac{{\nu_{12} E_{22} \left( z \right)}}{{1 - \nu_{12} \nu_{21} }};\quad Q_{22}^{C} \left( z \right) = \frac{{E_{22} \left( z \right)}}{{1 - \nu_{12} \nu_{21} }}; \\ Q_{44}^{C} \left( z \right) & = G_{23}^{C} \left( z \right);\quad Q_{55}^{C} \left( z \right) = G_{13}^{C} \left( z \right);\quad Q_{66}^{C} \left( z \right) = G_{12}^{C} \left( z \right). \\ \end{aligned} $$
(45)

The linear constitutive relations for an individual piezoelectric material layer can be expressed as [56,57,58]

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{x}^{k} } \\ {\sigma_{y}^{k} } \\ {\tau_{xy}^{k} } \\ {\tau_{yz}^{k} } \\ {\tau_{xz}^{k} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}l} {\overline{C}_{11} } \hfill & {\overline{C}_{12} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ {\overline{C}_{12} } \hfill & {\overline{C}_{11} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\frac{1}{2}\left( {\overline{C}_{11} - \overline{C}_{12} } \right)} \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {\overline{C}_{55} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\overline{C}_{55} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \right\} - \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & {\overline{e}_{31} } \hfill \\ 0 \hfill & 0 \hfill & {\overline{e}_{31} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & { - e_{15} } \hfill & 0 \hfill \\ { - e_{15} } \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {E_{x}^{k} } \\ {E_{y}^{k} } \\ {E_{z}^{k} } \\ \end{array} } \right\}, $$
(46)
$$ \left\{ {\begin{array}{*{20}c} {D_{x}^{k} } \\ {D_{y}^{k} } \\ {D_{z}^{k} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}l} 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - e_{15} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & { - e_{15} } \hfill & 0 \hfill \\ {\overline{e}_{31} } \hfill & {\overline{e}_{31} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{y} } \\ {\gamma_{xy} } \\ {\gamma_{yz} } \\ {\gamma_{xz} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}l} {p_{11} } \hfill & 0 \hfill & 0 \hfill \\ 0 \hfill & {p_{11} } \hfill & 0 \hfill \\ 0 \hfill & 0 \hfill & {\overline{p}_{33} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {E_{x}^{k} } \\ {E_{y}^{k} } \\ {E_{z}^{k} } \\ \end{array} } \right\}. $$
(47)

The elastic constants for the piezoelectric layer are

$$ \begin{aligned} \overline{C}_{11} & = C_{11} - \frac{{\left( {C_{13} } \right)^{2} }}{{C_{33} }};\quad \overline{C}_{12} = C_{12} - \frac{{\left( {C_{13} } \right)^{2} }}{{C_{33} }};\quad \overline{C}_{55} = C_{55} ; \\ \overline{e}_{31} & = e_{31} - \frac{{C_{13} }}{{C_{33} }}e_{33} ;\quad \overline{p}_{33} = p_{33} + \frac{{e_{33}^{2} }}{{C_{33} }} \\ \end{aligned} $$
(48)

where \({[}C_{{{\text{ij}}}} {]}\) is the elastic constant matrix of the piezoelectric layers, \({[}e_{{{\text{ij}}}} {]}\) is the electromechanical coupling matrix, \({[}p_{{{\text{ij}}}} {]}\) is the dielectric permittivity matrix, \({\text{\{ }}E{\text{\} }}\) is the electric field, and \({\text{\{ }}D{\text{\} }}\) is the electrical displacement in the piezoelectric layer. The coupling between the elastic and electric fields can be rewritten in short form as

$$ \begin{aligned} \left\{ \sigma \right\} & = \left[ Q \right]\left\{ \varepsilon \right\} - \left[ e \right]\left\{ E \right\}, \\ \left\{ D \right\} & = \left[ e \right]^{T} \left\{ \varepsilon \right\} + \left[ p \right]\left\{ E \right\}. \\ \end{aligned} $$
(49)

2.5 Governing equations of motion

The dynamic equations of the hybrid panel can be derived using Hamilton's variational principle,

$$ \delta \int_{{t_{1} }}^{{t_{2} }} {\left[ {T - U + W} \right]} dt = 0, $$
(50)

where \(T\), \(U\), and \(W\) are the kinetic energy, strain energy, and work done by the applied forces, respectively.

At the element level, the kinetic energy can be calculated as

$$ T^{e} = \frac{1}{2}\int_{{V_{e} }} {\rho \left\{ {\dot{d}} \right\}}^{T} \left\{ {\dot{d}} \right\}{\text{d}}V_{e}. $$
(51)

The strain energy can be written as

$$ U^{e} = \frac{1}{2}\int_{{V_{e} }} {\left[ {\left\{ \varepsilon \right\}^{T} \left\{ \sigma \right\} + \left\{ \gamma \right\}^{T} \left\{ \tau \right\} - \left\{ E \right\}^{T} \left\{ D \right\}} \right]} dV_{e}, $$
(52)

and the work done by the external forces is

$$ W^{e} = \int_{{V_{e} }} {\left\{ d \right\}}^{T} \left\{ {f_{b} } \right\}dV_{e} + \int_{{A_{e} }} {\left\{ d \right\}}^{T} \left\{ {f_{s} } \right\}{\text{d}}A_{e} + \left\{ d \right\}^{T} \left\{ {f_{c} } \right\} $$
(53)

where \(V_{e}\) is the volume of the element, \(\left\{ {f_{b} } \right\}\) is the body force, \(A_{e}\) is the surface area of the element where the surface force \(\left\{ {f_{s} } \right\}\) is specified, and \(\left\{ {f_{c} } \right\}\) is the concentrated load.

The elementary governing equation of motion can be derived by substituting Eqs. (21), (26), (39), and (49) into Eqs. (51), (52), (53), and Eq. (50),

$$ \left[ {\begin{array}{*{20}c} {M_{mm} } & 0 \\ 0 & 0 \\ \end{array} } \right]_{e} \left\{ {\begin{array}{*{20}c} {\ddot{d}} \\ {\ddot{\phi }} \\ \end{array} } \right\}_{e} + \left[ {\begin{array}{*{20}c} {K_{mm} } & {K_{m\phi } } \\ {K_{\phi m} } & {K_{\phi \phi } } \\ \end{array} } \right]_{e} \left\{ {\begin{array}{*{20}c} d \\ \phi \\ \end{array} } \right\}_{e} = \left\{ {\begin{array}{*{20}c} {F_{m} } \\ {F_{\phi } } \\ \end{array} } \right\}_{e}, $$
(54)

where

$$ \begin{aligned} \left[ {M_{mm} } \right]_{e} & = \int_{{A_{e} }} {\left[ {N_{m} } \right]}^{T} \left[ m \right]\left[ {N_{m} } \right]dA_{e}, \\ \left[ {K_{mm} } \right]_{e} & = \left[ {K_{mm}^{b} } \right]_{e} + \left[ {K_{mm}^{s} } \right]_{e} = \int_{{A_{e} }} {\left[ {B_{m}^{b} } \right]}^{T} \left[ {\overline{D}_{b} } \right]\left[ {B_{m}^{b} } \right]dA_{e} + \int_{{A_{e} }} {\left[ {B_{m}^{s} } \right]^{T} \left[ {\overline{D}_{s} } \right]\left[ {B_{m}^{s} } \right]} dA_{e}, \\ \left[ {K_{m\phi } } \right]_{e} & = \left[ {K_{\phi m} } \right]_{e}^{T} = \int_{{A_{e} }} {\left[ {B_{m} } \right]}^{T} \left[ e \right]\left[ {B_{m} } \right]dA_{e}, \\ \left[ {K_{\phi \phi } } \right]_{e} &; = \int_{{A_{e} }} {\left[ {B_{\phi } } \right]}^{T} \left[ p \right]\left[ {B_{\phi } } \right]dA_{e}. \\ \end{aligned} $$
(55)

Withdrawing \(\phi\) from the second equation and then substituting it into the first equation in Eq. (54), one obtains the final form of the governing equation in shortened form:

$$ \left[ {M_{mm} } \right]_{e} \left\{ {\ddot{d}} \right\}_{e} + \left( {\left[ {K_{mm} } \right]_{e} + \left[ {K_{m\phi } } \right]_{e} \left[ {K_{\phi \phi } } \right]_{e}^{ - 1} \left[ {K_{\phi m} } \right]_{e} } \right)\left\{ d \right\}_{e} = \left\{ {F_{m} } \right\}_{e} + \left[ {K_{m\phi } } \right]_{e} \left[ {K_{\phi \phi } } \right]_{e}^{ - 1} \left\{ {F_{\phi } } \right\}_{e}. $$
(56)

The global equations of motion can be obtained by assembling the element equations and are given by

$$ \left[ {M_{mm} } \right]\left\{ {\ddot{d}} \right\} + \left( {\left[ {K_{mm} } \right] + \left[ {K_{m\phi } } \right]\left[ {K_{\phi \phi } } \right]_{{}}^{ - 1} \left[ {K_{\phi m} } \right]} \right)\left\{ d \right\} = \left\{ {F_{m} } \right\} + \left[ {K_{m\phi } } \right]\left[ {K_{\phi \phi } } \right]_{{}}^{ - 1} \left\{ {F_{\phi } } \right\} $$
(57)

where

$$ \begin{aligned} \left[ {M_{mm} } \right] & = \sum\limits_{i = 1}^{m \times n} {\left[ \Lambda \right]_{i}^{T} \left[ {M_{mm} } \right]_{ei} \left[ \Lambda \right]_{i}^{{}} } ,\quad \left[ {K_{mm} } \right] = \sum\limits_{i = 1}^{m \times n} {\left[ \Lambda \right]_{i}^{T} \left[ {K_{mm} } \right]_{ei} \left[ \Lambda \right]_{i}^{{}} } ,\quad \left[ {F_{m} } \right] = \sum\limits_{i = 1}^{m \times n} {\left[ \Lambda \right]_{i}^{T} \left[ {F_{m} } \right]_{ei} } , \\ \left[ {K_{m\phi } } \right] & = \sum\limits_{i = 1}^{m \times n} {\left[ \Lambda \right]_{i}^{T} \left[ {K_{m\phi } } \right]_{ei} \left[ \Lambda \right]_{i}^{{}} } ,\quad \left[ {K_{\phi \phi } } \right] = \sum\limits_{i = 1}^{m \times n} {\left[ \Lambda \right]_{i}^{T} \left[ {K_{\phi \phi } } \right]_{ei} \left[ \Lambda \right]_{i}^{{}} } ,\quad \left[ {F_{\phi } } \right] = \sum\limits_{i = 1}^{m \times n} {\left[ \Lambda \right]_{i}^{T} \left[ {F_{\phi } } \right]_{ei} } , \\ \left[ {K_{\phi m} } \right] & = \sum\limits_{i = 1}^{m \times n} {\left[ \Lambda \right]_{i}^{T} \left[ {K_{\phi m} } \right]_{ei} \left[ \Lambda \right]_{i}^{{}} } . \\ \end{aligned} $$

Here, \(\left[ \Lambda \right]\) is the global–local transformation matrix.

2.6 Active control analysis

In this study, the piezoelectric actuator and sensor were bonded at the top and bottom surfaces, respectively. The actuator and sensor are denoted by subscripts a and s, respectively. Without an external charge, the generated potential on the sensor can be obtained from Eq. (54):

$$ \phi_{s} = \left[ {K_{\phi \phi }^{ - 1} } \right]_{s} \left[ {K_{\phi m} } \right]_{s} d_{s}. $$
(58)

By using closed-loop feedback control, the voltage on the actuator can be written as

$$ \phi_{a} = G_{d} \phi_{s} + G_{v} \dot{\phi }_{s} $$
(59)

where \(G_{d}\) and \(G_{v}\) are the displacement and feedback control gains, respectively. This implies that, when the panel is in the vibration state, electric charges are generated in the sensor layer and then amplified and converted into the signal. The signal is then fed back into the distributed actuator, and an input voltage for the actuator is generated. Owing to the piezoelectric effect, stresses and strains are generated. Substituting Eqs. (58), (59) into Eq. (54) gives

$$ F_{a} = \left[ {K_{\phi m} } \right]_{a} d_{a} - G_{d} \left[ {K_{\phi \phi } } \right]_{a} \left[ {K_{\phi \phi }^{ - 1} } \right]_{s} \left[ {K_{\phi m} } \right]_{s} d_{s} - G_{v} \left[ {K_{\phi \phi } } \right]_{a} \left[ {K_{\phi \phi }^{ - 1} } \right]_{s} \left[ {K_{\phi m} } \right]_{s} \dot{d}_{s}. $$
(60)

Substituting Eq. (59) into Eq. (56), one writes

$$ \left[ {M_{mm} } \right]\left\{ {\ddot{d}} \right\} + \left[ {C_{a} } \right]\left\{ {\dot{d}} \right\} + \left[ {K^{*} } \right]\left\{ d \right\} = \left\{ F \right\} $$
(61)

where

$$ \left[ {K^{*} } \right] = \left[ {K_{mm} } \right] + G_{d} \left[ {K_{m\phi } } \right]_{s} \left[ {K_{\phi \phi }^{ - 1} } \right]_{s} \left[ {K_{\phi m} } \right]_{{}}, $$
(62)
$$ \left[ {C_{a} } \right] = G_{v} \left[ {K_{m\phi } } \right]_{s} \left[ {K_{\phi \phi }^{ - 1} } \right]_{s} \left[ {K_{\phi m} } \right]_{s}. $$
(63)

Considering the structure damping effect, Eq. (60) can be rewritten as

$$ \left[ {M_{mm} } \right]\left\{ {\ddot{d}} \right\} + \left( {\left[ {C_{a} } \right] + \left[ {C_{R} } \right]} \right)\left\{ {\dot{d}} \right\} + \left[ {K^{*} } \right]\left\{ d \right\} = \left\{ F \right\} $$
(64)

with

$$ \left[ {C_{R} } \right] = \alpha_{R} \left[ {M_{mm} } \right] + \beta_{R} \left[ {K_{mm} } \right] $$
(65)

where \(\alpha_{R}\) and \(\beta_{R}\) are Rayleigh damping coefficients that can be determined from experiments.

3 Numerical results

Comparison studies were performed to prove the convergence and accuracy of the finite-element model. Furthermore, parametric studies were performed to study the effects of the CNT volume fraction, type of CNT distribution, thickness of the piezoelectric layer, laminate configurations, and mechanical and electrical boundary conditions on the natural frequencies of the panel. Finally, active vibration control results were obtained to illustrate the effectiveness of the type of load and feedback control gains on the dynamic behaviour of the PFG-CNTRC spherical shell panels. The following material properties are used in various examples.

  • Material 1 (Al2O3) [59]:

    E = 380 GPa, ν = 0.3, ρ = 3800 kg/m3.

  • Material 2 (PZT-4) [59]:

    C11 = 139 GPa, C12 = 77.8 GPa, C13 = 74.3 GPa, C33 = 115 GPa, C44 = C55 = 25.6 GPa, C66 = 30.6 GPa, ρ = 7500 kg/m3, \(e_{31}\) =  − 5.2 C/m2, \(e_{33}\) = 15.1 C/m2, \(e_{15}\) = 12.7 C/m2, \(p_{11}\) = 6.75 nF/m, \(p_{33}\) = 5.9 nF/m.

  • Material 3 (PZT-5A) [38]:

    E = 63 GPa, G = 23.3 GPa, ν = 0.35, ρ = 7750 kg/m3, \(e_{31} = e_{32}\) =  − 7.209 C/m2, \(e_{33}\) = 15.12 C/m2, \(e_{15} = e_{24}\) = 12.322 C/m2, \(p_{11} = p_{22}\) = 1.53 × 10−8 F/m, \(p_{33}\) = 1.5 × 10−8 F/m.

  • Material 4 [38]:

    Material 4 in this study is FG-CNTRC with the properties of the matrix and reinforcement as follows:

The matrix (PMMA): Em = (3.52 − 0.0034 \(\Delta T\)) GPa, νm = 0.34, and ρm = 1150 kg/m3. Here, \(\Delta T = T - T_{0}\) is the temperature change, and \(T_{0}\) is the reference temperature, which is set to 300 K.

The reinforcement (armchair SWCNT): E11CNT = 5.64 TPa, E22CNT = 7.0800 TPa, G12CNT = 1.9455 TPa, ν12CNT = 0.175, and ρCNT = 1400 kg/m3. For three different volume fractions of CNTs, the efficiency parameters are \(\eta_{1} = 0.137\) and \(\eta_{2} = 1.022\) for \(V_{{{\text{CNT}}}}^{*} = 0.12\), \(\eta_{1} = 0.142\) and \(\eta_{2} = 1.626\) for \(V_{{{\text{CNT}}}}^{*} = 0.17\), and \(\eta_{1} = 0.141\) and \(\eta_{2} = 1.585\) for \(V_{{{\text{CNT}}}}^{*} = 0.28\). For each case, the efficiency parameter \(\eta_{3}\) is \(0.7\eta_{2}\).

3.1 Convergence and comparison studies

The first example considered is the simply supported (SSSS) double-curved shell panel made of material 1 with integrated piezoelectric layers PZT4 at the top and bottom surfaces. Table 1 summarises a comparison of the fundamental natural frequencies in open-circuit (Opc) and closed-circuit (Clc) electrical conditions of the panel. It can be seen that, with a meshing of 20 × 20 elements, the results obtained by the present model are in good agreement with those obtained by Sayyadi [59] based on higher-order deformation theory. The difference between the present results and the results of Sayyadi [59] is less than 1% for various inlet parameters, such as a/Rx ratio, hp/h ratio, and closed and open electrical boundary conditions.

Table 1 Fundamental natural frequency of the doubly curved isotropic shell coupled with piezoelectric layers (a/b = 1, h/a = 0.1, and Ry/a = 5)
Full size table

The second example was considered for the PFG-CNTRC square plates. The results obtained were compared with those given by Nguyen-Quang et al. [38] based on an isogeometric approach and higher-order deformation theory. The dimensions of the plates were set to \(a = b = 0.4{\text{ m}}\), \(h = {a \mathord{\left/ {\vphantom {a {20}}} \right. \kern-\nulldelimiterspace} {20}}\), and \(h_{p} = {h \mathord{\left/ {\vphantom {h {10}}} \right. \kern-\nulldelimiterspace} {10}}\); the substrate was made of material 4; and the piezoelectric layers were made of material 3. Table 2 lists the first natural frequencies of the single-layer plates, while Table 3 lists those of the multilayer plates. A meshing of 20 × 20 elements was chosen to achieve extremely good agreement between the present results and the results reported elsewhere [38] for various mechanical and electrical boundary conditions, various CNT volume fractions, and different types of CNT distribution. Consequently, the meshing of 20 × 20 elements was used for all further analyses in this work.

Table 2 Fundamental natural frequency f (in Hz) of the single-layer PPG-CNTRC square plates (a = b, a/h = 20, [p/0/p], and \({{h_{p} } \mathord{\left/ {\vphantom {{h_{p} } h}} \right. \kern-\nulldelimiterspace} h} = {1 \mathord{\left/ {\vphantom {1 {10}}} \right. \kern-\nulldelimiterspace} {10}}\))
Full size table
Table 3 Fundamental natural frequency f (in Hz) of the multilayer PFG-CNTRC square plates (a = b, a/h = 20, and \({{h_{p} } \mathord{\left/ {\vphantom {{h_{p} } h}} \right. \kern-\nulldelimiterspace} h} = {1 \mathord{\left/ {\vphantom {1 {10}}} \right. \kern-\nulldelimiterspace} {10}}\))
Full size table

3.2 Free vibration analysis of PFG-CNTRC spherical shell panels

This example considers an FG-CNTRC spherical shell panel made of material 4. The panel has a square plane projection with a = 0.4 m, thickness h = 0.02 m, and radius R = 2 m. Two piezoelectric layers of PZT-5A with \(h_{p} = 0.002{\text{ m}}\) are bonded on the top and bottom surfaces of the panel. Tables 4 and 5 list the first natural frequencies of the PFG-CNTRC spherical shell panel for different parameters of material properties and different mechanical and electrical boundary conditions. The results illustrate that, with the increase in the CNT volume fraction, the frequency of the panel increases accordingly. The laminate configuration with [− 45/45]as is more effective than any other configuration. Among the four types of CNT distributions, the FG-X type has the highest frequency, whereas the FG-O type has the lowest frequency for the same other input parameters. The results show that the natural frequencies of the hybrid panel in the case of CCCC are higher than those of the other considered boundary conditions. It can also be seen that the natural frequencies of the hybrid panel are higher in the open-circuit case than in the closed-circuit case because the open circuit converts the electric potential to mechanical energy during vibration, while the closed circuit does not.

Table 4 Fundamental natural frequency f (in Hz) of the laminated PFG-CNTRC spherical shell panels (a/h = 20 and R/a = 5)
Full size table
Table 5 Fundamental natural frequency f (in Hz) of the laminated PFG-CNTRC spherical shell panels (a = b, a/h = 20, and R/a = 5)
Full size table

3.3 Dynamic vibration control of PFG-CNTRC spherical shell panels

A fully clamped (CCCC) PFG-CNTRC spherical panel, with lamination sequence [a/0/90/0/s], where a and s represent the piezoelectric actuator and sensor layers made of PZT-5A, bonded on the upper and lower surfaces, respectively, is considered. The substrate is made of material 4. The side dimension is a = 0.4 m, the thickness of the substrate h = 0.04 m, the thickness of each piezoelectric layer \(h_{p} = 0.004{\text{ m}}\), and radius R = 2 m. The panel is subjected to sinusoidally distributed transverse loads expressed as

$$ q = q_{0} \sin \left( {\frac{\pi x}{a}} \right)\sin \left( {\frac{\pi y}{b}} \right)F\left( t \right) $$
(66)

where \(F(t)\) is defined as

$$ F\left( t \right) = \left[ \begin{gathered} \left\{ {\begin{array}{*{20}l} 1 \hfill & {0 \le t \le t_{1} } \hfill & {{\text{Step}}\;{\text{load}}} \hfill \\ 0 \hfill & {t > t_{1} } \hfill & {} \hfill \\ \end{array} } \right. \hfill \\ \left\{ {\begin{array}{*{20}l} {1 - t/t_{1} } \hfill & {0 \le t \le t_{1} } \hfill & {{\text{Triangular}}\;{\text{load}}} \hfill \\ 0 \hfill & {t > t_{1} } \hfill & {} \hfill \\ \end{array} } \right. \hfill \\ \left\{ {\begin{array}{*{20}l} {e^{ - \gamma t} \, e^{ - \gamma t} \, } \hfill & {0 \le t \le t_{1} } \hfill & {{\text{Explosive}}\;{\text{blast}}\;{\text{load}}} \hfill \\ 0 \hfill & {t > t_{1} } \hfill & {} \hfill \\ \end{array} } \right. \hfill \\ \end{gathered} \right. $$
(67)

in which \(q_{0} = 10^{4} \;{\text{N/m}}^{{2}}\), \(\gamma = 330\;{\text{s}}^{ - 1}\), \(t_{1} = 0.002\;{\text{s}}\), and \(F(t)\) is plotted as shown in Fig. 3.

Fig. 3
figure 3

Types of load: step load, triangular load, and explosive load

Full size image

The transient response of the shell panel is solved by the Newmark-β direct integration method [60], and the parameters \(\alpha_{N}\) and \(\beta_{N}\) are taken to be 0.5 and 0.25, respectively. All the calculations for transient response were performed using a time step of 0.0005 s, and the initial modal damping ratio was assumed to be 0.8% [38]. The effects of the velocity feedback gain, CNT volume fraction, and CNT distribution type on the transient response of the centre point A (a/2, a/2) of the hybrid panel were investigated.

First, the active vibration control effect of the velocity feedback controller for the PFG-CNTRC spherical panel was studied. The transient responses of the panel with and without the velocity feedback gain are displayed in Figs. 4, 5 and 6. The Figures show that, in the case of a velocity feedback gain of zero, the transient responses of the panel decrease with time because of structural damping. These Figures also indicate that increasing the velocity feedback gain causes the active damping to become stronger, resulting in a smaller amplitude of the centre point deflection and faster suspension vibration of the hybrid panel. Moreover, the panel is in the free vibration state after the load is removed.

Fig. 4
figure 4

Central deflection of the PFG-CNTRC spherical panel subjected to step load (UD, \(V_{{{\text{CNT}}}}^{*} = 12\%\), CCCC)

Full size image
Fig. 5
figure 5

Central deflection of the PFG-CNTRC spherical panel subjected to triangular load (UD, \(V_{{{\text{CNT}}}}^{*} = 12\%\), CCCC)

Full size image
Fig. 6
figure 6

Central deflection of the PFG-CNTRC spherical panel subjected to explosive blast load (UD, \(V_{{{\text{CNT}}}}^{*} = 12\%\), CCCC)

Full size image

Next, the effects of the volume fraction of CNTs and the distribution type of CNTs on the transient response of the PFG-CNTRC spherical panel were investigated. The effect of the CNT volume fraction is indicated for the uniform distribution (UD) of CNTs with velocity feedback control gain Gv = 5e−5. The effect of the CNT distribution type is indicated for the CNT volume fraction \(V_{{{\text{CNT}}}}^{*} = 28\%\) with velocity feedback control gain Gv = 1.3e−5. Figures 7, 8, and 9 depict the transient responses of the panel associated with stepping load, triangular load, and explosive blast load, respectively. These Figures illustrate that, in all the study cases, the vibration is suppressed faster with an increase in the volume fraction of CNTs. This is compatible with the previous conclusion that addition of CNTs leads to more stiffness of the panels and results in a smaller deflection amplitude. In addition, among the five possible graded patterns of CNTs, FG-O has the largest central deflection, while FG-X has the smallest one. Therefore, the above numerical results demonstrate that, by the proper use of the velocity feedback gain, the vibration of the PFG-CNTRC spherical panels can be controlled as expected.

Fig. 7
figure 7

Transient response of the PFG-CNTRC spherical panel subjected to step load

Full size image
Fig. 8
figure 8

Transient response of the PFG-CNTRC spherical panel subjected to triangular load

Full size image
Fig. 9
figure 9

Transient response of the PFG-CNTRC spherical panel subjected to explosive blast load

Full size image

4 Conclusions

In this study, an efficient finite-element model based on the four-variable shear deformation refined theory was developed for the free vibration and active vibration control of a laminated functionally graded nanotube-reinforced composite with an integrated piezoelectric actuator and sensor layers. The free vibration results were in good agreement with those reported in the literature. Numerical results were provided to explore the effects of the CNT volume fraction, type of CNT distribution, thickness of the piezoelectric layer, laminate configurations, and mechanical and electrical boundary conditions on the natural frequencies of the hybrid spherical panel. A closed-loop control algorithm based on the displacement and velocity feedback was used for active vibration control of the piezoelectric FG-CNTRC spherical panel. As a result of the present formulation and numerical results, some conclusions can be drawn. (i) The volume fraction of CNTs has strong effects on the dynamic responses of the PFG-CNTRC panels. (ii) The natural frequencies of the PFG-CNTRC panel with an open-circuit electrical boundary condition are always higher than those in the closed-circuit case for the same other inlet parameters. (iii) Active vibration control is more effective for the panels with higher stiffness. (iv) The vibration of the PFG-CNTRC spherical panels can be controlled as expected by the proper use of the velocity feedback gain.