Active vibration control of rotating laminated composite truncated conical shells through magnetostrictive layers based on first-order shear deformation theory

Abstract

In this paper, for the first time active vibration control of rotating laminated composite truncated conical shells containing magnetostrictive layers by employing first-order shear deformation theory is investigated. The active vibration control task is done through magnetostrictive layers employing velocity feedback control law. The effects of initial hoop tension and centrifugal and Coriolis forces are considered in extraction of the partial differential equations through Hamilton principle. The ordinary differential equations are derived by employing modified Galerkin method. This study agrees with the mentioned results of the literature. Finally, the effects of several parameters on the vibration suppression are investigated.

1 Introduction

Undesirable vibration could cause bad effects on structural systems such as fatigue, noise and even severe damage. Therefore, one of the design parts of the modern structures should be vibration control. In this way, active vibration control which could be done through smart materials seems to be promising choice for this purpose. Shape memory alloys, piezoelectric and magnetostrictive materials are examples for smart materials which could be used as sensors and actuators [1]. In this paper, Terfenol-D which is a magnetostrictive material is selected for active vibration control of rotating conical shells. Magnetostriction is a phenomenon which takes place in ferromagnetic materials in a way that they undergo deformation in response to the change in their magnetic state [1]. Terfenol-D has great density of energy, wide bandwidth as well as comparatively great displacement [2]. Magnetostrictive materials especially Terfenol-D can have applications in micro-positioners, active damping systems, fluid injectors as well as helicopter blade control systems [3]. In order to learn more about the background of using smart materials in conical structures, in the following some of the papers are introduced.

Li et al. [4] have investigated active vibration control of clamped-free conical shells through laminated piezoelectric actuators. Li et al. [5] have controlled vibration of a conical shell via a diagonal piezoelectric sensor/actuator pair based on optimal approach. Shah and Ray [6] have presented the active vibration control responses of thin composite laminated conical shells through piezoelectric composite materials. Li et al. [7] have investigated active vibration control of conical shells with piezoelectric patches via velocity feedback and linear quadratic regulator approaches. Li et al. [8] have investigated optimal vibration control of conical shells with clamped-free boundary conditions via distributed helical piezoelectric sensor/actuator pairs. Kumar and Ray [9] have presented responses for active vibration control of thin rotating composite laminated conical shells via piezoelectric composite materials. Fan et al. [10] have developed vibration of piezoelectric functionally graded carbon nanotube-reinforced composite conical panels based on first-order shear deformation theory using Rayleigh–Ritz method. Sun et al. [11] have investigated vibration control of conical shells via piezoelectric ceramics using a multimodal fuzzy sliding mode controller. Hajmohammad et al. [12] have studied vibration and smart control of laminated sandwich conical shells containing piezoelectric layers based on layerwise first-order shear deformation theory by means of differential quadrature method. Chan et al. [13] have presented the nonlinear dynamic and vibration responses of functionally graded conical panel with piezoelectric actuators resting on elastic foundations in thermal environment based on Galerkin and Runge–Kutta methods. Mohammadrezazadeh and Jafari [14] have presented active vibration control of isotropic conical shells with magnetostrictive layers. Moghaddam and Ahmadi [15] have studied active vibration control of functionally graded conical shells in conjunction with piezoelectric layers using a semi-analytical approach while the shell is under harmonic excitation.

Rotating conical shells are widely used in industrial and engineering applications. The vibration behavior of rotating conical shells is investigated by several researchers. Lam and Hua [16] have employed the first approximation of the Love theory to investigate the free vibration of a rotating conical shell. Hua [17] has used Love first approximation theory and Galerkin method to find the free vibration responses of a rotating layered conical shell. Ng et al. [18] have studied the orthotropic influence of composite materials on frequency characteristics of rotating thin laminated composite conical shells. Civalek [19] has investigated the free vibration of rotating conical shells using a discrete singular convolution method. Talebitooti et al. [20] have presented an analytical solution for studying the free vibration of a rotating composite conical shell having stringers and rings. Malekzadeh and Heydarpour [21] have considered the effects of centrifugal and Coriolis forces to study the free vibration of a rotating functionally graded conical shell under different boundary conditions. Heydarpour et al. [22] have analyzed the influences of centrifugal and Coriolis forces on the free vibration of rotating carbon nanotube-reinforced composite conical shells. Nejati et al. [23] have studied the static and free vibration of rotating functionally graded conical shells reinforced with carbon nanotubes. Civalek [24] has investigated free vibration responses of rotating truncated conical shells, circular shells and panels. Sarkheil and Foumani [25] have presented improved formulation for free vibration of a rotating conical shell. Dai et al. [26] have studied the vibration of rotating conical shells using Love first approximation theory and the Haar wavelet method. Shakeri et al. [27] have investigated the free vibration of rotating sandwich conical shells. Talebitooti [28] has employed an approximate solution to study the effects of thermal load on the frequency of ring-stiffened rotating functionally graded conical shells. Dung et al. [29] have analyzed the free vibration of functionally graded rotating conical shells reinforced with rings and stringers. Shakouri [30] has investigated vibration of rotating conical shells from functionally graded materials considering their temperature dependency features. Singha et al. [31] have dealt the effect of elevated temperature and also moisture absorption on the vibration responses of rotating pretwisted sandwich conical shells.

It is obvious that vibration in rotating truncated conical shells is usually undesirable and can cause unwanted phenomena. In this way in this paper for the first time, active vibration control of rotating laminated composite truncated conical shells through magnetostrictive layers based on first-order shear deformation theory is studied. The velocity feedback control method is employed for extracting the control law. The vibration equations are obtained using Hamilton principle taking into consideration the effects of Coriolis and centrifugal forces and also initial hoop tension. The modified Galerkin method is used for obtaining ordinary differential equations from partial differential equations of the rotating conical shell. The correctness and accuracy of the study are obtained by comparison of some results with the results of open literature. The effects of several parameters such as circumferential wave number, rotational velocity, length, large edge radius, semi-vertex angle, the distance of magnetostrictive layers from middle surface, the thickness of magnetostrictive and orthotropic layers and the value of control gain on the active vibration control characteristics of these rotating conical shells are shown and illustrated.

2 Problem formulation

2.1 Basic formulations

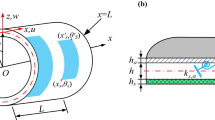
In this paper, active vibration control of a rotating laminated composite truncated conical shell containing two magnetostrictive layers on its inner and outer surfaces is considered. The rotating shell with the reference coordinate system x − θ − z is shown in Fig. 1. The terms x, θ and z are employed, respectively, for longitudinal, circumferential and thickness directions. The origin of the coordinate system is located on the middle surface of the small edge. The rotating laminated composite truncated conical shell consists of N layers, while 2 layers are from magnetostrictive smart material which used for vibration control. The variables L, α, h_mh, Ω, R₁ and R₂ are, respectively, used for the length, semi-vertex angle, magnetostrictive layer thickness, orthotropic layer thickness, constant rotational velocity of the shell about symmetric axis and the middle radiuses of small and large edges of the shell, respectively. In addition, the whole thickness of the shell is introduced by h_T.

Fig. 1

The schematic of the rotating laminated composite truncated conical shell and its reference coordinate system [16]

Using first-order shear deformation theory leads to the displacement components of the shell as below [32]:

$$u = u_{0} + z\psi_{x},\quad v = v_{0} + z\psi_{\theta},\quad w = w_{0}$$

(1)

where u, v and w are referred, respectively, to displacement of an arbitrary point on the shell along x, θ and z directions. In addition, ψ_x and ψ_θ denote total angular rotations about θ and x directions. In addition, u₀, v₀ and w₀ are used for displacement of a point on the middle surface of the rotating conical shell along x, θ and z directions. The relations of strains with displacements and rotations are obtained as follows [32]:

$$\begin{aligned} \varepsilon_{x} & = \varepsilon_{0x} + zk_{x} ,\quad \varepsilon_{\theta } = \varepsilon_{0\theta } + zk_{\theta } ,\quad \varepsilon_{x\theta } = \varepsilon_{0x\theta } + zk_{x\theta } , \\ \varepsilon_{0xz} & = \frac{{\partial w_{0} }}{\partial x} + \psi_{x} ,\quad \varepsilon_{0\theta z} = \frac{1}{R(x)}\frac{{\partial w_{0} }}{\partial \theta } - \frac{{v_{0} \cos \alpha }}{R(x)} + \psi_{\theta } \\ \end{aligned}$$

(2)

while the membrane strains ($\varepsilon_{0x} ,\varepsilon_{0\theta } ,\varepsilon_{0x\theta }$) and curvatures ($k_{x} ,k_{\theta } ,k_{x\theta }$) are given by [32]:

$$\begin{aligned} \varepsilon_{0x} & = \frac{{\partial u_{0} }}{\partial x},\quad \varepsilon_{0\theta } = \frac{1}{R(x)}\frac{{\partial v_{0} }}{\partial \theta } + \frac{{u_{0} \sin \alpha }}{R(x)} + \frac{{w_{0} \cos \alpha }}{R(x)},\quad \varepsilon_{0x\theta } = \frac{{\partial v_{0} }}{\partial x} + \frac{1}{R(x)}\frac{{\partial u_{0} }}{\partial \theta } - \frac{{v_{0} \sin \alpha }}{R(x)} \\ k_{x} & = \frac{{\partial \psi_{x} }}{\partial x},\quad k_{\theta } = \frac{1}{R(x)}\left( {\frac{{\partial \psi_{\theta } }}{\partial \theta } + \psi_{x} \sin \alpha } \right),\quad k_{x\theta } = \frac{{\partial \psi_{\theta } }}{\partial x} + \frac{1}{R(x)}\frac{{\partial \psi_{x} }}{\partial \theta } - \frac{{\psi_{\theta } \sin \alpha }}{R(x)} \\ \end{aligned}$$

(3)

It should be mentioned that the radius of each point on the middle surface of the rotating truncated conical shell is a function of the situation of the point along x axis ($R(x) = R_{1} + x\sin \alpha$). The relation of stresses of each orthotropic or magnetostrictive layer with strains is given by [33]:

$$\left\{ {\begin{array}{*{20}c} {\sigma_{x} } \\ {\sigma_{\theta } } \\ {\sigma_{\theta z} } \\ {\sigma_{xz} } \\ {\sigma_{x\theta } } \\ \end{array} } \right\}^{(k)} = \left[ {\begin{array}{*{20}c} {\bar{Q}_{11} } & {\bar{Q}_{12} } & 0 & 0 & {\bar{Q}_{16} } \\ {\bar{Q}_{12} } & {\bar{Q}_{22} } & 0 & 0 & {\bar{Q}_{26} } \\ 0 & 0 & {\bar{Q}_{44} } & {\bar{Q}_{45} } & 0 \\ 0 & 0 & {\bar{Q}_{45} } & {\bar{Q}_{55} } & 0 \\ {\bar{Q}_{16} } & {\bar{Q}_{26} } & 0 & 0 & {\bar{Q}_{66} } \\ \end{array} } \right]^{(k)} \left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{\theta } } \\ {\varepsilon_{\theta z} } \\ {\varepsilon_{xz} } \\ {\varepsilon_{x\theta } } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {\bar{e}_{31} } \\ {\bar{e}_{32} } \\ 0 \\ 0 \\ {\bar{e}_{36} } \\ \end{array} } \right\}^{(k)} H$$

(4)

In Eq. (4), H and also superscript k, respectively, denote the magnetic field and the number of the layers. It should be mentioned that the second part of Eq. (4) which contains H is only for magnetostrictive layers and does not exist for ordinary orthotropic layers. Furthermore, $\bar{Q}_{ij}$ denote the transformed reduced stiffnesses which are defined as follows [34]:

$$\begin{aligned} \bar{Q}_{11} & = Q_{11} \cos^{4} \zeta + Q_{22} \sin^{4} \xi + 2(Q_{12} + 2Q_{66} )\sin^{2} \xi \cos^{2} \xi \\ \bar{Q}_{12} & = Q_{12} (\sin^{4} \xi + \cos^{4} \xi ) + (Q_{22} + Q_{11} - 4Q_{66} )\sin^{2} \xi \cos^{2} \xi \\ \bar{Q}_{22} & = Q_{11} \sin^{4} \xi + Q_{22} \cos^{4} \xi + 2(2Q_{66} + Q_{12} )\sin^{2} \xi \cos^{2} \xi \\ \bar{Q}_{16} & = (Q_{12} + 2Q_{66} - Q_{22} )\cos \xi \sin^{3} \xi + (Q_{11} - 2Q_{66} - Q_{12} )\cos^{3} \xi \sin \xi \\ \bar{Q}_{26} & = (Q_{12} + 2Q_{66} - Q_{22} )\cos^{3} \xi \sin \xi + (Q_{11} - 2Q_{66} - Q_{12} )\cos \xi \sin^{3} \xi \\ \bar{Q}_{66} & = (Q_{22} + Q_{11} - 2Q_{66} - 2Q_{12} )\cos^{2} \xi \sin^{2} \xi + Q_{66} (\cos^{4} \xi + \sin^{4} \xi ) \\ \bar{Q}_{44} & = Q_{55} \sin^{2} \xi + Q_{44} \cos^{2} \xi \\ \bar{Q}_{45} & = (Q_{55} - Q_{44} )\sin \xi \cos \xi \\ \bar{Q}_{55} & = Q_{44} \sin^{2} \xi + Q_{55} \cos^{2} \xi \\ \end{aligned}$$

(5)

while ξ is the angle of each layer with longitudinal axis. The reduced stiffnesses Q_ij are defined as [34]:

$$\begin{aligned} Q_{11} & = \frac{{E_{1} }}{{1 - \nu_{12} \nu_{21} }},\quad Q_{12} = \frac{{\nu_{12} E_{2} }}{{1 - \nu_{12} \nu_{21} }},\quad Q_{22} = \frac{{E_{2} }}{{1 - \nu_{12} \nu_{21} }} \\ Q_{66} & = G_{12} ,\quad Q_{44} = G_{23} ,\quad Q_{55} = G_{13} \\ \end{aligned}$$

(6)

The variables E₁, E₂, v_ij, G₁₂, G₂₃ and G₁₃ are, respectively, used for Young’s moduli in x and θ directions, Poisson’s ratio, shear moduli in the x − θ, θ − z and x − z surfaces [34]. In addition, the magnetostrictive material coefficients $\bar{e}_{ij}$ are extracted as given by the following relations [33, 35]:

$$\begin{aligned} \bar{e}_{31} & = e_{31} \cos^{2} \xi + e_{32} \sin^{2} \xi \\ \bar{e}_{32} & = e_{32} \cos^{2} \xi + e_{31} \sin^{2} \xi \\ \bar{e}_{36} & = (e_{31} - e_{32} )\sin \xi \cos \xi \\ \end{aligned}$$

(7)

The in-plane forces ($N_{x} ,N_{\theta } ,N_{x\theta }$), moments ($M_{x} ,M_{\theta } ,M_{x\theta }$) and shear forces ($Q_{\theta } ,Q_{x}$) are derived by the following formulations [33]:

$$\left\{ {\begin{array}{*{20}c} {N_{x} } \\ {N_{\theta } } \\ {N_{x\theta } } \\ {M_{x} } \\ {M_{\theta } } \\ {M_{x\theta } } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {A_{11} } & {A_{12} } & {A_{16} } & {B_{11} } & {B_{12} } & {B_{16} } \\ {A_{12} } & {A_{22} } & {A_{26} } & {B_{12} } & {B_{22} } & {B_{26} } \\ {A_{16} } & {A_{26} } & {A_{66} } & {B_{16} } & {B_{26} } & {B_{66} } \\ {B_{11} } & {B_{12} } & {B_{16} } & {D_{11} } & {D_{12} } & {D_{16} } \\ {B_{12} } & {B_{22} } & {B_{26} } & {D_{12} } & {D_{22} } & {D_{26} } \\ {B_{16} } & {B_{26} } & {B_{66} } & {D_{16} } & {D_{26} } & {D_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{0x} } \\ {\varepsilon_{0\theta } } \\ {\varepsilon_{0x\theta } } \\ {k_{x} } \\ {k_{\theta } } \\ {k_{x\theta } } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {A_{31} } \\ {A_{32} } \\ {A_{36} } \\ {B_{31} } \\ {B_{32} } \\ {B_{36} } \\ \end{array} } \right\}H$$

(8)

$$\left\{ {\begin{array}{*{20}c} {Q_{\theta } } \\ {Q_{x} } \\ \end{array} } \right\} = K_{s} \left[ {\begin{array}{*{20}c} {A_{44} } & {A_{45} } \\ {A_{45} } & {A_{55} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{0\theta z} } \\ {\varepsilon_{0xz} } \\ \end{array} } \right\}$$

(9)

where K_s = 5/6 [34] and according to Ref. [33], the following relations exist:

$$\begin{aligned} \left( {A_{ij} ,B_{ij} ,D_{ij} } \right) & = \sum\limits_{k = 1}^{N} {\bar{Q}_{ij}^{(k)} \int\limits_{z} {\left( {1,z,z^{2} } \right){\text{d}}z\quad } } i,j = 1,2,6 \\ A_{ij} & = \sum\limits_{k = 1}^{N} {\bar{Q}_{ij}^{(k)} (z_{k + 1} - z_{k} )\quad i,j = 4,5} \\ \end{aligned}$$

(10)

$$\left( {A_{31} ,A_{32} ,A_{36} ,B_{31} ,B_{32} ,B_{36} } \right) = - ckc\sum\limits_{{k = m_{1} ,m_{2} , \ldots }}^{N} {\int\limits_{{z_{k} }}^{{z_{k + 1} }} {\left( {\bar{e}_{31} ,\bar{e}_{32} ,\bar{e}_{36} ,z\bar{e}_{31} ,z\bar{e}_{32} ,z\bar{e}_{36} } \right){\text{d}}z} }$$

(11)

while ckc is defined in Sect. 2.2.

2.2 Active vibration control law

The smart magnetostrictive layers which are placed in the rotating laminated composite conical shell are employed in order to control vibration actively. Induced magnetic field H is the result of passing current I from the magnetic coils. The relation between magnetic field and electric current is given as [33, 35]:

$$H = k_{\text{c}} I,\quad k_{\text{c}} = \frac{{n_{\text{c}} }}{{\sqrt {b_{\text{c}}^{2} + 4r_{\text{c}}^{2} } }}$$

(12)

In Eq. (12), n_c, b_c and r_c denote number of turns in the coil, coil width and coil radius, respectively. In order to control vibration of the shell actively, velocity feedback control law with the following equation is applied [33, 35]:

$$I = - C\dot{w}$$

(13)

Multiplying C by k_c leads to the control gain value which is shown by ckc ($ckc = C \times k_{\text{c}}$).

Figure 2a depicts a general quasi-static strain with magnetic field curve, while Fig. 2b shows the behavior of Terfenol-D magnetostrictive material.

Fig. 2

The curves of strain with magnetic field, a general quasi-static diagram, b diagram of Terfenol-D magnetostrictive material [1]

These figures illustrate symmetric behavior for positive and negative magnetic fields [1]. In addition, Fig. 2a, b shows that the curves saturate at great field values [1]. When magnetic field gets moderate values, the slope of the curves is comparatively constant [1]. It can be concluded from these figures that bipolar input magnetic field does not result in bipolar output strain [1]. In order to obtain bipolar output strain, it is necessary to operate around a bias point which is the midpoint of the linear section of the curve as shown in Fig. 2a [1]. Therefore, a steady magnetic field H_b must be accomplished to the magnetostrictive material. Therefore, the total magnetic field H_t is obtained as:

$$H_{t} = H + H_{\text{b}}$$

(14)

Figure 3 shows the control diagram which includes actuator and sensor.

Fig. 3

Schematic of the control system with sensor and actuator

2.3 Extraction of vibration equations

Hamilton principle is utilized in order to derive the vibration equations of the rotating laminated composite truncated conical shell by the following relation [36]:

$$\int\limits_{{t_{1} }}^{{t_{2} }} {\left( {\delta T - \delta U_{\varepsilon } - \delta U_{h} } \right){\text{d}}t} = 0$$

(15)

where the variable t denotes time. In addition, T [36], Uε [36] and δU_h [37] denote, respectively, kinetic energy, strain energy and the variation of work carried out on the shell due to centrifugal force. These variables are obtained through the following relations:

$$T = \sum\limits_{k = 1}^{N} {\frac{{\rho^{k} }}{2}\int\limits_{z} {\int\limits_{\theta } {\int\limits_{x} {\left\{ {{\mathbf{V}} \cdot {\mathbf{V}}} \right\}R(x){\text{d}}x{\text{d}}\theta {\text{d}}z} } } }$$

(16)

$$U_{\varepsilon } = \frac{1}{2}\int\limits_{z} {\int\limits_{\theta } {\int\limits_{x} {\left( {\sigma_{x} \varepsilon_{x} + \sigma_{\theta } \varepsilon_{\theta } + \sigma_{x\theta } \varepsilon_{x\theta } + \sigma_{xz} \varepsilon_{xz} + \sigma_{\theta z} \varepsilon_{\theta z} } \right)R(x){\text{d}}x{\text{d}}\theta {\text{d}}z} } }$$

(17)

$$\delta U_{h} = \int\limits_{\theta } {\int\limits_{x} {\frac{{N_{\theta }^{0} }}{{R(x)^{2} }}\left( \begin{aligned} \left( {R(x)\cos \alpha \frac{{\partial w_{0} }}{\partial x} - \frac{{\partial^{2} u_{0} }}{{\partial \theta^{2} }}} \right)\delta u_{0} \hfill \\ \quad \quad + \left( \begin{aligned} v_{0} \sin^{2} \alpha - R(x)\frac{{\partial^{2} u_{0} }}{\partial x\partial \theta } - \sin \alpha \frac{{\partial u_{0} }}{\partial \theta } \hfill \\ - R(x)\sin \alpha \frac{{\partial v_{0} }}{\partial x} \hfill \\ \end{aligned} \right)\delta v_{0} \hfill \\ \quad \quad + \left( {m_{kh} R(x)\cos \alpha \frac{{\partial u_{0} }}{\partial x} + os\frac{{\partial v_{0} }}{\partial \theta } - \frac{{\partial^{2} w_{0} }}{{\partial \theta^{2} }}} \right)\delta w_{0} \hfill \\ \end{aligned} \right)R(x){\text{d}}x{\text{d}}\theta } }$$

(18)

where for conical shell m_kh = 1 and os = 0 and for cylindrical shell m_kh = 0 and os = 1. Besides ρ^k is mass density of each layer of the rotating laminated composite truncated conical shell. In addition, $N_{\theta }^{0}$ and V express, respectively, initial hoop tension [37] and the shell velocity [36] which are given as:

$$N_{\theta }^{0} = I_{1} R(x)^{2} \varOmega^{2}$$

(19)

$$V = {\dot{\mathbf{r}}} + \left( { - \varOmega \cos \alpha {\hat{\mathbf{i}}} + \varOmega \sin \alpha {\hat{\mathbf{k}}}} \right) \times {\mathbf{r}},\quad {\mathbf{r}} = u{\hat{\mathbf{i}}} + v{\hat{\mathbf{j}}} + w{\hat{\mathbf{k}}}$$

(20)

Substituting Eq. (20) into Eq. (16) leads to the following relation for δT:

$$\begin{aligned} \delta T & = \int\limits_{\theta } {\int\limits_{x} {I_{1} \left\{ \begin{aligned} \left\{ { - \ddot{u}_{0} + 2\varOmega \sin \alpha \dot{v}_{0} + \varOmega^{2} u_{0} \sin^{2} \alpha + \varOmega^{2} w_{0} \cos \alpha \sin \alpha } \right\}\delta u_{0} \hfill \\ + \left\{ { - \ddot{v}_{0} - 2\varOmega \sin \alpha \dot{u}_{0} - 2\varOmega \cos \alpha \dot{w}_{0} + \varOmega^{2} v_{0} } \right\}\delta v_{0} \hfill \\ + \left\{ { - \ddot{w}_{0} + 2\varOmega \cos \alpha \dot{v}_{0} + \varOmega^{2} w_{0} \cos^{2} \alpha + \varOmega^{2} u_{0} \cos \alpha \sin \alpha } \right\}\delta w_{0} \hfill \\ \end{aligned} \right\}R(x){\text{d}}x{\text{d}}\theta } } \\ & \quad + \int\limits_{\theta } {\int\limits_{x} {I_{2} \left\{ \begin{aligned} + \left\{ { - \ddot{\psi }_{x} + 2\varOmega \sin \alpha \dot{\psi }_{\theta } + \psi_{x} \varOmega^{2} \sin^{2} \alpha } \right\}\delta u_{0} \hfill \\ + \left\{ { - \ddot{u}_{0} + 2\varOmega \sin \alpha \dot{v}_{0} + u_{0} \varOmega^{2} \sin^{2} \alpha + w_{0} \varOmega^{2} \cos \alpha \sin \alpha } \right\}\delta \psi_{x} \hfill \\ + \left\{ { - \ddot{\psi }_{\theta } - 2\varOmega \sin \alpha \dot{\psi }_{x} + \psi_{\theta } \varOmega^{2} } \right\}\delta v_{0} \hfill \\ + \left\{ { - \ddot{v}_{0} - 2\varOmega \sin \alpha \dot{u}_{0} - 2\varOmega \cos \alpha \dot{w}_{0} + v_{0} \varOmega^{2} } \right\}\delta \psi_{\theta } \hfill \\ + \left\{ {2\varOmega \cos \alpha \dot{\psi }_{\theta } + \psi_{x} \varOmega^{2} \cos \alpha \sin \alpha } \right\}\delta w_{0} \hfill \\ \end{aligned} \right\}R(x){\text{d}}x{\text{d}}\theta } } \\ & \quad + \int\limits_{\theta } {\int\limits_{x} {I_{3} \left\{ \begin{aligned} + \left\{ { - \ddot{\psi }_{x} + \varOmega \sin \alpha \dot{\psi }_{\theta } + \varOmega^{2} \psi_{x} \sin^{2} \alpha + \varOmega \sin \alpha \dot{\psi }_{\theta } } \right\}\delta \psi_{x} \hfill \\ + \left\{ { - \ddot{\psi }_{\theta } - \varOmega \sin \alpha \dot{\psi }_{x} + \varOmega^{2} \psi_{\theta } - \varOmega \sin \alpha \dot{\psi }_{x} } \right\}\delta \psi_{\theta } \hfill \\ \end{aligned} \right\}R(x){\text{d}}x{\text{d}}\theta } } \\ \end{aligned}$$

(21)

While mass moments of inertias are calculated using the following formulation [38]:

$$\left( {I_{1} ,I_{2} ,I_{3} } \right) = \sum\limits_{k = 1}^{N} {\int\limits_{{z_{k} }}^{{z_{k + 1} }} {\rho^{(k)} \left( {1,z,z^{2} } \right){\text{d}}z} }$$

(22)

Substituting relations (4), (8) and (9) into Eq. (17) and doing some mathematical simplifications leads to the following formulation for δU_ε:

$$\begin{aligned} \delta U_{\varepsilon } & = \int\limits_{x} {\int\limits_{\theta } {\left( \begin{aligned} \left( {N_{\theta } \sin \alpha - \frac{{\partial \left( {N_{x} R(x)} \right)}}{\partial x} - \frac{{\partial N_{x\theta } }}{\partial \theta }} \right)\delta u_{0} \hfill \\ \quad + \left( { - Q_{\theta } \cos \alpha - \frac{{\partial \left( {N_{x\theta } R(x)} \right)}}{\partial x} - \frac{{\partial N_{\theta } }}{\partial \theta } - N_{x\theta } \sin \alpha } \right)\delta v_{0} \hfill \\ \quad + \left( {N_{\theta } \cos \alpha - \frac{{\partial \left( {Q_{x} R(x)} \right)}}{\partial x} - \frac{{\partial Q_{\theta } }}{\partial \theta }} \right)\delta w_{0} \hfill \\ \quad + \left( { - \frac{{\partial \left( {M_{x} R(x)} \right)}}{\partial x} - \frac{{\partial M_{x\theta } }}{\partial \theta } + M_{\theta } \sin \alpha + Q_{x} R(x)} \right)\delta \psi_{x} \hfill \\ \quad + \left( { - \frac{{\partial \left( {M_{x\theta } R(x)} \right)}}{\partial x} - \frac{{\partial M_{\theta } }}{\partial \theta } - M_{x\theta } \sin \alpha + Q_{\theta } R(x)} \right)\delta \psi_{\theta } \hfill \\ \end{aligned} \right){\text{d}}x{\text{d}}\theta } } \\ & \quad + \frac{1}{2}\int\limits_{\theta } {(N_{x} R(x)\delta u_{0} )\left| {_{0}^{L} } \right.{\text{d}}\theta } + \frac{1}{2}\int\limits_{\theta } {(N_{x\theta } R(x)\delta v_{0} )\left| {_{0}^{L} } \right.{\text{d}}\theta } + \frac{1}{2}\int\limits_{\theta } {(M_{x} R(x)\delta \psi_{x} )\left| {_{0}^{L} } \right.{\text{d}}\theta } \\ & \quad + \frac{1}{2}\int\limits_{\theta } {(M_{x\theta } R(x)\delta \psi_{\theta } )\left| {_{0}^{L} } \right.{\text{d}}\theta } + \frac{1}{2}\int\limits_{\theta } {Q_{x} R(x)\delta w_{0} \left| {_{0}^{L} } \right.{\text{d}}\theta } \\ & \quad + \frac{1}{2}\int\limits_{x} {\left( {N_{\theta } \delta v_{0} + N_{x\theta } \delta u_{0} + M_{\theta } \delta \psi_{\theta } + M_{x\theta } \delta \psi_{x} + Q_{\theta } \delta w_{0} } \right)\left| {_{0}^{2\pi } } \right.{\text{d}}x} \\ \end{aligned}$$

(23)

Finally, by substituting Eqs. (18), (21) and (23) into Eq. (15), the partial differential equations for the vibration of the rotating laminated composite truncated conical shell are extracted in the following forms:

$$\begin{aligned} & \frac{{\partial N_{x} }}{\partial x}R(x) + \sin \alpha \left( {N_{x} - N_{\theta } } \right) + \frac{{\partial N_{x\theta } }}{\partial \theta } + \frac{{N_{\theta }^{0} }}{R(x)}\left[ {\frac{{\partial^{2} u}}{{\partial \theta^{2} }} - R(x)\cos \alpha \frac{\partial w}{\partial x}} \right] \\ & \quad \quad + I_{1} R(x)\left\{ { - \ddot{u}_{0} + 2\varOmega \sin \alpha \dot{v}_{0} + \varOmega^{2} u_{0} \sin^{2} \alpha + \varOmega^{2} w_{0} \cos \alpha \sin \alpha } \right\} \\ & \quad \quad + I_{2} R(x)\left\{ { - \ddot{\psi }_{x} + 2\varOmega \sin \alpha \dot{\psi }_{\theta } + \psi_{x} \varOmega^{2} \sin^{2} \alpha } \right\} = 0 \\ \end{aligned}$$

(24)

$$\begin{aligned} & \cos \alpha Q_{\theta } + R(x)\frac{{\partial N_{x\theta } }}{\partial x} + 2\sin \alpha N_{x\theta } + \frac{{\partial N_{\theta } }}{\partial \theta } + I_{2} R(x)\left\{ {\psi_{\theta } \varOmega^{2} - \ddot{\psi }_{\theta } - 2\varOmega \sin \alpha \dot{\psi }_{x} } \right\} \\ & \quad \quad + I_{1} R(x)\left\{ { - \ddot{v}_{0} - 2\varOmega \sin \alpha \dot{u}_{0} - 2\varOmega \cos \alpha \dot{w}_{0} + \varOmega^{2} v_{0} } \right\} \\ & \quad \quad + \frac{{N_{\theta }^{0} }}{R(x)}\left[ {R(x)\frac{{\partial^{2} u}}{\partial x\partial \theta } + \sin \alpha \frac{\partial u}{\partial \theta } + R(x)\sin \alpha \frac{\partial v}{\partial x} - v\sin^{2} \alpha } \right] = 0 \\ \end{aligned}$$

(25)

$$\begin{aligned} & \frac{{\partial Q_{x} }}{\partial x}R(x) - N_{\theta } \cos \alpha + Q_{x} \sin \alpha + \frac{{\partial Q_{\theta } }}{\partial \theta } + I_{2} R(x)\left\{ {2\varOmega \cos \alpha \dot{\psi }_{\theta } + \psi_{x} \varOmega^{2} \cos \alpha \sin \alpha } \right\} \\ & \quad \quad + I_{1} R(x)(2\varOmega \cos \alpha \dot{v}_{0} - \ddot{w}_{0} + \varOmega^{2} w_{0} \cos^{2} \alpha + \varOmega^{2} u_{0} \cos \alpha \sin \alpha ) \\ & \quad \quad + \frac{{N_{\theta }^{0} }}{R(x)}\left[ {\frac{{\partial^{2} w}}{{\partial \theta^{2} }} - m_{kh} R(x)\cos \alpha \frac{\partial u}{\partial x} - os\frac{\partial v}{\partial \theta }} \right] = 0 \\ \end{aligned}$$

(26)

$$\begin{aligned} & R(x)\frac{{\partial M_{x} }}{\partial x} + \sin \alpha \left( {M_{x} - M_{\theta } } \right) + \frac{{\partial M_{x\theta } }}{\partial \theta } - Q_{x} R(x) \\ & \quad \quad + I_{3} R(x)\left\{ {\varOmega^{2} \psi_{x} \sin^{2} \alpha - \ddot{\psi }_{x} + 2\varOmega \sin \alpha \dot{\psi }_{\theta } } \right\} \\ & \quad \quad + I_{2} R(x)\left\{ { - \ddot{u}_{0} + 2\varOmega \sin \alpha \dot{v}_{0} + u_{0} \varOmega^{2} \sin^{2} \alpha + w_{0} \varOmega^{2} \cos \alpha \sin \alpha } \right\} = 0 \\ \end{aligned}$$

(27)

$$\begin{aligned} & R(x)\frac{{\partial M_{x\theta } }}{\partial x} + 2\sin \alpha M_{x\theta } + \frac{{\partial M_{\theta } }}{\partial \theta } - Q_{\theta } R(x) + I_{3} R(x)\left\{ { - \ddot{\psi }_{\theta } - 2\varOmega \sin \alpha \dot{\psi }_{x} + \varOmega^{2} \psi_{\theta } } \right\} \\ & \quad \quad + I_{2} R(x)\left\{ { - \ddot{v}_{0} - 2\varOmega \sin \alpha \dot{u}_{0} - 2\varOmega \cos \alpha \dot{w}_{0} + v_{0} \varOmega^{2} } \right\} = 0 \\ \end{aligned}$$

(28)

Substituting Eqs. (2), (3), (8), (9), (12) and (13) into Eqs. (24)–(28) leads to the following matrix relationship:

$${\mathbf{L}}\left\{ {\begin{array}{*{20}c} {u_{0} } \\ {v_{0} } \\ {w_{0} } \\ {\psi_{x} } \\ {\psi_{\theta } } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\ \end{array} } \right\},\quad \quad {\mathbf{L}} = \left[ {\begin{array}{*{20}c} {L_{11} } & {L_{12} } & {L_{13} } & {L_{14} } & {L_{15} } \\ {L_{21} } & {L_{22} } & {L_{23} } & {L_{24} } & {L_{25} } \\ {L_{31} } & {L_{32} } & {L_{33} } & {L_{34} } & {L_{35} } \\ {L_{41} } & {L_{42} } & {L_{43} } & {L_{44} } & {L_{45} } \\ {L_{51} } & {L_{52} } & {L_{53} } & {L_{54} } & {L_{55} } \\ \end{array} } \right]$$

(29)

The elements of matrix L which denote differential operators are given in “Appendix” for cross-ply symmetric laminates. In addition, the geometric and natural boundary conditions for simply supported conical shells are, respectively, as shown in Eqs. (30) and (31) [32, 38]:

$$\begin{aligned} v_{0} (0,\theta ,z) & = 0,\quad w_{0} (0,\theta ,z) = 0,\quad \psi_{\theta } (0,\theta ,z) = 0 \\ v_{0} (L,\theta ,z) & = 0,\quad w_{0} (L,\theta ,z) = 0,\quad \psi_{\theta } (L,\theta ,z) = 0 \\ \end{aligned}$$

(30)

$$\begin{aligned} - N_{x} R(x)\left| {_{(0,\theta ,z)} } \right. & = 0,\quad - M_{x} R(x)\left| {_{(0,\theta ,z)} } \right. = 0 \\ - N_{x} R(x)\left| {_{(L,\theta ,z)} } \right. & = 0,\quad - M_{x} R(x)\left| {_{(L,\theta ,z)} } \right. = 0 \\ \end{aligned}$$

(31)

Natural boundary conditions of the shell which introduced in Eq. (31) can be rewritten as follows:

$${\mathbf{P}}\left\{ {\begin{array}{*{20}c} {u_{0} \left( {x,\theta ,t} \right)} \\ {v_{0} \left( {x,\theta ,t} \right)} \\ {w_{0} \left( {x,\theta ,t} \right)} \\ {\psi_{x} \left( {x,\theta ,t} \right)} \\ {\psi_{\theta } \left( {x,\theta ,t} \right)} \\ \end{array} } \right\} = {\mathbf{0}},\quad x = 0,\quad L,\quad {\mathbf{P}} = \left[ {\begin{array}{*{20}c} {P_{11} } & {P_{12} } & {P_{13} } & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & {P_{44} } & {P_{45} } \\ 0 & 0 & 0 & 0 & 0 \\ \end{array} } \right]$$

(32)

It should be mentioned that the elements of matrix P for symmetric cross-ply laminates are introduced in “Appendix”.

2.4 Problem solution

The trial function which satisfies geometric boundary conditions of Eq. (30) is introduced as follows:

$$\left\{ {\begin{array}{*{20}c} {{\mathbf{u}}_{{\mathbf{0}}} } \\ {{\mathbf{v}}_{{\mathbf{0}}} } \\ {{\mathbf{w}}_{{\mathbf{0}}} } \\ {{\varvec{\uppsi}}_{{\mathbf{x}}} } \\ {{\varvec{\uppsi}}_{{\varvec{\uptheta}}} } \\ \end{array} } \right\} = \left\{ {{\mathbf{\varphi }}_{{\mathbf{1}}} } \right\}\left\{ {\begin{array}{*{20}c} {{\mathbf{u}}_{{{\mathbf{t1}}}} (t)} \\ {{\mathbf{v}}_{{{\mathbf{t1}}}} (t)} \\ {{\mathbf{w}}_{{{\mathbf{t1}}}} (t)} \\ {{\varvec{\uppsi}}_{{{\mathbf{xt1}}}} (t)} \\ {{\varvec{\uppsi}}_{{{\mathbf{\theta t1}}}} (t)} \\ \end{array} } \right\} + \left\{ {{\mathbf{\varphi }}_{{\mathbf{2}}} } \right\}\left\{ {\begin{array}{*{20}c} {{\mathbf{u}}_{{{\mathbf{t2}}}} (t)} \\ {{\mathbf{v}}_{{{\mathbf{t2}}}} (t)} \\ {{\mathbf{w}}_{{{\mathbf{t2}}}} (t)} \\ {{\varvec{\uppsi}}_{{{\mathbf{xt2}}}} (t)} \\ {{\varvec{\uppsi}}_{{{\mathbf{\theta t2}}}} (t)} \\ \end{array} } \right\}$$

(33)

while

$$\left\{ {{\mathbf{\varphi }}_{{\mathbf{1}}} } \right\} = \left\{ {\begin{array}{*{20}c} {\sum\nolimits_{m = 1}^{{M_{\text{T}} }} {\cos \left( {\frac{m\pi x}{L}} \right)\cos n\theta } } \\ {\sum\nolimits_{m = 1}^{{M_{\text{T}} }} {\sin \left( {\frac{m\pi x}{L}} \right)\sin n\theta } } \\ {\sum\nolimits_{m = 1}^{{M_{\text{T}} }} {\sin \left( {\frac{m\pi x}{L}} \right)\cos n\theta } } \\ {\sum\nolimits_{m = 1}^{{M_{\text{T}} }} {\cos \left( {\frac{m\pi x}{L}} \right)\cos n\theta } } \\ {\sum\nolimits_{m = 1}^{{M_{\text{T}} }} {\sin \left( {\frac{m\pi x}{L}} \right)\sin n\theta } } \\ \end{array} } \right\},\quad \quad \left\{ {{\mathbf{\varphi }}_{{\mathbf{2}}} } \right\} = \left\{ {\begin{array}{*{20}c} { - \sum\nolimits_{m = 1}^{{M_{\text{T}} }} {\cos \left( {\frac{m\pi x}{L}} \right)\sin n\theta } } \\ {\sum\nolimits_{m = 1}^{{M_{\text{T}} }} {\sin \left( {\frac{m\pi x}{L}} \right)\cos n\theta } } \\ { - \sum\nolimits_{m = 1}^{{M_{\text{T}} }} {\sin \left( {\frac{m\pi x}{L}} \right)\sin n\theta } } \\ { - \sum\nolimits_{m = 1}^{{M_{\text{T}} }} {\cos \left( {\frac{m\pi x}{L}} \right)\sin n\theta } } \\ {\sum\nolimits_{m = 1}^{{M_{\text{T}} }} {\sin \left( {\frac{m\pi x}{L}} \right)\cos n\theta } } \\ \end{array} } \right\},n = 1,2, \ldots$$

(34)

where m and n denote longitudinal and circumferential wave numbers, respectively, and M_T denotes bounding value for longitudinal wave number. It should be mentioned that definitions of u₀, v₀ and w₀ in Eqs. (33) and (34) are similar to reference [39]. It is important to mention that in this study the inputs are considered in a way that the function of θ is not written in series forms. Galerkin method [32] can be employed in order to convert the differential equations into ordinary differential equations. The trial function of Galerkin method is necessary to satisfy both geometric and natural boundary conditions [32]. Since the introduced trial function in Eq. (33) only satisfies geometric boundary conditions, according to Hamilton principle and Eq. (23), the following modified formulation is introduced, named modified Galerkin method:

$$\int\limits_{0}^{L} {\int\limits_{0}^{2\pi } {\left( {{\mathbf{L}}\left\{ {{\mathbf{u}}_{{\mathbf{0}}} ,{\mathbf{v}}_{{\mathbf{0}}} ,{\mathbf{w}}_{{\mathbf{0}}} ,{\varvec{\uppsi}}_{{\mathbf{x}}} ,{\varvec{\uppsi}}_{{\varvec{\uptheta}}} } \right\}^{\text{T}} } \right)\left\{ {\mathbf{\varphi }} \right\}{\text{d}}\theta {\text{d}}x} } - \int\limits_{0}^{2\pi } {\left( {\left( {{\mathbf{P}}\left\{ {{\mathbf{u}}_{{\mathbf{0}}} ,{\mathbf{v}}_{{\mathbf{0}}} ,{\mathbf{w}}_{{\mathbf{0}}} ,{\varvec{\uppsi}}_{{\mathbf{x}}} ,{\varvec{\uppsi}}_{{\varvec{\uptheta}}} } \right\}^{\text{T}} } \right)\left\{ {\mathbf{\varphi }} \right\}} \right)\left| {_{0}^{L} } \right.} = {\mathbf{0}}$$

(35)

while

$$\left\{ {\mathbf{\varphi }} \right\} = \left\{ {cc, - cs,ss,sc,sc, - ss,cc, - cs,ss,sc} \right\}$$

(36)

where

$$\begin{aligned} cc & = \sum\limits_{m = 1}^{{M_{T} }} {\cos \left( {\frac{m\pi x}{L}} \right)} \cos n\theta ,\quad cs = \sum\limits_{m = 1}^{{M_{T} }} {\cos \left( {\frac{m\pi x}{L}} \right)} \sin n\theta \\ ss & = \sum\limits_{m = 1}^{{M_{T} }} {\sin \left( {\frac{m\pi x}{L}} \right)} \sin n\theta ,\quad sc = \sum\limits_{m = 1}^{{M_{T} }} {\sin \left( {\frac{m\pi x}{L}} \right)} \cos n\theta \\ \end{aligned}$$

(37)

Substituting Eq. (36) into Eq. (35) and doing some mathematical effort leads to the following formulation:

$${\mathbf{M\ddot{x}}} + \left( {{\mathbf{C}}_{{{\mathbf{damping}}}} + {\mathbf{C}}_{{{\mathbf{rotation}}}} } \right){\dot{\mathbf{x}}} + {\mathbf{Kx}} = {\mathbf{0}},{\mathbf{x}} = \left\{ {{\mathbf{u}}_{{{\mathbf{t1}}}} ,{\mathbf{u}}_{{{\mathbf{t2}}}} ,{\mathbf{v}}_{{{\mathbf{t1}}}} ,{\mathbf{v}}_{{{\mathbf{t2}}}} ,{\mathbf{w}}_{{{\mathbf{t1}}}} ,{\mathbf{w}}_{{{\mathbf{t2}}}} ,{\varvec{\uppsi}}_{{{\mathbf{xt1}}}} ,{\varvec{\uppsi}}_{{{\mathbf{xt2}}}} ,{\varvec{\uppsi}}_{{{\mathbf{\theta t1}}}} ,{\varvec{\uppsi}}_{{{\mathbf{\theta t2}}}} } \right\}^{\text{T}}$$

(38)

where M and K denote mass and stiffness matrices, respectively. Furthermore, C_dampling is the result of the damping characteristics caused by magnetostrictive layers. In addition, the components of C_rotation are related to the rotation speed of the rotating shell. In order to solve Eq. (38), state space form can be used [32]:

$${\dot{\mathbf{y}}} = {\mathbf{Ay}},\quad {\mathbf{y}} = \left[ {{\mathbf{x}},{\dot{\mathbf{x}}}} \right]^{\text{T}}$$

(39)

where

$${\mathbf{A}} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{I}} \\ { - {\mathbf{M}}^{ - 1} {\mathbf{K}}} & { - {\mathbf{M}}^{ - 1} \left( {{\mathbf{C}}_{{{\mathbf{damping}}}} + {\mathbf{C}}_{{{\mathbf{rotation}}}} } \right)} \\ \end{array} } \right]$$

(40)

Two eigenvalues $\lambda_{\text{b}} = - \beta_{\text{b}} \pm \omega_{\text{b}}$ and $\lambda_{\text{f}} = - \beta_{\text{f}} \pm \omega_{\text{f}}$ exist for matrix A, while β_b and β_f are backward and forward damping coefficients. Furthermore, ω_b and ω_f express, respectively, backward and forward frequencies. It should be mentioned that the absolute value of backward wave is generally larger than forward wave’s absolute value [37]. In addition, when the shell does not rotate (Ω = 0) backward and forward waves get the same values ($\lambda = - \beta \pm i\omega$), while β and ω are, respectively, referred to damping coefficient and frequency for the stationary conical shell. Doing some mathematical simplifications, the time response is obtained as follows:

$${\mathbf{y}} = {\mathbf{Y}}\exp (\left[ {\lambda_{i} } \right]t){\mathbf{Y}}^{ - 1} {\mathbf{y}}_{{\mathbf{0}}}$$

(41)

where Y, [λ_i] and y₀, respectively, denote matrix of right eigenvectors, diagonal matrix of eigenvalues and the vector of initial values, where

$${\mathbf{y}}_{{\mathbf{0}}} = \left\{ {\begin{array}{*{20}c} {{\mathbf{y}}_{{{\mathbf{01}}}} } \\ {{\mathbf{y}}_{{{\mathbf{02}}}} } \\ \end{array} } \right\}$$

(42)

where

$${\mathbf{y}}_{{{\mathbf{01}}}} = \left\{ {{\mathbf{u}}_{{{\mathbf{t1}}}} (0),{\mathbf{u}}_{{{\mathbf{t2}}}} (0),{\mathbf{v}}_{{{\mathbf{t1}}}} (0),{\mathbf{v}}_{{{\mathbf{t2}}}} (0),{\mathbf{w}}_{{{\mathbf{t1}}}} (0),{\mathbf{w}}_{{{\mathbf{t2}}}} (0),{\varvec{\uppsi}}_{{{\mathbf{xt1}}}} (0),{\varvec{\uppsi}}_{{{\mathbf{xt2}}}} (0),{\varvec{\uppsi}}_{{{\mathbf{\theta t1}}}} (0),{\varvec{\uppsi}}_{{{\mathbf{xt2}}}} (0)} \right\}^{\text{T}}$$

(43)

$${\mathbf{y}}_{{{\mathbf{02}}}} = \left\{ {{\dot{\mathbf{u}}}_{{{\mathbf{t1}}}} (0),{\dot{\mathbf{u}}}_{{{\mathbf{t2}}}} (0),{\dot{\mathbf{v}}}_{{{\mathbf{t1}}}} (0),{\dot{\mathbf{v}}}_{{{\mathbf{t2}}}} (0),{\dot{\mathbf{w}}}_{{{\mathbf{t1}}}} (0),{\dot{\mathbf{w}}}_{{{\mathbf{t2}}}} (0),{\dot{\mathbf{\psi }}}_{{{\mathbf{xt1}}}} (0),{\dot{\mathbf{\psi }}}_{{{\mathbf{xt2}}}} (0),{\dot{\mathbf{\psi }}}_{{{\mathbf{\theta t1}}}} (0),{\dot{\mathbf{\psi }}}_{{{\mathbf{xt2}}}} (0)} \right\}^{\text{T}}$$

(44)

Substituting Eq. (41) into Eq. (33) and then substituting the result in Eq. (1) leads to the displacement of each point of the rotating shell.

3 Results and discussion

In this paper, active vibration control of rotating laminated composite truncated conical shells embedded with two magnetostrictive layers is investigated. It should be mentioned that all of the results included in this section are for the shells with simply supported boundary conditions. At first, in order to validate this study, it is necessary to make comparison between some results of this study with published results of the literature. In this way, Table 1 presents the frequency parameter results ($\omega^{ * } = \omega R_{2} \sqrt {{{\left( {1 - \upsilon_{12}^{2} } \right)\rho } \mathord{\left/ {\vphantom {{\left( {1 - \upsilon_{12}^{2} } \right)\rho } {E_{1} }}} \right. \kern-0pt} {E_{1} }}}$) of this study and also literature for a non-rotating isotropic truncated conical shell with $\upsilon_{12} = 0.3,{{L\sin \alpha } \mathord{\left/ {\vphantom {{L\sin \alpha } {R_{2} }}} \right. \kern-0pt} {R_{2} }} = 0.25,{{h_{\text{T}} } \mathord{\left/ {\vphantom {{h_{\text{T}} } {R_{2} }}} \right. \kern-0pt} {R_{2} }} = 0.01$ while α = 45° and α = 60°. It should be mentioned that ρ is density. Table 1 reveals that there is good adaptation between the results of this study with the corresponding results of the literature. This fact demonstrates the correctness and validity of the present study. In order to show the validity of this study for rotating shells, Table 2 shows the non-dimensional backward and forward waves results ($\omega_{b(f)}^{ * } = \omega_{{b ( {\text{f)}}}} R_{2} \sqrt {{\rho \mathord{\left/ {\vphantom {\rho {E_{2} }}} \right. \kern-0pt} {E_{2} }}}$) obtained for a [0°/90°/0°] laminated rotating cylindrical shell which rotates with three different rotation speeds Ω = 0.1 rps, Ω = 0.4 rps and Ω = 1 rps (rps, revolutions per second) and compares the results of this study with the open literature. The constants of this rotating shell are considered to be:

$$\begin{aligned} m & = 1,\quad {h \mathord{\left/ {\vphantom {h {R_{2} }}} \right. \kern-0pt} {R_{2} }} = 0.002,\quad {L \mathord{\left/ {\vphantom {L {R_{2} }}} \right. \kern-0pt} {R_{2} }} = 1,\quad E_{2} = 7.6\,{{\text{GN}} \mathord{\left/ {\vphantom {{\text{GN}} {{\text{m}}^{2} }}} \right. \kern-0pt} {{\text{m}}^{2} }},\quad {{E_{1} } \mathord{\left/ {\vphantom {{E_{1} } {E_{2} }}} \right. \kern-0pt} {E_{2} }} = 2.5, \\ G_{12} & = 4.1\,{{\text{GN}} \mathord{\left/ {\vphantom {{\text{GN}} {{\text{m}}^{2} }}} \right. \kern-0pt} {{\text{m}}^{2} }},\quad \upsilon_{12} = 0.26,\quad \rho = 1643\,{{\text{kg}} \mathord{\left/ {\vphantom {{\text{kg}} {{\text{m}}^{3} }}} \right. \kern-0pt} {{\text{m}}^{3} }} \\ \end{aligned}$$

(45)

The results in Table 2 show good agreement between this study and literature results which corroborates the validity of this study.

Table 1 Frequency parameter results obtained for a non-rotating isotropic truncated conical shell

Table 2 Non-dimensional backward and forward waves ($\omega_{\text{b}}^{ * }$,$\omega_{f}^{ * }$) for a [0°/90°/0°] laminated rotating cylindrical shell with different values of rotation speed

After the validation of this study, it is time to demonstrate the effects of various parameters on the active vibration control of the rotating laminated composite truncated conical shell. In this way, a rotating laminated composite truncated conical shell with the lamination scheme of [mag/90°/0°/90°/0°]_s is considered, while the expression mag is used for magnetostrictive layers. Hence, the shell consists of 10 layers which are symmetrically placed according to middle surface, while all 8 orthotropic layers are from CFRP material unless mentioned otherwise and 2 layers are from Terfenol-D which is a smart magnetostrictive material. The active vibration control task lies with Terfenol-D magnetostrictive layers using velocity feedback control law. The rotating laminated composite truncated conical shell’s constants are considered to be: $\alpha = 30^{ \circ } ,L = 0.5{\text{ m}},R_{2} = 1{\text{ m}},h = 1{\text{ mm}},h_{m} = 1{\text{ mm}},M_{\text{T}} = 4,n = 4,ckc = 10^{4}$ unless mentioned other values.

The variation of backward and forward damping coefficients (β_b and β_f) with circumferential wave number n for several values of rotation speed is shown in Fig. 4a, b, respectively. The results of Fig. 4a, b are obtained for L = 0.1 m, M_T = 3. Figure 4 shows that for a constant value of rotational velocity, the values of β_b and β_f decrease with increase in n. In addition for a fixed value of n, the change of β_b and β_f values with increase in rotation speed is negligible.

Fig. 4

Variation of backward and forward damping coefficients with circumferential wave number for different values of rotational velocity

Figure 5a, b depicts, respectively, the variation of backward and forward frequencies with n for different values of rotation speed. Figure 5a, b is for a conical shell with L = 0.1 m, M_T = 3. Figure 5a, b demonstrates that for a fixed value of n in the range of n > 6, the absolute values of ω_b and ω_f increase with the increase in rotation speed. In addition, the values of both ω_b and ω_f in the range of n < 5 decrease with increase in circumferential wave number n for each rotational velocity; while in the range of n > 6, the values of ω_b and ω_f become larger with increase in n for each rotation speed.

Fig. 5

Variation of backward and forward frequencies with circumferential wave number for different values of rotation speed

Figure 6a, b shows, respectively, the variation of backward and forward damping coefficients and frequencies with rotation speed for different values of the rotating truncated conical shell’s length. One can conclude from Fig. 6a that for a fixed value of rotational velocity, the values of both backward and forward damping coefficients decrease with increase in the shell length. In addition for a constant value of length, the value of backward damping coefficient increases as the rotation speed becomes larger. On the other hand, the forward damping coefficient gets smaller value with increase in rotation speed. Figure 6b demonstrates that for a constant rotation speed, the values of backward and forward frequencies take smaller values with increase in the length. Besides, for a fixed value of the length, the increase in rotation speed leads to greater value for backward frequency.

Fig. 6

The effect of the length on the diagrams of backward and forward waves with rotational velocity, a damping coefficients, b frequencies

The effect of the large edge radius of the rotating conical shell on the curves of backward and forward damping coefficients with rotational velocity is shown in Fig. 7a. Figure 7a demonstrates that for a constant rotational velocity, increase in large edge radius leads to increase in the backward and forward damping coefficients. In addition, for a fixed value of R₂, the increase in rotation speed leads to increase in backward damping coefficient and decrease in forward damping coefficient; thus, the deference between the values of backward and forward damping coefficients in higher rotation speeds is greater. Figure 7b depicts the diagrams of backward and forward frequencies with rotation speed for different values of the large edge radius. According to Fig. 7b, it can be realized that for a fixed value of Ω, as the large edge radius R₂ becomes higher, the values of backward and forward frequencies become smaller. In addition, for a constant value of the large edge radius, the increase in rotation speed leads to increase in backward frequency.

Fig. 7

The effect of the large edge radius on the curves of backward and forward waves with rotation speed, a damping coefficients, b frequencies

Figure 8a depicts the variation of backward and forward damping coefficients with the semi-vertex angle α for different values of rotational velocity. It can be observed from Fig. 8a that for a fixed value of semi-vertex angle, the values of backward and forward damping coefficients become, respectively, greater and smaller as the rotation speed increases. Furthermore, for a determined value of rotation speed, backward and forward damping coefficients get smaller values as semi-vertex angle increases. Figure 8b demonstrates the curves of backward and forward frequencies with semi-vertex angle for different values of rotational velocity. According to Fig. 8b, one can conclude that when rotation speed is fixed, the values of backward and forward frequencies become smaller with increase in semi-vertex angle. Besides, for a constant value of semi-vertex angle, the increase in rotation speed leads to greater values for backward frequency.

Fig. 8

Variation of backward and forward waves with semi-vertex angle for different values of rotation speed, a damping coefficients, b frequencies

The effect of magnetostrictive layers distance from middle surface on the values of backward and forward damping coefficients and frequencies is presented in Table 3, while Ω = 10 rps and L = 0.6 m. According to Table 3, it can be realized that as the distance of magnetostrictive layers from middle surface increases the backward and forward frequencies get smaller values; but in general, the results in Table 3 demonstrate that the effect of the magnetostrictive layers’ location on the backward and forward damping coefficients and frequencies is small and negligible.

Table 3 The effect of the magnetostrictive layers’ position from middle surface on the backward and forward damping coefficients and frequencies

At the rest of this paper, the effect of several parameters on the diagrams of displacement in the thickness direction with time is investigated, while the values of rotation speed and initial velocity in thickness direction ($\dot{w}(0)$) are considered to be 10 rps and 3 mm/s, respectively. It should be mentioned that the displacement in thickness direction is for a point with position of x = 0.5L and θ = 0.

Figure 9a demonstrates the effect of the magnetostrictive layer’s thickness on the displacement of the conical shell in thickness direction. One can conclude from this figure that the vibration suppression rate increases with the increase in the magnetostrictive layer thickness. Figure 9b depicts the diagram of magnetic field H with time t for different values of the magnetostrictive layer’s thickness. This figure shows that the absolute value of magnetic field H is less than 40 Ampere/m. Figure 2b shows that in this range around the bias point ($\left| H \right| < 40{\text{ Ampere/m}}$) the behavior of the Terfenol-D magnetostrictive material is linear and matches the linear model that is considered in this study (Eq. 4); therefore, the selection of control gain and modeling of the control system is done correctly. In addition, Fig. 9b illustrates that the value of H becomes smaller for small values of time as the value of the thickness for magnetostrictive layer become higher.

Fig. 9

The effect of the magnetostrictive layer thickness on the curves of a displacement in thickness direction with time and b the magnetic field H with time

Figure 10a depicts the effects of CFRP layer’s thickness on the curves of displacement in thickness direction with time. This figure demonstrates that the increase in the CFRP layer’s thickness leads to slower vibration suppression. Figure 10b shows the curves of magnetic field H with time for different values of the orthotropic layer’s thickness. Figure 10b indicates that the absolute value of H is less than 50 Ampere/m. According to Fig. 2b, it can be concluded that this range around the bias point ($\left| H \right| < 50{\text{ Ampere/m}}$) belongs to linear region.

Fig. 10

The influence of the CFRP layer’s thickness on the curves of a displacement w with time, b magnetic field H with time

The effect of the control gain value ckc on the suppression of the displacement w of the rotating laminated composite conical shell is shown in Fig. 11a. When ckc = 0, the suppression does not take place, whereas the increase in control gain leads to faster suppression of the displacement in thickness direction. Figure 11b displays the curves of magnetic field H with time for different values of the control gain. This figure shows that the value of magnetic field H is zero for zero value of the control gain. On the other hand, the increase in the control gain leads to increase in the magnetic field H for small values of time; however, the magnetic field H is in the range that guarantees linear behavior according to Fig. 2b ($\left| H \right| < 300{\text{ Ampere/m}}$). As shown in Fig. 11a, when ckc = 10⁴, vibration suppression takes place almost in 0.2 s. According to this reason and also the fact that the increase in control gain leads to increase in magnetic field H for small times according to Fig. 11b, one can infer that the selection of ckc = 10⁴ is adequate. In addition, in references [33] and [35], the absolute value of ckc is considered to be 10⁴.

Fig. 11

The effect of the control gain on the curves of a displacement response w with time, b magnetic field H with time

4 Conclusion

In this paper, the active vibration control of rotating laminated composite truncated conical shells embedded with two magnetostrictive layers is studied. Feedback velocity control law is used for the purpose of active vibration control. The vibration equations of the rotating laminated composite truncated conical shell are extracted considering the effects of initial hoop tension and centrifugal and Coriolis forces by means of Hamilton principle based on first-order shear deformation theory. The task of reducing the differential equations into ordinary ones lies with modified Galerkin method. The validation of this study is investigated by comparison of some results with the results of other studies. Good agreement of this study’s results with the literature confirms the reliability of this study. The effects of several parameters such as circumferential wave number, rotation speed, length, large edge radius, semi-vertex angle, the location of magnetostrictive layers from middle surface, magnetostrictive and also orthotropic layers thickness and control gain value on the vibration attenuation of the rotating laminated composite conical shell are investigated.

Appendix

The differential operators of matrix L which is introduced in Eq. (29) are defined as the following for symmetric cross-ply lamination scheme:

$$\begin{aligned} L_{11} & = A_{11} R(x)\frac{{\partial^{2} }}{{\partial x^{2} }} + A_{11} \sin \alpha \frac{\partial }{\partial x} - \frac{{A_{22} \sin^{2} \alpha }}{R(x)} + \frac{{A_{66} }}{R(x)}\frac{{\partial^{2} }}{{\partial \theta^{2} }} - I_{1} R(x)\frac{{\partial^{2} }}{{\partial t^{2} }} \\ & \quad + I_{1} \varOmega^{2} R(x)\sin^{2} \alpha + I_{1} \varOmega^{2} R(x)\frac{{\partial^{2} }}{{\partial \theta^{2} }} \\ \end{aligned}$$

(46)

$$L_{12} = A_{12} \frac{{\partial^{2} }}{\partial x\partial \theta } - \frac{{A_{22} \sin \alpha }}{R(x)}\frac{\partial }{\partial \theta } + A_{66} \frac{{\partial^{2} }}{\partial x\partial \theta } - \frac{{A_{66} \sin \alpha }}{R(x)}\frac{\partial }{\partial \theta } + 2I_{1} \varOmega R(x)\sin \alpha \frac{\partial }{\partial t}$$

(47)

$$\begin{aligned} L_{13} & = A_{12} \cos \alpha \frac{\partial }{\partial x} - A_{31} R(x)\frac{{\partial^{2} }}{\partial x\partial t} - A_{31} \sin \alpha \frac{\partial }{\partial t} - \frac{{A_{22} \sin \alpha \cos \alpha }}{R(x)} + A_{32} \sin \alpha \frac{\partial }{\partial t} \\ & \quad + I_{1} \varOmega^{2} R(x)\sin \alpha \cos \alpha - I_{1} (R(x))^{2} \varOmega^{2} \cos \alpha \frac{\partial }{\partial x} \\ \end{aligned}$$

(48)

$$L_{14} = 0$$

(49)

$$L_{15} = 0$$

(50)

$$\begin{aligned} L_{21} & = A_{12} \frac{{\partial^{2} }}{\partial x\partial \theta } + \frac{{A_{22} \sin \alpha }}{R(x)}\frac{\partial }{\partial \theta } + A_{66} \frac{{\partial^{2} }}{\partial x\partial \theta } + \frac{{A_{66} \sin \alpha }}{R(x)}\frac{\partial }{\partial \theta } - 2I_{1} \varOmega R(x)\sin \alpha \frac{\partial }{\partial t} \\ & \quad + I_{1} \varOmega^{2} (R(x))^{2} \frac{{\partial^{2} }}{\partial x\partial \theta } + I_{1} \varOmega^{2} R(x)\sin \alpha \frac{\partial }{\partial \theta } \\ \end{aligned}$$

(51)

$$\begin{aligned} L_{22} & = \frac{{A_{22} }}{R(x)}\frac{{\partial^{2} }}{{\partial \theta^{2} }} + A_{66} R(x)\frac{{\partial^{2} }}{{\partial x^{2} }} + A_{66} \sin \alpha \frac{\partial }{\partial x} - \frac{{A_{66} }}{R(x)}\sin^{2} \\ & \quad\alpha - \frac{{K_{s} A_{44} \cos^{2} \alpha }}{R(x)} - I_{1} R(x)\frac{{\partial^{2} }}{{\partial t^{2} }} + I_{1} \varOmega^{2} R(x)\\ & \quad + I_{1} \varOmega^{2} (R(x))^{2} \sin \alpha \frac{\partial }{\partial x} - I_{1} \varOmega^{2} R(x)\sin^{2} \alpha \\ \end{aligned}$$

(52)

$$L_{23} = \frac{{A_{22} \cos \alpha }}{R(x)}\frac{\partial }{\partial \theta } - A_{32} \frac{{\partial^{2} }}{\partial \theta \partial t} + \frac{{K_{s} A_{44} \cos \alpha }}{R(x)}\frac{\partial }{\partial \theta } - 2I_{1} \varOmega R(x)\cos \alpha \frac{\partial }{\partial t}$$

(53)

$$L_{24} = 0$$

(54)

$$L_{25} = K_{\text{s}} A_{44} \cos \alpha$$

(55)

$$\begin{aligned} L_{31} & = - A_{12} \cos \alpha \frac{\partial }{\partial x} - \frac{{A_{22} \sin \alpha \cos \alpha }}{R(x)} + I_{1} \varOmega^{2} R(x)\sin \alpha \cos \alpha \\ & \quad - m_{kh} I_{1} \varOmega^{2} (R(x))^{2} \cos \alpha \frac{\partial }{\partial x} \\ \end{aligned}$$

(56)

$$ \begin{aligned}L_{32} &= - \frac{{A_{22} \cos \alpha }}{R(x)}\frac{\partial }{\partial \theta } - \frac{{K_{\text{s}} A_{44} \cos \alpha }}{R(x)}\frac{\partial }{\partial \theta } \\ &\quad+ 2I_{1} \varOmega R(x)\cos \alpha \frac{\partial }{\partial t} - I_{1} os\varOmega^{2} R(x)\frac{\partial }{\partial \theta }\end{aligned} $$

(57)

$$\begin{aligned} L_{33} & = - \frac{{A_{22} \cos^{2} \alpha }}{R(x)} + A_{32} \cos \alpha \frac{\partial }{\partial t} + K_{\text{s}} A_{55} R(x)\frac{{\partial^{2} }}{{\partial x^{2} }} + K_{s} A_{55} \sin \alpha \frac{\partial }{\partial x} \\ & \quad + \frac{{K_{\text{s}} A_{44} }}{R(x)}\frac{{\partial^{2} }}{{\partial \theta^{2} }} - I_{1} R(x)\frac{{\partial^{2} }}{{\partial t^{2} }} + I_{1} \varOmega^{2} R(x)\cos^{2} \alpha + I_{1} \varOmega^{2} R(x)\frac{{\partial^{2} }}{{\partial \theta^{2} }} \\ \end{aligned}$$

(58)

$$L_{34} = K_{\text{s}} A_{55} R(x)\frac{\partial }{\partial x} + K_{\text{s}} A_{55} \sin \alpha$$

(59)

$$L_{35} = K_{\text{s}} A_{44} \frac{\partial }{\partial \theta }$$

(60)

$$L_{41} = 0$$

(61)

$$L_{42} = 0$$

(62)

$$L_{43} = - K_{\text{s}} A_{55} R(x)\frac{\partial }{\partial x}$$

(63)

$$\begin{aligned} L_{44} & = D_{11} R(x)\frac{{\partial^{2} }}{{\partial x^{2} }} + D_{11} \sin \alpha \frac{\partial }{\partial x} - \frac{{D_{22} \sin^{2} \alpha }}{R(x)} + \frac{{D_{66} }}{R(x)}\frac{{\partial^{2} }}{{\partial \theta^{2} }} - K_{\text{s}} A_{55} R(x) \\ & \quad - I_{3} R(x)\frac{{\partial^{2} }}{{\partial t^{2} }} + I_{3} \varOmega^{2} R(x)\sin^{2} \alpha \\ \end{aligned}$$

(64)

$$ \begin{aligned}L_{45} &= D_{12} \frac{{\partial^{2} }}{\partial x\partial \theta } - \frac{{D_{22} \sin \alpha }}{R(x)}\frac{\partial }{\partial \theta } + D_{66} \frac{{\partial^{2} }}{\partial x\partial \theta } \\ &\quad- \frac{{D_{66} \sin \alpha }}{R(x)}\frac{\partial }{\partial \theta } + 2I_{3} \varOmega R(x)\sin \alpha \frac{\partial }{\partial t}\end{aligned} $$

(65)

$$L_{51} = 0$$

(66)

$$L_{52} = K_{\text{s}} A_{44} \cos \alpha$$

(67)

$$L_{53} = - K_{\text{s}} A_{44} \frac{\partial }{\partial \theta }$$

(68)

$$ \begin{aligned}L_{54} &= D_{12} \frac{{\partial^{2} }}{\partial x\partial \theta } + \frac{{D_{22} \sin \alpha }}{R(x)}\frac{\partial }{\partial \theta } + D_{66} \frac{{\partial^{2} }}{\partial x\partial \theta } \\ &\quad+ \frac{{D_{66} \sin \alpha }}{R(x)}\frac{\partial }{\partial \theta } - 2I_{3} \varOmega R(x)\sin \alpha \frac{\partial }{\partial t}\end{aligned} $$

(69)

$$\begin{aligned} L_{55} & = \frac{{D_{22} }}{R(x)}\frac{{\partial^{2} }}{{\partial \theta^{2} }} + D_{66} R(x)\frac{{\partial^{2} }}{{\partial x^{2} }} + D_{66} \sin \alpha \frac{\partial }{\partial x} \\ & \quad - \frac{{D_{66} \sin^{2} \alpha }}{R(x)} - K_{\text{s}} A_{44} R(x) - I_{3} R(x)\frac{{\partial^{2} }}{{\partial t^{2} }} + I_{3} \varOmega^{2} R(x) \\ \end{aligned}$$

(70)

The elements of matrix P which is presented in Eq. (32) can be obtained in the following types for cross-ply symmetric laminate scheme:

$$P_{11} = - A_{11} R(x)\frac{\partial }{\partial x} - A_{12} \sin \alpha$$

(71)

$$P_{12} = - A_{12} \frac{\partial }{\partial \theta }$$

(72)

$$P_{13} = - A_{12} \cos \alpha + A_{31} R(x)\frac{\partial }{\partial t}$$

(73)

$$P_{44} = - D_{11} R(x)\frac{\partial }{\partial x} - D_{12} \sin \alpha$$

(74)

$$P_{45} = - D_{12} \frac{\partial }{\partial \theta }$$

(75)