Effect of graphene nanoplatelet reinforcements on the dynamics of rotating truncated conical shells

Abstract

In this paper, a parametric study is presented for free vibration analysis of rotating truncated conical shells reinforced with graphene nanoplatelets (GNPs). The composite shell is considered to be composed of epoxy as the matrix and the GNPs which are distributed along the thickness direction based on the various distribution patterns. The shell is modeled based on the first-order shear deformation theory (FSDT), and effective material properties are calculated based on the Halpin–Tsai model and the rule of mixture. Incorporating centrifugal and Coriolis accelerations along with initial hoop tension, the set of the governing equations and boundary conditions are derived using Hamilton’s principle and are solved numerically using generalized differential quadrature method. Convergence and accuracy of the presented solution are confirmed, and influences of various parameters on the forward and backward frequencies are investigated including circumferential mode number, boundary conditions, rotational speed, semi-vertex angle and also mass fraction, distribution pattern, width and thickness of the GNPs. It is noteworthy that for the first time, the initial hoop tension is incorporated for a rotating conical shell modeled based on the FSDT.

1 Introduction

Due to their excellent mechanical and thermal properties, GNPs have been widely used as reinforcement in various engineering fields such as aerospace, automotive and civil engineering. Besides the experimental works on the material properties of GNP-reinforced composites, some theoretical and numerical works are presented on the mechanical behavior of such structures. Habibi et al. [1] studied wave propagation analysis of GNP-reinforced composite cylindrical nanoshells coupled with piezoelectric actuator and surrounded with viscoelastic foundation. They concluded that by adding GNPs in the pure epoxy matrix, the phase velocity of the nanoshells improves. Barati and Shahverdi [2] used finite element method (FEM) and studied forced vibration analysis of GNP-reinforced nanocomposite beams in thermal environments. They showed that dynamical deflection can be affected by weight fraction and distribution of GNPs, and resonance of nanocomposite beams can be controlled by the GNP content and distribution. Dynamic stability analysis of functionally graded (FG) porous arches reinforced with GNPs under the combined action of a static force and a dynamic uniform pressure in the radial direction was investigated by Zhao et al. [3]. They confirmed that stability of the porous arch can be enhanced by using symmetrically non-uniform porosity distribution and the addition of a small amount of GNPs. Afshari and Adab [4] presented exact solutions for size-dependent buckling and vibration analyses of GNP-reinforced rectangular microplates. It was shown by them that in order to have a better reinforcing effect, GNPs with larger surface area and fewer monolayer graphene sheets should be used. Static bending and free vibration analyses of FG porous plates reinforced with GNPs were studied by Nguyen et al. [5]. They confirmed that by adding a small amount of GNPs, the strength of FG plate structures can be significantly improved and distribution pattern of GNPs in matrix plays an important role in reinforcement. Shokrgozar et al. [6] studied viscoelastic dynamics and static responses of GNP-reinforced composite cylindrical microshells. They concluded that viscoelastic foundation, distribution pattern of GNPs, boundary condition and weight function of GNPs have remarkable effects on the stability of the GNP-reinforced cylindrical microshells. Tabatabaei Nejhad et al. [7] studied out-of-plane vibration analysis of laminated GNP-reinforced composite curved beams bonded by piezoelectric layers. It was revealed by them that by using only one percent weigh fraction of GNPs, natural frequencies increase about 100% regardless of GNPs distribution pattern.

Dynamic analysis of rotating shells is one the most practical and interesting problems in mechanical engineering, and there are a considerable number of paper regarding vibration analysis of rotating shells. Rotating shells have been extensively used in mechanical and aerospace applications, such as high-speed centrifugal separator, advanced gas turbine and high-power aircraft jet engine. The dynamics of rotating cylindrical shells have received much attention over the recent years. Hosseini-Hashemi [8] presented an exact analytical solution for free vibration analysis of rotating FG cylindrical shells. They concluded that unlike the transverse modes, rotational speed has no effect on the axial modes. Free vibration analysis of rotating FG GNP-reinforced porous cylindrical shells was studied by Dong et al. [9]. They discussed on the effect of initial hoop tension on the natural frequencies of the rotating cylindrical shells and concluded that initial hoop tension makes the critical rotating speed vanishes in some modes. Dong et al. [10] presented an analytical solution on linear and nonlinear free vibration analysis and dynamic responses of rotating FG GNP-reinforced cylindrical shells with various boundary conditions and subjected to a static axial load. They showed that subjoining a small amount of GNPs increases both linear and nonlinear frequencies and reduces the nonlinear to linear frequency ratio. Qin et al. [11] studied wave propagation in rotating FG GNP-reinforced composite cylindrical shells with general boundary conditions and confirmed that the natural frequencies increase by increasing boundary spring stiffness and weigh fraction of GNPs. An analytical study was presented by Dong et al. [12] to predict the low-velocity impact response of rotating FG GNP-reinforced cylindrical shells subjected to impact, external axial and thermal loads. It was shown by them that the peak values of the radial displacement of load points and the contact duration decrease with increase in weight fraction of GNPs. In comparison with the rotating cylindrical shells, there are fewer number of works regarding dynamics of rotating conical shells. Qinkai and Fulei [13] studied dynamic stability analysis of rotating truncated conical shells subjected to a periodic axial load and presented a parametric study on the effects of rotational speed, constant axial load and geometrical parameters on the location and width of instability regions. They showed that increase in rotational speed of the shell leads to movements of instability region along the frequency axis, while it has no considerable effect on the width of instability region. Malekzadeh and Heydarpour [14] studied free vibration analysis of rotating FG-truncated conical shells with different boundary conditions. They concluded that with increase in rotational speed of the shell, the effect of Coriolis acceleration on the natural frequencies increases and its impact depends on the shell boundary conditions. Heydarpour et al. [15] studied free vibration analysis of rotating truncated conical shells reinforced with carbon nanotubes (CNTs) and focused on the influences of angular velocity, Coriolis acceleration, geometrical parameters, distribution pattern and volume fraction of CNTs on the natural frequencies of the shell. They showed that effects of volume fraction and distribution of CNTs depend on the semi-vertex angle and angular velocity of the shell. With assumption of temperature-dependent material properties, Shakouri [16] studied free vibration analysis of FG rotating conical shells in thermal environment and concluded that reduction in natural frequencies created by temperature rise would be attenuated as the rotational speed of the shell increases.

Reduction in weight and increase in strength and stiffness of structures is one of the most important challenges for mechanical engineers which has been solved in the recent years using multi-phase materials [17,18,19] and different types of nano-reinforcements such as single-walled carbon nanotubes (SWCNTs), multi-walled carbon nanotubes (MWCNTs) and GNPs. In comparison with SWCNTs and MWCNTs, GNPs have bigger specific surface area which creates stronger bonding with the matrix and significantly enhanced load transfer capability [20]. Thus, a truncated conical shell made of a low-density polymer enriched with GNPs can be considered as a good choice to increase the strength and stiffness and decrease the weight of rotating shells. It can be seen in the literature review that free vibration analysis of rotating GNP-reinforced truncated conical shells is not studied which is the topic of the presented paper. The shell is modeled based on the FSDT, and effective mechanical properties are estimated based on the Halpin–Tsai model along with the rule of mixture. The set of the governing equations are solved analytically in circumferential direction via appropriate harmonic functions and are solved numerically in meridional direction via GDQM. Effects of various geometrical parameters of the shell and distribution pattern, mass fraction and dimensional parameters of the GNPs on the forward and backward frequencies are investigated. In most of the papers regarding vibration analysis of rotating shells, the initial hoop tension is modeled based on the classical shells theories, and recently, some authors have modeled the initial hoop tension in rotating cylindrical shells based on the FSDT [9,10,11,12]. To the best knowledge of author, this paper is the first attempt to model the initial hoop tension in a rotating conical shell modeled based on the FSDT.

2 Governing equations

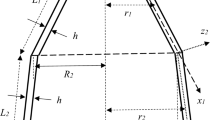
As depicted in Fig. 1, a truncated conical shell of small radius a, large radius b, semi-vertex angle α, length L and thickness h rotating at constant angular velocity Ω is considered. The radius of the shell changes linearly as r(x)= a + xsinα, and the shell is considered to be made of epoxy enriched with GNPs.

Fig. 1

Rotating GNP-reinforced truncated conical shell

Based on the FSDT and incorporating effect of the neutral surface (z = z₀), displacement filed in the shell can be considered as

$$\begin{aligned} u_{1} \left( {x,\theta ,z} \right) & = u\left( {x,\theta } \right) + \left( {z - z_{0} } \right)\phi_{x} \left( {x,\theta } \right), \\ u_{2} \left( {x,\theta ,z} \right) & = v\left( {x,\theta } \right) + \left( {z - z_{0} } \right)\phi_{\theta } \left( {x,\theta } \right), \\ u_{3} \left( {x,\theta ,z} \right) & = w\left( {x,\theta } \right), \\ \end{aligned}$$

(1)

in which u₁, u₂ and u₃ are components of displacement along x, θ and z directions, respectively. u, v and w stand for corresponding components of displacement at neutral surface (z = z₀) and φ_x and φ_θ are rotation about θ and x axes, respectively. The distance of the neutral surface from the mid-surface of the shell can be calculated as [21]

$$z_{0} = \frac{{\int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {zE\left( z \right){\text{d}}z} }}{{\int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {E\left( z \right){\text{d}}z} }}.$$

(2)

Components of the strain can be stated as [22]

$$\begin{aligned} & \begin{array}{*{20}c} {\varepsilon_{xx} = \frac{\partial u}{\partial x} + \left( {z - z_{0} } \right)\frac{{\partial \phi_{x} }}{\partial x},} & {\varepsilon_{\theta \theta } = \frac{\sin \alpha }{r}u + \frac{1}{r}\frac{\partial v}{\partial \theta } + \frac{\cos \alpha }{r}w + \left( {z - z_{0} } \right)\left( {\frac{\sin \alpha }{r}\phi_{x} + \frac{1}{r}\frac{{\partial \phi_{\theta } }}{\partial \theta }} \right),} \\ \end{array} \\ & \gamma_{x\theta } = \frac{1}{r}\frac{\partial u}{\partial \theta } + \frac{\partial v}{\partial x} - \frac{\sin \alpha }{r}v + \left( {z - z_{0} } \right)\left( {\frac{1}{r}\frac{{\partial \phi_{x} }}{\partial \theta } + \frac{{\partial \phi_{\theta } }}{\partial x} - \frac{\sin \alpha }{r}\phi_{\theta } } \right), \\ & \begin{array}{*{20}c} {\gamma_{xz} = \frac{\partial w}{\partial x} + \phi_{x} ,} & {\gamma_{\theta z} = - \frac{\cos \alpha }{r}v + \frac{1}{r}\frac{\partial w}{\partial \theta } + \phi_{\theta } ;} \\ \end{array} \\ \end{aligned}$$

(3)

and the constitutive equations can be written as follows:

$$\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{\theta \theta } } \\ {\sigma_{\theta z} } \\ {\sigma_{xz} } \\ {\sigma_{x\theta } } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 & 0 & 0 \\ {Q_{21} } & {Q_{22} } & 0 & 0 & 0 \\ 0 & 0 & {kQ_{44} } & 0 & 0 \\ 0 & 0 & 0 & {kQ_{55} } & 0 \\ 0 & 0 & 0 & 0 & {Q_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{\theta \theta } } \\ {\gamma_{\theta z} } \\ {\gamma_{xz} } \\ {\gamma_{x\theta } } \\ \end{array} } \right\},$$

(4)

where k = 5/6 is shear correction factor [22] and Q₁₁− Q₆₆ are defined as

$$\begin{array}{*{20}c} {Q_{11} = Q_{22} = \frac{E}{{1 - \nu^{2} }},} & {Q_{12} = Q_{21} = \nu Q_{11} ,} & {Q_{44} = Q_{55} = Q_{66} = G = \frac{E}{{2\left( {1 + \nu } \right)}}.} \\ \end{array}$$

(5)

in which E, G and ν are modulus of elasticity, shear modulus and Poisson’s ratio, respectively.

The effective modulus of elasticity can be calculated using the Halpin–Tsai model as [23]

$$E = \left( {\frac{3}{8}\frac{{1 + \xi_{\text{L}} \eta_{\text{L}} V_{\text{GNP}} }}{{1 - \eta_{\text{L}} V_{\text{GNP}} }} + \frac{5}{8}\frac{{1 + \xi_{\text{w}} \eta_{\text{w}} V_{\text{GNP}} }}{{1 - \eta_{\text{w}} V_{\text{GNP}} }}} \right)E_{\text{m}} ,$$

(6)

in which E_m is modulus of elasticity of the polymer matrix and ξ_L, ξ_w, η_L and η_w are some dimensionless parameters defined as follows:

$$\begin{array}{*{20}c} {\xi_{\text{L}} = 2\frac{{l_{\text{GNP}} }}{{h_{\text{GNP}} }},} & {\xi_{\text{w}} = 2\frac{{w_{\text{GNP}} }}{{h_{\text{GNP}} }},} & {\eta_{\text{L}} = \frac{\eta - 1}{{\eta + \xi_{\text{L}} }},} & {\eta_{\text{w}} = \frac{\eta - 1}{{\eta + \xi_{\text{w}} }},} & {\eta = \frac{{E_{\text{GNP}} }}{{E_{\text{m}} }},} \\ \end{array}$$

(7)

where E_GNP, l_GNP, w_GNP and h_GNP are modulus of elasticity, length, width and thickness of the GNPs, respectively.

In Eq. (6) V_GNP is volume fraction of GNPs which can be stated in terms of density of the matrix (ρ_m), density of GNPs (ρ_GNP) and mass fraction of GNPs (g_GNP) as follows:

$$V_{\text{GNP}} = \frac{{g_{\text{GNP}} }}{{g_{\text{GNP}} + \frac{{\rho_{\text{GNP}} }}{{\rho_{\text{m}} }}\left( {1 - g_{\text{GNP}} } \right)}}.$$

(8)

Using the rule of mixture, density and Poisson’s ratio of the shell can be calculated as

$$\rho = \rho_{\text{GNP}} V_{\text{GNP}} + \rho_{\text{m}} V_{\text{m}} ,\;\;\nu = \nu_{\text{GNP}} V_{\text{GNP}} + \nu_{\text{m}} V_{\text{m}} ,$$

(9)

where ν_m and ν_GNP are Poisson’s ratio of the polymer matrix and Poisson’s ratio of GNPs, respectively, and also V_m= 1 − V_GNP is volume fraction of the matrix.

As depicted in Fig. 2, five linear types of GNPs distribution patterns are considered in this paper. Mass fraction of GNPs for these patterns can be stated as [4]

$$\begin{array}{*{20}c} {{\text{UD}}:} & {g_{GNP} \left( z \right) = g_{GNP}^{*} ,} \\ {{\text{FG}} - A:} & {g_{\text{GNP}} \left( z \right) = \left( {1 - \frac{2z}{h}} \right)g_{\text{GNP}}^{*} ,} \\ {{\text{FG}} - V:} & {g_{\text{GNP}} \left( z \right) = \left( {1 + \frac{2z}{h}} \right)g_{\text{GNP}}^{*} ,} \\ {{\text{FG}} - O:} & {g_{\text{GNP}} \left( z \right) = 2\left( {1 - \frac{2\left| z \right|}{h}} \right)g_{\text{GNP}}^{*} ,} \\ {{\text{FG}} - X:} & {g_{\text{GNP}} \left( z \right) = 4\frac{\left| z \right|}{h}g_{\text{GNP}}^{*} ,} \\ \end{array}$$

(10)

in which g^*_GNP is total mass fraction of GNPs. It should be noted that in order to have a fair comparison between distribution patterns, Eq. (10) is regulated to have same total mass fraction of GNPs for all patterns [4].

Fig. 2

GNPs distribution patterns

The set of the governing equations can be derived using Hamilton’s principle as [10]

$$\int\limits_{{t_{1} }}^{{t_{2} }} {\left( {\delta T + \delta W_{{{\text{n}}.{\text{c}}.}} - \delta U_{\text{e}} - \delta U_{\text{h}} } \right){\text{d}}t} = 0,$$

(11)

where [t₁,t₂] is a desired time interval, δ stands for variational operator, T indicates to kinetic energy, W_n.c. is work done by non-conservative loads, U_e stands for the strain energy of the shell and U_h indicates the strain energy generated by initial hoop tension.

The strain energy of the shell can be calculated as [24]

$$U_{\text{e}} = \frac{1}{2}\iiint\limits_{V} {\sigma_{ij} \varepsilon_{ij} {\text{d}}V},$$

(12)

in which V is volume of the shell. Using Eqs. (3) and (12) and dV = dzdS, the variation of the strain energy of the shell can be stated as

$$\begin{aligned} \delta U_{\text{e}} & = \iint\limits_{S} {\left[ {N_{xx} \frac{\partial \delta u}{\partial x} + M_{xx} \frac{{\partial \delta \phi_{x} }}{\partial x} + N_{\theta \theta } \left( {\frac{\sin \alpha }{r}\delta u + \frac{1}{r}\frac{\partial \delta v}{\partial \theta } + \frac{\cos \alpha }{r}\delta w} \right)} \right.} \\ & \quad + M_{\theta \theta } \left( {\frac{\sin \alpha }{r}\delta \phi_{x} + \frac{1}{r}\frac{{\partial \delta \phi_{\theta } }}{\partial \theta }} \right) + N_{x\theta } \left( {\frac{1}{r}\frac{\partial \delta u}{\partial \theta } + \frac{\partial \delta v}{\partial x} - \frac{\sin \alpha }{r}\delta v} \right) \\ & \quad + M_{x\theta } \left( {\frac{1}{r}\frac{{\partial \delta \phi_{x} }}{\partial \theta } + \frac{{\partial \delta \phi_{\theta } }}{\partial x} - \frac{\sin \alpha }{r}\delta \phi_{\theta } } \right) + Q_{xz} \left( {\frac{\partial \delta w}{\partial x} + \delta \phi_{x} } \right) \\ & \quad \left. { + Q_{\theta z} \left( { - \frac{\cos \alpha }{r}\delta v + \frac{1}{r}\frac{\partial \delta w}{\partial \theta } + \delta \phi_{\theta } } \right)} \right]dS, \\ \end{aligned}$$

(13)

where S is surface of the shell and stress resultant components are defined as follows:

$$\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{\theta \theta } } \\ {N_{x\theta } } \\ \end{array} } \right\} = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{\theta \theta } } \\ {\sigma_{x\theta } } \\ \end{array} } \right\}{\text{d}}z} ,} & {\left\{ {\begin{array}{*{20}c} {M_{xx} } \\ {M_{\theta \theta } } \\ {M_{x\theta } } \\ \end{array} } \right\} = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left\{ {\begin{array}{*{20}c} {\sigma_{xx} } \\ {\sigma_{\theta \theta } } \\ {\sigma_{x\theta } } \\ \end{array} } \right\}\left( {z - z_{0} } \right){\text{d}}z} ,} & {\left\{ {\begin{array}{*{20}c} {Q_{xz} } \\ {Q_{\theta z} } \\ \end{array} } \right\} = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left\{ {\begin{array}{*{20}c} {\sigma_{xz} } \\ {\sigma_{\theta z} } \\ \end{array} } \right\}{\text{d}}z} .} \\ \end{array}$$

(14)

Substituting Eqs. (3) and (4) into Eq. (14) leads to the following relations:

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {N_{xx} } \\ {N_{\theta \theta } } \\ {M_{xx} } \\ {M_{\theta \theta } } \\ \end{array} } \right\} & = \left[ {\begin{array}{*{20}c} {A_{11} } & {B_{11} } & {A_{12} } & {B_{12} } \\ {A_{12} } & {B_{12} } & {A_{22} } & {B_{22} } \\ {B_{11} } & {D_{11} } & {B_{12} } & {D_{12} } \\ {B_{12} } & {D_{12} } & {B_{22} } & {D_{22} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\frac{\partial u}{\partial x}} \\ {\frac{{\partial \phi_{x} }}{\partial x}} \\ {\frac{\sin \alpha }{r}u + \frac{1}{r}\frac{\partial v}{\partial \theta } + \frac{\cos \alpha }{r}w} \\ {\frac{\sin \alpha }{r}\phi_{x} + \frac{1}{r}\frac{{\partial \phi_{\theta } }}{\partial \theta }} \\ \end{array} } \right\},\quad Q_{xz} = A_{55} \left( {\frac{\partial w}{\partial x} + \phi_{x} } \right), \\ \left\{ {\begin{array}{*{20}c} {N_{x\theta } } \\ {M_{x\theta } } \\ \end{array} } \right\} & = \left[ {\begin{array}{*{20}c} {A_{66} } & {B_{66} } \\ {B_{66} } & {D_{66} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\frac{1}{r}\frac{\partial u}{\partial \theta } + \frac{\partial v}{\partial x} - \frac{\sin \alpha }{r}v} \\ {\frac{1}{r}\frac{{\partial \phi_{x} }}{\partial \theta } + \frac{{\partial \phi_{\theta } }}{\partial x} - \frac{\sin \alpha }{r}\phi_{\theta } } \\ \end{array} } \right\},\quad Q_{\theta z} = A_{44} \left( { - \frac{\cos \alpha }{r}v + \frac{1}{r}\frac{\partial w}{\partial \theta } + \phi_{\theta } } \right), \\ \end{aligned}$$

(15)

in which

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {A_{ij} } \\ {B_{ij} } \\ {D_{ij} } \\ \end{array} } \right\} & = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {Q_{ij} \left\{ {\begin{array}{*{20}c} 1 \\ {\left( {z - z_{0} } \right)} \\ {\left( {z - z_{0} } \right)^{2} } \\ \end{array} } \right\}{\text{d}}z} ,\quad i,j = 1,2,6, \\ A_{ij} & = k\int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {Q_{ij} {\text{d}}z} ,\quad i,j = 4,5. \\ \end{aligned}$$

(16)

The strain energy created by initial hoop tension can be stated as [9, 10]

$$U_{\text{h}} = \iiint\limits_{V} {\sigma_{\theta \theta }^{0} \varepsilon_{\theta \theta }^{NL} {\text{d}}V},$$

(17)

in which $\sigma_{\theta \theta }^{0}$ and $\varepsilon_{\theta \theta }^{NL}$ indicate initial hoop tension and nonlinear part of circumferential strain which can be calculated using following relations [15, 25]:

$$\begin{aligned} \sigma_{\theta \theta }^{0} & = \rho r^{2}\Omega ^{2} , \\ \varepsilon_{\theta \theta }^{NL} & = \frac{1}{{2r^{2} }}\left[ {\left( {\frac{{\partial u_{2} }}{\partial \theta } + u_{1} \sin \alpha + u_{3} \cos \alpha } \right)^{2} + \left( {\frac{{\partial u_{3} }}{\partial \theta } - u_{2} \cos \alpha } \right)^{2} + \left( {\frac{{\partial u_{1} }}{\partial \theta } - u_{2} \sin \alpha } \right)^{2} } \right]. \\ \end{aligned}$$

(18)

Using Eqs. (1), (17) and (18) one can write

$$\begin{aligned} U_{\text{h}} & = \frac{{\Omega ^{2} }}{2}\iint\limits_{S} {\left\{ {I_{0} \left[ {\left( {\frac{\partial u}{\partial \theta }} \right)^{2} + \left( {\frac{\partial v}{\partial \theta }} \right)^{2} + \left( {\frac{\partial w}{\partial \theta }} \right)^{2} + u^{2} \sin^{2} \alpha + v^{2} + w^{2} \cos^{2} \alpha + 2\left( {u\frac{\partial v}{\partial \theta } - v\frac{\partial u}{\partial \theta }} \right)\sin \alpha } \right.} \right.} \\ & \quad \left. { + 2\left( {w\frac{\partial v}{\partial \theta } - v\frac{\partial w}{\partial \theta }} \right)\cos \alpha + uw\sin 2\alpha } \right] + 2I_{1} \left[ {u\left( {\frac{{\partial \phi_{\theta } }}{\partial \theta } + \phi_{x} \sin \alpha } \right)\sin \alpha } \right. \\ & \quad + \frac{\partial u}{\partial \theta }\left( {\frac{{\partial \phi_{x} }}{\partial \theta } - \phi_{\theta } \sin \alpha } \right) - v\left( {\frac{{\partial \phi_{x} }}{\partial \theta } - \phi_{\theta } \sin \alpha } \right)\sin \alpha + \frac{\partial v}{\partial \theta }\left( {\frac{{\partial \phi_{\theta } }}{\partial \theta } + \phi_{x} \sin \alpha } \right) \\ & \quad \left. { + w\left( {\frac{{\partial \phi_{\theta } }}{\partial \theta } + \phi_{x} \sin \alpha } \right)\cos \alpha + \phi_{\theta } \left( {v\cos \alpha - \frac{\partial w}{\partial \theta }} \right)\cos \alpha } \right] \\ & \quad \left. { + I_{2} \left[ {\left( {\frac{{\partial \phi_{x} }}{\partial \theta }} \right)^{2} + \left( {\frac{{\partial \phi_{\theta } }}{\partial \theta }} \right)^{2} + \phi_{x}^{2} \sin^{2} \alpha + \phi_{\theta }^{2} + 2\left( {\phi_{x} \frac{{\partial \phi_{\theta } }}{\partial \theta } - \phi_{\theta } \frac{{\partial \phi_{x} }}{\partial \theta }} \right)\sin \alpha } \right]} \right\}{\text{d}}S, \\ \end{aligned}$$

(19)

in which inertia terms are defined as follows:

$$I_{i} = \int\limits_{{ - \frac{h}{2}}}^{{\frac{h}{2}}} {\left( {z - z_{0} } \right)^{i} \rho \left( z \right){\text{d}}z} ,\quad i = 0,1,2.$$

(20)

The kinetic energy of the shell can be calculated as

$$T = \frac{1}{2}\iiint\limits_{V} {\rho \vec{v}.\vec{v}{\text{d}}V},$$

(21)

in which $\vec{v}$ is absolute velocity vector and the displacement vector can be written as [13]

$$\vec{r} = u_{1} \vec{i} + u_{2} \vec{j} + u_{3} \vec{k},$$

(22)

where u₁, u₂ and u₃ are presented based on FSDT in Eq. (1).

The absolute velocity vector can be stated using concept of relative velocity as follows [13]:

$$\vec{v} = \frac{{\partial u_{1} }}{\partial t}\vec{i} + \frac{{\partial u_{2} }}{\partial t}\vec{j} + \frac{{\partial u_{3} }}{\partial t}\vec{k} + {\vec{\Omega }} \times \vec{r},$$

(23)

where ${\vec{\Omega }}$ can be stated based on Fig. 1 as follows:

$${\vec{\Omega }} =\Omega \left( { - \cos \alpha \vec{i} + \sin \alpha \vec{k}} \right).$$

(24)

Substituting Eqs. (22) and (24) into Eq. (23) leads to the following equation:

$$\begin{aligned} \vec{v} & = \left( {\frac{{\partial u_{1} }}{\partial t} -\Omega u_{2} \sin \alpha } \right)\vec{i} + \left[ {\frac{{\partial u_{2} }}{\partial t} +\Omega \left( {u_{1} \sin \alpha + u_{3} \cos \alpha } \right)} \right]\vec{j} \\ & \quad + \left( {\frac{{\partial u_{3} }}{\partial t} -\Omega u_{2} \cos \alpha } \right)\vec{k}, \\ \end{aligned}$$

(25)

and using Eqs. (1), (21) and (25) one can write

$$\begin{aligned} T & = \frac{1}{2}\iint\limits_{S} {\left[ {I_{0} \left( {\frac{\partial u}{\partial t}} \right)^{2} + I_{0} \left( {\frac{\partial v}{\partial t}} \right)^{2} + I_{0} \left( {\frac{\partial w}{\partial t}} \right)^{2} + 2I_{1} \frac{\partial u}{\partial t}\frac{{\partial \phi_{x} }}{\partial t}} \right.} \\ & \quad + 2I_{1} \frac{\partial v}{\partial t}\frac{{\partial \phi_{\theta } }}{\partial t} + I_{2} \left( {\frac{{\partial \phi_{x} }}{\partial t}} \right)^{2} + I_{2} \left( {\frac{{\partial \phi_{\theta } }}{\partial t}} \right)^{2} + 2I_{0} \Omega \sin \alpha u\frac{\partial v}{\partial t} \\ & \quad + 2I_{1} \Omega \sin \alpha \frac{\partial v}{\partial t}\phi_{x} + 2I_{1} \Omega \sin \alpha \frac{{\partial \phi_{\theta } }}{\partial t}u + 2I_{2} \Omega \sin \alpha \frac{{\partial \phi_{\theta } }}{\partial t}\phi_{x} \\ & \quad + 2I_{0} \Omega \cos \alpha \frac{\partial v}{\partial t}w + 2I_{1} \Omega \cos \alpha \frac{{\partial \phi_{\theta } }}{\partial t}w - 2I_{0} \Omega \sin \alpha v\frac{\partial u}{\partial t} \\ & \quad - 2I_{1} \Omega \sin \alpha v\frac{{\partial \phi_{x} }}{\partial t} - 2I_{1} \Omega \sin \alpha \phi_{\theta } \frac{\partial u}{\partial t} - 2I_{2} \Omega \sin \alpha \phi_{\theta } \frac{{\partial \phi_{x} }}{\partial t} \\ & \quad - 2I_{0} \Omega \cos \alpha v\frac{\partial w}{\partial t} - 2I_{1} \Omega \cos \alpha \phi_{\theta } \frac{\partial w}{\partial t} + I_{0} \Omega^{2} \sin^{2} \alpha u^{2} \\ & \quad + I_{2} \Omega^{2} \sin^{2} \alpha \phi_{x}^{2} + 2I_{1} \Omega^{2} \sin^{2} \alpha u\phi_{x} + I_{0} \Omega^{2} v^{2} + I_{2} \Omega^{2} \phi_{\theta }^{2} + 2I_{1} \Omega^{2} v\phi_{\theta } \\ & \quad \left. { + I_{0} \Omega^{2} \cos^{2} \alpha w^{2} + I_{0} \Omega^{2} \sin 2\alpha uw + I_{1} \Omega^{2} \sin 2\alpha w\phi_{x} } \right]{\text{d}}S, \\ \end{aligned}$$

(26)

The work done by non-conservative loads can be stated as

$$W_{{{\text{n}}.{\text{c}} .}} = \iint\limits_{S} {q\left( {x,\theta } \right)w{\text{d}}S},$$

(27)

where q is load per unit area.

Substituting Eqs. (13), (19), (26) and (27) into Eq. (11) and using following relation for conical shells:

$${\text{d}}S = {r\left( x \right)}{\text{d}}\theta {\text{d}}x,$$

(28)

the set of the governing equations can be derived as

$$\begin{aligned} & \frac{{\partial N_{xx} }}{\partial x} + \frac{{N_{xx} - N_{\theta \theta } }}{r}\sin \alpha + \frac{1}{r}\frac{{\partial N_{x\theta } }}{\partial \theta } - I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} + 2\Omega \left( {I_{0} \sin \alpha \frac{\partial v}{\partial t} + I_{1} \sin \alpha \frac{{\partial \phi_{\theta } }}{\partial t}} \right) \\ & \quad + \Omega^{2} \left( {I_{0} \frac{{\partial^{2} u}}{{\partial \theta^{2} }} - 2I_{0} \sin \alpha \frac{\partial v}{\partial \theta } + I_{1} \frac{{\partial^{2} \varphi_{x} }}{{\partial \theta^{2} }} - 2I_{1} \sin \alpha \frac{{\partial \varphi_{\theta } }}{\partial \theta }} \right) = 0, \\ & \quad \frac{1}{r}\frac{{\partial N_{\theta \theta } }}{\partial \theta } + 2\frac{{N_{x\theta } }}{r}\sin \alpha + \frac{{Q_{\theta z} }}{r}\cos \alpha + \frac{{\partial N_{x\theta } }}{\partial x} - I_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{2} \phi_{\theta } }}{{\partial t^{2} }} \\ & \quad - 2\Omega \left( {I_{0} \sin \alpha \frac{\partial u}{\partial t} + I_{0} \cos \alpha \frac{\partial w}{\partial t} + I_{1} \sin \alpha \frac{{\partial \phi_{x} }}{\partial t}} \right) + \Omega^{2} \left( {2I_{0} \sin \alpha \frac{\partial u}{\partial \theta }} \right. \\ & \quad \left. { + I_{0} \frac{{\partial^{2} v}}{{\partial \theta^{2} }} + 2I_{0} \cos \alpha \frac{\partial w}{\partial \theta } + 2I_{1} \sin \alpha \frac{{\partial \varphi_{x} }}{\partial \theta } + I_{1} \frac{{\partial^{2} \varphi_{\theta } }}{{\partial \theta^{2} }}} \right) = 0, \\ & \quad - \frac{{N_{\theta \theta } }}{r}\cos \alpha + \frac{{\partial Q_{xz} }}{\partial x} + \frac{{Q_{xz} }}{r}\sin \alpha + \frac{1}{r}\frac{{\partial Q_{\theta z} }}{\partial \theta } - I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} \\ & \quad + 2\Omega \left( {I_{0} \cos \alpha \frac{\partial v}{\partial t} + I_{1} \cos \alpha \frac{{\partial \phi_{\theta } }}{\partial t}} \right) + \Omega^{2} \left( { - 2I_{0} \cos \alpha \frac{\partial v}{\partial \theta }} \right. \\ & \quad \left. { + I_{0} \frac{{\partial^{2} w}}{{\partial \theta^{2} }} - 2I_{1} \cos \alpha \frac{{\partial \varphi_{\theta } }}{\partial \theta }} \right) = - q,\frac{{\partial M_{xx} }}{\partial x} + \frac{{M_{xx} - M_{\theta \theta } }}{r}\sin \alpha \\ & \quad + \frac{1}{r}\frac{{\partial M_{x\theta } }}{\partial \theta } - Q_{xz} - I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} + 2\Omega \left( {I_{1} \sin \alpha \frac{\partial v}{\partial t} + I_{2} \sin \alpha \frac{{\partial \phi_{\theta } }}{\partial t}} \right) \\ & \quad + \Omega^{2} \left( {I_{1} \frac{{\partial^{2} u}}{{\partial \theta^{2} }} - 2I_{1} \sin \alpha \frac{\partial v}{\partial \theta } + I_{2} \frac{{\partial^{2} \varphi_{x} }}{{\partial \theta^{2} }} - 2I_{2} \sin \alpha \frac{{\partial \varphi_{\theta } }}{\partial \theta }} \right) = 0, \\ & \quad \frac{1}{r}\frac{{\partial M_{\theta \theta } }}{\partial \theta } + \frac{{\partial M_{x\theta } }}{\partial x} + 2\frac{{M_{x\theta } }}{r}\sin \alpha - Q_{\theta z} - I_{1} \frac{{\partial^{2} v}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{2} \phi_{\theta } }}{{\partial t^{2} }} \\ & \quad - 2\Omega \left( {I_{1} \sin \alpha \frac{\partial u}{\partial t} + I_{1} \cos \alpha \frac{\partial w}{\partial t} + I_{2} \sin \alpha \frac{{\partial \phi_{x} }}{\partial t}} \right) + \Omega^{2} \left( {2I_{1} \sin \alpha \frac{\partial u}{\partial \theta }} \right. \\ & \quad \left. { + I_{1} \frac{{\partial^{2} v}}{{\partial \theta^{2} }} + 2I_{1} \cos \alpha \frac{\partial w}{\partial \theta } + 2I_{2} \sin \alpha \frac{{\partial \varphi_{x} }}{\partial \theta } + I_{2} \frac{{\partial^{2} \varphi_{\theta } }}{{\partial \theta^{2} }}} \right) = 0. \\ \end{aligned}$$

(29)

and the boundary conditions can be written as follows:

$$\begin{array}{*{20}c} {{\text{Clamped}}\,\left( C \right):} & {u = 0,} & {v = 0,} & {w = 0,} & {\phi_{x} = 0,} & {\phi_{\theta } = 0,} \\ {{\text{Simply}}\;{\text{Supported}}\,\left( S \right):} & {N_{xx} = 0,} & {v = 0,} & {w = 0,} & {M_{xx} = 0,} & {\phi_{\theta } = 0,} \\ {{\text{Free}}\,\left( F \right):} & {N_{xx} = 0,} & {N_{x\theta } = 0,} & {Q_{xz} = 0,} & {M_{xx} = 0,} & {M_{x\theta } = 0.} \\ \end{array}$$

(30)

Substituting Eq. (15) into Eq. (29), the set of the governing equations can be written for free vibration analysis (q = 0) as follows:

$$\begin{aligned} & A_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{A_{11} \sin \alpha }}{r}\frac{\partial u}{\partial x} + \left( {\frac{{A_{66} }}{{r^{2} }} + I_{0} \Omega^{2} } \right)\frac{{\partial^{2} u}}{{\partial \theta^{2} }} - \frac{{A_{22} \sin^{2} \alpha }}{{r^{2} }}u \\ & \quad + \frac{{A_{12} + A_{66} }}{r}\frac{{\partial^{2} v}}{\partial x\partial \theta } - \sin \alpha \left( {\frac{{A_{22} + A_{66} }}{{r^{2} }} + 2I_{0} \Omega^{2} } \right)\frac{\partial v}{\partial \theta } + \frac{{A_{12} \cos \alpha }}{r}\frac{\partial w}{\partial x} \\ & \quad - \frac{{A_{22} \sin 2\alpha }}{{2r^{2} }}w + B_{11} \frac{{\partial^{2} \phi_{x} }}{{\partial x^{2} }} + \frac{{B_{11} \sin \alpha }}{r}\frac{{\partial \phi_{x} }}{\partial x} + \left( {\frac{{B_{66} }}{{r^{2} }} + I_{1} \Omega^{2} } \right)\frac{{\partial^{2} \varphi_{x} }}{{\partial \theta^{2} }} \\ & \quad - \frac{{B_{22} \sin^{2} \alpha }}{{r^{2} }}\phi_{x} + \frac{{B_{12} + B_{66} }}{r}\frac{{\partial^{2} \phi_{\theta } }}{\partial x\partial \theta } - \sin \alpha \left( {\frac{{B_{22} + B_{66} }}{{r^{2} }} + 2I_{1} \Omega^{2} } \right)\frac{{\partial \varphi_{\theta } }}{\partial \theta } \\ & \quad + 2\Omega I_{0} \sin \alpha \frac{\partial v}{\partial t} + 2\Omega I_{1} \sin \alpha \frac{{\partial \phi_{\theta } }}{\partial t} - I_{0} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} = 0, \\ & \frac{{A_{12} + A_{66} }}{r}\frac{{\partial^{2} u}}{\partial x\partial \theta } + \sin \alpha \left( {\frac{{A_{22} + A_{66} }}{{r^{2} }} + 2I_{0} \Omega^{2} } \right)\frac{\partial u}{\partial \theta } + A_{66} \frac{{\partial^{2} v}}{{\partial x^{2} }} \\ & \quad + \frac{{A_{66} \sin \alpha }}{r}\frac{\partial v}{\partial x} + \left( {\frac{{A_{22} }}{{r^{2} }} + I_{0} \Omega^{2} } \right)\frac{{\partial^{2} v}}{{\partial \theta^{2} }} - \frac{{A_{44} \cos^{2} \alpha + A_{66} \sin^{2} \alpha }}{{r^{2} }}v \\ & \quad + \cos \alpha \left( {\frac{{A_{22} + A_{44} }}{{r^{2} }} + 2I_{0} \Omega^{2} } \right)\frac{\partial w}{\partial \theta } + \frac{{B_{12} + B_{66} }}{r}\frac{{\partial^{2} \phi_{x} }}{\partial x\partial \theta } + \sin \alpha \\ & \quad \left( {\frac{{B_{22} + B_{66} }}{{r^{2} }} + 2I_{1} \Omega^{2} } \right)\frac{{\partial \varphi_{x} }}{\partial \theta } + B_{66} \frac{{\partial^{2} \phi_{\theta } }}{{\partial x^{2} }} + \frac{{B_{66} \sin \alpha }}{r}\frac{{\partial \phi_{\theta } }}{\partial x} \\ & \quad + \left( {\frac{{B_{22} }}{{r^{2} }} + I_{1} \Omega^{2} } \right)\frac{{\partial^{2} \varphi_{\theta } }}{{\partial \theta^{2} }} + \left( {\frac{{A_{44} \cos \alpha }}{r} - \frac{{B_{66} \sin^{2} \alpha }}{{r^{2} }}} \right)\phi_{\theta } - 2I_{0} \Omega \sin \\ & \quad \alpha \frac{\partial u}{\partial t} - 2I_{0} \Omega \cos \alpha \frac{\partial w}{\partial t} - 2I_{1} \Omega \sin \alpha \frac{{\partial \phi_{x} }}{\partial t} - I_{0} \frac{{\partial^{2} v}}{{\partial t^{2} }} - I_{1} \frac{{\partial^{2} \phi_{\theta } }}{{\partial t^{2} }} = 0, \\ & - \frac{{A_{12} \cos \alpha }}{r}\frac{\partial u}{\partial x} - \frac{{A_{22} \sin 2\alpha }}{{2r^{2} }}u - \cos \alpha \left( {\frac{{A_{22} + A_{44} }}{{r^{2} }} + 2I_{0} \Omega^{2} } \right) \\ & \quad \frac{\partial v}{\partial \theta } + A_{55} \frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{A_{55} \sin \alpha }}{r}\frac{\partial w}{\partial x} + \left( {\frac{{A_{44} }}{{r^{2} }} + I_{0} \Omega^{2} } \right)\frac{{\partial^{2} w}}{{\partial \theta^{2} }} - \frac{{A_{22} \cos^{2} \alpha }}{{r^{2} }}w \\ & \quad + \left( {A_{55} - \frac{{B_{12} \cos \alpha }}{r}} \right)\frac{{\partial \phi_{x} }}{\partial x} + \left( {\frac{{A_{55} \sin \alpha }}{r} - \frac{{B_{22} \sin 2\alpha }}{{2r^{2} }}} \right)\phi_{x} + \left[ {\frac{{A_{44} }}{r} - \left( {\frac{{B_{22} }}{{r^{2} }}} \right.} \right. \\ & \quad \left. {\left. { + 2I_{1} \Omega^{2} } \right)\cos \alpha } \right]\frac{{\partial \phi_{\theta } }}{\partial \theta } + 2I_{0} \Omega \cos \alpha \frac{\partial v}{\partial t} + 2I_{1} \Omega \cos \alpha \frac{{\partial \phi_{\theta } }}{\partial t} - I_{0} \frac{{\partial^{2} w}}{{\partial t^{2} }} = 0, \\ & B_{11} \frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{B_{11} \sin \alpha }}{r}\frac{\partial u}{\partial x} + \left( {\frac{{B_{66} }}{{r^{2} }} + I_{1} \Omega^{2} } \right)\frac{{\partial^{2} u}}{{\partial \theta^{2} }} - \frac{{B_{22} \sin^{2} \alpha }}{{r^{2} }}u \\ & \quad + \frac{{B_{12} + B_{66} }}{r}\frac{{\partial^{2} v}}{\partial x\partial \theta } - \sin \alpha \left( {\frac{{B_{22} + B_{66} }}{{r^{2} }} + 2I_{1} \Omega^{2} } \right)\frac{\partial v}{\partial \theta } - \left( {A_{55} - \frac{{B_{12} \cos \alpha }}{r}} \right)\frac{\partial w}{\partial x} \\ & \quad - \frac{{B_{22} \sin 2\alpha }}{{2r^{2} }}w + D_{11} \frac{{\partial^{2} \phi_{x} }}{{\partial x^{2} }} + \frac{{D_{11} \sin \alpha }}{r}\frac{{\partial \phi_{x} }}{\partial x} + \left( {\frac{{D_{66} }}{{r^{2} }} + I_{2} \Omega^{2} } \right)\frac{{\partial^{2} \varphi_{x} }}{{\partial \theta^{2} }} \\ & \quad - \left( {A_{55} + \frac{{D_{22} \sin^{2} \alpha }}{{r^{2} }}} \right)\phi_{x} + \frac{{D_{12} + D_{66} }}{r}\frac{{\partial^{2} \phi_{\theta } }}{\partial x\partial \theta } - \sin \alpha \left( {\frac{{D_{22} + D_{66} }}{{r^{2} }} + 2I_{2} \Omega^{2} } \right) \\ & \quad \frac{{\partial \varphi_{\theta } }}{\partial \theta } + 2I_{1} \Omega \sin \alpha \frac{\partial v}{\partial t} + 2I_{2} \Omega \sin \alpha \frac{{\partial \phi_{\theta } }}{\partial t} - I_{1} \frac{{\partial^{2} u}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{2} \phi_{x} }}{{\partial t^{2} }} = 0, \\ & \frac{{B_{12} + B_{66} }}{r}\frac{{\partial^{2} u}}{\partial x\partial \theta } + \sin \alpha \left( {\frac{{B_{22} + B_{66} }}{{r^{2} }} + 2I_{1} \Omega^{2} } \right)\frac{\partial u}{\partial \theta } + B_{66} \frac{{\partial^{2} v}}{{\partial x^{2} }} \\ & \quad + \frac{{B_{66} \sin \alpha }}{r}\frac{\partial v}{\partial x} + \left( {\frac{{B_{22} }}{{r^{2} }} + I_{1} \Omega^{2} } \right)\frac{{\partial^{2} v}}{{\partial \theta^{2} }} + \left( {\frac{{A_{44} \cos \alpha }}{r} - \frac{{B_{66} \sin^{2} \alpha }}{{r^{2} }}} \right)v \\ & \quad + \left[ { - \frac{{A_{44} }}{r} + \left( {\frac{{B_{22} }}{{r^{2} }} + 2I_{1} \Omega^{2} } \right)\cos \alpha } \right]\frac{\partial w}{\partial \theta } + \frac{{D_{12} + D_{66} }}{r}\frac{{\partial^{2} \phi_{x} }}{\partial x\partial \theta } \\ & \quad + \sin \alpha \left( {\frac{{D_{22} + D_{66} }}{{r^{2} }} + 2I_{2} \Omega^{2} } \right)\frac{{\partial \varphi_{x} }}{\partial \theta } + D_{66} \frac{{\partial^{2} \phi_{\theta } }}{{\partial x^{2} }} + \frac{{D_{66} \sin \alpha }}{r}\frac{{\partial \phi_{\theta } }}{\partial x} \\ & \quad + \left( {\frac{{D_{22} }}{{r^{2} }} + I_{2} \Omega^{2} } \right)\frac{{\partial^{2} \varphi_{\theta } }}{{\partial \theta^{2} }} - \left( {A_{44} + \frac{{D_{66} \sin^{2} \alpha }}{{r^{2} }}} \right)\phi_{\theta } - 2I_{1} \Omega \sin \alpha \frac{\partial u}{\partial t} \\ & \quad - 2I_{1} \Omega \cos \alpha \frac{\partial w}{\partial t} - 2I_{2} \Omega \sin \alpha \frac{{\partial \phi_{x} }}{\partial t} - I_{1} \frac{{\partial^{2} v}}{{\partial t^{2} }} - I_{2} \frac{{\partial^{2} \phi_{\theta } }}{{\partial t^{2} }} = 0. \\ \end{aligned}$$

(31)

It is worth mentioning that in Eq. (31), the terms containing second time derivatives of displacements are relative acceleration, the terms containing square of rotational speed denote the centrifugal acceleration along with initial hoop tension and the terms containing rotational speed and first time derivatives of displacements are Coriolis parts of acceleration.

In a similar manner, by substituting Eq. (15) into Eq. (30) and doing some simplifications for simply supported condition, the boundary conditions can be written as follows:

$$\begin{aligned} & {\text{Clamped}}\,\left( C \right):\quad u = 0,\;v = 0,\;w = 0,\;\phi_{x} = 0,\;\phi_{\theta } = 0, \\ & {\text{Simply}}\;{\text{Supported}}\,\left( S \right):\quad A_{11} \frac{\partial u}{\partial x} + \frac{{A_{12} \sin \alpha }}{r}u + B_{11} \frac{{\partial \phi_{x} }}{\partial x} + \frac{{B_{12} \sin \alpha }}{r}\phi_{x} = 0,v = 0, \\ & w = 0,\;B_{11} \frac{\partial u}{\partial x} + \frac{{B_{12} \sin \alpha }}{r}u + D_{11} \frac{{\partial \phi_{x} }}{\partial x} + \frac{{D_{12} \sin \alpha }}{r}\phi_{x} = 0,\;\phi_{\theta } = 0, \\ & {\text{Free}}\,\left( F \right): \\ & A_{11} \frac{\partial u}{\partial x} + B_{11} \frac{{\partial \phi_{x} }}{\partial x} + A_{12} \left( {\frac{\sin \alpha }{r}u + \frac{1}{r}\frac{\partial v}{\partial \theta } + \frac{\cos \alpha }{r}w} \right) + B_{12} \left( {\frac{\sin \alpha }{r}\phi_{x} + \frac{1}{r}\frac{{\partial \phi_{\theta } }}{\partial \theta }} \right) = 0, \\ & A_{66} \left( {\frac{1}{r}\frac{\partial u}{\partial \theta } + \frac{\partial v}{\partial x} - \frac{\sin \alpha }{r}v} \right) + B_{66} \left( {\frac{1}{r}\frac{{\partial \phi_{x} }}{\partial \theta } + \frac{{\partial \phi_{\theta } }}{\partial x} - \frac{\sin \alpha }{r}\phi_{\theta } } \right) = 0, \\ & \frac{\partial w}{\partial x} + \phi_{x} = 0, \\ & B_{11} \frac{\partial u}{\partial x} + D_{11} \frac{{\partial \phi_{x} }}{\partial x} + B_{12} \left( {\frac{\sin \alpha }{r}u + \frac{1}{r}\frac{\partial v}{\partial \theta } + \frac{\cos \alpha }{r}w} \right) + D_{12} \left( {\frac{\sin \alpha }{r}\phi_{x} + \frac{1}{r}\frac{{\partial \phi_{\theta } }}{\partial \theta }} \right) = 0, \\ & B_{66} \left( {\frac{1}{r}\frac{\partial u}{\partial \theta } + \frac{\partial v}{\partial x} - \frac{\sin \alpha }{r}v} \right) + D_{66} \left( {\frac{1}{r}\frac{{\partial \phi_{x} }}{\partial \theta } + \frac{{\partial \phi_{\theta } }}{\partial x} - \frac{\sin \alpha }{r}\phi_{\theta } } \right) = 0. \\ \end{aligned}$$

(32)

Using the following solution [25]:

$$\begin{array}{*{20}c} {\left\{ {\begin{array}{*{20}c} {u\left( {x,\theta ,t} \right)} \\ {v\left( {x,\theta ,t} \right)} \\ {w\left( {x,\theta ,t} \right)} \\ {\phi_{x} \left( {x,\theta ,t} \right)} \\ {\phi_{\theta } \left( {x,\theta ,t} \right)} \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {U\left( x \right)\cos \left( {n\theta + \omega t} \right)} \\ {V\left( x \right)\sin \left( {n\theta + \omega t} \right)} \\ {W\left( x \right)\cos \left( {n\theta + \omega t} \right)} \\ {X\left( x \right)\cos \left( {n\theta + \omega t} \right)} \\ {\Theta \left( x \right)\sin \left( {n\theta + \omega t} \right)} \\ \end{array} } \right\},} & {n = 1,2,3, \ldots ,} \\ \end{array}$$

(33)

in which ω is natural frequency and n is circumferential mode number, Eq. (31) can be written as follows:

$$\begin{aligned} & A_{11} U\prime \prime + \frac{{A_{11} \sin \alpha }}{r}U\prime - \left( {\frac{{A_{22} \sin^{2} \alpha + A_{66} n^{2} }}{{r^{2} }} + n^{2} I_{0} \Omega^{2} } \right)U + \frac{{n\left( {A_{12} + A_{66} } \right)}}{r}V\prime \\ & \quad - n\sin \alpha \left( {\frac{{A_{22} + A_{66} }}{{r^{2} }} + 2I_{0} \Omega^{2} } \right)V + \frac{{A_{12} \cos \alpha }}{r}W{\prime } - \frac{{A_{22} \sin 2\alpha }}{{2r^{2} }}W + B_{11} X\prime \prime \\ & \quad + \frac{{B_{11} \sin \alpha }}{r}X{\prime } - \left( {\frac{{B_{22} \sin^{2} \alpha + B_{66} n^{2} }}{{r^{2} }} + n^{2} I_{1} \Omega^{2} } \right)X + \frac{{n\left( {B_{12} + B_{66} } \right)}}{r}\Theta {\prime } \\ & \quad - n\sin \alpha \left( {\frac{{B_{22} + B_{66} }}{{r^{2} }} + 2I_{1} \Omega^{2} } \right)\Theta + 2\Omega \omega I_{0} \sin \alpha V + 2\Omega \omega I_{1} \sin \alpha \Theta \\ & \quad + I_{0} \omega^{2} U + I_{1} \omega^{2} X = 0, \\ & - \frac{{n\left( {A_{12} + A_{66} } \right)}}{r}U{\prime } - n\sin \alpha \left( {\frac{{A_{22} + A_{66} }}{{r^{2} }} + 2I_{0} \Omega^{2} } \right)U + A_{66} V{\prime \prime } + \frac{{A_{66} \sin \alpha }}{r}V{\prime } \\ & \quad - \left( {\frac{{A_{22} n^{2} + A_{44} \cos^{2} \alpha + A_{66} \sin^{2} \alpha }}{{r^{2} }} + n^{2} I_{0} \Omega^{2} } \right)V - n\cos \alpha \left( {\frac{{A_{22} + A_{44} }}{{r^{2} }} + 2I_{0} \Omega^{2} } \right)W \\ & \quad - \frac{{n\left( {B_{12} + B_{66} } \right)}}{r}X{\prime } - n\sin \alpha \left( {\frac{{B_{22} + B_{66} }}{{r^{2} }} + 2I_{1} \Omega^{2} } \right)X + B_{66} \Theta {\prime \prime } + \frac{{B_{66} \sin \alpha }}{r}\Theta {\prime } \\ & \quad + \left( {\frac{{A_{44} \cos \alpha }}{r} - \frac{{B_{22} n^{2} + B_{66} \sin^{2} \alpha }}{{r^{2} }} - n^{2} I_{1} \Omega^{2} } \right)\Theta + 2I_{0} \Omega \omega \sin \alpha U + 2I_{0} \Omega \omega \cos \alpha W \\ & \quad + 2I_{1} \Omega \omega \sin \alpha X + I_{0} \omega^{2} V + I_{1} \omega^{2} \Theta = 0, \\ & - \frac{{A_{12} \cos \alpha }}{r}U{\prime } - \frac{{A_{22} \sin 2\alpha }}{{2r^{2} }}U - n\cos \alpha \left( {\frac{{A_{22} + A_{44} }}{{r^{2} }} + 2I_{0} \Omega^{2} } \right)V + A_{55} W{\prime \prime } + \frac{{A_{55} \sin \alpha }}{r}W{\prime } \\ & \quad - \left( {\frac{{A_{22} \cos^{2} \alpha + A_{44} n^{2} }}{{r^{2} }} + n^{2} I_{0} \Omega^{2} } \right)W + \left( {A_{55} - \frac{{B_{12} \cos \alpha }}{r}} \right)X{\prime } + \left( {\frac{{A_{55} \sin \alpha }}{r} - \frac{{B_{22} \sin 2\alpha }}{{2r^{2} }}} \right)X \\ & \quad + n\left[ {\frac{{A_{44} }}{r} - \left( {\frac{{B_{22} }}{{r^{2} }} + 2I_{1} \Omega^{2} } \right)\cos \alpha } \right]\Theta + 2I_{0} \Omega \omega \cos \alpha V + 2I_{1} \Omega \omega \cos \alpha \Theta + I_{0} \omega^{2} W = 0, \\ & B_{11} U{\prime \prime } + \frac{{B_{11} \sin \alpha }}{r}U{\prime } - \left( {\frac{{B_{22} \sin^{2} \alpha + B_{66} n^{2} }}{{r^{2} }} + n^{2} I_{1} \Omega^{2} } \right)U + \frac{{n\left( {B_{12} + B_{66} } \right)}}{r}V{\prime } \\ & \quad - n\sin \alpha \left( {\frac{{B_{22} + B_{66} }}{{r^{2} }} + 2I_{1} \Omega^{2} } \right)V - \left( {A_{55} - \frac{{B_{12} \cos \alpha }}{r}} \right)W{\prime } - \frac{{B_{22} \sin 2\alpha }}{{2r^{2} }}W \\ & \quad + D_{11} X{\prime \prime } + \frac{{D_{11} \sin \alpha }}{r}X{\prime } - \left( {\frac{{D_{22} \sin^{2} \alpha + D_{66} n^{2} }}{{r^{2} }} + A_{55} + n^{2} I_{2} \Omega^{2} } \right)X \\ & \quad + \frac{{n\left( {D_{12} + D_{66} } \right)}}{r}\Theta {\prime } - n\sin \alpha \left( {\frac{{D_{22} + D_{66} }}{{r^{2} }} + 2I_{2} \Omega^{2} } \right)\Theta + 2I_{1} \Omega \omega \sin \alpha V \\ & \quad + 2I_{2} \Omega \omega \sin \alpha \Theta + I_{1} \omega^{2} U + I_{2} \omega^{2} X = 0, \\ & - \frac{{n\left( {B_{12} + B_{66} } \right)}}{r}U{\prime } - n\sin \alpha \left( {\frac{{B_{22} + B_{66} }}{{r^{2} }} + 2I_{1} \Omega^{2} } \right)U + B_{66} V{\prime \prime } + \frac{{B_{66} \sin \alpha }}{r}V{\prime } \\ & \quad + \left( {\frac{{A_{44} \cos \alpha }}{r} - \frac{{B_{22} n^{2} + B_{66} \sin^{2} \alpha }}{{r^{2} }} - n^{2} I_{1} \Omega^{2} } \right)V + n\left[ {\frac{{A_{44} }}{r} - \left( {\frac{{B_{22} }}{{r^{2} }} + 2I_{1} \Omega^{2} } \right)\cos \alpha } \right]W \\ & \quad - \frac{{n\left( {D_{12} + D_{66} } \right)}}{r}X{\prime } - n\sin \alpha \left( {\frac{{D_{22} + D_{66} }}{{r^{2} }} + 2I_{2} \Omega^{2} } \right)X + D_{66} \Theta {\prime \prime } + \frac{{D_{66} \sin \alpha }}{r}\Theta {\prime } \\ & \quad - \left( {\frac{{D_{22} n^{2} + D_{66} \sin^{2} \alpha }}{{r^{2} }} + A_{44} + n^{2} I_{2} \Omega^{2} } \right)\Theta + 2I_{1} \Omega \omega \sin \alpha U + 2I_{1} \Omega \omega \cos \alpha W \\ & \quad + 2I_{2} \Omega \omega \sin \alpha X + I_{1} \omega^{2} V + I_{2} \omega^{2} \Theta = 0. \\ \end{aligned}$$

(34)

in which prime denotes derivative with respect the spatial variable x. In a similar manner, using Eqs. (32) and (33), the boundary conditions can be written as follows:

$$\begin{aligned} & {\text{Clamped}}\,\left( C \right):\quad U = 0,\;V = 0,\;W = 0,\;X = 0,\;\Theta = 0, \\ & {\text{Simply}}\;{\text{Supported}}\,\left( S \right):\quad A_{11} U{\prime } + \frac{{A_{12} \sin \alpha }}{r}U + B_{11} X{\prime } + \frac{{B_{12} \sin \alpha }}{r}X = 0,\;V = 0, \\ & W = 0,\;B_{11} U{\prime } + \frac{{B_{12} \sin \alpha }}{r}U + D_{11} X{\prime } + \frac{{D_{12} \sin \alpha }}{r}X = 0,\;\Theta = 0, \\ & {\text{Free}}\,\left( F \right): \\ & A_{11} U{\prime } + B_{11} X{\prime } + \frac{{A_{12} }}{r}\left( {\sin \alpha U + nV + \cos \alpha W} \right) + \frac{{B_{12} }}{r}\left( {\sin \alpha X + n\Theta } \right) = 0, \\ & A_{66} \left( { - \frac{n}{r}U + V{\prime } - \frac{\sin \alpha }{r}V} \right) + B_{66} \left( { - \frac{n}{r}X + \Theta {\prime } - \frac{\sin \alpha }{r}\Theta } \right) = 0, \\ & W{\prime } + X = 0, \\ & B_{11} U{\prime } + D_{11} X{\prime } + \frac{{B_{12} }}{r}\left( {\sin \alpha U + nV + \cos \alpha W} \right) + \frac{{D_{12} }}{r}\left( {\sin \alpha X + n\Theta } \right) = 0, \\ & B_{66} \left( { - \frac{n}{r}U + V{\prime } - \frac{\sin \alpha }{r}V} \right) + D_{66} \left( { - \frac{n}{r}X + \Theta {\prime } - \frac{\sin \alpha }{r}\Theta } \right) = 0. \\ \end{aligned}$$

(35)

3 Solution procedure

Due to the mathematical complexities in the set of the governing equations and boundary conditions, a numerical solution is presented here using DQM. This method is based on this idea that all derivatives of a function like f(x) can be estimated by means of the weighted linear sum of the values of the function at N pre-selected grid of discrete points as [26]

$$\left. {\frac{{{\text{d}}^{r} f}}{{{\text{d}}x^{r} }}} \right|_{{x = x_{i} }} = \sum\limits_{j = 1}^{N} {A_{ij}^{\left( r \right)} f_{j} } ,$$

(36)

in which [A^(r)] is the weighting coefficient associated with the rth order derivative which can be calculated as follows [26]:

$$\begin{aligned} A_{ij}^{{^{\left( 1 \right)} }} & = \left\{ \begin{aligned} \frac{{\prod\limits_{\begin{subarray}{l} m = 1 \\ m \ne i,j \end{subarray} }^{N} {\left( {x_{i} - x_{m} } \right)} }}{{\prod\limits_{\begin{subarray}{l} m = 1 \\ m \ne j \end{subarray} }^{N} {\left( {x_{j} - x_{m} } \right)} }},\quad i,j = 1,2,3, \ldots ,N;\;i \ne j \hfill \\ \sum\limits_{\begin{subarray}{l} m = 1 \\ m \ne i \end{subarray} }^{N} {\frac{1}{{x_{i} - x_{m} }},\quad i = j = 1,2,3, \ldots ,N} \hfill \\ \end{aligned} \right., \\ A^{\left( r \right)} & = A^{\left( 1 \right)} A^{{\left( {r - 1} \right)}} ,\quad r = 2,3, \ldots ,N - 1. \\ \end{aligned}$$

(37)

Distribution of grid points plays an important role in convergence of the solution using DQM. A well-accepted set of the grid points is the Gauss–Lobatto–Chebyshev points given for 0≤ x ≤ L as [26]

$$x_{i} = \frac{L}{2}\left\{ {1 - \cos \left[ {\frac{{\left( {i - 1} \right)\pi }}{N - 1}} \right]} \right\},\quad i = 1,2,3, \ldots ,N.$$

(38)

Using the following notation:

$$\begin{array}{*{20}c} {\left[ A \right] = \left[ {A^{\left( 1 \right)} } \right],} & {\left[ B \right] = \left[ {A^{\left( 2 \right)} } \right]} \\ \end{array} ,$$

(39)

Equation (36) can be rewritten for the first two derivates as

$$\begin{array}{*{20}c} {\left\{ {\frac{{{\text{d}}f}}{{{\text{d}}x}}} \right\} = \left[ A \right]\left\{ f \right\},} & {\left\{ {\frac{{{\text{d}}^{2} f}}{{{\text{d}}x^{2} }}} \right\} = \left[ B \right]\left\{ f \right\}.} \\ \end{array}$$

(40)

Applying Eq. (40), the set of the governing Eq. (34) can be written in the following algebraic form:

$$\omega^{2} \left[ M \right]\left\{ s \right\} + \omega \left[ G \right]\left\{ s \right\} + \left[ K \right]\left\{ s \right\} = \left\{ 0 \right\},$$

(41)

where [M], [G], [K] and $\left\{ s \right\}$ are mass matrix, gyroscopic matrix, stiffness matrix and displacement vector which are presented in details in Appendix A.

Using Eqs. (35) and (40), the boundary conditions can be written in the following algebraic form:

$$\left[ T \right]\left\{ s \right\} = \left\{ 0 \right\},$$

(42)

in which matrix [T] is presented in Appendix B for various boundary conditions.

Simultaneous solution of algebraic Eqs. (41) and (42) leads to inconsistency between number of unknown variables and number of equations. In order to overcome this challenge, let us divide the grid points into two sets: boundary points (x₁ and x_N) and domain ones (x₂ − x_N−1). By neglecting satisfying Eq. (41) at the boundary points, this equation can be written as

$$\omega^{2} \left[ {\bar{M}} \right]\left\{ s \right\} + \omega \left[ {\bar{G}} \right]\left\{ s \right\} + \left[ {\bar{K}} \right]\left\{ s \right\} = \left\{ 0 \right\},$$

(43)

in which bar sign implies the corresponding non-square matrix. Equations (42) and (43) can be rearranged and partitioned in order to separate the boundary and domain points as follows:

$$\begin{aligned} & \omega^{2} \left( {\left[ {\bar{M}} \right]_{\text{b}} \left\{ s \right\}_{\text{b}} + \left[ {\bar{M}} \right]_{\text{d}} \left\{ s \right\}_{\text{d}} } \right) + \omega \left( {\left[ {\bar{G}} \right]_{\text{b}} \left\{ s \right\}_{\text{b}} + \left[ {\bar{G}} \right]_{\text{d}} \left\{ s \right\}_{\text{d}} } \right) \\ & \quad + \left[ {\bar{K}} \right]_{\text{b}} \left\{ s \right\}_{\text{b}} + \left[ {\bar{K}} \right]_{\text{d}} \left\{ s \right\}_{\text{d}} = \left\{ 0 \right\}, \\ \end{aligned}$$

(44-a)

$$\left[ T \right]_{\text{d}} \left\{ s \right\}_{\text{d}} + \left[ T \right]_{\text{b}} \left\{ s \right\}_{\text{b}} = \left\{ 0 \right\},$$

(44-b)

where subscripts “b” and “d” indicate to boundary and domain points, respectively. Substituting Eq. (44-b) into Eq. (44-a) leads to the following eigen value equation:

$$\omega^{2} \left[ {M^{*} } \right]\left\{ s \right\}_{\text{d}} + \omega \left[ {G^{*} } \right]\left\{ s \right\}_{\text{d}} + \left[ {K^{*} } \right]\left\{ s \right\}_{\text{d}} = \left\{ 0 \right\},$$

(45)

in which

$$\begin{aligned} & \left[ {M^{*} } \right] = \left[ {\bar{M}} \right]_{d} + \left[ {\bar{M}} \right]_{b} \left[ p \right],\;\;\left[ {K^{*} } \right] = \left[ {\bar{K}} \right]_{d} + \left[ {\bar{K}} \right]_{b} \left[ p \right], \\ & \quad \left[ {G^{*} } \right] = \left[ {\bar{G}} \right]_{d} + \left[ {\bar{G}} \right]_{b} \left[ p \right],\;\;\left[ p \right] = - \left[ T \right]_{b}^{ - 1} \left[ T \right]_{d} . \\ \end{aligned}$$

(46)

The eigenvalue Eq. (45) provides the natural frequencies of the rotating conical shells. Among all these frequencies, there are two sets of natural frequencies, the positive values which are known as forward frequencies and negative ones which are known as backward frequencies [27,28,29,30,31]. It is worth mentioning that the reverse definition is used by some authors as well [25, 32].

4 Numerical results

Numerical results are provided in this section to confirm convergence and accuracy of the presented numerical solution and examine the influences of different parameters on the forward and backward frequencies of rotating GNP-reinforced truncated conical shells. Except for the cases which are mentioned directly, in what follows, material properties of the epoxy and GNPs are considered as E_m= 3 GPa, ν_m= 0.34, ρ_m= 1200 kg/m³, E_GNP= 1.01 TPa, ν_GNP= 0.186 and ρ_GNP= 1060 kg/m³ [33,34,35] and results are presented for a rotating GNP-reinforced truncated conical shell clamped at x = 0 and simply supported at x = L (CS). The shell is of a = 0.5 m, α = 20°, L/a = 4, h/a = 0.1 which is rotating at Ω= 500 rad/s and FG-A distribution pattern is chosen for GNPs of g^*_GNP = 0.01, l_GNP/a = 2×10⁻⁶, w_GNP/l_GNP= 0.5 and h_GNP/l_GNP= 0.5 × 10⁻³. Also it should be noted that the natural frequencies are denoted by ω_mn in which “n” indicates to circumferential mode number [Eq. (33)] and m = 1,2,3,… shows the sequence of modes in meridional direction (x-axis).

Table 1 shows the effect of the number of grid points [N in Eq. (36)] on the values of forward and backward frequencies of the shell. As shown in this table, the presented solution converges rapidly and what follows, all of the numerical examples are reported based on N = 13.

Table 1 Convergence of the presented numerical solution

In order to confirm the accuracy of the presented solution, consider a CC stationary homogenous truncated conical shell of ν = 0.3, α = 45°, h/b = 0.01 and Lsinα/b = 0.5. For various values of circumferential mode number, values of dimensionless natural frequency (ω^*= ωb[ρ(1 − ν²)/E]^0.5) are presented in Table 2 for m = 1 against corresponding ones reported by Liew et al. [36] and Shu [37]. This table confirms that the presented solution has high accuracy and results are in agreement with those reported by other authors. It is worth mentioning that in Refs. [36, 37] the shear deformation and rotational inertia are neglected and the natural frequencies are obtained higher than the more accurate ones predicted in the presented paper based on the FSDT.

Table 2 Dimensionless natural frequencies of a CC stationary homogenous truncated conical shell (ν = 0.3, α = 45°, h/b = 0.01, Lsinα/b = 0.5, m = 1)

An homogenous rotating truncated conical shell of α = 30°, L/a = 6, h/a = 0.01 and ν = 0.3 is considered. For different boundary conditions, two selected values of dimensionless angular velocity (Ω^*= Ωb[ρ(1 − ν²)/E]^0.5) and n = m=1, dimensionless values of the forward and backward frequencies (ω^*= ωb[ρ(1 − ν²)/E]^0.5) are presented in Table 3 against corresponding ones reported by Dai et al. [32]. This table confirms that values of the frequencies are in high agreement and results with high accuracy can be obtained using the presented numerical solution. It should be noted that Dai et al. [32] used a classical shell theory to model the shell, and values of the both forward and backward frequencies reported by them are higher than the more accurate ones achieved in the presented paper. Also it is worth mentioning that the definition of forward and backward frequencies in Ref. [32] is reverse of the definition used in the current papers.

Table 3 Dimensionless forward and backward frequencies of a rotating homogenous truncated conical shell (ν = 0.3, α = 30°, h/a = 0.01, L/a = 6, n = m=1)

Effect of circumferential mode number on the values of forward and backward frequencies of the rotating GNP-reinforced truncated conical shells is illustrated in Fig. 3. This figure shows that for a special value of circumferential mode number, the minimum values of forward and backward frequencies can be obtained. Figure 3 reveals that this special value of circumferential mode number is same for forward and backward frequencies but is not same for different meridional mode numbers.

Fig. 3

Effect of circumferential mode number on the forward and backward frequencies of the shell

Effect of boundary conditions on the forward and backward frequencies of the rotating GNP-reinforced truncated conical shells is investigated in Table 4. This table shows that as was expected, using more constrained conditions at the edges of the shell leads to increase in values of forward and backward frequencies. A simple comparison between results for SC and CS or FC and CF shells reveals that in order to increase values of forward and backward frequencies it is better to use more constrained conditions at x = L (large radius of the cone) rather that x = 0 (small radius of the cone). It is noteworthy that result of this table can be used as benchmark results for other researchers.

Table 4 Effect of boundary conditions on the forward and backward frequencies of the shell

As rotational speed of the shell rises, both the Coriolis acceleration and initial hoop tension increase. The initial hoop tension leads to increase in stiffness of the shell and increases both forward and backward frequencies, but the Coriolis acceleration increases forward frequencies and reduces backward ones. Figure 4 shows the influence of rotational speed on the natural frequencies of the shell which is known as the Campbell diagram [27]. As depicted in this figure, with increase in rotational speed of the shell, all forward frequencies grow which shows the cooperative effects of initial hoop tension and the Coriolis acceleration on the forward modes. Figure 4 shows different trends for backward modes; for n = 1 and n = 2, with increase in rotational speed, some backward frequencies decrease, some of them increase and other ones decrease at first and increase subsequently, and for n ≥ 3, all backward frequencies grow with increase in rotational speed of the shell. This different trends can be explained by the contrast between effects of initial hoop tension and the Coriolis acceleration on the backward modes.

Fig. 4

Effect of angular velocity on the forward (-) and backward (–) frequencies of the shell

In Fig. 4, the line of Ω= ±ω is shown as well which is known as the line of synchronous whirling [27]. Intersection of this line with the Campbell diagram determines the critical resonance speeds of the rotating shell which should be strongly avoided. At these critical speeds, any residual unbalance increases the amplitude of vibration and leads to a catastrophic failure. As shown in this figure for the current case study, the resonance speeds can be found for n = 1 (Ω_cr ≈ 1000 rad/s) and n = 2 (Ω_cr≈ 914 rad/s), and for higher values of the circumferential mode number (n ≥ 3) the line of synchronous whirling has no intersection with the Campbell diagram and no resonance speed can be found.

In order to investigated the influences of centrifugal and Coriolis accelerations and initial hoop tension, variation of forward and backward frequencies is depicted in Fig. 5 versus rotational speed for m = 1, and three cases which are determined based on Eq. (31) as follows:

Fig. 5

Effect of centrifugal and Coriolis accelerations and initial hoop tension on the forward (-) and backward (–) frequencies of the shell

• Case 1 Centrifugal acceleration and initial hoop tension (terms contain square of rotational speed) are considered but Coriolis acceleration (terms contain rotational speed and first time derivatives of displacements) is neglected.

• Case 2 Coriolis acceleration is considered but centrifugal acceleration and initial hoop tension are neglected.

• Case 3 Coriolis and centrifugal accelerations and initial hoop tension are considered.

As depicted in Fig. 5, for a stationary shell there is no difference between three cases, but as rotating speed of the shell increases, significant differences can be seen between all cases. This figure shows that by neglecting Coriolis acceleration (Case 1) no difference can be detected between forward and backward frequencies and values of the natural frequencies are between corresponding values of forward and backward frequencies predicted in Case 3. Figure 5 reveals that centrifugal acceleration and initial hoop tension play predominant roles in determining values of critical speeds of the rotating shells. A comparison between cases 2 and 3 in this figure that reveals that for n = 1,2 neglecting centrifugal acceleration and initial hoop tension generates error in prediction of values of the critical speed, and for n > 2 the critical speeds predicted in case 2 vanish as the centrifugal acceleration and initial hoop tension are considered (case 3).

Figure 6 shows the influence of the semi-vertex angle on the forward and backward frequencies of the shell. As depicted in this figure, increase in value of the semi-vertex angle from α = 0 (cylindrical shell of radius r = a) to α = 90° (circular annular plate of inner radius r = a and outer radius r = b) leads to reduction in forward frequencies but no specific trend can be seen for backward ones, and these modes may increase or decrease with increase in value of semi-vertex angle. For explain this, it should be noted that with specific values of small radius and length of the shell, increase in value of semi-vertex angle of the shell affects both stiffness and inertia of the shell. Figure 6 also shows that for high values of semi-vertex angle forward and backward frequencies reach to same values which are corresponding natural frequencies of a rotating annular circular plate of inner radius r = a and outer radius r = b.

Fig. 6

Effect of semi-vertex angle on the forward (-) and backward (–) frequencies

Figure 7 shows the influence of total mass fraction of GNPs on the forward and backward frequencies of the rotating GNP-reinforced truncated conical shells for different values of circumferential mode number. As shown in this figure, subjoining a small amount of GNPs to the epoxy leads to a significant increase in the values of the forward and backward frequencies. It can be explained by high value of the modulus of elasticity of the GNPs which is significantly greater than modulus of elasticity of the epoxy.

Fig. 7

Effect of total mass fraction of GNPs on the forward (-) and backward (–) frequencies

Table 5 shows values of the forward and backward frequencies of the rotating GNP-reinforced truncated conical shell for different types of GNPs distribution patterns. This table reveals that among all studied patterns, the highest values of the forward and backward frequencies belong to FG-X pattern and the lowest ones belong to FG-O pattern. In other words, in order to make the most increase in the values of the forward and backward frequencies, it is better to put the GNPs as far as away from the middle surface of the shell which creates the highest flexural stiffness.

Table 5 Effect of distribution pattern of GNPs on the forward and backward frequencies

Variation of forward and backward frequencies of the GNP-reinforced truncated conical shells versus width of the GNPs is depicted in Fig. 8. As shown in this figure, increase in the width of the GNPs slightly increases both forward and backward frequencies of GNP-reinforced conical shells. In other words, increase in surface area of the GNPs increases the stiffness of a GNP-reinforced structure. To explain this, it can be pointed that a larger contact area between the GNPs and the polymer matrix provides better load transfer capability.

Fig. 8

Effect of width of the GNPs on the forward (-) and backward (–) frequencies

Figure 9 shows the influence of thickness of the GNPs on forward and backward frequencies of the GNP-reinforced truncated conical shells. This figure shows that increase in thickness of the GNPs leads to a slight reduction in both forward and backward frequencies which can be explained by increase in the monolayer graphene sheets. Figures 8 and 9 confirm that in order to have a better reinforcing effect, GNPs with larger surface area and fewer monolayer graphene sheets should be used.

Fig. 9

Effect of thickness of the GNPs on the forward (-) and backward (–) frequencies

5 Conclusions

Using GDQM, a numerical solution was presented for free vibration analysis of rotating truncated conical shells made of GNP-reinforced epoxy. The shell was modeled based on the FSDT incorporating centrifugal and Coriolis accelerations and initial hoop tension. Numerical results confirmed that presented solution is convergent, and for a special value of the circumferential mode number, the minimum values can be achieved for both forward and backward frequencies. It was shown that centrifugal and coriolis accelerations and initial hoop tension play predominant roles in dynamics of rotating conical shells. It was concluded that as rotational speed of the shell increases, forward frequencies increase, but no specific trend can be stated for variation of backward frequencies versus variation of rotational speed. Numerical results confirmed that increase in values of the semi-vertex angle decreases forward frequencies, but no specific trend can be stated for the effect of semi-vertex angle on the variation of backward frequencies. It was shown by numerical examples that increase in the value of the mass fraction of GNPs significantly increases values of both forward and backward frequencies, and in order to achieve higher reinforcing effect, it is better to use the GNPs with a larger surface area and fewer monolayer graphene and put them as far as away from the middle surface of the shell.

Appendices

Appendix A

In Eq. (41) mass, gyroscopic and stiffness matrices and displacement vector are defined as follows:

$$\begin{array}{*{20}c} {\left\{ s \right\}_{5N \times 1} = \left\{ {\begin{array}{*{20}c} {\left\{ U \right\}} \\ {\left\{ V \right\}} \\ {\left\{ W \right\}} \\ {\left\{ X \right\}} \\ {\left\{ \Theta \right\}} \\ \end{array} } \right\},} & {\left[ M \right] = \left[ {\begin{array}{*{20}c} {m_{11} } & {\left[ 0 \right]} & {\left[ 0 \right]} & {m_{14} } & {\left[ 0 \right]} \\ {\left[ 0 \right]} & {m_{22} } & {\left[ 0 \right]} & {\left[ 0 \right]} & {m_{25} } \\ {\left[ 0 \right]} & {\left[ 0 \right]} & {m_{33} } & {\left[ 0 \right]} & {\left[ 0 \right]} \\ {m_{41} } & {\left[ 0 \right]} & {\left[ 0 \right]} & {m_{44} } & {\left[ 0 \right]} \\ {\left[ 0 \right]} & {m_{52} } & {\left[ 0 \right]} & {\left[ 0 \right]} & {m_{55} } \\ \end{array} } \right],} \\ {\left[ G \right] = \left[ {\begin{array}{*{20}c} {\left[ 0 \right]} & {g_{12} } & {\left[ 0 \right]} & {\left[ 0 \right]} & {g_{15} } \\ {g_{21} } & {\left[ 0 \right]} & {g_{23} } & {g_{24} } & {\left[ 0 \right]} \\ {\left[ 0 \right]} & {g_{32} } & {\left[ 0 \right]} & {\left[ 0 \right]} & {g_{35} } \\ {\left[ 0 \right]} & {g_{42} } & {\left[ 0 \right]} & {\left[ 0 \right]} & {g_{45} } \\ {g_{51} } & {\left[ 0 \right]} & {g_{53} } & {g_{54} } & {\left[ 0 \right]} \\ \end{array} } \right],} & {\left[ K \right] = \left[ {\begin{array}{*{20}c} {k_{11} } & {k_{12} } & {k_{13} } & {k_{14} } & {k_{15} } \\ {k_{21} } & {k_{22} } & {k_{23} } & {k_{24} } & {k_{25} } \\ {k_{31} } & {k_{32} } & {k_{33} } & {k_{34} } & {k_{35} } \\ {k_{41} } & {k_{42} } & {k_{43} } & {k_{44} } & {k_{45} } \\ {k_{51} } & {k_{52} } & {k_{53} } & {k_{54} } & {k_{55} } \\ \end{array} } \right],} \\ \end{array}$$

(A-1)

in which [0] is zero matrix of order N and

$$\begin{aligned} & k_{11} = A_{11} \left[ B \right] + A_{11} \sin \alpha \left[ {a_{1} } \right]\left[ A \right] - \left( {A_{22} \sin^{2} \alpha + A_{66} n^{2} } \right)\left[ {a_{2} } \right] - n^{2} I_{0} \Omega^{2} I, \\ & k_{12} = n\left( {A_{12} + A_{66} } \right)\left[ {a_{1} } \right]\left[ A \right] - n\left( {A_{22} + A_{66} } \right)\sin \alpha \left[ {a_{2} } \right] - 2nI_{0} \Omega^{2} \sin \alpha I, \\ & k_{13} = A_{12} \cos \alpha \left[ {a_{1} } \right]\left[ A \right] - 0.5\sin 2\alpha A_{22} \left[ {a_{2} } \right], \\ & k_{14} = B_{11} \left[ B \right] + B_{11} \sin \alpha \left[ {a_{1} } \right]\left[ A \right] - \left( {B_{22} \sin^{2} \alpha + B_{66} n^{2} } \right)\left[ {a_{2} } \right] - n^{2} I_{1} \Omega^{2} I, \\ & k_{15} = n\left( {B_{12} + B_{66} } \right)\left[ {a_{1} } \right]\left[ A \right] - n\left( {B_{22} + B_{66} } \right)\sin \alpha \left[ {a_{2} } \right] - 2nI_{1} \Omega^{2} \sin \alpha I, \\ & g_{12} = 2\Omega I_{0} \sin \alpha I,\;g_{15} = 2\Omega I_{1} \sin \alpha I, \\ & m_{11} = I_{0} I,\;m_{14} = I_{1} I, \\ & k_{21} = - n\left( {A_{12} + A_{66} } \right)\left[ {a_{1} } \right]\left[ A \right] - n\left( {A_{22} + A_{66} } \right)\sin \alpha \left[ {a_{2} } \right] - 2nI_{0} \Omega^{2} \sin \alpha I, \\ & k_{22} = A_{66} \left[ B \right] + A_{66} \sin \alpha \left[ {a_{1} } \right]\left[ A \right] - \left( {A_{22} n^{2} + A_{44} \cos^{2} \alpha + A_{66} \sin^{2} \alpha } \right)\left[ {a_{2} } \right] - n^{2} I_{0} \Omega^{2} I, \\ & k_{23} = - n\left( {A_{22} + A_{44} } \right)\cos \alpha \left[ {a_{2} } \right] - 2nI_{0} \Omega^{2} \cos \alpha I, \\ & k_{24} = - n\left( {B_{12} + B_{66} } \right)\left[ {a_{1} } \right]\left[ A \right] - n\left( {B_{22} + B_{66} } \right)\sin \alpha \left[ {a_{2} } \right] - 2nI_{1} \Omega^{2} \sin \alpha I, \\ & k_{25} = B_{66} \left[ B \right] + B_{66} \sin \alpha \left[ {a_{1} } \right]\left[ A \right] + A_{44} \cos \alpha \left[ {a_{1} } \right] - \left( {B_{22} n^{2} + B_{66} \sin^{2} \alpha } \right)\left[ {a_{2} } \right] - n^{2} I_{1} \Omega^{2} I, \\ & g_{21} = 2I_{0} \Omega \sin \alpha I,\;g_{23} = 2I_{0} \Omega \cos \alpha I,\;g_{24} = 2I_{1} \Omega \sin \alpha I, \\ & m_{22} = I_{0} I,\;m_{25} = I_{1} I, \\ & k_{31} = - A_{12} \cos \alpha \left[ {a_{1} } \right]\left[ A \right] - 0.5\sin 2\alpha A_{22} \left[ {a_{2} } \right], \\ & k_{32} = - n\left( {A_{22} + A_{44} } \right)\cos \alpha \left[ {a_{2} } \right] - 2nI_{0} \Omega^{2} \cos \alpha I, \\ & k_{33} = A_{55} \left[ B \right] + A_{55} \sin \alpha \left[ {a_{1} } \right]\left[ A \right] - \left( {A_{22} \cos^{2} \alpha + A_{44} n^{2} } \right)\left[ {a_{2} } \right] - n^{2} I_{0} \Omega^{2} I, \\ & k_{34} = \left( {A_{55} I - B_{12} \cos \alpha \left[ {a_{1} } \right]} \right)\left[ A \right] + A_{55} \sin \alpha \left[ {a_{1} } \right] - 0.5B_{22} \sin 2\alpha \left[ {a_{2} } \right], \\ & k_{35} = n\left( {A_{44} \left[ {a_{1} } \right] - B_{22} \cos \alpha \left[ {a_{2} } \right]} \right) - 2nI_{1} \Omega^{2} \cos \alpha I, \\ & g_{32} = 2I_{0} \Omega \cos \alpha I,\;g_{35} = 2I_{1} \Omega \cos \alpha I, \\ & m_{33} = I_{0} I, \\ & k_{41} = B_{11} \left[ B \right] + B_{11} \sin \alpha \left[ {a_{1} } \right]\left[ A \right] - \left( {B_{22} \sin^{2} \alpha + B_{66} n^{2} } \right)\left[ {a_{2} } \right] - n^{2} I_{1} \Omega^{2} I, \\ & k_{42} = n\left( {B_{12} + B_{66} } \right)\left[ {a_{1} } \right]\left[ A \right] - n\left( {B_{22} + B_{66} } \right)\sin \alpha \left[ {a_{2} } \right] - 2nI_{1} \Omega^{2} \sin \alpha I, \\ & k_{43} = - A_{55} \left[ A \right] + B_{12} \cos \alpha \left[ {a_{1} } \right]\left[ A \right] - 0.5\sin 2\alpha B_{22} \left[ {a_{2} } \right], \\ & k_{44} = D_{11} \left[ B \right] + D_{11} \sin \alpha \left[ {a_{1} } \right]\left[ A \right] - \left( {D_{22} \sin^{2} \alpha + D_{66} n^{2} } \right)\left[ {a_{2} } \right] - \left( {A_{55} + n^{2} I_{2} \Omega^{2} } \right)I, \\ & k_{45} = n\left( {D_{12} + D_{66} } \right)\left[ {a_{1} } \right]\left[ A \right] - n\left( {D_{22} + D_{66} } \right)\sin \alpha \left[ {a_{2} } \right] - 2nI_{2} \Omega^{2} \sin \alpha I, \\ & g_{42} = 2I_{1} \Omega \sin \alpha I,\;g_{45} = 2I_{2} \Omega \sin \alpha I, \\ & m_{41} = I_{1} I,\;m_{44} = I_{2} I, \\ & k_{51} = - n\left( {B_{12} + B_{66} } \right)\left[ {a_{1} } \right]\left[ A \right] - n\left( {B_{22} + B_{66} } \right)\sin \alpha \left[ {a_{2} } \right] - 2nI_{1} \Omega^{2} \sin \alpha I, \\ & k_{52} = B_{66} \left[ B \right] + B_{66} \sin \alpha \left[ {a_{1} } \right]\left[ A \right] + A_{44} \cos \alpha \left[ {a_{1} } \right] - \left( {B_{22} n^{2} + B_{66} \sin^{2} \alpha } \right)\left[ {a_{2} } \right] - n^{2} I_{1} \Omega^{2} I, \\ & k_{53} = n\left( {A_{44} \left[ {a_{1} } \right] - B_{22} \cos \alpha \left[ {a_{2} } \right]} \right) - 2nI_{1} \Omega^{2} \cos \alpha I, \\ & k_{54} = - n\left( {D_{12} + D_{66} } \right)\left[ {a_{1} } \right]\left[ A \right] - n\left( {D_{22} + D_{66} } \right)\sin \alpha \left[ {a_{2} } \right] - 2nI_{2} \Omega^{2} \sin \alpha I, \\ & k_{55} = D_{66} \left[ B \right] + D_{66} \sin \alpha \left[ {a_{1} } \right]\left[ A \right] - \left( {D_{22} n^{2} + D_{66} \sin^{2} \alpha } \right)\left[ {a_{2} } \right] - \left( {A_{44} + n^{2} I_{2} \Omega^{2} } \right)I, \\ & g_{51} = 2I_{1} \Omega \sin \alpha I,\;g_{53} = 2I_{1} \Omega \cos \alpha I,\;g_{54} = 2I_{2} \Omega \sin \alpha I, \\ & m_{52} = I_{1} I,\;m_{55} = I_{2} I, \\ \end{aligned}$$

(A-2)

where I is identity matrix of order N and [a₁] and [a₂] are two diagonal matrices defined as follows:

$$\begin{array}{*{20}c} {\left[ {a_{1} } \right]_{ii} = \frac{1}{{r_{i} }},} & {\left[ {a_{2} } \right]_{ii} = \frac{1}{{r_{i}^{2} }}.} \\ \end{array}$$

(A-3)

Appendix B

In Eq. (42), matrix [T] is defined as

$$\left[ T \right]_{10 \times 5N} = \left[ {\begin{array}{*{20}c} {T_{11} } & {T_{12} } & {T_{13} } & {T_{14} } & {T_{15} } \\ {T_{21} } & {T_{22} } & {T_{23} } & {T_{24} } & {T_{25} } \\ \vdots & \vdots & \vdots & \vdots & \vdots \\ {T_{101} } & {T_{102} } & {T_{103} } & {T_{104} } & {T_{105} } \\ \end{array} } \right],$$

(B-1)

in which T₁₁ − T₅₅ are associated with the conditions at x = 0 and are defined as follows:

$$\begin{aligned} & {\text{Clamped}}\,\left( C \right): \\ & T_{11} = T_{22} = T_{33} = T_{44} = T_{55} = I_{1} , \\ & T_{12} = T_{13} = T_{14} = T_{15} = T_{21} = T_{23} = T_{24} = T_{25} = T_{31} = T_{32} = T_{34} = \\ & T_{35} = T_{41} = T_{42} = T_{43} = T_{45} = T_{51} = T_{52} = T_{53} = T_{54} = \left\{ 0 \right\}_{1 \times N} , \\ & {\text{Simply}}\;{\text{Supported}}\,\left( S \right): \\ & T_{11} = A_{11} A_{1} + \frac{{A_{12} \sin \alpha }}{a}I_{1} ,T_{14} = T_{41} = B_{11} A_{1} + \frac{{B_{12} \sin \alpha }}{a}I_{1} , \\ & T_{44} = D_{11} A_{1} + \frac{{D_{12} \sin \alpha }}{a}I_{1} ,T_{22} = T_{33} = T_{55} = I_{1} , \\ & T_{12} = T_{13} = T_{15} = T_{21} = T_{23} = T_{24} = T_{25} = T_{31} = T_{32} = T_{34} = \\ & T_{35} = T_{42} = T_{43} = T_{45} = T_{51} = T_{52} = T_{53} = T_{54} = \left\{ 0 \right\}_{1 \times N} , \\ & {\text{Free}}\,\left( F \right): \\ & T_{11} = A_{11} A_{1} + \frac{{A_{12} \sin \alpha }}{a}I_{1} ,T_{12} = \frac{{nA_{12} }}{a}I_{1} ,T_{13} = \frac{{A_{12} \cos \alpha }}{a}I_{1} , \\ & T_{14} = B_{11} A_{1} + \frac{{B_{12} \sin \alpha }}{a}I_{1} ,T_{15} = \frac{{nB_{12} }}{a}I_{1} , \\ & T_{21} = - \frac{{nA_{66} }}{a}I_{1} ,T_{22} = A_{66} A_{1} - \frac{{A_{66} \sin \alpha }}{a}I_{1} ,T_{23} = \left\{ 0 \right\}_{1 \times N} , \\ & T_{24} = - \frac{{nB_{66} }}{a}I_{1} ,T_{25} = B_{66} A_{1} - \frac{{B_{66} \sin \alpha }}{a}I_{1} , \\ & T_{31} = T_{32} = T_{35} = \left\{ 0 \right\}_{1 \times N} ,T_{33} = A_{1} ,T_{34} = I_{1} , \\ & T_{41} = B_{11} A_{1} + \frac{{B_{12} \sin \alpha }}{a}I_{1} ,T_{42} = \frac{{nB_{12} }}{a}I_{1} , \\ & T_{43} = \frac{{B_{12} \cos \alpha }}{a}I_{1} ,T_{44} = D_{11} A_{1} + \frac{{D_{12} \sin \alpha }}{a}I_{1} , \\ & T_{45} = \frac{{nD_{12} }}{a}I_{1} ,T_{51} = - \frac{{nB_{66} }}{a}I_{1} ,T_{52} = B_{66} A_{1} - \frac{{B_{66} \sin \alpha }}{a}I_{1} , \\ & T_{53} = \left\{ 0 \right\}_{1 \times N} ,T_{54} = - \frac{{D_{66} n}}{a}I_{1} ,T_{55} = D_{66} A_{1} - \frac{{D_{66} \sin \alpha }}{a}I_{1} , \\ \end{aligned}$$

(B-2)

in which the subscript 1 indicates to the first row of each matrix.

Also, with the following definitions, T₆₁ − T₁₀₅ are associated with the conditions at x = L:

$$\begin{aligned} & {\text{Clamped}}\,\left( C \right): \\ & T_{61} = T_{72} = T_{83} = T_{94} = T_{105} = I_{N} , \\ & T_{62} = T_{63} = T_{64} = T_{65} = T_{71} = T_{73} = T_{74} = T_{75} = T_{81} = T_{82} = T_{84} = \\ & T_{85} = T_{91} = T_{92} = T_{93} = T_{95} = T_{101} = T_{102} = T_{103} = T_{104} = \left\{ 0 \right\}_{1 \times N} , \\ & {\text{Simply}}\;{\text{Supported}}\,\left( S \right): \\ & T_{61} = A_{11} A_{N} + \frac{{A_{12} \sin \alpha }}{b}I_{N} ,T_{64} = T_{91} = B_{11} A_{N} + \frac{{B_{12} \sin \alpha }}{b}I_{N} , \\ & T_{94} = D_{11} A_{N} + \frac{{D_{12} \sin \alpha }}{b}I_{N} ,T_{72} = T_{83} = T_{105} = I_{N} , \\ & T_{62} = T_{63} = T_{65} = T_{71} = T_{73} = T_{74} = T_{75} = T_{81} = T_{82} = T_{84} = \\ & T_{85} = T_{92} = T_{93} = T_{95} = T_{101} = T_{102} = T_{103} = T_{104} = \left\{ 0 \right\}_{1 \times N} , \\ & {\text{Free}}\,\left( F \right): \\ & T_{61} = A_{11} A_{N} + \frac{{A_{12} \sin \alpha }}{b}I_{N} ,T_{62} = \frac{{nA_{12} }}{b}I_{N} ,T_{63} = \frac{{A_{12} \cos \alpha }}{b}I_{N} , \\ & T_{64} = B_{11} A_{N} + \frac{{B_{12} \sin \alpha }}{b}I_{N} ,T_{65} = \frac{{nB_{12} }}{b}I_{N} ,T_{71} = - \frac{{nA_{66} }}{b}I_{N} , \\ & T_{72} = A_{66} A_{N} - \frac{{A_{66} \sin \alpha }}{b}I_{N} ,T_{73} = \left\{ 0 \right\}_{1 \times N} ,T_{74} = - \frac{{nB_{66} }}{b}I_{N} , \\ & T_{75} = B_{66} A_{N} - \frac{{B_{66} \sin \alpha }}{b}I_{N} ,T_{81} = T_{82} = T_{85} = \left\{ 0 \right\}_{1 \times N} , \\ & T_{83} = A_{N} ,T_{84} = I_{N} ,T_{91} = B_{11} A_{N} + \frac{{B_{12} \sin \alpha }}{b}I_{N} ,T_{92} = \frac{{nB_{12} }}{b}I_{N} , \\ & T_{93} = \frac{{B_{12} \cos \alpha }}{b}I_{N} ,T_{94} = D_{11} A_{N} + \frac{{D_{12} \sin \alpha }}{b}I_{N} ,T_{95} = \frac{{nD_{12} }}{b}I_{N} , \\ & T_{101} = - \frac{{nB_{66} }}{b}I_{N} ,T_{102} = B_{66} A_{N} - \frac{{B_{66} \sin \alpha }}{b}I_{N} ,T_{103} = \left\{ 0 \right\}_{1 \times N} , \\ & T_{104} = - \frac{{D_{66} n}}{b}I_{N} ,T_{105} = D_{66} A_{N} - \frac{{D_{66} \sin \alpha }}{b}I_{N} , \\ \end{aligned}$$

(B-3)

in which the subscript N indicates to the last row of each matrix.