Optimal location of FG actuator/sensor patches on an FG rotating conical shell for active control of vibration

Abstract

In this paper, the optimization of piezoelectric patch positions is conducted in order to improve vibration performance of an FG-truncated conical shell. This investigation is done based upon a new optimization trend on a rotating cone for the first time, as well as, the piezoelectric material has been considered functionally graded. The vibration model is based on the classical theory, and the governing equation is obtained using the Lagrange equation. The sensor voltage change rate is selected as feedback signal to vibration control. Four different piezoelectric sets considered with different numbers of piezoelectric Patches. The settling time of the system and position of the piezoelectric patches in longitudinal direction is assumed as an objective function and optimization variable, respectively. Optimization is carried out using sequential quadratic programming and pattern search algorithms. Also, the symmetrical and asymmetrical layouts of the piezoelectric patches in order to study the settling time have been considered. Then, the effect of piezoelectric lengths and arcs on the settling time has been studied. The results show that the best position for piezoelectric placement is in a range between the middle and the base of the cone.

1 Introduction

Investigating the vibration of conical shells has particular importance due to its various applications in marine environments, aerospace, gas turbines, fluid transport pipelines, and so on. The importance of this vibration increases when the conical shell has rotational speed. Lots of research have been performed in the field of investigating the vibration of these structures. Li et al. [1] addressed the calculation of the natural frequency and forced vibration response of a conical shell by means of the Rayleigh–Ritz method. They investigated the vibration response in frequency domain. Setoodeh et al. [2] analyzed the dynamics and free vibrations of a functionally graded conical shell with variable thickness based on layerwise theory. The authors used differential quadrature method and Ansys software to discretize the equations and validate the results, respectively. Daneshjo et al. [3] presented an analysis of the dynamics and critical speed of a rotating conical shell with orthogonal stiffeners. In obtained results, the effect of parameters such as rotation speed, depth-to-width ratio of the stiffeners, number of stiffeners, cone angle, and boundary conditions on natural frequency is observed.

Nowadays, active and passive vibration control is important in most vibrating structures that use in aircraft, satellite, spacecraft, and pipelines. It is desirable for researchers to design an optimal closed-loop vibration control system with best performance. One impressive way to reduce cost and weight of the structure is to use piezoelectric patches instead of layers as sensors and actuators. In order to use these patches, designers deal with location, numbers, and dimensions of these patches, so a lot of choices are available. The basic questions that come up are what values for these three mentioned parameters should be considered so that the system shows best performance? To answer this question, it is necessary to examine the optimization topic. There are few studies about optimization in vibration control of shells. Karroubi and Irani [4] investigated vibration of rotating FG cylindrical shell with two piezoelectric layers. The piezoelectric materials was considered functionally graded (FG). They studied the effect of axial and circumferential wave number and piezoelectric thickness on the natural frequency. Also, Campbell’s diagram was depicted. Results show that using Galerkin's method leads to omitting the Coriolis effects.

Li et al. [5] studied the active control of free and forced vibration of a non-rotating conical shell using piezoelectric patches. To suppress vibrations, negative velocity feedback and linear quadratic regulator method were used. Numerical results of this paper illustrate that control gain is more effective than the piezoelectric size on vibration suppression. Jafari et al. [6] used the Lagrange method to study linear and nonlinear vibration of a functionally graded cylindrical shell with a piezoelectric layer. They investigated the effect of cylindrical radius, thickness, and circumferential wave number on the natural frequency. Moreover, they also studied vibrational behavior by changing the excitation force and applying an external voltage to the system. Heidari et al. [7] studied free vibrations of a porous cylindrical rotor with functionally graded piezoelectric patches based on first-order shear theory. In this study, various parameters such as porosity coefficient, fundamental natural frequency, critical speed, and piezoelectric characteristics are investigated. Based on the results of this research, higher value of piezoelectric angular pitch leads to a decrease in fundamental natural frequency. Song et al. [8] studied the active control of vibration of a composite cylindrical shell reinforced with carbon nanotubes using piezoelectric patches. They took into account thermal effects and used Reddy’s high-order shear deformation theory. They also proceeded to control the vibration amplitude by velocity feedback and LQR method. According to the results, vibration control effect of the velocity feedback method is more efficient in thin cylindrical shells than thick ones.

Biglar et al. [9] worked on optimizing of location of sensor and actuator to control vibration of cylindrical shell using genetic algorithm. The objective function they used was based on controllability and observability. Also, the optimization variables were the positions and orientations of piezoelectric patches. In order to improve the maximum power of actuator, a new control method was presented “saturated negative velocity feedback rule.” Active control of vibration of a simply supported thick cylindrical panel with optimally placed sensor and actuator pairs based on the linear three-dimensional exact piezo-elasticity theory was conducted by Hasheminejad and Oveisi [10]. The authors controlled the system under harmonic electromechanical excitations using the LQG method. It can be found from results that reducing the control input weighting factor causes a significant decrease in the closed-loop frequency response values. In [11], free and forced vibration reduction of non-rotating conical shells were investigated by Jamshidi and Jafari where four kinds of piezoelectric layer distributions were used. In this paper, the effect of control gain and piezoelectric distribution on closed-loop response and actuator voltage were analyzed simultaneously. Mohammadrezazadeh and Jafari [12] applied velocity feedback control method to nonlinear vibration suppression of laminated composite conical shell. In this study, the modified Galerkin method to discretize the PDE equations was used. Also, the asymptotic stability of the system was investigated using Lyapunov's indirect method.

Rostami and mohammadimehr [13] presented an analytical approach to the vibration control of a rotating sandwich cylindrical shell. The modeling and the control have been accomplished based on first-order shear deformation theory and Maxwell equations. The shell was considered porous, and functionally graded magneto‑electro‑elastic layers were used to suppress vibration. Dong et al. [14] focused on active control of dynamic behaviors and vibration characteristics of a sandwich cylindrical shell made of the graphene reinforced composite, considering thermal load. The results show that the velocity feedback gain does not affect the system's stiffness. Hoa et al. [15] analyzed nonlinear energy transfer of a flexible plate with arbitrary boundary conditions. The aim of this paper was to investigate low-frequency vibration isolation. Lagrange's approach was the method used to obtain equations of motion. Also, in order to validate frequency response and mode shapes, numerical method and finite element simulation were used, respectively. Xi et al. [16] presented a new coding metasurface based on fast optimization method to attain the reduction of wideband radar cross-section of the microstrip antenna array. Yan et al. [17] presented a novel complementary metal-oxide semiconductor latches design, namely Quadruple-Node-Upset-Tolerant Latch with optimized overhead for reliable computing. This design can stand multiple-node upset errors due to radiations.

In order to increase the efficiency of a ducted propeller system, Yu et al. [18] investigated its performance with considered weight penalty. For this purpose, optimization based on surrogate-based optimization (SBO) technique and momentum source method (MSM) was carried out. Wang et al. [19] designed a novel control method to make the teleoperation system more practical by amalgamating terminal sliding mode control and the neural network adaptive control method. Lu et al. [20] proposed a bilateral adaptive control approach to investigate the uncertainty of dynamic parameters and time delay. In this paper, the Lyapunov function was used to investigate stability and performance of the closed-loop system.

Regarding the wide application of autonomous underwater vehicles and the importance of their precise motion control in the presence of parameters uncertainty, Liu et al. [21] have presented a robust fractional-order proportional–integral–derivative (FOPID) controller. The authors gave simulation results to prove the correctness of proposed method. Liu et al. [22] investigated hybrid dynamic model of a high-speed thin-rimmed gear. The system is assumed six degrees of freedom, and the effects of centrifugal and inertia forces are present in the finite element model. In this article, the effect of the flexible gear body and high speed on the system was studied.

According to the literature, there are no studies that investigate and optimize the location of piezoelectric patches to improve the vibration behavior of a rotating FG conical shell. Therefore, in the present research, this issue has been addressed to optimize the position of FG piezoelectric sensors and actuators. In optimization procedure, settling time has been selected as objective function, and also the location of piezoelectric patches in the longitudinal direction has been considered as optimization variable. It should be noted that the sensors and actuators are modeled in pairs (sensor as inner layer and actuator as outer layer of the shell), and optimization is done in two different sensor and actuator sets: symmetric and asymmetric configurations with two optimization techniques, SQP¹ and PS² are used. SQP methods solve a sequence of optimization subproblems, each of which optimizes a quadratic model of the objective subject to a linearization of the constraints. Also, PS is one of the numerical optimization methods that is considered a derivative-free method. It aims to find the most desirable answer with the exploratory move by searching a number of mesh points. Therefore, the main innovations of this paper include: optimization of vibration control response of a rotating FG conical shell; considering piezoelectric patches properties to be functionally graded; choosing a simple function as an objective function unlike similar studies; using effective and simple procedures to optimize; and investigating the effect of the number, length, and angle of piezoelectric patches on the vibration behavior.

2 Modeling

In this research, a FG rotating cone with FG piezoelectric patches is modeled using energy method so that sensors and actuators are at inner and outer of the shell, respectively. Firstly, the kinetic and potential energies of system are obtained, and then, they are discretized, and finally, governing equations of motion are acquired in the ODE form using the Lagrange method.

2.1 Basic relationships

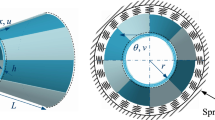
Schematic of the controlled rotating conical shell and piezoelectric arrangement is shown in Fig. 1. $a$ and $b$ are the radiuses at the two ends and $\alpha$ show semi-cone angle. The thickness of shell, actuator and sensor is indicated with $h$, ${h}_{a}$ and ${h}_{s}$, respectively. The radius of the cone is a function of $x$ as$r\left(x\right)=a+xsin\left(\alpha \right)$. $L$ and ${2l}_{p}$ refer to length of shell and piezoelectric in the longitudinal direction. Also, $2{\theta }_{p}$ shows patch angle; ${X}_{p}$ and ${\Theta }_{p}$ are the distance of middle point of each piezoelectric from the origin in $x$ and $\theta$ directions, respectively. ${V}_{a}$ is actuator voltage and ${V}_{s}$ is sensor voltage which investigate in further sections. It should be noted that system rotates at $\Omega$ rad/s about x axis. The stress–strain and electrical field–displacement relationships are expressed as [23]:

$$\sigma _{i} = \left\{ {\begin{array}{*{20}c} {\sigma _{x}^{i} } \\ {\sigma _{\theta }^{i} } \\ {\sigma _{{x\theta }}^{i} } \\ \end{array} } \right\}~,~\quad \varepsilon = \left\{ {\begin{array}{*{20}c} {\varepsilon _{x} } \\ {\varepsilon _{\theta } } \\ {\varepsilon _{{x\theta }} } \\ \end{array} } \right\}~ \to ~\left\{ {\begin{array}{*{20}l} {\sigma _{f} = C_{f} \varepsilon ~~~~~~~~~~~~~} \hfill \\ {\begin{array}{*{20}c} {\sigma _{p} = C_{p} \varepsilon - e^{T} E} \\ {D = e\varepsilon + \zeta E~~~~~~} \\ \end{array} } \hfill \\ \end{array} } \right. \to \left\{ {\begin{array}{*{20}l} {\text{shell}:~\frac{{ - h}}{2} < z < \frac{h}{2}~~~~~~~~~~~~} \hfill \\ {\text{sensor}:\frac{{ - h}}{2} - h_{s} < z < \frac{{ - h}}{2}} \hfill \\ {\text{actuator}:~~\frac{h}{2} < z < \frac{h}{2} + h_{a} } \hfill \\ \end{array} } \right.~\quad i = f,p$$

(1)

The subscripts $f$ and $p$ represent the shell and piezoelectric. $\sigma$ and $C$ are the stress and stiffness matrix. Also, mechanical strain and electrical field are indicated with $\varepsilon$ and $E$. $D$ is the electrical displacement vector, $e$ and $\zeta$ show effective piezoelectric and permittivity constants, respectively.

Fig. 1

Rotating conical shell with piezoelectric patches. a Three-dimensional, b side view, c front view

The, other parameters in Eq. (1) are as follows [5, 24]:

$$\left\{ {\begin{array}{*{20}l} { C_{f} = \left[ {\begin{array}{*{20}c} {Q_{11} } & {Q_{12} } & 0 \\ {Q_{21} } & {Q_{22} } & 0 \\ 0 & 0 & {Q_{66} } \\ \end{array} } \right] \quad \zeta = \left[ {\begin{array}{*{20}c} {\zeta_{1} } & 0 & 0 \\ 0 & {\zeta_{2} } & 0 \\ 0 & 0 & {\zeta_{3} } \\ \end{array} } \right] \quad E = \left\{ {\begin{array}{*{20}c} {E_{x} } \\ {E_{\theta } } \\ {E_{z} } \\ \end{array} } \right\} } \hfill \\ {C_{p} = \left[ {\begin{array}{*{20}c} {Q_{11}^{p} } & {Q_{12}^{p} } & 0 \\ {Q_{21}^{p} } & {Q_{22}^{p} } & 0 \\ 0 & 0 & {Q_{66}^{p} } \\ \end{array} } \right] \quad e = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ {e_{31} } & {e_{32} } & 0 \\ \end{array} } \right] \quad D = \left\{ {\begin{array}{*{20}c} {D_{x} } \\ {D_{\theta } } \\ {D_{z} } \\ \end{array} } \right\} } \hfill \\ \end{array} } \right.$$

(2)

In Eq. (2), $Q_{11} = Q_{22} = \frac{{E_{f} \left( z \right)}}{{1 - \upsilon^{2} }}; Q_{12} = Q_{21} = \upsilon E_{f} \left( z \right)/\left( {1 - \upsilon^{2} } \right) ; Q_{12} = Q_{21} = E_{f} \left( z \right)/\left[ {2\left( {1 - \upsilon^{2} } \right)} \right]$, where $E_{f} \left( z \right)$ is elasticity modulus and $\upsilon$ is Poisson ratio of shell that is assumed to be constant. For the piezoelectric layer, it is assumed that the electric field direction and polarity are parallel to each other and perpendicular to the piezoelectric surface. Therefore, it can be assumed that $E_{x} = E_{\theta } = 0$ [5, 25, 26]. Regarding [27], the electric potential is taken into account to be linear within the thickness of actuator layer:

$${\Phi }_{a} \left( {x,z,t} \right) = {\overline{\Phi }}_{a} \left( {x,t} \right) + \left( {z - z_{a} } \right)\frac{{V_{a} \left( {x,t} \right)}}{{h_{a} }},$$

(3)

where ${\overline{\Phi }}_{a} = \left( {{\Phi }^{ + } + {\Phi }^{ - } } \right)/2$; ${\Phi }^{ + }$ and ${\Phi }^{ - }$ are electrical boundary conditions at the top and bottom of actuator, respectively. Electric field in thickness direction is equal to

$$\left| {E_{z} } \right| = \left| { - \frac{{\partial {\Phi }_{a} }}{\partial z}} \right| = \frac{{V_{a} \left( {x,t} \right)}}{{h_{a} }},\quad x = x_{P},$$

(4)

while $V_{a}$ is the actuator voltage and $h_{a}$ refers to actuator thickness. In this study, the classical theory and Love strain–displacement relations have been used. In Love relations, normal and transverse shear stress and strain along the shell thickness are ignored, and only plane stresses are presented. The relationship between strain and displacement is as follows [28]:

$$\begin{aligned} &\left\{ {\begin{array}{*{20}c} {\varepsilon_{x} } \\ {\varepsilon_{\theta } } \\ {\varepsilon_{x\theta } } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\varepsilon_{x}^{0} } \\ {\varepsilon_{\theta }^{0} } \\ {\varepsilon_{x\theta }^{0} } \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {K_{x} } \\ {K_{\theta } } \\ {K_{x\theta } } \\ \end{array} } \right\},\\ &\varepsilon_{0x} = \frac{\partial u}{{\partial x}},\quad K_{x} = - \frac{{\partial^{2} w}}{{\partial x^{2} }}, \\ \end{aligned}$$

$${\varepsilon }_{\theta }^{0}=\frac{1}{r\left(x\right)}\frac{\partial v}{\partial \theta }+\frac{u{\rm sin}\left(\alpha \right)+w{\rm cos}\left(\alpha \right)}{r\left(x\right)}, \quad {K}_{\theta }=-\left(-\frac{1}{{r\left(x\right)}^{2}}\frac{{\partial }^{2}w}{\partial {\theta }^{2}}+\frac{1}{{r\left(x\right)}^{2}}\frac{\partial v}{\partial \theta }{\rm cos}\left(\alpha \right)-\frac{1}{r\left(x\right)}\mathrm{sin}(\alpha )\frac{\partial w}{\partial x}\right),$$

$${\varepsilon }_{x\theta }^{0}=\frac{\partial v}{\partial x}+\frac{1}{r\left(x\right)}\frac{\partial u}{\partial \theta }-\frac{\mathrm{sin}\left(\alpha \right)}{r\left(x\right)}v, \quad {K}_{x\theta }=-2\left(\frac{1}{r\left(x\right)}\frac{{\partial }^{2}w}{\partial x\partial \theta }-\frac{{\rm sin}\left(\alpha \right)}{{r\left(x\right)}^{2}}\frac{\partial w}{\partial \theta }-\frac{{\rm cos}\left(\alpha \right)}{r\left(x\right)}\frac{\partial v}{\partial x}+\frac{{\rm sin}\left(\alpha \right)\mathrm{cos}(\alpha )}{{r\left(x\right)}^{2}}v\right).$$

(5)

Both main and piezoelectric layers are considered to be FG, so the shell and piezoelectric properties are changed as [29, 30]:

$$\left\{ {\begin{array}{*{20}l} {\text{Shell}{\text{~~}}:{\text{~~}}Y_{f} \left( z \right) = \left( {Y_{C} - Y_{M} } \right)\left( {\frac{1}{2} + \frac{z}{h}} \right)^{P} + Y_{M} } \hfill & { \to {\text{~~~~}}Y = E{\text{~and~}}\rho } \hfill \\ {\text{Piezoelectric}{\text{~~~}}:{\text{~~}}Y\left( z \right) = Y^{0} \left( {\frac{z}{{{\raise0.7ex\hbox{$h$} \!\mathord{\left/ {\vphantom {h 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}}}} \right)^{N} } \hfill & { \to \left\{ {\begin{array}{*{20}c} {Y = Q_{{ij}}^{p} ~~~e_{{ij}} ~~~\zeta _{i} ~~~\rho _{p} ~~~~} \\ {Y^{0} = Q_{{ij}}^{0} ~~~e_{{ij}}^{0} ~~~\zeta _{i}^{0} ~~~\rho _{p}^{0} ~} \\ \end{array} } \right\}} \hfill \\ \end{array} } \right.$$

(6)

The Young's modulus and shell density vary in thickness of shell; also, $C$ and $M$ indices show ceramics and metals, respectively. $P$ and $N$ introduce power low index of the shell and piezoelectric layers that range of their changes are [0, ∞] and [−2, 2], respectively [31].

2.2 Equation of motion

To obtain the equation of motion by means of energy method, it is necessary to calculate the kinetic and potential energies:

$$\left\{ {\begin{array}{*{20}l} {T_{t} = \sum T_{i} } \hfill \\ {U_{t} = \sum U_{{\left( {st} \right)i}} + \sum U_{hi} } \hfill \\ \end{array} \quad i = f; a ;s} \right.$$

(7)

According to Eq. (7), kinetic energy $\left( {T_{t} } \right)$ of the system is the sum of kinetic energies of the main layer $\left( f \right)$, actuator $\left( a \right)$, and sensor patches $\left( s \right)$. Also, potential energy $\left( {U_{t} } \right)$ of system is divided into two parts: strain energy $\left( {U_{{\left( {st} \right)}} } \right)$ due to bending and strain energy $\left( {U_{h} } \right)$ due to hoop tension.

Equation (8) describes how to calculate kinetic energy of the system [32]. The range of integrals is defined according to area and thickness of each element as shown in Fig. 1:

$${T}_{t}=\frac{1}{2}{\int }_{0}^{2\pi }{\int }_{0}^{L}{\int }_{-\frac{h}{2}}^{\frac{h}{2}}\left({\rho }_{f}(z)\overrightarrow{V}.\overrightarrow{V}\right)dV+\frac{1}{2}\sum_{1}^{{n}_{a}}{\int }_{\frac{h}{2}}^{\frac{h}{2}+{h}_{a}}{\int }_{{\Theta }_{0}-{\theta }_{p}}^{{\Theta }_{0}+{\theta }_{p}}{\int }_{{X}_{p}-{l}_{p}}^{{X}_{p}+{l}_{p}}\left({\rho }_{p}\left(z\right)\overrightarrow{V}.\overrightarrow{V}\right)dV+\frac{1}{2}\sum_{1}^{{n}_{s}}{\int }_{-\frac{h}{2}-{h}_{s}}^{-h/2}{\int }_{{\Theta }_{0}-{\theta }_{p}}^{{\Theta }_{0}+{\theta }_{p}}{\int }_{{X}_{p}-{l}_{p}}^{{X}_{p}+{l}_{p}}\left({\rho }_{p}\left(z\right)\overrightarrow{V}.\overrightarrow{V}\right)dV \left(dV=r\left(x\right)dzdxd\theta \right),$$

(8)

$$\left\{ {\begin{array}{*{20}l} {\vec{R} = \left[ {\begin{array}{*{20}c} u \\ v \\ w \\ \end{array} } \right] } \\ {\vec{\Omega } = \left[ {\begin{array}{*{20}c} { - \Omega \cos \left( \alpha \right)} \\ 0 \\ {\Omega \sin \left( \alpha \right)} \\ \end{array} } \right]} \\ \end{array} } \right. \to \vec{V} = \frac{{{\text{d}}\vec{R}}}{{{\text{d}}t}} + \vec{\Omega } \times \vec{R} = \left[ {\begin{array}{*{20}c} {\dot{u}} \\ {\dot{v}} \\ {\dot{w}} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 & { - \Omega \sin \left( \alpha \right)} & 0 \\ {\Omega \sin \left( \alpha \right)} & 0 & {\Omega \cos \left( \alpha \right)} \\ 0 & { - \Omega \cos \left( \alpha \right)} & 0 \\ \end{array} } \right] \times \left[ {\begin{array}{*{20}c} u \\ v \\ w \\ \end{array} } \right],$$

(9)

where $\rho_{f}$ and $\rho_{p}$ refer to shell and piezoelectric density, respectively. Two parameters $n_{a}$ and $n_{s}$ represent the number of actuators and sensors. $\vec{V}$ vector also shows the velocity of each element, which can be calculated according to Eq. (9).

The strain energy due to bending is expressed in Eq. (10) [33]. As can be seen, integral related to the actuator has mechanical and electrical terms, but integral related to the sensor and core layers has only mechanical terms [8]:

$${U}_{(st)}=\frac{1}{2}{\int }_{0}^{2\pi }{\int }_{0}^{L}{\int }_{-\frac{h}{2}}^{\frac{h}{2}}\left({\sigma }_{f}^{T}.\varepsilon \right)dV+\frac{1}{2}\sum_{i=1}^{{n}_{a}}{\int }_{\frac{h}{2}}^{\frac{h}{2}+{h}_{a}}{\int }_{{\Theta }_{0}-{\theta }_{p}}^{{\Theta }_{0}+{\theta }_{p}}{\int }_{{X}_{p}-{l}_{p}}^{{X}_{p}+{l}_{p}}\left({\sigma }_{p}^{T}.\varepsilon -D.E\right)dV+\frac{1}{2}\sum_{1}^{{n}_{s}}{\int }_{-\frac{h}{2}-{h}_{s}}^{-\frac{h}{2}}{\int }_{{\Theta }_{0}-{\theta }_{p}}^{{\Theta }_{0}+{\theta }_{p}}{\int }_{{X}_{p}-{l}_{p}}^{{X}_{p}+{l}_{p}}\left({\sigma }_{p}^{T}.\varepsilon \right)dV \left(dV=r\left(x\right)dzdxd\theta \right).$$

(10)

The strain energy due to hoop tension can be obtained from Eq. (11) [33]:

$${U}_{h}=\frac{1}{2}{\int }_{0}^{2\pi }{\int }_{0}^{L}{\int }_{-\frac{h}{2}}^{\frac{h}{2}}\left({N}_{\theta f}{\varepsilon }_{\theta }^{0}\right)dV+\frac{1}{2}\sum_{1}^{{n}_{a}}{\int }_{\frac{h}{2}}^{\frac{h}{2}+{h}_{a}}{\int }_{{\Theta }_{0}-{\theta }_{p}}^{{\Theta }_{0}+{\theta }_{p}}{\int }_{{X}_{p}-{l}_{p}}^{{X}_{p}+{l}_{p}}\left({N}_{\theta p}{\varepsilon }_{\theta }^{0}\right)dV+\frac{1}{2}\sum_{1}^{{n}_{s}}{\int }_{-\frac{h}{2}-{h}_{s}}^{-h/2}{\int }_{{\Theta }_{0}-{\theta }_{p}}^{{\Theta }_{0}+{\theta }_{p}}{\int }_{{X}_{p}-{l}_{p}}^{{X}_{p}+{l}_{p}}\left({N}_{\theta p}{\varepsilon }_{\theta }^{0}\right)dV \left(dV=r\left(x\right)dzdxd\theta \right).$$

(11)

The hoop tension $\left({N}_{\theta }\right)$ and its related strain are expressed in Eq. (12) and Eq. (13) [33, 34].

$${N}_{\theta i}={\rho }_{i}\left(z\right){\Omega }^{2}{r}^{2}\left(x\right) \to i=f,p,$$

(12)

$${\varepsilon }_{\theta }^{0}=\frac{1}{{r}^{2}\left(x\right)}\left\{{\frac{\partial u}{\partial \theta }}^{2}+{\left(\frac{\partial v}{\partial \theta }+u{\rm sin}\left(\alpha \right)+w{\rm cos}\left(\alpha \right)\right)}^{2}+{\left(v-\frac{\partial w}{\partial \theta }\right)}^{2}\right\}.$$

(13)

In order to discretize the dynamic equation, the solution related to the simply supported boundary conditions has been considered as follows [34]:

$$u\left(x;\theta ;t\right)=\sum_{m=1}^{{M}_{T}}\sum_{n=1}^{{N}_{T}}\left[{u}_{1}^{mn}\left(t\right)\mathrm{cos}n\theta -{u}_{2}^{mn}\left(t\right)\mathrm{sin}n\theta \right]\mathrm{cos}\left(\frac{m\pi x}{L}\right),$$

$$v\left(x;\theta ;t\right)=\sum_{m=1}^{{M}_{T}}\sum_{n=1}^{{N}_{T}}\left[{v}_{1}^{mn}\left(t\right)\mathrm{sin}n\theta +{v}_{2}^{mn}\left(t\right)\mathrm{cos}n\theta \right]\mathrm{sin}\left(\frac{m\pi x}{L}\right),$$

$$w\left(x;\theta ;t\right)=\sum_{m=1}^{{M}_{T}}\sum_{n=1}^{{N}_{T}}\left[{w}_{1}^{mn}\left(t\right)\mathrm{cos}n\theta -{w}_{2}^{mn}\left(t\right)\mathrm{sin}n\theta \right]\mathrm{sin}\left(\frac{m\pi x}{L}\right),$$

(14)

where $u$, $v$, and $w$ are vibration displacements in the $x$, $y$, and $z$ direction, respectively. $m$ and $n$ show longitudinal and circumferential wavenumbers. Also, ${M}_{T}$ and ${N}_{T}$ are numbers of finite term to the approximation of exact solution. By substitution Eq. (14) into Eq. (7), the $x$ and $\theta$ variables are eliminated and kinetic and potential energies are calculated as a function of time. By making up $L={T}_{t}-{U}_{t}$ and using the Lagrange approach, differential equations of motion are obtained in the form ODE [34]:

$$L = T_{t} - U_{t} { } \to { }\frac{{\text{d}}}{{{\text{d}}t}}{ }\left( {\frac{\partial L}{{\partial \dot{q}_{i} }}} \right) - \frac{\partial L}{{\partial q_{i} }} = 0,$$

(15)

$$\begin{aligned} & M\ddot{q} + C\dot{q} + Kq + K_{a} V_{a} = 0, \\ & q = \left\{ {u_{1}^{mn} { };{ }u_{2}^{mn} { };{ }v_{1}^{mn} ;{ }v_{2}^{mn} { };{ }w_{1}^{mn} { };{ }w_{2}^{mn} } \right\}^{T}, \quad { }V_{a} = \left\{ {V_{a1} { };{ }V_{a2} { };{ }V_{a3} { }; \ldots { }V_{aj} { }} \right\}^{T}. \\ \end{aligned}$$

(16)

$M$, $C$ and $K$ are inertia, gyroscopic effect and stiffness matrices, respectively. The stiffness matrix $\left( K \right)$ is affected by the strain energy ($U_{t}$) and rotational terms in the kinetic energy. Unlike the stiffness and inertia matrices which are symmetric, the gyroscopic effect matrix is asymmetric. $V_{a}$ is the actuator voltage and $K_{a}$ also is the actuator voltage coefficient, which is defined as follows:

$$K_{a} = { }\left[ {k_{ij}^{a} } \right] \to i = 1 \ldots 6 \,\,\left({{\text{Number }}\;{\text{of}}\;{\text{ variables}}\;{\text{ of}}\;{\text{ Eq}}{.}\;{14}} \right) , j = 1 \ldots n_{a} \quad \left({{\text{Number }}\;{\text{of}}\;{\text{ actuators}}} \right).$$

(17)

As is known, the surface integral of sensor's electrical displacement in its thickness direction is equal to electrical charge produced on each sensor [8]:

$$Q_{sj} \left( t \right) = \mathop \int \limits_{{A_{sj} }}^{ } D_{z} \left( {z = z_{m} } \right) {\text{d}}A = \hat{K}_{sj} q,$$

(18)

where $A_{sj}$ is outer face area of each sensor, $z_{m}$ is transverse coordinate of the sensor mid-plane and also $\hat{K}_{sj}$ is a coefficient that is a row vector.

Using Eq. (18), the voltage of the jth sensor is calculated [8]:

$$V_{sj} \left( t \right) = \frac{{h_{s} }}{{\zeta_{3} A_{sj} }}Q_{sj} \left( t \right) = \left( {\frac{{h_{s} }}{{\zeta_{3} A_{sj} }}\hat{K}_{sj} q} \right) = K_{sj} q\left( t \right),$$

(19)

$$V_{s} \left( t \right) = K_{s} q\left( t \right),$$

(20)

$$K_{s} = \left[ {k_{ij}^{s} } \right] \to i = 1 \ldots n_{s}\, \left( {{\text{Number}}\;{\text{ of}}\;{\text{ sensors}}} \right) ; j = 1 \ldots 6 \quad \left( {{\text{Number}}\;{\text{ of}}\;{\text{ variables}}\;{\text{ of}}\;{\text{ Eq}}{.}\;{14}} \right).$$

(21)

Finally, the elements of $K_{s}$ matrix express the relationship between sensor voltage and displacements. These coefficients depend on the thickness, outer face area, material, and position of sensor.

The sensor voltage calculated in Eq. (20) has been considered as a feedback of the system output. In order to suppress vibration, negative velocity feedback is applied, so that voltage exerted to piezoelectric actuator is proportional to the derivative of the sensor voltage:

$$V_{a} = - K_{t} \frac{{{\text{d}}V_{s} \left( t \right)}}{{{\text{d}}t}} = - K_{t} K_{s} \dot{q}\left( t \right).$$

(22)

$K_{t}$ is feedback control gain, which is expressed as a matrix with dimensions $\left( {n_{a} \times n_{s} } \right)$. By substituting Eq. (22) into Eq. (16), the final form of the system equation is obtained as:

$$M\ddot{q} + \left( {C - K_{a} K_{t} K_{s} } \right)\dot{q} + \left( K \right)q = 0.$$

(23)

2.3 Optimization problem and algorithms

Details needed to implement the optimization problem are considered in this section to have optimal vibration reduction (Table 1). These details are objective function that is to be minimized; optimization parameters that are unknown parameters lead to minimize the objective function and optimization constraints that limit the parameters to the allowable region. As mentioned in the previous section, system settling time is considered as the objective function that is defined: “The time required for the response to reach and stay within 2% or 5% neighborhood of the final value” [35], where the system response is the vibration in three direction and the final value of response is zero. To achieve the settling time, the real part of dominant pole of system (the nearest pole to imaginary axis) must be calculated. For this purpose, it is necessary that using Eq. (23), the system characteristic equation $\left(M{s}^{2}+\left(C-{{K}_{a}K}_{t}{K}_{s}\right)s+K=0\right)$ is written and its roots are obtained. For this problem, three constraints have been defined: the first constraint is the static constraint that specifies the allowable range of piezoelectric position. The second one is considered the stability characteristic which means the acceptable optimization parameter is one that guarantees asymptotical stability. Finally, the third constraint is the system dynamic equation as an equality dynamic constraint.

Table 1 Details of optimization problem

As can be observed in Table 1, the static and the stability constraints have an inequality form and the dynamic constraint has equality form. The position of piezoelectric patch (${X}_{p}$) in the $x$ direction is assumed as optimization variable. ${l}_{p}$ is half-length of piezoelectric pairs in the longitudinal direction (see Fig.1), $G$ indicates state variables vector and ${A}_{c}$ is the dynamic matrix of closed-loop system and $Re(s)$ refers to real part of eigen values or ${A}_{c}$.

After defining the optimization problem and determining the details (objective function, constraints, and optimization parameter), it is needed to be specified optimization algorithms. In this paper, two algorithms, SQP and PS, have been used. Performance of algorithms is as follows:

The PS algorithm starts by creating points around the initial point, which can be provided by the user or obtained from the results of previous calculations. These points considered by the algorithm are called mesh points, and their distance to the starting point is called mesh size. The steps of the algorithm are as follows [36]:

• (a) Setting the starting or initial point (by user)

• (b) Constructing mesh points around the starting point

• (c) Calculation of the objective function at each mesh point

If the objective function at the mesh point is less than the value of it at starting point, the sampling is successful, and the following steps are followed:

• (A) The current point is set as the new starting point.

• (B) The mesh size is doubled.

• (C) The algorithm returns to step b.

If the sampling is unsuccessful, the mesh size is halved and the process continues from step b.

Termination conditions are as follows:

• (1) If the mesh size is less than the defined limit in advance.

• (2) If distance between two starting points is less than the set limit.

• (3) If number of iterations reaches the predefined number.

• (4) If difference of objective function between two successful samplings is less than the specified limit.

The SQP is a popular and strong algorithm used for constrained nonlinear problems. Its advantage is its high speed in optimization. In this method, in each iteration, a quadratic optimization problem is solved, in which a quadratic approximation of the objective function (based on approximation of the second order of Lagrange function) and a first-order linear approximation of the constraints are used. Unlike the PS algorithm, here the direction of searching is determined by calculating the gradient, and the termination condition is also established based on defining the limit on the difference between two consecutive values of the objective function [37].

3 Discussion and results

Before the discussion, to check the validity, the natural frequencies of system are compared with previous similar results. For this aim, a homogenous rotating conical shell without piezoelectric patches is considered, whose natural frequencies and rotational speed are made dimensionless using Eq. (24). In Table 2, the non-dimensional natural frequency of the simplified system is compared with reference [38] in different circumferential wave numbers.

Table 2 Comparison of frequency parameter of a rotating conical shell $\alpha =30^\circ ; h/a=0.01 ; L/a=6 ; m=1 ; \upsilon =0.3$

$${\Omega }^{*}=\Omega b\sqrt{\frac{\rho \left(1-{\upsilon }^{2}\right)}{E}} ;\quad {f}_{f}={\omega }_{f}b\sqrt{\frac{\rho \left(1-{\upsilon }^{2}\right)}{E} } ;\quad {f}_{b}={\omega }_{b}b\sqrt{\frac{\rho \left(1-{\upsilon }^{2}\right)}{E}}$$

(24)

As can be seen in Table 2, the backward and forward natural frequencies of the system are in good agreement with the reference [38].

To implement the optimization algorithm and determine the optimum position of piezoelectric patches, it is necessary to determine all system element’s mechanical and electrical properties. Piezoelectric patches are considered of type $PZT-4$; also, alumina and aluminum are used in inner and outer core layers, respectively. In Tables 3 and 4, the shell and piezoelectric properties are presented [39, 40]. Also, Table 5 gives other physical and geometrical parameters.

Table 3 Shell properties [39]

Table 4 Piezoelectric properties (PZT-4) [40]

Table 5 System parameters

3.1 Effect of number of piezoelectric patches

Figure 2 shows the four different cases A, B, C and D in which the number of piezoelectric pairs varies from 2 to 8. In order to compare the system response between these 4 cases, the feedback gain is chosen so that the maximum voltage of each actuator is equal to maximum allowable value. Also in each case the sum of the piezoelectric arc angles is considered to be equal with other cases, and also all other conditions are assumed to be same.

Fig. 2

Rotating conical shell with different numbers of piezoelectric pair. A 2 pairs, B 4 pairs, C 6 pairs and D 8 pairs

Figure 3 illustrates open- and close-loop response of point ${A}_{0}=\left(x;\theta \right)=\left(\frac{L}{4}; 0\right)$ to the initial displacement. Since the vibration has been controlled in time domain by reducing ${u}_{1}^{mn}\left(t\right)$, ${u}_{2}^{mn}\left(t\right)$, ${v}_{1}^{mn}\left(t\right)$, ${v}_{2}^{mn}\left(t\right)$, ${w}_{1}^{mn}\left(t\right)$ and ${w}_{2}^{mn}\left(t\right)$, and according to Eq. (14), the vibration of all points on the conical shell is controlled. The point ${A}_{0}=\left(\frac{L}{4}; 0\right)$ is selected only to show time history of resulted variables, and any other points can be selected.

Fig. 3

Non-controlled and controlled response in the transverse direction $\left(\mathrm{w}\right).$ A 2 pairs, B 4 pairs, C 6 pairs and D 8 pairs

As can be seen, the steady-state response in case A is oscillatory with constant amplitude, and this is because there is a conjugate pole with zero real part; therefore, the system cannot be asymptotically stable, but in three other cases, the system is asymptotically stable with the settling time in the same range. To prove this, the real parts of the closed-loop poles in four cases (A, B, C, D) are presented in Table 6. As can be seen in the first column of Table 6, (case A), there are two poles with a real part close to zero that have been bolded. The existence of a conjugate pole with zero real part (or in the other words, a pole on an imaginary axis) causes oscillatory steady-state response with constant amplitude, and the system cannot be asymptotically stable. Exactly the same result can be seen in Fig. 3a. On the other hand, all real parts of the poles of B, C, and D cases are negative, which means the system in these three cases is asymptotically stable.

Table 6 The real part of closed-loop poles corresponding to Fig. 3

3.2 Effect of piezoelectric patches position, symmetric optimization

In this section, the best position of sensor–actuator pairs is obtained in the longitudinal direction. It is assumed that $x$ coordinate of all piezoelectric is equal with each other, and therefore, the system is symmetric. Optimization procedure is implemented by means of two SQP and PS algorithms. The piezoelectric geometry and initial guess are given in Table 7.

Table 7 Initial guesses and piezoelectric dimensions (according to Fig. 1)

Table 8 presents the results of optimization procedure. By comparison of the third and fourth columns, it can be found that the obtained results by the PS algorithm are better than the SQP. In case A, the result obtained from the SQP algorithm was diverged. According to Table 8, the results of the three cases B, C, and D are equal together, and this shows that, as the same of previous section, the number of piezoelectric (except case A) does not effect on settling time. Also in the fifth column of Table 8, ${A}_{p}$ and ${A}_{f}$ are the ratio of total area of sensor–actuator pair and cone, respectively. The results of this column indicate that the higher the value of the ${X}_{p}$, the greater the ${A}_{p}/{A}_{f}$ ratio. The mass of piezoelectric patches is one of the important parameters; for this reason, the ratio of optimized to non-optimized value of piezoelectric mass is presented in the sixth column of Table 8. As another comparison, the area under curve of absolute value of the voltage–time in four cases is compared in the seventh column to show control effort (Eq. (25)). For this comparison, settling times in all cases must be the same. The last column of Table 8 expresses the S parameter, and as be seen, the minimum value is related to case D.

Table 8 Symmetric optimizing of piezoelectric position in the ${\varvec{x}}$ direction

$$S=\mathrm{max}\left({\int }_{0}^{t}\left|{V}_{ai}\right|\mathrm{d}t\right)\; i=\mathrm{num \;of \;actuator}$$

(25)

Figures 4, 5, and 6 show required actuator voltage signal according to the obtained results from Table 8, and, as expected, the highest voltage is observed in case A. It should be noted that in these diagrams, the settling time has been set at 1 s to have same conditions.

Fig. 4

Required voltage—PS (symmetric)—case A

Fig. 5

Required voltage—SQP (symmetric)—cases B, C, and D

Fig. 6

Required voltage—PS (symmetric)—cases B, C, and D

Figure 7 depicts the convergence of symmetric optimization process. Vertical and horizontal axes indicate settling time as objective function and number of iterations, respectively. It is clear that the results of the three cases B, C, and D have acceptable agreement using both algorithms. Also, it can be observed that the PS algorithm performs less iteration than the SQP algorithm. It should be noted that at the first step of optimization in case A, the system has a pole with zero real part and have infinite settling time, that's why the diagram of case A starts from 2.

Fig. 7

Symmetric optimization convergence

In Fig. 8, the settling time of the closed-loop system is plotted based on the position of piezoelectric patches. It appears that for the three cases B, C, and D, ${X}_{p} = 0.582L$ is the relative extremum point and ${X}_{p} = 0.742L$ is the absolute ones, also for case A, ${X}_{p} = 0.478L$ is a relative extremum.

Fig. 8

Settling time based on position of the sensor/actuator pairs. a For all cases. b With magnification of the discontinuity range for Cases B, C, and D

Figure 8a shows a discontinuity in range [0.68L; 0.72L], resulting of poles near to imaginary axis; therefore, the settling time in this range is great, and the diagram has a vertical asymptote. For further understanding of this discontinuity, Fig. 8b focuses on the discontinuity part, and also real parts of poles for cases A and B are presented in Tables 9 and 10, respectively. As shown in Fig. 8b, the settling time between points ${X}_{p}=0.625\mathrm{L}$ and ${X}_{p}=0.719\mathrm{L}$ has been enhanced to about 250 s. Tables 9 and 10 also demonstrate that at some ${X}_{p}$, the real part of dominant pole is very close to zero, so that the settling time increases sharply. For example, according to Table 9, the settling time at point ${X}_{p}=\frac{11}{16L}=0.687L$ is as follows:

Table 9 Real part of closed-loop poles in terms of ${{\varvec{X}}}_{{\varvec{p}}}$ for case A

Table 10 Real part of closed-loop poles in terms of ${{\varvec{X}}}_{{\varvec{p}}}$ for case B

$${t}_{s}\left({X}_{p}\right)=\frac{4}{\mathit{min}\left(\left|Re\left(s\right)\right|\right)} \to {X}_{p}=\frac{11}{16}L=0.687L \to {t}_{s}=\frac{4}{0.0165}=242\; {\rm (sec)}$$

(26)

Generally, considering the settling time and actuator voltage criterions, optimization results show that at least 4 numbers of piezoelectric pairs are needed to have a desirable closed-loop response.

In the first vibration mode, there is an antinode in${X}_{p}=\frac{L}{2}$. It makes sense for all of the piezoelectric patches to be located near to this point. On the other hand, the less the piezoelectric distance from the base of the cone, the larger the piezoelectric area. It means that the piezoelectric area in range $\left[0 ;\frac{L}{2}\right ]$ is smaller than in range$\left[ \frac{L}{2};L \right]$. Therefore, the best point for piezoelectric placement is in the $\left[ \frac{L}{2};L \right]$ range.

3.3 Asymmetric optimization

To improve closed-loop response, the position of each piezoelectric pair is optimized in the $x$ direction, separately. Initial guess and the other piezoelectric parameters have been considered like the previous section.

Tables 11 and 12 represent the results of asymmetric optimization of sensor/actuator position in the longitudinal direction. The results show that case B has the best settling time. Ratio of the area and the mass ratios has been calculated in the fourth and fifth columns of Table 11, respectively. To study the voltage effort of actuator in the last column of Table 11, the defined parameter in Eq. (25) has been calculated for all cases, and as can be seen, the maximum value has been obtained for case A. The optimal position of patches is reported in Table 12. A comparison of symmetric and asymmetric optimization results is displayed in Table 13. The results of this table show that in the cases B and C, mass and piezoelectric surface, in asymmetric optimization, have been reduced by about 10% compared with symmetric optimization.

Table 11 Asymmetric optimization of location of each piezoelectric pair

Table 12 Position of each piezoelectric pair obtained from asymmetric optimization

Table 13 Comparison of symmetric and asymmetric optimization results

In general, a comparison between the results of asymmetric optimization in cases B, C, and D and Sect. 3.1 expresses that the settling time has been decreased from 2 s in Fig. 3 to around 0.5 s, and the covered surface of the cone by piezoelectric has been reduced between 67 and 70% in comparison with Fig. 2, and also the piezoelectric mass for vibration control has been decreased by 21–16%.

Figures 9, 10, 11, and 12 indicate the required voltage of actuators according to the obtained results from Table 11 for the same settling time (${t}_{s}=1 sec$). Regarding figures, the most sudden increase in voltage at zero second is related to case D. As can be seen, these figures are in agreement with the numbers in the last column of Table 11.

Fig. 9

Required actuator voltage—asymmetric optimization—case A

Fig. 10

Required actuator voltage—asymmetric optimization—case B

Fig. 11

Required actuator voltage—asymmetric optimization—case C

Fig. 12

Required actuator voltage—asymmetric optimization—case D

3.4 Piezoelectric size effect

This part of the paper tries to answer this question: Does changing the piezoelectric area affect the vibration response? Changes in piezoelectric area depend on two factors: (1) change in piezoelectric length and (2) variations of piezoelectric arc. In order to find the answer to the question, the settling time $({t}_{s})$ versus piezoelectric half-length $({l}_{P})$ and arc ${(2\theta }_{P})$ in different curves, which show the position of the piezoelectric, is plotted in Figs. 13, 14, 15 and 16. It should be noted that these diagrams have been depicted for four piezoelectric arrangement modes: A, B, C, and D.

Fig. 13

Variations of the settling time in terms of piezoelectric pairs half-length in case A

Fig. 14

Variations of settling time in terms of piezoelectric half-length in cases B, C and D

Fig. 15

Settling time versus sum of the piezoelectric arcs in case A

Fig. 16

Settling time versus sum of the piezoelectric arcs in cases B, C and D

In Figs. 13 and 14, the effect of piezoelectric half-length on the settling time $({t}_{s})$ in various ${x}_{P}$ has been investigated. It is expected that the settling time decreases by piezoelectric half-length increase, but Figs. 13 and 14 illustrate that this is a misconception; therefore, these figures prove that increasing the stability of system (decreasing settling time) by increasing the piezoelectric length is not a suitable way.

The effect of piezoelectric arc on settling time is shown in Figs. 15 and 16. The horizontal axis shows the sum of arcs of all piezoelectric pairs:

$$\sum_{i=1}^{K}\left(2{\theta }_{Pi}\right)\; K={\rm number\; of \;piezoelectric \;pairs} \;(2, 4, 6, 8).$$

(27)

In Fig. 15, which is drawn for case A (2 piezoelectric pairs), it can be seen that, except for one curve, in the rest of curves with the increase in piezoelectric arc, the vibration suppression time (settling time) decreases. According to this figure, the best response reaches when piezoelectric pairs are at ${x}_{P}=0.5$ and each arc is 180 degrees. The trend of all curves in Fig. 16, which has drawn for three cases A, B, and C (four, six, and eight piezoelectric pairs), is descending, and the lowest settling time is seen at 360 degrees, where piezoelectric has encircled the cone, like a ring.

The four figures that have been investigated in this section contain this point: the size and dimensions of the piezoelectric definitely have an effect on the closed-loop response, and to suppress the vibrations in the shortest time, the piezoelectric pairs should be considered like a ring.

3.5 Stability of other modes

In Sects. 3.2 and 3.3, optimization was performed to improve the closed-loop response of the first mode of vibration. Considering that higher vibration modes are also of particular importance, in this section closed-loop response of the rotating conical shell in 8 vibration modes based on results of Table 11, in four different cases A, B, C, and D (number of piezoelectric pairs according to Fig. 2), is drawn in Figs. 17, 18, 19, and 20.

Fig. 17

Closed-loop response $({\varvec{w}}\boldsymbol{ }({\varvec{t}}))$ in different vibration modes for case A

Fig. 18

Closed-loop response $({\varvec{w}}\boldsymbol{ }({\varvec{t}}))$ in different vibration modes for case B

Fig. 19

Closed-loop response $({\varvec{w}}\boldsymbol{ }({\varvec{t}}))$ in different vibration modes for case C

Fig. 20

Closed-loop response $({\varvec{w}}\boldsymbol{ }({\varvec{t}}))$ in different vibration modes for case D

In Fig. 17, it can be observed that the response of modes $m=1, n=3$;$m=1, n=4$; $m=2 ,n=1$; and $m=2, n=3$ is oscillatory with a constant amplitude. This means that the negative velocity feedback with the help of two sensor/actuator pairs is not able to control the vibrations of mentioned modes. Therefore, more piezoelectric are needed to control all these modes. Figure 18 shows that the amplitude of all eight vibration modes is decreasing and the settling time (${t}_{s}$) in this figure is less than in Fig. 17, as well. Therefore, the result of increasing the number of piezoelectric pairs from 2 to 4 is the reduction of settling time and ability to control more modes. In Figs. 19 and 20, it can be seen that vibration has been controlled well. The clear difference between these two figures is the shorter settling time of the responses drawn in Fig. 20 compared with Fig. 19, which means more stability of a cone with 8 piezoelectric pairs patches compared with a cone with 6 pairs of piezoelectric patches.

By observing the plotted figures in this section, it can be claimed that as the number of piezoelectric patches enhances, sensor/actuator voltages are distributed better on the shell and as a result, the stability of the system increases.

4 Conclusion

The aim of this paper was to find the best position for the actuator and sensor patches on a rotating truncated conical shell made of functionally graded material in order to reduce the cost of vibration control by reducing the required voltage or reducing the vibration damping time. Modeling was accomplished based on the classical theory and using Lagrange approach. In order to vibration control, negative velocity was considered as feedback in this order that the required voltage to control (actuator voltage) was set proportional to sensor voltage changes rate. The optimization of the piezoelectric position was designed based on four different types of sensor–actuator pair arrangements, where the number of pairs was 2, 4, 6, and 8. The settling time and position of piezoelectric pairs are considered as the objective function and optimization variable, respectively. Also, constraints, static, stability and dynamic, were considered to limit the obtained answers. The optimization was done in two cases: 1. symmetrical layout, 2. asymmetric layout, in the first case, all the actuators/sensors pairs are located at the same distance from the edge of cone, and in the second case, each pair has an independent position.

In order to find the optimal position of the piezoelectric, two algorithms, SQP and PS, which have different process to optimize, were used. It should be noted that the size of actuators/sensors pairs was investigated in several figures. The most important results obtained from this research are as follows:

• 1. The optimization results illustrate that by placing the sensor and actuator in the right position on the cone, both the settling time (time of vibration suppression) and the amount of required piezoelectric to control the vibrations are reduced.

• 2. According to the symmetric optimization results, the best position for piezoelectric on the shell to control the first mode of vibrations is in the range [L/2, L].

• 3. Regarding parameters such as settling time and actuator voltage, at least four pairs of sensors and actuators are needed to have an appropriate control response.

• 4. In the first vibration mode, it makes no much difference if the system is controlled by 4, 6, or 8 pairs of piezoelectric. But increasing the number of sensors and actuators increases the stability of higher modes and decreases the settling time, as well.

• 5. The PS algorithm obtained absolute extremum points, while the SQP algorithm calculated the relative extremum ones, so the PS algorithm performs better results than SQP. On the other hand, the time of answer in the PS algorithm is more than the SQP algorithm.

• 6. It can be claimed that increasing the piezoelectric surface through increasing its arc improves closed-loop response. The most desirable value for each piezoelectric arc is that the sum of those arcs is 360, which means that the piezoelectric patches encircle the shell like a ring.