Nonlinear vibration and dynamic performance analysis of the inerter-based multi-directional vibration isolator

Abstract

Motivated by the demand of improving the multi-directional vibration dynamic performance, an inerter-based multi-directional (IMD) vibration isolator is proposed in this paper, which is composed of the inerter, damper and spring structures in multiple directions. The dynamic equation of the IMD vibration isolator is established using the Lagrange theory, its dynamic response under base harmonic excitation is obtained using the harmonic balance method and pseudo-arc-length method, and the stability of the dynamic response is considered. The dynamic performance of the IMD vibration isolator under harmonic and shock excitations is studied and compared with those of the conventional multi-directional (MD) vibration isolator consist of the damper and spring structure, and the effect of structural parameters on its dynamic performance is investigated in detail. The results show that the IMD vibration isolator has nonlinear inertial, damping and stiffness characteristics, and it further reduces the dynamic displacement and absolute displacement transmissibility peaks, widens the isolation frequency band than the MD vibration isolator and also has better shock performance in the middle severity parameter range. In order to obtain better isolation and shock performance, the vertical and horizontal inertance-to-mass ratios are chosen as larger values, and the stiffness ratio and the horizontal spring compression ratio are chosen as smaller values. Therefore, the design of the proposed IMD vibration isolator exhibits the advantages of applying the inerter and provides excellent isolation and shock performance in multiple directions.

1 Introduction

Vibration exists widely in practical engineering, and it could lead to fatigue damage of the engineering structures, deteriorate the dynamic performance and shorten their service time. Therefore, the vibration mitigation and isolation devices are used to reduce the vibration amplitude, which increases the reliability and durability of the engineering structures [1]. Traditional vibration mitigation and isolation devices focus on one-directional vibration, while in some practical engineering, the vibration is multi-directional, for instance, seismic and wind vibrations in civil engineering [2]. For multi-directional vibration, the vibration mitigation and isolation devices should have effectiveness in all directions.

Here, the vibration isolator is considered and some researchers have conducted studies in multi-directional vibration isolation area. Xu et al. [3] presented a comprehensive assessment of recent developments of multi-directional (MD) vibration isolator and the material used in these devices. Sun and Jing [4] designed a three-directional quasi-zero-stiffness (QZS) vibration isolator, and it is composed of two symmetrically scissor-like structures in the horizontal direction and a spring–mass–damper system in the vertical direction, which reduces the natural frequencies and resonant peak in both directions. Furthermore, Xu and Sun [5] exploit the potential benefits of time-delayed active control for the three-directional QZS vibration isolator. Wu et al. [6] constructed a 6 degree-of-freedom (DOF) vibration isolator which combines the X-shaped structure and Stewart platform, and it has good isolation performance in 6 directions. Zhou et al. [7] devised a 6 DOF vibration isolator using a cam-roller-beam mechanism, which broadens the vibration isolation bandwidth and has higher effectiveness in the lower frequency band. Dong et al. [8] constructed a MD vibration isolator with QZS structure and spatial pendulum, which achieves better low-frequency vibration isolation performance in multiple directions. Lu et al. [9] proposed an electromagnetic Stewart platform to reduce the vibration in 6 directions and simultaneously harvest energy. Chai et al. [10] presented a 3DOF X-shaped structure-based vibration isolator, which achieves low-frequency vibration isolation in 3 directions. Yang and Cao [11] designed a 6DOF micro-vibration isolator based on the hexagon structure and obtained a broader isolation bandwidth. In these researches, the MD vibration isolator is based on the spring and damper structure and has nonlinear stiffness or nonlinear damping characteristic, and the further improvement of the isolation performance is restricted by its inherent structure.

As a two-terminal inertial structure, the inerter possesses the characteristic that the generated force between its two ends is proportional to its relative acceleration [12]. This proportionality is expressed as inertance and has the unit of kilogram. The inerter retains the mass amplification affect and supplies a larger inertance compared with its own mass, and the total inertial of the system would be increased without the need of adding more mass and thus satisfies the lightweight requirement. The inerter has been used in different areas and illustrated favorable effects owing to its mechanical property. Wagg [13] presented a review of the mechanical inerter and analyzed its physical realizations and nonlinear applications. Hu et al. [14], Qin et al. [15] and Wang et al. [16] studied the dynamic response of the inerter-based suspension, and a better vehicle ride comfort can be realized than the traditional suspension. Li et al. [17] introduced an inerter-based mechanical passive suppression device to the design of the landing gear, and better shimmy performance can be obtained as the aircraft is landing. Zhang et al. [18], Wang and Giaralis [19] and Zhao et al. [20] utilized the inerter in the building isolation device, which reduces the seismic and wind vibrations. Hu and Chen [21], Barredo et al. [22], Shi et al. [23] proposed the inerter-based dynamic vibration absorber, which expands the bandwidth and reduces the vibration amplitude than the classic dynamic vibration absorber. Lewis et al. [24] used the inerter-based suspension to enhance both track wear and passenger comfort in the high-speed train. Dai et al. [25] designed a nonlinear tuned mass damper inerter to suppress the longitudinal vibration transmission in propulsion shaft system. Liu et al. [26] constructed linear and geometrically nonlinear inerter-based resonator in metamaterials and obtained a lower-frequency bandgap.

Some scholars have designed different kinds of inerter-based vibration isolators and acquired some fruitful results. Hu et al. [27] and Wang et al. [28] constructed different types of inerter-based linear vibration isolators, studied their dynamic characteristics and found that a better dynamic performance is obtained compared with the linear ones. Furthermore, Wang et al. [29] put forward a semi-active inerter-based linear vibration isolator based on the acceleration–velocity switch control strategy to improve the isolation performance. Čakmak et al. [30, 31] conducted a dynamic performance and optimization of vibration-induced fatigue in a 2DOF inerter-based vibration isolator. Dai et al. [32] proposed two kinds of inerter-based piecewise vibration isolators, which has both bilinear and mass magnification characteristics, and found that the parallel-connected one has smaller transmissibility peak than the traditional linear and piecewise vibration isolators. Moraes et al. [33], Wang et al. [34] and Yang et al. [35] designed a nonlinear vibration isolator with lateral inerters, which has nonlinear inertial characteristic, a wider isolation bandwidth and a smaller transmissibility which can be acquired. In addition, Wang et al. [36, 37] devised three types of inerter-based QZS vibration isolator, which further reduces the transmissibility and widens the isolation bandwidth than the QZS one. Dong et al. [38] proposed an inerter-based nonlinear passive joint device and applied it in the coupled systems to suppress the vibration transmission. Shi et al. [39] arranged an inerter in a diamond-shaped linkage mechanism to construct an inerter-based nonlinear vibration isolator, which can shift and bend transmissibility peaks and power flow to the lower frequency band and achieve a wider isolation frequency band.

Until now, the inerter has been applied in the linear and nonlinear vibration isolation areas, based on the layout of inerter, damper and spring structure, different kinds of inerter-based linear and nonlinear vibration isolators have been constructed, and the results indicate that the dynamic performance can be improved as the inerter is added. In the above researches, the vertical-directional vibration isolation is mainly considered, while the MD vibration isolation has been rarely studied. Thus, the authors introduce the inerter in the MD vibration isolation area and propose a novel inerter-based multi-directional (IMD) vibration isolator in this paper. In the three directions, the IMD vibration isolator is composed of the inerter, damper and spring structure, respectively, and the three elements are in the parallel-connected. The dynamic performance of the IMD vibration isolator under base harmonic and shock excitations is studied in detail, and the influence law of the structural parameters on its isolation performance is elucidated, especially the inerter. The purpose of this paper is to study how the inerter affects the isolation performance in the multiple directions, and whether the IMD vibration isolator could have beneficial dynamic performance than the conventional MD vibration isolator consisting of the damper and spring.

The paper is arranged as follows. In Sect. 2, the IMD vibration isolator is presented and the Lagrange theory is used to establish its dynamic equation. In Sect. 3, combining the harmonic balance method (HBM) and the pseudo-arc-length (PAL) method, the dynamic response of the IMD vibration isolator subjected to base harmonic excitation is acquired and the stability of the dynamic response is investigated; the isolation performance is analyzed and compared with the MD vibration isolator. The dynamic performance of the IMD vibration isolator under base shock excitation is investigated in Sect. 4. Section 5 summarizes the conclusions.

2 Structure and modeling

2.1 Structural diagram

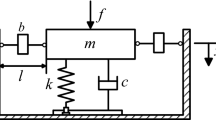
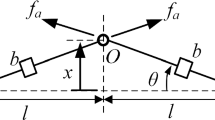
Figure 1 shows the structural diagram of the IMD vibration isolator, which is designed for three-directional vibration isolation. The isolation object is loaded in the support platform, and the support platform is connected with the base through the inerter-based isolation structure, which is composed of the inerter, damper and spring. The structural parameters of the IMD vibration isolator are displayed in Table 1. The displacement of the isolation object in the three directions is x_a, y_a and z_a, respectively, and the displacement of the base in the three directions is x_b, y_b and z_b, respectively. Due to the same structural parameters of the inerter, damper and spring in the x and z directions, the dynamic response of the isolation object in the x and z directions is the same, so the three-directional vibration isolation can be simplified as the x and y directions vibration isolation for brevity. Figure 2 shows the plane diagram of the IMD vibration isolator in the x and y directions. Aware that the pre-deformation of the horizontal spring is λ_h, it is pre-extended as λ_h > 0 or pre-compressed as λ_h < 0.

Fig. 1

Structural diagram of the IMD vibration isolator

Table 1 Structural parameters of the IMD vibration isolator

Fig. 2

Plane diagram of the IMD vibration isolator in the x and y plane

2.2 Dynamic modeling

The dynamic equation of the IMD vibration isolator is established using the Lagrange theory, and the kinetic energy of the IMD vibration isolator in the x and y directions is

$$T = \frac{1}{2}m\dot{x}_{a}^{2} + \frac{1}{2}m\dot{y}_{a}^{2} .$$

(1)

Denote the relative displacement of the isolation object and base in the x and y directions as

$$x_{r} = x_{a} - x_{b} \quad y_{r} = y_{a} - y_{b} ,$$

(2)

The deformation of the vertical and horizontal springs for the IMD vibration isolator is shown in Fig. 3, the length of the left and right horizontal spring changes from l_h0 to l_hl and l_hr, respectively, and the length of the vertical spring changes from l_v0 to l_v. The lengths l_hl, l_hr and l_v are expressed as

$$l_{{{\text{hl}}}} = \sqrt {\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} + x_{r} } \right)^{2} + y_{r}^{2} } \quad l_{{{\text{hr}}}} = \sqrt {\left( {l_{h0} + \lambda_{{\text{h}}} - x_{r} } \right)^{2} + y_{r}^{2} } \quad l_{{\text{v}}} = \sqrt {\left( {l_{{{\text{v0}}}} + y_{r} } \right)^{2} + x_{r}^{2} } .$$

(3)

Fig. 3

Deformation of the vertical and horizontal springs for the IMD vibration isolator

Thus, the potential energy of the IMD vibration isolator in the x and y directions is

$$\begin{aligned} V & = \frac{1}{2}k_{{\text{h}}} \left( {l_{{{\text{hl}}}} - l_{{{\text{h}}0}} } \right)^{2} + \frac{1}{2}k_{{\text{h}}} \left( {l_{{{\text{hr}}}} - l_{{{\text{h}}0}} } \right)^{2} + \frac{1}{2}k_{v} \left( {l_{v} - l_{v0} } \right)^{2} \\ & = \frac{1}{2}k_{{\text{h}}} \left[ {\sqrt {\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} + x_{r} } \right)^{2} + y_{r}^{2} } - l_{{{\text{h}}0}} } \right]^{2} + \frac{1}{2}k_{{\text{h}}} \left[ {\sqrt {\left( {l_{{{\text{h0}}}} + \lambda_{{\text{h}}} - x_{r} } \right)^{2} + y_{r}^{2} } - l_{{{\text{h0}}}} } \right]^{2} \\ & \quad + \frac{1}{2}k_{v} \left[ {\sqrt {\left( {l_{v0} + y_{r} } \right)^{2} + x_{r}^{2} } - l_{v0} } \right]^{2} , \\ \end{aligned}$$

(4)

which includes the elastic potential energy of the horizontal and vertical springs.

The absolute displacements of the isolation object in the x and y directions are chosen as the generalized coordinates, based on the Lagrange theory, and the Lagrange equations of the IMD vibration isolator in the two directions are given as

$$\begin{aligned} \frac{d}{dt}\left( {\frac{\partial T}{{\partial \dot{x}_{a} }}} \right) - \frac{\partial T}{{\partial x_{a} }} + \frac{\partial V}{{\partial x_{a} }} & = - c_{v} \frac{{dl_{v} }}{dt} \cdot \frac{{dl_{v} }}{{dx_{a} }} - c_{{\text{h}}} \frac{{dl_{{{\text{hl}}}} }}{dt} \cdot \frac{{dl_{{{\text{hl}}}} }}{{dx_{a} }} - c_{{\text{h}}} \frac{{dl_{{{\text{hr}}}} }}{dt} \cdot \frac{{dl_{{{\text{hr}}}} }}{{dx_{a} }} \\ & \quad - b_{v} \frac{{d^{2} l_{v} }}{{dt^{2} }} \cdot \frac{{dl_{v} }}{{dx_{a} }} - b_{h} \frac{{d^{2} l_{{{\text{hl}}}} }}{{dt^{2} }} \cdot \frac{{dl_{{{\text{hl}}}} }}{{dx_{a} }} - b_{{\text{h}}} \frac{{d^{2} l_{{{\text{hr}}}} }}{{dt^{2} }} \cdot \frac{{dl_{{{\text{hr}}}} }}{{dx_{a} }}, \\ \end{aligned}$$

(5)

$$\begin{aligned} \frac{d}{dt}\left( {\frac{\partial T}{{\partial \dot{y}_{a} }}} \right) - \frac{\partial T}{{\partial y_{a} }} + \frac{\partial V}{{\partial y_{a} }} & = - c_{v} \frac{{dl_{v} }}{dt} \cdot \frac{{dl_{v} }}{{dy_{a} }} - c_{h} \frac{{dl_{{{\text{hl}}}} }}{dt} \cdot \frac{{dl_{{{\text{hl}}}} }}{{dy_{a} }} - c_{{\text{h}}} \frac{{dl_{{{\text{hr}}}} }}{dt} \cdot \frac{{dl_{{{\text{hr}}}} }}{{dy_{a} }} \\ & \quad - b_{v} \frac{{d^{2} l_{v} }}{{dt^{2} }} \cdot \frac{{dl_{v} }}{{dy_{a} }} - b_{{\text{h}}} \frac{{d^{2} l_{{{\text{hl}}}} }}{{dt^{2} }} \cdot \frac{{dl_{{{\text{hl}}}} }}{{dy_{a} }} - b_{{\text{h}}} \frac{{d^{2} l_{{{\text{hr}}}} }}{{dt^{2} }} \cdot \frac{{dl_{hr} }}{{dy_{a} }}. \\ \end{aligned}$$

(6)

A detailed derivation process of the dynamic equation for the IMD vibration isolator in the x direction is provided, the partial derivative of kinetic energy T with respect to the displacement x_a and velocity $\dot{x}_{a}$ is given as

$$\frac{\partial T}{{\partial x_{a} }} = 0\quad \frac{\partial T}{{\partial \dot{x}_{a} }} = m\dot{x}_{a} = m\left( {\dot{x}_{r} + \dot{x}_{b} } \right),$$

(7)

which yields

$$\frac{d}{dt}\left( {\frac{\partial T}{{\partial \dot{x}_{a} }}} \right) = m\left( {\ddot{x}_{r} + \ddot{x}_{b} } \right),$$

(8)

and the partial derivative of potential energy V with respect to the displacement x_a is given by

$$\begin{aligned} \frac{\partial V}{{\partial x_{a} }} & = \frac{\partial V}{{\partial x_{r} }} \cdot \frac{\partial x}{{\partial x_{a} }} = \frac{\partial V}{{\partial x_{r} }} = k_{v} x_{r} \left[ {1 - \frac{{l_{v0} }}{{\sqrt {\left( {l_{v0} + y_{r} } \right)^{2} + x_{r}^{2} } }}} \right] \\ & \quad + k_{{\text{h}}} \left( {l_{h0} + \lambda_{{\text{h}}} + x_{r} } \right)\left[ {1 - \frac{{l_{{{\text{h}}0}} }}{{\sqrt {\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} + x_{r} } \right)^{2} + y_{r}^{2} } }}} \right] \\ & \quad - k_{{\text{h}}} \left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} - x_{r} } \right)\left[ {1 - \frac{{l_{{{\text{h}}0}} }}{{\sqrt {\left( {l_{h0} + \lambda_{{\text{h}}} - x_{r} } \right)^{2} + y_{r}^{2} } }}} \right], \\ \end{aligned}$$

(9)

Equation (9) can be approximated by using the Taylor series expansion, which yields

$$\frac{\partial V}{{\partial x_{r} }} = \frac{{k_{v} x_{r} y_{r} }}{{l_{v0} }} + \frac{{k_{v} x_{r}^{3} }}{{2l_{v0}^{2} }} - \frac{{k_{v} x_{r} y_{r}^{3} }}{{l_{v0}^{2} }} + 2k_{h} x_{r} - \frac{{2k_{{\text{h}}} l_{{{\text{h}}0}} x_{r} y_{r}^{2} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{3} }},$$

(10)

using Eq. (3), the generalized force provided by the damper is obtained as

$$\begin{aligned} c_{v} \frac{{dl_{v} }}{dt} \cdot \frac{{dl_{v} }}{{dx_{a} }} + c_{{\text{h}}} \frac{{dl_{{{\text{hl}}}} }}{dt} \cdot \frac{{dl_{hl} }}{{dx_{a} }} + c_{{\text{h}}} \frac{{dl_{{{\text{hr}}}} }}{dt} \cdot \frac{{dl_{{{\text{hr}}}} }}{{dx_{a} }} & = c_{v} \frac{{\left( {l_{v0} + y_{r} } \right)x_{r} \dot{y}_{r} + x_{r}^{2} \dot{x}_{r} }}{{\left( {l_{v0} + y_{r} } \right)^{2} + x_{r}^{2} }} \\ & \quad + c_{{\text{h}}} \frac{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} + x_{r} } \right)^{2} \dot{x}_{r} + \left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} + x_{r} } \right)y_{r} \dot{y}_{r} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} + x_{r} } \right)^{2} + y_{r}^{2} }} \\ & \quad + c_{{\text{h}}} \frac{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} - x_{r} } \right)^{2} \dot{x}_{r} - \left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} - x_{r} } \right)y_{r} \dot{y}_{r} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} - x_{r} } \right)^{2} + y_{r}^{2} }}, \\ \end{aligned}$$

(11)

and using the Taylor series expansion, Eq. (11) can be approximated as

$$\begin{aligned} c_{v} \frac{{dl_{v} }}{dt} \cdot \frac{{dl_{v} }}{{dx_{a} }} + c_{{\text{h}}} \frac{{dl_{{{\text{hl}}}} }}{dt} \cdot \frac{{dl_{{{\text{hl}}}} }}{{dx_{a} }} + c_{{\text{h}}} \frac{{dl_{{{\text{hr}}}} }}{dt} \cdot \frac{{dl_{{{\text{hr}}}} }}{{dx_{a} }} & = c_{v} \left( {\frac{{x_{r}^{2} \dot{x}_{r} }}{{l_{v0}^{2} }} + \frac{{x_{r} \dot{y}_{r} }}{{l_{v0} }} - \frac{{x_{r} y_{r} \dot{y}_{r} }}{{l_{v0}^{2} }}} \right) \\ & \quad + 2c_{{\text{h}}} \left[ {1 - \frac{{y_{r}^{2} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }}} \right]\dot{x}_{r} - \frac{{2c_{h} x_{r} y_{r} \dot{y}_{r} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }}, \\ \end{aligned}$$

(12)

The generalized force provided by the inerter is given as

$$\begin{aligned} b_{v} \frac{{d^{2} l_{v} }}{{dt^{2} }} \cdot \frac{{dl_{v} }}{{dx_{a} }} + b_{{\text{h}}} \frac{{d^{2} l_{{{\text{hl}}}} }}{{dt^{2} }} \cdot \frac{{dl_{{{\text{hl}}}} }}{{dx_{a} }} + b_{{\text{h}}} \frac{{d^{2} l_{{{\text{hr}}}} }}{{dt^{2} }} \cdot \frac{{dl_{{{\text{hr}}}} }}{{dx_{a} }} & = b_{v} \frac{{\left( {l_{v0} + y_{r} } \right)^{2} x_{r} \ddot{y}_{r} + x_{r}^{2} \ddot{x}_{r} }}{{\left( {l_{v0} + y_{r} } \right)^{2} + x_{r}^{2} }} \\ & \quad + b_{v} \frac{{x_{r} \left[ {\left( {l_{v0} + y_{r} } \right)\dot{x}_{r} - x_{r} \dot{y}_{r} } \right]^{2} }}{{\left[ {\left( {l_{v0} + y_{r} } \right)^{2} + x_{r}^{2} } \right]^{2} }} \\ & \quad + b_{{\text{h}}} \frac{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} + x_{r} } \right)^{2} \ddot{x}_{r} + \left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} + x_{r} } \right)y_{r} \ddot{y}_{r} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} + x_{r} } \right)^{2} + y_{r}^{2} }} \\ & \quad + b_{{\text{h}}} \frac{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} + x_{r} } \right)\left[ {\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} + x_{r} } \right)\dot{y}_{r} - \dot{x}_{r} y_{r} } \right]^{2} }}{{\left[ {\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} + x_{r} } \right)^{2} + y_{r}^{2} } \right]^{2} }} \\ & \quad + b_{{\text{h}}} \frac{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} - x_{r} } \right)^{2} \ddot{x}_{r} - \left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} - x_{r} } \right)y_{r} \ddot{y}_{r} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} - x_{r} } \right)^{2} + y_{r}^{2} }} \\ & \quad - b_{h} \frac{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} - x_{r} } \right)\left[ {\left( {l_{h0} + \lambda_{{\text{h}}} - x_{r} } \right)\dot{y}_{r} + \dot{x}_{r} y_{r} } \right]^{2} }}{{\left[ {\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} - x_{r} } \right)^{2} + y_{r}^{2} } \right]^{2} }}, \\ \end{aligned}$$

(13)

Equation (13) can be approximated by using the Taylor series expansion, which leads to

$$\begin{aligned} b_{v} \frac{{d^{2} l_{v} }}{{dt^{2} }} \cdot \frac{{dl_{v} }}{{dx_{a} }} + b_{{\text{h}}} \frac{{d^{2} l_{l} }}{{dt^{2} }} \cdot \frac{{dl_{l} }}{{dx_{a} }} + b_{{\text{h}}} \frac{{d^{2} l_{r} }}{{dt^{2} }} \cdot \frac{{dl_{r} }}{{dx_{a} }} & = b_{v} \left( {\frac{{x_{r} }}{{l_{v0} }} - \frac{{x_{r} y_{r} }}{{l_{v0}^{2} }}} \right)\ddot{y}_{r} + b_{v} \frac{{x_{r}^{2} }}{{l_{v0}^{2} }}\ddot{x}_{r} \\ & \quad + b_{v} \frac{{x_{r} \dot{x}_{r}^{2} }}{{l_{v0}^{2} }} + 2b_{{\text{h}}} \left[ {1 - \frac{{y_{r}^{2} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }}} \right]\ddot{x}_{r} \\ & \quad - \frac{{2b_{{\text{h}}} x_{r} y_{r} \ddot{y}_{r} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }} - \frac{{2b_{{\text{h}}} x_{r} \dot{y}_{r}^{2} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }} - \frac{{4b_{{\text{h}}} y_{r} \dot{x}_{r} \dot{y}_{r} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }}, \\ \end{aligned}$$

(14)

Combining Eqs. (7), (8), (10), (12) and (14) leads to the dynamic equation of the IMD vibration isolator in the x direction, which is given by

$$\begin{gathered} m\ddot{x}_{r} + b_{v} \left( {\frac{{x_{r} }}{{l_{v0} }} - \frac{{x_{r} y_{r} }}{{l_{v0}^{2} }}} \right)\ddot{y}_{r} + b_{v} \frac{{x_{r}^{2} }}{{l_{v0}^{2} }}\ddot{x}_{r} + b_{v} \frac{{x_{r} \dot{x}_{r}^{2} }}{{l_{v0}^{2} }} \hfill \\ \quad \quad + 2b_{{\text{h}}} \left[ {1 - \frac{{y_{r}^{2} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }}} \right]\dddot x_{r} - \frac{{2b_{{\text{h}}} x_{r} y_{r} \ddot{y}_{r} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }} - \frac{{2b_{{\text{h}}} x_{r} \dot{y}_{r}^{2} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }} - \frac{{4b_{{\text{h}}} y_{r} \dot{x}_{r} \dot{y}_{r} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }} \hfill \\ \quad \quad + c_{v} \left( {\frac{{x_{r}^{2} \dot{x}_{r} }}{{l_{v0}^{2} }} + \frac{{x_{r} \dot{y}_{r} }}{{l_{v0} }} - \frac{{x_{r} y_{r} \dot{y}_{r} }}{{l_{v0}^{2} }}} \right) + 2c_{h} \left[ {1 - \frac{{y_{r}^{2} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }}} \right]\dot{x}_{r} - \frac{{2c_{h} x_{r} y_{r} \dot{y}_{r} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }} \hfill \\ \quad \quad + \frac{{k_{v} x_{r} y_{r} }}{{l_{v0} }} + \frac{{k_{v} x_{r}^{3} }}{{2l_{v0}^{2} }} - \frac{{k_{v} x_{r} y_{r}^{2} }}{{l_{v0}^{2} }} + 2k_{{\text{h}}} x_{r} - \frac{{2k_{{\text{h}}} l_{{{\text{h}}0}} x_{r} y_{r}^{2} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{3} }} = - m\ddot{x}_{b} . \hfill \\ \end{gathered}$$

(15)

The dynamic equation of the IMD vibration isolator in the y direction can be obtained following the same derivation process, which yields

$$\begin{gathered} m\ddot{y}_{r} + b_{v} \left( {1 - \frac{{x_{r}^{2} }}{{l_{v0}^{2} }}} \right)\ddot{y}_{r} + b_{v} \left( {\frac{{x_{r} }}{{l_{v0} }} - \frac{{x_{r} y_{r} }}{{l_{v0}^{2} }}} \right)\ddot{x}_{r} + b_{v} \left( {\frac{1}{{l_{v0} }} - \frac{{y_{r} }}{{l_{v0}^{2} }}} \right)\dot{x}_{r}^{2} \hfill \\ \quad \quad - \frac{{2b_{v} x_{r} \dot{x}_{r} \dot{y}_{r} }}{{l_{v0}^{2} }} - \frac{{2b_{{\text{h}}} x_{r} y_{r} \ddot{x}_{r} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }} + \frac{{2b_{{\text{h}}} y_{r}^{2} \ddot{y}_{r} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }} + \frac{{2b_{{\text{h}}} y_{r} \dot{y}_{r}^{2} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }} \hfill \\ \quad \quad + c_{v} \left( {\dot{y}_{r} - \frac{{x_{r}^{2} \dot{y}_{r} }}{{l_{v0}^{2} }} + \frac{{x_{r} \dot{x}_{r} }}{{l_{v0} }} - \frac{{x_{r} y_{r} \dot{x}_{r} }}{{l_{v0}^{2} }}} \right) + \frac{{2c_{{\text{h}}} y_{r}^{2} \dot{y}_{r} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }} - \frac{{2c_{{\text{h}}} x_{r} y_{r} \dot{x}_{r} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{2} }} \hfill \\ \quad \quad + \left( {k_{v} + 2k_{h} - \frac{{2k_{{\text{h}}} l_{{{\text{h}}0}} }}{{l_{{{\text{h}}0}} + \lambda_{{\text{h}}} }}} \right)y_{r} + \frac{{k_{v} x_{r}^{2} }}{{2l_{v0} }} \hfill \\ \quad \quad - \left[ {\frac{{k_{v} }}{{l_{v0}^{2} }} + \frac{{2k_{{\text{h}}} l_{h0} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{3} }}} \right]x_{r}^{2} y_{r} + \frac{{k_{{\text{h}}} l_{{{\text{h}}0}} y_{r}^{3} }}{{\left( {l_{{{\text{h}}0}} + \lambda_{{\text{h}}} } \right)^{3} }} = - m\ddot{y}_{b} . \hfill \\ \end{gathered}$$

(16)

3 Base harmonic excitation

3.1 Dynamic equation

Firstly, the base harmonic excitation is considered, the excitation in the x and y directions is expressed as x_bmcos(ωt) and y_bmcos(ωt), respectively, which have the same excitation frequency ω, and the base amplitudes are x_bm and y_bm, respectively. Substituting the base harmonic excitations into Eqs. (15) and (16), also using the following non-dimensional parameters

$$\begin{gathered} \omega_{n} = \sqrt {\frac{{k_{v} }}{m}} \quad \zeta_{v} = \frac{{c_{v} }}{{2m\omega_{n} }}\quad \zeta_{v} = \frac{{c_{v} }}{{2m\omega_{n} }}\quad \delta_{v} = \frac{{b_{v} }}{m}\quad \delta_{{\text{h}}} = \frac{{b_{{\text{h}}} }}{m}\quad \gamma = \frac{{k_{{\text{h}}} }}{{k_{v} }} \hfill \\ \Omega = \frac{\omega }{{\omega_{n} }}\quad T = \omega_{n} t\quad \eta = \frac{{l_{{{\text{h}}0}} }}{{l_{v0} }}\quad \mu = \frac{{\lambda_{{\text{h}}} }}{{l_{{{\text{h}}0}} }}\quad X_{r} = \frac{{x_{r} }}{{l_{v0} }}\quad Y_{r} = \frac{{y_{r} }}{{l_{v0} }}\quad X_{{{\text{bm}}}} = \frac{{x_{{{\text{bm}}}} }}{{l_{v0} }}\quad Y_{{{\text{bm}}}} = \frac{{y_{{{\text{bm}}}} }}{{l_{v0} }}, \hfill \\ \end{gathered}$$

(17)

Equations (15) and (16) can be written in a non-dimensional form

$$\begin{gathered} \left\{ {1 + \delta_{v} X_{r}^{2} + 2\delta_{{\text{h}}} \left[ {1 - \frac{{Y_{r}^{2} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }}} \right]} \right\}X_{r}^{\prime \prime } + \left[ {\delta_{v} \left( {X_{r} - X_{r} Y_{r} } \right) - \frac{{2\delta_{{\text{h}}} X_{r} Y_{r} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }}} \right]Y_{r}^{\prime \prime } + \delta_{v} X_{r} X\prime_{r}^{2} - \frac{{2\delta_{{\text{h}}} X_{r} Y\prime_{r}^{2} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }} \hfill \\ \quad \quad - \frac{{4\delta_{{\text{h}}} Y_{r} X\prime_{r} Y\prime_{r} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }} + 2\zeta_{v} \left( {X_{r}^{2} X\prime_{r} + X_{r} Y^{\prime}_{r} - X_{r} Y_{r} Y^{\prime}_{r} } \right) + 4\zeta_{{\text{h}}} \left[ {1 - \frac{{Y_{r}^{2} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }}} \right]X^{\prime}_{r} - \frac{{4\zeta_{{\text{h}}} X_{r} Y_{r} Y\prime_{r} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }} \hfill \\ \quad \quad + X_{r} Y_{r} + \frac{{X_{r}^{3} }}{2} - X_{r} Y_{r}^{2} + 2\gamma X_{r} - \frac{{2\gamma X_{r} Y_{r}^{2} }}{{\eta^{2} \left( {1 + \mu } \right)^{3} }} = \Omega^{2} X_{{{\text{bm}}}} \cos \left( {\Omega T} \right), \hfill \\ \end{gathered}$$

(18)

$$\begin{gathered} \left[ {\delta_{v} \left( {X_{r} - X_{r} Y_{r} } \right) - \frac{{2\delta_{h} X_{r} Y_{r} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }}} \right]X_{r}^{\prime \prime } + \left[ {1 + \delta_{v} \left( {1 - X_{r}^{2} } \right) + \frac{{2\delta_{h} Y_{r}^{2} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }}} \right]Y_{r}^{\prime \prime } + \delta_{v} \left( {1 - Y_{r} } \right)X\prime_{r}^{2} - 2\delta_{v} X_{r} X\prime_{r} Y\prime_{r} \hfill \\ \quad \quad + \frac{{2\delta_{h} Y_{r} Y\prime_{r}^{2} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }} + 2\zeta_{v} \left( {Y_{r}^{\prime } - X_{r}^{2} Y\prime_{r} + X_{r} X\prime_{r} - X_{r} Y_{r} X\prime_{r} } \right) + \frac{{4\zeta_{h} Y_{r}^{2} Y\prime_{r} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }} - \frac{{4\zeta_{h} X_{r} Y_{r} X\prime_{r} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }} \hfill \\ \quad \quad + \left( {1 + 2\gamma - \frac{2\gamma }{{1 + \mu }}} \right)Y_{r} + \frac{{X_{r}^{2} }}{2} - \left[ {1 + \frac{2\gamma }{{\eta^{2} \left( {1 + \mu } \right)^{3} }}} \right]X_{r}^{2} Y_{r} + \frac{{\gamma Y_{r}^{3} }}{{\eta^{2} \left( {1 + \mu } \right)^{3} }} = \Omega^{2} Y_{{{\text{bm}}}} \cos \left( {\Omega T} \right), \hfill \\ \end{gathered}$$

(19)

where $( \cdot )\prime \prime = d^{2} ( \cdot )/dT^{2}$ and $( \cdot )\prime = d( \cdot )/dT$. As shown in Eqs. (18) and (19), for the IMD vibration isolator, adding the inerter generates additional nonlinear acceleration and velocity terms compared with those of the MD one, which yields nonlinear inertial and damping characteristics, respectively.

3.2 Natural frequency

For the IMD vibration isolator, the dynamic equation in the x and y directions is two nonlinear coupled equations, and if the excitation base amplitude and dynamic response are smaller; compared with the linear terms, the nonlinear terms in the dynamic equation are smaller, then the nonlinear and higher-order terms can be neglected. Thus in this case, the nonlinear dynamic equations can be simplified into the linear one, and the corresponding linear equations of Eqs. (18) and (19) are

$$(1 + 2\delta_{{\text{h}}} )X_{r}^{\prime \prime } + 4\zeta_{h} X\prime_{r} + 2\gamma X_{r} = \Omega^{2} X_{{{\text{bm}}}} \cos \left( {\Omega T} \right),$$

(20)

$$(1 + \delta_{v} )Y\prime \prime_{r} + 2\zeta_{v} Y\prime_{r} + \left( {1 + 2\gamma - \frac{2\gamma }{{1 + \mu }}} \right)Y_{r} = \Omega^{2} Y_{{{\text{bm}}}} \cos \left( {\Omega T} \right),$$

(21)

Equations (20) and (21) are two uncoupled linear equations. For a linear vibration isolation system, its isolation performance depends on its natural frequency and yields a beneficial isolation affect when the excitation frequency is larger than $\sqrt 2$ times its natural frequency. The natural frequencies of the simplified linear vibration isolator in the x and y directions are given as

$$\Omega_{x} = \sqrt {\frac{2\gamma }{{1 + 2\delta_{{\text{h}}} }}} \quad \Omega_{y} = \sqrt {\frac{1 + (1 + 2\gamma )\mu }{{(1 + \delta_{v} )(1 + \mu )}}} ,$$

(22)

which relies on the stiffness ratio γ, horizontal spring compression ratio μ, inertance-to-mass ratio (δ_v, δ_h).

The horizontal natural frequency of the simplified linear vibration isolator with a different horizontal inertance-to-mass ratio δ_h and stiffness ratio γ is shown in Fig. 4. The horizontal natural frequency becomes smaller as increasing the horizontal inertance-to-mass ratio δ_h or reducing the stiffness ratio γ. The vertical natural frequency also decreases as increasing the vertical inertance-to-mass ratio δ_v, and its changing tendency with other two structural parameters is shown in Fig. 5. So as to maintain the vertical natural frequency positive, the horizontal spring compression ratio μ should be equal to or larger than -1/(1 + 2γ). The vertical natural frequency becomes larger as increasing the horizontal spring compression ratio μ, and if the horizontal spring is pre-compressed, it increases as the stiffness ratio γ decreases, while if the horizontal spring is pre-extended, it increases as the stiffness ratio γ increases.

Fig. 4

Horizontal natural frequency with different δ_h and γ: a three-dimensional diagram, b plane diagram

Fig. 5

Vertical natural frequency with different μ and γ: a three-dimensional diagram, b plane diagram (δ_v = 1)

3.3 Approximate solution

For the IMD vibration isolator, Eqs. (18) and (19) are strongly coupled nonlinear equations, the HBM is acquired to obtain its dynamic response [40, 41], and taking the first-order and third-order harmonics, the approximate solutions are expressed as

$$\begin{gathered} X_{r} = a_{1} \cos \left( {\Omega T} \right) + a_{2} \sin \left( {\Omega T} \right) + a_{3} \cos \left( {3\Omega T} \right) + a_{4} \sin \left( {3\Omega T} \right) \hfill \\ Y_{r} = b_{1} \cos \left( {\Omega T} \right) + b_{2} \sin \left( {\Omega T} \right) + b_{3} \cos \left( {3\Omega T} \right) + b_{4} \sin \left( {3\Omega T} \right), \hfill \\ \end{gathered}$$

(23)

Substituting Eq. (23) into Eqs. (18) and (19), balancing the same harmonic terms in the two equations based on cos(ΩT), sin(ΩT), cos(3ΩT) and sin(3ΩT) yields the following equations

$$\begin{gathered} F_{1} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right)\cos \left( {\Omega T} \right) + F_{2} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right)\sin \left( {\Omega T} \right) \hfill \\ \quad + F_{3} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right)\cos \left( {3\Omega T} \right) + F_{4} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right)\sin \left( {3\Omega T} \right) = 0 \hfill \\ F_{5} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right)\cos \left( {\Omega T} \right) + F_{6} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right)\sin \left( {\Omega T} \right) \hfill \\ \quad + F_{7} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right)\cos \left( {3\Omega T} \right) + F_{8} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right)\sin \left( {3\Omega T} \right) = 0, \hfill \\ \end{gathered}$$

(24)

Letting the coefficients of the first-order and third-order harmonic terms equal to zero derives the following eight nonlinear equations

$$F_{1} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right) = 0, \cdots F_{i} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right) = 0, \cdots F_{8} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right) = 0,$$

(25)

The expressions of the eight nonlinear equations are shown in Appendix. Equation (25) can also be expressed as

$${\varvec{F}}\left( {{\varvec{A}},\Omega } \right) = 0,$$

(26)

where ${\varvec{F}} = [F_{1} , \cdots F_{8} ]^{T}$ and ${\varvec{A}} = [a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ]$, Eq. (26) can be rewritten as

$${\varvec{F}}({\varvec{w}}) = 0,$$

(27)

where ${\varvec{F}}:R^{9} \to R^{8}$, ${\varvec{w}} = [w_{1} , \cdots w_{9} ]$ and ${\varvec{w}} = \left( {{\varvec{A}},\Omega } \right)$. In the $R^{9}$ space, the solution of Eq. (27) is a one-dimensional manifold composed of the intersection of eight hypersurfaces, which derives

$$D{\varvec{F}}({\varvec{w}}) = \left[ {\begin{array}{*{20}c} {\frac{{\partial F_{1} }}{{\partial w_{1} }}} & {\frac{{\partial F_{1} }}{{\partial w_{2} }}} & \cdots & {\frac{{\partial F_{1} }}{{\partial w_{9} }}} \\ \vdots & \vdots & \ddots & \vdots \\ {\frac{{\partial F_{8} }}{{\partial w_{1} }}} & {\frac{{\partial F_{8} }}{{\partial w_{2} }}} & \cdots & {\frac{{\partial F_{8} }}{{\partial w_{9} }}} \\ \end{array} } \right]_{8 \times 9} ,$$

(28)

Defining the following nine-dimensional vector

$${\varvec{H}}\left( {\varvec{w}} \right) = \left[ {H_{1} , \cdots H_{9} } \right]^{T} \quad H_{i} = \left( { - 1} \right)^{i + 1} \det \left[ {\frac{\partial F}{{\partial w_{1} }}, \cdots \frac{\partial F}{{\partial w_{i - 1} }},\frac{{\partial \hat{F}}}{{\partial w_{i} }},\frac{\partial F}{{\partial w_{i + 1} }}, \cdots ,\frac{\partial F}{{\partial w_{9} }}} \right],$$

(29)

where ${{\partial \hat{F}} \mathord{/ {\vphantom {{\partial \hat{F}} {\partial w_{i} }}} \kern-\nulldelimiterspace} {\partial w_{i} }}$ indicates that this column vector is omit. The relationship between the matrix DF(w) and vector H(w) is

$$\left[ {\frac{{\partial F_{i} }}{{\partial w_{1} }}\quad \frac{{\partial F_{i} }}{{\partial w_{2} }}\quad \cdots \quad \frac{{\partial F_{i} }}{{\partial w_{9} }}} \right] \cdot {\varvec{H}} = 0\quad i = 1 \cdots 8,$$

(30)

which denotes that the vector H(w) is the tangential vector of the solution curve for Eq. (27) in the $R^{9}$ space, and the corresponding unit tangent vector is

$${\varvec{\varepsilon}}\left( {\varvec{w}} \right) = \frac{{\varvec{H}}}{{\left\| {\varvec{H}} \right\|}},$$

(31)

where $\left\| \cdot \right\|$ indicates the modulus.

The PAL method [42] is utilized to solve Eq. (25) which includes eight nonlinear equations, especially there exist folding points in the frequency response curve (FRC), and the arc length of the one-dimensional curve in the $R^{9}$ space is defined as

$$ds^{2} = \sum\limits_{i = 1}^{9} {dw_{i}^{2} } ,$$

(32)

Equation (27) contains nine variables (the eight amplitudes and the excitation frequency Ω), and an additional constraint equation should be added to make Eq. (27) solvable, which is given as

$${\varvec{\varepsilon}} \cdot \Delta {\varvec{w}} - \Delta s = 0,$$

(33)

where $\Delta ( \cdot )$ denotes smaller change of the variable; then, solving Eq. (27) can be converted to

$${\varvec{F}}\left( {\varvec{w}} \right) = 0\quad \varepsilon \cdot \Delta {\varvec{w}} - \Delta s = 0,$$

(34)

Equation (34) can also be transformed into solving the Cauchy problem

$$\frac{{d{\varvec{w}}}}{ds} = {\varvec{\varepsilon}}\left( {w_{0} } \right)\quad {\varvec{w}}\left( 0 \right) = {\varvec{w}}_{{\mathbf{0}}} ,$$

(35)

Using the modified Euler method to solve Eq. (35), the predicted solution is given as

$$w_{i} = w_{i - 1} + \varepsilon \left( {w_{i - 1} } \right)\left( {s_{i} - s_{i - 1} } \right) + \frac{{\left( {s_{i} - s_{i - 1} } \right)^{2} }}{2} \cdot \frac{{\varepsilon \left( {w_{i - 1} } \right) - \varepsilon \left( {w_{i - 2} } \right)}}{{s_{i - 1} - s_{i - 2} }}\quad i = 1,2, \ldots ,$$

(36)

Using the Newton-type iterative correction to dominate the precision of the solution

$$w_{i}^{0} = w_{i} \quad w_{i}^{j} = w_{i}^{j - 1} - \left[ {\begin{array}{*{20}c} {D{\varvec{F}}\left( {w_{i} } \right)} \\ {{\varvec{H}}\left( {w_{i} } \right)} \\ \end{array} } \right]^{ - 1} \left[ {\begin{array}{*{20}c} {{\varvec{F}}\left( {w_{i}^{j - 1} } \right)} \\ 0 \\ \end{array} } \right]\quad j = 1,2, \cdots ,$$

(37)

after a finite number of iteration steps, the solution converges to a point ${\varvec{w}}^{ * }$ which satisfies ${\varvec{F}}\left( {{\varvec{w}}^{ * } } \right) = 0$, it indicates that the point ${\varvec{w}}^{ * }$ is the solution of Eq. (35) in a certain precision; then, the solution of Eq. (27) is given, and the steady-state amplitudes of the IMD vibration isolator under base harmonic excitation can be obtained as

$$X_{{{\text{rm}}}} = \sqrt {a_{1}^{2} + a_{2}^{2} + a_{3}^{2} + a_{4}^{2} } ,\quad Y_{{{\text{rm}}}} = \sqrt {b_{1}^{2} + b_{2}^{2} + b_{3}^{2} + b_{4}^{2} } .$$

(38)

3.4 Stability analysis

In order to analyze the stability of the steady-state amplitudes, the formal approximate solutions (Eq. 23) are expressed as the time-varying ones, which are given as

$$\begin{aligned} X_{r} \left( T \right) & = a_{1} \left( T \right)\cos \left( {\Omega T} \right) + a_{2} \left( T \right)\sin \left( {\Omega T} \right) + a_{3} \left( T \right)\cos \left( {3\Omega T} \right) + a_{4} \left( T \right)\sin \left( {3\Omega T} \right) \\ Y_{r} \left( T \right) & = b_{1} \left( T \right)\cos \left( {\Omega T} \right) + b_{2} \left( T \right)\sin \left( {\Omega T} \right) + b_{3} \left( T \right)\cos \left( {3\Omega T} \right) + b_{4} \left( T \right)\sin \left( {3\Omega T} \right). \\ \end{aligned}$$

(39)

Substituting Eq. (39) into Eqs. (18) and (19), balancing the same harmonic terms in the two equations based on cos(ΩT), sin(ΩT), cos(3ΩT) and sin(3ΩT), letting the coefficients of the first-order and third-order harmonic terms equal to zero yields

$${\varvec{F}}^{ * } \left( {{\varvec{A}}^{\prime \prime } \left( {\varvec{t}} \right),{\varvec{A}}^{{\prime }} \left( {\varvec{t}} \right),{\varvec{A}}\left( {\varvec{t}} \right),\Omega } \right) = 0,$$

(40)

The second derivative of the time-varying amplitude is equal to zero $\left( {{\varvec{A}}\prime \prime \left( {\varvec{t}} \right) = 0} \right)$ in spite of the stability of the first derivative, which gives

$${\varvec{F}}^{ * } \left( {\user2{A^{\prime}}\left( {\varvec{t}} \right),{\varvec{A}}\left( {\varvec{t}} \right),\Omega } \right) = 0,$$

(41)

Equation (41) can be transformed into an explicit form which is composed of eight first-order differential equations

$${\varvec{A}}\prime \left( {\varvec{t}} \right) = {\varvec{F}}^{ * * } \left( {{\varvec{A}}\left( {\varvec{t}} \right),\Omega } \right),$$

(42)

where ${\varvec{F}}^{ * * }$ denotes a group of algebraic equations including the time-varying amplitudes ${\varvec{A}}\left( {\varvec{t}} \right)$ and excitation frequency Ω.

Therefore, the stability of the steady-state amplitudes transforms into the stability of the first derivative of the time-varying amplitude, which is defined by Eq. (42). Then, the first method of Lyapunov is adopted to judge the stability of Eq. (42), and the eigenvalues of the Jacobian determinant for Eq. (42) are given as

$$\left| {{\varvec{J}}({\varvec{A}}\left( {\varvec{t}} \right),\Omega ) - \lambda_{j} {\varvec{I}}} \right| = 0\quad j = 1 \cdots 8,$$

(43)

$${\varvec{J}} = \left[ {\begin{array}{*{20}c} {\frac{{\partial F_{1}^{ * * } }}{{\partial A_{1} (t)}}} & {\frac{{\partial F_{1}^{ * * } }}{{\partial A_{2} (t)}}} & \cdots & {\frac{{\partial F_{1}^{ * * } }}{{\partial A_{8} (t)}}} \\ \vdots & \vdots & \ddots & \vdots \\ {\frac{{\partial F_{8}^{ * * } }}{{\partial A_{1} (t)}}} & {\frac{{\partial F_{8}^{ * * } }}{{\partial A_{2} (t)}}} & \cdots & {\frac{{\partial F_{8}^{ * * } }}{{\partial A_{8} (t)}}} \\ \end{array} } \right]_{8 \times 8} ,$$

(44)

If all the eigenvalues of Eq. (43) are negative, the steady-state amplitude is stable, and if there exists at least one positive eigenvalue, the steady-state amplitude is unstable.

3.5 Dynamic response

Figure 6 shows the FRC of the IMD vibration isolator under different base amplitudes, which shows the representative changing trends. The horizontal and vertical inertance-to-mass ratios (δ_h, δ_v) are chosen as 0.5, which are relatively smaller values. The horizontal and vertical damping ratios (ζ_h, ζ_v) are chosen as 0.05, the stiffness ratio γ is chosen as 2, the length ratio η is chosen as 1, the horizontal spring compression ratio μ is chosen as 0 which indicates that it is in the original length state, and the vertical and horizontal base amplitudes are chosen as the same values. As can be seen from Fig. 6, the resonance frequency of the IMD vibration isolator in the y direction is smaller than that of the x direction, and while the resonance peak shows the reverse tendency. When the base amplitude is relatively smaller, the FRCs of the IMD vibration isolator in the x and y directions are single-valued, display linear characteristics and seem linear vibration system, and the steady-state amplitudes are stable, which is shown in Fig. 6a.

Fig. 6

FRC of the IMD vibration isolator in the x and y directions for smaller inertance-to-mass ratio (δ_h = δ_v = 0.5, γ = 2, η = 1, μ = 0, ζ_h = ζ_v = 0.05)

When the base amplitude increases, the FRC of the IMD vibration isolator in the y direction turns to the right, displays hardening characteristic and seems hardening Duffing vibration system; while the FRC in the x direction displays linear characteristic, except in a frequency band that is consistent with the resonance one of the y direction, there exists a folding point in the FRC and there are unstable steady-state amplitudes in this frequency band, and this tendency is exhibited in Fig. 6b. The eigenvalues in the resonance frequency band of the y direction are shown in Table 2, and the stability of the steady-state amplitudes can be determined based on the eigenvalues.

Table 2 The eigenvalues of the IMD vibration isolator with X_bm = 0.07 and Y_bm = 0.07 (δ_h = δ_v = 0.5, ζ_h = ζ_v = 0.05, γ = 2, η = 1, μ = 0)

When the base amplitude is a larger value, the FRC of the IMD vibration isolator in the y direction turns to the left, displays softening characteristic and seems softening Duffing vibration system; while the FRC in the x direction has two resonance frequencies, the FRC around the smaller resonance frequency turns to the left and shows softening characteristic, this resonance frequency band corresponds to the resonance one of the y direction, the FRC around the larger resonance frequency is linear, and this tendency is exhibited in Fig. 6c. The eigenvalues in the resonance frequency band can be also determined and are not shown for simplicity. Aware that when the excitation frequency falls into the range [0.95, 1], there exist five steady-state amplitudes, among the five steady-state amplitudes, three ones are stable and two ones are unstable, and the stability can be determined by calculating the corresponding eigenvalues. When the excitation frequency Ω = 0.98, there exist three stable steady-state amplitudes and the Fourier spectra for the three stable steady-state amplitudes are shown in Fig. 7.

Fig. 7

Fourier spectra of the IMD vibration isolator for the three stable steady-state amplitudes in the x and y directions with Ω = 0.98 (δ_h = δ_v = 0.5, γ = 2, η = 1, μ = 0, ζ_h = ζ_v = 0.05, X_bm = Y_bm = 0.01)

As the horizontal and vertical inertance-to-mass ratios (δ_h, δ_v) are chosen as 10, which are relatively larger values, the corresponding FRC of the IMD vibration isolator under different base amplitudes is shown in Fig. 8, and the other structural parameters are chosen as the same values with those of Fig. 6. When the base amplitudes (X_bm, Y_bm) are chosen as 0.1, the FRCs of the IMD vibration isolator in the x and y directions are single-valued and show linear characteristics, which is shown in Fig. 8a, and this changing trend is similar to Fig. 6a. As shown in Fig. 8b, when the base amplitudes (X_bm, Y_bm) increase to 0.4, a different changing trend of the FRC in the x direction is observed. The FRC in the x direction turns to the left, displays softening characteristic and seems softening Duffing vibration system; the FRC in the y direction turns to the right, displays hardening characteristic and seems hardening Duffing vibration system, another resonance frequency is found and its resonance peak is relatively smaller, and the stability of the FRC can be also determined by calculating the corresponding eigenvalues, which is not shown for brevity.

Fig. 8

FRC of the IMD vibration isolator in the x and y directions for larger inertance-to-mass ratio (δ_h = δ_v = 10, γ = 2, η = 1, μ = 0, ζ_h = ζ_v = 0.05)

The fourth-order Runge–Kutta method is used to solve Eqs. (18) and (19) to acquire the numerical results, which are shown as circles in Figs. 6 and 8. The analytical results exhibit good consistent with the numerical results, and it denotes that adopting the HBM and PAL method to acquire the analytical results can represent the real dynamic responses, which is an effective method to solve this type of strongly coupled nonlinear dynamic system. The asterisks shown in Figs. 6 and 8 denote the unstable analytical results, which is determined by the eigenvalues of the Jacobian determinant for Eq. (42). It should be noted that the non-dimensional dynamic displacement is normalized by the original length of the vertical spring, and if the base amplitude is larger, the dynamic displacement in the x and y directions can be larger, especially for the resonance peaks.

3.6 Isolation performance

For the IMD vibration isolator, its isolation performance in this paper is evaluated by three performance criteria: (1) dynamic displacement peak, (2) displacement transmissibility peak and (3) isolation frequency band, and the absolute displacements in the x and y directions are given as

$$\begin{aligned} X_{{{\text{am}}}} & = X_{{{\text{rm}}}} + X_{{{\text{bm}}}} \cos \left( {\Omega T} \right) = \left( {a_{1} + X_{{{\text{bm}}}} } \right)\cos \left( {\Omega T} \right) + a_{2} \sin \left( {\Omega T} \right) + a_{3} \cos \left( {3\Omega T} \right) + a_{4} \sin \left( {3\Omega T} \right) \\ Y_{{{\text{am}}}} & = Y_{{{\text{rm}}}} + Y_{{{\text{bm}}}} \cos \left( {\Omega T} \right) = \left( {b_{1} + Y_{{{\text{bm}}}} } \right)\cos \left( {\Omega T} \right) + b_{2} \sin \left( {\Omega T} \right) + b_{3} \cos \left( {3\Omega T} \right) + b_{4} \sin \left( {3\Omega T} \right), \\ \end{aligned}$$

(45)

Then, the corresponding absolute displacement transmissibilities are obtained as

$$\begin{gathered} T_{{{\text{ax}}}} = \left| {\frac{{x_{a} }}{{x_{b} }}} \right| = \frac{{\left| {X_{{{\text{am}}}} } \right|}}{{X_{{{\text{bm}}}} }} = \frac{{\sqrt {\left( {a_{1} + X_{{{\text{bm}}}} } \right)^{2} + a_{2}^{2} + a_{3}^{2} + a_{4}^{2} } }}{{X_{{{\text{bm}}}} }} \hfill \\ T_{{{\text{ay}}}} = \left| {\frac{{y_{a} }}{{y_{b} }}} \right| = \frac{{\left| {Y_{{{\text{am}}}} } \right|}}{{Y_{{{\text{bm}}}} }} = \frac{{\sqrt {\left( {b_{1} + Y_{{{\text{bm}}}} } \right)^{2} + b_{2}^{2} + b_{3}^{2} + b_{4}^{2} } }}{{Y_{{{\text{bm}}}} }}, \hfill \\ \end{gathered}$$

(46)

The dynamic displacement and absolute displacement transmissibility peaks should maintain smaller for the IMD vibration isolator, which determines the maximum dynamic displacement and absolute displacement transmissibility, respectively. The isolation frequency band determines the bandwidth where the IMD vibration isolator provides a advantageous isolation performance, which in this frequency band the absolute displacement transmissibility is smaller than 1.

For the IMD vibration isolator, the horizontal and vertical inertance-to-mass ratios (δ_h, δ_v) determine its inertial characteristic and the effect of inerter in the x and y directions, respectively; the stiffness ratio γ determines its stiffness characteristic; the horizontal spring compression ratio μ and the length ratio η determine the initial state of the horizontal spring and the acceleration, velocity and displacement terms in the dynamic equation (see Eqs. (18) and (19)), which has effect on the inertial, damping and stiffness characteristics.

The isolation performance of the IMD vibration isolator is compared with the conventional MD vibration isolator composed of the damper and spring, and denoting the horizontal and vertical inertance-to-mass ratios (δ_h, δ_v) equal to 0 in Eqs. (18) and (19) yields the corresponding non-dimensional dynamic equation subjected to base harmonic excitation

$$\begin{gathered} X^{\prime\prime}_{r} + 2\zeta_{v} \left( {X_{r}^{2} X^{\prime}_{r} + X_{r} Y^{\prime}_{r} - X_{r} Y_{r} Y^{\prime}_{r} } \right) + 4\zeta_{h} \left[ {1 - \frac{{Y_{r}^{2} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }}} \right]X^{\prime}_{r} - \frac{{4\zeta_{h} X_{r} Y_{r} Y^{\prime}_{r} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }} \hfill \\ \quad \quad + X_{r} Y_{r} + \frac{{X_{r}^{3} }}{2} - X_{r} Y_{r}^{2} + 2\gamma X_{r} - \frac{{2\gamma X_{r} Y_{r}^{2} }}{{\eta^{2} \left( {1 + \mu } \right)^{3} }} = \Omega^{2} X_{{{\text{bm}}}} \cos \left( {\Omega T} \right), \hfill \\ \end{gathered}$$

(47)

$$\begin{gathered} Y^{\prime\prime}_{r} + 2\zeta_{v} \left( {Y^{\prime}_{r} - X_{r}^{2} Y^{\prime}_{r} + X_{r} X^{\prime}_{r} - X_{r} Y_{r} X^{\prime}_{r} } \right) + \frac{{4\zeta_{h} Y_{r}^{2} Y^{\prime}_{r} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }} - \frac{{4\zeta_{h} X_{r} Y_{r} X^{\prime}_{r} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }} \hfill \\ \quad \quad + \left( {1 + 2\gamma - \frac{2\gamma }{{1 + \mu }}} \right)Y_{r} + \frac{{X_{r}^{2} }}{2} - \left[ {1 + \frac{2\gamma }{{\eta^{2} \left( {1 + \mu } \right)^{3} }}} \right]X_{r}^{2} Y_{r} + \frac{{\gamma Y_{r}^{3} }}{{\eta^{2} \left( {1 + \mu } \right)^{3} }} = \Omega^{2} Y_{{{\text{bm}}}} \cos \left( {\Omega T} \right), \hfill \\ \end{gathered}$$

(48)

Following the same solving procedure shown in Sect. 3.3, the HBM and PAL methods are used to acquire the dynamic response, and then, the absolute displacement transmissibility can be obtained.

The dynamic displacement and absolute displacement transmissibility of the IMD vibration isolator in the x and y directions with a different inertance-to-mass ratio (δ_h, δ_v), stiffness ratio γ, horizontal spring compression ratio μ and length ratio η are shown in Figs. 9, 10, 11, 12 and 13, respectively. In Figs. 9, 10, 11, 12 and 13, the horizontal and vertical base amplitudes (X_bm, Y_bm) are chosen as 0.01, which are smaller base amplitudes, and the FRC of the IMD vibration isolator displays linear characteristic.

Fig. 9

a Dynamic displacement in x direction, b dynamic displacement in y direction, c absolute displacement transmissibility in x direction and d absolute displacement transmissibility in y direction of the IMD vibration isolator with different δ_h (δ_v = 0.5, γ = 2, η = 1, μ = 0, ζ_h = ζ_v = 0.05, X_bm = Y_bm = 0.01)

Fig. 10

a Dynamic displacement in x direction, b dynamic displacement in y direction, c absolute displacement transmissibility in x direction and d absolute displacement transmissibility in y direction of the IMD vibration isolator with different δ_v (δ_h = 0.5, γ = 2, η = 1, μ = 0, ζ_h = ζ_v = 0.05, X_bm = Y_bm = 0.01)

Fig. 11

a Dynamic displacement in x direction, b dynamic displacement in y direction, c absolute displacement transmissibility in x direction and d absolute displacement transmissibility in y direction of the IMD vibration isolator with different γ (δ_h = δ_v = 0.5, η = 1, μ = 0, ζ_h = ζ_v = 0.05, X_bm = Y_bm = 0.01)

Fig. 12

a Dynamic displacement in x direction, b dynamic displacement in y direction, c absolute displacement transmissibility in x direction and d absolute displacement transmissibility in y direction of the IMD vibration isolator with different μ (δ_h = δ_v = 0.5, γ = 2, η = 1, ζ_h = ζ_v = 0.05, X_bm = Y_bm = 0.01)

Fig. 13

a Dynamic displacement in x direction, b dynamic displacement in y direction, c absolute displacement transmissibility in x direction and d absolute displacement transmissibility in y direction of the IMD vibration isolator with different η (δ_h = δ_v = 0.5, γ = 2, μ = 0, ζ_h = ζ_v = 0.05, X_bm = Y_bm = 0.01)

As shown in Fig. 9, for the IMD vibration isolator, when the horizontal inertance-to-mass ratio increases, the dynamic displacement and absolute displacement transmissibility peaks in the x direction decrease, the resonance frequency in the x direction becomes smaller, and the isolation frequency band in the x direction becomes wider, while the high-frequency absolute displacement transmissibility in the x direction increases. It should be noted that for the chosen horizontal inertance-to-mass ratio range (δ_hϵ[0, 10]), the isolation performance criteria in the y direction remain almost the same, which indicates that the horizontal inertance-to-mass ratio has less effect on the y direction isolation performance than that of the x direction.

As shown in Fig. 10, for the IMD vibration isolator, as the vertical inertance-to-mass ratio increases, the dynamic displacement and absolute displacement transmissibility peaks in the y direction decrease, the resonance frequency in the y direction decreases, and the isolation frequency band in the y direction widens, while the high-frequency absolute displacement transmissibility in the y direction increases. For the chosen vertical inertance-to-mass ratio range (δ_vϵ[0, 10]), the isolation performance criteria in the x direction remain almost the same, which suggests that the vertical inertance-to-mass ratio has less effect on the x direction isolation performance than that of the y direction.

Compared with the MD vibration isolator (δ_h = δ_v = 0), the IMD vibration isolator further reduces the dynamic displacement and absolute displacement transmissibility peaks and also widens the isolation frequency band; however, only the high-frequency absolute displacement transmissibility is larger. Therefore, adding the vertical and horizontal inerters on the basis of the MD vibration isolator to constitute the IMD one could further improve the isolation performance.

For the IMD vibration isolator, by increasing the stiffness ratio, the dynamic displacement and absolute displacement transmissibility peaks in the x direction increase, the resonance frequency in the x direction becomes larger and the isolation frequency band in the x direction becomes narrower, while the dynamic displacement and absolute displacement transmissibility peaks in the y direction increase a bit, and the resonance frequency and isolation frequency band in the y direction remains almost the same. This trend is shown in Fig. 11.

For the IMD vibration isolator, when the horizontal spring compression ratio increases, the isolation performance criteria in the x direction maintain the same which indicates that the horizontal spring compression ratio has little effect on the x direction isolation performance, while the dynamic displacement and absolute displacement transmissibility peaks in the y direction increase, the resonance frequency in the y direction becomes larger and the isolation frequency band in the y direction becomes narrower. It should be noted that if the horizontal spring compression ratio is equal to − 1/(1 + 2γ) for a fixed stiffness ratio, the natural frequency of the corresponding linear vibration isolator in the y direction is equal to 0 (see Eq. (22) and Fig. 5), and the IMD vibration isolator can achieve the full frequency band vibration isolation in the y direction, which is clearly shown in Fig. 12d. The overall trend is exhibited in Fig. 12.

For the IMD vibration isolator, the length ratio has little effect on the isolation performance in the x and y directions. The isolation performance criteria in the x direction retain the same with different length ratios. When the length ratio increases, the dynamic displacement and absolute displacement transmissibility peaks in the y direction decrease a bit, the resonance frequency in the y direction becomes a little smaller, and the isolation frequency band in the y direction becomes a little wider. This trend is illustrated in Fig. 13.

As the inertance-to-mass ratio is chosen as smaller and larger values, the dynamic displacement and absolute displacement transmissibility of the IMD vibration isolator in the x and y directions with different base amplitudes (X_bm, Y_bm) is shown in Figs. 14 and 15, respectively. When the inertance-to-mass ratio is chosen as smaller value, increasing the base amplitude results in larger dynamic displacement and absolute displacement transmissibility peaks in the x and y directions, while it has bit effect on the isolation frequency band. It should be noted that for larger horizontal base amplitude, there exists an additional smaller resonance frequency in the FRC for the x direction and the corresponding resonance peak is larger, which further deteriorates the isolation performance. When the inertance-to-mass ratio is chosen as larger value, increasing the base amplitude results in larger dynamic displacement peak in the x and y directions, while leads to smaller absolute displacement transmissibility peak in the x and y directions, widens the isolation frequency band in the x direction, while narrows the isolation frequency band in the y direction.

Fig. 14

a Dynamic displacement in x direction, b dynamic displacement in y direction, c absolute displacement transmissibility in x direction and d absolute displacement transmissibility in y direction of the IMD vibration isolator with different X_bm and Y_bm for smaller inertance-to-mass ratio (δ_h = δ_v = 0.5, γ = 2, η = 1, μ = 0, ζ_h = ζ_v = 0.05)

Fig. 15

a Dynamic displacement in x direction, b dynamic displacement in y direction, c absolute displacement transmissibility in x direction and d absolute displacement transmissibility in y direction of the IMD vibration isolator with different X_bm and Y_bm for larger inertance-to-mass ratio (δ_h = δ_v = 10, γ = 2, η = 1, μ = 0, ζ_h = ζ_v = 0.05)

Overall, the IMD vibration isolator can enhance the isolation performance of the MD vibration isolator significantly. The horizontal and vertical inertance-to-mass ratios are selected as larger values for better x and y directions isolation performance, the stiffness ratio is selected as smaller value that is especially better for x direction isolation performance, the horizontal spring compression ratio is selected as smaller value that is especially better for y direction isolation performance, and the length ratio is selected as larger value which is a bit better for y direction isolation performance.

4 Base shock excitation

Then, the base shock excitation is considered and the rounded displacement pulse [43] is used here, which can denote a bump or discrete irregularity of the road in practical engineering. The shock excitation in the x and y directions is expressed as

$$x_{b} = x_{{{\text{bm}}}} \left( {{{e^{2} } \mathord{\left/ {\vphantom {{e^{2} } 4}} \right. \kern-\nulldelimiterspace} 4}} \right)\left( {\nu \omega_{n} t} \right)^{2} e^{{ - \nu \omega_{n} t}} \quad y_{b} (t) = y_{{{\text{bm}}}} \left( {{{e^{2} } \mathord{\left/ {\vphantom {{e^{2} } 4}} \right. \kern-\nulldelimiterspace} 4}} \right)\left( {\nu \omega_{n} t} \right)^{2} e^{{ - \nu \omega_{n} t}} ,$$

(49)

where $\omega_{n} = \sqrt {k_{v} /m}$ and ν is the severity parameter; if the shock excitation is more severer, the parameter ν is larger. For the IMD vibration isolator, substituting Eq. (49) into Eqs. (15) and (16), and combined with Eq. (17) yields its non-dimensional dynamic equation subjected to shock excitation

$$\begin{gathered} \left\{ {1 + \delta_{v} X_{r}^{2} + 2\delta_{h} \left[ {1 - \frac{{Y_{r}^{2} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }}} \right]} \right\}X\prime \prime_{r} + \left[ {\delta_{v} \left( {X_{r} - X_{r} Y_{r} } \right) - \frac{{2\delta_{h} X_{r} Y_{r} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }}} \right]Y\prime \prime_{r} + \delta_{v} X_{r} X\prime_{r}^{2} - \frac{{2\delta_{h} X_{r} Y\prime_{r}^{2} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }} \hfill \\ \quad \quad - \frac{{4\delta_{h} Y_{r} X\prime_{r} Y\prime_{r} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }} + 2\zeta_{v} \left( {X_{r}^{2} X\prime_{r} + X_{r} Y\prime_{r} - X_{r} Y_{r} Y\prime_{r} } \right) + 4\zeta_{h} \left[ {1 - \frac{{Y_{r}^{2} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }}} \right]X\prime_{r} - \frac{{4\zeta_{h} X_{r} Y_{r} Y_{r}^{\prime } }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }} \hfill \\ \quad \quad + X_{r} Y_{r} + \frac{{X_{r}^{3} }}{2} - X_{r} Y_{r}^{2} + 2\gamma X_{r} - \frac{{2\gamma X_{r} Y_{r}^{2} }}{{\eta^{2} \left( {1 + \mu } \right)^{3} }} = - \frac{{e^{2} \nu^{2} }}{4}\left( {2 - 4\nu T + \nu^{2} T^{2} } \right)X_{bm} e^{ - \nu T} , \hfill \\ \end{gathered}$$

(50)

$$\begin{gathered} \left[ {\delta_{v} \left( {X_{r} - X_{r} Y_{r} } \right) - \frac{{2\delta_{h} X_{r} Y_{r} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }}} \right]X_{r}^{\prime \prime } + \left[ {1 + \delta_{v} \left( {1 - X_{r}^{{2}} } \right) + \frac{{2\delta_{h} Y_{r}^{2} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }}} \right]Y^{\prime\prime}_{r} + \delta_{v} \left( {1 - Y_{r} } \right)X_{r}^{{{\prime 2}}} - 2\delta_{v} X_{r} X_{r}^{{\prime }} Y_{r}^{{\prime }} \hfill \\ \quad \quad + \frac{{2\delta_{h} Y_{r} Y_{r}^{{{\prime 2}}} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }} + 2\zeta_{v} \left( {Y_{r}^{{\prime }} - X_{r}^{2} Y_{r}^{{\prime }} + X_{r} X_{r}^{{\prime }} - X_{r} Y_{r} X_{r}^{{\prime }} } \right) + \frac{{4\zeta_{h} Y_{r}^{{2}} Y_{r}^{{\prime }} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }} - \frac{{4\zeta_{h} X_{r} Y_{r} X_{r}^{{\prime }} }}{{\eta^{2} \left( {1 + \mu } \right)^{2} }} \hfill \\ \quad \quad + \left( {1 + 2\gamma - \frac{2\gamma }{{1 + \mu }}} \right)Y_{r} + \frac{{X_{r}^{{2}} }}{2} - \left[ {1 + \frac{2\gamma }{{\eta^{2} \left( {1 + \mu } \right)^{3} }}} \right]X_{r}^{{2}} Y_{r} + \frac{{\gamma Y_{r}^{3} }}{{\eta^{2} \left( {1 + \mu } \right)^{3} }} = - \frac{{e^{2} \nu^{2} }}{4}\left( {2 - 4\nu T + \nu^{2} T^{2} } \right)Y_{{{\text{bm}}}} e^{ - \nu T} , \hfill \\ \end{gathered}$$

(51)

Using the fourth-order Runge–Kutta method to acquire the corresponding dynamic response, then the absolute displacements in the x and y directions are given as

$$X_{{{\text{am}}}} = X_{{{\text{rm}}}} + \frac{{e^{2} \nu^{2} T^{2} }}{4}X_{{{\text{bm}}}} e^{ - \nu T} \quad Y_{{{\text{am}}}} = Y_{{{\text{rm}}}} + \frac{{e^{2} \nu^{2} T^{2} }}{4}Y_{{{\text{bm}}}} e^{ - \nu T} .$$

(52)

The time history of the absolute displacement in the x and y directions with different inertance-to-mass ratios is displayed in Fig. 16, where ν = 5 denotes less severe impact. The IMD vibration isolator can further reduce the displacement peak than the MD one, and the displacement peak has decreasing trend by increasing the inertance-to-mass ratio.

Fig. 16

Time history of the absolute displacement for the IMD vibration isolator under shock excitation with different δ_v and δ_h (γ = 2, η = 1, μ = 0, ν = 5, ζ_h = ζ_v = 0.05, X_bm = Y_bm = 0.01)

The shock performance of the IMD vibration isolator under shock excitation is assessed using the maximum absolute displacement ratio (MADR), which is defined as

$${\text{MADR}}_{x} = \frac{{\max \left| {X_{{{\text{am}}}} } \right|}}{{X_{{{\text{bm}}}} }}\quad {\text{MADR}}_{y} = \frac{{\max \left| {Y_{{{\text{am}}}} } \right|}}{{Y_{{{\text{bm}}}} }}.$$

(53)

Similar to the harmonic excitation, the effect of the inertance-to-mass ratio (δ_h, δ_v), stiffness ratio γ, horizontal spring compression ratio μ and length ratio η on the shock performance is mainly analyzed. The MADR of the IMD vibration isolator in the x and y directions is calculated in the ν range from 0.1 to 100, which covers the slight and severe impact, and Figs. 17, 18, 19 and 20 show the changing tendency of the MADR with different δ, γ, μ and η, respectively. The horizontal and vertical inertance-to-mass ratios are selected as the same values for brevity in this section. The horizontal and vertical damping ratios (ζ_h, ζ_v) are chosen as 0.05, and the horizontal and vertical base amplitudes (X_bm, Y_bm) are chosen as 0.01. When the severity parameter increases, the MADR of the IMD vibration isolator first increases, then reaches a peak value and finally decreases to a fixed value.

Fig. 17

MADR of the IMD vibration isolator with different δ_v and δ_h (γ = 2, η = 1, μ = 0, ζ_h = ζ_v = 0.05, X_bm = Y_bm = 0.01)

Fig. 18

MADR of the IMD vibration isolator with different γ (δ_h = δ_v = 0.5, η = 1, μ = 0, ζ_h = ζ_v = 0.05, X_bm = Y_bm = 0.01)

Fig. 19

MADR of the IMD vibration isolator with different μ (δ_h = δ_v = 0.5, γ = 2, η = 1, ζ_h = ζ_v = 0.05, X_bm = Y_bm = 0.01)

Fig. 20

MADR of the IMD vibration isolator with different η (δ_h = δ_v = 0.5, γ = 2, μ = 0, ζ_h = ζ_v = 0.05, X_bm = Y_bm = 0.01)

As shown in Fig. 17, for smaller severity parameter, the MADR decreases by increasing the inertance-to-mass ratio, while for larger severity parameter, the MADR increases by increasing the inertance-to-mass ratio. Compared with the MD vibration isolator (δ_h = δ_v = 0), the IMD vibration isolator further reduces the MADR in the middle severity parameter range, while it increases the MADR in the higher severity parameter range.

As displayed in Fig. 18, the stiffness ratio has little effect on the shock performance in the y direction. When the severity parameter is smaller, the MADR in the x direction decreases by increasing the stiffness ratio; when the severity parameter increases, the MADR in the x direction increases by increasing the stiffness ratio; as the severity parameter increases to a larger value (e.g., ν > 10), the MADR in the x direction remains almost the same with different stiffness ratios.

As exhibited in Fig. 19, the horizontal spring compression ratio has little effect on the shock performance in the x direction. When the severity parameter is smaller, the MADR in the y direction decreases as the horizontal spring compression ratio increases; when the severity parameter increases, the MADR in the y direction increases as the horizontal spring compression ratio increases; as the severity parameter increases to a larger value (e.g., ν > 10), the MADR in the y direction remains almost the same with different horizontal spring compression ratios. It should be noted that if the horizontal spring compression ratio is equal to − 1/(1 + 2γ) for a fixed stiffness ratio, the MADR in the y direction is smaller than 1 in the full severity parameter range, which achieves excellent shock performance and is the same with those of harmonic excitation shown in Sect. 3.6.

As illustrated in Fig. 20, the length ratio has little on the shock performance in the x and y directions, which the MADR in the x and y directions remains almost the same with different length ratios.

Overall, the IMD vibration isolator can improve the shock performance of the MD vibration isolator in the middle severity parameter range; in order to acquire a better shock performance, the vertical and horizontal inertance-to-mass ratios are chosen as larger values, and the stiffness ratio and the horizontal spring compression ratio are chosen as smaller values.

5 Conclusion

This paper adds the vertical and horizontal inerters on the basis of the MD vibration isolator and proposes the IMD vibration isolator consisting of the inerter, damper and spring structures. The Lagrange theory is used to establish its dynamic equation, combining the HBM and PAL method, the dynamic response subjected to base harmonic excitation is acquired and the stability of the dynamic response is investigated, the dynamic performance under harmonic and shock excitations is analyzed, and compared with those of the MD vibration isolator, the effect of structural parameters on its dynamic performance is studied in detail. This work yields the following conclusions:

• (1) The dynamic equation of the IMD vibration isolator in the multiple directions is strongly coupled nonlinear dynamic equations, the HBM and PAL method could be used to conveniently obtain its dynamic response, and the analytical results exhibit good accuracy with the numerical results, which confirms the validity of the analytical method.

• (2) The IMD vibration isolator has nonlinear inertial, damping and stiffness characteristics, and it further reduces the dynamic displacement and absolute displacement transmissibility peaks, widens the isolation frequency band than the MD vibration isolator and also has better shock performance in the middle severity parameter range.

• (3) In order to achieve better isolation and shock performance, the vertical and horizontal inertance-to-mass ratios (δ_v, δ_h) are chosen as larger values, and the stiffness ratio γ and the horizontal spring compression ratio μ are chosen as smaller values.

In summary, the proposed IMD vibration isolator is a original device and exhibits the advantages of applying the inerter, which provides excellent isolation and shock performance in multiple directions.

Appendix

The expressions of the eight nonlinear equations in Eq. (25) are given as

$$F_{1} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right) = - \frac{1}{{8\eta^{2} (\mu + 1)^{3} }}\left( {F_{11} + F_{12} + F_{13} } \right),$$

(A1)

$$\begin{aligned} F_{{11}} & = \left( {4a_{1} ^{3} \delta _{v} \eta ^{2} \mu ^{3} + 12a_{1} ^{2} a_{3} \delta _{v} \eta ^{2} \mu ^{3} + 4a_{1} a_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{3} + 24a_{1} a_{2} a_{4} \delta _{v} \eta ^{2} \mu ^{3} + 40a_{1} a_{3} ^{2} \delta _{v} \eta ^{2} \mu ^{3} + 40a_{1} a_{4} ^{2} \delta _{v} \eta ^{2} \mu ^{3} } \right. \\ & \quad - 6a_{1} b_{1} ^{2} \delta _{v} \eta ^{2} \mu ^{3} - 20a_{1} b_{1} b_{3} \delta _{v} \eta ^{2} \mu ^{3} - 2a_{1} b_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{3} - 20a_{1} b_{2} b_{4} \delta _{v} \eta ^{2} \mu ^{3} - 36a_{1} b_{3} ^{2} \delta _{v} \eta ^{2} \mu ^{3} - 36a_{1} b_{4} ^{2} \delta _{v} \eta ^{2} \mu ^{3} \\ & \quad - 12a_{2} ^{2} a_{3} \delta _{v} \eta ^{2} \mu ^{3} - 4a_{2} b_{1} b_{2} \delta _{v} \eta ^{2} \mu ^{3} - 20a_{2} b_{1} b_{4} \delta _{v} \eta ^{2} \mu ^{3} + 20a_{2} b_{2} b_{3} \delta _{v} \eta ^{2} \mu ^{3} - 2a_{3} b_{1} ^{2} \delta _{v} \eta ^{2} \mu ^{3} - 40a_{3} b_{1} b_{3} \delta _{v} \eta ^{2} \mu ^{3} \\ & \quad + 2a_{3} b_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{3} - 4a_{4} b_{1} b_{2} \delta _{v} \eta ^{2} \mu ^{3} - 40a_{4} b_{1} b_{4} \delta _{v} \eta ^{2} \mu ^{3} + 12a_{1} ^{3} \delta _{v} \eta ^{2} \mu ^{2} + 36a_{1} ^{2} a_{3} \delta _{v} \eta ^{2} \mu ^{2} + 12a_{1} a_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{2} \\ & \quad + 72a_{1} a_{2} a_{4} \delta _{v} \eta ^{2} \mu ^{2} + 120a_{1} a_{3} ^{2} \delta _{v} \eta ^{2} \mu ^{2} + 120a_{1} a_{4} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 18a_{1} b_{1} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 60a_{1} b_{1} b_{3} \delta _{v} \eta ^{2} \mu ^{2} + 8\eta ^{2} X_{{bm}} \\ & \quad - 6a_{1} b_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 60a_{1} b_{2} b_{4} \delta _{v} \eta ^{2} \mu ^{2} - 108a_{1} b_{3} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 108a_{1} b_{4} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 36a_{2} ^{2} a_{3} \delta _{v} \eta ^{2} \mu ^{2} + 8a_{1} \eta ^{2} \\ & \quad - 12a_{2} b_{1} b_{2} \delta _{v} \eta ^{2} \mu ^{2} - 60a_{2} b_{1} b_{4} \delta _{v} \eta ^{2} \mu ^{2} + 60a_{2} b_{2} b_{3} \delta _{v} \eta ^{2} \mu ^{2} - 6a_{3} b_{1} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 120a_{3} b_{1} b_{3} \delta _{v} \eta ^{2} \mu ^{2} - 20a_{3} b_{1} ^{2} \delta _{h} \\ & \quad + 6a_{3} b_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 12a_{4} b_{1} b_{2} \delta _{v} \eta ^{2} \mu ^{2} - 120a_{4} b_{1} b_{4} \delta _{v} \eta ^{2} \mu ^{2} + 12a_{1} ^{3} \delta _{v} \eta ^{2} \mu + 36a_{1} ^{2} a_{3} \delta _{v} \eta ^{2} \mu + 12a_{1} a_{2} ^{2} \delta _{v} \eta ^{2} \mu \\ & \quad + 72a_{1} a_{2} a_{4} \delta _{v} \eta ^{2} \mu + 120a_{1} a_{3} ^{2} \delta _{v} \eta ^{2} \mu + 120a_{1} a_{4} ^{2} \delta _{v} \eta ^{2} \mu - 18a_{1} b_{1} ^{2} \delta _{v} \eta ^{2} \mu - 60a_{1} b_{1} b_{3} \delta _{v} \eta ^{2} \mu - 6a_{1} b_{2} ^{2} \delta _{v} \eta ^{2} \mu \\ & \quad - 60a_{1} b_{2} b_{4} \delta _{v} \eta ^{2} \mu - 108a_{1} b_{3} ^{2} \delta _{v} \eta ^{2} \mu - 108a_{1} b_{4} ^{2} \delta _{v} \eta ^{2} \mu + 16a_{1} \delta _{h} \eta ^{2} \mu ^{3} - 36a_{2} ^{2} a_{3} \delta _{v} \eta ^{2} \mu - 12a_{2} b_{1} b_{2} \delta _{v} \eta ^{2} \mu \\ & \quad - 60a_{2} b_{1} b_{4} \delta _{v} \eta ^{2} \mu + 60a_{2} b_{2} b_{3} \delta _{v} \eta ^{2} \mu - 6a_{3} b_{1} ^{2} \delta _{v} \eta ^{2} \mu - 120a_{3} b_{1} b_{3} \delta _{v} \eta ^{2} \mu + 6a_{3} b_{2} ^{2} \delta _{v} \eta ^{2} \mu - 12a_{4} b_{1} b_{2} \delta _{v} \eta ^{2} \mu \\ & \quad - 120a_{4} b_{1} b_{4} \delta _{v} \eta ^{2} \mu + 4a_{1} ^{3} \delta _{v} \eta ^{2} + 12a_{1} ^{2} a_{3} \delta _{v} \eta ^{2} + 4a_{1} a_{2} ^{2} \delta _{v} \eta ^{2} + 24a_{1} a_{2} a_{4} \delta _{v} \eta ^{2} + 40a_{1} a_{3} ^{2} \delta _{v} \eta ^{2} + 40a_{1} a_{4} ^{2} \delta _{v} \eta ^{2} \\ & \quad - 6a_{1} b_{1} ^{2} \delta _{v} \eta ^{2} - 20a_{1} b_{1} b_{3} \delta _{v} \eta ^{2} - 2a_{1} b_{2} ^{2} \delta _{v} \eta ^{2} - 20a_{1} b_{2} b_{4} \delta _{v} \eta ^{2} - 36a_{1} b_{3} ^{2} \delta _{v} v\eta ^{2} - 36a_{1} b_{4} ^{2} \delta _{v} \eta ^{2} + 48a_{1} \delta _{h} \eta ^{2} \mu ^{2} \\ & \quad + 8a_{1} \eta ^{2} \mu ^{3} - 12a_{2} ^{2} a_{3} \delta _{v} \eta ^{2} - 4a_{2} b_{1} b_{2} \delta _{v} \eta ^{2} - 20a_{2} b_{1} b_{4} \delta _{v} \eta ^{2} + 20a_{2} b_{2} b_{3} \delta _{v} \eta ^{2} - 2a_{3} b_{1} ^{2} \delta _{v} \eta ^{2} - 40a_{3} b_{1} b_{3} \delta _{v} \eta ^{2} \\ & \quad + 2a_{3} b_{2} ^{2} \delta _{v} \eta ^{2} - 4a_{4} b_{1} b_{2} \delta _{v} \eta ^{2} - 40a_{4} b_{1} b_{4} \delta _{v} \eta ^{2} + 8\eta ^{2} \mu ^{3} X_{{bm}} - 12a_{1} b_{1} ^{2} \delta _{h} \mu - 8a_{1} b_{1} b_{3} \delta _{h} \mu - 4a_{1} b_{2} ^{2} \delta _{h} \mu \\ & \quad - 8a_{1} b_{2} b_{4} \delta _{h} \mu - 8a_{1} b_{3} ^{2} \delta _{h} \mu - 8a_{1} b_{4} ^{2} \delta _{h} \mu + 48a_{1} \delta _{h} \eta ^{2} \mu + 24a_{1} \eta ^{2} \mu ^{2} - 8a_{2} b_{1} b_{2} \delta _{h} \mu - 8a_{2} b_{1} b_{4} \delta _{h} \mu + 20a_{3} b_{2} ^{2} \delta _{h} \\ & \quad + 8a_{2} b_{2} b_{3} \delta _{h} \mu - 20a_{3} b_{1} ^{2} \delta _{h} \mu - 80a_{3} b_{1} b_{3} \delta _{h} \mu + 20a_{3} b_{2} ^{2} \delta _{h} \mu - 40a_{4} b_{1} b_{2} \delta _{h} \mu - 80a_{4} b_{1} b_{4} \delta _{h} \mu + 24\eta ^{2} \mu ^{2} X_{{bm}} \\ & \quad - 12a_{1} b_{1} ^{2} \delta _{h} - 8a_{1} b_{1} b_{3} \delta _{h} - 4a_{1} b_{2} ^{2} \delta _{h} - 8a_{1} b_{2} b_{4} \delta _{h} - 8a_{1} b_{3} ^{2} \delta _{h} - 8a_{1} b_{4} ^{2} \delta _{h} + 16a_{1} \delta _{h} \eta ^{2} + 24a_{1} \eta ^{2} \mu - 8a_{2} b_{1} b_{2} \delta _{h} \\ & \quad - \left. {8a_{2} b_{1} b_{4} \delta _{h} + 8a_{2} b_{2} b_{3} \delta _{h} - 80a_{3} b_{1} b_{3} \delta _{h} - 40a_{4} b_{1} b_{2} \delta _{h} - 80a_{4} b_{1} b_{4} \delta _{h} + 24\eta ^{2} \mu X_{{bm}} } \right)\Omega ^{2} , \\ \end{aligned}$$

(A2)

$$\begin{aligned} F_{{12}} & = \left( { - 4a_{1} ^{2} a_{2} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{1} ^{2} a_{4} \zeta _{v} \eta ^{2} \mu ^{3} + 8a_{1} a_{2} a_{3} \zeta _{v} \eta ^{2} \mu ^{3} + 8a_{1} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} + 8a_{1} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} } \right. \\ & \quad - 8a_{1} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{2} ^{3} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{2} ^{2} a_{4} \zeta _{v} \eta ^{2} \mu ^{3} - 8a_{2} a_{3} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} - 8a_{2} a_{4} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{2} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} \\ & \quad - 8a_{2} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{2} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} - 8a_{2} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} + 8a_{3} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} + 24a_{3} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} - 32a_{3} b_{1} b_{2} \zeta _{h} \\ & \quad + 8a_{3} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{4} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} - 24a_{4} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{4} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} + 8a_{4} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{2} ^{3} \zeta _{v} \eta ^{2} \\ & \quad - 12a_{1} ^{2} a_{2} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{1} ^{2} a_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 24a_{1} a_{2} a_{3} \zeta _{v} \eta ^{2} \mu ^{2} + 24a_{1} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} + 24a_{1} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} - 48a_{3} b_{1} b_{4} \zeta _{h} \\ & \quad - 24a_{1} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{2} ^{3} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{2} ^{2} a_{4} \zeta _{v} \eta ^{2} \mu ^{2} - 24a_{2} a_{3} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} - 24a_{2} a_{4} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} - 4a_{1} ^{2} a_{2} \zeta _{v} \eta ^{2} \\ & \quad - 12a_{2} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} - 24a_{2} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{2} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} - 24a_{2} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 24a_{3} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} - 32a_{2} \zeta _{h} \eta ^{2} \\ & \quad + 72a_{3} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 24a_{3} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{4} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} - 72a_{4} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{4} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} - 4a_{4} b_{1} ^{2} \zeta _{v} \eta ^{2} \\ & \quad + 24a_{4} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{1} ^{2} a_{2} \zeta _{v} \eta ^{2} \mu - 12a_{1} ^{2} a_{4} \zeta _{v} \eta ^{2} \mu + 24a_{1} a_{2} a_{3} \zeta _{v} \eta ^{2} \mu + 24a_{1} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu + 24a_{1} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu \\ & \quad - 24a_{1} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu - 12a_{2} ^{3} \zeta _{v} \eta ^{2} \mu + 12a_{2} ^{2} a_{4} \zeta _{v} \eta ^{2} \mu - 24a_{2} a_{3} ^{2} \zeta _{v} \eta ^{2} \mu - 24a_{2} a_{4} ^{2} \zeta _{v} \eta ^{2} \mu - 12a_{2} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu \\ & \quad - 24a_{2} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu + 12a_{2} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu - 24a_{2} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu - 32a_{2} \zeta _{h} \eta ^{2} \mu ^{3} + 24a_{3} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu + 72a_{3} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu \\ & \quad + 24a_{3} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu - 12a_{4} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu - 72a_{4} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu + 12a_{4} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu + 24a_{4} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu - 4a_{1} ^{2} a_{4} \zeta _{v} \eta ^{2} \\ & \quad + 8a_{1} a_{2} a_{3} \zeta _{v} \eta ^{2} + 8a_{1} b_{1} b_{2} \zeta _{v} \eta ^{2} + 8a_{1} b_{1} b_{4} \zeta _{v} \eta ^{2} - 8a_{1} b_{2} b_{3} \zeta _{v} \eta ^{2} + 4a_{2} ^{2} a_{4} \zeta _{v} \eta ^{2} - 8a_{2} a_{3} ^{2} \zeta _{v} \eta ^{2} - 8a_{2} a_{4} ^{2} \zeta _{v} \eta ^{2} \\ & \quad - 4a_{2} b_{1} ^{2} \zeta _{v} \eta ^{2} - 8a_{2} b_{1} b_{3} \zeta _{v} \eta ^{2} + 4a_{2} b_{2} ^{2} \zeta _{v} \eta ^{2} - 8a_{2} b_{2} b_{4} \zeta _{v} \eta ^{2} - 96a_{2} \zeta _{h} \eta ^{2} \mu ^{2} + 8a_{3} b_{1} b_{2} \zeta _{v} \eta ^{2} + 24a_{3} b_{1} b_{4} \zeta _{v} \eta ^{2} \\ & \quad + 8a_{3} b_{2} b_{3} \zeta _{v} \eta ^{2} - 24a_{4} b_{1} b_{3} \zeta _{v} \eta ^{2} + 4a_{4} b_{2} ^{2} \zeta _{v} \eta ^{2} + 8a_{4} b_{2} b_{4} \zeta _{v} \eta ^{2} + 16a_{2} b_{1} ^{2} \zeta _{h} \mu + 16a_{2} b_{2} ^{2} \zeta _{h} \mu + 16a_{2} b_{3} ^{2} \zeta _{h} \mu \\ & \quad + 16a_{2} b_{4} ^{2} \zeta _{h} \mu - 96a_{2} \zeta _{h} \eta ^{2} \mu - 32a_{3} b_{1} b_{2} \zeta _{h} \mu - 48a_{3} b_{1} b_{4} \zeta _{h} \mu + 16a_{3} b_{2} b_{3} \zeta _{h} \mu + 16a_{4} b_{1} ^{2} \zeta _{h} \mu + 48a_{4} b_{1} b_{3} \zeta _{h} \mu \\ & \quad - 16a_{4} b_{2} ^{2} \zeta _{h} \mu + 16a_{4} b_{2} b_{4} \zeta _{h} \mu + 16a_{2} b_{1} ^{2} \zeta _{h} + 16a_{2} b_{2} ^{2} \zeta _{h} + 16a_{2} b_{3} ^{2} \zeta _{h} + 16a_{2} b_{4} ^{2} \zeta _{h} + 16a_{3} b_{2} b_{3} \zeta _{h} + 16a_{4} b_{1} ^{2} \zeta _{h} \\ & \quad + \left. {48a_{4} b_{1} b_{3} \zeta _{h} - 16a_{4} b_{2} ^{2} \zeta _{h} + 16a_{4} b_{2} b_{4} \zeta _{h} } \right)\Omega , \\ \end{aligned}$$

(A3)

$$\begin{aligned} F_{13} = & - 3a_{1}^{3} \eta^{2} \mu^{3} - 3a_{1}^{2} a_{3} n^{2} \mu^{3} - 3a_{1} a_{2}^{2} \eta^{2} \mu^{3} - 6a_{1} a_{2} a_{4} \eta^{2} \mu^{3} - 6a_{1} a_{3}^{2} \eta^{2} \mu^{3} - 6a_{1} a_{4}^{2} \eta^{2} \mu^{3} + 6a_{1} b_{1}^{2} \eta^{2} \mu^{3} \\ & \quad + 4a_{1} b_{1} b_{3} \eta^{2} \mu^{3} + 2a_{1} b_{2}^{2} \eta^{2} \mu^{3} + 4a_{1} b_{2} b_{4} \eta^{2} \mu^{3} + 4a_{1} b_{3}^{2} \eta^{2} \mu^{3} + 4a_{1} b_{4}^{2} \eta^{2} \mu^{3} + 3a_{2}^{2} a_{3} \eta^{2} \mu^{3} + 4a_{2} b_{1} b_{2} \eta^{2} \mu^{3} \\ & \quad + 4a_{2} b_{1} b_{4} \eta^{2} \mu^{3} - 4a_{2} b_{2} b_{3} \eta^{2} \mu^{3} + 2a_{3} b_{1}^{2} \eta^{2} \mu^{3} + 8a_{3} b_{1} b_{3} \eta^{2} \mu^{3} - 2a_{3} b_{2}^{2} \eta^{2} \mu^{3} + 4a_{4} b_{1} b_{2} \eta^{2} \mu^{3} + 8a_{4} b_{1} b_{4} \eta^{2} \mu^{3} \\ & \quad - 9a_{1}^{3} \eta^{2} \mu^{2} - 9a_{1}^{2} a_{3} \eta^{2} \mu^{2} - 9a_{1} a_{2}^{2} \eta^{2} \mu^{2} - 18a_{1} a_{2} a_{4} \eta^{2} \mu^{2} - 18a_{1} a_{3}^{2} \eta^{2} \mu^{2} - 18a_{1} a_{4}^{2} \eta^{2} \mu^{2} + 18a_{1} b_{1}^{2} \eta^{2} \mu^{2} \\ & \quad + 12a_{1} b_{1} b_{3} \eta^{2} \mu^{2} + 6a_{1} b_{2}^{2} \eta^{2} \mu^{2} + 12a_{1} b_{2} b_{4} \eta^{2} \mu^{2} + 12a_{1} b_{3}^{2} \eta^{2} \mu^{2} + 12a_{1} b_{4}^{2} \eta^{2} \mu^{2} - 16a_{1} \eta^{2} \gamma \mu^{3} + 9a_{2}^{2} a_{3} \eta^{2} \mu^{2} \\ & \quad + 12a_{2} b_{1} b_{2} \eta^{2} \mu^{2} + 12a_{2} b_{1} b_{4} \eta^{2} \mu^{2} - 12a_{2} b_{2} b_{3} \eta^{2} \mu^{2} + 6a_{3} b_{1}^{2} \eta^{2} \mu^{2} + 24a_{3} b_{1} b_{3} \eta^{2} \mu^{2} - 6a_{3} b_{2}^{2} \eta^{2} \mu^{2} + 6a_{1} b_{2}^{2} \eta^{2} \mu \\ & \quad + 12a_{4} b_{1} b_{2} \eta^{2} \mu^{2} + 24a_{4} b_{1} b_{4} \eta^{2} \mu^{2} - 9a_{1}^{3} \eta^{2} \mu - 9a_{1}^{2} a_{3} \eta^{2} \mu - 9a_{1} a_{2}^{2} \eta^{2} \mu + 8a_{1} b_{2} b_{4} \gamma - 18a_{1} a_{3}^{2} \eta^{2} \mu + 4a_{1} b_{2}^{2} \gamma \\ & \quad - 18a_{1} a_{4}^{2} \eta^{2} \mu + 18a_{1} b_{1}^{2} \eta^{2} \mu + 12a_{1} b_{1} b_{3} \eta^{2} \mu + 12a_{1} b_{2} b_{4} \eta^{2} \mu + 12a_{1} b_{3}^{2} \eta^{2} \mu + 12a_{1} b_{4}^{2} \eta^{2} \mu + 8a_{1} b_{4}^{2} \gamma + 12a_{1} b_{1}^{2} \gamma \\ & \quad + 9a_{2}^{2} a_{3} \eta^{2} \mu + 12a_{2} b_{1} b_{2} \eta^{2} \mu + 12a_{2} b_{1} b_{4} \eta^{2} \mu - 12a_{2} b_{2} b_{3} \eta^{2} \mu + 6a_{3} b_{1}^{2} \eta^{2} \mu + 24a_{3} b_{1} b_{3} \eta^{2} \mu + 8a_{1} b_{3}^{2} \gamma + 8a_{1} b_{1} b_{3} \gamma \\ & \quad + 12a_{4} b_{1} b_{2} \eta^{2} \mu + 24a_{4} b_{1} b_{4} \eta^{2} \mu - 3a_{1}^{3} \eta^{2} - 3a_{1}^{2} a_{3} \eta^{2} - 3a_{1} a_{2}^{2} \eta^{2} - 6a_{1} a_{2} a_{4} \eta^{2} - 6a_{1} a_{3}^{2} \eta^{2} - 6a_{1} a_{4}^{2} \eta^{2} + 6a_{1} b_{1}^{2} \eta^{2} \\ & \quad + 4a_{1} b_{1} b_{3} \eta^{2} + 2a_{1} b_{2}^{2} \eta^{2} + 4a_{1} b_{2} b_{4} \eta^{2} + 4a_{1} b_{3}^{2} \eta^{2} + 4a_{1} b_{4}^{2} \eta^{2} - 48a_{1} \eta^{2} \gamma \mu + 3a_{2}^{2} a_{3} \eta^{2} + 4a_{2} b_{1} b_{2} \eta^{2} + 4a_{2} b_{1} b_{4} \eta^{2} \\ & \quad - 4a_{2} b_{2} b_{3} \eta^{2} + 2a_{3} b_{1}^{2} \eta^{2} + 8a_{3} b_{1} b_{3} \eta^{2} - 2a_{3} b_{2}^{2} \eta^{2} + 4a_{4} b_{1} b_{2} \eta^{2} + 8a_{4} b_{1} b_{4} \eta^{2} - 18a_{1} a_{2} a_{4} \eta^{2} \mu - 48a_{1} \eta^{2} \gamma \mu^{2} \\ & \quad - 6a_{3} b_{2}^{2} \eta^{2} \mu - 16a_{1} \eta^{2} \gamma + 8a_{2} b_{1} b_{2} \gamma + 8a_{2} b_{1} b_{4} \gamma - 8a_{2} b_{2} b_{3} \gamma + 4a_{3} b_{1}^{2} \gamma + 16a_{3} b_{1} b_{3} \gamma + 8a_{4} b_{1} b_{2} \gamma + 16a_{4} b_{1} b_{4} \gamma \\ \end{aligned}$$

(A4)

$$F_{2} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right) = - \frac{1}{{8\eta^{2} (\mu + 1)^{3} }}\left( {F_{21} + F_{22} + F_{23} } \right),$$

(A5)

$$\begin{aligned} F_{{21}} & = \left( {4a_{1} ^{2} a_{2} \delta _{v} \eta ^{2} \mu ^{3} + 12a_{1} ^{2} a_{4} \delta _{v} \eta ^{2} \mu ^{3} - 24a_{1} a_{2} a_{3} \delta _{v} \eta ^{2} \mu ^{3} - 4a_{1} b_{1} b_{2} \delta _{v} \eta ^{2} \mu ^{3} - 80a_{4} b_{2} b_{4} \delta _{h} + 8\eta ^{2} a_{2} } \right. \\ & \quad - 20a_{1} b_{1} b_{4} \delta _{v} \eta ^{2} \mu ^{3} + 20a_{1} b_{2} b_{3} \delta _{v} \eta ^{2} \mu ^{3} + 4a_{2} ^{3} \delta _{v} \eta ^{2} \mu ^{3} - 12a_{2} ^{2} a_{4} \delta _{v} \eta ^{2} \mu ^{3} + 40a_{2} a_{3} ^{2} \delta _{v} \eta ^{2} \mu ^{3} + 40a_{2} a_{4} ^{2} \delta _{v} \eta ^{2} \mu ^{3} \\ & \quad - 2a_{2} b_{1} ^{2} \delta _{v} \eta ^{2} \mu ^{3} + 20a_{2} b_{1} b_{3} \delta _{v} \eta ^{2} \mu ^{3} - 6a_{2} b_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{3} + 20a_{2} b_{2} b_{4} \delta _{v} \eta ^{2} \mu ^{3} - 36a_{2} b_{3} ^{2} \delta _{v} \eta ^{2} \mu ^{3} - 36a_{2} b_{4} ^{2} \delta _{v} \eta ^{2} \mu ^{3} \\ & \quad + 4a_{3} b_{1} b_{2} \delta _{v} \eta ^{2} \mu ^{3} - 40a_{3} b_{2} b_{3} \delta _{v} \eta ^{2} \mu ^{3} - 2a_{4} b_{1} ^{2} \delta _{v} \eta ^{2} \mu ^{3} + 2a_{4} b_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{3} - 40a_{4} b_{2} b_{4} \delta _{v} \eta ^{2} \mu ^{3} + 12a_{1} ^{2} a_{2} \delta _{v} \eta ^{2} \mu ^{2} \\ & \quad + 36a_{1} ^{2} a_{4} \delta _{v} \eta ^{2} \mu ^{2} - 72a_{1} a_{2} a_{3} \delta _{v} \eta ^{2} \mu ^{2} - 12a_{1} b_{1} b_{2} \delta _{v} \eta ^{2} \mu ^{2} - 60a_{1} b_{1} b_{4} \delta _{v} \eta ^{2} \mu ^{2} + 60a_{1} b_{2} b_{3} \delta _{v} \eta ^{2} \mu ^{2} + 12a_{2} ^{3} \delta _{v} \eta ^{2} \mu ^{2} \\ & \quad - 36a_{2} ^{2} a_{4} \delta _{v} \eta ^{2} \mu ^{2} + 120a_{2} a_{3} ^{2} \delta _{v} \eta ^{2} \mu ^{2} + 120a_{2} a_{4} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 6a_{2} b_{1} ^{2} \delta _{v} \eta ^{2} \mu ^{2} + 60a_{2} b_{1} b_{3} \delta _{v} \eta ^{2} \mu ^{2} - 18a_{2} b_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{2} \\ & \quad + 60a_{2} b_{2} b_{4} \delta _{v} \eta ^{2} \mu ^{2} - 108a_{2} b_{3} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 108a_{2} b_{4} ^{2} \delta _{v} \eta ^{2} \mu ^{2} + 12a_{3} b_{1} b_{2} \delta _{v} \eta ^{2} \mu ^{2} - 120a_{3} b_{2} b_{3} \delta _{v} \eta ^{2} \mu ^{2} - 8a_{2} b_{4} ^{2} \delta _{h} \\ & \quad - 6a_{4} b_{1} ^{2} \delta _{v} \eta ^{2} \mu ^{2} + 6a_{4} b_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 120a_{4} b_{2} b_{4} \delta _{v} \eta ^{2} \mu ^{2} + 12a_{1} ^{2} a_{2} \delta _{v} \eta ^{2} \mu + 36a_{1} ^{2} a_{4} \delta _{v} \eta ^{2} \mu - 72a_{1} a_{2} a_{3} \delta _{v} \eta ^{2} \mu \\ & \quad - 12a_{1} b_{1} b_{2} \delta _{v} \eta ^{2} \mu - 60a_{1} b_{1} b_{4} \delta _{v} \eta ^{2} \mu + 60a_{1} b_{2} b_{3} \delta _{v} \eta ^{2} \mu + 12a_{2} ^{3} \delta _{v} \eta ^{2} \mu - 36a_{2} ^{2} a_{4} \delta _{v} \eta ^{2} \mu + 120a_{2} a_{3} ^{2} \delta _{v} \eta ^{2} \mu \\ & \quad + 120a_{2} a_{4} ^{2} \delta _{v} \eta ^{2} \mu - 6a_{2} b_{1} ^{2} \delta _{v} \eta ^{2} \mu + 60a_{2} b_{1} b_{3} \delta _{v} \eta ^{2} \mu - 18a_{2} b_{2} ^{2} \delta _{v} \eta ^{2} \mu + 60a_{2} b_{2} b_{4} \delta _{v} \eta ^{2} \mu - 108a_{2} b_{3} ^{2} \delta _{v} \eta ^{2} \mu \\ & \quad - 108a_{2} b_{4} ^{2} \delta _{v} \eta ^{2} \mu + 16a_{2} \delta _{h} \eta ^{2} \mu ^{3} + 12a_{3} b_{1} b_{2} \delta _{v} \eta ^{2} \mu - 120a_{3} b_{2} b_{3} \delta _{v} \eta ^{2} \mu - 6a_{4} b_{1} ^{2} \delta _{v} \eta ^{2} \mu + 6a_{4} b_{2} ^{2} \delta _{v} \eta ^{2} \mu \\ & \quad - 120a_{4} b_{2} b_{4} \delta _{v} \eta ^{2} \mu + 4a_{1} ^{2} a_{2} \delta _{v} \eta ^{2} + 12a_{1} ^{2} a_{4} \delta _{v} \eta ^{2} - 24a_{1} a_{2} a_{3} \delta _{v} \eta ^{2} - 4a_{1} b_{1} b_{2} \delta _{v} \eta ^{2} - 20a_{1} b_{1} b_{4} \delta _{v} \eta ^{2} - 8a_{2} b_{3} ^{2} \delta _{h} \\ & \quad + 20a_{1} b_{2} b_{3} \delta _{v} \eta ^{2} + 4a_{2} ^{3} \delta _{v} \eta ^{2} - 12a_{2} ^{2} a_{4} \delta _{v} \eta ^{2} + 40a_{2} a_{3} ^{2} \delta _{v} \eta ^{2} + 40a_{2} a_{4} ^{2} \delta _{v} \eta ^{2} - 2a_{2} b_{1} ^{2} \delta _{v} \eta ^{2} + 20a_{2} b_{1} b_{3} \delta _{v} \eta ^{2} \\ & \quad - 6a_{2} b_{2} ^{2} \delta _{v} \eta ^{2} + 20a_{2} b_{2} b_{4} \delta _{v} \eta ^{2} - 36a_{2} b_{3} ^{2} \delta _{v} \eta ^{2} - 36a_{2} b_{4} ^{2} \delta _{v} \eta ^{2} + 48a_{2} \delta _{h} \eta ^{2} \mu ^{2} + 8\eta ^{2} a_{2} \mu ^{3} + 4a_{3} b_{1} b_{2} \delta _{v} \eta ^{2} \\ & \quad - 40a_{3} b_{2} b_{3} \delta _{v} \eta ^{2} - 2a_{4} b_{1} ^{2} \delta _{v} \eta ^{2} + 2a_{4} b_{2} ^{2} \delta _{v} \eta ^{2} - 40a_{4} b_{2} b_{4} \delta _{v} \eta ^{2} - 8a_{1} b_{1} b_{2} \delta _{h} \mu - 8a_{1} b_{1} b_{4} \delta _{h} \mu + 8a_{1} b_{2} b_{3} \delta _{h} \mu \\ & \quad - 4a_{2} b_{1} ^{2} \delta _{h} \mu + 8a_{2} b_{1} b_{3} \delta _{h} \mu - 12a_{2} b_{2} ^{2} \delta _{h} \mu + 8a_{2} b_{2} b_{4} \delta _{h} \mu - 8a_{2} b_{3} ^{2} \delta _{h} \mu - 8a_{2} b4^{2} \delta _{h} \mu + 48a_{2} \delta _{h} \eta ^{2} \mu \\ & \quad + 24a_{2} \eta ^{2} \mu ^{2} + 40a_{3} b_{1} b_{2} \delta _{h} \mu - 80a_{3} b_{2} b_{3} \delta _{h} \mu - 20a_{4} b_{1} ^{2} \delta _{h} \mu + 20a_{4} b_{2} ^{2} \delta _{h} \mu - 80a_{4} b_{2} b_{4} \delta _{h} \mu - 8a_{1} b_{1} b_{2} \delta _{h} \\ & \quad - 8a_{1} b_{1} b_{4} \delta _{h} + 8a_{1} b_{2} b_{3} \delta _{h} - 4a_{2} b_{1} ^{2} \delta _{h} + 8a_{2} b_{1} b_{3} \delta _{h} - 12a_{2} b_{2} ^{2} \delta _{h} + 8a_{2} b_{2} b_{4} \delta _{h} + 16a_{2} \delta _{h} \eta ^{2} + 24\eta ^{2} a_{2} \mu \\ & \quad + \left. {40a_{3} b_{1} b_{2} \delta _{h} - 80a_{3} b_{2} b_{3} \delta _{h} - 20a_{4} b_{1} ^{2} \delta _{h} + 20a_{4} b_{2} ^{2} \delta _{h} } \right)\Omega ^{2} , \\ \end{aligned}$$

(A6)

$$\begin{aligned} F_{{22}} & = \left( {4a_{1} ^{3} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{1} ^{2} a_{3} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{1} a_{2} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} + 8a_{1} a_{2} a_{4} \zeta _{v} \eta ^{2} \mu ^{3} + 8a_{1} a_{3} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} + 8a_{1} a_{4} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} } \right. \\ & \quad - 4a_{1} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} - 8a_{1} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{1} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} - 8a_{1} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{2} ^{2} a_{3} \zeta _{v} \eta ^{2} \mu ^{3} - 8a_{2} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} \\ & \quad - 8a_{2} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} + 8a_{2} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{3} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} - 8a_{3} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{3} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} + 24a_{3} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} \\ & \quad + 8a_{4} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} - 8a_{4} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} - 24a_{4} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} + 12a_{1} ^{3} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{1} ^{2} a_{3} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{1} a_{2} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} \\ & \quad + 24a_{1} a_{2} a_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 24a_{1} a_{3} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} + 24a_{1} a_{4} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{1} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} - 24a_{1} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{1} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} \\ & \quad - 24a_{1} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{2} ^{2} a_{3} \zeta _{v} \eta ^{2} \mu ^{2} - 24a_{2} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} - 24a_{2} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 24a_{2} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} - 16a_{1} b_{1} ^{2} \zeta _{h} \\ & \quad + 12a_{3} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} - 24a_{3} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{3} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} + 72a_{3} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 24a_{4} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} + 16a_{3} b_{2} ^{2} \zeta _{h} \\ & \quad - 24a_{4} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} - 72a_{4} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{1} ^{3} \zeta _{v} \eta ^{2} \mu + 12a_{1} ^{2} a_{3} \zeta _{v} \eta ^{2} \mu + 12a_{1} a_{2} ^{2} \zeta _{v} \eta ^{2} \mu + 24a_{1} a_{2} a_{4} \zeta _{v} \eta ^{2} \mu \\ & \quad + 24a_{1} a_{3} ^{2} \zeta _{v} \eta ^{2} \mu + 24a_{1} a_{4} ^{2} \zeta _{v} \eta ^{2} \mu - 12a_{1} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu - 24a_{1} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu + 12a_{1} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu - 24a_{1} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu \\ & \quad + 32a_{1} \zeta _{h} \eta ^{2} \mu ^{3} - 12a_{2} ^{2} a_{3} \zeta _{v} \eta ^{2} \mu - 24a_{2} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu - 24a_{2} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu + 24a_{2} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu + 12a_{3} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu \\ & \quad - 24a_{3} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu - 12a_{3} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu + 72a_{3} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu + 24a_{4} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu - 24a_{4} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu - 72a_{4} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu \\ & \quad + 4a_{1} ^{3} \zeta _{v} \eta ^{2} + 4a_{1} ^{2} a_{3} \zeta _{v} \eta ^{2} + 4a_{1} a_{2} ^{2} \zeta _{v} \eta ^{2} + 8a_{1} a_{2} a_{4} \zeta _{v} \eta ^{2} + 8a_{1} a_{3} ^{2} \zeta _{v} \eta ^{2} + 8a_{1} a_{4} ^{2} \zeta _{v} \eta ^{2} - 4a_{1} b_{1} ^{2} \zeta _{v} \eta ^{2} \\ & \quad - 8a_{1} b_{1} b_{3} \zeta _{v} \eta ^{2} + 4a_{1} b_{2} ^{2} \zeta _{v} \eta ^{2} - 8a_{1} b_{2} b_{4} \zeta _{v} \eta ^{2} + 96a_{1} \zeta _{h} \eta ^{2} u^{2} - 4a_{2} ^{2} a_{3} \zeta _{v} \eta ^{2} - 8a_{2} b_{1} b_{2} \zeta _{v} \eta ^{2} - 8a_{2} b_{1} b_{4} \zeta _{v} \eta ^{2} \\ & \quad + 8a_{2} b_{2} b_{3} \zeta _{v} \eta ^{2} + 4a_{3} b_{1} ^{2} \zeta _{v} \eta ^{2} - 8a_{3} b_{1} b_{3} \zeta _{v} \eta ^{2} - 4a_{3} b_{2} ^{2} \zeta _{v} \eta ^{2} + 24a_{3} b_{2} b_{4} \zeta _{v} \eta ^{2} + 8a_{4} b_{1} b_{2} \zeta _{v} \eta ^{2} - 8a_{4} b_{1} b_{4} \zeta _{v} \eta ^{2} \\ & \quad - 24a_{4} b_{2} b_{3} \zeta _{v} \eta ^{2} - 16a_{1} b_{1} ^{2} \zeta _{h} \mu - 16a_{1} b_{2} ^{2} \zeta _{h} \mu - 16a_{1} b_{3} ^{2} \zeta _{h} \mu - 16a_{1} b_{4} ^{2} \zeta _{h} \mu + 96a_{1} \zeta _{h} \eta ^{2} \mu - 16a_{3} b_{1} ^{2} \zeta _{h} \mu \\ & \quad - 16a_{3} b_{1} b_{3} \zeta _{h} \mu + 16a_{3} b_{2} ^{2} \zeta _{h} \mu - 48a_{3} b_{2} b_{4} \zeta _{h} \mu - 32a_{4} b_{1} b_{2} \zeta _{h} \mu - 16a_{4} b_{1} b_{4} \zeta _{h} \mu + 48a_{4} b_{2} b_{3} \zeta _{h} \mu - 16a_{1} b_{2} ^{2} \zeta _{h} \\ & \quad - 16a_{1} b_{3} ^{2} \zeta _{h} - 16a_{1} b_{4} ^{2} \zeta _{h} + 32a_{1} \zeta _{h} \eta ^{2} - 16a_{3} b_{1} ^{2} \zeta _{h} - 16a_{3} b_{1} b_{3} \zeta _{h} - 48a_{3} b_{2} b_{4} \zeta _{h} - 32a_{4} b_{1} b_{2} \zeta _{h} - 16a_{4} b_{1} b_{4} \zeta _{h} \\ & \quad + \left. {48a_{4} b_{2} b_{3} \zeta _{h} } \right)\Omega , \\ \end{aligned}$$

(A7)

$$\begin{aligned} F_{23} & = - 3a_{1}^{2} a_{2} \eta^{2} \mu^{3} - 3a_{1}^{2} a_{4} \eta^{2} \mu^{3} + 6a_{1} a_{2} a_{3} \eta^{2} \mu^{3} + 4a_{1} b_{1} b_{2} \eta^{2} \mu^{3} - 4a_{4} b_{2}^{2} \gamma + 16a_{4} b_{2} b_{4} - 12a_{3} b_{1} b_{2} \eta^{2} \mu^{2} \\ & \quad + 4a_{1} b_{1} b_{4} \eta^{2} \mu^{3} - 4a_{1} b_{2} b_{3} \eta^{2} \mu^{3} - 3a_{2}^{3} \eta^{2} \mu^{3} + 3a_{2}^{2} a_{4} \eta^{2} \mu^{3} - 6a_{2} a_{3}^{2} \eta^{2} \mu^{3} - 6a_{2} a_{4}^{2} \eta^{2} \mu^{3} + 2a_{2} b_{1}^{2} \eta^{2} \mu^{3} \\ & \quad - 4a_{2} b_{1} b_{3} \eta^{2} \mu^{3} + 6a_{2} b_{2}^{2} \eta^{2} \mu^{3} - 4a_{2} b_{2} b_{4} \eta^{2} \mu^{3} + 4a_{2} b_{3}^{2} \eta^{2} \mu^{3} + 4a_{2} b_{4}^{2} \eta^{2} \mu^{3} - 4a_{3} b_{1} b_{2} \eta^{2} \mu^{3} + 8a_{3} b_{2} b_{3} \eta^{2} \mu^{3} \\ & \quad + 2a_{4} b_{1}^{2} \eta^{2} \mu^{3} - 2a_{4} b_{2}^{2} \eta^{2} \mu^{3} + 8a_{4} b_{2} b_{4} \eta^{2} \mu^{3} - 9a_{1}^{2} a_{2} \eta^{2} \mu^{2} - 9a_{1}^{2} a_{4} \eta^{2} \mu^{2} + 18a_{1} a_{2} a_{3} \eta^{2} \mu^{2} + 12a_{1} b_{1} b_{2} \eta^{2} \mu^{2} \\ & \quad + 12a_{1} b_{1} b_{4} \eta^{2} \mu^{2} - 12a_{1} b_{2} b_{3} \eta^{2} \mu^{2} - 9a_{2}^{3} \eta^{2} \mu^{2} + 9a_{2}^{2} a_{4} \eta^{2} \mu^{2} - 18a_{2} a_{3}^{2} \eta^{2} \mu^{2} - 18a_{2} a_{4}^{2} \eta^{2} \mu^{2} + 6a_{2} b_{1}^{2} \eta^{2} \mu^{2} \\ & \quad - 12a_{2} b_{1} b_{3} \eta^{2} \mu^{2} + 18a_{2} b_{2}^{2} \eta^{2} \mu^{2} - 12a_{2} b_{2} b_{4} \eta^{2} \mu^{2} + 12a_{2} b_{3}^{2} \eta^{2} \mu^{2} + 12a_{2} b_{4}^{2} \eta^{2} \mu^{2} - 16a_{2} \eta^{2} \gamma \mu^{3} - 8a_{2} b_{2} b_{4} \gamma \\ & \quad + 24a_{3} b_{2} b_{3} \eta^{2} \mu^{2} + 6a_{4} b_{1}^{2} \eta^{2} \mu^{2} - 6a_{4} b_{2}^{2} \eta^{2} \mu^{2} + 24a_{4} b_{2} b_{4} \eta^{2} \mu^{2} - 9a_{1}^{2} a_{2} \eta^{2} \mu - 9a_{1}^{2} a_{4} \eta^{2} \mu + 18a_{1} a_{2} a_{3} \eta^{2} \mu \\ & \quad + 12a_{1} b_{1} b_{2} \eta^{2} \mu + 12a_{1} b_{1} b_{4} \eta^{2} \mu - 12a_{1} b_{2} b_{3} \eta^{2} \mu - 9a_{2}^{3} \eta^{2} \mu + 9a_{2}^{2} a_{4} \eta^{2} \mu - 18a_{2} a_{3}^{2} \eta^{2} \mu - 18a_{2} a_{4}^{2} \eta^{2} \mu \\ & \quad + 6a_{2} b_{1}^{2} \eta^{2} \mu - 12a_{2} b_{1} b_{3} \eta^{2} \mu + 18a_{2} b_{2}^{2} \eta^{2} \mu - 12a_{2} b_{2} b_{4} \eta^{2} \mu + 12a_{2} b_{3}^{2} \eta^{2} \mu + 12a_{2} b_{4}^{2} \eta^{2} \mu - 48a_{2} \eta^{2} \gamma \mu^{2} \\ & \quad - 12a_{3} b_{1} b_{2} \eta^{2} \mu + 24a_{3} b_{2} b_{3} \eta^{2} \mu + 6a_{4} b_{1}^{2} \eta^{2} \mu - 6a_{4} b_{2}^{2} \eta^{2} \mu + 24a_{4} b_{2} b_{4} \eta^{2} \mu - 3a_{1}^{2} a_{2} \eta^{2} - 3a_{1}^{2} a_{4} \eta^{2} + 12a_{2} b_{2}^{2} \gamma \\ & \quad + 6a_{1} a_{2} a_{3} \eta^{2} + 4a_{1} b_{1} b_{2} \eta^{2} + 4a_{1} b_{1} b_{4} \eta^{2} - 4a_{1} b_{2} b_{3} \eta^{2} - 3\eta^{2} a_{2}^{3} + 3a_{2}^{2} a_{4} \eta^{2} - 6a_{3}^{2} \eta^{2} a_{2} - 6a_{2} a_{4}^{2} \eta^{2} + 2b_{1}^{2} \eta^{2} a_{2} \\ & \quad - 4b_{1} \eta^{2} a_{2} b_{3} + 6b_{2}^{2} \eta^{2} a_{2} - 4a_{2} b_{2} b_{4} \eta^{2} + 4\eta^{2} a_{2} b_{3}^{2} + 4a_{2} b_{4}^{2} \eta^{2} - 48a_{2} \eta^{2} \gamma \mu - 4b_{2} a_{3} b_{1} \eta^{2} + 8b_{2} a_{3} \eta^{2} b_{3} + 2a_{4} b_{1}^{2} \eta^{2} \\ & \quad - 2a_{4} b_{2}^{2} \eta^{2} + 8a_{4} b_{2} b_{4} \eta^{2} + 8a_{1} b_{1} b_{2} \gamma + 8a_{1} b_{1} b_{4} \gamma - 8a_{1} b_{2} b_{3} \gamma + 4a_{2} b_{1}^{2} \gamma - 8a_{2} b_{1} b_{3} \gamma + 8a_{2} b_{3}^{2} \gamma + 8a_{2} b_{4}^{2} \gamma \\ & \quad - 16a_{2} \eta^{2} \gamma - 8a_{3} b_{1} b_{2} \gamma + 16a_{3} b_{2} b_{3} \gamma + 4a_{4} b_{1}^{2} \gamma , \\ \end{aligned}$$

(A8)

$$\begin{aligned} & F_{3} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right) = - \frac{1}{{8\eta ^{2} (\mu + 1)^{3} }}\left( {\left( {4a_{1} ^{3} \delta _{v} \eta ^{2} \mu ^{3} + 40a_{1} ^{2} a_{3} \delta _{v} \eta ^{2} \mu ^{3} - 12a_{1} a_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{3} - 2a_{1} b_{1} ^{2} \delta _{v} \eta ^{2} \mu ^{3} } \right.} \right. \\ & \quad - 40a_{1} b_{1} b_{3} \delta _{v} \eta ^{2} \mu ^{3} + 2a_{1} b_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{3} + 40a_{2} ^{2} a_{3} \delta _{v} \eta ^{2} \mu ^{3} + 4a_{2} b_{1} b_{2} \delta _{v} \eta ^{2} \mu ^{3} - 40a_{2} b_{2} b_{3} \delta _{v} \eta ^{2} \mu ^{3} + 36a_{3} ^{3} \delta _{v} \eta ^{2} \mu ^{3} \\ & \quad + 36a_{3} a_{4} ^{2} \delta _{v} \eta ^{2} \mu ^{3} - 4a_{3} b_{1} ^{2} \delta _{v} \eta ^{2} \mu ^{3} - 4a_{3} b_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{3} - 54a_{3} b_{3} ^{2} \delta _{v} \eta ^{2} \mu ^{3} - 18a_{3} b_{4} ^{2} \delta _{v} \eta ^{2} \mu ^{3} - 36a_{4} b_{3} b_{4} \delta _{v} \eta ^{2} \mu ^{3} \\ & \quad + 12a_{1} ^{3} \delta _{v} \eta ^{2} \mu ^{2} + 120a_{1} ^{2} a_{3} \delta _{v} \eta ^{2} \mu ^{2} - 36a_{1} a_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 6a_{1} b_{1} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 120a_{1} b_{1} b_{3} \delta _{v} \eta ^{2} \mu ^{2} + 6a_{1} b_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{2} \\ & \quad + 120a_{2} ^{2} a_{3} \delta _{v} \eta ^{2} \mu ^{2} + 12a_{2} b_{1} b_{2} \delta _{v} \eta ^{2} \mu ^{2} - 120a_{2} b_{2} b_{3} \delta _{v} \eta ^{2} \mu ^{2} + 108a_{3} ^{3} \delta _{v} \eta ^{2} \mu ^{2} + 108a_{3} a_{4} ^{2} \delta _{v} \eta ^{2} \mu ^{2} \\ & \quad - 12a_{3} b_{1} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 12a_{3} b_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 162a_{3} b_{3} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 54a_{3} b_{4} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 108a_{4} b_{3} b_{4} \delta _{v} \eta ^{2} \mu ^{2} + 12a_{1} ^{3} \delta _{v} \eta ^{2} \mu \\ & \quad + 120a_{1} ^{2} a_{3} \delta _{v} \eta ^{2} \mu - 36a_{1} a_{2} ^{2} \delta _{v} \eta ^{2} \mu - 6a_{1} b_{1} ^{2} \delta _{v} \eta ^{2} \mu - 120a_{1} b_{1} b_{3} \delta _{v} \eta ^{2} \mu + 6a_{1} b_{2} ^{2} \delta _{v} \eta ^{2} \mu + 120a_{2} ^{2} a_{3} \delta _{v} \eta ^{2} \mu \\ & \quad + 12a_{2} b_{1} b_{2} \delta _{v} \eta ^{2} \mu - 120a_{2} b_{2} b_{3} \delta _{v} \eta ^{2} \mu + 108a_{3} ^{3} \delta _{v} \eta ^{2} \mu + 108a_{3} a_{4} ^{2} \delta _{v} \eta ^{2} \mu - 12a_{3} b_{1} ^{2} \delta _{v} \eta ^{2} \mu - 12a_{3} b_{2} ^{2} \delta _{v} \eta ^{2} \mu \\ & \quad - 162a_{3} b_{3} ^{2} \delta _{v} \eta ^{2} \mu - 54a_{3} b_{4} ^{2} \delta _{v} \eta ^{2} \mu + 144a_{3} \delta _{h} \eta ^{2} \mu ^{3} - 108a_{4} a_{3} b_{4} \delta _{v} \eta ^{2} \mu + 4a_{1} ^{3} \delta _{v} \eta ^{2} + 40a_{1} ^{2} a_{3} \delta _{v} \eta ^{2} \\ & \quad - 12a_{1} a_{2} ^{2} \delta _{v} \eta ^{2} - 2a_{1} b_{1} ^{2} \delta _{v} \eta ^{2} - 40a_{1} b_{1} b_{3} \delta _{v} \eta ^{2} + 2a_{1} b_{2} ^{2} \delta _{v} \eta ^{2} + 40a_{2} ^{2} a_{3} \delta _{v} \eta ^{2} + 4a_{2} b_{1} b_{2} \delta _{v} \eta ^{2} - 40a_{2} b_{2} b_{3} \delta _{v} \eta ^{2} \\ & \quad + 36a_{3} ^{3} \delta _{v} \eta ^{2} + 36a_{3} a_{4} ^{2} \delta _{v} \eta ^{2} - 4a_{3} b_{1} ^{2} \delta _{v} \eta ^{2} - 4a_{3} b_{2} ^{2} \delta _{v} \eta ^{2} - 54a_{3} b_{3} ^{2} \delta _{v} \eta ^{2} - 18a_{3} b_{4} ^{2} \delta _{v} \eta ^{2} + 432a_{3} \delta _{h} \eta ^{2} \mu ^{2} \\ & \quad + 72a_{3} \eta ^{2} \mu ^{3} - 36a_{4} b_{3} b_{4} \delta _{v} \eta ^{2} - 20a_{1} b_{1} ^{2} \delta _{h} \mu - 80a_{1} b_{1} b_{3} \delta _{h} \mu + 20a_{1} b_{2} ^{2} \delta _{h} \mu + 40a_{2} b_{1} b_{2} \delta _{h} \mu - 80a_{2} b_{2} b_{3} \delta _{h} \mu \\ & \quad - 72a_{3} b_{1} ^{2} \delta _{h} \mu - 72a_{3} b_{2} ^{2} \delta _{h} \mu - 108a_{3} b_{3} ^{2} \delta _{h} \mu - 36a_{3} b_{4} ^{2} \delta _{h} \mu + 432a_{3} \delta _{h} \eta ^{2} \mu + 216a_{3} \eta ^{2} \mu ^{2} - 72a_{4} b_{3} b_{4} \delta _{h} \mu \\ & \quad - 20a_{1} b_{1} ^{2} \delta _{h} - 80a_{1} b_{1} b_{3} \delta _{h} + 20a_{1} b_{2} ^{2} \delta _{h} + 40a_{2} b_{1} b_{2} \delta _{h} - 80a_{2} b_{2} b_{3} \delta _{h} - 72a_{3} b_{1} ^{2} \delta _{h} - 72a_{3} b_{2} ^{2} bh - 108a_{3} b_{3} ^{2} bh \\ & \quad - \left. {36a_{3} b_{4} ^{2} \delta _{h} + 144a_{3} \delta _{h} \eta ^{2} + 216a_{3} \eta ^{2} \mu - 72a_{4} b_{3} b_{4} \delta _{h} + 72a_{3} \eta ^{2} } \right)\Omega ^{2} + \left( { - 12a_{1} ^{2} a_{2} \zeta _{v} \eta ^{2} \mu ^{3} - 24a_{1} ^{2} a_{4} \zeta _{v} \eta ^{2} \mu ^{3} } \right. \\ & \quad + 8a_{1} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} + 24a_{1} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} + 8a_{1} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{2} ^{3} \zeta _{v} \eta ^{2} \mu ^{3} - 24a_{2} ^{2} a_{4} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{2} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} \\ & \quad - 8a_{2} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{2} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} + 24a_{2} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} - 12a_{3} ^{2} a_{4} \zeta _{v} \eta ^{2} \mu ^{3} + 24a_{3} b_{3} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} - 12a_{4} ^{3} \zeta _{v} \eta ^{2} \mu ^{3} \\ & \quad - 12a_{4} b_{3} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} + 12a_{4} b_{4} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} - 36a_{1} ^{2} a_{2} \zeta _{v} \eta ^{2} \mu ^{2} - 72a_{1} ^{2} a_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 24a_{1} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} + 48a_{4} b_{3} ^{2} \zeta _{h} \\ & \quad + 72a_{1} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 24a_{1} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{2} ^{3} \zeta _{v} \eta ^{2} \mu ^{2} - 72a_{2} ^{2} a_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{2} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} + 48a_{4} b_{4} ^{2} \zeta _{h} \\ & \quad - 24a_{2} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{2} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} + 72a_{2} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} - 36a_{3} ^{2} a_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 72a_{3} b_{3} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} \\ & \quad - 36a_{4} ^{3} \zeta _{v} \eta ^{2} \mu ^{2} - 36a_{4} b_{3} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} + 36a_{4} b_{4} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} - 36a_{1} ^{2} a_{2} \zeta _{v} \eta ^{2} \mu - 72a_{1} ^{2} a_{4} \zeta _{v} \eta ^{2} \mu + 24a_{1} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu \\ & \quad + 72a_{1} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu + 24a_{1} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu + 12a_{2} ^{3} \zeta _{v} \eta ^{2} \mu - 72a_{2} ^{2} a_{4} \zeta _{v} \eta ^{2} \mu + 12a_{2} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu - 24a_{2} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu \\ & \quad - 12a_{2} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu + 72a_{2} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu - 36a_{3} ^{2} a_{4} \zeta _{v} \eta ^{2} \mu + 72a_{3} b_{3} b_{4} \zeta _{v} \eta ^{2} \mu - 36a_{4} ^{3} \zeta _{v} \eta ^{2} \mu - 36a_{4} b_{3} ^{2} \zeta _{v} \eta ^{2} \mu \\ & \quad + 36a_{4} b_{4} ^{2} \zeta _{v} \eta ^{2} \mu - 96a_{4} \zeta _{h} \eta ^{2} \mu ^{3} - 12a_{1} ^{2} a_{2} \zeta _{v} \eta ^{2} - 24a_{1} ^{2} a_{4} \zeta _{v} \eta ^{2} + 8a_{1} b_{1} b_{2} \zeta _{v} \eta ^{2} + 24a_{1} b_{1} b_{4} \zeta _{v} \eta ^{2} + 8a_{1} b_{2} b_{3} \zeta _{v} \eta ^{2} \\ & \quad + 4a_{2} ^{3} \zeta _{v} \eta ^{2} - 24a_{2} ^{2} a_{4} \zeta _{v} \eta ^{2} + 4a_{2} b_{1} ^{2} \zeta _{v} \eta ^{2} - 8a_{2} b_{1} b_{3} \zeta _{v} \eta ^{2} - 4a_{2} b_{2} ^{2} \zeta _{v} \eta ^{2} + 24a_{2} b_{2} b_{4} \zeta _{v} \eta ^{2} - 12a_{3} ^{2} a_{4} \zeta _{v} \eta ^{2} \\ & \quad + 24a_{3} b_{3} b_{4} \zeta _{v} \eta ^{2} - 12a_{4} ^{3} \zeta _{v} \eta ^{2} - 12a_{4} b_{3} ^{2} \zeta _{v} \eta ^{2} + 12a_{4} b_{4} ^{2} \zeta _{v} \eta ^{2} - 288a_{4} \zeta _{h} \eta ^{2} \mu ^{2} + 32a_{1} b_{1} b_{2} \zeta _{h} \mu + 48a_{1} b_{1} b_{4} \zeta _{h} \mu \\ & \quad - 16a_{1} b_{2} b_{3} \zeta _{h} \mu + 16a_{2} b_{1} ^{2} \zeta _{h} \mu + 16a_{2} b_{1} b_{3} \zeta _{h} \mu - 16a_{2} b_{2} ^{2} \zeta _{h} \mu + 48a_{2} b_{2} b_{4} \zeta _{h} \mu + 48a_{4} b_{1} ^{2} \zeta _{h} \mu + 48a_{4} b_{2} ^{2} \zeta _{h} \mu \\ & \quad + 48a_{4} b_{3} ^{2} \zeta _{h} \mu + 48a_{4} b_{4} ^{2} \zeta _{h} \mu - 288a_{4} \zeta _{h} \eta ^{2} \mu + 32a_{1} b_{1} b_{2} \zeta _{h} + 48a_{1} b_{1} b_{4} \zeta _{h} - 16a_{1} b_{2} b_{3} \zeta _{h} + 16a_{2} b_{1} ^{2} \zeta _{h} \\ & \quad + \left. {16a_{2} b_{1} b_{3} \zeta _{h} - 16a_{2} b_{2} ^{2} \zeta _{h} + 48a_{2} b_{2} b_{4} \zeta _{h} + 48a_{4} b_{1} ^{2} \zeta _{h} + 48a_{4} b_{2} ^{2} \zeta _{h} - 96a_{4} \zeta _{h} \eta } \right)^{2} \Omega + \left( { - a_{1} ^{3} \eta ^{2} \mu ^{3} - 6a_{1} ^{2} a_{3} \eta ^{2} \mu ^{3} } \right. \\ & \quad + 3a_{1} a_{2} ^{2} \eta ^{2} \mu ^{3} + 2a_{1} b_{1} ^{2} \eta ^{2} \mu ^{3} + 8a_{1} b_{1} b_{3} \eta ^{2} \mu ^{3} - 2a_{1} b_{2} ^{2} \eta ^{2} \mu ^{3} - 6a_{2} ^{2} a_{3} \eta ^{2} \mu ^{3} - 4a_{2} b_{1} b_{2} \eta ^{2} \mu ^{3} + 8a_{2} b_{2} b_{3} \eta ^{2} \mu ^{3} \\ & \quad - 3a_{3} ^{3} \eta ^{2} \mu ^{3} - 3a_{3} a_{4} ^{2} \eta ^{2} \mu ^{3} + 4a_{3} b_{1} ^{2} \eta ^{2} \mu ^{3} + 4a_{3} b_{2} ^{2} \eta ^{2} \mu ^{3} + 6a_{3} b_{3} ^{2} \eta ^{2} \mu ^{3} + 2a_{3} b_{4} ^{2} \eta ^{2} \mu ^{3} + 4a_{4} b_{3} b_{4} \eta ^{2} \mu ^{3} - 3a_{1} ^{3} \eta ^{2} \mu ^{2} \\ & \quad - 18a_{1} ^{2} a_{3} \eta ^{2} \mu ^{2} + 9a_{1} a_{2} ^{2} \eta ^{2} \mu ^{2} + 6a_{1} b_{1} ^{2} \eta ^{2} \mu ^{2} + 24a_{1} b_{1} b_{3} \eta ^{2} \mu ^{2} - 6a_{1} b_{2} ^{2} \eta ^{2} \mu ^{2} - 18a_{2} ^{2} a_{3} \eta ^{2} \mu ^{2} - 12a_{2} b_{1} b_{2} \eta ^{2} \mu ^{2} \\ & \quad + 24a_{2} b_{2} b_{3} \eta ^{2} \mu ^{2} - 9a_{3} ^{3} \eta ^{2} \mu ^{2} - 9a_{3} a_{4} ^{2} \eta ^{2} \mu ^{2} + 12a_{3} b_{1} ^{2} \eta ^{2} \mu ^{2} + 12a_{3} b_{2} ^{2} \eta ^{2} \mu ^{2} + 18a_{3} b_{3} ^{2} \eta ^{2} \mu ^{2} + 6a_{3} b_{4} ^{2} \eta ^{2} \mu ^{2} \\ & \quad - 16a_{3} \eta ^{2} \gamma \mu ^{3} + 12a_{4} b_{3} b_{4} \eta ^{2} \mu ^{2} - 3a_{1} ^{3} \eta ^{2} \mu - 18a_{1} ^{2} a_{3} \eta ^{2} \mu + 9a_{1} a_{2} ^{2} \eta ^{2} \mu + 6a_{1} b_{1} ^{2} \eta ^{2} \mu + 24a_{1} b_{1} b_{3} \eta ^{2} \mu - 6a_{1} b_{2} ^{2} \eta ^{2} \mu \\ & \quad - 18a_{2} ^{2} a_{3} \eta ^{2} \mu - 12a_{2} b_{1} b_{2} \eta ^{2} \mu + 24a_{2} b_{2} b_{3} \eta ^{2} \mu - 9a_{3} ^{3} \eta ^{2} \mu - 9a_{3} a_{4} ^{2} \eta ^{2} \mu + 12a_{3} b_{1} ^{2} \eta ^{2} \mu + 12a_{3} b_{2} ^{2} \eta ^{2} \mu \\ & \quad + 18a_{3} b_{3} ^{2} \eta ^{2} \mu + 6a_{3} b_{4} ^{2} \eta ^{2} \mu - 48a_{3} \eta ^{2} \gamma \mu ^{2} + 12a_{4} b_{3} b_{4} \eta ^{2} \mu - a_{1} ^{3} \eta ^{2} - 6a_{1} ^{2} a_{3} \eta ^{2} + 3a_{1} a_{2} ^{2} \eta ^{2} + 2a_{1} b_{1} ^{2} \eta ^{2} + 8a_{1} b_{1} b_{3} \eta ^{2} \\ & \quad - 2a_{1} b_{2} ^{2} \eta ^{2} - 6a_{3} \eta ^{2} a_{2} ^{2} - 4b_{2} b_{1} \eta ^{2} a_{2} + 8b_{2} \eta ^{2} a_{2} b_{3} - 3a_{3} ^{3} \eta ^{2} - 3a_{3} a_{4} ^{2} \eta ^{2} + 4a_{3} b_{1} ^{2} \eta ^{2} + 4b_{2} ^{2} a_{3} \eta ^{2} + 6a_{3} \eta ^{2} b_{3} ^{2} \\ & \quad + 2a_{3} b_{4} ^{2} \eta ^{2} - 48a_{3} \eta ^{2} \gamma \mu + 4a_{4} b_{3} b_{4} \eta ^{2} + 4a_{1} b_{1} ^{2} \gamma + 16a_{1} b_{1} b_{3} \gamma - 4a_{1} b_{2} ^{2} \gamma - 8a_{2} b_{1} b_{2} \gamma + 16a_{2} b_{2} b_{3} \gamma + 8a_{3} b_{1} ^{2} \gamma \\ & \quad + \left. {\left. {8a_{3} b_{2} ^{2} \gamma + 12a_{3} b_{3} ^{2} \gamma + 4a_{3} b_{4}^{2} \gamma - 16a_{3} \eta ^{2} \gamma + 8a_{4} b_{3} b_{4} \gamma } \right)} \right), \\ \end{aligned}$$

(A9)

$$\begin{aligned} & F_{4} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right) = - \frac{1}{{8\eta ^{2} \left( {\mu ^{3} + 3\mu ^{2} + 3\mu + 1} \right)}}\left( {\left( {12a_{1} ^{2} a_{2} \delta _{v} \eta ^{2} \mu ^{3} + 40a_{1} ^{2} a_{4} \delta _{v} \eta ^{2} \mu ^{3} - 4a_{1} b_{1} b_{2} \delta _{v} \eta ^{2} \mu ^{3} } \right.} \right. \\ & \quad - 40a_{1} b_{1} b_{4} \delta _{v} \eta ^{2} \mu ^{3} - 4a_{2} ^{3} \delta _{v} \eta ^{2} \mu ^{3} + 40a_{2} ^{2} a_{4} \delta _{v} \eta ^{2} \mu ^{3} - 2a_{2} b_{1} ^{2} \delta _{v} \eta ^{2} \mu ^{3} + 2a_{2} b_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{3} \\ & \quad - 40a_{2} b_{2} b_{4} \delta _{v} \eta ^{2} \mu ^{3} + 36a_{3} ^{2} a_{4} \delta _{v} \eta ^{2} \mu ^{3} - 36a_{3} b_{3} b_{4} \delta _{v} \eta ^{2} \mu ^{3} + 36a_{4} ^{3} \delta _{v} \eta ^{2} \mu ^{3} - 4a_{4} b_{1} ^{2} \delta _{v} \eta ^{2} \mu ^{3} \\ & \quad - 4a_{4} b_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{3} - 18a_{4} b_{3} ^{2} \delta _{v} \eta ^{2} \mu ^{3} - 54a_{4} b_{4} ^{2} \delta _{v} \eta ^{2} \mu ^{3} + 36a_{1} ^{2} a_{2} \delta _{v} \eta ^{2} \mu ^{2} + 120a_{1} ^{2} a_{4} \delta _{v} \eta ^{2} \mu ^{2} \\ & \quad - 12a_{1} b_{1} b_{2} \delta _{v} \eta ^{2} \mu ^{2} - 120a_{1} b_{1} b_{4} \delta _{v} \eta ^{2} \mu ^{2} - 12a_{2} ^{3} \delta _{v} \eta ^{2} \mu ^{2} + 120a_{2} ^{2} a_{4} \delta _{v} \eta ^{2} \mu ^{2} - 6a_{2} b_{1} ^{2} \delta _{v} \eta ^{2} \mu ^{2} \\ & \quad + 6a_{2} b_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 120a_{2} b_{2} b_{4} \delta _{v} \eta ^{2} \mu ^{2} + 108a_{3} ^{2} a_{4} \delta _{v} \eta ^{2} \mu ^{2} - 108a_{3} b_{3} b_{4} \delta _{v} \eta ^{2} \mu ^{2} + 108a_{4} ^{3} \delta _{v} \eta ^{2} \mu ^{2} \\ & \quad - 12a_{4} b_{1} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 12a_{4} b_{2} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 54a_{4} b_{3} ^{2} \delta _{v} \eta ^{2} \mu ^{2} - 162a_{4} b_{4} ^{2} \delta _{v} \eta ^{2} \mu ^{2} + 36a_{1} ^{2} a_{2} \delta _{v} \eta ^{2} \mu \\ & \quad + 120a_{1} ^{2} a_{4} \delta _{v} \eta ^{2} \mu - 12a_{1} b_{1} b_{2} \delta _{v} \eta ^{2} \mu - 120a_{1} b_{1} b_{4} \delta _{v} \eta ^{2} \mu - 12a_{2} ^{3} \delta _{v} \eta ^{2} \mu + 120a_{2} ^{2} a_{4} \delta _{v} \eta ^{2} \mu \\ & \quad - 6a_{2} b_{1} ^{2} \delta _{v} \eta ^{2} \mu + 6a_{2} b_{2} ^{2} \delta _{v} \eta ^{2} \mu - 120a_{2} b_{2} b_{4} \delta _{v} \eta ^{2} \mu + 108a_{3} ^{2} a_{4} \delta _{v} \eta ^{2} \mu - 108a_{3} b_{3} b_{4} \delta _{v} \eta ^{2} \mu \\ & \quad + 108a_{4} ^{3} \delta _{v} \eta ^{2} \mu - 12a_{4} b_{1} ^{2} \delta _{v} \eta ^{2} \mu - 12a_{4} b_{2} ^{2} \delta _{v} \eta ^{2} \mu - 54a_{4} b_{3} ^{2} \delta _{v} \eta ^{2} \mu - 162a_{4} b_{4} ^{2} \delta _{v} \eta ^{2} \mu \\ & \quad + 144a_{4} \delta _{h} \eta ^{2} \mu ^{3} + 12a_{1} ^{2} a_{2} \delta _{v} \eta ^{2} + 40a_{1} ^{2} a_{4} \delta _{v} \eta ^{2} - 4a_{1} b_{1} b_{2} \delta _{v} \eta ^{2} - 40a_{1} b_{1} b_{4} \delta _{v} \eta ^{2} - 4a_{2} ^{3} \delta _{v} \eta ^{2} \\ & \quad + 40a_{2} ^{2} a_{4} \delta _{v} \eta ^{2} - 2a_{2} b_{1} ^{2} \delta _{v} \eta ^{2} + 2a_{2} b_{2} ^{2} \delta _{v} \eta ^{2} - 40a_{2} b_{2} b_{4} \delta _{v} \eta ^{2} + 36a_{3} ^{2} a_{4} \delta _{v} \eta ^{2} - 36a_{3} b_{3} b_{4} \delta _{v} \eta ^{2} \\ & \quad + 36a_{4} ^{3} \delta _{v} \eta ^{2} - 4a_{4} b_{1} ^{2} \delta _{v} \eta ^{2} - 4a_{4} b_{2} ^{2} \delta _{v} \eta ^{2} - 18a_{4} b_{3} ^{2} \delta _{v} \eta ^{2} - 54a_{4} b_{4} ^{2} \delta _{v} \eta ^{2} + 432a_{4} \delta _{h} \eta ^{2} \mu ^{2} \\ & \quad + 72\eta ^{2} \mu ^{3} a_{4} - 40a_{1} b_{1} b_{2} \delta _{h} \mu - 80a_{1} b_{1} b_{4} \delta _{h} \mu - 20a_{2} b_{1} ^{2} \delta _{h} \mu + 20a_{2} b_{2} ^{2} \delta _{h} \mu - 80a_{2} b_{2} b_{4} \delta _{h} \mu \\ & \quad - 72a_{3} b_{3} b_{4} \delta _{h} \mu - 72a_{4} b_{1} ^{2} \delta _{h} \mu - 72a_{4} b_{2} ^{2} \delta _{h} \mu - 36a_{4} b_{3} ^{2} \delta _{h} \mu - 108a_{4} b_{4} ^{2} \delta _{h} \mu + 432a_{4} \delta _{h} n^{2} \mu \\ & \quad + 216a_{4} \eta ^{2} \mu ^{2} - 40a_{1} b_{1} b_{2} \delta _{h} - 80a_{1} b_{1} b_{4} \delta _{h} - 20a_{2} b_{1} ^{2} \delta _{h} + 20a_{2} b_{2} ^{2} \delta _{h} - 80a_{2} b_{2} b_{4} \delta _{h} - 72a_{3} b_{3} b_{4} \delta _{h} \\ & \quad - \left. {72a_{4} b_{1} ^{2} \delta _{h} - 72a_{4} b_{2} ^{2} \delta _{h} - 36a_{4} b_{3} ^{2} \delta _{h} - 108a_{4} b_{4} ^{2} \delta _{h} + 144a_{4} \delta _{h} \eta ^{2} + 216a_{4} \eta ^{2} \mu + 72a_{4} \eta ^{2} } \right)\Omega ^{2} \\ & \quad + \left( {4a_{1} ^{3} \zeta _{v} \eta ^{2} \mu ^{3} + 24a_{1} ^{2} a_{3} \zeta _{v} \eta ^{2} \mu ^{3} - 12a_{1} a_{2} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{1} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} - 24a_{1} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{1} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} } \right. \\ & \quad + 8a_{1} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} + 24a_{2} ^{2} a_{3} \zeta _{v} \eta ^{2} \mu ^{3} + 8a_{2} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} - 8a_{2} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} - 24a_{2} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} \\ & \quad + 12a_{3} ^{3} \zeta _{v} \eta ^{2} \mu ^{3} + 12a_{3} a_{4} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} - 12a_{3} b_{3} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} + 12a_{3} b_{4} ^{2} \zeta _{v} \eta ^{2} \mu ^{3} - 24a_{4} b_{3} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} \\ & \quad + 12a_{1} ^{3} \zeta _{v} \eta ^{2} \mu ^{2} + 72a_{1} ^{2} a_{3} \zeta _{v} \eta ^{2} \mu ^{2} - 36a_{1} a_{2} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{1} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} - 72a_{1} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} \\ & \quad + 12a_{1} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} + 24a_{1} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 72a_{2} ^{2} a_{3} \zeta _{v} \eta ^{2} \mu ^{2} + 24a_{2} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} \\ & \quad - 24a_{2} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} - 72a_{2} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} + 36a_{3} ^{3} \zeta _{v} \eta ^{2} \mu ^{2} + 36a_{3} a_{4} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} - 36a_{3} b_{3} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} + 36a_{3} b_{4} ^{2} \zeta _{v} \eta ^{2} \mu ^{2} \\ & \quad - 72a_{4} b_{3} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{1} ^{3} \zeta _{v} \eta ^{2} \mu + 72a_{1} ^{2} a_{3} \zeta _{v} \eta ^{2} \mu - 36a_{1} a_{2} ^{2} \zeta _{v} \eta ^{2} \mu - 12a_{1} b_{1} ^{2} \zeta _{v} \eta ^{2} \mu - 72a_{1} b_{1} b_{3} \zeta _{v} \eta ^{2} \mu \\ & \quad + 12a_{1} b_{2} ^{2} \zeta _{v} \eta ^{2} \mu + 24a_{1} b_{2} b_{4} \zeta _{v} \eta ^{2} \mu + 72a_{2} ^{2} a_{3} \zeta _{v} \eta ^{2} \mu + 24a_{2} b_{1} b_{2} \zeta _{v} \eta ^{2} \mu - 24a_{2} b_{1} b_{4} \zeta _{v} \eta ^{2} \mu - 72a_{2} b_{2} b_{3} \zeta _{v} \eta ^{2} \mu \\ & \quad + 36a_{3} ^{3} \zeta _{v} \eta ^{2} \mu + 36a_{3} a_{4} ^{2} \zeta _{v} \eta ^{2} \mu - 36a_{3} b_{3} ^{2} \zeta _{v} \eta ^{2} \mu + 36a_{3} b_{4} ^{2} \zeta _{v} \eta ^{2} \mu + 96a_{3} \zeta _{h} \eta ^{2} \mu ^{3} - 72a_{4} b_{3} b_{4} \zeta _{v} \eta ^{2} \mu \\ & \quad + 4a_{1} ^{3} \zeta _{v} \eta ^{2} + 24a_{1} ^{2} a_{3} \zeta _{v} \eta ^{2} - 12a_{1} a_{2} ^{2} \zeta _{v} \eta ^{2} - 4a_{1} b_{1} ^{2} \zeta _{v} \eta ^{2} - 24a_{1} b_{1} b_{3} \zeta _{v} \eta ^{2} + 4a_{1} b_{2} ^{2} \zeta _{v} \eta ^{2} + 8a_{1} b_{2} b_{4} \zeta _{v} \eta ^{2} \\ & \quad + 24a_{2} ^{2} a_{3} \zeta _{v} \eta ^{2} + 8a_{2} b_{1} b_{2} \zeta _{v} \eta ^{2} - 8a_{2} b_{1} b_{4} \zeta _{v} \eta ^{2} - 24a_{2} b_{2} b_{3} \zeta _{v} \eta ^{2} + 12a_{3} ^{3} \zeta _{v} \eta ^{2} + 12a_{3} a_{4} ^{2} \zeta _{v} \eta ^{2} - 12a_{3} b_{3} ^{2} \zeta _{v} \eta ^{2} \\ & \quad + 12a_{3} b_{4} ^{2} \zeta _{v} \eta ^{2} + 288a_{3} \zeta _{h} \eta ^{2} \mu ^{2} - 24a_{4} b_{3} b_{4} \zeta _{v} \eta ^{2} - 16a_{1} b_{1} ^{2} \zeta _{h} \mu - 48a_{1} b_{1} b_{3} \zeta _{h} \mu + 16a_{1} b_{2} ^{2} \zeta _{h} \mu - 16a_{1} b_{2} b_{4} \zeta _{h} \mu \\ & \quad + 32a_{2} b_{1} b_{2} \zeta _{h} \mu + 16a_{2} b_{1} b_{4} \zeta _{h} \mu - 48a_{2} b_{2} b_{3} \zeta _{h} \mu - 48a_{3} b_{1} ^{2} \zeta _{h} \mu - 48a_{3} b_{2} ^{2} \zeta _{h} \mu - 48a_{3} b_{3} ^{2} \zeta _{h} \mu - 48a_{3} b_{4} ^{2} \zeta _{h} \mu \\ & \quad + 288a_{3} \zeta _{h} \eta ^{2} \mu - 16a_{1} b_{1} ^{2} \zeta _{h} - 48a_{1} b_{1} b_{3} \zeta _{h} + 16a_{1} b_{2} ^{2} \zeta _{h} - 16a_{1} b_{2} b_{4} \zeta _{h} + 32a_{2} b_{1} b_{2} \zeta _{h} + 16a_{2} b_{1} b_{4} \zeta _{h} \\ & \quad - \left. {48a_{2} b_{2} b_{3} \zeta _{h} - 48a_{3} b_{1} ^{2} \zeta _{h} - 48a_{3} b_{2} ^{2} \zeta _{h} - 48a_{3} b_{3} ^{2} \zeta _{h} - 48a_{3} b_{4} ^{2} \zeta _{h} + 96a_{3} \zeta _{h} \eta ^{2} } \right)\Omega + \left( { - 3a_{1} ^{2} a_{2} \eta ^{2} \mu ^{3} } \right. \\ & \quad - 6a_{1} ^{2} a_{4} \eta ^{2} \mu ^{3} + 4a_{1} b_{1} b_{2} \eta ^{2} \mu ^{3} + 8a_{1} b_{1} b_{4} \eta ^{2} \mu ^{3} + a_{4} ^{3} \eta \mu ^{3} - 6a_{2} ^{2} a_{4} \eta ^{2} \mu ^{3} + 2a_{2} b_{1} ^{2} \eta ^{2} \mu ^{3} - 2a_{2} b_{2} ^{2} \eta ^{2} \mu ^{3} \\ & \quad + 8a_{2} b_{2} b_{4} \eta ^{2} \mu ^{3} - 3a_{3} ^{2} a_{4} \eta ^{2} \mu ^{3} + 4a_{3} b_{3} b_{4} \eta ^{2} \mu ^{3} - 3a_{4} ^{3} \eta ^{2} \mu ^{3} + 4a_{4} b_{1} ^{2} \eta ^{2} \mu ^{3} + 4a_{4} b_{2} ^{2} \eta ^{2} \mu ^{3} + 2a_{4} b_{3} ^{2} \eta ^{2} \mu ^{3} \\ & \quad + 6a_{4} b_{4} ^{2} \eta ^{2} \mu ^{3} - 9a_{1} ^{2} a_{2} \eta ^{2} \mu ^{2} - 18a_{1} ^{2} a_{4} \eta ^{2} \mu ^{2} + 12a_{1} b_{1} b_{2} \eta ^{2} \mu ^{2} + 24a_{1} b_{1} b_{4} \eta ^{2} \mu ^{2} + 3a_{2} ^{3} \eta ^{2} \mu ^{2} - 18a_{2} ^{2} a_{4} \eta ^{2} \mu ^{2} \\ & \quad + 6a_{2} b_{1} ^{2} \eta ^{2} \mu ^{2} - 6a_{2} b_{2} ^{2} \eta ^{2} \mu ^{2} + 24a_{2} b_{2} b_{4} \eta ^{2} \mu ^{2} - 9a_{3} ^{2} a_{4} \eta ^{2} \mu ^{2} + 12a_{3} b_{3} b_{4} \eta ^{2} \mu ^{2} - 9a_{4} ^{3} \eta ^{2} \mu ^{2} + 12a_{4} b_{1} ^{2} \eta ^{2} \mu ^{2} \\ & \quad + 12a_{4} b_{2} ^{2} \eta ^{2} \mu ^{2} + 6a_{4} b_{3} ^{2} \eta ^{2} \mu ^{2} + 18a_{4} b_{4} ^{2} \eta ^{2} \mu ^{2} - 16a_{4} \eta ^{2} \gamma \mu ^{3} - 9a_{1} ^{2} a_{2} \eta ^{2} \mu - 18a_{1} ^{2} a_{4} \eta ^{2} \mu + 12a_{1} b_{1} b_{2} \eta ^{2} \mu \\ & \quad + 24a_{1} b_{1} b_{4} \eta ^{2} \mu + 3a_{2} ^{3} \eta ^{2} \mu - 18a_{2} ^{2} a_{4} \eta ^{2} \mu + 6a_{2} b_{1} ^{2} \eta ^{2} \mu - 6a_{2} b_{2} ^{2} \eta ^{2} \mu + 24a_{2} b_{2} b_{4} \eta ^{2} \mu - 9a_{3} ^{2} a_{4} \eta ^{2} \mu \\ & \quad + 12a_{3} b_{3} b_{4} \eta ^{2} \mu - 9a_{4} ^{3} \eta ^{2} \mu + 12a_{4} b_{1} ^{2} \eta ^{2} \mu + 12a_{4} b_{2} ^{2} \eta ^{2} \mu + 6a_{4} b_{3} ^{2} \eta ^{2} \mu + 18a_{4} b_{4} ^{2} \eta ^{2} \mu - 48a_{4} \eta ^{2} r\mu ^{2} - 3a_{1} ^{2} a_{2} \eta ^{2} \\ & \quad - 6a_{1} ^{2} a_{4} \eta ^{2} + 4a_{1} b_{1} b_{2} \eta ^{2} + 8a_{1} b_{1} b_{4} \eta ^{2} + \eta ^{2} a_{2} ^{3} - 6a_{2} ^{2} a_{4} \eta ^{2} + 2b_{1} ^{2} \eta ^{2} a_{2} - 2b_{2} ^{2} \eta ^{2} a_{2} + 8a_{2} b_{2} b_{4} \eta ^{2} - 3a_{3} ^{2} a_{4} \eta ^{2} \\ & \quad + 4a_{3} b_{3} b_{4} \eta ^{2} - 3a_{4} ^{3} \eta ^{2} + 4a_{4} b_{1} ^{2} \eta ^{2} + 4a_{4} b_{2} ^{2} \eta ^{2} + 2a_{4} b_{3} ^{2} \eta ^{2} + 6a_{4} b_{4} ^{2} \eta ^{2} - 48a_{4} \eta ^{2} \gamma \mu + 8a_{1} b_{1} b_{2} \gamma + 16a_{1} b_{1} b_{4} \gamma \\ & \quad + \left. {\left. {4a_{2} b_{1} ^{2} \gamma - 4a_{2} b_{2} ^{2} \gamma + 16a_{2} b_{2} b_{4} \gamma + 8a_{3} b_{3} b_{4} \gamma + 8a_{4} b_{1} ^{2} \gamma + 8a_{4} b_{2} ^{2} \gamma + 4a_{4} b_{3} ^{2} \gamma + 12a_{4} b_{4} ^{2} \gamma - 16a_{4} \eta ^{2} \gamma } \right)} \right), \\ \end{aligned}$$

(A10)

$$\begin{aligned} & F_{5} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right) = \frac{1}{{4\eta ^{2} (\mu + 1)^{3} }}\left( {\left( {3a_{1} ^{2} b_{1} \delta _{v} \eta ^{2} \mu ^{3} + 5a_{1} ^{2} b_{3} \delta _{v} \eta ^{2} \mu ^{3} + 2a_{1} a_{2} b_{2} \delta _{v} \eta ^{2} \mu ^{3} + 10a_{1} a_{2} b_{4} \delta _{v} \eta ^{2} \mu ^{3} } \right.} \right. \\ & \quad + 2a_{1} a_{3} b_{1} \delta _{v} \eta ^{2} \mu ^{3} + 20a_{1} a_{3} b_{3} \delta _{v} \eta ^{2} \mu ^{3} + 2a_{1} a_{4} b_{2} \delta _{v} \eta ^{2} \mu ^{3} + 20a_{1} a_{4} b_{4} \delta _{v} \eta ^{2} \mu ^{3} + a_{2} ^{2} b_{1} \delta _{v} \eta ^{2} \mu ^{3} - 5a_{2} ^{2} b_{3} \delta _{v} \eta ^{2} \mu ^{3} \\ & \quad - 2a_{2} a_{3} b_{2} \delta _{v} \eta ^{2} \mu ^{3} + 2a_{2} a_{4} b_{1} \delta _{v} \eta ^{2} \mu ^{3} + 2a_{3} ^{2} b_{1} \delta _{v} \eta ^{2} \mu ^{3} + 2a_{4} ^{2} b_{1} \delta _{v} \eta ^{2} \mu ^{3} + 9a_{1} ^{2} b_{1} \delta _{v} \eta ^{2} \mu ^{2} + 15a_{1} ^{2} b_{3} \delta _{v} \eta ^{2} \mu ^{2} \\ & \quad + 6a_{1} a_{2} b_{2} \delta _{v} \eta ^{2} \mu ^{2} + 30\eta ^{2} a_{1} a_{2} b_{4} \delta _{v} \mu ^{2} + 6a_{1} a_{3} b_{1} \delta _{v} \eta ^{2} \mu ^{2} + 60\eta ^{2} a_{1} a_{3} b_{3} \delta _{v} \mu ^{2} + 6\eta ^{2} a_{1} a_{4} b_{2} \delta _{v} \mu ^{2} + 60\eta ^{2} a_{1} a_{4} b_{4} \delta _{v} \mu ^{2} \\ & \quad + 3a_{2} ^{2} b_{1} \delta _{v} \eta ^{2} \mu ^{2} - 15a_{2} ^{2} b_{3} \delta _{v} \eta ^{2} \mu ^{2} - 6a_{2} a_{3} b_{2} \delta _{v} \eta ^{2} \mu ^{2} + 6\eta ^{2} a_{2} a_{4} b_{1} \delta _{v} \mu ^{2} + 6\eta ^{2} a_{3} ^{2} b_{1} \delta _{v} \mu ^{2} + 6\eta ^{2} a_{4} ^{2} b_{1} \delta _{v} \mu ^{2} \\ & \quad + 9a_{1} ^{2} b_{1} \delta _{v} \eta ^{2} \mu + 15a_{1} ^{2} b_{3} \delta _{v} \eta ^{2} \mu + 6a_{1} a_{2} b_{2} \delta _{v} \eta ^{2} \mu + 30\eta ^{2} a_{1} a_{2} b_{4} \delta _{v} \mu + 6a_{1} a_{3} b_{1} \delta _{v} \eta ^{2} \mu + 60\eta ^{2} a_{1} a_{3} b_{3} \delta _{v} \mu \\ & \quad + 6\eta ^{2} a_{1} a_{4} b_{2} \delta _{v} \mu + 60\eta ^{2} a_{1} a_{4} b_{4} \delta _{v} \mu + 3a_{2} ^{2} b_{1} \delta _{v} \eta ^{2} \mu - 15a_{2} ^{2} b_{3} \delta _{v} \eta ^{2} \mu - 6a_{2} a_{3} b_{2} \delta _{v} \eta ^{2} \mu + 6\eta ^{2} a_{2} a_{4} b_{1} \delta _{v} \mu \\ & \quad + 6\eta ^{2} a_{3} ^{2} b_{1} \delta _{v} \mu + 6\eta ^{2} a_{4} ^{2} b_{1} \delta _{v} \mu - 4\eta ^{2} b_{1} \delta _{v} \mu ^{3} + 3a_{1} ^{2} b_{1} \delta _{v} \eta ^{2} + 5a_{1} ^{2} b_{3} \delta _{v} \eta ^{2} + 2a_{1} a_{2} b_{2} \delta _{v} \eta ^{2} + 10\eta ^{2} a_{1} a_{2} b_{4} \delta _{v} \\ & \quad + 2a_{1} a_{3} b_{1} \delta _{v} \eta ^{2} + 20\eta ^{2} a_{1} a_{3} b_{3} \delta _{v} + 2\eta ^{2} a_{1} a_{4} b_{2} \delta _{v} + 20\eta ^{2} a_{1} a_{4} b_{4} \delta _{v} + a_{2} ^{2} b_{1} \delta _{v} \eta ^{2} - 5a_{2} ^{2} b_{3} \delta _{v} \eta ^{2} - 2a_{2} a_{3} b_{2} \delta _{v} \eta ^{2} \\ & \quad + 2\eta ^{2} b_{1} \delta _{v} a_{2} a_{4} + 2\eta ^{2} b_{1} \delta _{v} a_{3} ^{2} + 2\eta ^{2} b_{1} \delta _{v} a_{4} ^{2} - 12\eta ^{2} b_{1} \delta _{v} \mu ^{2} - 4b_{1} \eta ^{2} \mu ^{3} - 4\eta ^{2} \mu ^{3} Y_{{bm}} + 6a_{1} ^{2} b_{1} \delta _{h} \mu + 2a_{1} ^{2} b_{3} \delta _{h} \mu \\ & \quad + 4a_{1} a_{2} b_{2} \delta _{h} \mu + 4\mu \delta _{h} a_{1} b_{4} a_{2} + 20a_{1} a_{3} b_{1} \delta _{h} \mu + 40\mu \delta _{h} b_{3} a_{3} a_{1} + 20\mu \delta _{h} b_{2} a_{1} a_{4} + 40\mu \delta _{h} a_{1} b_{4} a_{4} + 2a_{2} ^{2} b_{1} \delta _{h} \mu \\ & \quad - 2a_{2} ^{2} b_{3} \delta _{h} \mu - 20a_{2} a_{3} b_{2} \delta _{h} \mu + 20\mu \delta _{h} a_{2} b_{1} a_{4} + 36\mu \delta _{h} a_{3} ^{2} b_{1} + 36\mu \delta _{h} b_{1} a_{4} ^{2} - 4b_{1} ^{3} \delta _{h} \mu - 12b_{1} ^{2} b_{3} \delta _{h} \mu \\ & \quad - 4b_{1} b_{2} ^{2} \delta _{h} \mu - 24b_{1} b_{2} b_{4} \delta _{h} \mu - 40b_{1} b_{3} ^{2} \delta _{h} \mu - 40b_{1} b_{4} ^{2} \delta _{h} \mu - 12b_{1} \delta _{v} \eta ^{2} \mu - 12b_{1} \eta ^{2} \mu ^{2} + 12b_{2} ^{2} b_{3} \delta _{h} \mu \\ & \quad - 12\eta ^{2} \mu ^{2} Y_{{bm}} + 6a_{1} ^{2} b_{1} \delta _{h} + 2a_{1} ^{2} b_{3} \delta _{h} + 4a_{1} a_{2} b_{2} \delta _{h} + 4a_{1} a_{2} b_{4} \delta _{h} + 20a_{1} a_{3} b_{1} \delta _{h} + 40a_{1} a_{3} b_{3} \delta _{h} + 20a_{1} a_{4} b_{2} \delta _{h} \\ & \quad + 40a_{1} a_{4} b_{4} \delta _{h} + 2a_{2} ^{2} b_{1} \delta _{h} - 2a_{2} ^{2} b_{3} \delta _{h} - 20a_{2} a_{3} b_{2} \delta _{h} + 20a_{2} a_{4} b_{1} \delta _{h} + 36a_{3} ^{2} b_{1} \delta _{h} + 36a_{4} ^{2} b_{1} \delta _{h} - 4b_{1} ^{3} \delta _{h} \\ & \quad - 12b_{1} ^{2} b_{3} \delta _{h} - 4b_{1} b_{2} ^{2} \delta _{h} - 12b_{1} ^{2} b_{3} \delta _{h} - 4b_{1} b_{2} ^{2} \delta _{h} - 24b_{1} b_{2} b_{4} \delta _{h} - 40b_{1} b_{3} ^{2} \delta _{h} - 40b_{1} b_{4} ^{2} \delta _{h} - 4b_{1} \delta _{v} \eta ^{2} \\ & \quad - \left. {12b_{1} \eta ^{2} \mu + 12b_{2} ^{2} b_{3} \delta _{h} - 12\eta ^{2} \mu Y_{{bm}} - 4b_{1} n^{2} - 4\eta ^{2} Y_{{bm}} } \right)\Omega ^{2} + \left( { - 4a_{1} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{1} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} } \right. \\ & \quad + 8a_{1} a_{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} - 12a_{1} a_{3} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} + 12a_{1} a_{4} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{2} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{2} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{2} a_{3} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} \\ & \quad - 4a_{2} a_{4} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{3} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{4} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} - 12a_{1} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{1} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 24a_{1} a_{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} \\ & \quad - 36a_{1} a_{3} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 36a_{1} a_{4} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{2} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{2} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{2} a_{3} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} \\ & \quad - 12a_{2} a_{4} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{3} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{4} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{1} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu - 12a_{1} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu + 24a_{1} a_{2} b_{3} \zeta _{v} \eta ^{2} \mu \\ & \quad - 36a_{1} a_{3} b_{4} \zeta _{v} \eta ^{2} \mu + 36a_{1} a_{4} b_{3} \zeta _{v} \eta ^{2} \mu - 12a_{2} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu + 12a_{2} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu - 12a_{2} a_{3} b_{3} \zeta _{v} \eta ^{2} \mu - 12a_{2} a_{4} b_{4} \zeta _{v} \eta ^{2} \mu \\ & \quad - 12a_{3} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu - 12a_{4} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu + 8b_{2} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{1} ^{2} b_{2} \zeta _{v} \eta ^{2} - 4a_{1} ^{2} b_{4} \zeta _{v} \eta ^{2} + 8a_{1} a_{2} b_{3} \zeta _{v} \eta ^{2} - 12a_{1} a_{3} b_{4} \zeta _{v} \eta ^{2} \\ & \quad + 12a_{1} a_{4} b_{3} \zeta _{v} \eta ^{2} - 4a_{2} ^{2} b_{2} \zeta _{v} \eta ^{2} + 4a_{2} ^{2} b_{4} \zeta _{v} \eta ^{2} - 4a_{2} a_{3} b_{3} \zeta _{v} \eta ^{2} - 4a_{2} a_{4} b_{4} \zeta _{v} \eta ^{2} - 4a_{3} ^{2} b_{2} \zeta _{v} \eta ^{2} - 4a_{4} ^{2} b_{2} \zeta _{v} \eta ^{2} \\ & \quad + 24b_{2} \zeta _{v} \eta ^{2} \mu ^{2} + 4a_{1} ^{2} b_{2} \zeta _{h} \mu + 4a_{1} ^{2} b_{4} \zeta _{h} \mu - 8a_{1} a_{2} b_{1} \zeta _{h} \mu - 8a_{1} a_{2} b_{3} \zeta _{h} \mu + 8a_{1} a_{3} b_{2} \zeta _{h} \mu + 24a_{1} a_{3} b_{4} \zeta _{h} \mu \\ & \quad - 8a_{1} a_{4} b_{1} \zeta _{h} \mu - 24a_{1} a_{4} b_{3} \zeta _{h} \mu - 4a_{2} ^{2} b_{2} \zeta _{h} \mu - 4a_{2} ^{2} b_{4} \zeta _{h} \mu + 8a_{2} a_{3} b_{1} \zeta _{h} \mu - 8a_{2} a_{3} b_{3} \zeta _{h} \mu + 8a_{2} a_{4} b_{2} \zeta _{h} \mu \\ & \quad - 8a_{2} a_{4} b_{4} \zeta _{h} \mu + 4b_{1} ^{2} b_{2} \zeta _{h} \mu + 4b_{1} ^{2} b_{4} \zeta _{h} \mu - 8b_{1} b_{2} b_{3} \zeta _{h} \mu + 4b_{2} ^{3} \zeta _{h} \mu - 4b_{2} ^{2} b_{4} \zeta _{h} \mu + 8b_{2} b_{3} ^{2} \zeta _{h} \mu + 8b_{2} b_{4} ^{2} \zeta _{h} \mu \\ & \quad + 24b_{2} \zeta _{v} \eta ^{2} \mu + 4a_{1} ^{2} b_{2} \zeta _{h} + 4a_{1} ^{2} b_{4} \zeta _{h} - 8a_{1} a_{2} b_{1} \zeta _{h} - 8a_{1} a_{2} b_{3} e\zeta _{h} + 8a_{1} ab_{2} \zeta _{h} + 24a_{1} a_{3} b_{4} \zeta _{h} - 8a_{1} a_{4} b_{1} \zeta _{h} \\ & \quad - 24a_{1} a_{4} b_{3} \zeta _{h} - 4a_{2} ^{2} b_{2} \zeta _{h} - 4a_{2} ^{2} b_{4} \zeta _{h} + 8a_{2} a_{3} b_{1} \zeta _{h} - 8a_{2} a_{3} b_{3} \zeta _{h} + 8a_{2} a_{4} b_{2} \zeta _{h} - 8a_{2} a_{4} b_{4} \zeta _{h} + 4b_{1} ^{2} b_{2} \zeta _{h} \\ & \quad + \left. {4b_{1} ^{2} b_{4} \zeta _{h} - 8b_{1} b_{2} b_{3} \zeta _{h} + 4b_{2} ^{3} \zeta _{h} - 4b_{2} ^{2} b_{4} \zeta _{h} + 8b_{2} b_{3} ^{2} \zeta _{h} + 8b_{2} b_{4} ^{2} \zeta _{h} + 8b_{2} \zeta _{v} \eta ^{2} } \right)\Omega + \left( { - 3a_{1} ^{2} b_{1} \eta ^{2} \mu ^{3} } \right. \\ & \quad - a_{1} ^{2} b_{3} \eta ^{2} \mu ^{3} - 2a_{1} a_{2} b_{2} \eta ^{2} \mu ^{3} - 2a_{1} a_{2} b_{4} \eta ^{2} \mu ^{3} - 2a_{1} a_{3} b_{1} \eta ^{2} \mu ^{3} - 4a_{1} a_{3} b_{3} \eta ^{2} \mu ^{3} - 2a_{1} a4b_{2} \eta ^{2} \mu ^{3} - 4a_{1} a_{4} b_{4} \eta ^{2} \mu ^{3} \\ & \quad - a_{2} ^{2} b_{1} \eta ^{2} \mu ^{3} + a_{2} ^{2} b_{3} \eta ^{2} \mu ^{3} + 2a_{2} a_{3} b_{2} \eta ^{2} \mu ^{3} - 2a_{2} a_{4} b_{1} \eta ^{2} \mu ^{3} - 2a_{3} ^{2} b_{1} \eta ^{2} \mu ^{3} - 2a_{4} ^{2} b_{1} \eta ^{2} \mu ^{3} - 9a_{1} ^{2} b_{1} \eta ^{2} \mu ^{2} \\ & \quad - 3a_{1} ^{2} b_{3} \eta ^{2} \mu ^{2} - 6a_{1} a_{2} b_{2} \eta ^{2} \mu ^{2} - 6a_{1} a_{2} b_{4} \eta ^{2} \mu ^{2} - 6a_{1} a_{3} b_{1} \eta ^{2} \mu ^{2} - 12a_{1} a_{3} b_{3} \eta ^{2} \mu ^{2} - 6a_{1} a_{4} b_{2} \eta ^{2} \mu ^{2} \\ & \quad - 12a_{1} a_{4} b_{4} \eta ^{2} \mu ^{2} - 3a_{2} ^{2} b_{1} \eta ^{2} \mu ^{2} + 3a_{2} ^{2} b_{3} \eta ^{2} \mu ^{2} + 6a_{2} a_{3} b_{2} \eta ^{2} \mu ^{2} - 6a_{2} a_{4} b_{1} \eta ^{2} \mu ^{2} - 6a_{3} ^{2} b_{1} \eta ^{2} \mu ^{2} - 6a_{4} ^{2} b_{1} \eta ^{2} \mu ^{2} \\ & \quad + 8b_{1} \eta ^{2} \gamma \mu ^{3} - 9a_{1} ^{2} b_{1} \eta ^{2} \mu - 3a_{1} ^{2} b_{3} \eta ^{2} \mu - 6a_{1} a_{2} b_{2} \eta ^{2} \mu - 6a_{1} a_{2} b_{4} \eta ^{2} \mu - 6a_{1} a_{3} b_{1} \eta ^{2} \mu - 12a_{1} a_{3} b_{3} \eta ^{2} \mu \\ & \quad - 6a_{1} a_{4} b_{2} \eta ^{2} \mu - 12a_{1} a_{4} b_{4} \eta ^{2} \mu - 3a_{2} ^{2} b_{1} \eta ^{2} \mu + 3a_{2} ^{2} b_{3} \eta ^{2} \mu + 6a_{2} a_{3} b_{2} \eta ^{2} \mu - 6a_{2} a_{4} b_{1} \eta ^{2} \mu - 6a_{3} ^{2} b_{1} \eta ^{2} \mu \\ & \quad - 6a_{4} ^{2} b_{1} \eta ^{2} \mu + 16b_{1} \eta ^{2} \gamma \mu ^{2} + 4b_{1} \eta ^{2} \mu ^{3} - 3a_{1} ^{2} b_{1} \eta ^{2} - a_{1} ^{2} b_{3} \eta ^{2} - 2a_{1} a_{2} b_{2} \eta ^{2} - 2a_{1} a_{2} b_{4} \eta ^{2} - 2a_{1} a_{3} b_{1} \eta ^{2} \\ & \quad - 4a_{1} a_{3} b_{3} \eta ^{2} - 2a_{1} a_{4} b_{2} \eta ^{2} - 4a_{1} a_{4} b_{4} \eta ^{2} - a_{2} ^{2} b_{1} \eta ^{2} + a_{2} ^{2} b_{3} \eta ^{2} + 2a_{2} a_{3} b_{2} \eta ^{2} - 2a_{2} a_{4} b_{1} \eta ^{2} - 2a_{3} ^{2} b_{1} \eta ^{2} \\ & \quad - 2a_{4} ^{2} b_{1} \eta ^{2} + 8b_{1} \eta ^{2} \gamma \mu + 12b_{1} \eta ^{2} \mu ^{2} - 6a_{1} ^{2} b_{1} \gamma - 2a_{1} ^{2} b_{3} \gamma - 4a_{1} a_{2} b_{2} \gamma - 4a_{1} a_{2} b_{4} \gamma - 4a_{1} a_{3} b_{1} \gamma - 8a_{1} a_{3} b_{3} \gamma \\ & \quad - 4a_{1} a_{4} b_{2} \gamma - 8a_{1} a_{4} b_{4} \gamma - 2a_{2} ^{2} b_{1} \gamma + 2a_{2} ^{2} b_{3} \gamma + 4a_{2} a_{3} b_{2} \gamma - 4a_{2} a_{4} b_{1} \gamma - 4a_{3} ^{2} b_{1} \gamma - 4a_{4} ^{2} b_{1} \gamma + 3b_{1} ^{3} \gamma + 3b_{1} ^{2} b_{3} r \\ & \quad + \left. {\left. {3b_{1} b_{2} ^{2} \gamma + 6b_{1} b_{2} b_{4} \gamma + 6b_{1} b_{3} ^{2} \gamma + 6b_{1} b_{4} ^{2} \gamma + 12b_{1} \eta ^{2} \mu - 3b_{2} ^{2} b_{3} \gamma + 4b_{1} \eta ^{2} } \right)} \right), \\ \end{aligned}$$

(A11)

$$\begin{aligned} & F_{6} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right) = \frac{1}{{4\eta ^{2} (\mu + 1)^{3} }}\left( {\left( {a_{1} ^{2} b_{2} \delta _{v} \eta ^{2} \mu ^{3} + 5a_{1} ^{2} b_{4} \delta _{v} \eta ^{2} \mu ^{3} + 2a_{1} a_{2} b_{1} \delta _{v} \eta ^{2} \mu ^{3} - 10a_{1} a_{2} b_{3} \delta _{v} \eta ^{2} \mu ^{3} } \right.} \right. \\ & \quad - 2a_{1} a_{3} b_{2} \delta _{v} \eta ^{2} \mu ^{3} + 2a_{1} a_{4} b_{1} \delta _{v} \eta ^{2} \mu ^{3} + 3a_{2} ^{2} b_{2} \delta _{v} \eta ^{2} \mu ^{3} - 5a_{2} ^{2} b_{4} \delta _{v} \eta ^{2} \mu ^{3} - 2a_{2} a_{3} b_{1} \delta _{v} \eta ^{2} \mu ^{3} + 20a_{2} a_{3} b_{3} \delta _{v} \eta ^{2} \mu ^{3} \\ & \quad - 2a_{2} a_{4} b_{2} \delta _{v} \eta ^{2} \mu ^{3} + 20a_{2} a_{4} b_{4} \delta _{v} \eta ^{2} \mu ^{3} + 2a_{3} ^{2} b_{2} \delta _{v} \eta ^{2} \mu ^{3} + 2a_{4} ^{2} b_{2} \delta _{v} \eta ^{2} \mu ^{3} + 3a_{1} ^{2} b_{2} \delta _{v} \eta ^{2} \mu ^{2} + 15a_{1} ^{2} b_{4} \delta _{v} \eta ^{2} \mu ^{2} \\ & \quad + 6a_{1} a_{2} b_{1} \delta _{v} \eta ^{2} \mu ^{2} - 30a_{1} a_{2} b_{3} \delta _{v} \eta ^{2} \mu ^{2} - 6a_{1} a_{3} b_{2} \delta _{v} \eta ^{2} \mu ^{2} + 6a_{1} a_{4} b_{1} \delta _{v} \eta ^{2} \mu ^{2} + 9a_{2} ^{2} b_{2} \delta _{v} \eta ^{2} \mu ^{2} - 15a_{2} ^{2} b_{4} \delta _{v} \eta ^{2} \mu ^{2} \\ & \quad - 6a_{2} a_{3} b_{1} \delta _{v} \eta ^{2} \mu ^{2} + 60a_{2} a_{3} b_{3} \delta _{v} \eta ^{2} \mu ^{2} - 6a_{2} a_{4} b_{2} \delta _{v} \eta ^{2} \mu ^{2} + 60a_{2} a_{4} b_{4} \delta _{v} \eta ^{2} \mu ^{2} + 6a_{3} ^{2} b_{2} \delta _{v} \eta ^{2} \mu ^{2} + 6a_{4} ^{2} b_{2} \delta _{v} \eta ^{2} \mu ^{2} \\ & \quad + 3a_{1} ^{2} b_{2} \delta _{v} \eta ^{2} \mu + 15a_{1} ^{2} b_{4} \delta _{v} \eta ^{2} \mu + 6a_{1} a_{2} b_{1} \delta _{v} \eta ^{2} \mu - 30a_{1} a_{2} b_{3} \delta _{v} \eta ^{2} \mu - 6a_{1} a_{3} b_{2} \delta _{v} \eta ^{2} \mu + 6a_{1} a_{4} b_{1} \delta _{v} \eta ^{2} \mu \\ & \quad + 9a_{2} ^{2} b_{2} \delta _{v} \eta ^{2} \mu - 15a_{2} ^{2} b_{4} \delta _{v} \eta ^{2} \mu - 6a_{2} a_{3} b_{1} \delta _{v} \eta ^{2} \mu + 60a_{2} a_{3} b_{3} \delta _{v} \eta ^{2} \mu - 6a_{2} a_{4} b_{2} \delta _{v} \eta ^{2} \mu + 60a_{2} a_{4} b_{4} \delta _{v} \eta ^{2} \mu \\ & \quad + 6a_{3} ^{2} b_{2} \delta _{v} \eta ^{2} \mu + 6a_{4} ^{2} b_{2} \delta _{v} \eta ^{2} \mu - 4b_{2} \delta _{v} \eta ^{2} \mu ^{3} + a_{1} ^{2} b_{2} \delta _{v} \eta ^{2} + 5a_{1} ^{2} b_{4} \delta _{v} \eta ^{2} + 2a_{1} a_{2} b_{1} \delta _{v} \eta ^{2} - 10a_{1} a_{2} b_{3} \delta _{v} \eta ^{2} \\ & \quad - 2a_{1} a_{3} b_{2} \delta _{v} \eta ^{2} + 2a_{1} a_{4} b_{1} \delta _{v} \eta ^{2} + 3a_{2} ^{2} b_{2} \delta _{v} \eta ^{2} - 5a_{2} ^{2} b_{4} \delta _{v} \eta ^{2} - 2a_{2} a_{3} b_{1} \delta _{v} \eta ^{2} + 20a_{2} a_{3} b_{3} \delta _{v} \eta ^{2} - 2a_{2} a_{4} b_{2} \delta _{v} \eta ^{2} \\ & \quad + 20a_{2} a_{4} b_{4} \delta _{v} \eta ^{2} + 2a_{3} ^{2} b_{2} \delta _{v} \eta ^{2} + 2a_{4} ^{2} b_{2} \delta _{v} \eta ^{2} - 12b_{2} \delta _{v} \eta ^{2} \mu ^{2} - 4b_{2} \eta ^{2} \mu ^{3} + 2a_{1} ^{2} b_{2} \delta _{h} \mu + 2a_{1} ^{2} b_{4} \delta _{h} \mu \\ & \quad + 4a_{1} a_{2} b_{1} \delta _{h} \mu - 4a_{1} a_{2} b_{3} \delta _{h} \mu - 20a_{1} a_{3} b_{2} \delta _{h} \mu + 20a_{1} a_{4} b_{1} \delta _{h} \mu + 6a_{2} ^{2} b_{2} \delta _{h} \mu - 2a_{2} ^{2} b_{4} \delta _{h} \mu - 20a_{2} a_{3} b_{1} \delta _{h} \mu \\ & \quad + 40a_{2} a_{3} b_{3} \delta _{h} \mu - 20a_{2} a_{4} b_{2} \delta _{h} \mu + 40a_{2} a_{4} b_{4} \delta _{h} \mu + 36a_{3} ^{2} b_{2} \delta _{h} \mu + 36a_{4} ^{2} b_{2} \delta _{h} \mu - 4b_{1} ^{2} b_{2} \delta _{h} \mu - 12b_{1} ^{2} b_{4} \delta _{h} \mu \\ & \quad + 24b_{1} b_{2} b_{3} \delta _{h} \mu - 4b_{2} ^{3} \delta _{h} \mu + 12b_{2} ^{2} b_{4} \delta _{h} \mu - 40b_{2} b_{3} ^{2} \delta _{h} \mu - 40b_{2} b_{4} ^{2} \delta _{h} \mu - 12b_{2} \delta _{v} \eta ^{2} \mu - 12b_{2} \eta ^{2} \mu ^{2} + 2\delta _{h} b_{2} a_{1} ^{2} \\ & \quad + 2\delta _{h} b_{4} a_{1} ^{2} + 4\delta _{h} a_{1} a_{2} b_{1} - 4\delta _{h} a_{1} a_{2} b_{3} - 20\delta _{h} b_{2} a_{1} a_{3} + 20\delta _{h} a_{1} a_{4} b_{1} + 6\delta _{h} b_{2} a_{2} ^{2} - 2\delta _{h} a_{2} ^{2} b_{4} - 20\delta _{h} a_{2} a_{3} b_{1} \\ & \quad + 40\delta _{h} a_{2} a_{3} b_{3} - 20\delta _{h} a_{2} a_{4} b_{2} + 40\delta _{h} a_{2} a_{4} b_{4} + 36\delta _{h} b_{2} a_{3} ^{2} + 36\delta _{h} b_{2} a_{4} ^{2} - 4\delta _{h} b_{2} b_{1} ^{2} - 12\delta _{h} b_{4} b_{1} ^{2} + 24\delta _{h} b_{2} b_{3} b_{1} \\ & \quad - \left. {4\delta _{h} b_{2} ^{3} + 12\delta _{h} b_{2} ^{2} b_{4} - 40\delta _{h} b_{2} b_{3} ^{2} - 40b_{2} b_{4} ^{2} \delta _{h} - 4b_{2} \delta _{v} \eta ^{2} - 12b_{2} \eta ^{2} \mu - 4b_{2} \eta ^{2} } \right)\Omega ^{2} + \left( {4a_{1} ^{2} b_{1} \zeta _{v} \eta ^{2} \mu ^{3} } \right. \\ & \quad + 4a_{1} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} + 8a_{1} a_{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{1} a_{3} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{1} a_{4} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{2} ^{2} b_{1} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{2} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} \\ & \quad - 12a_{2} a_{3} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} + 12a_{2} a_{4} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{3} ^{2} b_{1} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{4} ^{2} b_{1} \zeta _{v} \eta ^{2} \mu ^{3} + 12a_{1} ^{2} b_{1} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{1} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} \\ & \quad + 24a_{1} a_{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{1} a_{3} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{1} a_{4} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{2} ^{2} b_{1} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{2} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} \\ & \quad - 36a_{2} a_{3} b_{4} \zeta _{v} ^{2} \mu ^{2} + 36a_{2} a_{4} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{3} ^{2} b_{1} \zeta _{v} \eta ^{2} \mu ^{2} + 12a4^{2} b_{1} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{1} ^{2} b_{1} \zeta _{v} \eta ^{2} \mu \\ & \quad + 12a_{1} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu + 24a_{1} a_{2} b_{4} \zeta _{v} \eta ^{2} \mu + 12a_{1} a_{3} b_{3} \zeta _{v} \eta ^{2} \mu + 12a_{1} a_{4} b_{4} \zeta _{v} \eta ^{2} \mu + 12a2^{2} b_{1} \zeta _{v} \eta ^{2} \mu \\ & \quad - 12a_{2} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu - 36a_{2} a_{3} b_{4} \zeta _{v} \eta ^{2} \mu + 36a_{2} a_{4} b_{3} \zeta _{v} \eta ^{2} \mu + 12a_{3} ^{2} b_{1} \zeta _{v} \eta ^{2} \mu + 12a_{4} ^{2} b_{1} \zeta _{v} \eta ^{2} \mu - 8b_{1} \zeta _{v} \eta ^{2} \mu ^{3} \\ & \quad + 4a_{1} ^{2} b_{1} \zeta _{v} \eta ^{2} + 4a_{1} ^{2} b_{3} \zeta _{v} \eta ^{2} + 8a_{1} a_{2} b_{4} \zeta _{v} \eta ^{2} + 4a_{1} a_{3} b_{3} \zeta _{v} \eta ^{2} + 4a_{1} a_{4} b_{4} \zeta _{v} \eta ^{2} + 4a_{2} ^{2} b_{1} \zeta _{v} \eta ^{2} - 4a_{2} ^{2} b_{3} \zeta _{v} \eta ^{2} \\ & \quad - 12a_{2} a_{3} b_{4} \zeta _{v} \eta ^{2} + 12a_{2} a_{4} b_{3} \zeta _{v} \eta ^{2} + 4a_{3} ^{2} b_{1} \zeta _{v} \eta ^{2} + 4a_{4} ^{2} b_{1} \zeta _{v} \eta ^{2} - 24b_{1} \zeta _{v} \eta ^{2} \mu ^{2} + 4a_{1} ^{2} b_{1} \zeta _{h} \mu - 4a_{1} ^{2} b_{3} \zeta _{h} \mu \\ & \quad + 8a_{1} a_{2} b_{2} \zeta _{h} \mu - 8a_{1} a_{2} b_{4} \zeta _{h} \mu + 8a_{1} a_{3} b_{1} \zeta _{h} \mu + 8a_{1} a_{3} b_{3} \zeta _{h} \mu + 8a_{1} a_{4} b_{2} \zeta _{h} \mu + 8a_{1} a_{4} b_{4} \zeta _{h} \mu - 4a_{2} ^{2} b_{1} \zeta _{h} \mu \\ & \quad + 4a_{2} ^{2} b_{3} \zeta _{h} \mu - 8a_{2} a_{3} b_{2} \zeta _{h} \mu + 24a_{2} a_{3} b_{4} \zeta _{h} \mu + 8a_{2} a_{4} b_{1} \zeta _{h} \mu - 24a_{2} a_{4} b_{3} \zeta _{h} \mu - 4b_{1} ^{3} \zeta _{h} \mu - 4b_{1} ^{2} b_{3} \zeta _{h} \mu \\ & \quad - 4b_{1} b_{2} ^{2} \zeta _{h} \mu - 8b_{1} b_{2} b_{4} \zeta _{h} \mu - 8b_{1} b_{3} ^{2} \zeta _{h} \mu - 8b_{1} b_{4} ^{2} \zeta _{h} \mu - 24b_{1} \zeta _{v} \eta ^{2} \mu + 4b_{2} ^{2} b_{3} \zeta _{h} \mu + 4a_{1} ^{2} b_{1} \zeta _{h} - 4a_{1} ^{2} b_{3} \zeta _{h} \\ & \quad + 8a_{1} a_{2} b_{2} \zeta _{h} - 8a_{1} a_{2} b_{4} \zeta _{h} + 8a_{1} a_{3} b_{1} \zeta _{h} + 8a_{1} a_{3} b_{3} \zeta _{h} + 8a_{1} a_{4} b_{2} \zeta _{h} + 8a_{1} a_{4} b_{4} \zeta _{h} - 4a_{2} ^{2} b_{1} \zeta _{h} + 4a_{2} ^{2} b_{3} \zeta _{h} \\ & \quad - 8a_{2} a_{3} b_{2} \zeta _{h} + 24a_{2} a_{3} b_{4} \zeta _{h} + 8a_{2} a_{4} b_{1} \zeta _{h} - 24a_{2} a_{4} b_{3} \zeta _{h} - 4b_{1} ^{3} \zeta _{h} - 4b_{1} ^{2} b3\zeta _{h} - 4b_{1} b_{2} ^{2} \zeta _{h} - 8b_{1} b_{2} b_{4} \zeta _{h} \\ & \quad - \left. {8b_{1} b_{3} ^{2} \zeta _{h} - 8b_{1} b_{4} ^{2} \zeta _{h} - 8b_{1} \zeta _{v} \eta ^{2} + 4b_{2} ^{2} b_{3} \zeta _{h} } \right)\Omega + \left( { - a_{1} ^{2} b_{2} \eta ^{2} \mu ^{3} - a_{1} ^{2} b_{4} \eta ^{2} \mu ^{3} - 2a_{1} a_{2} b_{1} \eta ^{2} \mu ^{3} + 2a_{1} a_{2} b_{3} \eta ^{2} \mu ^{3} } \right. \\ & \quad + 2a_{1} a_{3} b_{2} \eta ^{2} \mu ^{3} - 2a_{1} a_{4} b_{1} \eta ^{2} \mu ^{3} - 3a_{2} ^{2} b_{2} \eta ^{2} \mu ^{3} + a_{2} ^{2} b_{4} \eta ^{2} \mu ^{3} + 2a_{2} a_{3} b_{1} \eta ^{2} \mu ^{3} - 4a_{2} a_{3} b_{3} \eta ^{2} \mu ^{3} + 2a_{2} a_{4} b_{2} \eta ^{2} \mu ^{3} \\ & \quad - 4a_{2} a_{4} b_{4} \eta ^{2} \mu ^{3} - 2a_{3} ^{2} b_{2} \eta ^{2} \mu ^{3} - 2a_{4} ^{2} b_{2} \eta ^{2} \mu ^{3} - 3a_{1} ^{2} b_{2} \eta ^{2} \mu ^{2} - 3a_{1} ^{2} b_{4} \eta ^{2} \mu ^{2} - 6a_{1} a_{2} b_{1} \eta ^{2} \mu ^{2} + 6a_{1} a_{2} b_{3} \eta ^{2} \mu ^{2} \\ & \quad + 6a_{1} a_{3} b_{2} \eta ^{2} \mu ^{2} - 6a_{1} a_{4} b_{1} \eta ^{2} \mu ^{2} - 9a_{2} ^{2} b_{2} \eta ^{2} \mu ^{2} + 3a_{2} ^{2} b_{4} \eta ^{2} \mu ^{2} + 6a_{2} a_{3} b_{1} \eta ^{2} \mu ^{2} - 12a_{2} a_{3} b_{3} \eta ^{2} \mu ^{2} + 6a_{2} a_{4} b_{2} \eta ^{2} \mu ^{2} \\ & \quad - 12a_{2} a_{4} b_{4} \eta ^{2} \mu ^{2} - 6a_{3} ^{2} b_{2} \eta ^{2} \mu ^{2} - 6a_{4} ^{2} b_{2} \eta ^{2} \mu ^{2} + 8b_{2} \eta ^{2} \gamma \mu ^{3} - 3a_{1} ^{2} b_{2} \eta ^{2} \mu - 3a_{1} ^{2} b_{4} \eta ^{2} \mu - 6a_{1} a_{2} b_{1} \eta ^{2} \mu \\ & \quad + 6a_{1} a_{2} b_{3} \eta ^{2} \mu + 6a_{1} a_{3} b_{2} \eta ^{2} \mu - 6a_{1} a_{4} b_{1} \eta ^{2} \mu - 9a_{2} ^{2} b_{2} \eta ^{2} \mu + 3a_{2} ^{2} b_{4} \eta ^{2} \mu + 6a_{2} a_{3} b_{1} \eta ^{2} \mu - 12a_{2} a_{3} b_{3} \eta ^{2} \mu \\ & \quad + 6a_{2} a_{4} b_{2} \eta ^{2} \mu - 12a_{2} a_{4} b_{4} \eta ^{2} \mu - 6a_{3} ^{2} b_{2} \eta ^{2} \mu - 6a_{4} ^{2} b_{2} \eta ^{2} \mu + 16b_{2} \eta ^{2} \gamma \mu ^{2} + 4b_{2} \eta ^{2} \mu ^{3} - a_{1} ^{2} b_{2} \eta ^{2} - a_{1} ^{2} b_{4} \eta ^{2} \\ & \quad - 2a_{1} a_{2} b_{1} \eta ^{2} + 2a_{1} a_{2} b_{3} \eta ^{2} + 2a_{1} a_{3} b_{2} \eta ^{2} - 2a_{1} a_{4} b_{1} \eta ^{2} - 3a_{2} ^{2} b_{2} \eta ^{2} + a_{2} ^{2} b_{4} \eta ^{2} + 2a_{2} a_{3} b_{1} \eta ^{2} - 4a_{2} a_{3} b_{3} \eta ^{2} \\ & \quad + 2a_{2} a_{4} b_{2} \eta ^{2} - 4a_{2} a_{4} b_{4} \eta ^{2} - 2a_{3} ^{2} b_{2} \eta ^{2} - 2a_{4} ^{2} b_{2} \eta ^{2} + 8b_{2} \eta ^{2} \gamma \mu + 12b_{2} \eta ^{2} \mu ^{2} - 2a_{1} ^{2} b_{2} \gamma - 2a_{1} ^{2} b_{4} \gamma - 4a_{1} a_{2} b_{1} \gamma \\ & \quad + 4a_{1} a_{2} b_{3} \gamma + 4a_{1} a_{3} b_{2} \gamma - 4a_{1} a_{4} b_{1} \gamma - 6a_{2} ^{2} b_{2} \gamma + 2a_{2} ^{2} b_{4} r + 4a_{2} a_{3} b_{1} \gamma - 8a_{2} a_{3} b_{3} r + 4a_{2} a_{4} b_{2} \gamma - 8a_{2} a_{4} b4\gamma - 4a_{3} ^{2} b_{2} \gamma \\ & \quad - \left. {\left. {4a_{4} ^{2} b_{2} \gamma + 3b_{1} ^{2} b_{2} \gamma + 3b_{1} ^{2} b_{4} \gamma - 6b_{1} b_{2} b_{3} \gamma + 3b_{2} ^{3} \gamma - 3b_{2} ^{2} b_{4} \gamma + 6b_{2} b_{3} ^{2} \gamma + 6b_{2} b_{4} ^{2} \gamma + 12b_{2} \eta ^{2} \mu + 4b_{2} \eta ^{2} } \right)} \right), \\ \end{aligned}$$

(A12)

$$\begin{aligned} & F_{7} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right) = \frac{1}{{4\eta ^{2} (\mu + 1)^{3} }}\left( {\left( {5a_{1} ^{2} b_{1} \delta _{v} \eta ^{2} \mu ^{3} + 18a_{1} ^{2} b_{3} \delta _{v} \eta ^{2} \mu ^{3} - 10a_{1} a_{2} b_{2} \delta _{v} \eta ^{2} \mu ^{3} + 20a_{1} a_{3} b_{1} \delta _{v} \eta ^{2} \mu ^{3} } \right.} \right. \\ & \quad - 5a_{2} ^{2} b_{1} \delta _{v} \eta ^{2} \mu ^{3} + 18a_{2} ^{2} b_{3} \delta _{v} \eta ^{2} \mu ^{3} + 20a_{2} a_{3} b_{2} \delta _{v} \eta ^{2} \mu ^{3} + 27a_{3} ^{2} b_{3} \delta _{v} \eta ^{2} \mu ^{3} + 18a_{3} a_{4} b_{4} \delta _{v} \eta ^{2} \mu ^{3} + 9a_{4} ^{2} b_{3} \delta _{v} \eta ^{2} \mu ^{3} \\ & \quad + 15a_{1} ^{2} b_{1} \delta _{v} \eta ^{2} \mu ^{2} + 54a_{1} ^{2} b_{3} \delta _{v} \eta ^{2} \mu ^{2} - 30a_{1} a_{2} b_{2} \delta _{v} \eta ^{2} \mu ^{2} + 60a_{1} a_{3} b_{1} \delta _{v} \eta ^{2} \mu ^{2} - 15a_{2} ^{2} b_{1} \delta _{v} \eta ^{2} \mu ^{2} + 54a_{2} ^{2} b_{3} \delta _{v} \eta ^{2} \mu ^{2} \\ & \quad + 60a_{2} a_{3} b_{2} \delta _{v} \eta ^{2} \mu ^{2} + 81\eta ^{2} a_{3} ^{2} b_{3} \delta _{v} \mu ^{2} + 54\eta ^{2} a_{3} a_{4} b_{4} \delta _{v} \mu ^{2} + 27\eta ^{2} a_{4} ^{2} b_{3} \delta _{v} \mu ^{2} + 15\eta ^{2} a_{1} ^{2} b_{1} \delta _{v} \mu + 54\eta ^{2} a_{1} ^{2} b_{3} \delta _{v} \mu \\ & \quad - 30\eta ^{2} a_{1} a_{2} b_{2} \delta _{v} \mu + 60\eta ^{2} a_{1} a_{3} b_{1} \delta _{v} \mu - 15\eta ^{2} a_{2} ^{2} b_{1} \delta _{v} \mu + 54\eta ^{2} a_{2} ^{2} b_{3} \delta _{v} \mu + 60\eta ^{2} a_{2} a_{3} b_{2} \delta _{v} \mu + 81\eta ^{2} a_{3} ^{2} b_{3} \delta _{v} \mu \\ & \quad + 54\eta ^{2} a_{3} a_{4} b_{4} \delta _{v} \mu + 27\eta ^{2} a_{4} ^{2} b_{3} \delta _{v} \mu - 36\eta ^{2} b_{3} \delta _{v} \mu ^{3} + 5\eta ^{2} \delta _{v} b_{1} a_{1} ^{2} + 18\eta ^{2} b_{3} \delta _{v} a_{1} ^{2} - 10\eta ^{2} \delta _{v} b_{2} a_{2} a_{1} + 20\eta ^{2} \delta _{v} a_{3} b_{1} a_{1} \\ & \quad - 5\eta ^{2} \delta _{v} b_{1} a_{2} ^{2} + 18\eta ^{2} b_{3} \delta _{v} a_{2} ^{2} + 20\eta ^{2} \delta _{v} b_{2} a_{3} a_{2} + 27\eta ^{2} b_{3} \delta _{v} a_{3} ^{2} + 18\eta ^{2} \delta _{v} b_{4} a_{3} a_{4} + 9\eta ^{2} b_{3} \delta _{v} a_{4} ^{2} - 108\eta ^{2} b_{3} \delta _{v} \mu ^{2} \\ & \quad - 36\eta ^{2} b_{3} \mu ^{3} + 2\mu \delta _{h} b_{1} a_{1} ^{2} + 4\mu \delta _{h} b_{3} a_{1} ^{2} - 4\mu \delta _{h} b_{2} a_{2} a_{1} + 40\mu \delta _{h} a_{3} b_{1} a_{1} - 2\mu \delta _{h} b_{1} a_{2} ^{2} + 4\mu \delta _{h} a_{2} ^{2} b_{3} + 40\mu \delta _{h} b_{2} a3a_{2} \\ & \quad + 54\mu \delta _{h} a_{3} ^{2} b_{3} + 36\mu \delta _{h} b_{4} a_{3} a_{4} + 18\mu \delta _{h} b_{3} a_{4} ^{2} - 4\mu \delta _{h} b_{1} ^{3} - 40\mu \delta _{h} b_{1} ^{2} b_{3} + 12\mu \delta _{h} b_{2} ^{2} b_{1} - 40\mu \delta _{h} b_{2} ^{2} b_{3} - 36\mu \delta _{h} b_{3} ^{3} \\ & \quad - 36b_{3} b_{4} ^{2} \delta _{h} \mu - 108b_{3} \delta _{v} \eta ^{2} \mu - 108b_{3} \eta ^{2} \mu ^{2} + 2a_{1} ^{2} b_{1} \delta _{h} + 4a_{1} ^{2} b_{3} \delta _{h} - 4a_{1} a_{2} b_{2} \delta _{h} + 40a_{1} a_{3} b_{1} \delta _{h} - 2a_{2} ^{2} b_{1} \delta _{h} + 4a_{2} ^{2} b_{3} \delta _{h} \\ & \quad + 40a_{2} a_{3} b_{2} \delta _{h} + 54a_{3} ^{2} b_{3} \delta _{h} + 36a_{3} a_{4} b_{4} \delta _{h} + 18a_{4} ^{2} b_{3} \delta _{h} - 4b_{1} ^{3} \delta _{h} - 40b_{1} ^{2} b_{3} \delta _{h} + 12b_{1} b_{2} ^{2} \delta _{h} - 40b_{2} ^{2} b_{3} \delta _{h} - 36b_{3} ^{3} \delta _{h} \\ & \quad - \left. {36b_{3} b_{4} ^{2} \delta _{h} - 36b_{3} \delta _{v} \eta ^{2} - 108b_{3} \eta ^{2} \mu - 36b_{3} \eta ^{2} } \right)\Omega ^{2} + \left( { - 4a_{1} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} - 12a_{1} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} - 8a_{1} a_{2} b_{1} \zeta _{v} \eta ^{2} \mu ^{3} } \right. \\ & \quad - 4a_{1} a_{3} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} - 12a_{1} a_{4} b_{1} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{2} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} - 12a_{2} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{2} a_{3} b_{1} \zeta _{v} \eta ^{2} \mu ^{3} - 12a_{2} a_{4} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} \\ & \quad - 12a_{3} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} - 12a_{4} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{3} - 12a_{1} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} - 36a_{1} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} - 24a_{1} a_{2} b_{1} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{1} a_{3} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} \\ & \quad - 36a_{1} a_{4} b_{1} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{2} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} - 36a_{2} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{2} a_{3} b_{1} \zeta _{v} \eta ^{2} \mu ^{2} - 36a_{2} a_{4} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} - 36a_{3} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} \\ & \quad - 36a_{4} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{1} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu - 36a_{1} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu - 24a_{1} a_{2} b_{1} \zeta _{v} \eta ^{2} \mu - 12a_{1} a_{3} b_{2} \zeta _{v} \eta ^{2} \mu - 36a_{1} a_{4} b_{1} \zeta _{v} \eta ^{2} \mu \\ & \quad + 12a_{2} ^{2} b_{2} \zeta _{v} \eta ^{2} \mu - 36a_{2} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu + 12a_{2} a_{3} b_{1} \zeta _{v} \eta ^{2} \mu - 36a_{2} a_{4} b_{2} \zeta _{v} \eta ^{2} \mu - 36a_{4} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu - 36a_{4} ^{2} b_{4} \zeta _{v} \eta ^{2} \mu \\ & \quad + 24b_{4} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{1} ^{2} b_{2} \zeta _{v} \eta ^{2} - 12a_{1} ^{2} b_{4} \zeta _{v} \eta ^{2} - 8a_{1} a_{2} b_{1} \zeta _{v} \eta ^{2} - 4a_{1} a_{3} b_{2} \zeta _{v} \eta ^{2} - 12a_{1} a_{4} b_{1} \zeta _{v} \eta ^{2} + 4a_{2} ^{2} b_{2} \zeta _{v} \eta ^{2} \\ & \quad - 12a_{2} ^{2} b_{4} \zeta _{v} \eta ^{2} + 4a_{2} a_{3} b_{1} \zeta _{v} \eta ^{2} - 12a_{2} a_{4} b_{2} \zeta _{v} \eta ^{2} - 12a_{3} ^{2} b_{4} \zeta _{v} \eta ^{2} - 12a_{4} ^{2} b_{4} \zeta _{v} \eta ^{2} + 72b_{4} \zeta _{v} \mu ^{2} \mu ^{2} - 4a_{1} ^{2} b_{2} \zeta _{h} \mu \\ & \quad - 8a_{1} a_{2} b_{1} \zeta _{h} \mu + 8a_{1} a_{3} b_{2} \zeta _{h} \mu - 24a_{1} a_{4} b_{1} \zeta _{h} \mu + 4a_{2} ^{2} b_{2} \zeta _{h} \mu - 8a_{2} a_{3} b_{1} \zeta _{h} \mu - 24a_{2} a_{4} b_{2} \zeta _{h} \mu + 12a_{3} ^{2} b_{4} \zeta _{h} \mu \\ & \quad - 24a_{3} a_{4} b_{3} \zeta _{h} \mu - 12a_{4} ^{2} b_{4} \zeta _{h} \mu + 12b_{1} ^{2} b_{2} \zeta _{h} \mu + 24b_{1} ^{2} b4\zeta _{h} \mu - 4b_{2} ^{3} \zeta _{h} \mu + 24b_{2} ^{2} b_{4} \zeta _{h} \mu + 12b_{3} ^{2} b_{4} \zeta _{h} \mu \\ & \quad + 12b_{4} ^{3} \zeta _{h} \mu + 72b4\zeta _{v} \eta ^{2} \mu - 4a_{1} ^{2} b_{2} \zeta _{h} - 8a_{1} a_{2} b_{1} \zeta _{h} + 8a_{1} a_{3} b_{2} \zeta _{h} - 24a_{1} a_{4} b_{1} \zeta _{h} + 4a_{2} ^{2} b_{2} \zeta _{h} - 8a_{2} a_{3} b_{1} \zeta _{h} \\ & \quad - 24a_{2} a_{4} b_{2} \zeta _{h} + 12a_{3} ^{2} b_{4} \zeta _{h} - 24a_{3} a_{4} b_{3} \zeta _{h} - 12a_{4} ^{2} b_{4} \zeta _{h} + 12b_{1} ^{2} b_{2} \zeta _{h} + 24b_{1} ^{2} b_{4} \zeta _{h} - 4b_{2} ^{3} eh + 24b_{2} ^{2} b_{4} \zeta _{h} \\ & \quad + \left. {12b_{3}^{2} b_{4} \zeta _{h} + 12b_{4} ^{3} \zeta _{h} + 24b_{4} \zeta _{v} \eta ^{2} } \right)\Omega + \left( { - a_{1} ^{2} b_{1} \eta ^{2} \mu ^{3} - 2a_{1} ^{2} b_{3} \eta ^{2} \mu ^{3} + 2a_{1} a_{2} b_{2} \eta ^{2} \mu ^{3} - 4a_{1} a_{3} b_{1} \eta ^{2} \mu ^{3} + a_{2} ^{2} b_{1} \eta ^{2} \mu ^{3} } \right. \\ & \quad - 2a_{2} ^{2} b_{3} \eta ^{2} \mu ^{3} - 4a_{2} a_{3} b_{2} \eta ^{2} \mu ^{3} - 3a_{3} ^{2} b_{3} \eta ^{2} \mu ^{3} - 2a_{3} a_{4} b_{4} \eta ^{2} \mu ^{3} - a_{4} ^{2} b_{3} \eta ^{2} \mu ^{3} - 3a_{1} ^{2} b_{1} \eta ^{2} \mu ^{2} \\ & \quad - 6a_{1} ^{2} b_{3} \eta ^{2} \mu ^{2} + 6a_{1} a_{2} b_{2} \eta ^{2} \mu ^{2} - 12a_{1} a_{3} b_{1} \eta ^{2} \mu ^{2} + 3a_{2} ^{2} b_{1} \eta ^{2} \mu ^{2} - 6a_{2} ^{2} b_{3} \eta ^{2} \mu ^{2} - 12a_{2} a_{3} b_{2} \eta ^{2} \mu ^{2} - 9a_{3} ^{2} b_{3} \eta ^{2} \mu ^{2} \\ & \quad - 6a_{3} a_{4} b_{4} \eta ^{2} \mu ^{2} - 3a_{4} ^{2} b_{3} \eta ^{2} \mu ^{2} + 8b_{3} \eta ^{2} \gamma \mu ^{3} - 3a_{1} ^{2} b_{1} \eta ^{2} \mu - 6a_{1} ^{2} b_{3} \eta ^{2} \mu + 6a_{1} a_{2} b_{2} \eta ^{2} \mu - 12a_{1} a_{3} b_{1} \eta ^{2} \mu + 3a_{2} ^{2} b_{1} \eta ^{2} \mu \\ & \quad - 6a_{2} ^{2} b_{3} \eta ^{2} \mu - 12a_{2} a_{3} b_{2} \eta ^{2} \mu - 9a_{3} ^{2} b_{2} \eta ^{2} \mu - 6a_{3} a_{4} b_{4} \eta ^{2} \mu - 3a_{4} ^{2} b_{3} \eta ^{2} \mu + 16b_{3} \eta ^{2} \gamma \mu ^{2} + 4\eta ^{2} b_{3} \mu ^{3} - a_{1} ^{2} b_{1} \eta ^{2} - 2a_{1} ^{2} b_{3} \eta ^{2} \\ & \quad + 2a_{1} a_{2} b_{2} \eta ^{2} - 4a_{1} a_{3} b_{1} \eta ^{2} + b_{1} \eta ^{2} a_{2} ^{2} - 2a_{2} ^{2} \eta ^{2} b_{3} - 4b2a_{3} \eta ^{2} a_{2} - 3a_{3} ^{2} \eta ^{2} b_{3} - 2a_{3} a_{4} b_{4} \eta ^{2} - a_{4} ^{2} b_{3} \eta ^{2} + 8b_{3} \eta ^{2} \gamma \mu + 12\eta ^{2} b_{3} \mu ^{2} \\ & \quad - 2a_{1} ^{2} b_{1} \gamma - 4a_{1} ^{2} b_{3} \gamma + 4a_{1} a_{2} b_{2} \gamma - 8a_{1} a_{3} b_{1} \gamma + 2a_{2} ^{2} b_{1} \gamma - 4a_{2} ^{2} b_{3} \gamma - 8a_{2} a_{3} b_{2} \gamma - 6a_{3} ^{2} b_{3} \gamma - 4a_{3} a_{4} b_{4} \gamma - 2a_{4} ^{2} b_{3} \gamma + b_{1} ^{3} \gamma \\ & \quad + \left. {\left. {6b_{1} ^{2} b_{3} \gamma - 3b_{1} b_{2} ^{2} \gamma + 6b_{2} ^{2} b_{3} \gamma + 3b_{3} ^{3} \gamma + 3b_{3} b_{4} ^{2} \gamma + 12b_{3} \eta ^{2} \mu + 4b_{3} \eta ^{2} } \right)} \right), \\ \end{aligned}$$

(A13)

$$\begin{aligned} & F_{8} \left( {a_{1} , \cdots a_{4} ,b_{1} , \cdots b_{4} ,\Omega } \right) = \frac{1}{{4\eta ^{2} (\mu + 1)^{3} }}\left( {\left( {5a_{1} ^{2} b_{2} \delta _{v} \eta ^{2} \mu ^{3} + 18a_{1} ^{2} b_{4} \delta _{v} \eta ^{2} \mu ^{3} + 10a_{1} a_{2} b_{1} \delta _{v} \eta ^{2} \mu ^{3} + 20a_{1} a_{4} b_{1} \delta _{v} \eta ^{2} \mu ^{3} } \right.} \right. \\ & \quad - 5a_{2} ^{2} b_{2} \delta _{v} \eta ^{2} \mu ^{3} + 18a_{2} ^{2} b_{4} \delta _{v} \eta ^{2} \mu ^{3} + 20a_{2} a_{4} b_{2} \delta _{v} \eta ^{2} \mu ^{3} + 9a_{3} ^{2} b_{4} \delta _{v} \eta ^{2} \mu ^{3} + 18a_{3} a_{4} b_{3} \delta _{v} \eta ^{2} \mu ^{3} + 27a_{4} ^{2} b_{4} \delta _{v} \eta ^{2} \mu ^{3} \\ & \quad + 15a_{1} ^{2} b_{2} \delta _{v} \eta ^{2} \mu ^{2} + 54a_{1} ^{2} b_{4} \delta _{v} \eta ^{2} \mu ^{2} + 30a_{1} a_{2} b_{1} \delta _{v} \eta ^{2} \mu ^{2} - 15a_{2} ^{2} b_{2} \delta _{v} \eta ^{2} \mu ^{2} + 54a_{2} ^{2} b_{4} \delta _{v} \eta ^{2} \mu ^{2} + 60a_{2} a_{4} b_{2} \delta _{v} \eta ^{2} \mu ^{2} \\ & \quad + 54a_{3} a_{4} b_{3} \delta _{v} \eta ^{2} \mu ^{2} + 27a_{3} ^{2} b_{4} \delta _{v} \eta ^{2} \mu ^{2} + 81a_{4} ^{2} b_{4} \delta _{v} \eta ^{2} \mu ^{2} + 54a_{1} ^{2} b_{4} \delta _{v} \eta ^{2} \mu + 30a_{1} a_{2} b_{1} \delta _{v} \eta ^{2} \mu + 60a_{1} a_{4} b_{1} \delta _{v} \eta ^{2} \mu ^{2} \\ & \quad + 15a_{1} ^{2} b_{2} \delta _{v} \eta ^{2} \mu + 60a_{1} a_{4} b_{1} \delta _{v} \eta ^{2} \mu - 15a_{2} ^{2} b_{2} \delta _{v} \eta ^{2} \mu + 54a_{2} ^{2} b_{4} \delta _{v} \eta ^{2} \mu + 60a_{2} a_{4} b_{2} \delta _{v} \eta ^{2} \mu + 27a_{3} ^{2} b_{4} \delta _{v} \eta ^{2} \mu \\ & \quad + 54a_{3} a_{4} b_{3} \delta _{v} \eta ^{2} \mu + 81a_{4} ^{2} b_{4} \delta _{v} \eta ^{2} \mu + 5a_{1} ^{2} b_{2} \delta _{v} \eta ^{2} + 18a_{1} ^{2} b_{4} \delta _{v} \eta ^{2} + 10a_{1} a_{2} b_{1} \delta _{v} \eta ^{2} + 20a_{1} a_{4} b_{1} \delta _{v} \eta ^{2} - 5a_{2} ^{2} b_{2} \delta _{v} \eta ^{2} \\ & \quad + 9a_{3} ^{2} b_{4} \delta _{v} \eta ^{2} - 36b_{4} \delta _{v} \eta ^{2} \mu ^{3} + 18a_{2} ^{2} b_{4} \delta _{v} \eta ^{2} + 20a_{2} a_{4} b_{2} \delta _{v} \eta ^{2} + 2a_{1} ^{2} b_{2} \delta _{h} \mu + 54a_{4} ^{2} b_{4} \delta _{h} \mu - 12b_{1} ^{2} b_{2} \delta _{h} \mu \\ & \quad - 40b_{1} ^{2} b_{4} \delta _{h} \mu + 4b_{2} ^{3} \delta _{h} \mu - 40b_{2} ^{2} b_{4} \delta _{h} \mu - 36b_{3} ^{2} b_{4} \delta _{h} \mu + 4a_{2} ^{2} b_{4} \delta _{h} \mu + 18a_{3} a_{4} b_{3} \delta _{v} \eta ^{2} - 108b_{4} \delta _{v} \eta ^{2} \mu ^{2} - 36b_{4} \eta ^{2} \mu ^{3} \\ & \quad + 4a_{1} ^{2} b_{4} \delta _{h} \mu + 4a_{1} a_{2} b_{1} \delta _{h} \mu - 2a_{2} ^{2} b_{2} \delta _{h} \mu + 40a_{2} a_{4} b_{2} \delta _{h} \mu + 18a_{3} ^{2} b_{4} \delta _{h} \mu + 36a3a_{4} b_{3} \delta _{h} \mu - 36b_{4} ^{3} \delta _{h} \mu - 108b_{4} \delta _{v} \eta ^{2} \mu \\ & \quad - 108b_{4} \eta ^{2} \mu ^{2} + 2a_{1} ^{2} b_{2} \delta _{h} + 4a_{1} ^{2} b_{4} \delta _{h} + 4a_{1} a_{2} b_{1} \delta _{h} + 40a_{1} a_{4} b_{1} \delta _{h} - 2a_{2} ^{2} b_{2} \delta _{h} + 4a_{2} ^{2} b_{4} \delta _{h} + 40a_{2} a_{4} b_{2} \delta _{h} + 18a_{3} ^{2} b_{4} \delta _{h} \\ & \quad + 36a_{3} a_{4} b_{3} \delta _{h} + 54a_{4} ^{2} b_{4} \delta _{h} - 12b_{1} ^{2} b_{2} \delta _{h} - 40b_{1} ^{2} b_{4} \delta _{h} + 4b_{2} ^{3} \delta _{h} - 40b_{2} ^{2} b_{4} \delta _{h} - 36b_{3} ^{2} b_{4} \delta _{h} - 36b_{4} ^{3} \delta _{h} - 36b_{4} \delta _{v} \eta ^{2} \\ & \quad - \left. {108b_{4} \eta ^{2} \mu - 36b_{4} \eta ^{2} + 40a_{1} a_{4} b_{1} \delta _{h} \mu } \right)\Omega ^{2} + \left( {4a_{1} ^{2} b_{1} \zeta _{v} \eta ^{2} \mu ^{3} + 12a_{1} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} - 8a_{1} a_{2} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} + 12a_{1} a_{3} b_{1} \zeta _{v} \eta ^{2} \mu ^{3} } \right. \\ & \quad - 4a_{1} a_{4} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} - 4a_{2} ^{2} b_{1} \zeta _{v} \eta ^{2} \mu ^{3} + 12a_{2} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} + 12a_{2} a_{3} b_{2} \zeta _{v} \eta ^{2} \mu ^{3} + 4a_{2} a_{4} b_{1} \zeta _{v} \eta ^{2} \mu ^{3} + 12a_{3} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} \\ & \quad + 12a_{4} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{3} + 12a_{1} ^{2} b_{1} \zeta _{v} \eta ^{2} \mu ^{2} + 36a_{1} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} - 24a_{1} a_{2} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} + 36a_{1} a_{3} b_{1} \zeta _{v} \eta ^{2} \mu ^{2} - 12a_{1} a_{4} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} \\ & \quad - 12a_{2} ^{2} b_{1} \zeta _{v} \eta ^{2} \mu ^{2} + 36a_{2} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} + 36a_{2} a_{3} b_{2} \zeta _{v} \eta ^{2} \mu ^{2} + 12a_{2} a_{4} b_{1} \zeta _{v} \eta ^{2} \mu ^{2} + 36a_{3} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} + 36a_{4} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu ^{2} \\ & \quad + 12a_{1} ^{2} b_{1} \zeta _{v} \eta ^{2} \mu - 24a_{1} a_{2} b_{2} \zeta _{v} \eta ^{2} \mu + 36a_{1} a_{3} b_{1} \zeta _{v} \eta ^{2} \mu - 12a_{1} a_{1} b_{2} \zeta _{v} \eta ^{2} u - 12a_{2} ^{2} b_{1} \zeta _{v} \eta ^{2} \mu + 36a_{2} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu + 4a_{1} ^{2} b_{1} \zeta _{v} \eta ^{2} \\ & \quad + 36a_{2} a_{3} b_{2} \zeta _{v} \eta ^{2} \mu + 12a_{2} a_{4} b_{1} \zeta _{v} \eta ^{2} \mu + 36a_{3} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu + 36a_{4} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu - 24b_{3} \zeta _{v} \eta ^{2} \mu ^{3} + 12a_{1} ^{2} b_{3} \zeta _{v} \eta ^{2} - 8a_{1} a_{2} b_{2} \zeta _{v} \eta ^{2} \\ & \quad + 12a_{1} a_{3} b_{1} \zeta _{v} \eta ^{2} - 4a_{1} a_{4} b_{2} \zeta _{v} \eta ^{2} - 4a_{2} ^{2} b_{1} \zeta _{v} \eta ^{2} + 12a_{2} ^{2} b_{3} \zeta _{v} \eta ^{2} + 12a_{2} a_{3} b_{2} \zeta _{v} \eta ^{2} + 4a_{2} a_{4} b_{1} \zeta _{v} \eta ^{2} + 4a_{1} ^{2} b_{1} \zeta _{h} - 8a_{1} a_{2} b_{2} \zeta _{h} \\ & \quad + 24a_{1} a_{3} b_{1} \zeta _{h} + 8a_{1} a_{4} b_{2} \zeta _{h} - 4a_{2} ^{2} b_{1} \zeta _{h} + 24a_{2} a_{3} b_{2} \zeta _{h} - 8a_{2} a_{4} b_{1} \zeta _{h} + 12a_{3} ^{2} b_{3} \zeta _{h} + 24a_{3} a_{4} b_{4} \zeta _{h} - 12a_{4} ^{2} b_{3} \zeta _{h} - 4b_{1} ^{3} \zeta _{h} \\ & \quad - 24b_{1} ^{2} b_{3} \zeta _{h} + 12b_{1} b_{2} ^{2} \zeta _{h} - 24b_{2} ^{2} b_{3} \zeta _{h} - 12b_{3} ^{3} \zeta _{h} - 12b_{3} b_{4} ^{2} \zeta _{h} - 24b_{3} \zeta _{v} \eta ^{2} + 12a_{3} ^{2} b_{3} \zeta _{v} \eta ^{2} + 12a_{4} ^{2} b_{3} \zeta _{v} \eta ^{2} - 72b_{3} \zeta _{v} \eta ^{2} \mu ^{2} \\ & \quad + 4a_{1} ^{2} b_{1} \zeta _{h} \mu - 8a_{1} a_{2} b_{2} \zeta _{h} \mu + 24a_{1} a_{3} b_{1} \zeta _{h} \mu + 8a_{1} a_{4} b_{2} \zeta _{h} \mu - 4a_{2} ^{2} b_{1} \zeta _{h} \mu + 24a_{2} a_{3} b_{2} \zeta _{h} \mu - 8a_{2} a_{4} b_{1} \zeta _{h} \mu + 12a_{3} ^{2} b_{3} \zeta _{h} \mu \\ & \quad + 24a_{3} a_{4} b_{4} \zeta _{h} \mu - 12a_{4} ^{2} b_{3} \zeta _{h} \mu - 4b_{1} ^{3} \zeta _{h} \mu - 24b_{1} ^{2} b_{3} \zeta _{h} \mu + 12b_{1} b_{2} ^{2} \zeta _{h} \mu - 24b_{2} ^{2} b_{3} \zeta _{h} \mu - 12b_{3} ^{3} \zeta _{h} \mu - 12b_{3} b_{4} ^{2} \zeta _{h} \mu \\ & \quad - \left. {72b_{3} \zeta _{v} \eta ^{2} \mu + 36a_{1} ^{2} b_{3} \zeta _{v} \eta ^{2} \mu } \right)\Omega + \left( { - a_{1} ^{2} b_{2} \eta ^{2} \mu ^{3} - 2a_{1} ^{2} b_{4} \eta ^{2} \mu ^{3} - 2a_{1} a_{2} b_{1} \eta ^{2} \mu ^{3} - 4a_{1} a_{4} b_{1} \eta ^{2} \mu ^{3} + a_{2} ^{2} b_{2} \eta ^{2} \mu ^{3} } \right. \\ & \quad - 2a_{2} ^{2} b_{4} \eta ^{2} \mu ^{3} - 4a_{2} a_{4} b_{2} \eta ^{2} \mu ^{3} - a_{3} ^{2} b_{4} \eta ^{2} \mu ^{3} - 2a3a_{4} b_{3} \eta ^{2} \mu ^{3} + 27a_{4} ^{2} b_{4} \delta _{v} \eta ^{2} w^{2} - 3a_{4} ^{2} b_{4} \eta ^{2} \mu ^{3} - 3a_{1} ^{2} b_{2} \eta ^{2} \mu ^{2} - 6a_{1} ^{2} b_{4} \eta ^{2} \mu ^{2} \\ & \quad - 6a_{1} a_{2} b_{1} \eta ^{2} \mu ^{2} - 12a_{1} a_{4} b_{1} \eta ^{2} \mu ^{2} + 3a_{2} ^{2} b_{2} \eta ^{2} \mu ^{2} - 6a_{2} ^{2} b_{4} \eta ^{2} \mu ^{2} - 12a_{2} a_{4} b_{2} \eta ^{2} \mu ^{2} - 3a_{3} ^{2} b_{4} \eta ^{2} \mu ^{2} - 6a_{3} a_{4} b_{3} \eta ^{2} \mu ^{2} + 8b_{4} \eta ^{2} \gamma \mu ^{3} \\ & \quad - 3a_{1} ^{2} b_{2} \eta ^{2} \mu - 6a_{1} ^{2} b_{4} \eta ^{2} \mu - 6a_{1} a_{2} b_{1} \eta ^{2} \mu - 12a_{1} a_{4} b_{1} \eta ^{2} \mu + 3a_{2} ^{2} b_{2} \eta ^{2} \mu - 6a_{2} ^{2} b_{4} \eta ^{2} \mu - 12a_{2} a_{4} b_{2} \eta ^{2} \mu - 3a_{3} ^{2} b_{4} \eta ^{2} \mu \\ & \quad - 6a_{3} a_{4} b_{3} \eta ^{2} \mu - 9a_{4} ^{2} b_{4} \eta ^{2} \mu + 16b_{4} \eta ^{2} \gamma \mu ^{2} + 4b_{4} \eta ^{2} \mu ^{3} - a_{1} ^{2} b_{2} \eta ^{2} - 2a_{1} ^{2} b_{4} \eta ^{2} - 2a_{1} a_{2} b_{1} \eta ^{2} - 4a_{1} a_{4} b_{1} \eta ^{2} + a_{2} ^{2} b_{2} \eta ^{2} - 2a_{2} ^{2} b_{4} \eta ^{2} \\ & \quad - 4a_{2} a_{4} b_{2} \eta ^{2} - a_{3} ^{2} b_{4} \eta ^{2} - 2a_{3} a_{4} b_{3} \eta ^{2} - 3a4^{2} b_{4} \eta ^{2} + 8b_{4} \eta ^{2} \gamma \mu + 12b_{4} \eta ^{2} \mu ^{2} - 2a_{1} ^{2} b_{2} \gamma - 4a_{1} ^{2} b_{4} \gamma - 4a_{1} a_{2} b_{1} \gamma - 8a_{1} a_{4} b_{1} \gamma \\ & \quad + 2a_{2} ^{2} b_{2} \gamma - 4a_{2} ^{2} b_{4} \gamma - 8a_{2} a_{4} b_{2} \gamma - 2a_{3} ^{2} b_{4} \gamma - 4a_{3} a_{4} b_{3} \gamma - 6a_{4} ^{2} b_{4} \gamma + 3b_{1} ^{2} b_{2} \gamma + 6b_{1} ^{2} b_{4} \gamma - b_{2} ^{3} \gamma + 6b_{2} ^{2} b_{4} \gamma + 3b_{3} ^{2} b_{4} \gamma + 3b_{4} ^{3} \gamma \\ & \quad + \left. {\left. {12b_{4} \eta ^{2} \mu + 4b_{4} \eta ^{2} - 9a_{4} ^{2} b_{4} \eta ^{2} \mu ^{2} } \right)} \right), \\ \end{aligned}$$

(A14)