Performance analysis of a quasi-zero stiffness vibration isolation system with scissor-like structures

Abstract

To isolate low-frequency vibration, a novel single-degree-of-freedom vibration isolation system with quasi-zero stiffness (QZS) and nonlinear damping using geometric nonlinearity is proposed in this study. One of the remarkable features of this system is the use of scissor-like structures (SLSs) to achieve the nonlinear stiffness and damping. The length difference between the connecting rods in SLS is considered. First, both the stiffness and damping characteristics are derived and analyzed in detail. Then, the frequency response and force transmissibility are obtained using the harmonic balance method. Finally, the effects of structural parameters on the isolation performance are investigated. Theoretical results show that the proposed QZS vibration system can not only isolate low-frequency vibration but also suppress the high-amplitude vibration in the resonant region. Besides, increasing nonlinear damping has little influence on the isolation performance in high frequencies. The proposed QZS vibration system can outperform a classical counterpart.

1 Introduction

Vibrations exist everywhere in engineering applications such as construction machinery, aerospace, vehicles, and precision equipment. High-amplitude vibration could result in disastrous accidents [1]. Moreover, how to isolate low-frequency vibration effectively is a challenging research hot spot. Vibrations can be generally suppressed by applying passive vibration isolators, absorbers [2], or active control methods [3,4,5]. Compared with other techniques, passive vibration isolators are more widely used in engineering because of high reliability and low cost. However, linear vibration isolators have a common dilemma that decreasing the natural frequency can lead to the reduction of bearing capacity. Therefore, it is necessary to design nonlinear vibration isolators that can isolate the low-frequency vibration effectively.

The design of quasi-zero stiffness (QZS) vibration isolator has always been the focus of research [6]. The QZS vibration isolators are generally obtained by combining the linear vibration isolator with the negative stiffness corrector (NSC) which is used to produce the negative stiffness in the direction of vibration isolation using a geometric relationship [7]. The positive stiffness can be counteracted by the negative one, which can result in zero stiffness at the equilibrium position by designing appropriate structural parameters. Therefore, a high-static-low-dynamic stiffness (HSLDS) is obtained, which can make sure that the vibration isolator has a small static deflection and a low natural frequency simultaneously [8]. There are various NSCs to realize QZS vibration isolators. Carrella et al. [9] designed a QZS vibration isolator using two oblique springs as NSC. Then, Xu et al. [10] improved this QZS vibration isolator by replacing the NSC with four oblique springs. The investigation results showed that the QZS vibration isolator has an excellent performance in isolating low-frequency vibration. Le and Ahn [11] designed a QZS vehicle seat whose NSC consisted of connecting rods and horizontal springs. Liu et al. [12] proposed a QZS vibration isolator using four Euler buckled beams as the NSC. The authors also considered the effects of load imperfection which can lead to asymmetric stiffness [13]. The results showed that the QZS vibration isolator with load imperfection can exhibit purely softening, softening-to-hardening, and purely hardening characteristics. Zhou et al. [14] built a QZS vibration isolator based on two cam-roller-spring mechanisms and found that the isolator can exhibit piecewise nonlinear stiffness characteristics. The negative stiffness corrector also can be realized with the application of magnetic forces. Zheng et al. [15] developed an HSLDS vibration isolator whose NSC consisted of a pair of coaxial ring permanent magnets. A similar QZS vibration isolator was developed and further applied to neonatal transport to protect new-born infants [16]. Yang et al. [17] proposed an NSC consisting of four connecting rods and four horizontal springs. Furthermore, QZS vibration isolator also can be designed to isolate torsional vibration. Zheng et al. [18] developed a QZS torsional vibration isolator whose NSC mainly consisted of two coaxial ring magnets.

The scissor-like structure (SLS) is also a good choice for low-frequency vibration isolation and is generally comprised of connecting rods and joints. Sun et al. [19] proposed a nonlinear vibration isolator consisting of an n-layer SLS with the same rod length and horizontal springs. The results showed that this isolator can realize quasi-zero stiffness by designing appropriate structural parameters and is superior to an existing QZS vibration isolator. Wu et al. [20] also proposed a similar vibration isolator in which the connecting rods of the SLS were of different lengths. The authors verified its good performance by experiment. Then, Wang et al. [21] analyzed the subharmonic and ultra-subharmonic resonances of this nonlinear vibration isolator. The results indicated that the subharmonic resonance can be suppressed by adjusting structural parameters. Note that these mentioned vibration isolators were not developed by combining the SLS and the linear vibration isolator. The SLS had multiple layers and was installed vertically. Therefore, these vibration isolators cannot guarantee the high static stiffness, and the structures are complicated. Sun et al. [22, 23] designed a three-dimensional QZS vibration isolation system based on the SLSs and further applied it to the sensor. In our previous work [24, 25], we also designed a QZS vibration isolator whose NSC consisted of an SLS and a horizontal spring. In this design, the NSC was also installed vertically.

It is worth noting that the performance of the QZS vibration isolator in the resonant region could be deteriorated when the excitation amplitude increases. This phenomenon is caused by the existence of nonlinear stiffness [26]. It is well known that increasing the linear viscous damping can suppress the transmissibility in the resonant region, while the performance in the isolation region can be deteriorated [27]. This dilemma can be overcome by applying the nonlinear damping. Cubic nonlinear viscous damping is commonly used in the vibration system. It has been demonstrated that applying cubic nonlinear damping can suppress the force transmissibility in the resonant region effectively and has little effect on the performance in the isolation region [28]. However, it is detrimental to the performance in the isolation region under base excitation [29]. Thus, the geometric nonlinear damping was subsequently proposed by scholars. Tang and Brennan [30] proposed geometric nonlinear damping based on an oblique linear viscous damper and made a comparison with cubic nonlinear damping. The results showed that applying the geometric nonlinear damping can reduce the force transmissibility in the resonant region effectively, while the performance in the isolation region remains unaffected. Besides, the geometric nonlinear damping can outperform the linear one when isolating the base excitation. Sun and Jing [31] applied a horizontal viscous damper in an n-layer SLS vibration isolator and obtained geometric nonlinear damping. The authors found that SLS can also achieve beneficial damping characteristics. Dong et al. [32] obtained geometric nonlinear damping using semi-active electromagnetic shunt damping and applied it in an HSLDS vibration isolator. Recently, Liu et al. [33] achieved geometric nonlinear damping by combining a cam-roller mechanism and a horizontal linear viscous damper. In our previous work [24], geometric nonlinear damping was also proposed based on the SLS. How the geometric nonlinear damping affects the isolation performance was explained from the perspective of equivalent damping.

The above-mentioned literature shows that applying the SLS can achieve the geometric nonlinear stiffness and damping and is beneficial for isolating low-frequency vibration. Inspired by the SLS proposed in Ref. [23], a novel QZS vibration system is designed using single-layer SLSs and springs as NSC. The proposed QZS vibration isolation system has a simpler structure than the counterpart proposed in Ref. [23] and is used to isolate one-dimensional vibration. The rods with different lengths are considered to reveal the effect of rod length on the isolation performance.

The rest of this paper is organized as follows. In Sect. 2, a model of the proposed QZS vibration system is established, and the analysis of the nonlinear stiffness and damping is conducted. In Sect. 3, the frequency response of the system is derived based on the harmonic balance method and further verified by numerical simulation. In Sect. 4, the parametric analysis on the frequency response and the performance is conducted in detail. Section 5 draws the conclusions.

2 Mathematical model

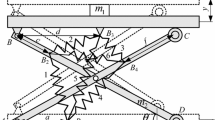
Figure 1 shows the schematic diagram of the proposed QZS vibration system. The negative stiffness corrector is composed of two same SLSs and two springs. Each SLS consists of two pairs of connecting rods with different lengths and four joints. A spring and a linear viscous damper are installed in parallel in each SLS. The SLSs are obliquely installed between the base wall and the supporting platform, which is different from most of the prior studies [19,20,21]. The supporting platform is used to support the isolation object. In the vertical direction, a supporting spring and a linear viscous damper are installed in parallel between the base and the supporting platform. The sliding bar acts as a guide mechanism with the help of a linear bearing to ensure that the isolation object can only move in the vertical direction.

Fig. 1

Schematic diagram of the proposed QZS vibration system

2.1 Geometric nonlinear stiffness characteristics

A simplified plane diagram of the designed QZS vibration system is shown in Fig. 2. When the vibration system supports an object with rated mass m, it will stabilize from an initial position to the static equilibrium position where the diagonals of SLSs coincide, and the static deflection is $\Delta x$. At the equilibrium position, the distance between the left and right joints of each SLS is $L_{e}$. The lengths of two pairs of connecting rods are $L_{\mathrm {1}}$ and $L_{\mathrm {2}}$, respectively. In the two SLSs, the stiffness of springs is $k_{h}$, and the damping coefficients of dampers are $c_{h}$. The stiffness of the spring and the damping coefficient of the damper between the object and the base are $k_{v}$ and $c_{v}$, respectively. It is assumed that the prestretching length of springs in the SLSs is d at the equilibrium position. The displacement of the object from its static equilibrium position in the vertical direction is x.

Fig. 2

Plane diagram of the proposed QZS vibration system

It is assumed that the mass of rods, springs, dampers, and supporting platform is neglected. The rotational frictions of joints are also neglected. The motion and the static analysis of the right-side SLS are shown in Fig. 3. In Fig. 3a, capital letters A, B, C, D, and O represent four joints and intersection of the two diagonals of the SLS, respectively, at the equilibrium position. $B'$, $C'$, $D'$, and $O'$ represent corresponding points when the displacement of the isolation object is x. $\alpha$ is the angle between diagonals AB and $AB'$.

Fig. 3

a Motion and b static analysis of the right-side SLS

It is assumed that the distance between points A and O is $L_{OA}$, and the distance between points B and O is $L_{OB}$. According to the geometric relationship, the following equations can be obtained

$$\begin{aligned} L_{1}^{2} -L_{OB}^{2}= & {} L_{2}^{2} -L_{OA}^{2} \end{aligned}$$

(1)

$$\begin{aligned} L_{OA} +L_{OB}= & {} L_{e} \end{aligned}$$

(2)

Thus, $L_{OA}$ and $L_{OB}$ can be obtained by combining Eqs. (1) and (2), which yields

$$\begin{aligned} L_{OA}= & {} \frac{L_{e}^{2} -L_{1}^{2} +L_{2}^{2} }{2L_{e} } \end{aligned}$$

(3)

$$\begin{aligned} L_{OB}= & {} \frac{L_{e}^{2} +L_{1}^{2} -L_{2}^{2} }{2L_{e} } \end{aligned}$$

(4)

The distance between points C and D is given by

$$\begin{aligned} L_{CD} =\sqrt{4L_{1}^{2} -\left( {\frac{L_{e}^{2} +L_{1}^{2} -L_{2}^{2} }{L_{e} }} \right) ^{2}} \end{aligned}$$

(5)

When the isolation object is subjected to a force F, it will deviate from the static equilibrium position by a displacement x. The distance between points A and $B'$ and the distance between points $C'$ and $D'$ are separately given by

$$\begin{aligned} L_{A{B}'}= & {} \sqrt{L_{e}^{2} +x^{2}} \end{aligned}$$

(6)

$$\begin{aligned} L_{{C}'{D}'}= & {} \sqrt{4L_{1}^{2} -\left( {\frac{x^{2}+L_{e}^{2} +L_{1}^{2} -L_{2}^{2} }{\sqrt{x^{2}+L_{e}^{2} } }} \right) ^{2}} \end{aligned}$$

(7)

Therefore, the force generated by the spring in the SLS is given by

$$\begin{aligned} f_{1} =k_{h} \left( {d-\left( {L_{CD} -L_{{C}'{D}'} } \right) } \right) \end{aligned}$$

(8)

Note that the prestretching length d cannot be greater than $L_{CD}$ due to the size limitation of the SLS. It is impractical if d is greater than $L_{CD}$.

The forces $f_{1}$, $f_{2}$, $f_{3}$, $f_{4}$, and F have the following relationships according to Fig. 3b.

$$\begin{aligned} f_{2} \sin \alpha _{1}= & {} f_{3} \sin \alpha _{2} \end{aligned}$$

(9)

$$\begin{aligned} f_{1}= & {} f_{2} \cos \alpha _{1} +f_{3} \cos \alpha _{2} \end{aligned}$$

(10)

$$\begin{aligned} \frac{f_{4} }{2}= & {} \frac{F}{2}+\frac{mg}{2}+2f_{2} \sin \alpha _{1} \sin \alpha \end{aligned}$$

(11)

where $f_{2}$ and $f_{3}$ denote the forces acting on the connecting rods, and $f_{4} =k_{v} \left( {x+\Delta x} \right)$ is the force generated by the vertical spring. Note that $mg=k_{v} \Delta x$, and g is the gravitational acceleration. $\alpha _{1}$ and $\alpha _{2}$ denote the angles between the diagonal $C'$ $D'$ and its adjacent connecting rods, respectively.

Combining Eqs. (9), (10), and (11) can derive

$$\begin{aligned} F=f_{4} -mg-\frac{4f_{1} \sin \alpha }{\cot \alpha _{1} +\cot \alpha _{2} } \end{aligned}$$

(12)

Thus, the restoring force of the vibration system can be further written as

$$\begin{aligned} F\left( x \right) =k_{v} x-2k_{h} \left( {d-\sqrt{4L_{1}^{2} -\left( {\frac{L_{e}^{2} +L_{1}^{2} -L_{2}^{2} }{L_{e} }} \right) ^{2}} +\sqrt{4L_{1}^{2} -\left( {\frac{x^{2}+L_{e}^{2} +L_{1}^{2} -L_{2}^{2} }{\sqrt{x^{2}+L_{e}^{2} } }} \right) ^{2}} } \right) \cdot \frac{2\sin \alpha }{\cot \alpha _{1} +\cot \alpha _{2} } \end{aligned}$$

(13)

where

$$\begin{aligned} \cot \alpha _{1}= & {} \frac{\sqrt{4L_{1}^{2} \left( {x^{2}+L_{e}^{2} } \right) -\left( {x^{2}+L_{e}^{2} +L_{1}^{2} -L_{2}^{2} } \right) ^{2}} }{x^{2}+L_{e}^{2} +L_{1}^{2} -L_{2}^{2} } \end{aligned}$$

(14)

$$\begin{aligned} \cot \alpha _{2}= & {} \frac{\sqrt{4L_{1}^{2} \left( {x^{2}+L_{e}^{2} } \right) -\left( {x^{2}+L_{e}^{2} +L_{1}^{2} -L_{2}^{2} } \right) ^{2}} }{x^{2}+L_{e}^{2} -L_{1}^{2} +L_{2}^{2} } \end{aligned}$$

(15)

$$\begin{aligned} \sin \alpha= & {} \frac{x}{\sqrt{x^{2}+L_{e}^{2} } } \end{aligned}$$

(16)

Writing Eq. (13) in a nondimensional form can yield

$$\begin{aligned} f\left( u\right)= & {} u-2\beta \left( {\delta -\sqrt{4l_{1}^{2} -\left( {1+l_{1}^{2} -l_{2}^{2} } \right) ^{2}} +\sqrt{4l_{1}^{2} -\left( {\frac{u^{2}+1+l_{1}^{2} -l_{2}^{2} }{\sqrt{u^{2}+1} }} \right) ^{2}} } \right) \cdot \nonumber \\&\frac{u\left( {\left( {u^{2}+1} \right) ^{2}-\left( {l_{1}^{2} -l_{2}^{2} } \right) ^{2}} \right) }{\left( {u^{2}+1} \right) ^{{\text{3 }}/{\text{2 }}}\sqrt{4l_{1}^{2} \left( {u^{2}+1} \right) -\left( {u^{2}+1+l_{1}^{2} -l_{2}^{2} } \right) ^{2}} } \end{aligned}$$

(17)

where $f=F / {\left( {k_{v} L_{e} } \right) }$, $\beta ={k_{h} } /{k_{v} }$, $u=x / {L_{e} }$, $\delta =d / {L_{e} }$, $l_{1} ={L_{1} } / {L_{e} }$, and $l_{2} ={L_{2} } / {L_{e} }$.

Equation (17) can be further rewritten in the following form for simplicity:

$$\begin{aligned} f\left( u \right) =u-2\beta \left( {\delta -l_{h} +\sqrt{4l_{1}^{2} -\left( {\frac{u^{2}+1+l_{\text{0 }} }{\sqrt{u^{2}+1} }} \right) ^{2}} } \right) \cdot \;\frac{u\left( {\left( {u^{2}+1} \right) ^{2}-l_{0}^{2} } \right) }{\left( {u^{2}+1} \right) ^{{\text{3 }} / {\text{2 }}}\sqrt{4l_{1}^{2} \left( {u^{2}+1} \right) -\left( {u^{2}+1+l_{\text{0 }} } \right) ^{2}} } \end{aligned}$$

(18)

where $l_{h} =\sqrt{4l_{1}^{2} -\left( {1+l_{0} } \right) ^{2}}$ and $l_{0} =l_{1}^{2} -l_{2}^{2}$.

Differentiating Eq. (18) with respect to u can obtain the stiffness of the vibration system, which yields

$$\begin{aligned} k\left( u \right)= & {} 1+\frac{2\beta u^{2}\left( {\left( {u^{2}+1} \right) ^{2}-l_{0}^{2} } \right) ^{2}}{\left( {u^{2}+1} \right) ^{3}\left( {4l_{1}^{2} \left( {u^{2}+1} \right) -\left( {u^{2}+l_{0} +1} \right) ^{2}} \right) }+\frac{\beta \left( {\delta \sqrt{u^{2}+1} -l_{h} \sqrt{u^{2}+1} +\sqrt{4l_{1}^{2} -\left( {u^{2}+l_{0} +1} \right) ^{2}} } \right) }{\left( {u^{2}+1} \right) ^{2}\sqrt{4l_{1}^{2} \left( {u^{2}+1} \right) -\left( {u^{2}+l_{0} +1} \right) ^{2}} }\cdot \nonumber \\&\left( {2l_{0}^{2} -2\left( {u^{2}+1} \right) \left( {5u^{2}+1} \right) +2u^{2}\left( {\left( {u^{2}+1} \right) ^{2}-l_{0}^{2} } \right) \left( {\frac{3}{u^{2}+1}+\frac{4l_{1}^{2} -2u^{2}-2l_{0} -2}{4l_{1}^{2} \left( {u^{2}+1} \right) -\left( {u^{2}+l_{0} +1} \right) ^{2}}} \right) } \right) \end{aligned}$$

(19)

Therefore, letting $k\left( {u=0} \right) =0$ can obtain the quasi-zero stiffness condition, which leads to

$$\begin{aligned} l_{h} +2\beta \delta \left( {l_{0}^{2} -1} \right) =0 \end{aligned}$$

(20)

The QZS condition can be further written as

$$\begin{aligned} \beta =\frac{l_{h} }{2\delta \left( {1-l_{0}^{2} } \right) } \end{aligned}$$

(21)

Substituting Eq. (21) into Eqs. (18) and (19) can obtain the restoring force $f_{q}(u)$ and the stiffness $k_{q}(u)$ of the QZS vibration system, which are listed in “Appendix A.” The effect of rod length $l_{1}$ on the stiffness of the QZS vibration system is shown in Fig. 4. The stiffness at $u=0$ is zero, indicating that the QZS property is obtained. Increasing $l_{1}$ can reduce the stiffness of the QZS vibration system and expand the negative stiffness interval. Note that the stiffness is less than that of the linear system in the selected displacement range.

$l_{0}$ represents the length difference between the two adjacent connecting rods of the SLS. Its effect on the stiffness of the QZS vibration system is shown in Fig. 5. It can be observed that increasing $l_{0}$ leads to an increase in system stiffness and narrows the negative stiffness interval. Note that the greater the length difference $l_{0}$, the smaller the rod length $l_{2}$.

Fig. 4

Nondimensional stiffness for various $l_{1}$ when $l_{0} =0$ and $\delta =0.4$

Fig. 5

Nondimensional stiffness for various $l_{0}$ when $l_{1} =0.75$ and $\delta =0.4$

Fig. 6

Nondimensional stiffness for various $\delta$ when $l_{1} =0.75$ and $l_{0} =0$

The effect of prestretching length $\delta$ on the stiffness of the QZS vibration system is shown in Fig. 6. It can be observed that increasing $\delta$ can reduce the system stiffness and expand the negative stiffness interval. Note that $\delta$ cannot be greater than $l_{h}$ due to the size limitation of the SLS.

To simplify the subsequent dynamic analysis, the nondimensional restoring force of the QZS vibration system can be replaced approximately by a fifth-order Taylor series when the oscillations are small [9], which yields

$$\begin{aligned} f_{q}^{a} \left( u \right) =\gamma _{1} u^{3}+\gamma _{2} u^{5} \end{aligned}$$

(22)

where

$$\begin{aligned} \gamma _{1}= & {} \frac{2l_{0}^{2} }{l_{0}^{2} -1}+\left( {l_{0}^{2} -1} \right) \frac{\delta -l_{h} }{2\delta l_{h}^{2} }\\ \gamma _{2}= & {} \frac{\text{2 }\left( {l_{h}^{2} +l_{0}^{2} -1} \right) \left( {\delta l_{h} \left( 3l_{0}^{2} +1\right) -\left( {l_{0}^{2} -1} \right) ^{2}} \right) + \delta l_{h}^{3} +15\delta l_{h}^{3} l_{0}^{2} +2l_{h}^{2} \left( {5l_{0}^{2} +1} \right) \left( {1-l_{0}^{2} } \right) -\left( {l_{0}^{2} -1} \right) ^{3}}{8\delta l_{h}^{3} \left( {1-l_{0}^{2} } \right) } \\&-\frac{3\left( {l_{h}^{2} +l_{0}^{2} -1} \right) ^{2}+4l_{h}^{2} }{8l_{h}^{4} } \end{aligned}$$

Thus, the approximate nondimensional stiffness is given by

$$\begin{aligned} k_{q}^{a} \left( u \right) =3\gamma _{1} u^{2}+5\gamma _{2} u^{4} \end{aligned}$$

(23)

The exact restoring force and stiffness with their approximations are shown in Fig. 7a, b, respectively. Generally, the approximate curves are in great agreement with exact ones in the displayed displacement range. Therefore, it is reasonable to use approximate restoring force for the following dynamic analysis.

Fig. 7

a Exact restoring force and its approximation and b exact stiffness and its approximation when $l_{1} =0.75$, $l_{0} =0$, and $\delta =0.4$

2.2 Geometric nonlinear damping characteristics

The geometric nonlinear damping also can be realized by combining the SLS with linear viscous damper. It can be observed from Fig. 3a that when the displacement of the isolation object is x, the variation of the distance $L_{{C}'{D}'}$ is given by

$$\begin{aligned} \Delta L_{{C}'{D}'} =\sqrt{4L_{1}^{2} -\left( {\frac{L_{e}^{2} +L_{1}^{2} -L_{2}^{2} }{L_{e} }} \right) ^{2}} -\sqrt{4L_{1}^{2} -\left( {\frac{x^{2}+L_{e}^{2} +L_{1}^{2} -L_{2}^{2} }{\sqrt{x^{2}+L_{e}^{2} } }} \right) ^{2}} \end{aligned}$$

(24)

Differentiating Eq. (24) with respect to the time can obtain the relative velocity between points $C'$ and $D'$ along the diagonal, which yields

$$\begin{aligned} V_{{C}'{D}'} =\frac{x\left( {x^{2}+L_{e}^{2} +L_{1}^{2} -L_{2}^{2} } \right) \left( {x^{2}+L_{e}^{2} -L_{1}^{2} +L_{2}^{2} } \right) }{\left( {x^{2}+L_{e}^{2} } \right) \sqrt{\left( {x^{2}+L_{e}^{2} } \right) \left( {4L_{1}^{2} \left( {x^{2}+L_{e}^{2} } \right) -\left( {x^{2}+L_{e}^{2} +L_{1}^{2} -L_{2}^{2} } \right) ^{2}} \right) } }\dot{{x}} \end{aligned}$$

(25)

Thus, the total nonlinear damping force $F_{d} \left( {x,\;\dot{{x}}} \right)$ transmitted to the isolation object in the vertical direction is given by

$$\begin{aligned} F_{d} \left( {x,\;\dot{{x}}} \right) =2F_{d1} \left( {x,\;\dot{{x}}} \right) \frac{2}{\cot \alpha _{1} +\cot \alpha _{2} }\cdot \sin \alpha \end{aligned}$$

(26)

where $F_{d1} \left( {x,\;\dot{{x}}} \right) =c_{h} V_{{C}'{D}'}$ is the damping force generated by the linear viscous damper in the SLS. Equation (26) can be further expanded as

$$\begin{aligned} F_{d} \left( {x,\;\dot{{x}}} \right) =c_{h} \frac{2x^{2}\left( {\left( {x^{2}+L_{e}^{2} } \right) ^{2}-\left( {L_{1}^{2} -L_{2}^{2} } \right) ^{2}} \right) ^{2}}{\left( {x^{2}+L_{e}^{2} } \right) ^{3}\left( {4L_{1}^{2} \left( {x^{2}+L_{e}^{2} } \right) -\left( {x^{2}+L_{e}^{2} +L_{1}^{2} -L_{2}^{2} } \right) ^{2}} \right) }\dot{{x}} \end{aligned}$$

(27)

Rewriting the nonlinear damping force in the nondimensional form leads to

$$\begin{aligned} f_{d} \left( {u,\;{u}'} \right) =\frac{2\zeta _{2} u^{2}\left( {\left( {u^{2}+1} \right) ^{2}-l_{0}^{2} } \right) ^{2}}{\left( {u^{2}+1} \right) ^{3}\left( {4l_{1}^{2} \left( {u^{2}+1} \right) -\left( {u^{2}+l_{0}^{2} +1} \right) ^{2}} \right) }{u}' \end{aligned}$$

(28)

where $f_{d} ={F_{d} } /{\left( {k_{v} L_{e} } \right) }$, $\zeta _{2} ={c_{h} } / {\left( {m\omega _{0}} \right) }$, $\omega _{{0}} \text{= }\sqrt{{k_{v} } / m}$, ${u}'={\mathrm{d}u}/{\mathrm{d}\tau }$, $\tau =\omega _{0} t$, and t is time.

The effect of rod length $l_{1}$ on the nonlinear damping coefficient is shown in Fig. 8. It can be observed that the nonlinear damping coefficient becomes greater with the increase of displacement. When the displacement is zero, the damping coefficient also becomes zero. Thus, the vibration system can achieve heavy damping for high vibration and low damping for small vibration. Besides, increasing $l_{1}$ leads to a decrease in the nonlinear damping coefficient.

The effect of rod length difference $l_{0}$ on the nonlinear damping coefficient is shown in Fig. 9. Increasing $l_{0}$ can lead to an increase in the nonlinear damping coefficient. Thus, it can be concluded that increasing the rod lengths of the SLS can reduce the nonlinear damping coefficient.

Fig. 8

Nonlinear damping coefficient for various $l_{1}$ when $l_{0} =0$ and $\zeta _{2} =1$

Fig. 9

Nonlinear damping coefficient for various $l_{0}$ when $l_{1} =0.75$ and $\zeta _{2} =1$

To simplify the subsequent analysis, a fourth-order Taylor series is applied to replace Eq. (28) approximately [30], which yields

$$\begin{aligned} f_{d}^{a} \left( {u,\;\dot{{u}}} \right) =\zeta _{2} \left( {\lambda _{1} u^{2}+\lambda _{2} u^{4}} \right) {u}' \end{aligned}$$

(29)

where

$$\begin{aligned} \lambda _{1} =\frac{2\left( {1-l_{0}^{2} } \right) ^{2}}{l_{h}^{2} }\,,\lambda _{2} =\frac{2\left( {2l_{0}^{2} -3l_{0}^{4} +1} \right) }{l_{h}^{2} }-\frac{2\left( {l_{0}^{2} -1} \right) ^{2}\left( {l_{h}^{2} +l_{0}^{2} -1} \right) }{l_{h}^{4} } \end{aligned}$$

The comparison of the exact nonlinear damping coefficient and its approximation is given in Fig. 10. Generally, the approximate damping coefficient curve matches well with the exact one in the displayed displacement range. Therefore, it is suitable to apply the approximate nonlinear damping force in the following dynamic analysis.

Fig. 10

Comparison of the exact nonlinear damping coefficient and its approximation when $l_{1} =0.75$, $l_{0} =0$, and $\zeta _{2} =1$

3 Frequency response

The equation of motion of the isolation object subjected to a force excitation can be expressed as

$$\begin{aligned} m\ddot{{x}}+c_{v} \dot{{x}}+F_{d} \left( {x,\;\dot{{x}}} \right) +F\left( x \right) =F_{e} \cos \omega t \end{aligned}$$

(30)

where $F_{e}$ and $\omega$ represent the amplitude and frequency of the force excitation, respectively. Writing Eq. (30) in a nondimensional form and replacing the exact restoring force and the nonlinear damping force with their approximations, respectively, can obtain

$$\begin{aligned} {u}''+2\zeta _{1} {u}'+\zeta _{2} \left( {\lambda _{1} u^{2}+\lambda _{2} u^{4}} \right) {u}'+\gamma _{1} u^{3}+\gamma _{2} u^{5}=f_{e} \cos \Omega \tau \end{aligned}$$

(31)

where

$$\begin{aligned} \omega _{0} =\sqrt{\frac{k_{v} }{m}} , \quad \zeta _{1} =\frac{c_{v} }{2m\omega _{0} }, \quad \zeta _{2} =\frac{c_{h} }{m\omega _{0} }, \quad \Omega =\frac{\omega }{\omega _{0} }, \quad f_{e} =\frac{F_{e} }{k_{v} L_{e} }, \quad \tau =\omega _{0} t, \quad \left( \cdot \right) ^{\prime }=\frac{d\left( \cdot \right) }{d\tau } \end{aligned}$$

The harmonic balance method (HBM) is applied to obtain the approximate solution. It is assumed that the first-order steady-state solution is expressed as

$$\begin{aligned} u=A\cos \left( {\Omega \tau +\theta } \right) \end{aligned}$$

(32)

where A and $\theta$ are the amplitude and initial phase of the steady-state solution, respectively. Letting $\varphi =\Omega \tau +\theta$ and substituting Eqs. (32) into (31) can obtain

$$\begin{aligned} \begin{array}{l} -\zeta _{2} \left( {\lambda _{1} A^{3}\Omega \left( {\frac{1}{4}\sin \varphi +\frac{1}{4}\sin \left( {3\varphi } \right) } \right) +\lambda _{2} A^{5}\Omega \left( {\frac{1}{8}\sin \varphi +\frac{3}{16}\sin \left( {3\varphi } \right) +\frac{1}{16}\sin \left( {5\varphi } \right) } \right) }\right) -A\Omega ^{2}\cos \varphi \\ -2\zeta _{1} A\Omega \sin \varphi +\frac{1}{4}\gamma _{1} A^{3}\left( {3\cos \varphi +\cos \left( {3\varphi } \right) } \right) +\frac{1}{16}\gamma _{2} A^{5}\left( {10\cos \varphi +5\cos \left( {3\varphi } \right) +\cos \left( {5\varphi } \right) } \right) \\ \quad =f_{e} \cos \varphi \cos \theta +f_{e} \sin \varphi \sin \theta \end{array} \end{aligned}$$

(33)

Neglecting the terms containing $\sin ({3\varphi })$, $\cos (3\varphi )$, $\sin ({5\varphi })$, and $\cos (5\varphi )$ can obtain

$$\begin{aligned} f_{e} \cos \theta= & {} -A\Omega ^{2}+\frac{3}{4}\gamma _{1} A^{3}+\frac{5}{8}\gamma _{2} A^{5} \end{aligned}$$

(34)

$$\begin{aligned} f_{e} \sin \theta= & {} -2\zeta _{1} A\Omega -\frac{1}{4}\zeta _{2} \lambda _{1} A^{3}\Omega -\frac{1}{8}\zeta _{2} \lambda _{2} A^{5}\Omega \end{aligned}$$

(35)

Thus, the amplitude–frequency equation can be obtained using $\sin ^{2}\theta +\cos ^{2}\theta =1$, which yields

$$\begin{aligned} \left( {A\Omega ^{2}-\frac{3}{4}\gamma _{1} A^{3}-\frac{5}{8}\gamma _{2} A^{5}} \right) ^{2}+\left( {2\zeta _{1} A\Omega +\frac{1}{4}\zeta _{2} \lambda _{1} A^{3}\Omega +\frac{1}{8}\zeta _{2} \lambda _{2} A^{5}\Omega } \right) ^{2}=f_{e}^{2} \end{aligned}$$

(36)

The force transmissibility is used to evaluate the vibration isolation performance of the proposed QZS vibration system. The force transmitted to the base can be expressed as

$$\begin{aligned} f_{s} =2\zeta _{1} {u}'+\zeta _{2} \left( {\lambda _{1} u^{2}+\lambda _{2} u^{4}} \right) {u}'+\gamma _{1} u^{3}+\gamma _{2} u^{5} \end{aligned}$$

(37)

Substituting Eq. (32) into Eq. (37) can obtain the amplitude of $f_{s}$, which yields

$$\begin{aligned} f_{t} =\left( {\left( {\frac{3}{4}\gamma _{1} A^{3}+\frac{5}{8}\gamma _{2} A^{5}} \right) ^{2}+\left( {2\zeta _{1} A\Omega +\frac{1}{4}\zeta _{2} \lambda _{1} A^{3}\Omega +\frac{1}{8}\zeta _{2} \lambda _{2} A^{5}\Omega } \right) ^{2}} \right) ^{1 / 2} \end{aligned}$$

(38)

Thus, the force transmissibility is given by

$$\begin{aligned} T_{f} =20\lg \left( {\frac{f_{t} }{f_{e} }} \right) \end{aligned}$$

(39)

The amplitude–frequency curve obtained by the HBM is shown in Fig. 11. To verify the analytical result, the amplitudes of the first harmonic components obtained by the Runge–Kutta method are also given for comparison. It can be observed that the analytical solutions match well with the numerical ones, demonstrating the feasibility of the HBM. It is worth noting that the numerical solutions in the shaded area cannot be obtained due to that they are unstable [34]. In the following analysis, the excitation amplitude and the linear damping ratio default to $f_{e} =0.01$ and $\zeta _{1} =0.02$, unless otherwise stated.

Fig. 11

Amplitude–frequency curves when $l_{1} =0.75$, $l_{0} =0.1$, $\delta =0.4$, $\zeta _{\text{1 }} =0.02$, $\zeta _{2} =0.02$, and $f_{e} =0.01$

4 Vibration isolation performance analysis

4.1 Effect of connecting rod length $l_{\mathrm {1}}$

The above analysis indicates that the rod length $l_{1}$ can affect both the stiffness and nonlinear damping of the QZS vibration system. The amplitude–frequency curves for various $l_{1}$ are shown in Fig. 12. When there is no nonlinear damping, increasing $l_{1}$ can reduce the resonant frequency but leads to an increase in the peak amplitude, as shown in Fig. 12a. However, it has little effect on the response amplitude in high frequencies. When $\zeta _{2} =0.2$, increasing $l_{1}$ can lead to an increase in the resonant frequency, as shown in Fig. 12b. The peak amplitude keeps the same trend.

The force transmissibility curves for various $l_{1}$ are shown in Fig. 13. When there is no nonlinear damping, increasing $l_{1}$ can reduce peak transmissibility. Note that there is little effect on the force transmissibility in high frequencies. The result is the opposite for the case of $\zeta _{2} =0.2$, as shown in Fig. 13b. Increasing $l_{1}$ leads to an increase in the peak transmissibility. Therefore, selecting a smaller rod length is beneficial when the nonlinear damping is considered.

Fig. 12

Amplitude–frequency curves for various $l_{1}$ when $l_{0} =\text{0 }$ and $\delta =0.4$

Fig. 13

Force transmissibility curves for various $l_{1}$ when $l_{0} =\text{0 }$ and $\delta =0.4$

4.2 Effect of connecting rod length difference $l_{\mathrm {0}}$

The amplitude–frequency curves for various $l_{0}$ are shown in Fig. 14. It can be observed that the rod length difference $l_{0}$ has little effect on the response amplitude in high frequencies. When there is no nonlinear damping, increasing $l_{0}$ can lead to an increase in the resonant frequency and a decrease in the peak amplitude. When $\zeta _{2} =0.2$, the resonant frequency increases at first and then decreases with the increase of $l_{0}$, as shown in Fig. 14b. However, the peak amplitude keeps decreasing.

Fig. 14

Amplitude–frequency curves for various $l_{0}$ when $l_{1} =\text{0.75 }$ and $\delta =0.4$

The force transmissibility curves for various $l_{0}$ are shown in Fig. 15. It is worth noting that increasing $l_{0}$ also has little effect on the performance in high frequencies. When there is no nonlinear damping, increasing $l_{0}$ can lead to an increase in the peak transmissibility. For the case of $\zeta _{2} =0.2$, the peak transmissibility keeps decreasing when $l_{0}$ increases. Therefore, selecting a larger rod length difference is beneficial when the nonlinear damping is considered.

Fig. 15

Force transmissibility curves for various $l_{0}$ when $l_{1} =\text{0.75 }$ and $\delta =0.4$

4.3 Effect of prestretching length $\delta$

The amplitude–frequency curves for various $\delta$ are shown in Fig. 16. It can be found that increasing $\delta$ can reduce the resonant frequency but lead to an increase in the peak amplitude. Besides, it leads to an increase in the response amplitude over low frequencies, but has little influence on the response amplitude in high frequencies.

Fig. 16

Amplitude–frequency curves for various $\delta$ when $l_{1} =0.75$, $l_{0} =\text{0 }$, and $\zeta _{2} =0.2$

Fig. 17

Force transmissibility curves for various $\delta$ when $l_{1} =0.75$, $l_{0} =\text{0 }$, and $\zeta _{2} =0.2$

The force transmissibility curves for various $\delta$ are shown in Fig. 17. Generally, increasing $\delta$ can reduce the peak transmissibility and expand the vibration isolation frequency band. There is little effect on the performance in high frequencies. Thus, selecting a larger prestretching length is beneficial to the low-frequency vibration isolation.

4.4 Effect of damping ratio $\zeta _{2}$

The amplitude–frequency curves for various $\zeta _{2}$ are shown in Fig. 18. Generally, increasing $\zeta _{2}$ can lead to a decrease in both the resonant frequency and the peak amplitude. Moreover, it can also suppress the response amplitude in the resonant region, but has little effect on the amplitude in high frequencies.

The force transmissibility curves for various $\zeta _{2}$ are shown in Fig. 19. Similarly, increasing $\zeta _{2}$ can effectively reduce the transmissibility in the resonant region. Meanwhile, there is little effect on the performance in the isolation region.

Fig. 18

Amplitude–frequency curves for various $\zeta _{2}$ when $l_{1} =0.75$, $l_{0} =\text{0 }$, and $\delta =0.4$

Fig. 19

Force transmissibility curves for various $\zeta _{2}$ when $l_{1} =0.75$, $l_{0} =\text{0 }$, and $\delta =0.4$

Fig. 20

A classical QZS vibration system at the equilibrium position

4.5 Comparison with an existing QZS vibration system

To verify the superior performance of the proposed QZS vibration system, an existing QZS vibration system [35] is given for comparison, as shown in Fig. 20. This classical QZS vibration system is composed of three springs and three linear viscous dampers. Concretely, the stiffness of the horizontal and vertical springs is $k_{h}$ and $k_{v}$, respectively. The damping coefficients of the horizontal and vertical viscous dampers are separately $c_{h}$ and $c_{v}$. The distance between the base wall and the isolation object with rated mass m is $L_{e}$. It is assumed that the precompression length of the horizontal springs is d at the equilibrium position. The displacement of the object from the static equilibrium position in the vertical direction is x.

The nondimensional restoring force, stiffness, and damping force of the system are separately given by

$$\begin{aligned} f\left( u \right)= & {} u+2\beta u\left( {1-\frac{\delta +1}{\sqrt{u^{2}+1} }} \right) \end{aligned}$$

(40)

$$\begin{aligned} k\left( u \right)= & {} 1+\frac{2\beta u^{2}}{u^{2}+1}-\frac{2\beta \left( {\delta +1-\sqrt{u^{2}+1} } \right) }{\left( {u^{2}+1} \right) ^{3 / 2}}\end{aligned}$$

(41)

$$\begin{aligned} f_{d} \left( {u,\;\dot{{u}}} \right)= & {} \frac{2\zeta _{2} u^{2}}{u^{2}+1}{u}' \end{aligned}$$

(42)

The QZS condition is given by

$$\begin{aligned} \beta =\frac{1}{2\delta } \end{aligned}$$

(43)

Therefore, the approximate restoring force and the approximate damping force using Taylor series expansion are separately given by

$$\begin{aligned} f_{q}^{a} \left( u \right)= & {} \frac{\delta +1}{2\delta }u^{3}-\frac{3\left( {\delta +1} \right) }{8\delta }u^{5} \end{aligned}$$

(44)

$$\begin{aligned} f_{d}^{a} \left( {u,\;\dot{{u}}} \right)= & {} 2\zeta _{2} \left( {u^{2}-u^{4}} \right) {u}' \end{aligned}$$

(45)

Fig. 21

Isolation performance comparison between the proposed QZS vibration system, an existing QZS vibration system, and the linear one when $l_{1} =0.75$, $l_{0} =\text{0 }$, $\zeta _{1} =0.02$, and $\delta =0.4$

Substituting Eqs. (44) and (45) into Eq. (30) and following the same procedure in Sect. 3 can obtain the same amplitude–frequency equation as Eq. (36). The isolation performance comparison between the proposed QZS vibration system, an existing QZS vibration system, and the linear one is shown in Fig. 21. Compared with an existing QZS vibration system, the proposed one not only has lower peak transmissibility but also has a wider vibration isolation frequency band for different levels of excitation amplitude no matter if there is nonlinear damping. Moreover, compared with the linear vibration system, the proposed QZS vibration system has a much wider vibration isolation frequency band and lower force transmissibility in high frequencies. Therefore, the proposed QZS vibration system can achieve excellent isolation performance.

5 Conclusions

A novel QZS vibration system with scissor-like structures is proposed. The mathematical model of the proposed system is established, and the length difference between the connecting rods in the SLS is considered. It is demonstrated that the QZS property and the nonlinear damping all can be obtained using the SLS. The parametric analysis shows that the geometric nonlinear stiffness can ensure that the system has a wide frequency band of vibration isolation. Applying geometric nonlinear damping can suppress the high-amplitude vibration in the resonant region, while the isolation performance in high frequencies remains unaffected. The performance of the QZS vibration system can be adjusted flexibly by four parameters. Moreover, the proposed QZS vibration system can outperform a classical one.

Appendix A

$$\begin{aligned} f_{q} \left( u \right)= & {} u-\frac{l_{h} }{\delta \left( {1-l_{0}^{2} } \right) }\left( {\delta -l_{h}+\sqrt{4l_{1}^{2} -\left( {\frac{u^{2}+1+l_{\text{0 }} }{\sqrt{u^{2}+1} }} \right) ^{2}} } \right) \nonumber \\&\cdot \;\frac{u\left( {\left( {u^{2}+1} \right) ^{2}-l_{0}^{2} } \right) }{\left( {u^{2}+1} \right) ^{{\text{3 }}/{\text{2 }}}\sqrt{4l_{1}^{2} \left( {u^{2}+1} \right) -\left( {u^{2}+1+l_{\text{0 }} } \right) ^{2}} } \end{aligned}$$

(A.1)

$$\begin{aligned} k_{q} \left( u \right)= & {} 1+\frac{l_{h} u^{2}\left( {\left( {u^{2}+1} \right) ^{2}-l_{0}^{2} } \right) ^{2}}{\delta \left( {1-l_{0}^{2} } \right) \left( {u^{2}+1} \right) ^{3}\left( {4l_{1}^{2} \left( {u^{2}+1} \right) -\left( {u^{2}+l_{0} +1} \right) ^{2}} \right) }\nonumber \\&+\frac{l_{h} \left( {\delta \sqrt{u^{2}+1} -l_{h} \sqrt{u^{2}+1} +\sqrt{4l_{1}^{2} -\left( {u^{2}+l_{0} +1} \right) ^{2}} } \right) }{2\delta \left( {1-l_{0}^{2}} \right) \left( {u^{2}+1} \right) ^{2}\sqrt{4l_{1}^{2} \left( {u^{2}+1} \right) -\left( {u^{2}+l_{0} +1} \right) ^{2}} }\nonumber \\&\cdot \,\left[ {2l_{0}^{2} -2\left( {u^{2}+1} \right) \left( {5u^{2}+1} \right) +2u^{2}\left( {\left( {u^{2}+1} \right) ^{2}-l_{0}^{2} } \right) \left( {\frac{3}{u^{2}+1}+\frac{4l_{1}^{2} -2u^{2}-2l_{0} -2}{4l_{1}^{2} \left( {u^{2}+1} \right) -\left( {u^{2}+l_{0} +1} \right) ^{2}}} \right) } \right] \end{aligned}$$

(A.2)