${\mathcal {H}}_{2}$ optimization and numerical study of inerter-based vibration isolation system helical spring fatigue life

Abstract

This paper presents an optimization and numerical analysis of vibration-induced fatigue in a two degree-of-freedom inerter-based vibration isolation system. The system is comprised of a primary, e.g. source body, and a secondary, e.g. receiving body, mutually connected through an isolator. The isolator includes a spring, a dashpot and an inerter. Inerter is a mechanical device which produces a force proportional to relative acceleration between its terminals. A broadband frequency force excitation of the primary body is imposed throughout the study. The goal of the proposed optimization is to prolong the fatigue life of the ground connecting helical spring of the secondary body. The optimization is based on minimizing separately the displacement and velocity amplitudes. Both optimization criteria are compared with regard to spring fatigue life improvement for fair benchmark comparison. The inerter-based optimized systems, in which the ${\mathcal {H}}_{2}$ index of the receiving body is minimized, are also compared with the optimized systems without inerter. Notable improvements are observed in inerter-based systems due to the inclusion of an optimally tuned inerter in the isolator. The proposed analytical vibration fatigue method optimization results are compared with the finite element method results, and a very good agreement is observed. Most accurate helical spring deflection and stress correction factors are discussed and determined. Furthermore, the inerter concept is successfully implemented into finite element-based dynamic solution.

1 Introduction

The cylindrical helical coil spring is one of the fundamental and most important key mechanical components found in many industrial applications (e.g. vehicle suspension components, automotive valve springs, stamping presses, brakes). Springs are typically used to perform required mechanical functions (i.e. apply, transfer, indicate or maintain a force/torque, store energy and provide the system with the flexibility [1]).

Vibration isolation systems [2] (e.g. car suspension) are often subjected to high dynamic loading during service. These loadings can cause harmful vibrations and may result with premature failure from aggressive fatigue mechanisms which are especially prominent in case of resonant harmonic excitations [2, 3]. Massive spring used in the suspension systems [3, 4] is a common example where the crack may initiate at a high stress location and eventually propagate. This can lead to fatigue failure, especially due to vibration-induced fatigue effects [2, 3, 5]. In order to estimate the vibration fatigue, it is necessary to predetermine stiffness, strength and damping parameters of the system. In particular, all of the above-mentioned parameters should be taken into account while evaluating the helical spring fatigue life [2]. The springs as machine elements should withstand long exploitation period. Hence, they are commonly evaluated with appropriate high-cycle fatigue (HCF) calculation method (above $10^{3}$ life cycles) [2]. Shear-governed life criterion is normally considered for spring fatigue calculation where highly stressed region is usually located at the inner side of the helix [1, 2]. Contrary to that traditional concept, Todinov [6] in accordance with Del Llano-Vizcaya et al. [7] states that the highest stress region is reported at the outer surface of the helical compression springs with a large coil to wire radius ratio, rather than usual inside of the helix. Consequently, the fatigue crack origin will presumably also be located on the outer surface where the maximum amplitude of the principal tensile stress occurs. Furthermore, it is in accordance with the stress field obtained from numerical fatigue analysis via finite element method (FEM) [7]. As discussed in [2], the problem with unambiguous definition of the stress field and the corresponding fatigue life is noted in the literature since multiple stress correction factors for helical spring are proposed. One of the most often used and cited expressions originate from Wahl [8], Bergsträsser [2], Göhner [9,10,11] and Ancker and Goodier (A/G) [2, 12,13,14,15,16,17,18,19]. The investigation conducted by Calder et al. [14] reported that A/G and Wahl stress correction factors differ only slightly for small spring pitch angles. Moreover, the Wahl correction factor matched with their experimental stress measurements of a helical coil automobile spring within less than $\pm \, 1\%$ difference. It is often discussed whether using aforementioned stress correction factors may result with highly conservative fatigue life prediction [1, 2].

Numerically determining the vibration fatigue life is an increasingly evolving field. Various researchers use mostly FEM-based software for calculation depending on the availability, application and functionality [5, 20,21,22]. Rahman et al. [23] used FEM for obtaining stress amplitudes of engine components and performing corresponding fatigue calculation. Authors employed a power spectral density (PSD) load and obtained fatigue results in the frequency domain. According to Halfpenny [24] and also reported by Mršnik et al. [25, 26], operating with a PSD proves to be rather beneficial when working with complicated and computationally expensive FEM models. Hence, the calculation of the frequency response functions (FRFs) is convenient and much faster than a long-term transient dynamic analysis in the time domain [5]. When loading conditions are prescribed in the form of PSD which is defined in a frequency domain, structural response of systems can be computed by using the transfer function (TF), i.e. FRF of target systems and PSD of excitation loads [24]. Mršnik et al. also gave important scientific contribution to further understanding of the vibration-induced fatigue phenomena by studying multi-axial stress effects [25] and various frequency domain methods [26]. In [25], authors used both FEM and experimental approaches where similar numerical model was analysed as in [27]. Česnik and Slavič [27] investigated harmonic and random kinematic/base excitation load on the aluminium alloy “Y”-shaped specimen and used custom vibration fatigue plug-in developed for the commercial FEM package analysis environment. Furthermore, the numerically predicted fatigue life was compared to the experimental results. The results obtained via numerical analysis estimated substantially more conservative fatigue life compared to the actual fatigue life. Opposed to common unimodal (i.e. narrow-band PSD), Braccesi et al. [28] considered bimodal PSD for random stress process and created custom FE-based fatigue life calculation code valid for the frequency domain. Additionally, Bonte et al. [29] used combination of various FEM packages for the calculation of the vibration fatigue life. They developed a commercially used simulation method for the fatigue analysis of automotive and other products that are subjected to multiple random excitations by adopting PSD. Furthermore, Zhou et al. [30] used modal stress approach in random vibration fatigue assessment by employing FEM. The conducted investigations consisted of a two-step procedure. In the first step, modal stress analysis is conducted to locate the fatigue hotspots in a dynamic structure, while in the second step the frequency domain-based approach for random fatigue evaluation is performed at fatigue hotspots through PSD.

Vibration systems are commonly tuned (i.e. optimized) according to some optimization criterion. One of the metrics for vibrations of the dynamic structures is square vibration amplitude over the entire frequency range. Proposing the optimization of this quantity is first attributed to Warburton [31] and is generally referred to as ${\mathcal {H}}_{2}$ optimization [32,33,34]. ${\mathcal {H}}_{2}$ optimization has the objective function of minimizing the total vibration energy, i.e. mean square motion of the dynamic structure under the white noise of the PSD excitation [31]. Studies which incorporate this method usually employ the minimization of specific kinetic energy (i.e. vibration velocity amplitudes) [2, 32, 35]. However, alternate studies such as minimization of displacement amplitudes can also be applied [34]. Inerter is a novel mechanical element conceived and developed by Smith [4]. Inerter produces a force which is proportional to relative acceleration ($a_{2}-a_{1}$) between its terminals where equation $F_{\mathrm{inerter}}=b(a_{2~}-a_{1})$ holds. The coefficient of inerter resistance force $F_{\mathrm{inerter}}$ is called inertance. It is denoted by label “b” and is measured in kilograms, in SI units. Inerters are mathematically approximated in the same sense as, for example, springs and dashpots. Consequently, it is assumed that inerter mass is rather small compared to inertance it provides [2, 4, 35].

In the preceding work [2], all the above presented concepts were implemented into an analytical solution. Although this problem is discussed in other studies [34,35,36,37,38], reference [2] is further suitably referred to, as this previously proposed approach addresses vibration isolation and fatigue life assessment simultaneously. The unit PSD load was applied on the dynamic system. The minimization of the specific kinetic energy of inerter-based system in the frequency domain yielded substantial reduction in vibration velocity amplitudes. Consequently, extension of the corresponding cylindrical spring fatigue life was reported. However, concerns were raised whether the exclusively fatigue-based optimization would prove more efficient with regard to the spring fatigue life when compared to solely kinetic energy-based optimization. The aim of this study is to revisit and address this question by employing alternate displacement-based criterion and utilizing linear FEM to assess the accuracy of the adopted expressions [2], especially with regard to before discussed approximate spring stress and displacement correction factors. Using FEM as control verification tool with a purpose of benchmark comparison is a common practice used in conjunction with complex analytical calculations [39].

In this study, which is a direct continuation leading the approach of the same problem from previous work [2], the goal is to model the fatigue load of a helical spring acting as a linear elastic element in a simplified two degree-of-freedom (2-DOF) inerter-based vibration isolation system. Analytical and numerical methods are employed by means of specialized software packages: FEM-based Abaqus [40] and Fe-Safe [41]. Fe-Safe can import and analyse FEM generated static/dynamic multi-axial complex stress fields with the aim of assessing the fatigue life. The paper is structured as follows. In Sect. 2, analytical mathematical 2-DOF inerter-based vibration isolation system model is established where optimized parameters for both viscous damper and inerter are determined. ${\mathcal {H}}_{2}$ optimization of the newly proposed displacement and referent velocity amplitudes [2] is used as a criterion. Novel displacement-based optimization parameters for inertance and damping are derived and explicitly given. In Sect. 3, various dimensionless spring deflection and stress correction factors from the referent literature are revisited from [2] and discussed. The accuracy of previously derived Timoshenko/Cowper (T/C)-based deflection factor [2, 8] is determined. The most accurate spring correction factors are later used in the context of analytically calculating displacement and stress amplitudes under PSD force loading. In Sect. 4, previously established deflection and stress correction factors are further discussed by comparing analytically obtained results with FEM. Final Sect. 5 presents a benchmark example adopted from [2] by utilizing all before proposed methods and finally comparing analytical and numerical results of the vibration fatigue optimization study. Previously derived analytical expression [2] based on the von Mises energy criterion for shear-governed biaxial and proportional stress is verified. The proposed expression explicitly ties vibration displacement amplitudes with HCF life of the helical spring. Moreover, the ideal inerter concept is implemented in the commercial FEM code Abaqus.

2 2-DOF inerter-based vibration isolator mathematical model

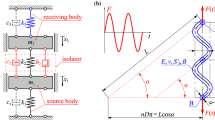
In this chapter, the generalized analytical model for the discrete 2-DOF inerter-based vibration isolation system optimization process is established as a straightforward closed-form solution. The studied problem is fully adopted from [2] and represented by a simple model shown in Fig. 1a. It is assumed that the critical fatigue component is a helical spring $k_{3,}$ shown in Fig. 1b. The material parameters of the spring are as follows: E is Young modulus, $\nu$ is Poisson’s ratio, $S'_{\mathrm{f}}$ is fatigue strength coefficient and B is Basquin’s exponent [2] denoted in capital letter in order not to be mistaken for inertance b. Number of active coils is designated as n ($n=2$ in Fig. 1b), h is spring total length where $h=n\cdot l$ for $n=$ arbitrary $\hbox {integer}\ge 1$, and l is the spring pitch. D and d are large and small spring diameters, respectively, while $C=D/d$ is defined as spring index [1, 2]. Recommended values of spring index C for practical engineering purposes lie in between $C=4{-}12$ [2]. Angle $\alpha$ represents the pitch angle which can be calculated according to usual geometric expression $\alpha =\hbox {arctan}[l/(\pi D)]$ (Fig. 1b).

Fig. 1

a 2-DOF linear discrete vibration isolation system, b helical spring $k_{3}$ properties [2]

The goal of the vibration-based optimization is to minimize vibrations of the secondary or receiving body, i.e. vibrations of mass $m_{2}$ which are proportional to the maximum deflection amplitudes of the spring $k_{3}$. In this optimization, the excitation of the primary/source body $F_{1}(t)$ is assumed to contain white noise spectral properties [2, 35], i.e. unit PSD loading amplitude $F_{01}(\varOmega )=1$ over the entire frequency range. The whole vibration system consists of discrete masses $m_{1}$ and $m_{2}$, ideally massless springs $k_{1}$, $k_{2}$ and $k_{3}$, viscous dampers $c_{1}$, $c_{2}$ and $c_{3}$ and an inerter of inertance $b_{2}$. Isolator consists of spring $k_{2}$, damper $c_{2}$ and inerter $b_{2}$. The ideal inerter produces a force $F_{\mathrm{inerter}}$ proportional to the relative acceleration [4] between masses $m_{1}$ and $m_{2}$. The described discrete parameter approximation may represent a reduced-order model [36] of a system of a more complex nature [37] which includes distributed mass, stiffness and damping parameters, as discussed in [35, 38]. The damping of the source and receiving bodies is assumed to be negligible (i.e. $c_{1}\approx c_{3}\approx$0) which provides for substantially more simple solution derivation. However, the relations are also approximately valid for the systems with small inherent damping [35].

The equations of motion [2, 3, 35] for system in Fig. 1a can be written in the general matrix form as

$$\begin{aligned} \mathbf{M}{{\ddot{\mathbf{x}}}}\left( t \right) +\mathbf{C}{{{\dot{\mathbf{x}}}}}\left( t \right) +\mathbf{Kx}\left( t \right) =\mathbf{F}\left( t \right) , \end{aligned}$$

(1)

where M is the global mass matrix, C is the global damping matrix, K is the global stiffness matrix and F(t) is the excitation column force vector. Displacement of the masses $m_{1}$ and $m_{2}$ from static equilibrium position, velocity and acceleration vectors are denoted by x(t), ${{{\dot{{\mathbf{x}}}}}}(t)$ and ${{{\ddot{{\mathbf{x}}}}}}(t)$, respectively.

Global matrices and vectors from Eq. (1), accounting for negligible damping $c_{1}$ and $c_{3}$, can be written as

$$\begin{aligned}&\mathbf{M}=\left[ {{\begin{array}{cc} {m_1 +b_2 }&{}\quad {-b_2 } \\ {-b_2 }&{}\quad {m_2 +b_2 } \\ \end{array} }} \right] , \quad \mathbf{C}=\left[ {{\begin{array}{cc} {c_2 }&{}\quad {-c_2 } \\ {-c_2 }&{}\quad {c_2 } \\ \end{array} }} \right] , \quad \mathbf{K}=\left[ {{\begin{array}{cc} {k_1 +k_2 }&{}\quad {-k_2 } \\ {-k_2 }&{}\quad {k_2 +k_3 } \\ \end{array} }} \right] , \end{aligned}$$

(2a, b, c)

$$\begin{aligned}&\mathbf{x}=\left[ {{\begin{array}{cc} {x_1 \left( t \right) } \\ {x_2 \left( t \right) } \\ \end{array} }} \right] , \quad \mathbf{F}=\left[ {{\begin{array}{cc} {F_1 \left( t \right) } \\ 0 \\ \end{array} }} \right] , \end{aligned}$$

(3a, b)

where the parameters and functions in the matrices and vectors are denoted in Fig. 1a. Due to influence of inerter $b_{2}$, mass matrix M from Eq. (2a) is no longer diagonal [3]; however, it is still symmetric [2, 35].

By assuming harmonic excitation and expressing the excitation and the steady-state response in the complex form $\mathbf{F}(t)=\mathbf{F}_{0}\hbox {e}^{\mathrm{{i}}\varOmega t}$ and $\mathbf{x}(t)=\mathbf{x}_{0}\hbox {e}^{\mathrm{{i}}\varOmega t}$, where $\hbox {i}=\sqrt{-1}$, the solution of Eq. (1) can be directly written as

$$\begin{aligned} \mathbf{x}_0 \left( \varOmega \right) =\left[ {{\begin{array}{lllll} {x_{01} }&{} {x_{02} } \\ \end{array} }} \right] ^{\mathrm {T}}=\left[ {\left( {\mathrm{{i}}\varOmega } \right) ^{2}{} \mathbf{M}+\mathrm{{i}}\varOmega \mathbf{C}+\mathbf{K}} \right] ^{-1}\mathbf{F}, \end{aligned}$$

(4)

where terms inside the square bracket denote dynamic stiffness matrix and $\mathbf{x}_{0}(\varOmega )$ is the complex displacement amplitude. Multiplying Eq. (4) with the term i $\varOmega$ yields complex velocity amplitude $\mathbf{v}_{0}$ expression which can be written as

$$\begin{aligned} {{{{\dot{\mathbf{x}}}}}}_0 \left( \varOmega \right) \equiv \mathbf{v}_0 \left( \varOmega \right) =\left[ {{\begin{array}{lllll} {{\dot{x}}_{01} }&{} {{\dot{x}}_{02} } \\ \end{array} }} \right] ^{\mathrm {T}}=\hbox {i}\varOmega \mathbf{x}_0 \left( \varOmega \right) . \end{aligned}$$

(5)

By considering M, C and K matrices from Eq. (2a–c), the steady-state (i.e. time-invariant) complex response of the mass $m_{2}$ can now be expressed in simplified form as the following FRFs

$$\begin{aligned} \frac{x_{02} \left( \varOmega \right) }{F_{01} }=\frac{B_0 +\left( {\hbox {i}\varOmega } \right) B_1 +\left( {\hbox {i}\varOmega } \right) ^{2}B_2 +\left( {\hbox {i}\varOmega } \right) ^{3}B_3 }{A_0 +\left( {\hbox {i}\varOmega } \right) A_1 +\left( {\hbox {i}\varOmega } \right) ^{2}A_2 +\left( {\hbox {i}\varOmega } \right) ^{3}A_3 +\left( {\hbox {i}\varOmega } \right) ^{4}A_4 },\quad \frac{{\dot{x}}_{02} \left( \varOmega \right) }{F_{01} }\equiv \frac{v_{02} \left( \varOmega \right) }{F_{01} }=\hbox {i}\varOmega \frac{x_{02} \left( \varOmega \right) }{F_{01} }, \end{aligned}$$

(6a, b)

where coefficients $A_{0 }-A_{4 }$ and $B_{0 }-B_{3}$ with respect to Eq. (6a, b) are defined as

$$\begin{aligned} \begin{array}{lllll} A_0 =\left( {k_2 +k_3 } \right) k_1 +k_2 k_3 \\ A_1 =c_2 \left( {k_1 +k_3 } \right) \\ A_2 =\left( {m_2 +b_2 } \right) k_1 +\left( {m_1 +m_2 } \right) k_2 +\left( {m_1 +b_2 } \right) k_3 \\ A_3 =c_2 \left( {m_1 +m_2 } \right) \\ A_4 =\left( {m_2 +b_2 } \right) m_1 +b_2 m_2 \\ \end{array}, \quad \begin{array}{lllll} B_0 \left( {x_0 } \right) =k_2 \\ B_1 \left( {x_0 } \right) =c_2 \\ B_2 \left( {x_0 } \right) =b_2 \\ B_3 \left( {x_0 } \right) =0 \\ \\ \end{array}, \quad \begin{array}{lllll} B_0 \left( {v_0 } \right) =0 \\ B_1 \left( {v_0 } \right) =k_2 \\ B_2 \left( {v_0 } \right) =c_2 \\ B_3 \left( {v_0 } \right) =b_2 \\ \\ \end{array}. \end{aligned}$$

(7a--m)

The transfer admittance (i.e. FRF ${x_{02} }/{F_{01} }$) from Eq. (6a) represents the complex displacement amplitude of the receiving body per unit forcing $F_{01 }=$1 of the source body. The transfer mobility (i.e. FRF ${v_{02} }/{F_{01} })$ from Eq. (6b) represents the complex velocity amplitude of the receiving body per unit forcing $F_{01 }=1$ of the source body. Coefficients $B_{0 }-B_{3}$ from Eq. (7) are different with regard to variables of displacement $x_{02}$ and velocity $v_{02}$ amplitudes, respectively [i.e. Eqs. (4) and (5)]. FRFs from Eq. (6a, b) are further used to assess the effectiveness of the vibration isolation. Considering that the excitation force $F_{1 }$ with the unit PSD is assumed, the ${\mathcal {H}}_{2}$ index of the receiving body $I_{{\mathcal {H}}2}$ per unit excitation force can be calculated with relations that write as

$$\begin{aligned} I_{{{\mathcal {H}}}2} \left( {x_0 } \right) =\mathop \int \limits _{-\infty }^\infty {\left| {\frac{x_{02} \left( \varOmega \right) }{F_{01} }} \right| ^{2}} \hbox {d}\varOmega ,\quad I_{{{\mathcal {H}}}2} \left( {v_0 } \right) =\mathop \int \limits _{-\infty }^\infty {\left| {\frac{v_{02} \left( \varOmega \right) }{F_{01} }} \right| ^{2}} \hbox {d}\varOmega , \end{aligned}$$

(8a, b)

according to [31] and demonstrated in [2, 32,33,34,35]. The ${\mathcal {H}}_{2}$ indices of the receiving body (i.e. $I_{{\mathcal {H}}2})$ from Eq. (8a, b) are used throughout this study as a quantitative measure of the broadband frequency vibration isolation performance quality. The objective is to minimize this quantity for all vibration isolation systems analysed in the scope of the conducted investigation. Vibration-based optimization with the goal of vibration reduction by using this particular method can be found in [2, 32,33,34,35]. The ${\mathcal {H}}_{2}$ index in Eq. (8) for $I_{{\mathcal {H}}2 }=I_{4}$ can according to [2, 35] analytically be calculated with closed-form polynomial expression which can be written as

$$\begin{aligned} I_{{{\mathcal {H}}}2\left( 4 \right) } ={\pi }\frac{A_0 B_3^2 \left( {A_0 A_3 -A_1 A_2 } \right) +A_0 A_1 A_4 \left( {2B_1 B_3 -B_2^2 } \right) -A_0 A_3 A_4 \left( {B_1^2 -2B_0 B_2 } \right) +A_4 B_0^2 \left( {A_1 A_4 -A_2 A_3 } \right) }{A_0 A_4 \left( {A_0 A_3^2 +A_1^2 A_4 -A_1 A_2 A_3 } \right) },\nonumber \\\end{aligned}$$

(9)

where substituting coefficients $A_{0 }-A_{4 }$ and $B_{0 }-B_{3 }$ from Eq. (7) into Eq. (9) yields with the final ${\mathcal {H}}_{2}$ index $I_{{\mathcal {H}}2}$ analytical expression, which is herein omitted for substantial length [2]. In Eq. (9), index “4” denotes fourth-order polynomial of the denominator with regard to the term i$\varOmega$ in Eq. (6).

Two fundamental circular natural frequencies $\omega _{n1,2}$ of the given 2-DOF vibration system can be analytically obtained by solving the classic eigenvalue problem [2, 3] which readily writes as

$$\begin{aligned} \left[ {\mathbf{K}-\left( {\omega _{n1,2} } \right) ^{2}{} \mathbf{M}} \right] \mathbf{x}\left( t \right) =0, \end{aligned}$$

(10)

where influence of inertance $b_{2}$ on eigenvalues is demonstrated later on. The following expressions

$$\begin{aligned} \varOmega _{\mathrm{A}} =\sqrt{\frac{k_2 }{b_2 }},\quad \mathop {\lim }\limits _{c_2 ,k_2 \rightarrow \infty } \varOmega _{\mathrm{a}} =\sqrt{\frac{k_1 +k_3 }{m_1 +m_2 }}, \end{aligned}$$

(11a, b)

denote anti-resonance $\varOmega _{\mathrm{A}}$ and isolator-locking circular frequency $\varOmega _{\mathrm{a}}$, respectively, as reported in [2, 35].

In the next subchapters of this study, two main types of the vibration transmission control are analysed with respect to minimizing the index $I_{{\mathcal {H}}2}$. The isolation control without inerter (i.e. $b_{2 }=0$) and the isolation control with optimized inertance $b_{\mathrm{opt}}$ are considered. The optimized isolator damping and inertance parameters are obtained by minimizing the frequency averaged index $I_{{\mathcal {H}}2}$ of the receiving body denoted symbolically in Eq. (9). The displacement and velocity amplitudes criteria are used, respectively. As discussed in [2], due to this particular problem definition, spring $k_{2}$ cannot be optimized and is further considered as constrained/fixed value bound by physical limits [35].

2.1 Isolation optimization considering displacement amplitudes

The parameters from Eq. (7a–i) are considered. The procedure explained in [2] is applied. Differentiating Eq. (9) with respect to damping $c_{2}$, equalling with zero and again solving for damping $c_{2}$ yield with

$$\begin{aligned} c_{\mathrm {2}\left( {b_2 \ne 0} \right) } \left[ {{{\mathcal {H}}}_2 \left( {x_0 } \right) } \right] =\sqrt{\frac{{\begin{array}{c} \left( {m_1 +m_2 } \right) ^{2}k_2 ^{3}+\left[ {k_3 m_1 ^{2}+m_2 ^{2}k_1 -2{}\left( {m_1 +m_2 } \right) \left( {k_3 +k_1 } \right) b_2 } \right] k_2 ^{2} \\ +\left[ {\left( {k_3 +k_1 } \right) ^{2}b_2 -2{}k_1 k_3 \left( {m_1 +m_2 } \right) } \right] b_2 k_2 +\left( {k_3 +k_1 } \right) b_2 ^{2}k_1 k_3 \\ \end{array}}}{\left[ {\left( {k_2 +k_3 } \right) k_1 +k_2 k_3 } \right] \left( {m_1 +m_2 } \right) }}, \end{aligned}$$

(12)

where $c_{2}$ now represents optimum damping $c_{\mathrm{opt}}(b_{2})$ for any given inertance $b_{2}$. By substituting Eq. (12) into Eq. (9), differentiating with respect to $b_{2}$, equalling with zero and solving for $b_{2}$, optimum inertance parameter $b_{\mathrm{opt}}$ is obtained. Inserting $b_{2~}= b_{\mathrm{opt}}$ into Eq. (12) results with optimum damping $c_{\mathrm{opt2}}$. These expressions write as

$$\begin{aligned} c_{\mathrm {opt2}} \left[ {{{\mathcal {H}}}_2 \left( {x_0 } \right) } \right] =\frac{k_2 \left| {k_1 m_2 -m_1 k_3 } \right| }{\sqrt{\left[ {\left( {k_2 +k_3 } \right) k_1 +k_2 k_3 } \right] \left( {m_1 +m_2 } \right) \left( {k_1 +k_3 } \right) }}, \quad b_{\mathrm {opt}} \left[ {{{\mathcal {H}}}_2 \left( {x_0 } \right) } \right] =\frac{k_2 \left( {m_1 +m_2 } \right) }{k_1 +k_3 }. \end{aligned}$$

(13a, b)

By setting the inertance $b_{2 }=0$ in Eq. (12), the optimum damping $c_{\mathrm{opt}}$ for the case without inerter is

$$\begin{aligned} c_{\mathrm {opt}\left( {b_2 =0} \right) } \left[ {{{\mathcal {H}}}_2 \left( {x_0 } \right) } \right] =k_2 \frac{\sqrt{\left( {m_1 +m_2 } \right) ^{2}k_2 +k_1 m_2^2 +k_3 m_1^2 }}{\sqrt{\left[ {\left( {k_2 +k_3 } \right) k_1 +k_2 k_3 } \right] \left( {m_1 +m_2 } \right) }}. \end{aligned}$$

(14)

Derived Eqs. (13, 14) unambiguously represent closed-form algebraic solutions for optimized damping and inertance parameters regarding displacement-based, i.e. consequently fatigue-based optimization.

2.2 Isolation optimization considering velocity amplitudes

The proposed procedure described in [2] is further utilized for optimization process. The parameters from Eq. (7a–e, j–m) are considered further. Differentiating Eq. (9) with respect to damping $c_{2}$, equalling with zero and again solving for damping $c_{2}$ yield with already known solution

$$\begin{aligned} c_{\mathrm {2}\left( {b_2 \ne 0} \right) } \left[ {{{\mathcal {H}}}_2 \left( {v_0 } \right) } \right] =\sqrt{\frac{m_1 +m_2 }{k_1 +k_3 }k_2 ^{2}-2{}b_2 k_2 +\frac{m_1 k_3 ^{2}+m_2 k_1 ^{2}+b_2 \left( {k_1 +k_3 } \right) ^{2}}{\left( {k_1 +k_3 } \right) \left[ {m_1 \left( {b_2 +m_2 } \right) +b_2 m_2 } \right] }b_2 ^{2}}, \end{aligned}$$

(15)

where $c_{2}$ represents optimum damping $c_{\mathrm{opt}}(b_{2})$ for any given inertance $b_{2}$, but now in the context of velocity amplitudes, i.e. kinetic energy optimization. For inertance $b_{2 }=$0, Eq. (15) morphs into simpler relation

$$\begin{aligned} c_{\mathrm {opt}\left( {b_2 =0} \right) } \left[ {{{\mathcal {H}}}_2 \left( {v_0 } \right) } \right] =k_2 \sqrt{\frac{m_1 +m_2 }{k_1 +k_3 }}, \end{aligned}$$

(16)

which represents the optimum damping coefficient $c_{2 }=c_{\mathrm{opt}}$. As reported in [2], explicit expressions for $b_{\mathrm{opt}}$ and $c_{\mathrm{opt2}}$ in the context of velocity-based optimization are not shown due to the fact that they are rather lengthy and cannot be expressed in the convenient algebraic form although they are purely analytical. Interestingly, displacement-based optimization yields with much simpler final expressions for optimized parameters. Albeit, initial Eq. (15) seems more straightforward for further manipulation when compared to Eq. (12).

3 Helical spring displacement and stress correction factors

In this chapter, spring stiffness and stress corrections from the literature are reviewed. A simple expression for determining the spring fatigue life is recapitulated from [2] where HCF life is addressed and employed. Obtained displacement amplitudes in the frequency domain from previous chapter [see Eq. (4)] can now be tied to stress amplitudes necessary for performing the vibration fatigue analysis. The cylindrical spring can for simplicity be viewed as a thin/slender and curved rod/beam subjected to torsion load [1]. In the case curvature, pitch and thickness effects are considered [2], and the analytical expressions for true spring stiffness $k_{\mathrm{true}}$ and maximum shear stress $\tau _{\mathrm{max}}$ are

$$\begin{aligned} k_{\mathrm {true}} =\frac{1}{K_\delta }\frac{F_0 }{\delta _{\mathrm {nom}} }=\frac{1}{K_\delta }\frac{Gd}{8C^{3}n},\quad \tau _{\max } =K_\tau \frac{8F_0 C}{{\pi }d^{2}}, \end{aligned}$$

(17a, b)

where $\delta _{\mathrm{nom }}=8C^{3}n$/(Gd) is nominal spring deflection, $K_{\delta }$ is displacement correction factor, $K_{\tau }$ is (shear) stress correction factor and $G =E/[2(1+\nu )]$ is the shear modulus. As linear elastic/small deformation and deflection conditions are assumed, Eq. (17) is valid for both tensile and compressive applied force amplitudes $\pm F_{0}$. For previously defined simple harmonic conditions, equation  $F(t)=F_{0}\hbox {e}^{i\varOmega t}$ holds. The helical spring geometry, parameters, loading and boundary conditions (BCs) are the same as schematically shown in Fig. 1b. For a more general approach in the scope of this study, boundaries of spring index C are varied both inside and outside of the recommended values $C =4{-}12$, in order to parametrically test all physically valid solutions. As already noted, additional correction factors $K_{\delta }$ and $K_{\tau }$ need to be applied for displacement and shear stress, where relations $\delta _{\mathrm{max}}=K_{\delta }\delta _{\mathrm{nom}}$ and $\tau _{\mathrm{max}}=K_{\tau }\tau _{\mathrm{nom}}$ now hold [2], while $\tau _{\mathrm{nom }}=8F_{0}C/(\pi d^{2})$ is designated as nominal shear stress.

Table 1 is adopted from [2, 13], expanded and fitly modified. It sums up all the expressions from the referent literature used in the scope of this paper. T/C deflection correction factor is proposed in [2] by adopting Timoshenko thick cantilevered shear-deformable beam analogy and Cowper’s shear correction factor for circular cross-sectional area. Göhner-based Castigliano/Timoshenko (C/T) deflection correction factor is previously derived [2] in dimensionless form and denoted in Table 1 in a more convenient and simplified form.

Table 1 Expressions for stress correction factors $K_{\tau }$ and deflection correction factors $K_{\delta }$

Furthermore, additional stress correction factors can be found in the literature. The investigation conducted by Göhner [9] directly influenced Henrici [10] who derived similar approximate stress correction factor by using Legendre power series function which yielded with more complex expression

$$\begin{aligned} K_{\tau ,\mathrm{Henrici}} =1+\frac{5}{4C}+\frac{7}{8C^{2}}+\frac{155}{256C^{3}}+\frac{11 911}{24576C^{4}}+\cdots . \end{aligned}$$

(18)

Berry [11], for instance, gives alternate Göhner stress correction equation compared to one denoted in Table 1.

$$\begin{aligned} K_{\tau ,{\mathrm{G}}\ddot{\mathrm{o}}{\mathrm{hner}}\left( {alt} \right) } =\left( {\frac{C}{C-1}+\frac{1}{4C}+\frac{1}{16C^{2}}} \right) \left( {\frac{C^{2}-1}{C^{2}-0.8125}} \right) . \end{aligned}$$

(19)

Interestingly, Eqs. (18), (19) and four-term Göhner equation from Table 1 give almost the same results for any physically acceptable value of spring index C. Moreover, Calder [14] gives alternate version of A/G correction

$$\begin{aligned} K_{\tau ,\mathrm{A/G}\left( {\hbox {Calder}} \right) } =1+\frac{5}{4C}+\frac{7}{8C^{2}}+\frac{1}{C}\tan ^{2}\left( \alpha \right) , \end{aligned}$$

(20)

which differs from the expression in Table 1, by comparing the last term denominator. However, for small pitch angle the difference is negligible compared to original A/G relation, which is in return very similar to fundamental Göhner expression [2]. A/G deflection correction factor from Table 1 can also be found in their original paper [12], and it is considered to be one of the most accurate ones found in the literature [15, 17, 19]. A/G derived detailed equations for the stresses and deflections in a helical spring using the theory of elasticity approach and employing thin slice method. They used truncated, doubly infinite power series in the terms of spring index, coil curvature and spring’s initial pitch angle or helix angle combined effects [12, 15,16,17].

All deflection correction expressions from Table 1 are shown in Fig. 2. Fully compressible material (i.e. $\nu =0$) and incompressible material (i.e. $\nu =0.5$) are considered in Fig. 2a, b, respectively. Similar study was conducted by Burns [18] where dependency of Poisson’s ratio on helical spring stiffness was evaluated.

Fig. 2

Deflection correction factors, $K_{\delta }$: a fully compressible material, $\nu =0.0$, b incompressible material, $\nu =0.5$

Simple Wood deflection correction largely deviates from rest of the curves as reported in [2], although it is included here for the sake of completeness. It is interesting to note that for $\nu =0.0$ curves are somewhat scattered for small spring indices C. However, for $\nu =0.5$ the curves based on the theory of elasticity (A/G, C/T and Göhner) uniformly converge to lower values while the rest of the curves converge to higher values.

By using appropriate vibration terminology [i.e. obtained displacement amplitudes from Eq. (4)] and considering appropriate spring stress and displacement factors with embedded von Mises distortion energy criterion, Basquin’s equation and number of cycles $N_{\mathrm{f}}$ can according to [2] finally be explicitly written as

$$\begin{aligned} N_{\mathrm{f}} =\left( {\frac{S_{\mathrm{a}} }{S^{\prime }_{\mathrm{f}} }} \right) ^{\frac{1}{B}} \Rightarrow N_{\mathrm{f}} \left( \varOmega \right) =\left[ {\sqrt{3}\frac{K_\tau }{K_\delta }\frac{G}{C^{2}n{\pi }d}\frac{\left| {x_{02} \left( \varOmega \right) } \right| }{S^{\prime }_{\mathrm{f}} }} \right] ^{\frac{1}{B}}. \end{aligned}$$

(21a, b)

The benefit of simple Eq. (21b) is that it is not obligatory to explicitly define force amplitude $F_{0}$ acting on spring $k_{3}$ (i.e. mass $m_{2}$). In the next chapter, FEM is employed for alternative $K_{\delta }$ and $K_{\tau }$ identification.

4 Finite element method helical spring displacement and stress analysis

In this chapter, spring stiffness and stress corrections are determined numerically by employing FEM-based software suite Abaqus [40]. Analytical/empirical solutions and referent relations for various deflection and stress correction factors from Table 1 are benchmarked and verified.

Table 2 shows example spring parameters used in this parametric evaluation. Mean coil diameter D is fixed at referent value $D=50$ mm, and spring wire diameter d is varied in steps of $\Delta d=3$ mm in order to obtain discrete numerical values for different spring indices C. For simplicity and computational efficiency, only one active coil is used (i.e. $n = 1$). Spring pitch l is parameterized with relation $l=2\cdot d$, analogue to the analytical model. Young’s modulus denotes standard steel material properties. However, Poisson’s ratio value is varied from $0-0.5$ in order to test the robustness and wide applicability of benchmarked displacement and stress correction factors.

Table 2 Helical spring geometric and material parametric properties

Abaqus computational model consists of structured 3D second-order 20 node hexahedron continuum elements C3D20R FE mesh. The chosen mesh employs reduced integration and shows superior performance compared to first-order elements, due to additional nodes on mid-sides of finite element [40]. Structured mesh is enabled by partitioning 3D spring geometry accordingly. Preliminary analysis is defined as linear and quasi-static (i.e. time is dimensionless). Convergence study/mesh sensitivity check is performed beforehand, and it is found that eight second-order hexahedron elements per spring thickness (i.e. wire diameter d) give sufficiently accurate results for analysed linear deflection/stress class of problems.

Figure 3a shows the FEM model with the fully defined RPs A and B and kinematic couplings with highlighted surfaces. BCs are defined through two reference points (RPs) A and B, analogue to Fig. 1b. The moving-pinned and fixed-pinned conditions are assumed as they comply with open-coil analytical assumption where the pitch angle $\alpha \ne$0 [1, 2]. Full definition of BCs is: $B(u,v,w,\varphi _{y }=0)$ and $A(u,w = 0)$. RPs A and B are coupled to belonging spring sides (i.e. outer highlighted surfaces) through kinematic attachment of type distributing. The imposed kinematic attachment allows for deformation of the connecting surfaces by using uniform weighting factors [40], i.e. surfaces coupled with RPs are still freely deformable. Special care is needed with employing such kinematic relations in the vicinity of high stress gradient locations since forcing additional rotational DOFs on otherwise 3-DOF per node continuum FE mesh can result with numerical anomalies and stress singularities in some cases.

Furthermore, referent FE model mesh convergence is reported in Fig. 3b. The convergence of model with zero Poisson’s ratio (i.e. fully compressible material) is denoted herein. However, similar convergence behaviour is observed for arbitrary value of $\nu =0{-}0.5$ which is hence not separately displayed.

Fig. 3

Abaqus computational model, $n=1$, $C=50/17$, $\nu =0.0$: a RPs (A, B) definition, b convergence study

As shown in Fig. 3a, relatively thick spring of small index $C=D/d=50/17$ with sufficiently large pitch angle $\alpha$ is chosen as the representative model for convergence check. Arbitrary large force $F_{0}$ is acting on RP A. Displacement of RP A and maximum von Mises equivalent stress of the entire spring model are measured. Monotonous and quick convergence is observed in Fig. 3b. As expected, the deflections converge much quicker compared to calculated stresses. The relative error $E_{\mathrm{rel}}$ is defined as a difference between two successive meshes where every next mesh is considered as a referent solution and the previous mesh is a measured numerical solution, i.e. Equation $E_{\mathrm{rel}}=(x_{(i+1)}/x_{i}- 1)\cdot 100\%$ holds. Since for this case analytical solution is unknown, more convenient term is still relative difference rather than relative error. Spring deflections and stresses are divided with nominal analytical deflection and stress solutions from Eq. (17) in order to obtain adequate correction factors. Figure 4 shows Abaqus normalized deflection and stress results, respectively, for referent converged FE mesh.

Fig. 4

Abaqus C3D20R normalized results: a deflection $\delta _{\mathrm{ynorm}}$, b equivalent stress $\sigma _{\mathrm{eqv(HMH)norm}}$

Linear displacement field and relatively uniform, singularity-free stress field are observed through entire spring in Fig. 4. Homogeneity of the numerical stress field also implies that appropriate BCs are enforced in the model, and therefore, no stress singularities due to kinematic constraints or BCs occurred. It is also interesting to note the shift of the spring neutral line further away from the Y axis in Fig. 4b, also reported in [2]. As already observed by Timoshenko [8] and Wahl [1], maximum shear stress $\tau _{\mathrm{max}}$ and corresponding equivalent von Mises stress $\sigma _{\mathrm{eqv(HMH),max}}$ can be consequently observed at the inner side of the spring coil. That also agrees with Abaqus results in Fig. 4b. Thus, potential crack initiation location is uniformly identified nearest to the spring Y axis. As stress field is homogenous through entire isolated one coil numerical spring, the terminology of stress correction is favourable compared to stress concentration. The beneficiary effects of using relatively coarse and efficient but converged FE mesh needs to be highlighted.

Next, six parametric Abaqus models similar to one discussed beforehand are defined with regard to Table 2. The spring pitch $l=2\cdot d$ and incremental steps of $\Delta d=3$ mm are applied. Eight FEs are used per spring thickness for obtaining accurate results according to Fig. 3b convergence guideline. Figures 5, 6 and 7 show comparison of selected best matching continuous analytical results and Abaqus results for six discrete C values ($C=50/2;50/5;50/8;50/11;50/14;50/17$) and three different values of Poisson’s ratio ($\nu =0;0.3;0.5$). Considered analytical expressions for deflection correction are: A/G, Shigley, Göhner, C/T and T/C. Furthermore, Wahl, Bergsträsser, Göhner and A/G stress correction analytical expressions are taken into account. Wahl stress correction is for this analysis considered to be Poisson’s ratio $\nu$ dependent, i.e. $\hbox {Wahl} = \hbox {Wahl}(\nu$) [2], as presented in Figs. 5, 6 and 7 legends. Vertical lines ($C_{\mathrm{lower}}$ and $C_{\mathrm{upper}})$ denote practical spring index C limits. Circle markers represent Abaqus discrete results.

Fig. 5

Analytical and FEM correction factors, fully compressible, $\nu =0.0$: a deflection correction $K_{\delta }$, b stress correction $K_{\tau }$

For Poisson’s ratio $\nu =0$ (i.e. fully compressible material), the best correlation with FEM displacement is observed for A/G. Shigley and T/C overestimate while Göhner and C/T slightly underestimate FEM results. From the series of conducted analyses, it can be concluded that all authors show very similar results regarding obtained stress corrections and slightly underestimate FEM.

Fig. 6

Analytical and FEM correction factors, compressible, $\nu =0.3$: a deflection correction $K_{\delta }$, b stress correction $K_{\tau }$

At the second test case, Poisson’s ratio $\nu =0.3$ (i.e. compressible material). The best agreement with displacements obtained via FEM is still observed for A/G. Shigley and T/C overestimate FEM even more compared to $\nu =0.0$ test case. Considering the stress correction, Wahl now agrees rather closely with FEM. However, all the other authors still somewhat underestimate FEM.

Fig. 7

Analytical and FEM correction factors, incompressible, $\nu =0.5$: a deflection correction $K_{\delta }$, b stress correction $K_{\tau }$

Finally, for Poisson’s ratio $\nu =0.5$ (i.e. perfectly incompressible material) the best agreement with the FEM displacements is again reported for A/G. Shigley and T/C now overestimate FEM results much more compared to previous two cases. However, Göhner and C/T for all $\nu$ values constantly provide rather similar results compared to both A/G and FEM. Regarding stress correction factors, it is notable that for this test case Wahl somewhat overestimates FEM. Furthermore, all other authors continue to underestimate FEM, but Wahl is still closest to the FEM solution.

Considering this parametric analysis, A/G ($K_{\delta ,\mathrm{A/G}})$ deflection correction expression shows the best overall agreement with Abaqus model. Even though Göhner and C/T slightly underestimate the deflection, they can still be considered as a “reserve” or “backup” referent solution. Wahl ($K_{\tau ,\mathrm{Wahl}})$ stress correction expression agrees excellently with Abaqus model for $\nu =0.3$ while Bergsträsser, Göhner and A/G constantly somewhat underestimate the stress field. However, they give almost identical mutual results. Based on the conducted numerical investigation, the currently adopted deflection and stress correction factors are

$$\begin{aligned} K_{\delta ,\hbox {Ancker Goodier}\left( {\hbox {A/G}} \right) } =1-\frac{3}{16C^{2}}+\frac{3+\nu }{2\left( {1+\nu } \right) }\tan ^{2}\left( \alpha \right) , \quad K_{\tau ,\hbox {Wahl}} =\frac{4C-1}{4C-4}+\frac{0.615}{C}. \end{aligned}$$

(22a, b)

By inspecting Wahl expression from Eq. (22b), it should be noted that pitch angle $\alpha$ is not considered and $k_{\mathrm{w}}=0.615$ is hard-coded. Although, Wahl results still apparently show the all-around best agreement with FEM compared to solutions from other authors. Wahl correction is further examined. For comparison purpose, Poisson’s ratio influence on deflection correction is summarized in Fig. 8a where differences are clearly visible, especially for lower spring indices C. Analytical A/G and numerical deflection correction solutions agree very well for all tested parametric cases. However, almost insignificant sensitivity of Poisson’s ratio influence on Abaqus numerical stress correction can be detected by inspecting Fig. 8b. Thus, Eq. (22b) with fixed $k_{w}=0.615$ (i.e. Wahl original solution) is adopted as approximate stress correction for further analyses.

Fig. 8

Analytical and numerical correction factors, $\nu =0{-}0.5$: a deflection correction $K_{\delta }$, b stress correction $K_{\tau }$

In conclusion, both numerical and analytical (i.e. A/G) $K_{\delta }$ diminish with rising Poisson’s ratio, even though numerical $K_{\tau }$ insignificantly rises with rising of Poisson’s ratio for small $\alpha$. That fact justifies excluding Poisson’s ratio influence in further stress correction. Figure 9 correlates with Fig. 8 by denoting relative differences between analytical (A/G, Wahl) and numerical solutions for all given cases. Relative error/difference $E_{\mathrm{rel}}$ is well below ${\vert }1{\vert }$% for all shown parametric values. Largest differences in stress correction are observed for fully incompressible material (i.e. $\nu =0.5$), especially for very high and low spring indices C presented in Fig. 9b.

Fig. 9

Analytical and numerical correction factors relative difference $E_{\mathrm{rel}}$ comparison, $\nu =0{-}0.5$: a deflection correction difference $E_{\mathrm{rel}}(K_{\delta ,A/G})$, b stress correction difference $E_{\mathrm{rel}}(K_{\tau ,\mathrm{Wahl}})$

Figure 10a shows relative difference between Wahl stress correction factors by varying Poisson’s ratio $\nu$. In order to check the relative differences for the other stress correction candidates (i.e. Bergsträsser, Göhner and A/G), they are contrasted to Wahl. The corresponding results are denoted in Fig. 10b. While comparing the obtained results (see Fig. 10b), the relative difference smaller than 2% is observed in most regions for practical C limits. Since much smaller relative difference $< {\vert }1{\vert }$% is achieved for FEM and Wahl comparison (see Fig. 9b), the selection of the Wahl stress correction factor is verified. The Wahl stress correction factor outperforms all the other authors based on the FEM results obtained herein.

Fig. 10

Analytical stress correction factors relative difference $E_{\mathrm{rel}}(K_{\tau })$ comparison: a Wahl correction factor difference with respect to Poisson’s ratio $\nu$$E_{\mathrm{rel}}(\nu$), b Wahl correction factor difference with respect to Bergsträsser, Göhner and A/G

Finally, one specific case is used as a definitive benchmark for correction factors by setting the pitch angle $\alpha =0$, analogue to the study conducted in [13]. Steel Poisson’s ratio $\nu =0.3$ is considered. A/G (i.e. Eq. (22a)) is again employed against Abaqus C3D20R solution. Derived T/C Eq. [2] is also evoked in order to contrast it with Abaqus B32 Timoshenko-based second-order beam elements. B32 FEs are formulated as shear flexible with quadratic interpolation [40]. It is interesting to compare these analytical and numerical solutions since Abaqus also uses Cowper [2] correction, according to [40]. From the analytical and numerical 1D and 3D correction factors, comparison (Fig. 11a) can be seen that A/G solution again follows Abaqus C3D20R (Abq,3D in legend) solution closely and that T/C derived solution matches Abaqus B32 (Abq,1D in legend) solution almost perfectly. For higher spring index C values, all analytical and numerical correction factors tend to unity. However, two concurrent solutions completely diverge for small spring indices C. Analytical and numerical 3D model even show concordant below unity trend. Analytical T/C solution is apparently correctly derived according to the thick beam theory [2] as it agrees with the corresponding Timoshenko beam FE element solution. However, T/C solution should not be used in the context of approximating real, thick cylindrical springs with small indices C because it overestimates the spring compliance. The trends reported in Fig. 2 already suggested aforementioned. Additionally, Fig. 11b demonstrates that beam elements (Abq,1D in legend) expectedly cannot capture stress correction because the value constantly remains at unity for any C value. Interestingly, numerical values for zero pitch angle (Abq,3D in legend, triangle symbol) now lie in between Wahl and A/G stress correction factors which implies that Wahl stress correction solution may be overly conservative when pitch angle $\alpha \approx 0$.

Fig. 11

Analytical and numerical 1D and 3D correction factors comparison, $\nu = 0.3$, $\alpha = 0$: a deflection correction $K_{\delta }$, b stress correction $K_{\tau }$

In summary, setting $\nu =0$ underestimates the numerical stresses while setting $\nu =0.5$ somewhat overestimates the numerical stresses considering generalized Wahl equation from Table 1. By setting $\nu =0$, Wahl yields almost identical results to A/G, Göhner and Bergsträsser stress correction factors as demonstrated in Fig. 5b. Keeping in mind that smaller spring index C results with larger stresses and deflections, the question of larger pitch angle $\alpha$ influence still remains unanswered.

A/G model is now firmly adopted for deflection correction. Furthermore, Wahl approximate model with fixed $k_{\mathrm{w}}=0.615$ is finally adopted for stress correction although it is a bit deficient according to performed parametric investigation. However, the advantage of the Wahl equation is that it best coincides with the current FEM solutions which embody relatively small, but nonzero pitch angle $\alpha$. The main concern is whether the linear numerical solution should be considered as a referent one, compared to other available analytical/empirical/approximate models. In order to obtain objective/nonbiased numerical results, alternate linear FEM solver Catia, Elfini [42] is also employed for double checking of Abaqus computational accuracy, analogue to method used in [39]. Catia Elfini solver matches Abaqus numerical results rather closely for both 3D continuum solution and 1D Timoshenko beam-based solution. Thus, it is not separately shown, nor further discussed in detail. Moreover, it reassures about the accuracy of both adopted approximate correction factors and Abaqus detailed computational model. The implied correct choice of employing A/G for deflection correction and Wahl for stress correction used in previously published results [2] is confirmed.

5 Example: inerter-based isolator helical spring vibration fatigue optimization study

In this chapter, vibration optimization and fatigue analysis are performed on a general 2-DOF system shown in Fig. 1a. Table 3 shows parameters used in the isolator optimization process example. While following recommendations given in [2], the system is detuned (i.e. $m_{2}k_{1 }\ne m_{1}k_{3})$ and the spring $k_{2}$ is compliant compared to springs $k_{1,3}$.

Table 3 Example 2-DOF vibration isolation system parameters [2]

The mass parameter value is chosen as $m_{0 }=100$kg and spring stiffness $k_{0}$ is yet to be determined from helical spring parameters proposed in Table 4. Material parameters (E, $\nu$, $S'_{\mathrm{f}}$ and B) of the spring in this example are chosen in such way to represent physical elastic and fatigue properties of regular, common steel, adopted from [2].

Table 4 Example helical spring of stiffness $k_{0}$ geometric and material properties [2]

Diameters D and d are chosen so $C=D/d=50/17\approx 2.941$ in order to provide a very small spring index. However, such small spring index C results with a relatively large stress correction factor which makes it a convenient fatigue benchmark. The ideal massless springs are considered for simplicity and straightforwardness. Spring stiffness is calculated according to introduced Eq. (17a) where $K_{\delta }F_{0 }=k_{0}\delta _{\mathrm{nom}}$. Obtained 2-DOF key values/factors and optimized parameters are listed in Table 5. Equations (12–16) are used in the process of optimization. Velocity amplitude optimization results are taken from [2]. Some differences in obtained parameters with regard to optimization criterion are observed. Hence, it will be interesting to observe the impact of those differences to fatigue life assessment.

Fig. 12

Mass $m_{2}$ normalized ${\mathcal {H}}_{2}$ index $I_{{{\mathcal {H}}}2{\mathrm{norm}}}$: a displacement index $I_{{\mathcal {H}}2\mathrm{norm}}(x_0 )$, b velocity index $I_{{\mathcal {H}}2\mathrm{norm}}(v_0 )$

Table 5 Example 2-DOF vibration isolation system referent values and optimized parameters

Figure 12 shows contour-plotted normalized results of the optimization process with regard to Table 5 for the prescribed parameters defined in Tables 3 and 4. The minimum (i.e. optimum ${\mathcal {H}}_{2})$ indices $I_{{\mathcal {H}}2norm}$ are represented as diamond markers. The contours of displacement-based optimization (Fig. 12a) and velocity-based optimization (Fig. 12b) are rather similar as expected from the results denoted in Table 5. Darker contours in both plots imply regions of higher ${\mathcal {H}}_{2}$ index (i.e. undesired effect). Dash-dotted curved lines denote implicit plots of function $c_{2}$ when $b_{2 }\ne$0, i.e. Eqs. (12) and (15), respectively. Circles at the bottom of the both figures correspond to the optimized damping case $c_{\mathrm{opt}}$ when $b_{2}$ = 0, defined in Eqs. (14) and (16). Finally, diamond markers denote the position of both optimized damping $c_{\mathrm{opt2}}$ and inertance $b_{2}$ simultaneously from Eq. (13a, b) and previously omitted equations for the velocity-based optimization due to extensive length [2, 35]. Consequently, diamond markers are located at the lightest region centre as they represent the global minimum of the displacement and velocity-based functions from Eq. (9).

The upper limit of the plots is defined as $b_{\mathrm{2max }}=2b_{\mathrm{opt}}$. Furthermore, bow and arrow-like shapes outline the contours. Implicit functions from Eqs. (12) and (15) denote dashed-dotted bow while horizontal dashed lines $b_{2~}= b_{\mathrm{opt}}$ denote arrow and vertical dashed lines connecting circle with down-pointing triangle shown at the top with the corresponding coordinates $\triangledown (c_{\mathrm{opt}},2b_{\mathrm{opt}})$ denote string. Similarly shaped contour optimization diagrams are reported in [2, 35]. In conclusion, dash-dotted bow curve connects all three markers: circle, diamond and triangle.

Next, the analytical and numerical quasi-static results are compared for the displacement and stress correction. Results are shown in Table 6 with the corresponding maximum relative difference $E_{\mathrm{rel,max }}<0.4\%$.

Table 6 Example 2-DOF vibration isolation system numerical values and relative difference comparison

Although only minor discrepancies are observed for this static benchmark case, it should be noted that the vibration fatigue study conducted in the further investigation depends exponentially (Basquin) on both displacement and stress simultaneously as witnessed from structure of Eq. (21). Thus, special considerations are taken into account in the following.

With that in mind, two separate Abaqus vibration fatigue models are defined. First model is simplified and denotes closely Fig. 1a. Instead of real continuum helical spring $k_{3}$ analogue to Fig. 1b, a single 3D C3D8R first-order hexahedron continuum element with reduced integration is employed. It is acting as a simple truss/rod connector element which serves as both equivalent stiffness and fatigue stress concentrator. In order to approximate the real 3D spring presented in Fig. 1b, an equivalent ideal spring is defined by matching both stiffness $k_{0}$ and equivalent stress $\sigma _{\mathrm{eqv(HMH),max}}$ of the original spring which are prescribed as equal. This is performed in order to verify proposed dynamic procedure regardless of the chosen deflection and the stress correction accuracy. For pure normal axial load, stiffness and stress equations for truss can be, respectively, written as

$$\begin{aligned} k_{\mathrm {truss}} \equiv k_0 =\frac{A_{\mathrm {truss}} E_{\mathrm {truss}} }{l},\quad \left| {\sigma _{\mathrm {eqv}\left( {\hbox {HMH}} \right) \hbox {,max}} } \right| \equiv \left| {\sigma _{0\hbox {n}} } \right| =\frac{k_0 }{A_{\mathrm {truss}} }\left| {x_{\mathrm {02}} } \right| , \end{aligned}$$

(23a, b)

where $A_{\mathrm{truss }}=a_{\mathrm{truss}}^{2}$ is truss axial quadratic surface area and $E_{\mathrm{truss}}$ is an equivalent Young’s modulus of the truss. Since stress is uniaxial, equivalent stress amplitude $\sigma _{\mathrm{eqv(HMH)}}$ according to von Mises is equal to normal stress amplitude $\sigma _{0 \mathrm n}$. Thus, the truss equivalent parameters follow from equalling Eqs. (23a, b) with previously established stiffness and stress relations for helical spring which consider both deflection and stress correction factors i.e.

$$\begin{aligned} k_{\mathrm {true}} \equiv k_0 =\frac{1}{K_\delta }\frac{Gd}{8C^{3}n},\quad \left| {\sigma _{\mathrm {eqv}\left( {\hbox {HMH}} \right) \hbox {,max}} } \right| =\sqrt{3}K_\tau \left| {\tau _{\mathrm {nom}} } \right| =\sqrt{3}\frac{K_\tau }{K_\delta }\frac{G}{C^{2}n{\pi }d}\left| {x_{\mathrm {02}} } \right| . \end{aligned}$$

(24a, b)

Solving for the two unknowns from Eqs. (23–24) yields $E_{\mathrm{truss }}\approx 15075.385$ MPa and $a_{\mathrm{truss}}\approx 3.737$ mm. Ideal and realAbaqus isolator FE models are shown in Fig. 13. The model schematics are denoted in Fig. 13a, b, while Fig. 13c, d illustrates actual Abaqus FE model screenshots.

Fig. 13

2-DOF Abaqus isolator FE models: aideal scheme, breal scheme, cideal screenshot, dreal screenshot

In Abaqus, springs $k_{1,2}$ and dashpot $c_{2}$ are utilized through SpringA and DashpotA FEs, respectively. They add axial spring/dashpot between the two nodes whose line of action is the line joining the two nodes [40]. Abaqus does not yet possess ideal inerter functionality which is similar to ideal spring/dashpot. Hence, analogue to Smith original rack and pinion inerter concept [4] the required optimum inertance $b_{\mathrm{opt}}$ is utilized alternatively by defining discrete dynamic inertia moment $J_\mathrm{O}$ and using embedded Abaqus *Equation functionality. The imposed feature ties relative nodal displacement between masses $m_{1}$ and $m_{2}$ to rotation of inertia $J_\mathrm{{O}}$ through custom created relation

$$\begin{aligned} r_{\mathrm {unit}} =1\;{m} \Rightarrow r\cdot \underbrace{\varphi _z \left( {J_{\mathrm{O}} } \right) }_{\mathrm {DOF6}}-\underbrace{y_1 \left( {m_1 } \right) }_{\mathrm {DOF2}}+\underbrace{y_2 \left( {m_2 } \right) }_{\mathrm {DOF2}}=0, \end{aligned}$$

(25)

where nodal displacement y is measured in metres and nodal rotation $\varphi _{z}$ is measured in radians. Equation (25) implies that if using SI units, one metre relative displacement between masses $m_{1}$ and $m_{2}$ yields one radian rotation of $J_\mathrm{{O}}$. If the relative displacement between the two terminals (i.e. masses $m_{1}$ and $m_{2})$ is zero, no rotation occurs and inerter does not contribute to functionality of the isolator. Consequently, dynamic moment of inertia $J_\mathrm{{O}}$ in current configuration serves as an ideal inerter whose inertia characteristics can be calculated according to a simple expression

$$\begin{aligned} J_{\mathrm{O}} =b_{\mathrm {opt}} \cdot r_{\mathrm {unit}}^2 . \end{aligned}$$

(26)

By adopting convenient unit radius $r_{\mathrm{unit}}=1$ m, dynamic moment of inertia for the displacement-based optimization is $J_\mathrm{{O}}=15\,\hbox {kg}\,\hbox {m}^{2}$ and $J_\mathrm{{O}}\approx 13.701\,\hbox {kg}\,\hbox {m}^{2}$ for the velocity-based optimization (Table 5). Moreover, it can be concluded that $J_{\mathrm{O}} \propto b_{\mathrm {opt}}$ and stated that Eqs. (25, 26) are exact for both small and large rotation effects.

In Abaqus, Lánczos method is used as eigensolver. Steady-state dynamics, Direct Step is employed for obtaining linear response in frequency domain analogue to direct method Eq. (4). In order to obtain sufficient visual resolution of results, 500 equally spaced discrete frequency steps per analysis are requested. First, velocity-based optimization results from [2] and Sect. 2.1 are taken into account. Figure 14 denotes comparison of the analytical and Abaqus ideal models from Eq. (23a, b) for mass $m_{2}$ displacement amplitudes. Two extreme cases are taken under consideration. The first case includes super-optimal extremely high damping $c_{\mathrm{sup}}=100\cdot c_{\mathrm{opt}}$. It effectively locks the isolator and produces new resonance $\varOmega _{\mathrm{a}}$ (Fig. 14a) from Eq. (11b). The second test case sets zero damping $c_{2 }=0$ and considers optimal inertance $b_{2 }=b_{\mathrm{opt}}$ which unveils anti-resonance $\varOmega _{\mathrm{A}}$ (Fig. 14b) from Eq. (11a). Since damping $c_{2}$ in Fig. 14b is prescribed to zero, responses at natural frequencies tend to infinity at eigenvalues obtained from Eq. (10). All desired effects, previously derived analytically [2, 35], are successfully captured by FEM solutions. Abaqus ideal and real models yield almost the same displacement amplitudes results. Hence, they are purposely not distinguished here.

Fig. 14

Mass $m_{2}$ displacement amplitudes ${\vert } x_{02} {\vert }$ comparison: a super-optimal damping, b optimal inertance, no damping

Figure 15 shows comparison of analytical, Abaqus ideal and Abaqus real models for spring $k_{3}$ stress amplitudes in fatigue nomenclature ${\vert }S_{a}(k_{3}){\vert }$. Optimum damping $c_{\mathrm{opt}}$ and inertance $b_{\mathrm{opt}}$ parameters for the velocity-based optimization from Table 5 are considered. A very good agreement is observed between all models. Thus, the correct numerical inerter implementations and approximately correct displacement and stress correction factors adoption for analytical calculations is strongly implied. There is virtually no discrepancy noted between analytical and Abaqus ideal models.

Fig. 15

Spring $k_{3}$ stress amplitudes ${\vert } S_{a}(k_{3}) {\vert }$ comparison: a optimal damping, b optimal damping and inertance

Fe-Safe [41] software suite is further employed with von Mises criterion evoked for fatigue analysis. The converged FEM complex nodal stress amplitudes from Abaqus are taken into account for the most destructive frequency (i.e. first natural frequency where $\varOmega =\omega _{n1}(b_{\mathrm{opt}}))$. Custom created Fe-Safe material $S-N (i.e.$ Stress amplitude–No. of cycles to fatigue) curve [2, 41] is defined with respect to parameters $S'_{\mathrm{f}}$ and B (Basquin) from Table 4. The entire ideal and real FE spring models are analysed. Figure 16 shows the final results of performed HCF real spring analysis for the velocity-based optimization, analogue to [2]. Explicit Basquin’s curve $S_{\mathrm{a}}=S'_{\mathrm{f}}\cdot (N_{\mathrm{f}})^{B}$ is superimposed and shown as inclined dashed line in Fig. 16. The presented curve is ranged from $10^{3}$–$10^{7}$ fatigue life cycles.

Fig. 16

Real spring $k_{3}$ fatigue life: a number of cycles to failure $N_{\mathrm{f}}(k_{3})$, bAbaqus/Fe-Safe$N_{\mathrm{f}}(k_{3})_{\mathrm{(log)}}$

Figure 16b shows particular vibration fatigue life results of real spring, post-processed in Abaqus. Analogue to analytical solution [1, 2, 8], the shortest fatigue life is expected on the inner-coil side of spring numerical model. Abaqus/Fe-Safe LOGLife legend shows homogenous life field scaled according to expression [41]

$$\begin{aligned} \left( {N_{\mathrm{f}} } \right) _{\mathrm {LOGLife-Repeats}} =\log _{10} \left( {N_{\mathrm{f}} } \right) \Leftrightarrow N_{\mathrm{f}} =10^{\left( {N_{\mathrm{f}} } \right) _{\mathrm {LOGLife-Repeats}} }, \end{aligned}$$

(27a, b)

where actual minimum number of cycles $N_{\mathrm{f}}$ compared to analytical results is shown in Table 7. These results correspond to the velocity-based optimization study conducted in [2]. Rigid benchmark method is adopted herein. All the results are compared for analytically calculated natural frequencies $\omega _{n1\mathrm{(Anlt)}}$.

Table 7 Vibration fatigue optimization study analytical and numerical results comparison for $c_{2 }=c_{\mathrm{opt2}}$ and $b_{2 }=b_{\mathrm{opt}}$

By comparing analytical and Abaqus ideal model, the difference $E_{\mathrm{rel}} \quad \approx 0.000\%$ can be observed for all quantities. With regard to number of cycles $N_{\mathrm{f}}$, only negligible numerical rounding error occurred. However, some minor discrepancies can be observed while comparing analytical and Abaqus real model. It is necessary to emphasize that smaller differences are noted in Table 6 for the displacement and stress correction factors if compared to differences observed in Table 7 for displacement ${\vert }x_{02}(\omega _{n1}){\vert }$ and stress ${\vert }S_{\mathrm{a}}(\omega _{n1}){\vert }$ amplitudes, respectively. In conclusion, it is important to point out that these are a cumulative consequence of mismatch between the fundamental natural frequency $\omega _{n1 }$ obtained analytically and numerically.

The results for the stress amplitude $S_{\mathrm{a}}(\omega _{n1})$ reported in Table 7 differ by only $\sim$0.556%; however, difference is magnified in fatigue analysis to considerably larger $\sim {\vert }5.390{\vert }\%$. This is due to the fact that Eq. (21) presents exponential relation where small differences in stress yield with much larger dissipation for general fatigue analysis results. By taking into account stress amplitude $S_{\mathrm{a}}(\omega _{n1})\approx 230.998$ MPa computed by Abaqus, difference between hand calculated fatigue from Eq. (21a) and the one from FE complex nodal stress and Fe-Safe results now completely vanishes, i.e. falls to $E_{\mathrm{rel}}\approx 0.000\%$. Hence, only analytical computational error lies in the helical spring adopted displacement and stress approximate correction factors (i.e. $K_{\delta ,\mathrm{A/G}}$ and $K_{\tau ,\mathrm{Wahl}})$. As a final consequence, analytical results are now on the safety side and provide more conservative approximate fatigue life assessment compared to FEM.

In the following, four specific optimized cases are considered regarding Table 5. The displacement-based optimization parameters with ($b_{\mathrm{opt}})$ and without inerter ($b_{0})$, and the velocity-based optimization parameters with ($b_{\mathrm{opt}})$ and without inerter ($b_{0})$ are taken into account. Comparison of analytical and FEM results is shown in Table 8. Influence of inerter on circular natural frequencies is presented, and it can be observed that due to the added apparent mass—frequencies diminish. Results are reported for the most destructive, e.g. first resonant excitation frequency where $\varOmega =\omega _{n1\mathrm{(Anlt)}}$.

Table 8 Vibration fatigue displacement and velocity optimization study analytical and numerical result comparison

Very good agreement is generally observed in Table 8. Analogue to results denoted in Table 7, Abaqus ideal spring results show almost no relative error compared to analytical solution with the exception of small fatigue life assessment errors attributed to numerical rounding. Taking into account Abaqus real spring results, natural frequencies always seem to be a bit lower compared to analytical solution. Larger discrepancies are observed for fatigue calculation as a result of mismatch. If the inerter is present in the isolator, analytical results yield with more conservative fatigue life assessment compared to FEM. However, excluding the inerter from the isolator leads to less conservative analytical fatigue results compared to FEM.

Results are recapitulated and visually presented in Fig. 17. Inverse number of cycles to fatigue as a function of circular excitation frequency is shown in Fig. 17a for all four cases. The small rectangular detail represents range of response for near-resonant conditions. This detail also implies that the highest $1/N_{\mathrm{f}}$ FRF peaks correspond to the lowest fatigue life. Labels $c_{\mathrm{opt2}}$ in legend imply both optimum damping and optimum inertance $b_{\mathrm{opt}}$. Cases without inerter and with optimum damping (i.e. $c_{\mathrm{opt}}(x_{0})$ and $c_{\mathrm{opt}}(v_{0}))$ almost cannot be visually distinguished, except near resonance conditions as shown in rectangular detail. Improvements are observed for optimum damping $c_{\mathrm{opt2}}$ and inertance $b_{\mathrm{opt}}$, compared to only optimum damping $c_{\mathrm{opt}}$ on almost all frequencies, except in the vicinity of the second natural frequency $\omega _{ n2b\mathrm{opt}}$. Bar chart shown in Fig. 17b denotes the most conservative criterion (i.e. number of cycles in resonant conditions) which corresponds to Table 8. It is organized as follows: bars are aligned so that the highest number of achieved life cycles is positioned far left and the lowest number of cycles is positioned right. The line dashing and colour definition of the FRFs (Fig. 17a) corresponds to line dashing and colour of bars (Fig. 17b).

Fig. 17

Spring $k_{3}$ number of cycles to fatigue failure $N_{\mathrm{f}}(k_{3})$: a$1/N_{\mathrm{f}}({\varOmega })$ FRFs, b$N_{\mathrm{f}}(\omega _n1{\mathrm{(Anlt)}})$

As expected, displacement-based optimization criterion ${\mathcal {H}}_{2}(x_{0})$ yields general further improvement compared to velocity-based criterion ${\mathcal {H}}_{2}(v_{0})$ previously proposed in [2]. This is true for the test cases with and without inerter. Moreover, by inspecting results from Table 8 and Fig. 17b, improvements are much more pronounced for the displacement-based optimization compared to velocity-based optimization when utilizing combined optimum damping $c_{\mathrm{opt2}}$ and inertance $b_{\mathrm{opt}}$. For the velocity-based optimization, over 1 million cycles are achieved [2]. However, for herein proposed displacement (i.e. fatigue)-based optimization, over 3.5 times more cycles are achieved. It can be considered as further substantial improvement. Thus, for shown family of vibration isolation systems it is justifiable to include inerter in the isolator and perform displacement-based optimization analysis if stress of coupling elastic components is of crucial importance.

It can finally be concluded that spring correction factors used in the context of this study and embedded in the analytical method provide sufficiently correct approximate solution compared to FEM. However, it should be noted that this direct dynamic stiffness analytical method provides for more transparent solution and computationally inexpensive model. That is especially evident when compared to direct FEM solution. If the real spring model is considered for the range denoted in Fig. 15, computational process takes considerable amount of time on high-end PC desktop computer. At first glance, relatively simple FEM model is utilized. However, due to complex real spring geometry and many additional kinematic relations, the incremental numerical process in frequency domain tends to get saturated and rather slow. This only includes Abaqus complex stress direct computation, where Fe-Safe takes additional/considerable CPU time for PSD-based fatigue life calculation. Moreover, analytical expressions derived and used throughout this investigation are approximately true even for continuous systems with distributed mass across the spring with the assumption that ratios between spring mass to primary and secondary mass are small. This makes proposed analytical method more appealing and time effective for this class of systems.

Considering that pitch angle in this study is defined through relation $l=2\cdot d$ and $\alpha =\hbox {arctan}[l/(\pi D)]$, it would be logical to further investigate the influence of arbitrary large pitch angle $\alpha$ on deflection and stress correction. The future study notably applies to further testing of Wahl approximate stress correction factor in detail as it does not contain the pitch angle in its formulation, compared to, for example, A/G. On the other hand, it is reassuring that Wahl currently demonstrates the highest accuracy compared to FEM for a wide variety of tested parameters. Additionally, the method proposed in this work could find its applicability on other types of springs used in suspension systems (e.g. leaf springs) [1, 43]. Automobile leaf spring can act as both road shock absorber and carrier of lateral loads [1]. Thus, it could prove beneficiary to examine the effects of including both helical and leaf spring in conjunction with inerter in the isolator. Moreover, simplified analytical leaf spring vibration fatigue model analogue to one proposed in the scope of this investigation may be established.

6 Conclusion

A novel cylindrical helical spring solely displacement-based (i.e. vibration fatigue-based) ${\mathcal {H}}_{2 }$ optimization method for inerter-based vibration isolation system is presented in this paper. The analysed spring couples receiving body (i.e. mass that needs to be isolated from vibrations) to the fixed ground. The optimization method is based on the previous findings which imply that the stresses in the spring are directly proportional to spring maximum displacement amplitudes. Power spectral density principle in the broadband frequency domain is employed for spring life assessment and complemented with the direct inversion of dynamic stiffness matrix method. The efficiency of the proposed method is studied on a two degree-of-freedom system which represents reduced-order model of a potentially much more complex general dynamic system. Results are compared to previous study which was based on broadband minimization of the specific kinetic energy as a vibration optimization criterion. Substantial improvement regarding prolonging spring high-cycle fatigue life is observed by utilizing currently proposed method.

Two types of referent isolators are studied throughout the paper. First referent isolator incorporates optimal inerter and optimal viscous damping, while the second one contains only the optimal damping (i.e. inerter is excluded). Based on the previous research, it is confirmed that simultaneous optimization of isolator damper and inerter connected in parallel convincingly outperforms any isolator configuration that contains only damper (i.e. system without inerter). Furthermore, in the scope of this work it is additionally reported that displacement-based optimization always outperforms kinetic energy (i.e. velocity-based) optimization if the ground-coupling spring fatigue life of the receiving body is a primary optimization criterion objective.

Spring deflection and stress correction factors from the referent literature are benchmarked versus finite element method. Previously derived approximate Timoshenko/Cowper displacement correction factor based on the strength of materials principles assumption, thick shear-deformable Timoshenko beam theory and enriched with Cowper shear correction is set to test against finite element method. It is found that proposed deflection correction factor matches excellently with the beam-based finite element solution. However, the obtained results are completely divergent compared to theory of elasticity based on approximate Ancker and Goodier solution and complementary continuum finite element method solution alike. Thus, it can be concluded that beam-based theory is not appropriate and should not be used for helical spring calculation, especially for small spring indices. The most convenient correction factors are adopted for further vibration fatigue study based on benchmark comparison results. Ancker and Goodier factor is confidently adopted for the spring displacement correction, while for the spring stress correction, Wahl factor is conditionally adopted. Despite the fact that some discrepancies and inconsistencies were found in the formulation of the Wahl stress correction factor, the parametric analyses and comparisons with numerical solutions have apparently shown the best agreement with adopted Wahl stress correction solution.

Previously introduced simplified analytical method for calculating cylindrical spring high-cycle fatigue life is verified herein by comparing the analytical and finite element method results. The proposed method employs von Mises energy criterion for shear-governed biaxial proportional stress and Basquin’s relation. The only reported discrepancies between the analytical and numerical methods are related to adopted approximate displacement and stress correction factors. Otherwise excellent agreement is noted between the two employed methods.

Furthermore, the optimum inertance concept is integrated into finite element-based numerical solution by following the original rack and pinion analogy taken from Smith. Moreover, an excellent agreement with analytical solution is reported. The novel inerter-induced effects (e.g. anti-resonance of the receiving body and reduction in natural frequencies) are successfully reproduced within finite element-based solution.

The future work regarding investigation presented herein will be to further study the influence of much larger spring pitch angles on the displacement and stress fields. Consequently, a more general correction models could be developed with the aim to capture both small spring index and large pitch angle effects simultaneously. Finally, the alternate ways of implementing the both ideal inerter (e.g. massless) and real inerter into a more general and robust finite element-based solution will be investigated. In the future, possible benefits of additionally including the leaf spring in the inerter-based isolator with regard to absorbing shocks and carrying lateral load could be studied.