On the dynamics of a vibration isolator with geometrically nonlinear inerter

Abstract

The inerter is a two-terminal mechanical element that produces forces directly proportional to the relative acceleration between these terminals. The linear behaviour of this element has already been described in the literature. In this work, the nonlinear effects of the geometrical arrangement of the inerter are investigated in terms of vibration isolation and compared to the traditional arrangement. The analysis comprises the use of harmonic-balanced method applied to the exact equation, as well as approximations for low amplitude and high amplitude. Numerical analysis is used to complement the investigation. Comparison with classic vibration isolators shows possible benefits for high frequency regimes. The effects from the geometrical nonlinearity vanish when the amplitude of motion is large.

1 Introduction

The classical isolator consisting a parallel combination of a linear spring and viscous damper supporting a lumped mass has been the foundation for the study of vibration transmissibility in mechanical systems. There are registers of patents on the study of mechanical isolators from the beginning of the twentieth century [3, 7].

Nonlinear isolators are considered to obtain low amplitude response in a wide range of excitation frequencies. Ibrahim [13] presented a comprehensive review of many designs of nonlinear vibration isolators which were developed prior to 2008, including applications for vibro-impact, chaotic regimes and stochastic excitation.

Nonlinear absorbers were also extensively explored. An absorber using cubic nonlinear stiffness attached to the main mass was presented by Roberson [22]. A similar concept with only nonlinear term was formalised as a Nonlinear Energy Sink (NES), as the one studied by Vakakis [32]. Similar absorbers with nonlinear damping were studied as well [28]. Sapsis et al. [23] have discussed types of nonlinear attachments including spring and damper elements that work in a similar way to the proposal of this paper.

The concept of transmissibility (displacement or force) is generally used to describe the performance of an isolator, which is often represented in the frequency domain considering both the external excitation and system response as harmonic functions.

In 2002, Smith [25] proposed the synthesis of a mechanical device that reacted with forces directly proportional to the relative acceleration of its terminals. However, it is known that there are other similar mechanical elements which were developed prior to 1997 and presents similar behaviour to the Smith’s inerter, for instance, the ones presented by Flannelly [6] and Goodwin [10].

The inerter can be composed of hydraulic or pneumatic elements [31], with concentrated masses and levers [36], and also by a combination of pinion, rack, gears and inertia fly wheel [26].

The inerter device has several types of applications such as vibration isolator in hydraulic mounting of motors [31, 37], in passive and active vehicle suspensions [27], in civil engineering substituting the tuned mass damper with the benefit of a lower weight [9], in mechanical steering compensator of high performance motorcycles [5], in aircraft landing gear controlling shimmy vibration [16, 35], in railways improving the performance of train suspension systems [33], among others.

Papageorgiu and Smith [20, 21] and Gonzalez Buelga et al. [9] have investigated using experimental tests the nonlinearity effects on two types of inerters, such as friction.

Backlash, unwanted gaps have also been reported as important nonlinear phenomenon present in inerters [19, 38]. Wang and Su [33, 34] studied the effects of blacklash, elastic effect and friction nonlinearities applied to automotive suspension, indicating that the performance was slightly degraded by inerter nonlinearities, although overall suspension performance with a nonlinear inerter was still superior to traditional suspension system.

Nonlinear geometrically arranged elements have been considered previously, the concept of snap-through mechanism to provide the conditions HSLDS (high-static low-dynamic stiffness) has been considered in many works [2, 4, 12, 15, 24]. Tang and Brennan [30] studied the vibration transmissibility characteristics of geometrically arranged viscous damper. Sun et al. [29] have also considered the case of geometrically nonlinear damping using velocity n-th power damper.

This paper presents an analysis of a vibration isolator with an inerter with geometrical nonlinearity. Many applications of vibration isolators have operating angles presenting this type of geometrical nonlinearity, and the effect of an inerter in this arrangement is not well understood. The analysis comprises the exact solution, as well as approximations for low amplitude and high amplitude.

The paper is organised as follows. Section 2 presents the mathematical modelling, including the exact and two approximated equations of the system. In Sect. 3, the full equation of motion and the two approximations are analysed using the method of harmonic balance, showing the free response, frequency response and stability of the periodic response for relative and absolute displacement. In Sect. 4, a detailed numerical analysis is performed, illustrating parameter sensitivity in time domain, phase planes and basins of attraction. Section 5 presents the study conclusions.

2 Mathematical modelling

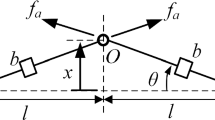
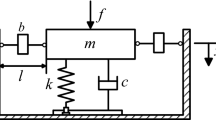
The system considered in this work is illustrated in Fig. 1, which consists of a traditional mass–spring–damper model subjected to base excitation, and an added inerter elements mounted with horizontal arrangement, with one end attached to the moving base and the other end attached to the mass. The mass is restricted to move only in the vertical direction and the horizontal forces acting on the mass are not cancelled due to the symmetric configuration of the inerters and are not considered in this analysis. For comparison, the usual arrangement with the inerter in a vertical configuration is shown in Fig. 2.

Fig. 1

Representation of the mass–spring–damper system with an inerter in horizontal arrangement

Fig. 2

Representation of the mass–spring–damper system with an inerter in vertical arrangement

The equation of motion for the system presented in Fig. 1 is obtained in terms of the relative displacement $z = x - x_0$, where x and $x_0$ are the displacements of the mass and the base, respectively. The dynamic force equilibrium given by

$$\begin{aligned} m\ddot{x} = - k z - c\dot{z} - 2 f_b \frac{z}{\sqrt{L^2+z^2}}, \end{aligned}$$

(1)

in which m is the lumped mass, k is the spring stiffness, c is the viscous damping coefficient and $f_b$ is the inerter force produced along its axis. The parameter L is the length of the inerter mechanism attached to the base and the mass.

An illustrative example of an inerter is shown in Fig. 3, which consists of a rack and pinion mechanism with a case. The two terminals of the inerter have accelerations $\ddot{x}_1$ and $\ddot{x}_2$. According to ref.  [25], the force acting on this mechanism is proportional to the relative acceleration, given by $f_b=b\left( {\ddot{x}_2-\ddot{x}_1}\right)$, where b is the inertance, which is a function of the mass and geometric parameters of the rack/pinion elements.

Fig. 3

Illustration of an inerter mechanism consisting of a rack and pinion

The rightmost term in Eq. 1 $\left( z/\sqrt{L^2+z^2} \right)$ represents the vertical decomposition factor of the inerter force acting on the mass m and the overdots represent differentiation with respect to time t. It is assumed that on the the equilibrium position ($x=0$), the inerter is arranged horizontally. When the mass m moves up and down, it stretches the inerter device by a length

$$\begin{aligned} \Delta = \sqrt{L^2+z^2}-L, \end{aligned}$$

(2)

The relative acceleration between the endpoints of the inerter is obtained by differentiating Eq. 2 twice with respect to time, and the force on the inerter is given by multiplying the acceleration by the inertance coefficient b, which gives

$$\begin{aligned} f_b = \frac{b}{2} \frac{\left( z\ddot{z}+\dot{z}^2 \right) L^2 + z^3\ddot{z}}{\left( L^2+z^2\right) ^{3/2}}, \end{aligned}$$

(3)

Substituting Eq. 3 into Eq. 1, the equation of motion is obtained as

$$\begin{aligned}&\left( 1 + \mu \frac{z^2 L^2+z^4}{(L^2+z^2)^2}\right) \ddot{z} + 2\xi \omega _0\dot{z} \nonumber \\&\qquad + \,\left( \omega _0^2 + \mu \frac{\dot{z}^2L^2}{(L^2+z^2)^2}\right) z \nonumber \\&\quad =-\ddot{x}_0, \end{aligned}$$

(4)

in which $\mu = b/m$ is the inertia ratio (non dimensional), $\omega _0 = \sqrt{k/m}$ is the natural frequency and $\xi = 2 m \omega _0$ is the damping factor. The last two parameters are related to the single degree of freedom mass–spring–damper system, used here for convenience of the analysis (note that $\omega _0$ and $\xi$ are not the natural frequency and damping factor of the systems in Figs. 1 and 2).

Considering the non dimensional time $\uptau =\omega _0 t$, such that $\dot{z} = \omega _0 z'$, with $z' = dz/d \uptau$, and also considering that the system is subject to harmonic base excitation of the form $x_0=X_0\cos {(\omega t)}$, where $\omega$ is the excitation frequency, Eq. 4 is rewritten as

$$\begin{aligned}&\left( 1 + \mu \frac{z^2 L^2+z^4}{(L^2+z^2)^2}\right) z'' + 2\xi z'\nonumber \\&\qquad + \,\left( 1 + \mu \frac{{z'}^2L^2}{(L^2+z^2)^2}\right) z \nonumber \\&\quad = \varOmega ^2 X_0 \cos {(\varOmega \uptau )}, \end{aligned}$$

(5)

in which $\varOmega = \omega /\omega _0$ is the frequency ratio. The final form of the equation of motion is obtained by dividing Eq. 5 by the length L, giving

$$\begin{aligned}&\left( 1+\mu \frac{h^2}{(1+h^2)}\right) h'' {+} 2\xi h' {+} \left( 1+ \mu \frac{{h'}^2}{(1+h^2)^2} \right) h \nonumber \\&\quad = \varOmega ^2 \hat{X}_0 \cos {(\varOmega \uptau )}, \end{aligned}$$

(6)

in which $h=z/L$ is a normalised relative displacement and $\hat{X}_0 = X_0/L$ is a normalised base displacement.

2.1 Approximated equations for high and low amplitudes

Analysing Eq. 6, for a value of $\mu >0$, it is possible to obtain two limiting approximations. The first approximation is obtained considering low values of the relative displacement h, such that the denominator terms can be approximated as $1+h^2\approx 1$, providing

$$\begin{aligned}&\left( 1+\mu {h}^2\right) h'' + 2\xi h' + \left( 1+\mu {h'}^2\right) h \nonumber \\&\quad =\varOmega ^2 \hat{X}_0 \cos {(\varOmega \uptau )}, \end{aligned}$$

(7)

Equation 7 will be refereed to as LA (Low Amplitude) approximation. This equation is still nonlinear, where the nonlinearity influences the inertia forces and the elastic forces. The term $(1+\mu {h'}^2)h$ does not have a significant effect on the system dynamics when the mass is at its maximum displacement or close to the equilibrium position, because the displacement and velocity have $90^{\circ }$ phase shift. Consequently, when the displacement is maximum, the velocity is zero and vice-versa.

One interesting observation is that, except for a nonlinear stiffness term, this system is similar to the equation defining the single mode of a uniform cantilever beam carrying an intermediate lumped mass and rotary inertia described by [11] and [17]. These results are also similar to the nonlinear oscillator proposed by [1] when the exponent $p=1$.

The second approximation occurs when h is large. In this situation, the term $1+h^2 \approx h^2$, and the equation of motion becomes linear with a change in the inertia force

$$\begin{aligned} \left( 1+\mu \right) h'' + 2\xi h' + h = \varOmega ^2 \hat{X}_0 \cos {(\varOmega \uptau )}, \end{aligned}$$

(8)

Equation 8 will be refereed to as HA (high amplitude) approximation. This equation represents the case of a mass supported by the linear combination of spring–damper–inerter in parallel configuration (Fig. 2). This is an interesting result which shows that the nonlinearity of the system vanishes for large relative displacements.

3 First-order harmonic balance solution

In this section, the equations of motion, exact (Eq. 6) and approximated LA (Eq. 7) and HA (Eq. 8) are analysed using the method of harmonic balance. Considering firstly the exact equation (Eq. 6), which can be modified by multiplying the left- and right-hand sides by the term $(1+h^2)^2$, this way, eliminating the rational terms, it is possible to write

$$\begin{aligned}&\left( (1+h^2)^ 2+\mu h^2(1+h^2)\right) h'' + 2\xi h'(1+h^2)^2\nonumber \\&\quad + \,\left( (1+h^2)^ 2+ \mu {h'}^2 \right) h\nonumber \\&\quad = \varOmega ^2\hat{X}_0 \cos {(\varOmega \uptau )}(1+h^2)^2. \end{aligned}$$

(9)

In this format, Eq. 9 is used in the following section together with Eqs. 7 and 8 to obtain expressions for the oscillatory frequency as a function of the displacement amplitude.

3.1 Backbone curves of free vibration response

The first investigation is carried out considering the case of free motion ($\hat{X}_0=0$). Assuming that the response can be written as a harmonic function of the form $h(\uptau )=H\cos {(\varPhi )}$, where $\varPhi = \varOmega \uptau + \phi$. Calculating the first and second derivatives of this expression and replacing the respective terms in Eq. 9, allows to obtain an equation in terms of sine and cosine multiplicands, and their higher-order harmonics.

$$\begin{aligned}&C_1 \cos {(\varPhi )} + S_1\sin {(\varPhi )} + C_3 \cos {(3 \varPhi )} + S_3 \sin {(3\varPhi )}\nonumber \\&\quad + \,C_5 \cos {(5 \varPhi )} + S_5\sin {(5 \varPhi )} = 0. \end{aligned}$$

(10)

By neglecting the higher-order harmonics, there are two equations which are factors of $\cos {(\varPhi )}$ and $\sin {(\varPhi )}$. Solving the cosine equation ($C_1 = 0$) for $\varOmega$ gives the expression for the oscillatory frequency as a function of the relative displacement H, written as

$$\begin{aligned} \varOmega = \left( \frac{5H^4 + 12H^2 + 8}{(5\mu +5)H^4+(4\mu +12)H^2+8}\right) ^{1/2}, \end{aligned}$$

(11)

carrying out a similar procedure for equation (Eq. 7), the oscillatory frequency as a function of the displacement H is given by

$$\begin{aligned} \varOmega = \left( \frac{2}{2+\mu H^2}\right) ^{1/2}, \end{aligned}$$

(12)

the last case is for Eq. 8, which is linear and has a fixed frequency, given by

$$\begin{aligned} \varOmega = \left( \frac{1}{1+\mu }\right) ^{1/2}, \end{aligned}$$

(13)

Equations 11, 12 and 13 describe the oscillatory frequency as a function of the amplitude, known as backbone curves. These curves have been plotted for a range of displacement amplitudes and are shown in Fig. 4.

Fig. 4

Backbone curves of oscillatory frequency $\varOmega$ as a function of H with $\mu =0.3$. Thin blue line—exact equation; thick red line—low amplitude approximation; dashed line – high amplitude approximation. (Color figure online)

As shown in Fig. 4, Eqs. 11 and 12 agree well for small values of displacement (less than one). For higher values of the displacement, Eq. 11 approximates to Eq. 13, which confirms the assumptions adopted in Sect. 2.1.

3.2 Free motion: phase plane

The phase plane (displacement/velocity) also helps to understand the behaviour described by Eqs. 4, 7 and 8. For this, the viscous damping element has been neglected and numerical simulations considering initial conditions and free motion were performed. The results are shown in Figs. 5, 6 and 7 for three different initial conditions, Fig. 5 $(h_0,h_0')=(5,0)$, Fig. 6 $(h_0,h_0')=(2,0)$, Fig. 7 $(h_0,h_0')=(0.1,0)$.

The results shown in Fig. 5 consider large displacement, and it is possible to note the difference between the trajectories in the phase plane obtained by the exact equation and the LA approximation when displacement is far from zero. In contrast, the exact equation and HA equation agree well unless for values of displacement close to zero.

By reducing the amplitude of the initial displacement, the trajectories on the phase plane given by the exact equation are approximated to the results defined by LA approximation, as shown in the sequence of Figs. 6 and 7. The low amplitude solution also reaches the correct maximum amplitude because of the initial conditions given to system.

Fig. 5

Trajectories on the phase plane for exact equation (thin blue line), LA approximation (thick red line) and HA approximation (dashed line) with initial conditions $(h_0,h_0')=(5,0)$. (Color figure online)

Fig. 6

Trajectories on the phase plane for exact equation (thin blue line), LA approximation (thick red line) and HA approximation (dashed line) with initial conditions $(h_0,h_0')=(2,0)$. (Color figure online)

Fig. 7

Trajectories on the phase plane for exact equation (thin blue line), LA approximation (thick red line) and HA approximation (dashed line) with initial conditions $(h_0,h_0')=(0.1,0)$. (Color figure online)

3.3 Frequency response

The proposal of this section is to describe the behaviour of system due to harmonic excitation. The initial analysis is described using LA approximation. Typically, in this type of analysis, for the excitation of the form $\varOmega ^2 \hat{X}_0 \cos {(\varOmega \uptau )}$ described in Eq. 7, it is assumed a motion of the form $h(\uptau ) = H\cos {\varPhi }$, with $\varPhi =\varOmega \uptau + \phi$. Replacing this expression in Eq. 6 and keeping only the fundamental frequency terms in cosine and sine, it is obtained:

$$\begin{aligned}&\left( 1-\varOmega ^2\left( 1 + \frac{\mu H^2}{2} \right) \right) H\cos {(\varOmega \uptau + \phi )} \nonumber \\&\quad -\,2\xi \varOmega H\sin {(\varOmega \uptau + \phi )} = \varOmega ^2 \hat{X}_0 \cos {(\varOmega \uptau )}. \end{aligned}$$

(14)

Expanding the trigonometric functions, such that the terms in the right- and left-hand side are balanced, Eq. 14 is split in two equations in terms of sine and cosine, such as

$$\begin{aligned}&\left( 1-\varOmega ^2\left( 1 + \frac{\mu H^2}{2} \right) \right) H = \varOmega ^2 \hat{X}_0 \cos {(\phi )}, \end{aligned}$$

(15)

$$\begin{aligned}&-\,2\xi \varOmega H = \varOmega ^2 \hat{X}_0 \sin {(\phi )}, \end{aligned}$$

(16)

In the free motion case ($\hat{X}_0 = 0$), using Eq. 15 and solving it for $\varOmega$, it is possible to obtain the backbone curve for the resonance frequency as a function of the relative displacement H. The response to harmonic base excitation is obtained by summing the square of Eqs. 15 and 16, which results in a polynomial equation in terms of H

$$\begin{aligned}&\frac{\mu ^2 \varOmega ^4}{4}H^6 + \mu \varOmega ^2\left( \varOmega ^2-1\right) H^4\nonumber \\&\quad + \,\left( 4\xi ^2\varOmega ^2 + \left( 1-\varOmega ^2\right) ^2\right) H^2 -\varOmega ^4\hat{X}_0^2 = 0,\nonumber \\ \end{aligned}$$

(17)

or in terms of $\varOmega$

$$\begin{aligned}&\left( H^2\left( 1+\frac{\mu H^2}{2}\right) ^2 - \hat{X}_0^2\right) \varOmega ^4 \nonumber \\&\quad +\, \left( -2H^2\left( 1+\frac{\mu H^2}{2}\right) +4\xi ^2+H^2\right) \varOmega ^2 \nonumber \\&\quad +\, H^2 = 0, \end{aligned}$$

(18)

Equation 17 is a sextic equation in H, but can be converted to a cubic equation, allowing to obtain three roots which may be of interest. Similarly, Eq. 18 is a bi-quadratic equation in $\varOmega$ and can be solved for the roots of interest.

3.4 Results obtained by using the harmonic balance method: approximated model

The magnitude of H was obtained by solving the polynomial equation (Eq. 17) for values of $\varOmega$, using $\xi =0.1$ and $\hat{X}_0=0.1$. Three values of inertia ratio $\mu$ were compared and are shown in Fig. 8. This figure illustrates effect similar to a softening spring, in which the resonance frequency is reduced by increasing the amplitude of motion, but instead, this reduction is due to the influence of the inertia ratio.

Fig. 8

Magnitude of the relative transmissibility ($|H/\hat{X}_0|$) as a function of frequency varying the inertia ratio $\mu =0.1, 0.2, 0.3$, with $\xi = 0.01$ and $\hat{X}_0 = 0.1$

The detailed behaviour of the relative transmissibility is shown in Fig. 9. The low and high frequency asymptotes are equal to the asymptotes of the linear system. The backbone curve is calculated using Eq. 12. The inner part of the curve (red dashed line) represents unstable periodic motion.

Fig. 9

Magnitude of the relative transmissibility ($|H/\hat{X}_0|$) as a function of frequency and some of its defining features. $\hat{X}_0 = 0.1$, $\mu =0.3$, $\xi =0.01$

The two black dots (a) and (b) are, respectively, the jump-up and jump-down frequencies. The jump-up frequency can be obtained from the solutions of Eq. 18, making $d\varOmega / dH = 0$ and solve for $\varOmega$, to obtain

$$\begin{aligned} \varOmega _a = \frac{2^{1/2}\mu ^{1/3}\hat{X}_0^{1/6}}{\left( 3\mu \hat{X}_0+2\mu ^{2/3}\hat{X}_0^{1/3}\right) ^{1/2}}, \end{aligned}$$

(19)

The respective magnitude for the jump-up frequency is given by

$$\begin{aligned} |H_a| = \left( \frac{\hat{X}_0}{\mu }\right) ^{\frac{1}{3}}, \end{aligned}$$

(20)

Obtaining an expression for the jump-down frequency seems to be more difficult using the same strategy, since it produces a relatively long analytical expression. Therefore, an approximation for the jump-down frequency was obtained from the solutions of Eq. 17, making $\hbox {d}H/\hbox {d}\varOmega = 0$, to obtain

$$\begin{aligned} \varOmega _b = \frac{1}{\hat{X}_0}\sqrt{\frac{2\xi }{\mu }\left( \sqrt{2\mu }\hat{X}_0-2\xi \right) }, \end{aligned}$$

(21)

Equation 21 is not exactly the portion of the frequency response where the slope is vertical ($90^{\circ }$), instead, it corresponds to the resonance peak where the slope is zero.

The respective magnitude for the jump-down frequency is also a long analytical expression which depends on the amount of damping and due to practical reasons is not presented here. Nevertheless, it can be obtained substituting the expression for $\varOmega _b$ in the solution of Eq. 17.

3.5 Absolute displacement

So far, the analysis of transmissibility has been based on the study of relative displacement, but in practice, it is interesting to consider the absolute displacement transmissibility. This can be calculated considering the magnitude and phase of the relative transmissibility, given by

$$\begin{aligned} X= & {} \sqrt{H^2+\hat{X}_0^2 + 2 H \hat{X}_0 \cos {(\phi )}}, \end{aligned}$$

(22)

$$\begin{aligned} \phi= & {} {{\mathrm{atan}}}{\left( -\frac{4\xi \varOmega }{2-\varOmega ^2(2+\mu H^2)}\right) }, \end{aligned}$$

(23)

Using Eq.  22, the absolute displacement is plotted in Figs. 10 and 11 and compared to two other linear systems. In these figures, the thin red line corresponds to the absolute displacement transmissibility of the traditional mass–spring–damper system; the black dashed line, represents the displacement transmissibility of the mass–spring–damper–inerter (shown in Fig. 2) and the thick blue line represents the results obtained using Eq. 22. The transmissibility of the linear systems is given in “Appendix C”.

The difference between Figs. 10 and 11 is the amplitude of the base displacement $\hat{X}_0$.

Fig. 10

Comparison of absolute displacement magnitudes with base excitation for mass–spring–damper, mass–spring–damper-inerter and proposed system, considering $\xi = 0.01$, $\mu = 0.3$ and $\hat{X}_0 = 0.3$

Fig. 11

Comparison of absolute displacement magnitudes with base excitation for mass–spring–damper, mass–spring–damper–inerter and proposed system, considering $\xi = 0.01$, $\mu = 0.3$ and $\hat{X}_0 = 0.6$

Figures 10 and 11 show the frequency response, comparing the proposed system to the classical mass–spring–damper and the mass–spring–damper with inerter in vertical configuration. The resonance peak is similar to a softening stiffness system, as consequence of the geometrical arrangement. The anti-resonance in the frequency response is a characteristic of isolators with an inerter element, also the high frequency asymptote is a drawback when the inerter is used. For the system under study, with the inerter in horizontal arrangement, the anti-resonance is shifted to a higher frequency, and the response at high frequencies is reduced to lower amplitudes. As the amplitude of base displacement ($X_0$) is increased, the resonance peak is shifted to the left.

3.6 Results obtained by using the harmonic balance method: exact model

So far, the transmissibility of the system described by the approximated equation could be obtained using the harmonic balance method, resulting in analytical expressions such as those described by Eqs. 15 and 16. When considering the exact model described by Eq. 9, it becomes difficult to obtain analytical expressions that define the transmissibility as a function of frequency. To overcome this issue, the procedure to obtain the transmissibility function for the exact system was also developed considering that $h(\uptau ) = H \cos {(\varPhi )}$. Replacing this term in Eq. 9, results in expression in terms of the multiplicands $\cos {(\varOmega \tau )}$ and $\sin {(\varOmega \tau )}$ and higher-order harmonics. Neglecting the higher-order harmonics results in the set of nonlinear equations:

$$\begin{aligned} P_1\cos {(\phi )} + P_2\sin {(\phi )} + P_3\cos {(2\phi )}= & {} 0, \end{aligned}$$

(24)

$$\begin{aligned} P_2\cos {(\phi )} - P_1\sin {(\phi )} - P_3\sin {(2\phi )}= & {} 0, \end{aligned}$$

(25)

in which the terms $P_1, P_2, P_3$ are functions of H and are described in “Appendix A”. Equations 24 and 25 can be solved numerically with the unknowns H and $\phi$ for each frequency.

When solving Eqs. 24 and 25 numerically, there is the necessity of initial guess for H and $\phi$. For some frequency ranges, there may exist more than one solution, which makes necessary to solve these equations for different initial guesses. These equations were solved using the Python–Scipy library [14] and the fsolve function, which consists of a modification of Powell’s Hybrid Method for finding the roots of N-nonlinear equations.

Figure 12 shows the relative transmissibility obtained using this procedure for different values of base displacement $\hat{X}_0$. The values of base displacement adopted were $\hat{X}_0 = 0.025, 0.05, 0.075, 0.1$ and the respective resonance peaks moving from the right to the left-hand side as the base displacement increases. This behaviour is similar to line defining the backbone curve defined in Eq. 11 and shown in Fig. 4.

Fig. 12

Comparison of the relative transmissibility considering the exact equation for base displacement $\hat{X}_0 = 0.025, 0.05, 0.075, 0.1$. (with the respective resonance peaks from right- to left-hand side). Results were normalised to base displacement $\hat{X}_0=0.1$

Figures 13 and 14 show a comparison of the transmissibility for the proposed system considering the exact equation with the classical mass–spring–damper system and the mass–spring–damper and inerter in vertical configuration. The difference between Figs. 13 and 14 is the amplitude of the base displacement $\hat{X}_0$, respectively, $\hat{X}_0=0.3$ and $\hat{X}_0=0.6$.

Fig. 13

Comparison of the absolute transmissibility considering the exact equation, the mass–spring–damper and the mass–spring–damper–inerter isolators. $X_0=0.3$, $\mu =0.3$, $\xi =0.01$

In Fig. 13, it is possible to observe that the transmissibility of the proposed system has some advantages for specific frequency ranges when compared to the other two systems. The high frequency amplitude has some benefits when compared to the mass–spring–damper–inerter in vertical configuration isolator.

The results shown in Fig. 14 present a similar behaviour, with a slight change in the anti-resonance frequency.

Fig. 14

Comparison of the absolute transmissibility considering the exact equation, the mass–spring–damper and the mass–spring–damper–inerter isolators. $X_0=0.6$, $\mu =0.3$, $\xi =0.01$

The results of these figures show that there may be some advantage of using the inerter in horizontal configurations depending on the amplitude of the base excitation and the frequency range of interest.

4 Stability of the periodic response

The conditions leading to jumps in the frequency response, which are defined by the jump-up and jump-down frequencies, are important in the analysis of nonlinear systems since these conditions produce undesired behaviour of a vibration isolator. The analysis of the regions of instability can be obtained considering perturbation in the periodic response, defined by

$$\begin{aligned} h(\tau ) = u(\tau ) + e(\tau ) = U\cos {(\varOmega \tau )} + e(\tau ), \end{aligned}$$

(26)

in which u is a solution of the differential equation and e is a small perturbation parameter. Replacing Eq. 26 for the free motion case into Eq. 7 gives

$$\begin{aligned}&\left( 1+\mu \left( u+e\right) ^2\right) \left( u'' + e''\right) + 2\xi \left( u'+e'\right) \nonumber \\&\quad + \,\left( 1 + \mu \left( u'+e'\right) ^2\right) \left( u+e \right) = 0, \end{aligned}$$

(27)

expanding Eq. 27, and reminding that $u(\uptau )$ is a solution

$$\begin{aligned} \left( 1+\mu {u}^2\right) u'' + 2\xi u' + \left( 1+\mu {u'}^2\right) u = 0, \end{aligned}$$

(28)

replacing Eq. 28 into Eq. 27, results in

$$\begin{aligned}&(1+\mu u^2)e''+\mu (2ue+e^2)(u''+e'')\nonumber \\&\quad +\, 2\xi e'+(1+\mu {u'}^2)e \nonumber \\&\quad + \,\mu (2u'e'+{e'}^ 2)(u+e)=0, \end{aligned}$$

(29)

assuming $e(\uptau ) = \mathbf {A}\sin {(\varOmega \uptau )} + \mathbf {B}\cos {(\varOmega \uptau )}$ and, since e is a small parameter, the higher-order terms can be neglected ($\mathbf {A}^2, \mathbf {B}^2, \mathbf {AB}, \mathbf {A}^2\mathbf {B}, \mathbf {A}\mathbf {B}^2, \ldots$), allowing to rewrite Eq. 29 as

$$\begin{aligned}&\left[ \left( 1-\varOmega ^2(1+\frac{3}{2}\mu U^2\right) \mathbf {A} +2\xi \varOmega \mathbf {B}\right] \cos {(\varOmega \uptau )} \nonumber \\&\quad +\,\left[ \left( 1-\varOmega ^2(1+\frac{1}{2}\mu U^2\right) \mathbf {B} -2\xi \varOmega \mathbf {A} \right] \sin {(\varOmega \uptau )} = 0,\nonumber \\ \end{aligned}$$

(30)

the parameters $\mathbf {A}$ and $\mathbf {B}$ are small but nonzero; therefore, Eq. 30 can be rearranged in two equations in terms of sine and cosine terms and put in the matrix form,

$$\begin{aligned}&\left[ \begin{array}{cc} 1-\varOmega ^2\left( 1+\frac{3}{2}\mu U^2\right) &{} 2\xi \varOmega \\ -2\xi \varOmega &{} 1-\varOmega ^2\left( 1+\frac{1}{2}\mu U^2\right) \end{array} \right] \left[ \begin{array}{c} \mathbf {A} \\ \mathbf {B} \end{array} \right] \nonumber \\&\quad =\left[ \begin{array}{c} 0 \\ 0 \end{array} \right] , \end{aligned}$$

(31)

for nonzero $\mathbf {A}$ and $\mathbf {B}$, the determinant of Eq. 31 provides the equation which defines the regions of instability

$$\begin{aligned}&\frac{3 \mu ^2 \varOmega ^4}{4} U^4 - 2\mu \varOmega ^2\left( 1-\varOmega ^2\right) U^2 + 4\xi ^2\varOmega ^2\nonumber \\&\quad + \left( 1-\varOmega ^2\right) ^2 = 0, \end{aligned}$$

(32)

among the four solutions of Eq. 32 in terms of U, two are of interest, which can be plotted as a function of the frequency in Fig. 15. The red areas define the regions where the system is subject to jumps.

Fig. 15

Relative displacement and stability region obtained by harmonic balance method. $\hat{X}_0=0.1$, $\mu =0.3$, $\xi =0.01$ (LA approximation)

4.1 Stability of the periodic response: exact model

Carrying out a similar procedure for the exact model, the equivalence of Eq. 32 is given by

$$\begin{aligned} T_8 U^8 + T_6 U^6 + T_4 U^4 + T_2 U^2 + T_0 = 0, \end{aligned}$$

(33)

this equation can also be written as a function of $\varOmega$ as

$$\begin{aligned} W_4 \varOmega ^4 + W_2 \varOmega ^2 + W_0 = 0, \end{aligned}$$

(34)

and the terms $T_i$ and $W_i$ are given in “Appendix B”. Solving any of Eqs. 33 or 34 allows to obtain the region of instability of the periodic response. In the case of the exact system equation, the regions of instability are plotted in Fig. 16

Fig. 16

Relative displacement and stability region obtained by harmonic balance method. $\mu =0.3$, $\xi =0.01$. Two values of base displacement were used $\hat{X}_0=0.05, 0.025$, (exact equation)

As it is possible to observe in Fig. 16, the regions of instability differ from the results shown in Fig. 15. For values large values of base displacement, the displacement curves do not cross the red regions and the system does not present jumps. In the case of the two curves shown in this figure, the jump-down frequency is coincident with the top part of the instability region. The jump-up frequency is not coincident, mainly because of the approximations described in Sect. 4.

5 Numerical analysis

In the previous sections, the relative and absolute transmissibility functions were calculated using the method of harmonic balance and considering the exact and approximated equations of motion. In this section, a detailed analysis is performed using numerical integration. For this, an implementation in C-language using the GNU–GSL library [8] was used. The method for numerical integration chosen was the explicit Runge–Kutta–Fehlberg (4, 5) method. In some cases, parallel computation using the multiprocessing module [18] in Python programming language was used.

Recalling the full equation of motion written as

$$\begin{aligned}&\left( 1+\mu \frac{h^2}{(1+h^2)}\right) h'' + 2\xi h' + \left( 1+ \mu \frac{{h'}^2}{(1+h^2)^2} \right) h \nonumber \\&\quad = \varOmega ^2 \hat{X}_0 \cos {(\varOmega \uptau )} \end{aligned}$$

(35)

and the usual choice of state variables as $q_1=h$ and $q_2=h'$, the state equations are given by

$$\begin{aligned}&q_1' = q_2 \end{aligned}$$

(36)

$$\begin{aligned}&q_2' = -\left( 1+\mu \frac{h^2}{(1+h^2)}\right) ^{-1} \nonumber \\&\qquad \left( 2 \xi ' + \left( 1+ \mu \frac{{h'}^2}{(1+h^2)^2} \right) h \right. \nonumber \\&\qquad \left. -\, \varOmega ^2 \hat{X}_0 \cos {(\varOmega \uptau )} \right) \end{aligned}$$

(37)

The first investigation was performed by integrating Eqs. 36 and 37 in the frequency range $\varOmega = [0.8, 1.2]$ using small incremental steps in frequency. The numerical integration was performed with the system initially at rest for a time $\tau = 2000$. Only a small portion at the end of each time history was considered to reduce the influence of transient behaviour. The amplitude of the steady state was then recorded. This procedure was repeated for different values of base displacement $\hat{X}_0$ and is shown in Fig. 17.

Fig. 17

Magnitude of the relative transmissibility $|H/\hat{X}_0|$ for different values of base displacement ($X_0$), using $\mu =0.3$ and $\xi =0.02$

Fig. 18

Magnitude of the relative transmissibility ($|H/\hat{X}_0|$) obtained by frequency sweep up and sweep down. Results were obtained for $X_0=0.1$, $\mu =0.3$ and $\xi =0.01$. The detail shows the frequency range with co-existing solutions

Fig. 19

a Time history and b steady-state response on the phase plane for excitation frequency $\varOmega = 0.91$ with $h_0=0$ and $h'_0=-\,4.0$, (b)

Fig. 20

a Time history and b steady-state response on the phase plane for excitation frequency $\varOmega = 0.91$ with $h_0=2$ and $h'_0=-\,4.0$

Fig. 21

a Basins of attraction for $\varOmega =0.91$, $\mu =0.3$, $\xi =0.01$ and $\hat{X}_0=0.1$, where the yellow area represents the high amplitude limit cycle and the dark area represents the small amplitude limit cycle; b zoom region

It is possible to observe in Fig. 17 that increasing the base motion amplitude, the resonance peak is shifted to the left in the frequency axis. There are values of base displacement that produces discontinuities in the frequency response, for instance when $\hat{X}_0 = 0.1$. By further increasing the base displacement, the discontinuities tend to disappear and the resonance peak tends to a fixed value which is in agreement with what was described in the previous sections.

5.1 Evolution of basins of attraction

In the previous section, it was shown that there is a range of $X_0$ for which the response has two co-existing solutions. For example, Fig. 18 shows the overlapping solutions between the up and down jumps. These co-existing solutions are low and high amplitude limit cycles. These limit cycles at $\varOmega =0.91$ are shown in Figs. 19, 20.

The basins of attraction of these two periodic attractors were calculated and are shown in Fig. 21, in which the yellow area is the basin of the high amplitude limit cycle, and the dark area is the basin of the small amplitude limit cycle. Figure 22 shows the evolution of the basins as the inertance ratio $\mu$ is varied, showing that larger $\mu$ results in larger probability of finding larger amplitude response.

Fig. 22

Effect of the mass ratio ($\mu$) on the basins of attraction. The last figure on the bottom right shows the ratio between the low and high amplitude limit cycles as a function of the mass ratio. a $\mu =0.28$. b $\mu =0.29$. c $\mu =0.30$. d $\mu =0.31$. e $\mu =0.32$. f ratio of the areas leading to low and high amplitude limit cycles as a function of the parameter $\mu$

6 Final remarks

This work presented a study on the dynamic behaviour of a vibration isolator consisting of a mass supported by linear spring and a viscous damper in combination with an inerter in horizontal arrangement.

It has been shown that the equation of motion for this system has two approximating conditions, one for low amplitude of motion and one of high amplitude of motion.

The harmonic balance method was used to obtain approximated solutions for the relative and absolute displacement transmissibility, showing that, depending on the frequency range and amplitude of the base excitation, the proposed system can have benefits when compared to the traditional spring–damper and spring–damper–inerter in vertical arrangement isolators.

An interesting observation about the nonlinearity in this system is that it vanishes when the amplitude of motion becomes high, so that there is a limited amplitude range where the nonlinearity plays important role in the system response.

The last section of the paper presented a numerical analysis showing that the system may exhibit two different co-existing limit cycles, one large and one smaller, both period-1. The basins of attraction suggest that increasing the value of inertance makes the system more likely to exhibit large amplitude limit cycle.

Appendices

Polynomial terms

The polynomial terms defining Eqs. 24 and 25:

$$\begin{aligned} P_1= & {} -\frac{5}{8}\left( \left( \mu + 1\right) \varOmega ^2 - 1\right) H^5 \nonumber \\&- \,\frac{1}{2} \left( \left( 1 \mu +3\right) \varOmega ^2-3\right) H^3\nonumber \\&+ \,\left( 1- \varOmega ^2 \right) H \end{aligned}$$

(38)

$$\begin{aligned} P_2= & {} -\frac{1}{4}\left( \xi \varOmega H^5 + 4 \xi \varOmega H^3 + 8 \xi \varOmega H \right) \end{aligned}$$

(39)

$$\begin{aligned} P_3= & {} -\frac{1}{4}\left( \varOmega ^2 H^4 + 2\varOmega ^2 H^2 \right) \hat{X}_0 \end{aligned}$$

(40)

Polynomial terms: stability

The polynomial terms defining the stability Eqs. 33 and 34:

$$\begin{aligned} T8= & {} \frac{125}{64}\left( \mu ^2 + 2\mu + 1\right) \varOmega ^4 \nonumber \\&+ \,\frac{1}{32}\left( 10\xi ^2 -125\mu - 125\right) \varOmega ^2 + \frac{125}{64} \end{aligned}$$

(41)

$$\begin{aligned} T_6= & {} \frac{1}{2}\left( 5\mu ^ 2 + 20 \mu + 15\right) \varOmega ^4 \nonumber \\&+\, \left( 2\xi ^2 - 10 \mu - 15\right) \varOmega ^2 + \frac{15}{2} \end{aligned}$$

(42)

$$\begin{aligned} T_4= & {} \frac{1}{4}\left( 3\mu ^2 + 33\mu + 43\right) \varOmega ^4 \nonumber \\&+\, \frac{1}{4} \left( 24\xi ^2 -33\mu - 84 \right) \varOmega ^2 + 1 \end{aligned}$$

(43)

$$\begin{aligned} T_2= & {} \left( 2\mu + 6\right) \varOmega ^4 + \left( 8\xi ^2 -2\mu - 12\right) \varOmega ^2 + 6 \end{aligned}$$

(44)

$$\begin{aligned} T_0= & {} \varOmega ^4 + \left( 4\xi ^2 -2\right) \varOmega ^2 + 1 \end{aligned}$$

(45)

$$\begin{aligned} W_4= & {} \frac{1}{64} \left( 125\mu ^2+250\mu +125\right) U^8\nonumber \\&+ \,\left( \frac{5}{2}\mu ^2+10\mu +\frac{15}{2}\right) U^{6} \nonumber \\&+\,\frac{1}{64}\left( 48\mu ^2+528\mu +672\right) U^4 \nonumber \\&+\, \left( 2\mu +6\right) U^2 + 1 \end{aligned}$$

(46)

$$\begin{aligned} W_2= & {} \frac{1}{32} \left( 10{\xi }^2-125\mu -125\right) U^8 \nonumber \\&+\,\left( 2{\xi }^2-10\mu -15\right) U^6 \nonumber \\&+\,\frac{1}{4}\left( 24{\xi }^2-33\mu -84\right) U^4 \nonumber \\&+ \,\left( 8 \xi ^2-2\mu -12\right) U^2 + 4 \xi ^2 - 1 \end{aligned}$$

(47)

$$\begin{aligned} W_0= & {} \frac{125}{64} U^8 + \frac{15}{2}U^{6} + \frac{21}{2} U^4 + 6 U^2+1 \end{aligned}$$

(48)

Fig. 23

Comparison of the absolute transmissibility considering the exact equation, the mass–spring–damper, the mass–spring–damper–inerter isolators and a system with an auxiliary TMD. $X_0=0.3$, $\mu =0.3$, $\xi =0.01$

Absolute transmissibility of linear systems

The absolute transmissibility of a linear spring–mass–damper system is given by

$$\begin{aligned} T = \frac{1+j2\xi \varOmega }{1-\varOmega ^2 + j2\xi \varOmega } \end{aligned}$$

(49)

The absolute transmissibility of a linear spring–mass–damper–inerter system of Fig. 2 is given by

$$\begin{aligned} T = \frac{1 -\mu \varOmega ^2 + j2\xi \varOmega }{1-(1+\mu )\varOmega ^2 + j2\xi \varOmega } \end{aligned}$$

(50)

Comparison with tuned mass damper (TMD)

To complement the analysis described in this paper, a comparison of the proposed system with the tuned mass damper is shown in Fig. 23. In this analysis, the natural frequency of the auxiliary system was tuned in the same resonance frequency of the primary system.