1 Introduction

Bio-inspired isolators that imitate the special structures of living organisms, such as animal limbs and bird necks, have become the focus of investigation with the aim of improving the performance of engineering systems. These isolation systems have favorable geometrical nonlinearities [1,2,3,4] that have led researchers to study the effect of these nonlinearities with added geometric nonlinear stiffness [5,6,7,8] and nonlinear damping [9,10,11,12,13,14,15,16]. For example, an X-shaped vibration isolation mount has desirably weak nonlinearities and structural parameters. The addition of an oblique spring can ensure good stability, loading capacity, and adjustable isolation. The negative stiffness effect of the X-shaped structure can be eliminated by the vertical positive stiffness resulting from the contact stiffness of the oblique spring [1]. Abbasi et al. [17] investigated the optimal design of asymmetric high-static-low-dynamic-stiffness (HSLDS) suspensions to mitigate the vibration of a symmetric rotating system excited by an unbalanced force. Zhang et al. [18] analysed the dynamic characteristics of a quasi-zero stiffness (QZS) system with geometric nonlinear damping, friction, and inertia of the connection rods. Dai et al. [19] proposed a novel bio-inspired anti-impact manipulator that offers high efficiency and anti-impact performance; moreover, the manipulator can be adjusted with respect to different targets. Feng et al. [3] and Jing et al. [20] proposed a novel passive human body-inspired anti-vibration structure (HBIAVS) and an HBIAVS with a coupled nonlinear inertia (HBIAVS-NI) design [4], which can be easily realised, both in terms of size and loading capacity. Gatti [2] presented an analytical insight into the elastic performance of a bio-inspired nonlinear spring, which consists of four linear mechanical springs arranged in a K-shaped configuration to achieve a specific form of nonlinearity. Recently, multi-layer structures with geometrical nonlinearities have been established to provide new advantages, such as anti-vibration capability [21, 22]. Jiang et al. [21] studied a unique bio-inspired multi-joint leg-like or limb-like vibration isolation structure by mimicking the skeleton and joint structures of animal legs; and achieved the desired vibration isolation performance, including the resonant frequency, loading capacity, and effective vibration displacement range. By imitating the structure of a bird neck and the gazing stability of the head, Deng et al. [22] investigated a multi-layered QZS nonlinear isolator with high-performance isolation for low- and ultra-low-frequency vibrations.

In the aforementioned studies, the harmonic balance method (HBM) was applied to solve the equations of motion for single-layer and two-layer nonlinear systems. However, increasing the number of system layers solved by the HBM increases the number of harmonic components included, which increases the complexity of balancing equations resulting in a comparatively large truncation error, which is induced by neglecting high-order harmonic components [23,24,25]. To improve the accuracy of the HBM, modified methods, such as the two-timescale HBM [26], incremental HBM (IHBM) [27], linearisation of the governing equation with the HBM [28], and a combination of Newton’s iteration with HBM [29], have been presented. Moreover, von Wagner and Lentz presented the methods of harmonic balance and slowly changing phase and amplitude to solve simple and modified Duffing oscillators [30]. Zhou et al. [31] proposed a new analytical approximate technique by combining system linearisation with the HBM. Donmez et al. [32] utilised the HBM, which transforms the nonlinear differential equations of motion into a set of nonlinear algebraic equations to solve the steady-state response of a QZS isolator with dry friction damping. Furthermore, to obtain accurate results for high-dimensional systems or systems with complex nonlinearities, the high-dimensional harmonic balance method is relatively simple despite the complexity of the nonlinearities; however, it may produce spurious solutions in addition to the physically meaningful ones [33]. Using linear equations, Khodaparast et al. [34] controlled the nonlinear restoring function of multiple-degree-of-freedom nonlinear dynamic systems using an extended HBM.

Jacobi elliptic functions have been widely used to obtain accurate results by assuming the general solutions of several nonlinear dynamical system responses to be in the form of Jacobi elliptic functions [23, 35,36,37,38]. Okabe et al. [39] improved the averaging method using the Jacobi elliptic sine, cosine, and delta functions, as well as the delta and zeta functions [40], to obtain highly accurate periodic solutions for highly nonlinear dynamical systems. The approximation solutions of conservative oscillators with a non-negative real power restoring force were derived using Jacobi elliptic functions [41, 42]. Recently, Jacobi elliptic functions were used to obtain the exact closed-form solutions of several oscillatory systems that contain pure cubic stiffness nonlinearity [43] and to achieve the desired response by tuning the external excitation [44]. However, when the EHBM is used to solve the equations of motion of two- or multi-degrees of freedom (DOF) nonlinear oscillator systems, the number of balancing equations is not equal to that of the unknowns [45]. To address this issue in two-DOF systems, Chen and Liu [45] extended the EHBM for an analysis using an additional equation prior to initial harmonic balancing. By transforming the sinusoidal driving function into its corresponding equivalent Jacobian elliptic function form, Elias-Zuniga and Beatty [46] obtained the solution of a system of two coupled nonhomogeneous undamped ordinary differential equations with a cubic nonlinear and sinusoidal driving force. Using a combination of a Jacobi elliptic function and a trigonometric function as the analytical solution, Cveticanin proposed an approximate method for solving coupled highly nonlinear differential equations with small nonlinearities based on the Krylov–Bogolubov procedure [47]. Wu and Tang modified the harmonic components of the geometric nonlinear damping and nonlinear stiffness force of single- and two-DOF nonlinear vibration isolation systems using Jacobi elliptic functions, which perform well in resonance regimes [48, 49].

In this study, the isolation characteristics of a bio-inspired multistage nonlinear vibration isolator were analysed using a modified elliptic harmonic balance method (EHBM). As detailed in Sect. 2, by imitating the structure of a bird neck, a bio-inspired multistage isolator with both geometric stiffness and damping nonlinearities, which are incorporated in each stage of the configuration, was realised. Simultaneously, by imitating the space-fixed gazing stability of the bird head, a large mass was used in the first stage of the multistage configuration. The equations of motion for both force excitation and base excitation were established in a matrix form after decoupling the stiffness and damping matrix of the multistage nonlinear isolator. Section 3 discusses how the dynamic equilibrium force at each steady-state stage is obtained. The relationship between the excitation frequency and Jacobi elliptic frequency and modulus was analysed. The modified stiffness and damping force components were obtained to improve the solution accuracy of the amplitude–frequency results. The amplitude and phase relationship of the excitation, damping, stiffness, and inertia force components are presented as vectors with an orthogonal relationship. Further, as detailed in Sect. 4, the force and displacement transmissibilities of the multistage nonlinear vibration isolation system are solved using the first-order harmonic balance method (HB1) and EHBM. The results of a three-stage isolation system, which is a simple multistage system, and a twelve-stage isolation system, such as that of twelve cervical vertebrae in birds, are compared with the numerical solutions.

2 A bio-inspired multistage nonlinear isolation system

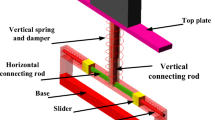
The bird neck not only performs a variety of demanding tasks, such as feeding, manipulation of the head, and combat behaviour [50], but also performs the stable gazing action of the head and helps control flight and stabilisation of vision [51]. Normally, 8–25 vertebrae in bird necks are connected by a complex network of tendons and muscles; the low-frequency vibrations are isolated to protect the bird organs that have lower resonance frequencies [22]. A multistage nonlinear isolation system, shown in Fig. 1a, was used to imitate the multi-vertebral structure of a bird neck. The bio-inspired isolation system with HSLDS property may realise the isolation of low- and ultra-low-frequency vibrations. For simplicity, we focused on the motion along the neck direction and neglected the motion in the transverse direction of the bird neck. When the connection between the concave and convex structures of the bird’s vertebrae is considered, the forces of the tendons and muscles that are in the horizontal direction, are modelled by horizontal springs and dampers. The muscles and tendons that provide the forces in the vertical direction are simplified to vertical springs and dampers. Each adjacent vertebra of the neck, connected by muscles and tendons, is modelled by a stage of the nonlinear vibration isolation system. For the ith stage of the isolator shown in Fig. 1b, xi is the displacement, ms(i) is the equivalent mass, kv(i) and kh(i) are the stiffness values of the vertical and horizontal springs, and cv(i) and ch(i) are the damping coefficients of the vertical and horizontal dampers, respectively; xe is the displacement of the base, and \({1} \le i \le N\). The vertical dampers and springs are orientated in the direction of the displacement; the horizontal dampers and springs, which induce nonlinear geometric characteristics, are orientated in the perpendicular direction of the displacement.

Fig. 1
figure 1

Simple model of a bio-inspired multistage isolation system: a overall model; b ith stage

Full size image

In this study, we investigate the displacement and force transmissibilities of a bio-inspired multistage nonlinear vibration isolator. A displacement excitation is induced to imitate the bio-inspired case in which the bird neck isolates the low-frequency motion of the body and maintains the gazing stability. When the base displacement is zero and the excitation force is not zero, the force excitation case is also investigated to provide further insight into the potential engineering applications of the bio-inspired multistage nonlinear vibration isolator.

When the base displacement is \(x_{e} = 0\) and the excitation force is \(f_{e} \left( t \right) = F_{e} \cos \left( {\omega_{e} t} \right)\), where fe(t) is the excitation force added to ms(1), the equation of motion in the matrix form is given by

$${\mathbf{M}}{\ddot{\mathbf{X} + \mathbf{C}}}_{t} {\dot{\mathbf{X} + \mathbf{K}}}_{t} {\mathbf{X = F}}_{e} ,$$
(1)

where \({\mathbf{M}} = \left[ {\begin{array}{*{20}c} {m_{s\left( 1 \right)} } & 0 & \cdots & 0 \\ 0 & {m_{s\left( 2 \right)} } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {m_{s\left( N \right)} } \\ \end{array} } \right]_{N \times N}\), \({\mathbf{C}}_{t} = \left[ {\begin{array}{*{20}c} {c_{t\left( 1 \right)} } & { - c_{t\left( 1 \right)} } & \cdots & 0 \\ { - c_{t\left( 1 \right)} } & {c_{t\left( 1 \right)} + c_{t\left( 2 \right)} } & \ddots & \vdots \\ \vdots & \ddots & \ddots & { - c_{{t\left( {N - 1} \right)}} } \\ 0 & \cdots & { - c_{{t\left( {N - 1} \right)}} } & {c_{{t\left( {N - 1} \right)}} + c_{t\left( N \right)} } \\ \end{array} } \right]_{N \times N}\), \({\mathbf{K}}_{t} { = }\left[ {\begin{array}{*{20}c} {k_{t\left( 1 \right)} } & { - k_{t\left( 1 \right)} } & \cdots & 0 \\ { - k_{t\left( 1 \right)} } & {k_{t\left( 1 \right)} + k_{t\left( 2 \right)} } & \ddots & \vdots \\ \vdots & \ddots & \ddots & { - k_{{t\left( {N - 1} \right)}} } \\ 0 & \cdots & { - k_{{t\left( {N - 1} \right)}} } & {k_{{t\left( {N - 1} \right)}} + k_{t\left( N \right)} } \\ \end{array} } \right]_{N \times N}\), \({\mathbf{F}}_{e} = \left[ {\begin{array}{*{20}c} {F_{e} \cos \left( {\omega_{e} t} \right)} & 0 & \cdots & 0 \\ \end{array} } \right]^{T}_{1 \times N}\), \({\mathbf{X}} = \left[ {\begin{array}{*{20}c} {x_{1} } & {x_{2} } & \cdots & {x_{N} } \\ \end{array} } \right]^{T}_{1 \times N}\), \(k_{t\left( i \right)} = k_{v\left( i \right)} + 2k_{h\left( i \right)} \left( {1 - {{l_{0\left( i \right)} } \mathord{\left/ {\vphantom {{l_{0\left( i \right)} } {\sqrt {\left( {x_{i} - x_{i + 1} } \right)^{2} + l_{i}^{2} } }}} \right. \kern-\nulldelimiterspace} {\sqrt {\left( {x_{i} - x_{i + 1} } \right)^{2} + l_{i}^{2} } }}} \right)\),\(c_{t\left( i \right)} = c_{v\left( i \right)} + {{2c_{h\left( i \right)} \left( {x_{i} - x_{i + 1} } \right)^{2} } \mathord{\left/ {\vphantom {{2c_{h\left( i \right)} \left( {x_{i} - x_{i + 1} } \right)^{2} } {\left( {l_{i}^{2} + \left( {x_{i} - x_{i + 1} } \right)^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {l_{i}^{2} + \left( {x_{i} - x_{i + 1} } \right)^{2} } \right)}}\), \(1 \le i \le N\), and Fe and ωe are the amplitude and frequency of the excitation force, respectively.

The transmitted force of the ith stage is given by

$$f_{t\left( i \right)} \left( {z_{i} ,\dot{z}_{i} } \right) = c_{v\left( i \right)} \dot{z}_{i} + 2c_{h\left( i \right)} \frac{{z_{i}^{2} }}{{z_{i}^{2} + l_{i}^{2} }}\dot{z}_{i} + k_{v\left( i \right)} z_{i} + 2k_{h\left( i \right)} \left( {1 - \frac{{l_{0\left( i \right)} }}{{\sqrt {z_{i}^{2} + l_{i}^{2} } }}} \right)z_{i} ,$$
(2)

where \(z_{i} = x_{i} - x_{i + 1}\) is the relative displacement between ms(i) and ms(i+1) for \(1 \le i \le N - 1\), \(z_{N} = x_{N} - x_{e}\) is the relative displacement between ms(N) and the base, li is the length of the horizontal springs of the ith stage in the state of rest, and l0(i) is the unstretched length of the horizontal springs of the ith stage.

If zi is sufficiently small and \(\left| {z_{i} } \right| < 0.2l_{i}\), then the transmitted force ft(i), as shown in Eq. (2), can be approximated using the series expansion to the third-order for zi as follows:

$$f_{t\left( i \right)} \left( {z_{i} ,\dot{z}_{i} } \right) = f_{d\left( i \right)} + f_{s\left( i \right)} \approx c_{v\left( i \right)} \dot{z}_{i} + 2c_{h\left( i \right)} \left( {\frac{{z_{i} }}{{l_{i} }}} \right)^{2} \dot{z}_{i} + k_{i} z_{i} + k_{c\left( i \right)} z_{i}^{3} ,$$
(3)

where fd(i) is the approximate damping force when \({{z_{i}^{2} } \mathord{\left/ {\vphantom {{z_{i}^{2} } {\left( {z_{i}^{2} + l_{i}^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {z_{i}^{2} + l_{i}^{2} } \right)}} \approx \left( {{{z_{i} } \mathord{\left/ {\vphantom {{z_{i} } {l_{i} }}} \right. \kern-\nulldelimiterspace} {l_{i} }}} \right)^{2}\), and fs(i) is the approximate spring force when \(k_{v\left( i \right)} z_{i} + 2k_{h\left( i \right)} \left( {1 - {{l_{0\left( i \right)} } \mathord{\left/ {\vphantom {{l_{0\left( i \right)} } {\sqrt {z_{i}^{2} + l_{i}^{2} } }}} \right. \kern-\nulldelimiterspace} {\sqrt {z_{i}^{2} + l_{i}^{2} } }}} \right)z_{i} \approx k_{i} z_{i} + k_{c\left( i \right)} z_{i}^{3}\) where \(k_{i} = k_{v\left( i \right)} - 2k_{h\left( i \right)} \left( {{{l_{0\left( i \right)} } \mathord{\left/ {\vphantom {{l_{0\left( i \right)} } {l_{i} }}} \right. \kern-\nulldelimiterspace} {l_{i} }} - 1} \right)\) and \(k_{c\left( i \right)} = {{k_{h\left( i \right)} l_{0\left( i \right)} } \mathord{\left/ {\vphantom {{k_{h\left( i \right)} l_{0\left( i \right)} } {l_{i}^{3} }}} \right. \kern-\nulldelimiterspace} {l_{i}^{3} }}\).

The base displacement \(x_{e} = 0\), \(x_{i} = \sum\limits_{j = i}^{N} {z_{j} }\) can be obtained. The equations of motion of the force-excited vibration isolation system are given by

$$\begin{aligned} {\mathbf{MU}\ddot{\mathbf{Z}}} + \left( {{\mathbf{C}}_{v} { + }{\mathbf{C}}_{h} } \right){\dot{\mathbf{Z}}} + {\mathbf{K}}_{1} {\mathbf{\rm Z}}{ + }{\mathbf{K}}_{c} {\mathbf{\rm Z}}^{\left( 3 \right)} {\mathbf{ = }} & {\mathbf{F}}_{e} + \left[ {\begin{array}{*{20}c} 0 & {\mathbf{0}} \\ {\mathbf{0}} & {\left( {{\mathbf{C}}_{v} { + }{\mathbf{C}}_{h} } \right)_{{\left( {N - 1} \right) \times \left( {N - 1} \right)}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 \\ {{\dot{\mathbf{Z}}}_{{\left( {N - 1} \right) \times 1}} } \\ \end{array} } \right] \\ & \; + \left[ {\begin{array}{*{20}c} 0 & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{K}}_{{1\left( {N - 1} \right) \times \left( {N - 1} \right)}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 \\ {{\mathbf{Z}}_{{\left( {N - 1} \right) \times 1}} } \\ \end{array} } \right]{ + }\left[ {\begin{array}{*{20}c} 0 & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{K}}_{{c\left( {N - 1} \right) \times \left( {N - 1} \right)}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 \\ {{\mathbf{\rm Z}}^{\left( 3 \right)}_{{\left( {N - 1} \right) \times 1}} } \\ \end{array} } \right], \\ \end{aligned}$$
(4)

where \({\mathbf{U}} = \left[ {\begin{array}{*{20}c} 1 & 1 & \cdots & 1 \\ 0 & 1 & \ddots & \vdots \\ \vdots & \ddots & \ddots & 1 \\ 0 & \cdots & 0 & 1 \\ \end{array} } \right]_{N \times N}\), \({\mathbf{C}}_{v} = \left[ {\begin{array}{*{20}c} {c_{v\left( 1 \right)} } & 0 & \cdots & 0 \\ 0 & \ddots & \ddots & \vdots \\ \vdots & \ddots & {c_{{v\left( {N - 1} \right)}} } & 0 \\ 0 & \cdots & 0 & {c_{v\left( N \right)} } \\ \end{array} } \right]_{N \times N}\), \({\mathbf{C}}_{h} = \left[ {\begin{array}{*{20}c} {\frac{{2c_{h\left( 1 \right)} z_{1}^{2} }}{{l_{1}^{2} }}} & 0 & \cdots & 0 \\ 0 & \ddots & \ddots & \vdots \\ \vdots & \ddots & {\frac{{2c_{{h\left( {N - 1} \right)}} z_{N - 1}^{2} }}{{l_{N - 1}^{2} }}} & 0 \\ 0 & \cdots & 0 & {\frac{{2c_{h\left( N \right)} z_{N}^{2} }}{{l_{N}^{2} }}} \\ \end{array} } \right]_{N \times N}\), \({\mathbf{K}}_{1} = \left[ {\begin{array}{*{20}c} {k_{1} } & 0 & \cdots & 0 \\ 0 & \ddots & \ddots & \vdots \\ \vdots & \ddots & {k_{N - 1} } & 0 \\ 0 & \cdots & 0 & {k_{N} } \\ \end{array} } \right]_{N \times N}\), \(\quad{\mathbf{K}}_{c} = \left[ {\begin{array}{*{20}c} {k_{c\left( 1 \right)} } & 0 & \cdots & 0 \\ 0 & \ddots & \ddots & \vdots \\ \vdots & \ddots & {k_{{c\left( {N - 1} \right)}} } & 0 \\ 0 & \cdots & 0 & {k_{c\left( N \right)} } \\ \end{array} } \right]_{N \times N}\), \(\quad{\mathbf{Z}} = \left[ {\begin{array}{*{20}c} {z_{1} } & \cdots & {z_{N - 1} } & {z_{N} } \\ \end{array} } \right]^{T}_{1 \times N}\), \({\mathbf{Z}}^{\left( 3 \right)} = \left[ {\begin{array}{*{20}c} {z_{1}^{3} } & \cdots & {z_{N - 1}^{3} } & {z_{N}^{3} } \\ \end{array} } \right]^{T}_{1 \times N}\). The matrices, \(\left( {{\mathbf{C}}_{v} { + }{\mathbf{C}}_{h} } \right)_{{\left( {N - 1} \right) \times \left( {N - 1} \right)}}\), \({\mathbf{K}}_{{1\left( {N - 1} \right) \times \left( {N - 1} \right)}}\), and \({\mathbf{K}}_{{c\left( {N - 1} \right) \times \left( {N - 1} \right)}}\) are the first N − 1 rows and the first N − 1 columns of \({\mathbf{C}}_{v} { + }{\mathbf{C}}_{h}\), \({\mathbf{K}}_{1}\), and \({\mathbf{K}}_{c}\); \({\mathbf{Z}}_{{\left( {N - 1} \right) \times 1}}\) and \({\mathbf{Z}}^{\left( 3 \right)}_{{\left( {N - 1} \right) \times 1}}\) are the first N − 1 rows of \({\mathbf{Z}}\) and \({\mathbf{Z}}^{\left( 3 \right)}\), respectively.

Considering the multi-vertebral structure of the bird neck, we assumed that \(l_{0\left( 1 \right)} = l_{0\left( 2 \right)} = \cdots = l_{0\left( N \right)}\) and \(l_{1} = l_{2} = \cdots = l_{N}\). The non-dimensional form of Eq. (4) can be expressed as follows:

$${{\varvec{\upmu}}}{\mathbf{U}\hat{\mathbf{Z}^{\prime\prime}}} + {\hat{\mathbf{F}}}_{{\mathbf{t}}} = \left[ {\begin{array}{*{20}c} {\hat{F}_{e} \cos \left( {\Omega \tau } \right)} \\ {{\hat{\mathbf{F}}}_{{{\mathbf{t}}\left( {N - 1} \right) \times 1}} } \\ \end{array} } \right],$$
(5)

where \({{\varvec{\upmu}}} = \left[ {\begin{array}{*{20}c} {\mu_{1} } & 0 & \cdots & 0 \\ 0 & {\mu_{2} } & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & {\mu_{N} } \\ \end{array} } \right]\), \({\hat{\mathbf{F}}}_{{\mathbf{t}}} = \left[ {\begin{array}{*{20}c} {\hat{f}_{t\left( 1 \right)} } & \cdots & {\hat{f}_{{t\left( {N - 1} \right)}} } & {\hat{f}_{t\left( N \right)} } \\ \end{array} } \right]^{T}_{1 \times N}\), \({\hat{\mathbf{F}}}_{{{\mathbf{t}}\left( {N - 1} \right) \times 1}}\) are the first N − 1 rows of \({\hat{\mathbf{F}}}_{{\mathbf{t}}}\), \({\hat{\mathbf{Z}}} = \left[ {\begin{array}{*{20}c} {\hat{z}_{1} } & \cdots & {\hat{z}_{N - 1} } & {\hat{z}_{N} } \\ \end{array} } \right]^{T}_{1 \times N}\), and the corresponding non-dimensional variables are defined by \(x_{s} = \sqrt {l_{0\left( i \right)}^{2} - l_{i}^{2} }\), \(\hat{z}_{i} = {{z_{i} } \mathord{\left/ {\vphantom {{z_{i} } {x_{s} }}} \right. \kern-\nulldelimiterspace} {x_{s} }}\), \(\hat{l} = {{l_{i} } \mathord{\left/ {\vphantom {{l_{i} } {l_{0\left( i \right)} }}} \right. \kern-\nulldelimiterspace} {l_{0\left( i \right)} }}\), \(\tau = \omega_{n} t\), \(\omega_{n} = \sqrt {{{k_{v\left( 1 \right)} } \mathord{\left/ {\vphantom {{k_{v\left( 1 \right)} } {m_{s\left( 1 \right)} }}} \right. \kern-\nulldelimiterspace} {m_{s\left( 1 \right)} }}}\), \(\Omega = {{\omega_{e} } \mathord{\left/ {\vphantom {{\omega_{e} } {\omega_{n} }}} \right. \kern-\nulldelimiterspace} {\omega_{n} }}\), \(\hat{F}_{e} = {{F_{e} } \mathord{\left/ {\vphantom {{F_{e} } {k_{v\left( 1 \right)} x_{s} }}} \right. \kern-\nulldelimiterspace} {k_{v\left( 1 \right)} x_{s} }}\), \(\mu_{i} = {{m_{s\left( i \right)} } \mathord{\left/ {\vphantom {{m_{s\left( i \right)} } {m_{s\left( 1 \right)} }}} \right. \kern-\nulldelimiterspace} {m_{s\left( 1 \right)} }}\), \(\zeta_{v\left( i \right)} = {{c_{v\left( i \right)} } \mathord{\left/ {\vphantom {{c_{v\left( i \right)} } {2m_{s\left( 1 \right)} \omega_{n} }}} \right. \kern-\nulldelimiterspace} {2m_{s\left( 1 \right)} \omega_{n} }}\), \(\zeta_{h\left( i \right)} = {{c_{h\left( i \right)} } \mathord{\left/ {\vphantom {{c_{h\left( i \right)} } {2m_{s\left( 1 \right)} \omega_{n} }}} \right. \kern-\nulldelimiterspace} {2m_{s\left( 1 \right)} \omega_{n} }}\), \(\zeta_{n\left( i \right)} = \zeta_{h\left( i \right)} {{\left( {1 - \hat{l}^{2} } \right)} \mathord{\left/ {\vphantom {{\left( {1 - \hat{l}^{2} } \right)} {\hat{l}^{2} }}} \right. \kern-\nulldelimiterspace} {\hat{l}^{2} }}\), \(\Omega_{i}^{2} = {{k_{i} } \mathord{\left/ {\vphantom {{k_{i} } {k_{v\left( 1 \right)} }}} \right. \kern-\nulldelimiterspace} {k_{v\left( 1 \right)} }}\), \(\gamma_{i} = {{k_{c\left( i \right)} x_{s}^{2} } \mathord{\left/ {\vphantom {{k_{c\left( i \right)} x_{s}^{2} } {k_{v\left( 1 \right)} }}} \right. \kern-\nulldelimiterspace} {k_{v\left( 1 \right)} }}\), \(\hat{f}_{t\left( i \right)} = \hat{f}_{d\left( i \right)} + \hat{f}_{s\left( i \right)}\), \(\hat{f}_{d\left( i \right)} = 2\left( {\zeta_{v\left( i \right)} + 2\zeta_{n\left( i \right)} \hat{z}_{i}^{2} } \right)\hat{z}^{\prime}_{i}\), \(\hat{f}_{s\left( i \right)} = \Omega_{i}^{2} \hat{z}_{i} + \gamma_{i} \hat{z}_{i}^{3}\).

From Eq. (5), the transmitted force of the ith stage can be expressed as

$$\hat{f}_{t\left( i \right)} = \hat{f}_{d\left( i \right)} + \hat{f}_{s\left( i \right)} = \hat{F}_{e} \cos \left( {\Omega \tau } \right) - \sum\limits_{k = 1}^{i} {\left( {\mu_{k} \sum\limits_{j = k}^{N} {\hat{z}^{\prime\prime}_{j} } } \right)} .$$
(6)

When the excitation force is \(f_{e} = 0\) and the base displacement is \(x_{e} = X_{e} \cos (\omega_{e} t)\), \(X_{e}\) and \(\omega_{e}\) are the base excitation amplitude and frequency, respectively. The equation of motion in matrix form for the base-excited system is given by

$$\left[ {\begin{array}{*{20}c} {\mathbf{M}} & {\mathbf{0}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\ddot{\mathbf{X}}}} \\ {\ddot{x}_{e} } \\ \end{array} } \right]{\mathbf{ + }}\left[ {\begin{array}{*{20}c} {{\mathbf{C}}_{t} } & {{\mathbf{c}}_{t\left( N \right)} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\dot{\mathbf{X}}}} \\ {\dot{x}_{e} } \\ \end{array} } \right]{\mathbf{ + }}\left[ {\begin{array}{*{20}c} {{\mathbf{K}}_{t} } & {{\mathbf{k}}_{t\left( N \right)} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\mathbf{X}} \\ {x_{e} } \\ \end{array} } \right]{\mathbf{ = 0}}.$$
(7)

where \({\mathbf{c}}_{t\left( N \right)} = \left[ {\begin{array}{*{20}c} 0 & \cdots & 0 & { - c_{v\left( N \right)} } \\ \end{array} } \right]^{T}_{1 \times N}\) and \({\mathbf{k}}_{t\left( N \right)} = \left[ {\begin{array}{*{20}c} 0 & \cdots & 0 & { - k_{t\left( N \right)} } \\ \end{array} } \right]^{T}_{1 \times N}\).

As shown in Fig. 1, when the base displacement is \(x_{e} = X_{e} \cos \left( {\omega_{e} t} \right)\) and the excited force is \(f_{e} \left( t \right) = 0\), \(x_{i} = x_{e} + \sum\limits_{j = i}^{N} {z_{j} }\) can be obtained, where \(1 \le i \le N\). Equation (7) can be rewritten as follows:

$$\begin{aligned} {\mathbf{MU}\ddot{\mathbf{Z}}} + \left( {{\mathbf{C}}_{v} { + }{\mathbf{C}}_{h} } \right){\dot{\mathbf{Z}}} + {\mathbf{K}}_{1} {\mathbf{Z}}{ + }{\mathbf{K}}_{c} {\mathbf{Z}}^{\left( 3 \right)} + \ddot{x}_{e} {\mathbf{MI}}_{1} {\mathbf{ = }} & \left[ {\begin{array}{*{20}c} 0 & {\mathbf{0}} \\ {\mathbf{0}} & {\left( {{\mathbf{C}}_{v} { + }{\mathbf{C}}_{h} } \right)_{{\left( {N - 1} \right) \times \left( {N - 1} \right)}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 \\ {{\dot{\mathbf{Z}}}_{{\left( {N - 1} \right) \times 1}} } \\ \end{array} } \right] \\ & \; + \left[ {\begin{array}{*{20}c} 0 & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{K}}_{{1\left( {N - 1} \right) \times \left( {N - 1} \right)}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 \\ {{\mathbf{Z}}_{{\left( {N - 1} \right) \times 1}} } \\ \end{array} } \right]{ + }\left[ {\begin{array}{*{20}c} 0 & {\mathbf{0}} \\ {\mathbf{0}} & {{\mathbf{K}}_{{c\left( {N - 1} \right) \times \left( {N - 1} \right)}} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 \\ {{\mathbf{Z}}^{\left( 3 \right)}_{{\left( {N - 1} \right) \times 1}} } \\ \end{array} } \right], \\ \end{aligned}$$
(8)

where \({\mathbf{I}}_{1} = \left[ {\begin{array}{*{20}c} 1 & \cdots & 1 & 1 \\ \end{array} } \right]^{T}_{1 \times N}\). The non-dimensional form of Eq. (8) can be expressed as follows:

$${\varvec{\upmu}}{\mathbf{U}\hat{\mathbf{Z}^{\prime\prime}}} + {\hat{\mathbf{F}}}_{{\mathbf{t}}} = \left[ {\begin{array}{*{20}c} 0 \\ {{\hat{\mathbf{F}}}_{{{\mathbf{t}}\left( {N - 1} \right) \times 1}} } \\ \end{array} } \right] + {\varvec{\upmu}}{\mathbf{I}}_{1} \hat{X}_{e} \Omega^{2} \cos (\Omega \tau ),$$
(9)

where \(\hat{X}_{e} = {{X_{e} } \mathord{\left/ {\vphantom {{X_{e} } {x_{s} }}} \right. \kern-\nulldelimiterspace} {x_{s} }}\). From Eq. (9), the transmitted force of the ith stage can be expressed as

$$\hat{f}_{t\left( i \right)} = \sum\limits_{k = 1}^{i} {\mu_{k} \left( {\hat{X}_{e} \Omega^{2} \cos (\Omega \tau ) - \sum\limits_{j = k}^{N} {\hat{z}^{\prime\prime}_{j} } } \right)} .$$
(10)

3 Elliptic harmonic balance method

3.1 Harmonic balance method

The first-order solution of Eq. (6) is assumed to be

$$\hat{z}_{i} = \hat{Z}_{i} \cos \left( {\Omega \tau + \phi_{i} } \right),$$
(11)

where \(\hat{Z}_{i}\) is the non-dimensional amplitude of \(\hat{z}_{i}\), and \(\phi_{i}\) is the phase difference between the relative displacement \(\hat{z}_{i}\) and excitation force.

Assume that the non-dimensional damping and stiffness force can be written as \(\hat{f}_{d\left( i \right)} \approx \tilde{\alpha }_{i} \left( {\hat{Z}{}_{i}} \right){\text{sin}}\left( {\Omega \tau + \phi_{i} } \right)\) and \(\hat{f}_{s\left( i \right)} \approx \tilde{\beta }_{i} \left( {\hat{Z}{}_{i}} \right){\text{cos}}\left( {\Omega \tau + \phi_{i} } \right)\), respectively, where \(\tilde{\alpha }_{i}\) and \(\tilde{\beta }_{i}\) are the harmonic components of the first-order series expansion of \(\hat{f}_{d\left( i \right)}\) and \(\hat{f}_{s\left( i \right)}\) at steady-state, and can be expressed as follows:

$$\tilde{\alpha }_{i} \left( {\hat{Z}{}_{i}} \right) \approx \frac{\Omega }{\pi }\mathop \int \nolimits_{0}^{{\frac{2\pi }{\Omega }}} \hat{f}_{d\left( i \right)} \left( {\hat{Z}{}_{i}{\text{cos}}\left( {\Omega \tau + \phi_{i} } \right), - \hat{Z}{}_{i}\Omega {\text{sin}}\left( {\Omega \tau + \phi_{i} } \right)} \right){\text{sin}}\left( {\Omega \tau + \phi_{i} } \right){\text{d}}\tau ,$$
(12a)
$$\tilde{\beta }_{i} \left( {\hat{Z}{}_{i}} \right) \approx \frac{\Omega }{\pi }\mathop \int \nolimits_{0}^{{\frac{2\pi }{\Omega }}} \hat{f}_{s\left( i \right)} \left( {\hat{Z}{}_{i}{\text{cos}}\left( {\Omega \tau + \phi_{i} } \right), - \hat{Z}{}_{i}\Omega {\text{sin}}\left( {\Omega \tau + \phi_{i} } \right)} \right){\text{cos}}\left( {\Omega \tau + \phi_{i} } \right){\text{d}}\tau .$$
(12b)

Substituting Eq. (11) into Eq. (6), the equations for the harmonic components of \(\sin \left( {\Omega \tau + \phi_{i} } \right)\) and \(\cos \left( {\Omega \tau + \phi_{i} } \right)\) are obtained as follows:

$$- \frac{{\Omega^{2} \sum\nolimits_{k = 1}^{i} {\left( {\mu_{k} \sum\nolimits_{j = k}^{N} {\left( {\hat{Z}_{j} \sin \left( {\phi_{j} - \phi_{i} } \right)} \right)} } \right)} }}{{\Omega \hat{Z}_{i} }}\hat{z}_{i}^{\prime } \left( \tau \right) + \hat{f}_{d\left( i \right)} = - \frac{{\hat{F}_{e} \sin \left( {\phi_{i} } \right)}}{{\Omega \hat{Z}_{i} }}\hat{z}_{i}^{\prime } \left( \tau \right),$$
(13a)
$$\frac{{\sum\nolimits_{k = 1}^{i} {\left( {\mu_{k} \sum\nolimits_{j = k}^{N} {\left( {\hat{Z}_{j} \cos \left( {\phi_{j} - \phi_{i} } \right)} \right)} } \right)} }}{{\hat{Z}_{i} }}\hat{z}_{i}^{\prime \prime } \left( \tau \right) = - \hat{f}_{s\left( i \right)} + \frac{{\hat{F}_{e} \cos \left( {\phi_{i} } \right)}}{{\hat{Z}_{i} }}\hat{z}_{i} \left( \tau \right),$$
(13b)

where \(\hat{z}_{i}^{\prime } \left( \tau \right) = - \Omega \hat{Z}_{i} \sin \left( {\Omega \tau + \phi_{i} } \right)\) and \(\hat{z}_{i}^{\prime \prime } \left( \tau \right) = - \Omega^{2} \hat{Z}_{i} \cos \left( {\Omega \tau + \phi_{i} } \right)\). The equilibrium relationship given in Eq. (3), is shown in Fig. 2.

Fig. 2
figure 2

Dynamic equilibrium force on ms(i) at steady-state response

Full size image

By combining Eqs. (12) and (13), the amplitude–frequency equations of Eq. (6) are given by

$$\tilde{\alpha }_{i} \approx \hat{F}_{e} \sin \left( {\phi_{i} } \right) - \Omega^{2} \sum\limits_{k = 1}^{i} {\left( {\mu_{k} \sum\limits_{j = k}^{N} {\left( {\hat{Z}_{j} \sin \left( {\phi_{j} - \phi_{i} } \right)} \right)} } \right)} ,$$
(14a)
$$\tilde{\beta }_{i} \approx \hat{F}_{e} \cos \left( {\phi_{i} } \right) + \Omega^{2} \sum\limits_{k = 1}^{i} {\left( {\mu_{k} \sum\limits_{j = k}^{N} {\left( {\hat{Z}_{j} \cos \left( {\phi_{j} - \phi_{i} } \right)} \right)} } \right)} .$$
(14b)

3.2 Jacobi elliptic function solutions

The steady-state responses of Eqs. (6) can be represented by the Jacobi elliptic functions as follows:

$$\hat{z}_{i} \left( \tau \right) = \hat{Z}_{i} cn\left( {\psi_{i} \left| {m_{i} } \right.} \right),\;\;\hat{z}_{i}^{\prime } \left( \tau \right) = - \hat{Z}_{i} \omega_{i} sn\left( {\psi_{i} \left| {m_{i} } \right.} \right){\text{d}}n\left( {\psi_{i} \left| {m_{i} } \right.} \right),$$
(15)

where \(\psi_{i} = \omega_{i} \tau + \varphi_{i}\) is the complete phase, \(m_{i}\) is the square of the elliptic modulus, \(\omega_{i}\) is the Jacobi elliptic frequency, and \(\varphi_{i}\) is the Jacobi phase of the corresponding displacement response of the ith stage system. \({{\partial {\text{cn}}\left( {\psi_{i} |m_{i} } \right)} \mathord{\left/ {\vphantom {{\partial {\text{cn}}\left( {\psi_{i} |m_{i} } \right)} {\partial \psi_{i} }}} \right. \kern-\nulldelimiterspace} {\partial \psi_{i} }} = - {\text{sn}}\left( {\psi_{i} |m_{i} } \right){\text{dn}}\left( {\psi_{i} |m_{i} } \right)\) was used to derive Eq. (15). Following a procedure similar to that in [48], the second derivative of the relative displacement \(\hat{z}_{i}\) can be expressed as follows:

$$\hat{z}_{i}^{\prime \prime } \left( \tau \right) = - \omega_{i}^{2} \left( {1 - 2m_{i} } \right)\hat{z}_{i} \left( \tau \right) - \frac{{2m_{i} \omega_{i}^{2} \hat{z}_{i} \left( \tau \right)^{3} }}{{\hat{Z}_{i}^{2} }}.$$
(16)

Substituting Eq. (15) and Eq. (16) into Eq. (13b), the equations of the cosine harmonic component become

$$\frac{{\sum\limits_{k = 1}^{i} {\left( {\mu_{k} \sum\limits_{j = k}^{N} {\left( {\hat{Z}_{j} \cos \left( {\phi_{j} - \phi_{i} } \right)} \right)} } \right)} }}{{\hat{Z}_{i} }}\left( {\omega_{i}^{2} \left( {1 - 2m_{i} } \right)\hat{z}_{i} \left( \tau \right) + \frac{{2m_{i} \omega_{i}^{2} \hat{z}_{i} \left( \tau \right)^{3} }}{{\hat{Z}_{i}^{2} }}} \right) = \left( {\Omega_{i}^{2} - \frac{{\hat{F}_{e} \cos \left( {\phi_{i} } \right)}}{{\hat{Z}_{i} }}} \right)\hat{z}_{i} \left( \tau \right) + \gamma_{i} \hat{z}_{i} \left( \tau \right)^{3} .$$
(17)

Equating the coefficients of \(\hat{z}_{i} \left( \tau \right)\) and \(\hat{z}_{i} \left( \tau \right)^{3}\) of Eq. (17) gives

$$\omega_{i}^{{2}} = \frac{{\Omega_{i}^{2} - \frac{{\hat{F}_{e} \cos \left( {\phi_{i} } \right)}}{{\hat{Z}_{i} }} + \gamma_{i} \hat{Z}_{i}^{2} }}{{\sum\limits_{k = 1}^{i} {\left( {\mu_{k} \sum\limits_{j = k}^{N} {\left( {\hat{Z}_{j} \cos \left( {\phi_{j} - \phi_{i} } \right)} \right)} } \right)} }}\hat{Z}_{i} ,\;\;m_{i} = \frac{{\gamma_{i} \hat{Z}_{i}^{2} }}{{2\left( {\Omega_{i}^{2} - \frac{{\hat{F}_{e} \cos \left( {\phi_{i} } \right)}}{{\hat{Z}_{i} }} + \gamma_{i} \hat{Z}_{i}^{2} } \right)}}.$$
(18)

For the ith stage of the nonlinear vibration isolation system shown in Fig. 1b, where \(\Omega_{i}^{2} > 0\) and \(\gamma_{i} > 0\), the excited frequency \(\Omega\) equals the Jacobi elliptic frequency \(\omega_{i}\) with the same period, which can be expressed as follows:

$$\Omega = \frac{{\pi \omega {}_{i}}}{{2K\left( {m_{i} } \right)}},$$
(19)

where \(K\left( {m_{i} } \right)\) is the complete elliptic integral of the first type when \(0 < m_{i} < {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-\nulldelimiterspace} 2}\).

3.3 Modified stiffness force component

Because the high-order harmonic components are truncated in Eq. (12), both the damping force component \(\tilde{\alpha }_{i}\) and stiffness force component \(\tilde{\beta }_{i}\) are approximate terms. To improve the accuracy of the solutions of the amplitude–frequency characteristics, the stiffness force component \(\tilde{\beta }_{i}\) is first modified using Jacobi elliptic functions.

Using Eq. (19) and \(\phi_{i} = {{\pi \varphi_{i} } \mathord{\left/ {\vphantom {{\pi \varphi_{i} } {2K\left( {m_{i} } \right)}}} \right. \kern-\nulldelimiterspace} {2K\left( {m_{i} } \right)}}\), Eq. (12b) can be rewritten as follows:

$$\tilde{\beta }_{i} \approx \frac{{\omega_{i} }}{{2K\left( {m_{i} } \right)}}\mathop \int \nolimits_{0}^{{\frac{{4K\left( {m_{i} } \right)}}{{\omega_{i} }}}} \hat{f}_{s\left( i \right)} \left( {\hat{z}_{i} ,\hat{z}^{\prime}_{i} } \right){\text{cos}}\left( {\frac{{\pi \psi_{i} }}{{2K\left( {m_{i} } \right)}}} \right){\text{d}}\tau .$$
(20)

Substituting the first Fourier series expansion of \({\text{cn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right) \approx c_{i} \cos \left( {{{\pi \psi_{i} } \mathord{\left/ {\vphantom {{\pi \psi_{i} } {2K(m_{i} )}}} \right. \kern-\nulldelimiterspace} {2K(m_{i} )}}} \right)\) into Eq. (20), where \({{\pi \psi_{i} } \mathord{\left/ {\vphantom {{\pi \psi_{i} } {2K(m_{i} )}}} \right. \kern-\nulldelimiterspace} {2K(m_{i} )}}\) is the approximate phase of the relative displacement \(\hat{z}_{i}\), the modified stiffness component becomes

$$\tilde{\beta }_{e\left( i \right)} \approx \frac{1}{{2c_{i} K\left( {m_{i} } \right)}}\mathop \int \nolimits_{0}^{{4K\left( {m_{i} } \right)}} \hat{f}_{s\left( i \right)} \left( {\hat{z}_{i} ,\hat{z}^{\prime}_{i} } \right){\text{cn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right){\text{d}}\psi_{i} ,$$
(21)

where \(c_{i} = {{2\pi \sqrt {q_{i} } } \mathord{\left/ {\vphantom {{2\pi \sqrt {q_{i} } } {\sqrt {m_{i} } }}} \right. \kern-\nulldelimiterspace} {\sqrt {m_{i} } }}K\left( {m_{i} } \right)\left( {1 + q_{i} } \right)\) and \(q_{i} = \exp \left( {{{ - \pi K\left( {1 - m_{i} } \right)} \mathord{\left/ {\vphantom {{ - \pi K\left( {1 - m_{i} } \right)} {K\left( {m_{i} } \right)}}} \right. \kern-\nulldelimiterspace} {K\left( {m_{i} } \right)}}} \right)\).

3.4 Modified damping force component

To improve the accuracy of the damping force components \(\tilde{\alpha }_{i}\) in Eq. (12a), following a procedure similar to that described in Sect. 3.3, Eq. (12a) can be expressed as

$$\tilde{\alpha }_{i} \approx \frac{{\omega_{i} }}{{2K\left( {m_{i} } \right)}}\mathop \int \nolimits_{0}^{{\frac{{4K\left( {m_{i} } \right)}}{{\omega_{i} }}}} \hat{f}_{d\left( i \right)} \left( {\hat{z}_{i} ,\hat{z}^{\prime}_{i} } \right){\text{sin}}\left( {\frac{{\pi \psi_{i} }}{{2K\left( {m_{i} } \right)}}} \right){\text{d}}\tau .$$
(22)

Substituting the first Fourier series expansion of \({\text{sn}}\left( {\left. {\psi_{i} } \right|m_{i} } \right){\text{dn}}\left( {\left. {\psi_{i} } \right|m_{i} } \right) \approx a_{i} \sin \left( {{{\pi \psi_{i} } \mathord{\left/ {\vphantom {{\pi \psi_{i} } {2K\left( {m_{i} } \right)}}} \right. \kern-\nulldelimiterspace} {2K\left( {m_{i} } \right)}}} \right)\) into Eq. (22), the modified damping component becomes

$$\tilde{\alpha }_{e\left( i \right)} \approx \frac{1}{{2a_{i} K\left( {m_{i} } \right)}}\mathop \int \nolimits_{0}^{{4K\left( {m_{i} } \right)}} \left( {\hat{f}_{d\left( i \right)} \left( {\hat{z}_{i} ,\hat{z}_{i}^{\prime } } \right)} \right){\text{sn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right){\text{dn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right){\text{d}}\psi_{i} ,$$
(23)

where \(a_{i} = {{\pi^{2} \sqrt {q_{i} } } \mathord{\left/ {\vphantom {{\pi^{2} \sqrt {q_{i} } } {\sqrt {m_{i} } }}} \right. \kern-\nulldelimiterspace} {\sqrt {m_{i} } }}K^{2} \left( {m_{i} } \right)\left( {1 + q_{i} } \right)\).

3.5 Elliptic harmonic balance method (EHBM)

When the modified stiffness force component given in Eq. (21) and the modified damping force component given in Eq. (23) are obtained, the HBM given in Eq. (14) can be rewritten as follows

$$\tilde{\alpha }_{e\left( i \right)} \approx \hat{F}_{e} \sin \left( {\phi_{i} } \right) - \Omega^{2} \sum\limits_{k = 1}^{i} {\left( {\mu_{k} \sum\limits_{j = k}^{N} {\left( {\hat{Z}_{j} \sin \left( {\phi_{j} - \phi_{i} } \right)} \right)} } \right)} ,$$
(24a)
$$\tilde{\beta }_{e\left( i \right)} \approx \hat{F}_{e} \cos \left( {\phi_{i} } \right) + \Omega^{2} \sum\limits_{k = 1}^{i} {\left( {\mu_{k} \sum\limits_{j = k}^{N} {\left( {\hat{Z}_{j} \cos \left( {\phi_{j} - \phi_{i} } \right)} \right)} } \right)} .$$
(24b)

Using Eqs. (14a, b) and (24a, b), the orthogonal relationship of the non-dimensional force components on ms(i) determined using HB1 and EHBM is shown in Fig. 3, where the stiffness and damping force components on ms(i) are shown on the horizontal and vertical coordinates, respectively. The phase difference between the excitation force \(\hat{F}_{e}\), indicated by the green vector in Fig. 3, and the horizontal coordinate is \(\phi_{i}\). The inertia force components are indicated by orange vectors; the vector of the inertia force on ms(j) is termed as vector-jth, where \(1 \le j \le N\). The phase difference between vector-jth and the horizontal coordinates is \(\phi_{i} - \phi_{j}\), and the amplitude of vector-jth is \(\sum\nolimits_{k = 1}^{j} {\mu_{k} \Omega^{2} } \hat{Z}_{j}\) when \(1 \le j \le i - 1\) and \(\sum\nolimits_{k = 1}^{i} {\mu_{k} \Omega^{2} } \hat{Z}_{j}\) when \(i \le j \le N\). Note that the phase difference between the vector-ith (\(j = i\)) and horizontal coordinates is \({\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-\nulldelimiterspace} 2}\). The improvement in EHBM is shown in Fig. 3.

Fig. 3
figure 3

Orthogonality relationship of force components on ms(i)

Full size image

4 Force and displacement transmissibilities

In this section, the force and displacement transmissibilities of the bio-inspired nonlinear vibration isolation system are solved using HB1 and EHBM, and the results are discussed.

4.1 Amplitude–frequency characteristics

By considering the motion equation provided in Eq. (6), \(\tilde{\alpha }_{i}\) and \(\tilde{\beta }_{i}\) can be obtained from Eqs. (12a, b). The amplitude–frequency solution obtained using HB1 can be expressed as follows:

$$- \hat{Z}{}_{i}\Omega \left( {2\zeta_{v\left( i \right)} + \zeta_{n\left( i \right)} \hat{Z}{}_{i}^{2} } \right) = \hat{F}_{e} \sin \left( {\phi_{i} } \right) - \Omega^{2} \sum\limits_{k = 1}^{i} {\left( {\mu_{k} \sum\limits_{j = k}^{N} {\left( {\hat{Z}_{j} \sin \left( {\phi_{j} - \phi_{i} } \right)} \right)} } \right)} ,$$
(25a)
$$\Omega_{i}^{2} \hat{Z}{}_{i} + \frac{{3\gamma_{i} \hat{Z}{}_{i}^{3} }}{4} = \hat{F}_{e} \cos \left( {\phi_{i} } \right) + \Omega^{2} \sum\limits_{k = 1}^{i} {\left( {\mu_{k} \sum\limits_{j = k}^{N} {\left( {\hat{Z}_{j} \cos \left( {\phi_{j} - \phi_{i} } \right)} \right)} } \right)} .$$
(25b)

The relative displacement amplitudes and phases were determined for each excitation frequency using Newton methods, which can be simply achieved using the Mathematica function, FindRoot [52]. Subsequently, the amplitude–frequency curve can be plotted.

Integrating Eqs. (21) and (23), the non-dimensional nonlinear stiffness force \(\hat{f}_{s\left( i \right)} = \Omega_{i}^{2} {\hat{\text{Z}}}_{i} {\text{cn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right) + \gamma_{i} \left( {{\hat{\text{Z}}}_{i} {\text{cn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)} \right)^{3}\) and the non-dimensional nonlinear damping force \(\hat{f}_{d\left( i \right)} = \left( {2\zeta_{v\left( i \right)} { + 4}\zeta_{n\left( i \right)} \left( {{\hat{\text{Z}}}_{i} {\text{cn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)} \right)^{2} } \right)\left( { - {\hat{\text{Z}}}_{i} \omega_{i} {\text{sn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right){\text{dn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)} \right)\), respectively, gives

$$\tilde{\alpha }_{e\left( i \right)} \approx \frac{{ - 4\hat{Z}_{i} \omega_{i} }}{{a_{i} }}\left( {\zeta_{v\left( i \right)} R_{a\left( i \right)} + 2\zeta_{n\left( i \right)} \hat{Z}_{i}^{2} R_{b\left( i \right)} } \right),$$
(26a)
$$\tilde{\beta }_{e\left( i \right)} \approx \frac{{2\hat{Z}_{i} }}{{c_{i} }}\left( {\Omega_{i}^{2} R_{c\left( i \right)} + \gamma_{i} \hat{Z}_{i}^{2} R_{d\left( i \right)} } \right),$$
(26b)

where,

$$\begin{aligned} R_{a\left( i \right)} = & {{\int_{0}^{{4{\text{K}}\left( {m_{i} } \right)}} {{\text{sn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)^{2} } {\text{dn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)^{2} d\psi_{i} } \mathord{\left/ {\vphantom {{\int_{0}^{{4{\text{K}}\left( {m_{i} } \right)}} {{\text{sn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)^{2} } {\text{dn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)^{2} d\psi_{i} } {4K\left( {m_{i} } \right)}}} \right. \kern-\nulldelimiterspace} {4K\left( {m_{i} } \right)}} \\ = & {{\left[ {\left( {1 - m_{i} } \right)K\left( {m_{i} } \right) + \left( {2m_{i} - 1} \right)E\left( {m_{i} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\left( {1 - m_{i} } \right)K\left( {m_{i} } \right) + \left( {2m_{i} - 1} \right)E\left( {m_{i} } \right)} \right]} {3m_{i} K\left( {m_{i} } \right)}}} \right. \kern-\nulldelimiterspace} {3m_{i} K\left( {m_{i} } \right)}}, \\ \end{aligned}$$
$$\begin{aligned} R_{b\left( i \right)} = & {{\int_{0}^{{4{\text{K}}\left( {m_{i} } \right)}} {{\text{cn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)^{2} {\text{dn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)^{2} {\text{sn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)^{2} } d\psi_{i} } \mathord{\left/ {\vphantom {{\int_{0}^{{4{\text{K}}\left( {m_{i} } \right)}} {{\text{cn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)^{2} {\text{dn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)^{2} {\text{sn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)^{2} } d\psi_{i} } {4K\left( {m_{i} } \right)}}} \right. \kern-\nulldelimiterspace} {4K\left( {m_{i} } \right)}} \\ = & {{\left[ {2\left( {m_{i}^{2} - m_{i} + 1} \right)E\left( {m_{i} } \right) - \left( {m_{i}^{2} - 3m_{i} + 2} \right)K\left( {m_{i} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {2\left( {m_{i}^{2} - m_{i} + 1} \right)E\left( {m_{i} } \right) - \left( {m_{i}^{2} - 3m_{i} + 2} \right)K\left( {m_{i} } \right)} \right]} {15m_{i}^{2} K\left( {m_{i} } \right)}}} \right. \kern-\nulldelimiterspace} {15m_{i}^{2} K\left( {m_{i} } \right)}}, \\ \end{aligned}$$
$$\begin{aligned} R_{c\left( i \right)} = & {{\mathop \int \nolimits_{0}^{{4K\left( {m_{i} } \right)}} {\text{cn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)^{2} {\text{d}}\psi_{i} } \mathord{\left/ {\vphantom {{\mathop \int \nolimits_{0}^{{4K\left( {m_{i} } \right)}} {\text{cn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)^{2} {\text{d}}\psi_{i} } {4K\left( {m_{i} } \right)}}} \right. \kern-\nulldelimiterspace} {4K\left( {m_{i} } \right)}} \\ = & {{\left( {\left( {m_{i} - 1} \right)K\left( {m_{i} } \right) + E\left( {m_{i} } \right)} \right)} \mathord{\left/ {\vphantom {{\left( {\left( {m_{i} - 1} \right)K\left( {m_{i} } \right) + E\left( {m_{i} } \right)} \right)} {m_{i} K\left( {m_{i} } \right)}}} \right. \kern-\nulldelimiterspace} {m_{i} K\left( {m_{i} } \right)}}, \\ \end{aligned}$$
$$\begin{aligned} R_{d\left( i \right)} = & {{\mathop \int \nolimits_{0}^{{4K\left( {m_{i} } \right)}} {\text{cn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)^{4} {\text{d}}\psi_{i} } \mathord{\left/ {\vphantom {{\mathop \int \nolimits_{0}^{{4K\left( {m_{i} } \right)}} {\text{cn}}\left( {\psi_{i} \left| {m_{i} } \right.} \right)^{4} {\text{d}}\psi_{i} } {4K\left( {m_{i} } \right)}}} \right. \kern-\nulldelimiterspace} {4K\left( {m_{i} } \right)}} \\ = & {{\left( {2\left( {2m_{i} - 1} \right)E\left( {m_{i} } \right) + \left( {m_{i} - 1} \right)\left( {3m_{i} - 2} \right)K\left( {m_{i} } \right)} \right)} \mathord{\left/ {\vphantom {{\left( {2\left( {2m_{i} - 1} \right)E\left( {m_{i} } \right) + \left( {m_{i} - 1} \right)\left( {3m_{i} - 2} \right)K\left( {m_{i} } \right)} \right)} {3m_{i}^{2} K\left( {m_{i} } \right)}}} \right. \kern-\nulldelimiterspace} {3m_{i}^{2} K\left( {m_{i} } \right)}}, \\ \end{aligned}$$

E(m) is the complete elliptic integral of the second type.

By substituting Eq. (26a) into Eq. (24a), and combining Eq. (19), the amplitude \(\hat{Z}_{i}\) and phase \(\phi_{i}\) of the steady-state response of the bio-inspired nonlinear vibration isolator, as indicated by Eq. (6) can be numerically solved using the Mathematica function, FindRoot [52]. Subsequently, the amplitude–frequency solutions obtained by the EHBM can be calculated.

Three-stage and twelve-stage nonlinear vibration isolation systems were chosen as the basic causes of the bio-inspired multistage vibration isolation system. The values of the related parameters were studied in [22], and the non-dimensional parameters were given by \(\mu_{1} = 1\), \(\mu_{i} = 0.05\) (\(i \ne 1\)), \(\zeta_{v\left( i \right)} = 0.02\), \(\zeta_{h\left( i \right)} = 0.2\), \({{k_{v\left( i \right)} } \mathord{\left/ {\vphantom {{k_{v\left( i \right)} } {k_{{v\left( {1} \right)}} }}} \right. \kern-\nulldelimiterspace} {k_{{v\left( {1} \right)}} }} = 1\), \({{k_{h\left( i \right)} } \mathord{\left/ {\vphantom {{k_{h\left( i \right)} } {k_{v\left( 1 \right)} }}} \right. \kern-\nulldelimiterspace} {k_{v\left( 1 \right)} }} = 2\), \(\hat{l} = 0.8\), and \(\hat{F}_{e} = 0.001\), where \({1} \le i \le 3\), which are used for the three-stage isolation system, and \({1} \le i \le 12\) are used for the twelve-stage isolation system. Both HB1 and EHBM can calculate the displacement response for each stage. The amplitude–frequency solutions of each stage of the three-stage nonlinear isolation system are shown in Fig. 4, and for simplicity, the amplitude–frequency solutions of the 3rd-, 6th-, 9th- and 12th-stage of the twelve-stage nonlinear isolation system are shown in Fig. 5. The results of the EHBM exhibit better performance than those of HB1 within the peak region.

Fig. 4
figure 4

Amplitude–frequency curves of a relative displacement between ms(1) and ms(2), b relative displacement between ms(2) and ms(3), and c displacement of ms(3), of the three-stage nonlinear vibration isolation system when μ1 = 1, μ2 = μ3 = 0.05, ζv(i) = 0.02, ζh(i) = 0.2, kv(i)/kv(1) = 1, kh(i)/kv(1) = 2, where 1 ≤ i ≤ 3, \(\hat{l} = 0.8\), and \(\hat{F}_{e} = 0.001\). Dashed line, HB1; red solid line, EHBM; filled black dot, numerical results

Full size image
Fig. 5
figure 5

Amplitude–frequency curves of the relative displacement between a ms(3) and ms(4), b ms(6) and ms(7), c ms(9) and ms(10), and d ms(12) and base, of the twelve-stage nonlinear vibration isolation system when μ1 = 1, μi = 0.05 (i ≠ 1), ζv(i) = 0.02, ζh(i) = 0.2, kv(i)/kv(1) = 1, kh(i)/kv(1) = 2, where 1 ≤ i ≤ 12, \(\hat{l} = 0.8\), and \(\hat{F}_{e} = 0.001\). Dashed line, HB1; red solid line, EHBM; filled black dot, numerical results

Full size image

4.2 Force transmissibility

The force transmissibility of the bio-inspired N-stage nonlinear vibration isolator is given by

$$\left| {T_{F} } \right| = {\text{20log}}_{10} \left( {\frac{{\hat{F}_{N} }}{{\hat{F}_{e} }}} \right),$$
(27)

where the non-dimensional force from ms(N) transmitted to the base by the springs and dampers is given by

$$\hat{f}_{t\left( N \right)} \left( {\hat{z}_{N} ,\hat{z}^{\prime}_{N} } \right) = 2\left( {\zeta_{v\left( N \right)} + 2\zeta_{n\left( N \right)} \hat{z}_{N}^{2} } \right)\hat{z}^{\prime}_{N} + \Omega_{N}^{2} \hat{z}_{N} + \gamma_{N} \hat{z}_{N}^{3} ,$$
(28)

When the amplitude of the first-order component \(\hat{F}_{N}\) is obtained using Eq. (28), the force transmissibility can be obtained as follows:

$$\left| {T_{F} } \right| = \frac{1}{{\hat{F}_{e} }}\sqrt {\left( { - \Omega \hat{Z}_{N} \left( {2\zeta_{v\left( N \right)} + \zeta_{n\left( N \right)} \hat{Z}_{N}^{2} } \right)} \right)^{2} + \left( {\Omega_{N}^{2} \hat{Z}{}_{N} + \frac{{3\gamma_{N} \hat{Z}_{N}^{3} }}{4}} \right)^{2} } ,$$
(29a)
$$\left| {T_{F} } \right| = \frac{1}{{\hat{F}_{e} }}\sqrt {\left( {\frac{{ - 4\omega_{N} \hat{Z}_{N} }}{{a_{N} }}\left( {\zeta_{v\left( N \right)} R_{a\left( N \right)} + 2\zeta_{n\left( N \right)} \hat{Z}_{N}^{2} R_{b\left( N \right)} } \right)} \right)^{2} + \left( {\frac{{2\hat{Z}_{N} }}{{c_{N} }}\left( {\Omega_{N}^{2} R_{c\left( N \right)} + \gamma_{N} \hat{Z}_{N}^{2} R_{d\left( N \right)} } \right)} \right)^{2} } ,$$
(29b)

which are the results obtained by HB1 and EHBM, respectively.

After obtaining the numerical solution to Eq. (5), the force transmissibility can be solved using Eqs. (29a, b), as shown in Fig. 6. The performance of EHBM was better than that of HB1 compared with the numerical solutions.

Fig. 6
figure 6

Force transmissibility when μ1 = 1, μi = 0.05 (\(i \ne 1\)), ζv(i) = 0.02, ζh(i) = 0.2, kv(i)/kv(1) = 1, kh(i)/kv(1) = 2, \(\hat{l} = 0.8\), and \(\hat{F}_{e} = 0.001\). a Three-stage nonlinear isolation system where 1 ≤ i ≤ 3, b twelve-stage nonlinear isolation system where 1 ≤ i ≤ 12. Dashed line, HB1; red solid line, EHBM; filled black dot, numerical results

Full size image

4.3 Displacement transmissibility

The solution of Eq. (10) can be assumed as follows: Eq. (11) or Eq. (15). Following a similar procedure to solve the case of force excitation given in Sect. 3, the amplitude–frequency equations of the bio-inspired N-stage nonlinear vibration isolation system with base excitation obtained using HB1 are given by

$$\tilde{\alpha }_{i} \approx \Omega^{2} \sum\limits_{k = 1}^{i} {\left( {\mu_{k} \left( {\hat{X}_{e} \sin \left( {\phi_{i} } \right) - \sum\limits_{j = k}^{N} {\left( {\hat{Z}_{j} \sin \left( {\phi_{j} - \phi_{i} } \right)} \right)} } \right)} \right)} ,$$
(30a)
$$\tilde{\beta }_{i} \approx \Omega^{2} \sum\limits_{k = 1}^{i} {\left( {\mu_{k} \left( {\hat{X}_{e} \cos \left( {\phi_{i} } \right) + \sum\limits_{j = k}^{N} {\left( {\hat{Z}_{j} \cos \left( {\phi_{j} - \phi_{i} } \right)} \right)} } \right)} \right)} ,$$
(30b)

where \(\tilde{\alpha }_{i}\) and \(\tilde{\beta }_{i}\) are the same as those in Eqs. (25a, b).

Substituting \(\tilde{\alpha }_{e\left( i \right)}\) and \(\tilde{\beta }_{e\left( i \right)}\), which are given in Eqs. (26a, b), into Eqs. (30a, b), respectively, the EHBM results were obtained. The square of the elliptic modulus and Jacobi frequency functions are given by \(m_{i} = {{\gamma_{i} \hat{Z}_{i}^{2} } \mathord{\left/ {\vphantom {{\gamma_{i} \hat{Z}_{i}^{2} } {2\left( {\Omega_{i}^{2} + \gamma_{i} \hat{Z}_{i}^{2} } \right)}}} \right. \kern-\nulldelimiterspace} {2\left( {\Omega_{i}^{2} + \gamma_{i} \hat{Z}_{i}^{2} } \right)}}\) and \(\omega_{i}^{{2}} = {{\left( {\Omega_{i}^{2} + \gamma_{i} \hat{Z}_{i}^{2} } \right)\hat{Z}_{i} } \mathord{\left/ {\vphantom {{\left( {\Omega_{i}^{2} + \gamma_{i} \hat{Z}_{i}^{2} } \right)\hat{Z}_{i} } {\sum\limits_{k = 1}^{i} {\left( {\mu_{k} \left( {\hat{X}_{e} \cos \left( {\phi_{i} } \right) + \sum\limits_{j = k}^{N} {\left( {\hat{Z}_{j} \cos \left( {\phi_{j} - \phi_{i} } \right)} \right)} } \right)} \right)} }}} \right. \kern-\nulldelimiterspace} {\sum\limits_{k = 1}^{i} {\left( {\mu_{k} \left( {\hat{X}_{e} \cos \left( {\phi_{i} } \right) + \sum\limits_{j = k}^{N} {\left( {\hat{Z}_{j} \cos \left( {\phi_{j} - \phi_{i} } \right)} \right)} } \right)} \right)} }}\), respectively. Using \(\Omega = {{\pi \omega {}_{i}} \mathord{\left/ {\vphantom {{\pi \omega {}_{i}} {2K\left( {m_{i} } \right)}}} \right. \kern-\nulldelimiterspace} {2K\left( {m_{i} } \right)}}\) and Eq. (30a), the amplitude \(\hat{Z}_{i}\) and phase \(\phi_{i}\) of the steady-state response when \(1 \le i \le N\) can be solved using the EHBM. The relative displacement and absolute displacement transmissibilities can be determined by \(\left| {T_{r} } \right| = {{\left| {\hat{x}_{1} - \hat{x}_{e} } \right|} \mathord{\left/ {\vphantom {{\left| {\hat{x}_{1} - \hat{x}_{e} } \right|} {\hat{X}_{e} }}} \right. \kern-\nulldelimiterspace} {\hat{X}_{e} }} = {{\left| {\sum\limits_{i = 1}^{N} {\hat{z}_{i} } } \right|} \mathord{\left/ {\vphantom {{\left| {\sum\limits_{i = 1}^{N} {\hat{z}_{i} } } \right|} {\hat{X}_{e} }}} \right. \kern-\nulldelimiterspace} {\hat{X}_{e} }} = {{\sqrt {\left( {\sum\limits_{i = 1}^{N} {\hat{Z}_{i} \sin \left( {\phi_{i} } \right)} } \right)^{2} + \left( {\sum\limits_{i = 1}^{N} {\hat{Z}_{i} \cos \left( {\phi_{i} } \right)} } \right)^{2} } } \mathord{\left/ {\vphantom {{\sqrt {\left( {\sum\limits_{i = 1}^{N} {\hat{Z}_{i} \sin \left( {\phi_{i} } \right)} } \right)^{2} + \left( {\sum\limits_{i = 1}^{N} {\hat{Z}_{i} \cos \left( {\phi_{i} } \right)} } \right)^{2} } } {\hat{X}_{e} }}} \right. \kern-\nulldelimiterspace} {\hat{X}_{e} }}\) and \(\left| {T_{d} } \right|{ = }{{\left| {\hat{x}_{1} } \right|} \mathord{\left/ {\vphantom {{\left| {\hat{x}_{1} } \right|} {\hat{X}_{e} }}} \right. \kern-\nulldelimiterspace} {\hat{X}_{e} }} = {{\left| {\sum\limits_{i = 1}^{N} {\hat{z}_{i} } + \hat{x}_{e} } \right|} \mathord{\left/ {\vphantom {{\left| {\sum\limits_{i = 1}^{N} {\hat{z}_{i} } + \hat{x}_{e} } \right|} {\hat{X}_{e} }}} \right. \kern-\nulldelimiterspace} {\hat{X}_{e} }}{ = }{{\sqrt {\left( {\sum\limits_{i = 1}^{N} {\hat{Z}_{i} \sin \left( {\phi_{i} } \right)} } \right)^{2} + \left( {\sum\limits_{i = 1}^{N} {\hat{Z}_{i} \cos \left( {\phi_{i} } \right) + \hat{X}_{e} } } \right)^{2} } } \mathord{\left/ {\vphantom {{\sqrt {\left( {\sum\limits_{i = 1}^{N} {\hat{Z}_{i} \sin \left( {\phi_{i} } \right)} } \right)^{2} + \left( {\sum\limits_{i = 1}^{N} {\hat{Z}_{i} \cos \left( {\phi_{i} } \right) + \hat{X}_{e} } } \right)^{2} } } {\hat{X}_{e} }}} \right. \kern-\nulldelimiterspace} {\hat{X}_{e} }}\), respectively. The relative displacement and absolute displacement transmissibilities of the three-stage and twelve-stage nonlinear vibration isolation systems are shown in Fig. 7. EHBM improved the accuracy of the displacement transmissibility solutions within the resonance regimes.

Fig. 7
figure 7

a, c Relative displacement transmissibility, and b, d absolute displacement transmissibility for (a) and (b) three-stage geometrically nonlinear isolation system with 1 ≤ i ≤ 3 and \(\hat{X}_{e} = 0.08\), and c, d twelve-stage geometrically nonlinear isolation system with 1 ≤ i ≤ 12 and \(\hat{X}_{e} = 0.12\), when μ1 = 1, μi = 0.05 (\(i \ne 1\)), ζv(i) = 0.02, ζh(i) = 0.2, kv(i)/kv(1) = 1, kh(i)/kv(1) = 2, and \(\hat{l} = 0.8\). Dashed line, HB1; red solid line, EHBM; black filled dot, numerical results

Full size image

5 Conclusions

In this study, an elliptic harmonic balance method (EHBM) was used to analyse the isolation performance of a bio-inspired multistage vibration isolator. The bio-inspired isolator has both geometric stiffness and damping nonlinearities, which are incorporated in each stage of the configuration by imitating the structure of a bird neck and the space-gazing stability of a bird head. The equation of motion and the analysis of the dynamic force equilibrium of each stage were conducted in the steady-state. Using the relationship between the excitation frequency and the Jacobi elliptic frequency and modulus, EHBM can improve the accuracy of the stiffness and damping force components, which are obtained using the first-order harmonic balance method (HB1). The force components at each stage are presented in an orthogonal vector plot. Using the EHBM and HB1, the force and displacement transmissibilities of a three-stage and twelve-stage nonlinear isolation system are obtained and compared with the numerical solutions. With the same form and number of balancing equations as HB1, the EHBM can reduce the truncation error induced by neglecting the high-order harmonic components and obtain better results for the amplitude–frequency response and transmissibility than that of the HB1. Furthermore, nonlinear systems with polynomial-type nonlinearities can be analysed using the proposed procedure.