Dynamic analysis and performance evaluation of nonlinear inerter-based vibration isolators

Abstract

This paper investigates a nonlinear inertance mechanism (NIM) for vibration mitigation and evaluates the performance of nonlinear vibration isolators employing such mechanism. The NIM comprises a pair of oblique inerters with one common hinged terminal and the other terminals fixed. The addition of the NIM to a linear spring-damper isolator and to nonlinear quasi-zero-stiffness (QZS) isolators is considered. The harmonic balance method is used to derive the steady-state frequency response relationship and force transmissibility of the isolators subjected to harmonic force excitations. Different performance indices associated with the dynamic displacement response and force transmissibility are employed to evaluate the performance of the resulting isolators. It is found that the frequency response curve of the inerter-based nonlinear isolation system with the NIM and a linear stiffness bends towards the low-frequency range, similar to the characteristics of the Duffing oscillator with softening stiffness. It is shown that the addition of NIM to a QZS isolator enhances vibration isolation performance by providing a wider frequency band of low amplitude response and force transmissibility. These findings provide a better understanding of the functionality of the NIM and assist in better designs of nonlinear passive vibration mitigation systems with inerters.

1 Introduction

There has been a growing demand for high-performance vibration control devices that change the vibration transmission within a dynamic system to meet specific design requirements. Such devices can be categorised into active or passive vibration control systems, depending on whether external energy input is required. Even though active control systems can achieve effective vibration isolation, their disadvantages, such as their complexity, the need of external energy supply and maintenance issues confine their engineering applications. Passive vibration isolators have been extensively studied and widely used for mitigation of excessive vibration transmission [1]. Nevertheless, there is still much interest in design and analysis of new passive vibration suppression systems for enhanced performance. For instance, by configuring a nonlinear negative-stiffness mechanism with a linear isolator, it is possible to achieve a high-static low-dynamic stiffness characteristic, such that the static deflection is small, and the natural frequency is low to enlarge the frequency range of effective vibration isolation [2]. Nonlinear passive vibration isolators have also been proposed and demonstrated to outperform their linear counterparts [3]. Many studies on passive vibration control systems have been focused on the parameter optimisation of springs and dampers to modify the stiffness and damping characteristics. For example, in the classic design approach for the dynamic vibration absorber, the spring and damping coefficients of the absorber are carefully chosen so as to achieve tuning and also to reduce the peak responses. Some recent investigations considered the possibility of employing nonlinear geometric configuration of multiple springs and dampers to enhance vibration attenuation [3]. There is much less work reported on the use of the inertia in nonlinear passive devices to improve vibration isolation performance.

In the search for the mechanical counterpart of capacitors using the force–current analogy, a new element, the inerter, has been proposed [4]. The one-port, two-terminal device has the property that the applied force is proportional to the relative accelerations across the terminals, i.e. $F_b=b(\dot{V_1}-\dot{V_2})$, where $F_b$ is the coupling inertial force, b is a parameter named inertance and $\dot{V_1}$ and $\dot{V_2}$ are the accelerations of the two terminals. The work also showed that it is possible to construct such element using a flywheel and a rack-pinion mechanism. Benefits of introducing inerter in vibration mitigation have been demonstrated in many applications such as automobile shock absorbers and railway suspension systems [5,6,7], building vibration control systems [8,9,10] and landing gear shimmy vibration suppression systems [11]. These works identified beneficial network configurations consisting of springs, dampers and inerters through optimisation of either low-complexity network structures or positive real admittance functions. Network synthesis techniques (e.g. [12,13,14]) are then used to obtain networks which are able to realise such admittances.

Previous studies of inerter-based vibration mitigation systems usually adopt linear models and configurations of inerters. The dynamic characteristics and performance of inerter-based nonlinear vibration isolators remain largely unexplored. Note that passive nonlinear quasi-zero-stiffness (QZS) isolators which employ the geometric nonlinearities of a pair of compressed horizontal springs, bars or buckled beams to create negative-stiffness mechanisms and a high-static-low-dynamic characteristic have shown favourable vibration isolation performance [2, 15, 16]. These investigations provide insights into the possibility of incorporating inerters alongside the horizontal springs of QZS isolators to achieve better suppression of vibration transmission. Vibration isolator with geometrically nonlinear inerter subjected to base motion excitation was investigated, and it was shown to have performance benefits at high frequencies as compared to classical isolators [17]. It should be noted that in many engineering systems, there is a strong need for vibration isolation of force excitation, and it is thus necessary to carry out detailed dynamic analysis to reveal the associated vibration transmission characteristics and performance of nonlinear inerter-based vibration isolators for enhanced application. There is also limited study on power flow properties of inerter-based vibration mitigation systems. Vibration power flow analysis (PFA) approach has been widely used to assess the performance of linear vibration mitigation systems [18, 19], including linear inerter-based vibration isolators [20, 21]. This approach has been developed to reveal dynamics of nonlinear systems from energy flow viewpoint [22,23,24] and to evaluate nonlinear isolators [2, 25] and dynamic vibration absorbers [26].

This paper investigates a nonlinear geometric configuration of inerters and examines its dynamics and performance when used in nonlinear vibration isolators. A nonlinear inertance mechanism (NIM) is presented and configured to a conventional spring-damper isolator and also a QZS isolator. The steady-state response characteristics of the system subjected to harmonic excitation are obtained using analytical approximation based on the harmonic balance method and verified by numerical integrations. The influence of the NIM on vibration isolation performance is evaluated using different performance indices including peak dynamic displacement, peak force transmissibility and unity isolation frequency band. The effects of the addition of a NIM to a QZS nonlinear vibration isolator on dynamic properties and isolation performance are examined. Power flow behaviour of the isolator is discussed. The remaining content of the paper is organised as follows. The mathematical model of a NIM and its application as an isolator both with a linear and a nonlinear QZS spring arrangements are introduced in Sect. 2. In Sect. 3, the frequency response relationship is derived by the harmonic balance method. Then, the characteristics of the backbone curves are studied analytically. Section 4 defines and formulates the force transmissibility for performance evaluations of the inerter-based nonlinear isolators. Section 5 provides the results and discussion of the dynamics and performance of the NIM isolator and also the nonlinear NIM QZS mount. Conclusions are provided at the end of the paper.

2 Mathematical modelling

2.1 The NIM

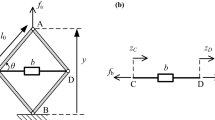
Figure 1 provides a schematic representation of the proposed NIM created by using a pair of inerters positioned obliquely and hinged together at terminal O while their other terminals are fixed at points A and B, which are separated horizontally by 2l. The two inerters are assumed to be ideal with inertance b so that the inertance force in the axial direction is proportional to relative acceleration across the terminals. The motion of the NIM is restricted to this two-dimensional plane. It is assumed that the inerter axis is horizontal at $x=0$ when point O lies on midpoint of line AB. As the system is symmetrical, the terminals of the inerters at O move in the vertical direction.

Fig. 1

Schematic model of the NIM

Fig. 2

Nonlinear inertial force characteristics of the NIM ($b=0.5\,\text {kg},\,l=1\,\text {m}$)

Fig. 3

Different configurations of vibration isolators. a QZS isolator, b NIM isolator, c NIM QZS mount and d linear isolator

Based on the geometric configurations of the system, the velocity of the moving terminal O is ${\dot{x}}$, in the vertical direction. Thus, the velocity component of point O along the axis of the inerter is $v={\dot{x}}\sin {\theta }$, where $\theta$ denotes the angle between the inerter axis and the horizontal line AB, with $\sin {\theta }=x / \sqrt{l^2+x^2}$. Therefore, the force applied to each inerter is along the axial direction of the inerter and is calculated by

$$\begin{aligned} f_a= & {} b\frac{\mathrm {d} ({\dot{x}}\sin {\theta })}{\mathrm {d} t}\nonumber \\= & {} b\left( \ddot{x}\sin {\theta }+\frac{{\dot{x}}^2l^2}{(l^2+x^2)\sqrt{l^2+x^2}}\right) . \end{aligned}$$

(1)

It shows that geometric nonlinearity is introduced by the NIM. The total force introduced by the NIM to point O is:

$$\begin{aligned} f_b= & {} 2f_a\sin {\theta }\nonumber \\= & {} 2b\left( \frac{x^2\ddot{x}}{l^2+x^2} +\frac{l^2x{\dot{x}}^2}{(l^2+x^2)^2}\right) =f_{b1}+f_{b2}, \end{aligned}$$

(2)

where $f_{b1}=2b x^2\ddot{x}/(l^2+x^2)$ and $f_{b2}=2b l^2x{\dot{x}}^2/(l^2+x^2)^2$. Equation (2) shows that the nonlinear inertial force by the NIM depends on the displacement, velocity and acceleration of the moving terminal O. This is of contrast to an ideal linear inerter, of which the applied force is only proportional to the accelerations of its terminals. The nonlinear inertial forces $f_{b1}$ and $f_{b2}$ for a NIM with inertance $b=0.5 \text {kg},l=1 \text {m}$ are shown in Fig. 2. It shows that $f_{b1}$ depends on the displacement and acceleration of point O. The value of $f_{b1}$ is approximately proportional to acceleration $\ddot{x}$ when x / l is large. This is reasonable as the NIM should provide an inertance of 2b in the extreme case of x / l tending to infinity, i.e. the inerters are oriented in the vertical direction. Figure 2b shows that $f_{b2}$ depends on the displacement and the velocity. Its value is sensitive to changes in velocity ${\dot{x}}$ in the neighbourhood of $x=0$. The magnitude of the nonlinear inertance force component $f_{b2}$ tends to zero when the displacement x becomes large.

2.2 Inerter-based nonlinear vibration isolators

Figure 3 shows several configurations of inerter-based linear and nonlinear vibration isolators. Figure 3a shows a nonlinear quasi-zero-stiffness (QZS) isolator that has been studied previously [15, 16]. It comprises a pair of lateral springs each with stiffness coefficient $k_h/2$, a vertical spring with stiffness coefficient k and a vertical viscous damper with damping coefficient c. This paper will investigate the use of inerters in this context. As shown in Fig. 3b, a nonlinear NIM isolator can be obtained by replacing the lateral springs in Fig. 3a with a NIM created by a pair of oblique inerters, each with inertance b / 2. Figure 3c shows a more complex vibration isolator named NIM QZS mount comprising both QZS and NIM. In these systems, the mass m represents a vibrating machine subjected to a harmonic force excitation. The motion of the system is restricted to be in the two-dimensional plane. As the system is symmetrical, the mass only has vertical movement denoted by x. It is assumed that the mass is in static equilibrium and the inerters are oriented in the horizontal direction when $x=0$. This can be achieved through the adjustment of the vertical spring. The two terminals of the inerters and the lateral springs are of a distance of l when $x=0$, and the original un-stretched length of the lateral springs is $l_0$. To achieve QZS characteristics, the lateral springs are initially compressed by setting $l<l_0$.

For comparisons of dynamic characteristics and performance of inerter-based linear and nonlinear isolators, Fig. 3d shows a linear isolator with a mass m, a spring with stiffness coefficient k, a viscous damper with damping coefficient c and an inerter with inertance b. The mass is subjected to a harmonic force with amplitude $f_e$ and frequency $\omega$ with its equation of motion being

$$\begin{aligned} m\ddot{x}+c{\dot{x}}+kx+b\ddot{x}=f_e\cos {\omega t}. \end{aligned}$$

(3)

As the nonlinear QZS and NIM isolators shown in Fig. 3a and b are special cases of the one illustrated by Fig. 3c, the governing equation of motion of the mass in Fig. 3c is formulated here. Note that the combined restoring force of the QZS mechanism provided by the vertical and lateral springs as shown in Fig. 3c is

$$\begin{aligned} f_s(x)=kx+k_hx\left( 1-\frac{l_0}{\sqrt{x^2+l^2}}\right) . \end{aligned}$$

(4)

Based on Eqs. (2) and (4), the equation of motion of the mass in Fig. 3c is

$$\begin{aligned}&m\ddot{x}+c{\dot{x}}+kx+k_hx\left( 1-\frac{l_0}{\sqrt{x^2+l^2}}\right) \nonumber \\&\quad +b\left( \frac{x^2\ddot{x}}{l^2+x^2}+\frac{l^2x{\dot{x}}^2}{(l^2+x^2)^2}\right) =f_e \cos {\omega t} , \end{aligned}$$

(5)

where $f_e$ and $\omega$ are the amplitude and frequency of the harmonic excitation force, respectively. Note that the equation of motion of the mass in Fig. 3a is obtained by setting inertance $b=0$ in Eq. (5). By setting stiffness coefficient $k_h=0$ in Eq. (5), the equation of motion of a nonlinear NIM isolation system illustrated by Fig. 3b is found.

To facilitate later formulations, the following non-dimensional parameters are introduced:

$$\begin{aligned}&\omega _0 =\sqrt{\frac{k}{m}}, \quad \tau =\omega _0 t,\quad \zeta =\frac{c}{2m\omega _0}, \quad L=\frac{l_0}{l}, \\&X =\frac{x}{l}, \quad K=\frac{k_h}{k}, \quad F_e=\frac{f_e}{kl}, \quad \\&\varOmega =\frac{\omega }{\omega _0}, \quad \lambda =\frac{b}{m}, \end{aligned}$$

where $\omega _0$ is the linearised natural frequency of the system in Fig. 3c without the NIM and the lateral springs, $\tau$ is the non-dimensional time, $\zeta$ denotes the damping ratio, L is the ratio of the initial length $l_0$ of the lateral springs when $x=0$ and their free length l with $L>1$ and X, K, $F_e$, $\varOmega$ and $\lambda$ are the non-dimensional displacement, the stiffness ratio of the lateral springs and the vertical spring, the non-dimensional excitation amplitude, the non-dimensional excitation frequency and the inertance ratio, respectively. By using these dimensionless parameters and variables, Eqs. (3) and (5) can be written in a dimensionless form as

$$\begin{aligned}&(1+\lambda )X''+2\zeta X'+X=F_e\cos {\varOmega \tau }, \end{aligned}$$

(6a)

$$\begin{aligned}&X''+2\zeta X'+H(X)+G(X,X',X'')=F_e\cos {\varOmega \tau }, \end{aligned}$$

(6b)

respectively, where the primes denote differentiation with respect to $\tau$, H(X) and $G(X,X',X'')$ are the total restoring force from the vertical and lateral springs (i.e. the QZS mechanism), and the total inertial force arising from the geometric nonlinearity of the NIM, respectively, with

$$\begin{aligned}&H(X)=(1+K)X-\frac{KL}{\sqrt{X^2+1}} \approx \alpha X+\beta X^3, \end{aligned}$$

(7a)

$$\begin{aligned}&G(X,X',X'')= \frac{\lambda X^2 X''}{1+X^2}+ \frac{\lambda X X'^2}{(1+X^2)^2}, \end{aligned}$$

(7b)

where $\alpha =1-K(L-1)$ and $\beta =KL/2$. Note that in Eq. (7a), the effects of the pair of oblique springs are approximated by Duffing-type stiffness nonlinearity [27]. They also lead to the addition of a linear stiffness term. This approximation is in line with previous studies of QZS isolators [15, 16]. Equation (6b) becomes:

$$\begin{aligned}&X''+2\zeta X'+\alpha X+\beta X^3+G(X,X',X'')\nonumber \\&\quad =F_e\cos {\varOmega \tau }. \end{aligned}$$

(8)

Note that $K>0$ and $L>1$, we have $\alpha <1$. By adjusting L and K values, we can have $\alpha =0$, and correspondingly, the quasi-zero-stiffness characteristic of the QZS isolator is achieved. Also note that as L and K are both positive, the dimensionless stiffness parameter $\beta$ is also positive. Therefore, the QZS isolator exhibits hardening stiffness characteristics.

Equation (7b) shows that the nonlinear force $G(X,X',X'')$ depends on displacement, velocity and acceleration of the harmonically excited mass. When its displacement response X is small, $G(X,X',X'')$ may be Taylor expanded at $X=0$ to have

$$\begin{aligned} G(X,X',X'') \approx \lambda X^2 X''+\lambda (1-2X^2)X X'^2. \end{aligned}$$

(9)

By replacing $G(X,X',X'')$ in Eq. (8) using the approximations in Eq. (9), we have a simplified non-dimensional governing equation

$$\begin{aligned}&X''+2\zeta X'+\alpha X+\beta X^3+\lambda X^2 X''\nonumber \\&\quad +\lambda (1-2X^2)X X'^2=F_e\cos {\varOmega \tau }. \end{aligned}$$

(10)

This equation suggests that the non-dimensional linearised natural frequency of the inerter-based vibration nonlinear isolation system is $\sqrt{\alpha }$. It shows that the addition of the NIM does not alter the linearised natural frequency of the system.

3 Forced response

3.1 Frequency response relationship

The steady-state frequency response relationship of the nonlinear isolation system with the NIM QZS mount as shown in Fig. 3c subjected to a harmonic force excitation will be derived here using the harmonic balance method. It is assumed that the non-dimensional steady-state displacement of the mass is

$$\begin{aligned} X=r\cos (\varOmega \tau +\phi ), \end{aligned}$$

(11)

where r and $\phi$ represent the response amplitude and the phase angle. The corresponding velocity and acceleration are expressed by:

$$\begin{aligned} X'&=-r\varOmega \sin (\varOmega \tau +\phi ), \end{aligned}$$

(12a)

$$\begin{aligned} X''&=-r\varOmega ^2\cos (\varOmega \tau +\phi ). \end{aligned}$$

(12b)

By inserting Eqs. (11), (12a) and (12b) into Eq. (10) and following some mathematical transformation, we have:

$$\begin{aligned}&\left( \alpha r+\frac{3\beta r^3}{4}-r\varOmega ^2-\frac{\lambda r^3 \varOmega ^2}{2}-\frac{\lambda r^5\varOmega ^2}{4}\right) \cos (\varOmega \tau + \phi )\nonumber \\&\qquad +\left( \frac{\beta r^3}{4} -\frac{\lambda r^3 \varOmega ^2}{2}+\frac{\lambda r^5\varOmega ^2}{8}\right) \cos (3\varOmega \tau +3\phi ) \nonumber \\&\qquad \frac{\lambda r^5\varOmega ^2}{8} \cos (5\varOmega \tau +5\phi )-2\zeta r\varOmega \sin (\varOmega \tau + \phi )\nonumber \\&\quad =F_e \cos \varOmega \tau . \end{aligned}$$

(13)

By considering only the response component at the excitation frequency and omitting the trigonometric terms with harmonics at $3\varOmega$ and $5\varOmega$, it follows that

$$\begin{aligned}&\left( \alpha r+\frac{3\beta r^3}{4}-r\varOmega ^2-\frac{\lambda r^3 \varOmega ^2}{2}-\frac{\lambda r^5\varOmega ^2}{4}\right) \nonumber \\&\quad \cos (\varOmega \tau +\phi )\nonumber \\&\quad -2\zeta r\varOmega \sin (\varOmega \tau + \phi )=F_e \cos \varOmega \tau . \end{aligned}$$

(14)

Using trigonometric identities, the right-hand side of Eq. (14) may be rewritten as

$$\begin{aligned}&F_e \cos \varOmega \tau =F_e\cos (\varOmega \tau + \phi -\phi ) \nonumber \\&\quad =F_e \cos (\varOmega \tau + \phi )\cos \phi +F_e \sin (\varOmega \tau + \phi )\sin \phi . \end{aligned}$$

(15)

By inserting Eq. (15) into Eq. (14) and balancing the coefficients of $\cos (\varOmega \tau + \phi )$ and $\sin (\varOmega \tau + \phi )$ in Eq. (14), we have

$$\begin{aligned}&\alpha r+\frac{3\beta r^3}{4}-r\varOmega ^2-\frac{\lambda r^3 \varOmega ^2}{2}-\frac{\lambda r^5\varOmega ^2}{4}=F_e\cos \phi , \end{aligned}$$

(16a)

$$\begin{aligned}&-2\zeta r\varOmega =F_e\sin \phi . \end{aligned}$$

(16b)

After cancelling out the trigonometric terms with $\phi$ by combining Eqs. (16a) and (16b), we obtain the frequency response relationship between the response amplitude and the system parameters:

$$\begin{aligned}&F_e^2=(2\zeta \varOmega )^2 r^2\nonumber \\&\qquad +\Big (\alpha +\frac{3\beta r^2}{4}-\Big (1+\frac{\lambda r^2}{2}+\frac{\lambda r^4}{4}\Big )\varOmega ^2\Big )^2 r^2.\nonumber \\ \end{aligned}$$

(17)

Equation (17) provides a nonlinear algebraic equation for the response amplitude r. When the system parameter values are set, it can be solved by using a standard bisection method to obtain the steady-state displacement response characteristics.

Note that for the nonlinear QZS isolator without the NIM as shown by Fig. 3a, we have $\lambda =0$. Thus, the corresponding frequency response relationship is

$$\begin{aligned} F_e^2=(2\zeta \varOmega )^2 r^2+\Big (\alpha +\frac{3\beta r^2}{4}-\varOmega ^2\Big )^2 r^2. \end{aligned}$$

(18)

For the nonlinear NIM isolator shown in Fig. 3b with $k_h=0$ (i.e.$\alpha =1,\beta =0$), the corresponding frequency response relationship is

$$\begin{aligned} F_e^2=(2\zeta \varOmega )^2 r^2+\Big (1-\Big (1+\frac{\lambda r^2}{2}+\frac{\lambda r^4}{4}\Big )\varOmega ^2\Big )^2 r^2.\nonumber \\ \end{aligned}$$

(19)

For the inerter-based linear isolator represented by Fig. 3d, the frequency response relationship has been derived previously and introduced here [20]:

$$\begin{aligned} F_e^2=(2\zeta \varOmega )^2 r^2+\Big (1-(1+\lambda )\varOmega ^2\Big )^2 r^2. \end{aligned}$$

(20)

Fig. 4

Backbone curves of a different types of vibration isolators and b nonlinear NIM isolators. In (a), solid line: linear isolator ($\lambda =15$), dashed line: QZS isolator ($\alpha =0,\beta =1.5,\lambda =0$), dash–dot line: nonlinear NIM QZS mount ($\alpha =0,\beta =1.5,\lambda =15$) and dotted line: NIM isolator ($\alpha =1,\beta =0,\lambda =15$)

3.2 Backbone curves

The backbone curve is widely used to describe relationship between the displacement amplitude of a undamped and unforced nonlinear vibration system with the oscillation frequency, i.e. the free vibration behaviour, [28,29,30]. For the NIM QZS mount shown in Fig. 3c, the backbone curve is obtained by setting the damping and external excitation to be zero in Eq. (17):

$$\begin{aligned} \alpha +\frac{3\beta r^2}{4}-(1+\frac{\lambda r^2}{2}+\frac{\lambda r^4}{4})\varOmega ^2=0. \end{aligned}$$

(21)

The peak displacement amplitude of the damped, forced system relates closely to the point where its frequency response curve intersects with the backbone curve. For a system with prescribed parameters $\zeta$, $\alpha$, $\beta$ and $\lambda$, the displacement amplitude and the response frequency corresponding to the crossing point of the frequency response curve and the backbone curve are expressed by

$$\begin{aligned} r_p&=\frac{F_e}{2\zeta \varOmega _b}, \end{aligned}$$

(22a)

$$\begin{aligned} \varOmega _b&=\sqrt{\frac{4\alpha +3\beta r_p^2}{4+2\lambda r_p^2+\lambda r_p^4}}, \end{aligned}$$

(22b)

respectively, where Eqs. (17) and (21) are used to find the intersection point.

For the QZS isolator illustrated by Fig. 3a, the corresponding backbone curve is obtained by setting $\lambda =0$ in Eq. (21):

$$\begin{aligned} \alpha +\frac{3\beta r^2}{4}-\varOmega ^2=0. \end{aligned}$$

(23)

The oscillation frequency associated with the cross point of the frequency response curve and the backbone curve is expressed by:

$$\begin{aligned} \varOmega _b=\sqrt{\alpha +\frac{3}{4}\beta r_p^2}, \end{aligned}$$

(24)

which agrees with the expression reported in ref. [16]. The displacement amplitude can be calculated by using Eq. (22a).

For the nonlinear NIM isolator shown in Fig. 3b, the backbone curve is obtained by setting $\alpha =1, \beta =0$ in Eqs. (21):

$$\begin{aligned} 1-(1+\frac{\lambda r^2}{2}+\frac{\lambda r^4}{4})\varOmega ^2=0. \end{aligned}$$

(25)

Thus, at intersection point of the frequency response curve and the backbone curve, we have

$$\begin{aligned} \varOmega _b=\frac{2}{\sqrt{4+2\lambda r_p^2+\lambda r_p^4}}. \end{aligned}$$

(26)

Again, Eq. (22a) can then be used to determine the corresponding displacement amplitude.

The backbone curve of the linear inerter-based vibration isolator shown in Fig. 3d is obtained by setting $F_e=\zeta =0$ in Eq. (20):

$$\begin{aligned} 1-\varOmega ^2 (1+\lambda )=0, \end{aligned}$$

(27)

which indicates $\varOmega _b=1/\sqrt{1+\lambda }$, i.e. the free vibration frequency of the undamped inerter-based linear isolation system is independent of the displacement amplitude.

Figure 4a shows the backbone curves associated with the four different types of vibration isolators shown in Fig. 3. Figure 4a shows that the backbone curve of the QZS isolator is hardening, i.e. the natural frequency increases with the amplitude of oscillation. This can be explained by Eq. (24), which shows that the oscillation frequency is an increasing function of amplitude r. Physically, the QZS isolator may be approximated via a Taylor series expansion, to a hardening Duffing oscillator [27]. In contrast, the backbone curve associated with the nonlinear NIM isolator shown by Fig. 3b bends to the left. The reason is that the forced response frequency $\varOmega$ is a decreasing function of displacement amplitude r, as suggested by Eq. (26). This characteristic is similar to that of the backbone curve associated with the softening stiffness Duffing oscillator. The backbone curve of the inerter-based linear vibration isolator shown in Fig. 3d is a straight vertical line at $\varOmega _b=1/\sqrt{1+\lambda }$. When a NIM is added to the QZS isolator to achieve a NIM QZS isolator, it is found that the backbone curve firstly extends to the high frequencies until a turning point A at approximately $\varOmega =0.3145,r=0.719$. As the response amplitude r continues to increase, the curve turns and bends to the low-frequency range. Figure 4b plots backbone curves that are associated with nonlinear NIM isolators, as shown in Fig. 3b with NIM of different inertance ratios of 5, 15, and 40 and that of the conventional linear isolator with $\alpha =1,\beta =0,\lambda =0$. Figure 4b shows that with the increase in inertance ratio $\lambda$, the backbone curve associated with the nonlinear NIM isolator shifts more to the low-frequency range.

It is of interest to investigate the characteristics of the backbone curve of the NIM QZS mount as they are closely related to the dynamics and isolation performance. Note that Eq. (22b) has shown that the oscillation frequency $\varOmega _b$ is a function of displacement amplitude $r_p$. The derivative information can be used to determine the bending behaviour of the backbone curve. Based on Eq. (22b), a differentiation of $\varOmega _b$ with respect to $r_p$ leads to

$$\begin{aligned}&\frac{\mathrm {d}\varOmega _b}{\mathrm {d}r_p}\nonumber \\&\quad =\frac{r_p\Big (3\beta (4-\lambda r_p^4)-8\alpha \lambda (1+r_p^2)\Big )}{(4+2\lambda r_p^2+\lambda r_p^4)^2}\nonumber \\&\qquad \times \sqrt{\frac{4\alpha +3\beta r_p^2}{4+2\lambda +\lambda r_p^4}}. \end{aligned}$$

(28)

Clearly, the parameters $\alpha$, $\beta$ and $\lambda$ of the nonlinear isolator can be designed so as to achieve desirable characteristics of the backbone curves. For the QZS isolator with $\alpha =0$, $\beta >0$ and $\lambda =0$, as shown in Fig. 3a, we have $\mathrm {d}\varOmega _b/\mathrm {d}r_p>0$. Therefore, the oscillation frequency $\varOmega _b$ is a monotonically increasing function of $r_p$ and the backbone curve associated with the QZS isolator bends to the high-frequency range. For the NIM isolator (i.e. $\alpha =1,\beta =0$) as shown in Fig. 3b, we have $\mathrm {d}\varOmega _b/\mathrm {d}r_p<0$, suggesting that the $\varOmega _b$ is a monotonically decreasing function of $r_p$. Consequently, the backbone curves of the isolators with NIM extend to the low-frequency range, as shown in Fig. 4a and b.

For the inerter-based nonlinear isolator with both QZS and NIM, i.e. $\alpha =0, \beta >0$, as shown in Fig. 3c, the backbone curve initially bends to the right as we have $\mathrm {d}\varOmega _b/\mathrm {d}r_p>0$ for small-amplitude oscillations. As the displacement amplitude $r_p$ increases until the derivative $\mathrm {d}\varOmega _b/\mathrm {d}r_p$ becomes zero, a turning point appears on the backbone curve. This is illustrated by point A in Fig. 4a. The turning point is found by setting $\mathrm {d}\varOmega _b/\mathrm {d}r_p=0$ in Eq. (28). Consequently, we have one equation for the location of the turning point on the backbone curve:

$$\begin{aligned} 3\beta (4-\lambda r_p^4)-8\alpha \lambda (1+r_p^2)=0, \end{aligned}$$

(29)

which is a quadratic equation of $r_p^2$, and thus, the solutions can be found analytically for prescribed system parameters $\alpha$, $\beta$ and $\lambda$. For the NIM and QZS isolator (i.e. $\alpha =0,\beta>0,\lambda >0$), we have $r_p=\sqrt{2}\lambda ^{-0.25}$ at the turning point. It suggests that the corresponding response amplitude $r_p$ at the turning point only depends on inertance ratio $\lambda$ when $\alpha =0$. Therefore, for the case considered in Fig. 4a with $\alpha =0,\beta =1.5,\lambda =15$, the turning point is found at $r_p=0.719$ and $\varOmega =0.3145$. This analytical prediction agrees with the location of Point A shown in Fig. 4a.

Figure 5 shows that backbone curves of NIM QZS mount comprising QZS with $\alpha =0,\beta =1.5$ and NIM with different inertance ratios $\lambda$ of 5, 10, 20 and 40. The figure shows that as $\lambda$ increases from 5 to 40, the backbone curve shifts to the low-frequency range. The locus of turning point is also obtained by using Eqs. (22b) and (29). It shows that as the inertance ratio $\lambda$ increases, the turning point position moves to the left with the decrease in $r_p$ and $\varOmega _b$. This property demonstrates that the inertance ratio $\lambda$ can be designed for favourable turning point position for the design of inerter-based nonlinear isolators.

Fig. 5

Backbone curves of the nonlinear NIM QZS mount ($\alpha =0,\beta =1.5$). The dash–dot–dot line is for the locus of the turning point as $\lambda$ changes

4 Force transmissibility

Force transmissibility has been widely used for performance evaluation of vibration isolators [1]. For nonlinear vibration isolators, the following performance indices may be used [2, 3, 15, 16]:

• (a) Peak dynamic displacement;

• (b) Peak transmissibility;

• (c) Unity isolation frequency band, in which the value of transmissibility is less than unity.

They are used in this paper to evaluate the nonlinear inerter-based vibration isolators. In this section, the force transmissibility of the NIM QZS mount as represented by Fig. 3c is defined and derived.

Note that other performance indicators such as time-averaged power flow transmission and kinetic energy of the mass have also been used in previous studies of linear and nonlinear vibration isolators [2, 18, 19, 25, 31]. A power flow analysis is carried out for the current nonlinear NIM QZS mount, and the detailed formulations are provided in “Appendix”.

The total non-dimensional force transmitted to the ground is

$$\begin{aligned}&F_T=2\zeta X'+H(X)+G(X,X',X'') \nonumber \\&\quad \approx r\Big (\alpha +\frac{3}{4}\beta r^2 \nonumber \\&\quad -\frac{\lambda r^2\varOmega ^2(2+r^2)}{4}\Big )\cos (\varOmega \tau +\phi )\nonumber \\&\quad -2\zeta r \varOmega \sin (\varOmega \tau +\phi ), \end{aligned}$$

(30)

where the Taylor expansions of H(X) and $G(X,X',X'')$ as shown in Eqs. (7a) and (9) as well as the first-order approximate expressions of the steady-state response were employed. Also, only the component at the excitation frequency $\varOmega$ has been considered in the analytical approximation. Consequently, the analytical approximate expression of the amplitude of the transmitted force is

$$\begin{aligned} |F_T|=r\sqrt{(2\zeta \varOmega )^2+\Big (\alpha +\frac{3}{4}\beta r^2-\frac{\lambda r^2\varOmega ^2(2+r^2)}{4}\Big )^2}.\nonumber \\ \end{aligned}$$

(31)

For nonlinear isolators, the force transmissibility can be defined as the ratio of the maximum transmitted force to that of the excitation force, and we have

$$ \begin{aligned}&TR_{\mathrm{NIM} \& \mathrm{QZS}}=\frac{|F_T|}{F_e} \approx \nonumber \\&\frac{\sqrt{(2\zeta \varOmega )^2+\Big (\alpha +\frac{3}{4}\beta r^2-\Big (\frac{\lambda r^2}{2}+\frac{\lambda r^4}{4}\Big )\varOmega ^2\Big )^2}}{\sqrt{(2\zeta \varOmega )^2+\Big (\alpha +\frac{3}{4}\beta r^2-\Big (1+\frac{\lambda r^2}{2}+\frac{\lambda r^4}{4}\Big )\varOmega ^2\Big )^2}}, \end{aligned}$$

(32)

where the frequency response relation expressed by Eq. (17) is used to replace $F_e$. Note that for numerical integration solutions of the force transmissibility, the maximum value of the transmitted force in the steady-state motion is used in this paper.

Note that by removing the NIM in Fig. 3a, we have a QZS nonlinear vibration isolator as shown in Fig. 3a. Thus, the force transmissibility is obtained by setting the inertance ratio $\lambda =0$ in Eq. (32):

$$\begin{aligned} TR_\mathrm{QZS}= \frac{\sqrt{(2\zeta \varOmega )^2+\left( \alpha +\frac{3}{4}\beta r^2\right) ^2}}{\sqrt{(2\zeta \varOmega )^2+\left( \alpha +\frac{3}{4}\beta r^2-\varOmega ^2\right) ^2}}. \end{aligned}$$

(33)

For the NIM isolator as the one represented by Fig. 3b, the force transmissibility is obtained by setting $\alpha =1,\beta =0$ in Eq. (32):

$$\begin{aligned} TR_\mathrm{NIM}= \frac{\sqrt{(2\zeta \varOmega )^2+\Big (1-\Big (\frac{\lambda r^2}{2}+\frac{\lambda r^4}{4}\Big )\varOmega ^2\Big )^2}}{\sqrt{(2\zeta \varOmega )^2+\Big (1-\Big (1+\frac{\lambda r^2}{2}+\frac{\lambda r^4}{4}\Big )\varOmega ^2\Big )^2}}.\nonumber \\ \end{aligned}$$

(34)

For the inerter-based linear vibration isolator as shown in Fig. 3d, the force transmissibility is [20]:

$$\begin{aligned} TR_\mathrm{linear}= \frac{\sqrt{(2\zeta \varOmega )^2+\big (1-\varOmega ^2\big )^2}}{\sqrt{(2\zeta \varOmega )^2+\big (1-\varOmega ^2(1+\lambda )\big )^2}}. \end{aligned}$$

(35)

For the nonlinear NIM QZS mount shown in Fig. 3c to be effective in terms of force transmission, we need $TR_{\mathrm{NIM} \& \mathrm{QZS}} <1$ , i.e.

$$\begin{aligned} \frac{(2\zeta \varOmega )^2+\Big (\alpha +\frac{3}{4}\beta r^2-\Big (\frac{\lambda r^2}{2}+\frac{\lambda r^4}{4}\Big )\varOmega ^2\Big )^2}{(2\zeta \varOmega )^2+\Big (\alpha +\frac{3}{4}\beta r^2-\Big (1+\frac{\lambda r^2}{2}+\frac{\lambda r^4}{4}\Big )\varOmega ^2\Big )^2}<1,\nonumber \\ \end{aligned}$$

(36)

Fig. 6

Effects of a inertance ratio $\lambda$ and b excitation amplitude $F_e$ on the response amplitude. In a$F_e=0.01$. Circles, triangles and squares are the RK results for $\lambda$=10, 20 and 40, respectively. In b$\lambda =20$. Circles, triangles and squares are the RK results for $F_e$=0.005, 0.01 and 0.05, respectively

which is equivalent to the condition:

$$\begin{aligned}&\Big (\alpha +\frac{3}{4}\beta r^2-\Big (\frac{\lambda r^2}{2}+\frac{\lambda r^4}{4}\Big )\varOmega ^2\Big )^2 \nonumber \\&\quad -\Big (\alpha +\frac{3}{4}\beta r^2-\Big (1+\frac{\lambda r^2}{2}+\frac{\lambda r^4}{4}\Big )\varOmega ^2\Big )^2<0. \end{aligned}$$

(37)

Using the relationship $y^2-z^2=(y+z)(y-z)$, the inequality (37) is transformed into:

$$\begin{aligned} \Big (2\alpha +&\frac{3}{2}\beta r^2-\Big (1+\lambda r^2+\frac{\lambda r^4}{2}\Big )\varOmega ^2\Big )\varOmega ^2<0, \end{aligned}$$

(38)

which is mathematically equivalent to

$$\begin{aligned}&2\alpha +\frac{3}{2}\beta r^2<\left( 1+\lambda r^2+\frac{\lambda r^4}{2}\right) \varOmega ^2. \end{aligned}$$

(39)

Therefore, the requirement for effective isolation of transmitted force is:

$$\begin{aligned} \varOmega >\sqrt{\frac{8\alpha +6\beta r^2}{4+4\lambda r^2+2\lambda r^4}}=\varOmega _\mathrm{low}. \end{aligned}$$

(40)

This expression provides the lower limit $\varOmega _\mathrm{low}$ of the frequency range where the force transmission is attenuated by using the inerter-based nonlinear isolator. The isolation range of some special cases can then be derived from expression (40). For the QZS isolator without NIM (i.e. $\lambda =0$) as shown in Fig. 3a, the lower limit $\varOmega _\mathrm{low}$ reduces with $\alpha$, and correspondingly the addition of the QZS mechanism can be used to enhance low-frequency vibration isolation. For the NIM isolator as the one shown in Fig. 3b, we have $\alpha =1,\beta =0$ and $\lambda >0$, and thus, the frequency range of effective vibration isolation, i.e. the unity isolation frequency band, can be enlarged by introducing the NIM. For the conventional spring-damper isolator, we have $\alpha =1,\beta =\lambda =0$, and therefore, the lower limit of effective isolation frequency range is $\sqrt{2}$. This agrees with the classical vibration isolation theory. It is noted that for nonlinear NIM QZS mount, the lower limit $\varOmega _\mathrm{low}$ of effective isolation frequency band depends on the response amplitude r and hence the external forcing amplitude $F_e$.

5 Performance of inerter-based nonlinear vibration isolators

5.1 The NIM isolator

The configuration of the NIM isolator has been presented previously in Fig. 3b. The effects of the inertance ratio $\lambda$ and the external forcing amplitude $F_e$ on the steady-state displacement amplitude are investigated and shown in Fig. 6a and b, respectively. The isolator investigated here does not contain lateral springs, i.e. $\alpha =1, \beta =0$, and the damping ratio $\zeta$ is set to 0.01. In Fig. 6a, the dashed, dash–dot and dotted lines represent the analytical approximation results based on harmonic balance (HB) method, while the symbols denote direct numerical integrations of Eq. (10) based on the fourth-order Runge–Kutta (RK) method. In Fig. 6a, $F_e=0.01$ and the inertance ratio $\lambda$ changes from 10 to 20 and then to 40. For engineering applications, a large value of the inertance to mass ratio $\lambda$ may be desirable as inerters are geared and so their device mass is significantly lower than their apparent mass, and hence, the suspension system is lighter. Correspondingly, the effectiveness of the isolators when $\lambda$ is large is of interest and is investigated in this section. The response amplitude curve of the linear spring-damper isolator without NIM (i.e. $\lambda =0$) is also included and represented by the solid line for comparison.

Figure 6a shows the steady-state response obtained by analytical approximations and numerical integrations, which generally agree well, and thus, the harmonic balance formulations are verified. The differences between the numerical and analytical results are due to the fixed number of the response components considered in the harmonic balance method. It shows that the addition of the NIM into the isolator bends the frequency response curve to the low-frequency range and reduces the response at the original peak value around $\varOmega =1$. With the increase in $\lambda$ from 10 to 40, the displacement response curve bends further to the low frequencies. This bending characteristic of the frequency response curves is similar to those of the harmonically excited Duffing oscillator with softening stiffness [22, 27]. An explanation for this behaviour is that with an increase in the deflection |X|, the nonlinearity introduced by the NIM becomes stronger. Consequently, the nonlinear inertance force by the NIM and the effective mass of the system increase with |X| as well. The effects of having the effective mass increase with the deflection |X| on the steady-state response may be similar to the situation of having the stiffness reduce with an increase in deflection |X|, i.e. a softening stiffness characteristic. Figure 6a also shows that the introduction of the NIM in the isolator results in higher peak displacement amplitude, compared to that of the conventional isolator case with $\lambda =0$. In the non-resonant frequency range away from the response peaks, the response curves for the four examined cases merge with each other. This property arises from the fact that for small-amplitude oscillations, the corresponding nonlinear force term introduced by the NIM is negligible. At low excitation frequencies, multiple possible solutions may be encountered at a single excitation frequency, suggesting a dependence of the steady-state response on the initial conditions of the isolation system with NIM. Figure 6b investigates the effects of the external forcing amplitude on the frequency response characteristics of the system with $\lambda =20$. The external forcing amplitude varies from 0.005, 0.01 and then 0.05. The backbone curve of the system with $\alpha =1, \beta =0, \lambda =20$ is also plotted in the figure. It shows that the backbone curve provides good indication of the bending direction of the frequency response curves. The figure also shows that a larger external excitation leads to higher response amplitude in the low- and high-frequency ranges. However, as the associated backbone curve is independent of the excitation force amplitude $F_e$, the extent of the bending of the frequency response curve is almost the same for the three cases regardless of the change in the value of $F_e$.

Fig. 7

a Effects of inertance ratio $\lambda$ on the force transmissibility for the NIM isolator and b force transmissibility of the linear inerter isolator ($\lambda =10$). In a, the circles, triangles and squares present the RK results for $\lambda$=0, 10, 20 and 40, respectively

Figure 7a presents the force transmissibility characteristics of the NIM isolators (i.e. $\alpha =1, \beta =0$). The other parameters are set as $F_e=0.01,\zeta =0.01$, and the inertance ratio $\lambda$ changes from 10 to 20 and then to 40. The force transmissibility curve of the corresponding linear system with a spring-damper isolator (i.e. $\lambda =0$) is also provided for comparisons. The dash, dash–dot and dotted lines shown in the figure represent first-order approximations of force transmissibility TR based on the harmonic balance method. Figure 7a shows that the use of NIM in the inerter-based nonlinear isolator bends the force transmissibility curves to the low-frequency range. This behaviour is desirable for improvement in vibration isolation performance. The force transmissibility in the vicinity of $\varOmega =1$, the original peak frequency of the linear isolator case, is also reduced. With the increase in the inertance ratio $\lambda$ of the NIM from 10 to 20 and then to 40, the peak transmissibility becomes smaller. It is shown that inertance nonlinearity due to NIM created by the pair of lateral inerters may also yield multiple possible levels of force transmission at a predetermined excitation frequency in the low-frequency range. It is also observed that the nonlinear inertance introduced by the NIM affects force transmissibility locally in the resonant region. Away from the resonant region, the curves corresponding to different levels of inertance ratios and the linear isolator case coincide. This is again due to the fact that the nonlinear force introduced by the NIM is small when the system exhibits small-amplitude oscillations. Figure 7b shows the force transmissibility curve of the inerter-based linear isolator for a comparison of NIM isolator with the linear isolator. The inertance ratio $\lambda$ is set to be 10. Figure 7b shows that while the inerter-based linear isolator provides a large frequency band in which $TR<1$, its performance at high excitation frequencies is weak as the value of TR remains close to unity. This asymptotic behaviour of force transmissibility TR of inerter-based linear isolator has been shown analytically [20]. This deficiency is overcome by having the inerters in the lateral configuration, i.e. adding a NIM, as the NIM isolator provides much better attenuation of force transmission at high excitation frequencies with force transmissibility reducing with the excitation frequency $\varOmega$.

5.2 The NIM QZS mount

The steady-state dynamic response characteristics and performance of nonlinear inerter-based vibration isolators with a combination use of NIM and QZS are investigated herein. Figure 8 examines the steady-state displacement amplitude of inerter-based nonlinear isolator with both QZS and NIM. The system parameters are set as $\zeta =0.01,K=2,L=1.5,F_e=0.005$. Correspondingly, we have $\alpha =0, \beta =1.5$, i.e. the isolator is characterised by quasi-zero-stiffness (QZS) and also exhibits hardening stiffness behaviour. The inertance ratio $\lambda$ for the NIM changes from 0, representing a nonlinear QZS isolator, to 10, then to 20 and finally to 40, denoting a nonlinear isolator with both NIM and QZS. The solid, dashed, dash–dot and dotted lines in the figure represent analytical solutions of the frequency response equation (17) obtained from the harmonic balance method. For the QZS isolator without NIM, the frequency response curve bends to the right towards the high-frequency range. This is due to the hardening stiffness characteristics introduced by the QZS mechanism. After introducing the NIM with $\lambda =10$, the resonance peak bends less to the left, compared to the QZS isolator. As the inertance ratio $\lambda$ increases to 20, the frequency response curves initially extend to the right when the response amplitude r is relatively small and then to the left as r becomes larger. When the NIM with $\lambda =40$ is included in the nonlinear isolator, the resonant peak shifts and bends further into the low-frequency range. The bending behaviour of the frequency response curves is captured by the backbone curves, the characteristics of which have been explained previously in Sect. 3. The figure also shows that the peak displacement amplitude increases with inertance ratio $\lambda$. Away from the resonant region, the effects of inertance ratio on the displacement amplitude are observed to be small. The figure shows that the addition of the NIM to the QZS isolator enlarges the bandwidth of low response amplitude but at the expense of higher response peak.

Fig. 8

Response characteristics of the NIM QZS mount. Solid, dashed, dash–dot and dotted lines for the HB results of $\lambda$ = 0, 10, 20 and 40, respectively. The circles, triangles, squares and diamonds are for the RK results of $\lambda$ = 0, 10, 20 and 40, respectively

Fig. 9

Effects of the lateral spring stiffness on the response characteristics of the QZS isolator a with NIM ($\lambda = 10$) and b without NIM ($\lambda = 0$). Parameters set as $\zeta$ = 0.01, $F_e$ = 0.005, L = 2. Solid curve 1: K = 0; Solid curve 2:K = 0.5; Solid curve 3: K = 1; Solid curve 4: K = 1.5; Solid curve 5: K = 1.8; Solid curve 6: K = 2. Dash–dot–dot lines: backbone curves

Figure 8 shows that the response curve characteristics for the NIM QZS mount are quite different with those for the NIM only isolator shown in Fig. 6. It is of interest to investigate the effects of the lateral spring stiffness on the response characteristics. In Fig. 9a, b, displacement responses associated with the QZS isolator shown in Fig. 3c with NIM ($\lambda =10$) and without the NIM ($\lambda =0$) are examined, respectively. The other parameter values are set to be $\zeta$=0.01,$F_e$=0.005 and L=1.5. The responses are obtained with the stiffness ratio K increased from 0 to 0.5, 1, 1.5, 1.8 and finally to 2. Correspondingly, there are six sets of system parameter values, with $\alpha =0,\beta =1$(Case one), $\alpha =0.75, \beta =0.375$ (Case two), $\alpha$=0.5, $\beta$=0.75 (Case three), $\alpha$=0.25, $\beta$=1.125 (Case four), $\alpha$=0.1, $\beta$=1.35 (Case five) and $\alpha$=0, $\beta$=1.5 (Case six). In Fig. 9a, Case one represents the use of the NIM isolator, while Case six is for the NIM QZS mount. The corresponding backbone curves of the six cases are also included. Figure 9a shows that the curves associated with the NIM isolator (i.e. $K=0$) bends to the low-frequency range. With the increase in K, the curves extend to the high frequencies when $K=1.8$ and $K=2$. The increase in the lateral spring stiffness also leads to the shift of the resonance peak to the low-frequency range. This is due to the fact that the linearised natural frequency of system is $\sqrt{\alpha }$, and an increase in K will lead to a smaller value of $\alpha$. Consequently, there are shifts of the resonance peak. The figure also shows that the response peak value increases with the stiffness ratio K. In Fig. 9b, solid curve 1 shows the response of a conventional isolator with vertical spring-damper unit, without lateral springs ($K=0)$. With the addition of lateral springs with an increase in non-dimensional stiffness coefficient K, the displacement response curve shifts to the low-frequency range with the peak bending to the right. When the lateral spring stiffness K increases to 2 (solid line 6), the response curves twist significant to the left. The corresponding peak value is the highest, compared to other cases with lower values of K. Comparing Fig. 9b with Fig. 9a, it is clear that the use of lateral springs alone leads to the shift and right-hand side bending of response curves. The addition of the NIM, as in Fig. 9a, may alter the bending direction and yield left-hand side bending response curves.

Fig. 10

Force transmissibility characteristics of the NIM QZS mounts ($\zeta = 0.01, F_e = 0.005, K = 2, L = 1.5$). Solid, dashed, dash–dot and dotted lines for the HB results of $\lambda$ = 0, 10, 20 and 40, respectively. The triangles, squares and diamonds are for the RK results of $\lambda$ = 10, 20 and 40, respectively

Fig. 11

Effects of inertance ratio $\lambda$ on the maximum kinetic energy $K_{\max }$ for a NIM only isolator and b the NIM QZS mounts. The circles, triangles and squares are for the RK results of $\lambda$ = 10, 20 and 40, respectively

Figure 10 presents the performance of the nonlinear NIM QZS mount in terms of force transmissibility. The system parameters are set as $\zeta =0.01,K=2,L=1.5,F_e=0.005$ so as to represent a system with quasi-zero-stiffness characteristics. Four different values of the inertance ratio $\lambda$ with $\lambda$=0, 10, 20 and 40 are selected to evaluate the effects of NIM on the isolation of force transmission. The force transmissibility TR is obtained by harmonic balance analytical formulations based on Eqs. (17) and (32) and also by the direct numerical integration results of the maximum transmitted force in the steady-state motion. The figure shows that the force transmissibility curve of the nonlinear QZS isolator extends to the high-frequency range. By the introduction of the NIM with $\lambda$ = 10 to the QZS isolator, the force transmissibility curve bends less to the right. Further increases in the inertance ratio $\lambda$ to 20 and then to 40 lead to less twisting of the force transmissibility to the high-frequency range. Meanwhile, the peak force transmissibility is reduced by the increase in $\lambda$. The figure shows that by increasing the inertance ratio $\lambda$, the horizontal line of unity transmissibility, i.e. $TR=1$, crosses the force transmissibility curve at lower frequencies. This agrees with the analytical formulation of the lower limit of the effective isolation frequency band in expression (48).

These characteristics show potential benefits of adding the NIM to a QZS nonlinear vibration isolator. More specifically, the addition of the NIM increases the effective isolation bandwidth while reducing the peak value of TR. Away from the resonant solution branches, the effects of inertance ratio $\lambda$ on force transmissibility TR are observed to be small.

5.3 Discussion of vibration power flow behaviour

Power flow analysis of inerter-based nonlinear isolator is carried out, and the formulations are presented in “Appendix”. Figure 11 investigates the influence of the inertance ratio $\lambda$ on the maximum kinetic energy $K_{\max }$ of the mass for the NIM only isolator and also the NIM QZS mount cases. Three different values inertance ratio of the NIM are selected with $\lambda$ varying from 10 to 20 and then to 40. In Fig. 11a, the system parameters for the NIM isolator are set as $\zeta =0.01, F_e=0.01, \alpha =1, \beta =0$. The figure shows that the addition of the NIM into the vibration isolator twists peaks of $K_{\max }$ to the low-frequency range. With the increase in the inertance ratio $\lambda$, the curves of $K_{\max }$ bend further to the low frequencies. The peak values in the curves of $K_{\max }$ are suppressed by introducing the NIM and increasing the inertance ratio $\lambda$. These characteristics may be beneficial for vibration isolation. It is seen that the level of the maximum kinetic energy is also reduced at the original peak frequency of the system with a linear spring-damper isolator (i.e. $\lambda =0$). In Fig. 11b, the parameters are set to be $\zeta =0.01,F_e=0.005,K=2,L=1.5$ (i.e. $\alpha =0, \beta =1.5$). The inertance ratio $\lambda$ is initially set as 0 to represent a nonlinear QZS isolator while three other values of the inertance ratio with $\lambda =10, 20$ and 50 are considered for nonlinear NIM QZS mounts. Figure 11b shows that the peak of $K_{\max }$ for the QZS only isolator (with $\lambda$=0) extends to the high-frequency range due to the hardening stiffness characteristics of QZS mechanism. When the NIM with $\lambda =10$ is used together with the QZS mechanism, the peak of $K_{\max }$ bends less to the right. A further increase in the inertance ratio $\lambda$ to 20 leads to less bending of the curves to the high frequencies. When $\lambda$ increases to 40, the kinetic energy curve extends to the low-frequency range. The figure also shows that the peak values of $K_{\max }$ are almost the same for the four cases of $\lambda$ values considered. This behaviour was shown by analytical derivations in “Appendix”, i.e. the upper limits of $K_{\max }$ are independent of $\lambda$. Figure 11 shows that for different cases considered, the non-resonant solution branches for $K_{\max }$ merge. This is due to small oscillation amplitude as shown in Figs. 6a and 8, and correspondingly the associated nonlinear effects introduced by NIM may be ignored. In summary, the addition of the NIM to the QZS isolator does not have a detrimental effect on the peak value of $K_{\max }$ but does shift the frequency at which it occurs.

6 Conclusions

This paper presented a nonlinear inertance mechanism (NIM) that can be used to enhance vibration isolation performance and demonstrated its application to nonlinear inerter-based isolators. The NIM is created by arranging a pair of inerters obliquely with the one common end hinged together and the other ends fixed. Two configurations of inerter-based nonlinear vibration isolators, with one comprising the NIM and a conventional spring-damper isolator, and another one consisting of the NIM with a nonlinear QZS isolator were examined. The frequency response relationship was obtained using the harmonic balance method. Performance indices associated with dynamic response and force transmissibility were used to evaluate the effectiveness of the vibration isolators.

The addition of the NIM to a linear isolator provides performance benefits to vibration isolation. This was evident by showing that the presence of the NIM results in: (1) the bending the frequency response curves towards the low-frequency range and reducing the original peak values in dynamic response; (2) bending of force transmissibility curve and potential reduction in peak transmissibility; and (3) lower transmissibility are achieved at high frequencies comparing to the inerter-based linear isolator.

The introduction of NIM to a QZS isolator can provide enhanced performance as shown by: (1) a larger frequency range of small dynamic response amplitude and kinetic energy of the mass; 2) a wider frequency band of unity force transmissibility; and (3) potential reduction in peak force transmissibility.

Overall, the study suggests that the added NIM can have a beneficial effect on both the linear isolator and the nonlinear QZS isolators. These findings improve the understanding of the dynamic properties of the NIM and provide design guidance for nonlinear inerter-based vibration isolators for enhanced vibration attenuation.

Appendix: Vibration power flow analysis

The non-dimensional power flow balance equations of the systems shown by Fig. 3d and c are obtained by multiplying by non-dimensional velocity $X'$ on both sides of the original governing equations (6a) and (6b):

$$\begin{aligned}&(1+\lambda )X''X'+2\zeta X'X'+XX'=X'F_e\cos {\varOmega \tau }, \end{aligned}$$

(41a)

$$\begin{aligned}&X''X'+2\zeta X'X'+H(X)X'+G(X,X',X'')X'\nonumber \\&\quad =X'F_e\cos {\varOmega \tau }, \end{aligned}$$

(41b)

Thus, for the vibration isolation systems shown in Fig. 3, the non-dimensional instantaneous time-averaged input power by the external excitation force and the dissipated power by the damper in the isolator are expressed by the products of the forces and the corresponding velocities:

$$\begin{aligned} p_\mathrm{in}&=X'F_e\cos {\varOmega \tau }, \end{aligned}$$

(42a)

$$\begin{aligned} p_{d}&=2\zeta X'X', \end{aligned}$$

(42b)

respectively. Interested readers may refer to ref. [18] for the basic concept and definition of vibration power flow as well as its application to dynamic analysis of linear and nonlinear vibration suppression systems as in Refs. [2, 19, 20, 22, 25, 26]. In the steady-state motion, the non-dimensional time-averaged input and dissipated powers over one period of the external excitation are

$$\begin{aligned} {\bar{p}}_\mathrm{in}(\varOmega )&=\frac{1}{T}\int _{\tau _0}^{\tau _0+T} X'F_e\cos {\varOmega \tau } \,\mathrm {d}\tau \approx -\frac{r\varOmega }{2}F_e \sin \phi , \end{aligned}$$

(43a)

$$\begin{aligned} {\bar{p}}_{d}(\varOmega )&=\frac{1}{T}\int _{\tau _0}^{\tau _0+T} 2\zeta X'X'\,\mathrm {d}\tau \approx \zeta r^2 \varOmega ^2, \end{aligned}$$

(43b)

respectively, where $\tau _0$ is the starting time while T is the averaging time, set to be a period of excitation, i.e. $T=2\pi /\varOmega$, and a first-order approximation of the velocity with $X'=-r\varOmega \sin (\varOmega \tau +\phi )$ was used for the inerter-based nonlinear isolation system shown in Fig. 3c. Note that based on Eqs. (16b) and (43a), the first-order approximation of the time-averaged input power into the system shown in Fig. 3c is

$$\begin{aligned} {\bar{p}}_\mathrm{in}(\varOmega )=\zeta r^2 \varOmega ^2. \end{aligned}$$

(44)

Note that it has been shown that Eq. (44) presents the exact analytical expression of the time-averaged input power into the inerter-based linear isolator [20]. Equations (43b) and (44) show that the first-order approximate expressions for the time-averaged input and dissipated powers are identical. This is due to the fact that over a cycle of steady-state periodic oscillation, there is no net change in potential and kinetic energies of the integrated nonlinear isolation system. Consequently, the vibration power input from the external excitation is all dissipated by damping.

The maximum kinetic energy of the excited system is widely used as a performance index of vibration control systems [19]. The non-dimensional maximum kinetic energy of the mass in the steady-state motion is

$$\begin{aligned} K_{\max }=\frac{1}{2}X'^2 \approx \frac{1}{2} r^2 \varOmega ^2. \end{aligned}$$

(45)

where a first-order approximation the steady-state velocity response was used for the inerter-based nonlinear isolator shown in Fig. 3. Note that a comparison of Eqs. (44) and (45) shows that

$$\begin{aligned} {\bar{p}}_\mathrm{in}=2\zeta K_{\max }. \end{aligned}$$

(46)

Equation (46) shows that for the system with a predetermined damping coefficient $\zeta$, the time-averaged input power is proportional to the maximum kinetic energy of the harmonically excited mass.

With reference to the frequency response relationship expressed by Eq. (17), the time-averaged input power and the maximum kinetic energy of the mass for the system shown in Fig. 3c can be rewritten as:

$$\begin{aligned}&{\bar{p}}_\mathrm{in}=\frac{\zeta \varOmega ^2 F_e^2}{(2\zeta \varOmega )^2+\Big (\alpha +\frac{3}{4}\beta r^2-\Big (1+\frac{\lambda }{2}r^2+\frac{\lambda }{4}r^4\Big )\varOmega ^2\Big )^2} \nonumber \\&\quad \le \frac{F_e^2}{4\zeta }, \end{aligned}$$

(47a)

$$\begin{aligned}&K_{\max }=\frac{\varOmega ^2 F_e^2}{2(2\zeta \varOmega )^2+2\Big (\alpha +\frac{3}{4}\beta r^2-\Big (1+\frac{\lambda }{2}r^2+\frac{\lambda }{4}r^4\Big )\varOmega ^2\Big )^2} \nonumber \\&\quad \le \frac{F_e^2}{8\zeta ^2}. \end{aligned}$$

(47b)

These equations show that there are upper limits for both the time-averaged input power and the maximum kinetic energy of the mass, respectively. The upper limits are only determined by the damping coefficient $\zeta$ and the excitation force amplitude $F_e$. These upper limits of the time-averaged power flow and the maximum kinetic energy of the mass may be reached when

$$\begin{aligned} \alpha +\frac{3\beta r^2}{4}-\left( 1+\frac{\lambda r^2}{2}+\frac{\lambda r^4}{4}\right) \varOmega ^2=0. \end{aligned}$$

(48)

Recalling the backbone curve expression in Eq. (21) and frequency response relationship in (17), it is found that the upper limits of input power and kinetic energy of the mass are reached at the intersection point of the backbone curve and the displacement response curve.