Study of transversely isotropic nonlocal thermoelastic thin nano-beam resonators with multi-dual-phase-lag theory

Abstract

This study deals with a novel model of forced vibrational analysis of nonlocal transversely isotropic thermoelastic nanobeam resonators due to ramp-type heating and due to time varying exponentially decaying load with multi-dual-phase-lag theory of thermoelasticity. The mathematical model is prepared for the nanobeam in a closed form with the application of Euler–Bernoulli (E–B) beam theory using nonlocal generalized thermoelasticity with multi-dual phase lags. The nonlocal nanobeam theory has a nonlocal parameter to depict small-scale effect. The Laplace Transform technique has been used to find the expressions for lateral deflection, conductive temperature, thermal moment, nonlocal axial stress and thermodynamic temperature for (i) clamped–clamped, (ii) simply supported–simply supported, (iii) clamped–simply supported, (iv) clamped–free, and (v) free–free nanobeam in the transformed domain. The general algorithm of the inverse Laplace Transform is developed to compute the results numerically in physical domain. The results exhibit that the amplitude of deflection and thermal moment is attenuated and depends upon the schematic design of the nanobeam being considered. Also, it can be found from both the numerical calculations and the analytic results that nonlocal multi-dual-phase-lag theory of thermoelasticity with two temperatures due to time varying exponentially decaying load has significant effect on deflection and thermal moment. The effect of different theories of nonlocal thermoelasticity, due to time varying exponentially decaying load, has been depicted on the various quantities. Some particular cases have also been deduced.

1 Introduction

In last decade, nanomaterials have gained interest in the field of engineering due to their special properties like electronic, electrical and mechanical. Due to these properties, nano-materials are used in nano-beams as elementary structural components in micro-electromechanical system (MEMS)/nano-electromechanical systems (NEMS) and piezoelectric devices.

Nonlocal theory of elasticity is adopted to deal with many applications in nano-mechanics. Eringen [1,2,3] introduced the theory of nonlocal continuum mechanics to deal with the small-scale structure problems. The theories of nonlocal continuum consider the state of stress at a point as a function of the states of strain of all points in the medium. But in classical continuum mechanics the state of stress at a certain point uniquely depends on the state of strain on that same point. Lu et al. [4] proposed a model on nonlocal plate depending upon nonlocal Kirchhoff and Mindlin plate theories using the Eringen’s theory of nonlocal continuum mechanics.

The thermoelastic damping in a micro-beam resonator by the modified couple stress theory was examined by Ghader et al. [5]. Guo et al. [6] presented the problem of thermoelastic damping in vented MEMS beam with Galerkin finite element and eigenvalue formulation method. Simsek and Reddy [7] and Shaat et al. [8] examined the bending and vibration of functionally graded micro-beams using the modified couple stress theory and higher order beam theory. Allam and Abouelregal [9] investigated the thermoelastic waves prompted by pulsed laser and varying heat of nano-beam. Abouelregal and Zenkour [10] discussed the axially moving micro-beam with combined effects of the pulse-width of thermally originated vibration, varying speed and the transverse excitation. Zenkour [11] discussed the nonlocal elasticity theory for analysing the vibration in a single-layered graphene sheet fixed in viscoelastic medium. Abouelregal and Zenkour [12] studied the linear nonlocal theory for isotropic and semi-infinite medium using an ultra-short pulsed laser heating. Abouelregal [13] presented a new model for thermo-elastic vibrations using fractional derivatives in a nonlocal nanobeams.

Despite these several researchers as Marin [14, 15], Yu et al. [16], Park and Gao [17], Sun et al. [18] Li and Cheng [19], Sharma [20], Chakraborty [21], Lazar and Agiasofitou [22], Abd-Elaziz et al. [23, 24], Zhang and Fu [25], Abbas and Marin [26], Sharma and Kaur [27], Zenkour and Abouelregal [28], Fantuzzi et al. [29], Abouelregal and Zenkour [30], Aksoy [31], Kumar and Devi [32], Riaz et al. [33], Karami et al. [34, 35], Zhang et al. [36], Bhatti et al. [37, 38], Sharma and Marin [39], Sharma and Grover [40], Marin and Craciun [41, 42], AbbasR [43],Lata and Kaur [44,45,46,47,48,49], Bhatti and Michaelides [50] worked on different theory of thermoelasticity.

The present investigation deals with the problem of forced vibrations in a transversely Isotropic thermoelastic thin nanobeam in the context of nonlocal thermoelasticity theory with multi-dual-phase-lag heat transfer due to ramp-type heating and due to time varying exponentially decaying load. The Laplace Transform technique has been used to find the expressions for lateral deflection, conductive temperature, thermal moment, nonlocal axial stress and thermodynamic temperature for (i) clamped–clamped (CC), (ii) simply supported–simply supported (SS), (iii) clamped–simply supported (CS), (iv) clamped–free (CF), and (v) free–free (FF) nanobeam in the transformed domain.

2 Basic equations

Following Eringen [1], Chakraborty [21] the constitutive relation for an anisotropic thermoelastic medium is:

$$\begin{aligned} t_{ij}-\xi \nabla ^{2}t_{ij}=c_{ijkl}e_{kl}-\beta _{ij}T, \end{aligned}$$

(1)

where $\xi =\left( e_{0}a \right) ^{2}$, a is internal characteristic length and $e_{0}$ is a constant appropriate to each material, the characteristic length for macro-scale problems is relatively small, i.e. $\xi =0$, so Eq. (1) changes to classical stress–strain relations. Following Zenkour [51] heat conduction equation with multi-dual-phase-lag heat transfer is:

$$\begin{aligned} {K_{ij}{\mathrm {L}}_{\theta }\varphi }_{{,}ij}= {\mathrm {L}}_{\mathrm {q}}\frac{{\partial }}{{\partial t}}\left( \beta _{ij}T_{{0}}u_{i,j}{+}{\rho C}_\mathrm{E}T \right) . \end{aligned}$$

(2)

Here the superimposed dot indicates derivative w.r.t. time variable t and a comma denotes derivative w.r.t. space variable x. The two differential parameters ${L}_{{\theta }}$ and ${L}_{\mathrm {q}}$ are of the form

$$\begin{aligned} {\mathrm {L}}_{\theta }=1+\sum \limits _{{\mathrm {j}=1}}^{\mathrm {R}_{1}} \frac{{\tau }_{\theta }^{j}{\partial }^{j}}{j{!\partial }{\mathrm {t}}^{j}}, \end{aligned}$$

and

$$\begin{aligned} {\mathrm {L}}_{\mathrm {q}}=\left( {\varrho +}{\tau }_{{0}} \frac{{\partial }}{{\partial t}}{+}\mathop {\sum }\nolimits _{j=2}^{\mathrm {R}_{{2}}} \frac{{\tau }_{\mathrm {q}}^{j}{\partial }^{j}}{j{!\partial }{\mathrm {t}}^{j}} \right) . \end{aligned}$$

($0\le {\tau \theta }<\tau _q$), and $\varrho$ is a non-dimension parameter (= 0 or 1 as per the thermoelasticity theory).

where

$$\begin{aligned}&T= \varphi -a_{ij}\varphi _{,ij}, \end{aligned}$$

(3)

$$\begin{aligned}&\quad {\beta _{ij}=c}_{ijkl}\alpha _{ij}, \end{aligned}$$

(4)

$$\begin{aligned}&\quad e_{ij}= \frac{1}{2}\left( u_{i,j}+ u_{j,i} \right) , i,j=1,2,3. \end{aligned}$$

(5)

$$\begin{aligned} \beta _{ij}=\beta _{i}\delta _{ij}, { K}_{ij}=K_{i}\delta _{ij}, \end{aligned}$$

i is not summed [47].

$c_{ijkl}$are elastic parameters and having symmetry due to homogeneous transversely isotropic medium. The basis of these symmetries of $c_{ijkl}$ is due to the following facts

• i. The stress tensor is symmetric, which is only possible if $(c_{ijkl}= c_{jikl})$

• ii. If a strain energy density exists for the material, the elastic stiffness tensor must satisfy $c_{ijkl}= c_{klij}$

• iii. From stress tensor and elastic stiffness tensor symmetries infer $(c_{ijkl}= c_{ijlk})$ and $c_{ijkl}= c_{klij}= c_{jikl}= c_{ijlk}$

3 Formulation of the problem

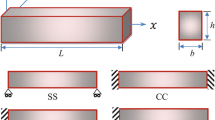
We study a homogeneous TIT rectangular nano-beam (Fig. 1) of length $(0\le x \le L)$, width $\left( -\frac{b}{2}\le y\le \frac{b}{2} \right)$ and thickness $\left( -\frac{h}{2}\le z\le \frac{h}{2} \right) ,$ where x, y and z are the Cartesian axes denotes the length, width and thickness of the nano-beam. The x-axis coincides with the nano-beam axis and y, z axis coincide with the end ($x=0$) with the origin located at the axis of the beam. In equilibrium, the nano-beam is kept at uniform temperature $\hbox {T}_{{0,}}$ unstrained and unstressed. Moreover, initially there is no flow of heat along the upper and lower surface of the nanobeam so that

$$\begin{aligned} \frac{\partial \varphi }{\partial z}=0, at \,\, z=\pm \frac{h}{2}, {\mathrm {t}}=0. \end{aligned}$$

(6)

and its axial ends are presumed to be at isothermal conditions.

Fig. 1

Schematic design of the nanobeam: (i) clamped–clamped (CC), (ii) simply supported–simply supported (SS), (iii) clamped–simply supported (CS), (iv) clamped–free (CF), (v) free–free (FF) nanobeam

According to the fundamental E-B theory for small deflection of a simple bending problem, the displacement components are given by Rao (2007)

$$\begin{aligned} u\left( x,y,z,t \right) = -z\frac{\partial w}{\partial x},\quad v\left( x,y,z,t \right) =0,\quad w\left( x,y,z,t \right) = w\left( x,t \right) , \end{aligned}$$

(7)

where $w\left( x,t \right)$ is the lateral deflection of the nanobeam and t is the time. Also the temperature distribution function T and conductive temperature $\varphi$ can be expressed as

$$\begin{aligned} T=T\left( x,z,t \right) ,\varphi =\varphi \left( x,z,t \right) \end{aligned}$$

(8)

From Eqs. (3) and (8), we have

$$\begin{aligned} T=\varphi -a_{1}\frac{\partial ^{2}\varphi }{\partial x^{2}}-a_{3}\frac{\partial ^{2}\varphi }{\partial z^{2}} \end{aligned}$$

(9)

According to Eringen’s nonlocal theory of elasticity the one-dimensional constitutive equation obtained from Eq. (1) with the help of Eq. (7) becomes

$$\begin{aligned} t_{11}-\xi \frac{\partial ^{2}t_{11}}{{\partial x}^{2}}= -c_{11}z\frac{\partial ^{2}w}{\partial x^{2}}- \beta _{1}T \end{aligned}$$

(10)

where $t_{11}$ is the nonlocal stress, ${\beta }_{1}= {(c}_{11}+c_{13})\alpha _{1}+C_{13}\alpha _{3}$ is the thermoelastic coupling parameter and $\alpha _{1},\alpha _{3}$ are the coefficient of linear thermal expansion along and perpendicular to plane of isotropy. The thermoelastic parameter $\beta _{3}= \mathrm {2}c_{13}\alpha _{1}+c_{33}\alpha _{3}$ along z-axis does not appear due to E-B hypothesis.

The flexural moment of the cross section of the nanobeam following Rao [52] is given by

$$\begin{aligned} M\left( x,z, t \right) =-\int _\frac{-h}{2}^\frac{h}{2} {bt_{11}z\mathrm{d}z} \end{aligned}$$

(11)

Multiply Eq. (10) by z and integrate w.r.t z and by using Eq. (11) we obtain

$$\begin{aligned} M\left( x, t \right) -\xi \frac{\partial ^{2}M}{{\partial x}^{2}}=c_{11}I\frac{\partial ^{2}w}{\partial x^{2}} - \beta _{1}{ M}_\mathrm{T} \end{aligned}$$

(12)

where

$$\begin{aligned} { M}_\mathrm{T}\left( x,z,t \right) =b\int _\frac{-h}{2}^\frac{h}{2} {Tz\mathrm{d}z} \end{aligned}$$

(13)

${M}_\mathrm{T}$ is the thermal moment of inertia of the nano-beam and $\beta _{1}M_\mathrm{T}$ is the thermal moment of the nano-beam. In addition, $I=\frac{bh^{3}}{\mathrm {12}}$ is the moment of inertia of cross section and $c_{11}I$ is the flexural rigidity of the nano-beam.

The equation of transverse motion of the nano-beam is given by Rao [52]

$$\begin{aligned} \frac{\partial ^{2}M}{\partial x^{2}}+ \rho A\frac{\partial ^{2}w}{\partial t^{2}}=q\left( x,t \right) , \end{aligned}$$

(14)

where $A=bh$ is the area of cross section and q(x, t) represents the load acting on the nano-beam along the thickness direction. Using Eq. (12) in Eq. (14), we get

$$\begin{aligned} c_{11}I\frac{\partial ^{4}w}{\partial x^{4}}+\rho A\frac{\partial ^{2}}{\partial t^{2}}\left( 1+\xi \frac{\partial ^{2}w}{\partial x^{2}} \right) +\beta _{1}\frac{\partial ^{2}M_\mathrm{T}}{\partial x^{2}}=\left( 1-\xi \frac{\partial ^{2}}{\partial x^{2}} \right) q(x,t). \end{aligned}$$

(15)

According to Lifshitz and Roukes [53] no thermal gradient exists in the y-direction. Therefore, Eq. (1) under such situation using Eq. (7) becomes

$$\begin{aligned}&K_{1}\left( {1+}\mathop \sum \nolimits _{{\mathrm {r}=1}}^{\mathrm {R}_{{1}}} \frac{{\tau }_{{\theta }}^{{r}}{\partial }^{\mathrm {r}}}{{\mathrm {r}!\partial }{\mathrm {t}}^{\mathrm {r}}} \frac{\partial ^{2}\varphi }{\partial x^{2}} \right) +K_{3}\left( {1+}\mathop \sum \nolimits _{{\mathrm {r}=1}}^{\mathrm {R}_{{1}}} \frac{{\tau }_{{\theta }}^{\mathrm {r}}{\partial }^{\mathrm {r}}}{{\mathrm {r}!\partial }{\mathrm {t}}^{\mathrm {r}}} \frac{\partial ^{2}\varphi }{{\partial z}^{2}} \right) = \left( {\varrho +}{\tau }_{{0}}\frac{{\partial }}{{\partial t}}\nonumber \right. \\&\quad \left. +\mathop \sum \nolimits _{{r=2}}^{\mathrm {R}_{{2}}} \frac{{\tau }_{\mathrm {q}}^{\mathrm {r}}{\partial }^{\mathrm {r}}}{{\mathrm {r}!\partial }{\mathrm {t}}^{\mathrm {r}}} \right) \left[ T_{0}\left( \beta _{1}\frac{\partial ^{2}w}{\partial x^{2}} \right) +\rho C_\mathrm{E}\left\{ \varphi -a_{1}\frac{\partial ^{2}\varphi }{{\partial x}^{2}}-a_{3}\frac{\partial ^{2}\varphi }{{\partial z}^{2}} \right\} \right] . \end{aligned}$$

(16)

To facilitate the solution, the following dimensionless quantities are introduced:

$$\begin{aligned} x^{'}= & {} \frac{x}{L}, z^{'}= \frac{z}{h}, { w}^{'}= \frac{w}{h}, \beta _{1}^{,}= \frac{\beta _{1}T_{0}}{C_{11}}, M_\mathrm{T}^{'}= \frac{M_\mathrm{T}}{T_{0}Ah}, T^{'}\nonumber \\&\quad = \frac{T}{T_{0}}, \varphi ^{'}= \frac{\varphi }{T_{0}},K= \frac{K_{3}}{K_{1}},a_{R}=\frac{L}{h}, a_{1}^{'}\nonumber \\&\quad = \frac{a_{1}}{L^{2}}, a_{3}^{'}= \frac{a_{3}}{h^{2}}, {\rho c}_{1}^{2}=c_{11},{ q}_{1}\left( x^{'},t^{'} \right) \nonumber \\&\quad =\frac{L^{2}}{c_{11}Ah}q\left( x,t \right) , { t}_{11}^{'}=\frac{t_{11}}{c_{11}},\xi ^{'}=\frac{\xi }{L^{2}},{(\tau }_{0}^{'}{,\tau }_{\theta }^{'}{,\tau }_{q}^{'},t^{'})\nonumber \\&\quad =\frac{c_{1}}{L}{(\tau }_{0},\tau _{\theta }{,\tau }_{q},t). \end{aligned}$$

(17)

Now applying the dimensionless quantities from (17) in Eqs. (12) and (13), after, suppressing the prime, we get

$$\begin{aligned}&\frac{1}{12a_{R}^{2}}\frac{\partial ^{4}w}{\partial x^{4}}+\frac{\partial ^{2}}{\partial t^{2}}\left( 1+\xi \frac{\partial ^{2}w}{\partial x^{2}} \right) +\beta _{1}\frac{\partial ^{2}M_\mathrm{T}}{\partial x^{2}}+\frac{\partial ^{2}w}{\partial t^{2}}=\left( 1-\xi \frac{\partial ^{2}}{\partial x^{2}} \right) q_{1}(x,t), \end{aligned}$$

(18)

$$\begin{aligned}&\frac{1}{Ka_{R}^{2}}\left( {1+}\mathop \sum \nolimits _{{\mathrm {r}=1}}^{\mathrm {R}_{{1}}} \frac{{\tau }_{{\theta }}^{\mathrm {r}}{\partial }^{\mathrm {r}}}{{\mathrm {r}!\partial }{\mathrm {t}}^{\mathrm {r}}} \right) \frac{\partial ^{2}\varphi }{\partial x^{2}}+\left( {1+}\mathop \sum \nolimits _{{\mathrm {r}=1}}^{\mathrm {R}_{{1}}} \frac{{\tau }_{{\theta }}^{\mathrm {r}}{\partial }^{\mathrm {r}}}{{\mathrm {r}!\partial }{\mathrm {t}}^{\mathrm {r}}} \right) \frac{\partial ^{2}\varphi }{{\partial z}^{2}}= \left( {\varrho +}{\tau }_{{0}}\frac{{\partial }}{{\partial t}}\nonumber \right. \\&\quad \left. +\mathop \sum \nolimits _{{\mathrm {r}=2}}^{\mathrm {R}_{{2}}} \frac{{\tau }_{\mathrm {q}}^{\mathrm {r}}{\partial }^{\mathrm {r}}}{{\mathrm {r}!\partial }{\mathrm {t}}^{\mathrm {r}}} \right) \left[ \delta _{{1}}\left( z\frac{\partial ^{2}w}{\partial x^{2}} \right) +\delta _{2}\left\{ \varphi -a_{1}\frac{\partial ^{2}\varphi }{\partial x^{2}}-a_{3}\frac{\partial ^{2}\varphi }{{\partial z}^{2}} \right\} \right] , \end{aligned}$$

(19)

where

$$\begin{aligned} \delta _{{1}}=- \frac{\beta _{1}T_{{0}}h^{2}}{K_{3}a_{R}^{2}}{, }\delta _{{2}}=\frac{\rho C_\mathrm{E}h^{2}}{K_{3}} \end{aligned}$$

The nonlocal axial stress defined in Eq. (10) after using Eq. (9) and the dimensionless quantities defined by Eq. (17) and suppressing primes become

$$\begin{aligned} t_{11}-\xi \frac{\partial ^{2}t_{11}}{{\partial x}^{2}}= -\frac{1}{a_{R}^{2}}z\frac{\partial ^{2}w}{\partial x^{2}}- \beta _{1}\left\{ \varphi -a_{1}\frac{\partial ^{2}\varphi }{{\partial x}^{2}}-a_{3}\frac{\partial ^{2}\varphi }{{\partial z}^{2}} \right\} , \end{aligned}$$

(20)

For a very thin nano-beam, assuming that the increase in temperature varies along the thickness of the nano-beam as function of $\sin \frac{\pi z}{h}$ (i.e. varies sinusoidally) given by

$$\begin{aligned} \varphi \left( x,z,t \right) ={\Theta }\left( x,t \right) \sin \frac{\pi z}{h}, \end{aligned}$$

(21)

The temperature in Eq. (9) after using dimensionless quantities and suppressing primes and using (21) becomes

$$\begin{aligned} T\left( x,z,t \right) =\sin \frac{\pi z}{h}\left[ \left( 1+a_{3}\frac{\pi ^{2}}{h^{2}} \right) {\Theta }\left( x,t \right) -a_{1}\frac{\partial ^{2}{\Theta }\left( x,t \right) }{\partial x^{2}} \right] \end{aligned}$$

(22)

Using Eq. (21) in Eq. (20) gives nonlocal axial stress as

$$\begin{aligned} t_{11}-\xi \frac{\partial ^{2}t_{11}}{{\partial x}^{2}}= -\frac{1}{a_{R}^{2}}z\frac{\partial ^{2}w}{\partial x^{2}}- \beta _{1}\sin \frac{\pi z}{h}\left[ \left( 1+a_{3}\frac{\pi ^{2}}{h^{2}} \right) {\Theta }\left( x,t \right) -a_{1}\frac{\partial ^{2}{\Theta }\left( x,t \right) }{\partial x^{2}} \right] \end{aligned}$$

(23)

Using Eq. (9) in Eq. (13) and then using Eq. (21)

$$\begin{aligned} {M}_\mathrm{T}\left( x,t \right) =\delta _{3}{\Theta }\left( x,t \right) +\delta _{4}\frac{\partial ^{2}{\Theta }\left( x,t \right) }{\partial x^{2}} \end{aligned}$$

(24)

where $\delta _{3}=\frac{2h^{2}}{\pi ^{2}}\left\{ \left( 1+a_{3}\frac{\pi ^{2}}{h^{2}} \right) \right\} ,\delta _{4}=-\frac{2h^{2}a_{1}}{\pi ^{2}}.$

Now using the value of ${ M}_\mathrm{T}$ from Eq. (24) in (18) we get

$$\begin{aligned} \frac{1}{12a_{R}^{2}}\frac{\partial ^{4}w}{\partial x^{4}}+\frac{\partial ^{2}}{\partial t^{2}}\left( 1+\xi \frac{\partial ^{2}}{\partial x^{2}} \right) w+\beta _{1}\frac{\partial ^{2}}{\partial x^{2}}\left( \delta _{3}{\Theta }+\delta _{4}\frac{\partial ^{2}{\Theta }}{\partial x^{2}} \right) =\left( 1-\xi \frac{\partial ^{2}}{\partial x^{2}} \right) q_{1}(x,t), \end{aligned}$$

(25)

Using Eq. (21) in Eq. (19) and multiplying by z and integrating both sides w.r.t z for $\frac{-h}{2}\le z\le \frac{h}{2},$ gives

$$\begin{aligned}&\frac{1}{Ka_{R}^{2}}\left( {1+}\mathop \sum \nolimits _{{\mathrm {r}=1}}^{\mathrm {R}_{{1}}} \frac{{\tau }_{{\theta }}^{\mathrm {r}}{\partial }^{\mathrm {r}}}{{\mathrm {r}!\partial }{\mathrm {t}}^{\mathrm {r}}} \right) \frac{\partial ^{2}{\Theta }}{\partial x^{2}}\nonumber \\&\qquad -\frac{\pi ^{2}}{h^{2}}\left( {1+}\mathop \sum \nolimits _{{\mathrm {r}=1}}^{\mathrm {R}_{{1}}} \frac{{\tau }_{{\theta }}^{\mathrm {r}}{\partial }^{\mathrm {r}}}{{\mathrm {r}!\partial }{\mathrm {t}}^{\mathrm {r}}} \right) {\Theta }= \left( {\varrho +}{\tau }_{{0}}\frac{{\partial }}{{\partial t}}\nonumber \right. \\&\qquad \left. +\mathop \sum \nolimits _{{\mathrm {r}=2}}^{\mathrm {R}_{{2}}} \frac{{\tau }_{\mathrm {q}}^{\mathrm {r}}{\partial }^{\mathrm {r}}}{{\mathrm {r}!\partial }{\mathrm {t}}^{\mathrm {r}}} \right) \left[ \frac{\delta _{{1}}h\pi ^{2}}{12}\left( \frac{\partial ^{2}w}{\partial x^{2}} \right) +\delta _{2}\left( 1+a_{3}\frac{\pi ^{2}}{h^{2}} \right) {\Theta }-\delta _{2}a_{1}\frac{\partial ^{2}{\Theta }}{\partial x^{2}} \right] . \end{aligned}$$

(26)

Let us take the Laplace transform defined by

$$\begin{aligned} L\left[ f(t) \right] = \int \limits _0^\infty {e^{-st}f\left( t \right) \mathrm{d}t={\bar{f}}(s)}. \end{aligned}$$

(27)

By applying Laplace Transform defined by Eq. (27) in Eqs. (21) and (22), we get

$$\begin{aligned} \bar{\varphi }\left( x,z,s \right)= & {} \bar{\Theta }\left( x,s \right) \sin \frac{\pi z}{h}, \end{aligned}$$

(28)

$$\begin{aligned} {\bar{T}}\left( x,z,s \right)= & {} \bar{\mathrm{T}}\left( x,s \right) \sin \frac{\pi z}{h}=\sin \frac{\pi z}{h}\left[ \left( 1+a_{3}\frac{\pi ^{2}}{h^{2}} \right) -a_{1}D^{2} \right] \bar{\Theta }\left( x,s \right) \end{aligned}$$

(29)

Which implies

$$\begin{aligned} \bar{\mathrm{T}}\left( x,s \right) =\left[ \left( 1+a_{3}\frac{\pi ^{2}}{h^{2}} \right) -a_{1}D^{2} \right] \bar{\Theta }\left( x,s \right) . \end{aligned}$$

(30)

By applying Eq. (27) in Eq. (24)–(26), we get

$$\begin{aligned}&{\bar{M}}_\mathrm{T}\left( x,s \right) =\left( \delta _{3}+\delta _{4}D^{2} \right) \bar{\Theta }\left( x,s \right) \end{aligned}$$

(31)

$$\begin{aligned}&\quad \left[ \delta _{5}D^{4}+s^{2}\left( {1+\xi D}^{2} \right) \right] {\bar{w}}\left( x,s \right) +\left[ \beta _{1}\delta _{3}D^{2}+\beta _{1}\delta _{4}D^{4} \right] \bar{\Theta }\left( x,s \right) =\left( 1-\xi \frac{\partial ^{2}}{\partial x^{2}} \right) {\bar{q}}_{1}(x,s){,} \end{aligned}$$

(32)

$$\begin{aligned}&\quad \delta _{6}D^{2}{\bar{w}}\left( x,s \right) +\left\{ \delta _{7}D^{2}+\delta _{8} \right\} \bar{\Theta }\left( x,s \right) =0 , \end{aligned}$$

(33)

where

$$\begin{aligned} D=\frac{d}{\mathrm{d}x} , \delta _{5}= & {} \frac{1+s^{2}\xi }{12a_{R}^{2}},\delta _{6}=\left( {\varrho +}{\tau }_{{0}}{\mathrm {s}+}\mathop \sum \nolimits _{{\mathrm {r}=2}}^{\mathrm {R}_{{2}}} \frac{{\tau }_{\mathrm {q}}^{\mathrm {r}}\mathrm {s}^{\mathrm {r}}}{\mathrm {r!}} \right) \frac{\delta _{{1}}h\pi ^{2}}{12},\delta _{7} \\= & {} -\left[ \frac{1}{Ka_{R}^{2}}\left( {1+}\mathop \sum \nolimits _{{\mathrm {r}=1}}^{\mathrm {R}_{{1}}} \frac{{\tau }_{{\theta }}^{\mathrm {r}}\mathrm {s}^{\mathrm {r}}}{\mathrm {r!}} \right) +\delta _{2}a_{1}\left( {\varrho +}{\tau }_{{0}}{\mathrm {s}+}\mathop \sum \nolimits _{{\mathrm {r}=2}}^{\mathrm {R}_{{2}}} \frac{{\tau }_{\mathrm {q}}^{\mathrm {r}}\mathrm {s}^{\mathrm {r}}}{\mathrm {r!}} \right) \right] ,\delta _{8}=\left[ \frac{\pi ^{2}}{h^{2}}\left( {1+}\mathop \sum \nolimits _{{\mathrm {r}=1}}^{\mathrm {R}_{{1}}} \frac{{\tau }_{{\theta }}^{\mathrm {r}}\mathrm {s}^{\mathrm {r}}}{\mathrm {r!}} \right) \right. \\&\left. +\delta _{2}\left( 1+a_{3}\frac{\pi ^{2}}{h^{2}} \right) \left( {\varrho +}{\tau }_{{0}}{\mathrm {s}+}\mathop \sum \nolimits _{{\mathrm {r}=2}}^{\mathrm {R}_{{2}}} \frac{{\tau }_{\mathrm {q}}^{\mathrm {r}}\mathrm {s}^{\mathrm {r}}}{\mathrm {r!}} \right) \right] . \end{aligned}$$

Now consider a dimensionless time varying exponentially decaying load of the form

$$\begin{aligned} q_{1}(x,t)=-q_{0}\left( 1-\delta e^{-{\Omega }t}\right) \end{aligned}$$

(34)

where $q_{0}$ is the dimensionless magnitude of the point load and ${\Omega }$ represents the dimensionless frequency of the applied load. For uniformly distributed load we take $\delta =0$. Taking Laplace transform of Eq. (34), we have

$$\begin{aligned} {\bar{q}}_{1}\left( x,s \right) ==-q_{0}\left( \frac{1}{s}-\frac{\delta }{s+{\Omega }} \right) \end{aligned}$$

(35)

Therefore Eq. (31) using Eq. (34) becomes

$$\begin{aligned} \left[ \delta _{5}D^{4}+s^{2}\left( {1+\xi D}^{2} \right) \right] {\bar{w}}\left( x,s \right) +\left[ \beta _{1}\delta _{3}D^{2}+\beta _{1}\delta _{4}D^{4} \right] \bar{\Theta }=-q_{0}\left( \frac{1}{s}-\frac{\delta }{s+{\Omega }} \right) {,} \end{aligned}$$

(36)

Eliminating $\bar{\Theta }$ from Eqs. (33) and (36), we get

$$\begin{aligned} \left[ D^{6}-pD^{4}+qD^{2}-r \right] {\bar{w}}\left( x,s \right) =Q{,} \end{aligned}$$

(37)

where

$$\begin{aligned} p= & {} \frac{{-\delta }_{7}s^{2}\xi +\delta _{3}\delta _{6}\beta _{1}-\delta _{8}\delta _{5}}{\delta _{7}\delta _{5}-\delta _{4}\delta _{6}\beta _{1}},q=\frac{\delta _{8}s^{2}\xi +\delta _{7}s^{2}}{\delta _{7}\delta _{5}-\delta _{4}\delta _{6}\beta _{1}},\\&\qquad r=\frac{-\delta _{8}s^{2}}{\delta _{7}\delta _{5}-\delta _{4}\delta _{6}\beta _{1}},Q=\frac{q_{0}\delta _{8}}{\delta _{7}\delta _{5}-\delta _{4}\delta _{6}\beta _{1}}\left( \frac{1}{s}-\frac{\delta }{s+{\Omega }} \right) \end{aligned}$$

For simplification of solution let us take $q_{0}=0$, i.e. load on nano-beam is assumed to be zero.

The differential equation governing the lateral deflection ${\bar{w}}\left( x,s \right) ,$ Eq. (37) can take the form

$$\begin{aligned} \left( D^{2}-\lambda _{1}^{2} \right) \left( D^{2}-\lambda _{2}^{2} \right) \left( D^{2}-\lambda _{3}^{2} \right) {\bar{w}}(x,s)=0, \end{aligned}$$

(38)

where $\pm \lambda _{1}, \pm \lambda _{2}$ and $\pm \lambda _{3}$ are the characteristics roots of the equation $\lambda ^{6}-p\lambda ^{4}+q\lambda ^{2}-r=0$ and hence,

$$\begin{aligned} \lambda _{1}^{2}+\lambda _{2}^{2}+ \lambda _{3}^{2}= & {} p,\\ \lambda _{1}^{2}\lambda _{2}^{2}+\lambda _{2}^{2}\lambda _{3}^{2}+\lambda _{1}^{2}\lambda _{3}^{2}= & {} q,\\ \lambda _{1}^{2}{\lambda _{2}^{2}\lambda }_{3}^{2}= & {} \mathrm {r}, \end{aligned}$$

Let the lateral deflection ${\bar{w}}\left( x,s \right)$ is given by

$$\begin{aligned} {\bar{w}}\left( x,s \right) = \sum \nolimits _{i=1}^3 \left[ A_{i}e^{-\lambda _{i}x}+A_{i+3}e^{\lambda _{i}x} \right] , \end{aligned}$$

(39)

where $A_{i}=A_{i}(s)$ and $A_{i+3}=A_{i+3}(s), \mathrm {i}=1,2,3$.

Now using Eq. (32) in Eq. (35) gives

$$\begin{aligned} \bar{\Theta }\left( x,s \right) =\zeta _{1}Q+\left( {\zeta _{2}D}^{4}+\zeta _{3}D^{2}{+\zeta }_{4} \right) {\bar{w}}\left( x,s \right) \end{aligned}$$

(40)

where $\zeta _{1}=\frac{\delta _{7}^{2}}{\beta _{1}\delta _{8}^{2}\delta _{4}-\delta _{3}\delta _{7}\delta _{8}\beta _{1}},\zeta _{2}=\frac{-\left( \delta _{7}^{2}\delta _{5}+\delta _{4}\delta _{6}\delta _{7}\beta _{1} \right) }{\beta _{1}\delta _{8}^{2}\delta _{4}-\delta _{3}\delta _{7}\delta _{8}\beta _{1}},\zeta _{3}=\frac{\delta _{3}\delta _{6}\delta _{7}\beta _{1}-\delta _{4}\delta _{6}\delta _{8}\beta _{1}-s^{2}\xi \delta _{7}^{2}}{\beta _{1}\delta _{8}^{2}\delta _{4}-\delta _{3}\delta _{7}\delta _{8}\beta _{1}}{,\zeta }_{4}=\frac{-s^{2}\delta _{7}^{2}}{\beta _{1}\delta _{8}^{2}\delta _{4}-\delta _{3}\delta _{7}\delta _{8}\beta _{1}}$

The general solution for Eq. (39) using Eq. (38) is given by

$$\begin{aligned} \bar{\Theta }\left( x,s \right) =\sum \limits _{i=1}^3 {B_{i}\left[ A_{i}e^{{-\lambda }_{i}x}+A_{i+3}e^{\lambda _{i}x} \right] } +\zeta _{1}Q, \end{aligned}$$

(41)

where $B_{i}=\left( \zeta _{2}\lambda _{i}^{4}+\zeta _{3}\lambda _{i}^{2}{+\zeta }_{4} \right) , i=1,2,3.$

Using Eq. (41) in Eq. (28) the expression for conductive temperature is given by

$$\begin{aligned} \bar{\varphi }\left( x,z,s \right) =\left\{ \sum \nolimits _{i=1}^3 {B_{i}\left[ A_{i}e^{{-\lambda }_{i}x}+A_{i+3}e^{\lambda _{i}x} \right] }+\zeta _{1}Q \right\} \sin \frac{\pi z}{h}. \end{aligned}$$

(42)

By putting the value of $\bar{\Theta }\left( x,s \right)$ from Eq. (41) in Eq. (31), we get thermal moment of inertia of the nano-beam which is $\bar{M}_\mathrm{T}\left( x,s \right)$ as

$$\begin{aligned} {\bar{M}}_\mathrm{T}\left( x,s \right) =\sum \limits _{i=1}^3 {C_{i}\left[ A_{i}e^{{-\lambda }_{i}x}+A_{i+3}e^{\lambda _{i}x}\right] } +\delta _{3}\zeta _{1}Q \end{aligned}$$

(43)

where

$$\begin{aligned} C_{i}=B_{i}\left( \delta _{3}+\delta _{4}\lambda _{i}^{2} \right) , i=1,2,3. \end{aligned}$$

The expression for thermal moment of nano-beam is $\beta _{1}\bar{M}_\mathrm{T}\left( x,s \right)$ as

$$\begin{aligned} {\beta _{1} \bar{M}}_\mathrm{T}\left( x,s \right) =\sum \limits _{i=1}^3 {{\beta _{1}C}_{i}\left[ A_{i}e^{{-\lambda }_{i}x}+A_{i+3}e^{\lambda _{i}x} \right] } +\beta _{1}\delta _{3}\zeta _{1}Q \end{aligned}$$

(44)

using (23) and (27) the nonlocal axial stress $\bar{t}_{11}\left( x,z,s \right)$ can be written as

$$\begin{aligned} \left( \xi D^{2}-1 \right) \bar{t}_{11}\left( x,z,s \right) = \frac{1}{a_{R}^{2}}zD^{2}{\bar{w}}\left( x,s \right) + \beta _{1}\sin \frac{\pi z}{h}\left[ \left( 1+a_{3}\frac{\pi ^{2}}{h^{2}} \right) -a_{1}D^{2} \right] \bar{\Theta }\left( x,s \right) \end{aligned}$$

(45)

Using Eqs. (39) and (41) in Eq. (42) gives

$$\begin{aligned} \left( D^{2}-\frac{1}{\xi } \right) \bar{t}_{11}\left( x,z,s \right) = \sum \limits _{i=1}^3 {D_{i}\left[ A_{i}e^{-\lambda _{i}x}+A_{i+3}e^{\lambda _{i}x} \right] } + \frac{\beta _{1}}{\xi }\sin \frac{\pi z}{h}\zeta _{1}Q \end{aligned}$$

(46)

where $D_{i}=\left\{ \frac{1}{a_{R}^{2}\xi }z\lambda _{i}^{2}+ \frac{\beta _{1}}{\xi }\sin \frac{\pi z}{h}B_{i}\left[ \left( 1+a_{3}\frac{\pi ^{2}}{h^{2}} \right) -a_{1}\lambda _{i}^{2} \right] \right\} ,\xi =\left( e_{0}a \right) ^{2}, i=1,2,3$.

Solving Eq. (44) gives nonlocal axial stress as

$$\begin{aligned} \bar{t}_{11}\left( x,z,s \right) =E_{1}e^{\frac{x}{\sqrt{\xi }}}+E_{2}e^{\frac{-x}{\sqrt{\xi }}}+\sum \limits _{i=1}^3 {\frac{D_{i}}{\lambda _{i}^{2}-\xi }\left[ A_{i}e^{-\lambda _{i}x}+A_{i+3}e^{\lambda _{i}x} \right] } - \frac{\beta _{1}}{\xi ^{2}}\sin \frac{\pi z}{h}\zeta _{1}Q \end{aligned}$$

(47)

where $E_{1},E_{2}$ are constants.

The expression for thermodynamic temperature from Eq. (30) and (41) is given by

$$\begin{aligned} {\bar{T}}\left( x,z,s \right) =\sin \frac{\pi z}{h}\sum \limits _{i=1}^3 {F_{i}\left[ A_{i}e^{{-\lambda }_{i}x}+A_{i+3}e^{\lambda _{i}x} \right] } +\zeta _{1}Q \end{aligned}$$

(48)

where $F_{i}=B_{i}\left[ \left( 1+a_{3}\frac{\pi ^{2}}{h^{2}} \right) -a_{1}\lambda _{i}^{2} \right]$ and $B_{i}=\left( \zeta _{2}\lambda _{i}^{4}+\zeta _{3}\lambda _{i}^{2}{+\zeta }_{4} \right) , i=1,2,3$.

4 Initial conditions

The homogeneous nanobeam is initially at rest, is undeformed state and is at uniform temperature $T_{0}$. Thus the dimensionless initial conditions will be

$$\begin{aligned} \left. w\left( x,t \right) \right| _{t=0}=\left. \frac{\partial w\left( x,t \right) }{\partial t} \right| _{t=0}=0,\left. {\Theta }\left( x,t \right) \right| _{t=0}=\left. \frac{\partial {\Theta }\left( x,t \right) }{\partial t} \right| _{t=0}=0, \end{aligned}$$

(49)

Using the Laplace transform defined by Eq. (27) in the boundary conditions (45) yields

$$\begin{aligned} \left. {\bar{w}}\left( x,s \right) \right| _{s=0}=0,\left. \bar{\Theta }\left( x,s \right) \right| _{s=0}=0, \end{aligned}$$

(50)

5 Mechanical boundary conditions

Consider the ends of the nanobeam are subjected to (i) clamped–clamped (CC), (ii) simply supported–simply supported (SS), (iii) clamped–simply supported (CS), (iv) clamped–free (CF), and (v) free–free (FF) conditions. Thus at its dimensionless ends $x=0$ and $x=1$, the boundary conditions are:

Case I:

Clamped–clamped (CC) or pinned or hinged nanobeam

At the fixed ends the lateral deflection and the slope of lateral deflection are zero.

$$\begin{aligned} \left. w\left( x,t \right) \right| _{x=0,1}=\left. \frac{\partial w\left( x,t \right) }{\partial x} \right| _{x=0,1}=0, \end{aligned}$$

(51)

Using the Laplace transform defined by Eq. (27) in the boundary conditions (51) yields

$$\begin{aligned} \left. {\bar{w}}\left( x,s \right) \right| _{x=0,1}=\left. \frac{\partial {\bar{w}}\left( x,s \right) }{\partial x} \right| _{x=0,1}=0, \end{aligned}$$

(52)

Case II:

Simply supported–simply supported (SS) nanobeam. Here the transverse lateral deflection and bending moment are zero at the ends.

$$\begin{aligned} \left. w\left( x,t \right) \right| _{x=0,1}=\left. \frac{\partial ^{2}w\left( x,t \right) }{\partial x^{2}} \right| _{x=0,1}=0, \end{aligned}$$

(53)

Using the Laplace transform defined by Eq. (27) in the boundary conditions (53) yields

$$\begin{aligned} \left. {\bar{w}}\left( x,s \right) \right| _{x=0,1}=\left. \frac{\partial ^{2}{\bar{w}}\left( x,s \right) }{\partial x^{2}} \right| _{x=0,1}=0, \end{aligned}$$

(54)

Case III:

Clamped–simply supported (CS) nanobeam.

At the fixed ends the transverse lateral deflection and the slope of lateral deflection are zero and at simply supported end the transverse displacement and bending moment are zero. If the beam is clamped at $x=0$ and simply supported at $x=1$, then boundary conditions can be written as

$$\begin{aligned} \left. w\left( x,t \right) \right| _{x=0,1}=\left. \frac{\partial w\left( x,t \right) }{\partial x} \right| _{x=0}=\left. \frac{\partial ^{2}w\left( x,t \right) }{\partial x^{2}} \right| _{x=1}, \end{aligned}$$

(55)

Using the Laplace transform defined by Eq. (27) in the boundary conditions (55) yields

$$\begin{aligned} \left. {\bar{w}}\left( x,s \right) \right| _{x=0,1}=\left. \frac{\partial w\left( x,s \right) }{\partial x} \right| _{x=0}=\left. \frac{\partial ^{2}{\bar{w}}\left( x,s \right) }{\partial x^{2}} \right| _{x=1}, \end{aligned}$$

(56)

Case IV:

Clamped–free (CF)/cantilever nanobeam. The bending moment and shear force are zero at the free end and at the fixed ends the transverse lateral deflection and the slope of displacement are zero. If the nanobeam is fixed at $x=0$ and free at $x=1$, then the boundary conditions are:

$$\begin{aligned} \left. w\left( x,t \right) \right| _{x=0}=\left. \frac{\partial w\left( x,t \right) }{\partial x} \right| _{x=0}=\left. \frac{\partial ^{2}w\left( x,t \right) }{\partial x^{2}} \right| _{x=1}=\left. \frac{\partial ^{3}w\left( x,t \right) }{\partial x^{3}} \right| _{x=1}, \end{aligned}$$

(57)

Using the Laplace transform defined by Eq. (27) in the boundary conditions (57) yields

$$\begin{aligned} \left. {\bar{w}}\left( x,s \right) \right| _{x=0}=\left. \frac{\partial {\bar{w}}\left( x,s \right) }{\partial x} \right| _{x=0}=\left. \frac{\partial ^{2}{\bar{w}}\left( x,s \right) }{\partial x^{2}} \right| _{x=1}=\left. \frac{\partial ^{3}{\bar{w}}\left( x,s \right) }{\partial x^{3}} \right| _{x=1}, \end{aligned}$$

(58)

Case V:

Free–free (FF) nanobeam The bending moment and shear force are zero at the ends in this case.

$$\begin{aligned} \left. \frac{\partial ^{2}w\left( x,t \right) }{\partial x^{2}} \right| _{x=0,1}=\left. \frac{\partial ^{3}w\left( x,t \right) }{\partial x^{3}} \right| _{x=0,1}=0, \end{aligned}$$

(59)

Using the Laplace transform defined by Eq. (27) in the boundary conditions (59) yields

$$\begin{aligned} \left. \frac{\partial ^{2}{\bar{w}}\left( x,s \right) }{\partial x^{2}} \right| _{x=0,1}=\left. \frac{\partial ^{3}{\bar{w}}\left( x,s \right) }{\partial x^{3}} \right| _{x=0,1}=0, \end{aligned}$$

(60)

6 Applications: thermal boundary conditions

Consider the nanobeam is thermally loaded on the boundary $x=0$. Therefore by Eq. (21) we have

$$\begin{aligned} {\Theta }\left( x,t \right) =\theta _{0}f\left( x,t \right) \hbox {on} x=0 \end{aligned}$$

(61)

where $\theta _{0}$ is a constant and $f\left( x,t \right)$ is a ramp-type function given by

$$\begin{aligned} \left. f\left( x,t \right) \right| _{x=0}=\left\{ {\begin{array}{l} 0 for t\le 0 \\ \frac{t}{t_{0}}for 0\le t\le t_{0} \\ 1for t>t_{0} \\ \end{array}} \right. \end{aligned}$$

(62)

where $t_{0}$ is ramp-type parameter. The temperature at the boundary $x=1$ is given by

$$\begin{aligned} \left. \frac{\partial {\Theta }\left( x,t \right) }{\partial x} \right| _{x=1}=0, \end{aligned}$$

(63)

Using the Laplace transform defined by Eq. (27) in the thermal boundary conditions defined by (61)–(63) yields

$$\begin{aligned} \left. \bar{\Theta }\left( x,s \right) \right| _{x=0}=\theta _{0}\left( \frac{1-e^{-t_{0}s}}{t_{0}s^{2}} \right)= & {} \bar{G}\left( s \right) , \end{aligned}$$

(64)

$$\begin{aligned} \left. \frac{\partial \bar{\Theta }\left( x,s \right) }{\partial x} \right| _{x=1}= & {} 0 \end{aligned}$$

(65)

By applying the mechanical boundary conditions and thermal boundary conditions, we have

Case I:

Substituting the values of ${\bar{w}}$ and $\bar{\Theta }$ from Eqs. (39) and (41) in the mechanical and thermal boundary conditions (52), (64) and (65), we obtain the value of $A_{i}$ as

$$\begin{aligned} A_{i}=\frac{{\Delta }_{i}}{{\Delta }} , i=1,2,3,4,5,6. \end{aligned}$$

(66)

and

$$\begin{aligned} {\Delta =}\left| {\begin{array}{*{20}c} {\begin{array}{*{20}c} {1} &{} {1} &{} {1}\\ \mathrm {e}^{{{-\lambda }}_{{1}}} &{} \mathrm {e}^{{{-\lambda }}_{{2}}} &{} \mathrm {e}^{{{-\lambda }}_{{3}}}\\ -{\lambda }_{{1}} &{} -{\lambda }_{{2}} &{} -{\lambda }_{{3}}\\ \end{array}} &{} {\begin{array}{*{20}c} {1} &{} {1} &{} {1}\\ \mathrm {e}^{{\lambda }_{{1}}} &{} \mathrm {e}^{{\lambda }_{{2}}} &{} \mathrm {e}^{{\lambda }_{{3}}}\\ {\lambda }_{{1}} &{} {\lambda }_{{2}} &{} {\lambda }_{{3}}\\ \end{array}}\\ {\begin{array}{*{20}c} -{\lambda }_{{1}}\mathrm {e}^{{{-\lambda }}_{{1}}} &{} -{\lambda }_{{2}}\mathrm {e}^{{{-\lambda }}_{{2}}} &{} -{\lambda }_{{3}}\mathrm {e}^{-{\lambda }_{{3}}}\\ B_{1} &{} B_{2} &{} B_{3}\\ B_{1}\mathrm {e}^{-{\lambda }_{{1}}} &{} B_{2}\mathrm {e}^{{{-\lambda }}_{{2}}} &{} B_{3}\mathrm {e}^{{{-\lambda }}_{{3}}}\\ \end{array}} &{} {\begin{array}{*{20}c} {\lambda }_{{1}}\mathrm {e}^{{\lambda }_{{1}}} &{} {\lambda }_{2}\mathrm {e}^{{\lambda }_{{2}}} &{} {\lambda }_{3}\mathrm {e}^{{\lambda }_{{3}}}\\ B_{1} &{} B_{2} &{} B_{3}\\ B_{1}\mathrm {e}^{{\lambda }_{{1}}} &{} B_{2}\mathrm {e}^{{\lambda }_{{2}}} &{} B_{3}\mathrm {e}^{{\lambda }_{{3}}}\\ \end{array}}\\ \end{array}} \right| \end{aligned}$$

${\Delta }_{i}(i=1,2,3,\ldots ,6)$ are obtained by replacing the columns by $\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {0,} &{} {0,} &{} {0,}\\ \end{array} } &{} {\begin{array}{*{20}c} {0,} &{} \bar{G}\left( s \right) -\zeta _{1}Q{,} &{} 0\\ \end{array}}\\ \end{array}} \right]$ in ${\Delta }$.

Case II:

Substituting the values of ${\bar{w}}$ and $\bar{\Theta }$ from Eqs. (39) and (41) in the mechanical and thermal boundary conditions (54), (64) and (65), we obtain the value of $A_{i}$ as

$$\begin{aligned} A_{i}=\frac{{\Delta }_{i}}{{\Delta }} , i=1,2,3,4,5,6. \end{aligned}$$

(67)

and

$$\begin{aligned} {\Delta } =\left| {\begin{array}{*{20}c} {\begin{array}{*{20}c} {1} &{} {1} &{} {1}\\ \mathrm {e}^{{{-\lambda }}_{{1}}} &{} \mathrm {e}^{{{-\lambda }}_{{2}}} &{} \mathrm {e}^{{{-\lambda }}_{{3}}}\\ {\lambda }_{{1}}^{{2}} &{} {\lambda }_{{2}}^{{2}} &{} {\lambda }_{{3}}^{{2}}\\ \end{array} } &{} {\begin{array}{*{20}c} {1} &{} {1} &{} {1}\\ \mathrm {e}^{{\lambda }_{{1}}} &{} {e}^{{\lambda }_{{2}}} &{} \mathrm {e}^{{\lambda }_{{3}}}\\ {\lambda }_{{1}}^{{2}} &{} {\lambda }_{{2}}^{{2}} &{} {\lambda }_{{3}}^{{2}}\\ \end{array}}\\ {\begin{array}{*{20}c} {\lambda }_{{1}}^{{2}}\mathrm {e}^{{{-\lambda }}_{{1}}} &{} {\lambda }_{{2}}^{{2}}\mathrm {e}^{{{-\lambda }}_{{2}}} &{} {\lambda }_{{3}}^{{2}}\mathrm {e}^{-{\lambda }_{{3}}}\\ B_{1} &{} B_{2} &{} B_{3}\\ B_{1}\mathrm {e}^{-{\lambda }_{{1}}} &{} B_{2}\mathrm {e}^{{{-\lambda }}_{{2}}} &{} B_{3}\mathrm {e}^{{{-\lambda }}_{{3}}}\\ \end{array}} &{} {\begin{array}{*{20}c} {\lambda }_{{1}}^{{2}}\mathrm {e}^{{\lambda }_{{1}}} &{} {\lambda }_{{2}}^{{2}}\mathrm {e}^{{\lambda }_{{2}}} &{} {\lambda }_{{3}}^{{2}}\mathrm {e}^{{\lambda }_{{3}}}\\ B_{1} &{} B_{2} &{} B_{3}\\ B_{1}\mathrm {e}^{{\lambda }_{{1}}} &{} B_{2}\mathrm {e}^{{\lambda }_{{2}}} &{} B_{3}\mathrm {e}^{{\lambda }_{{3}}}\\ \end{array}}\\ \end{array}} \right| \end{aligned}$$

${\Delta }_{i}(i=1,2,3,\ldots ,6)$ are obtained by replacing the columns by $\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {0,} &{} {0,} &{} {0,}\\ \end{array} } &{} {\begin{array}{*{20}c} {0,} &{} \bar{G}\left( s \right) -\zeta _{1}Q{,} &{} 0\\ \end{array}}\\ \end{array}} \right]$ in ${\Delta }$.

Case III:

Substituting the values of ${\bar{w}}$ and $\bar{\Theta }$ from Eqs. (39) and (41) in the mechanical and thermal boundary conditions (56), (64) and (65), we obtain the value of $A_{i}$ as

$$\begin{aligned} A_{i}=\frac{{\Delta }_{i}}{{\Delta }} , i=1,2,3,4,5,6. \end{aligned}$$

(68)

and

$$\begin{aligned} {\Delta =}\left| {\begin{array}{*{20}c} {\begin{array}{*{20}c} {1} &{} {1} &{} {1}\\ \mathrm {e}^{{{-\lambda }}_{{1}}} &{} \mathrm {e}^{{{-\lambda }}_{{2}}} &{} \mathrm {e}^{{{-\lambda }}_{{3}}}\\ -{\lambda }_{{1}} &{} -{\lambda }_{{2}} &{} -{\lambda }_{{3}}\\ \end{array}} &{} {\begin{array}{*{20}c} {1} &{} {1} &{} {1}\\ \mathrm {e}^{{\lambda }_{{1}}} &{} \mathrm {e}^{{\lambda }_{{2}}} &{} \mathrm {e}^{{\lambda }_{{3}}}\\ {\lambda }_{{1}} &{} {\lambda }_{{2}} &{} {\lambda }_{{3}}\\ \end{array}}\\ {\begin{array}{*{20}c} \mathrm {\lambda }_{{1}}^{{2}}\mathrm {e}^{{{-\lambda }}_{{1}}} &{} {\lambda }_{{2}}^{{2}}\mathrm {e}^{{{-\lambda }}_{{2}}} &{} {\lambda }_{{3}}^{{2}}\mathrm {e}^{-{\lambda }_{{3}}}\\ B_{1} &{} B_{2} &{} B_{3}\\ B_{1}\mathrm {e}^{-{\lambda }_{{1}}} &{} B_{2}\mathrm {e}^{{{-\lambda }}_{{2}}} &{} B_{3}\mathrm {e}^{{{-\lambda }}_{{3}}}\\ \end{array} } &{} {\begin{array}{*{20}c} {\lambda }_{{1}}^{{2}}\mathrm {e}^{{\lambda }_{{1}}} &{} {\lambda }_{{2}}^{{2}}\mathrm {e}^{{\lambda }_{{2}}} &{} {\lambda }_{{3}}^{{2}}\mathrm {e}^{{\lambda }_{{3}}}\\ B_{1} &{} B_{2} &{} B_{3}\\ B_{1}\mathrm {e}^{{\lambda }_{{1}}} &{} B_{2}\mathrm {e}^{{\lambda }_{{2}}} &{} B_{3}\mathrm {e}^{{\lambda }_{{3}}}\\ \end{array}}\\ \end{array}} \right| \end{aligned}$$

${\Delta }_{i}(i=1,2,3,\ldots ,6)$ are obtained by replacing the columns by $\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {0,} &{} {0,} &{} {0,}\\ \end{array} } &{} {\begin{array}{*{20}c} {0,} &{} \bar{G}\left( s \right) -\zeta _{1}Q{,} &{} 0\\ \end{array}}\\ \end{array}}\right]$ in ${\Delta }$.

Case IV:

Substituting the values of ${\bar{w}}$ and $\bar{\Theta }$ from Eqs. (39) and (41) in the mechanical and thermal boundary conditions (58), (64) and (65), we obtain the value of $A_{i}$ as

$$\begin{aligned} A_{i}=\frac{{\Delta }_{i}}{{\Delta }} ,i=1,2,3,4,5,6. \end{aligned}$$

(69)

and

$$\begin{aligned} {\Delta =}\left| {\begin{array}{*{20}c} {\begin{array}{*{20}c} {1} &{} {1} &{} {1}\\ {\lambda }_{{1}}^{{2}}\mathrm {e}^{{{-\lambda }}_{{1}}} &{} {\lambda }_{{2}}^{{2}}\mathrm {e}^{{{-\lambda }}_{{2}}} &{} {{\lambda }_{{3}}^{{2}}\mathrm {e}}^{{{-\lambda }}_{{3}}}\\ -{\lambda }_{{1}} &{} -{\lambda }_{{2}} &{} -{\lambda }_{{3}}\\ \end{array} } &{} {\lambda }_{{1}}^{{2}}{\begin{array}{*{20}c} {1} &{} {1} &{} {1}\\ \mathrm {e}^{{\lambda }_{{1}}} &{} {\lambda }_{{2}}^{{2}}\mathrm {e}^{{\lambda }_{{2}}} &{} {{\lambda }_{{3}}^{{2}}\mathrm {e}}^{{\lambda }_{{3}}}\\ {\lambda }_{{1}} &{} {\lambda }_{{2}} &{} {\lambda }_{3}\\ \end{array}}\\ {\begin{array}{*{20}c} {{-\lambda }}_{{1}}^{{3}}\mathrm {e}^{{{-\lambda }}_{{1}}} &{} -{\lambda }_{{2}}^{{3}}\mathrm {e}^{{{-\lambda }}_{{2}}} &{} {{-\lambda }}_{{3}}^{3}\mathrm {e}^{-{\lambda }_{{3}}}\\ B_{1} &{} B_{2} &{} B_{3}\\ B_{1}\mathrm {e}^{-{\lambda }_{{1}}} &{} B_{2}\mathrm {e}^{{{-\lambda }}_{{2}}} &{} B_{3}\mathrm {e}^{{{-\lambda }}_{{3}}}\\ \end{array} } &{} {\begin{array}{*{20}c} {\lambda }_{{1}}^{3}\mathrm {e}^{{\lambda }_{{1}}} &{} {\lambda }_{{2}}^{{3}}\mathrm {e}^{{\lambda }_{{2}}} &{} {\lambda }_{{3}}^{{3}}\mathrm {e}^{{\lambda }_{{3}}}\\ B_{1} &{} B_{2} &{} B_{3}\\ B_{1}\mathrm {e}^{{\lambda }_{{1}}} &{} B_{2}\mathrm {e}^{{\lambda }_{{2}}} &{} B_{3}\mathrm {e}^{{\lambda }_{{3}}}\\ \end{array}}\\ \end{array} } \right| \end{aligned}$$

${\Delta }_{i}(i=1,2,3,\ldots ,6)$ are obtained by replacing the columns by $\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {0,} &{} {0,} &{} {0,}\\ \end{array} } &{} {\begin{array}{*{20}c} {0,} &{} \bar{G}\left( s \right) -\zeta _{1}Q{,} &{} 0\\ \end{array}}\\ \end{array}} \right]$ in ${\Delta }$.

Case V:

Substituting the values of ${\bar{w}}$ and $\bar{\Theta }$ from Eqs. (39) and (41) in the mechanical and thermal boundary conditions (60), (64) and (65), we obtain the value of $A_{i}$ as

$$\begin{aligned} A_{i}=\frac{{\Delta }_{i}}{{\Delta }} , i=1,2,3,4,5,6. \end{aligned}$$

(70)

and

$$\begin{aligned} {\Delta =}\left| {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\lambda }_{{1}}^{{2}} &{} {\lambda }_{{2}}^{{2}} &{} {\lambda }_{{3}}^{{2}}\\ {{\lambda }_{{1}}^{{2}}\mathrm {e}}^{{{-\lambda }}_{{1}}} &{} {{\lambda }_{{2}}^{{2}}\mathrm {e}}^{{{-\lambda }}_{{2}}} &{} {{\lambda }_{{3}}^{{2}}\mathrm {e}}^{{{-\lambda }}_{{3}}}\\ -{\lambda }_{{1}}^{{3}} &{} -{\lambda }_{{2}}^{{3}} &{} {{-\lambda }}_{{3}}^{{3}}\\ \end{array} } &{} {\begin{array}{*{20}c} {\lambda }_{1}^{{2}} &{} {\lambda }_{2}^{{2}} &{} {\lambda }_{{3}}^{{2}}\\ {{\lambda }_{{1}}^{{2}}\mathrm {e}}^{{\lambda }_{{1}}} &{} {\lambda }_{{2}}^{{2}}\mathrm {e}^{{\lambda }_{{2}}} &{} {{\lambda }_{{3}}^{{2}}\mathrm {e}}^{{\lambda }_{{3}}}\\ {\lambda }_{{1}}^{{3}} &{} {\lambda }_{{2}}^{{3}} &{} {\lambda }_{{3}}^{{3}}\\ \end{array}}\\ {\begin{array}{*{20}c} {{-\lambda }}_{{1}}^{{3}}\mathrm {e}^{{{-\lambda }}_{{1}}} &{} {{-\lambda }}_{{2}}^{{3}}\mathrm {e}^{{{-\lambda }}_{{2}}} &{} {{-\lambda }}_{{3}}^{3}\mathrm {e}^{-{\lambda }_{\mathrm {3}}}\\ B_{1} &{} B_{2} &{} B_{3}\\ B_{1}\mathrm {e}^{-{\lambda }_{{1}}} &{} B_{2}\mathrm {e}^{{{-\lambda }}_{{2}}} &{} B_{3}\mathrm {e}^{{{-\lambda }}_{{3}}}\\ \end{array} } &{} {\begin{array}{*{20}c} {\lambda }_{{1}}^{3}\mathrm {e}^{{\lambda }_{{1}}} &{} {\lambda }_{{2}}^{3}\mathrm {e}^{{\lambda }_{{2}}} &{} {\lambda }_{{3}}^{{3}}\mathrm {e}^{{\lambda }_{{3}}}\\ B_{1} &{} B_{2} &{} B_{3}\\ B_{1}\mathrm {e}^{{\lambda }_{{1}}} &{} B_{2}\mathrm {e}^{{\lambda }_{{2}}} &{} B_{3}\mathrm {e}^{{\lambda }_{{3}}}\\ \end{array}}\\ \end{array}} \right| \end{aligned}$$

${\Delta }_{i}(i=1,2,3,\ldots ,6)$ are obtained by replacing the columns by $\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {0,} &{} {0,} &{} {0,}\\ \end{array} } &{} {\begin{array}{*{20}c} {0,} &{} \bar{G}\left( s \right) -\zeta _{1}Q{,} &{} 0\\ \end{array}}\\ \end{array}}\right]$ in ${\Delta }$.

7 Inversion of Laplace transform

To find the solution of the problem in physical domain, we must invert the transforms in equations (40), (42), (43), (46)–(48), (66)–(70). These equations are functions of x, the parameter of Laplace transform s and hence, are of the form ${\bar{f}}\left( x,s \right)$. To get the function $f\left( x,t \right)$ in the physical domain, first we invert the Laplace transform using

$$\begin{aligned} f\left( x,t \right) =\frac{1}{2\pi i} \int \limits _{e^{-i\infty }}^{e^{+i\infty }}{{\bar{f}}\left( x,s \right) e^{-st}\mathrm{d}s} . \end{aligned}$$

(71)

The integral in Eq. (71) is evaluated using the method described in Press et al. [54].

8 Particular cases

• i. If we take $q_{0}=0$, in equations (39), (42), (44), (47) and (48) we obtain expressions for lateral deflection, conductive temperature, thermal moment, nonlocal axial stress and thermodynamic temperature of a transversely isotropic thermoelastic nanobeam for nonlocal thermoelasticity with free vibrations and two temperatures for all the five mechanical boundary conditions.

• ii. If we take $q_{0}=0{, }c_{11}=c_{33}=\lambda +2\mu , c_{12}=c_{13}=\lambda ,c_{44}=\mu ,a_{1}=a_{3}=a,\beta _{{1}}=\beta _{{3}}=\beta {,} \alpha _{1}=\alpha _{3}=\alpha ^{'}, K_{1}=K_{3}=K,K_{1}^{*}=K_{3}^{*}=K^{*}$, in equations (39), (42), (44), (47) and (48), we obtain expressions for lateral deflection, conductive temperature, thermal moment, nonlocal axial stress and thermodynamic temperature of an isotropic thermoelastic nanobeam for nonlocal thermoelasticity with free vibrations and two temperatures for all the five mechanical boundary conditions.

• iii. If we take $c_{11}=c_{33}=\lambda +2\mu , c_{12}=c_{13}=\lambda ,c_{44}=\mu ,a_{1}=a_{3}=a,\beta _{{1}}=\beta _{{3}}=\beta {,} \alpha _{1}=\alpha _{3}=\alpha ^{'}, K_{1}=K_{3}=K,K_{1}^{*}=K_{3}^{*}=K^{*}$, in equations (39), (42), (44), (47) and (48), we obtain expressions for lateral deflection, conductive temperature, thermal moment, nonlocal axial stress and thermodynamic temperature of an isotropic thermoelastic nanobeam for nonlocal thermoelasticity with forced vibrations and two temperatures for all the five mechanical boundary conditions.

• iv. If $\tau _{\theta },\tau _{q}\rightarrow 0, \tau _{0}>0$ and ${\varrho =1}$, in equations (39), (42), (44), (47) and (48) we obtain expressions for lateral deflection, conductive temperature, thermal moment, nonlocal axial stress and thermodynamic temperature of a transversely isotropic thermoelastic nanobeam for nonlocal thermoelasticity with forced vibrations and two temperatures with Lord-Shulman (LS) theory for all the five mechanical boundary conditions.

• v. If $\tau _{\theta }=\tau _{q}=\tau _{0}=0$ and ${\varrho =1, }$ in equations (39), (42), (44), (47) and (48), we obtain expressions for lateral deflection, conductive temperature, thermal moment, nonlocal axial stress and thermodynamic temperature of a transversely isotropic thermoelastic nanobeam for nonlocal thermoelasticity with forced vibrations and two temperature with Coupled Theory of Thermoelasticity (CTE) for all the five mechanical boundary conditions.

• vi. If $\tau _{0}\rightarrow \tau _{q} ,\mathrm {R}_{{1}}=\mathrm {R}_{{2}}=1$ and ${\varrho =1}$, in equations (39), (42), (44), (47) and (48), we obtain expressions for lateral deflection, conductive temperature, thermal moment, nonlocal axial stress and thermodynamic temperature of a transversely isotropic thermoelastic nanobeam for nonlocal thermoelasticity with forced vibrations and two temperatures with dual phase-lag theory for all the five mechanical boundary conditions.

• vii. If $\tau _{0}\rightarrow \tau _{q} ,\mathrm {R}_{{1}}=1,\mathrm {R}_{{2}}=2$ and $\varrho =1$, in Eqs. (39), (42), (44), (47) and (48) we obtain expressions for lateral deflection, conductive temperature, thermal moment, nonlocal axial stress and thermodynamic temperature of a transversely isotropic thermoelastic nanobeam for nonlocal thermoelasticity with forced vibrations and two temperatures with refined multi-dual-phase-lag heat transfer theory and more refinement may be obtained by taking higher values of $\mathrm {R}_{{1}}$ and $\mathrm {R}_{\mathrm {2}}$ for all the five mechanical boundary conditions.

9 Numerical results and discussion

In order to illustrate our theoretical results in the proceeding section and to show the effect of different theories of nonlocal thermoelasticity, we now present some numerical results. Cobalt material is chosen from Dhaliwal and Singh [55] for the purpose of numerical calculation, which is transversely isotropic. Physical data for a single crystal of cobalt is given by:

$$\begin{aligned} c_{11}= & {} 3.07\times {10}^{11}\,\hbox {Nm}^{-2},\qquad c_{12}=1.650\times {10}^{11}\,\hbox {Nm}^{-2},\\ c_{13}= & {} 1.027\times {10}^{10}\,\hbox {Nm}^{-2},\qquad {c}_{33}=3.581\times {10}^{11}\,\hbox {Nm}^{-2},\\ c_{44}= & {} 1.510\times {10}^{11}\,\hbox {Nm}^{-2},\qquad { C}_\mathrm{E}=4.27\times {10}^{2}\,\hbox {J\,kg}^{-1}\mathrm{deg}^{-1},\\ \beta _{1}= & {} 7.04\times {10}^{6}\,\hbox {Nm}^{-2}{rm deg}^{-1},\qquad {\beta }_{3}=6.90\times {10}^{6}\hbox {Nm}^{-2}{rm deg}^{-1},\\ K_{1}= & {} 0.690\times {10}^{2}\,\hbox {Wm}^{-1}{rm K\,deg}^{-1},\qquad {K}_{3}=0.690\times {10}^{2}\,\hbox {Wm}^{-1}K^{-1},\\ K_{1}^{*}= & {} 0.02\times {10}^{2}\,\hbox {Ns}^{-2}{rm deg}^{-1},\quad K_{3}^{*}=0.04\times {10}^{2}N{Sec}^{-2}{rm deg}^{-1},\\ L/h= & {} 10,b /h=0.5, \qquad \rho =8.836\times {10}^{3}\,\hbox {kg}^{-3}. \end{aligned}$$

The following five cases are considered in numerical computations for dimensionless lateral deflection, thermal moment, conductive temperature and thermodynamic temperature studied with various theories of thermoelasticity (like LS, CTE, DPL and MDPL) by taking $\xi =0.1,h=0.1,a_{1}=0.03, a_{3}=0.06$, and $0<L<1$.

Case I:

Clamped–clamped (CC) or pinned or hinged nanobeam

Case II:

Simply supported–simply supported (SS) nanobeam.

Case III:

Clamped–simply supported (CS) nanobeam.

Case IV:

Clamped–free (CF)/cantilever nanobeam.

Case V:

Free–free (FF) nanobeam

The numerical results are obtained and graphically presented in Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 1617, 18, 19, 20 and 21. In the graphs, the solid red line with centre symbol circle represents CTE Theory and solid black line represents LS theory, the solid blue line with centre symbol diamond represents DPL Theory and the solid green line with centre symbol circle represents MDPL Theory.

Case I: Clamped–clamped (CC) or pinned or hinged nanobeam

Figure 2 shows the variation in the lateral deflection w w.r.t. length of the beam for various theories of thermoelasticity (like LS, CTE, DPL and MDPL). It is found that the DPL has the highest effect and CTE theory has the least effect on the lateral deflection w. Lateral deflection decreases gradually and reaches to zero for all the theories of thermoelasticity. Figure 3 illustrates the variation of thermal moment w.r.t. length of the beam for various theories of thermoelasticity (like LS, CTE, DPL and MDPL). It is found that the DPL has the highest effect and CTE theory has the least effect on the thermal moment. Thermal moment decreases gradually and reaches to zero for all the theories of thermoelasticity.

Fig. 2

Variation in lateral deflection w with length of nanobeam

Figure 4 demonstrates the variation of conductive temperature w.r.t. length of the beam for various theories of thermoelasticity (like LS, CTE, DPL and MDPL). It is found that the DPL has the highest effect and MPDL theory has the least effect on the conductive temperature. Conductive temperature decreases gradually and reaches to zero for all the theories of thermoelasticity.

Fig. 3

Variation of thermal moment with length of the nanobeam

Fig. 4

Variation in the conductive temperature with respect to length of nanobeam

Fig. 5

Variation in the thermodynamic temperature with respect to length of nanobeam

Figure 5 exhibits the variation of thermodynamic temperature w.r.t. length of the beam for various theories of thermoelasticity (like LS, CTE, DPL and MDPL). It is found that the DPL has the highest effect and CTE theory has the least effect on the thermodynamic temperature. Thermodynamic temperature decreases gradually and reaches to zero for all the theories of thermoelasticity.

Case II: Simply supported–simply supported (SS) nanobeam

Figures 6, 7, 8 and 9 show the variation in the lateral deflection, thermal moment, conductive temperature and thermodynamic temperature w.r.t. length of the beam for various various theories of thermoelasticity (like LS, CTE, DPL and MDPL). It is found that the CTE has the highest effect and MDPL theory of thermoelasticity has the least effect on lateral deflection, thermal moment, conductive temperature in simply supported–simply supported (SS) nanobeam, whereas DPL has the highest effect and CTE theory of thermoelasticity has the least effect thermodynamic temperature. All these parameters decrease gradually and reach to zero for all the theories of thermoelasticity.

Fig. 6

Variation in lateral deflection w with length of nanobeam

Fig. 7

Variation of thermal moment with length of the nanobeam

Fig. 8

Variation in the conductive temperature with respect to length of nanobeam

Fig. 9

Variation in the thermodynamic temperature with respect to length of nanobeam

Case III: Clamped–simply supported (CS) nanobeam

Figures 10, 11, 12 and 13 show the variation in the lateral deflection, thermal moment, conductive temperature and thermodynamic temperature w.r.t. length of the beam for various various theories of thermoelasticity (like LS, CTE, DPL and MDPL). It is found that the LS has the highest effect and CTE theory of thermoelasticity has the least effect on these parameters in clamped–simply supported (CS) nanobeam, whereas DPL and MDPL have approximately equal effect on these parameters.

Fig. 10

Variation in lateral deflection w with length of nanobeam

Fig. 11

Variation of thermal moment with length of the nanobeam

Fig. 12

Variation in the conductive temperature with respect to length of nanobeam

Fig. 13

Variation in the thermodynamic temperature with respect to length of nanobeam

Case IV: Clamped–free (CF)/cantilever nanobeam

Figures 14, 15, 16 and 17 show the variation in the lateral deflection, thermal moment, conductive temperature and thermodynamic temperature w.r.t. length of the beam for various theories of thermoelasticity (like LS, CTE, DPL and MDPL). It is found that the LS has the highest effect on lateral deflection and thermal moment and DPL theory of thermoelasticity has the highest effect on conductive temperature and thermodynamic temperature in clamped–simply supported (CS) nanobeam, whereas MDPL has approximately lowest effect on these parameters.

Fig. 14

Variation in lateral deflection w with length of nanobeam

Fig. 15

Variation of thermal moment with length of the nanobeam

Fig. 16

Variation in the conductive temperature with respect to length of nanobeam

Fig. 17

Variation in the thermodynamic temperature with respect to length of nanobeam

Case V: Free–free (FF) nanobeam

Figures 18, 19, 20 and 21 show the variation in the lateral deflection, thermal moment, conductive temperature and thermodynamic temperature w.r.t. length of the beam for various various theories of thermoelasticity (like LS, CTE, DPL and MDPL). It is found that the CTE has the highest effect and MDPL theory of thermoelasticity has the least effect on these parameters in free–free (FF) nanobeam. All these parameters decrease gradually and reach to zero for all the theories of thermoelasticity.

Fig. 18

Variation in lateral deflection w with length of nanobeam

Fig. 19

Variation of thermal moment with length of the nanobeam

Fig. 20

Variation in the conductive temperature with respect to length of nanobeam

Fig. 21

Variation in the thermodynamic temperature with respect to length of nanobeam

10 Conclusions

• The proposed model is designed to predict the thermomechanical response of transversely isotropic thermoelastic thin nanobeam in the context of nonlocal and multi-dual-phase-lag theories of thermoelasticity with two temperatures due to time varying exponentially decaying load and due to ramp-type heating at the end $x=0$ by using E–B Beam theory and Laplace transform technique.

• The ends of the nanobeam are subjected to: clamped–clamped (CC), simply supported–simply supported (SS), clamped–simply supported (CS), clamped–free (CF), free–free (FF) boundary conditions.

• Sinusoidally varying conductive temperature has been considered.

• Variation in the lateral deflection, thermal moment, conductive temperature and thermodynamic temperature with various theories of nonlocal thermoelasticity (like LS, CTE, DPL and MDPL with two temperatures) due to time varying exponentially decaying load are studied and shown graphically to depict the effects successfully.

• From the analysis, it is observed that the nonlocal multi-dual-phase-lag theory of thermoelasticity with two temperatures due to time varying exponentially decaying load has significant effect on lateral deflection, thermal moment, conductive temperature and thermodynamic temperature. In addition, for the change in boundary conditions at the ends of the nanobeam, there is significant effect on the lateral deflection, thermal moment, conductive temperature and thermodynamic temperature with different theories.

• A novel mathematical solutions has been given for the thin nanobeam in the context of nonlocal and multi-dual-phase-lag theories of thermoelasticity with two temperatures due to time varying exponentially decaying load, which is consequently easier for design and construction of beam-type MEMS/NEMS, accelerometers, sensors, resonators and other branches of engineering.