Study of Arrhenius activation energy on the thermo-bioconvection nanofluid flow over a Riga plate

Abstract

This article deals with a study of Arrhenius activation energy on thermo-bioconvection nanofluid propagates through a Riga plate. The Riga plate is filled with nanofluid and microorganisms suspended in the base fluid. The fluid is electrically conducting with a varying, parallel Lorentz force, which changes exponentially along the vertical direction, due to the lower electrical conductivity of the base fluid and the arrangements of the electric and magnetic fields at the lower plate. We consider only the electromagnetic body force over a Riga plate. The governing equations are formulated including the activation energy and viscous dissipation effects. Numerical results are obtained through the use of shooting method and are depicted graphically. It is noticed from the results that the magnetic field and the bioconvection Rayleigh number weaken the velocity profile. The bioconvection Schmidt and the Peclet number decrease the microorganism profile. The concentration profile is enhanced due to the increment in activation energy and the Brownian motion tends to increase the temperature profile. The latter is suppressed by an increment of the Prandtl number.

Introduction

In the recent decade, nanofluids received significant attention due to its major demand in diverse areas of science and technology. Nanofluids are produced by suspending particles in the base fluid with sizes less than 100 nm. Because nanomaterials have distinctive magnetic, mechanical, electrical, optical, and thermal features, appending small amounts of nanoparticles stably and uniformly in the base fluids results in dramatic enhancements of the thermal properties of the base fluids. The main objective of the nanofluids is to obtain the maximum thermal conductivity at the minimum possible concentrations, better if less than 1% by volume. Additional applications of nanofluids in multiple systems involve micro-reactors [1], enzyme biosensors [2], micro-channel heat sinks [3], bio-separation systems [4], and micro-heat pipes [5].

Bashirnezhad et al. [6] presented a detailed experimental review on the viscosity of the nanofluids, and Michaelides [7] presented a review of all their transport properties. Ayub et al. [8] studied the consequences of slip on the electro-magneto-hydro-dynamics nanofluid flow on a Riga plate using a viscous fluid model. Radiative heat transfers and slip flow over a dusty fluid filled with nanoparticles were investigated by Souayeh et al. [9]. Uddin et al. [10] discussed the nanoparticles’ behavior on the propagation of blood through a cylindrical tube using a singular kernel. Saif et al. [11] studied the hydromagnetic flow using Jeffrey’s nanofluid model over a curvy stretching surface. Alamri [12] presented an application for Stefan convection with the help of a Poiseuille flow model past a porous medium filled with nanoparticles. A few other important studies on thermal analysis and nanofluids may be found from the references [13,14,15,16,17,18,19].

Bioconvection occurs because of the formation of an apparent fluid pattern, i.e., falling plumes. Bioconvection is guided by the directional movement of microorganisms (self-driven) that are denser than water. Each microorganism swims on the physical phenomenon of mesoscale. The comprehensive density gradient, due to the up swimming of a large number of microorganisms, causes convection, which results in the generation of a spatially periodic apparent fluid circulation. Bioconvection has many implementations in bio-micro-systems, due to the improvement in mass migration and mixing, which are essential issues in various micro-systems [20, 21]. Shitanda et al. [22] considered the bioconvection flow through a toxic compound sensor and concluded that some toxic compounds constrain the movement of flagella and thus diminish the bioconvection. Iqbal et al. [23] numerically explored the flow of nanofluids with microorganisms over a Riga plate. Balla et al. [24] presented a bioconvection model with oxytactic microorganism propagating through a porous enclosure under the thermal impact. Shahid et al. [25] studied the behavior of microorganisms and nanofluids through a stretching surface using a numerical scheme. Pal and Mondal [26] presented a bioconvection model with a non-Newtonian Eyring–Powell fluid model under the consequences of Joule heating, magnetic fields, and thermal radiation. Other relevant studies on the gyrotactic microorganism migration are given in references [23, 27, 28].

Activation energy with mass and heat transfer plays an essential role in free convection boundary layer flows. The activation energy is also important in the fields of oil reservoir engineering and geothermal reservoirs. Several authors studied the behavior of activation energy in various media: Lu et al. [29] presented a three-dimensional numerical survey on the activation energy with slip and binary chemical reactions. Hayat et al. [30] discussed the consequences of variable thermal conductivity and activation energy on peristaltic induced flow through a curvy channel. Waqas et al. [31] examined the behavior of nonlinear radiative heat flow using Neild’s condition and activation energy over a stretching surface. Khan et al. [32] studied the bio-convective Sisko fluid model contains microorganisms under the effects of activation energy. Other relevant studies on the activation energy and the gyrotactic microorganisms are given in references [33,34,35].

From the above studies in mind, the main objective of the present analysis is to study the effects of the Arrhenius activation energy on the thermo-bioconvection nanofluid flow over a Riga plate. The effects of viscous dissipation under the influence of the electromagnetic force are also taken into account. Numerical solutions are acquired for the nonlinear coupled differential equations with the help of the shooting method. Shooting method is more efficient method and provides more convergence when compared with other similar methods [36,37,38,39].

Mathematical modeling

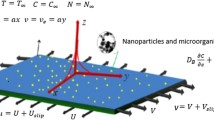
We consider an electro-magneto-hydro-dynamics flow of a nanofluid comprising gyrotactic toward a Riga plate. The flow occurs by a Riga plate at $\tilde{y} = 0$ as shown in Fig. 1. The Riga plate is composed of electrodes and magnets that are placed on a plain sheet. The nanoparticle concentration, motile microorganisms, and temperature at the Riga plate are $\tilde{C}_{\text{w}} ,\tilde{n}_{\text{w}} ,\tilde{T}_{\text{w}}$, respectively.

Fig. 1

Geometry of Riga plate composed of electrodes and magnets

The governing equation of continuity and momentum are as follows [40]:

$$\nabla \cdot {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{V} }} = 0,$$

(1)

$$\rho_{\text{f}} \left( {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{V} }} \cdot \nabla {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{V} }} + \frac{{\partial {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{V} }}}}{{\partial \tilde{t}}}} \right) = \mu \nabla^{2} \cdot {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{V} }} - \nabla \cdot \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{p} + \left[ { - \rho_{\text{f}} \left( {\tilde{T} - \tilde{T}_{1} } \right)\beta + \left( {\tilde{C} - \tilde{C}_{0} } \right)\left( {\rho_{\text{p}} - \rho_{\text{f}} } \right) + \Theta \tilde{n}\Delta \rho } \right]{\mathbf{g}} + {\mathbf{F}},$$

(2)

where ${\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{V} }}$ the velocity vector; $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{p}$ represents the pressure; $\rho$ the density; the subscripts f and p denote the base fluid and nanoparticles, respectively; $\tilde{T}$ the temperature of the fluid; $T_{1}$ the reference temperature; $\Theta$ the average volume of a microorganism; $\tilde{t}$ the time; $\tilde{C}_{0}$ the nanoparticle concentration; $\tilde{n}$ the concentration of microorganisms; $\beta$ represents the volumetric coefficient of thermal expansion; $\Delta \rho \left( { = \rho_{\text{mo}} - \rho_{\text{nf}} } \right)$ is the density difference betwixt the base fluid and a microorganism; ${\mathbf{g}}$ the gravity vector; and the viscosity of the suspension is denoted by $\mu$, which is composed of the microorganisms, the nanoparticles, and the base fluid.

The volume density of the Lorentz force ${\mathbf{F}}$ for the Riga plate is [8]

$${\mathbf{F}} = \frac{{M_{0} J_{0} \pi }}{8}\exp \left[ { - \tilde{y}\frac{\pi }{a}} \right],$$

(3)

where the magnetization of the permanent magnets is denoted by $M_{0}$; the width of electrodes and magnets is denoted by $a$; and the extrinsic current density in the electrodes is denoted $J_{0}$ (see Fig. 1).

The energy equation is [35]:

$$\left( {\rho c} \right)_{\text{f}} \left( {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{V} }} \cdot \nabla \tilde{T} + \frac{{\partial \tilde{T}}}{{\partial \tilde{t}}}} \right) = \nabla \cdot \left( {k_{\text{f}} \nabla \tilde{T}} \right) + \left( {\rho c} \right)_{\text{p}} \nabla \tilde{T}\left[ {d_{\text{T}} \nabla \tilde{T} + T_{1} d_{\text{B}} \nabla \tilde{C}} \right]\frac{1}{{T_{1} }} + \mu \left( {\nabla \cdot {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{V} }}} \right)^{2} ,$$

(4)

where Brownian motion parameter is denoted by d_B and the thermophoretic diffusion coefficient is denoted by d_T; k_f the thermal conductivity; and $\left( {\rho c} \right)_{\text{f}}$ and $\left( {\rho c} \right)_{\text{p}}$ represent the volumetric heat capacities for the nanoparticles and nanofluid, respectively. For the current analysis, the temperature gradient is considered to be very small so that it would not kill the microorganisms. Also, the stipulation of dilute suspension confirms that the theory introduced for oxytactic microorganisms must hold [3, 4]. It must be noted that thermophoresis is the result of Brownian movement when a temperature gradient is applied and that when the Brownian movement of nanoparticles is correctly simulated, the thermophoresis coefficients may be derived [41, 42]. In the continuum description of the nanofluids, such as the current one, the phenomenological coefficients d_T and d_B may be considered as independent variables.

The mass transfer equation is [35]:

$$\left( {{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{V} }} \cdot \nabla \tilde{C} + \frac{{\partial \tilde{C}}}{{\partial \tilde{t}}}} \right) = \nabla \cdot \left[ {\frac{{d_{\text{T}} }}{{T_{1} }}\nabla \cdot \tilde{T} + d_{\text{B}} \nabla \cdot \tilde{C}} \right] - K_{\text{r}}^{2} \left( {\frac{T}{{T_{1} }}} \right)^{\text n} {\text e}^{{\left( {\frac{{ - {\text E}_{\text{a}} }}{\upkappa \text T}} \right)}} \left( {C - C_{1} } \right),$$

(5)

where $\left( {\frac{T}{{T_{1} }}} \right)^{\text n} \text{e}^{{\left( {\frac{{ - {\text E}_{\text{a}} }}{\upkappa \text T}} \right)}}$ is the Arrhenius function, $K_{\text{r}}^{2}$ the chemical reaction rate constant, $E_{\text{a}}$ the activation energy, $n \, \left( { - 1 < n < 1} \right)$ is a dimensionless exponent, and the Boltzmann constant is denoted by $k = \frac{8.61}{{10^{5} }} \,$ eV K⁻¹.

The conservation equation of microorganisms derived in the presence of oxytactic microorganisms is:

$$\frac{{\partial \tilde{n}}}{{\partial \tilde{t}}} = - \nabla \cdot {\varvec{\upchi}},$$

(6)

with

$${\varvec{\upchi}} = \tilde{n}{\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{V} }} + \tilde{n}\Xi - D_{\text{mo}} \nabla \cdot \tilde{n},$$

(7)

where $D_{\text{mo}}$ the diffusivity of microorganisms, ${\varvec{\upchi}}$ the flux of microorganisms because of the macroscopic fluid movement (the diffusion that results from all the random movement of microorganisms, and the directional swimming of the microorganisms up the oxygen gradients).

The average form of directional swimming velocity of a microorganism is:

$$\Xi = \overline{H} \left( {\tilde{C}} \right)\bar{b}W_{\text{mo}} \nabla \cdot \tilde{C},$$

(8)

where $\bar{b},W_{\text{mo}}$ are the chemotaxis constant and the maximal speed of cell swimming, ($\bar{b}W_{\text{mo}}$ is considered as a constant), and $\overline{H} \left( {\tilde{C}} \right)$ is the Heaviside step function which is deemed to be unity here.

The complete model for the flow is summarized as:

$$\frac{{\partial \tilde{v}}}{{\partial \tilde{y}}} = - \frac{{\partial \tilde{u}}}{{\partial \tilde{x}}},$$

(9)

$$\begin{aligned} & \rho_{f} \left( {\tilde{v}\frac{{\partial \tilde{u}}}{{\partial \tilde{y}}} + \tilde{u}\frac{{\partial \tilde{u}}}{{\partial \tilde{x}}}} \right) - \frac{{J_{0} M_{0} \pi }}{8}\exp \left( { - \frac{\pi }{a}\tilde{y}} \right) = \mu \frac{{\partial^{2} \tilde{u}}}{{\partial \tilde{y}^{2} }} \\ & \quad + \left[ { - \rho_{\text{f}} \left( {T - T_{1} } \right)\beta + \left( {C - C_{0} } \right)\left( {\rho_{\text{p}} - \rho_{\text{f}} } \right) + n\Delta \rho \Theta } \right]g, \\ \end{aligned}$$

(10)

$$\tilde{v}\frac{{\partial \tilde{T}}}{{\partial \tilde{y}}} = \frac{k}{{\left( {\rho c} \right)_{\text{f}} }}\frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{y}^{2} }} + \frac{\tau }{{T_{1} }}\frac{{\partial \tilde{T}}}{{\partial \tilde{y}}}\left[ {d_{\text{T}} \frac{{\partial \tilde{T}}}{{\partial \tilde{y}}} + T_{1} d_{\text{B}} \frac{{\partial \tilde{C}}}{{\partial \tilde{y}}}} \right] - \tilde{u}\frac{{\partial \tilde{T}}}{{\partial \tilde{x}}} + \frac{\mu }{{\left( {\rho c} \right)_{\text{f}} }}\left( {\frac{{\partial \tilde{u}}}{{\partial \tilde{y}}}} \right)^{2} ,$$

(11)

where $\tau = \frac{{\left( {\rho c} \right)_{\text{p}} }}{{\left( {\rho c} \right)_{\text{f}} }}.$

$$\tilde{v}\frac{{\partial \tilde{C}}}{{\partial \tilde{y}}} = \frac{{d_{T} }}{{T_{1} }}\frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{y}^{2} }} + d_{\text{B}} \frac{{\partial^{2} \tilde{C}}}{{\partial \tilde{y}^{2} }} - \tilde{u}\frac{{\partial \tilde{C}}}{{\partial \tilde{x}}} - K_{\text{r}}^{2} \left( {\frac{T}{{T_{1} }}} \right)^{n} \exp \left( {\frac{{ - E_{\text{a}} }}{\kappa T}} \right)\left( {C - C_{1} } \right),$$

(12)

$$\tilde{u}\frac{{\partial \tilde{n}}}{{\partial \tilde{x}}} + \tilde{v}\frac{{\partial \tilde{n}}}{{\partial \tilde{y}}} = D_{\text{mo}} \frac{{\partial^{2} \tilde{n}}}{{\partial \tilde{y}^{2} }} - \frac{{\bar{b}W_{\text{mo}} }}{{C_{\text{w}} - C_{1} }}\left[ {\frac{\partial }{{\partial \tilde{y}}}\left( {\tilde{n}\frac{{\partial \tilde{C}}}{{\partial \tilde{y}}}} \right)} \right].$$

(13)

The boundary conditions are:

$$\tilde{n} = \tilde{n}_{\text{w}} ,\quad \tilde{T} = \tilde{T}_{\text{w}} ,\quad \tilde{v} = \tilde{v}_{\text{w}} ,\quad \tilde{C} = \tilde{C}_{\text{w}} ,\quad \tilde{u} = \tilde{u}_{\text{w}} ,\quad {\text{at}}\; \, \tilde{y} = 0,$$

(14)

$$\tilde{n} \to \tilde{n}_{1} ,\quad \tilde{u} \to 0,\quad \tilde{C} \to \tilde{C}_{1} ,\quad \tilde{T} \to \tilde{T}_{1} ,\quad {\text{ at}}\; \, \tilde{y} \to \infty ,$$

(15)

The set of equations may be rendered non-dimensional using the following parameters:

$$\left( \begin{aligned} & u = \frac{{\tilde{u}}}{{\tilde{u}_{\text{w}} }},\quad l = \frac{{\tilde{u}_{\text{w}} L^{2} }}{\nu },\quad v = \frac{{\tilde{v}}}{{\tilde{v}_{0} }},\quad y = \frac{{\tilde{y}}}{L},\quad \tilde{v}_{0} = \nu \frac{\pi }{a},\quad L = \frac{a}{\pi },\quad \phi = \left( {\tilde{C} - \tilde{C}_{1} } \right)\left( {\tilde{C}_{\text{w}} - \tilde{C}_{1} } \right)^{ - 1} ,\quad x = \frac{{\tilde{x}}}{l}, \\ & \Phi = \frac{{\tilde{n} - \tilde{n}_{1} }}{{\tilde{n}_{\text{w}} - \tilde{n}_{1} }},\quad \theta = \frac{{\tilde{T} - \tilde{T}_{1} }}{{\tilde{T}_{\text{w}} - \tilde{T}_{1} }}, \\ \end{aligned} \right.$$

(16)

Applying Eq. (16) into Eqs. (10–15), we obtain

$$u\frac{\partial u}{\partial x} = \frac{{\partial^{2} u}}{{\partial y^{2} }} - v\frac{\partial u}{\partial y} - R_{\text{a}} \theta + R_{\text{n}} \Phi + R_{\text{b}} \phi + H_{\text{m}} e^{ - \text y} ,$$

(17)

$$u\frac{\partial \theta }{\partial x} = N_{\text{b}} \frac{\partial \theta }{\partial y}\left( {\frac{\partial \phi }{\partial y} - \frac{v}{{N_{\text{b}} }} + \frac{{N_{\text{t}} }}{{N_{\text{b}} }}\frac{\partial \theta }{\partial y}} \right) + \frac{1}{{P_{\text{r}} }}\frac{{\partial^{2} \theta }}{{\partial y^{2} }} + E_{\text{k}} \left( {\frac{\partial u}{\partial y}} \right)^{2} ,$$

(18)

$$u\frac{\partial \phi }{\partial x} = \frac{1}{{S_{\text{c}} }}\frac{{\partial^{2} \phi }}{{\partial y^{2} }} - v\frac{\partial \phi }{\partial y} + \frac{{N_{\text{b}} }}{{S_{\text{c}} N_{\text{t}} }}\frac{{\partial^{2} \theta }}{{\partial y^{2} }} - \omega \left( {\theta \Gamma + 1} \right)^{\text n} \phi e^{{\frac{ - \text A}{{\left( {1 + \Gamma \uptheta } \right)}}}} ,$$

(19)

$$S_{\text{b}} v\frac{\partial \Phi }{\partial y} + P_{\text{e}} \left[ {\frac{\partial \Phi }{\partial y}\frac{\partial \phi }{\partial y} + \left( {\Phi + \eta } \right)\frac{{\partial^{2} \phi }}{{\partial y^{2} }}} \right] = \frac{{\partial^{2} \Phi }}{{\partial y^{2} }},$$

(20)

In the above equations,

$$\left( \begin{aligned} & R_{\text{a}} = \frac{{\beta \left( {T_{\text{w}} - T_{1} } \right)gl}}{{u_{\text{w}} }},\quad R_{\text{n}} = \frac{{\left[ {\left( {\rho_{\text{p}} - \rho_{\text{f}} } \right)\left( {C_{\text{w}} - C_{1} } \right)} \right]gl}}{{\rho_{\text{f}} u_{\text{w}} }},\quad \Gamma = \frac{{\left( {T_{\text{w}} - T_{1} } \right)}}{{T_{1} }}, \\ & R_{\text{b}} = \frac{{n\Theta \left( {n_{\text{w}} - n_{\infty } } \right)gl}}{{\rho_{\text{f}} u_{\text{w}} }},\quad H_{\text{m}} = \frac{{j_{0} M_{0} a^{2} }}{{8\rho_{\text{f}} \pi u_{\text{w}} \upsilon }},\quad N_{\text{b}} = \frac{{d_{\text{B}} \tau \Delta T}}{{\upsilon T_{1} }},\quad A = \frac{{ - E_{\text{a}} }}{\kappa T}, \\ & \alpha = \frac{\gamma \Delta nl}{{\Delta Ou_{\text{w}} }},\quad N_{\text{t}} = \frac{{d_{\text{T}} \tau \Delta \phi }}{\upsilon },\quad S_{\text{c}} = \frac{\upsilon }{{d_{\text{B}} }},\quad S_{\text{b}} = \frac{\upsilon }{{D_{\text{mo}} }},\quad \eta = \frac{{n_{1} }}{{n_{\text{w}} - n_{1} }}, \\ & P_{\text{e}} = \frac{{\bar{b}W_{\text{mo}} }}{{D_{\text{mo}} }},\quad P_{\text{r}} = \frac{\upsilon }{{\bar{\alpha }}},\quad \bar{\alpha } = \frac{k}{{\left( {\rho c} \right)_{\text{f}} }},\quad E_{\text{k}} = \frac{{u_{\text{w}}^{2} }}{{c_{\text{f}} \left( {C_{\text{w}} - C_{1} } \right)}},\quad \omega = \frac{{K_{\text{r}}^{2} L^{2} }}{\upsilon }. \\ \end{aligned} \right.$$

(21)

that the symbols in the above equations are as follows: $A$ the activation energy, R_m the basic-density Rayleigh number, $\omega$ the chemical reaction parameter, $\Gamma$ the temperature difference, E_k the Eckert number, R_b the bioconvection Rayleigh number, R_a the thermal Rayleigh number, H_m describes the balance between the viscous and electromagnetic forces, S_c the Schmidt number, R_n the nanoparticle concentration number, N_b the Brownian motion parameter, P_e the Peclet number, R_d the radiation parameter, N_t the thermophoresis parameter, S_b the bioconvection Schmidt number, traditional Lewis number is denoted by L_b, and P_r the Prandtl number.

The dimensionless boundary conditions are:

$$\left( \begin{aligned} & u = 1,\;\theta = 1,\;\phi = 1,\;v = v_{w} ,\;\Phi = 1,\quad {\text{at}}\;y = 0, \\ & \phi \to 0,\;\theta \to 0,\;u \to 0,\;\Phi \to 0,\quad {\text{at}}\; \, y \to \infty . \\ \end{aligned} \right.$$

(22)

The flow between the plates is considered as fully developed, which means that the horizontal velocity depends on $y$ only. Under the approximation of suction/injection, the resulting equations after invoking $v = v_{\text{w}}$ read as

$$v_{\text{w}} \frac{\partial u}{\partial y} = \frac{{\partial^{2} u}}{{\partial y^{2} }} - R_{\text{a}} \theta + R_{\text{n}} \Phi + R_{\text{b}} \phi + H_{\text{m}} e^{ - \text y} ,$$

(23)

$$N_{\text{b}} \frac{\partial \theta }{\partial y}\left[ {\frac{\partial \phi }{\partial y} - \frac{{v_{\text{w}} }}{{N_{\text{b}} }} + \frac{{N_{\text{t}} }}{{N_{\text{b}} }}\frac{\partial \theta }{\partial y}} \right] + \Omega \frac{{\partial^{2} \theta }}{{\partial y^{2} }} + E_{\text{k}} \left( {\frac{\partial u}{\partial y}} \right)^{2} = 0,$$

(24)

$$\frac{1}{{S_{\text{c}} }}\frac{{\partial^{2} \phi }}{{\partial y^{2} }} - v_{\text{w}} \frac{\partial \phi }{\partial y} + \frac{{N_{\text{b}} }}{{S_{\text{c}} N_{\text{t}} }}\frac{{\partial^{2} \theta }}{{\partial y^{2} }} - \left( {\theta \Gamma + 1} \right)^{\text n} \omega \phi e^{{\frac{\text A}{{\left( {1 + \Gamma \uptheta } \right)}}}} = 0,$$

(25)

$$S_{\text{b}} v_{\text{w}} \frac{\partial \Phi }{\partial y} + P_{\text{e}} \left( {\frac{\partial \Phi }{\partial y}\frac{\partial \phi }{\partial y} + \left\{ {\Phi + \eta } \right\}\frac{{\partial^{2} \phi }}{{\partial y^{2} }}} \right) = \frac{{\partial^{2} \Phi }}{{\partial y^{2} }}.$$

(26)

Numerical solutions

Equations (23) through (26) are nonlinear, and exact solutions for them are impossible to obtain. For this reason, we employ a shooting scheme, which is efficient and provides accurate results. We have used the computational software Mathematica (10.3v) to solve the equations. Initially, we reduce the formulated equations into first-order equations and obtain the following forms:

$$\left( \begin{aligned} & \frac{\partial u}{\partial y} = \beta_{1} , \\ &\frac{{\partial \beta_{1} }}{\partial y} = v_{\text{w}} D_{1} + R_{\text{a}} \theta - R_{\text{n}} \Phi - R_{\text{b}} \phi - H_{\text{m}} e^{ - \text y} , \\ \end{aligned} \right.$$

(27)

$$\left( \begin{aligned} & \frac{\partial \theta }{\partial y} = \beta_{2} , \\ & v_{\text{w}} \beta_{2} = \frac{1}{{P_{\text{r}} }}\frac{{\partial \beta_{2} }}{\partial y} + N_{\text{b}} \beta_{2} \beta_{3} + N_{\text{t}} \beta_{2}^{2} + E_{\text{k}} \beta_{1}^{2} , \\ \end{aligned} \right.$$

(28)

$$\left( \begin{aligned} & \frac{\partial \phi }{\partial y} = \beta_{3} , \\ & v_{\text{w}} \beta_{3} = \frac{1}{{S_{\text{c}} }}\frac{{\partial \beta_{3} }}{\partial y} + \frac{{N_{\text{b}} }}{{S_{\text{c}} N_{t} }}\frac{{\partial \beta_{2} }}{\partial y} - \omega \left( {1 + \Gamma \theta } \right)^{n} \phi e^{{\frac{A}{{\left( {1 + \Gamma \theta } \right)}}}} , \\ \end{aligned} \right.$$

(29)

$$\left( \begin{aligned} & \frac{\partial \Phi }{\partial y} = \beta_{4} , \\ & S_{\text{b}} v_{\text{w}} \beta_{4} + P_{\text{e}} \left( {\beta_{3} \beta_{4} + \left\{ {\Phi + \eta } \right\}\frac{{\partial \beta_{3} }}{\partial y}} \right) = \frac{{\partial \beta_{4} }}{\partial y}, \\ \end{aligned} \right.$$

(30)

and the boundary conditions become

$$u = 1,\;\beta_{1} = \alpha_{1} ,\;\theta = 1,\;\beta_{2} = \alpha_{2} ,\;\phi = 1,\;\beta_{3} = \alpha_{3} ,\;\Phi = 1,\;\beta_{4} = \alpha_{4} ,\quad {\text{as}}\;y = 0.$$

(31)

For the present flow, the suction velocity is assumed to be $v_{\text{w}} = - \ell , \, \ell > 0$. An appropriate numerical initial guess is selected $\alpha_{\text{j}} \, \left( {j = 1, \ldots ,4} \right)$ for the computations.

The dimensionless quantities of interest used for the engineering applications are:

$${\text{Nu}}_{\text{x}} = - \theta (0),\quad {\text{Sh}}_{\text{x}} = - \phi (0),\quad {\text{Nn}}_{\text{x}} = - \Phi (0).$$

(32)

where ${\text{Nu}}_{\text{x}}$ the Nusselt number, ${\text{Sh}}_{\text{x}}$ the Sherwood number, and ${\text{Nn}}_{\text{x}}$ the motile density number.

Results and discussion

The following figures show graphically the effects the several parameters have in the problem at hand. Figure 1 shows the geometrical structure of the flow over a Riga plate. Figures 2–4 depict the numerical results of the several parameters examined here on the Nusselt number, the motile density number, and the Sherwood number against all the governing parameters.

Fig. 2

Data analysis of the Nusselt number against various parameters

Fig. 3

Data analysis of the Sherwood number against various parameters

Fig. 4

Data analysis of the motile density number against various parameters

Figure 5 demonstrates the behavior of the magnetic parameter $H_{\text{m}}$ and bioconvection Rayleigh number $R_{\text{b}}$ on the velocity profile. It is noticed in this figure that, when the magnetic parameter is higher, the velocity increases. However, any negative values of the magnetic parameter oppose the flow and reduce the velocity. One may also see that the bioconvection Rayleigh number also increases the velocity profile. Figure 6 demonstrates that the nanoparticle concentration number has a greater effect on the velocity than the thermal Rayleigh number. A strengthening the thermal Rayleigh number causes a decrease in the velocity profile, while the opposite happens for the nanoparticle concentration number.

Fig. 5

Velocity curves for several values of H_m. Solid line: $R_{\text{b}} = 0.1$, dashed line: $R_{\text{b}} = 0.4$

Fig. 6

Velocity curves for several values of $R_{\text{n}}$. Solid line: $R_{\text{a}} = 0.1$, dashed line: $R_{\text{a}} = 1.5$

Figure 7 demonstrates the temperature profile with the intention to determine the consequence of the thermophoresis parameter $N_{\text{t}}$ and the Prandtl number $P_{\text{r}}$. We can see that the temperature profile significantly increases for the higher numbers of the thermophoresis parameter. However, the temperature profile is reduced with the increase of the Prandtl number. Further, we notice that the momentum diffusivity is more supreme than the thermal diffusivity. It can be seen in Fig. 8 that the Brownian motion parameter $N_{\text{b}}$ and the Eckert number $E_{\text{k}}$ increase the temperature profile. Advection transport is more significant and outcomes in the intensification of the temperature profile at the higher values of Eckert number. On the other hand, the enhancement of Brownian motion causes the particles to move faster, and this creates a fuller temperature profile.

Fig. 7

Temperature distribution for several values of $N_{\text{t}}$. Solid line: $P_{\text{r}} = 6.8$, dashed line: $P_{\text{r}} = 8.0$

Fig. 8

Temperature distribution for several values of $N_{\text{b}}$. Solid line: $E_{\text{k}} = 0.1$, dashed line: $E_{\text{k}} = 0.2$

Figure 9 shows the effects of the variation of $N_{\text{b}}$ and $n$ on the concentration profile. We observe that the parameter $n$ does not produce a noticeable impact and that the Brownian motion suppresses the concentration profile. It follows from Fig. 10 that the chemical reaction parameter $\omega$ substantially strengthens the concentration profile. We can also see that the activation energy $A$ intensify the concentration profile. This type of analysis is helpful for various industrial processes in chemical engineering.

Fig. 9

Concentration distribution for several values of $N_{\text{b}}$. Solid line: $n = 0.9$, dashed line: $n = - 0.9$

Fig. 10

Concentration distribution for several values of $\omega$. Solid line: $A = 1$, dashed line: $A = 2$

The six curves of Fig. 11 show that the Schmidt number S_c reduces the concentration profile but the thermophoresis parameter increases the concentration. Figure 12 shows the effect of bioconvection Schmidt number S_b and the Peclet number P_e on the motile microorganism profile. It is noticed that both parameters strongly decrease the motile microorganism profile. This happens because the advection transport rate is more dominant than the diffusive transport rate.

Fig. 11

Concentration distribution for several values of $N_{\text{t}}$. Solid line: $S_{\text{c}} = 0.5$, dashed line: $S_{\text{c}} = 1$

Fig. 12

Motile microorganism density profile for several values of $P_{\text{e}}$. Solid line: $S_{\text{b}} = 0.3$, dashed line: $S_{\text{b}} = 0.4$

Conclusions

We have performed calculations for the effect of the Arrhenius activation energy on the thermo-bioconvection nanofluid flow over a Riga plate with a magnetic field. The Riga plate is filled with a nanofluid containing microorganisms suspended in the base fluid. The fluid is electrically conducting with a varying Lorentz force parallel to it. The formulated equations are examined numerically by employing the shooting technique. The main observations are summarized as:

• 1. The velocity profile strengthens with the increase of the bioconvection Rayleigh number and magnetic field, while it mitigates when the magnetic field decreases.

• 2. The nanoparticle concentration number suppresses the velocity profile while the thermal Rayleigh number enhances it.

• 3. Both the Eckert number and the Brownian motion parameter enhance the temperature profile, whereas the Prandtl number has an opposite effect.

• 4. The thermophoresis parameter enhances both the temperature and concentration profiles.

• 5. The activation energy boosts the concentration profile, whereas the chemical reaction parameter decreased it.

• 6. The bioconvection Schmidt and the Peclet number significantly oppose the microorganism concentration profile.

It must be noted that any non-Newtonian behavior of the fluid model has been ignored.