1 Introduction

During the recent decades, the study of mass and heat transfer on nanofluid flow past a stretching plate has grabbed the attention of many investigators due to applications of nanofluids in industries such as, compact heat exchangers, production of plastic sheets, transportation, the design of nuclear reactors, electronics, cooling of metallic plates, etc. Adequate cooling methods are required for cooling high energy devices. Some conventional heat transfer fluids such as ethylene glycol, water, engine oil, etc. have poor and limited heat transfer capability because of their very bad heat transfer characteristics. Various investigators made great efforts to break this limit by suspending small-sized particles (millimeter or micrometer) in base fluids. These particles are known as nanoparticles, which are of different materials such as metals, oxides, non-metals, etc. The involvement of nanoparticles can improve heat transfer and thermal conductivity performances. The fantastic features of nanofluids are helpful in different applications which need active and quick heat transfer. Moreover, it is also found that the suspension of nanoparticles in a water-cooled nuclear system tends to improve the safety margins significantly and creates a substantial economic gain [1]. A few more applications of nanofluid involve chillers, diesel-electric generator, the coolant of machining, and in different industrial process [2]. Further, the utilisation of nanofluid in heat pipes markedly enhances the rate of heat transfer by reducing heat resistance [3].

Mass and heat transfer with thermo-diffusion and diffusion-thermo have much applications in applied physics and engineering, i.e. chemical engineering, geothermal insulation, and drying technology. Thermo-diffusion and diffusion-thermo play significant roles in the proximity of a flow regime. The inverse mechanism is called Dufour effect, and this influence becomes more critical in the vicinity of density differences in a flow regime. Soret and Dufour effects have significant importance in a combined process of flow through a binary system which can be observed in chemical engineering. These effects also have a remarkable influence when different species are imported at stretching plate / surface having less density than that of the encircling fluid. Various researchers investigated the Dufour and Soret effect with mass and heat transfer on nanofluid flow over a stretching plate. For instance, Akbar et al [4] explored the Williamson nanofluid numerically through an asymmetric channel. Nadeem et al [5] presented optimised solutions for Casson nanofluid with various surface conditions. Rashidi et al [6] analysed the nanofluid dynamics through a nonlinear permeable surface with transpiration and presented the analytic solution utilising homotopy analysis method. Sheikholeslami et al [7] presented the simultaneous impact of thermophoresis and Brownian motion on a steady stream of nanofluid through parallel plates. Hayat et al [8, 9] addressed the stagnation point flow of non-Newtonian Jeffrey fluid model with combined effects of convective boundary conditions and magnetohydrodynamics (MHD). Mohyud-Din et al [10] analysed the consequences of mass and heat transfer on nanofluid flow through parallel plates. Khan et al [11] examined the tridimensional nanofluid flow. Mustafa et al [12] studied numerically and analytically the nanofluid flow through a nonlinearly stretching sheet. Hayat et al [13] explored the power-law nanofluid model with convection boundary through a vertical stretching sheet. Bhatti et al [14] numerically studied the flow of nanofluid past a porous shrinking plate. Bhatti and Rashidi [15] analysed the combined impact of radiation and Soret effect on the flow through a stretching / shrinking porous sheet with non-Newtonian (Williamson) nanofluid.

MHD nanofluid has significant importance in an extensive temperature process and has numerous applications in geothermal engineering, underground nuclear wastes disposal, space technology, etc. Moreover, they are also useful in cancer therapy, magnetic resonance imaging, removal of the blockage in the artery, hyperthermia, magnetic drug targeting, wound treatment, etc. Magnetic nanofluids, also known as ferrofluids, consist of a mixture of ferromagnetic particles having 10 nm diameter in a base fluid. Such types of fluids depict innovative characteristics on exposure to a magnetic field [16, 17]. In biomedical science such as in the treatment of cancer, small particles (made up of iron) are suspended in the blood, which is helpful to transport radiations and drugs using an external magnetic field. MHD and thermal radiation effects of nanofluid with convective boundary conditions through a stretching sheet were analysed by Akbar et al [18]. Sheikholeslami et al [19] numerically considered the impact of MHD with viscous dissipation and heat transfer on nanofluid flow. Sheikholeslami and Abelman [20] presented a simulation on the two-phase flow of nanofluid through an annulus under an axial magnetic field. Sheikholeslami and Ellahi [21] addressed the natural convection on three-dimensional (3D) mesoscopic simulation of MHD nanofluid flow. The MHD effects on the nanofluid flow and hydrothermal behaviour between collateral plates have been analysed analytically by Sheikholeslami et al [22]. MHD nanofluid flow with natural convection with multiwalled and single CNTs added in salt water solution were presented by Ellahi et al [23]. Free convective MHD flow of the nanofluids have been investigated by Zeeshan et al [24]. Qing et al [25] explored the concurrent impact of entropy on MHD Casson nanofluid through a porous sheet. Bhatti et al [26] studied the Eyring–Powell nanofluid past a permeable stretching surface and also analysed the entropy generation with MHD. Some of the important studies on our present subject are available in refs [27,28,29,30,31] and several other studies.

The study of chemical reaction on mass and heat transfer has become substantial due to its growing need in hydrometallurgical industries. Various transport procedures exist which are regulated by a simultaneous process of buoyancy force due to the combined mass and thermal diffusion with chemical reaction effect. This phenomenon can also be found in solar collectors, chemical engineering, nuclear combustion systems, and nuclear reactor safety. The chemical reaction is categorised as either heterogeneous or homogenous. Both the responses mainly rely on whether they originated in a single-phase volume reaction or in an interface. The heterogeneous reaction occurs within the boundary of the phase or in a restricted region while the homogenous reaction appears uniformly along with the phase. In different engineering processes, chemical reaction plays a vital role. Such processes arise in various industrial applications such as the production of glassware or ceramics, manufacturing of polymers, food processing, etc. Therefore, numerical applications of chemical reactions with mass and heat transfer are given significant importance in hydrometallurgical and chemical industries. Kameswaran et al [32] analysed the effects of chemical reaction and viscous dissipation on hydromagnetic nanofluid flow through a shrinking / stretching surface. El-Aziz [33] inspected the stagnation point flow of nanofluid in the presense of chemical reaction with heat transfer flow through a stretching sheet. Zhang et al [34] considered the combined effects of radiation, chemical reaction with MHD, and variable surface heat flux on nanofluid flow past a porous surface. Pal and Mandal [35] addressed the impact of chemical reaction, mixed convection with thermal radiation on a stagnation point nanofluid flow through a porous shrinking / stretching plate. Reddy and Shankar [36] explored the stagnation point flow of MHD nanofluid under the effects of chemical reaction towards an exponentially stretching surface. Ramesh et al [37] considered the influence of MHD Maxwell flow of nanofluid with thermal radiation and chemical reaction. The studies on heat and mass transfer of nanofluids with chemical reaction are available in refs [38,39,40,41,42].

The study of convective boundary conditions flow through a porous surface has been analysed theoretically and experimentally due to its wide applications in fields such as petroleum processing, solid matrix, transpiration cooling, microporous heat exchangers, chemical and catalytic particle beds, geothermal engineering, heat transfer enhancement, and microthrusters. Freidoonimehr et al [43] investigated the 3D nanofluid flow through a rotating channel having porous walls and presented the analytical solutions. Kameswaran et al [44] considered the combined effects of heterogeneous–homogeneous reactions on the nanofluid flow towards a permeable stretching sheet. Rosmila et al [45] presented the Lie symmetric group transformation of MHD nanofluid flow with thermal stratification through linearly porous stretching walls. Sheikholeslami et al [46] explored the heat transfer on copper–water nanofluid through a permeable stretching surface in a rotating system. Malvandi et al [47] analytically analysed the stagnation point flow with heat transfer on the nanofluid flow towards a stretching porous sheet. Combined effects of MHD and thermal radiation for the stagnation point nanofluid flow through a permeable stretching surface was presented by Reddy et al [48]. Pal et al [49] considered the influence of non-uniform heat source / sink on the stagnation point nanofluid flow towards a porous shrinking / stretching sheet. Shaw et al [50] addressed the heterogeneous and homogeneous reactions with dual solutions for stagnation point nanofluid flow through a non-Darcy porous medium.

The main purpose of our present study is to explore the impact of diffusion-thermo and thermo-diffusion on hyperbolic tangent nanofluid with magnetic field through a nonlinear porous stretching sheet. Simultaneous effects of Hall current and chemical reaction are also considered in our present analysis. The behaviour of thermal slip condition is also observed. Formulation of the problem is done using similarity transformation variables. Runge–Kutta–Merson method and shooting method are used to obtain solutions of the nonlinear differential equations using the computational software MATLAB. A numerical comparison is also presented with previously published data [51,52,53,54] for the power-law exponent and Prandtl number. The impact of all the significant parameters is shown using graphs and tables. The novelty of the current work is the simultaneous inclusion of Soret and Dufour effects, and wall slip, which is known to have a significant influence in magnetic materials processing [55, 56]. The Dufour effect relates to the energy flux due to a species concentration gradient occurring and is the reverse phenomenon to the Soret effect. Both effects exert some influence on heat, mass, and momentum characteristics in sheet processing, as elaborated in due course. The current investigation constitutes a novel contribution to the scientific literature on nanomaterial fabrication process simulation.

2 Mathematical formulation

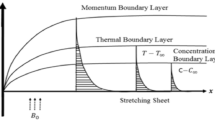
Consider a hyperbolic tangent nanofluid flow through a stretching sheet at the stagnation point \({{\bar{y}}}=0\). An extrinsic magnetic field \(B_0 \) is activated while due to very less magnetic Reynolds number the induced magnetic field is ignored (see figure 1). Cartesian coordinate system is considered in which x- and y-axes are considered along horizontal and vertical directions, respectively. \({{\tilde{C}}}_w \) and \({{\tilde{T}}}_{w}\) are the nanoparticle concentration and temperature at the surface and \({{\tilde{C}}}_{\infty }\) and \({{\tilde{T}}} _{\infty }\) are at infinity. The non-Newtonian hyperbolic tangent fluid model reads [57] as

$$\begin{aligned} {\bar{\mathbf{S}}}=-[ {\eta _\infty +( {\eta _0 +\eta _\infty } )\tanh ( {{\Gamma }{\bar{{\dot{\gamma }}}} } )^{n}} ], \end{aligned}$$
(1)

For the present case, we have considered \({\Gamma }\bar{{\dot{\gamma }}}<1\) and \(\eta _\infty =0\). Therefore, eq. (1) takes the following form:

$$\begin{aligned} {\bar{\mathbf{S}}}=\eta _0[ 1+n( {\Gamma }{{\bar{{\dot{\gamma }}}}}-1 ) ]{\dot{\gamma }}. \end{aligned}$$
(2)
Fig. 1
figure 1

Structure for the flow.

Full size image

The governing equation of continuity reads as

$$\begin{aligned} \frac{\partial {{\tilde{v}}}}{\partial {{\bar{y}}}}+\frac{\partial {{\tilde{u}}}}{\partial {{\bar{x}}}}=0. \end{aligned}$$
(3)

In view of eq. (2), the momentum equation in the presence of magnetic field and porosity reads as

$$\begin{aligned} {{\tilde{u}}}\frac{{\partial {{\tilde{u}}}}}{{\partial {{\bar{x}}}}} + \tilde{v}\frac{{\partial {{\tilde{v}}}}}{{\partial {{\bar{y}}}}}= & {} \frac{{{\mu _{nf}}}}{{{\rho _{nf}}}}\left( {1 - n} \right) \frac{{{\partial ^2}{{\tilde{u}}}}}{{\partial {{{{\bar{y}}}}^2}}} + 2{{\Gamma }}n\frac{{{\mu _{nf}}}}{{{\rho _{nf}}}}\frac{{{\partial ^2}{{\tilde{u}}}}}{{\partial {{{{\bar{y}}}}^2}}}\frac{{\partial {{\tilde{u}}}}}{{\partial {{\bar{y}}}}} \nonumber \\&- \frac{{{\mu _{nf}}}}{{{\rho _{nf}}{{\bar{k}}}}}{{\tilde{u}}} + {{\bar{\mathbf{J}}}} \times {\bar{\mathbf{B}}} - \frac{{{\nu _{nf}}}}{{{{\bar{k}}}}}\tilde{u}\nonumber \\&+ \frac{{{{\left( {\rho {\beta _{{{\tilde{T}}}}}} \right) }_{nf}}}}{{{{( {{{\tilde{T}}} - {{{{\tilde{T}}}}_\infty }} )}^{ - 1}}{\rho _{nf}}}}g \nonumber \\&+ \frac{{{{( {\rho {\beta _{{{\tilde{C}}}}}} )}_{nf}}}}{{{{( {{{\tilde{C}}} - {{\tilde{C}}_\infty }} )}^{ - 1}}{\rho _{nf}}}}g. \end{aligned}$$
(4)

The results for Newtonian fluid can be achieved by \(n=0\) in the above equation. The detailed expression of the generalised Ohm’s law \({\bar{\mathbf{J}}}\times {\bar{\mathbf{B}}}\) can be found from ref. [58]. The energy equation takes the following form:

$$\begin{aligned} {{\tilde{u}}}\frac{{\partial {{\tilde{T}}}}}{{\partial {{\bar{x}}}}} + \tilde{v}\frac{{\partial {{\tilde{T}}}}}{{\partial {{\bar{y}}}}} = \frac{{{D_m}{K_{{{\tilde{T}}}}}}}{{{c_s}{c_p}}}\frac{{{\partial ^2}\tilde{C}}}{{\partial {{{{\bar{y}}}}^2}}} + {{\bar{\alpha }}} \frac{{{\partial ^2}{{\tilde{T}}}}}{{\partial {{{{\bar{y}}}}^2}}}, \end{aligned}$$
(5)

The nanoparticle concentration equation under the influence of chemical reaction reads as

$$\begin{aligned} {{\tilde{u}}}\frac{{\partial {{\tilde{C}}}}}{{\partial {{\bar{x}}}}} + \tilde{v}\frac{{\partial {{\tilde{C}}}}}{{\partial {{\bar{y}}}}}= & {} \frac{{{D_m}{K_{{{\tilde{T}}}}}}}{{{{{{\tilde{T}}}}_m}}}\frac{{{\partial ^2}{{\tilde{C}}}}}{{\partial {{{{\bar{y}}}}^2}}} \nonumber \\&+ {D_m}\frac{{{\partial ^2}{{\tilde{T}}}}}{{\partial {{{{\bar{y}}}}^2}}} - {k_1}( {{{{{\tilde{C}}}}_w} - {{{{\tilde{C}}}}_\infty }} ). \end{aligned}$$
(6)

Their respective boundary conditions become

$$\begin{aligned}&\left. \begin{array}{l}\displaystyle {{\tilde{u}}} = {u_w}\left( {{{\bar{x}}}} \right) = \pm {C_1}{{\bar{x}}^{2m}}\\ \displaystyle {{\tilde{T}}} = {{{{\tilde{T}}}}_w} = {{{{\tilde{T}}}}_\infty } + {C_2}{{{{\bar{x}}}}^{2m - 1}} + k'\frac{{\partial {{\tilde{T}}}}}{{\partial {{\bar{y}}}}}\\ \displaystyle {{\tilde{v}}} = {{{{\tilde{v}}}}_w},\quad {{\tilde{C}}} = {{{{\tilde{C}}}}_w} = {{{{\tilde{C}}}}_\infty } + {C_3}{{{{\bar{x}}}}^{2m - 1}} \end{array}\right| _{{{\bar{y}}} = 0}, \end{aligned}$$
(7)
$$\begin{aligned}&{\left. {{{\tilde{C}}} = {{{{\tilde{C}}}}_\infty },\quad {{\tilde{T}}} = {{\tilde{T}}_\infty },\quad {{\tilde{u}}} \rightarrow 0} \right| _{{{\bar{y}}} \rightarrow \infty }}. \end{aligned}$$
(8)

In eq. (7), \(+\) sign represents the stretching surface and −sign represents the shrinking surface.

However, for the present study we only considered the case of stretching surface.

The steam functions are given as follows:

$$\begin{aligned} {{\tilde{u}}} = \frac{{\partial {{\bar{\varphi }}} }}{{\partial \bar{y}}},\quad ~{{\tilde{v}}} = - \frac{{\partial {{\bar{\varphi }}} }}{{\partial \bar{x}}}. \end{aligned}$$
(9)

The similarity transformation variables are described as

$$\begin{aligned} \zeta= & {} \sqrt{\frac{{\left( {m + 1} \right) {{{{\bar{y}}}}^2}{u_w}\left( {{{\bar{x}}}} \right) }}{{2{\nu _f}{{\bar{x}}}}}} ,\quad {{\bar{\varphi }}} = \sqrt{\frac{{2{{\bar{x}}}{\nu _f}{u_w}\left( {{{\bar{x}}}} \right) }}{{\left( {m + 1} \right) }}~} F, \nonumber \\ \theta= & {} \frac{{{{\tilde{T}}} - {{{{\tilde{T}}}}_\infty }~}}{{{{{{\tilde{T}}}}_w} - {{{{\tilde{T}}}}_\infty }}},\quad ~{{\Phi }} = \frac{{{{\tilde{C}}} - {{{{\tilde{C}}}}_\infty }}}{{{{{{\tilde{C}}}}_w} - {{\tilde{C}}_\infty }}}. \end{aligned}$$
(10)

Using eqs (3)–(8), we get

$$\begin{aligned}&\left( {1 - n} \right) F''' - \frac{{2m}}{{\left( {m + 1} \right) }}{F'^2} + n\text {We}F'''F'' - \frac{M}{{1 + m_e^2~}}F' \nonumber \\&\quad - kF' + \frac{2}{{m + 1}}{\text {Ri}}\left( {\theta + \eta {\Phi }} \right) + F''F = 0, \end{aligned}$$
(11)
$$\begin{aligned}&\frac{1}{{{\text {Pr}}}}\theta '' + \frac{{2\left( {1 - 2m} \right) }}{{\left( {m + 1} \right) }}\theta F' + \theta 'F = - {\text {Du}}{\Phi ''}, \end{aligned}$$
(12)
$$\begin{aligned}&\frac{1}{{{\text {Sc}}}}{{\Phi ''}} + \frac{{2\left( {1 - 2m} \right) }}{{\left( {m + 1} \right) }}{{\Phi }}F' + F{{\Phi '}} = - {\text {Sr}}\theta '' + \gamma {{\Phi }}.\nonumber \\ \end{aligned}$$
(13)

Their associated boundary conditions are

$$\begin{aligned}&F\left( 0 \right) =s,\quad {\Phi }\left( 0 \right) =1, \end{aligned}$$
(14)
$$\begin{aligned}&F'\left( 0 \right) = \pm 1, \quad \theta \left( 0 \right) = 1 + \xi \theta '\left( 0 \right) ,~ \end{aligned}$$
(15)
$$\begin{aligned}&{F}'\left( \infty \right) =0,\quad {\Phi }\left( \infty \right) =0,\quad \theta \left( \infty \right) =0. \end{aligned}$$
(16)

It is worth mentioning that eq. (11) can be reduced for a Newtonian fluid by taking \(n=0\). The physical quantities such as Sherwood number \((\mathrm{Sh}_r)\), Nusselt number \((\mathrm{Nu}_r)\) and skin friction coefficient \((C_F)\) can be described in dimensionless form as [26, 27]

$$\begin{aligned}&{C_F} = \left[ {\left( {1 - n} \right) F^{\prime \prime }\left( 0 \right) + \frac{n}{2}\text {We}{F^{\prime \prime 2}}\left( 0 \right) } \right] ,~\nonumber \\&\mathrm{Nu}_{r} = ~ -\theta '\left( 0 \right) ,~\mathrm{Sh}_{r} = - {{\Phi '}}\left( 0 \right) . \end{aligned}$$
(17)

The other parameters are

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle {\text {Du}} = \frac{{{D_m}{K_{{{\tilde{T}}}}}}}{{{\nu _f}{c_s}{c_p}}}\left( {\frac{{{{{{\tilde{C}}}}_w} - {{{{\tilde{C}}}}_\infty }}}{{{{{{\tilde{T}}}}_w} - {{{{\tilde{T}}}}_\infty }}}} \right) ,\quad {\text {Sr}} = \frac{{{D_m}{K_{{{\tilde{T}}}}}}}{{{{{{\tilde{T}}}}_m}{\nu _f}}},\\ \displaystyle \eta = \frac{{{{\left( {\rho {\beta _{{{\tilde{C}}}}}} \right) }_{nf}}}}{{{{\left( {\rho {\beta _{{{\tilde{T}}}}}} \right) }_{nf}}}}\left( {\frac{{{{{{\tilde{C}}}}_w} - {{{{\tilde{C}}}}_\infty }}}{{{{{{\tilde{T}}}}_w} - {{{{\tilde{T}}}}_\infty }}}} \right) ,\\ \displaystyle {\text {Ri}} = \frac{{{{\bar{x}}}{{\left( {\rho {\beta _{{{\tilde{T}}}}}} \right) }_{nf}}}}{{{\rho _{nf}}{u_w}}}( {{{{{\tilde{T}}}}_w} - {{{{\tilde{T}}}}_\infty }} ),\quad s = - \frac{{{{{{\tilde{v}}}}_w}}}{{{{\left( {{C_1}{\nu _f}} \right) }^{{1}/{2}}}}},\\ \displaystyle \text {We} = \frac{{{{\Gamma }}u_w^{{3}/{2}}{{{{\bar{x}}}}^{{{(3m - 1)}}/{2}}}\sqrt{m + 1} }}{{\sqrt{{\nu _{nf}}} }},\\ \displaystyle {\mathrm{R}}{{\mathrm{e}}_x} = \frac{{{{{{\tilde{u}}}}_w}{{\bar{x}}}}}{\nu },\quad k = \frac{{2{\nu _{nf}}}}{{\left( {m + 1} \right) {{{{\bar{x}}}}^{ - 1}}{u_w}{{\bar{k}}}}},\quad {{\bar{\alpha }}} = \frac{{{k_f}}}{{\rho {c_p}}},\\ \displaystyle \xi = k'\sqrt{\frac{{\left( {m + 1} \right) {u_w}\left( {{{\bar{x}}}} \right) }}{{2{\nu _f}}}} ,\\ \displaystyle M = \sqrt{\frac{{2B_0^2\sigma }}{{{C_1}{\rho _{nf}}{u_w}{{{{\bar{x}}}}^{ - 1}}\left( {m + 1} \right) }}} ,\,{\text {Pr}} = \frac{{{\nu _f}}}{{{{{{\bar{\alpha }}} }_f}}},\,{\text {Sc}} = \frac{{{\nu _f}}}{{{D_m}}}. \end{array} \right. \end{aligned}$$
(18)

3 Solution methodology: Runge–Kutta–Merson method and shooting method

The Runge–Kutta–Merson numerical quadrature is a technique to solve the following equations:

$$\begin{aligned} \frac{{\mathrm{d}{{\bar{y}}}}}{{\mathrm{d}{{\bar{x}}}}} = F\left( {{{{{\bar{x}}}}_i},{{{{\bar{y}}}}_i}} \right) ,\quad {{\bar{y}}}\left( {{{{{\bar{x}}}}_i}} \right) = {{{\bar{y}}}_i}. \end{aligned}$$
(19)

It is known as RK45 because it consists of fourth-order together with five stages have been used with a combination of fifth-order technique and six steps that are utilised with all the points with the first. The stepping formulae are designed for nonlinear and linear problems [59, 60]. This approach has been successfully applied to various problems [59, 60]. The efficiency and stability of this technique are excellent, and it is highly adaptive, and it can adjust the location and quantity of the grid points during the iteration process. This technique has a process if a proper value of \({\tilde{h}}\) is selected. Two different approximations are determined and estimated at each step during the solution procedure. If the resulting solutions are in good agreement then we can proceed further, otherwise the value of \(\tilde{h}\) should be reduced to achieve accuracy. Therefore, the accuracy mainly depends upon the value. The comparison (see tables 2 and 3) shows that the present methodology has a higher rate of convergence compared to other techniques [62], and it is expected that it will have a good rate of convergence while presenting approximation solutions to lump solutions [61] and interaction solutions [62, 63] as well. In each step, the following values will be used to approximate the results:

$$\begin{aligned}&{\ell _1} = F\left( {{{{{\bar{x}}}}_i},{{{{\bar{y}}}}_i}} \right) , \end{aligned}$$
(20)
$$\begin{aligned}&{\ell _2} = F\left( {{{{{\bar{x}}}}_i} + \frac{1}{4}{{\tilde{h}}},{{{{\bar{y}}}}_i} + \frac{1}{4}{\ell _1}{{\tilde{h}}}} \right) , \end{aligned}$$
(21)
$$\begin{aligned}&{\ell _3} = F\left( {{{{{\bar{x}}}}_i} + \frac{3}{8}{{\tilde{h}}},{{{{\bar{y}}}}_i} + \left( {\frac{3}{{32}}{\ell _1} + \frac{9}{{32}}{\ell _2}} \right) {{\tilde{h}}}} \right) , \end{aligned}$$
(22)
$$\begin{aligned}&{\ell _4} = F\left( {{{{\bar{x}}}}_i} + \frac{{12}}{{13}}{{\tilde{h}}},{{\bar{y}}_i} + \left( \frac{{1932}}{{2197}}{\ell _1}\right. \right. \nonumber \\&\quad \qquad \left. \left. - \frac{{7200}}{{2197}}{\ell _2} + \frac{{7296}}{{2197}}{\ell _3} \right) {{\tilde{h}}} \right) , \end{aligned}$$
(23)
$$\begin{aligned}&{\ell _5} = F\left( {{{{\bar{x}}}}_i} + {{\tilde{h}}},{{{{\bar{y}}}}_i} + \left( \frac{{439}}{{216}}{k_0} - 8{\ell _2} \right. \right. \nonumber \\&\quad \qquad \left. \left. + \frac{{3860}}{{513}}{\ell _3} - \frac{{845}}{{4104}}{\ell _4} \right) {{\tilde{h}}} \right) , \end{aligned}$$
(24)
$$\begin{aligned}&{\ell _6} = F\left( {{{{\bar{x}}}}_i} + \frac{1}{2}{{\tilde{h}}},{{{{\bar{y}}}}_i} + \left( - \frac{8}{{27}}{\ell _1} + 2{\ell _2} \right. \right. \nonumber \\&\quad \qquad \left. \left. - \frac{{3544}}{{2565}}{\ell _3} + \frac{{1859}}{{4104}}{\ell _4} - \frac{{11}}{{40}}{\ell _5} \right) {{\tilde{h}}} \right) , \end{aligned}$$
(25)
$$\begin{aligned}&{{\bar{y}}}_{i + 1} = {{{\bar{y}}}_i} + \left( {\frac{{25}}{{216}}{\ell _1} - \frac{{1408}}{{2565}}{\ell _3} + \frac{{2197}}{{4104}}{\ell _4} - \frac{1}{5}{\ell _5}} \right) {{\tilde{h}}}, \nonumber \\ \end{aligned}$$
(26)
$$\begin{aligned}&{{{\bar{z}}}_{i + 1}} = {{{\bar{z}}}_i} + \left( \frac{{16}}{{135}}{\ell _1} + \frac{{6656}}{{12825}}{\ell _3} + \frac{{28561}}{{56430}}{\ell _4}\right. \nonumber \\&\qquad \qquad \left. - \frac{9}{{50}}{\ell _5} + \frac{2}{{55}}{\ell _6} \right) \tilde{h}. \end{aligned}$$
(27)

In the above equations, \({{\bar{z}}}\) is the fifth-order Runge–Kutta phase and \({\bar{y}}\) is the fourth-order Runge–Kutta phase. The procedure to approximate new step size can be written as

$$\begin{aligned} {{{\tilde{h}}}_{{\mathrm{new}}}} = {{{\tilde{h}}}_{{\mathrm{old}}}}{\left( {\frac{{{{\bar{\varepsilon }}} {{{{\tilde{h}}}}_{{\mathrm{old}}}}}}{{2|{{{{\bar{z}}}}_{i + 1}} - {{{{\bar{y}}}}_{i + 1}}|}}} \right) ^{1/4}}, \end{aligned}$$
(28)

where \(\bar{{\varepsilon }}\) is the specified error control tolerance.

Table 1 Numerical comparability of skin friction coefficient, Nusselt number and Sherwood number against numerous values of \(\hbox {Pr} ,\gamma ,M,m_e ,\hbox {Du} ,\hbox {Sc} ,\hbox {Sr} ,k\).
Full size table

The dimensionless form of velocity, temperature and concentration equations (11)–(13) with their compatible boundary conditions in eqs. (14)–(16) have been formulated by using shooting method. Firstly, we transform the ODEs into first-order ODEs by setting

$$\begin{aligned} {{{\mathcal {U}}}}_1= & {} F,\quad {{{{\mathcal {U}}}}_2} = F',\quad {{{{\mathcal {U}}}}_3} = \mathcal{U}'',\quad {{{{\mathcal {U}}}}_4} = \theta ,\nonumber \\ {{{{\mathcal {U}}}}_5}= & {} \theta ',\quad {{{{\mathcal {U}}}}_6} = \Phi \quad \mathrm{and}\quad {{{{\mathcal {U}}}}_7} = {{\Phi '}}, \end{aligned}$$
(29)

which gives

$$\begin{aligned}&\left[ \begin{array}{l} {{{\mathcal {U}}}}_1^\prime \\ {{{\mathcal {U}}}}_2^\prime \\ {{{\mathcal {U}}}}_3^\prime \\ {{{\mathcal {U}}}}_4^\prime \\ {{{\mathcal {U}}}}_5^\prime \\ {{{\mathcal {U}}}}_6^\prime \\ {{{\mathcal {U}}}}_7^\prime \end{array} \right] = \left[ \begin{array}{c} {{{{\mathcal {U}}}}_2}\\ {{{{\mathcal {U}}}}_3}\\ \displaystyle \frac{{\frac{{2m}}{{m + 1}}{{{\mathcal {U}}}}_2^2 - {{{{\mathcal {U}}}}_1}{{{{\mathcal {U}}}}_3} - n\mathrm{We}{{{{\mathcal {U}}}}_3}{{{{\mathcal {U}}}}_3^{\prime }} + \frac{M}{{1 + m_e^2~}}{{{\mathcal {U}}}}_2^{\prime } + k{{{{\mathcal {U}}}}_2} - \frac{2}{{m + 1}}{\mathrm{Ri}}\left( {{{{{\mathcal {U}}}}_4} + \eta {{{{\mathcal {U}}}}_6}} \right) }}{{({1 - n})}}\\ {{\mathcal {U}}_5}\\ {\mathrm{Pr}}\left( { - {{{{\mathcal {U}}}}_1}{{{{\mathcal {U}}}}_5} + \frac{{2\left( {2m - 1} \right) }}{{m + 1}}{{{{\mathcal {U}}}}_4}{{{{\mathcal {U}}}}_2} - {\mathrm{Du}}{{{\mathcal {U}}}}_7^\prime } \right) \\ {{{{\mathcal {U}}}}_7}\\ {\mathrm{Sc}}\left( { - {{{{\mathcal {U}}}}_1}{{{{\mathcal {U}}}}_7} + \frac{{2\left( {2m - 1} \right) }}{{m + 1}}{{{{\mathcal {U}}}}_6}{{{{\mathcal {U}}}}_2} - {\mathrm{Sr}}{{{\mathcal {U}}}}_5^\prime + \gamma {{{{\mathcal {U}}}}_6}} \right) \end{array} \right] . \end{aligned}$$
(30)

and the corresponding initial conditions are

$$\begin{aligned} \left[ {\begin{array}{l} {{{\mathcal {U}}}}_1 \\ {{{\mathcal {U}}}}_2 \\ {{{\mathcal {U}}}}_3 \\ {{{\mathcal {U}}}}_4 \\ {{{\mathcal {U}}}}_5 \\ {{{\mathcal {U}}}}_6 \\ {{{\mathcal {U}}}}_7 \\ \end{array}} \right] =\left[ {\begin{array}{c} s \\ 1 \\ U_1 \\ 1+\xi U_2 \\ U_2 \\ 1 \\ U_3 \\ \end{array}} \right] . \end{aligned}$$
(31)

Equations (11)–(13) are now converted into an initial value problem. We require the values of \(U_1 ,U_2\) and \(U_3\) but these values are missing. Appropriate guesses for \({F}''(0),\theta '(0)\) and \({\Phi }'(0)\) are taken to obtain the solution. The step size is selected as ‘0.0001’. Numerical computations are executed in MATLAB symbolic software.

4 Results and discussion

This section interprets the numerical and graphical outcomes of the influence of governing parametric quantities of our prevalent flow problem. Computational software MATLAB is utilised to incorporate the impact of Hartmann number (M), porous parameter (k), concentration buoyancy ratio (\(\eta )\), Weissenberg number \(\left( {\hbox {We}} \right) \), Richardson number (\(\hbox {Ri}\)), Prandtl number \((\hbox {Pr})\), fluid parameter (n), Dufour parameter \(\left( {\hbox {Du} } \right) \), power-law exponent \(m\left( {\ne -1} \right) \), chemical reaction parameter \(\left( \gamma \right) \), Schmidt number (Sc), and Soret number \((\hbox {Sr}\)) on velocity profile (\({F}'(\zeta )\)), temperature profile (\(\theta \left( \zeta \right) )\) and nanoparticle concentration profile (\({\Phi }\left( \zeta \right) \)). The numerical values for \(\mathrm{Sh}_r ,\mathrm{Nu}_r\) and \(C_F\) against numerous values of \(\mathrm{Pr}, \gamma , M,m_e,\mathrm{Du},\mathrm{Sc} ,\mathrm{Sr},k\) are presented in table 1. Tables 2 and 3 exhibit the numerical comparability for skin friction coefficient by taking \(M=m_e =n=\mathrm{We}=\mathrm{Ri} =k=\mathrm{Du} =\xi =\mathrm{Sr} =(\gamma ) =0\) against different values of power-law exponent (m), and for Nusselt number by taking \(M=m_e =\hbox {Ri} =n=\mathrm{We}=k=\hbox {Du} =\hbox {Sr} =\gamma =\xi =0\) and \(m=1\) against different values of \(\hbox {Pr} \) respectively. From tables 2 and 3, we can conclude that our current data are in excellent agreement which ratifies the efficacy of the this technique.

Table 2 Numerical comparability of \(F^{{\prime }{\prime }}(0)\) against multiple values of m.
Full size table
Table 3 Numerical comparison of \(-\theta ^{\prime }(0)\) against multiple values of \(\mathrm{Pr}\).
Full size table

Figures 2–5 represent the variation of velocity profile against m, n, \(\hbox {Ri}\), Hall current parameter (\(m_{\mathrm{e}}\)), M and porous parameter (k). Figure 2 portrays that increasing the values of m does not bring forth a significant change in the velocity profile. Moreover, in figure 2, the extreme values of We create a resistance in the velocity profile. We is the proportion between the viscous forces and elastic forces. Higher values of We corresponds to higher viscous forces, and as a result, the velocity of the fluid diminishes. Figure 3 demonstrates the simultaneous variation of n and \(\mathrm{Ri} \). It is worthy to mention here that the prevalent results reduce to the Newtonian fluid by taking \(n=0\) (see eq. (11)). It can be examined from figure 3 that an increase in \(\mathrm{Ri}\) causes a significant enhancement in the velocity profile. Higher values of \(\mathrm{Ri}\) create a tremendous buoyancy force and kinetic energy. However, if \(\mathrm{Ri} =1\), then the governing flow is known as buoyancy-driven flow. In figure 3 we can also notice that when the fluid parameter increases, the velocity of the fluid increases. Another important thing we can see is that as the fluid depicts non-Newtonian behaviour, the velocity of the fluid decreases more as opposed to its boundary layer thickness. Figure 4 shows the response of the Hall parameter and concentration buoyancy ratio on the velocity profile. It is seen that both parameters give significant assistance to boost the velocity of the flow. Figure 5 shows that the velocity profile decreases for M. The reduction in magnitude of the fluid velocity occurs due to an influence of Lorentz force, which arises when a magnetic field is applied to the fluid. This force which moves in the opposite direction of the flow causes a flow retardation. Figure 5 also indicates the behaviour of k. This figure shows that higher values of porous parameter causes decrease in the velocity profile and its boundary layer thickness.

Fig. 2
figure 2

Variation of m and \(\hbox {We}\) for velocity distribution.

Full size image
Fig. 3
figure 3

Variation of n and \(\hbox {Ri}\) for velocity distribution.

Full size image
Fig. 4
figure 4

Variation of \(\eta \) and \(m_e \) for velocity distribution.

Full size image
Fig. 5
figure 5

Variation of M and k for velocity distribution.

Full size image
Fig. 6
figure 6

Variation of \(\xi \) and m for temperature distribution.

Full size image
Fig. 7
figure 7

Variation of \(\hbox {Pr}\) and \(\hbox {Du}\) for temperature distribution.

Full size image
Fig. 8
figure 8

Variation of \(\hbox {Sr}\) and \(\hbox {Sc}\) for concentration distribution.

Full size image
Fig. 9
figure 9

Variation of m and \(\gamma \) for concentration distribution.

Full size image

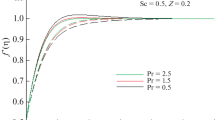
Figures 6 and 7 represent the variation of temperature distribution against thermal slip parameter \(\xi \), \(\mathrm{Du}\), m and \(\mathrm{Pr}\). Figure 6 shows that an increment in m tends to diminish the temperature profile. However, we can notice from this figure that the temperature profile reduces in the region \(\zeta \in \left[ {0,1.5} \right] \), whereas no variation is observed for \(\zeta >1.5\). From figure 6 we can also see that by enhancing \(\xi \) the magnitude of the temperature profile decreases. Further, by taking \(\xi =0\) there will not be any thermal slip. It can be observed from figure 7 that an enhancement in \(\mathrm{Du}\) causes a marked improvement in the temperature profile. It is the opposite mechanism of Soret effect, and it arises due to the coupled influence of irreversible process. When \(\mathrm{Du}\) is high then the combined impact of solutal buoyancy force and thermal source increases the convection velocity, which result in enhancing the temperature profile. Furthermore, we can also notice in figure 7 that higher values of \(\mathrm{Pr}\) produces a strong resistance in boundary layer thickness and temperature profiles. Physically, the increment in \(\mathrm{Pr}\) corresponds to weaker thermal diffusivity, and different Newtonian and non-Newtonian fluids have lower thermal diffusivity. Lower thermal diffusivity causes lower temperature.

Figures 8 and 9 are sketched for concentration profile against various values of \(\mathrm{Sc}\), \(\gamma \), \(\mathrm{Sr}\), and m. Figure 8 shows the simultaneous behaviour of \(\mathrm{Sc}\) and \(\mathrm{Sr}\). It can be seen from this figure that an increase in \(\mathrm{Sc} \) shows strong resistance to its boundary layer thickness and concentration profile. The proportion between mass diffusivity and momentum diffusivity is called \(\mathrm{Sc}\). An enhancement in \(\mathrm{Sc}\) corresponds to higher mass diffusion rate which causes decrease in its relevant boundary layer thickness and concentration profile. In this figure, it is also noticed that an increase in \(\mathrm{Sr}\) (also known as thermophoresis) contributes to raising the concentration profile and its skin boundary layer thickness. When \(\mathrm{Sr}\) increases, then a thermophoresis force originated which tends to propagate the particles due to a temperature gradient. The force tends to separate the particles from mixing or have been mixed. Figure 9 shows that larger values m tend to diminish its boundary layer thickness and the concentration profile. Furthermore, \(\gamma \) shows similar behaviour in the region \(\zeta \in \left[ {0,2.5} \right] \) where the expression of concentration profile become opposite for \(\zeta >2.5.\)

5 Conclusion

Effect of thermo-diffusion and diffusion-thermo on hyperbolic tangent nanofluid with Hall current and magnetic field are examined through a nonlinear porous stretching sheet. The concurrent consequence of chemical reaction and thermal slip are also considered. The governing nonlinear coupled ODEs are numerically solved using the Runge–Kutta–Merson method and shooting method. The impact of pertinent parametric quantities is displayed and illustrated using tables and graphs. We have reached the following conclusions

  1. i.

    An enhancement in fluid parameter and M creates a marked reduction in the velocity of the fluid.

  2. ii.

    Hall parameter and concentration buoyancy ratio significantly boost the fluid velocity.

  3. iii.

    The velocity of the fluid reduces due to the porosity parameter and \(\mathrm{W}\mathrm{e}\).

  4. iv.

    Thermal slip parameter and m create a decrement in the temperature distribution as well as its corresponding boundary layer thickness.

  5. v.

    \(\mathrm{Pr}\) and \(\mathrm{Du}\) depict contrary behaviour on the temperature profile.

  6. vi.

    Concentration distribution and skin boundary layer thickness decrease due to \(\mathrm{Sr}\) and \(\gamma \).

  7. vii.

    An enhancement in \(\mathrm{Sc}\) reduces the concentration distribution as well as its boundary layer thickness.