1 Introduction

Mechanical behavior of heterogeneous (disordered) materials has been an interest of researchers. Microstructure plays a critical role in mechanical behavior of materials which exhibits power law scaling such as colloidal aggregates, porous materials and two phase materials with inclusions [23, 30, 45, 54]. Continuum theories have been developed in order to account for the effects of heterogeneities (voids, grains, material phases) on material behavior such as micropolar and microstretch theories [20]. Homogenization techniques such as effective medium theories or multiscale methods have also been widely used in modeling the effect of microstructure on macroscopic material behavior [35]. Both effective medium theories and multiscale methods are originally developed for boundary value problems and can be applied successfully to a limited number of problems where the problem is static or quasi-static and material behavior is linear elastic with periodic topological structure or dynamic problems in which length scale of the microstructure is much smaller than the wavelength [36]. Dynamic homogenization of heterogeneous materials by using effective medium theory, in which the length scale of the microstructure is comparable to the corresponding wavelength, is an active research area due to its use in metamaterial design [53] and limited to problems with linear or weakly nonlinear material behavior.

There has been growing interest in using fractional calculus in modeling complex media [9, 14, 50]. History of fractional derivatives and therefore calculus goes back to 17th century and depends on a question asked by L’Hopital to Leibniz [46]. Fractional calculus has found many applications in electromagnetics, mechanics of materials and particle physics [31, 46, 51]. Fractional integral is a generalization of n fold integration and fractional derivative is inverse operator of the fractional integral on a function [34, 38, 46]. Even though the definition of fractional integral is unique, fractional derivative has different definitions. Riemann-Liouville, Caputo and Marchaud fractional derivatives are nonlocal fractional derivatives or integro-differential operators on a function [34, 38, 46]. Local fractional derivatives are also proposed and have been used [5, 28, 39, 50]. The type of problem and method of solution determines the choice of the fractional derivative [8, 46]. Fractional integro-differential equations are solved either by using Fourier and Laplace transforms [34, 38, 46] or by using different numerical methods including finite elements [1, 22, 48] and fractional finite differences [15, 55].

Fractional derivatives and fractional integrals are used in three different types of problems. The first type of problems are problems in which the field variables do not have a derivative in the classical sense such as random processes and problems with singularities [11, 46]. The second type of problems are problems that have some retarded effects such as problems with memory effect [31, 42, 44]. The third type of problems are problems with a discrete or disordered domain where the topology of the domain has a significant role on the problem [9, 39]. Topological disorder of the domain is measured by fractal dimension of the domain [8, 9, 32] namely box counting dimension in the case of quasi-fractals and Hausdorff dimension for fractals. Relation between an open fractal set and fractional integral and derivative has been recently shown [42, 43].

Disordered, quasi-fractal (self-similar structures within certain length scales) structures have been seen in nature [32]. There has been a growing interest in understanding size and scale effects on the mechanical behavior of material at the macro scale [7], force transmission mechanism and structural behavior of hierarchical, biomimetic and biological materials [18, 21]. Such media exhibits quasi-fractal structure [39] and fractional calculus is a good candidate for the homogenization of disordered and self similar media. Fractional calculus has been used in solid mechanics for modeling viscoelastic and hereditarily elastic material behavior. The reader can consult to Refs. [31, 44] for an extensive review of the subject and references therein. Use of fractional calculus on a fractal set in solid mechanics is first presented in [9] where the Kolwankar-Gangal derivative [28] is suggested as a fractional derivative and the virtual work principle is proposed for a finite element solution. The elastic potential for fractal media is proposed in [10] and scaling properties of kinematic and equilibrium equations are investigated with examples given on the Cantor set. Balance laws for thermoelastic fractal media are presented in [39] based on the local fractional derivative proposed in [50]. The Jacobian between the fractal media and Euclidean space is calculated using the modified Riemann-Liouville fractional derivative [26] in [14]. In addition, balance equations for equivalent continuum media, geometric and kinematic compatibility and equilibrium equations around a shock front are presented. Recently, a continuum mechanics model based on the Riesz potential [38, 46] is proposed in [16], where the mapping of field variables to Euclidean space is done via the Riesz potential. In addition to modeling fractal media, inelastic models and nonlocal elastic models are proposed or reformulated in various studies [11, 13, 29, 33, 40, 47].

It has been known that a material point in a linear elastic body gets information from either side of the point with left and right running characteristics [17] which makes the symmetry properties of the operators used in modeling the problem important [33]. Local fractional derivatives, which are used in modeling continuum problems [39, 50], are based on one sided fractional derivatives and do not have the symmetry property. Riesz-Feller fractional derivatives are symmetric integro-differential operators [46]. In this study, wave propagation in heterogeneous material with self-similar structure is investigated via fractional calculus along with the discontinuous Galerkin method, considering that each element has a quasi-fractal structure. Riesz-Feller fractional derivatives and their local counter parts are used. A suddenly loaded 1D bar and a suddenly loaded plate under plane strain conditions are studied assuming that the material is elastic. An outline of the paper is as follows: In Sect. 2, some fundamentals of fractional calculus are given. Equilibrium equations for fractal media are given in Sect. 3. Homogenization of fractal media and a finite element formulation is given in Sect. 4. Results of numerical calculations are presented in Sect. 5. Conclusions are drawn in Sect. 6.

2 Fractional Calculus

In this section some of the properties of fractional integrals and derivatives are revisited. For details the reader can consult to [34, 38, 46].

Let us define an interval \(\mathbb{A}= [a,b ]\subseteq \mathbb{R}\). f is a locally integrable function [24] such that \(f(x)\in\mathbb{R}\) and \(x\in\mathbb{A}\). The left and right fractional integral of f is defined as

$$\begin{aligned} _{a}I^{\alpha}_{x}f(x) =&\frac{1}{\varGamma(\alpha)} \int _{a}^{x}\frac{f(y)}{(x-y)^{1-\alpha}} dy, \end{aligned}$$
(1)
$$\begin{aligned} _{x}I^{\alpha}_{b}f(x) =&\frac{1}{\varGamma(\alpha)} \int _{x}^{b}\frac{f(y)}{(y-x)^{1-\alpha}}dy. \end{aligned}$$
(2)

In Eqs. (1) and (2), α is the order of the fractional integral and α>0. Thus in this study we restrict ourselves to 0<α≤1. Γ is Euler’s Gamma function which is defined as \(\varGamma(z)=\int_{0}^{1}(\log x)^{-z-1} dx\), \(\forall z \in\mathbb{C}\). Left and right Riemann-Liouville fractional derivatives are defined as \({}_{a}D^{\alpha}_{x}=~_{a}I^{-\alpha}_{x}\) and \({}_{x}D^{\alpha}_{b}=~_{x}I^{-\alpha}_{b}\) and written as follows

$$\begin{aligned} _{a}D^{\alpha}_{x}f(x) =&\frac{d}{dx} \bigl({}_{a}I^{1-\alpha}_{x}f(x) \bigr), \end{aligned}$$
(3)
$$\begin{aligned} _{x}D^{\alpha}_{b}f(x) =&-\frac{d}{dx} \bigl({}_{x}I^{1-\alpha}_{b}f(x) \bigr). \end{aligned}$$
(4)

The Riemann-Liouville fractional derivative can be applied to locally non-differentiable functions such as functions with singularities. On the other hand, the Riemann-Liouville fractional derivative of f is not zero when f(x)=C and C is a constant [36, 40, 48]. In physical systems, when field variable is constant, its derivative is zero. Therefore, the Caputo derivative has been used in physical systems in order to calculate the fractional derivative of a field variable, similar to that in viscoelasticity [33]. Caputo derivatives are defined as

$$\begin{aligned} _{a}\tilde{D}^{\alpha}_{x}f(x) =&{}_{a}I^{1-\alpha}_{x}f^{(1)}(x), \end{aligned}$$
(5)
$$\begin{aligned} _{x}\tilde{D}^{\alpha}_{b}f(x) =&- _{x}I^{1-\alpha}_{b}f^{(1)}(x). \end{aligned}$$
(6)

One can see from the definitions of Caputo derivatives, that the function f must have a first derivative in the interval [a,b] for 0<α≤1. In order to calculate the fractional derivative of a non-differentiable field variable in a physical system, the modified Riemann-Liouville derivative is proposed in [26] which is called the Jumarie derivative. Left and right Jumarie derivatives are defined as

$$\begin{aligned} _{a}^j D^{\alpha}_{x}f(x) =&~_{a}D^{\alpha}_{x} \bigl(f(x)-f(a) \bigr), \end{aligned}$$
(7)
$$\begin{aligned} _{x}^j D^{\alpha}_{b}f(x) =&~_{x}D^{\alpha}_{b} \bigl(f(x)-f(b) \bigr). \end{aligned}$$
(8)

Jumarie derivatives are equivalent to Caputo derivatives when the function f is differentiable and equivalent to the Riemann-Liouville derivatives when f(a)=f(b)=0 and the derivative of a constant is zero.

The left fractional derivative and right fractional derivative of a function are not equal. The Riesz fractional integral and derivative [46] has been used to circumvent this problem, which is more appropriate for defining the physics of a problem in spatial coordinates. Thus in a linear elastic material, a point in the material gets information carried by both left and right running characteristics [17]. Therefore the Riesz-Feller fractional integral and derivative [46] are used based on Jumarie’s modified Riemann-Liouville derivative. The Riesz-Feller integral and derivative are the conjugate of the Riesz integral and derivative, respectively [24]. In addition, the Riesz fractional integral and derivative exhibit singular behavior in the limiting case as α limits to one [24]. The Riesz-Feller fractional integral and derivative, based on the Jumarie derivative, can be written as

$$\begin{aligned} _{a}R^{\alpha}_{b}f(x) =&\frac{1}{2 \sin(\frac{\pi}{2} \alpha)} \bigl({}_{a}I^{\alpha}_{x}f(x)-~_{x}I^{\alpha}_{b}f(x) \bigr), \end{aligned}$$
(9)
$$\begin{aligned} _{a}^r D^{\alpha}_{b}f(x) =& \frac{1}{2 \sin(\frac{\pi}{2} \alpha)} \bigl({}_{a}^j D^{\alpha}_{x}f(x)-~_{x}^j D^{\alpha}_{b}f(x) \bigr). \end{aligned}$$
(10)

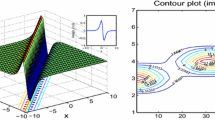
The Riesz-Feller fractional derivative, based on the Jumarie fractional derivative, combines the advantages of the Riemann-Liouville and the Caputo fractional derivatives, such as when function f(x) is constant the Riesz-Feller fractional derivative based on the Jumarie fractional derivative of the function is zero. It can be applied to non-differentiable functions. Moreover, the Riesz derivative is singular as α→1 whereas the Riesz-Feller fractional derivative is continuous with respect to α. In addition, the Kolwankar-Gangal derivative gives the strength of a singularity which has an order of α. This property of the Kolwankar-Gangal derivative is used in modeling of the localization of strain in [9]. The Riemann-Liouville derivative, and therefore the Riesz-Feller derivative, is the derivative of a function on a fractal set with Hausdorff dimension α [42, 43]. It is shown in [42, 43] that the relation between the fractional derivative and the derivative of a function f(x) is given as \(\frac{\partial^{\alpha}f(x)}{\partial x^{\alpha}}=C(L,\alpha)\ _{a}^{r} D^{\alpha}_{b}f(x)\) where L is the characteristic length and \(\frac{\partial^{\alpha}(\cdot)}{\partial x^{\alpha}}\) is the differential operator in fractal space. The Riesz-Feller derivative of f(x)=x is shown in Fig. 1 for different values of α.

Fig. 1
figure 1

Riesz-Feller derivative of a linear function f(x)=x, where x∈[0,1]

Full size image

Local fractional derivatives have also been used either as an approximation of nonlocal fractional derivatives [6] or in relation to fractional finite differences [28]. In this study, we focus on local fractional derivatives which are approximations of nonlocal fractional derivatives. The basic idea arises from replacing the Lebesgue measure with the Lebesgue-Stieltjes measure,

$$\begin{aligned} d^{n}x \rightarrow d \varrho(x). \end{aligned}$$
(11)

In Eq. (11), n is the number of topological dimensions and ϱ is a distribution. In the case that ϱ is continuous, one can write

$$\begin{aligned} d\varrho(x)=c(\beta,x)d^{n}x, \end{aligned}$$
(12)

where β is the Hausdorff dimension of the fractional space and n>β>n−1. c(β,x) is the Jacobian, which is analogous to the density of states [6].

Assuming that coordinate transformation from the fractional space to the Euclid space is a parallelepiped (Fig. 2), one can write the differential volume element in the fractional media as follows

$$\begin{aligned} d\varOmega^{\alpha} =&(dx_{1})^{\alpha_{1}} (dx_{2})^{\alpha_{2}}(dx_{3})^{\alpha_{3}} \\ =&c_3(\beta,\mathbf{x})d\varOmega_{3} \\ =&c_{1}(\alpha_{1},x_{1}) c_{1}( \alpha_{2},x_{2}) c_{1}(\alpha_{3},x_{3})dx_{1} dx_{2}dx_{3}. \end{aligned}$$
(13)
Fig. 2
figure 2

Coordinate transformation

Full size image

In Eq. (13), dΩ α is the differential volume element in fractional space. dΩ 3 is the differential volume element in 3 dimensional Euclid space and \((dx_{i})^{\alpha_{i}} \) is the differential line element in \(x_{i}^{\alpha_{i}}\). α i is the dimension of the fractional space in the direction of x i . The reader can consult Ref. [8] for a detailed discussion on differential forms.

Let us consider a differentiable function f(x i ). Following [6, 39, 50], we obtain the local fractional derivative for the Riesz-Feller potential as follows

$$\begin{aligned} _{a} ^{rl} D^{\alpha_{i}}_{b}f(x_{i})= \frac{1}{c_{1}(\alpha _i,x_i)}\frac{\partial f(x_{i})}{\partial x_{i}}, \end{aligned}$$
(14)

where

$$\begin{aligned} c_{1}(\alpha_i,x_i)= \biggl( \frac{(b-x_{i})^{1-\alpha _{i}}+(x_{i}-a)^{1-\alpha_{i}}}{2 \sin{(\frac{\pi}{2} \alpha _{i})}\varGamma(2-\alpha_{i})} \biggr)^{-1}. \end{aligned}$$
(15)

3 Equilibrium Equations

Let us review equilibrium equations for a linear elastic body occupying a space \(\varOmega\subset\mathbb{R}^{3}\). The boundary of Ω is denoted by ∂Ω. ∂Ω D and ∂Ω N denote the subregions of ∂Ω, and the displacement vector and traction are specified such that

$$\begin{aligned} \partial\varOmega=\overline{\partial\varOmega_N \cup \partial\varOmega_D}\quad \mbox{and}\quad \partial \varOmega_N \cap \partial\varOmega_D= \emptyset. \end{aligned}$$
(16)

The equilibrium equation for elastodynamics can be written as follows

$$\begin{aligned} \rho\ddot{\mathbf{u}}=\nabla\cdot\boldsymbol{\sigma}+ \mathbf{b} \quad \mbox{in } \varOmega. \end{aligned}$$
(17)

In Eq. (17), ρ is the density, σ is the Cauchy stress tensor, b represents the body forces per unit mass, u is the displacement and overdot represents derivation with respect to time.

The boundary conditions are as follows

$$ \begin{aligned} \boldsymbol{\sigma}\cdot\mathbf{n}&= \bar{\mathbf{t}}\quad \mbox{in } \partial\varOmega_N, \\ \mathbf{u}&=\bar{\mathbf{u}} \quad \mbox{in }\partial\varOmega_D, \end{aligned} $$
(18)

where \(\bar{\mathbf{t}}\) and \(\bar{\mathbf{u}}\) are the specified traction and displacement, respectively.

For a linear elastic material, the stress tensor is given as

$$\begin{aligned} \boldsymbol{\sigma}=\mathbf{C}:\boldsymbol{\varepsilon}, \end{aligned}$$
(19)

where

$$\begin{aligned} \boldsymbol{\varepsilon}=\frac{1}{2} \bigl(\nabla \mathbf{u}+ \nabla \mathbf{u}^{\mathbf{T}} \bigr), \end{aligned}$$
(20)

where C is the stiffness tensor and ε is the strain tensor.

The dynamical equations for elastic and thermoelastic materials on a fractal media are given in [9, 16, 39] and, also, recently in [5], by using local fractional derivatives. Following the studies done by using local fractional derivatives, one can write the equations for a quasi-fractal media with nonlocal fractional derivatives without loss of generality. Thus it is straight forward to prove their validity with nonlocal fractional derivatives by using the Gauss divergence theorem for fractional calculus [3, 52], which is given in Eq. (21). A detailed derivation of Eq. (21) is given in Appendix A for the nonlocal fractional derivatives. The reader can consult Refs. [39] and [5] for the case of local fractional derivatives.

Let us consider a body occupying a space Ω α such that Ω α⊂Ω in \(\mathbb{R}^{3}\) and \(\beta \in \mathbb{R}^{+}\) is the Hausdorff dimension or box counting dimension of Ω α. \(\partial\varOmega^{\alpha}_{D}\) and \(\partial\varOmega^{\alpha}_{N}\) denote the non-overlapping boundary regions of Ω α, where, respectively, the displacement and traction are given.

In this study, we consider an isotropic fractal media where α 1=α 2=α 3=α. Therefore β=3α. The dynamical equation for elastodynamics on a fractal media can be written as follows

$$\begin{aligned} \rho\ddot{\mathbf{u}}=\nabla^{\alpha}\cdot \boldsymbol{\sigma}+\mathbf{b}\quad \mbox{in } \varOmega^{\alpha}. \end{aligned}$$
(21)

In Eq. (21) \(\nabla^{\alpha}= (\frac{\partial^{\alpha}}{\partial x_{1}^{\alpha}},\frac{\partial^{\alpha}}{\partial x_{2}^{\alpha}},\frac{\partial^{\alpha}}{\partial x_{3}^{\alpha}} )\) is the nabla operator either with local fractional derivative components which are defined in Eq. (14) or with nonlocal fractional derivative components which are defined in Eq. (10). One must note that Eq. (21) is a integro-differential equation defined in fractal space. The fractional divergence of the Cauchy stress σ arises as an effect of the heterogeneous structure in Euclid space Ω on the fractal space Ω α. In addition, material properties, such as density, are the properties of the bulk material. Boundary conditions are given as follows

$$\begin{aligned} \begin{aligned} \boldsymbol{\sigma}\cdot\mathbf{n}&= \bar{\mathbf{t}}\quad \mbox{in }\partial\varOmega^{\alpha}_N, \\ \mathbf{u}&=\bar{\mathbf{u}}\quad \mbox{in }\partial\varOmega^{\alpha}_D. \end{aligned} \end{aligned}$$
(22)

Similar to the linear elastic material, the stress and strain tensor can be defined as

$$\begin{aligned} \boldsymbol{\sigma} =&\mathbf{C}:\boldsymbol{\varepsilon}, \end{aligned}$$
(23)
$$\begin{aligned} \boldsymbol{\varepsilon} =& \frac{1}{2} \bigl( \nabla^\alpha\mathbf{u}+\nabla^\alpha\mathbf {u}^{\mathbf{T}} \bigr). \end{aligned}$$
(24)

In Eq. (24), ε is the strain tensor in Euclid space. Proof of the validity of Eq. (24) can be done by using a geometric interpretation of strain in classical continuum [19] and is given in Appendix B. One must mention that both the Riesz derivative and the Riesz-Feller derivative do not admit the derivation of a metric tensor. Thus both the right Riemann-Liouville and the Jumarie derivative do not have a natural distribution function ϱ(x,ν), and this results in \({}_{x}^{j} D^{\mu}_{b}\varrho(x,\nu)\neq\delta_{\mu}^{\nu}\) and \({}_{x}D^{\mu}_{b}\varrho(x,\nu)\neq\delta_{\mu}^{\nu}\) [8]. Therefore it is not possible to define a metric tensor either for the Riesz derivative or for the Riesz-Feller derivative, which is done for left fractional derivatives in [8, 12, 27].

Fractional calculus has been seen as a natural candidate in describing continuum properties of fractal media due its non-integer order. The relation between the fractional derivative and integral of a function and the derivative and integral of function on a Cantor set is shown by [43] by using Laplace transform in the asymptotic limit of p→∞ where p is the Laplace parameter. The order of approximation is L 2α where L is the characteristic length. It is also shown that derivative of a function on a Cantor bar is equivalent to the fractional derivative of a function multiplied by a constant C. This constant is a function of the Hausdorff dimension of the Cantor bar and characteristic length of it is such that C∝1/L 1−α, which makes the strain on a Cantor bar dimensionless as is the case in classical continuum mechanics [19]. In this study, we assume that C=1 regardless of the Hausdorff or box counting dimension and the characteristic length in order to make a comparison between the nonlocal fractional derivative and it’s local approximation. It is observed from Eq. (24) that in a fractional space which is the case when C=1, the strain has a dimension of L 1−α similar to that of the strain in a fractal media [9]. Even though they posses mathematically identical results, the fractal strain defined in [9] differs from the definition given in this study. In this study the structure is composed of discrete set of material points and the deformation localizes at all material points as a result of the discrete structure. In [9], localization in strain occurs as a result of loading or the material property and the structure is continuous.

When the bulk material is linear elastic and isotropic, the dynamical equation can be written as follows

$$\begin{aligned} \rho \ddot{\mathbf{u}}=(\lambda+\mu) \nabla^\alpha \nabla^\alpha\cdot\mathbf{u}+\mu\nabla^\alpha\cdot\nabla ^\alpha \mathbf{u} \end{aligned}$$
(25)

where λ and μ are the Lamè parameters.

4 Coarse Graining and Finite Element Formulation

Let x,y∈Ω 0 and let φ be a contraction mapping from Ω 0 to Ω. If \(|\varphi(\mathbf{x)}-\varphi(\mathbf{y)}|=c |\mathbf{x}-\mathbf{y}|\) where 0<c<1, then the structure is self-similar (Fig. 3). From a topological point of view the structure repeats itself at lower scales.

Fig. 3
figure 3

Homogenization of self-similar structure

Full size image

Different than the previous studies in the literature, where the whole structure is fractal or quasi fractal [9, 39], each element is quasi-fractal with upper cut off (Fig. 4) in this study. This introduces the element size as a parameter for modeling the structure. This is obtained by replacing the derivatives of the base functions with fractional derivatives of the base functions in the finite element formulation.

Fig. 4
figure 4

Coarse grained element

Full size image

The discontinuous Galerkin method [2], in which the continuity of the displacement is weakly enforced, is used in this study for modeling problems. Weak enforcement of the continuity of displacements allows us to capture discontinuities at the element interfaces as a result of non-vanishing inter-element terms which arise from integration by parts. The integration by parts rule in fractional calculus contains integral terms in the boundary integrals [37] which makes the numerical implementation complicated. Thus [26] approximated the fractional differential of a continuous function f(x) in the generalized Taylor series expansion with a fractional order differential as d α f=Γ(α+1)df+O(h 2α), where h is a small number. For 0<α<0.5, the error due to the truncated terms in the approximation of fractional differential increases. Therefore we limit our analysis to 0.5≤α≤1.0. In addition, this approximation of fractional differential allows one to write the integration by parts rule similar to that of classical calculus for the nonlocal case [26], which is given in Eq. (26)

$$\begin{aligned} \int_a^b f^{(\alpha)}(x) g(x) (dx)^{\alpha} =&\varGamma(\alpha+1) f(x)g(x)|_a^b-\int_a^b f(x) g^{(\alpha)}(x) (dx)^{\alpha}. \end{aligned}$$
(26)

The integration by parts rule for the local fractional derivative is the same as in classical calculus with the exception of the coefficients which arise from the mapping of fractional space onto Euclid space; these will not be given here.

Before presenting the discontinuous Galerkin formulation, let us give some definitions.

Let \(\mathcal{P}_{h}(\varOmega^{\alpha})\) be a regular partition of the domain Ω α, such that \(\mathcal{P}_{h}(\varOmega ^{\alpha})\) is generated by dividing Ω α in to N e number of \(\varOmega^{\alpha}_{e}\) subdomains. \(\varGamma^{\alpha}_{\mathrm{int}}\) defines the interelement boundaries. \(\varGamma^{\alpha}_{D}\) and \(\varGamma^{\alpha}_{N}\) define the Dirichlet and Neumann boundaries. A Greek superscript α shows that it is a fractal surface or volume. Let I n =(t n ,t n+1) be a time interval for the integer n. Then each space-time slab is defined as S=Ω α×I n .

Let us define a broken space of basis functions V n , in which u(x,t) and v(x,t) are smooth and continuous vector functions for every \(S_{e}=\varOmega^{\alpha}_{e} \times I_{n}\). Similarly, a broken space of weighting functions W n is defined for each n, in which w u (x,t) and w v (x,t) are smooth and continuous vector functions for every \(S_{e}=\varOmega^{\alpha}_{e} \times I_{n}\). Elements of V n and W n are vector functions different from zero in S e , and zero elsewhere. The weak formulation of space-time discontinuous Galerkin form can be written as follows

$$\begin{aligned} &\int_{I_n}\int _{\varOmega^{\alpha}_e}\mathbf{w}_v \rho\dot{\mathbf{v}}d \varOmega^{\alpha}_e dt+\int_{I_n}A( \mathbf{u},\mathbf{w}_v)dt-\int_{I_n}L(\mathbf {w}_v)dt \\ &\qquad {}+\int_{I_n}A(\dot{\mathbf{u}},\mathbf{w}_u)dt- \int_{I_n}A(\mathbf {v},\mathbf{w}_u)dt \\ &\qquad {}+\int_{\varOmega^{\alpha}_e}\mathbf{w}_v \bigl(t^+_n \bigr)\rho \bigl({\mathbf {v}} \bigl(t^+_n \bigr)-{\mathbf{v}} \bigl(t^-_n \bigr) \bigr)d\varOmega^{\alpha}_e \\ &\qquad {}+A \bigl(\mathbf{u} \bigl(t^+_n \bigr), \mathbf{w}_u \bigl(t^+_n \bigr) \bigr)-A \bigl(\mathbf {u} \bigl(t^-_n \bigr),\mathbf{w}_u \bigl(t^+_n \bigr) \bigr) \\ &\quad {}=A \bigl(\mathbf{u} \bigl(0^+ \bigr),\mathbf{w}_u \bigl(0^+ \bigr) \bigr)+\int_{\varOmega^{\alpha }_e}\mathbf{w}_v \bigl(0^+ \bigr) \rho\bigl({\mathbf{v}} \bigl(0^+ \bigr)\bigr)d\varOmega^{\alpha}_e. \end{aligned}$$
(27)

In Eq. (27), A(⋅,⋅) and L(⋅) are the bilinear and linear operators respectively and are given in Appendix C. Details of the numerical implementation can be found in Appendix D.

5 Numerical Experiments

In this section, two different problems are studied in order to determine the wave propagation characteristics in heterogeneous media with self similar structure. Numerical results obtained with different box counting measures, different element sizes, local and nonlocal fractional derivatives are compared with numerical results obtained for a homogeneous material. A 1D bar connected to a rigid wall is studied in order to expose the dispersion properties of the proposed model. A 2D suddenly loaded plate at its center is studied in order to determine the wave propagation characteristics for multi-dimensional problems.

5.1 1D Bar Connected to a Rigid Wall

In this example, a suddenly end loaded 1D bar connected to a rigid wall under tension is studied. The geometry of the problem is shown in Fig. 5. Linear basis functions are used. Young’s modulus E is 1 N/m2 and the density ρ is 1.0 kg/m3. Element sizes are chosen as Δx=0.5 m, Δx=0.25 m and Δx=0.125 m with corresponding time steps Δt=0.04 s, Δt=0.02 s and Δt=0.01 s. In order to eliminate the effect of the fixed end on the monitoring points, length of the bar is taken as L=40 m. Two monitoring points are chosen in order to determine the dispersion diagram and phase velocity. The first monitoring point is 2 m away from the loaded end and the second one is 6 m away from the loaded end. Dispersion diagrams and phase velocities are calculated by assuming that the waves are planar by using the Fourier transform of the stress values at the monitoring points.

Fig. 5
figure 5

Bar connected to a rigid wall and loading history

Full size image

The dispersion curve and phase velocity is shown in Fig. 6 for Δx=0.5. It is seen from the figure that the dispersion curves are almost linear for a wide number of wave numbers. When the wave number is close to 6, deviation from linearity is seen in the solutions with fractal dimensions α=0.8 to α=1. Thus α=1 is theoretically non-dispersive for a linear elastic material. Therefore, the phase velocities corresponding to frequencies higher than the wave number k=6 1/m are not presented. In the case of α=1, the phase velocity tends to increase after f=0.6 Hz, but is expected to be constant for all frequencies. Similar behavior is observed for the phase velocity of fractal media. In addition, results with nonlocal derivatives give smaller values of phase velocity and have the same characteristics with results obtained by using local fractional derivatives. When α=0.9, the phase velocity tends to increase after f=0.5 Hz in the case of local fractional derivatives, whereas the phase velocity tends to decrease when nonlocal derivatives are used.

Fig. 6
figure 6

Dispersion curves and phase velocity for Δx=0.5; —: local fractional derivative, - - -: nonlocal fractional derivative

Full size image

In Fig. 7, the dispersion curves and phase velocities are shown for Δx=0.25. The dispersion curves are almost linear similar to the case Δx=0.5. As the box counting dimension decreases, slopes of dispersion curves become closer. It is seen from the curve that the phase velocity is higher in the nonlocal case than in the local case when α=0.9. Contrarily, higher values of the phase velocity are observed in the local case when compared to the nonlocal case for lower values of α. In addition, the phase velocity increases with increasing frequency for all values of α.

Fig. 7
figure 7

Dispersion curves and phase velocity for Δx=0.25; —: local fractional derivative, - - -: nonlocal fractional derivative

Full size image

Dispersion curves and phase velocities are given in Fig. 8 for Δx=0.125. The dispersion curves are linear for both the nonlocal and the local cases for all box counting dimensions. The phase velocity is almost constant for a wide range of frequencies for all cases and decreases with decreasing box counting dimension. Similar to the previous element sizes, the phase velocity is higher in the local case than in the nonlocal case, apart from α=0.9.

Fig. 8
figure 8

Dispersion curves and phase velocity for Δx=0.125; —: local fractional derivative, - - -: nonlocal fractional derivative

Full size image

In Fig. 9 a space-time plot of stress is shown for Δx=0.125 as a representative case. It is observed that the pulse shape changes with the box counting dimension. The peak stress increases from 0.6 when α=0.9 to 0.75 when α=0.5 in both computations with nonlocal and local fractional derivatives. As the stress wave propagates, the peak stress decreases and the pulse gets wider. This effect becomes significant with decreasing box counting dimension and decreasing Δx. The decrease in peak stress is smaller than 8 %. In addition, it is observed that the results obtained with nonlocal fractional derivatives are very close to the results with local fractional derivatives.

Fig. 9
figure 9

Space-time plots of stress for Δx=0.125

Full size image

5.2 Suddenly Loaded Plate

In this example, a plate suddenly loaded in a central zone is studied under plane strain conditions. The geometry of the problem is shown in Fig. 10. Bilinear basis functions are used. Young’s modulus E is 70 GPa, Poisson’s ratio ν is 0.33 and the density ρ is 2700 kg/m3. Element sizes are chosen as Δx=1.25 mm, Δx=0.625 mm and Δx=0.3125 mm with a time step Δt=0.25 μs. The half-length and width of the plate are taken as L=0.1 m and W=0.02 m ant the loading zone is characterized by a=0.005 m (Fig. 10).

Fig. 10
figure 10

Suddenly loaded plate from its center and loading history

Full size image

The effective stress values at point x=60.0 mm, y=10.0 mm are shown for different element sizes in Fig. 11. It is seen that as the order of the fractional derivative decreases, effective stress values decrease and time lag increases. The transient part of the effective stress exhibits a similar behavior for all α. As the flexural waves develop, difference between the local and nonlocal fractional derivatives increases. In addition, it is also observed that the effective stress decreases with a decrease of the element size.

Fig. 11
figure 11

Comparison of effective stress values at x=60.0 mm, y=10.0 mm; —: local fractional derivative, - - -: nonlocal fractional derivative

Full size image

The maximum effective stress and the time (t max.) where maximum effective stress (\(\sigma_{\mathrm{eff}.}^{\mathrm{max}.}\)) is observed at point x=20.0 mm and y=10.0 mm is shown in a semi-logarithmic graph in Fig. 12. The maximum effective stress value decreases with a decrease of the order of the fractional derivative. A scaling behavior is observed from the figure with \(\alpha=a_{s}\log(\sigma_{\mathrm{eff.}}^{\mathrm{max}.})\) as a s varies between 3.07 and 5.64. The difference between the local and the nonlocal cases is negligible. On the other hand, t max. increases with increasing α. A similar scaling behavior is also observed between α and \(t_{\mathrm{max.}}\). A relation between α and \(t_{\mathrm{max.}}\) can be written as \(\alpha=a_{s}\log(t_{\mathrm{max.}})\) where the coefficient a s varies between 3.62 and 6.85.

Fig. 12
figure 12

Maximum effective stress and time it is determined at point x=20.0 mm, y=10.0 mm

Full size image

The directions and magnitude of the Poynting vector, which is defined as power flow per unit area and is given as p=−σ⋅v [4], is shown at the center line of the plate for two different points in Fig. 13 for the element size Δx=1.25 mm. It is seen that the power flow happens in the direction of thickness on the symmetry axis. The direction of the Poynting vector shows a ±35∘ scatter around the symmetry axis in the results for the case of local derivatives. In addition, the maximum value of magnitude of the Poynting vector is seen when α=0.9. In the results for the case of nonlocal derivatives, the direction of the power flow gets narrower and exhibits a ±30∘ scatter around the y axis of the plate. The magnitudes of the Poynting vectors are higher in the results for the case of nonlocal derivatives as compared to the results for the case of local derivatives. There is no preferred direction of the power flow observed at the point x=40.0 mm, y=10 mm for both cases of local and the nonlocal derivatives. The Poynting vector exhibits distinct bands for each order of the fractional derivative in results for the case of local derivatives. Similar to the results in the case of local derivatives, the results obtained for the case of nonlocal derivatives does not have any preferred direction. The transition between the magnitude of the Poynting vectors is not distinct and bands are entwined in the results for the case of nonlocal derivatives. The magnitudes of the Poynting vectors are higher in the nonlocal case as compared to results for the case of local fractional derivatives.

Fig. 13
figure 13

Directions and magnitudes of Poynting vectors at different instances, (Δx=1.25 mm)

Full size image

The direction of the Poynting vector and its magnitude is shown in Fig. 14 for Δx=0.625 mm. Similar to the results obtained with the element size Δx=1.25 mm, the Poynting vectors on symmetry axis have direction through the thickness of the plate both in the results for the cases of local and nonlocal derivatives. The scattering angle of the direction of the Poynting vectors about the symmetry axis decreases with a decrease of the order of the fractional derivative, and in addition with the magnitude of the Poynting vector, for both of the cases of local and nonlocal fractional derivatives. The scatter angle is approximately ±30∘ in the local derivative case and ±25∘ in the case of nonlocal derivatives. The results in the case of nonlocal derivatives have higher magnitudes as compared to results for the case of local derivatives. Moreover, the results with the nonlocal derivatives exhibit lower scattering angle on the symmetry axis as compared to results obtained with the local fractional derivatives. At point x=40 mm, y=10 mm, there is no preferred direction of the Poynting vector observed for both results with the local and the nonlocal fractional derivatives. The magnitude of the Poynting vector is higher in the results for the case of nonlocal derivatives. In Fig. 15, the direction and magnitude of the Poynting vector is presented for Δx=0.3125 mm. Similar behavior with larger element sizes is observed. The scattering of the direction of propagation decreases to ±20∘ in the results with local derivatives and ±15∘ in the results with nonlocal derivatives. The magnitude of the Poynting vectors differs with the change of order of the fractional derivative in the results with local derivatives. On the other hand, entwining in the magnitude of the Poynting vectors is seen in the results with the nonlocal derivatives.

Fig. 14
figure 14

Directions and magnitudes of Poynting vectors, (Δx=0.625 mm)

Full size image
Fig. 15
figure 15

Directions and magnitudes of Poynting vectors, (Δx=0.3125 mm)

Full size image

The longitudinal and Rayleigh wave speeds are compared in a semi-logarithmic graph in Fig. 16. The longitudinal wave speed is predicted via time of flight on the symmetry axis of the plate. Scaling behavior is observed both for the cases of local and nonlocal derivatives, with \(\alpha=a_{s}\log(c_{l}/c^{1}_{l})\), where \(c^{1}_{l}\) is the longitudinal wave speed for α=1 and is calculated as 6198.0 m/s for the material used in this study. It is observed that the longitudinal wave speed decreases with decreasing α and element size. The predicted value of a s varies between 3.38 and 5.43. The difference between the results in the cases of local and nonlocal derivative is small. A similar behavior is observed for the Rayleigh wave speed. The Rayleigh wave speed for the homogeneous media is predicted to be \(c^{1}_{R}=2857~\mbox{m}/\mbox{s}\). The slope of the semi-logarithmic graph is predicted to vary between 4.27 and 5.74.

Fig. 16
figure 16

Longitudinal and Rayleigh wave speeds

Full size image

Snapshots of the effective stress distributions are shown in Fig. 17 for Δx=0.635, for two different instances as a representative case. Even though it is not presented here, the results obtained for the case of local fractional derivatives are very close to those for the case of nonlocal fractional derivatives. Wave fronts obtained from computations with different box counting dimensions exhibit similar behavior except in the case of slow propagation. In addition, the effective stress values decrease with a decrease of the box counting dimension.

Fig. 17
figure 17

Effective stresses for Δx=0.625 mm obtained with nonlocal fractional derivatives

Full size image

6 Conclusion

In this study, wave propagation in heterogeneous material with self similar microstructure, such as porous materials [30], is studied by using fractional calculus. Due to the lack of an analytical solution and the absence of experimental results, the results presented in this study do not include validation.

A one dimensional bar suddenly loaded at its free end is studied and the dispersion relation and phase velocity is presented for different box counting dimensions and element sizes. It is observed that as the box counting dimension decreases, the phase velocity decreases as seen in porous materials with increasing porosity [41]. It is known that the porosity is inversely proportional to the fractal dimension in porous materials [49]. In addition, we found that the dispersion curve is almost linear and exhibits a weakly dispersive character for all box counting dimensions within the range of our analysis. The difference between the results obtained in the cases of local derivatives and nonlocal derivatives is negligible for one dimensional problems.

A two dimensional suddenly loaded plate under the assumption of plane strain conditions is studied in order to demonstrate the multi-dimensional behavior of the proposed model. It is observed that the amplitude of the maximum effective stress decreases with a decrease of the box counting dimension, which seems to mimic elastic wave scattering in porous materials. In addition, as the stress wave propagates in the plate and as the flexural waves dominate the problem, the difference in the results between the material models with local and nonlocal fractional derivatives becomes significant. One can conclude that the local fractional derivative can be used as an approximation to nonlocal counterparts for transient problems. On the other hand, the difference in the results may be significant when studying the dynamic behavior of material for harmonic problems or in the prediction of failure such as crack propagation. Similar to the wave speeds in the one dimensional case, both the Rayleigh and the longitudinal wave speeds decrease with decreasing box counting dimension and exhibit a power law scaling. Such scaling is also seen in the maximum effective stresses. It is observed that the difference in the wave speeds between the two material models with local and nonlocal derivatives is negligible. In addition, this difference may be significant and has an effect on the Poynting vector which shows the direction and magnitude of the power flow per unit area, as is seen from the comparison of the Poynting vectors. Difference in the Poynting vectors may cause misprediction of the location of the maximum effective stress, which is used as a criteria for most of the failure models.

As a summary, the one dimensional and two dimensional results show that the model which is based on local fractional derivatives can be used as an approximation to the model based on nonlocal fractional derivatives only for a limited number of cases. One can conclude that the model presented in this study is a good candidate for modeling the dynamic mechanical of the behavior of heterogeneous structures. Experimental studies are needed in order to validate the relations we have reported between the wave speeds, fractal dimension and topology.