Transversely isotropic thermoelastic thin circular plate with constant and periodically varying load and heat source

Abstract

The present research deals with the deformation in transversely isotropic thermoelastic (TIT) thin circular plate. Rotation effect is studied under thermally insulated as well as isothermal boundaries. The Laplace and Hankel transform techniques have been used to find the solution to the problem. The displacement components, conductive temperature distribution, and stress components with the radial distance are computed in the transformed domain and further calculated in the physical domain using numerical inversion techniques. The effects of rotation and two temperatures are represented graphically. Some specific cases are also figured out from the current research.

Introduction

A lot of research has been carried out to predict deformation and heat flow in a continuum using thermoelasticity theories during the past few years. Thick plate, thin plate, and a membrane have a large difference according to their structure. Circular thin plates and membranes are widely used in pressure sensors, microphones, loudspeakers, gas flow metres, optical telescopes, solar powers, radio and radar antennae, and many other devices. Plate theories are beneficial for designs and analyses of these devices. Zhao (2008) described the flexural properties of a plate influenced by its thickness. According to Ventsel and Krauthammer (2001) and Zhao (2008), plates can be classified into three categories: membranes, thin plates, and thick plates depending upon the aspect ratio. The aspect ratio is defined as a/h, where a is the diameter of a plate and h is the thickness of a plate. The plates with aspect ratio a/h ≥ 80...100 are referred as membranes. It is termed as thin plate with aspect ratio as 8…10 ≤ a/h ≤ 80….100. Moreover, if a/h ≤ 8...10, the plate is termed as thick plate.

Kar and Kanoria (2011) studied the thermoelastic response of fibre-reinforced thin circular disc with three phase lag due to axisymmetric thermoelastic loading. Tripathi, Warbhe, Deshmukh, & Verma, (2017a; Tripathi, Warbhe, Deshmukh, & Verma, 2017b) investigated a quasi-static uncoupled theory of thermoelasticity based on time fractional heat conduction equation for a thin circular plate and studied a thin hollow circular disc with quasi-static uncoupled theory of thermoelasticity with the time fractional derivative of order alpha subjected to a time-dependent heat flux. Bhad and Varghese (2014) studied thermoelastic deformation with annular heat supply on a thin circular plate. Tikhe and Deshmukh (2005; Tikhe & Deshmukh, 2006) considered the inverse problem of transient heat conduction in a thin finite circular plate with integral transform technique and the thin circular plate for unknown heating temperatures in the form of Bessel functions and with integral techniques. Gaikwad (2016; Gaikwad & Deshmukh, 2005; Gaikwad, Ghadle, & Mane, 2012) described the circular plate for known interior temperature under steady-state field, a thin circular plate due to uniform internal energy generation using Hankel transform technique for its solution, and the inverse problem of thermoelasticity in a thin isotropic circular plate. Parveen, Lamba, & Khobragade (2012) examined the thermal deflection of a thin circular plate using boundary conditions of radiation type. Ahire, Hamoud, & Ghadle (2019) studied a problem of thermal stresses in circular plate due to internal moving heat sources with integral transform technique. Also, researchers such as Marin (1998, 1999), Hassan, Marin, Ellahi, & Alamri (2018; Marin, Baleanu, & Vlase, 2017), Marin and Craciun (2017; Marin, Craciun, & Pop, 2016), Marin and Öchsner (2017), Lata and Kaur (Kaur & Lata, 2019; Lata & Kaur, 2019a; Lata & Kaur, 2019c; Lata & Kaur, 2019d), Othman and Marin (2017), and Kumar, Sharma, & Lata (2016a) worked on different theories of thermoelasticity. In spite of all these efforts, no attempt has been made for coupled theory of thermoelasticity of thin circular plate with rotation.

In this paper, we have attempted to study the deformation in transversely isotropic thin circular plate due to isothermal/thermally insulated boundaries. The Laplace and Hankel transform has been used to obtain the general solution of the field equations. The analytical expressions of stresses, conductive temperature, and displacement components are computed in transformed domain. However, the resulting quantities are obtained in the physical domain by using numerical inversion technique. Some particular cases are also discussed.

Basic equations

Following Lata (2017a, 2017b), the constitutive relations and field equations for an anisotropic thermoelastic medium in the absence of body forces and heat sources are:

$$ {t}_{ij}={C}_{ij kl}{e}_{kl}-{\beta}_{ij}T, $$

(1)

$$ {C}_{ij kl}{e}_{kl,j}-{\beta}_{ij}{T}_{,j}=\rho {\ddot{u}}_i, $$

(2)

$$ \left({K}_{ij}^{\ast }+{K}_{ij}\frac{\partial }{\partial t}\right){\varphi}_{, ij}=\left(1+{\tau}_0\frac{\partial }{\partial t}\right)\left({\beta}_{ij}{T}_0{\dot{e}}_{ij}+{\rho C}_E\dot{T}\right) $$

(3)

where

$$ T=\varphi -{a}_{ij}{\varphi}_{, ij}, $$

(4)

$$ {\beta}_{ij}={C}_{ij kl}{\alpha}_{ij}, $$

(5)

$$ {e}_{ij}=\frac{1}{2}\left({u}_{i,j}+{u}_{j,i}\right).\kern0.5em i=1,2,3 $$

(6)

β_ij is the thermal tensor, T is the thermodynamic temperature, τ₀ is the relaxation time, T₀ is the reference temperature, t_ij are the components of stress tensor, e_ij are the components of strain tensor, u_i are the displacement components, φ is the conductive temperature, ρ is the density, C_E is the specific heat, K_ij is the thermal conductivity parameter, ${K}_{ij}^{\ast }$ is the materialistic constant,  a_ij are the two temperature parameters, and α_ijis the coefficient of linear thermal expansion. C_ijkl are the elastic parameters with symmetry (C_ijkl = C_klij = C_jikl = C_ijlk). These symmetries of C_ijkl are due to the following:

• The stress tensor is symmetric, which is only possible if (C_ijkl = C_jikl).

• If a strain energy density exists for the material, the elastic stiffness tensor must satisfy C_ijkl = C_klij.

• From stress tensor and elastic stiffness, tensor symmetries infer (C_ijkl = C_ijlk) and C_ijkl = C_klij = C_jikl = C_ijlk.

And following Kumar, Sharma, & Lata (2016b), the equation of motion for a uniformly rotating medium with an angular velocity Ω is:

$$ {t}_{ij,j}=\rho {\left\{{\ddot{\boldsymbol{u}}}_i+\left(\boldsymbol{\Omega} \times \boldsymbol{\Omega} \times \mathbf{u}\right)\right\}}_i+\Big(2\boldsymbol{\Omega} \times {\dot{\boldsymbol{u}\Big)}}_i, $$

(7)

where Ω = Ωn, n is a unit vector representing the direction of axis of rotation, the term Ω × (Ω × u) is the additional centripetal acceleration due to the time-varying motion only, and the term $2\boldsymbol{\Omega} \times \dot{\boldsymbol{u}}$is the Coriolis acceleration.

The components of Lorentz force are:

$$ {F}_i={\mu}_0\left(\overrightarrow{j}\times {\overrightarrow{H}}_0\right), $$

where ${\overrightarrow{H}}_0$ the is magnetic field intensity vector and $\overrightarrow{j}$ is the current density vector.

Method and formulation of the problem

We consider a transversely isotropic thin circular plate of thickness 2b occupying space D defined by 0 ≤ r ≤ ∞,−h ≤ z ≤ h. Thin plates are usually characterised by the ratio a/h (the ratio between the length of a side, a, and the thickness of the material, h, falling between the values of 8 and 80 as mentioned by Ventsel and Krauthammer (2001). Let the plate be subjected to axisymmetric heat supply thermal shock load applied into its inner boundary having initially undisturbed state at a uniform temperature T₀. We use plane cylindrical coordinates (r, θ, z) with the centre of the plate as the origin (Fig. 1).

Fig. 1

Geometry of the problem

As the problem considered is plane axisymmetric, (u, v, w, and φ) are independent of θ. We restrict our analysis to two-dimension problem with $\overrightarrow{u}=\left(u,0,w\right)$, also applying the transformation:

$$ {x}^{\prime }=x\cos \phi +y\sin \phi, {y}^{\prime }=-x\sin \phi +y\cos \phi, \kern0.5em {z}^{\prime }=z. $$

where ϕ is the angle of rotation in x-y plane, on the set of Eqs. (1)–(3) to derive the equations for TIT solid with two temperatures and with energy dissipation, to obtain:

$$ {C}_{11}\left(\frac{\partial^2u}{{\partial r}^2}+\frac{1}{r}\frac{\partial u}{\partial r}-\frac{1}{r^2}u\right)+{C}_{13}\left(\frac{\partial^2w}{\partial r\partial z}\right)+{C}_{44}\frac{\partial^2u}{{\partial z}^2}+{C}_{44}\left(\frac{\partial^2w}{\partial r\partial z}\right)-{\beta}_1\frac{\partial }{\partial r}\left\{\varphi -{a}_1\left(\frac{\partial^2\varphi }{{\partial r}^2}+\frac{1}{r}\frac{\partial \varphi }{\partial r}\right)-{a}_3\frac{\partial^2\varphi }{{\partial z}^2}\right\}=\rho \left(\frac{\partial^2u}{\partial {t}^2}-{\varOmega}^2u+2\varOmega \frac{\partial w}{\partial t}\right), $$

(8)

$$ \left({C}_{11}+{C}_{44}\right)\left(\frac{\partial^2u}{\partial r\partial z}+\frac{1}{r}\frac{\partial u}{\partial z}\right)+{C}_{44}\left(\frac{\partial^2w}{{\partial r}^2}+\frac{1}{r}\frac{\partial w}{\partial r}\right)+{C}_{33}\frac{\partial^2w}{{\partial z}^2}-{\beta}_3\frac{\partial }{\partial z}\left\{\varphi -{a}_1\left(\frac{\partial^2\varphi }{{\partial r}^2}+\frac{1}{r}\frac{\partial \varphi }{\partial r}\right)-{a}_3\frac{\partial^2\varphi }{{\partial z}^2}\right\}=\rho \left(\frac{\partial^2w}{\partial {t}^2}-{\varOmega}^2w-2\varOmega \frac{\partial u}{\partial t}\right), $$

(9)

$$ \left({K}_1^{\ast }+{K}_1\frac{\partial }{\partial t}\right)\left(\frac{\partial^2\varphi }{{\partial r}^2}+\frac{1}{r}\frac{\partial \varphi }{\partial r}\right)+\left({K}_3^{\ast }+{K}_3\frac{\partial }{\partial t}\right)\frac{\partial^2\varphi }{{\partial z}^2}={T}_0\left(1+{\tau}_0\frac{\partial }{\partial t}\right)\left({\beta}_1\frac{\partial \dot{u}}{\partial r}+{\beta}_3\frac{\partial \dot{w}}{\partial z}\right)+\rho {C}_E\left(1+{\tau}_0\frac{\partial }{\partial t}\right)\left\{\dot{\varphi}-{a}_1\left(\frac{\partial^2\dot{\varphi}}{{\partial r}^2}+\frac{1}{r}\frac{\partial \dot{\varphi}}{\partial r}\right)-{a}_3\frac{\partial^2\dot{\varphi}}{{\partial z}^2}\right\}. $$

(10)

In above equations, we use the contracting subscript notations (1 → 11, 2 → 22, 3 → 33, 5 → 23, 4 → 13, 6 → 12) to relate C_ijkl to C_mn. Also a₁ and a₃ are two temperature parameters.

For axisymmetric problem following Lata and Kaur (2019b), the constitutive relations are:

$$ {t}_{rr}={c}_{11}{e}_{rr}+{c}_{12}{e}_{\theta \theta}+{c}_{13}{e}_{zz}-{\beta}_1T, $$

$$ {t}_{zr}=2{c}_{44}{e}_{rz}, $$

$$ {t}_{zz}={c}_{13}{e}_{rr}+{c}_{13}{e}_{\theta \theta}+{c}_{33}{e}_{zz}-{\beta}_3T, $$

$$ {t}_{\theta \theta}={c}_{12}{e}_{rr}+{c}_{11}{e}_{\theta \theta}+{c}_{13}{e}_{zz}-{\beta}_1T, $$

where

$$ {e}_{rz}=\frac{1}{2}\left(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial r}\right), $$

$$ {e}_{rr}=\frac{\partial u}{\partial r}, $$

$$ {e}_{\theta \theta}=\frac{u}{r}, $$

$$ {e}_{zz}=\frac{\partial w}{\partial z}, $$

$$ T=\varphi -{a}_1\left(\frac{\partial^2\varphi }{{\partial r}^2}+\frac{1}{r}\frac{\partial \varphi }{\partial r}\right)-{a}_3\frac{\partial^2\varphi }{{\partial z}^2}, $$

$$ {\beta}_{ij}={\beta}_i{\delta}_{ij},\kern0.5em {K}_{ij}={K}_i{\delta}_{ij,} $$

$$ {\beta}_1=\left({c}_{11}+{c}_{12}\right){\alpha}_1+{c}_{13}{\alpha}_3, $$

$$ {\beta}_3=2{c}_{13}{\alpha}_1+{c}_{33}{\alpha}_3. $$

To facilitate the solution, the following dimensionless quantities are introduced:

$$ {r}^{\prime }=\frac{r}{L},\kern0.75em {z}^{\prime }=\frac{z}{L},{t}^{\prime }=\frac{c_1}{L}t,{u}^{\prime }=\frac{{\rho c}_1^2}{L{\beta}_1{T}_0}u,{w}^{\prime }=\frac{{\rho c}_1^2}{L{\beta}_1{T}_0}w,{T}^{\prime }=\frac{T}{T_0},{t}_{zr}^{\prime }=\frac{t_{zr}}{\beta_1{T}_0},{t}_{zz}^{\prime }=\frac{t_{zz}}{\beta_1{T}_0},{\varOmega}^{\prime }=\frac{L}{C_1}\varOmega, {\varphi}^{\prime }=\frac{\varphi }{T_0},{a}_1^{\prime }=\frac{a_1}{L^2},{a}_3^{\prime }=\frac{a_3}{L^2}, $$

(11)

where ${c}_1^2=\frac{c_{11}}{\rho }$, and L is a constant of dimension of length.

Using the dimensionless quantities defined by Eq. (11) in Eqs. (8)–(10) and after that suppressing the primes and applying the Laplace and Hankel transforms defined by:

$$ {f}^{\ast}\left(r,z,s\right)=\underset{0}{\overset{\infty }{\int }}f\left(r,z,t\right){e}^{- st} dt, $$

(12)

$$ \overset{\sim }{f}\left(\xi, z,s\right)=\underset{0}{\overset{\infty }{\int }}{f}^{\ast}\left(r,z,s\right)r{J}_n\left( r\xi \right) dr. $$

(13)

on the resulting quantities, we obtain:

$$ \left(-{\xi}^2-{s}^2+{\varOmega}^2+{\delta}_2{D}^2\right)\overset{\sim }{u}+\left[{\xi \delta}_1D-2\varOmega s\right]\overset{\sim }{w}+\left(\xi \left(1-{a}_3{D}^2\Big)+{a}_1{\xi}^3\right)\right)\overset{\sim }{\varphi }=0, $$

(14)

$$ \left({\delta}_1\xi D+2\varOmega s\right)\overset{\sim }{u}+\left({\delta}_3{D}^2-{\delta}_2{\xi}^2-{s}^2+{\varOmega}^2\right)\overset{\sim }{w}-\left(\frac{\beta_3}{\beta_1}D\left[\left(1-{a}_3{D}^2\right)+{\xi}^2{a}_1\right]\right)\overset{\sim }{\varphi }=0, $$

(15)

$$ {\delta}_4\left(s+{\tau}_0{s}^2\right)\xi \overset{\sim }{u}-{\delta}_5\left(s+{\tau}_0{s}^2\right)D\overset{\sim }{w}+\left(-{\delta}_6\left(s+{\tau}_0{s}^2\right)\left(1+{\xi}^2{a}_1\right)-\left({K}_1^{\ast }+\frac{C_1}{L}{K}_1s\right){\xi}^2+{D}^2\left({K}_3^{\ast }+\frac{C_1}{L}{K}_3s+{a}_3{\delta}_6\left(s+{\tau}_0{s}^2\right)\right)\right)\overset{\sim }{\varphi }=0, $$

(16)

where

$$ {\delta}_1=\frac{c_{13}+{c}_{44}}{c_{11}},\kern0.5em {\delta}_2=\frac{c_{44}}{c_{11}},\kern0.5em {\delta}_3=\frac{c_{33}}{c_{11}},\kern0.5em {\delta}_4=\frac{\beta_1^2{T}_0}{\rho },\kern0.75em {\delta}_5=\frac{\beta_1{\beta}_3{T}_0}{\rho },\kern0.5em {\delta}_6=\rho {C}_E{C}_1^2, $$

and

$$ D\equiv \frac{d}{dz}, $$

$$ \overset{\sim }{t_{zz}}=\frac{C_{13}}{C_{11}}\xi \overset{\sim }{u}+{\delta}_3D\overset{\sim }{w}-\frac{\upbeta_3}{\upbeta_1}\left(1+{a}_1{\xi}^2-{a}_3{D}^2\right)\overset{\sim }{\varphi }, $$

(17)

$$ \overset{\sim }{t_{rz}}={\delta}_2D\overset{\sim }{u}-\xi {\delta}_2\overset{\sim }{w}, $$

(18)

$$ \overset{\sim }{t_{rr}}=-\xi \overset{\sim }{u}+\frac{C_{12}\xi }{C_{11}}\overset{\sim }{u}+\frac{C_{13}}{C_{11}}D\overset{\sim }{w}-\left(1+{a}_1{\xi}^2-{a}_3{D}^2\right)\overset{\sim }{\varphi }. $$

(19)

We will obtain the non-trivial solution of Eqs. (14)–(16) if the determinant of the coefficient$\overset{\sim }{\ u}$, $\overset{\sim }{w}$, and $\overset{\sim }{\varphi\ }$vanishes, which yields to the following characteristic equation:

$$ {AD}^6+{BD}^4+{CD}^2+E=0, $$

(20)

where

$$ \mathrm{A}={\updelta}_2{\updelta}_3{\upzeta}_{12}-{\updelta}_2{\upzeta}_{10}{\upzeta}_8, $$

$$ \mathrm{B}={\upzeta}_1{\upzeta}_{12}{\updelta}_3-{\zeta}_1{\zeta}_{10}{\upzeta}_8+{\updelta}_2{\updelta}_3{\upzeta}_{11}+{\updelta}_2{\upzeta}_{12}{\upzeta}_6-{\updelta}_2{\upzeta}_{10}{\upzeta}_7-{\zeta}_2^2{\upzeta}_{12}-{\zeta}_2{\zeta}_9{\upzeta}_8+{\zeta}_5{\zeta}_{10}{\upzeta}_2-{\upzeta}_5{\upzeta}_9{\updelta}_3, $$

$$ C={\updelta}_3{\upzeta}_1{\upzeta}_{11}+{\updelta}_2{\upzeta}_6{\upzeta}_{11}+{\upzeta}_1{\upzeta}_6{\upzeta}_{12}-{\upzeta}_1{\upzeta}_{10}{\upzeta}_7-{\zeta}_2^2{\upzeta}_{11}+{\upzeta}_2{\upzeta}_7{\upzeta}_9-{\upzeta}_5{\upzeta}_6{\upzeta}_9+{\upzeta}_4{\upzeta}_2{\upzeta}_{10}-{\updelta}_3{\upzeta}_4{\upzeta}_9+{\zeta}_3^2{\upzeta}_{12}, $$

$$ E={\upzeta}_6{\upzeta}_1{\upzeta}_{11}-{\upzeta}_4{\upzeta}_6{\upzeta}_9. $$

$$ {\upzeta}_1=-{\xi}^2-{\mathrm{s}}^2+{\Omega}^2, $$

$$ {\upzeta}_2={\delta}_1\xi, $$

$$ {\upzeta}_3=2\Omega s, $$

$$ {\upzeta}_4=\upxi \left(1+{\mathrm{a}}_1{\upxi}^2\right), $$

$$ {\upzeta}_5={a}_3\xi, $$

$$ {\upzeta}_6=-{\delta}_2{\xi}^2-{s}^2+{\Omega}^2, $$

$$ {\upzeta}_7=-\frac{\upbeta_3}{\upbeta_1}\left(1+{\mathrm{a}}_1{\upxi}^2\right), $$

$$ {\upzeta}_8=\frac{\upbeta_3}{\upbeta_1}{\mathrm{a}}_3, $$

$$ {\upzeta}_9={\delta}_4\left(s+{\tau}_0{s}^2\right)\xi, $$

$$ {\upzeta}_{10}=-{\delta}_5\left(s+{\tau}_0{s}^2\right), $$

$$ {\zeta}_{11}=-{\delta}_6\left(s+{\tau}_0{s}^2\right)\left(1+{\mathrm{a}}_1{\upxi}^2\right)-{\xi}^2\left({K}_1^{\ast }+\frac{C_1}{L}{K}_1s\right), $$

$$ {\zeta}_{12}=\left({K}_3^{\ast }+\frac{C_1}{L}{K}_3s+{a}_3{\delta}_6\left(s+{\tau}_0{s}^2\right)\right). $$

The solutions of Eq. (20) can be written in the form by making use of the radiation condition that $\overset{\sim }{\ u}$, $\overset{\sim }{w}$, $\overset{\sim }{\varphi\ }\to 0$ as z →  ∞ :

$$ \overset{\sim }{u}=\sum {A}_i\left(\xi, s\right)\cosh \left({q}_iz\right), $$

(21)

$$ \overset{\sim }{w}=\sum {d}_i{A}_i\left(\xi, s\right)\cosh \left({q}_iz\right), $$

(22)

$$ \overset{\sim }{\varphi }=\sum {l}_i{A}_i\left(\xi, s\right)\cosh \left({q}_iz\right), $$

(23)

where A_i, being arbitrary constants,±q_i are the roots of Eq. (20), and

$$ {d}_i=\frac{\left({\zeta}_2{\zeta}_{12}-{\zeta}_8{\zeta}_9\right){q}_i^3+{\zeta}_3{\zeta}_{12}{q}_i^2+\left({\zeta}_2{\zeta}_{11}-{\zeta}_7{\zeta}_9\right){q}_i+{\zeta}_3{\zeta}_{11}}{\left(-{\zeta}_8{\zeta}_{10}+{\delta}_3{\upzeta}_{12}\right){q}_i^4+\left({\delta}_3{\zeta}_{11}+{\zeta}_6{\zeta}_{12}-{\zeta}_7{\zeta}_{10}\right){q}_i^2+{\zeta}_6{\zeta}_{11}}, $$

(24)

$$ {l}_i=\frac{\left(-{\zeta}_9{\delta}_3+{\zeta}_1{\zeta}_{10}\right){q}_i^2+{\zeta}_3{\zeta}_{10}{q}_i-{\zeta}_8{\zeta}_9}{\left(-{\zeta}_8{\zeta}_{10}+{\delta}_3{\upzeta}_{12}\right){q}_i^4+\left({\delta}_3{\zeta}_{11}+{\zeta}_6{\zeta}_{12}-{\zeta}_7{\zeta}_{10}\right){q}_i^2+{\zeta}_6{\zeta}_{11}}, $$

(25)

where i = 1, 2, 3.

Also, using Eqs. (21)–(23) in expressions (17)–(19), we obtain stress components as:

$$ \overset{\sim }{t_{zz}}=\sum {A}_i\left(\xi, s\right){\eta}_i\cosh \left({q}_iz\right)+\sum {\mu}_i{A}_i\left(\xi, s\right)\sinh \left({q}_iz\right), $$

(26)

$$ \overset{\sim }{t_{rz}}=\sum {A}_i\left(\xi, s\right){M}_i\cosh \left({q}_iz\right)+\sum {N}_i{A}_i\left(\xi, s\right)\sinh \left({q}_iz\right), $$

(27)

$$ {t}_{rr}=\sum {A}_i\left(\xi, s\right){R}_i\cosh \left({q}_iz\right)+\sum {S}_i{A}_i\left(\xi, s\right)\sinh \left({q}_iz\right), $$

(28)

where

$$ {\eta}_i=\frac{C_{13}}{C_{11}}\xi -\frac{\upbeta_3}{\upbeta_1}{l}_i\left(1+{a}_1{\xi}^2-{\mathrm{a}}_3{\mathrm{q}}_{\mathrm{i}}^2\right), $$

$$ {R}_i=-\xi +\frac{C_{12}\xi }{C_{11}}-\left(1+{a}_1{\xi}^2-{a}_3{\mathrm{q}}_{\mathrm{i}}^2\right), $$

$$ {S}_i=\frac{C_{13}}{C_{11}}{d}_i{q}_i, $$

$$ {\mu}_i={\delta}_3{d}_i{q}_i, $$

$$ {M}_i={\delta}_2{d}_i\xi, $$

$$ {N}_i={\delta}_2{q}_i,i=1,2,3. $$

Boundary conditions

We consider a cubical thermal source and normal force along with vanishing of tangential stress components at the stress-free surface at z = ± h. Mathematically, these can be written as:

$$ {h}_1\frac{\partial \varphi }{\partial z}+{h}_2\varphi =\pm {g}_oF\left(r,z\right), $$

(29)

$$ {t}_{zz}\left(r,z,t\right)=f\left(r,t\right), $$

(30)

$$ {t}_{rz}\left(r,z,t\right)=0. $$

(31)

Here, h₂ → 0 corresponds to thermally insulated boundaries and h₁ → 0 corresponds to isothermal boundaries. Using the dimensionless quantities defined by Eq. (11) on Eqs. (29)–(31) and taking Hankel and Laplace transform of the resulting equations and then using Eqs. (26) and (27) and Eqs. (21)–(23) yields:

$$ \sum {A}_i{l}_i\left({h}_1{q}_i+{h}_2\right)\sinh \left({q}_ih\right)=\pm {g}_o\overset{\sim }{F}\left(\xi, h\right), $$

(32)

$$ \sum {A}_i\left(\xi, s\right){\eta}_i\cosh \left({q}_ih\right)+\sum {\mu}_i{A}_i\left(\xi, s\right)\sinh \left({q}_ih\right)=\overset{\sim }{f}\left(\xi, s\right), $$

(33)

$$ \sum {A}_i\left(\xi, s\right){M}_i\cosh \left({q}_ih\right)+\sum {N}_i{A}_i\left(\xi, s\right)\sinh \left({q}_ih\right),=0. $$

(34)

Solving Eqs. (21)–(23) with the aid of Eqs. (32)–(34) and hence solving Eqs. (26)–(28), we obtain:

$$ \overset{\sim }{u}=\frac{\overset{\sim }{f}\left(\xi, s\right)}{\Delta}\left\{-{\chi}_1{\vartheta}_1+{\chi}_2{\vartheta}_2-{\chi}_3{\vartheta}_3\right\}+\frac{g_o\overset{\sim }{F}\left(\xi, h\right)}{\Delta}\left\{{\chi}_4{\vartheta}_1-{\chi}_5{\vartheta}_2+{\chi}_6{\vartheta}_3\right\}, $$

(35)

$$ \overset{\sim }{w}=\frac{\overset{\sim }{f}\left(\xi, s\right)}{\Delta}\left\{-{\chi}_1{d}_1{\vartheta}_1+{\chi}_2{d}_2{\vartheta}_2-{\chi}_3{d}_3{\vartheta}_3\right\}+\frac{g_o\overset{\sim }{F}\left(\xi, h\right)}{\Delta}\left\{{\chi}_4{d}_1{\vartheta}_1-{\chi}_5{d}_2{\vartheta}_2+{\chi}_6{d}_3{\vartheta}_3\right\}, $$

(36)

$$ \overset{\sim }{\varphi }=\frac{\overset{\sim }{f}\left(\xi, s\right)}{\Delta}\left\{-{\chi}_1{l}_1{\vartheta}_1+{\chi}_2{l}_2{\vartheta}_2-{\chi}_3{l}_3{\vartheta}_3\right\}+\frac{g_o\overset{\sim }{F}\left(\xi, h\right)}{\Delta}\left\{{\chi}_4{l}_1{\vartheta}_1-{\chi}_5{l}_2{\vartheta}_2+{\chi}_6{l}_3{\vartheta}_3\right\}, $$

(37)

$$ \overset{\sim }{t_{zz}}=\frac{\overset{\sim }{f}\left(\xi, s\right)}{\Delta}\left\{-{\chi}_1{G}_4+{\chi}_2{G}_5-{\chi}_3{G}_6\right\}+\frac{g_o\overset{\sim }{F}\left(\xi, h\right)}{\Delta}\left\{{\chi}_4{G}_4-{\chi}_5{G}_5+{\chi}_6{G}_6\right\}, $$

(38)

$$ \overset{\sim }{t_{zr}}=\frac{\overset{\sim }{f}\left(\xi, s\right)}{\Delta}\left\{-{\chi}_1{G}_7+{\chi}_2{G}_8-{\chi}_3{G}_9\right\}+\frac{g_o\overset{\sim }{F}\left(\xi, h\right)}{\Delta}\left\{{\chi}_4{G}_7-{\chi}_5{G}_8+{\chi}_6{G}_9\right\}, $$

(39)

$$ \overset{\sim }{t_{rr}}=\frac{\overset{\sim }{f}\left(\xi, s\right)}{\Delta}\left\{-{\chi}_1{G}_{10}+{\chi}_2{G}_{11}-{\chi}_3{G}_{12}\right\}+\frac{g_o\overset{\sim }{F}\left(\xi, h\right)}{\Delta}\left\{{\chi}_4{G}_{10}-{\chi}_5{G}_{11}+{\chi}_6{G}_{12}\right\}, $$

(40)

where

$$ {G}_i={l}_i\left({h}_1{q}_i+{h}_2\right){\theta}_i, $$

$$ {G}_{i+3}={\eta}_i{\vartheta}_i+{\mu}_i{\theta}_i, $$

$$ {G}_{i+6}={N}_i{\theta}_i+{M}_i{\vartheta}_i, $$

$$ {G}_{i+9}={S}_i{\theta}_i+{R}_i{\vartheta}_i,i=1,2,3. $$

$$ \Delta ={\mathrm{G}}_1{\chi}_4-{\mathrm{G}}_2{\chi}_5+{\mathrm{G}}_3{\chi}_6, $$

$$ {\Delta}_1=-\overset{\sim }{f}\left(\xi, s\right){\chi}_1+{g}_o\overset{\sim }{F}\left(\xi, h\right){\chi}_4, $$

$$ {\Delta}_2=\overset{\sim }{f}\left(\xi, s\right){\chi}_2-{g}_o\overset{\sim }{F}\left(\xi, h\right){\chi}_5, $$

$$ {\Delta}_3=-\overset{\sim }{f}\left(\xi, s\right){\chi}_3+{g}_o\overset{\sim }{F}\left(\xi, h\right){\chi}_6, $$

$$ {\chi}_1=\left[{\mathrm{G}}_2{\mathrm{G}}_9-{\mathrm{G}}_8{\mathrm{G}}_3\right], $$

$$ {\chi}_2=\left[{\mathrm{G}}_1{\mathrm{G}}_9-{\mathrm{G}}_7{\mathrm{G}}_3\right], $$

$$ {\chi}_3=\left[{\mathrm{G}}_1{\mathrm{G}}_8-{\mathrm{G}}_2{\mathrm{G}}_7\right], $$

$$ {\chi}_4=\left[{\mathrm{G}}_5{\mathrm{G}}_9-{\mathrm{G}}_8{\mathrm{G}}_6\right], $$

$$ {\chi}_5=\left[{\mathrm{G}}_4{\mathrm{G}}_9-{\mathrm{G}}_6{\mathrm{G}}_7\right], $$

$$ {\chi}_6=\left[{\mathrm{G}}_4{\mathrm{G}}_8-{\mathrm{G}}_5{\mathrm{G}}_7\right], $$

$$ {\vartheta}_i=\cosh \left({q}_ih\right),{\theta}_i=\sinh \left({q}_ih\right),i=1,2,3 $$

Applications

In this section, we discuss the effect of various heat sources on the transversely isotropic thin circular plate.

Constant load and heat source

For constant load and heat source which decays moving away from the centre of the thin circular plate in the radial direction as well as along the axial directions:

$$ f\left(r,t\right)=H(t),F\left(\mathrm{r},\mathrm{z}\right)=\frac{1}{\sqrt{r^2+{z}^2}} $$

(41)

where H(t) denotes the Heaviside function. Applying the Laplace and Hankel transform, on Eq. (41), gives:

$$ \overline{f}\left(\xi, s\right)=\frac{1}{s},\overset{\sim }{F}\left(\xi, z\right)=\frac{e^{-\xi \left|z\right|}}{\xi } $$

(42)

Periodically varying load and heat source

For periodically varying load and heat source which decays moving away from the centre of the thin circular plate in the radial direction as well as along the axial directions:

$$ f\left(r,t\right)={T}_0\left\{\begin{array}{c}\sin \frac{\pi t}{\gamma },0\le t\le \gamma, \\ {}0,t>\gamma .\end{array}\right.F\left(\mathrm{r},\mathrm{z}\right)=\frac{1}{r^2+{z}^2} $$

(43)

Applying the Laplace and Hankel transform, on Eq. (43), gives:

$$ \overline{f}\left(\xi, s\right)=\frac{T_0\pi \gamma \left(1+{e}^{- s\gamma}\right)}{\left({\pi}^2+{s}^2{\gamma}^2\right)},\overset{\sim }{F}\left(\xi, z\right)={K}_0\left(\xi z\right) $$

(44)

Inversion of the transforms

To find the solution of the problem in physical domain, we must invert the transforms in Eqs. (34)–(39). These equations are functions of ξ and z and hence are of the form$\overset{\sim }{f}\left(\xi, z,\omega \right)$. To get the function f(r, z, ω) in the physical domain, first, we invert the Hankel transform using:

$$ f\left(r,z,\omega \right)=\underset{0}{\overset{\infty }{\int }}\xi \overset{\sim }{f}\left(\xi, z,\omega \right){J}_n\left(\xi r\right) d\xi . $$

(45)

The last step is to calculate the integral in Eq. (45). The method for evaluating this integral is described in Press, Teukolshy, Vellerling, & Flannery (1986), which uses Romberg’s integration with adaptive step size. This also uses the results from successive refinements of the extended trapezoidal rule followed by extrapolation of the results to the limit when the step size tends to zero.

Particular cases

The cases are as follows:

• If ${K}_{ij}^{\ast }=0,{\tau}_0=0,$ then Eqs. (35)–(40) give results for TIT thin plate for classical coupled thermoelasticity.

• If angular velocity of thin plate is taken zero, i.e. Ω = 0, then Eqs. (35)–(40) give results for TIT thin plate without rotation.

• If K_ij = 0, τ₀ = 0,we obtain a TIT thin plate without energy dissipation, i.e. GN II theory from Eqs. (35)–(40).

• If ${K}_{ij}\ne 0\ne {K}_{ij}^{\ast },{\tau}_0=0$, we obtain a TIT thin plate with and without energy dissipation, i.e. GN III theory from Eqs. (35)–(40).

• If we take ${c}_{11}={c}_{22}={c}_{33},{c}_{12}={c}_{13},{c}_{44}={c}_{66},{\beta}_1={\beta}_3=\beta, {K}_1={K}_3=K,{K}_1^{\ast }={K}_3^{\ast }={K}^{\ast }$, then we obtain the results for the case of cubic crystal materials from Eqs. (35)–(40).

• If we take c₁₁ = c₃₃ = λ + 2μ, c₁₂ = c₁₃ = λ, c₄₄ = μ, β₁ = β₃ = β = (3λ + 2μ)α,${K}_1={K}_3=K,{K}_1^{\ast }={K}_3^{\ast }={K}^{\ast }$, then we obtain results for isotropic rotating thin plate with and without energy dissipation from Eqs. (35)–(40).

Numerical results and discussion

In order to illustrate our theoretical results in the proceeding section and to show the effect of rotation in different forms of boundary conditions as mentioned in applications in above part, we now present some numerical results. Cobalt material is chosen for the purpose of numerical calculation, which is transversely isotropic. The physical data for cobalt material, which is transversely isotropic, is taken from Dhaliwal and Singh (1980) which is given by:

$$ {c}_{11}=3.07\times {10}^{11}N{m}^{-2}, $$

$$ {c}_{12}=1.650\times {10}^{11}N{m}^{-2}, $$

$$ {c}_{13}=1.027\times {10}^{10}N{m}^{-2}, $$

$$ {c}_{33}=3.581\times {10}^{11}N{m}^{-2} $$

$$ {c}_{44}=1.510\times {10}^{11}N{m}^{-2}, $$

$$ {C}_E=4.27\times {10}^2 JK{g}^{-1}{\mathit{\deg}}^{-1}, $$

$$ {\beta}_1=7.04\times {10}^6N{m}^{-2}{\mathit{\deg}}^{-1},\rho =8.836\times {10}^3K{gm}^{-3} $$

$$ {\beta}_3=6.90\times {10}^6N{m}^{-2}{\mathit{\deg}}^{-1}, $$

$$ {K}_1=0.690\times {10}^2W{m}^{-1}{Kdeg}^{-1},\kern0.5em {K}_3=0.690\times {10}^2W{m}^{-1}{K}^{-1}, $$

$$ {K}_1^{\ast }=0.02\times {10}^2N{Sec}^{-2}{\mathit{\deg}}^{-1}, $$

$$ {K}_3^{\ast }=0.04\times {10}^2N{Sec}^{-2}{\mathit{\deg}}^{-1}. $$

$$ L=1,{\tau}_0=1,h=0.01m $$

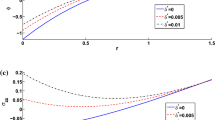
The values of normal force stress t_zz, tangential stress t_zr, radial stress t_rr, and conductive temperature φ for a TIT solid with two temperature and thermal relaxation times are illustrated graphically to show the effect of two temperatures.

• The solid black line with centre symbol square corresponds to thermal insulated boundaries without rotation.

• The solid red line with centre symbol circle corresponds to thermal insulated boundaries with rotation.

• The solid green line with centre symbol triangle corresponds to isothermal boundaries without rotation.

• The solid blue line with centre symbol diamond corresponds to isothermal boundaries with rotation.

Case 1: Constant load and heat source

Figure 2 shows the variations of displacement component u with radius r for constant load and heat source. In the initial range of radius r, there is a sharp decrease in the value of displacement component for all the cases. However, for thermal insulated boundary, the displacement component varies more as compared to isothermal boundary conditions. Moreover, away from source applied, it follows oscillatory behaviour. We can see that the rotation has a significant effect on the displacement component in all the cases as there are more variations in u in case of rotation as compared to when rotation is zero.

Fig. 2

variations of displacement component u with radius r

Figure 3 illustrates the variations of displacement component w with radius r for constant load and heat source. In the initial range of radius r, there is a decrease in the value of displacement component for all the cases. However, for thermal insulated boundary and rotation, the displacement component varies more as compared to isothermal boundaries, with and without rotation. Moreover, away from source applied, it follows opposite oscillatory behaviour. We can see that the rotation has a major effect on the displacement component as there are more variations in w in case of rotation, and it behaves opposite for thermal insulated and isothermal boundary conditions.

Fig. 3

variations of displacement component w with radius r

Figure 4 illustrates the variations of conductive temperature φ with radius r for constant load and heat source. In the initial range of radius r, there is a sharp increase in the value of φ for all the cases. However, for thermal insulated boundary and rotation, the conductive temperature varies more as compared to isothermal boundaries, with and without rotation. Moreover, away from source applied, it follows opposite oscillatory behaviour nearby the zero value.

Fig. 4

Variations of conductive temperature φ with radius r

Figure 5 illustrates the variations of tangential stress component t_zr with radius r for constant load and heat source. In the initial range of radius r, there is a small oscillation in the value of stress component t_zr for all the cases. However, for isothermal boundary and without rotation, the stress component t_zr varies more as compared to thermal insulated boundaries for both with and without rotation. Moreover, away from source applied, it follows opposite oscillatory behaviour nearby the zero value.

Fig. 5

Variations of tangential stress component t_zr with radius r

Figure 6 illustrates the variations of radial stress with radius r. In the initial range of radius r for constant load and heat source, there is a large oscillation in the value of radial stress for all the cases. However, for thermal insulated boundaries, the radial stress varies more as compared to isothermal boundary for both with and without rotation.

Fig. 6

Variations of radial stress with radius r

Case II: Periodically varying load and heat source

Figure 7 shows the variations of displacement component uwith radius r due to periodically varying load and heat source. For thermally insulated boundary in the initial range of radius r, there is a sharp decrease in the value of displacement component for all the cases; however, rotation case displacement w shows oscillations. However, for thermal insulated boundary, the displacement component varies more as compared to isothermal boundaries conditions. Moreover, away from source applied, it follows oscillatory behaviour. We can see that the rotation has a significant effect on the displacement component as there are more variations in u in case of rotation as compared to when rotation is zero.

Fig. 7

Variations of displacement component u with radius r

Figure 8 illustrates the variations of displacement component wwith radius r due to periodically varying load and heat source. In the initial range of distance x, there is a decrease in the value of displacement component for all the cases. However, for thermal insulated boundary and rotation, the displacement component varies more and is almost opposite as compared to isothermal boundaries, with and without rotation. Moreover, away from source applied, it follows opposite oscillatory behaviour nearby the zero value. We can observed that the rotation as well as isothermal boundary conditions has a significant effect on the displacement component in all the cases as there are more variations in w in case of rotation, and it behaves opposite for thermal insulated and isothermal boundary conditions.

Fig. 8

Variations of displacement component w with radius r

Figure 9 illustrates the variations of conductive temperature φ with radius r due to periodically varying load and heat source. In the initial range of distance x, there is a sharp increase in the value of φ for all the cases. However, for thermal insulated boundary and rotation, the conductive temperature varies less and rather oscillates near the plate as compared to isothermal boundaries, with and without rotation. Moreover, away from source applied, it follows opposite oscillatory behaviour near the zero value.

Fig. 9

Variations of conductive temperature φ with radius r

Figure 10 illustrates the variations of tangential stress component t_zr with radius r due to periodically varying load and heat source. In the initial range of radius r, there is a small oscillation in the value of stress component t_zr for all the cases. However, for isothermal boundary and without rotation, the stress component t_zr varies more as compared to thermal insulated boundaries for both with and without rotation. Moreover, away from source applied, it follows opposite oscillatory behaviour near the zero value.

Fig. 10

Variations of tangential stress with radius r

Figure 11 illustrates the variations of radial stress t_rr with radius r due to periodically varying load and heat source. For thermally insulated boundary and without rotation, the value of radial stress increases for 0 ≤ r ≤ 3.0 and then decreases, while for thermally insulated boundary and with rotation, radial stress t_rr first decreases for the range 0 ≤ r ≤ 2.5 and then increases. For isothermal boundary and without rotation, the value oscillates with small amplitude, and for isothermal boundary and with rotation, the value increases but has small increase as opposite of thermally insulated boundary. However, for thermal insulated boundaries, the radial stress varies more as compared to isothermal boundary for both with and without rotation. Moreover, away from source applied, it follows oscillatory behaviour near the zero value.

Fig. 11

Variations of radial stress with radius r

Conclusion

In this paper, we have discussed the thermoelastic problem for a transversely isotropic thin circular plate with and without rotation and with relaxation time and GN III model. Thermally insulated and isothermal boundary cases for circular edges are considered, and temperature is maintained on upper and lower surface of the circular thin plate. The Laplace and finite Hankel transform technique is used to obtain the numerical results.

In the present research article, conductive temperature, displacement, and stresses along with rotation, two temperatures with thermally insulated and isothermal boundary for constant and periodically varying load have been outlined. Since the thickness of plate is very small, the series solution given here will be definitely convergent. The temperature, displacement, and thermal stresses that are obtained can be applied to the design of pressure sensors, microphones, gas flow metres, optical telescopes, radar antennae, and many other device structures or machines in engineering applications.