1 Introduction

In the high-precision GNSS applications, IAR is a fundamental problem. After the integer ambiguities are fixed, users can take advantage of the precise pseudo-range data in positioning and navigation. Many GNSS models have been developed for IAR applications. The principle of them can be referred to Leick (2004) and Misra and Enge (2006).

The procedures of IAR usually consist of four steps. In the first step, the integer constraint of ambiguities \(a \in \mathbb {Z}^n\) is disregarded. The float solutions together with their variance–covariance (vc) matrix are estimated based on least-square adjustment as \(\Big [ \begin{array}{c} \hat{a} \\ \hat{b} \\ \end{array} \Big ]\), \(\Big [ \begin{array}{ll} Q_{\hat{a} \hat{a}}&{} Q_{\hat{a} \hat{b}}\\ Q_{\hat{b} \hat{a}}&{}Q_{\hat{b} \hat{b}} \end{array} \Big ]\). The quality control to float solutions Moore et al. (2002) and Teunissen and De Bakker (2013) is also implemented in this step, which includes the adaptation of outliers in code observations and cycle slips in phase observations.

In the second step, the integer constraint of ambiguities is taken into consideration in the fixing process of float ambiguities. It can be described as a many to one mapping

$$\begin{aligned} {\check{a}} = S(\hat{a}), \quad S: R^n \rightarrow Z^n \end{aligned}$$
(1)

Many mapping methods can be used, such as integer rounding (IR), integer bootstrapping (IB), and integer least-square (ILS). ILS is optimal and proved to have the highest success rate among these methods (Teunissen 1999). However, the correlations between different ambiguities lead to that the efficiency of integer mapping is very low. The Least-square Ambiguity Decorrelation Adjustment (LAMBDA) method, Teunissen (1993, 1995, 2010) and De Jonge and Tiberius (1996) is introduced to improve the efficiency and can effectively solve the ambiguity searching problems. Other decorrelation methods, such as Xu (2001) and Wang and Wang (2010), can also be used, and are effective to improve the efficiency of ambiguity resolution.

The third step is to test whether the fixed solution should be accepted, the so-called ambiguity validation. It can be realized by many acceptance tests, including R ratio test (RT) (Frei and Beutler 1990), F ratio test (FT) (Euler and Schaffrin 1991), difference test (DT) (Tiberius 1995), W ratio test (WT) (Wang et al. 1998), projector test (PT) (Han 1997). The optimal ambiguity (OA) tests, including constrained maximum success rate test and minimum mean penalty test, are introduced in (Teunissen , 2004b; Teunissen , 2005a; Teunissen , 2013). Note that the motivation of acceptance test is to exclude the suspected integers, and accept the most possible ones, since we do not know the true integer ambiguity.

After the ambiguities are accepted, other parameters can be adjusted based on correlation with the ambiguities

$$\begin{aligned} {\check{b}}= \hat{b} - Q_{{\hat{b}} {\hat{a}}}Q_{\hat{a} \hat{a}}^{-1}(\hat{a}-{\check{a}}) \end{aligned}$$
(2)

where \(Q_{\hat{b} \hat{a}}\) is the vc-matrix between ambiguity vector and other parameters. After these four steps and ambiguities are correctly fixed, all estimated parameters can benefit from the high-precision phase data.

Actually, the second and third steps are realized by the IA estimator. It can be simply regarded as the overall approach of ILS estimation and validation. If critical value of acceptance test is set so that all validation results are passed, then IA estimator is equivalent to ILS estimator. Three judgements are generated after IA estimation: success, failure, and undecided. The undecided part is formed by the interval or holes between different aperture pull-in regions (Teunissen 2004a). Its probability is determined by the choice of a maximum allowed failure rate. The ranges of failure rate and other probabilities can be referred to Li and Wang 2013). The benefit of IA estimators is that their estimation process and quality can be totally controlled by adjusting the threshold of acceptance test. It has been realized by the so-called fixed failure rate IA estimator (Verhagen and Teunissen 2006), and already applied into practice (Teunissen and Zhang 2010; Odolinski et al. 2014). Its critical value is determined by Monte Carlo simulation in advance. A feasible approach to apply this kind of IA estimator into practice is detailed analyzed and proposed in Verhagen (2013).

Though IA estimation theory provides the foundations from principle to practice for ambiguity validation, there are still several problems to be resolved in the application of fixed failure rate approach:

  • The determination of critical value in fixed failure rate approach relies on Monte Carlo sampling. Since the geometry of IA pull-in regions is complicate, it is difficult to derive analytical formula of IA success rate or failure rate based on multi-variate integral, especially when ambiguities are correlated. The precision of Monte Carlo sampling depends on the number of samples. Though we can improve the precision with more effective sampling methods, such as sample average approximation, importance sampling, stratified sampling (Rubinstein and Kroese 2011), the time cost still cannot satisfy the lowest requirement in GNSS instantaneous applications;

  • The practical way to apply the fixed failure rate approach is based on look-up table. This table is created based on a large amount of GNSS samples for certain IA estimator. The aim of look-up table is to satisfy the requirements world widely. However, it is impossible to globally collect all the required GNSS scenarios. Until now, only RT has the public look-up table for certain fixed failure rates (Verhagen 2013). Besides this, there is no evaluation indicator for quality of the released look-up table. At present, since the advantages and disadvantages of all acceptance tests have not been fully studied, there is no need to create look-up table for all acceptance tests. Furthermore, the performance comparisons between different tests based on fixed failure approach still take too much time. A more efficient approach to study the properties of acceptance tests is necessary;

  • Though properties of other IA estimators are investigated (Li and Wang 2014; Verhagen 2005), the gaps between IA estimation theory and application still have not been completely bridged. Recently, some researchers (Wang 2015) start to focus on the properties of DTIA, and the threshold function is proposed. Similar method also can be seen in Brack (2015). This kind of method can be applied to other IA estimators. Unfortunately, their solutions still depend on Monte Carlo simulation and fixed failure rate approach. Since there is no performance evaluation for fixed failure rate approach, it is difficult to evaluate the effectiveness of look-up table or fitting function;

  • Last but not least, fixed failure rate approach tries to realize controllable failure rate. Actually, the meaning of controllability needs further discussion. The requirement of users is to control the threshold or upper bound of failure rate within certain range. However, since fixed failure rate approach relies on Monte Carlo simulation, its critical value is determined by stochastically generated samples. Then the critical value and its corresponding failure rate will behave with certain statistical characteristics.

To tackle these problems, this contribution mainly focuses on exploiting the following topics:

  1. 1.

    The performance evaluation of fixed failure rate approach based on Monte Carlo simulation;

  2. 2.

    The probability approximation methods for the resolvable IA estimators which have analytical probability formulas;

  3. 3.

    Relation between the probability evaluations of ILS and IA estimators;

  4. 4.

    Instantaneous critical value determination method with controllable failure rate;

Based on research about these topics, we propose the instantaneous and controllable ambiguity resolution approach named as iCON. It can be applied to all IA estimators which have analytical formulas of probability evaluation. The stronger GNSS model, the better performance.

Note that the ’instantaneous’ in this contribution means the time of critical value determination is much less than 1 s. Most precise GNSS applications do not have strict requirement to the observations output with high frequency except some high dynamic situations.

The whole contribution is organized as follows. Section 2 briefly reviews the statistical inference theory in GNSS ambiguity resolution, which paves the theoretical foundation of IA estimation. Here the IA estimators are divided into resolvable and unresolvable classes according to whether they have analytical probability evaluation formulas. In Sect. 3, fixed failure rate approach based on Monte Carlo sampling and its performance are analyzed and investigated. Analytical formulas to evaluate the precision of fixed failure approach are firstly given and verified. Section 4 gives the approximation formulas for those resolvable IA estimators. The accuracy of the approximation formulas are analyzed based on simulation experiment. According to previous analysis in Sect. 5, the iCON approach is derived by analyzing the relation between ILS and IA probability evaluations. To verify the performance of IA estimation based on iCON approach, three kinds of comparison experiments are designed: (1) iCON approach and fixed failure rate approach; (2) different IA estimators based on iCON approach; (3) DTIA or IALS based on iCON approach, and RTIA based on look-up table. All these results show that iCON approach is effective in realizing better controllable ambiguity resolution than the fixed failure rate approach in practice.

2 Statistical inference in GNSS ambiguity resolution

2.1 Integer least-square estimator

In IAR, the integer solution is realized by a many-to-one mapping with the consideration of its integer constraint, \( {\check{a}} = S(\hat{a}) \in \mathbb {Z}^n \). It means that different float vectors can be mapped to the same integer vectors. The subset of float vectors mapped to the same integer is called integer pull-in region (Teunissen 1998a)

$$\begin{aligned} S_z= \{ x \in \mathbb {R}^n, z \in \mathbb {Z}^n | z= S(x)\} \end{aligned}$$
(3)

Integer pull-in regions are the basic cells to construct integer estimators. Different integer estimators are classified based on the construction principle of their pull-in regions, such as IR, IB and ILS. All of these integer estimators have the following properties

  1. (1)

    \( \bigcup _{z \in \mathbb {Z}^n} S_z= \mathbb {R}^n \)

  2. (2)

    \( \text {Int}(S_u) \bigcap \text {Int}(S_v)= \emptyset ,\quad \forall u,v \in \mathbb {Z}^n \quad \text {and} \quad u \ne v \)

  3. (3)

    \( S_z=S_0+z,\quad \forall z \in \mathbb {Z}^n \)

Their common expression is given as

$$\begin{aligned} {\check{a}} = \underset{z \in \mathbb {Z}^n}{\Sigma } z s_z(\hat{a}) \end{aligned}$$
(4)

with the indicator function \(s_z(x)\)

$$\begin{aligned} s_z(x)= \left\{ \begin{array}{c@{\quad }c@{\quad }c} 1 &{} \text {if} &{} x \in S_z \\ 0 &{} \text {if} &{} x \notin S_z \end{array} \right. \end{aligned}$$

If the float ambiguity is fixed to the true ambiguity z, IAR is ‘success’. Otherwise, it will be ‘failure’. Note that the integer pull-in regions are translational and not overlapped, hence there is no ‘false alarm’ and ‘failure detected’ judgments. Among various integer estimators, ILS is optimal and can maximize the success rate (Teunissen 1999).

According to the normal distribution of float solution \(\hat{a} \sim N(a,Q_{\hat{a} \hat{a}})\), the probability density function (PDF) of float solutions is given as \( f_{\hat{a}}(x|a) = C \text {exp}\{ -\frac{1}{2} \Vert x-a \Vert ^2_{Q_{\hat{a} \hat{a}}} \} \), where C is a normalizing constant and \(\Vert \cdot \Vert ^2_{Q_{\hat{a} \hat{a}}}=(\cdot )^\mathrm{T} Q_{\hat{a} \hat{a}}^{-1} (\cdot )\). To evaluate the confidence of the successful IAR, the probability mass function (PMF) is defined as Teunissen (1998a)

$$\begin{aligned} P_{\mathrm{s},\text {ILS}} = P({\check{a}}=a)= \int _{\mathrm{s}_a}{f_{\hat{a}}(x|a)\mathrm{d} x} \end{aligned}$$
(5)

Besides the success rate, the failure rate of integer estimator can also be calculated

$$\begin{aligned} P_{\mathrm{f},\text {ILS}} = \sum \limits _{z\in \mathbb {Z}^n /\{a\} } P({\check{a}}=z)= \sum _{z \in \mathbb {Z}^n /\{a\} } \int _{\ S_z}{f_{\hat{a}}(x|a)\mathrm{d}x} \end{aligned}$$
(6)

In Eq. (5), the size of \(P({\check{a}}=a)\) mainly depends on PDF of float solutions. Due to the multi-variate normal distribution of float vectors and the correlation between different elements of these vectors, it is difficult to compute the integral in Eq. (5). Its value is usually obtained by Monte Carlo sampling or approximated by upper or lower bounding (Verhagen et al. 2013). Note that the success rate of ambiguity resolution is positively correlated with GNSS model strength. The stronger GNSS model, the higher success rate. It means once the GNSS model is chosen, its success rate is fixed and cannot be adjusted by users.

Once the PMF is obtained, the failure rate can be directly computed in another way besides Eq. (6), \(P_{\mathrm{f},\text {ILS}}=1-P_{\mathrm{s},\text {ILS}}\).

2.2 IA estimator

For strong GNSS models, the success rates of IAR are close to 1, and we can omit the trivial influence of possible failures. However, if the GNSS model cannot satisfy the requirement of IAR success rate, we need to take measure to exclude the potential failures in IAR. This is the function of acceptance testing. The reformed pull-in regions based on acceptance test are named as integer aperture (IA) pull-in regions (Verhagen 2005). Here, the IA pull-in region is defined as \(\Omega \), \(\Omega \subset \mathbb {R}^n\) and \( \Omega _z = \Omega \cap S_z \). The properties of IA pull-in regions are given below

  1. (1)

    \( \bigcup _{z \in \mathbb {Z}^n } \Omega _z = \Omega \)

  2. (2)

    \( \text {Int}(\Omega _u) \bigcap \text {Int}(\Omega _v)= \emptyset , \forall u,v \in \mathbb {Z}^n \quad \text {and} \quad u \ne v \)

  3. (3)

    \( \Omega _z=\Omega _0+z, \forall z \in \mathbb {Z}^n \)

Here \(\Omega \) can be chosen as \(\mathbb {R}^n\) or its subset. Hence, integer pull-in regions are the limiting case of IA pull-in regions. The IA estimator is also given below

$$\begin{aligned} {\check{a}}_{\text {IA}} = \hat{a} + \underset{z \in \mathbb {Z}^n}{\sum } (z- \hat{a}) \delta _z(\hat{a}) \end{aligned}$$
(7)

with \( \delta _z (\hat{a})\) the indicator function of \(\Omega _z\). The standard form of acceptance test is given in Teunissen (2013)

$$\begin{aligned} \Omega = \{ x\in \mathbb {R}^n | \gamma (x) \le \mu \} \end{aligned}$$
(8)

with \(\gamma (\cdot )\) the testing function, and \(\mu \) the critical value. Most of IA estimators can be transformed into this form. Be different from integer pull-in regions, the volume of IA pull-in regions depends on the threshold of acceptance test. Hence, we can control the success rate and failure rate by adjusting the value of \(\mu \).

The geometry of IA pull-in regions is mainly determined by acceptance test. Various 2-D geometry reconstruction of IA estimators can be referred to Verhagen and Teunissen (2006). Note that all 1-D IA estimators have the same pull-in intervals when the failure rates are the same.

To evaluate the performance of an IA estimator, we give four judgements to the outcomes of IA estimators, including: success, \(P_{\mathrm{s},\text {IA}}\); failure, \(P_{\mathrm{f},\text {IA}}\); false alarm, \(P_{\text {fa}}\) and failure detection, \(P_{\text {fd}}\). \(P_{\text {fa}}\) and \(P_{\text {fd}}\) are also named as undecided probabilities. The computation formulas and their relations are summarized as

$$\begin{aligned} \begin{aligned}&P_{\mathrm{s},\text {IA}} = \int _{\Omega _a}{f_{\hat{a}}(x|a)\mathrm{d}x} \\&P_{\mathrm{f},\text {IA}} = \sum \limits _{z\in \mathbb {Z}^n /{a}} \int _{\Omega _z}{f_{\hat{a}}(x|a)\mathrm{d}x} \\&P_{\text {fa}} = P_{\mathrm{s},\text {ILS}}-P_{\mathrm{s},\text {IA}} \\&P_{\text {fd}} = 1-P_\mathrm{f}- P_{\mathrm{s},\text {ILS}} \end{aligned} \end{aligned}$$
(9)

\(P_{\mathrm{f},\text {IA}}\) is a critical quality indicator and can be set by users. \(P_{\mathrm{s},\text {IA}}\) is the critical element to determine \(P_{\text {fa}}\). However, its computation is not so easy as \(P_{\mathrm{s}, \text {ILS}}\), since the scaling brought by the acceptance test in each direction maybe nonlinear. Hence, we cannot directly use the bounding method as integer estimator to approximate \(P_{\mathrm{s},\text {IA}}\). The only exception discovered until now is DTIA estimator. Since its IA pull-in region is linearly scaled based on integer pull-in estimator in each dimension, the success rate of DTIA estimator can be directly approximated based on the corresponding scaling ratio. The details about DTIA estimator can be referred to Zhang et al. (2015). Besides the approximation method, Monte Carlo sampling method can also be used in the computation of IA success rate. Note that, though Monte Carlo sampling can be seen as globally optimal, it is time consuming and its accuracy and precision depend on the number of samples.

2.3 Resolvable IA estimators

Though there are various IA estimators, only parts of them have the analytical or resolvable probability evaluations until now. These estimators all have well-organized pull-in regions. Since their pull-in regions are constructed based on certain geometry which is easy to be approximated, their probability evaluations can be derived based on the geometry information. Here we list all the resolvable IA estimators until now, including ellipsoidal IA (EIA) (Teunissen 2003), DTIA and IA least-square (IALS) estimators. Though IAB estimator is also resolvable, its success rate is always the lower bound for that of IALS. Hence, our attention is focused on IALS. Besides these resolvable IA estimators, other popular IA estimators, such as RT, WT, FT, PT and OA estimators, their pull-in regions do not have obvious characteristics to be approximated, and need further investigation. However, once they can be approximated or become resolvable, they are also available to the approach introduced in Sect. 5.

When the failure rates of these resolvable IA estimators are chosen, then their success rates and other probabilities can be determined. Hence, here we only reveal the computations of success rates and failure rates, which are the main indicators users focus on.

2.3.1 EIA estimator

Be different from other IA estimators, the procedure to compute the EIA estimator is rather straightforward. Its definition is given as Teunissen (2003)

$$\begin{aligned} \Omega _z=\Omega _0+z, \quad \Omega _{0,\text {EIA}}=S_0 \cap C_{\mu _{\text {ET}},0} \end{aligned}$$
(10)

with \(S_0\) the original ILS pull-in region and

$$\begin{aligned} C_{\mu _{\text {ET}},0}=\{ x \in \mathbb {R}^n\,|\,\Vert x \Vert ^2_{Q_{\hat{z} \hat{z}}} \le \mu _{\text {ET}}^2 \} \end{aligned}$$

an origin-centered ellipsoidal region of which the size is controlled by the aperture parameter \(\mu _{\text {ET}}\). The motivation to design EIA estimator is due to its simplicity in the computation of success rate and failure rate.

Based on the float solution x and its decorrelated vc-matrix \(Q_{\hat{z} \hat{z}}\), we can complete the validation by verifying the inequality

$$\begin{aligned} \Vert x - \check{z}_1 \Vert ^2_{Q_{\hat{z} \hat{z}}} \le \mu _{\text {ET}}^2 \end{aligned}$$
(11)

is satisfied, where \(\check{z}_1\) is the best or first integer candidate. If not, the float solution is used. It seems that EIA only concerns with the best integer candidate. Actually, we can generalize EIA from RTIA. Since RTIA is given as

$$\begin{aligned} \frac{ \Vert x - \check{z}_1 \Vert ^2_{Q_{\hat{z} \hat{z}}} }{ \Vert x - \check{z}_2 \Vert ^2_{Q_{\hat{z} \hat{z}}} } \le \mu _{\text {RT}} \end{aligned}$$
(12)

If we add the constraint: \( \mu _{\text {RT}} \Vert \hat{z} - \check{z}_2 \Vert ^2_{Q_{\hat{z} \hat{z}}} = \mu _{\text {ET}} \), then we can conclude that EIA is essentially one kind of constrained RTIA. Its pull-in region can be interpreted as

$$\begin{aligned} \begin{array}{ll} \Omega _{\mu _{\text {ET}},0}\\ \quad = \left\{ x \in \mathbb {R}^n \bigg | \frac{ \Vert x \Vert ^2_{Q_{\hat{z} \hat{z}}} }{ \Vert x - \check{z} \Vert ^2_{Q_{\hat{z} \hat{z}}} } \le \mu _{\text {RT}}, \mu _{\text {RT}} \Vert x - \check{z} \Vert ^2_{Q_{\hat{z} \hat{z}}} = \mu _{\text {ET}} \right\} \end{array}\nonumber \\ \end{aligned}$$
(13)

Note that no matter how to set the value of \(\mu _{\text {ET}}\), there is no overlapping between different EIA pull-in regions. Since the maximum boundaries of EIA are constrained by ILS pull-in region.

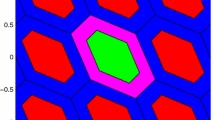
Here we give the 2-D geometry reconstruction of EIA estimator with \(\mu _{\text {ET}} = 0.1\) in Fig. 1, with the ambiguity model

$$\begin{aligned} \left[ \begin{array}{ll} 0.0865 &{}\quad -0.0364 \\ -0.0364 &{}\quad 0.0847 \end{array} \right] \end{aligned}$$
(14)
Fig. 1
figure 1

2-D pull-in regions of EIA estimator. Green part success region; red parts failure regions

Full size image

The success rate and failure rate of EIA are explicitly given as Teunissen (2003)

$$\begin{aligned} \left\{ \begin{array}{ll} P_{\mathrm{s},\text {EIA}} &{}= P( \chi ^2 (n,0) \le \mu _{\text {ET}}^2 ) \\ P_{\mathrm{f},\text {EIA}} &{}= \sum _{z \in \mathbb {Z}^n \slash \{0\}} P( \chi ^2 (n,\lambda _z) \le \mu _{\text {ET}}^2 ) \end{array} \right. \end{aligned}$$
(15)

with \( \mu _{\text {ET}} \le \frac{1}{2} \underset{ z \in \mathbb {Z}^n \slash \{ 0 \} }{\text {min}} \Vert z \Vert _{Q_{\hat{z} \hat{z}}}\). n is the freedom of Chi-square distribution, and the non-centrality parameter \(\lambda _z = z^\mathrm{T} Q_{\hat{z} \hat{z}}^{-1}z\). Thus, failure rate for each integer candidate can also be derived. Once \( \mu _{\text {ET}} > \frac{1}{2} \underset{ z \in \mathbb {Z}^n \slash \{ 0 \} }{\text {min}} \Vert z \Vert _{Q_{\hat{z} \hat{z}}}\), \(P_{\mathrm{s},\text {EIA}}\) and \(P_{\mathrm{f},\text {EIA}}\) become the upper bounds of EIA.

Hence, it is concluded that PMF of EIA estimator can be precisely calculated once \(\mu _{\text {ET}}\) is determined within certain range.

2.3.2 DTIA estimator

The pull-in region of DT is defined as

$$\begin{aligned} \Omega _{\text {DTIA},0} = \{ x \in \mathbb {R}^n \, | \, \Vert x - u \Vert _{Q_{\hat{z} \hat{z}}}^2 - \Vert x \Vert _{Q_{\hat{z} \hat{z}}}^2 \ge \mu _{\text {DT}} \} \end{aligned}$$
(16)

with \(u \in \mathbb {Z}^n \slash \{0\}\). The range of \(\mu _{\text {DT}}\) based on LAMBDA method has the easy-to-compute \([0, \frac{1}{d(1,1)})\), in which d(1, 1) is the first element of D in the LDL-decomposition of the decorrelated matrix \(Q_{\hat{z} \hat{z}}\). This is proved in Zhang et al. (2015).

Its 2-D geometry reconstruction is given in Fig. 2 with \(\mu _{\text {DT}} = 1.4723 \). The ambiguity model matrix is the same as (14).

Fig. 2
figure 2

2-D pull-in regions of DTIA estimator. Green part success region; red parts failure regions

Full size image

There is no analytical formula to directly compute the probability evaluations of DTIA. However, we can give indirect evaluation by various bounds. The first results for the lower bound and upper bound of the success rate of DTIA are derived and proved in Zhang et al. (2015).

$$\begin{aligned} \left\{ \begin{array}{ll} P_{\mathrm{s},\text {DTIA}} &{} \ge \prod _{i=1}^n \left[ 2 \Phi \left( \frac{|x_i|}{\sigma _{z_{i|I}}} \right) -1 \right] \\ P_{\mathrm{s},\text {DTIA}} &{} \le P\left( \chi ^2 (n,0) \le \frac{4 \bar{x} c_n}{\text {ADOP}^2} \right) \end{array} \right. \end{aligned}$$

with the \(\sigma _{z_{i|I}}\) standard deviation from LDL-decomposition of the decorrelated \(Q_{\hat{z} \hat{z}}\), and the scaling factor \(|x_i|\) is computed by

$$\begin{aligned} |x_i| = \frac{ \Vert c_i\Vert _{Q_{\hat{z} \hat{z}}}^2-\mu _{\text {DT}}}{2\Vert c_i\Vert _{Q_{\hat{z} \hat{z}}}^2}, \quad i=1,2,\ldots ,n \end{aligned}$$
(17)

where \(0< |x_i|\le 0.5\) and \(c_i\) is the canonical vector of the i-th coordinate axis. \(\bar{x} = \frac{ \sum ^n_{i=1} |x_i| }{n}\), and \(c_n = \frac{ (\frac{\pi }{2} \Gamma (\frac{\pi }{2}))^\frac{\pi }{2} }{\pi } \). Besides scaling factor, \(|x_i|\) can also be seen as the intersecting points between original pull-in region of DT integer aperture bootstrapping (DTIAB) with the coordinate axes. The success rate of DTIA can be approximated by that of DTIAB in decorrelated space. The definition and properties of DTIAB can be referred to Zhang et al. (2015).

Actually, the lower bounds based on DTIAB have small differences with DTIA. It can be used to approximate the success rate of DTIA for rough evaluation. Due to the similar algebraic formation between DTIA and ILS, DTIA can be seen as the linearly scaling ILS estimator.

According to the formula of ILS failure rate in (6), the failure rate of IA estimator can also be decomposed into the sum of failure rates for each IA pull-in region. Hence, the failure rate of DTIA can be approximated by the analytical formula

$$\begin{aligned} P_{\mathrm{f},\text {DTIA}} \approx \sum \limits _{z \in \mathbb {Z}^n \slash \{0\}} \prod _{i=1}^n \left[ \Phi \left( \frac{z_i+ |x_i|}{\sigma _{z_{i|I}}}\right) - \Phi \left( \frac{z_i- |x_i| }{\sigma _{z_{i|I}}} \right) \right] \nonumber \\ \end{aligned}$$
(18)

with \(z=(z_1,z_2,\ldots ,z_n)^\mathrm{T}\). The proof is given in the Appendix. The accuracy of approximation will be verified in Sect. 4.

2.3.3 IALS estimator

The IALS estimator can be seen as the scaled version of ILS estimator (Teunissen 2004a, 2005b). The motivation for introducing this estimator stems from the known optimality of the ILS estimator. Its aperture pull-in region is defined as

$$\begin{aligned} \Omega _{z,\text {IALS}} = \beta S_{z,\text {ILS}} \end{aligned}$$
(19)

with

$$\begin{aligned} \left\{ \begin{array}{ll} \beta S_{z,\text {ILS}}&{} = \{ x\in \mathbb {R}^n \,| \, \frac{1}{\beta } (x-z) \in S_{0,\text {ILS}} \} \\ S_{0,\text {ILS}} &{}= \{ x\in \mathbb {R}^n \, | \, \Vert x\Vert _{Q_{\hat{z} \hat{z}}}^2 \le \Vert x-u\Vert _{Q_{\hat{z} \hat{z}}}^2 , \forall u \in \mathbb {Z}^n \slash \{ 0\} \} \end{array} \right. \end{aligned}$$

The aperture parameter is \(\beta , 0 \le \beta \le 1 \). When \(\beta = 1\), the IALS estimator can be seen as the ILS estimator. The 2-D geometry reconstruction is given in Fig. 3, in which the aperture parameter is chosen as \(\beta = 0.7\).

Fig. 3
figure 3

2-D pull-in regions of IALS estimator. Green part success pull-in region; red parts failure pull-in regions

Full size image

Be different from other IA estimators, the estimation process and the determination of aperture parameter are more complicated, which can be referred to Teunissen (2005b).

Furthermore, since the ILS estimation in IALS actually is implemented twice. Hence, it is more time consuming for IALS than other IA estimators in estimation. However, the optimality inherited from ILS also brings benefits to IALS, which will be verified later.

Be similar as ILS, there are various ways of probability evaluation for IALS. Its probability lower bounds and upper bounds are detailed given in Teunissen (2005b). Here we list the lower bound and upper bound for the success rate of IALS

$$\begin{aligned} \left\{ \begin{array}{ll} P_{\mathrm{s},\text {IALS}} &{} \ge \prod _{i=1}^n \left[ 2 \Phi \left( \frac{\beta }{2 \sigma _{z_{i|I}}} \right) -1 \right] \\ P_{\mathrm{s},\text {IALS}} &{} \le P \left( \chi ^2(n,0) \le \frac{\lambda ^2 c_n}{\text {ADOP}^2} \right) \end{array} \right. \end{aligned}$$

Be similar as DTIA, the failure rate of IALS also has analytical formula

$$\begin{aligned} P_{\mathrm{f},\text {IALS}} \approx \sum \limits _{z \in \mathbb {Z}^n \slash \{0\}} \prod _{i=1}^n \left[ \Phi \left( \frac{2 z_i+ \beta }{2 \sigma _{z_{i|I}}} \right) - \Phi \left( \frac{2 z_i- \beta }{2 \sigma _{z_{i|I}}} \right) \right] \nonumber \\ \end{aligned}$$
(20)

with \(z_i\) the i-th element of integer vector z, whose proof is also given in the Appendix.

According to Zhang et al. (2015), DTIA is the generalized IALS with different scaling factors for different directions. When all directions have the same scaling factor, which means \(|x_1|=\dots =|x_n|=\frac{\beta }{2}\), DTIA will be transformed into IALS. Besides this, just as the relation between IB and ILS, DTIA has similar relation with DTIAB. Due to previous relation between IALS and DTIA, the performances of DTIA and IALS have some similarities, which can be seen later.

3 Fixed failure rate approach based on Monte Carlo sampling and performance evaluation

According to the theory of IA estimation, the quality of ambiguity resolution is controllable. As previous analysis, critical values of acceptance tests are the elements to control the probability evaluations of IA estimation. However, based on the formula of \(P_{\mathrm{f},\text {IA}}\), it is difficult to find the analytical relation between critical value and failure rate for most of IA estimators, such as RT, OA. To solve this problem, IA ambiguity resolution based on Monte Carlo sampling method is proposed in Teunissen (1998a) and Verhagen and Teunissen (2006). Their procedures can be summarized into the following steps:

  1. 1.

    Set fixed failure rate \(P_{\mathrm{f}}\), and other initial parameters;

  2. 2.

    Generate N float ambiguities with normal distribution: \( \hat{a}_i \sim N(0, Q_{\hat{a} \hat{a}}), i = 1, \ldots , N \);

  3. 3.

    Implement ambiguity resolution and acceptance test \(\mu _i = \gamma (\hat{a}_i)\) for each sample;

  4. 4.

    Count the number of failed points for which: \(\mu _i \le \mu \) and \({\check{a}}_i \ne 0\);

  5. 5.

    Based on rooting finding method to determine the critical value \(\mu \) so that \(P_{\mathrm{f},\text {IA}}(\mu )-P_\mathrm{f}=0\).

According to the principle of Monte Carlo sampling, the precision of sampling result depends on the number of simulation samples, N. If these stochastic samples are drawn independently from the normal distribution \(N(0, Q_{\hat{a} \hat{a}})\), we can interpret the IA ambiguity resolution results as a binomial distribution process. It means the decision parts only include failure and the other part. If the number of failure rate, \(N_{\mathrm{f},IA}\), is known, then the probability of failure rate can be written as

$$\begin{aligned} P_{N_{\mathrm{f},IA}} = \frac{ N ! }{ (N - N_{\mathrm{f},IA}) ! N_{\mathrm{f},IA} !}P_{\mathrm{f},\text {ILS}}^{N_{\mathrm{f},IA}} (1- P_{\mathrm{f},\text {ILS}})^{N-N_{\mathrm{f},IA}}\nonumber \\ \end{aligned}$$
(21)

Once \(\mu \) is determined based on fixed failure rate approach or other approaches, the IA ambiguity resolution failure rate and its dispersion can be derived as the following formulas:

$$\begin{aligned} \begin{array}{ll} E\left( \frac{N_{\mathrm{f},\text {IA}}}{N}\right) &{}= P_{\mathrm{f},\text {IA}} \\ D\left( \frac{N_{\mathrm{f},\text {IA}}}{N}\right) &{}= \frac{ (1- P_{\mathrm{f},\text {IA}}) P_{\mathrm{f},\text {IA}} }{N} = \sigma ^2_{\mathrm{f},\text {IA}} \end{array} \end{aligned}$$
(22)

with \(N_{\mathrm{f},\text {IA}}\) the number of failure samples in IA ambiguity resolution. Here \(\sigma ^2_{\mathrm{f},\text {IA}}\) can be used to describe the precision of failure rate in IA ambiguity resolution. Notice that the precision of fixed failure approach is independent of the model strength.

Based on the above mean and variance, the Chebyshev inequality can be used to obtain an upper bound on the probability that \(\frac{N_{\mathrm{f},\text {IA}}}{N}\) differs more than any \(\tau >0\) from \(P_{\mathrm{f},\text {IA}}\). It can be written as

$$\begin{aligned} P\left( \left| \frac{N_{\mathrm{f},\text {IA}}}{N} - P_{\mathrm{f},\text {IA}}\right| \ge \tau \right) \le \frac{(1- P_{\mathrm{f},\text {IA}}) P_{\mathrm{f},\text {IA}}}{ N_{\mathrm{f},\text {IA}} \tau ^2} \end{aligned}$$
(23)

It is obvious that the number of samples is critical to guarantee the precision and its confidence interval of the computed failure rate.

To explicitly present the relation between simulation samples, critical value and failure rate, simulation experiment is implemented for ambiguity model matrix

$$\begin{aligned} Q = \left[ \begin{array}{c@{\quad }c@{\quad }c} 0.0865 &{} -0.0357 &{} 0.0421\\ -0.0357 &{} 0.0847 &{} -0.0258 \\ 0.0421 &{} -0.0258 &{} 0.0797 \end{array} \right] \end{aligned}$$
(24)

When the critical value is fixed, the relation between simulation samples and failure rate is presented in Fig. 4. Here the DT critical value is randomly chosen as \(\mu _{\text {DT}}=5\).

Fig. 4
figure 4

Relation between simulation samples and failure rate with fixed critical value

Full size image

It is obvious that in Fig. 4, as the increase of samples, the values of failure rate gradually become stable, which means the precision of failure rate is improved as the increase of number of simulation samples. This is consistent with the second formula in (22).

Note that in Fig. 4, the critical value of DT is chosen regardless of the quality control. Now we will analyze the performance of IA estimator based on the critical value determined by fixed failure rate approach.

In the procedures of fixed failure rate approach, the critical value is determined based on the stochastically generated N samples. Just as the formula shown in (23), the confidence level we can give to the determined critical value is also inversely proportional to the number of simulation samples. In other words, it means that the determined critical value is a local result, and we may obtain different values in different trials of Monte Carlo simulation. Besides this, if we implement N times IA ambiguity resolution based on the obtained critical value, the failure rate may not be the fixed failure rate \(P_{\mathrm{f}}\). The range and precision of failure rate are determined by Eq. (22).

To verify previous analysis, we use the ambiguity model matrix (24) to verify the performance of fixed failure rate approach. The simulation procedures are designed as follows:

  1. 1.

    Based on fixed failure rate approach, the critical value of DT for fixed failure rate \(P_\mathrm{f}=0.001\) is determined;

  2. 2.

    Use this critical value to implement K trials of Monte Carlo simulation, in which each simulation includes \(N=50{,}000\) samples for IA ambiguity resolution;

  3. 3.

    Compute the value of \(P_{\mathrm{f},\text {IA}}\) and \(\sigma _{{f,\text {IA}}}\), and compare them with \(P_{\mathrm{f}}\).

The simulation results are summarized in Table 1, in which the theoretical precision of fixed failure rate \(P_{\mathrm{f},0}\) is

$$\begin{aligned} \sigma _{P_{\mathrm{f}}} = \frac{ (1- P_{\mathrm{f}}) P_{\mathrm{f}}}{N} = 1.4135\times 10^{-4} \end{aligned}$$
(25)

Notice that as the increase of Monte Carlo trials,

$$\begin{aligned} \begin{array}{ll} \underset{K \rightarrow \infty }{\text {lim}} P_{\mathrm{f},\text {IA}} &{}= P_{\mathrm{f}} \\ \underset{K \rightarrow \infty }{\text {lim}} \sigma _{\mathrm{f},\text {IA}} &{}= \sigma _{P_{\mathrm{f}}} \end{array} \end{aligned}$$
(26)

According to central limit theorem (Breiman 1992), when \(K \rightarrow \infty \), \(\frac{N_{\mathrm{f},\text {IA}}}{N}\) will behave as a random variable with normal distribution, \(N(P_{\mathrm{f}}, \sigma ^2_{P_{\mathrm{f}}})\). Hence, in practice, if we only use the critical value in IA estimation just once, the IA failure rate actually behaves as random value but not the fixed failure rate.

Table 1 Relation between Monte Carlo simulation trials and precision
Full size table

Now we can conclude that the fixed failure rate approach is actually one kind of statistical control to the failure rate of IA ambiguity resolution. It is impossible to make the failure rate of IA ambiguity resolution always smaller than the required failure rate. That is the reason why the look-up table of RTIA chooses the conservative value to ensure its feasibility. Besides this, the controllability (precision) of fixed failure rate approach has no relation with the ambiguity model strength. In another words, the model information does not take much effect in this method.

As a summary, the controllability expressed by the fixed failure rate approach is essentially the control of their statistics. The confidence level of its controllability within certain range can be given by analytical formula. To improve the confidence level of look-up table or threshold function, the artificial measure has to be taken, which can be seen in Verhagen (2013) and Wang (2015). To delete the influence of artificial measure, the ambiguity model information is necessary to be used. Though Wang (2015) indirectly includes the ambiguity model information, that method is not general and cannot be expanded to other IA estimators.

4 Analysis to the success rate approximation of IA estimator

In the forgoing sections, probability evaluations of resolvable IA estimators are given. These probability evaluations provide important reference for the performance of IA ambiguity resolution. Besides this, probability evaluation is also the direct indicator which correlates with critical value of acceptance test. The controlling of failure rate has to rely on the adjustment of critical value. Hence, it is necessary to study how to approximate numerical values of probability evaluations of IA estimators.

Actually, there already exist many literatures exploring the probability evaluations of ILS ambiguity resolution. According to Feng and Wang (2011) and Verhagen et al. (2013), lower bounds based on IB provide quite sharp bounds for ambiguity resolution. Hence, it is natural to approximate probability evaluations of IA ambiguity resolution with their analytical bounds. Here we choose the lower bound as the approximation method. According to Teunissen (1998b) and Feng and Wang (2011)

$$\begin{aligned} P_{\mathrm{s},\text {IB}} = \prod ^n_{i=1} \left[ 2 \Phi \left( \frac{1}{2 \sigma _{z_{i|I}}}\right) -1 \right] \end{aligned}$$
(27)

In decorrelated space, ILS will behave similarly as IB. Hence, we can use the success rate of IB to approximate ILS, which means

$$\begin{aligned} P_{\mathrm{s},\text {ILS}} \ge \prod ^n_{i=1} \left[ 2 \Phi \left( \frac{1}{2 \sigma _{z_{i|I}}}\right) -1 \right] \end{aligned}$$
(28)

Of course, there exist differences between the approximated ILS probability evaluations and actual values. They are caused by the influence of correlation which cannot be totally eliminated due to integer constraint of ambiguity.

Besides the success rate, the failure rate of ILS for each pull-in region is approximated by

$$\begin{aligned} P_{\mathrm{f},\text {ILS}} (k) \approx \prod _{i=1}^n \left[ \Phi \left( \frac{z_i(k)+0.5}{\sigma _{z_{i|I}}} \right) - \Phi \left( \frac{z_i(k)-0.5}{\sigma _{z_{i|I}}} \right) \right] \nonumber \\ \end{aligned}$$
(29)

with \(z(k) = (z_1(k),\dots ,z_i(k),\dots ,z_n(k))^\mathrm{T}\) and \(z(k) \ne 0\). \(z(k), k\ge 1\), is the k-th failure integer candidate. The proof of (29) is given in the Appendix.

The ILS failure rate is

$$\begin{aligned} P_{\mathrm{f},\text {ILS}} \le \sum \limits _{k=1}^{\infty } P_{\mathrm{f},\text {ILS}} (k) \end{aligned}$$
(30)

As to IA estimators, they are based on ILS estimation. Some probability evaluations are directly derived from ILS. Hence, we also can use those lower bounds to approximate the probability evaluations of IA estimators. In the following part, we directly give the approximation formula of previous solvable IA estimators, and analyze the accuracy of approximation based on simulation experiments.

Be different from other IA estimators, the probability evaluation of EIA can be accurately given within certain range. As to DTIA and IALS, success rates and failure rates can be approximated by their lower bounds in decorrelated space, which are explicitly given in Sect. 3. Note that success rates and failure rates of IA estimators are independent of true integer ambiguity. In other words, the critical value and ambiguity model matrix determine the probability evaluation of ambiguity resolution.

To evaluate the accuracy of these approximation formulas, this section will give a comprehensive experimental study to these approximations. The simulation setting is presented in Table 2. Multi-frequency, multi-GNSS environments are constructed. In this simulation, we will use two methods to calculate success rates: Monte Carlo sampling and approximation formulas. The former one can be used as reference if the number of simulation samples is large enough. The latter one will be compared with the former one to evaluate the accuracy of approximation.

Table 2 Simulation settings for GNSS models
Full size table

Here we only give the simulation results within 1 day. Only when \(P_{\mathrm{s},\text {ILS}}>0.8\), IA ambiguity resolution is implemented. 50, 000 samples are generated in Monte Carlo sampling. The success rates of three IA estimator are computed based on two methods. Critical value of IA estimators are determined by fixed failure rate approach with \(P_\mathrm{f}=0.001\).

The success rates of EIA and the approximation errors for success rates are demonstrated in Fig. 5. It is obvious that two methods obtain almost the same success rates for each epoch. This is because the success rate formula of EIA is obtained by accurate integration within a hyper-ellipsoidal. The trivial success rate approximation errors are due to numerical errors. Note that the setting of \(P_\mathrm{f}\) ensures that \( \mu _{\text {ET}} \le \frac{1}{2} \underset{ c \in \mathbb {Z}^n \slash \{ 0 \} }{\text {min}} \Vert c \Vert _{Q_{\hat{z} \hat{z}}}\) with \(c = \check{z}_2 -\check{z}_1\) based on the generated GNSS models.

Fig. 5
figure 5

Comparison of EIA success rates between two methods and their difference. Blue line Monte Carlo integration; red line approximated formula; black line approximation errors

Full size image

Then the results of DTIA is given in Fig. 6. Comparing with EIA, though red line cannot so accurately approximate blue line, their approximation error is acceptable, and the maximum approximation error is smaller than 0.05.

Results of IALS is presented in Fig. 7. Notice that the overall success rates are almost the same as those of DTIA, which conforms to the relation between IALS and DTIA. Their approximation formulas of success rates will be equivalent under certain numerical conditions. However, as to the approximation errors, we still can see that IALS has smaller approximation errors than those of DTIA. The maximum approximation error is smaller than that of DTIA. This shows that the approximation formula of IALS is more accurate than that of DTIA.

In Table 3, the expectations of approximation errors are listed. Obviously, EIA has the smallest approximation error. IALS is better than DTIA.

Fig. 6
figure 6

Comparison of DTIA success rates between two methods and their difference. Blue line Monte Carlo integration; red line approximated formula; black line approximation errors

Full size image
Fig. 7
figure 7

Comparison of IALS success rates between two methods and their difference. Blue line Monte Carlo integration; red line approximated formula; black line approximation errors

Full size image
Table 3 Expectation of approximation errors for three IA estimators, \(\delta P_{\mathrm{s},\text {IA}} = P'_{\mathrm{s},\text {IA}} - P_{\mathrm{s},\text {IA}} \)
Full size table

Note that here we only talk about the approximation of success rates. Of course, there must exist approximation errors in failure rates. The critical problem is how to constrain the approximation errors of failure rates within certain range. In next section, we will propose an efficient approach in detail.

As a summary, EIA can accurately compute its success rate with the fixed failure rate. However, its IA estimation is most conservative. This is understandable, since it can be interpreted as a RTIA with extra constraint. Its theoretical performance is worse than RTIA. IALS and DTIA basically have the same success rates. The trivial difference lies on that IALS has smaller approximation errors.

5 Instantaneous and controllable IA ambiguity resolution

5.1 Relation between failure rates of IA and ILS estimators

According to IA estimation theory, integer estimator is the limiting case of IA estimator. This is the reason why ILS success rate and failure rate are the extreme values of IA estimator. Besides this, the ILS and IA probability evaluations can also be connected by their probability ratio factor.

In this part, we will take DTIA and ILS estimator as example to reveal the relation between failure rates of IA and ILS for each pull-in region. Those derived results can be generalized to other IA estimators which have analytical probability evaluation formulas.

To obtain the so-called probability ratio factor for each pull-in region, the failure rates of DTIA and ILS are computed based on the initial setting \(\mu \). We define the probability ratio factor as

$$\begin{aligned} r(k,\mu )= & {} \frac{P_{\mathrm{f},\text {DTIA}}(k,\mu )}{P_{\mathrm{f},\text {ILS}}(k)} \nonumber \\\approx & {} \prod _{i=1}^n \frac{ \Phi \left( \frac{z_i(k)+ |x_i|}{\sigma _{z_{i|I}}}\right) - \Phi \left( \frac{z_i(k)- |x_i| }{\sigma _{z_{i|I}}}\right) }{ \Phi \left( \frac{z_i(k)+0.5}{\sigma _{z_{i|I}}}\right) - \Phi \left( \frac{z_i(k)-0.5 }{\sigma _{z_{i|I}}}\right) } \end{aligned}$$
(31)

with \(r(k,\mu )\) the ratio factor. Further derivation can be implemented to Eq. (31) based on the mean value theorem of integral

$$\begin{aligned}&\Phi \left( \frac{z_i(k)+|x_i|}{\sigma _{z_{i|I}}}\right) - \Phi \left( \frac{z_i(k)-|x_i| }{\sigma _{z_{i|I}}}\right) \nonumber \\&\quad = \int _{z_i(k)-|x_i| }^{z_i(k) + |x_i|} \frac{1}{ \sqrt{2 \pi } \sigma _{z_{i|I}}} \text {exp} \left( -\frac{x^2}{2 \sigma _{z_{i|I}}^2}\right) \mathrm{d}x\nonumber \\&\quad = 2 |x_i| f( \xi _x(k) ) \end{aligned}$$
(32)

and

$$\begin{aligned}&\Phi \left( \frac{z_i(k)+0.5 }{\sigma _{z_{i|I}}}\right) - \Phi \left( \frac{z_i(k)-0.5 }{\sigma _{z_{i|I}}}\right) \nonumber \\&\quad = \int _{z_i(k)-0.5 }^{z_i(k)+0.5 } \frac{1}{ \sqrt{2 \pi } \sigma _{z_{i|I}}} \text {exp} \left( -\frac{x^2}{2 \sigma _{z_{i|I}}^2}\right) \mathrm{d}x \nonumber \\&\quad = f( \xi (k) ) \end{aligned}$$
(33)

In Eqs. (32) and (33), \(f(\cdot )\) is the PDF of normal distribution and

$$\begin{aligned}&\xi _x(k)\in ( z_i(k)- |x_i|, z_i(k)+|x_i|) = U_x\nonumber \\&\xi (k)\in ( z_i(k)-0.5, z_i(k)+0.5) = U \end{aligned}$$
(34)

with \(U_x \subset U\). Besides this, \(r(k,\mu )\), \(\xi _x(k)\) and \(\xi (k)\) have the following properties:

Property 1

There exists the threshold \(\sigma , \sigma >0\), if

$$\begin{aligned} U \subset (-\infty ,-\sigma ) \bigcup (\sigma ,+\infty ) \end{aligned}$$

then \(f(\xi _x(k)) \le f(\xi (k))\), in which \( \xi _x (k) \le \xi (k) \) in \((-\infty ,-\sigma )\), and \( \xi _x (k) \ge \xi (k) \) in \((\sigma ,+\infty )\).

Property 2

The probability ratio factor between DTIA and ILS estimator can be seen as an approximated decreasing function, though it is not monotonous. Its limiting value converges to zero

$$\begin{aligned} \underset{ k \rightarrow \infty }{ \text {lim}} r(k,\mu )= \underset{ k \rightarrow \infty }{ \text {lim}} \frac{P_{\mathrm{f},\text {DTIA}}(k,\mu )}{P_{\mathrm{f},\text {ILS}}(k)} = 0 \end{aligned}$$
(35)

Proofs of two properties are given in the Appendix.

To demonstrate the relation between ILS failure rate and DTIA failure rate, Fig. 8 gives the numerical values of original ILS failure rate, sorted ILS failure rate and its corresponding failure rate for integer candidates from 2 to 150.

Fig. 8
figure 8

ILS and DTIA failure rate for each integer candidate. The critical value of DTIA is chosen as 6

Full size image

In Fig. 8, it is obvious that \(P_{\mathrm{f},\text {ILS}}(k)\) is not monotonous. The sorting operation is to obtain a better approximation value with finite integer candidates. Though the corresponding DTIA failure rate is not monotonous, its influence can be neglected due to the trivial fluctuation of magnitude.

To approximate ILS failure rate with finite integer candidates, we implement the following procedures:

  1. 1.

    Choose a large number of failure rates for ILS pull-in region, such as M;

  2. 2.

    Sort these failure rates into descending order;

  3. 3.

    Choose the threshold, \(P_{\mu } (0< P_{\mu }\ll P_{\mathrm{f}})\). If \(P_{\mathrm{f},\text {ILS}}(m)> P_{\mu }\) and \(P_{\mathrm{f},\text {ILS}}(m+1)< P_{\mu }\) , the failure rate will be decomposed into two parts

    $$\begin{aligned} \left\{ \begin{array}{ll} &{} P_{\mathrm{f},\text {ILS}} \approx \sum \limits _{k=1}^m P_{\mathrm{f},\text {ILS}}(k) , \quad 1<m \le M \\ &{} P_{0,\text {ILS}} = \sum \limits _{k=m+1}^{M} P_{\mathrm{f},\text {ILS}}(k) \end{array} \right. \end{aligned}$$

    with \(P_{0,\text {ILS}}\) the remaining part of ILS failure rate approximation and \( 0< P_{0,\text {ILS}}\ll P_{\mathrm{f}} \).

Note that \(P_{\mu }\) should be very small, so that the approximation error in \(P_{\mathrm{f},\text {ILS}}\) is as small as possible. In step 1, the reason why we choose M is to limit the range of integer candidates, so that the approximation is possible. Based on many trials, the M is chosen as 300 in this contribution to balance precision and time cost. While, the m in step 3 is to decrease the time consumption in the following nonlinear optimization, which will be introduced later.

There exists the relation in ILS probability evaluations

$$\begin{aligned} P_{\mathrm{s},\text {ILS}}+P_{\mathrm{f},\text {ILS}} + P_{0,\text {ILS}} = 1 \end{aligned}$$
(36)

It is explicitly demonstrated in Fig. 9.

Fig. 9
figure 9

The composition of ILS probability for 2-D ambiguity model. Green region \(P_{\mathrm{s},\text {ILS}} + P_{\mathrm{f},\text {ILS}}\); red region \(P_{0,\text {ILS}}\)

Full size image

If the initial critical value \(\mu _0\) is given, failure rate of DTIA can be approximated by

$$\begin{aligned} P_{\mathrm{f},\text {DTIA}}(\mu _0) \approx \sum ^m_{k=1} P_{\mathrm{f},\text {DTIA}} (k,\mu _0) \end{aligned}$$
(37)

Besides the approximated part in (37), the remaining part of failure rate is written as

$$\begin{aligned} P_{0,\text {DTIA}}(\mu _0) = \sum ^{M}_{k=m+1} r(k,\mu _0) P_{\mathrm{f},\text {ILS}}(k) \end{aligned}$$
(38)

To be convenient, we choose \(r(m)= \text {max} \{r(i)\},i=m+1,\dots ,M\). Then

$$\begin{aligned} P_{0,\text {DTIA}}(\mu _0) \approx r(m,\mu _0) P_{0,\text {ILS}} \end{aligned}$$
(39)

Eventually, if we want to compute the critical value so that the failure rate of DTIA is fixed to \(P_{\mathrm{f}}\), the nonlinear equation must be solved

$$\begin{aligned} P_{\mathrm{f},\text {DTIA}}(\mu )+ r(m,\mu ) P_{0,\text {ILS}} = P_{\mathrm{f}} \end{aligned}$$
(40)

It can be changed into a nonliear optimization problem and solved by the trust-region-dogleg method (Nocedal and Wright 1999). In MATLAB, the function ’fsolve’ can be used.

The numerical optimization is time consuming. The bigger m, the more accurate \(\mu \) and more time consumption. Hence, m should be chosen based on the balance of time cost and accuracy, and \(P_{\mu }\) is to control this balance.

Summarizing previous derivations, we will have a new fast and controllable method to determine critical value, which we name as iCON approach. Previously, we take DTIA as example. Actually, the iCON approach can be applied to any IA estimators with analytical PMF formula.

5.2 iCON approach

The overall procedures of iCON approach are listed below:

  1. 1.

    Set initial parameters \(P_{\mathrm{f}}\), \(\mu _0\), \(P_{\mu }\) and other parameters. Calculate the PMF for M integer candidates and sort them into descending order. Choose m so that

    $$\begin{aligned} P_{\mathrm{f},\text {ILS}}(m) > P_{\mu } \quad P_{\mathrm{f},\text {ILS}}(m+1) < P_{\mu } \end{aligned}$$
    (41)

    Then \(P_{0,\text {ILS}} = \sum ^{M}_{k=m+1} P_{\mathrm{f},\text {ILS}}(k)\);

  2. 2.

    Compute the failure rates for \(P_{\mathrm{f},\text {IA}}(i,\mu _0)\) and \(i= 1,\ldots , M\). Besides this, the values of probability ratio factors are computed based on the initial settings

    $$\begin{aligned} r(j,\mu _0) = \frac{P_{\mathrm{f},\text {IA}}(j,\mu _0)}{P_{\mathrm{f},ILS}(j)} \quad j=m+1,\dots ,M \end{aligned}$$

    Choose \(r(m,\mu _0)= \text {max} \{r(j,\mu _0)\}\);

  3. 3.

    Construct the nonlinear equation and implement numerical optimization to

    $$\begin{aligned} \sum _{i=1}^m P_{\mathrm{f},\text {IA}}(i,\mu ) + r(m,\mu ) P_{0,\text {ILS}} = P_\mathrm{f} \end{aligned}$$
    (42)

    with \(0<r(m,\mu ) < 1\).

Note that those initial parameters have influence to the performance of iCON approach:

  • \(P_{\mu }\), which determines the value of m. The smaller \(P_{\mu }\), the bigger m and the less approximation error in \(P_{\mathrm{f},\text {ILS}}\);

  • \(\mu _0\), which influences the time cost in numerical optimization. The better choice of \(\mu _0\) will decrease the iterative times in nonlinear optimization of step 3.

Here we give two remarks about the application of iCON approach. First, a simplified version of iCON approach can be used under certain numerical condition. Previously, we mentioned that to decrease the approximation error of \(P_{\mathrm{f},\text {ILS}}\), we have to choose a rather small \(P_{\mu }\). For instance, if the failure rate is \(P_\mathrm{f}=0.001\), according to the variation of order of magnitude in Fig. 8, \(P_{\mu }\) is better to be smaller than \(10^{-8}\). This is because \(\sum _{k=m+1}^{\infty } P_{\mathrm{f},\text {ILS}}(k)\) may lead to large \(P_{0,\text {ILS}}\). Then the determined \(\mu \) with (42) will not be so accurate, which directly influences the controllability of failure rate.

If \(P_{\mu }\) is trivial, such as less than \(10^{-10}\), then \(P_{0,\text {ILS}}\) is also very trial. Since \(r(m,\mu )<1\), \(r(m,\mu )P_{0,\text {ILS}}\) can be neglected in numerical optimization. Then the iCON approach can be simplified into two steps:

  1. 1.

    Set initial parameters \(P_{\mathrm{f}}\), \(\mu _0\), \(P_{\mu }\) and other parameters. Sort the calculated PMF of M integer candidates into descending order. Choose m so that

    $$\begin{aligned} P_{\mathrm{f},\text {ILS}}(m) > P_{\mu } \quad P_{\mathrm{f},\text {ILS}}(m+1) < P_{\mu } \end{aligned}$$
    (43)
  2. 2.

    Construct the nonlinear equation and implement numerical optimization to

    $$\begin{aligned} \sum _{i=1}^m P_{\mathrm{f},\text {IA}}(i,\mu ) = P_\mathrm{f} \end{aligned}$$
    (44)

Note that this simplified approach would be better used when GNSS model is strong.

Second, it is noted that \(P_{\mathrm{f}}\) should be chosen based on model strength. If model is weak, it is meaningless to have high requirement to reliability. The users should take measure to strengthen the GNSS model, such as using the constraint of baseline information. For strong GNSS model, \(P_{\mathrm{f}}\) should not be too small, which would reject many correct integer candidates and lead to high false alarm.

6 Experiments verification

6.1 The performance of iCON approach

In Sect. 5, the iCON approach was introduced and analyzed. This section will verify those conclusions based on multi-frequency and multi-GNSS simulation experiments. The simulation settings are the same as Table 2. The failure rates in Monte Carlo and iCON approach are chosen as \(P_\mathrm{f}=0.001\). The number of simulation samples in Monte Carlo is 50,000 and all IAR are implemented epoch by epoch. The flow diagram of simulation experiment is presented in Fig. 10. Note that we only implement IAR to the GNSS models whose ILS success rates are larger than 0.8. The GNSS models which have low ILS success rates are difficult to realize the ambiguity fixing.

Fig. 10
figure 10

The flow diagram of the simulation experiment. \(P_{\mathrm{f},\text {iCON}}\),\(T_{\text {iCON}}\), \(P_{\mathrm{f},\text {MC}}\) and \(T_{\text {MC}}\) denote the failure rates and time consumptions of iCON and Monte Carlo approach, respectively

Full size image

To evaluate the performance of iCON approach, we will first take the DTIA estimator as example. The comparison of time consumption between Monte Carlo and iCON approaches are presented in Fig. 11. The simulation ephemeris is chosen from July 12 to July 17, 2014, including all the systems and their combinations 6934 samples.

Fig. 11
figure 11

Time consumptions of iCON and Monte Carlo sampling approaches based on DTIA estimator. Black lines Monte Carlo sampling; blue lines iCON approach; red line 1 s line

Full size image

As presented in Fig. 11, the time consumptions of Monte Carlo sampling are much longer than that of iCON approach. All the time consumptions of iCON approach are much less than 1 s, which means we can realize the instantaneous IA ambiguity resolution based on iCON. Notice that there are several similar curves obviously overlapping each other for Monte Carlo approach. This is because the time consumptions of Monte Carlo sampling have the positive correlation with the dimension of GNSS model. The more number of satellites, the more time will be taken to implement IAR. Double or triple system combinations will obviously have more time consumptions. Besides this, all GNSS ephemeris will repeat several times in 6 days. Hence, we can see similar periodical phenomenon for the time consumptions of Monte Carlo. Of course, they will also appear in those of iCON approach.

Table 4 Statistics of simulation experiment for both approaches
Full size table
Fig. 12
figure 12

The controlled failure rates based on Monte Carlo sampling approach. Red dots failure rates based on Monte Carlo; black lines \(P_{\mathrm{f}} \pm 3\sigma _{\mathrm{f},\text {DTIA}}\) bounds

Full size image
Fig. 13
figure 13

The controlled failure rates based on iCON approach. Blue dots failure rates based on iCON; black line 2\(P_\mathrm{f}\) bound

Full size image

Besides the time consumptions, the controlled failure rates based on both approaches are demonstrated in Figs. 12 and 13. According to both figures, we can see that the controlled failure rates of both approaches have different scattering range. Here we give the detailed statistics of experiment results for both approaches based on DTIA estimator. According to Table 4, we give more characteristics of both approaches. They are summarized as:

  1. 1.

    As analyzed in Sect. 4, fixed failure rate approach based on Monte Carlo sampling is essentially the approach of stochastic control. Based on formula (22), the standard deviation of controlled failure rate \(\sigma _{\mathrm{f},\text {DTIA}}= 1.42 \times 10^{-4}\), which is close to the theoretical precision in (25). The expectation of controlled failure rates is \(E(P_{\mathrm{f},\text {DTIA}}) \approx P_\mathrm{f}\) with \(|E(P_{\mathrm{f},\text {DTIA}})-P_\mathrm{f} |<10^{-5}\). These results indicate that the controlled failure rates based on Monte Carlo sampling will obey the normal distribution \(N(P_\mathrm{f}, \sigma _{P_{\mathrm{f},\text {DTIA}}})\) when the number of epochs is infinite. In Fig. 12, the \(P_{\mathrm{f}} \pm 3\sigma _{\mathrm{f},\text {DTIA}}\) bounds are plotted, which means the controlled failure rates have \(99.7\,\%\) probability falling into this region.

  2. 2.

    iCON approach can realize the instantaneous and controllable IA ambiguity resolution. Note that the expectation of \(P_{\mathrm{f},\text {DTIA}}\) is smaller than 0.001. This is because the failure rate of DTIA is approximated by the formula of DTIAB, which is the lower bound for that of DTIA. To make DTIA approximate to DTIAB, its critical value has to be chosen a little conservative so that success rates are reduced to lower bound. Hence, the expectation of its actual failure rate will be less than \(P_\mathrm{f}\).

  3. 3.

    The interval of failure rates for iCON approach is shorter than that of Monte Carlo. Though there exist points pass the fixed failure rate \(P_\mathrm{f}\), the maximum is smaller than \(1.5 P_\mathrm{f}\). However, that of Monte Carlo is larger than \(2 P_\mathrm{f}\). It shows that the model information used by iCON is helpful to lower the range of controlled failure rate.

As a summary, it is obvious that iCON approach has better controllability than Monte Carlo sampling.

To give clearer demonstration for the time consumptions of iCON approach, various GNSS models within 1 day are generated, including single and multiple frequencies, single and GNSS combinations. The relations between time consumptions and success rates of DTIA estimators are presented in Fig. 14.

Fig. 14
figure 14

Relation between DTIA success rates and time consumptions for iCON approach

Full size image

Obviously, the maximum time consumptions of iCON approach is gradually decreasing as the increase of DTIA success rate. This proves that the stronger GNSS model, the less time consumption of iCON approach. As analyzed previously, if the GNSS model is rather strong, less pull-in regions is included in the iCON approach, then its time consumption will decrease in nonlinear optimization. Note that more efficient nonlinear optimization method can further save the time consumption, which will be exploited in future.

6.2 Performance of resolvable IA estimators based on iCON approach

Previously, the performance of iCON approach is compared with the fixed failure rate approach based on Monte Carlo sampling by DTIA estimator. Actually, iCON approach can be applied into other resolvable IA estimators, such as EIA and IALS listed before. Though iCON is proved to be instantaneous and can effectively control failure rate, it is not clear that which IA estimator will have better performance based on iCON. In this part, we will apply iCON into three IA estimators and compare their performances. It is noted that here the ’better performance’ means higher IA success rate for the same setting of \(P_\mathrm{f}\).

The experiment settings are the same as those of Table 2, and the flow diagram is similar. More than 500 epochs of ’GPS+BeiDou’ systems are generated within 2 days. The controlled failure rates for three IA estimators are presented in Fig. 16, and their corresponding success rates are shown in Fig. 15. The statistics for both figures are summarized in Table 5. Specifically, here we only compare the mean of IA success rates and failure rates. The former one reflects the performance of IA estimator, and the latter one indicates the controllability of failure rate.

Fig. 15
figure 15

IA success rates of three resolvable IA estimators based on iCON approach. Green line EIA; blue line IALS; red line DTIA

Full size image
Fig. 16
figure 16

Failure rates of three resolvable IA estimators based on iCON approach. Green line EIA; blue line IALS; red line DTIA; black line \(2P_\mathrm{f}\) bound

Full size image

Based on Figs. 15 and 16 and their statistics, we give the following remarks:

  1. 1.

    iCON can be applied into IA estimators which have analytical formulas of probability evaluations;

  2. 2.

    The failure rates of IA estimators are all controlled within small range based on iCON. However, EIA has the shortest range of controlled failure rates. Besides this, we also can see that EIA always has the smallest success rates. This is caused by the small \(P_\mathrm{f}\). If \(P_\mathrm{f}\) is chosen large or GNSS model is strong enough so that its aperture regions are constrained by ILS region, then EIA will behave similarly as ILS estimators.

  3. 3.

    DTIA has almost the same performance as IALS. Their controlled failure rates and success rates are almost overlapped each other. Note that there still exist small differences, and the mean for the success rates of DTIA is a little larger than that of IALS. This is due to that DTIA is the generalized IALS and can be seen as the approximated optimal IA estimator when GNSS model is strong. Note that IALS has better controllability of failure rate than that of DTIA. This is benefitted from the optimality of ILS estimation and less approximation errors. However, since the implementation procedure of IALS is rather complicate, it is not so applicable as DTIA in practice.

According to previous analysis, we can conclude that DTIA is more suitable to be used in practice, especially in the multi-GNSS, multi-frequency GNSS applications.

Table 5 Statistics of three resolvable IA estimators
Full size table

6.3 Comparison between iCON approach and fixed failure rate approach with look-up table

Until now, we have verified the performance of resolvable IA estimators based on iCON approach. However, we still do not know the performance difference between the instantaneous IA estimator based on iCON approach and RTIA estimator based on look-up table. In this section, we will compare the performance of DTIA and IALS based on iCON approach and RTIA based on look-up table. Here the look-up table of RTIA is released in Verhagen (2013). The simulation settings and experiment flow diagram are not changed.

Fig. 17
figure 17

IA success rates of DTIA, IALS and RTIA. Green line RTIA; blue line IALS; red line DTIA

Full size image

In this simulation experiment, the dual-frequency, ’GPS +Galileo+BeiDou’ combination system is chosen. More than 500 epochs are chosen within 2 days. Results are demonstrated in Figs. 17 and 18. The statistics for them are listed in Table 6. According to the simulation results, we can give the following remarks:

  • DTIA and IALS based on iCON approach basically have similar performance as RTIA based on look-up table. All estimators can realize fast and controllable IAR;

  • Specifically, we can see that DTIA and IALS have little higher success rates than that of RTIA most of times in Fig. 17 and Table 6. That is the reason why the expectations of success rates for DTIA and IALS are higher than that of RTIA;

  • Comparing with RTIA, the controlled failure rates of DTIA and IALS are not so conservative. Their expectation values are closer to \(P_\mathrm{f}\). It means DTIA and IALS have better controllability to the approximation errors based on iCON approach than that of RTIA, even if RTIA has the a priori information of look-up table;

  • We can see that the failure rates of RTIA based on look-up table are not fluctuating around \(P_\mathrm{f}\). This is because the critical values in look-up table already choose the conservative ones, which will artificially change the statistics of fixed failure rate results.

As a summary, DTIA and IALS based on iCON approach can realize better instantaneous and controllable ambiguity resolution than the RTIA based on look-up table. Note that more detailed performance comparison and application for DTIA and RTIA can be referred to Li et al. (2015). Furthermore, as analyzed previously, the look-up table has to be created based on numerous simulation, whose precision is limited by the corresponding setting in simulation. Hence, it cannot be quickly applied into practice for other IA estimators. While, based on iCON approach, the users only need the information of ambiguity model matrix and set the required failure rate upper bound requirement. It is very convenient and feasible to other IA estimator with analytical probability evaluations.

Fig. 18
figure 18

IA failure rates of DTIA, IALS and RTIA. Green line RTIA; blue line IALS; red line DTIA

Full size image
Table 6 Statistics of three resolvable IA estimators
Full size table

Furthermore, since iCON approach is suitable to all IA estimators with analytical PMF formulas, this gives a new viewpoint to study other IA estimators. Some IA estimators can be connected by their PMF relations. Besides this, how to decrease the approximation errors in probability evaluations also need further research.

7 Conclusion

Instantaneous and precise quality control is an important topic in IAR. In this contribution, we firstly reviewed the development of IAR and then analyzed the unresolved problems in the IA estimation theory, especially its difficulties in the instantaneous applications. Though fixed failure rate approach combined with the look-up table can provide the initial solution, the longtime consumptions in creating the look-up table made it difficult to be widely applied. Besides this, fixed failure rate approach was essentially one kind of statistical control to the failure rate. This may bring unexpected trouble in quality control.

To tackle these problems, in this contribution, we proposed an original approach to realize instantaneous and precise quality control for IA ambiguity resolution. The so-called iCON approach is instantaneous and controllable without resorting to external information. The only requirement is that the IA estimator should have simple and analytical probability evaluation formulas. Besides this, the stronger GNSS models, the shorter time consumptions iCON will take. Furthermore, this approach has better controllability than fixed failure rate approach.

To verify these conclusions, multi-frequency and multi-GNSS simulation experiments were implemented to test the performance of iCON approach by different comparisons. Experiment results verified the advantages of iCON approach. Specifically, DTIA and IALS based on iCON had almost the same performance in controllability of failure rates, since DTIA can be seen as the generalized IALS. Both estimators slightly outperformed RTIA with look-up table based on the same controlled failure rates. However, due to the complicate process in IALS ambiguity resolution, DTIA based on iCON approach would be a better choice for the instantaneous and controllable IAR.

In the future, the connection between IA estimators and more efficient nonlinear optimization method will be the main research topics, which are helpful to better solve the ambiguity validation problem.