Keywords

1 Introduction

In the rapid and high precision GNSS applications, IAR is a fundamental and difficult problem. Once the integer ambiguities are fixed, users can take advantage of the precise pseudo range data in positioning and navigation. Many GNSS models are developed for IAR applications. The principle of them can refer to [1, 2].

As the point of departure, most of GNSS models can be casted in the following conceptual frame of linear(ized) observation equations:

$$ {\mathbf{E(y) = Aa + Bb;}}\,{\mathbf{D(y) = Q}}_{{{\mathbf{yy}}}} $$
(49.1)

where \( {\mathbf{E}}( \cdot ) \) and \( {\mathbf{D}}( \cdot ) \) are the expectation and dispersion operators, and y the ‘observed minus computed’ single- or dual-frequency carrier phase or/and code observations. \( {\mathbf{Q}}_{{{\mathbf{yy}}}} \) is the variance covariance (vc)-matrix of observations y.

The procedure of IAR usually consists of four steps. In the first step, the integer constraint of ambiguities \( {\mathbf{a}} \in {\mathbb{Z}}^{{\mathbf{n}}} \) is disregarded. The float solutions together with their vc-matrix are estimated based on least-square adjustment as \( \left[ {\begin{array}{*{20}c} {{\hat{\mathbf{a}}}} \\ {{\hat{\mathbf{b}}}} \\ \end{array} } \right],\;\left[ {\begin{array}{*{20}c} {{\mathbf{Q}}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{a}}}}}}} } & {{\mathbf{Q}}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{b}}}}}}} } \\ {{\mathbf{Q}}_{{{{\hat{{\mathbf{b}}}\hat{{\mathbf{a}}}}}}} } & {{\mathbf{Q}}_{{{{\hat{{\mathbf{b}}}\hat{{\mathbf{b}}}}}}} } \\ \end{array} } \right] \). Their estimation formulas are given as

$$ \begin{aligned} {\hat{\mathbf{a}}} & = ({\bar{\mathbf{A}}}^{{\mathbf{T}}} {\mathbf{Q}}_{{{\mathbf{yy}}}}^{ - 1} {\bar{\mathbf{A}}})^{ - 1} {\bar{\mathbf{A}}}^{{\mathbf{T}}} {\mathbf{Q}}_{{{\mathbf{yy}}}}^{ - 1} {\mathbf{y}} \\ {\hat{\mathbf{b}}} & = ({\mathbf{B}}^{{\mathbf{T}}} {\mathbf{Q}}_{{{\mathbf{yy}}}}^{ - 1} {\mathbf{B}})^{ - 1} {\mathbf{B}}^{{\mathbf{T}}} {\mathbf{Q}}_{{{\mathbf{yy}}}}^{ - 1} ({\mathbf{y}} - {\mathbf{A}\hat{{\mathbf{a}}}}) \\ \end{aligned} $$
(49.2)

where \( {\bar{\mathbf{A}}} = {\mathbf{P}}_{{\mathbf{B}}}^{ \bot } {\mathbf{A}},\;{\mathbf{P}}_{{\mathbf{B}}}^{ \bot } = {\mathbf{I}}_{{\mathbf{m}}} - {\mathbf{P}}_{{\mathbf{B}}} \) and \( {\mathbf{P}}_{{\mathbf{B}}} = {\mathbf{B}}({\mathbf{B}}^{{\mathbf{T}}} {\mathbf{Q}}_{{{\mathbf{yy}}}}^{ - 1} {\mathbf{B}})^{ - 1} {\mathbf{B}}^{{\mathbf{T}}} {\mathbf{Q}}_{{{\mathbf{yy}}}}^{ - 1} \). With the metric of \( {\mathbf{Q}}_{{{\mathbf{yy}}}} ,\;{\mathbf{P}}_{{\mathbf{B}}} \) is the projector that projects orthogonally onto the range space of B. Quality control steps, such as detection, identification and adaption of outliers are implemented in this step.

The second step takes into the previous integer constraint, and realizes the fixing process of float ambiguities. It can be described as a many-to-one mapping

$$ {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} }} = {\mathbf{S}(\hat{{\mathbf{a}}})},\;{\mathbf{S}}:{\mathbf{R}}^{{\mathbf{n}}} \to {\mathbb{Z}}^{{\mathbf{n}}} $$
(49.3)

The mapping process is realized by many integer estimators, such as integer rounding (IR), integer bootstrapping (IB), and integer least-square (ILS). Among them, ILS is the optimal one and can maximize the success rate of estimation [3]. Due to the influence of correlation between different ambiguities, the efficiency of integer estimators is often very low. In order to tackle this problem, LAMBDA method [4]; Teunissen [5–7] is introduced to improve the estimation efficiency and success rate [8].

After integer mapping, the third step is to test whether the fixed solutions should be accepted. This step is also called ambiguity validation and realized by many acceptance tests, including F-ratio test (FT) [9], R-ratio test (RT) [10], W-ratio test (WT) [11], Difference test (DT) [12], Projector test (PT) [13]. Note that the function of testing is to exclude the suspected integers, and accept the most possible one, since most of times we do not know the correct ambiguity.

According to previous testing result, other parameters can be adjusted based on the estimated ambiguities in the last step

$$ {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{b} }} = {\hat{\mathbf{b}}} - {\mathbf{Q}}_{{{{\hat{{\mathbf{b}}}\hat{{\mathbf{a}}}}}}} {\mathbf{Q}}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{a}}}}}}}^{ - 1} {{(\hat{{\mathbf{a}}}}} - {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} )}} $$
(49.4)

where \( {\mathbf{Q}}_{{{{\hat{{\mathbf{b}}}\hat{{\mathbf{a}}}}}}} \) is the vc-matrix between ambiguity vector and other parameters. After four steps, the carrier phase observations based on correctly fixed result will behave as the high precision range data.

In this contribution, we will focus on the third step. As is known, the combination of second step and third step is the so-called IA estimator. Be different from ILS estimator, there are three judgments after IA estimation: success, failure or undecided. The undecided part is formed by the intervals or holes between different aperture pull-in regions [14]. The benefit of IA estimators is that their failure rates and success rates can be adjusted by the controlling to critical values of acceptance tests. Since failure rate is the critical indicator for the performance of ambiguity resolution, In order to realize its controlling, FFR approach based on Monte Carlo integral is proposed by [15]. The IA estimation theory and FFR approach provide the ambiguity validation foundation and an initial solution to this problem. However, there still exist the following problems in this solution and the theory:

  1. 1.

    The critical values of IA estimators are determined by Monte Carlo integral with the GNSS models as input. Its precision depends on the simulation times. Hence, if we want to obtain a precise value, a large amount of simulation samples must be generated which is rather time-consuming. Since the pull-in regions of IA estimators are constructed by complicated geometries, most of the relations between critical value and success rate or failure rate are nonlinear. The computation for them cannot be realized analytically. The only choice is Monte Carlo integral, though we can improve the precision of Monte Carlo integral with more effective sampling methods, such as sample average approximation, importance sampling, stratified sampling [16], the contradiction between precision and time cost still hinders its application;

  2. 2.

    The practical way to apply the FFR approach is to create the look-up table for certain acceptance test. This work was firstly completed for RT in [17]. The look-up table is created based on numerous GNSS samples with FFR approach for local and global applications. It is constructed according to the number of satellites and failure rates and must satisfy the failure rate requirement for any GNSS samples for certain location. Hence, the choice of critical values in the table is chosen for the worst GNSS model with certain number of satellites. Essentially, the fixed failure-rate approach realized by look-up table actually constraints the failure rate within the user’s requirement. Though this approach is applicable, it will be a huge workload for the global application and various acceptance tests;

  3. 3.

    At present, the research about the IA estimators and its application mainly focus on RT-IA estimator. Though properties of other IA estimator are investigated in [18, 19], the gaps between IA estimation theory and practice still have not been bridged. One of the difficult problems is the probability evaluation to IA estimators. Those popular estimators, such as RTIA, and optimal IA estimator, do not have analytical expression for the IA success rates and failure rates, which hinder the further investigation.

Fortunately, recent research about DT reveals the clue to resolve these problems. In [20], RT and DT are compared based on a large number of GNSS samples. Then in [21], the essence between their differences are revealed from geometry and mathematical analysis, which proves that DT is more suitable to the multi-frequency and multi-GNSS applications. According to the results in [22], the properties of DT-IA is derived and its analytical expression for success rate and failure rate are firstly given. This provides the necessary tools to realize the application of DT-IA estimator.

In this contribution, we will introduce an effective method to realize instantaneously controlling to the failure rate of DTIA estimator. This method takes full advantage of DT in strong GNSS scenarios. By using the relationship between ILS and IA probability evaluations of pull-in regions, the failure rate of DT-IA estimator can be effectively and instantaneously controlled by using the constraint of the pre-setting failure rate.

The whole contribution is organized as follows. In Sect. 49.2, we briefly review the previous research about DTIA estimator and present its corresponding properties. The analytical expressions for the success rates of ILS and DTIA estimators are presented. The probability ratio to connect both probability evaluations is defined and analyzed. Then the new controllable IA ambiguity resolution method is introduced in Sect. 49.3. Its principle is detailed presented. In order to verify the effectiveness of this method, simulation experiments based on multi-frequencies, multi-GNSS are implemented. The experiment results show that this method can instantaneously realize the controlling of failure rate within certain range, which has the same performance as FFR approach. The stronger GNSS model, the better instantaneity and the stronger capacity of quality control the iCON method will have.

2 Difference Test and Its Properties

2.1 Aperture Pull-in Regions Based on DT

The purpose of acceptance test is to exclude the suspected ambiguities. This is realized by the aperture pull-in region in geometry. If the float ambiguity falls into the aperture pull-in region, it will be more likely fixed to the corresponding integer vector than those in integer pull-in region. Hence, it is a necessary quality control step. The overall definition of aperture pull-in region is given in [23]

$$ \Omega _{{\mathbf{z}}} = \{ {\mathbf{x}} \in {\mathbb{R}}^{{\mathbf{n}}} ,{\mathbf{z}} \in {\mathbb{Z}}^{{\mathbf{n}}} |{\mathbf{S}}({\mathbf{x}}) = {\mathbf{z}},{\mathbf{\gamma (x)}} \le {\varvec{\upmu}}\} $$
(49.5)

where \( {\varvec{\upgamma}}( \cdot ) \) is the acceptance testing function and μ its critical value. Then the IA estimator is defined as

$$ {\bar{\mathbf{a}}}_{{{\mathbf{IA}}}} = \left\{ {\begin{array}{*{20}l} {{\mathbf{z}}\,\,{\mathbf{if}}\,{\hat{\mathbf{a}}} \in {\varvec{\Omega}}_{{\mathbf{z}}} } \hfill \\ {{\hat{\mathbf{a}}}\,\,{\mathbf{if}}\,{\hat{\mathbf{a}}} \notin {\varvec{\Omega}}_{{\mathbf{z}}} } \hfill \\ \end{array} } \right. $$
(49.6)

The aperture pull-in regions satisfy the following properties

$$ \left\{ {\begin{array}{*{20}l} {\mathop \cup \limits_{{{\mathbf{z}} \in {\mathbb{Z}}^{{\mathbf{n}}} }} {\varvec{\Omega}}_{{\mathbf{z}}} = {\varvec{\Omega}},\,{\varvec{\Omega}} \subset {\mathbb{R}}^{{\mathbf{n}}} } \hfill \\ {{\mathbf{Int}}({\varvec{\Omega}}_{{\mathbf{u}}} ) \cap {\mathbf{Int}}({\varvec{\Omega}}_{{\mathbf{v}}} ) = \emptyset ,\,{\mathbf{u}} \ne {\mathbf{v}}} \hfill \\ {{\varvec{\Omega}}_{{\mathbf{z}}} = {\mathbf{z}} + {\varvec{\Omega}}_{0} } \hfill \\ \end{array} } \right. $$

Thus the aperture pull-in regions \( \Omega _{{\mathbf{z}}} \) are no overlapping subsets of \( {\mathbb{R}}^{{\mathbf{n}}} \). The explicit expression of DT is given below

$$ \left\| {{\hat{\mathbf{a}}} - {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} }}_{2} } \right\|_{{{\mathbf{Q}}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{a}}}}}}} }}^{2} - \left\| {{\hat{\mathbf{a}}} - {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} }}_{1} } \right\|_{{{\mathbf{Q}}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{a}}}}}}} }}^{2} \ge\,{\varvec{\upmu}}_{{{\mathbf{DT}}}} $$
(49.7)

with \( {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} }}_{1} \) and \( {\mathbf{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} }}_{2} \) the best and second best integer candidates, and \( {\varvec{\upmu}}_{{{\mathbf{DT}}}} \) the critical value. The geometry of origin-center pull-in region for DTIA is

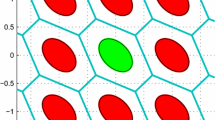
$$ \begin{aligned}\Omega _{{0,{\mathbf{DTIA}}}} & = \{ {\hat{\mathbf{a}}} \in {\mathbb{R}}^{{\mathbf{n}}} |{\mathbf{S}}({\hat{\mathbf{a}}}) = \text{0},\left\| {{\hat{\mathbf{a}}} - {\mathbf{u}}} \right\|_{{{\mathbf{Q}}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{a}}}}}}}}}^{2} -\,\left\| {{\hat{\mathbf{a}}}} \right\|_{{{\mathbf{Q}}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{a}}}}}}} }}^{2} \ge\,{\varvec{\upmu}}_{{{\mathbf{DT}}}} \} \\ & = \{ {\hat{\mathbf{a}}} \in {\mathbb{R}}^{{\mathbf{n}}} |{\mathbf{S}}({\hat{\mathbf{a}}}) = \text{0},\frac{{{\mathbf{uQ}}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{a}}}}}}}^{ - 1} {\hat{\mathbf{a}}}}}{{\left\| {\mathbf{u}} \right\|_{{{\mathbf{Q}}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{a}}}}}}}}} }} \ge \frac{{\left\| {\mathbf{u}} \right\|_{{{\mathbf{Q}}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{a}}}}}}}}}^{2} -\,{\varvec{\upmu}}_{{{\mathbf{DT}}}} }}{{2\left\|{\mathbf{u}}\right\|_{{{\mathbf{Q}}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{a}}}}}}} }} }}\} \\ \end{aligned} $$
(49.8)

with \( {\mathbf{u}} \in {\mathbb{Z}}^{{\mathbf{n}}} \backslash \{ \text{0}\} \). It means that \( \Omega _{{\text{0},{\mathbf{DTIA}}}} \) are formed by intersecting half-spaces that are constrained by hyper-planes orthogonal to u and passing through the points \( \frac{1}{2}(1 - \frac{{{\varvec{\upmu}}_{{{\mathbf{DT}}}} }}{{\left\| {\mathbf{u}} \right\|_{{{\mathbf{Q}}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{a}}}}}}} }}^{2} }}){\mathbf{u}} \). The two-dimensional geometry construction of aperture pull-in region is demonstrated in Fig. 49.1. The two dimensional vc-matrix is \( \left[ {\begin{array}{*{20}c} {0.0865} & { - 0.0364} \\ { - 0.0364} & {0.0847} \\ \end{array} } \right] \).

Fig. 49.1
figure 1

Two-dimensional construction of DT aperture pull-in region with \( {\varvec{\upmu}}_{{{\mathbf{DT}}}} = {5} \). The red stars denote the intersecting points between pull-in regions and coordinate axes

Full size image

2.2 Probability Evaluations of DTIA Estimator

In [22], the definition of DTIAB is firstly given, which can be seen as the generalized IA bootstrapping estimator. Its success rate is given as

$$ {\mathbf{P}}_{{{\mathbf{s}},{\mathbf{DTIAB}}}} = \prod\limits_{{{\mathbf{i}} = 1}}^{{\mathbf{n}}} {\left( {2{\varvec{\Phi}}(\frac{{|{\mathbf{x}}_{{\mathbf{i}}} |}}{{{\varvec{\upsigma}}_{{{\mathbf{i}}|{\mathbf{I}}}} }}) - 1} \right)} $$
(49.9)

with \( |{\mathbf{x}}_{{\mathbf{i}}} | \) the intersecting points between DTIAB and coordinate axes and \( {\varvec{\upsigma}}_{{{\mathbf{i}}|{\mathbf{I}}}} \) the standard deviation from the LDL decomposition of \( {\mathbf{Q}}_{{{{\hat{{\mathbf{z}}}\hat{{\mathbf{z}}}}}}}\text{,}\;{\mathbf{Q}}_{{{{\hat{{\mathbf{z}}}\hat{{\mathbf{z}}}}}}} = {Z}^{T{\mathbf{Q}}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{a}}}}}}}}Z \), with Z the decorrelation matrix of \( {\mathbf{Q}}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{a}}}}}}} \). The analytical expression to compute \( |{\mathbf{x}}_{{\mathbf{i}}} | \) can be determined in decorrelated space when the GNSS model \( {\mathbf{Q}}_{{{{\hat{{\mathbf{z}}}\hat{{\mathbf{z}}}}}}} \) and critical value \( {\varvec{\upmu}}_{{{\mathbf{DT}}}} \) are given, just as shown below

$$ {\mathbf{x}}_{{\mathbf{i}}} = \frac{{\left\| {{\mathbf{c}}_{{\mathbf{i}}} } \right\|_{{{\mathbf{Q}}_{{{{\hat{{\mathbf{z}}}\hat{{\mathbf{z}}}}}}} }}^{2} - {\varvec{\upmu}}_{{{\mathbf{DT}}}} }}{{2\left\| {{\mathbf{c}}_{{\mathbf{i}}} } \right\|_{{{\mathbf{Q}}_{{{{\hat{{\mathbf{z}}}\hat{{\mathbf{z}}}}}}} }}^{2} }},\;{\mathbf{i}} = 1,2, \ldots ,{\mathbf{n}} $$
(49.10)

where \( {\mathbf{c}}_{{\mathbf{i}}} \) is the canonical vector with 1 at the i-th entry and 0 for other entries. Actually, DTIA and DTIAB have the same intersecting points between correct pull-in regions and coordinate axes. This means that the scaling ratios are the same for DTIA and DTIAB in the coordinate directions, which is consistent with the relationship between IB and ILS [22]. Hence, we can use the properties of DTIAB to approximate DTIA estimator after decorrelation step.

Based on the scaling ratios in different directions, the size of DT-IAB pull-in region can be derived as

$$ {\mathbf{V}}_{{{\mathbf{DTIAB}}}} = \prod\limits_{{{\mathbf{i}} = 1}}^{{\mathbf{n}}} {2\left| {{\mathbf{x}}_{{\mathbf{i}}} } \right|} = \prod\limits_{{{\mathbf{i}} = 1}}^{{\mathbf{n}}} {\left| {1 - \frac{{{\varvec{\upmu}}_{{{\mathbf{DT}}}} }}{{\left\| {{\mathbf{c}}_{{\mathbf{i}}} } \right\|_{{{\mathbf{Q}}_{{{{\hat{{\mathbf{z}}}\hat{{\mathbf{z}}}}}}} }}^{2} }}} \right|} $$
(49.11)

There exists the maximization condition for computation of Eq. (49.11), and the proof is given in [22]. According to the formula (49.11), the size of DTIAB is variant and depends on \( {\varvec{\upmu}}_{{{\mathbf{DT}}}} \) and \( {\mathbf{Q}}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{a}}}}}}} \), and the decorrelation step is helpful to improve the success rate of DTIAB.

Just as proven in [22], \( {\mathbf{P}}_{{{\mathbf{s}}\text{,}{\mathbf{DTIAB}}}} \) can be seen as the lower bound for that of DTIA. Hence, we also can use it to approximate the success rate of DTIA. Its upper bound can be constrained by the scaling Euclidean ball based on ADOP. It is given below

$$ {\mathbf{P}}_{{{\mathbf{s}}\text{,}{\mathbf{DTIA}}}} \le {\mathbf{P}}({\varvec{\upchi}}^{2} ({\mathbf{n}}\text{,}{0}) \le \frac{{{2}{\bar{\mathbf{x}}}^{2} {\mathbf{c}}_{{\mathbf{n}}} }}{{{\mathbf{ADOP}}^{2} }}) $$
(49.12)

with \( {\bar{\mathbf{x}}} = \frac{{\sum\nolimits_{{{\mathbf{i}} = {1}}}^{{\mathbf{n}}} {|{\mathbf{x}}_{{\mathbf{i}}} |} }}{{\mathbf{n}}}\text{,}\;{\mathbf{c}}_{{\mathbf{n}}} = \frac{{(\frac{{\varvec{\uppi}}}{2}{\varvec{\Gamma}}(\frac{{\varvec{\uppi}}}{2}))^{{\frac{{\varvec{\uppi}}}{2}}} }}{{\varvec{\uppi}}} \) and \( {\mathbf{ADOP}} = \sqrt {|{\mathbf{Q}}_{{{{\hat{{\mathbf{z}}}\hat{{\mathbf{z}}}}}}} |}^{{\frac{1}{{\mathbf{n}}}}} \).

Actually this is a rather loose upper bound for DTIA estimator. A little sharper bound can be given, which is also based on ADOP and derived from the DTIAB

$$ {\mathbf{P}}_{{{\mathbf{s}}\text{,}{\mathbf{DTIAB}}}} \le \prod\limits_{{{\mathbf{i}} = {1}}}^{{\mathbf{n}}} {\left( {{2}{\varvec{\Phi}}(\frac{{\varvec{\upbeta}}}{{{\mathbf{ADOP}}}}) - {1}} \right)} $$
(49.13)

with \( {\varvec{\upbeta}} = \sqrt{\frac{1}{{\mathbf{n}}}}{{\prod\nolimits_{{{\mathbf{i}} = 1}}^{{\mathbf{n}}} {\left| {{\mathbf{x}}_{{\mathbf{i}}} } \right|} }} \). After enlarging twice by β and ADOP, the upper bound for DTIAB can be regarded as the upper bound of DTIA.

The effectiveness of these probability evaluations are verified in [22].

2.3 Probability Evaluations for Pull-in Regions of ILS and DTIA

In practice, the success rate is the probability evaluation to the correct or central pull-in region. It can provide the information about the GNSS model strength and reliability. Actually, probabilities of other pull-in regions are also important. They give us the reference for the design of ambiguity resolution. In this part, we will give the global analytical expressions for all pull-in regions, including ILS and DTIA pull-in regions.

Since DTIA can be seen as the generalized IALS which have different scaling ratios in different directions [22]. ILS can be seen as the special case for DTIA or IALS. Hence, we will take similar approach in the approximation of probability evaluations for both estimators.

The ILS probability evaluation for the correct integer vector can be approximated by

$$ {\mathbf{P}}_{{{\mathbf{s}}\text{,}{\mathbf{ILS}}}} \approx \prod\limits_{{{\mathbf{i}} = {1}}}^{{\mathbf{n}}} {\left( {{2}{\varvec{\Phi}}(\frac{1}{{{2}{\varvec{\upsigma}}_{{{\mathbf{i}}|{\mathbf{I}}}} }}) - {1}} \right)} $$
(49.14)

This is the probability of central pull-in region. For the probabilities of other pull-in region, or the failing pull-in region, we have

$$ {\mathbf{P}}_{{{\mathbf{f}},{\mathbf{ILS}}}} ({\mathbf{i}}) \approx \prod\limits_{{{\mathbf{i}} = {1}}}^{{\mathbf{n}}} {\left| {{\varvec{\Phi}}(\frac{{{\mathbf{x}}_{{\mathbf{i}}} }}{{{\varvec{\upsigma}}_{{{\mathbf{i}}|{\mathbf{I}}}} }}) - {\varvec{\Phi}}(\frac{{{\mathbf{x}}_{{\mathbf{i}}} - {1}}}{{{\varvec{\upsigma}}_{{{\mathbf{i}}|{\mathbf{I}}}} }})} \right|} $$
(49.15)

where i is the i-th integer candidate, \( {\mathbf{x}}_{{\mathbf{i}}} = \frac{1}{2} + {\mathbf{z}}_{{\mathbf{i}}} \text{,}{\mathbf{z}}_{{\mathbf{i}}} \in {\mathbb{Z}} \) is the intersecting element for each entry of integer vector.

Corresponding to the probabilities of ILS pull-in regions, the probabilities of the DTIA pull-in regions can also be derived

$$ {\mathbf{P}}_{{{\mathbf{f}}\text{,}{\mathbf{DTIA}}}} ({\mathbf{i}}) \approx \prod\limits_{{i = {1}}}^{n} {\left| {{\varvec{\Phi}}(\frac{{{\mathbf{v}}_{{\mathbf{i}}} }}{{{\varvec{\upsigma}}_{{{\mathbf{i}}|{\mathbf{I}}}} }}) - {\varvec{\Phi}}(\frac{{{\mathbf{v}}_{{\mathbf{i}}} - {2}{\mathbf{x}}_{{\mathbf{i}}} }}{{{\varvec{\upsigma}}_{{{\mathbf{i}}|{\mathbf{I}}}} }})} \right|} $$
(49.16)

where \( {\mathbf{x}}_{{\mathbf{i}}} \) is given in (49.10) and \( {\mathbf{v}}_{{\mathbf{i}}} = {\mathbf{x}}_{{\mathbf{i}}} + {\mathbf{z}}_{{\mathbf{i}}} \).

In order to find the relationship between ILS and DTIA pull-in regions, here we give the definition to the ratio between probabilities of pull-in regions

$$ {\mathbf{R}}({\mathbf{i}}) = \frac{{{\mathbf{P}}_{{{\mathbf{f}}\text{,}{\mathbf{DTIA}}}} ({\mathbf{i}})}}{{{\mathbf{P}}_{{{\mathbf{f}}\text{,}{\mathbf{ILS}}}} ({\mathbf{i}})}} $$
(49.17)

where \( {\mathbf{P}}_{{{\mathbf{f}}\text{,}{\mathbf{DTIA}}}} ({\mathbf{i}}) \) and \( {\mathbf{P}}_{{{\mathbf{f}}\text{,}{\mathbf{ILS}}}} ({\mathbf{i}}) \) are the i-th failure rate of the pull-in region, and calculated based on (49.16) and (49.15). Actually, \( {\mathbf{R}}({\mathbf{i}}) \) is within the range \( [{0}\text{,}\;{1}] \).

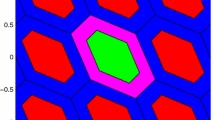
Based on the GNSS model matrix given in Figs. 49.1 and 49.2 gives the trend of probability ratios for different integer candidates.

Fig. 49.2
figure 2

The trend of probability ratio between ILS and DTIA probability of pull-in regions for different integer candidates

Full size image

Hence, the value of \( {\mathbf{R}}({\mathbf{i}}) \) is basically a monotone decreasing function of different integer candidates. This is a useful property in approximation, which will be used in the computation of critical values for acceptance tests.

3 Instantaneous and Controllable IA Ambiguity Resolution

3.1 FFR Approach Based on Monte Carlo Integral

As the beginning of the discussion to tackle the IA ambiguity resolution, we will start from the review to Monte Carlo integral. The start point to use Monte Carlo integral is to resolve the problem of multivariate integral for irregular figures. Since the geometries of pull-in regions is not the regular shape, most of times we cannot directly compute their size. The computation of the probability evaluations for points falling into the pull-in regions are based on the multivariate integral for certain probability density function. One of the most direct and convenient approach is to implement Monte Carlo integral. It is firstly proposed by [24]. The procedures to determine the critical value of FFR IA estimator can be summarized into the following steps [19]:

  1. 1.

    Generate N float ambiguity samples which have normal distribution and conform to \( {\hat{\mathbf{a}}}_{{\mathbf{i}}} \sim {\mathbf{N}}(0,{\mathbf{Q}}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{a}}}}}}} ) \);

  2. 2.

    Set the fixed failure rate \( {\mathbf{P}}_{{\mathbf{f}}} \). Implement ambiguity resolution to each float ambiguities and compute the values of acceptance tests;

  3. 3.

    Based on the root finding method and pre-setting \( {\mathbf{P}}_{{\mathbf{f}}} \), determine the critical value μ which satisfies the fixed failure rate so that \( {\mathbf{P}}_{{\mathbf{f}}} ({\varvec{\upmu}}) - {\mathbf{P}}_{{\mathbf{f}}} = {0} \);

  4. 4.

    Count the number of failing samples \( {\mathbf{N}}_{{\mathbf{f}}} \) and successful samples \( {\mathbf{N}}_{{\mathbf{s}}} \), then the failure rate and success rate can be determined \( {\mathbf{P}}_{{\mathbf{f}}} = \frac{{{\mathbf{N}}_{{\mathbf{f}}} }}{{\mathbf{N}}}\text{,}\,{\mathbf{P}}_{{\mathbf{s}}} = \frac{{{\mathbf{N}}_{{\mathbf{s}}} }}{{\mathbf{N}}} \).

According to the principle of Monte Carlo integral, the precision of this method will improve as the increase of simulation times. An enough large number of samples can ensure the optimality of this method. However, though we can obtain the critical value which has enough precision, it is rather time-consuming and has limited reference value for the instantaneous application. Here we give the relationship between simulation samples and critical values in Fig. 49.3, which is based on the GNSS model matrix

$$ {\mathbf{Q}} = \left[ {\begin{array}{*{20}c} {0.0865} & { - 0.0357} & {0.0421} \\ { - 0.0357} & {0.0847} & { - 0.0258} \\ {0.0421} & { - 0.0258} & {0.0797} \\ \end{array} } \right]. $$
Fig. 49.3
figure 3

Relationship between simulation times and corresponding critical values

Full size image

In Fig. 49.3, it is obvious that as the increase of simulation times, the variation of critical values keep steady. It proves that large simulation times can improve the precision of FFR approach. However, the huge time-consumption makes it almost unavailable in practice.

Even if the FFR approach is realized by look-up table, it is essentially to realize the controlling of failure rate below the certain failure. Strictly speaking, fixed failure rate cannot be realized.

In order to tackle this problem, we propose the instantaneous and CONtrollable (iCON) IA ambiguity resolution method. Based on its characteristics, we name it as iCON.

3.2 ICON IA Ambiguity Resolution

In order to overcome the disadvantages of Monte Carlo integral, the iCON method is proposed here. Its procedures are listed below

  1. (1)

    Set the fixed failure rate and initial critical value as \( {\mathbf{P}}_{{\mathbf{f}}} \text{,}\,{\varvec{\upmu}}_{0} \) and \( {\mathbf{P}}_{0} \). Calculate the probability evaluations for pull-in regions of ILS and determine the number of pull-in regions needed by the equation

    $$ {\mathbf{P}}_{{{\mathbf{s}}\text{,}{\mathbf{ILS}}}} + \sum\limits_{{{\mathbf{i}} = {1}}}^{{\mathbf{n}}} {{\mathbf{P}}_{{{\mathbf{f}}\text{,}{\mathbf{ILS}}}} ({\mathbf{i}})} = {\mathbf{P}}_{0} $$
    (49.18)

    where n is the number of pull-in regions used below. \( {\mathbf{P}}_{0} \) can be set as \( {1} - {\mathbf{P}}_{{\mathbf{f}}} \) for the first time;

  2. (2)

    Calculate the probabilities of n IA pull-in regions and the value of probability ratio in (49.17)

    $$ {\mathbf{R}}({\mathbf{n}}) = \frac{{{\mathbf{P}}_{{{\mathbf{f}}\text{,}{\mathbf{DTIA}}}} ({\mathbf{n}})}}{{{\mathbf{P}}_{{{\mathbf{f}}\text{,}{\mathbf{ILS}}}} ({\mathbf{n}})}} $$
    (49.19)
  3. (3)

    According to the probability ratio in step 2, we can determine the critical value \( {\varvec{\upmu}}_{{{\mathbf{DT}}}} \) for certain GNSS model by

    $$ \sum\limits_{{{\mathbf{i}} = 1}}^{{\mathbf{n}}} {{\mathbf{P}}_{{{\mathbf{f}},{\mathbf{DTIA}}}} ({\mathbf{i}},{\varvec{\upmu}}_{{{\mathbf{DT}}}} )} + {\mathbf{R}}({\mathbf{n}})*{\mathbf{P}}_{{\mathbf{f}}} = {\mathbf{P}}_{{\mathbf{f}}} $$
    (49.20)

In this method, two elements are the critical points. The first one is \( {\mathbf{P}}_{0} \). The larger \( {\mathbf{P}}_{0} \), the more pull-in regions needed in step 1 and 3. Since the resolution in step 3 is a recursive process, the most time-consumption for this method lies on this step. The other one is the GNSS model \( {\mathbf{Q}}{}_{{{{\hat{{\mathbf{a}}}\hat{{\mathbf{a}}}}}}} \). Though it does not appear in previous equations, it determines the values of \( {\mathbf{P}}_{{{\mathbf{s}}\text{,}{\mathbf{ILS}}}} \text{,}\;{\mathbf{P}}_{{{\mathbf{f}}\text{,}{\mathbf{ILS}}}} \text{,}\;{\mathbf{P}}_{{{\mathbf{f}}\text{,}{\mathbf{DTIA}}}} \) and \( {\mathbf{R}}({\mathbf{n}}) \). In other words, it indirectly influences the number of pull-in regions and time-consumption in this method. The stronger GNSS model, the less pull-in regions can be required and the less time the iCON method needed.

Equation (49.20) is the critical step to realize the controlling of failure rate. According to this equation, even if we can give precisely evaluation to \( {\mathbf{P}}_{{{\mathbf{s}}\text{,}{\mathbf{DTIA}}}} ({\mathbf{i}}) \) and \( {\mathbf{P}}_{{{\mathbf{s}}\text{,}{\mathbf{ILS}}}} \), we still can constrain the range of approximation error in the left side by the constraining of \( {\mathbf{P}}_{{\mathbf{f}}} \). It is because

$$ {\mathbf{R}}({\mathbf{n}})*{\mathbf{P}}_{{\mathbf{f}}} < {\mathbf{P}}_{{\mathbf{f}}} $$
(49.21)

In the FFR approach, Eq. (49.20) should be written as

$$ \sum\limits_{{\mathbf{i}} = 1}^{\infty } {{\mathbf{P}}_{{{\mathbf{f}}\text{,}{\mathbf{DTIA}}}} ({\mathbf{i}}\text{,}{\varvec{\upmu}}_{{{\mathbf{DT}}}} )} = {\mathbf{P}}_{{\mathbf{f}}} $$
(49.22)

Equation (49.20) is essentially the approximation for the pull-in regions which can almost be neglected. At the same time

$$ \sum\limits_{{\mathbf{i} = {1}}}^{\mathbf{n}} {{\mathbf{P}}_{{{\mathbf{f}}\text{,}{\mathbf{DTIA}}}} ({\mathbf{i}}\text{,}\,{\varvec{\upmu}}_{{{\mathbf{DT}}}} )} < {\mathbf{P}}_{{\mathbf{f}}} $$
(49.23)

Hence, the range of the controlled failure rate is \( \left( {0,2{\mathbf{P}}_{{\mathbf{f}}} } \right) \). If we want to obtain the same failure rate range as Monte Carlo by iCON, we can apply \( \frac{{{\mathbf{P}}_{{\mathbf{f}}} }}{2} \) into this approach.

4 Experiment Verification

In order to verify the performance of the iCON algorithm, we design the simulation experiment for a medium length baseline with the basic setting in Table 49.1. The \( {\mathbf{P}}_{{\mathbf{f}}} \) in FFR approach and iCON are both chosen as 0.001. Here, the Monte Carlo simulation times is chosen as 50,000. The flow diagram of the simulation experiment is presented in Fig. 49.4.

Table 49.1 Simulation settings for GNSS models
Full size table
Fig. 49.4
figure 4

The flow diagram for the simulation experiment

Full size image

In Fig. 49.4, \( {\mathbf{P}}_{{{\mathbf{f}}\text{,}\,{\mathbf{iCON}}}} \text{,}\,{\mathbf{P}}_{{{\mathbf{f}},{\mathbf{MC}}}} \text{,}\,{\varvec{\upmu}}_{{{\mathbf{iCON}}}} \text{,}\,{\varvec{\upmu}}_{{{\mathbf{MC}}}} \text{,}\,{\mathbf{T}}_{{{\mathbf{iCON}}}} \) and \( {\mathbf{T}}_{{{\mathbf{MC}}}} \) are the failure rates, critical values and time consumptions based on iCON and FFR approach.

Since if the model strength is weak, the IA success rates will be very low. It is not significant to analyse the GNSS samples whose success rates are very low. Hence, we set a threshold to do the comparison for GNSS model strength. If their ILS success rates are larger than 0.8, we will implement previous comparison.

Here we give the comparison of time consumptions and failure rates for both methods based on ‘GPS + BeiDou + Galieo’combination within 1 day in Figs. 49.4 and 49.5, whose statistics are summarized in Table 49.2.

Fig. 49.5
figure 5

The comparison of time consumptions between iCON and FFR approach within 1 day

Full size image
Table 49.2 Statistics for FFR and iCON comparison
Full size table

According to Table 49.2, it is obvious that the iCON has rather shorter time consumptions in the computation of critical values, which can be realized instantaneously. Besides this, the controlling of failure rates is within the theoretical range. The controlling of iCON is also more precise than FFR approach. This comparison reveals one problem in FFR approach in Fig. 49.6. In order to keep its failure rate within the required range, its simulation times must be large enough, and the critical value should choose the worst GNSS scenario so that others can be satisfied. However, iCON method does not have these considerations. This proves that iCON is a better choice than the FFR approach based on Monte Carlo integral.

Fig. 49.6
figure 6

The comparison of failure rates between iCON and FFR approach within 1 day

Full size image

In order to explicitly demonstrate the relations between time consumptions and IA success rates of both methods, we generate more GNSS samples based on the settings in Table 49.1. Their experiment results are demonstrated in Figs. 49.7 and 49.8.

Fig. 49.7
figure 7

Relations between IA success rates and time consumptions for Monte Carlo

Full size image
Fig. 49.8
figure 8

Relations between IA success rates and time consumptions for iCON method

Full size image

According to Fig. 49.7, it is obvious that as the increase of IA success rate, the time consumptions will gradually increase. This is due to that FFR approach relies on the time cost of ambiguity resolution. The more dimension of ambiguity, the more time it will take in ambiguity resolution. Notice that there exist some gaps for the IA success (0.8, 0.9). This is due to the number of simulation samples. However, the maximizations of time consumptions increase as the GNSS models become strong. Besides this, the minimizations of the time consumptions basically keep constant. Since the strengthening of GNSS models can be realized by using several epochs in one estimation step. Then the dimension of GNSS model will keep constant and their time consumptions also do not change.

However, in Fig. 49.8 we can see that the time consumption gradually decreases as the increase of IA success rate. It means that the stronger model can decrease the number of pull-in regions needed, and then less time consumption of iCON method will be taken in the recursive process. Actually, the number of pull-in regions taken into consideration in the approximation process is no more than 300. The less time consumptions in iCON, the more pull-in regions can be added by enlarging \( {\mathbf{P}}_{0} \) to increase the precision of failure rate controlling. Note that the increasing trend within (0, 0.1) is caused by the insufficient samples at that interval, since the ILS success rates of GNSS samples must be larger than 0.8.

5 Conclusions

Ambiguity validation is an important step to realize the quality control of ambiguity resolution. Its foundation is based on the IA ambiguity resolution theory and can be realized by many acceptance tests.

Due to the good properties of DT in previous research, this contribution firstly introduced the properties of DT. Then, the FFR approach based on Monte Carlo integral was introduced and analysed. Though the FFR approach can realize the controlling of failure rate, it is time-consuming and its precision relies on simulation times. In order to overcome these disadvantages, this contribution proposed the iCON method. This method can instantaneously compute the critical value of acceptance test based on pre-setting failure rate and constrain the failure rate within certain range. Both time consumptions and controlling of failure rate can be better than Monte Carlo integral. Besides this, as the GNSS models become strong, iCON will have better performance in time consumption and failure rate control. The simulation experiment based on single and multi-frequency, single and multi-GNSS combinations proves the effectiveness of this method. It will be a better choice in the instantaneous scenarios of next generation GNSS.

Furthermore, the iCON method can be used by any IA estimator whose success rate and failure rates have analytical expressions, such as the IAB, IALS and ellipsoid IA estimators. This will be the topic studied in the future.