Introduction

Integer carrier-phase ambiguity resolution is required for rapid and high-precision GNSS positioning and navigation. Once the ambiguities are fixed, one can take advantage of the precise phase measurements to realize highly demanding application such as attitude determination, integrity monitoring, and formation flying of satellites. Integer ambiguity resolution is a nontrivial problem, especially when one attempts to fix ambiguities instantaneously and reliably.

Each GNSS model including ambiguities can be casted in the linearized observation equation with a dispersion matrix

$$E(y) = Aa + Bb,\;D(y) = Q_{yy}$$
(1)

where E(·) and D(·) are the expectation and dispersion operators, y the m-vector of “observed minus computed” single- or dual-frequency GNSS data, usually the carrier phase and/or code observations, a the n-vector of unknown double-difference ambiguities and a ∊ Z n, the p-vector b consisting of the remaining unknown parameters, and \(b \in {\mathbb{R}}^{p}\). The combined design matrix (A, B) is the m × (n + p) design matrix and Q yy the m × m variance–covariance matrix of GNSS data. In the following parts, \({\hat{\text{a}}}\) and \(\hat{b}\) denote the float solutions of ambiguities and unknown parameters, and \(\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}\) and \(\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{b}\) denote their fixed values.

The procedures of integer ambiguity resolution are usually divided into the following four steps:

  1. 1.

    Float solution. In the first step, one estimates the ambiguities by least-square adjustment as real-valued parameters. These are the so-called float solutions. The float parameters and their covariance matrix are usually denoted as \(\left[ {\begin{array}{*{20}c} {\hat{a}} \\ {\hat{b}} \\ \end{array} } \right],\left[ {\begin{array}{*{20}c} {Q_{{\hat{a}\hat{a}}} } & {Q_{{\hat{a}\hat{b}}} } \\ {Q_{{\hat{b}\hat{a}}} } & {Q_{{\hat{b}\hat{b}}} } \\ \end{array} } \right]\) and

    $$\begin{aligned} \hat{a} & = (\bar{A}^{T} Q_{yy}^{ - 1} \bar{A})^{ - 1} \bar{A}^{T} Q_{yy}^{ - 1} y \\ \hat{b} & = (B^{T} Q_{yy}^{ - 1} B)^{ - 1} B^{T} Q_{yy}^{ - 1} (y - A\hat{a}) \\ \end{aligned}$$
    (2)

    where \(\bar{A} = P_{B}^{ \bot } A\), P ⊥ B  = I m  − P B , P B  = B(B T Q −1 yy B)−1 B T Q −1 yy and \(Q_{{\hat{a}\hat{a}}} = (\bar{A}^{T} Q_{yy}^{ - 1} \bar{A})^{ - 1}\). P B is the projector that projects orthogonally onto the range space of B with the metric of Q yy . Covariance matrix of other float parameters, such as baseline vectors, also can be obtained. Quality control steps are also implemented in this step.

  2. 2.

    Integer solution. The float solution \(\hat{a}\) is further adjusted to take its integer nature into account and constrained to the integer vector \(\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}\). It can be obtained by different methods, which are essentially realized by a many-to-one mapping just as

    $$\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} = S(\hat{a}),{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} S:{\mathbb{R}}^{n} \mapsto {\mathbb{Z}}^{n}$$
    (3)

    where S is the many-to-one integer mapping operator. Among various integer estimators, integer least square (ILS) is the optimal one and has the highest success rate. In order to improve the computational efficiency, the LAMBDA method (de Jonge and Tiberius 1996; Teunissen 1993, 1995, 2010a) can be used.

  3. 3.

    Acceptance test. In practice, one can never ensure the correctness of the integer identification, but one can exclude integer candidates who are most likely suspected. Through acceptance testing, one can avoid the severe influence brought by incorrectly fixed integers. Various tests have been proposed in the literature, such as RT (Frei and Beutler 1990), DT (Tiberius and De Jonge 1995), projector test (Han 1997; Wang et al. 1998), and others. RT and DT, basically outperforming other tests, are analyzed in detail in Verhagen and Teunissen (2006). Note that, the combination of steps 2 and 3 is the so-called IA estimator (Teunissen 2004).

  4. 4.

    Fixed solution. Once the integer ambiguities are determined, the constrained adjustment must be completed. The so-called fixed solution can be achieved as follows

    $$\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{b} = \hat{b} - Q_{{\hat{b}\hat{a}}} Q_{{\hat{a}\hat{a}}}^{ - 1} (\hat{a} - \overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} )$$
    (4)

    with \(Q_{{\hat{b}\hat{a}}}\) the covariance matrix between the ambiguity vector and other unknown parameters. Once ambiguities are successfully fixed, the estimation results will have accuracy in accordance with the precise phase observations.

An incorrectly fixed ambiguity will lead to severe biases in real-valued parameters. Hence, the failure rate, which users mainly pay attention to, should be controlled to be close to 0. It can be realized by adjusting the critical value of acceptance test according to the requirement of failure rate, the so-called fixed failure rate approach (Teunissen 2003b, c). However, the precise control to failure rate is not a trivial problem due to the difficulty in precisely evaluating the performance of IA estimators, which is usually realized by Monte Carlo simulation. Besides quality control of ambiguity resolution, the failure rate can also be chosen as a comparing criterion between different acceptance tests (Teunissen and Verhagen 2008). A better acceptance test should have higher success rate than those of other tests with the same controlled failure rate.

In order to apply the fixed failure rate approach into practice, the look-up table for RTIA estimator is created based on a large amount of Monte Carlo simulations to various GNSS models (Verhagen and Teunissen 2013). Users can check the critical value of fixed failure rate by inputting the number of double-difference ambiguities and the failure rate of ILS for certain GNSS model. This method first provides a feasible way for the applications of the controllable IA ambiguity resolution. Based on this method, the next step is to find the most suitable acceptance test which can be applied in practice. Verhagen and Teunissen (2006) give an initial investigation about the comparison of IA estimators and finding the good performance of RTIA and DTIA estimators. Furthermore, in Wang and Verhagen (2014), DT and RT are compared in detail. However, those comparisons only give initial explanations to the phenomena in simulation experiments. The essence of their difference in different models is not revealed. In addition, the instantaneous and controllable ambiguity resolution approach based on DTIA is shown in Zhang et al. (2015b). At this time, we have two available choices for instantaneous and controllable IA ambiguity resolution: RTIA and DTIA. In this contribution, we focus on exploiting the following two aspects:

  1. (1)

    the relations and differences between both IA estimators;

  2. (2)

    the comparison for instantaneous application of both IA estimators.

First, both acceptance tests are analyzed from the perspectives of geometry reconstruction and algebra. Their differences are explicitly illustrated in weak and strong GNSS models, so that their advantages and drawbacks are clear and easy to be compared and analyzed. Second, as a reference, the relations between RT and DT are studied through OA from numerical perspective. Then, the instantaneous approach for both IA estimators is reviewed and compared. Finally, in order to verify previous conclusions, RTIA and DTIA are compared in simulation experiments and field test.

Acceptance test and integer aperture estimator

Acceptance testing is one part of quality control for ambiguity resolution. It has a close relation with GNSS model strength. When the GNSS model is strong enough, its success rate almost approximates to 1, and then, its ambiguities can be directly fixed without any testing. Unfortunately, many GNSS models, such as single-frequency, single-epoch solutions, are not strong enough, and acceptance testing must be implemented for quality control.

As to acceptance tests, they are the necessary parts of IA estimators introduced in Verhagen (2005). They can be summarized into the unified form (Teunissen 2013a)

$$T(x) \le \mu$$
(5)

where T(·) is the acceptance testing function and μ the critical value.

An IA estimator can be interpreted as integer estimation whose results satisfy a certain acceptance test, which is defined as

$$\varOmega_{z} = \left\{ {x \in {\mathbb{R}}^{n} , \quad z \in {\mathbb{Z}}^{n} |S(x) = z, \quad T( \cdot ) \le \mu } \right\}$$
(6)

where the properties of Ω z are given in Teunissen (2004). It is the combination of integer estimator and acceptance test. The detailed theory about integer estimator and IA estimator can be referred to Teunissen (2010b). The theory of IA estimation provides the foundation of ambiguity validation and gives the feasible way to realize quality control of ambiguity resolution. In order to provide users with controllable failure rate, the so-called fixed failure rate approach is recommended in Teunissen and Verhagen (2008), which can make the failure rate of ambiguity resolution equal to or below the required failure rate. The difference between acceptance test and IA estimator is that the former one is just a test, while the latter represents one region whose samples also satisfy the test. Hence, in the following parts, we will use IA to denote the performance or geometry properties of certain estimators, while RT or DT will be used when we analyze their algebra or numerical properties of testing.

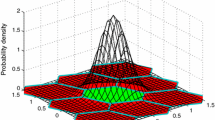
As an illustration, Fig. 1 demonstrates the two-dimensional (2D) DTIA estimator. There are four judgments for the estimation results of IA estimator:

Fig. 1
figure 1

2D geometry reconstruction for DTIA estimation results. Success and detection represent correct judgments, while failure and false alarm represent incorrect judgments. Green success; blue detection; pink false alarm; and red failure

Full size image
  1. 1.

    Success, denoted as P s,IA: The float solution resides in the correct IA pull-in region and passes acceptance test as the green part shows. The mathematical expression for P s,IA is given as \(P_{{{\text{s}},{\text{IA}}}} = \int\limits_{{\varOmega_{a} }} {f(x|a)} {\text{d}}x\), where a is the correct integer vector, f(x|a) the probability density function (PDF) of normal distribution, and \(\varOmega_{a} ,a \in {\mathbb{Z}}^{n}\) the correct IA pull-in region.

  2. 2.

    Failure, denoted as P f,IA: It resides in the wrong IA pull-in region and passes acceptance test, just as the red parts show. Its computation formula is \(P_{\text{f,IA}} = \int\limits_{{\varOmega_{z} ,z \in {\mathbb{Z}}^{n} /\{ a\} }} {f(x|a)} {\text{d}}x\).

  3. 3.

    False alarm, denoted as P fa: It does not reside in any IA pull-in region and does not pass acceptance test, but fall into the correct ILS pull-in region, just as the pink part shows. It can be deduced from the known P s,IA and P s,ILS, since P fa = P s,ILS − P s,IA, where \(P_{\text{s,ILS}} = \int\limits_{{S_{a} }} {f(x|a)} {\text{d}}x\) and S a is the correct ILS pull-in region.

  4. 4.

    Detection, denoted as P d: It does not reside in any IA pull-in region or does not pass acceptance test, while it falls in the wrong ILS pull-in region, just as the blue parts show. It also can be directly obtained by P d = 1 − P s,ILS − P f,IA.

The size of Ω a is controlled by the critical value of acceptance test. The adjustments of P s,IA and P f,IA are realized by choosing critical values based on a certain rule. From another point of view, due to the corresponding relations between critical value and size of IA pull-in region, critical value can be determined by adjusting the size of IA pull-in regions. Since the properties of IA estimators are much discussed in the literature, here we do not list their definitions. Their properties are directly compared and summarized.

The differences between difference test and ratio test

The original definitions of both tests are given here. Let the squared norm of ambiguity residuals for ith integer candidate with the metric of \(Q_{{{\hat{\text{a}}}\hat{a}}}\) be given as

$$R_{i} = \left\| {\hat{a} - \overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{i} } \right\|_{{Q_{{\hat{a}\hat{a}}} }}^{2} = (\hat{a} - \overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{i} )^{T} Q_{{\hat{a}\hat{a}}}^{ - 1} (\hat{a} - \overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{i} )\quad i = 1,2,3, \ldots, n$$
(7)

where \(Q_{{\hat{a}\hat{a}}}\) is the covariance matrix of float ambiguities, and \(\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\text{a}}_{i}\) is the ith integer candidate of float ambiguities. \(R_{\text{i}}\) can be interpreted as the Mahalanobis distance (MD) (Maesschalck et al. 2000) between float ambiguities and the ith integer candidates.

Based on previous definition, RT is given as

$${\text{Accept }}\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} {\text{ iff:}} \, \frac{{R_{1} }}{{R_{2} }} \le \mu_{\text{RT}} , \quad { 0} \le \mu_{\text{RT}} \le 1$$
(8)

with R 1 and R 2 the two smallest values of \(R_{\text{i}}\). When μ RT = 0, all testing results are rejected, and only float solutions are accepted. If μ RT = 1, RTIA pull-in region is overlapping with ILS pull-in region. RTIA estimator will be the same as ILS estimator.

DT is shown below

$${\text{Accept}}\,\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} {\text{ iff:}}R_{2} - R_{1} \ge \mu_{\text{DT}} , \quad \mu_{\text{DT}} \ge 0$$
(9)

when μ DT = 0, the DTIA is also equivalent to ILS estimator. The upper bound of critical value and more properties for DT is deduced in Zhang et al. (2015a). In order to explicitly present the differences in both tests, the geometry reconstruction of 2D IA pull-in regions for both tests is shown in Fig. 2. Their ambiguity model matrix is chosen as \(Q_{{\hat{a}\hat{a}}} { = }\left[ {\begin{array}{*{20}c} {0.0865} & {{ - }0.0364} \\ {{ - }0.0364} & {0.0847} \\ \end{array} } \right]\).

Fig. 2
figure 2

2D geometry reconstruction for the IA pull-in regions of RT and DT (Verhagen and Teunissen 2006). Top panel RTIA pull-in region with \(\mu_{RT} { = }0.4\); bottom panel DTIA pull-in region with \(\mu_{DT} { = }5\). Green parts in both panels are the IA pull-in regions of both tests

Full size image

Notice that in (8) and (9), the tests are designed based on different calculations of two smallest MDs, and then testing judgments are made. Explicitly, RT is realized by calculating the quotient, while DT is based on subtraction. Eventually, we can obtain the ratio of two MDs by RT and absolute difference by DT. The construction of two IA pull-in regions in Fig. 2 reflects this difference. The ratio of MDs preserves the quadratic items of \(R_{\text{i}}\); hence, the boundary of RTIA is constructed by ellipses. While the absolute difference removes the influence of quadratic items, DTIA pull-in region is bounded by linear functions.

The comparisons for both tests from weak model to strong model are directly demonstrated in Fig. 3. Please note that the ranges of coordinate are different in both panels. Hence, the size of IA pull-in region in top panel is much smaller than that of bottom panel. The critical values of both tests are determined based on the fixed failure rate approach and P f = 0.001. The IA regions for both tests are denoted with different colors. Besides this, the contours of MDs to the origin point are presented by colored ellipses.

Fig. 3
figure 3

2D comparison of RTIA and DTIA in weak ambiguity model and strong model with the fixed failure rates P f = 0.001. The weak model is chosen as \(10Q_{{\hat{a}\hat{a}}}\), and that of strong model is \(Q_{{\hat{a}\hat{a}}}\). Green parts: samples pass DT and RT; blue parts: samples pass DT and fail RT; magenta parts: samples pass RT and fail DT. Red star is the coordinate origin. Contours of MDs to the origin for all points are plotted with colored ellipses

Full size image

The performance evaluations for DTIA and RTIA are realized by calculating the size (volume) of three regions. Here, we denote the green, blue, and magenta parts in each panel as Ω a,0, Ω a,RT, and Ω a,DT, respectively, with Ω a,DTIA = Ω a,0 ∪ Ω a,DT, Ω a,RTIA = Ω a,0 ∪ Ω a,RT. P s,DTIA − P s,RTIA is deduced as follows

$$P_{\text{s,DTIA}} - P_{\text{s,RTIA}} = \int\limits_{{\varOmega_{a} \cup \varOmega_{{a,{\text{DT}}}} }} {f(x|a){\text{d}}x} - \int\limits_{{\varOmega_{a} \cup \varOmega_{{a,{\text{RT}}}} }} {f(x|a){\text{d}}x} = \int\limits_{{\varOmega_{{a,{\text{DT}}}} }} {f(x|a)} {\text{d}}x - \int\limits_{{\varOmega_{{a,{\text{RT}}}} }} {f(x|a)} {\text{d}}x$$
(10)

Hence, the sign of P s,DTIA − P s,RTIA depends on Ω a,DT and Ω a,RT. In addition, the distribution of Ω a,DT and Ω a,RT in f(x|a) also plays certain role. The MD of x to the vector a is given as \(R_{a} (x) = \left\| {x - a} \right\|_{{Q_{{\hat{a}\hat{a}}} }}^{2}\), then

$$f(x|a) = \frac{1}{{\sqrt {\det (2\pi Q_{{\hat{a}\hat{a}}} )} }}\exp \left( - \frac{{R_{a} (x)}}{2}\right)$$
(11)

The smaller the R a (x), the larger the f(x|a). Based on Fig. 3, theorem 1 can be deduced:

Theorem 1

Let \(\varOmega_{a,RT} = \{ x \in {\mathbb{R}}^{n} |x \in \varOmega_{a,RTIA} /\varOmega_{a,DTIA} \}\), \(\varOmega_{a,DT} = \{ x \in {\mathbb{R}}^{n} |x \in \varOmega_{a,DTIA} /\varOmega_{a,RTIA} \}\) , and Ω a,RT  ∩ Ω a,DT  = ∅. Points in both sets conform to the normal distribution N(a, Q aa ). Ω a,RTIA and Ω a,DTIA are determined based on fixed failure rate approach. If x RT  ∊ Ω a,RT and x DT  ∊ Ω a,DT , then

$$f(x_{RT} |a) > f(x_{DT} |a)$$
(12)

Proof

See the “Appendix”.□

It means that samples are more likely to fall into Ω a,RT rather than Ω a,DT when both sizes are equal. However, different sizes of Ω a,RT and Ω a,DT may counteract this result. There exist two definite cases and one indefinite case for Eq. (10):

  1. 1.

    Ω a,DT ≤ Ω a,RT, then P s,DTIA − P s,RTIA ≤ 0;

  2. 2.

    Ω a,DT ≫ Ω a,RT, then P s,DTIA − P s,RTIA > 0;

  3. 3.

    Ω a,DT > Ω a,RT, then the sign of P s,DTIA − P s,RTIA is uncertain.

These cases can be seen in Fig. 3. The strength of GNSS model \(Q_{{\hat{a}\hat{a}}}\) varies from weak to strong from the top panel to the bottom panel. For the top panel, when model is weak, both case 1 and case 3 may happen. When the model becomes strong, which refers to the bottom panel, case 2 is more probable since the size of Ω a,DT is obviously larger than that of Ω a,RT at that time. If the model is strong enough, the size difference between Ω a,RT and Ω a,DT is trivial, then case 3 happens, and |P s,DTIA − P s,RTIA| is also trivial. In other words, when \(Q_{{\hat{a}\hat{a}}}\) gradually varies from weak to strong, |P s,DTIA − P s,RTIA| may first increase and then decrease to 0. This can be observed in the following simulation experiments part.

We note that in case 3, the sign of P s,DTIA − P s,RTIA is influenced by the randomness in Monte Carlo integral. We may obtain different signs for P s,DTIA − P s,RTIA for the same GNSS model in different Monte Carlo simulations. We choose the sign which appears more frequently.

The relations between difference test and ratio test

Based on statistical inference and IA theory, we can realize the optimally controlled failure rate based on a certain rule, the so-called optimal IA (OIA). OIA is defined such that its success rate is maximized based on a fixed failure rate. Its principle and derivation can be referred to Teunissen 2003a, 2005, 2013b). For simplicity, here we directly give the definition of OA

(13)

where \(f_{{\hat{a}}} ( \cdot )\) is the PDF of float ambiguities, \(f_{{\hat{\varepsilon }}} ( \cdot )\) is the PDF of ambiguity residuals, with \(f_{{\hat{\varepsilon }}} (\hat{a} - \overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} ) = C\sum\nolimits_{i = 1}^{\infty } {\exp \left\{ { - \frac{1}{2}R} \right\}_{i} }\). μ OA is the critical value, and C is the normalization constant. Notice that OA is much more complicate than DT and RT, and its nominator is impossible to be completely known. This is the reason why it cannot be widely applied in practice.

Previous research (Verhagen and Teunissen 2006) showed that RT and DT have a good performance close to OA in many GNSS situations. Therefore, some potential relations should exist between RT and DT. Here, we connect both tests by OA.

According to (13), we can deduce that

$$\frac{{f_{{\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{\varepsilon } }} (\hat{a} - \overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} )}}{{f_{{\hat{a}}} (\hat{a} - \overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a})}} = \frac{{\sum\limits_{i = 1}^{\infty } {\exp \left\{ { - \frac{1}{2}R_{i} } \right\}} }}{{\exp \left\{ { - \frac{1}{2}R_{1} } \right\}}} = 1 + \frac{{\exp \left\{ { - \frac{1}{2}R_{2} } \right\}}}{{\exp \left\{ { - \frac{1}{2}R_{1} } \right\}}} + \frac{{\sum\limits_{i = 3}^{\infty } {\exp \left\{ { - \frac{1}{2}R_{i} } \right\}} }}{{\exp \left\{ { - \frac{1}{2}R_{1} } \right\}}} \le \mu_{\text{OA}}$$
(14)

Rearranging inequality (14) gives

$$1 + \exp \left\{ { - \frac{1}{2}(R_{2} - R_{1} )} \right\} + \sum\limits_{i = 3}^{\infty } {\exp \left\{ { - \frac{1}{2}(R_{i} - R_{1} )} \right\}} \le \mu_{\text{OA}}$$
(15)

Equation (15) can be further simplified as

$$R_{2} - R_{1} \ge 2\ln \frac{1}{{\mu_{\text{OA}} - \sum\limits_{i = 3}^{\infty } {\exp \left\{ { - \frac{1}{2}(R_{i} - R_{1} )} \right\} - 1} }} = \mu_{\text{DT}}$$
(16)

It is obvious that the critical value of DT is coupled with R 1 and R i , i ≥ 3. If condition

$$\sum\limits_{i = 3}^{\infty } {\exp \left\{ { - \frac{1}{2}(R_{i} - R_{1} )} \right\} \approx 0}$$
(17)

is satisfied, Eq. (16) will be transformed into

$$R_{2} - R_{1} \ge - 2\ln (\mu_{OA} - 1)$$
(18)

Condition (17) only happens when GNSS model is very strong, and then, DT is equivalent to OA.

Unfortunately, it is not easy to deduce similar relation between RT and OA. However, this relation can be investigated from a numerical perspective. Introducing RT into (14) is only feasible when the following approximation exists

$$\exp \left\{ { - \frac{1}{2}R_{i} } \right\} \approx \frac{1}{2}R_{i} \;i = 1$$
(19)

This transcendental equation is established within a certain numerical interval, as shown below

$${\text{if}}\;\left| {\exp \left\{ { - \frac{{R_{1} }}{2}} \right\} - \frac{{R_{1} }}{2}} \right| < 0.001\quad {\text{then}}\quad R_{1} \in [1.1331,1.1335]$$
(20)

Within this numerical interval, RT can realize its approximation to OA. R i satisfies the following inequality

(21)

where λ max and λ min are the maximum and minimum eigenvalues of \(Q_{{\hat{a}\hat{a}}}\), respectively. The variation in R i can be analyzed from two cases: \(Q_{{\hat{a}\hat{a}}}\) is changed or \(\hat{a}\) changed.

For the first case, if \(Q_{{\hat{a}\hat{a}}}\) becomes more precise, λ max and λ min will become smaller. As to the same \(\hat{a}\) and \(\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{i}\) of different GNSS models, \((\hat{a} - \overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{i} )^{T} (\hat{a} - \overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{i} )\) keeps constant; hence, the lower bound and upper bound will increase in (21), and then, R i will also be enlarged. Note that in this case, we only talk about the constant float vector and integer candidate, \(\hat{a}\) and \(\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{i}\), under the varying GNSS model \(Q_{{\hat{a}\hat{a}}}\). It is possible that two different GNSS models may generate the same samples. We admit that \(\bar{Q}_{{\hat{a}\hat{a}}}\) may make \(\hat{a}\) get closer to \(\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{i}\), but it is impossible to analyze R i when both \(\hat{a}\) and \(Q_{{\hat{a}\hat{a}}}\) are changed. For the second case, if a new ambiguity item is added to the original vector, \((\hat{a}' - \overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} '_{i} )^{T} (\hat{a}' - \overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} '_{i} )\), \(\hat{a}' = [\hat{a}_{1} , \ldots ,\hat{a}_{n} ,\hat{a}_{n + 1} ]^{T}\), and \(\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} ' = [\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{1} , \ldots ,\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{n} ,\overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a}_{n + 1} ]^{T}\), which means the number of visible satellites increases, \((\hat{a}' - \overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} '_{i} )^{T} (\hat{a}' - \overset{\lower-0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{a} '_{i} )\) also increase. Under this situation, the added satellite will not worsen the GNSS model, so λ max and λ min will decrease or basically keep constant. Then, the lower and upper bounds will increase in (21), and R i also will increase.

If the approximation in (19) is satisfied, we have

$$\frac{{\exp \left\{ { - \frac{1}{2}R_{2} } \right\}}}{{\exp \left\{ { - \frac{1}{2}R_{1} } \right\}}} \approx \frac{{2\exp \left\{ { - \frac{{R_{1} }}{2}} \right\}^{{\frac{{R_{2} }}{{R_{1} }}}} }}{{R_{1} }}$$
(22)

then (14) can be rearranged as

$$\begin{aligned} 1 + \frac{{2\exp \left\{ { - \frac{1}{2}R_{2} } \right\}^{{\frac{{R_{2} }}{{R_{1} }}}} }}{{R_{1} }} + \sum\limits_{i = 3}^{\infty } {\exp \left\{ { - \frac{1}{2}(R_{i} - R_{1} )} \right\}} \le \mu_{\text{OA}} \hfill \\ \quad \exp \left\{ { - \frac{1}{2}R_{2} } \right\}^{{\frac{{R_{2} }}{{R_{1} }}}} \le \frac{{R_{1} }}{2}\left( {\mu_{\text{OA}} - 1 - \sum\limits_{i = 3}^{\infty } {\exp \left\{ { - \frac{1}{2}(R_{i} - R_{1} )} \right\}} } \right) \hfill \\ \end{aligned}$$
(23)

Finally, the following relation can be deduced

$$\frac{{R_{2} }}{{R_{1} }} \ge \frac{2}{{R_{1} }}\ln \frac{2}{{R_{1} \left( {\mu_{\text{OA}} - 1 - \sum\limits_{i = 3}^{\infty } {\exp \left\{ { - \frac{1}{2}(R_{i} - R_{1} )} \right\}} } \right)}} = \frac{1}{{\mu_{\text{RT}} }}$$
(24)

Obviously, the critical value of RT is also coupled with R 1 and R i , i ≥ 3. It cannot be independently determined as DT in (18). This essentially means that RT cannot realize optimal testing in any GNSS situation. However, when the GNSS model is very strong, just as condition (17), DT is equivalent to OA and its critical value is independent of the candidates. Hence, the following inequality between the success rates of three IA estimators finally can be established based on condition (17)

$$P_{s,OA} \ge P_{\text{s,DTIA}} \ge P_{\text{s,RTIA}}$$
(25)

Here, some remarks should be added regarding inequality (25):

  1. a.

    According to the theorem on loss of precision (Kincaid and Cheney 2003), DT loses more precision (significant binary bits) than RT when R 2 is very close to R 1. This is the intrinsic drawback of subtraction or DT, but it will rarely happen in GNSS situations.

  2. b.

    Based on the analysis in previous section about the difference between RTIA and DTIA, when there is trivial difference between the size of Ω a,RT and Ω a,DT, it is also possible that P s,OA ≥ P s,RTIA ≥ P s,DTIA;

  3. c.

    Theoretically, if the critical value of OA is determined based on the fixed failure rate approach and other integer candidates are also known, the critical values of both tests can also be derived and both tests would have the same fixed failure rate. However, this is impossible in practice, and commonly we only know the first and second integer candidates. That is the reason why DT and RT are always suboptimal.

  4. d.

    The numerical condition (19) reveals that RT is not the best choice for strong GNSS models or multi-GNSS models. Fortunately, these requirements are just the conditions of DT to approximate OA. This proves that DT is more suitable for multi-frequency, multi-GNSS ambiguity resolution than RT.

Combining condition (16) with (24), the relation between μ DT and μ RT can be found as

$$\mu_{\text{RT}} = \frac{{R_{1} }}{{\mu_{\text{DT}} - 2\ln \frac{{R_{1} }}{2}}}$$
(26)

This formula proves that the critical values of both tests are coupled with the first integer candidate, which means that this relation depends on each sample or each first integer candidate. Notice that the RT approximation condition (19) also depends on R 1. Hence, this determines that RT and DT are not equivalent in most GNSS situations. Though theoretically DT outperforms RT under condition (17), it may be trivially worse than RT when both IA regions have trivial difference, which will lead to case 3 in the analysis of the previous section. All in all, when multi-frequency and multi-GNSS are widely applied into practice, DT will reveal its advantages in theory.

Instantaneous application for difference test and ratio test

Though the fixed failure rate approach is an effective method for the quality control of ambiguity resolution, it cannot be instantaneously realized due to time consumption in Monte Carlo simulation. That is the reason why a look-up table is created for RT. Based on the created look-up table, RTIA can realize controllable ambiguity resolution by checking the critical value in the look-up table. However, until now only RT has such table. Of course, we can create such a table for other acceptance tests as the method shown (Verhagen and Teunissen 2013). But the numerous GNSS models and time cost in creating tables are the main obstacles for the widely applications of other tests. Hence, an instantaneous approach independent of look-up table is necessary to be found. Fortunately, we can realize instantaneous IA ambiguity resolution for the estimators with analytical probability evaluation formulas based on the instantaneous and CONtrollable (iCON) approach introduced in Zhang et al. (2015b). Here, we only take DTIA as example due to its distinct performance.

Based on the iCON approach, DTIA can realize instantaneous ambiguity resolution with controllable failure rate. Here, we briefly give an introduction to the iCON approach:

Set the fixed failure rate and initial critical value as P f, μ 0, and P μ . Calculate the probability for N integer candidates, and sort them into descending order. Choose n(1 < n ≤ N), so that

$$P_{\text{f,ILS}} (n) > P_{\mu } ,\;P_{\text{f,ILS}} (n + 1) < P_{\mu }$$
(27)

Then, P 0 = ∑ N k=n+1 P f,ILS(k) and P f,ILS ≈ ∑  n k=1 P f,ILS(k), with P f,ILS the approximated ILS failure rate and 0 < P 0 ≪ P f.

Calculate the approximated failure rates for P f,DTIA(k, μ 0), k = 1,…, N. The values of ratio factor are calculated as

$$R(k,\mu_{0} ) = \frac{{P_{\text{f,DTIA}} (k,\mu_{0} )}}{{P_{\text{f,ILS}} (k)}}\quad k = n + 1, \ldots ,N$$
(28)

Choose R(n, μ 0) = max{R(k, μ 0)}.

According to the ratio factor in step 2, we can determine the critical value μ for a certain GNSS model by

$$\sum\limits_{k = 1}^{n} {P_{f,{\hbox{DTIA}}} (i,\mu )} + R(n,\mu )P_{0} = P_{f}$$
(29)

where P f,DTIA(i, μ) is the DTIA failure rate of the ith integer candidate.

Look-up table and iCON have in common that both approaches are suboptimal methods. Specifically, look-up table is created based on numerous simulated GNSS samples, and the most conservative case is chosen to ensure that it can be applied globally. For the iCON approach, the determination of μ is approximated by n failure rates of IA estimators. The GNSS model information is used in iCON approach. In addition, the approximation errors in P f,DTIA also lead to uncertainty in μ. However, by the constraining of P f, we can limit those errors within very small range.

Simulation verifications

The foregoing analysis reveals the differences, relations, and their instantaneous application of DTIA and RTIA. Now, we construct different GNSS models and compare the ambiguity resolution performances of both IA estimators.

Three GNSS cases are designed here. The first case varies the model strength by including more epochs in the ambiguity resolution; the second case compares the performances between both IA estimators based on fixed failure rate approach. The comparison of their performance in instantaneous applications is implemented in case 3. All these GNSS models are generated by means of “Visual” software (Verhagen 2006) with GNSS ephemeris as input. The basic simulation settings for single medium-length baseline GNSS model are listed in Table 1. The ambiguity resolution will be implemented epoch by epoch for 100,000 samples.

Table 1 Basic simulation settings for three cases
Full size table

Case 1

DTIA and RTIA comparison with varying GNSS models.

GNSS model strength in this case varies from weak to strong by including 1 to 10 epochs in the ambiguity resolution. The difference in the success rates between both tests is presented in Fig. 4. Note that the first value at the left side is negative.

Fig. 4
figure 4

Success rate differences between both IA estimators with different number of epochs. From left to right, the number of epochs increases from one to 10, and δP s = P s,DTIA − P s,RTIA

Full size image

In Fig. 4, as the number of epochs increases, the ILS success rate gradually increases, and the value of |P s,DTIA − P s,RTIA| first increases and then decreases almost to zero. This is possible according to the previous analysis. When the model is weak, both P s,DTIA and P s,RTIA are small, and then |P s,DTIA − P s,RTIA| is trivial. Due to the trivial difference between Ω a,RTIA and Ω a,DTIA, the sign of P s,DTIA − P s,RTIA is uncertain. However, because samples are more likely to fall into Ω a,RTIA, P s,DTIA − P s,RTIA tends to be negative. That is the reason why the first value at the left side is negative but trivial. When the model becomes strong, Ω a,DT ≫ Ω a,RT, then P s,DTIA − P s,RTIA will be positive and increase to the maximum as the size of Ω a,DT − Ω a,RT increases. When the GNSS model is strong enough, the IA pull-in regions start to overlap with the ILS pull-in regions. The size of Ω a,DT − Ω a,RT is small, and P s,DTIA − P s,RTIA becomes small again. When the ILS success rate is larger than 1 − P f, the acceptance test is not necessary and P s,DTIA − P s,RTIA will be 0.

Case 2

DTIA and RTIA comparison based on fixed failure rate approach.

Here, we mainly investigate the overall performance comparison between DTIA and RTIA with 12110 GNSS samples. This simulation experiment includes multi-frequency, multi-GNSS samples. The samples with ILS success rates larger than 0.8 are chosen since these samples are more likely to be fixed. The ambiguity resolutions are implemented epoch by epoch based on the fixed failure rate approach.

Among the 12110 samples, the number of samples which makes P s,DTIA > P s,RTIA is 11,626, and the number of P s,DTIA < P s,RTIA is 484. Notice that the negative points in Fig. 5 mostly appear when the ILS success rates are larger than 0.95, and their absolute values are very small. This conforms to previous analysis. When GNSS models are strong enough, the pull-in regions of DTIA and RTIA will be very similar. Their performances will have a trivial difference, and both negative and positive δP s are possible. In future, multi-frequency, multi-GNSS ambiguity resolution will be common, which will benefit from DTIA.

Fig. 5
figure 5

Relations between success rates difference δP s = P s,DTIA − P s,RTIA and ILS success rates. Blue dots P s,DTIA > P s,RTIA; red dots P s,DTIA < P s,RTIA

Full size image
Fig. 6
figure 6

Flow diagram of the simulation experiment for two IA estimators. P f,DTIA and P f,RTIA are the failure rates of two IA estimators; P s,DTIA and P s,RTIA are their success rates, and μ DTIA and μ RTIA are their critical values

Full size image

Case 3

Instantaneous application comparison for DTIA and RTIA with their corresponding approaches.

In this part, we will compare the performances of both IA estimators by the simulation experiment shown in Fig. 6. The better IA estimator should have higher success rates with controlled failure rates. The 4039 GNSS samples are generated based on GPS, Galileo, BeiDou, and three combinations, including GPS+Galileo, GPS+BeiDou, and GPS+BeiDou+Galileo.

Here, we set a threshold, P s,ILS > 0.8, to select effective GNSS samples as in case 2, since samples with lower ILS success rates cannot realize reliable ambiguity resolution in practice. Experiment results are presented in Figs. 7 and 8, and their statistics are summarized in Table 2. Note that the number of epochs involved in P f = 0.01 is less than those of P f = 0.001. This is because only when P s,ILS < 1 − P f will the IA ambiguity resolution be implemented. Otherwise, we directly set P s,IA = 1 − P f, and P f,IA = P f.

Fig. 7
figure 7

Controlled ranges of failure rates for two instantaneous IA estimators. Top panel P f = 0.01; bottom panel P f = 0.001

Full size image
Fig. 8
figure 8

Success rate differences between two IA estimators based on their corresponding controllable failure rate approach, in which δP s = P s,DTIA − P s,RTIA. Top panel P f = 0.01; bottom panel P f = 0.001

Full size image
Table 2 Statistics for the comparison results of IA estimators. “std” denotes the standard deviation
Full size table

According to Fig. 7 and 8 and their statistics in Table 2, we can see that DTIA based on the iCON approach has almost the same controllability performance as that of RTIA based on look-up table. Notice that RTIA based on look-up table actually does not constrain the failure rate within (0, P f), because the critical values in the look-up table choose the worst GNSS model based on limited locations and samples, which is only locally available.

Due to the approximation error in the computation of DTIA success rates and failure rates, the variation range of P f,DTIA for DTIA is slightly broader when P f = 0.001, but its influence can be neglected. According to the IA success rates, DTIA obviously has better performance since most of times its success rates are larger than those of RTIA. When P f = 0.01, DTIA has obviously a smaller range of controlled failure rates and higher IA success rates.

When the DTIA success rates approach 1, the success rates of DTIA and RTIA gradually approximate each other. This conforms to previous analysis that when the GNSS model is very strong, both estimators have similar performance. Hence, we still can conclude that DTIA has better performance than RTIA most of the times for instantaneous applications. Note that the horizontal axis indicates the DTIA success rates not ILS success rates, since P s,ILS falls into the range (0.8, 1.0), which is too narrow to clearly demonstrate the difference in both IA estimators.

In addition to the previous remarks, the look-up table for RTIA has a big drawback. Only 0.001 and 0.01 are available as the choice of fixed failure rates. This means that users do not have many choices in the quality control of ambiguity resolution. However, DTIA based on iCON does not have this shortcoming, whose failure rates can be set randomly, and the only consideration is its upper bound.

Field test verification

In order to give a final evaluation to the instantaneous applications of both IA estimators, a field test was carried out on January 9, 2013 at Delft University of Technology, the Netherlands. Two low-cost, single-frequency mu-blox receivers are connected with the baseline length 9.71 m. One GNSS observation station with high-precision Septentrio receiver is used as reference receiver. The layout of three receivers is presented in Fig. 9. More than 1-h GPS single-frequency observations are collected in the field test. IA ambiguity resolutions are implemented based on Kalman filter, so that most of the epochs can be fixed as reliable as possible. The outliers are adapted before ambiguity resolution. Then, IA estimation is implemented based on two controllable methods. The IA estimation results are listed in Table 3. Here, we only talk about the controlled failure rates, P f,IA, to compare the performance of both estimators. The fixed rate is P fix,IA = 1 − P f,IA. Note that the fixed rate includes success rate and failure rate. Since the true ambiguities are not known, here we only compare the controlled failure rates.

Fig. 9
figure 9

Configuration of three receivers. R1 and R2 are two low-cost mu-blox receivers, and R is a high-end Septentrio receiver

Full size image
Table 3 Results for the field test of two IA estimators. “Failure RT” means the failure rate of RTIA, and “Failure DT” the failure rate of DTIA
Full size table

In Table 3, we can see that DTIA always has lower failure rates than those of RTIA, especially when P f chooses the smaller value. Hence, the fixed rates of DTIA are higher than those of RTIA. This means that comparing with RTIA, DTIA is more likely to accept the testing result. Hence, its failure rate is lower than that of RTIA. In addition, we also can see that the short baseline R1–R2 has lower failure rates than the two long baselines. This is because the atmospheric delays and other common errors are cancelled when the baseline is short. Hence, according to the results of the field test, we still can conclude that DTIA has a better performance than that of RTIA in ambiguity resolution.

Furthermore, in practice, the failure or fixing rates of IA estimation are not the only quality indicators of ambiguity resolution. Precision of positioning or attitude determination should also be taken into consideration. Hence, the relation between quality of ambiguity resolution and positioning will be studied in the future.

Conclusion

The performances of DTIA and RTIA are analyzed and compared in detail. In order to find the differences between DTIA and RTIA, their pull-in regions and success rates were compared in different GNSS models. Two definite cases and one indefinite case are summarized to deduce the explicit conditions. For the purpose of finding the mathematical relations between both IA estimators, optimal test was introduced, and its relations with both tests were revealed from numerical considerations. The conditions for the mathematical equivalence between three IA estimators were investigated, and the probability relations between DTIA, RTIA, and optimal IA were established. The analysis showed that the critical value of DTIA was perturbed by other integer candidates. Only when the model was strong, the DTIA was mathematically equivalent to the optimal IA estimator. RTIA is a numerical approximation of optimal IA estimator under certain numerical condition. Its critical value is also perturbed, and their influences cannot be eliminated given its approximation condition. Hence, DTIA outperforms RTIA when the model is strong. However, when the model is strong enough and its ILS success rate approaches 1, both IA pull-in regions are almost the same, and their probability differences are small and influenced by the randomness in Monte Carlo simulation. If model is weak, samples are more likely to fall into the RTIA pull-in region. Hence, RTIA may be better in weak models. Unfortunately, this advantage is not useful in practice, since ambiguity resolution in weak GNSS models is difficult. The available choice is to first strengthen the GNSS model by adding constraints or decreasing the observation errors and then implement ambiguity resolution. Finally, the instantaneous approaches for both IA estimators, which were the fixed failure rate approach and the iCON approach, were compared and analyzed.

In order to verify the above conclusions, three simulation experiments and a field test were implemented to compare the performances of both IA estimators. The comparison results show that DTIA is better than RTIA in practice. It can realize better failure rate control and have higher fixed rate most of the times. Hence, DTIA based on the iCON approach will be a better choice for the future IA ambiguity resolution.