1 Introduction

Integer ambiguity resolution (IAR) is a fundamental problem to realize rapid and high-precision GNSS positioning and navigation. One can take advantage of the precise pseudo range data after the ambiguities are fixed. IAR applies to a great variety of GNSS models and extends to a wide range of applications, such as surveying, positioning, navigation, and precision agriculture. The principle of these GNSS applications can be found in Leick (2004) and Misra and Enge (2006).

Considering the common carrier-phase GNSS model with integer ambiguities, its linearized model is formulated as:

$$\begin{aligned} E(y)=Aa+Bb; \quad D(y)=Q_{yy} \end{aligned}$$
(1)

with \(E(\cdot )\) and \(D(\cdot )\) the expectation and dispersion operators, and \(y\) the \(m \times 1\) vector ’observed minus computed’ single- or dual-frequency carrier phase or/and code observations. \(Q_{yy}\) is the \(m \times m\) covariance matrix of \(y\). \(a\) is the \(n\times 1\) vector unknown double-difference ambiguities, and \(b\) is the \(p \times 1\) vector other unknown parameters. \([A,B]\) are the \(m \times (n+p)\) design matrix.

The procedures of IAR usually include four steps. In the first step, the integer constraint of ambiguities is disregarded and their float solutions are estimated based on least-square adjustment. The float solutions and their variance–covariance matrix are usually given as: \(\left[ \begin{array}{c} \hat{a} \\ \hat{b} \\ \end{array} \right] \), \(\left[ \begin{array}{ll} Q_{\hat{a} \hat{a}}&{} Q_{\hat{a} \hat{b}}\\ Q_{\hat{b} \hat{a}}&{}Q_{\hat{b} \hat{b}} \end{array} \right] \) and

$$\begin{aligned} \hat{a}= & {} (\bar{A}^T Q_{yy}^{-1} \bar{A})^{-1}\bar{A}^T Q_{yy}^{-1}y \\ \hat{b}= & {} (B^T Q_{yy}^{-1} B)^{-1}B^T Q_{yy}^{-1}(y-A\hat{a}) \end{aligned}$$

where \(\bar{A}= P^{\perp }_B A\), \(P^{\perp }_B=I_m-P_B\), and \(P_B=B(B^T Q_{yy}^{-1} B)^{-1} B^T Q_{yy}^{-1}\). With the metric of \(Q_{yy}\), \(P_B\) is the projector that projects orthogonally onto the range space of \(B\). Quality control steps, such as detection, identification and adaptation of outliers, are implemented in this step.

In the second step, the integer constraint of ambiguities is taken into account and float solution is fixed into integer solutions. This is realized by a many-to-one mapping as:

$$\begin{aligned} \check{a} = S(\hat{a}), \quad S: R^n \rightarrow Z^n \end{aligned}$$
(2)

There are many mapping methods, such as integer rounding, integer bootstrapping (IB), and integer least-square (ILS). ILS is optimal and has the highest success rate among these methods Teunissen (1999a). However, due to the influence of the correlations between different ambiguities, the efficiency of integer mapping is very low. The Least-square Ambiguity Decorrelation Adjustment (LAMBDA) method, Teunissen (1993, 1995, 2010), De Jonge and Tiberius (1996), is introduced to improve the efficiency and effectively solve the ambiguity searching problems. The LAMBDA method usually consists of two parts. In the first part, an invertible transformation \(Z\) is constructed that allows one to reparametrize the original double-difference ambiguities, so that the new ambiguities have the required properties. Hence, the original float ambiguity vector \(\hat{a}\) and its corresponding covariance matrix \(Q_{\hat{a} \hat{a}}\) are transformed as:

$$\begin{aligned} \check{z}&= Z^T \check{a} \nonumber \\ \hat{z}&= Z^T \hat{a} \\ Q_{\hat{z} \hat{z}}&= Z^T Q_{\hat{a} \hat{a}} Z\nonumber \end{aligned}$$
(3)

Then

$$\begin{aligned} (\hat{a}-\check{a})^T Q^{-1}_{\hat{a} \hat{a}}(\hat{a}-\check{a})=(\hat{z} - \check{z})^T Q^{-1}_{\hat{z} \hat{z}} (\hat{z} - \check{z}) \end{aligned}$$
(4)

The ambiguity transformation matrix \(Z\) is required to be integral and volume preserving. Here, the \(Z\) transformation is actually performed as a sequence of integer Gaussian elimination and permutations. The \(Z\) matrix in (3) can be decomposed into the multiplication of a series transformation matrix

$$\begin{aligned} Z = Z_n \ldots Z_2 Z_1 \end{aligned}$$
(5)

The decorrelation times can be adjusted based on certain additional conditions to achieve better decorrelation results, as shown in Xu (2001) and Wang and Wang (2010). However, due to the integer constraint for ambiguities, it is impossible to realize perfect decorrelation (De Jonge and Tiberius 1996). Note that once the criterion to stop decorrelation is determined, the transformation matrix \(Z\) is unique. Then, the unique \(Q_{\hat{z} \hat{z}}\) is obtained when we cannot further decorrelate \(Q_{\hat{a} \hat{a}}\).

To evaluate the effect of decorrelation, the decorrelation number is defined (Teunissen 1993)

$$\begin{aligned} \gamma = \sqrt{\text {det}( \{\text {diag}(Q_{\hat{a} \hat{a}})\}^{-1/2} Q_{\hat{a} \hat{a}} \{\text {diag}(Q_{\hat{a} \hat{a}})\}^{-1/2})} \end{aligned}$$
(6)

with \(\{ \text {diag}(Q_{\hat{a} \hat{a}}) \}\) the diagonal matrix whose diagonal elements are identical to \(Q_{\hat{a} \hat{a}}\). Besides this, condition number can also be used (Wang 2012).

Once the transformed ambiguities are obtained, searching process for the integer ambiguities is efficiently performed in the second part.

The third step needs to determine whether the estimated integers are accepted. This is completed by various kinds of acceptance tests, including R-ratio test (RT) (Euler and Schaffrin 1991), F-ratio test (FT) (Frei and Beutler 1990), W-ratio test (WT) (Wang et al. 1998), DT (Tiberius and De Jonge 1995), Projector test (PT) (Han 1997), etc. This step is to exclude the suspected integers, and accept the most possible ones. In the last step, after the ambiguities are fixed, other parameters can be corrected by virtue of their correlation with the ambiguities

$$\begin{aligned} \check{b}= \hat{b} - Q_{\hat{b} \hat{a}}Q_{\hat{a} \hat{a}}^{-1}(\hat{a}-\check{a}) \end{aligned}$$
(7)

with \(Q_{\hat{b} \hat{a}}\) the covariance matrix between ambiguity vector and other unknown parameters. Once the ambiguities are successfully fixed, estimation results will behave the same as high-precision phase observations.

Actually, the third and fourth steps can be realized within one estimator, which is the so-called IA estimator. IA estimator can be simply regarded as the overall approach of ILS estimation and validation. The ILS estimator can also be seen as the a special class of IA estimator without validation. There are three cases for the probabilities of IA estimators: success rate, failure rate, and undecided rate. The undecided rate is formed by the interval or holes between different aperture pull-in regions, and its size is determined by the choice of a maximum allowed fail rate. Actually, failure rate cannot be chosen randomly. It has theoretical upper bound and lower bound as analyzed in Li and Wang (2013).

The performance of ILS can be evaluated by success rate and failure rate. Due to rather complicated geometry of integer pull-in region, it is difficult to derive its analytical probability formula. However, its upper and lower bounds can easily be obtained by other estimators. Furthermore, the LAMBDA method mentioned previously can make the bounding sharper. The explicit formulas for bounding are given in Feng and Wang (2011) and Teunissen (1998b, 1999b). Unfortunately, the corresponding probability evaluations for IA estimators are lack of research, especially those popular ones, such as RT and DT. The critical problem lies on how to connect the scaling ratio with the GNSS model and the computation of IA success rate. Though some results are given in Verhagen (2005), they are not applicable in practice.

Monte Carlo simulation is another way to obtain the probability evaluations of IA estimators. However, they are time-consuming and cannot be implemented in practice. The solution to tackle these problems is realized by creating the look-up table based on fixed failure rate. This table is created based on various GNSS scenarios in one or many locations. When the critical value based on certain failure rate is chosen, IA estimator can realize the control of failure rate within certain range. The shortcoming is that other probability evaluations of IA estimator are still unknown. Theoretically, if we know how to evaluate these probabilities, it is possible to realize the controlling of success rate and failure rate based on their analytical formulas. Without the direct probability evaluations of IA estimators, we have to resort to the time-consuming Monte Carlo simulation. This contribution will firstly focus on the problem how to evaluate the probability DT-IA estimators with the analytical formulas. It will pave the way for the probability evaluations of other IA estimators.

Why do we choose DT-IA estimator? According to the principle of IAR and IA theory, most IA estimators can be seen as nonlinearly scaling to ILS estimators. However, these nonlinear scalings have no common rules. Different ways of nonlinear scaling lead to that it is difficult to summarize a global approach. Fortunately, DT-IA estimator is based on linear scaling. This advantage simplifies the process of derivation and avoids the approximation errors in nonlinear problem.

This contribution is organized as follows. In Sect. 2, we briefly review the concepts in IAR and its probability evaluations. To clearly discriminate the difference between the second best integer candidate of integer estimator and that of ambiguity resolution, the remarks to the second best integer candidates are given in detail. After analyzing the pull-in regions of DT, the bounds of DT, which means the testing results, are derived from the perspective of geometry in Sect. 3. Though similar sharp bound can also be found in Li and Wang (2014), here we give a further simpler and easier way to deduce and calculate it. We can obtain this upper bound without extra computation in IAR. This result can provide the range of critical values for DT. Section 4 reveals the explicit way of bounding DT-IA success rate and other probability evaluations. The definition of DT-IAB estimator is given, and its relationships with DT-IA are studied. This part also gives us a new perspective to review IAB and IALS estimators. By the way, other properties of DT-IAB and DT-IA are also proved. Then, both upper bounds and lower bounds of DT-IA estimator are investigated. Finally, all these bounding methods for DT and DT-IA estimators are verified based on single and multi-GNSS simulation experiments.

2 Integer estimation and probability evaluations

2.1 ILS pull-in regions and probability evaluations

In the second step of ambiguity resolution, integer solution is mathematically obtained by a many-to-one mapping. It means that a subset of float solutions, denoted as \(S_z\), \(S_z \subset R^n\), has the biggest probability to obtain one integer solution. To be convenient, we define \(S_z\) as the integer pull-in region of \(z\)

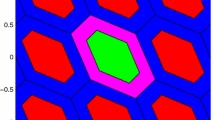
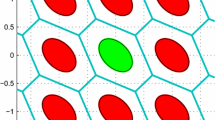
$$\begin{aligned} S_z= \{ x \in \mathbb {R}^n, z \in \mathbb {Z}^n | z= S(x)\} \end{aligned}$$
(8)

Integer pull-in regions are translational invariant over the integers and cover the whole \( \mathbb {R}^n \) space without gaps and overlap (Teunissen 1998a). Based on the definition of integer pull-in region, we can make two judgments: success and fail. As shown in Figs. 1 and 2, the whole \(\mathbb {R}^2\) spaces are constructed by success and fail pull-in regions. Note that when one float sample falls into \(S_z\), it only means that it is closer to \(z\) than other integers, hence it is more possible to be fixed to \(z\).

Fig. 1
figure 1

PDF and 2-Dimensional (2-D) pull-in regions of ILS float ambiguity. Green success region; red fail regions

Full size image
Fig. 2
figure 2

Corresponding probability mass and ILS pull-in regions. Green success probability; red fail probabilities

Full size image

Here, we take the ILS for example. Its pull-in region in decorrelated space follows that (Verhagen 2005)

$$\begin{aligned} S_{z,\text {ILS}} = \bigcap _{c\in \mathbb {Z}^n /\{0\}} \left\{ x \in \mathbb {R}^n,z \in \mathbb {Z}^n | |c^T Q^{-1}_{\hat{z} \hat{z}}(x-z)| \le \frac{1}{2} \Vert c \Vert _{Q_{\hat{z} \hat{z}}}^2 \right\} \end{aligned}$$
(9)

with \(Q_{\hat{z} \hat{z}}\) the variance matrix of \(x\). According to Eq. (9), the ILS pull-in regions are constructed as intersecting half-spaces, which are bounded by the planes orthogonal to \(c\), and passing through \(\frac{1}{2}(c+2z)\). When \(z\) is chosen as the origin or zero vector, the passing points of these planes are \(\frac{1}{2}c\). When \(c\) choose the canonical vectors, \(\frac{1}{2}c\) will lie on the coordinate axes. In other words, the absolute value of passing points between the planes of origin pull-in region and coordinate axis is \(\frac{1}{2}\). This is an useful property, which will be used in Sect. 4.

The distribution of ambiguity float solution conforms the multivariate integer normal distribution \(\hat{a} \backsim N(a,Q_{\hat{a} \hat{a}})\). The probability density function (PDF) of \(\hat{a}\) is given as:

$$\begin{aligned} f_{\hat{a}}(x|a)= \frac{1}{\sqrt{ \text {det} (2 \pi Q_{\hat{a} \hat{a}})}} \text {exp} \left\{ -\frac{1}{2}\Vert x-a \Vert _{Q_{\hat{a} \hat{a}}}^2 \right\} \end{aligned}$$
(10)

with the weighted squared norm \(\Vert \cdot \Vert ^2_{Q_{\hat{a} \hat{a}}}=(\cdot )^T Q_{\hat{a} \hat{a}}^{-1} (\cdot )\).

When ambiguity is fixed, the integer ambiguity \(\check{a}\) will have the so-called probability mass function (PMF). PMF of \(\check{a}\) is derived from the PDF of \(\hat{a}\). Hence, when \(\hat{a} \in S_z \), the PMF of \(\check{a}\) follows as:

$$\begin{aligned} P(\check{a}=z)= P(\hat{a} \in S_z)= \int _{S_z}{f_{\hat{a}}(x|z)dx} \end{aligned}$$
(11)

If the correct integer ambiguity is \(a\) and \(\hat{a}\) is correctly fixed, the successful probability is given as:

$$\begin{aligned} P(\check{a} =a)= \int _{S_a} {f_{\hat{a}}(x|a)dx} \end{aligned}$$
(12)

Otherwise, it will be wrongly fixed with the probability

$$\begin{aligned} P(\check{a} \ne a)=1- \int _{S_a} {f_{\hat{a}}(x|a)dx} \end{aligned}$$
(13)

The PDF and PMF of ambiguity are also demonstrated in Figs. 1 and 2. The success and fail probabilities in different pull-in regions are presented by the size of pillars. The 2-dimensional (2-D) ambiguity model matrix is chosen as:

$$\begin{aligned} Q_{\hat{a} \hat{a}} = \left[ \begin{array}{cc} 0.0865 &{} -0.0364 \\ -0.0364 &{} 0.0847 \end{array} \right] . \end{aligned}$$

2.2 Bounds of ILS estimator

Success rate is an important measure, since it can directly give the quality measure of IAR without actual measurements. In Teunissen (1999a), it is proved that

$$\begin{aligned} P(\check{a}_{ \text {ILS}}=a) \ge P(\check{a} = a) \end{aligned}$$
(14)

for any admissible integer estimator. Though ILS estimator is optimal, its success rate is very complicated to compute and can only be obtained by approximation or bounding. The two most popular bounds for ILS success rate are based on IB and ambiguity dilution of precision (ADOP) (Verhagen et al. 2013). Properties of ADOP can be referred to Teunissen and Odijk (1997).

IB success rate is usually regarded as that of ILS lower bound, and its evaluation formula is easy to be given

$$\begin{aligned} P_{s,\text {IB}}= P(\check{a}_{\text {IB}}=a)= \prod _{i=1}^n \left( 2 \Phi (\frac{1}{2 \sigma _{a_{i|I}}})-1 \right) \end{aligned}$$
(15)

with \(\sigma _{a_{i|I}}\) the conditional standard deviation from \(Q_{\hat{a} \hat{a}}\) based on LDL decomposition. The IB success rate is not \(Z\) transformation invariant. It is close to optimal when the decorrelated ambiguity \(\hat{z}\) is applied

$$\begin{aligned} P(\check{z}_{\text {IB}}=z) \ge P(\check{a}_{\text {IB}}=a) \end{aligned}$$
(16)

in which \(\hat{z}= Z^T \hat{a}\) and \(Q_{\hat{z} \hat{z}}=Z^T Q_{\hat{a} \hat{a}} Z\). Besides the lower bound, an upper bound is also useful. In Teunissen (2000), it proves that this upper bound can be given as:

$$\begin{aligned} P_{s,\text {IB}} \le \left( 2 \Phi \left( \frac{1}{2 \text {ADOP}}\right) -1 \right) ^n \end{aligned}$$
(17)

where ADOP is defined as:

$$\begin{aligned} \text {ADOP}= \sqrt{\text {det}(Q_{\hat{a} \hat{a}}) }^{\frac{1}{n}} \end{aligned}$$
(18)

with units of cycles. This upper bound is \(Z\) transformation invariant. Note that the upper bound in Eq. (17) is not that of ILS success rate, though most of times this upper bound is larger than the computed ILS success rate.

Since ILS estimator is optimal, its success rate is

$$\begin{aligned} P_{s,\text {ILS}}&=P(\check{z}_{ \text {ILS}}=z ) \nonumber \\&\ge P\left( \check{z}_{\text{ IB }}=z\right) \nonumber \\&= \prod _{i=1}^n \left( 2\Phi (\frac{1}{2 \sigma _{z_{i|I}}} ) -1 \right) \end{aligned}$$
(19)

The conditional standard deviation \(\sigma _{z_{i|I}} \) is derived from \(Q_{\hat{z} \hat{z}}\) and LDL decomposition, with \(I = \{ 1, ...,(i-1) \}\). Another useful bound for ILS success rate is the ADOP based upper bound. It is given as:

$$\begin{aligned} P_{s,\text {ILS}} \le P\left( \chi ^2(n,0) \le \frac{c_n}{\text {ADOP}^2}\right) \end{aligned}$$
(20)

with \(c_n= \frac{(\frac{n}{2} \Gamma ({\frac{n}{2}}))^{\frac{2}{n}}}{\pi } \). This bound is firstly introduced in Hassibi and Boyd (1998), and proved in Teunissen (2000).

To verify the performances of bounds for ILS estimator, simulation experiment is implemented based on the setting in Table 1. The computation of actual ILS success rate is by means of Monte Carlo simulation (Teunissen 1998a). The functional model is geometry-based model. Original measurements include phase and code, and double-difference measurements are used. The number of samples is chosen to guarantee that the influence of sample number is smaller than the order of \(10^{-3}\). The IAR is implemented epoch by epoch.

Table 1 Simulation settings for GNSS models
Full size table

Figure 3 shows the comparison between actual success rate, IB lower bound, IB upper bound and ILS upper bound based on ADOP. According to Fig. 3, it is obvious that IB lower bound is a good and sharp bound for the ILS success rate. This conforms to the property of ILS and IB. Since when the ambiguity covariance matrix is fully decorrelated, both ILS and IB will have the same performance as integer rounding (Verhagen 2005). Hence, we can directly use the IB lower bounds based on \(Z\) transformation to approximate the ILS success rate

$$\begin{aligned} P_{s,\text {ILS}} \approx P(\check{z}_{\text {IB}}=z) \end{aligned}$$
(21)

For Fig. 3, we give the following remarks:

  1. 1.

    The lower bound based on IB is a better approximation to the ILS success rate. The approximation error comes from the decorrelation step. The better ambiguities are decorrelated, the smaller approximation error will be;

  2. 2.

    The IB upper bound based on ADOP most of times can give the upper bound reference for ILS. However, notice that these upper bounds sometimes are smaller than the ILS computed values. This means that this upper bound is always an upper bound of IB, but not always that of ILS estimator;

  3. 3.

    The ILS upper bound based on ADOP provides the upper constraint for ILS computed values. Since it is deduced for ILS estimator, their values are always larger than the computed ILS success rates;

  4. 4.

    The horizontal points are generated based on the complete constellation of BeiDou. Since BeiDou has 5 GEO-stationary satellites, the ADOP-based upper bound directly reflects this influence of BeiDou and its combined systems.

Of course, there are other bounding ways for ILS success rate. More details about their analysis can be referred to Teunissen (2000), Verhagen (2005).

Fig. 3
figure 3

ILS computed success rates and their lower or upper bounds: lower bound based on IB (green); ADOP-based upper bound for IB (blue); ILS upper bound based on ADOP (red); the computed ILS success rates (black)

Full size image

2.3 Remarks to the second best integer candidate

Here, we discuss the topic of the second best integer candidate. The second best integer candidates can be seen as those adjacent integer candidates of the best candidate. They have the second closest distance (with the metric of \(Q_{\hat{a} \hat{a}}\)) to float solution, and have the highest possibility to be fixed except the best candidate.

As we know that LAMBDA method is based on the ILS principle, and always has the same estimation result as ILS. Hence, they also have the same second integer candidate. However, be different from the ILS principle, there are two kinds of second best integer candidates in LAMBDA method: original second best integer candidates and decorrelated second best integer candidates. Because the acceptance testing is always implemented in the decorrelation space, here we only talk about the properties of decorrelated second best integer candidates.

In Fig. 4, both the original and decorrelated ILS pull-in regions are demonstrated. The 2-D ambiguity model matrix is chosen as \( \left[ \begin{array}{cc} 0.0640 &{} -0.0350 \\ -0.0350 &{} 0.0200 \end{array} \right] \). Note that after decorrelation, the negative correlation between two ambiguities is changed into trivial positive correlation.

Fig. 4
figure 4

The comparison of two kinds of ILS pull-in regions. Left panel original ILS pull-in region; right panel decorrelated ILS pull-in regions. Green success pull-in region; red fail pull-in region

Full size image

According to the comparison in Fig. 4, though two ambiguities cannot be totally decorrelated, the decorrelated pull-in regions have better geometry formation than those of original. Here, we only focus on the decorrelated part due to its better properties in algebraic and geometry.

As reviewed previously, after decorrelation, ILS will behave similarly as IB. Hence, we can analyze the properties of decorrelated ILS based on IB. However, due to the existence of trivial correlation, decorrelated ILS still has few differences from IB.

Obviously, as demonstrated in Verhagen (2005), the second best integer candidates of IB are the canonical vectors on each axis. Similarly, the decorrelated second best integer candidates of ILS also have these properties, which can be summarized as:

$$\begin{aligned} \text {min}(\check{z}_2 - \check{z}_1)^T(\check{z}_2 - \check{z}_1) = 1 \end{aligned}$$
(22)

with \(\check{z}_2\) the second best integer candidate, and \(\check{z}_1\) the best integer candidate.

The reason why ‘min’ is added in (22) is due to the existence of correlation in the decorrelated ambiguity model matrix. According to the 2-D decorrelated ILS in Fig. 4, its second best integer candidates include not only those canonical vectors, but also \((1,1)\) and \((-1,-1)\). Notice that this decorrelated model matrix is positive correlated. If the model matrix is negative correlated, the other two second best integer candidates are \((-1,1)\) and \((1,-1)\).

Hence, we can summarize the relation between the best and second best integer candidates for their corresponding element in decorrelated space

$$\begin{aligned} (\check{z}^i_2-\check{z}^i_1)^T(\check{z}^i_2-\check{z}^i_1) \le 1 \quad i = 1,2,\ldots ,n \end{aligned}$$
(23)

where \(z^i_1\) and \(z^i_2\) are the \(i\)th elements of the best and second best integer candidate, respectively. Note that this property depends on the decorrelation process, which means perfectly decorrelated or trivial existence of correlation. This is understandable. Since if \((\check{z}^i_2-\check{z}^i_1)^T(\check{z}^i_2-\check{z}^i_1) > 1 \) for certain \(i\), we always can find a closer second best integer vector to \(z_1\) based on IB or decorrelated ILS.

To demonstrate the relation between ILS pull-in region and its second best integer candidates, the 2-D geometry reconstruction for the ambiguity model of Fig. 1 is given in Fig. 5. Notice that the best integer pull-in region can be divided into six parts based on their corresponding second best integer candidate. Since two ambiguities of this model matrix are negative correlated, this pull-in region has two different second integer candidates from that of Fig. 4. We can interpret this relation for ILS pull-in region as:

$$\begin{aligned} S_{0,\text {ILS}} = \bigcup _{c \in \mathbb {Z}^n / \{0\}} S_{0,\text {ILS}} (c) \end{aligned}$$

with \(c\) the second best integer candidates and \(S_{0,\text {ILS}} (c)\) the pull-in region part whose second best integer candidate is \(c\).

Fig. 5
figure 5

ILS origin pull-in region and their corresponding second best integer candidates. Blue (0, 1); black (0, \(-\)1); magenta (1, 0); red (\(-\)1, 0); yellow (1, \(-\)1); cyan (\(-\)1, 1). Red stars the second best integers to be fixed

Full size image

3 IA ambiguity resolution based on DT

3.1 Aperture pull-in region based on DT

Though integer estimation can fix the ambiguities, it cannot realize quality control to the ambiguity resolution. This is the reason why IA estimation is proposed. IA estimation is realized by implementing the acceptance testing in the third step. This overall formation of acceptance test is defined in Teunissen (2013) as:

$$\begin{aligned} \Omega = \{ x\in \mathbb {R}^n | \gamma (x) \le \mu \} \end{aligned}$$
(24)

where \(\gamma (\cdot )\) is the acceptance testing function, \(x\) lies in the decorrelated space, and \(\mu \) its critical value. \(\Omega \) is named as the set of aperture pull-in regions. The success aperture pull-in region within the success ILS pull-in region is

$$\begin{aligned} \Omega _z = \{ x \in \mathbb {R}^n, z\in \mathbb {Z}^n | S(x)=z, \gamma (x) \le \mu \} \end{aligned}$$
(25)

and \(\Omega _z \in \Omega \).

Now we give the definition of IA (Teunissen 2004):

Definition 1

Let \(\Omega \subset \mathbb {R}^n\) and \(\Omega _z= \Omega \cap S_z\). Then, the estimator

$$\begin{aligned} \check{a}_{\text {IA}}= \left\{ \begin{array}{c} z \quad \text {if} \quad \hat{a} \in \Omega _z \\ \hat{a} \quad \text {if} \quad \hat{a} \notin \Omega _z \end{array} \right. \end{aligned}$$
(26)

is an IA estimator only if its aperture pull-in regions satisfy the following requirements

$$\begin{aligned} (1)&\quad \bigcup _{z \in \mathbb {Z}^n} \Omega _z=\Omega \\ (2)&\quad \text {Int} (\Omega _u)\bigcap \text {Int}(\Omega _v)= \emptyset , u\ne v \\ (3)&\quad \Omega _z = z+\Omega _0, z\in \mathbb {Z}^n \end{aligned}$$

Thus, the aperture pull-in regions \(\Omega _z\) have no overlapping and are subsets of \(\mathbb {R}^n\). As previously reviewed, there are various kinds of acceptance tests. Here, we choose to talk about the ambiguity solution based on DT. It is defined as the difference between two quadratic forms, \(\Vert x -\check{z}_2 \Vert ^2_{Q_{\hat{z} \hat{z}}} \) and \(\Vert x -\check{z}_1 \Vert ^2_{Q_{\hat{z} \hat{z}}} \)

$$\begin{aligned} \Vert x -\check{z}_2 \Vert ^2_{Q_{\hat{z} \hat{z}}} - \Vert x -\check{z}_1 \Vert ^2_{Q_{\hat{z} \hat{z}}} \ge \mu _{\text {DT}} \end{aligned}$$
(27)

where \(\hat{z}\) is the float solution, \(\check{z}_1\) and \(\check{z}_2\) are the best and second best integer candidates, and \(\mu _{\text {DT}}\) the critical value of DT. Inequality (27) can be transformed into (25) by multiplying a negative constant to both sides. When \(\check{z}_1 = 0\) and \(u = \check{z}_2 - \check{z}_1\), the origin-centered aperture pull-in region based on DT can be determined as:

$$\begin{aligned} \Omega _{0,\text {DTIA}}&= \{ x \in \mathbb {R}^n| S(x)=0, \Vert x - u \Vert ^2_{Q_{\hat{z} \hat{z}}} - \Vert x \Vert ^2_{Q_{\hat{z} \hat{z}}} \ge \mu _{\text {DT}} \} \nonumber \\&= \left\{ x \in \mathbb {R}^n| S(x)=0, \frac{u^T Q^{-1}_{\hat{z} \hat{z}} x }{ \Vert u\Vert _{Q_{\hat{z} \hat{z}}}} \le \frac{\Vert u\Vert ^2_{Q_{\hat{z} \hat{z}}}- \mu _{\text {DT}} }{2 \Vert u\Vert _{Q_{\hat{z} \hat{z}}} } \right\} \end{aligned}$$
(28)

with \(u \in \mathbb {Z}^n \backslash \{0\}\). This shows that \( \Omega _{0,\text {DTIA}} \) are formed by intersecting half-spaces that are constrained by hyper-planes orthogonal to \(u\) and passing through the points \( \frac{1}{2}\left( 1- \frac{\mu _{\text {DT}}}{ \Vert u\Vert ^2_{Q_{\hat{z} \hat{z}}}}\right) u \). The 2-D demonstration of DT aperture pull-in regions is presented in Fig. 6. Based on the properties of aperture pull-in regions, four different judgments to DT-IA estimator can be made, which are indicated by different colors.

Fig. 6
figure 6

The 2-D DT-IA pull-in regions. Four colors denote different judgments. Green success; red fail; blue failure detected; pink false alarm

Full size image

3.2 Bounds of DT

Based on the DT in (27), its bounds can be derived in various GNSS models. For simplification, in decorrelated space, we use \(R_2\) denoting \(\Vert x -\check{z}_2 \Vert ^2_{Q_{\hat{z} \hat{z}}} \), and \(R_1\) for \(\Vert x -\check{z}_1 \Vert ^2_{Q_{\hat{z} \hat{z}}} \)

$$\begin{aligned} R_2-R_1&= ( x \!-\check{z}_2)^T Q^{-1}_{\hat{z} \hat{z}}( x \!-\check{z}_2)-( x -\check{z}_1)^T Q^{-1}_{\hat{z} \hat{z}}( x\!-\check{z}_1) \nonumber \\&= 2 x^T Q^{-1}_{\hat{z} \hat{z}}(\check{z}_1 - \check{z}_2)+ \check{z}_2^T Q^{-1}_{\hat{z} \hat{z}} \check{z}_2^T -\check{z}_1^T Q^{-1}_{\hat{z} \hat{z}} \check{z}_1^T \nonumber \\&= [2 x -(\check{z}_1 + \check{z}_2)]^T Q^{-1}_{\hat{z} \hat{z}} (\check{z}_1 - \check{z}_2 ) \end{aligned}$$
(29)

Based on previous discussion about \(\check{z}_2\), though \(Q_{\hat{z} \hat{z}}\) is not totally decorrelated (De Jonge and Tiberius 1996), it does not influence the properties of the second best or adjacent integer candidate. Hence, the difference between each element for \( \check{z}_1\) and its second best candidate \(\check{z}_2\) is

$$\begin{aligned} | \check{z}^i_2- \check{z}^i_1 | \le 1 \quad i=1,2,\cdots ,n \end{aligned}$$
(30)

Then, the range of the difference between \( \check{z}_1\) and \(\check{z}_2\) is

$$\begin{aligned} 1 \le (\check{z}_2 - \check{z}_1)^T (\check{z}_2 - \check{z}_1) \le n \end{aligned}$$
(31)

According to (29), DT can be seen as the projection of \(2 x -(\check{z}_1 + \check{z}_2) \) on \( \check{z}_1 - \check{z}_2 \) with the metric of \( Q_{\hat{z} \hat{z}}\). Since \(\hat{z}\) must be chosen within the pull-in region, the upper bound of DT will appear when \(2 x -(\check{z}_1 + \check{z}_2)\) and \( \check{z}_1 - \check{z}_2 \) have the same direction, which means \(x=\check{z}_1\). Hence

$$\begin{aligned} R_2-R_1&= [2x-(\check{z}_1 + \check{z}_2)]^T Q^{-1}_{\hat{z} \hat{z}} (\check{z}_1 - \check{z}_2 ) \nonumber \\&\le (\check{z}_1 - \check{z}_2)^T Q^{-1}_{\hat{z} \hat{z}} (\check{z}_1 - \check{z}_2) \nonumber \\&= (\check{z}_2 - \check{z}_1)^T Q^{-1}_{\hat{z} \hat{z}} (\check{z}_2 - \check{z}_1) \end{aligned}$$
(32)

When the equality is built, we have the sharpest upper bound. Here we denote \(c= \check{z}_2 - \check{z}_1\). Based on the property of the second best integer candidate and the best one in (23) for each axis, we have \(c_j^Tc_j=1\), and \(c_j\) is the canonical vector at the \(j\)-th axis. Then, the sharpest bound of DT is given as:

$$\begin{aligned} R_2-R_1&\le \text {min} \{ c^T Q^{-1}_{\hat{z} \hat{z}} c \} \nonumber \\&= c_j^T Q^{-1}_{\hat{z} \hat{z}} c_j, j=1,2,\cdots ,n \end{aligned}$$
(33)

According to LDL decomposition

$$\begin{aligned} Q_{\hat{z} \hat{z}} = L^T D L \quad Q^{-1}_{\hat{z} \hat{z}} = L^{-1} D^{-1} (L^{-1})^T \end{aligned}$$
(34)

where \(L\) is a lower triangular matrix. It is already known that \(\text {diag}\{L\}= \left[ \begin{array}{ccc} 1&\ldots&1 \end{array} \right] ^T\). Based on the choice of \(c\) in (33)

$$\begin{aligned} c_j^T L^{-1} = \left[ \begin{array}{llllllll} l_{j,1}&\ldots&l_{j,j-1}&1&0&\ldots&0 \end{array} \right] \end{aligned}$$
(35)

Then, we can derive that

$$\begin{aligned} \text {{min}} \{ c^T Q^{-1}_{\hat{z} \hat{z}} c \}&= c_j^T L^{-1} D^{-1} (L^{-1})^T c_j \nonumber \\&= \frac{l_{j,1}^2}{d_{1,1}}+\frac{l_{j,2}^2}{d_{2,2}}+\cdots +\frac{1}{d_{j,j}} \end{aligned}$$
(36)

with \(d_{j,j}\) the \(j\)th element of diagonal matrix \(D\). The \(j\) depends on the method of ordering and parametrization in the decorrelation step. Obviously, the sharpest upper bound is obtained when \(j=1\).

Formula (36) is the general result for ambiguity resolution in decorrelated space. As to the LAMBDA method, for the actual integer minimization we strive for largely decorrelated ambiguities and, furthermore, to have the most precise ambiguity at position \(n\). The purpose is striving for De Jonge and Tiberius (1996).

$$\begin{aligned} d_{n,n} \le \dots \le d_{1,1} \end{aligned}$$
(37)

Of course, (37) is just an objective, and this monotonously decreasing from \(n\) to \(1\) may not be realized in practice. No matter what the correct integer vector is, after decorrelation in LAMBDA method, we can find that the relation between the best and second best integer candidates as (22):

$$\begin{aligned} \text {min} (\check{z}_2 - \check{z}_1 )^T (\check{z}_2 - \check{z}_1 ) = 1 \end{aligned}$$
(38)

The minimum choice for \(\check{z}_2 - \check{z}_1\) satisfying both the requirements in (38) and in (36) is \(\left[ \begin{array}{cccc} \pm 1&0&...&0 \end{array} \right] ^T\). Of course, other \(\check{z}_2 - \check{z}_1\) satisfying (38) also can derive an upper bound of DT; however, it is not the sharpest one.

Eventually, combining (36) and (38), we obtain the IA pull-in region based on DT and its simple but the sharpest bound based on LAMBDA method

$$\begin{aligned} \!\Omega _{0,\text {DTIA}}\!=\! \left\{ x \in \mathbb {R}^n | S(x)\!=\!0, \!\mu _{\text {DT}} \le R_2(x)\!-\! R_1(x)\! \le \!\frac{1}{ d_{1,1}} \right\} \end{aligned}$$
(39)

This is an interesting result, since we can directly obtain this upper bound after decorrelation without extra computation and measurement.

The upper bound of DT can also be seen as the upper bound of the critical value for DT. The obtained critical value based on fixed-failure rate or other approaches should be smaller than the upper bound in Li and Wang (2014). Furthermore, based on the bounds of covariance matrix, we give the loose upper bound of DT based on (33) after decorrelation. Note that we also can obtain the upper bound without decorrelation; however, it is rather loose.

According to Rayleigh-Ritz theorem (Golub and Loan 1996), we have

$$\begin{aligned} \frac{1}{ \lambda _{ \text {max}}} \le \frac{ c^T Q^{-1}_{\hat{z} \hat{z}} c }{c^Tc} \le \frac{1}{ \lambda _{\text {min}}} \end{aligned}$$
(40)

where \(\lambda _{\text {min}} \) and \(\lambda _{\text {max}} \) are the minimum and maximum eigenvalues of \(Q_{\hat{z} \hat{z}}\). When we choose the minimum of \(c^T Q^{-1}_{\hat{z} \hat{z}} c\) based on the condition in Eq. (33), then the loose upper bound based on covariance matrix can be deduced

$$\begin{aligned} R_2-R_1&\le \text {min} (c^T Q^{-1}_{\hat{z} \hat{z}} c) \nonumber \\&\le \frac{ \text {min}(c^Tc)}{\lambda _{\text {min}}} = \frac{1}{\lambda _{\text {min}}} \end{aligned}$$
(41)

Eventually, the IA pull-in region based on DT and its loose bound is

$$\begin{aligned}&\Omega _{0,\text {DTIA}}\nonumber \\&\quad =\left\{ x \in \mathbb {R}^n | S(x)\!=\!0, \mu _{\text {DT}} \le R_2(x)\!-\! R_1(x) \le \frac{1}{\lambda _{\text {min}}} \right\} \nonumber \\ \end{aligned}$$
(42)

As to the lower bound of DT, it is the so-called critical value and not trivial to choose for various GNSS models in practice. Since incorrect integer estimation may impose severe impact to baseline solution, it is desirable to realize the control of failure rate. Therefore, the fixed failure rate acceptance testing is introduced (Verhagen and Teunissen 2006). \(\mu _{DT}\) is better to be chosen based on this approach. DT has good performance in various GNSS models, especially when GNSS model is strong. There exists direct mathematical relation between DT and optimal test (Verhagen 2005), and DT can be seen as optimal test when model is strong enough.

To verify the previous bounds for DT, we implement the following simulation experiments. Based on the setting in Table 1, choose one epoch of GPS at one location in China, \(28^{\circ }\)N, \(113^{\circ }\)E, and implement 10,000 simulation times for this epoch. The DT values, its sharp and loose upper bounds are demonstrated in Fig. 7. Then, collect one day samples at the same location, with time interval 300 s. The same three items are presented in Fig. 8. Figure 7 is presented to verify the effectiveness of the upper bounds for different samples from the same GNSS model. Since these samples have the same GNSS model \(Q_{\hat{a} \hat{a}}\), their upper bounds keep constant. Figure 8 is to verify their effectiveness for different GNSS models. Hence, we can see different upper bounds for different epochs. In both figures, red lines are sharp upper bounds of DT, and black lines are loose upper bounds. Blue line denoted as ’DT’ means the testing values computed by \(R_2-R_1\) as in (29) based on each stochastically generated sample from GNSS models. Obviously, the red line imposes sharp constraints to the maximum value of DT, and the black line gives loose constraints.

Fig. 7
figure 7

DT’s loose bound and sharp bound for the same GNSS model with 10,000 simulation times

Full size image
Fig. 8
figure 8

DT’s loose bound and sharp bound for the GNSS models in 1 day with 300 s interval

Full size image

4 Probability evaluations of DT-IA estimator

4.1 DT-IAB and DT-IA estimators

One problem to be resolved for IA estimator is probability evaluation. Before we tackle this problem, we will study the properties of DT-IAB and DT-IA estimator.

The nonlinear scaling from ILS estimator to IA estimator results in that it is unlikely to find a global approach to the probability evaluations of all IA estimators. Hence, DT-IA estimator is chosen and studied here due to its linear scaling property and potential applications in future GNSS IAR. Since IA theory assumes that users pay more attention to failure rate, success rate is not so critical. However, the analytical relation between critical value, GNSS model and IA estimator success rate is very useful. It can help users give more accurate evaluation to the estimation results. Once critical value is determined by fixed-failure rate approach or other ways, users can directly obtain the quality of IA estimator without specific measurements. Here, we will give the approximation of the success rate of DT-IA estimator, which can provide reference for other IA estimators. According to previous discussion and simulation results about ILS estimator, the lower bound success rate based on IB can be chosen as a good approximation to the computed ILS success rate. Hence, it is natural to approximate IA success rate in this way.

Here, we firstly give the definition of IB based on DT, which we name as DT-IAB. In Teuniseen (2005), the IAB estimator is firstly given as the scaled version of integer pull-in region. Note that the IAB estimator chooses the scaling ratio as the acceptance testing. Similarly, DT-IAB uses these scaling ratios to complete the testing. The definition of DT-IAB is given below.

Definition 2

(The DT-IAB estimator)

The pull-in region of DT-IAB estimator is defined as

$$\begin{aligned} \Omega _{z,\text {DTIAB}} = \bigcap _{i = 1}^n \left\{ x \in \mathbb {R}^n \, | \, \frac{|c_i^T L^{-1} ( x -z)|}{T(c_i)} \le \frac{1}{2} \right\} \end{aligned}$$
(43)

It can also be interpreted as the combination of different parts which have different second best integer candidates. It means

$$\begin{aligned} \Omega _{z,\text {DTIAB}} = \bigcup _{c_i \in \mathbb {Z}^n / \{0\}} T(c_i) S_{z,\text {IB}} (c_i+z) \quad i = 1,2,\ldots ,n \end{aligned}$$
(44)

with

$$\begin{aligned} \left\{ \begin{array}{ll} &{}T(c_i) S_{z,IB}(c_i+z) = \{ x \in \mathbb {R}^n \quad | \quad \frac{x-z}{T(c_i)} \in S_{0,IB}(c_i) \} \\ &{}S_{0,IB} = \bigcup _{c_i \in \mathbb {Z}^n / \{0\}} S_{0,IB} (c_i) \\ &{}S_{0,IB} = \bigcap _{i = 1}^n \{ x \in \mathbb {R}^n \quad | \quad |c_i^T L^{-1} x| \le \frac{1}{2} \} \end{array} \right. \end{aligned}$$
(45)

where \(T(c_i), 0 < T(c_i) \le 1,\) is the scaling ratio based on the canonical vector \(c_i\) at the \(i\)th axis. \(L\) is the unique lower triangular matrix of the decomposition \(Q_{\hat{z} \hat{z}}=L^TDL\). \(S_{0,\text {IB}}(c_i)\) and \(S_{z,\text {IB}}(c_i+z)\) are parts of the IB pull-in region whose second best integer candidates are \(c_i\) and \(c_i+z\), respectively.

Note that in (44) and (2), \(S_{0,\text {IB}}(c_i)\) and \(S_{z,\text {IB}}(c_i+z)\) are just intermediate symbols to be better interpreted, and have no explicit expressions. All their properties can only be derived from \(S_{0,\text {IB}}\) or \(S_{z,\text {IB}}\). Besides this, it is emphasized here that the linear scaling by \(T(c_i)\) to \(S_{z,\text {IB}}(c_i+z)\) can only be interpreted as single direction scaling or compression from the second best integer candidate to the best integer candidate.

Those similar statements will be omitted for the following analysis to DTIA estimator.

The analytical expression to compute \(T(c_i)\) will be derived later. The difference between DT-IAB and IAB lies on the determination method of scaling ratios. These scaling ratios in all directions of IAB are the same, which may be different for DT-IAB. However, when \(T(c_1) = T(c_2) = \cdots = T(c_{n})\), DT-IAB will be the same as IAB. Hence, we can say that DT-IAB is the generalized IAB.

Based on the definition of DT-IAB, its success rate is deduced in the corollary below:

Corollary 1

(DT-IAB success rate)

Let the float solution be distributed as \(\hat{a} \sim N(a,Q_{\hat{a} \hat{a}})\). The success rate of DT-IAB estimator is directly given as:

$$\begin{aligned} P(\check{a}_{\text {DTIAB}}=a)=\prod ^n_{i=1} \left( 2\Phi \left( \frac{|x_i|}{\sigma _{\hat{a}_{i|I}}}\right) -1\right) \end{aligned}$$
(46)

with \(|x_i|\) the intersecting points between DT-IAB origin pull-in region and the \(i-\)th coordinate axis. Each axis has only one \(|x_i|\).

Proof

see the Appendix.

Here, we give the details to compute \(|x_i|\), which are computed based on Eq. (28) after the decorrelation process. Note that, here, the computation of the intersecting points between ILS or IA pull-in regions and coordinate axes only considers the situation without the presence of bias in ambiguities, just as analyzed in Teunissen (2001). \(|x_i|\) under biased situation will have different properties, which will be studied in the future.

To compute \(|x_i|\), we need to know \(\mu _{\text {DT}}\), which can be determined based on fixed failure-rate approach or other methods. It is emphasized here that the function of decorrelation is to make DT-IA approach to DT-IAB, so that using DT-IAB to approximate DT-IA is feasible. Note that different \(Z\) transformation or \(Q_{\hat{z} \hat{z}}\) leads to different values of \(|x_i|\). However, its computation formula will not change.

In (28), \(x\) is chosen as \([0,\ldots ,x_i,\ldots 0]^T\) and \(x_i>0\), which means that \(x\) is the intersecting point at the \(i\)th axis. The second best integer candidate of \(x_i\) is \(u=c_i\) and \(u\) is not zero vector. \(c_i\) is the canonical vector at the \(i\)th axis, or the second best integer candidate of the IB origin pull-in region. When the equality is built in (28) and \(x_i>0\), we have

$$\begin{aligned} x_i = \frac{ \Vert c_i\Vert ^2_{Q_{\hat{z} \hat{z}}} - \mu _{\text {DT}} }{ 2 \Vert c_i\Vert ^2_{Q_{\hat{z} \hat{z}}} } \end{aligned}$$
(47)

and \(\Vert c_i\Vert ^2_{Q_{\hat{z} \hat{z}}} - \mu _{\text {DT}}>0\). If \(x_i<0\), then

$$\begin{aligned} -x_i = \frac{ \Vert c_i\Vert ^2_{Q_{\hat{z} \hat{z}}} - \mu _{\text {DT}} }{ 2 \Vert c_i\Vert ^2_{Q_{\hat{z} \hat{z}}} } \end{aligned}$$
(48)

Hence,

$$\begin{aligned} |x_i| = \frac{ \Vert c_i\Vert ^2_{Q_{\hat{z} \hat{z}}} - \mu _{\text {DT}} }{ 2 \Vert c_i\Vert ^2_{Q_{\hat{z} \hat{z}}} } \end{aligned}$$
(49)

Note that \(|x_i|\) only denotes the intersecting points between origin pull-in region and coordinate axes. Intersecting points from other pull-in regions can be obtained by integer translation along the coordinate axes. \(\square \)

Now, we can deduce the relationship between DT-IA and IALS estimator.

If we rearrange Eq. (28)

$$\begin{aligned}&\Omega _{0,\text {DTIA}} = \bigcap _{c \in \mathbb {Z}^n/ \{0\}} \left\{ x \in \mathbb {R}^n | \frac{ \Vert c\Vert ^2_{Q_{\hat{z} \hat{z}}} c^T Q^{-1}_{\hat{z} \hat{z}}x}{ \Vert c\Vert ^2_{Q_{\hat{z} \hat{z}}}- \mu _{\text {DT}}} \le \frac{ \Vert c\Vert ^2_{Q_{\hat{z} \hat{z}}} }{2} \right\} \end{aligned}$$
(50)

with \(c\) the second best integer candidate. We can see that

$$\begin{aligned} \Omega _{0,\text {DTIA}} = \bigcap _{c \in \mathbb {Z}^n/ \{0\}} \left\{ x \in \mathbb {R}^n | \frac{1}{T(c)} \frac{ c^T Q^{-1}_{\hat{z} \hat{z}}x }{ \Vert c\Vert _{Q_{\hat{z} \hat{z}}} } \le \frac{ \Vert c\Vert _{Q_{\hat{z} \hat{z}}} }{2} \right\} \end{aligned}$$
(51)

with

$$\begin{aligned} T(c) = \frac{ \Vert c\Vert ^2_{Q_{\hat{z} \hat{z}}}- \mu _{\text {DT}}}{ \Vert c\Vert ^2_{Q_{\hat{z} \hat{z}}} } \end{aligned}$$
(52)

with \( 0<T(c)\le 1 \) and the definition of \(S_{0,\text {ILS}}\) given in (9). \(S_{0,\text {ILS}}(c)\) is to denote one part of ILS pull-in region whose second best integer candidate is \(c\).

The properties of \(T(c)\) are summarized below:

  1. 1.

    The second best integer candidates \(c\) are determined once \(Q_{\hat{z} \hat{z}}\) is given. Then, \(T(c)\) will be determined if \(\mu _{\text {DT}}\) is chosen.

  2. 2.

    After decorrelation, ILS can be approximated by IB, and their second best integer candidates can be seen as the same, which means that the set of c is equal to the set of \(c_i\).

  3. 3.

    \(T(c)\) are not influenced by the sign of \(c\), which means \(T(c)=T(-c)\). They do not change the properties of \(S_{z,\text {ILS}}\) or \(S_{z,\text {IB}}\) after linear scaling.

Hence, after decorrelation, we can say \(c\) will be the same as \(c_i\), and \(S_{z,\text {ILS}} \approx S_{z,\text {IB}}\). Here, we still can find that the decorrelation step is necessary to realize the approximation from DT-IAB to DT-IA. \(S_{z,\text {ILS}} (c+z)\) is one part of the ILS pull-in region with the second best integer candidate \(c+z\). Note that the second best integer candidates of \(S_{z,\text {ILS}}\) and \(\Omega _{0,\text {DTIA}}\) are different due to the integer translation.

From another point of view, \(\Omega _{z,\text {DTIA}}\) can also be seen as the combination of different parts. It is decomposed into

$$\begin{aligned} \begin{aligned}&\Omega _{z,\text {DTIA}} = \bigcup _{c \in \mathbb {Z}^n/\{0\}} \Omega _{z,\text {DTIA}} (c+z)\\&\Omega _{z,\text {DTIA}} (c+z) = T(c) S_{z,\text {ILS}} (c+z) \end{aligned} \end{aligned}$$
(53)

where \(\Omega _{z,\text {DTIA}} (c+z)\) is one part of DTIA pull-in region with the second best integer candidate \(c+z\).

As a summarization, we can give another definition of DT-IA estimator, which is mathematically equivalent to (28).

Definition 3

(The DT-IA estimator)

The pull-in region of DT-IA estimator is defined as:

$$\begin{aligned} \Omega _{z,\text {DTIA}} \!=\! \bigcap _{c \in \mathbb {Z}^n/ \{0\}} \left\{ x \in \mathbb {R}^n | \frac{ \Vert c\Vert ^2_{Q_{\hat{z} \hat{z}}} c^T Q^{-1}_{\hat{z} \hat{z}} (x-z) }{ (\Vert c\Vert ^2_{Q_{\hat{z} \hat{z}}}\!-\! \mu _{\text {DT}}) \Vert c\Vert _{Q_{\hat{z} \hat{z}}} } \le \frac{ \Vert c\Vert _{Q_{\hat{z} \hat{z}}} }{2} \right\} \end{aligned}$$
(54)

It can also be interpreted as the combination of different scaling parts, \(S_{z,\text {ILS}}(c+z)\) , whose second best integer candidates are \(c+z\). It means

$$\begin{aligned} \Omega _{z,\text {DTIA}} = \bigcup _{c \in \mathbb {Z}^n/\{0\}} T(c) S_{z,\text {ILS}} (c+z) \end{aligned}$$
(55)

with

$$\begin{aligned} \left\{ \begin{array}{ll} &{} T(c) S_{z,\text {ILS}}(c+z) = \left\{ x \in \mathbb {R}^n \quad | \quad \frac{x-z}{T(c)} \in S_{0,\text {ILS}}(c) \right\} \\ &{} S_{0,\text {ILS}} = \bigcup _{c \in \mathbb {Z}^n / \{0\}} S_{0,\text {ILS}} (c) \\ &{} S_{0,\text {ILS}} = \bigcap _{c \in \mathbb {Z}^n/ \{0\}} \left\{ x \in \mathbb {R}^n \quad | \quad \frac{ c^T Q^{-1}_{\hat{z} \hat{z}}x }{ \Vert c\Vert _{Q_{\hat{z} \hat{z}}} } \le \frac{ \Vert c\Vert _{Q_{\hat{z} \hat{z}}} }{2} \right\} \end{array} \right. \end{aligned}$$

with \(T(c)\) computed in (52).

Obviously, DT-IA is connected with IALS by different scaling ratios for the different second best integer candidates. Scaling ratios \(T(c)\) depend on the choice of \(c\), \(Q_{\hat{z} \hat{z}}\) and \(\mu _{\text {DT}}\). When scaling ratios in all directions \(T(c)\) are equal, DT-IA will behave the same as IALS. Hence, DT-IA can be seen as the generalized IALS estimator.

Note that the difference between \(T(c_i)\) in (44) and \(T(c)\) in (54) is that DT-IA has more second best integer candidates \(c\) than \(c_i\) of DT-IAB. Of course, the decorrelation step can decrease this kind of difference. Hence, when DT-IA and DT-IAB are fully decorrelated, the set of \(c\) is the same as that of \(c_i\), and both estimators will be equal. This property is consistent with the relation between IB and ILS. Note that even if DT-IA is not perfectly decorrelated, we still can use DT-IAB to approximate DT-IA. Of course, this will lead to approximation errors.

To analyze the properties of DT-IA estimator in detail, the 2-D reconstruction of DT-IA pull-in region and their corresponding second best integer candidates are presented in Fig. 9. Its ambiguity model matrix is the same as that of Fig. 1.

Fig. 9
figure 9

2-D reconstruction of DT-IA origin pull-in region with \(\mu _{DT}=5\), and their corresponding second best integer candidates denoted with different colors. Blue (0,1); black (0, \(-\)1); magenta (1, 0); red (\(-\)1, 0); yellow (1, \(-\)1); cyan (\(-\)1, 1). Red stars the second best integers to be fixed

Full size image

According to Fig. 9, \(\Omega _{0,\text {DTIA}}\) is very similar to the ILS pull-in region \(S_{0,\text {ILS}}\). However, the intersecting points between ILS pull-in regions and coordinate axes are different from those of DT-IA estimator. ILS pull-in regions have fixed intersecting points, \(\frac{1}{2} c_i\) and \(c_i \in \mathbb {Z}^2 / \{ 0 \}\), whereas those of DT aperture pull-in regions depend on \(\Vert c_i \Vert ^2_{Q_{\hat{z} \hat{z}}} \) and \(\mu _{\text {DT}}\). When \(Q_{\hat{z} \hat{z}}\) is given, its second best integer candidates of origin pull-in region are determined, then these scaling ratios are determined values based on fixed \(\mu _{\text {DT}}\).

Furthermore, it is noted that the sizes of the ILS and IB pull-in regions are the same and invariant for different \(Q_{\hat{z} \hat{z}}\). Unfortunately, the volumes of aperture pull-in regions for DT-IA and DT-IAB do not keep this property. Here, we give the size of DT-IAB below. Since DT-IA and DT-IAB have few differences when \(Q_{\hat{z} \hat{z}}\) is decorrelated, we will analyze the property of their size based on DT-IAB.

Corollary 2

(Size of DT-IAB pull-in region)

The size of DT-IAB estimator is variant and depends on the chosen \(Q_{\hat{z} \hat{z}}\). It can be calculated based on the analytical expression below

$$\begin{aligned} V_{DTIAB} = \prod _{i=1}^n 2|x_i| = \prod _{i=1}^n | 1 - \frac{\mu _{\text {DT}} }{ \Vert c_i\Vert ^2_{Q_{\hat{z} \hat{z}}}} | \end{aligned}$$
(56)

There exists maximum for \(V_{DTIAB}\) based on the condition

$$\begin{aligned} \Vert c_1\Vert ^2_{Q_{\hat{z} \hat{z}}} = \cdots = \Vert c_i\Vert ^2_{Q_{\hat{z} \hat{z}}} = \cdots = \Vert c_n\Vert ^2_{Q_{\hat{z} \hat{z}}} \end{aligned}$$
(57)

with \(c_i\) the second best integer candidate of the origin DT-IAB pull-in region at the \(i\)th axis.

Proof

We briefly give the proof of this corollary.

$$\begin{aligned} \prod _{i=1}^n | 1 - \frac{\mu _{\text {DT}} }{ \Vert c_i\Vert ^2_{Q_{\hat{z} \hat{z}}}} | \le \frac{ \left( | 1 - \frac{\mu _{\text {DT}} }{ \Vert c_1\Vert ^2_{Q_{\hat{z} \hat{z}}}} |+ \cdots + | 1 - \frac{\mu _{\text {DT}} }{ \Vert c_n\Vert ^2_{Q_{\hat{z} \hat{z}}}} | \right) ^n }{n} \end{aligned}$$
(58)

The equality is built when condition (57) is satisfied.

Note that here each axis only chooses one \(c_i\) in computation of the DT-IAB size, since \(c_i\) at the same axis have equal \(T(c_i)\).

Since \(c_i\) is always fixed for each coordinate axis, the condition (57) is totally determined by \(Q_{\hat{z} \hat{z}}\). In Teunissen (1995), it analyzes that the decorrelation will make the spectrum of conditional variance become flat. In other words, it will make the condition (57) easier to be achieved. Hence, we can say that the decorrelation will enlarge the size of DT-IAB pull-in region. This will also lead to the result in (60).

Note that the size of DT-IAB pull-in region is always smaller than the size of integer pull-in region

$$\begin{aligned} 0<\prod _{i=1}^n 2|x_i| \le 1 \end{aligned}$$
(59)

When \(\mu _{\text {DT}}=0\), DT-IAB estimator will degenerate into IB estimator and \(V_{\text {DTIAB}}=1\).

Since DT-IA and DT-IAB have similar performances after decorrelation, most of times we can use the size of DT-IAB to approximate that of DT-IA after ambiguity decorrelation. Similar to DT-IAB, once \(Q_{\hat{z} \hat{z}}\), and \(\mu _{\text {DT}}\) are determined, the intersecting points between coordinate axes and pull-in regions are determined, and its size is also fixed. \(\square \)

4.2 Probability bounds of DT-IA estimator

Based on \(Z\) transformation, we can deduce a higher DT-IAB success rate (Teunissen 2000)

$$\begin{aligned} P(\check{z}_{\text {DTIAB}}=z)&=\prod ^n_{i=1} \left( 2\Phi \left( \frac{|x_i|}{\sigma _{ z_{i|I}}}\right) -1 \right) \nonumber \\&\ge \prod ^n_{i=1}\left( 2\Phi \left( \frac{|x_i|}{\sigma _{ a_{i|I}}}\right) -1\right) \nonumber \\&= P(\check{a}_{\text {DTIAB}}=a) \end{aligned}$$
(60)

When GNSS model is strong enough, acceptance testing is not necessary, and \(\mu _{\text {DT}}\) will be set as 0. When \(\mu _{\text {DT}}=0\), we can obtain the ILS success rate approximation as Eq. (15). Under this situation, DT-IA estimator can be directly regarded as ILS estimator.

Like the upper bound of IB based on ADOP, DT-IAB also has its ADOP based upper bound. It is derived based on the following idea. The pull-in region of DT-IAB is a cube constructed by different side lengths. Note that the volume of this cube depends on the size of critical value. This volume reaches its maximum when all side lengths are all equal to the geometrical average of the reciprocal sequential conditional standard deviation. It means

$$\begin{aligned} \frac{|x_1|}{\sigma _{\hat{a}_{1|2,\cdots ,n}}} = \cdots = \frac{|x_n|}{\sigma _{\hat{a}_{n}}} \end{aligned}$$
(61)

Actually, this condition is impossible to be obtained in practice. It imposes extremely strict requirements to GNSS model.

Similarly, we have

$$\begin{aligned}&P \left( \underset{i=1}{\overset{n}{\bigcap }} \left( \frac{| \hat{a}_{i|I}-a_i|}{\sigma _{\hat{a}_{i|I}}} \le \frac{|x_i|}{\sigma _{\hat{a}_{i|I}}} \right) \right) \nonumber \\&\le P \left( \underset{i=1}{\overset{n}{\bigcap }} \left( \frac{| \hat{a}_{i|I}-a_i|}{\sigma _{\hat{a}_{i|I}}} \le \sqrt{ \prod _{i=1}^n \frac{|x_i|}{\sigma _{\hat{a}_{i|I}}} }^{\frac{1}{n}} \right) \right) \nonumber \\&\qquad = \prod ^n_{i=1} \left( 2\Phi (\frac{\beta }{\text {ADOP}})-1\right) \end{aligned}$$
(62)

with \(\beta = \sqrt{\prod ^n_{i=1} |x_i|}^{\frac{1}{n}}\).

Be different from the invariant upper bound of IB (Teunissen 1998b), this upper bound in Eq. (62) is not invariant and is influenced by the decorrelation process to \(Q_{\hat{a} \hat{a}}\). However, when the termination criterion of decorrelation process is determined, then the \(Z\) matrix will be unique and eventually \(|x_i|\) and \(\beta \) also will be unique.

Then, we obtain that

$$\begin{aligned} P(\check{a}_{\text {DTIAB}}=a) \le \prod ^n_{i=1} \left( 2\Phi \left( \frac{\beta }{\text {ADOP}}\right) -1\right) \end{aligned}$$
(63)

Since ADOP is \(Z\) transformation invariant, we also can deduce similar result as (62)

$$\begin{aligned} P(\check{z}_{\text {DTIAB}}=z) \le \prod ^n_{i=1} \left( 2\Phi \left( \frac{\beta }{\text {ADOP}}\right) -1\right) \end{aligned}$$
(64)

Combining (60) and (64), we have

$$\begin{aligned} \prod ^n_{i=1} \left( 2\Phi \left( \frac{|x_i|}{\sigma _{\hat{a}_{i|I}}}\right) -1\right) \le P(\check{z}_{\text {DTIAB}}=z) \le \prod ^n_{i=1} \left( 2\Phi \left( \frac{\beta }{\text {ADOP}}\right) -1\right) \end{aligned}$$
(65)

Due to the similarity between DT-IAB and DT-IA under the weak correlation situation, most of times we can use formula (65) to bound DT-IA estimator. However, due to the optimality of ILS estimator (Teunissen 1999a), we still can deduce similar lower bound for DT-IA estimator.

Corollary 3

(Lower bound of DT-IA estimator)

Based on the definition of DT-IAB estimator, and the PDF of \(\hat{a} \in \Omega _{a,\text {DTIA}}\) is given in (10), we have the inequality between DT-IA and DT-IAB estimators

$$\begin{aligned} P(\check{z}_{\text {DTIA}}=z) \ge P(\check{a}_{\text {DTIAB}}=a) \end{aligned}$$
(66)

Proof

See the Appendix.

Note that \(P(\check{z}_{\text {DTIA}}=z) \ne P(\check{a}_{\text {DTIA}}=a)\) since the size of DT-IA is variant in \(Z\) transformation.

Hence, for DT-IA estimator, \(P(\check{z}_{\text {DTIAB}}=z)\) can be chosen as its sharp lower bound. Its upper bound based on ADOP can also be derived. We directly give it in Corollary 4. \(\square \)

Corollary 4

(Upper bound of DT-IA estimator)

For the determined admissible ambiguity parametrization, the success rate of DT-IA estimator can be bounded from above as:

$$\begin{aligned} P(\check{z}_{\text {DTIA}}=z) \le P\left( \chi ^2(n,0)\le \frac{ 4 \bar{x}^2 c_n}{\text {ADOP}^2} \right) \end{aligned}$$
(67)

with \(\bar{x}^2 = \left( \frac{\sum _{i=1}^n |x_i| }{n}\right) ^2\).

Proof

See the Appendix.

Of course, no matter which upper bound to choose, the following upper bound always exists:

$$\begin{aligned} P(\check{z}_{\text {DTIA}}=z) \le P_{s,\text {ILS}} \end{aligned}$$
(68)

Eventually, we obtain the bounds of DT-IA estimator

$$\begin{aligned} P(\check{z}_{\text {DTIAB}}=z)\le & {} P(\check{z}_{\text {DTIA}}=z)\nonumber \\\le & {} P\left( \chi ^2(n,0)\le \frac{ 4 \bar{x}^2 c_n}{\text {ADOP}^2} \right) \end{aligned}$$
(69)

After \(\mu _{DT}\) is obtained by fixed-failure rate approach, other probability evaluations of IA estimator can be derived. Assume that the fixed-failure rate is set as \(P_f\), and the false alarm rate and the failure detection rate are denoted as \(P_{fa}\) and \(P_{fd}\) respectively, then we have

$$\begin{aligned} \begin{aligned} P_{fa}&= P_{s,\text {ILS}}- P(\check{z}_{\text {DTIA}}=z)\\ P_{fd}&= 1-P_f- P_{s,\text {ILS}} \end{aligned} \end{aligned}$$
(70)

The probability evaluations for all judgments in DTIA estimator are obtained once \(P(\check{z}_{\text {DTIA}}=z)\) and \(P_{s,\text {ILS}}\) are known. \(\square \)

4.3 Simulation verification

To verify these conclusions, the simulation experiments are also implemented based on the settings in Table 1. Here, critical values of DT are determined based on fixed failure rate approach and \(P_f=0.001\). For Fig. 10, we give the following remarks:

  1. 1.

    The lower bound based on DT-IAB success rate can realize good approximation to the DT-IA computed success rate. It is noted that incomplete decorrelation to the ambiguity variance matrix leads to the deviation of approximation;

  2. 2.

    The ADOP-based upper bound for DT-IAB also provides the upper constraint of the DT-IA. Be different from the ADOP based upper bound for ILS, all these upper bounds are always larger than the DT-IAB based lower bounds. This is the result for the geometric average of scaling ratios \(|x_i|\) and ADOP;

  3. 3.

    The ADOP-based upper bound for DT-IA provides the loose upper constraint for DT-IA estimator, which is also the upper bound of previous bounds.

Based on the approximated DT-IA success rates by DT-IAB lower bound, the false alarm rates are approximated and compared with the computed false alarm rates. The comparison results in the Fig. 11 show that the false alarm rate can realize good approximation to the actual computed values. Similarly, approximation errors mainly come from the DT-IA success rate approximation errors, which are mainly brought by the decorrelation step.

Fig. 10
figure 10

The success rates of DT-IA estimator and their corresponding lower bounds, upper bounds based on IB and DT-IA upper bounds based on ADOP. Black computed IA success rates; green lower bounds based on IB; red upper bounds based on IB; blue DT-IA upper bounds based on ADOP

Full size image

As a summary, these simulation experiments verified the effectiveness of the conclusions for DT-IA estimators.

Fig. 11
figure 11

False alarm rates and its approximation of DT-IA estimator. Black computed IA false alarm rates; green IA false alarm rates approximation

Full size image

5 Conclusions

Quality control is of great importance in GNSS ambiguity resolution, especially in the reliable GNSS application. Acceptance testing is one of the most important quality control measures. There are various acceptance tests and different IA estimators have distinctive properties (Verhagen 2005). This contribution is mainly focused on DT-IA estimator and studied the overall properties of DT-IA ambiguity resolution based on the theory of IA ambiguity resolution.

First, after reviewing the principle of integer estimation, this contribution paid attention to the second best integer candidates in integer estimation and analyzed their properties in decorrelated space. The second best integer candidates have close relation with the geometry formation of pull-in region.

Then, the properties and bounds of DT were studied from the algebraic perspective. Its sharp bound and loose upper bound were derived and verified based on simulation experiments. These bounds were simple and easy to be computed, which can provide direct reference for DT-IA ambiguity resolution. The sharp upper bound of DT gave a clear range for the choice of critical values.

Based on the probability evaluation theory in ILS estimator, the probability evaluations of DT-IA estimators were further exploited. The DT-IA success rate can realize quick approximation based on the IB lower bound like ILS estimator. This is more efficient and time saving than the conventional Monte Carlo method. The other quality items, such as false alarm and failure detection rates, are easy to be derived. During the investigation process, the definition of DT-IAB was firstly given, and the relationships between DT-IA and DT-IAB estimators were deeply investigated. They can be seen as the generalized IAB and IALS estimators, and both estimators can be approximated after decorrelation. Based on the studies of the second best integer candidates in ILS, a new definition of DT-IA was given based on the linear scaling perspective, which was equivalent to its original definition. This perspective gives us a new perspective to study other IA estimators.

The derived results for DT-IA success rates and false alarm rates were verified in the simulation experiments including single and GNSS combination models. Results showed that DT-IA success rate can realize good approximation based on DT-IAB success rate. The approximation of the false alarm rate gave similar performance to that of the success rate. The research frame for DT-IA estimator can provide reference for the investigation of other IA estimators.