1 Introduction

The width control in continuous hot rolling process is mainly realized by vertical rolling. During width reduction process, complicated deformation occurs at the slab edge, leading to the rolling force acting on the vertical rolling mechanism. However, the distance between the vertical rolling mill and horizontal rolling mill is short, and the detection devices of rolling force and slab shape are delayed. It is difficult to realize online adjustment of width reduction [1]. Comprehensive research on the whole rolling mechanism to accurately predict rolling force and plastic deformation is essential for parameter presetting and online control.

There are three ways for vertical rolling research: physical experiment method, finite element simulation and theoretical model. Experimental method can be summarized as follow: Select appropriate materials to roll by a small mill, which is scaled down from industrial rolling mill. Then measure the edge deformation and fit the curves with process parameters. Okado et al. [2] and Xiong et al. [3] used pure Lead to simulate vertical rolling and fitted empirical formulas of edge deformation parameters including the height of peak and edge, the position of peak, and the length of plastic zone. Shibahara et al. [4] developed a mathematical model for edger set-up by regressing measured values of edge bulge. Tazoe et al. [5] obtained an exponential formula of dog–bone peak height considering vertical roller diameter, width reduction and initial slab size. Later, the result was modified by Ginzburg et al. [6].

Benefiting from the development of computer technology, the finite element simulation method has been widely used. Huisman et al. [7] proposed a 3D FEM method to analyze edge deformation, and the reliability of model was verified by the plastic mud experiment. Chung et al. [8] put forward an explicit dynamic finite element method with appropriate damping to investigate optimum rolling procedure to minimize crop losses. The effect of flat vertical roller and grooved vertical roller on vertical–horizontal mill is compared. Based on rigid–plastic theory, Xiong et al. [9] predicted the slab shape, the spread and the sectional distribution of temperature in vertical–horizontal rolling process by a full 3D thermal coupling FEM. By finite element method and updated geometrical method, Yu et al. [10] simulated the rough rolling and finish rolling of stainless steel plate to analyze the influences of width reduction on the stress change at strip edge. Yun et al. [11] set up a FEM based on the hypothetical mode of vertical rolling process and the least–squares regression analysis from the result of the FE approach. The model reflects rolling force affected by dimensionless process variables including shape factor, reduction ratio and width–to–thickness ratio. To improve the theoretical prediction accuracy of extra-thick plate rolling process, Zhang et al. [12] used the genetic algorithm as an enhancing means to optimize the global searching ability of the BP model and then combined the neural network model with a theoretical model.

Due to the complicated and non–uniform plastic deformation, it is quite difficult to establish the equilibrium differential equation. Scholars prefer to give a kinematically admissible velocity field, and then solve total power functional according to upper bound energy method. In order to analyze edge rolling of steel, copper and aluminum, Lundberg et al. [13,14,15] simplified the edge bulge into a trapezoid and drew the speed end diagram of metal flow under the assumption of plane deformation. Triangular velocity fields considering friction and smoothness were established respectively, and the calculation formulas of rolling force and torque were deduced based on the achieved energy model. To improve the prediction accuracy, a feasible way is to describe the process of edge deformation by more appropriate curves. Assuming the entire slab section as deformation area, Yun et al. [16] used high–order power function curves to describe the cross section of edge deformation, and set a velocity field based on stream function and volume invariance. Then, a regression model was established according to the results of finite element simulation. Liu et al. [17] proposed a sine function dog–bone model and built a stream function velocity field. The total power functional is derived based on rigid–plastic theory and the incompressibility of flow. With the same deformation assumption, Zhang et al. [18] determined the maximal width of a dog–bone region by slip–line method. By repeatedly optimizing the weighted coefficient b of intermediate principal shear stress on the yield criterion, the rolling force and edge shape are obtained analytically. Liu et al. [19], Cao et al. [20] and Li et al. [21] calculated the plastic deformation power of a parabolic dog–bone model based on angular bisector (ID) yield criterion, twin shear stress (TSS) yield criterion, and mean (MY) yield criterion, respectively. The shear power and friction power are obtained according to integral mean value theorem and Pavlov projection principle. The simplified analytical solutions of total power functional and rolling force are given by using energy method. Ding et al. [22] analyze parabolic dog–bone deformation in chamfer edge rolling of ultra–heavy plate and obtained a velocity field with fixed angle. Zhang et al. [23] constructed a quadratic velocity field and established a three-dimensional rolling model of extra-thick plate by using energy method. The model considered the temperature difference of the workpiece and the result is much closer to the measured data. Later, dual–stream function (DSF) method was carried out in 3D edge rolling research. Sine [24], parabolic [25], and cubic [1] dog–bone model with their corresponding velocity fields and strain rate fields are derived. The obtained dog–bone height is lower than that of 2D models but closer to measurement. In order to satisfy the requirement of low computation cost, the author provided a rather simple 3D velocity field through global weighted method in previous study [26]. A combination of Γ function and parabola function is carried out to describe edge deformation. The total power functional is solved numerically.

In the above studies, the slab was analyzed in isolation and the vertical rolling mechanism is assumed to be a rigid body. Actually, although the flattening of roller can be ignored in hot rolling process [27], the vertical roller leads to deflection inevitably result from the large rolling force. Moreover, the support bearing could also produce radial displacement. In order to accurately predict rolling force and edge deformation, the elastic deformation of mechanism needs to be considered. However, the relevant research is poor at present. Base on Γ–parabola dog–bone model developed in our previous study, a 3D velocity field consisting of a 2D steam function velocity field and an additional velocity field in rolling direction at the slab edge is proposed. By applying geometric midline yield criterion and Pavlov projection principle, the total power functional is derived. During the numerical solution of the rolling force via the principle of minimum power, the deflection of rollers and the radial displacement of support bearings are fully considered. Further, the comprehensive research on vertical rolling mechanism is carried out according to the established force–displacement coupling model.

2 Energy model of vertical rolling process

2.1 Assumptions of vertical rolling mechanism and steel slab

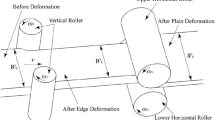
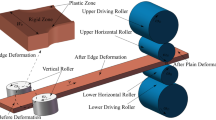
Figure 1 shows that a steel slab passes through the vertical rolling mechanism. The vertical rolling mill has no complex roller system and the rollers are directly driven by the motor. The rolling force is only supported by bearings. Due to the high ratio of width to thickness, the bulge in thickness direction only occurs at slab edge while the middle part remains rigid. The formation of the dog–bone cross section can be seen in Fig. 2(a). Simultaneously, the rolling mechanism causes elastic deformation under the rolling force, and the whole system is in a static equilibrium state.

Fig. 1
figure 1

The working principle of vertical rolling mechanism

Full size image
Fig. 2
figure 2

The edge deformation during vertical rolling process

Full size image

The assumptions before mechanical analysis are given as follows:

(1) For hot rolling, the strength of the roller is far more than that of workpiece, the elastic flattening of the roller is ignored. (2) The steel slab is rigid–plastic material with uniform and isotropic microstructure. (3) There is no fore and aft tension and impact load during vertical rolling process. The slab in bite zone is in steady state without width lose. (4) The vertical roller and the inner raceway of the bearing are rigidly connected. The extrusion deformation and the relative sliding are neglected. (5) The deformation between the bearing rolling element and the raceway is in the range of elasticity.

2.2 Dog–bone deformation at the edge

A 3D coordinate system is located at the center of the entrance cross section, which is shown in Fig. 2. The axis x, y, and z represent rolling, thickness, and width directions, respectively. Because of the symmetry, a quarter of the deformation zone is studied.

As Fig. 2(a) shows, half of the slab width before and after rolling is given by \({w}_{0}\) and \({w}_{1}\), respectively. The unilateral width reduction \(\Delta w={w}_{0}-{w}_{1}\). The vertical roller radius is denoted by R. The bite angle \(\theta ={cos}^{-1}\left[\left(R-\Delta w/R\right)\right]\). The projected length of the roller–slab contact arc in rolling direction \(l=\sqrt{{R}^{2}-{\left(R-\Delta w\right)}^{2}}\). Half of the width, the unilateral width reduction, and the contact angle at arbitrary position in bite zone are \({w}_{x}={w}_{1}+R-\sqrt{{R}^{2}-{\left(l-x\right)}^{2}}\), \(\Delta {w}_{x}={w}_{0}-{w}_{x}\), and \(\phi ={sin}^{-1}\left[\left(l-x\right)/R\right]\), respectively.

It can be seen in Fig. 2(b) that the middle part is rigid zone, and the edge part is plastic zone with bulge. The half thickness of steel slab in bite zone is expressed by \({h}_{\left(x,z\right)}\). The peak height, the edge height, the peak position, and the length of dog–bone is given by \({h}_{bx}\), \({h}_{rx}\), \({l}_{px}\), and \({l}_{cx}\), respectively. Take the peak of dog–bone as boundary, the dog–bone is divided into zone α \(\left(0<z<{w}_{x}-2{d}_{x}\right)\) and zone β \(\left({w}_{x}-2{d}_{x}<z<{w}_{x}\right)\). In order to well mark the slow change of thickness between dog–bone peak and rigid zone, Γ function is selected to describe the half thickness in zone α. In zone β, the half thickness is assumed to change as a parabola function. Detailed explanation can be found in our previous study [26], of which the result is given by:

$${h}_{\alpha }={h}_{0}+k{h}_{0}\frac{\Delta {w}_{x}}{{d}_{x}}{u}^{2}{e}^{-u}$$
(1)
$${h}_{\beta }={h}_{0}+\frac{4k{h}_{0}}{{e}^{2}}\frac{\Delta {w}_{x}}{{d}_{x}}-\frac{mk{h}_{0}}{{e}^{2}}\frac{\Delta {w}_{x}}{{d}_{x}}{\left(u-2\right)}^{2}$$
(2)

where k is the undetermined constant, m is the friction factor, \(u=\frac{{w}_{x}-z}{{d}_{x}}\), and \({d}_{x}=\frac{d}{{w}_{1}}{w}_{x}\) expresses the half of peak position at arbitrary cross section.

2.3 Velocity field and strain rate field of plastic flow

The total velocity field and strain rate field in bite zone can be expressed by two fields. The velocity field I assumes a plain deformation with constant velocity in rolling direction \({v}_{0}\). All the metal at the edge pressed by roller flows to thickness direction.

According to the property of stream function, incompressibility of the material and the boundary condition \({w}_{\alpha }\left({w}_{x}-2{d}_{x}\right)={w}_{\beta }\left({w}_{x}-2{d}_{x}\right)\), the velocity field I and strain rate field I can be derived. The solution of stream function can be seen in Ref. [17, 19, 20]. In zone α and zone β, there are [26]:

$$\left\{\begin{array}{c}v_{\alpha x\mathrm I}=v_0\\v_{\alpha y\mathrm I}=\frac{v_0y}{h_0}\frac{\partial h_\alpha}{\partial x}=kv_0y\left({t'}_xu^2-tu'_xu^2+2tu'_xu\right)e^{-u}\\v_{\alpha z\mathrm I}=v_0\frac{\partial w_\alpha}{\partial x}=kv_0\left[{w'}_x\left(u^2+2u+2\right)+\Delta w_x{u'}_xu^2\right]e^{-u}\end{array}\right.$$
(3)
$$\left\{\begin{array}{c}{\dot\varepsilon}_{\alpha x\mathrm I}=0\\{\dot\varepsilon}_{\alpha y\mathrm I}=\frac{v_0}{h_0}\frac{\partial h_\alpha}{\partial x}=kv_0\left(t'_x\;u^2-tu'_xu^2+2tu'_xu\right)e^{-u}\\{\dot\varepsilon}_{\alpha z\mathrm I}=-\frac{v_0}{h_0}\frac{\partial h_\alpha}{\partial x}=-kv_0\left({t'}_xu^2-t{u'}_{x\;}u^2+2t{u'}_xu\right)e^{-u}\end{array}\right.$$
(4)
$$\left\{\begin{array}{c}v_{\beta x\mathrm I}=v_0\\v_{\beta y\mathrm I}=\frac{v_0y}{h_0}\frac{\partial h_\beta}{\partial x}=\frac k{e^2}v_0y\left[4t'_x-mt'_x\left(u-2\right)^2-2mt\left(u-2\right)u'_x\right]\\v_{\beta z\mathrm I}=v_0\frac{\partial w_\beta}{\partial x}=\frac{4k}{e^2}v_0\left(\Delta w_x{u'}_x+\frac92\;w'_x-w'_xu\right)\text{+}\frac{mk}{e^2}v_0\left[\frac13\;w'_x\left(u-2\right)^3-\Delta w_x\left(u-2\right)^2\;u'_x\right]\end{array}\right.$$
(5)
$$\left\{\begin{array}{c}{\dot\varepsilon}_{\beta x\mathrm I}=0\\{\dot\varepsilon}_{\beta y\mathrm I}=\frac{v_0}{h_0}\frac{\partial h_\beta}{\partial x}=\frac k{e^2}v_0\left[4t'_x-mt'_x\left(u-2\right)^2-2mt\left(u-2\right)\;u'_x\right]\\{\dot\varepsilon}_{\beta z\mathrm I}=-\frac{v_0}{h_0}\frac{\partial h_\beta}{\partial x}=-\frac k{e^2}v_0\left[4t'_x-mt'_x\left(u-2\right)^2-2mt\left(u-2\right)\;u'_x\right]\end{array}\right.$$
(6)

where \(t=\frac{\Delta {w}_{x}}{{d}_{x}}\), \(t_x^1=-\frac{w'_xd_x+\Delta w_xd'_x}{d_x^2}\), \(u'_x=\frac{zd'_x}{d_x^2}\); \({w}_{\alpha }=-k\Delta {w}_{x}\left[{u}^{2}+2u+2\right]{e}^{-u}\), \({w}_{\beta }=\frac{4k\Delta {w}_{x}}{{e}^{2}}\left[u-\frac{9}{2}-\frac{m}{12}{\left(u-2\right)}^{3}\right]\) are lateral displacement functions in zone α and zone β.

Under the contact and friction of roller–slab, there is a visible velocity change in rolling direction at the edge, and the change decreases gradually along the width direction. Assuming no velocity in thickness direction and the velocity in rolling direction decreases exponentially, an additional field II conforming to Cauchy equation, incompressible law and the boundary conditions is proposed:

$$\left\{\begin{array}{c}v_{x\mathrm{II}}=v_0\left(\frac{w_1}{w_x}-1\right)e^{-\frac{w_x-z}{b_x}}\\v_{y\mathrm{II}}=0\\v_{z\mathrm{II}}=v_0\left[\frac{w_1w'_z}{w_x^2}\text{+}\frac{b'_x}{b_x^2}\left(\frac{w_1}{w_x}-1\right)\left(z-b_x\right)\right]b_xe^{-\frac{w_x-z}{b_x}}\end{array}\right.$$
(7)
$$\left\{\begin{array}{c}\varepsilon_{x\mathrm{II}}=-v_0\left[\frac{w_1w'_x}{w_x^2}+\left(\frac{w_1}{w_x}-1\right)\frac{b'_x}{b_x^2}z\right]e^{-\frac{w_x-z}{b_x}}\\\varepsilon_{y\mathrm{II}}=0\\\varepsilon_{z\mathrm{II}}=v_0\left[\frac{w_1w'_x}{w_x^2}\text{+}\left(\frac{w_1}{w_x}-1\right)\frac{b'_x}{b_x^2}z\right]e^{-\frac{w_x-z}{b_x}}\end{array}\right.$$
(8)

where \({b}_{x}=\frac{b}{{w}_{1}}{w}_{x}=\frac{2d}{{w}_{1}}{w}_{x}\).

Superposing components of Eqs. (3)–(8) in three directions, the kinematically admissible velocity field is obtained:

$$\left\{\begin{array}{c}{v}_{ix}={v}_{ix\mathrm{I}}+{v}_{ix\mathrm{II}}\\ {v}_{iy}={v}_{iy\mathrm{I}}+{v}_{iy\mathrm{II}}\\ {v}_{iz}={v}_{iz\mathrm{I}}+{v}_{iz\mathrm{II}}\end{array}\right.$$
(9)
$$\left\{\begin{array}{c}{\dot{\varepsilon }}_{ix}={\dot{\varepsilon }}_{ix\mathrm{I}}+{\dot{\varepsilon }}_{ix\mathrm{II}}\\ {\dot{\varepsilon }}_{iy}={\dot{\varepsilon }}_{iy\mathrm{I}}+{\dot{\varepsilon }}_{iy\mathrm{II}}\\ {\dot{\varepsilon }}_{iz}={\dot{\varepsilon }}_{iz\mathrm{I}}+{\dot{\varepsilon }}_{iz\mathrm{II}}\end{array}\right.$$
(10)

where \(i=\alpha ,\beta\).

According to the continuity equation, the mass flow is equal at the inlet and outlet:

$${h}_{0}{\int }_{0}^{{w}_{0}}{v}_{x0}dz={v}_{0}{\int }_{0}^{{w}_{1}-2d}{h}_{\alpha }dz+{v}_{0}{\int }_{{w}_{1}-2d}^{{w}_{1}}{h}_{\beta }dz$$
(11)

Substituting Eqs. (1) and (2) into Eq. (11), the relationship between the undetermined coefficient k and d can be derived:

$$k=\frac{{e}^{2}}{18-\frac{8}{3}m}\left(1-\frac{2d}{{w}_{1}}\right)$$
(12)

The above velocity fields satisfy the following boundary conditions:

At the entry cross section: \({v}_{\alpha y}\left(0,0,z\right)={v}_{\beta y}\left(0,0,z\right)=0\)

At the exit cross section: \({v}_{\alpha y}\left(l,y,z\right)={v}_{\beta y}\left(l,y,z\right)=0\); \({v}_{\alpha z}\left(l,y,z\right)={v}_{\beta z}\left(l,y,z\right)=0\)

At the boundary of two parts: \({v}_{\alpha x}\left(x,y,{w}_{x}-2{d}_{x}\right)={v}_{\beta x}\left(x,y,{w}_{x}-2{d}_{x}\right)\)

$${v}_{\alpha y}\left(x,y,{w}_{x}-2{d}_{x}\right)={v}_{\beta y}\left(x,y,{w}_{x}-2{d}_{x}\right)$$
$${v}_{\alpha z}\left(x,y,{w}_{x}-2{d}_{x}\right)={v}_{\beta z}\left(x,y,{w}_{x}-2{d}_{x}\right)$$

The strain rate fields satisfy incompressible law:

$${\dot{\varepsilon }}_{\alpha x}+{\dot{\varepsilon }}_{\alpha y}+{\dot{\varepsilon }}_{\alpha z}=0; {\dot{\varepsilon }}_{\beta x}+{\dot{\varepsilon }}_{\beta y}+{\dot{\varepsilon }}_{\beta z}=0$$

2.4 Geometric midline yield criterion

The nonlinear Mises yield criterion leads to the integral difficulty of deformation power. In order to solve the above problem, Zhao et al. [28] linked up the geometric midlines of error triangles or gaps between Tresca and Twin shear stress yield loci on π–plane together to form a linear yield locus called Geometric midline (GM) yield criterion. It can be seen in Fig. 3 that the obtained yield criterion is an equilateral and non–equiangular dodecagon, which can greatly simplify the calculation burden of deformation power with sufficient calculation accuracy. The yield criterion in Haigh Westergaard stress space and the specific plastic power can be calculated as follows [29]:

$$\begin{array}{c}{\sigma }_{1}-\frac{2}{7}{\sigma }_{2}-\frac{5}{7}{\sigma }_{3}={\sigma }_{s} \, {\text{f}}{\text{o}}{\text{r}} \, {\sigma }_{2}\le \frac{1}{2}\left({\sigma }_{1}\text{+}{\sigma }_{3}\right)\\ \frac{5}{7}{\sigma }_{1}\text{+}\frac{2}{7}{\sigma }_{2}-{\sigma }_{3}={\sigma }_{s} \, {\text{f}}{\text{o}}{\text{r}} \, {\sigma }_{2}\ge \frac{1}{2}\left({\sigma }_{1}\text{+}{\sigma }_{3}\right)\end{array}$$
(13)
$$D\left({\dot{\varepsilon }}_{ij}\right)=\frac{7}{12}{\sigma }_{s}\left({\dot{\varepsilon }}_{\mathrm{max}}-{\dot{\varepsilon }}_{\mathrm{min}}\right)$$
(14)

where \({\dot{\varepsilon }}_{\mathrm{max}}\) and \({\dot{\varepsilon }}_{\mathrm{min}}\) (\({s}^{-1}\)) are the maximum and minimum principal strain rates respectively.

Fig. 3
figure 3

The locus of GM yield criterion on the π–plane

Full size image

2.5 Total power functional

According to the first variational principle of rigid–plastic material, the total power functional consists of plastic deformation power, shear power and friction power:

$${J}^{*}={\dot{W}}_{i}+{\dot{W}}_{s}+{\dot{W}}_{f}$$
(15)

The plastic deformation power can be expressed by using GM yield criterion:

$$\begin{array}{c}{\dot{W}}_{i}\text{=}\underset{V}{\iiint }D\left({\dot{\varepsilon }}_{ij}\right)dV=\frac{7}{12}{\sigma }_{s}\underset{V}{\iiint }{\dot{\varepsilon }}_{\mathrm{max}}-{\dot{\varepsilon }}_{\mathrm{min}}dV\\ =\frac{7}{12}{\sigma }_{s}{\int }_{0}^{l}{\int }_{0}^{{w}_{x}-2{d}_{x}}{\int }_{0}^{{h}_{\alpha }}{\dot{\varepsilon }}_{\mathrm{max}}-{\dot{\varepsilon }}_{\mathrm{min}}dydzdx+{\int }_{0}^{l}{\int }_{{w}_{x}-2{d}_{x}}^{{w}_{x}}{\int }_{0}^{{h}_{\beta }}{\dot{\varepsilon }}_{\mathrm{max}}-{\dot{\varepsilon }}_{\mathrm{min}}dydzdx\end{array}$$
(16)

The tangential velocity discontinuity only exists at entry section:

$${\dot{W}}_{s}\text{=}{\int }_{{S}_{0}}{\tau }_{s}\left|\Delta {\overrightarrow{v}}_{s}\right|ds\text{=}{\tau }_{s}{\int }_{0}^{{w}_{0}}{\int }_{0}^{{h}_{0}}\sqrt{{\left(\Delta {v}_{x}\left|{ }_{x=0}\right.\right)}^{2}+{\left({v}_{y}\left|{ }_{x=0}\right.\right)}^{2}+{\left({v}_{z}\left|{ }_{x=0}\right.\right)}^{2}}dydz$$
(17)

where \({\tau }_{s}={\sigma }_{s}/\sqrt{3}\) is the shear yield strength.

Noticing that the friction shear stress \({\tau }_{f}=m{\tau }_{s}\) and the velocity discontinuity on the interface are collinear vectors. The friction power can be obtained by Pavlov projection principle [30]:

$$\begin{array}{c}{\dot{W}}_{f}={\int }_{{S}_{f}}\left|{\overrightarrow{\tau }}_{f}\right|\left|\Delta {\overrightarrow{v}}_{f}\right|\mathrm{cos}\left({\overrightarrow{\tau }}_{f},\Delta {\overrightarrow{v}}_{f}\right)d{s}_{f}\\ \, \, \, \, \, \, \text{=}m{\tau }_{s}{\int }_{0}^{l}{\int }_{0}^{{h}_{rx}}\sqrt{{{v}_{z}\left|{ }_{z={w}_{x}}\right.}^{2}+{\left({v}_{x}\left|{ }_{z={w}_{x}}\right.-{v}_{R}\mathrm{cos}\phi \right)}^{2}+{\left({v}_{z}\left|{ }_{z={w}_{x}}\right.-{v}_{R}\mathrm{sin}\phi \right)}^{2}}sec\phi dydx\end{array}$$
(18)

Substituting Eqs. (16), (17), and (18) into Eq. (14), the total power functional is given as follow:

$$\begin{array}{c}{J}^{*}=\frac{7}{3}{\sigma }_{s}{\int }_{0}^{l}{\int }_{0}^{{w}_{x}-2{d}_{x}}{\int }_{0}^{{h}_{\alpha }}{\dot{\varepsilon }}_{\mathrm{max}}-{\dot{\varepsilon }}_{\mathrm{min}}dydzdx+\frac{7}{3}{\sigma }_{s}{\int }_{0}^{l}{\int }_{{w}_{x}-2{d}_{x}}^{{w}_{x}}{\int }_{0}^{{h}_{\beta }}{\dot{\varepsilon }}_{\mathrm{max}}-{\dot{\varepsilon }}_{\mathrm{min}}dydzdx\\ \, \, \, \, \, \, \, \, \text{+}{\tau }_{s}{\int }_{0}^{{w}_{0}}{\int }_{0}^{{h}_{0}}\sqrt{{\left({v}_{y}\left|{ }_{z=0}\right.\right)}^{2}+{\left({v}_{z}\left|{ }_{z=0}\right.\right)}^{2}}dydz\\ +m{\tau }_{s}{\int }_{0}^{l}{\int }_{0}^{{h}_{rx}}\sqrt{{v}_{y}\left|{ }_{z={w}_{x}}\right.+{\left({v}_{x}\left|{ }_{z={w}_{x}}\right.-{v}_{R}\mathrm{cos}\phi \right)}^{2}+{\left({v}_{z}\left|{ }_{z={w}_{x}}\right.-{v}_{R}\mathrm{sin}\phi \right)}^{2}}sec\phi dydx\end{array}$$
(19)

When the parameters, such as \({h}_{0}\), \(\Delta w\), \({v}_{R}\), \(R\), \({\sigma }_{s}\), and \(m\) are given, d is the only unknown variable. Based on the principle of minimum energy, the optimal d and the corresponding power \({J}_{\mathrm{min}}^{*}\) can be calculated numerically by MATLAB. The rolling force per unit slab thickness \({F}_{0}\) is determined as follow [31]:

$${J}_{\mathrm{min}}^{*}=\frac{2M{v}_{R}}{R}=\frac{{4h}_{0}l\chi {F}_{0}{v}_{R}}{R}$$
(20)

where \(M\) is the rolling torque, \(\chi\) is the arm factor, which is selected as 0.42 [32].

2.6 Load and displacement analysis of support bearing

The support of vertical roller is selected as double–row tapered roller bearing in this paper whose structure is shown in Fig. 4. The contact angle of roller–inner ring and roller–outer ring is \({\alpha }_{i}\) and \({\alpha }_{o}\), respectively. The contact angle between the big end of rolling element and the inner ring rib is \({\alpha }_{f}\). The diameter of roller pitch circle and the axial distance between two rows of roller centroids are \({d}_{m}\) and \({d}_{c}\), respectively. The effect length, average diameter and big end spherical radius of the rolling element are \({L}_{e}\), \({D}_{w}\), and \({R}_{s}\), respectively.

Fig. 4
figure 4

The structure and load of double–row tapered roller bearing

Full size image

As shown in Fig. 5(a), the contact load of roller–inner ring, roller–outer ring, and roller–rib on jth rolling element is \({Q}_{ij}\), \({Q}_{oj}\), and \({Q}_{fj}\). The static balance equation of the whole bearing is:

$$\left\{\begin{array}{c}F_x=\sum\limits_{\zeta=1}^2\;\overset{Z_B}{\underset{j=1}{\sum\limits\;}}Q_{\zeta oj}\;\cos\;\alpha_o\sin\;\psi_j\\F_y=\overset2{\underset{\zeta=1}{\sum\limits\;}}\sum\limits_{j=1}^{Z_B}\;Q_{\zeta oj}\cos\;\alpha_o\cos\;\psi_j\end{array}\right.$$
(21)

where \(\zeta\) is the number of bearing row, \({Z}_{B}\) is the number of rolling elements, the azimuth angle of jth rolling element is \({\psi }_{j}={\psi }_{1}+\frac{2\pi }{{Z}_{B}}\left(j-1\right)\).

Fig. 5
figure 5

The (a) load and (b) deformation of tapered rolling elements

Full size image

The deformation of rolling element can be seen in Fig. 5(b). \({\delta }_{ij}\) and \({\delta }_{oj}\) represent the inside and outside displacement.

According to Hertz line contact theory, the relationship between displacement and load of roller–inner ring and roller–outer ring is:

$$\left\{\begin{array}{c}{\delta }_{i}={G}_{i}{\mathrm{c}}_{i}^{0.9}{{Q}_{o}}^{0.9}\\ {\delta }_{o}={G}_{o}{{Q}_{o}}^{0.9}\end{array}\right.$$
(22)

where \({c}_{i}=\frac{sin\left({\alpha }_{o}+{\alpha }_{f}\right)}{sin\left({\alpha }_{i}+{\alpha }_{f}\right)}\), \({G}_{i}\), and \({G}_{o}\) are the flexibility coefficient of roller–inner ring and roller–outer ring contact pair. In the modified formula proposed by Palmgren, there is:

$$\left\{\begin{array}{c}{G}_{i}=4.80{\left(\frac{1-{\mu }_{1}^{2}}{\pi {E}_{1}}+\frac{1-{\mu }_{2}^{2}}{\pi {E}_{2}}\right)}^{0.9}\frac{{\left(1+{s}_{i}\right)}^{0.1}}{{L}_{e}^{0.74}{D}_{w}^{0.1}}\\ {G}_{o}=4.80{\left(\frac{1-{\mu }_{1}^{2}}{\pi {E}_{1}}+\frac{1-{\mu }_{2}^{2}}{\pi {E}_{2}}\right)}^{0.9}\frac{{\left(1-{s}_{o}\right)}^{0.1}}{{L}_{e}^{0.74}{D}_{w}^{0.1}}\end{array}\right.$$
(23)

where \({s}_{i}\) and \({s}_{o}\) represent the ratio of average rolling element diameter (\({D}_{w}\)) to inner and outer ring diameter (\({D}_{ri}\), \({D}_{ro}\)), \({\mu }_{1}\) and \({\mu }_{2}\) are Poisson ratio, \({E}_{1}\) and \({E}_{2}\) are elastic modulus.

The projection of \({\delta }_{i}\) in \({\delta }_{o}\) direction is:

$${\delta }_{io}={\delta }_{i}cos\left({\alpha }_{o}-{\alpha }_{i}\right)$$
(24)

For optional rolling elements, the relationship between total normal displacement and load in outer ring direction is:

$${\delta }_{nj}={\delta }_{oj}+{\delta }_{ioj}=\left[{G}_{o}+{G}_{i}{\mathrm{c}}_{i}^{0.9}\mathrm{cos}\left({\alpha }_{o}-{\alpha }_{i}\right)\right]{\mathrm{Q}}_{oj}^{0.9}$$
(25)

The radial displacement \({\delta }_{rj}\) of optional rolling elements can be expressed as:

$${\delta }_{rj}={\delta }_{x}sin{\psi }_{j}+{\delta }_{y}cos{\psi }_{j}$$
(26)

where \({\delta }_{xj}\) and \({\delta }_{yj}\) are the displacement of bearing center along x and y direction.

When the bearing is acted under the pre load \({P}_{0}\) only, the axial static balance can be established according to Eq. (25) [33]:

$${P}_{0}-{Z}_{B}{\left[{G}_{o}+{G}_{i}{c}_{i}\mathrm{cos}\left({\alpha }_{o}-{\alpha }_{i}\right)\right]}^{-\frac{10}{9}}{\left({\delta }_{0}\mathrm{sin}{\alpha }_{o}\right)}^\frac{10}{9}\mathrm{sin}{\alpha }_{o}=0$$
(27)

The pre displacement can be sorted as:

$${\delta }_{0}={\left(\frac{{P}_{0}}{{Z}_{B}}\right)}^{0.9}{sin\alpha }_{0}^{-1.9}\left[{G}_{o}+{G}_{i}{c}_{i}\mathrm{cos}\left({\alpha }_{o}-{\alpha }_{i}\right)\right]$$
(28)

Then, the total normal displacement in outer ring direction can also be expressed by radial displacement and pre displacement:

$${\delta }_{nj}={\delta }_{rj}\mathrm{cos}{\alpha }_{o}+{\delta }_{0}\mathrm{sin}{\alpha }_{o}$$
(29)

Substituting Eq. (29) into Eq. (25), the relationship between the displacement of bearing and the load of roller–outer ring is obtained. Taking the result into Eq. (21), the displacement can be solved iteratively.

2.7 Displacement of vertical rolling mechanism

The vertical roller consists of body part, neck part and head part, whose diameter and length are \({l}_{b}\), \({D}_{b}=2R\); \({l}_{n}\), \({D}_{n}\) and \({l}_{h}\), \({D}_{h}\), respectively, as shown in Fig. 6. The roller body is actually involved in rolling and bears rolling force. The roller neck is equipped with the support bearing (with a length of \({l}_{r}\)) to transmit the rolling force to rack through bearing seat and screw–down device. The head part is connected with gear housing through connecting shaft for transmitting the rotating torque of motor.

Fig. 6
figure 6

The vertical rolling mechanism and its simplified model

Full size image

The slab thickness is far less than the length of vertical roller, so the rolling force can be treated as a concentrated load. During rolling process, the vertical roller causes bending deformation under the effect of rolling force and bearing supports. Due to the gap at the supports, the support bearings cannot restrict the minor deflection of the roller. Moreover, the contact between the shaft shoulder and the bearing limits the axial displacement. Thus, the support bearings at both sides can be regarded as fixed hinged support and movable hinged support, respectively [34].

Thus, the total radial displacement of rolling position is composed of two parts:

$$\eta ={\eta }_{1}+{\eta }_{2}$$
(30)

where \({\eta }_{1}\) and \({\eta }_{2}\) are the axis displacement and deflection of rolling position, respectively.

From the analysis in Sect. 2.6, the value of \({\eta }_{1}\) is equal to the radial displacement of the bearing \({\delta }_{rj}\) when the bending moment is ignored. The deflection of the vertical roller can be derived according to the superposition principle or mathematical integration:

$${\eta }_{2}=\frac{{F}_{b}{l}_{n}^{3}}{24{E}_{r}{I}_{n}}+\frac{{F}_{b}{l}_{b}}{24{E}_{r}{I}_{b}}\left({l}_{b}^{2}+3{l}_{b}{l}_{n}+3{l}_{n}^{2}\right)$$
(31)

where \({I}_{n}=\frac{\pi {D}_{n}^{4}}{32}\), \({I}_{b}=\frac{\pi {D}_{b}^{4}}{32}\), \({E}_{r}\) are the elastic modulus of the vertical roller.

2.8 Coupling of rolling force and total radial displacement

In rolling process, the total radial displacement of mechanism at rolling position causes the insufficiency of width reduction, which should be compensated when presetting in order to satisfy the requirements of process. After establishing the equilibrium equation of support force and rolling force, the compensation value of width reduction and the corresponding rolling force can be modified by iterative method. The detailed calculation flow of the coupling model is illustrated in Fig. 7.

Fig. 7
figure 7

The calculation flow of coupling model

Full size image

3 Result and discussion

3.1 Influence of bearing structure on rolling force

The detailed parameters of vertical rolling mechanism, including the double–row tapered roller bearing and the vertical roller, are given in Table 1. The rolling force varies with azimuth angle exhibited in Fig. 8. The axis track of bearing fluctuates with the azimuth angle, which leads to the periodic change of total radial displacement and the rolling force. But the fluctuation range of rolling force is no more than 16 N. Because of the tiny influence, the azimuth angle is no longer considered in later research of this paper. The average radial displacement of bearing during a cycle is selected for iterative calculation.

Table 1 The structure and mechanical parameters of vertical rolling mechanism
Full size table
Fig. 8
figure 8

The variation of rolling force with azimuth angle

Full size image

3.2 Verification of model accuracy

The presented model predicted the cross section of dog–bone shape at exit when considering three–dimensional flow and ignoring the edge velocity field (\({v}_{x}={v}_{0}\)), respectively. The results are compared with the shape obtained by Shibahara’s experiment [4], Okado’s [2], and Xiong’s [3] exponential regression model and Yun’s [16] model, which is shown in Fig. 9(a). Since the consideration of plastic flow in rolling direction, 3D model predicted a remarkably lower dog–bone peak and a more uniform deformation than 2D model. The comparison of peak position (\({l}_{p}\)) shows that the presented model is more accurate than the other models and the error with measurement is only 3.2%. Moreover, the predicted height of dog–bone is closer to the fitted result by Xiong’s model and slightly higher than the experiment data, but the error of \({h}_{b}/{h}_{r}\) is within 5%.

Fig. 9
figure 9

The dog–bone deformation predicted by several models

Full size image

The comparison of dog–bone shape at outlet predicted by the presented model and several models is shown in Fig. 9(b). The presented model predicted a more uniform deformation than sine function model [17] and double parabolic models [19, 20], which can be attributed to the properties of Γ function. The presented curve well reflects the slow increase of deformation from rigid zone to plastic zone. Compared with global weighted model [26], the presented model obtained a more inward peak position and is closer to the results of exponential regression models [2, 3] and Yun’s model [16]. It seems that the velocity field of the presented model is more reasonable.

When the equipment and process parameters are \({h}_{0}=0.07\sim 0.11\mathrm{m}\), \({w}_{0}=0.5\sim 0.95\mathrm{m}\), \(\Delta w/{w}_{0}=0.011\sim 0.026\), \(R=0.475\sim 0.5\mathrm{m}\), 92 groups of rolling force were recorded and compared with numerical results as shown in Fig. 10. It is obvious that the predicted result is in good agreement with measurement, and the error is no more than 8%. The effect of displacement compensation on rolling force is further analyzed in Fig. 11. Dimensionless coefficient, relative error \(\left|{F}_{a}-{F}_{m}\right|/\left|{F}_{b}-{F}_{m}\right|\), is used to describe the correction. \({F}_{b}\) and \({F}_{a}\) are the predictive rolling force before and after compensation, and \({F}_{m}\) is the measurement. After displacement compensation, the improvement of accuracy is around 10%. The width reduction rate of the last group is bigger, the radial displacement becomes greater by reason of the increasing rolling force. As a result, the effect of displacement compensation is more remarkable. From the above studies, the reliability and accuracy of the model is proved.

Fig. 10
figure 10

The comparison of rolling force between prediction and measurement

Full size image
Fig. 11
figure 11

The effect of displacement compensation on rolling force

Full size image

3.3 Edge deformation

Figure 12 shows the dog–bone parameters change with various process parameters. In Fig. 12(a) and (b), the increase of width reduction rate and slab thickness enlarges the pressed metal volume in width and height directions, respectively. The plastic deformation becomes more severe, and the dog–bone expands inward noticeably. Vertical roller radius and slab width play a less role in edge deformation because of the unchanged pressed volume, which is indicated in Fig. 12(c) and (d). The interface of roller–slab contact increases with larger roller radius, which suppress the plastic flow in height direction. Increasing the width of slab is equivalent to raise rigid area in the middle, which will certainly restrain the transverse flow of metal. As a result, the dog–bone moves outwards with a higher peak. Moreover, the inhibition is more obvious when the slab width is narrow.

Fig. 12
figure 12

The effects of (a) \(\Delta w/{w}_{0}\), (b) \({h}_{0}\), (c) \(R\), and (d) \({w}_{0}\) on dog–bone shape

Full size image

3.4 Rolling force and power

With the same equipment and process parameters in Sect. 3.3, the research on rolling force and power ratio is displayed in Fig. 13. The increase of pressed metal volume and deformation resistance causes the rise of rolling force, but the former, that is, the width reduction rate and slab thickness have more prominent effects. The deformation power is the largest, which account for 50–60% of total power, followed by shear power, and the friction power is the least. The result is consistent with the previous studies [1, 25, 26]. From the above analysis, the width reduction rate and slab thickness have greater impact on edge deformation and rolling force than roller radius and slab width. For the consideration of engineer and economy, adjusting the width reduction rate is the most effective method to control the mechanical parameters.

Fig. 13
figure 13

The effects of (a) \(\Delta w/{w}_{0}\), (b) \({h}_{0}\), (c) \(R\), and (d) \({w}_{0}\) on rolling force and power ratio

Full size image

3.5 Displacement compensation

Dimensionless rolling force parameter \(\left({F}_{a}-{F}_{b}\right)/{F}_{a}\) is used to describe force compensation. The compensation of displacement and rolling force changes with various main process parameters is expressed in Fig. 14. It can be seen from each figure that both of the dependent variables have almost the same change trend. In Fig. 14(b) and (c), the compensation variables increase linearly with the rise of slab thickness and roller radius. It is worth noting that the growth of compensation value has a visible weakness with wider width as shown in Fig. 14(d). The similar nonlinearity is also indicated in Fig. 12(d) and 13(d), which reveals the gradually diminished influence of rigid zone on deformation law. Differently, the force compensation moves slower than displacement compensation apparently in Fig. 14(a). This can be attributed to the change of yield strength that affects the displacement compensation, while the dimensionless rolling force parameter is unaffected.

Fig. 14
figure 14

The effects of (a) \(\Delta w/{w}_{0}\), (b) \({h}_{0}\), (c) \(R\), and (d) \({w}_{0}\) on force and displacement compensation

Full size image

Figure 15 illustrates the proportion of axis displacement and deflection in total radial displacement of rolling position changes with main process parameters. It can be seen that axis displacement is far greater than deflection. Obviously, optimizing bearing structure is more effective in the control of radial displacement. A similar law which can be summarized as rises first and then falls is found in Fig. 15(a) and (b). This can be explained by the properties of rolling bearing, the stiffness of rolling elements gradual increase with the increase of load [35]. But the above rule disappears in Fig. 15(c) and (d) because of the less influence of roller radius and slab width on rolling force, which result in the limited change range of rolling force, so the properties of rolling bearing cannot be fully reflected.

Fig. 15
figure 15

The effects of (a) \(\Delta w/{w}_{0}\), (b) \({h}_{0}\), (c) \(R\), and (d) \({w}_{0}\) on the proportion of axis displacement and deflection

Full size image

4 Conclusions

The 3D plastic flow is considered to derive the kinematically admissible velocity field of Γ–parabola dog–bone model, including the planar stream function velocity field and the exponential velocity field. The numerical functional of vertical rolling process consists of the plastic deformation power, the shear power at the inlet cross section and the friction power on the interface. According to the superposition principle, the deflection formula of rolling position is derived. Taking double–row tapered roller bearing as an example, the axis displacement is solved by Palmgren’s modified formula. Finally, a coupling model of rolling force and radial displacement is developed. The specific conclusions are listed as follows:

1. With specific example, the proposed model is applied to predict the shape of dog–bone at the exit cross section, and the results are compared with those obtained by other models and measurement. It shows that the predicted shape of the presented model is closer to the experimental result. 92 groups of typical vertical rolling processes in hot rolling plant are studied. The displacement compensation method can effectively improve the prediction accuracy, of which the error of rolling force is only 8%.

2. The volume of the pressed metal becomes larger with the increase of width reduction rate and slab thickness result in significant increase of edge deformation and rolling force. The roller radius and slab width affect the resistance of plastic flow in rolling direction and width direction, respectively, but their influences on edge deformation and rolling force are weaker compared with the influences of width reduction rate and slab thickness.

3. The rolling force compensation and displacement compensation have a similar trend with the variation of main rolling parameters. Axis displacement is dominant in the total radial displacement of rolling position, and its proportion increases at first and then decreases with the increase of width reduction rate and slab thickness. In contrast, the proportion of roller deflection is smaller.