1 Introduction

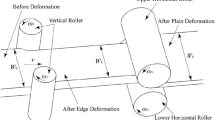
With the development of rolling technology, continuous casting and rolling have been extensively applied in many iron and steel enterprises. The width accuracy of hot-rolled strip steel products is an extremely important technical indicator in continuous casting and rolling processes. At present, the task of controlling the width of continuously cast slabs is mainly undertaken by vertical rolling and a sizing press (SP), and the reduction of vertical rolling is much smaller than that of the SP process. Owing to a small reduction and high width-to-thickness ratio, plastic deformation is concentrated on a tiny edge zone of the slab and presents an obvious dog bone shape after vertical rolling [1], as shown in Fig. 1. The dog-bone shape has a significant influence on the width spread of the subsequent flat rolling process and cannot be measured online, so the accurate prediction of dog-bone shape and rolling force is of enormous significance to automatic control.

Fig. 1
figure 1

Vertical-horizontal rolling in roughing mill and dog-bone shape

Full size image

Okado et al. [2], Toaze et al. [3], and Shibahara et al. [4] investigated the dog-bone shape by simulating the vertical-rolling process with pure lead and obtained a series of empirical formulas. Ginzburg et al. [5] modified Toaze’s formulas and drew the conclusion that the relative dog-bone peak height increased with increasing reduction and decreased with increasing initial slab thickness. Xiong et al. [6, 7] obtained an experiential model of dog-bone shape after vertical rolling through physical simulation experiments on a laboratory rolling mill. However, these formulas can only describe the shape of the exit deformation zone, and prediction accuracy is affected considerably by different rolling conditions.

The finite element method (FEM) has been one of the best ways to analyze vertical rolling because it is suitable for solving intricate geometric deformation. Huisman and Huetink [8] investigated the effect of different vertical roll radii on the dog-bone shape after vertical rolling and verified the FEM results using plasticine as the experimental material. Chuang et al. [9] considered the geometric and material nonlinearities and established three-dimensional (3D) vertical-rolling and subsequent flat-rolling models based on the explicit dynamic equations by using the dynamic relaxation method, and obtained shape parameter data of the dog bone after edge rolling. Using the ABAQUS Explicit Solver, Forouzan et al. [10] proposed a 3D elastic-viscoplastic FEM model for vertical-rolling, studied the characteristics of geometric shape change and deformation law, and compared it with the SP. Ruan et al. [11] set up a 3D rigid-plastic FEM model with DEFORM to discuss the displacement velocity field of the deformation zone and the distribution of the dog-bone shape under different technological rolling parameters. Nevertheless, although the results obtained by the use of a FEM have high accuracy, a FEM cannot be used for online automatic control in practical production due to a large amount of computation time required.

In relation to the development of the analytical solution of vertical rolling force and a dog bone shape model, Yun et al. [12] proposed a mathematical model consisting of exponential and quartic functions, but the parameters of the dog-bone shape and vertical-rolling force were obtained by fitting FEM simulation data. Since the model did not offer the expression of the deformation power functional, Yun did not obtain the analytical solution of the vertical-rolling process. The present author previously proposed a method for calculating the vertical rolling force and dog-bone shape by combining a slip line and exponential velocity field [13]. Unfortunately, although an accurate prediction of the maximum width of the dog bone region, the error in calculating vertical-rolling force is slightly larger due to the selection of the upper-bound method, and the proposed dog-bone shape model is somewhat rough.

The unified yield (UY) criterion was proposed by Yu after noticing the nonlinearity of Mises’s yield criterion, which is not a single yield criterion but a series of continuously variable linear yield criteria [14]. Then, Zhao et al. deduced the linear plastic work rate per unit volume of the UY criterion by a flow rule [15]. Therefore, herein, for the purpose of improving the prediction accuracy of edge rolling force, a new mathematical model is proposed by the energy method with the UY criterion, and the calculated accuracy of vertical rolling force is further improved by optimizing the weight coefficient in the UY criterion. Finally, the calculated shape and mechanical parameters are verified, and the variation law of the stress-state coefficient under different rolling conditions is discussed.

2 Optimization of sine function dog bone shape model

In the vertical rolling process, owing to the large width-to-thickness ratio of the slabs, the plastic deformation is mainly restricted in a small area on the slab edge [12]. Therefore, the vertical rolling process can be approximately regarded as a plane deformation process and is suitable to be solved by the slip-line method.

As shown in Fig. 2, the maximum depth of the dog-bone region has been determined by the geometric characteristics of the vertical-rolling slip-line field in our previous study [16] and is expressed as follows:

$${d_0} = B^{\prime}D^{\prime} = BD = AB = 2{h_0}$$
(1)
Fig. 2
figure 2

Slip-line field and hodograph for edge rolling

Full size image

Based on Eq. (1), Liu’s sine-function dog-bone-shape model was optimized [17], as shown in Fig. 3, and the mathematical expressions of half thickness \(h\left( {x,y} \right)\) are the following:

Fig. 3
figure 3

Definition sketch of a sine-function dog-bone profile and b bite zone in vertical rolling

Full size image

Zone I: (\(0 < y < {W_E} - {d_E}\)); half thickness \({h_I}{ = }{h_{II}}\left( {x,y} \right)\) is

$${h_I} = {h_0}$$
(2)

Zone II: (\({W_E} - {d_E} < y < {W_x}\)); half thickness \({h_I}{ = }{h_{II}}\left( {x,y} \right)\) is

$${h_{II}} = {h_0} + \beta \Delta {W_x} - \beta \Delta {W_x}\sin \left[ {\frac{{3\pi \left( {y - {W_x}} \right)}}{{2{d_\varphi }}}} \right]$$
(3)

where \(\beta\) is an undetermined parameter, and on the basis of the incompressibility condition \(\beta { = }\frac{{3\pi {h_0}}}{{{d_\varphi }\left( {2 + 3\pi } \right)}}\), \({W_x}\) is half of the slab width, \({W_x} = R + {W_E} - \sqrt {{R^2} - {{\left( {l - x} \right)}^2}}\).

The peak height of the deformation zone is

$${h_p} = {h_{II}}\left( {l,{W_E} - \frac{{d_E}}{3}} \right) = {h_0} + \frac{{6\pi {h_0}\Delta W}}{{{d_E}\left( {2 + 3\pi } \right)}}$$
(4)

and its edge height is

$${h_r} = {h_{II}}\left( {l,{W_E}} \right) = {h_0} + \frac{{3\pi {h_0}\Delta W}}{{{d_E}\left( {2 + 3\pi } \right)}}$$
(5)

where \({d_E}\) is the width of the dog-bone zone after edge rolling, \({d_E}{ = }{d_0} - \Delta W{ = }2{h_0} - \Delta W\).

3 Velocity and strain rate fields

\(dc - dC\) is the lateral variation of an infinitesimal segment in the direction of length, and \(w = w\left( {x,y} \right)\) is the lateral displacement as shown in Fig. 3.

$$\frac{dw}{{dy}} = \frac{dc - dC}{{dC}}$$
(6)

The half-thickness is \(h = h\left( {x,y} \right)\), and considering the incompressibility condition, the velocity of the rolling direction is

$${v_x} = \frac{{{v_0}{h_0}}}{h}\frac{dC}{{dc}}$$
(7)

Substituting Eq. (7) into Eq. (6) and noting that \(\frac{dw}{{dy}} \ll 1\) and \(\frac{{{{dw} \mathord{\left/ {\vphantom {{dw} {dy}}} \right. \kern-\nulldelimiterspace} {dy}}}}{{1 + {{dw} \mathord{\left/ {\vphantom {{dw} {dy}}} \right. \kern-\nulldelimiterspace} {dy}}}} \approx \frac{dw}{{dy}}\), then

$${v_x} = \frac{{{v_0}{h_0}}}{h}\left( {1 - \frac{dw}{{dy}}} \right)$$
(8)

According to the properties of stream function

$$\frac{{v_y}}{{v_x}} = \frac{dw}{{dx}}$$
(9)

Substituting Eq. (8) into Eq. (9), the metal flow velocity of the width direction is derived as follows:

$${v_y} = \frac{{{v_0}{h_0}}}{h}\left( {1 - \frac{\partial w}{{\partial y}}} \right)\frac{\partial w}{{\partial x}}$$
(10)

Based on the plane-deformation assumption,

$${v_x} = {v_0}$$
(11)

Then in accordance with the incompressibility condition,

$$\begin{aligned} {{\dot \varepsilon }_z} &= - \left( {{{\dot \varepsilon }_x} + {{\dot \varepsilon }_y}} \right) = - \left( {\frac{{\partial {v_x}}}{\partial x} + \frac{{\partial {v_y}}}{\partial y}} \right) \\& = {v_0}{h_0}\left\{ {\frac{\partial }{\partial y}\left( \frac{1}{h} \right)\left[ {\frac{\partial w}{{\partial x}}\left( {\frac{\partial w}{{\partial y}} - 1} \right)} \right] + \frac{1}{h}\frac{{{\partial^2}w}}{\partial x\partial y}\left( {\frac{\partial w}{{\partial y}} - 1} \right) + \frac{1}{h}\frac{\partial }{\partial w}\frac{{{\partial^2}w}}{{\partial {y^2}}}} \right\} \\ \end{aligned}$$
(12)

Noting that when \(z = 0\), \({v_z} = 0\), the metal flow velocity of the vertical direction, \({v_z}\) can be obtained by integrating \({\dot \varepsilon_z}\):

$$\begin{aligned}{v_z} &= \int {{{\dot \varepsilon }_y}} dy \\& = {v_0}{h_0}z\left\{ {\frac{\partial }{\partial y}\left( \frac{1}{h} \right)\left[ {\frac{\partial w}{{\partial x}}\left( {\frac{\partial w}{{\partial y}} - 1} \right)} \right] + \frac{1}{h}\frac{{{\partial^2}w}}{\partial x\partial y}\left( {\frac{\partial w}{{\partial y}} - 1} \right) + \frac{1}{h}\frac{\partial }{\partial w}\frac{{{\partial^2}w}}{{\partial {y^2}}}} \right\} \\ \end{aligned}$$
(13)

From Eqs. (8) and (11):

$$w = w\left( {x,y} \right){ = }\int_0^y {\left( {1 - {h \mathord{\left/ {\vphantom {h {h_0}}} \right. \kern-\nulldelimiterspace} {h_0}}} \right)} dy$$
(14)

From Eqs. (2), (3), and (14), and the boundary conditions, the lateral displacement of each region can be obtained as follows:

Zone I:

$${w_I}{ = }\int_0^{{W_E} - {d_E}} {\left( {1 - {{h_I} \mathord{\left/ {\vphantom {{h_I} {h_0}}} \right. \kern-\nulldelimiterspace} {h_0}}} \right)} dy = 0$$
(15)

Zone II:

$${w_{II}} = - \frac{{3\pi \Delta {W_x}}}{{\left( {2 + 3\pi } \right){d_\varphi }}}\left[ {y - \left( {{W_x} - d\varphi } \right)} \right] - \frac{{2\Delta {W_x}}}{2 + 3\pi }\cos \left[ {\frac{{3\pi \left( {y - {W_x}} \right)}}{{2{d_\varphi }}}} \right]$$
(16)

It can be obtained from Eq. (16), \({w_{II}}\left( {x,{W_x}} \right) = - \Delta {W_x}\) and the boundary condition is satisfied.

Substituting Eq. (15) into Eqs. (10) and (13), the velocity field of zone I is derived as follows:

$${v_{xI}} = {v_0},{v_{yI}} = {v_{zI}} = 0$$
(17)

Then, the axial strain-rate field in zone I can be deduced on the basis of the Cauchy equation,

$${\dot \varepsilon_{xI}} = {\dot \varepsilon_{yI}} = {\dot \varepsilon_{zI}} = 0$$
(18)

Inserting Eq. (16) into Eqs. (10) and (13), the velocity field of zone II is

$$\begin{gathered} {v_{xII}} = {v_0} \hfill \\ {v_{yII}} = \frac{{3\pi {v_0}\left( {y - {W_x} + {d_\varphi }} \right)}}{{\left( {2 + 3\pi } \right){d_\varphi }^2}}\left[ {2{h_0} - \Delta {W_x}sin\left( {\frac{{3\pi \left( {y - {W_x}} \right)}}{{2{d_\varphi }}}} \right)} \right]\frac{{{\text{d}}{W_x}}}{{{\text{d}}x}} + \frac{{2{v_0}}}{2 + 3\pi }\cos \left( {\frac{{3\pi \left( {y - {W_x}} \right)}}{{2{d_\varphi }}}} \right)\frac{{{\text{d}}{W_x}}}{{{\text{d}}x}} \hfill \\ {v_z}_{II} = - \frac{{\pi {v_0}z}}{{\left( {2 + 3\pi } \right)}}\left\{ {\frac{{6{h_0}}}{{{d_\varphi }^2}}\left[ {1 - sin\left( {\frac{{3\pi \left( {y - {W_x}} \right)}}{{2{d_\varphi }}}} \right)} \right] - \frac{{9\pi \left( {y - {W_x} + {d_\varphi }} \right)\Delta {W_x}}}{{2{d_\varphi }^3}}\cos \left( {\frac{{3\pi \left( {y - {W_x}} \right)}}{{2{d_\varphi }}}} \right)} \right\}\frac{{{\text{d}}{W_x}}}{{{\text{d}}x}} \hfill \\ \end{gathered}$$
(19)

From Eqs. (17) and (19), \(\left. {{v_{zI}}} \right|_{\begin{subarray}{l} x = 0 \\ z = 0 \end{subarray}} = \left. {{v_{zII}}} \right|_{\begin{subarray}{l} x = 0 \\ z = 0 \end{subarray}} = 0\), \(\left. {{v_{yII}}} \right|_{\begin{subarray}{l} x = l \\ y = {W_E} - {d_E} \end{subarray} } = 0\), \(\left. {{v_{zI}}} \right|_{\begin{subarray}{l} x = l \\ z = 0 \end{subarray} } = \left. {{v_{zII}}} \right|_{\begin{subarray}{l} x = l \\ z = 0 \end{subarray} } = 0\),

\(\left. {{v_{zI}}} \right|_{\begin{subarray}{l} x = l \\ z = h \end{subarray} } = \left. {{v_{zII}}} \right|_{\begin{subarray}{l} x = l \\ z = h \end{subarray} } = 0\),\({\left. {{v_{xI}}} \right|_{y = {W_E} - {d_E}}} = {\left. {{v_{xII}}} \right|_{y = {W_E} - {d_E}}} = {v_0}\), \({\left. {{v_{yI}}} \right|_{y = {W_E} - {d_E}}} = {\left. {{v_{yII}}} \right|_{y = {W_E} - {d_E}}} = 0\), and

\({\left. {{v_{zI}}} \right|_{y = {W_E} - {d_E}}} = {\left. {{v_{zII}}} \right|_{y = {W_E} - {d_E}}} = 0\). These equations satisfy the boundary conditions.

Based on the Cauchy equation, the axial strain rate field in zone II is determined as follows:

$$\begin{gathered} {{\dot \varepsilon }_{xII}} = 0 \hfill \\ {{\dot \varepsilon }_{yII}} = \frac{{\pi {v_0}}}{{\left( {2 + 3\pi } \right)}}\left\{ {\frac{{6{h_0}}}{d_\varphi^2}\left[ {1 - sin\left( {\frac{{3\pi \left( {y - {W_x}} \right)}}{{2{d_\varphi }}}} \right)} \right] - \frac{{9\pi \left( {y - {W_x} + {d_\varphi }} \right)\Delta {w_x}}}{2d_\varphi^3}\cos \left( {\frac{{3\pi \left( {y - {W_x}} \right)}}{{2{d_\varphi }}}} \right)} \right\}\frac{{{\text{d}}{W_x}}}{{{\text{d}}x}} \hfill \\ {{\dot \varepsilon }_{zII}} = - \frac{{\pi {v_0}}}{{\left( {2 + 3\pi } \right)}}\left\{ {\frac{{6{h_0}}}{d_\varphi^2}\left[ {1 - sin\left( {\frac{{3\pi \left( {y - {W_x}} \right)}}{{2{d_\varphi }}}} \right)} \right] - \frac{{9\pi \left( {y - {W_x} + {d_\varphi }} \right)\Delta {W_x}}}{2d_\varphi^3}\cos \left( {\frac{{3\pi \left( {y - {W_x}} \right)}}{{2{d_\varphi }}}} \right)} \right\}\frac{{{\text{d}}{W_x}}}{{{\text{d}}x}} \hfill \\ \end{gathered}$$
(20)

From Eqs. (18) and (20), \({\dot \varepsilon_{xI}} + {\dot \varepsilon_{yI}} + {\dot \varepsilon_{zI}} = 0\) and \({\dot \varepsilon_{xII}} + {\dot \varepsilon_{yII}} + {\dot \varepsilon_{zII}} = 0\).

Thus, Eqs. (19) and (20) are the kinematically admissible velocity and strain-rate field, respectively.

4 Total power functional

4.1 UY criterion

The UY criterion is a unified expression of various linear yield criteria in the error triangle between Tresca’s and the twin shear stress (TSS) yield loci on the π plane [14], as shown in Fig. 4.

Fig. 4
figure 4

Yield loci in π plane

Full size image

Through an in-depth study, it is found that the UY yield criterion is more generalized than other linear yield criteria that have exact physical significance. The UY criterion is usually expressed by

$$\left\{ \begin{gathered} {\sigma_1} - \frac{{b{\sigma_2}}}{1 + b} - \frac{{\sigma_3}}{1 + b} = {\sigma_s}\begin{array}{*{20}{c}} {}&{{\text{if}}\begin{array}{*{20}{c}} {}&{{\sigma_2} \leq \frac{{{\sigma_1} + {\sigma_3}}}{2}} \end{array}} \end{array} \hfill \\ \frac{{\sigma_1}}{1 + b} + \frac{b}{1 + b}{\sigma_2} - {\sigma_3} = {\sigma_s}\begin{array}{*{20}{c}} {}&{{\text{if}}\begin{array}{*{20}{c}} {}&{{\sigma_2} \geq \frac{{{\sigma_1} + {\sigma_3}}}{2}} \end{array}} \end{array} \hfill \\ \end{gathered} \right.$$
(21)

where \(b\) is the yield-criterion parameter, which represents the effect of the intermediate principal shear stress on the yield of materials, and \(0 \leq b \leq 1\). \({\sigma_1}\), \({\sigma_2}\), and \({\sigma_3}\) are principal stresses.

The specific plastic work rate per unit volume of the UY criterion was derived by Zhao [15]

$$D\left( {{\varepsilon_{ij}}} \right) = \frac{1 + b}{{2 + b}}{\sigma_s}\left( {{{\dot \varepsilon }_{\max }} - {{\dot \varepsilon }_{\min }}} \right)$$
(22)

where \({\dot \varepsilon_{\max }}\) and \({\dot \varepsilon_{\min }}\) are the maximum and minimum strain rates, respectively, in deformation; \({\dot \varepsilon_{\max }} = {\dot \varepsilon_z}\) and \({\dot \varepsilon_{\min }} = {\dot \varepsilon_y}\). When b takes any value between 0 and 1, the corresponding specific plastic power can be obtained. Zhao’s research made considerable progress in the physical linearization of forming the energy-rate functional integral, which provides a necessary basis for the first application of the UY criterion in this paper to improve the accuracy of the vertical-rolling force calculation by repeatedly optimizing the value of b in the UY yield criterion.

4.2 Inter-deformation power

Substituting Eqs. (18) and (20) into Eq. (22), the inter-deformation power can be calculated as follows:

$$\begin{aligned}{\dot W_i} &= \frac{{4\left( {1 + b} \right)}}{2 + b}\int_0^l {\int_{{W_E} - {d_E}}^{W_x} {\int_0^{h_I} {{\sigma_s}\left( {{{\dot \varepsilon }_{\max }} - {{\dot \varepsilon }_{\min }}} \right)} } } {\text{d}}z{\text{d}}y{\text{d}}x\\&= \frac{{4\left( {1 + b} \right){\sigma_s}}}{2 + b}\int_0^l {\int_{{W_E} - {d_E}}^{W_x} {\int_0^{h_I} {\left( {\frac{{ - 2\pi {v_0}}}{{\left( {2 + 3\pi } \right)}}\left\{ {\frac{{6{h_0}}}{d_\varphi^2}\left[ {1 - sin\left( {\frac{{3\pi \left( {y - {W_x}} \right)}}{{2{d_\varphi }}}} \right)} \right] - \frac{{9\pi \left( {y - {W_x} + {d_\varphi }} \right)\Delta {W_x}}}{2d_\varphi^3}\cos \left( {\frac{{3\pi \left( {y - {W_x}} \right)}}{{2{d_\varphi }}}} \right)} \right\}\frac{{{\text{d}}{W_x}}}{{{\text{d}}x}}} \right)} } } {\text{d}}z{\text{d}}y{\text{d}}x\\&= \frac{{ - 4\left( {1 + b} \right){\sigma_s}}}{2 + b}\frac{{\pi {v_0}{h_0}}}{{\left( {2 + 3\pi } \right)}}\int_{W_0}^{W_E} {\left[ {\frac{{\left( {4 + 6\pi } \right){h_0}}}{{\pi {d_\varphi }}} + \frac{{\left( {8 + 9\pi } \right){h_0}}}{2 + 3\pi }\frac{{3\Delta {W_x}}}{d_\varphi^2} - \frac{{\left( {8 + 3\pi } \right)}}{{4\left( {2 + 3\pi } \right)}}\frac{3\Delta W_x^2}{{d_\varphi^2}} - \frac{2}{\pi }\frac{{\Delta {W_x}}}{{d_\varphi }}} \right]} d{W_x}\\&= \frac{1 + b}{{2 + b}}\frac{{3{\sigma_s}{v_0}{h_0}}}{{{{\left( {2 + 3\pi } \right)}^2}\left( {2{h_0} - \Delta W} \right)}}\left[ {16\pi \left( {2{h_0} - \Delta W} \right){h_0}\ln \left( {\frac{{2{h_0}}}{{2{h_0} - \Delta W}}} \right) + \frac{{4\left( {2{h_0} - \Delta W} \right)}}{3}\left( {4 + 6\pi + 9{\pi^2}} \right)\Delta W + \left( {8 + 15\pi } \right)\pi \Delta {W^2}} \right]\end{aligned}$$
(23)

4.3 Friction power

Friction acts on the contact surface between the slab and vertical roll (\(y = {W_x}\)), and the tangential velocity discontinuity is

$$\Delta {v_t} = {v_R} - \frac{{v_0}}{\cos \varphi }$$
(24)

while the velocity discontinuity is

$$\Delta {v_f} = \sqrt {{{\left( {{{\left. {{v_{zII}}} \right|}_{y = {W_x}}}} \right)}^2} + \Delta v_t^2}$$
(25)

It is noted that the friction stress \({\tau_f} = mk = {{m{\sigma_s}} \mathord{\left/ {\vphantom {{m{\sigma_s}} {\sqrt 3 }}} \right. \kern-\nulldelimiterspace} {\sqrt 3 }}\) and velocity discontinuity \(\Delta {v_f}\) are always in the same direction, and the friction power is then deduced using the collinear vector inner product

$$\begin{gathered} {{\dot W}_f} = 4\int_0^l {\int_0^{{h_{rx}}} {|{\tau_f}|} } |\Delta {v_f}|\cos (\Delta {v_f},{\tau_f}){\text{d}}s \\ {\kern 1pt} = 4\int_0^l {\int_0^{{h_{rx}}} {\tau_f} } |\Delta {v_f}|{\text{d}}s = 4mk\int_0^l {\int_0^{{h_{rx}}} {\sqrt {{{\left( {{{\left. {{v_{zII}}} \right|}_{y = {W_x}}}} \right)}^2} + \Delta v_t^2} \frac{{{\text{d}}z{\text{d}}x}}{\cos \varphi }{\kern 1pt} } } \\ \end{gathered}$$
(26)

For the purpose of obtaining the analytical solution of the friction power, the mean-value theorem of the integral is used to calculate the average value of \(\Delta {v_t}\),\({h_r}\), and \({v_{zII}}\):

$$\Delta {\bar v_t} = \frac{{\int_\theta^0 {\left( {{v_R} - \frac{{v_0}}{\cos \varphi }} \right){\text{d}}\varphi } }}{ - \theta } = {v_R} - \frac{{v_0}}{2\theta }\ln \left( {\frac{R + l}{{R - l}}} \right)$$
(27)
$${\bar h_r} = \frac{{{h_{rl}} + {h_0}}}{2} = {h_0} + \frac{{3\pi {h_0}\Delta W}}{{2\left( {2 + 3\pi } \right)\left( {2{h_0} - \Delta W} \right)}}$$
(28)
$$\begin{aligned}{\bar v_{zII}} =& \frac{1}{{l{{\bar h}_r}}}\int_0^l {\int_0^{{{\bar h}_r}} {\left( {{{\left. {{v_{zII}}} \right|}_{y = {W_x}}}} \right)} } {\text{d}}z{\text{d}}x = \frac{{\pi {v_0}{{\bar h}_r}}}{{4\left( {2 + 3\pi } \right)l}}\\&\left[ {9\pi \ln \left( {\frac{{2{h_0}}}{{2{h_0} - \Delta W}}} \right) + \frac{{3\left( {3\pi - 2} \right)\Delta W}}{{2{h_0} - \Delta W}}} \right]\end{aligned}$$
(29)

Substituting \({\text{d}}s = \frac{{{\text{d}}x{\text{d}}y}}{\cos \varphi }\) and \({\text{d}}x = - R\cos \varphi {\text{d}}\varphi\) into Eq. (26),

$$\begin{aligned} {{\dot W}_f} &= 4\int_0^l {\int_0^{{h_{rx}}} {\tau_f} } |\Delta {v_f}|{\text{d}}s = 4\int_0^l {\int_0^{{h_{rx}}} {|{\tau_f}|} } |\Delta {v_f}|\cos (\Delta {v_f},{\tau_f}){\text{d}}s \\&= 4\int_0^l {\int_0^{{h_{rx}}} {\Delta {v_f}{\tau_f}} } {\text{d}}s = \frac{{4m{\sigma_s}{{\bar h}_r}R\theta }}{\sqrt 3 }\bigg\{ \Delta {{\bar v}_t}{{\left[ {1 + {{\left( {{{{{\bar v}_{zII}}} \mathord{\left/ {\vphantom {{{{\bar v}_{zII}}} {\Delta {{\bar v}_t}}}} \right.} {\Delta {{\bar v}_t}}}} \right)}^2}} \right]}^{ - 1/2}} \\&+ {{\bar v}_{zII}}{{\left[ {1 + {{\left( {{{\Delta {{\bar v}_t}} \mathord{\left/ {\vphantom {{\Delta {{\bar v}_t}} {{{\bar v}_{zII}}}}} \right.} {{{\bar v}_{zII}}}}} \right)}^2}} \right]}^{ - 1/2}} \bigg\} \\ \end{aligned}$$
(30)

4.4 Shear power

On the basis of the mean value theorem, the velocity field in the transverse region of the entrance becomes the following:

Zone I:

$${\bar v_{yI}}{ = }{\bar v_{zI}} = 0$$
(31)

Zone II:

$$\begin{aligned} {{\bar v}_{yII}} &= - \frac{{3{v_0}{\text{tan}}\theta }}{{2\left( {2 + 3\pi } \right){h_0}}}\frac{{\int_{{W_0} - 2{h_0}}^{W_0} {\left[ {\pi \left( {y - {W_0} + 2{h_0}} \right) + \frac{4}{3}{h_0}\cos \left( {\frac{{3\pi \left( {y - {W_0}} \right)}}{{4{h_0}}}} \right)} \right]} {\text{d}}y}}{{2{h_0}}} \\&= - \frac{{{\text{tan}}\theta {v_0}\left( {9{\pi^2} - 8} \right)}}{{6\pi \left( {2 + 3\pi } \right)}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\bar v}_{zII}} = \frac{{3\pi {\text{tan}}\theta {v_0}z}}{{2\left( {2 + 3\pi } \right){h_0}}}\frac{{\int_{{W_0} - 2{h_0}}^{W_0} {\left[ {1 - sin\left( {\frac{{3\pi \left( {y - {W_0}} \right)}}{{4{h_0}}}} \right)} \right]} {\text{d}}y}}{{2{h_0}}} \hfill \\&= \frac{{{\text{tan}}\theta {v_0}z}}{{2{h_0}}} \hfill \\ \end{aligned}$$
(32)

The shear power can then be expressed as

$$\begin{aligned} {{\dot W}_s} &= 4k\int_{{W_0} - 2{h_0}}^{W_0} {\int_0^{h_0} {\sqrt {{{({{\bar v}_{yII}})}^2} + {{({{\bar v}_{zII}})}^2}} } } {\text{d}}z{\text{d}}y \\&= \frac{{4k{\text{tan}}\theta {v_0}}}{{2{h_0}}}\int_{{W_0} - 2{h_0}}^{W_0} {\int_0^{h_0} {\sqrt {{z^2} + {{\left[ {\frac{{9{\pi^2} - 8}}{{3\pi \left( {2 + 3\pi } \right)}}{h_0}} \right]}^2}} } } {\text{d}}z{\text{d}}y \\& = \frac{{2{\sigma_s}{\text{tan}}\theta {v_0}h_0^2}}{\sqrt 3 }\left[ \sqrt {{1 + }{{\left[ {\frac{{9{\pi^2} - 8}}{{3\pi \left( {2 + 3\pi } \right)}}} \right]}^2}} { + }{{\left[ {\frac{{9{\pi^2} - 8}}{{3\pi \left( {2 + 3\pi } \right)}}} \right]}^2}\right.\\&\qquad\left.\ln \frac{{{1 + }\sqrt {{1 + }{{\left[ {{{(9{\pi^2} - 8)} / {3\pi \left( {2 + 3\pi } \right)}}} \right]}^2}} }}{{{{(9{\pi^2} - 8)} / {3\pi \left( {2 + 3\pi } \right)}}}} \right] \\ \end{aligned}$$
(33)

4.5 Total power and its optimization

Substituting Eqs. (23), (30), and (33) into \({J^*}{ = }{\dot W_i}{ + }{\dot W_f} + {\dot W_s}\) yields the analytical solution of the total power functional

$$\begin{aligned}{J^*} =& \frac{1 + b}{{2 + b}}\frac{{3{\sigma_s}{v_R}{h_0}\cos \theta }}{{{{\left( {2 + 3\pi } \right)}^2}\left( {2{h_0} - \Delta W} \right)}}\bigg[ 16\pi \left( {2{h_0} - \Delta W} \right){h_0}\ln \left( {\frac{{2{h_0}}}{{2{h_0} - \Delta W}}} \right) \\&+ \frac{{4\left( {2{h_0} - \Delta W} \right)}}{3}\left( {4 + 6\pi + 9{\pi^2}} \right)\Delta W + \left( {8 + 15\pi } \right)\pi \Delta {W^2} \bigg]\\&+ \frac{{4m{\sigma_s}{{\bar h}_r}R\theta }}{\sqrt 3 }\left\{ {\Delta {{\bar v}_t}{{\left[ {1 + {{\left( {{{{{\bar v}_{zII}}} / {\Delta {{\bar v}_t}}}} \right)}^2}} \right]}^{ - 1/2}} + {{\bar v}_{zII}}{{\left[ {1 + {{\left( {{{\Delta {{\bar v}_t}} / {{{\bar v}_{zII}}}}} \right)}^2}} \right]}^{ - 1/2}}} \right\}\\&+ \frac{{2{\sigma_s}{\text{tan}}\theta {v_0}h_0^2}}{\sqrt 3 }\left[ {\sqrt {{1 + }{{\left[ {\frac{{9{\pi^2} - 8}}{{3\pi \left( {2 + 3\pi } \right)}}} \right]}^2}} { + }{{\left[ {\frac{{9{\pi^2} - 8}}{{3\pi \left( {2 + 3\pi } \right)}}} \right]}^2}\ln \frac{{{1 + }\sqrt {{1 + }{{\left[ {{{(9{\pi^2} - 8)} / {3\pi \left( {2 + 3\pi } \right)}}} \right]}^2}} }}{{{{(9{\pi^2} - 8)} / {3\pi \left( {2 + 3\pi } \right)}}}}} \right]\end{aligned}$$
(34)

\({J^*}\) is only relevant to the yield criterion parameter \(b\) when the deformation resistance \({\sigma_s}\), reduction \(\Delta W\), radius of edge roll \(R\), peripheral velocities \({v_R}\), initial thickness of slabs \(2{h_0}\), and friction factor of edge roll-slab arc m are given. Therefore, the value of \(b\) can be repeatedly optimized between 0 and 1 according to the measured vertical rolling force data to improve the accuracy of Eq. (34). Then, the corresponding values of rolling torque M, rolling force \(\bar P\), and stress state coefficient \({n_\sigma }\) can be achieved separately as follows [18]:

$$M{ = }\frac{{J^* }}{2\omega },\bar P{ = }\frac{M}{\chi l},{n_\sigma }{ = }\frac{\bar P}{{\sigma_s}}$$
(35)

The arm coefficient \(\chi\) = 0.3–0.6 was researched in the hot-rolling process [19], and \(\chi { = }0.5\) is selected in this paper under the relevant equipment and process parameters.

5 Results

5.1 Dog-bone shape

To verify the accuracy of the dog-bone-shape model proposed in this paper, the ratio of dog-bone peak height to width, \({{h_p} \mathord{\left/ {\vphantom {{h_p} {W_0}}} \right. \kern-\nulldelimiterspace} {W_0}}\), was calculated by Eq. (4) under different engineering strains \({{\Delta W} \mathord{\left/ {\vphantom {{\Delta W} {W_0}}} \right. \kern-\nulldelimiterspace} {W_0}}\), initial thicknesses \({h_0}\), and vertical-roll radii \(R\). In addition, a comparison between the optimized sine-function-model results and those of other models is shown in Figs. 5 and 6. The comparison results demonstrate that the deviation between Eq. (4) and Ginzburg’s model is within 5.7% and that between Eq. (4) and Xiong’s model is within 8%. As can be seen from Fig. 5, the deflections between the present model and the other two models will increase with increasing reduction \(\Delta W\). When the value of \({{\Delta W} \mathord{\left/ {\vphantom {{\Delta W} {W_0}}} \right. \kern-\nulldelimiterspace} {W_0}}\) is less than 0.015, the comparative deflections are reduced to 1.5% and 5%. Because the present model assumed that the edge rolling process is a plane-deformation process, it is reasonable that the value of \({{h_p} \mathord{\left/ {\vphantom {{h_p} {W_0}}} \right. \kern-\nulldelimiterspace} {W_0}}\) is higher than those of both Xiong’s and Ginzburg’s models.

Fig. 5
figure 5

Influence of \({{\Delta W} \mathord{\left/ {\vphantom {{\Delta W} {W_0}}} \right. \kern-\nulldelimiterspace} {W_0}}\) on \({{h_p} \mathord{\left/ {\vphantom {{h_p} {W_0}}} \right. \kern-\nulldelimiterspace} {W_0}}\)

Full size image
Fig. 6
figure 6

Influence of \({{h_0} \mathord{\left/ {\vphantom {{h_0} {W_0}}} \right. \kern-\nulldelimiterspace} {W_0}}\) on \({{h_p} \mathord{\left/ {\vphantom {{h_p} {W_0}}} \right. \kern-\nulldelimiterspace} {W_0}}\)

Full size image

5.2 Edge rolling force

To validate the vertical rolling force model proposed in this paper, the authors collected a large amount of actual measurement data in the hot rolling production line of a Chinese steel company. Its roughing mill group consists of two vertical roll stands and two horizontal rolling stands, and Fig. 7 shows its schematic diagram and main electrical characteristics.

Fig. 7
figure 7

Schematic diagram and main characteristics of the roughing mill group

Full size image

Taking the material of Q235 steel product for instance, the cast slab with dimension of \(180 \times 480 \times 7000\;\left( {{\text{m}}{{\text{m}}^3}} \right)\) is reduced from 480 to 455 mm by vertical roll stands E1 and E2 in the roughing mills. The radius of vertical roll, peripheral velocity \({v_R}\), temperature \(t\), and true strain \(\varepsilon = \ln \left( {{W_0}/{W_E}} \right)\) for vertical stands are shown in Table 1, and the deformation resistance of the slabs is also included. Then the rolling process parameters in Table 1 are substituted into Eqs. (33) and (34) to calculate the vertical-rolling force and compare with the rolling force values monitored by two force transducers located over the bearing blocks of the vertical roll. By repeatedly optimizing the value of b, the error between the calculated force and actual measured data is within 5% when b = 0.613, as shown in Table 1.

Table 1 Comparison of vertical rolling force calculated by present model with measured one
Full size table

The model of deformation resistance for the Q235 steel used in the calculation is determined by Wang et al. [20], which can be expressed mathematically as

$${\sigma_s} = {\sigma_0}{e^{\left( {{a_1}T - {a_2}} \right)}}{\left( {\frac{\dot \varepsilon }{{10}}} \right)^{\left( {{a_3}T - {a_4}} \right)}}\left[ {{a_6}{{\left( {\frac{\varepsilon }{0.4}} \right)}^{a_5}} - \left( {{a_6} - 1} \right)\frac{\varepsilon }{0.4}} \right]$$
(36)

where \({\sigma_0}\) = 150 MPa, \({a_1}\) = −2.8685, \({a_2}\) = 3.6573, \({a_3}\) = 0.2121, \({a_4}\) = −0.1531, \({a_5}\) = 0.3912, \({a_6}\) = 1.4403, \(T{ = }\left( {t + 273} \right)/1000\).

In addition, the authors also used the TSS (b = 1) and the Tresca yield criteria (b = 0) for calculating the vertical-rolling force with a maximum error of 12% and 15%, as shown in Fig. 8. This indicates that the application of the UY criterion can effectively improve the accuracy of the vertical rolling-force calculation by the energy method.

Fig. 8
figure 8

Comparison between calculated rolling force under different b values and actual measured data

Full size image

6 Discussion

Based on the dog-bone-shape model, Eq. (4), and the vertical rolling-force model, Eqs. (33) and (34), proposed in the present paper, the influence of different rolling process parameters on dog-bone peak height \({h_p}\) and vertical rolling force is studied, and the results are shown in Figs. 5 and 6 and in Figs. 9 and 10.

Fig. 9
figure 9

Influence of \(\Delta W/{W_0}\) and \({h_0}/{W_0}\) on stress state coefficient \({n_\sigma }\)

Full size image
Fig. 10
figure 10

Influence of \(\Delta W/{W_0}\) and friction factor m on stress state coefficient \({n_\sigma }\)

Full size image

Figure 5 shows the significant increase in dog-bone peak height during the vertical rolling process with increasing engineering strain \({{\Delta W} \mathord{\left/ {\vphantom {{\Delta W} {W_0}}} \right. \kern-\nulldelimiterspace} {W_0}}\). This is caused by the length of the contact arc and the volume of the deformed metal, increasing while \(\Delta W\) increases. Since the plastic deformation is concentrated on the edge of the slab, \({h_p}\) obviously increases. In Fig. 6, the dog-bone peak height \({h_p}\) shows a linear growth trend with the increase of the slab’s initial thickness \({h_0}\), which is consistent with Xiong’s and Ginzburg’s models. This is because, when only \({h_0}\) increases, the contact-arc length between the slab and vertical roll remains unchanged, but the contact surface of the rolling slab becomes larger, which increases the volume of metal involved in plastic deformation, resulting in an increase in the value of \({h_p}\). Furthermore, although \({h_p}\) increases with \({h_0}\), the increase in \({h_p}\) is much smaller than that in \({h_0}\), which is why the curves in Fig. 6 are linear.

The vertical rolling force is another key parameter studied in the present paper, and according to the calculation results shown in Fig. 8, it can be seen that the variation of the yield criterion parameter b has a drastic positive effect on the calculated value of the vertical rolling force. This is because the inter-deformation power accounts for a large proportion of the total power in the vertical rolling process. After optimizing the vertical rolling force model by adjusting the value of the yield criterion parameter b, the impact of slab thickness \({h_0}\) and reduction \(\Delta W\) on the vertical rolling force is studied, and the results are shown in Fig. 9. Figure 9 shows that the stress-state coefficient \({n_\sigma }\) increases significantly with increasing \({h_0}/{W_0}\) and engineering strain \(\Delta W/{W_0}\), and the increasing trend of \({n_\sigma }\) is from sharp to gentle as \({h_0}/{W_0}\) and \(\Delta W/{W_0}\) increase. In addition, it is evident from Fig. 9 that the influence of engineering strain on the stress state coefficient is much greater than that of the initial thickness, and it is the main factor affecting the change of rolling force.

Figure 10 shows the influence law of friction coefficient m and \(\Delta W/{W_0}\) on the influence coefficient of the stress state. When the engineering strain is small, the friction coefficient has little influence on the rolling force, but as the engineering strain becomes larger, the friction coefficient exhibits a rapid increase in the influence of the rolling force.

7 Conclusions

  1. 1.

    The UY criterion is first proposed establishing the vertical rolling force model, and the yield criterion parameter b is converted into an optimal parameter of the vertical rolling force. Then, the value of b is repeatedly optimized, and it is determined that the mechanical model in this paper achieves the highest accuracy when b = 0.613, the error between the optimized model calculation results and the field measured data is within 5%.

  2. 2.

    The vertical rolling forces calculated by UY, TSS, and Tresca yield criteria are compared with actual measured data. It is noted that the prediction accuracy of the rolling force is effectively improved by optimizing the yield parameter b. This proves that it is feasible and effective to use the UY criterion to optimize the solution accuracy of mechanical parameters.

  3. 3.

    The sine-function dog-bone-shape model is optimized by using the slip line field to determine the maximum depth of the dog bone area, which ensures the prediction accuracy and simplifies the calculation steps, which can improve the prediction efficiency of the slab shape after vertical rolling.

  4. 4.

    Engineering strain is the primary factor that affects the height of the bone peak of the dog bone shape. The increase of the initial thickness of the slab also increases the height of the bone peak, but it is far from the obvious influence of the engineering strain on the height of the bone peak. In addition, the increases of engineering strain, initial slab thickness, and friction coefficient will cause different degrees of increase in the rolling force. The co-increasing of engineering strain and friction coefficient will make the rolling force present the most obvious increasing trend.