Mathematical model for vertical rolling deformation based on energy method

Abstract

An approach to analyzing three-dimensional vertical rolling is presented on the basis of energy method. The double parabola function model is applied to describe dog bone shape in the deformed region between the vertical rolls. The DSF (dual stream function) method is utilized to obtain three-dimensional velocity and strain rate fields. The values of dog bone shape dimensions and roll force are obtained when the total power functional achieves minimum, which is received according to double parabola model, velocity field, and the first variational principle. The validity of the proposed approach is discussed by contradistinguishing the present predictions with other models’ results and measured data in a hot strip plant in miscellaneous rolling conditions. Moreover, the impacts of different rolling conditions on the dog bone shape and stress state coefficient are researched, respectively.

1 Introduction

Due to the needs for energy and resource conservation, traditional slabs are now replaced by continuous casting slabs. The number of mold sizes needs to be restricted for the purpose of efficient operation of the continuous casting equipment, and then width control is mostly carried out by vertical rolling. Plastic deformation is principally restricted in a small edge zone, so the dog bone shape is generated [1] after vertical rolling. To forecast the dimension of dog bone shape and vertical roll force requirement would help automate the process [2].

The earlier experience formulas to express the characteristic parameters of dog bone were researched by Shibahara et al. [3], Okado et al. [4], and Tazoe et al. [5] using physical experiments of lead. Ginzburg et al. [6] conducted experiments and established the dog bone height model by modifying Tazoe’s model. The model of dog bone characteristic parameters was built by Xiong et al. [7, 8] on the basis of physical experiments in a laboratorial rolling mill. However, the shape at the exit is only expressed after vertical rolling in these formulas, and the theoretical studies are relatively few. Yun et al. [9] proposed a mathematical model of the dog bone which contains exponential function, power function, and some unknown parameters. Unfortunately, the parameters of dog bone shape and rolling force were gained by matching FEM simulation’s data. The dog bone shape of double parabola function model and two-dimensional velocity fields on the basis of the plane strain deformation were established in our previous study [1]. But, the values of dog bone are larger than others’ researches on account of ignoring the variation of velocity in rolling direction.

The axial spread during ring rolling of plain rings was researched by Lugora et al. [10] utilizing DSF based on Hill’s [11] general method of analysis. The metal deformation including extrusion, forging, piercing, and rolling were researched by Nagpal [12] using DSF method. A mathematical model using DSF method was proposed by Hwang et al. [13] to predict the roll torque and initial velocity of the product during planetenshra¨gwalzwerk rolling processes. Metal flow in upsetting of polygonal blocks which expressed as exponential function and kinematically admissible velocity field was derived by Aksakal et al. [14]. Sezek et al. [15] introduced DSF to analyze three-dimensional process of cold rolling. However, the dual stream functions proposed by above researchers are hardly applied to solve vertical rolling process.

A new three-dimensional admissible velocity field is built with DSF method according to the double parabola model for vertical rolling. The calculated shape and force parameters are verified, and the change mechanism of stress state coefficient in various conditions is discussed.

2 Double parabola function dog bone shape model

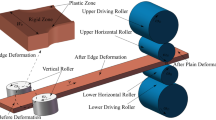
As demonstrated in Fig. 1, the dog bone shape of double parabola function model was established in our previous study [1]. The mathematical expressions of half thickness h(x,z) in three zones are as follows:

Fig. 1

Double parabola dog bone in vertical rolling

Zone I: (0 < z < W_E − 3A); half thickness h_I = h_I(x, z) is

$$ {h}_I={h}_0 $$

(1)

Zone II: (W_E − 3A < z < W_x − 2A_x); half thickness h_II = h_II(x, z) is

$$ {h}_{\mathrm{II}}={h}_0+\frac{\beta {h}_0\varDelta {W}_x}{A_x^3}{\left(z-{W}_x+3{A}_x\right)}^2 $$

(2)

Zone III: (W_x − 2A_x < z < W_x); half thickness h_III = h_III(x, z) is

$$ {h}_{\mathrm{III}}={h}_0+\frac{2\beta {h}_0\varDelta {W}_x\kern0.1em }{A_x}-\frac{\beta {h}_0\varDelta {W}_x}{A_x^3}{\left(z-{W}_x+{A}_x\right)}^2 $$

(3)

where W_x is half of the width, ${W}_x=R+{W}_E-\sqrt{R^2-{\left(l-x\right)}^2}$; A_x is the width parameter, A_x = (W_x − W_E + 3A)/3. A and β are undetermined parameters, which can be got by energy method in various production conditions.

3 Three-dimensional velocity and strain rate fields

Plane strain was assumed in our previous study [1], and the value of β was obtained based on this assumption and incompressibility condition. Due to this assumption that ignored the variation of velocity in rolling direction, the vertical rolling was treated as two-dimensional deformation, and metal flow in rolling direction was neglected; in other words, the pressed metal in the direction of width were all translated into the metal raised in the direction of thickness. And then, the shape of dog bone was larger than that in actual conditions. The values of A and β are simultaneously obtained using DSF and energy methods in this study.

The energy method is an analysis approach to predicting plate dimensions and load requirements in plastic deformation considering conditions which have to be met by the velocity field. Two stream functions ϕ and ψ can denote the velocity components for an incompressible body on the basis of DSF method [16]. The velocity field in three dimension is

$$ {\displaystyle \begin{array}{c}{v}_x=\frac{\partial \phi }{\partial y}\frac{\partial \psi }{\partial z}-\frac{\partial \phi }{\partial z}\frac{\partial \psi }{\partial y}\\ {}{v}_y=\frac{\partial \phi }{\partial z}\frac{\partial \psi }{\partial x}-\frac{\partial \phi }{\partial x}\frac{\partial \psi }{\partial z}\\ {}{v}_z=\frac{\partial \phi }{\partial x}\frac{\partial \psi }{\partial y}-\frac{\partial \phi }{\partial y}\frac{\partial \psi }{\partial x}\end{array}} $$

(4)

where the stream surfaces of ϕ and ψ are given, while ϕ=constant and ψ=constant, and the intersection of ϕ and ψ is streamline.

Zone I is rigid zone; no metal flow occurs in this zone. Metal flow in the x–z plane of zones II and III is related to the (x, z) coordinate location of metal and presented by metal flow stream function ϕ

$$ \phi =-\frac{U\left(z-{W}_E+3A\right)}{3{A}_x} $$

(5)

Metal flow in the x–y plane of zone II is related to the (x, y) coordinate location of metal and presented by metal flow stream function ψ_II:

$$ {\psi}_{\mathrm{II}}=\frac{y}{h_{\mathrm{II}}} $$

(6)

Similarity, metal flow stream function ψ_III of x–y plane in zone III is

$$ {\psi}_{\mathrm{III}}=\frac{y}{h_{\mathrm{III}}} $$

(7)

Placing Eqs. (5) and (6) into Eq. (4) receives the velocity field of zone II as follows:

$$ {v}_{x\mathrm{II}}=\frac{U}{3{A}_x{h}_{\mathrm{II}}}{v}_{y\mathrm{II}}=-\frac{Uy}{3{A}_x}\frac{\partial }{\partial x}\left(\frac{1}{h_{\mathrm{II}}}\right)+\frac{U\left(z-{W}_E+3A\right)y}{3}\frac{\partial }{\partial x}\left(\frac{1}{A_x}\right)\frac{\partial }{\partial z}\left(\frac{1}{h_{\mathrm{II}}}\right){v}_{z\mathrm{II}}=-\frac{U\left(z-{W}_E+3A\right)}{3{h}_{\mathrm{II}}}\frac{\partial }{\partial x}\left(\frac{1}{A_x}\right) $$

(8)

The strain rate field of zone II is

$$ {\displaystyle \begin{array}{c}{\overset{.}{\varepsilon}}_{x\mathrm{II}}=\frac{\partial {v}_{x\mathrm{II}}}{\partial x}=-\frac{U}{3{A}_x{h}_{\mathrm{II}}^2}\frac{\partial {h}_{\mathrm{II}}}{\partial x}-\frac{U{A}_x^{\hbox{'}}}{3{A}_x^2{h}_{\mathrm{II}}}\\ {}{\overset{.}{\varepsilon}}_{y\mathrm{II}}=\frac{\partial {v}_{y\mathrm{II}}}{\partial y}=\frac{U}{3{A}_x{h}_{\mathrm{II}}^2}\frac{\partial {h}_{\mathrm{II}}}{\partial x}+\frac{U\left(z-{W}_E+3A\right){A}_x^{\hbox{'}}}{3{A}_x^2{h}_{\mathrm{II}}^2}\frac{\partial {h}_{\mathrm{II}}}{\partial z}\\ {}{\overset{.}{\varepsilon}}_{z\mathrm{II}}=\frac{\partial {v}_{z\mathrm{II}}}{\partial z}=\frac{U{A}_x^{\hbox{'}}}{3{A}_x^2{h}_{\mathrm{II}}}-\kern0.3em \frac{U\left(z-{W}_E+3A\right){A}_x^{\hbox{'}}}{3{A}_x^2{h}_{\mathrm{II}}^2}\frac{\partial {h}_{\mathrm{II}}}{\partial z}\\ {}{\overset{.}{\varepsilon}}_{xy\mathrm{II}}=\frac{1}{2}\left(\frac{\partial {v}_{x\mathrm{II}}}{\partial y}+\frac{\partial {v}_{y\mathrm{II}}}{\partial x}\right)=\frac{Uy}{6{A}_x^2{h}_{\mathrm{II}}^3}\left\{{A}_x{h}_{\mathrm{II}}\frac{\partial^2{h}_{\mathrm{II}}}{\partial {x}^2}-{A}_x^{\hbox{'}}{h}_{\mathrm{II}}\frac{\partial {h}_{\mathrm{II}}}{\partial x}-2{A}_x{\left(\frac{\partial {h}_{\mathrm{II}}}{\partial x}\right)}^2\right.+\\ {}\left.\left(z-{W}_{\mathrm{E}}+3A\right)\left[{h}_{\mathrm{II}}\left({A}_x^{\hbox{'}}\frac{\partial^2{h}_{\mathrm{II}}}{\partial z\partial x}+{A}_x^{{\prime\prime}}\frac{\partial {h}_{\mathrm{II}}}{\partial z}\right)-2{A}_x^{\hbox{'}}\left(\frac{A_x^{\hbox{'}}{h}_{\mathrm{II}}}{A_x}+\frac{\partial {h}_{\mathrm{II}}}{\partial x}\right)\frac{\partial {h}_{\mathrm{II}}}{\partial z}\right]\right\}\\ {}{\overset{.}{\varepsilon}}_{xz\mathrm{II}}=\frac{1}{2}\left(\frac{\partial {v}_{x\mathrm{II}}}{\partial z}+\frac{\partial {v}_{z\mathrm{II}}}{\partial x}\right)=\frac{U}{6{A}_x{h}_{\mathrm{II}}^2}\left\{-\frac{\partial {h}_{\mathrm{II}}}{\partial z}+\left(z-{W}_{\mathrm{E}}+3A\right)\left[\frac{A_x^{{\prime\prime} }{h}_{\mathrm{II}}}{A_x}-\frac{A_x^{\hbox{'}}}{A_x^2}\left(2{A}_x^{\hbox{'}}{h}_{\mathrm{II}}+{A}_x\frac{\partial {h}_{\mathrm{II}}}{\partial x}\right)\right]\right\}\\ {}{\overset{.}{\varepsilon}}_{yz\mathrm{II}}=\frac{1}{2}\left(\frac{\partial {v}_y\mathrm{II}}{\partial z}+\frac{\partial {v}_{z\mathrm{II}}}{\partial y}\right)\\ {}=\frac{Uy}{6{A}_x{h}_{\mathrm{II}}^3}\left\langle {h}_{\mathrm{II}}\frac{\partial^2{h}_{\mathrm{II}}}{\partial x\partial z}-2\frac{\partial {h}_{\mathrm{II}}}{\partial x}\frac{\partial {h}_{\mathrm{II}}}{\partial z}+\frac{A_x^{\hbox{'}}}{A_x}\left\{{h}_{\mathrm{II}}\frac{\partial {h}_{\mathrm{II}}}{\partial z}+\left(z-{W}_E+3A\right)\left[{h}_{\mathrm{II}}\frac{\partial^2{h}_{\mathrm{II}}}{\partial {z}^2}-2{\left(\frac{\partial {h}_{\mathrm{II}}}{\partial z}\right)}^2\right]\right\}\right\rangle \end{array}} $$

(9)

where ${A}_x^{\hbox{'}}=d{W}_x/ dx={W}_x^{\hbox{'}}/3$ and ${A}_x^{{\prime\prime} }=d{A}_x^{\hbox{'}}/ dx$. Placing Eqs. (5) and (7) into Eq. (4), the velocity field is given directly in the plastic zone III:

$$ {\displaystyle \begin{array}{c}{v}_{x\mathrm{III}}=\frac{U}{3{A}_x{h}_{\mathrm{III}}}\\ {}{v}_{y\mathrm{III}}=-\frac{Uy}{3{A}_x}\frac{\partial }{\partial x}\left(\frac{1}{h_{\mathrm{III}}}\right)+\frac{U\left(z-{W}_E+3A\right)y}{3}\frac{\partial }{\partial x}\left(\frac{1}{A_x}\right)\frac{\partial }{\partial z}\left(\frac{1}{h_{\mathrm{III}}}\right)\\ {}{v}_{z\mathrm{III}}=-\frac{U\left(z-{W}_E+3A\right)}{3{h}_{\mathrm{III}}}\frac{\partial }{\partial x}\left(\frac{1}{A_x}\right)\end{array}} $$

(10)

The strain rate field of zone III is

$$ {\displaystyle \begin{array}{c}{\dot{\varepsilon}}_{x\mathrm{III}}=\frac{\partial {v}_{x\mathrm{III}}}{\partial x}=-\frac{U}{3{A}_x{h}_{\mathrm{III}}^2}\frac{\partial {h}_{\mathrm{III}}}{\partial x}-\frac{U{A}_x^{\hbox{'}}}{3{A}_x^2{h}_{\mathrm{III}}}\\ {}{\overset{.}{\varepsilon}}_{y\mathrm{III}}=\frac{\partial {v}_{y\mathrm{III}}}{\partial y}=\frac{U}{3{A}_x{h}_{\mathrm{III}}^2}\frac{\partial {h}_{\mathrm{III}}}{\partial x}+\frac{U\left(z-{W}_E+3A\right){A}_x^{\hbox{'}}}{3{A}_x^2{h}_{\mathrm{III}}^2}\frac{\partial {h}_{\mathrm{III}}}{\partial z}\\ {}{\overset{.}{\varepsilon}}_{z\mathrm{III}}=\frac{\partial {v}_{z\mathrm{III}}}{\partial z}=\frac{U{A}_x^{\hbox{'}}}{3{A}_x^2{h}_{\mathrm{III}}}-\kern0.3em \frac{U\left(z-{W}_E+3A\right){A}_x^{\hbox{'}}}{3{A}_x^2{h}_{\mathrm{III}}^2}\frac{\partial {h}_{\mathrm{III}}}{\partial z}\\ {}{\overset{.}{\varepsilon}}_{xy\mathrm{III}}=\frac{1}{2}\left(\frac{\partial {v}_{x\mathrm{III}}}{\partial y}+\frac{\partial {v}_{y\mathrm{III}}}{\partial x}\right)=\frac{Uy}{6{A}_x^2{h}_{\mathrm{III}}^3}\left\{{A}_x{h}_{\mathrm{III}}\frac{\partial^2{h}_{\mathrm{III}}}{\partial {x}^2}-{A}_x^{\hbox{'}}{h}_{\mathrm{III}}\frac{\partial {h}_{\mathrm{III}}}{\partial x}-2{A}_x{\left(\frac{\partial {h}_{\mathrm{III}}}{\partial x}\right)}^2\right.+\\ {}\left.\left(z-{W}_E+3A\right)\left[{h}_{\mathrm{III}}\left({A}_x^{\hbox{'}}\frac{\partial^2{h}_{\mathrm{III}}}{\partial z\partial x}+{A}_x^{{\prime\prime}}\frac{\partial {h}_{\mathrm{III}}}{\partial z}\right)-2{A}_x^{\hbox{'}}\left(\frac{A_x^{\hbox{'}}{h}_{\mathrm{III}}}{A_x}+\frac{\partial {h}_{\mathrm{III}}}{\partial x}\right)\frac{\partial {h}_{\mathrm{III}}}{\partial z}\right]\right\}\\ {}{\overset{.}{\varepsilon}}_{xz\mathrm{III}}=\frac{1}{2}\left(\frac{\partial {v}_{x\mathrm{III}}}{\partial z}+\frac{\partial {v}_{z\mathrm{III}}}{\partial x}\right)=\frac{U}{6{A}_x{h}_{\mathrm{III}}^2}\left\{-\frac{\partial {h}_{\mathrm{III}}}{\partial z}+\left(z-{W}_E+3A\right)\left[\frac{A^{{\prime\prime} }{h}_{\mathrm{III}}}{A_x}-\frac{A_x^{\hbox{'}}}{A_x^2}\left(2{A}_x^{\hbox{'}}{h}_{\mathrm{III}}+{A}_x\frac{\partial {h}_{\mathrm{III}}}{\partial x}\right)\right]\right\}\\ {}{\overset{.}{\varepsilon}}_{yz\mathrm{III}}=\frac{1}{2}\left(\frac{\partial {v}_{y\mathrm{III}}}{\partial z}+\frac{\partial {v}_{z\mathrm{III}}}{\partial y}\right)\\ {}\kern2.2em =\frac{Uy}{6{A}_x{h}_{\mathrm{III}}^3}\left\langle {h}_{\mathrm{III}}\frac{\partial^2{h}_{\mathrm{III}}}{\partial x\partial z}-2\frac{\partial {h}_{\mathrm{III}}}{\partial x}\frac{\partial {h}_{\mathrm{III}}}{\partial z}+\frac{A_x^{\hbox{'}}}{A_x}\left\{{h}_{\mathrm{III}}\frac{\partial {h}_{\mathrm{III}}}{\partial z}+\left(z-{W}_E+3A\right)\left[{h}_{\mathrm{III}}\frac{\partial^2{h}_{\mathrm{III}}}{\partial {z}^2}-2{\left(\frac{\partial {h}_{\mathrm{III}}}{\partial z}\right)}^2\right]\right\}\right\rangle \end{array}} $$

(11)

Based on Eqs. (8) and (10), ${\left.{v}_{y\mathrm{I}}\right|}_{\begin{array}{c}x=0\\ {}y=0\end{array}}={\left.{v}_{y\mathrm{I}\mathrm{I}}\right|}_{\begin{array}{c}x=0\\ {}y=0\end{array}}={\left.{v}_{y\mathrm{I}\mathrm{I}\mathrm{I}}\right|}_{\begin{array}{c}x=0\\ {}y=0\end{array}}=0$; ${\left.{v}_{y\mathrm{I}}\right|}_{\begin{array}{c}x=l\\ {}y=0\end{array}}={\left.{v}_{y\mathrm{I}\mathrm{I}}\right|}_{\begin{array}{c}x=l\\ {}y=0\end{array}}={\left.{v}_{y\mathrm{I}\mathrm{I}\mathrm{I}}\right|}_{\begin{array}{c}x=l\\ {}y=0\end{array}}=0$, ${\left.{v}_{y\mathrm{I}}\right|}_{\begin{array}{c}x=l\\ {}y=h\end{array}}={\left.{v}_{y\mathrm{I}}\right|}_{\begin{array}{c}x=l\\ {}y=h\end{array}}=$${\left.{v}_{y\mathrm{III}}\right|}_{\begin{array}{c}x=l\\ {}y=h\end{array}}=0$, ${\left.{v}_{y\mathrm{I}}\right|}_{z={W}_E-3A}={\left.{v}_{y\mathrm{I}\mathrm{I}}\right|}_{z={W}_E-3A}=0$;${\left.{v}_{z\mathrm{I}}\right|}_{z={W}_E-3A}={\left.{v}_{z\mathrm{I}\mathrm{I}}\right|}_{z={W}_E-3A}=0$; ${\left.{v}_{x\mathrm{II}}\right|}_{z={W}_x-2{A}_x}={\left.{v}_{x\mathrm{II}\mathrm{I}}\right|}_{z={W}_x-2{A}_x}$, ${\left.{v}_{y\mathrm{II}}\right|}_{z={W}_x-2{A}_x}={\left.{v}_{y\mathrm{II}\mathrm{I}}\right|}_{z={W}_x-2{A}_x}$, ${\left.{v}_{z\mathrm{II}}\right|}_{z={W}_x-2{A}_x}={\left.{v}_{z\mathrm{II}\mathrm{I}}\right|}_{z={W}_x-2{A}_x}$, ${\left.{v}_{z\mathrm{III}}/{v}_{x\mathrm{III}}\right|}_{z={W}_x}=3{A}_x^{\hbox{'}}={W}_x^{\hbox{'}}$. The boundary conditions are satisfied in Eqs. (8) and (10). Based on Eqs. (9) and (11), ${\dot{\varepsilon}}_{x\mathrm{II}}+{\dot{\varepsilon}}_{y\mathrm{II}}+{\dot{\varepsilon}}_{z\mathrm{II}}=0$ and ${\dot{\varepsilon}}_{x\mathrm{III}}+{\dot{\varepsilon}}_{y\mathrm{III}}+{\dot{\varepsilon}}_{z\mathrm{III}}=0$, so they are kinematically admissible velocity and strain rate fields [17].

4 Mathematical model establishment

The vertical rolls are assumed as rigid, and slab is supposed as a rigid plastic material. The internal plastic deformation ${\overset{.}{W}}_i$ based on Mises yield criterion in bite zone is

$$ {\overset{.}{W}}_i={\int}_V\overline{\sigma}\kern0.1em \overset{.}{\overline{\varepsilon}} dV=4{\int}_0^l{\int}_{W_x-3{A}_x}^{W_x-2{A}_x}{\int}_0^{h_{\mathrm{II}}}\kern0.1em {\sigma}_s\kern0.1em {\overset{.}{\overline{\varepsilon}}}_{\mathrm{II}} dydzdx+4{\int}_0^l{\int}_{W_x-2{A}_x}^{W_x}{\int}_0^{h_{\mathrm{II}}}{\sigma}_s\kern0.1em {\overset{.}{\overline{\varepsilon}}}_{\mathrm{II}\mathrm{I}} dydzdx $$

(12)

The effective strain rate ${\overset{.}{\overline{\varepsilon}}}_{\mathrm{II}}$ and ${\overset{.}{\overline{\varepsilon}}}_{\mathrm{III}}$ are

$$ {\overset{.}{\overline{\varepsilon}}}_{\mathrm{II}}=\sqrt{\frac{2}{3}}\sqrt{{\overset{.}{\varepsilon}}_{x\mathrm{II}}^2+{\overset{.}{\varepsilon}}_{y\mathrm{II}}^2+{\overset{.}{\varepsilon}}_{z\mathrm{II}}^2+2{\overset{.}{\varepsilon}}_{xy\mathrm{II}}^2+2{\overset{.}{\varepsilon}}_{xz\mathrm{II}}^2+2{\overset{.}{\varepsilon}}_{yz\mathrm{II}}^2} $$

(13)

$$ {\overset{.}{\overline{\varepsilon}}}_{\mathrm{III}}=\sqrt{\frac{2}{3}}\sqrt{{\overset{.}{\varepsilon}}_{x\mathrm{III}}^2+{\overset{.}{\varepsilon}}_{y\mathrm{III}}^2+{\overset{.}{\varepsilon}}_{z\mathrm{III}}^2+2{\overset{.}{\varepsilon}}_{xy\mathrm{III}}^2+2{\overset{.}{\varepsilon}}_{xz\mathrm{III}}^2+2{\overset{.}{\varepsilon}}_{yz\mathrm{III}}^2} $$

(14)

In Eqs. (8) and (10), the velocity discontinuity exists at entrance section. The shear power ${\overset{.}{W}}_s$ is

$$ {\overset{.}{W}}_s={\int}_Sk\mid \varDelta {v}_s\mid dS\kern0.3em =4k{\int}_{W_0-3{A}_0}^{W_0-2{A}_0}{\int}_0^{h_0}\sqrt{{\left({\left.{v}_{y\mathrm{II}}\right|}_{x=0}\right)}^2+{\left({\left.{v}_{z\mathrm{II}}\right|}_{x=0}\right)}^2} dydz+4k{\int}_{W_0-2{A}_0}^{W_0}{\int}_0^{h_0}\sqrt{{\left({\left.{v}_{y\mathrm{II}\mathrm{I}}\right|}_{x=0}\right)}^2+{\left({\left.{v}_{z\mathrm{II}\mathrm{I}}\right|}_{x=0}\right)}^2} dydz $$

(15)

The friction force produces on contact surface between slab and vertical roll, and the velocity discontinuity in tangential direction is

$$ \varDelta {v}_t={v}_R-{v}_{x\mathrm{III}}/\cos \alpha $$

(16)

The velocity discontinuity is

$$ \varDelta {v}_f=\sqrt{{\left({\left.{v}_{y\mathrm{III}}\right|}_{z={W}_x}\right)}^2+{\left({\left.\varDelta {v}_t\right|}_{z={W}_x}\right)}^2} $$

(17)

The velocity discontinuity Δv_f of Eq. (17) and friction stress ${\tau}_f= mk=m{\sigma}_s/\sqrt{3}$ are in the same direction invariably on contact surface. The friction power ${\dot{W}}_f$ [18] is

$$ {\dot{W}}_f=4{\int}_0^l{\int}_0^{h_{rx}}\mid {\tau}_f\Big\Vert \varDelta {v}_f\mid \cos \left(\varDelta {v}_f,{\tau}_f\right) ds=4{\int}_0^l{\int}_0^{h_{rx}}{\tau}_f\mid \varDelta {v}_f\mid ds=4 mk{\int}_0^l{\int}_0^{h_{rx}}\sqrt{{\left({\left.{v}_{y\mathrm{III}}\right|}_{z={W}_x}\right)}^2+{\left({\left.\varDelta {v}_t\right|}_{z={W}_x}\right)}^2}\kern0.1em \frac{dydx}{\cos \alpha}\kern0.30em $$

(18)

According to the first variational principle of rigid plastic, substituting Eqs. (12), (15), and (18) into ${J}^{\ast }={\dot{W}}_i+{\dot{W}}_s+{\dot{W}}_f\kern0.30em$ gets the solution of total power function

$$ {J}^{\ast }=4\sqrt{\frac{2}{3}}{\sigma}_s{\int}_0^l{\int}_{W_x-3{A}_x}^{W_x-2{A}_x}{\int}_0^{h_{\mathrm{II}}}\sqrt{{\overset{.}{\varepsilon}}_{x\mathrm{II}}^2+{\overset{.}{\varepsilon}}_{y\mathrm{II}}^2+{\overset{.}{\varepsilon}}_{z\mathrm{II}}^2+2{\overset{.}{\varepsilon}}_{xy\mathrm{II}}^2+2{\overset{.}{\varepsilon}}_{xz\mathrm{II}}^2+2{\overset{.}{\varepsilon}}_{yz\mathrm{II}}^2} dydz dx+4\sqrt{\frac{2}{3}}{\sigma}_s{\int}_0^l{\int}_{W_x-2{A}_x}^{W_x}{\int}_0^{h_{\mathrm{II}\mathrm{I}}}\sqrt{{\overset{.}{\varepsilon}}_{x\mathrm{II}\mathrm{I}}^2+{\overset{.}{\varepsilon}}_{y\mathrm{II}\mathrm{I}}^2+{\overset{.}{\varepsilon}}_{z\mathrm{II}\mathrm{I}}^2+2{\overset{.}{\varepsilon}}_{xy\mathrm{II}\mathrm{I}}^2+2{\overset{.}{\varepsilon}}_{xz\mathrm{II}\mathrm{I}}^2+2{\overset{.}{\varepsilon}}_{yz\mathrm{II}\mathrm{I}}^2} dydz dx+4k{\int}_{W_0-3{A}_0}^{W_0-2{A}_0}{\int}_0^{h_0}\sqrt{{\left({\left.{v}_{y\mathrm{II}}\right|}_{x=0}\right)}^2+{\left({\left.{v}_{z\mathrm{II}}\right|}_{x=0}\right)}^2} dydz+4k{\int}_{W_0-2{A}_0}^{W_0}{\int}_0^{h_0}\sqrt{{\left({\left.{v}_{y\mathrm{II}\mathrm{I}}\right|}_{x=0}\right)}^2+{\left({\left.{v}_{z\mathrm{II}\mathrm{I}}\right|}_{x=0}\right)}^2} dydz+4 mk{\int}_0^l{\int}_0^{h_{rx}}\sqrt{{\left({\left.{v}_{y\mathrm{II}\mathrm{I}}\right|}_{z={W}_x}\right)}^2+{\left({\left.\varDelta {v}_t\right|}_{z={W}_x}\right)}^2}\kern0.1em \frac{dydx}{\cos \alpha}\kern0.20em $$

(19)

The optimal values of A and β are acquired, while J^∗ attains the minimum value ${J}_{\mathrm{min}}^{\ast }$ [19, 20]. The calculation procedure is shown in Fig. 2. Substituting optimal values of A and β into Eqs. (1)–(3) and Eq. (19) attains the results of dog bone shape and total power’s minimum ${J}_{\mathrm{min}}^{\ast }$, respectively. Then, the corresponding values of force parameters of roll force F, roll torque M, and stress state coefficient n_σ can be achieved separately as [21]

$$ M=\frac{R{J}_{\mathrm{min}}^{\ast }}{2{\nu}_R},\kern0.5em F=\frac{M}{\chi l},\kern0.5em {n}_{\sigma }=\frac{F}{4 hlk} $$

(20)

Fig. 2

Flowchart of the calculation

5 Results and discussions

The ratio of peak height to width h_b/W₀ in dog bone shape is received under different engineering strain ΔW/W₀, initial thickness h₀, and roll radius R. The contrasts among present double parabola model’s results, the data collected from Xiong’s [7] and Ginzburg’s [6] models, and Ref. [1] model’s results are shown in Figs. 3–5. Comparing the calculated results, the deviation between present model and Xiong’s model is within 0.72%. The deflection between present model and Ginzburg’s model is less than 1.0%, and deviation between present model and Ref. [1]’s model is within 1.8%. Because the metal flow in rolling direction is considered in present model, the dog bone’s peak height is smaller than Ref [1]’s model.

Fig. 3

Influence of ΔW/W₀ on h_b/W₀

Fig. 4

Influence of h₀ on h_b/W₀

Fig. 5

Influence of R on h_b/W₀

Figure 3 reflects the dog bone’s peak height increases obviously when the engineering strain increases. This is because the area of contact arc increases, while ΔW increases. The flow resistance of deformed metal increases in rolling direction, and then the deformation goes to the center of slab width. In Fig. 4, the changes of h_b with diverse initial thickness h₀ are shown. The contact surface of roll slab and volume of deformed metal increase, while the initial thickness increases. So the value of h_b increases as h₀ increases. Figure 5 demonstrates the influence of roll radius R on the value of h_b. The peak height of dog bone decreases with the increasing of roll radius R.

The values of roll force F calculated by present double parabola model under different rolling conditions agree well with predictions from Yun’s model [9] and measured values, as found in Figs. 6 and 7. Compared with Yun’s predicted values, the double parabola model’s results are closer to the measured values, and the former deviation is within 7%, and the latter is within 6%. The validity and precision of the present model are proven.

Fig. 6

Roll force contrast between present and Yun’s models

Fig. 7

Roll force comparison between present double parabola model and measured value

Figure 8 shows the proportions of plastic deformation, friction, and shear powers in different engineering strain ΔW/W₀. The plastic deformation power is larger than the friction and shear powers, which also illustrates, in vertical rolling, that the contact area of roll slab is small. The friction power decreases and shear power increases slightly while the engineering strain increase, but the change of plastic deformation proportion is not obvious.

Fig. 8

Proportion of ${\dot{W}}_i$, ${\dot{W}}_f$, and ${\dot{W}}_s$ in ${J}_{min}^{\ast }$

The stress state coefficient n_σ reflects the effect of slab size, contact area of roll slab, friction, the shape of tool, etc. on roll force. The influences of engineering strain ΔW/W₀, friction factor m, vertical roll radius R, and slab thickness h₀ on stress state coefficient are shown in Figs. 9 and 10 based on Eq. (20). The stress state coefficient increases nonlinearly as the engineering strain, friction factor, or vertical roll radius increases, while the stress state coefficient increases linearly as slab thickness increases. The impacts of engineering strain and friction factor on stress state coefficient are more obvious than slab thickness and vertical roll radius. In addition, the smaller engineering strain, the larger influence of friction factor on stress state coefficient.

Fig. 9

Influence of engineering strain and friction factor on stress state coefficient

Fig. 10

Influence of vertical roll radius and slab thickness on stress state coefficient

6 Conclusions

A successful approach is proposed to investigate three-dimensional vertical rolling based on DSF and energy method. Three-dimensional velocity field is established on the basis of double parabola dog bone model and DSF method. Therefore, dog bone parameters and required roll force predictions, which are very important in actual production, are attained when total power reaches minimum. A comprehensive examination of this present method is performed by contrasting the present model’s values with data in previous researches and measured values. The peak height of dog bone shape gets large when initial thickness or engineering strain increases but decreases while roll radius increases. The stress state coefficient augments when engineering strain, slab thickness, vertical roll radius, or friction factor augments. And the influences of engineering strain and friction factor on stress state coefficient are more obvious.

Financial information

This study is financially supported by the National Natural Science Foundation of China (Nos. 51904206, 51975398, 51774084, 51634002, 51805359, 51504156), National Key R&D Program of China (Nos. 2018YFB1308700, 2017YFB0304100), Natural Science Foundation of Shanxi Province (No. 201801D221130), Shanxi Province Science and Technology Major Projects (No. 20181102015), Major Program of National Natural Science Foundation of China (No. U1710254), Taiyuan City Science and Technology Major Projects (No. 170203), Key Research and Development Program of Shanxi Province (No. 201703D111003), Outstanding Youth Fund of Jiangsu Province (No. BK20180095), the Fundamental Research Funds for the Central Universities (Nos. N160704004, N170708020), and Scientific and Technologial Innovation Programs of Higher Education Institutions in Shanxi (No. 2019 L0258).