1 Introduction

In roughing rolling stage, vertical rolling is usually arranged before plain rolling to control the width precision and restrain the non-rectangularization of slab. During rolling, the deformation (dog-bone deformation) only occurs at the slab edge, and the deformation law is very complex. Theoretical research on metal forming process has been proven to be of great significance in improving production yield and quality (Bari and Kumar 2023a). Therefore, in-depth research on vertical rolling process is necessary.

Scholars have conducted several experimental research on vertical rolling process. Okado et al. (1981) simulated vertical rolling by pure lead and firstly proposed the empirical formulas of four deformation parameters (peak height, peak position, edge thickness and deformation length) to describe the dog-bone shape. Shibahara et al. (1981) built a vertical rolling model through the regression analysis of measured value. Based on Shibahara’s results, Tazoe et al. (1984) obtained an empirical formula of peak height and pointed out that the dog-bone length and the peak position are directly proportion to width reduction. Later, the formula was modified by Ginzburg et al. (1991), and the result is consistent with the plastic mud model put forward by Huisman and Huètink (1985). Xiong et al. (1997) developed a vertical rolling experiment with the simulation ratio of 10. The fitted dog-bone formulas consider the width reduction, roller diameter, initial slab thickness and width. However, the results are greatly affected by experimental conditions.

With the widespread popularity of computer technology, the simulation of vertical rolling process is carried out by finite element software. Xiong et al. (2003) obtained the friction characteristics of 3D contact based on micro-compressible plastic theory and the simplified Euler formula. By using 3D elastic–viscoplastic FEM, Forouzan et al. (2009) studied the sizing press and vertical rolling under heavy width reduction. The influences of slab size and width reduction on edge deformation and the head and end quality of slab were studied. Ruan et al. (2014) used a 3D thermo-mechanical coupled rigid–plastic FEM to analyze the non-rectangular shape and the evolution rules of wide and heavy plate in hot rolling process.

Theoretical researches have been carried out later. Based on plane deformation assumption, Lundberg (1986; 2008) and Lundberg and Gustafsson (1993) established a triangular velocity field of vertical rolling process considering friction and smoothness condition, respectively. Then, the hodograph of plastic flow and the torque formulas were obtained. Zhang et al. (2018; 2020) drew the slip line field and hodograph of edge deformation zone under full adhesive contact, and the analytical solutions of mechanics parameters and dog-bone shape were deduced. Yun et al. (2012) assumed that the deformation was distributed in the entire width and then established a theoretical model with several power functions. Meanwhile, some deformation parameters and rolling force were fitted according to FEM result. But the slope growth of the high-power function is too fast, so the predicted deformation zone of the dog-bone is often too wide. Li et al. (2016) established an upper bound power functional for edge rolling by using complex mathematical functions. The edge rolling force and torque are calculated by minimizing the power functional. Cao et al. (2016) used sine function to describe edge deformation and established the energy model by stream function method. Simplifying the peak position and the dog-bone length as 1:3 as well as full sliding assumption of the contact interface, Liu et al. (2015; 2016) deduced the total power functional. However, the dog-bone shapes are more concentrate at the edge, which result in the higher dog-bone peak and the predicted rolling force. Later, Liu et al. (2020; 2022) built double stream function velocity fields to build the numerical and analytical model.

Through the analysis of the above studies, the research on vertical rolling force and edge deformation is still insufficient. The predicted force and shape are quite different and cannot be in good agreement with measurements (Yun et al. 2012; Liu et al. 2016). The difficulty of energy method in vertical rolling process is to choose suitable deformation curves and kinematically admissible velocity field. In this paper, cubic function is combined with gamma distribution function to form the edge deformation model. The velocity and strain rate fields are built based on stream function method. The plastic deformation power and inlet shear power are calculated based on Mises yield criterion and the velocity discontinuity. After fully considering the adhesion of the contact interface, the friction power is calculated by using inner product of collinear principle. The total power functional is derived based on the new method. Then, the calculated edge shape and rolling force are compared with other results, which verified the precision of the proposed method. Finally, the effects of slab and equipment parameters on mechanical properties and edge deformation are studied.

2 Mechanics Model of Vertical Rolling Process

2.1 Vertical–Horizontal Rolling Process

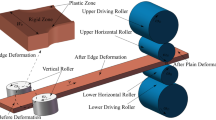
The basic process of continuous hot rolling is shown in Fig. 1. The vertical rollers are driven by motors with a constant speed \(\omega_{{\text{V}}}\).The steel slab moves forward and passes through the clearance between a pair of vertical rollers at the initial velocity \(v_{0}\). Under the extrusion of the vertical rollers, the slab width reduces from \(W_{0}\) to \(W_{1}\). Then the slab is rolled by a pair of horizontal rollers. The slab length increases with the decrease in thickness under the compression plastic deformation.

Fig. 1
figure 1

Continuous hot rolling process

Full size image

2.2 Edge Deformation Model

As shown in Fig. 2, the steel slab occurs non-uniform plastic deformation when rolled by vertical rollers. For the high ratio of width to thickness, the deformation is mainly restricted at the edge with obvious bulge in the thickness direction. Finally, the dog-bone deformation is formed, which is exhibited in Fig. 2.

Fig. 2
figure 2

Plastic deformation in vertical rolling process

Full size image

Before analyzing, the assumptions are given as follows:

(1) The microstructure of steel slab and vertical rollers is uniform and isotropic. (2) The vertical rollers are rigid bodies. (3) The elastic deformation of the steel slab is ignored. The tension and width lose are ignored. (4) The force and plastic deformation rules of the steel slab are symmetrical. So, a quarter of the deformation zone is analyzed.

As shown in Fig. 2a, the center of entrance cross section is selected as the coordinate origin to establish a three-dimensional coordinate system. \(H_{0}\) represents the initial thickness of steel slab. \(W_{0}\) and \(W_{1}\) represent the slab width before and after rolling, respectively. The unilateral reduction \(\Delta w = \frac{\Delta W}{2} = \frac{{W_{0} - W_{1} }}{2}\). R represents the vertical roller radius. The projected length of the roller–slab contact arc in rolling direction is \(l = R\sin \theta\). The bite angle is given by \(\theta = \cos^{ - 1} \left( {\frac{R - \Delta w}{R}} \right)\). Half of the width and half of the width reduction at any position are \(w_{x} = \frac{{W_{1} }}{2} + R - \sqrt {R^{2} - (l - x)^{2} }\) and \(\Delta w_{x} = \frac{{W_{0} }}{2} - w_{x}\). The contact angle \(\phi\) has the following relationship with \(x\) direction:

$$\phi = \sin^{ - 1} \left( {\frac{l - x}{R}} \right)$$

\({\text{d}}\phi = - \frac{{{\text{d}}x}}{R\cos \phi }\)

The first- and second-order derivative equations of \(w_{x}\) are:

$$w_{x}^{\prime } = - \frac{l - x}{{\sqrt {R^{2} - (l - x)^{2} } }} = - \tan \phi$$

\(w_{x}^{\prime \prime } = \frac{{R^{2} }}{{\left[ {R^{2} - \left( {l - x} \right)^{2} } \right]^{\frac{3}{2}} }}\)

Half of the thickness is denoted by \(h(x,z)\). On arbitrary cross section along rolling direction, the height and position of dog-bone peak are expressed by \(h_{bx}\) and \(l_{px}\), respectively. The height of dog-bone edge is expressed by \(h_{rx}\). The length of dog-bone zone (plastic deformation zone) is expressed by \(l_{bx}\), respectively.

In order to describe and analyze the edge deformation, it is essential to use appropriate functions to describe the edge shape of slab. In this paper, the dog-bone peak is used as the boundary, and the bite zone is divided into zone α and zone β.

Gamma distribution function in statistics is the product of power function and exponential function. It has both extreme value and the property of exponential function and can well describe the slow change of thickness between dog-bone peak and rigid zone. Thus, in zone α (\(0 < z < w_{x} - l_{px}\)), half of the slab thickness is expressed as:

$$h_{\alpha } = h_{0} + \frac{{ah_{{0}} \Delta w_{x} }}{{l_{px} }}\left( {\frac{{w_{x} - z}}{{l_{px} }}} \right)^{2} e^{{ - {2}\left( {\frac{{w_{x} - z}}{{l_{px} }}} \right)}}$$
(1)

The cubic curve function has a simple form and is easy to integrate. It has been applied to describe the edge deformation of vertical rolling process and has been proven to have high accuracy (Liu et al. 2022). In zone β (\(w_{x} - l_{px} < z < w_{x}\)), half of the slab thickness is expressed by cubic function:

$$h_{\beta } = h_{0} + \frac{{ah_{{0}} \Delta w_{x} }}{{e^{2} l_{px} }} - \frac{{bc_{m} h_{{0}} \Delta w_{x} }}{{l_{px} }}\left[ {{2}\left( {\frac{{w_{x} - z}}{{l_{px} }}} \right)^{3} - 3\left( {\frac{{w_{x} - z}}{{l_{px} }}} \right)^{2} + {1}} \right]$$
(2)

where a and b are the undetermined parameters, \(c_{m}\) is the coefficient related to friction factor m

In previous researches, the friction factor of roller–slab contact is generally between 0.2 and 0.8, and the calculated \({{\left( {h_{r} - h_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {h_{r} - h_{0} } \right)} {\left( {h_{b} - h_{0} } \right)}}} \right. \kern-0pt} {\left( {h_{b} - h_{0} } \right)}}\) is 0.3–0.75 (Okado et al. 1981; Xiong et al. 1997; Shibahara et al. 1981). According to the relationship between the friction factor and \({{\left( {h_{r} - h_{0} } \right)} \mathord{\left/ {\vphantom {{\left( {h_{r} - h_{0} } \right)} {\left( {h_{b} - h_{0} } \right)}}} \right. \kern-0pt} {\left( {h_{b} - h_{0} } \right)}}\), a simplified rule is assumed as:

$$c_{m} = \left\{ \begin{gathered} \begin{array}{*{20}c} { - {2}\left( {m - \frac{1}{2}} \right)^{2} + \frac{1}{2}} & {m \in \left( {0,\frac{1}{2}} \right)} \\ \end{array} \hfill \\ \begin{array}{*{20}c} {2\left( {m - \frac{1}{2}} \right)^{2} + \frac{1}{2}} & {m \in \left( {\frac{1}{2},1} \right)} \\ \end{array} \hfill \\ \end{gathered} \right.$$
(3)

When the friction factor \(m = 1\), the slab and the vertical roller are in full adhesion without any relative sliding, that is \(c_{m} = 0\). Substituting into Eq. (2) yields:

$$b = \frac{a}{{e^{2} }}$$

According to plane deformation assumption and constant volume, the FEM established by Yun et al. (2012) shows that the maximum variation is less than 3%. Thus, in every cross section, there is:

$$\Delta w_{x} h_{0} = \int_{0}^{{w_{x} - l_{px} }} {\left( {h_{\alpha } - h_{0} } \right)} {\text{d}}z + \int_{{w_{x} - l_{px} }}^{{w_{x} }} {\left( {h_{\beta } - h_{0} } \right)} {\text{d}}z$$
(4)

Substituting Eqs. (1) and (2) and the coefficient b into Eq. (4), there is:

$$a = \frac{{{4}e^{2} }}{{{9} - {2}c_{m} }}$$

Then, the expressions of dog-bone model can be written as follows:

$$h_{\alpha } = h_{0} + \frac{{{4}e^{2} h_{{0}} \Delta w_{x} }}{{\left( {{9} - {2}c_{m} } \right)l_{px} }}\left( {\frac{{w_{x} - z}}{{l_{px} }}} \right)^{2} e^{{ - {2}\left( {\frac{{w_{x} - z}}{{l_{px} }}} \right)}}$$
(5)
$$h_{\beta } = h_{0} + \frac{{{4}h_{{0}} \Delta w_{x} }}{{\left( {{9} - {2}c_{m} } \right)l_{px} }} - \frac{{{4}c_{m} h_{{0}} \Delta w_{x} }}{{\left( {{9} - {2}c_{m} } \right)l_{px} }}\left[ {{2}\left( {\frac{{w_{x} - z}}{{l_{px} }}} \right)^{3} - 3\left( {\frac{{w_{x} - z}}{{l_{px} }}} \right)^{2} + {1}} \right]$$
(6)

Then, the dog-bone deformation model only contains one unknown parameter \(l_{px}\). For edge rolling process, the peak position of dog-bone \(l_{px}\) in bite zone can be simplified as a constant (Yun et al. 2012).

2.3 Velocity Field and Strain Rate Field of Plastic Flow

The stream function method is widely used to analyze plastic deformation. The premise of this method is the principle of volume invariance. Firstly, a differential equilibrium equation is established based on the relationship between volume flow components, and then the plastic flow field is determined through integration and the boundary conditions. The plastic flow in bite zone is shown in Fig. 3. \({\text{d}}s\) and \({\text{d}}S\) represent the front and back lateral width of the infinitesimal element in length direction, respectively, and \(w(x,z)\) represents the function of lateral displacement.

Fig. 3
figure 3

Plastic flow diagram

Full size image

According to the properties of stream function:

$$\frac{\partial w}{{\partial z}} = \frac{{{\text{d}}s - {\text{d}}S}}{{{\text{d}}S}}$$
(7)

Based on the incompressibility of plastic flow, the speed in rolling direction is:

$$v_{x} = \frac{{v_{0} h_{0} }}{h}\frac{{{\text{d}}S}}{{{\text{d}}s}}$$
(8)

Substituting Eq. (8) into Eq. (7), and considering when \(\frac{\partial w}{{\partial z}} \ll 1\), \(\frac{\partial w/\partial z}{{1 + \partial w/\partial z}} \approx \frac{\partial w}{{\partial z}}\), then:

$$v_{x} = \frac{{v_{0} h_{0} }}{h}\left( {1 - \frac{\partial w}{{\partial z}}} \right)$$
(9)

The velocity in rolling direction and width direction has the following relationship:

$$\frac{{v_{z} }}{{v_{x} }} = \frac{\partial w}{{\partial x}}$$
(10)

Substituting Eq. (9) into Eq. (10) yields:

$$v_{z} = \frac{{v_{0} h_{0} }}{h}\left( {1 - \frac{\partial w}{{\partial z}}} \right)\frac{\partial w}{{\partial x}}$$
(11)

According to Cauchy equation:

$$\dot{\varepsilon }_{y} = \frac{{\partial v_{y} }}{\partial y} = - \frac{{\partial v_{x} }}{\partial x} - \frac{{\partial v_{z} }}{\partial z}$$
(12)

Substituting Eqs. (9) and (11) into Eq. (12) and noticing when \(y = 0\), \(v_{y} = 0\), the velocity in thickness direction can be obtained by solving the differential equation:

$$v_{y} = v_{0} h_{0} y\left\{ {\left( {\frac{\partial w}{{\partial z}} - 1} \right)\left[ {\frac{\partial }{\partial x}\left( \frac{1}{h} \right) + \frac{\partial }{\partial z}\left( \frac{1}{h} \right)\frac{\partial w}{{\partial x}}} \right] + \frac{1}{h}\left( {\frac{\partial w}{{\partial z}}\frac{{\partial^{2} w}}{\partial x\partial z} + \frac{\partial w}{{\partial x}}\frac{{\partial^{2} w}}{{\partial z^{2} }}} \right)} \right\}$$
(13)

For vertical rolling, the rolling velocity can be approximately regarded as constant:

$$v_{x} = v_{0}$$
(14)

The lateral displacement can be obtained by substituting Eq. (14) into Eq. (9):

$$w = \int\limits_{0}^{z} {\left( {1 - \frac{h(x,z)}{{h_{0} }}} \right)} {\text{d}}z$$
(15)

Substituting Eqs. (5) and (6) into Eq. (15) and considering the boundary condition \(w_{\alpha } \left( {w_{x} - l_{px} } \right) = w_{\beta } \left( {w_{x} - l_{px} } \right)\), there are:

$$w_{\alpha } = - \frac{{e^{2} \Delta w_{x} }}{{\left( {{9} - {2}c_{m} } \right)}}\left[ {{2}\left( {\frac{{w_{x} - z}}{{l_{px} }}} \right)^{2} + {2}\left( {\frac{{w_{x} - z}}{{l_{px} }}} \right) + {1}} \right]e^{{ - {2}\left( {\frac{{w_{x} - z}}{{l_{px} }}} \right)}}$$
(16)
$$w_{\beta } = \frac{{4\Delta w_{x} }}{{\left( {{9} - {2}c_{m} } \right)}}\left( {\frac{{w_{x} - z}}{{l_{px} }} - \frac{9}{{4}}} \right) + \frac{{{2}c_{m} \Delta w_{x} }}{{\left( {{9} - {2}c_{m} } \right)}}\left[ {{1} - \left( {\frac{{w_{x} - z}}{{l_{px} }}} \right)^{4} + {2}\left( {\frac{{w_{x} - z}}{{l_{px} }}} \right)^{3} - {2}\left( {\frac{{w_{x} - z}}{{l_{px} }}} \right)} \right]$$
(17)

The above formulas satisfy the boundary condition:

$$w_{\beta } \left( {x,w_{x} } \right) = - \Delta w_{x}$$

Through further calculation, the velocity and strain rate fields in zone α and zone β are obtained:

$$\left\{ {\begin{array}{*{20}l} {v_{\alpha x} = v_{0} } \hfill \\ {v_{\alpha y} = \frac{{v_{0} y}}{{h_{0} }}\frac{{\partial h_{\alpha } }}{\partial x} = \frac{{{4}e^{2} v_{0} \tan \phi y}}{{\left( {{9} - {2}c_{m} } \right)l_{px} }}\left( {u^{2} + {2}\frac{{\Delta w_{x} }}{{l_{px} }}u^{2} - {2}\frac{{\Delta w_{x} }}{{l_{px} }}u} \right)e^{{ - {2}u}} } \hfill \\ {v_{\alpha z} = v_{0} \frac{{\partial w_{\alpha } }}{\partial x} = - \frac{{e^{2} v_{0} \tan \phi }}{{{9} - {2}c_{m} }}\left( {{2}u^{2} + {4}\frac{{\Delta w_{x} }}{{l_{px} }}u^{2} + {2}u + {1}} \right)e^{{ - {2}u}} } \hfill \\ \end{array} } \right.$$
(18)
$$\left\{ {\begin{array}{*{20}l} {\dot{\varepsilon }_{\alpha x} = 0} \hfill \\ {\dot{\varepsilon }_{\alpha y} = \frac{{v_{0} }}{{h_{0} }}\frac{{\partial h_{\alpha } }}{\partial x} = \frac{{{4}e^{2} v_{0} \tan \phi }}{{\left( {{9} - {2}c_{m} } \right)l_{px} }}\left( {u^{2} + {2}\frac{{\Delta w_{x} }}{{l_{px} }}u^{2} - {2}\frac{{\Delta w_{x} }}{{l_{px} }}u} \right)e^{{ - {2}u}} } \hfill \\ {\dot{\varepsilon }_{\alpha z} = - \frac{{v_{0} }}{{h_{0} }}\frac{{\partial h_{\alpha } }}{\partial x} = - \frac{{{4}e^{2} v_{0} \tan \phi }}{{\left( {{9} - {2}c_{m} } \right)l_{px} }}\left( {u^{2} + {2}\frac{{\Delta w_{x} }}{{l_{px} }}u^{2} - {2}\frac{{\Delta w_{x} }}{{l_{px} }}u} \right)e^{{ - {2}u}} } \hfill \\ \end{array} } \right.$$
(19)
$$\left\{ {\begin{array}{*{20}l} \begin{gathered} \dot{\varepsilon }_{\alpha xy} = \dot{\varepsilon }_{\alpha yx} = \frac{1}{2}\left( {\frac{{\partial v_{x} }}{\partial y}{ + }\frac{{\partial v_{y} }}{\partial x}} \right){ = }\frac{{v_{0} y}}{{2h_{0} }}\frac{{\partial^{2} h_{\alpha } }}{{\partial x^{2} }} \hfill \\ = \frac{{{4}e^{2} v_{0} \tan^{2} \phi y}}{{\left( {{9} - {2}c_{m} } \right)l_{px}^{2} }}e^{ - 2u} \left[ {2u^{2} - 2u + \frac{{\Delta w_{x} }}{{l_{px} }}\left( {2u^{2} - 4u + 1} \right)} \right] - \frac{{v_{0} w_{xx}^{\prime \prime } y}}{{2h_{0} \tan \phi }}\frac{{\partial h_{\alpha } }}{\partial x} \hfill \\ \end{gathered} \hfill \\ \begin{gathered} \dot{\varepsilon }_{\alpha xz} = \varepsilon_{\alpha zx} = \frac{1}{2}\left( {\frac{{\partial v_{x} }}{\partial z}{ + }\frac{{\partial v_{z} }}{\partial x}} \right) = \frac{1}{2}v_{0} \frac{{\partial^{2} w_{\alpha } }}{{\partial x^{2} }} \hfill \\ { = }\frac{{e^{2} v_{0} }}{{{18} - {4}c_{m} }}e^{ - 2u} \left[ {w_{x}^{\prime \prime } \left( {2u^{2} + 2u + 1} \right) + \frac{{\Delta w_{x} w_{xx}^{\prime \prime } - 2\tan^{2} \phi }}{{l_{px} }}4u^{2} - \frac{{{8}\Delta w_{x} \tan^{2} \phi }}{{l_{px}^{2} }}\left( {u^{2} - u} \right)} \right] \hfill \\ \end{gathered} \hfill \\ \begin{gathered} \dot{\varepsilon }_{\alpha yz} = \dot{\varepsilon }_{\alpha zy} = \frac{1}{2}\left( {\frac{{\partial v_{y} }}{\partial z}{ + }\frac{{\partial v_{z} }}{\partial y}} \right){ = }\frac{{v_{0} y}}{{2h_{0} }}\frac{{\partial^{2} h_{\alpha } }}{\partial x\partial z} \hfill \\ { = }\frac{{{4}e^{2} v_{0} \tan \phi \Delta w_{x} y}}{{\left( {{9} - {2}c_{m} } \right)l_{px}^{3} }}e^{ - 2u} \left( {2u^{2} - 4u + 1} \right) + \frac{{{4}e^{2} v_{0} \tan \phi y}}{{\left( {{9} - {2}c_{m} } \right)l_{px}^{2} }}e^{ - 2u} \left( {u^{2} - u} \right) \hfill \\ \end{gathered} \hfill \\ \end{array} } \right.$$
(20)
$$\left\{ {\begin{array}{*{20}l} {v_{\beta x} = v_{0} } \hfill \\ {v_{\beta y} = \frac{{v_{0} y}}{{h_{0} }}\frac{{\partial h_{\beta } }}{\partial x} = \frac{{4c_{m} v_{0} \tan \phi y}}{{\left( {9 - 2c_{m} } \right)l_{px} }}\left[ {\frac{1}{{c_{m} }} - 2u^{3} - {3}u^{2} + 1 + \frac{{{6}\Delta w_{x} }}{{l_{px} }}\left( {u^{2} - u} \right)} \right]} \hfill \\ {v_{\beta z} = v_{0} \frac{{\partial w_{\beta } }}{\partial x} = \frac{{2c_{m} v_{0} \tan \phi }}{{9 - 2c_{m} }}\left[ {\frac{1}{{c_{m} }}\left( {{2}u - {2}\frac{{\Delta w_{x} }}{{l_{px} }} - \frac{9}{2}} \right){ + }1 - u^{4} + 2u^{3} - 2u + \frac{{\Delta w_{x} }}{{l_{px} }}\left( {4u^{3} - 6u^{2} + 2} \right)} \right]} \hfill \\ \end{array} } \right.$$
(21)
$$\left\{ {\begin{array}{*{20}l} {\dot{\varepsilon }_{\beta x} = 0} \hfill \\ {\dot{\varepsilon }_{\beta y} = \frac{{v_{0} }}{{h_{0} }}\frac{{\partial h_{\beta } }}{\partial x} = \frac{{4c_{m} v_{0} \tan \phi }}{{\left( {9 - 2c_{m} } \right)l_{px} }}\left[ {\frac{1}{{c_{m} }} - 2u^{3} + 3u^{2} - 1 + \frac{{{6}\Delta w_{x} }}{{l_{px} }}\left( {u^{2} - u} \right)} \right]} \hfill \\ {\dot{\varepsilon }_{\beta z} = - \frac{{v_{0} }}{{h_{0} }}\frac{{\partial h_{\beta } }}{\partial x} = - \frac{{4c_{m} v_{0} \tan \phi }}{{\left( {9 - 2c_{m} } \right)l_{px} }}\left[ {\frac{1}{{c_{m} }} - 2u^{3} + 3u^{2} - 1 + \frac{{{6}\Delta w_{x} }}{{l_{px} }}\left( {u^{2} - u} \right)} \right]} \hfill \\ \end{array} } \right.$$
(22)
$$\left\{ {\begin{array}{*{20}l} \begin{aligned} \dot{\varepsilon }_{\beta xy} = \dot{\varepsilon }_{\beta yx} = & \frac{1}{2}\left( {\frac{{\partial v_{x} }}{\partial y}{ + }\frac{{\partial v_{y} }}{\partial x}} \right){ = }\frac{{v_{0} y}}{{2h_{0} }}\frac{{\partial^{2} h_{\beta } }}{{\partial x^{2} }} \\ { = } & \frac{{2c_{m} v_{0} y}}{{9 - 2c_{m} }}\left[ \begin{gathered} \frac{{w_{x}^{\prime \prime } }}{{l_{px} }}\left( {2u^{3} - 3u^{2} + 1 - \frac{1}{{c_{m} }}} \right) - \frac{{\tan^{2} \phi \Delta w_{x} }}{{l_{px}^{3} }}\left( {12u - 6} \right) \hfill \\ + \left( {\frac{{2\tan^{2} \phi - \Delta w_{x} w_{x}^{\prime \prime } }}{{l_{px}^{2} }}} \right)\left( {6u^{2} - 6u} \right) \hfill \\ \end{gathered} \right] \\ \end{aligned} \hfill \\ \begin{aligned} \dot{\varepsilon }_{\beta xz} = \dot{\varepsilon }_{\beta zx} = & \frac{1}{2}\left( {\frac{{\partial v_{x} }}{\partial z}{ + }\frac{{\partial v_{z} }}{\partial x}} \right){ = }\frac{1}{2}v_{0} \frac{{\partial^{2} w_{\beta } }}{{\partial x^{2} }} \\ { = } & \frac{{c_{m} v_{0} }}{{9 - 2c_{m} }}\left[ \begin{gathered} \frac{{{2}w_{x}^{\prime \prime } }}{{c_{m} }}\left( { - u + \frac{{\Delta w_{x} }}{{l_{px} }} + \frac{9}{{8}}} \right) - 4n_{2} \frac{{\tan^{2} \phi }}{{l_{px} }} - w_{x}^{\prime \prime } \left( {1 - u^{4} + 2u^{3} - 2u} \right) \hfill \\ + \frac{{2\tan^{2} \phi - \Delta w_{x} w_{xx}^{\prime \prime } }}{{l_{px} }}\left( {4u^{3} - 6u^{2} + 2} \right) - \frac{{{12}\Delta w_{x} \tan^{2} \phi }}{{l_{px}^{2} }}\left( {u^{2} - u} \right) \hfill \\ \end{gathered} \right] \\ \end{aligned} \hfill \\ \begin{aligned} \dot{\varepsilon }_{\beta yz} = \dot{\varepsilon }_{\beta zy} = & \frac{1}{2}\left( {\frac{{\partial v_{y} }}{\partial z}{ + }\frac{{\partial v_{z} }}{\partial y}} \right){ = }\frac{{v_{0} y}}{{2h_{0} }}\frac{{\partial^{2} h_{\beta } }}{\partial x\partial z} \\ = & \frac{{{12}c_{m} v_{0} \tan \phi y}}{{\left( {9 - 2c_{m} } \right)l_{px}^{2} }}\left[ {u^{2} - u - \frac{{\Delta w_{x} }}{{l_{px} }}\left( {{2}u - {1}} \right)} \right] \\ \end{aligned} \hfill \\ \end{array} } \right.$$
(23)

In the formulas, \(u = \frac{{w_{x} - z}}{{l_{px} }}\).

Taking the boundary conditions in Eqs. (18) and (21), there are:

At the entrance cross section: \(v_{\alpha y} \left( {0,0,z} \right) = v_{\beta y} \left( {0,0,z} \right) = 0\).

At the exit cross section: \(v_{\alpha y} \left( {l,y,z} \right) = v_{\beta y} \left( {l,y,z} \right) = 0\), \(v_{\alpha z} \left( {l,y,z} \right) = v_{\beta z} \left( {l,y,z} \right) = 0\).

At the boundary of zone α and zone β: \(v_{\alpha x} \left( {x,y,w_{x} - l_{px} } \right) = v_{\beta x} \left( {x,y,w_{x} - l_{px} } \right) = v_{0}\)

$$v_{\alpha y} \left( {x,y,w_{x} - l_{px} } \right) = v_{\beta y} \left( {x,y,w_{x} - l_{px} } \right)$$

\(v_{\alpha z} \left( {x,y,w_{x} - l_{px} } \right) = v_{\beta z} \left( {x,y,w_{x} - l_{px} } \right)\)

According to Eqs. (19) and (22), the incompressible property is satisfied:

$$\dot{\varepsilon }_{\alpha x} + \dot{\varepsilon }_{\alpha y} + \dot{\varepsilon }_{\alpha z} = 0,\dot{\varepsilon }_{\beta x} + \dot{\varepsilon }_{\beta y} + \dot{\varepsilon }_{\beta z} = 0$$

2.4 Total Power Functional

The total power functional of vertical rolling process is obtained by using the first variation principle of rigid–plastic material:

$$J^{ * } = N_{i} + N_{{\text{s}}} + N_{{\text{f}}}$$
(24)

where \(N_{i}\), \(N_{{\text{s}}}\) and \(N_{{\text{f}}}\) represent plastic deformation power, shear power and friction power, respectively.

Based on Mises yield criterion, the plastic deformation power is:

$$\begin{aligned} N_{i} { = } & \iiint\limits_{V} {D\left( {E_{ij} } \right)}{\text{d}}V = \sqrt{\frac{2}{3}} \sigma_{s} \iiint\limits_{V} {\sqrt {\dot{\varepsilon }_{ij} \dot{\varepsilon }_{ij} } }{\text{d}}V \\ = & \frac{4\sqrt 6 }{3}\sigma_{s} \int_{0}^{l} {\int_{0}^{{w_{x} - l_{px} }} {\int_{0}^{{h_{\alpha } }} {\sqrt {\dot{\varepsilon }_{ax}^{2} + \dot{\varepsilon }_{\alpha y}^{2} + \dot{\varepsilon }_{\alpha z}^{2} + 2\dot{\varepsilon }_{\alpha xy}^{2} { + 2}\dot{\varepsilon }_{\alpha xz}^{2} { + 2}\dot{\varepsilon }_{\alpha yz}^{2} } } } } {\text{d}}y{\text{d}}z{\text{d}}x \\ & \;{ + }\frac{4\sqrt 6 }{3}\sigma_{s} \int_{0}^{l} {\int_{{w_{x} - l_{px} }}^{{w_{x} }} {\int_{0}^{{h_{\beta } }} {\sqrt {\dot{\varepsilon }_{\beta x}^{2} + \dot{\varepsilon }_{\beta y}^{2} + \dot{\varepsilon }_{\beta z}^{2} + 2\dot{\varepsilon }_{\beta xy}^{2} { + 2}\dot{\varepsilon }_{\beta xz}^{2} { + 2}\dot{\varepsilon }_{\beta yz}^{2} } } } } {\text{d}}y{\text{d}}z{\text{d}}x \\ \end{aligned}$$
(25)

At the exit section, there is no shear power because of the continuous velocity field. At entrance section, the discontinuity of velocity exists and the shear power can be expressed as:

$$N_{{\text{s}}} { = }\int_{{S_{0} }} {\tau_{{\text{s}}} \left| {\Delta v_{{\text{s}}} } \right|{\text{d}}S} { = }4\tau_{{\text{s}}} \int\limits_{0}^{{w_{0} }} {\int\limits_{0}^{{h_{0} }} {\sqrt {\left( {v_{y} \left| {_{x = 0} } \right.} \right)^{2} + \left( {v_{z} \left| {_{x = 0} } \right.} \right)^{2} } {\text{d}}y{\text{d}}z} }$$
(26)

where \(\tau_{{\text{s}}} { = }\sigma_{s} /\sqrt 3\) is the shear yield stress.

In vertical rolling process, the plastic deformation and the relative motion between roller and slab lead to extremely complicated tangential force and displacement on the contact interface. In the 3D rolling model proposed by Lian et al. (1984), the contact surface is divided into sliding zone and deformation stagnation zone (adhesion zone).

There is an initial displacement of sliding friction on the contact interface. Only when the calculated velocity discontinuity \(\Delta v_{f}\) becomes larger than the initial velocity discontinuity \(\Delta v_{c}\), the sliding and the friction power exist. The friction shear stress in the adhesive zone is assumed to be proportional to the displacement as:

$$\tau_{{\text{f}}} { = }m\tau_{{\text{s}}} \frac{{\Delta v_{f} }}{{\Delta v_{c} }}$$
(27)

According to the empirical formula obtained from the experiments of hot plain rolling (Shchepinsky 1987), the length of adhesion zone is given by:

$$l_{c} = 0.{2}mRl$$
(28)

For plain rolling, the adhesion zone is located on both sides of the neutral point. Differently in vertical rolling, the linear velocity of the roller surface is consistent with the rolling speed of the slab. From the above principle, the point with the same velocity of vertical roller and slab is located at the exit section, that is, the adhesion zone only exists on single side of the neutral point. So, the length of adhesion zone can be rewritten as:

$$l_{c} = 0.1mRl$$
(29)

In the sliding zone, the friction factor is constant and the friction shear stress is:

$$\tau_{{\text{f}}} = m\tau_{{\text{s}}}$$
(30)

On the sliding interface, the friction shear stress and the velocity discontinuity are collinear vectors. The friction power is:

$$N_{f} = \int_{{S_{f} }} {\left| {\tau _{f} } \right|\left| {\Delta v_{f} } \right|\cos \left( {\tau _{f} ,\Delta v_{f} } \right){\text{d}}s} = 4m\tau _{s} \int_{0}^{{l - l_{c} }} {\int_{0}^{{h_{{rx}} }} {\sqrt {\left( {v_{y} \left| {_{{z = w_{x} }} } \right.} \right)^{2} + \Delta v_{t}^{2} } } } \sec \phi {\text{d}}y{\text{d}}x$$
(31)

where \(\Delta v_{{\text{t}}} = \frac{{v_{0} }}{\cos \phi } - v_{R}\) is the tangential velocity discontinuity on the interface.

Substituting Eqs. (25), (26) and (31) into Eq. (24), the expression of total power functional changes into:

$$\begin{aligned} J^{ * } = & \frac{4\sqrt 6 }{3}\sigma_{s} \int_{0}^{l} {\int_{0}^{{w_{x} - l_{px} }} {\int_{0}^{{h_{\alpha } }} {\sqrt {\dot{\varepsilon }_{ax}^{2} + \dot{\varepsilon }_{\alpha y}^{2} + \dot{\varepsilon }_{\alpha z}^{2} + 2\dot{\varepsilon }_{\alpha xy}^{2} { + 2}\dot{\varepsilon }_{\alpha xz}^{2} { + 2}\dot{\varepsilon }_{\alpha yz}^{2} } } } } {\text{d}}y{\text{d}}z{\text{d}}x \\ & \;{ + }\frac{4\sqrt 6 }{3}\sigma_{s} \int_{0}^{l} {\int_{{w_{x} - l_{px} }}^{{w_{x} }} {\int_{0}^{{h_{\beta } }} {\sqrt {\dot{\varepsilon }_{\beta x}^{2} + \dot{\varepsilon }_{\beta y}^{2} + \dot{\varepsilon }_{\beta z}^{2} + 2\dot{\varepsilon }_{\beta xy}^{2} { + 2}\dot{\varepsilon }_{\beta xz}^{2} { + 2}\dot{\varepsilon }_{\beta yz}^{2} } } } } {\text{d}}y{\text{d}}z{\text{d}}x \\ & \;{ + }4\tau_{s} \int_{0}^{{w_{0} }} {\int_{0}^{{h_{0} }} {\sqrt {\left( {v_{y} \left| {_{x = 0} } \right.} \right)^{2} + \left( {v_{z} \left| {_{x = 0} } \right.} \right)^{2} } } } dydz + 4\tau_{f} \int_{0}^{{l - l_{c} }} {\int_{0}^{{h_{rx} }} {\sqrt {\left( {v_{y} \left| {_{{z = w_{x} }} } \right.} \right)^{2} + \Delta v_{t}^{2} } } } \sec \phi {\text{d}}y{\text{d}}x \\ \end{aligned}$$
(32)

The calculation procedure of energy model is shown in Fig. 4. When known the geometry size and movement speed of steel slab and rollers, the physical parameters of material, the width reduction and the friction factor, the total power functional are defined by the only undetermined constant parameter \(l_{px}\) (Zhang 2016). Continuously changing the unknown parameter \(l_{px}\), numerical calculation is carried out by using MATLAB to solve the corresponding total power functional until \(l_{px} = w_{1}\). The minimum of total power \(J_{\min }^{ * }\) is selected as the actual solution based on minimum energy principle. The rolling torque \(M\) and the rolling force per unit slab thickness \(F_{0}\) are determined by the following equation (Zhang et al. 2014):

$$J_{\min }^{ * } = 2M\frac{{v_{R} }}{R} = 4h_{0} l\chi F_{0} \omega_{V}$$
(33)

where \(\chi\) is the arm factor. In this paper, it is selected as 0.44 (Qi and Wang 2012).

Fig. 4
figure 4

Flowchart of the calculation

Full size image

3 Numerical Research

3.1 Validation of the Model

The dog-bone shape at outlet predicted by the presented model is compared with several results. As shown in Fig. 5a, the presented model predicted a lower and wider dog-bone than sine (Liu et al. 2015) and double parabolic (Liu et al. 2016) function model. The presented shape is more uniform than that of global weighted model (Yang et al. 2022), which seems that the global weighted velocity field is not very applicable when the width reduction is small. The predicted length of dog-bone is closer to the value predicted by Yun et al. (2012). Compared with other theoretical and fitted (Okado et al. 1981; Xiong et al. 1997) results in Fig. 5c, the dog-bone peak position (\(l_{px}\)) obtained by presented model is closer to the experimental result (Shibahara et al. 1981) with a less error of \(h_{r} /h_{b}\) value (within 0.5%). In addition, the presented curve is more accurate in describing the end part of dog-bone deformation, and the calculated length of plastic deformation zone (\(l_{bx}\)) is rather credible. However, the predicted height of dog-bone peak is higher than the other result. This is due to the assumption of plane deformation, which neglects the metal flow along rolling direction. The comparison of rolling force shows that the calculated values are very close to the results obtained by Yun et al. (2012) and Lundberg (2008), and the error is less than 7%. In Fig. 5b, when the width reduction rate is small, the predicted rolling force of global weighted model is sharply smaller than other results. It seems that the presented model is more reasonable.

Fig. 5
figure 5

Comparison of edge shape and rolling force predicted by several models

Full size image

It is effective to validate the theoretical model through experiments (Bari and Kumar 2023a, b). The vertical rolling experiments are performed on a small rolling mill in laboratory. The radius of vertical rollers is 50 mm. Pressure sensors are installed at the vertical rollers on both sides, respectively, to measure the total rolling force. Heavy strain hardened copper specimens and precipitation hardened aluminum specimens are selected as experimental material. By continuous casting, the materials are made into 25-mm thick plates, and then cold rolled to 8 and 6 mm to avoid strain hardening during further deformation. And thus, it would be approximately ideally plastic during edge rolling experiment. The length and width of slabs are 300 mm and 60 mm, respectively. The shear yield strength of the materials was determined by a simple tensile test (EN 10002) (Lundberg 1993;2008).

When the width reduction rate is selected between 1.8 and 4.25%, the rolling force predicted by the presented model is compared with 10 groups of experiments (Li et al. 2016). Table 1 shows the mechanics and process parameters of the experimental materials. Figure 6 shows that the total error of the presented values compared with measurements is less than 14%. When the width reduction rate is small, the presented model performs better. As the width reduction rate increasing, the numerical results become slightly higher than the experimental values, which can be explained that the plane deformation assumption (\(v_{x} = v_{0}\)) predicted a bigger edge deformation.

Table 1 Parameters of materials and processes
Full size table
Fig. 6
figure 6

Comparison of rolling force obtained by presented model and measurement

Full size image

3.2 Dog-bone deformation

Based on the above calculation method, the edge deformation was calculated with the value of \(\frac{\Delta w}{{w_{0} }} = 0.01 - 0.05\), \(\frac{{h_{0} }}{{w_{0} }} = 0.08 - 0.16\), \(\frac{R}{{w_{0} }} = 0.65 - 1.05\), \(m = 0.3 - 0.7\). The relationship between the cross section of dog-bones at outlet and the rolling parameters is shown in Fig. 7. The predicted peak position is compared with the results predicted by Xiong et al. (1997). All the parameters were non-dimensionalized. In the study of width reduction rate, thickness, width and roller radius, the friction factors are given as 0.3 (Byon et al. 2018) uniformly.

Fig. 7
figure 7

Effects of a, b \(\Delta w/w_{0}\) c, d \(h_{0}\) e, f \(h_{0} /w_{0}\) g, h \(R\) i, j \(m\) on dog-bone shape and peak position

Full size image

Figure 7a shows that with the width reduction rate increasing, the deformation zone becomes larger and extends obviously. Accordingly, \(h_{b}\) and \(h_{r}\) increase as well as the dog-bone peak moves inward. The influence of initial thickness is similar to width reduction rate, as shown in Fig. 7c and d. The increase of initial thickness enlarges the deformation extent and area, which let \(l_{b}\) and \(l_{p}\) linear rise approximately. It is worth to note that in Fig. 7e, with the decrease of \(h_{0} /w_{0}\), \(h_{r} /h_{0}\) and \(h_{b} /h_{0}\) rise, while the peak moves outward, which indicates that the deformation will be more concentrated at the edge. In other words, it will aggravate the non-uniform deformation. The deformation area extends inward slightly and the peak has a small decrease with the increase of vertical roller radius, as Fig. 7g and h shown. The expansion of the interface will enhance the resistance along rolling direction, and the movement tendency toward the center of width becomes stronger. It can be seen in Fig. 7i and j that the effect of friction factor on dog-bone deformation is limited and mainly concentrated in zone β.

3.3 Rolling Power and Rolling Force

The comparison of presented function model and sine DSF Model (Liu et al. 2018) in the proportion of three kinds of power in total power is exhibited in Fig. 8. It can be seen that plastic deformation power is dominant (more than 60%). The second one is shear power, and friction power is the minimum. Further analysis found that the presented model predicted a less proportion of friction power, which can be attributed to the consideration of adhesion zone. The comparison model assumes that the entire contact interface is in sliding condition and generates friction power while in the presented model, the adhesion within the contact zone is considered. In the adhesion zone, there is no sliding; thus, no friction power exists, which results in a smaller predicted friction power (Lian et al. 1984; Chen et al. 2018).

Fig. 8
figure 8

The proportion of powers calculated by a presented model and b sine DSF model

Full size image

Figure 9 shows the ratio of several power in total power varies with rolling parameters. In Fig. 9a, with the increase of width reduction rate, plastic deformation zone becomes larger, while the increase of the entrance shear plane and the contact interface is smaller. So, the proportion of plastic deformation power increases obviously. The increase of slab thickness sharply enlarges the contact interface and the entrance shear plane, which increases the proportion of friction power and shear power, as shown in Fig. 9b. From Fig. 9c, the increase of radius makes the deformation expands slightly to the width center, resulting in a minor increase of deformation power. As shown in Fig. 9d, the growth of friction factor increases the friction power, while the proportion of deformation power and shear power changes slightly.

Fig. 9
figure 9

Effects of a \(\Delta w/w_{0}\) b \(h_{0}\) c \(R\) d \(m\) on power ratio in total power

Full size image

The change of rolling force with rolling parameters is shown in Fig. 10. The increase of width reduction rate and slab thickness cause the expansion of deformation region and the obvious rise of rolling force, as Fig. 10a and b shows, respectively. As shown in Fig. 10c, the increase of vertical roller radius expands the deformation zone and the contact interface, which result in a minor increase of rolling force. In Fig. 10d, the increase of friction factor leads to a growth of rolling force. However, the change range of rolling force is tiny, which can be attributed to the limited proportion of friction power in total power.

Fig. 10
figure 10

Effects of a \(\Delta w/w_{0}\) b \(h_{0}\) c \(R\) d \(m\) on rolling force

Full size image

4 Conclusions

  1. 1.

    This is a crossover study on both mathematic and mechanics. Based on the incompressibility and rigid–plastic of the steel slab, a combination of theory and engineering is carried out to analyze the vertical rolling process. A new model called gamma distribution–cubic function dog-bone model is put forward and the velocity and strain rate fields are derived according to stream function method. According to the first variation principle of rigid–plastic material and fully considering the adhesion and sliding of the friction interface, the total power functional is given. The proposed model can be applied for accurate prediction of the dog-bone deformation at the edge and rolling force.

  2. 2.

    The developed method is compared with several models and the reliability is well verified by experiment results. On this basis, the influences of several process parameters on rolling power, rolling force and dog-bone shape are discussed. The increase of slab thickness and width reduction rate leads to a significant expansion of edge deformation. The height of dog-bone decreases and moves inward, which can lighten the non-uniform edge deformation by increasing the ratio of thickness to width or changing the rollers with larger radius. The effect of friction factor on dog-bone shape is slight. Plastic deformation power accounts for the largest proportion in total power, and friction power accounts for the least. The width reduction rate and initial slab thickness have considerable impacts on power proportion and rolling force. By comparison, the effects of vertical roller radius and friction factor are rather smaller.