1 Introduction

Uncertainties are often encountered in the practical systems and mathematical models (Iman et al. 2005; Nannapaneni et al. 2016; Xiao et al. 2012), which lead to uncertain performance. Uncertainty analysis has been widely used to help decision makers understand the degree of confidence of the model results so that they can know the degree of confidence in the decision they made and assess the risk (Borgonovo and Peccati 2006). However, most applications of uncertainty analysis do not provide information on how the uncertainty of model output can be apportioned to the uncertainty of model inputs, and therefore, on which factors to devote data collection resources so as to reduce the uncertainty most effectively (Wang 2017; Xiong et al. 2010). Global sensitivity analysis (GSA) has been widely used to apportion the uncertainty of model output to different sources of uncertainty in the model inputs (Saltelli et al. 2008). Thus, GSA can help researchers find the significant or non-significant input factors (Morris 1991), measure the respective contributions of input factors to the uncertainty of model output or detect the interaction effect between different input factors. Then, researchers can reduce the uncertainty of model output effectively through the calibration of the most influential input factors and simplify the model by fixing the non-influential input factors into nominal values. In addition, it can also help researchers obtain a comprehensive insight on the model behavior and structure (Xu et al. 2017). Due to this property, GSA has been widely used in risk assessment and decision making, etc. For example, Saltelli and Tarantola (2002) used GSA on the safety assessment for nuclear waste disposal, Hu and Mahadevan (2016) proposed an enhanced surrogate model-based reliability analysis method based on GSA, Patil and Frey (2004) used GSA for the food safety risk assessment, Borgonovo and Peccati (2006) used GSA techniques in the investment decisions, Lamboni et al. (2009) used GSA for dynamic crop models to help researchers make better decisions in the growing season of crops. More details of GSA can be found in the reviews of other researchers, such as Refs. (Borgonovo and Plischke 2016; Wei et al. 2015).

The traditional GSA methods, such as the nonparametric methods (Helton 1999), variance based methods (Saltelli et al. 2010; Sobol 2001), distribution based methods (Borgonovo 2007; Liu and Homma 2010; Pianosi and Wagener 2015), the relative entropy based method (Liu et al. 2006), the probability distance based method (Greegar and Manohar 2015), etc. focus on the models with scalar output, which can be considered as a random variable. However, many practical models with dynamic output, which can be considered as random process, are widely used in engineering. In these models, time-dependent model outputs are usually considered (in practical, time-dependent output is often discretized, which leads to high dimensional multivariate output). Usually, an appropriate scalar objective function (such as an aggregated statistic like sum, average or maximum value) is selected at first, then GSA is performed on the selected objective function (Saltelli et al. 2000). While if no appropriate scalar objective function can be obtained, then the GSA should be performed on model output at each time moment separately (Lilburne and Tarantola 2009). Although performing GSA on a pre-defined scalar function of the dynamic output can be convenient and useful when the selected scalar function has a meaningful interpretation, it leads to many potential scalar functions, and sometimes it is impossible to find a proper scalar function (Li et al. 2016). On the other hand, conducting GSA on the model output at each instant can give information on how the sensitivity of input variable evolves over time, however, it may lead to redundancy since strong correlation often exists between outputs from one instant to another (Garcia-Cabrejo and Valocchi 2014) and can not get how the input variables affect the whole model output in an entire time interval. As mentioned by Campbell et al. (2006), it may be insufficiently informative to perform GSA on a specific scalar function of the outputs or on the output at each time instant separately. Thus, it is more appropriate to apply GSA on the dynamic model output as a whole.

Similar to the variance based GSA method for models with scalar output, which utilizes the variance to describe the uncertainty of model output, the uncertainty of dynamic output (multivariate output) can be represented by the covariance matrix. Then Gamboa et al. (2013) proposed a set of multivariate global sensitivity indices based on the decomposition of the covariance matrix of model output which are equivalent to the Sobol’ indices (Sobol 1993) in the scalar case. These indices can be considered as the average of all the Sobol’ indices for each output weighted by the variance of the corresponding output, and they do not consider the covariance among different outputs. Based on the idea of the output decomposition method proposed by Campbell et al. (2006), Lamboni et al. (2011) used principal component analysis (PCA) to perform the decomposition of model output and proposed a set of multivariate global sensitivity indices according to the variance based GSA method. These indices can still be considered as averaging all the Sobol’ indices for the principal components weighted by the variance of each principal component. Since the total variance of all the principal components is equal to the total variance of the original model output, these two sets of indices are equivalent if the selected principal components preserve all the variance of the original model output. This has also been pointed out by Garcia-Cabrejo and Valocchi (2014). The PCA based method still misses the covariance among different model outputs.

The multivariate sensitivity analysis methods mentioned above are all based on the variance of the model output, which implicitly assume that the variance is sufficient to describe output variability (Saltelli 2002). However, the variance only provides a summary of the whole distribution and it will result in inevitable loss of information when representing the uncertainty of output with variance alone (Helton and Davis 2003). Thus, a sensitivity index based on the whole distribution of dynamic output is preferable to have a comprehensive assessment of the influence of model inputs on the dynamic output. Based on the density based GSA method for scalar output (Borgonovo 2007), Cui et al. (2010) proposed a multivariate sensitivity index based on the joint probability density function (PDF) of the multivariate output. Although this method can take both the whole distribution and the correlation of the multivariate output into consideration, it suffers the “curse of dimensionality” for calculating the high dimensional integration and the difficulty in estimating the joint PDF of the high dimensional output variables. Later, Li et al. (2016) utilized the joint cumulative distribution function (CDF) to describe the whole uncertainty of multivariate output since the CDF is easier to be estimated than the PDF (Liu and Homma 2009). Then the multivariate global sensitivity index was defined based on the multivariate probability integral transformation (PIT) distribution of the multivariate output. It is recognized that valuable information of the correlation structure is contained in the joint CDF of the multivariate output. In addition, due to the univariate nature of the multivariate PIT, this index can be calculated through a univariate integration. Although the multivariate PIT based method is easier to be implemented than the joint PDF-based method, it still needs to estimate the joint CDF of the multivariate output, which is very difficult in the case of high dimension model outputs. This is often the case when the time-dependent output is discretized, which usually will lead to a very high dimensional model output.

In this work, we propose a new multivariate global sensitivity index which measures the effect of the input uncertainty on the whole probability distribution of the model output, and it takes the correlation among different outputs into consideration. This new sensitivity index is defined based on the energy distance (Rizzo and Székely 2016; Székely and Rizzo 2013), which is used to measure the difference between the unconditional distribution of the multivariate output and the conditional one when a certain input variable is fixed. Compared to the joint PDF based method and the multivariate PIT based method, the new method does not need to estimate the joint PDF or CDF of the multivariate output and can be estimated through a surprisingly simple form of expectation.

The rest of this paper is organized as follows: Section 2 briefly reviews the covariance decomposition based method and the multivariate PIT based method. In Section 3, the energy distance is briefly introduced at first, then the new multivariate global sensitivity index is defined based on the energy distance and the properties of the new sensitivity index are discussed. Section 4 gives the comparison of the proposed sensitivity index with the existent indices and the estimation of the proposed sensitivity index. A numerical example and two engineering examples are employed in Section 5 to show the validity and the benefits of the proposed sensitivity index. Section 6 gives the conclusion.

2 Review of the multivariate global sensitivity analysis methods

Let X i (i = 1 , 2 ,  …  , d) be a set of independent random input variables with PDFs \( {f}_{X_i}\left({x}_i\right) \) (i = 1 , 2 ,  …  , d). The dynamic output is defined as

$$ Y(t)= g\left({X}_1.{X}_2,\dots, {X}_d, t\right),\kern0.5em t\in \mathcal{T} $$
(1)

where Y(t) is the dynamic output and g represents the deterministic model response function. The model output becomes a vector Y = (Y(t 1), Y(t 2),  … , Y(t m )) if the \( \mathrm{domain}\kern0.2em \mathcal{T} \) is discrete or more generally a function Y(t) (\( t\in \mathcal{T} \)) \( \mathrm{if}\kern0.2em \mathcal{T} \) is continuous. In practical application, many continuous functions are often discretized for a more convenient calculation and analysis. Here, we will consider the discrete case.

2.1 Covariance decomposition based method

The multivariate sensitivity analysis based on covariance decomposition proposed by Gamboa et al. (2013) is established on the high dimensional model representation (HDMR) (Sobol 1993) of the outputs, i.e.

$$ \begin{array}{l} Y\left({t}_r\right)={g}_{0,{t}_r}+\sum_{i=1}^d{g}_i\left({X}_i,{t}_r\right)+\sum_{1\le i< j\le d}{g}_{i,\; j}\left({X}_i,{X}_j,{t}_r\right)\hfill \\ {}+\dots +{g}_{1,2,\dots, d}\left({X}_1,{X}_2,\dots, {X}_d,{t}_r\right),\kern1em r=1,\dots, m\hfill \end{array} $$
(2)

where

$$ \begin{array}{l}{g}_{0,{t}_r}= E\left( Y\left({t}_r\right)\right)\hfill \\ {}{g}_i\left({X}_i,{t}_r\right)= E\left( Y\left({t}_r\right)\left|{X}_i\right.\right)-{g}_{0,{t}_r}\hfill \\ {}{g}_{i, j}\left({X}_i,{X}_j,{t}_r\right)= E\left( Y\left({t}_r\right)\left|{X}_i,{X}_j\right.\right)-{g}_i\left({X}_i,{t}_r\right)-{g}_j\left({X}_j,{t}_r\right)-{g}_{0,{t}_r}\hfill \\ {}\cdots \hfill \end{array} $$
(3)

and t r (r = 1 , 2 ,  …  , m, and m is the number of the time instant) is the time instant which indicates different outputs and E(•) denotes the expectation operator.

Take the covariance matrices for both sides of (2), then the following equation can be obtained

$$ \begin{array}{c}\hfill \mathbf{C}\left( Y\left({t}_1\right),\dots, Y\left({t}_m\right)\right)=\sum_{i=1}^d{\mathbf{C}}_i\left( Y\left({t}_1\right),\dots, Y\left({t}_m\right)\right)+\sum_{1\le i< j\le d}{\mathbf{C}}_{i, j}\left( Y\left({t}_1\right),\dots, Y\left({t}_m\right)\right)\hfill \\ {}\hfill +\cdots +{\mathbf{C}}_{1,2,\dots, d}\left( Y\left({t}_1\right),\dots, Y\left({t}_m\right)\right)\hfill \end{array} $$
(4)

Equation (4) denotes that the covariance matrix of multivariate output can be partitioned into the sum of covariance matrices that comes from changes in single, pairs, triplets, etc. of input variables (Garcia-Cabrejo and Valocchi 2014). For the scalar output, this equation becomes the decomposition of the variance, which is used to define the traditional variance based global sensitivity indices. For the case of multivariate output, Gamboa et al. (2013) showed that the covariance matrix C can be projected onto a scalar through multiplication by a matrix M and then taking the trace. They also showed that the matrix M can be taken as the identify matrix, i.e. M = I. Then it leads to

$$ \begin{array}{c}\hfill \mathrm{Tr}\left[\mathbf{C}\left( Y\left({t}_1\right),\dots, Y\left({t}_m\right)\right)\right]=\sum_{i=1}^d\mathrm{Tr}\left[{\mathbf{C}}_i\left( Y\left({t}_1\right),\dots, Y\left({t}_m\right)\right)\right]+\sum_{1\le i< j\le d}\mathrm{Tr}\left[{\mathbf{C}}_{i, j}\left( Y\left({t}_1\right),\dots, Y\left({t}_m\right)\right)\right]\hfill \\ {}\hfill +\cdots +\mathrm{Tr}\left[{\mathbf{C}}_{1,2,\dots, d}\left( Y\left({t}_1\right),\dots, Y\left({t}_m\right)\right)\right]\hfill \end{array} $$
(5)

Thus, the multivariate main effect index of input variable X i is defined as

$$ S{1}_i^M\left( Y\left({t}_1\right),\dots, Y\left({t}_m\right)\right)=\frac{\mathrm{Tr}\left[{\mathbf{C}}_i\right]}{\mathrm{Tr}\left[\mathbf{C}\right]}=\frac{\sum_{r=1}^m V\left({g}_i\left({X}_i,{t}_r\right)\right)}{\sum_{r=1}^m V\left( Y\left({r}_j\right)\right)} $$
(6)

And the multivariate total effect index of X i can be defined as

$$ \begin{array}{l}{ST}_i^M\left( Y\left({t}_1\right),\dots, Y\left({t}_m\right)\right)\hfill \\ {}=\frac{\mathrm{Tr}\left[{\mathbf{C}}_i\right]+\sum_{j=1, j\ne i}^d\mathrm{Tr}\left[{\mathbf{C}}_{i, j}\right]+\cdots +\mathrm{Tr}\left[{\mathbf{C}}_{1,2,\dots, d}\right]}{\mathrm{Tr}\left[\mathbf{C}\right]}\hfill \\ {}=\frac{\sum_{r=1}^m V\left({g}_i\left({X}_i,{t}_r\right)\right)+\sum_{j=1, j\ne i}^d{\sum}_{r=1}^m V\left({g}_{i, j}\left({X}_i,{X}_j,{t}_r\right)\right)+\cdots +{\sum}_{r=1}^m V\left({g}_{1,2\dots, d}\left({X}_1,{X}_2,\dots, {X}_d,{t}_r\right)\right)}{\sum_{r=1}^m V\left( Y\left({t}_r\right)\right)}\hfill \end{array} $$
(7)

Since all the elements along diagonal in C are positive, the trace of C is positive. This trace is equal to the sum of variances of all the outputs Y(t r ) (r = 1 ,  …  , m), i.e., the total variance of all the output variables. The trace of C i is the total variance of all the output variables associated with changes in input variable X i . According to the law of total variance, the numerator in (6) can be represented as \( {\sum}_{j=1}^m V\left({g}_i\left({X}_i,{t}_r\right)\right)={\sum}_{j=1}^m V\left( E\left( Y\left({t}_r\right)\left|{X}_i\right.\right)\right)={\sum}_{j=1}^m V\left( Y\left({t}_r\right)\right)- E\left( V\left( Y\left({t}_r\right)\left|{X}_i\right.\right)\right) \). V(Y(t r )|X i ) is the conditional variance of Y(t r ) when X i is fixed at a certain value. E(V(Y(t r )|X i )) denotes the average residual variance of Y(t r ) when X i can be fixed. Thus, \( {\sum}_{j=1}^m V\left( Y\left({t}_r\right)\right)- E\left( V\left( Y\left({t}_r\right)\left|{X}_i\right.\right)\right) \) represents the average reduction of the total variance of all the output variables when X i can be fixed. \( S{1}_i^M \) can be interpreted as the expected percentage reduction in the total variance of output variables when the uncertainty of X i is eliminated. \( {ST}_i^M \) is the summation of all the sensitivity indices related to input variable X 1, thus \( {ST}_i^M \) can measure both the individual effect of X i and the interaction effects between X i and other input variables on the outputs.

According to the definition of \( S{1}_i^M \) in (6), \( S{1}_i^M \) can also be represented as

$$ S{1}_i^M=\frac{\sum_{j=1}^m V\left( E\left( Y\left({t}_j\right)\left|{X}_i\right.\right)\right)}{\sum_{r=1}^m V\left( Y\left({t}_r\right)\right)}=\sum_{j=1}^m\frac{V\left( Y\left({t}_j\right)\right)}{\sum_{r=1}^m V\left( Y\left({t}_r\right)\right)} S{1}_{i,{t}_j} $$
(8)

where \( S{1}_{i,{t}_j}=\frac{V\left( E\left( Y\left({t}_j\right)\left|{X}_i\right.\right)\right)}{V\left( Y\left({t}_j\right)\right)} \) is the main effect index of X i on the single output Y(t j ). Thus, \( S{1}_i^M \) can be regarded as the weighted average of the main effect indices of X i on the single output Y(t j ) (j = 1 ,  …  , m), and the weight of each term is proportional to the variance of each output. Similarly, \( {ST}_i^M \) can also be represented as

$$ {ST}_i^M=\frac{\sum_{j=1}^m E\left( V\left( Y\left({t}_j\right)\left|{\mathbf{X}}_{\sim i}\right.\right)\right)}{\sum_{r=1}^m V\left( Y\left({t}_r\right)\right)}=\sum_{j=1}^m\frac{V\left( Y\left({t}_j\right)\right)}{\sum_{r=1}^m V\left( Y\left({t}_r\right)\right)}{ST}_{i,{t}_j} $$
(9)

where X ~i denotes all the input variables except X i , \( {ST}_{i,{t}_j}=\frac{E\left( V\left( Y\left({t}_j\right)\left|{\mathbf{X}}_{\sim i}\right.\right)\right)}{V\left( Y\left({t}_j\right)\right)} \) is the total effect index of X i on the single output Y(t j ). Thus, \( {ST}_i^M \) is also the weighted average of the total effect indices of X i on the single output Y(t j ) (j = 1 ,  …  , m).

According to the definition, it can be seen that the covariance decomposition based indices mainly concern the variance of model outputs, which may be insufficient for representing the uncertainty of model output. In addition, they also ignore the covariance terms in the covariance matrix, which represent the correlation between different outputs.

2.2 Multivariate probability integral transformation based method

The base of the multivariate sensitivity analysis method proposed by Li et al. (2016) is the multivariate probability integral transformation (PIT) (Genest and Rivest 2001). Let F Y (y 1, y 2,  … , y m ) be the joint CDF of the multivariate output Y = (Y(t 1), Y(t 2),  … , Y(t m )), then the m-dimensional PIT of Y can be obtained by taking the CDF of Y, i.e., V = F Y (y 1, y 2,  … , y m ). The CDF of V, represented by K V (v), is known as the PIT distribution of Y. For the univariate case, K V (v)is a standard uniform distribution. While for the multivariate case, K V (v) is not a standard uniform distribution since it relies on the correlation structure of the joint CDF of Y. Specifically, K V (v) is distributed in [0, 1] for the multivariate case and it can be represented as K V (v) = P(V ≤ F Y (y 1, y 2,  … , y m ), where P(•) denotes the probability of event • in the bracket. Since K V (v) is obtained from the joint CDF of the multivariate output Y, it contains valuable information about the joint CDF of Y.

Denote \( {F}_{\mathbf{Y}\left|{X}_i\right.}\left({y}_1,{y}_2,\dots, {y}_m\right) \) as the conditional joint CDF of Y when fixing a input variable X i at a certain value. Then the corresponding conditional PIT distribution is \( {K}_{V\left|{X}_i\right.}(v)= P\Big( V\le {F}_{Y\left|{X}_i\right.}\left({y}_1,{y}_2,\dots, {y}_m\right) \). Thus, the effect of input variable fixed in a certain value on the multivariate output can be measured through the difference between K V (v) and \( {K}_{V\left|{X}_i\right.}(v) \), which can be represented as

$$ s\left({X}_i\right)={\int}_0^1\left|{K}_V(v)-{K}_{V\left|{X}_i\right.}(v)\right|\mathrm{d} v $$
(10)

Since X i is a random variable with PDF \( {f}_{X_i}\left({x}_i\right) \), the average effect of X i on the multivariate output can be measured through the expectation of s(X i ), i.e.

$$ {E}_{X_i}\left( s\left({X}_i\right)\right)={\int}_{-\infty}^{+\infty }{f}_{X_i}\left({x}_i\right)\left({\int}_0^1\left|{K}_V(v)-{K}_{V\left|{X}_i\right.}(v)\right|\mathrm{d} v\right)\mathrm{d}{x}_i $$
(11)

The final multivariate sensitivity index is defined as

$$ {\eta}_i=\frac{1}{2}{E}_{X_i}\left( s\left({X}_i\right)\right) $$
(12)

η i represents the normalized average effect of X i on the PIT distribution of Y. Larger value of η i will indicate greater effect of X i on the multivariate output.

It can be seen that the multivariate PIT based index η i focuses on the joint CDF of model output, which contains all the uncertainty information of model output. However, it needs to estimate the joint CDF of model output, which is a difficult task, especially for the cases of high dimensional output. In addition, when the model output becomes a scalar random variable, the index η i is not suitable. Since the PIT distribution of an one-dimensional variable is standard uniform distribution, thus K V (v) is equal to \( {K}_{V\left|{X}_i\right.}(v) \), which leads to that η i is zero.

3 Multivariate global sensitivity analysis based on energy distance

In this section, we will propose a new multivariate sensitivity index which will take the whole distribution of the multivariate output into consideration. Firstly, the energy distance, which is used for the definition of the new index, will be introduced.

3.1 Energy distance

Energy distance is a distance between probability distributions (Rizzo and Székely 2016; Székely and Rizzo 2013), which is analogous to the potential energy between objects in a gravitational space. For two independent random vectors X and Y in ℝ d, the energy distance between them is defined as

$$ \varepsilon \left(\mathbf{X},\mathbf{Y}\right)=2 E\left\Vert \mathbf{X}-\mathbf{Y}\right\Vert - E\left\Vert \mathbf{X}-{\mathbf{X}}^{\mathbf{\prime}}\right\Vert - E\left\Vert \mathbf{Y}-{\mathbf{Y}}^{\mathbf{\prime}}\right\Vert $$
(13)

where E denotes expectation operator, ‖•‖ denotes the Euclidean norm if the argument is real and the complex norm when the argument is complex, E‖X‖ < ∞, E‖Y‖ < ∞, X ′ denotes an independent and identically distributed (iid) copy of X and Y ′ denotes an iid copy of Y.

A significant advantage of the energy distance is that ε(X, Y) = 0 if and only if X and Y are identically distributed. Thus, the energy distance has been used for testing of equal distributions (Székely and Rizzo 2004; Székely et al. 2007). This advantage of energy distance can be explained with the following proposition (Székely and Rizzo 2013).

Proposition

For d-dimensional independent random vectors X and Y with E‖X‖ + E‖Y‖ < ∞, ϕ X (t) and ϕ Y (t) denote the characteristic functions of X and Y separately, then their energy distance can be represented as

$$ \varepsilon \left(\mathbf{X},\mathbf{Y}\right)=2 E\left\Vert \mathbf{X}-\mathbf{Y}\right\Vert - E\left\Vert \mathbf{X}-{\mathbf{X}}^{\mathbf{\prime}}\right\Vert - E\left\Vert \mathbf{Y}-{\mathbf{Y}}^{\mathbf{\prime}}\right\Vert =\frac{1}{C_d}{\int}_{R^d}\frac{{\left\Vert {\phi}_{\mathbf{X}}\left(\mathbf{t}\right)-{\phi}_{\mathbf{Y}}\left(\mathbf{t}\right)\right\Vert}^2}{{\left\Vert \mathbf{t}\right\Vert}^{d+1}}\mathrm{d}\mathbf{t} $$
(14)

where

$$ {C}_d=\frac{\pi^{\left( d+1\right)/2}}{\Gamma \left(\frac{d+1}{2}\right)} $$
(15)

with Γ(•) is the complete gamma function. Thus, ε(X, Y) ≥ 0 with equality to zero if and only if X and Y are identically distributed.

The proof of this proposition can be found in (Székely and Rizzo 2005). Equation (14) shows that energy distance is the weighted L 2 distance between characteristic functions, with the weight function w(t) = ‖t‖−(d + 1). The characteristic function is the Fourier transform of the PDF, and it also contains all the information of the distribution of random vectors. Thus, the energy distance measures the difference between the distributions of two random vectors.

Another advantage of energy distance is that it is distribution free, i.e., the estimated value of energy distance does not depend on the distribution form of random vectors, although it can be represented as the form of characteristic function. Due to the form of expectation in (13), the energy distance can be estimated with the following surprisingly simple form. Let \( {\mathbf{x}}_1,\dots, {\mathbf{x}}_{n_1} \) denote the samples of X and \( {\mathbf{y}}_1,\dots, {\mathbf{y}}_{n_2} \) denote the samples of Y, then the energy distance can be estimated as follows (Rizzo and Székely 2016)

$$ {\varepsilon}_{n_1,{n}_2}\left(\mathbf{X},\mathbf{Y}\right)=2 A- B- C $$
(16)

where A, B, C are simply the average of the pairwise distance:

$$ \begin{array}{l} A=\frac{1}{n_1{n}_2}\sum_{i=1}^{n_1}\sum_{j=1}^{n_2}\left\Vert {\mathbf{x}}_i-{\mathbf{y}}_j\right\Vert \\ {} B=\frac{1}{n_1^2}\sum_{i=1}^{n_1}\sum_{j=1}^{n_2}\left\Vert {\mathbf{x}}_i-{\mathbf{x}}_j\right\Vert \\ {} C=\frac{1}{n_2^2}\sum_{i=1}^{n_1}\sum_{j=1}^{n_2}\left\Vert {\mathbf{y}}_i-{\mathbf{y}}_j\right\Vert \end{array} $$
(17)

Since the value of the energy distance does not has a upper bound, a normalized energy distance \( \overline{\varepsilon}\left(\mathbf{X},\mathbf{Y}\right) \) can be obtained as follows (Rizzo and Székely 2016)

$$ \overline{\varepsilon}\left(\mathbf{X},\mathbf{Y}\right)=\frac{2 E\left\Vert \mathbf{X}-\mathbf{Y}\right\Vert - E\left\Vert \mathbf{X}-{\mathbf{X}}^{\mathbf{\prime}}\right\Vert - E\left\Vert \mathbf{Y}-{\mathbf{Y}}^{\mathbf{\prime}}\right\Vert }{2 E\left\Vert \mathbf{X}-\mathbf{Y}\right\Vert } $$
(18)

Then \( 0\le \overline{\varepsilon}\left(\mathbf{X},\mathbf{Y}\right)\le 1 \) with \( \overline{\varepsilon}\left(\mathbf{X},\mathbf{Y}\right)=0 \) if and only if X and Y are identically distributed. In the next subsection, the normalized energy distance is applied to define the multivariate global sensitivity index.

3.2 The new sensitivity index

Consider the dynamic model Y(t) = g(X 1 . X 2,  … , X d , t) used in Section 2 with the discrete model output Y = (Y(t 1), Y(t 2),  … , Y(t m )). Let Y|X i denote the conditional multivariate output when one input variable X i is fixed at a certain value. The effect of the fixed value of X i on the multivariate output can be measured by the energy distance between Y and Y|X i as follows

$$ d\left({X}_i\right)=\overline{\varepsilon}\left(\mathbf{Y},\mathbf{Y}\left|{X}_i\right.\right) $$
(19)

Then d(X i ) is a function only dependent on X i . Since X i is a random variable with PDF \( {f}_{X_i}\left({x}_i\right) \), the average effect of X i on the multivariate output can be described by the expectation of d(X i ) as follows

$$ {E}_{X_i}\left( d\left({X}_i\right)\right)=\int d\left({X}_i\right){f}_{X_i}\left({x}_i\right)\mathrm{d}{x}_i $$
(20)

Then the multivariate global sensitivity index is defined as follows

$$ {\xi}_i={E}_{X_i}\left( d\left({X}_i\right)\right) $$
(21)

ξ i denotes the expected difference between the distributions of the unconditional output Y and the conditional output Y when fixing X i . Larger value of ξ i means that the input variable X i has a greater effect on the multivariate output.

Similarly, the multivariate global sensitivity index for any group of input variables (\( {X}_{i_1},{X}_{i_2},\dots, {X}_{i_p} \)) can also be defined as follows

$$ \begin{array}{l}{\xi}_{i_1,{i}_2,\dots, {i}_p}={E}_{X_{i_1},{X}_{i_2},\dots, {X}_{i_p}}\left( d\left({X}_{i_1},{X}_{i_2},\dots, {X}_{i_p}\right)\right)\hfill \\ {}={E}_{X_{i_1},{X}_{i_2},\dots, {X}_{i_p}}\left(\overline{\varepsilon}\left(\mathbf{Y},\mathbf{Y}\left|\left({X}_{i_1},{X}_{i_2},\dots, {X}_{i_p}\right)\right.\right)\right)\hfill \\ {}\hfill ={\int}_{{\mathbb{R}}^r}\overline{\varepsilon}\left(\mathbf{Y},\mathbf{Y}\left|\left({X}_{i_1},{X}_{i_2},\dots, {X}_{i_p}\right)\right.\right){f}_{X_{i_1},{X}_{i_2},\dots, {X}_{i_p}}\left({x}_{i_1},{x}_{i_2},\dots, {x}_{i_p}\right)\mathrm{d}{x}_{i_1}\mathrm{d}{x}_{i_2}\cdots \mathrm{d}{x}_{i_p}\hfill \end{array} $$
(22)

The properties of the proposed sensitivity index are listed in Table 1.

Table 1 Properties of the sensitivity index proposed in this work
Full size table

Proof of property 1

Since

$$ 0\le \overline{\varepsilon}\left(\mathbf{Y},\mathbf{Y}\left|{X}_i\right.\right)\le 1 $$

Thus, it can be obtained that

$$ 0= E(0)\le E\left(\overline{\varepsilon}\left(\mathbf{Y},\mathbf{Y}\left|{X}_i\right.\right)\right)\le E(1)=1 $$

Namely

$$ 0\le {\xi}_i\le 1 $$

Proof of property 2 and 3

If Y is independent of X i , then the distribution of Y would be the same with the distribution of Y|X i , thus, it can be obtained that \( \overline{\varepsilon}\left(\mathbf{Y},\mathbf{Y}\left|{X}_i\right.\right)=0 \), i.e., \( {\xi}_i= E\left(\overline{\varepsilon}\left(\mathbf{Y},\mathbf{Y}\left|{X}_i\right.\right)\right)=0 \).

If Y is dependent on X i but independent on X j , then the distribution of Y|(X i , X j ) will be equal to the distribution of Y|X i , thus, \( \overline{\varepsilon}\left(\mathbf{Y},\mathbf{Y}\left|\left({X}_i,{X}_j\right)\right.\right)=\overline{\varepsilon}\left(\mathbf{Y},\mathbf{Y}\left|{X}_i\right.\right) \), i.e., \( {\xi}_{i, j}=\overline{\varepsilon}\left(\mathbf{Y},\mathbf{Y}\left|\left({X}_i,{X}_j\right)\right.\right)=\overline{\varepsilon}\left(\mathbf{Y},\mathbf{Y}\left|{X}_i\right.\right)={\xi}_i \).

4 Discussion and estimation of the proposed sensitivity index

4.1 Discussion of the proposed sensitivity index

The proposed sensitivity index ξ i measures the effect of input variables on the multivariate output through the average energy distance between the unconditional multivariate output and the conditional one. Since the energy distance can be used to measure the difference between the distributions of two random vectors through the weighted L 2 distance between characteristic functions, ξ i can measure the effect of input variables on the whole distribution of the multivariate output. For the covariance decomposition based indices, they just utilize a certain moment (variance) of whole distribution for the multivariate output, which can not represent the whole uncertainty information of multivariate output. In addition, they only use the variances of the multivariate output, but neglect the covariance (correlation) between different outputs. Thus, compared to the covariance decomposition based indices, the proposed index captures more information of the uncertainty of model output and can obtain more reasonable results.

Both ξ i and the multivariate PIT based index measure the effect of input variables on the whole distribution of the multivariate output, the main difference is that ξ i utilizes the weighted L 2 distance between characteristic functions but the PIT based index uses the L 1 distance between the PIT distributions. The multivariate PIT transforms the joint CDF of multivariate output into a univariate function, which may miss some useful information. The characteristic function still contains all the information of model output. Another advantage of ξ i is that it can be easily calculated due to the form of expectation in (13). For the PIT based method, it needs to calculate the joint CDF of the multivariate output, which is quite difficult compared to the proposed method, especially for the cases of high dimensional output. When the time-dependent output is discretized, which will lead to a very high dimension of model outputs, the PIT based method will not be appropriate.

For the special case of scalar variables X and Y, the energy distance can also be represented as follows

$$ \varepsilon \left( X, Y\right)=2\int {\left({F}_X(t)-{F}_Y(t)\right)}^2\mathrm{d} t $$
(23)

where F X (•) and F Y (•) are the CDFs of X and Y, separately. It can be seen that, the energy distance for scalar variables is also the L 2 distance between the CDFs. Thus, for the scalar model output, the proposed sensitivity index can also be represented as the average difference between the unconditional CDF and conditional CDF of model output. This is similar to the sensitivity index proposed by Liu and Homma (Liu and Homma 2010), which used the absolute operator instead of the square operator. As mentioned before, the multivariate PIT based index is not suitable for the special case of scalar model output since the index will always be zero.

4.2 Estimation of the proposed sensitivity index

According to the definition of the proposed index, a direct way to estimate ξ i needs a double loop sampling, which is similar to the method used in Refs.(Borgonovo 2007; Li et al. 2016). However, the double loop sampling method is not efficient enough, especially for the computationally intensive models. Later, Plischke et al. (2013) proposed an efficient method to estimate the distribution based index proposed in (Borgonovo 2007) with just one set of input-output samples, and it also has been developed into a general and consistent method for estimating many sensitivity indices (Borgonovo et al. 2016). In this subsection, this idea is adopted to estimate the proposed index ξ i .

For a certain input X i , suppose the corresponding sample space is [b 1, b 2], and partition the sample space of X i into L successive and non-overlapping subintervals A l  = [a l − 1, a l ], where b 1 = a 0 < a 1 <  ⋯  < a l  <  ⋯  < a L  = b 2 and l = 1 , 2 ,  …  , L. Then the following theorem can be obtained (The proof similar to that in (Zhai et al. 2014) is given in Appendix).

Theorem 1

Suppose the model Y = g(X, t) is continuous with respect to X. Then, when \( \Delta a=\underset{l}{ \max}\left|{a}_l-{a}_{l-1}\right| \) approaches zero, the following equation can be obtained

$$ \underset{\Delta a\to 0}{ \lim}\sum_{l=1}^L{P}_l\overline{\varepsilon}\left(\mathbf{Y},\mathbf{Y}\left|{X}_i\in {A}_l\right.\right)={E}_{X_i}\left(\overline{\varepsilon}\left(\mathbf{Y},\mathbf{Y}\left|{X}_i\right.\right)\right) $$
(24)

where \( {P}_l={\int}_{a_{l-1}}^{a_l}{f}_{X_i}\left({x}_i\right)\mathrm{d}{x}_i={F}_{X_i}\left({a}_l\right)-{F}_{X_i}\left({a}_{l-1}\right) \) and \( {F}_{X_i}\left(\cdot \right) \) is the CDF of X i .

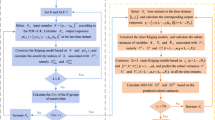
Theorem 1 shows that when the maximum length of intervals Δa approaches zero (the number of intervals approaches infinity), the estimator \( {\widehat{\xi}}_i=\sum_{l=1}^L{P}_l\overline{\varepsilon}\left(\mathbf{Y},\mathbf{Y}\left|{X}_i\in {A}_l\right.\right) \) approaches ξ i . Then based on Theorem 1, the following steps are proposed to estimate the sensitivity indices and the flow chart is shown in Fig. 1.

  1. 1)

    Generate N samples {x 1,  … , x N} according to the joint PDF f X (x) of model inputs, and then obtain the corresponding output sample set B = {y 1,  … , y N} through running the model Y = g(X, t).

  2. 2)

    Partition the sample space of model input X i into L successive and non-overlapping subintervals A l  = [a l − 1, a l ], l = 1 , 2 ,  …  , L.

  3. 3)

    Partition the output samples into L subsets based on the partition of X i , i.e.,

Fig. 1
figure 1

The flow chart for estimating the proposed sensitivity index

Full size image
$$ \begin{array}{cc}\hfill {B}_l=\left\{{\mathbf{y}}^j\left|{x}_i^j\in {A}_l\right.\right\},\hfill & \hfill l=1,2,\dots, L\hfill \end{array} $$
(25)

Then estimate the energy distance between Y and Y|X i  ∈ A l using the sample sets B and B l according to (16) and (17). Denote the estimated value as \( \widehat{\overline{\varepsilon}}\left(\mathbf{Y},\mathbf{Y}\left|{X}_i\in {A}_l\right.\right) \) (l = 1 , 2 ,  …  , L).

  1. 4)

    Estimate ξ i as follows

$$ {\widehat{\xi}}_i=\sum_{l=1}^L{P}_l\widehat{\overline{\varepsilon}}\left(\mathbf{Y},\mathbf{Y}\left|{X}_i\in {A}_l\right.\right) $$
(26)
  1. 5)

    Repeat steps 2) to 4) to estimate the sensitivity index for all the input variables.

For a group of input variables (\( {X}_{i_1},{X}_{i_2},\dots, {X}_{i_p} \)), the procedure above can also be used to estimate the corresponding sensitivity index \( {\xi}_{i_1,{i}_2,\dots, {i}_p} \). The difference is that one needs to partition the joint sample space of (\( {X}_{i_1},{X}_{i_2},\dots, {X}_{i_p} \)) into subspaces. Then partition the output samples based on the partition of (\( {X}_{i_1},{X}_{i_2},\dots, {X}_{i_p} \)).

The same output samples {y 1,  … , y N} can be partitioned into different subsets for different X i , thus, one group of samples will be enough to estimate the sensitivity indices for each model input. The sampling process for generating the samples of model input can be realized by many different methods (simple random sampling, Latin hypercube sampling, quasi random sampling, etc.). In this work, the Sobol’ quasi random sequence (Sobol” 1976; Sobol’ et al. 2011) is utilized to generate the samples due to its low discrepancy property. Several partition strategies are available in (Plischke 2012). In this paper, the equiprobability partition (Zhai et al. 2014) is adopted, which is a widely used and effective scheme. The previous studies showed that there exists a tradeoff of selecting the number of subintervals for a given set of input-output samples, it should be guaranteed that both the number of subintervals and the number of samples in each subinterval are enough. A recommended strategy for selecting the number of subintervals is \( L=\left[\sqrt{N}\right] \) (take the integer part of \( \sqrt{N} \), and N is the total sample size) to achieve a balance of number of subintervals and the number of samples in each subinterval (Li and Mahadevan 2016). This strategy is used in this work.

5 Examples

In this section, a numerical example and two engineering examples with high dimensional model output are adopted. Since the estimation of the PIT based method is very difficult in the case with high dimensional model output, only the covariance decomposition method and the proposed method are applied on these example to have a comparison.

5.1 Numerical example

Here, a numerical example with time-dependent output is adopted. The model response function can be represented as

$$ g\left(\mathbf{x}, t\right)={x}_1^2{x}_3 \cos \left(2\pi \cdot 20 t\right){\mathrm{e}}^{-{x}_2 t}-3{x}_2 \cos \left(2\pi \cdot 40 t\right){\mathrm{e}}^{-{x}_1 t}+\left({x}_1+1\right) \cos \left(2\pi \cdot 60 t\right){\mathrm{e}}^{-{x}_2 t}-2{x}_3 $$
(27)

Each value of the time parameter t corresponds to a model output. Here, t lies in the interval [0, 5] and it is discretized into 128 time points equally distributed in [0, 5], which correspond to 128 model outputs. The independent input variables x 1, x 2, x 3 follow normal distribution and their distribution parameters are shown in Table 2.

Table 2 Distribution parameters of the input variables for the numerical example
Full size table

Figure 2 shows the estimated values of the proposed index for the three input variables with different sample sizes by the proposed method in Section 4.2. It shows that the proposed estimation method can obtain a stable result as the sample size increases.

Fig. 2
figure 2

Values of the proposed index with different sample sizes for the numerical example

Full size image

Table 3 shows the values of different indices. The results indicate that the importance rankings of the input variables based on the proposed sensitivity index and the covariance decomposition based sensitivity indices are different. For the covariance decomposition based sensitivity indices, the importance ranking is x 2 > x 1 > x 3, while for the proposed sensitivity index, the importance ranking is x 1 > x 2 > x 3. The difference of the importance ranking is caused by the fact that covariance decomposition based sensitivity indices measure the effect of input variables on the variance of the model output and do not consider the correlation between different model outputs, while the proposed sensitivity index measure the effect of input variables on the entire probability distribution (represented by the characteristic function) of the model outputs. Thus, x 2 has the most effect on the variance of the model output and x 1 has the most effect on the entire probability distribution of the model output. This also denotes that the variable having the most effect on the variance of model output may not have the most effect on the entire probability distribution of model outputs. In addition, x 2 has more effect on the variance of model output than x 3, but almost has the same effect on the entire probability distribution of model output with x 3.

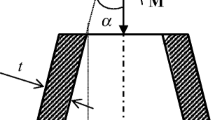
Table 3 Values of different indices for the numerical example
Full size table

5.2 A vibration problem

In this example, a vibration problem used in (Hu and Du 2015) is adopted and it is shown in Fig. 3. The stiffness of spring k 2, damping coefficient c 2, mass m 2, stiffness of spring k 1, and mass m 1 are considered as random input variables, and they are described in Table 4. The amplitude of the vibration of mass m 1 subjected to force f 0 sin(Ωt) is given by

$$ {q}_{1 \max }={f}_0{\left(\frac{c_2^2{\Omega}^2+{\left({k}_2-{m}_2{\Omega}^2\right)}^2}{c_2^2{\Omega}^2{\left({k}_1-{m}_1{\Omega}^2-{m}_2{\Omega}^2\right)}^2+{\left({k}_2{m}_2{\Omega}^2-\left({k}_1-{m}_1{\Omega}^2\right)\left({k}_2-{m}_2{\Omega}^2\right)\right)}^2}\right)}^{1/2} $$
(28)
Fig. 3
figure 3

A vibration problem

Full size image
Table 4 Distribution parameters of the input variables for the vibration problem
Full size table

This equation can be non-dimensionalized using a static deflection of main system, defined by \( {q}_{1\mathrm{st}}=\frac{f_0}{k_1} \). Thus, the non-dimensional displacement of m 1 is considered as the output and can be given as

$$ Y= g\left(\mathbf{X},\Omega \right)=\frac{q_{1 \max }}{q_{1\mathrm{st}}}={k}_1{\left({K}_1/\left({K}_2+{K}_3^2\right)\right)}^{1/2} $$
(29)

where

$$ \begin{array}{l}{K}_1={c}_2^2{\Omega}^2+{\left({k}_2-{m}_2{\Omega}^2\right)}^2\hfill \\ {}{K}_2={c}_2^2{\Omega}^2{\left({k}_1-{m}_1{\Omega}^2-{m}_2{\Omega}^2\right)}^2\hfill \\ {}{K}_3={k}_2{m}_2{\Omega}^2-\left({k}_1-{m}_1{\Omega}^2\right)\left({k}_2-{m}_2{\Omega}^2\right)\hfill \end{array} $$
(30)

The parameter Ω is the excitation frequency in [8, 28] rad/s. Different values of Ω will lead to different model outputs. In this example, Ω will take the values from 8 rad/s to 28 rad/s with a step size of 0.2 rad/s, which correspond to 101 model outputs.

The estimated values of the proposed sensitivity index through the method proposed in Section 4.2 with different sample sizes are shown in Fig. 4, which indicates that as the sample size increases, the proposed method can converge toward a stable result.

Fig. 4
figure 4

Values of the proposed index with different sample sizes for the vibration problem

Full size image

The values of different sensitivity indices are shown in Table 5. For both kinds of indices, k 1 is the most important variable, which means that k 1 not only has the most effect on variance of model output but also has the most effect on the entire probability distribution of model output. For the covariance decomposition based indices, m 2 is the second important variable and it almost has the same effect on the variance of model output with k 1, the other variables have little effect on the variance of model output. However, for the proposed sensitivity index, k 2 and m 1 are the second and third important variables separately, and they almost have the same effect on the entire probability distribution of model output, but has less effect on the entire probability distribution of model output than k 1 apparently. m 2 and c 2 have the least effect on the whole probability distribution of model output, and they are just a little less important than m 1 and k 2. The results also show that the relative importance of input variables based on these two kinds of indices may not be the same. Since k 1 is the most important variable based on these two kinds of sensitivity indices, more attention should be paid on k 1 to have a more accurate estimation of the output.

Table 5 Values of different indices for the vibration problem
Full size table

5.3 Automobile front axle

In this example, an automobile front axle beam used in (Shi et al. 2017) is adopted. In the automobile engineering, the front axle beam is used to carry the weight of the front part of the vehicle (Fig. 5(a)). Since the whole front part of the automobile rests on the front axle beam, it must be robust enough in construction to make sure it is reliable. The I-beam is often used in the design of the front axle due to its high bend strength and light weight. Figure 5(b) shows the dangerous cross-section. The maximum normal stress and shear stress are σ = M/W x and τ = T/W ρ separately, where M and T are time-dependent bending moment and torque, i.e., \( M={M}_0\left(\frac{1}{10} \cos \frac{1}{10} z+\frac{1}{10}\right) \) and \( T={T}_0 \sin \frac{1}{3} z \), where M 0 and T 0 are the basic bending moment and torque, z is the time parameter which lies in the interval [0, 10] second. W x and W ρ are section factor and polar section factor which are given as

$$ \begin{array}{l}{W}_x=\frac{a{\left( h-2 t\right)}^3}{6 h}+\frac{b}{6 h}\left[{h}^3-{\left( h-2 t\right)}^3\right]\\ {}{W}_{\rho}=0.8{ b t}^2+0.4\left[{a}^3\left( h-2 t\right)/ t\right]\end{array} $$
(31)
Fig. 5
figure 5

Diagram of the automobile front axle

Full size image

The limit state function for checking the strength of front axle can be expressed as:

$$ g={\sigma}_s-\sqrt{\sigma^2+3{\tau}^2} $$
(32)

where σ s is the ultimate stress of yielding. According to the material property of the front axle, the ultimate stress of yielding σ s is 460 MPa. The geometry variables of I-beam a , b , t , h and the basic bending moment M 0 and torque T 0 are independent normal variables with distribution parameters listed in Table 6. The time parameter z will take the values from 0.1 to 10 s with a step size of 0.1 s, which will lead to 100 model outputs.

Table 6 Distribution parameters of the input variables for automobile front axle
Full size table

Fig. 6 shows the estimated values of the proposed sensitivity index through the proposed method with increasing sample sizes. It denotes that the estimated values converge to a stable value as the sample size increases. Table 7 shows the values of different sensitivity indices. For the covariance decomposition based sensitivity indices, T 0 has the most significant effect on the variance of model output and b comes at the second. The other variables has little effect on the variance of model output. For the proposed sensitivity index, h has the most significant effect on the whole probability distribution of model output. The second and third important input variables are M 0 and b separately, and they almost have the same effect on the whole probability distribution of model output. The other variables have the least effect on the whole probability distribution of model output. Based on the results, if one focuses on the variance of model output, more attention should be paid on T 0 and b. While if one is interested in the whole probability distribution of model output, then more attention should be paid on h, M 0 and b.

Fig. 6
figure 6

Values of the proposed index with different sample sizes for the automobile front axle

Full size image
Table 7 Values of different indices for the automobile front axle
Full size table

6 Conclusion

A multivariate global sensitivity index is proposed in this work to measure the effect of input variables on the entire probability distribution of the discretized dynamic output. Compared to the covariance decomposition based indices, which just considers the variance of model output and neglects the correlation between different model outputs, the proposed sensitivity index considers the whole probability distribution of the model output, which contains more information of model output. Compared to the multivariate PIT based method, which needs to estimate the joint CDF of multivariate output and is quite difficult to implement for high dimensional outputs, the proposed sensitivity index can be represented as the form of expectations and can be easily estimated, especially for high dimensional outputs. To estimate the proposed sensitivity index more efficiently, the given-data method is adopted in this work, which just needs one set of input-output sample. The numerical and engineering examples are used to compare the proposed method and the covariance decomposition based method. It can be seen that the input rankings based on these two kinds of sensitivity indices are not necessarily the same. This is caused by the fact that the covariance decomposition based indices consider the effect of input variables on the variance of model output while the proposed index considers the effect of input variables on the whole distribution of model output. Through these two kinds of sensitivity indices, one can easily obtain the input variables which have significant effect on the whole probability distribution of output and the input variables which have the significant effect on the variance of output separately. When the output variable is normally distributed or the response function is a quadratic utility function, variance is sufficient to describe the uncertainty of model output. Otherwise, the whole probability distribution is preferable to have a more comprehensive description of the uncertainty of model output.