1 Introduction

The key point of reliability analysis is to estimate the probability that a system fails to meet the design requirement, considering the randomness of input variables. Obtaining the failure probability needs to frequently call the performance function. In practical engineering, the performance function usually needs to be calculated by time-consuming finite element method (FEM), computational fluid dynamics (CFD), etc. Then the computational effort of reliability analysis will become unacceptable. Therefore, reducing the number of function evaluations without sacrificing the accuracy is state of the art in the field of reliability analysis. The approaches can be classified into three groups.

The first group comprises FORM or SORM (first or second order reliability method) (Der Kiureghian and Dakessian 1998). Both of them behave poorly for highly nonlinear performance functions or performance functions with multiple most probabilistic points (MPPs) (Qin et al. 2006; Yang et al. 2015). The second group is the sampling methods which comprises direct Monte Carlo simulation (MCS) method, importance sampling (IS) methods (Ditlevsen and Madsen 1996; Au and Beck 1999; Kurtz and Song 2013), Subset simulation method (Au and Beck 2001), etc. The vital shortcoming of sampling methods is the poor efficiency. More than thousands of function evaluations are usually needed for such kind of methods. The third group is the surrogate-model-based methods (Bourinet et al. 2011; Kim and Na 1997; Papadopoulos et al. 2012). Such methods firstly approximate the original performance function by a surrogate model and then obtain the failure probability with a sampling method. The major drawback of such methods is that it is hard to keep the approximation error under control (Cadini et al. 2014).

Recently, adaptive strategies based on Kriging model (Echard et al. 2011; Bichon et al. 2008; Dubourg et al. 2011) have been proposed in the field of reliability analysis. The major achievement of such methods lies in locally approximating the performance function in the narrow region close to the limit-state surface. They are uniformly referred to as active learning Kriging (ALK) model in this paper. EGRA (Bichon et al. 2008) and AK-MCS (Echard et al. 2011) are two most representative strategies. Serial benchmark tests reveal that such kind of methods have great potential to accurately assess the failure probability with a minimizing number of function evaluations (Echard et al. 2011; Bichon et al. 2008; Wen et al. 2016). However, the estimation of low failure probability still remains an issue for those methods (Echard et al. 2013).

EGRA approximates the limit state in a fixed design space of ±5 standard deviation of random variables. If the size of design space exceeds the demand, wasted expense will arise in EGRA; otherwise, the accuracy will not be assured. In AK-MCS, the simulated samples of MCS are used to represent the design space which is verified as a good strategy. With this strategy, the ALK model just meets the necessity of MCS. However, for rare event with a very low failure probability (10−6~10−9), the size of simulated samples required by MCS will be very large (108 to 1011). In AK-MCS, the responses at all the samples should be predicted by the Kriging model in each iteration. Then, the process of purely building an ALK model will become very time-demanding (Echard et al. 2013). In reliability based design optimization, to build an ALK model in an approximate region as small as possible, an local adaptive sampling (LAS) region was proposed in Refs. (Li et al. 2016; Chen et al. 2014). In those methods, to calculate the failure probability at each design point, the LAS region should be predicted by a Kriging model and then choose optimal training points until the ALK model is accurate enough in the LAS region. However, in the initial process, the Kriging model is too inaccurate to predict a proper LAS region and the LAS region will be very inaccurate and much larger than necessity. However, the whole process of choosing training points should be executed in such a much larger approximate region. An adaptive sampling region (ASR) based on the Kriging model was defined in Ref. (Wen et al. 2016). However, in each iteration, the ASR should be predicted by the current Kriging based on MCS. In addition, various learning criteria (Sun et al. 2017; Wang and Wang 2013; Wang and Wang 2016; Hu and Mahadevan 2016), diverse stopping conditions (Sun et al. 2017; Zhu and Du 2016) have been proposed to improve the performance of AK-MCS. In each iteration of those methods, MCS should also be used. Therefore, for the estimation of low failure probability, those method are also very time-demanding just like AK-MCS.

To avoid this shortcoming, replacing MCS method by IS method is a wise option. The basic idea of IS strategies is forcing the simulated samples to fall into the most probable failure region (MPFR) so that the rare event can occur more often (Ditlevsen and Madsen 1996). By doing so, an IS method is able to accomplish the estimation of low failure probability with a remarkably reduced size of simulated samples. Then the vital drawback of AK-MCS will be overcome. Several schemes have been proposed during the past several years. The method fusing ALK model with FORM-based IS method was proposed and termed as AK-IS in Ref. (Echard et al. 2013). Recently, an improved method of AK-IS which combined ALK model with a trust region method was proposed in Ref. (Gaspar et al. 2017). However, the adoption of FORM-based IS method limits its application to performance functions with one single MPFR (Cadini et al. 2014). In Ref. (Zhao et al. 2015), Markov chain Monte Carlo (MCMC) method (Au and Beck 2001; Yuan et al. 2013) calling the true performance function was adopted to identify the MPFR(s) and then AK-IS was used to predict the failure probability. As is known to us, purely identifying all the MPFRs by MCMC frequently needs hundreds to thousands of function evaluations (Au and Beck 1999; Yuan et al. 2013). Therefore, this method is not efficient in practice. In Ref. (Cadini et al. 2014), a metamodel-based IS (meta-IS) method developed in Ref. (Dubourg et al. 2013) was adopted to identify all the MPPs and the method termed as MetaAK-IS2 was proposed. However, MetaAK-IS2 is not efficient dealing with low failure probability estimation demonstrated from Ref. (Cadini et al. 2014).

This paper is aimed at fusing ALK model with IS method to deal with the issue of rare event estimation. The work comprises two main stages like other methods in Refs. (Cadini et al. 2014; Echard et al. 2013; Zhao et al. 2015): (1) identify all the MPFRs; (2) update an ALK model with IS samples. To efficiently recognize all the MPFRs, a brand-new scheme combining ALK model with a so-called concentric ring approaching (CRA) method is proposed. And then ALK model is updated in the framework of IS method. The proposed method is denoted as ALK-CRA-IS. Compared with other methods (Cadini et al. 2014; Echard et al. 2013; Zhao et al. 2015), the points evaluated in Stage (1) are all optimal points for improving the sign prediction of Kriging model. Therefore, they can be made full use and fewer additional training points are required in Stage (2). Thus, ALK-CRA-IS is more efficient than other methods in general.

The organization of this paper is summarized as follows. ALK model applied in the field of reliability analysis is reviewed in Section 2. The ALK-CRA-IS method is formulated in Section 3. The performance of the proposed method is compared with other methods through four case studies in Section 4. Conclusions are made in the last section.

2 Review of ALK model and important sampling

In the standard normal space, denote the performance function as G(u) with u = [u1, u2, ⋯, un] the n input random variables. Given the failure region F = {u|G(u) < 0}, the failure probability can be obtained by

$$ {P}_f=P\left\{\boldsymbol{u}\in F\right\}=\iint \cdots \int I\left(\boldsymbol{u}\in F\right)f\left(\boldsymbol{u}\right)d\boldsymbol{u}=E\left[I\left(\boldsymbol{u}\in F\right)\right] $$
(1)

where P{·} is the probability of an event; f(·) is the joint probability density function (PDF); E(·) is the expectation operator; I(·) is the indicator function of an event, with value 1 if the event is true and 0 otherwise. With MCS, the failure probability can be estimated as

$$ {\hat{P}}_f=\frac{1}{N_{MC}}\sum \limits_{j=1}^{N_{MC}}I\left(G\left({\boldsymbol{u}}^{(j)}\right)<0\right) $$
(2)

in which {u(j), j = 1, 2, ⋯, NMC} is the NMC simulated samples. (2) reveals that only the sign of G(u) can affect the value of \( {\hat{P}}_f \). Therefore, during constructing a surrogate model with as few training points as possible, it is wise to only accurately predict the sign of G(u) rather than its specific value. This idea can be perfectly accomplished by ALK model.

Kriging model is a Gaussian process model. Given a design of experiments (DoE), it offers not only the predicted value μG(u), but also the specific uncertainty information of this prediction, i.e. \( \hat{G}\left(\boldsymbol{u}\right)\sim N\left({\mu}_G\left(\boldsymbol{u}\right),{\sigma}_G\left(\boldsymbol{u}\right)\right) \) (Jones et al. 1998; Ranjan et al. 2008). The predicted value μG(u) is given as

$$ {\mu}_G\left(\boldsymbol{u}\right)=\hat{\beta}+\mathbf{r}{\left(\boldsymbol{\uptheta}, \boldsymbol{u}\right)}^T\mathbf{R}{\left(\boldsymbol{\uptheta} \right)}^{-1}\left(\mathbf{g}-\hat{\beta}\mathbf{1}\right) $$
(3)

The predicted variance \( {\sigma}_G^2\left(\mathbf{u}\right) \) is given as

$$ {\sigma}_G^2\left(\boldsymbol{u}\right)={\sigma}^2\left[1+\frac{{\left({\mathbf{1}}^T\mathbf{R}{\left(\boldsymbol{\uptheta} \right)}^{-1}\mathbf{r}\left(\boldsymbol{\uptheta}, \boldsymbol{u}\right)-1\right)}^2}{{\mathbf{1}}^T\mathbf{R}{\left(\boldsymbol{\uptheta} \right)}^{-1}\mathbf{1}}-{\mathbf{r}}^T\left(\boldsymbol{\uptheta}, \boldsymbol{u}\right)\mathbf{R}{\left(\boldsymbol{\uptheta} \right)}^{-1}\mathbf{r}\left(\boldsymbol{\uptheta}, \boldsymbol{u}\right)\right] $$
(4)

In (3)–(4), g is the vector of response in a DoE; 1 is a unit column vector; r(θ, u) is a correlation vector and R(θ) is a correlation matrix; \( \hat{\beta} \), σ2 and θ are parameters of a Kriging model. On details of Kriging model, people can refer to Ref. (Yang et al. 2016).

The basic procedure of ALK model applied in reliability analysis is listed as follows:

  1. (1)

    Define a candidate region.

  2. (2)

    Construct an initial Kriging model with a small number of training points.

  3. (3)

    Find out an optimal point u∗ from the candidate region. u∗ is the point at which the sign of performance function has the largest risk to be wrongly predicted. This step is fulfilled with a so-call learning criterion.

  4. (4)

    Add u∗ into the DoE and update the Kriging model.

  5. (5)

    Repeat (3)–(4) until the risk of wrong sign prediction is small enough.

Following the five steps listed above, people will find out that most training points will be located in the vicinity of the limit state G(u) = 0. That means ALK model only finely approximates G(u) in this narrow region rather than throughout the candidate region. That is the main advantage of ALK model compared with other surrogate models.

Learning criterion or learning function is the key to construct an ALK model. Recall that Kriging offers the specific uncertainty information of the prediction, i.e. \( \hat{G}\left(\boldsymbol{u}\right)\sim N\left({\mu}_G\left(\boldsymbol{u}\right),{\sigma}_G\left(\boldsymbol{u}\right)\right) \). Making full use of this property, several criteria can be elaborated. Learning function U was proposed in AK-MCS (Echard et al. 2011). The famous learning function named expected feasible function (EFF) was proposed in Ref. (Bichon et al. 2008). The expected risk function (ERF) was proposed in Ref. (Yang et al. 2015), which measures the expected risk that the sign of a point is wrongly predicted by the Kriging model. The so-called failure potential-based function (FPF) was proposed in Ref. (Wang and Wang 2016), to find points probably located in the failure region and with large predicted error. Similar idea with FPF can be seen in Refs. (Chen et al. 2014; Lee and Jung 2008). Other criteria can be seen in Refs. (Sun et al. 2017; Wang and Wang 2013; Bect et al. 2012).

The size of candidate region determines the size of approximating space where the ALK model should precisely predict the sign of performance function. If the size exceeds the demand, some computational expense will be wasted; contrariwise, accuracy will be sacrificed. The candidate region of EGRA is fixed as [−5,5]n. Apparently, it is not the optimal option. Ref. (Wen et al. 2016) suggested that the minimal candidate region (MCR) should be a sphere centered on the origin with a radius

$$ \beta =\sqrt{\chi_n^{-2}\left(1-\alpha {P}_f\right)} $$
(5)

in which \( {\chi}_n^{-2}\left(\cdotp \right) \) is the inverse cumulative distribution function (CDF) of Chi-square distribution, n is the degree of freedom of Chi-square distribution or the number of input variables. The joint PDF of region outside the MCR is P{‖u‖ ≥ β} = 1 − χn(β2) = αPf. By setting the constant α as 0.05, an ALK model built in the MCR will have a relative error less than 5% during predicting Pf with MCS. However, such a MCR is infeasible because Pf is the quantity to be computed. In AK-MCS, the simulated samples of MCS are used to represent the candidate region which is verified as a good strategy. With this strategy, the ALK model just meets the necessity of MCS. This strategy has been extensively adopted by other researchers (Yang et al. 2015; Hu and Mahadevan 2016; Fauriat and Gayton 2014; Perrin 2016). However, it is not applicable to the estimation of a rare event where the size of simulated samples is required to be very large (108 to 1011). To avoid this shortcoming, replacing MCS method by IS method is a wise option.

Introducing an instrumental density function (IDF) h(u), (1) can be rewritten as

$$ {P}_f=P\left\{G\left(\boldsymbol{u}\right)<0\right\}=\int I\left(\mathbf{u}\in F\right)\frac{f\left(\boldsymbol{u}\right)}{h\left(\mathbf{u}\right)}h\left(\boldsymbol{u}\right)d\mathbf{x}=E\left[I\left(\boldsymbol{u}\in F\right)\frac{f\left(\boldsymbol{u}\right)}{h\left(\boldsymbol{u}\right)}\right] $$
(6)

Then the failure probability can be estimated as

$$ {\hat{P}}_f^{IS}=\frac{1}{N_{IS}}\sum \limits_{i=1}^{N_{IS}}I\left[G\left({\boldsymbol{u}}^{(i)}\right)<0\right]\frac{f\left({\boldsymbol{u}}^{(i)}\right)}{h\left({\boldsymbol{u}}^{(i)}\right)} $$
(7)

The corresponding variance and the coefficient of variation (Cov) are respectively given as

$$ Var\left({\hat{P}}_f^{IS}\right)=\frac{1}{N_{IS}}\left(\frac{1}{N_{IS}}\sum \limits_{i=1}^{N_{IS}}I\left[G\left({\boldsymbol{u}}^{(i)}\right)<0\right]{\left(\frac{f\left({\boldsymbol{u}}^{(i)}\right)}{h\left({\boldsymbol{u}}^{(i)}\right)}\right)}^2-{\left({\hat{P}}_f^{IS}\right)}^2\right) $$
(8)
$$ Cov\left({\hat{P}}_f^{IS}\right)=\frac{\sqrt{Var\left({\hat{P}}_f^{IS}\right)}}{{\hat{P}}_f^{IS}} $$
(9)

If the IDF is properly devised, IS method can unbiasedly estimate the failure probability with a remarkably smaller number of simulated samples than MCS. The word ‘properly’ means that the IDF should help samples of IS populate all the most probable failure regions (MPFRs) (Au and Beck 1999; Au and Beck 2001). A MPFR is a failure domain with large probability density where the main contribution of the failure probability comes from. Therefore, the main task of IS methods is the identification of MPFR.

IS methods consist of two stages: (1) identify all the MPFRs; (2) generate the simulated samples populating MPFRs and estimate the failure probability. To improve the efficiency of IS with ALK model, both stages should be elaborately tackled. In Refs. (Echard et al. 2011; Bichon et al. 2008; Dubourg et al. 2011), it has been demonstrated that ALK model is very good at efficiently predicting the sign of performance function. Therefore, it is natural to utilize ALK model to predict the sign of performance function in Stage (2). That means treating the simulated samples \( \left\{{\boldsymbol{u}}^{(1)},{\boldsymbol{u}}^{(2)},\cdots, {\boldsymbol{u}}^{\left({N}_{IS}\right)}\right\} \) as candidate points and iteratively updating the Kriging model by adding an optimal training point into the DoE until the risk of wrong sign prediction is small enough. Consequentially, the training points will be located in the neighborhood of G(u) = 0.

The key of Stage (1) lies in identifying the MPFR(s). Several methods are available to fulfill this task. AK-IS used FORM, Ref. (Zhao et al. 2015) chose MCMC, MetaAK-IS2 adopted Meta-IS. All of them are not efficient and cannot assure obtaining all the MPFRs. Moreover, the points evaluated in Stage (1) are not necessary the optimal points capable of remarkably improving the sign prediction of a Kriging model. Therefore, much more training points are still needed in Stage (2). This paper elaborates a brand-new strategy to identify the MPFRs with ALK model. That means, in Stage (1), most of the training points will be located in the neighborhood of G(u) = 0. Those training points will be made full use to improve the sign prediction of ALK model. And thus much fewer training points are required in Stage (2) than other methods.

3 ALK-CRA-IS

3.1 Basic idea

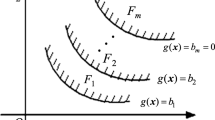
The basic idea of our strategy is to formulate a series of concentric rings to asymptotically approach the MPFR(s). As shown in Fig. 1, in the standard normal space, the center of the rings is the origin and the circular band of them is narrow. Therefore, the points in the same ring have approximate probability density and the points in the larger ring have smaller probability density. By expanding the rings step by step, the MPFR(s) will be approached by our method.

Fig. 1
figure 1

Basic idea of ALK-CRA-IS

Full size image

The basic procedure is listed as follows.

  1. (1)

    Configure an initial ring with small inner and outer radiuses.

  2. (2)

    Judge if failure region arises in the ring with ALK model.

  3. (3)

    If so, stop. Otherwise, expand the ring and do the same judgment as Step (2) until failure region arises.

The key of the proposed method lies in Step (2), i.e., how to judge if failure region exists in the current ring. We generate a population of uniformly distributed points to fill this ring. Because the circular band of the ring is narrow, an acceptable number of points can fulfill this task. Then we treat them as candidate points and build an ALK model with the procedures stated in Section 2. The ALK model is competent to predict whether failure points exist among the samples. If no failure points exist, we deem failure region does not exist or the failure region is very small; otherwise, failure region must be located in the ring. Here we expound the CRA method in detail.

3.2 Concentric ring approaching strategy

The inner radius of initial circular ring is chosen as

$$ {\beta}_{in}^{(1)}=\sqrt{\chi_n^{-2}\left(1-{P}_0\right)} $$
(10)

Here, P0 is the joint probability of the region outside the sphere centered on the origin with a radius \( {\beta}_{in}^{(1)} \) because there is \( P\left\{\left\Vert \mathbf{u}\right\Vert \ge {\beta}_{in}^{(1)}\right\}=1-{\chi}_n\left[{\left({\beta}_{in}^{(1)}\right)}^2\right]={P}_0 \); here we assign a value 0.1 to P0 so that the inner radius of initial circular ring is remarkably smaller than MCR if Pf is less than 0.1.

The outer radius is chosen as

$$ {\beta}_{out}^{(1)}=\sqrt{\chi_n^{-2}\left(1-{P}_0/{N}_{\mathrm{step}}\right)} $$
(11)

in which Nstep is a constant. \( {\beta}_{out}^{(1)}-{\beta}_{in}^{(1)} \) is the width of a circular ring and the value of Nstep determines this width. The width should not be too large or too small. If the width is too small, the number of iteration will increase. If the width is too large, the region scanned by concentric rings will be much larger than necessity and the efficiency will be reduced. In this paper, the value of Nstep is uniformly chosen as 10.

Then we generate a large number of points uniformly covering the circular band of the ring. Note that those points obey conditional distribution, i.e., they are situated in the circular band of the ring. Although MCS can be used to generate those points, we resort to MCMC which is more efficient. Denote the set of points in the ith ring as C(i). Then we build an ALK model by treating those points as candidate points. In C(i), only the sign of performance function is our concern. The uncertain information provided by a Kriging model is \( \hat{G}\left(\mathbf{u}\right)\sim N\left({\mu}_G\left(\boldsymbol{u}\right),{\sigma}_G\left(\boldsymbol{u}\right)\right) \). Therefore, the probability that \( \hat{G}\left(\boldsymbol{u}\right) \) and μG(u) have different signs can be obtained by

$$ P\left\{\hat{G}\left(\boldsymbol{u}\right){\mu}_G\left(\mathbf{u}\right)<0\right\}=1-\Phi \left(\frac{\left|{\mu}_G\left(\boldsymbol{u}\right)\right|}{\sigma_G\left(\mathbf{u}\right)}\right) $$
(12)

In which Φ(·) is the CDF of standard normal distribution. In Ref. (Echard et al. 2011), learning function U was proposed, which is given as

$$ U\left(\mathbf{u}\right)=\frac{\left|{\mu}_G\left(\boldsymbol{u}\right)\right|}{\sigma_G\left(\mathbf{u}\right)} $$
(13)

It can be seen that U(u) is inversely proportional to (12). In C(i), find out the point at which the sign of \( \hat{G}\left(\boldsymbol{u}\right) \) has the largest probability to be wrongly predicted (i.e. the point with minimum value of U(u)) and add it to the DoE, then the sign prediction of Kriging model will be largely improved. Therefore, learning function U is adopted in this paper. As stated above, various learning functions have been proposed in the field of reliability analysis until now. Several of them can be applied into our ALK-CRA-IS method and note that the adoption of different learning functions may influence the efficiency of the proposed method.

Then we develop a stopping condition to tell the ALK model when to stop in each ring. According to Refs. (Dubourg et al. 2011; Yang et al. 2018; Haeri and Fadaee 2016), the region with large probability to be negative was defined as

$$ {S}^N=\left\{\boldsymbol{u}\left|{\mu}_G\left(\boldsymbol{u}\right)\le -{\delta \sigma}_G\left(\boldsymbol{u}\right)\right.\right\} $$
(14)

In which δ = 1.96, then the probability is larger than 95%. The region with large probability to be positive was defined as

$$ {S}^P=\left\{\boldsymbol{u}\left|{\mu}_G\left(\boldsymbol{u}\right)\ge {\delta \sigma}_G\left(\boldsymbol{u}\right)\right.\right\} $$
(15)

The region in which the sign of performance function remains uncertain was defined as

$$ {S}^O=\left\{\mathbf{u}\left|-{\delta \sigma}_G\left(\boldsymbol{u}\right)\le {\mu}_G\left(\boldsymbol{u}\right)\le {\delta \sigma}_G\left(\boldsymbol{u}\right)\right.\right\} $$
(16)

Apparently, a point in SO has the minimal value of U(u) compared with points in SP and SN. Therefore, the added points must be located in SO. According to Ref. (Dubourg et al. 2011), the size of SO will shrink along with sequentially adding training points into SO. That means the size of SN will sequentially approximate to that of SN ∪ SO or the size of SP will sequentially approximate to that of SP ∪ SO. From a discrete point of view, the number of points located in SN will sequentially approximate to that of SN ∪ SO or the number of points located in SP will sequentially approximate to that of SP ∪ SO. In ALK-CRA-IS method, only the failure region is our most concern. Therefore, the stopping criterion is defined as

$$ Ratio=\frac{eps+\sum \limits_{j=1}^{N_C}I\left({\boldsymbol{u}}_C^{(j)}\in {S}^N\right)}{eps+\sum \limits_{j=1}^{N_C}I\left({\boldsymbol{u}}_C^{(j)}\in {S}^N\cup {S}^O\right)}=\frac{eps+\sum \limits_{j=1}^{N_C}I\left({\mu}_G\left({\boldsymbol{u}}_C^{(j)}\right)\le -{\delta \sigma}_G\left({\boldsymbol{u}}_i^{(j)}\right)\right)}{eps+\sum \limits_{j=1}^{N_C}I\left({\mu}_G\left({\boldsymbol{u}}_C^{(j)}\right)\le {\delta \sigma}_G\left({\boldsymbol{u}}_i^{(j)}\right)\right)} $$
(17)

where eps is a small constant to prevent the denominator from being zero, and \( \left\{{\boldsymbol{u}}_C^{(1)},{\boldsymbol{u}}_C^{(2)},\cdots, {\boldsymbol{u}}_C^{\left({N}_C\right)}\right\} \) are the set of current candidate samples. If Ratio ≥ 0.99, the Kriging model is accurate enough to predict the signs of performance function at current candidate samples.

If no points are located in SN or the size is very small, we expand the current circular ring. The ith ring closely clings to the former one so that every part of the uncertain region can be scanned. Therefore, the inner and outer radiuses of the ith(i ≥ 1) ring are defined as

$$ {\beta}_{in}^{(i)}=\sqrt{\chi_n^{-2}\left(1-{P}_{i-1}/{N}_{\mathrm{step}}\right)} $$
(18)
$$ {\beta}_{out}^{(i)}=\sqrt{\chi_n^{-2}\left(1-{P}_{i-1}/{N}_{\mathrm{step}}^2\right)} $$
(19)

Then we build an ALK model in the ith ring. Note that the previous training points can be used as the initial training points of the current ALK model. Then no training points will be wasted. The process is repeated until failure region or failure points firstly arise in a ring. However, if the number of failure points is very small, that means the size of MPFR is very small. Then we continue to expand the ring. According to our experience, for medium to low dimensional problems, one more iteration can meet the size requirement of MPFR.

Executing the iterative process stated above, NF failure points in MPFR are identified by ALK model. Denote them as \( \left\{{\boldsymbol{u}}_F^{(1)},{\boldsymbol{u}}_F^{(2)},\cdots, {\boldsymbol{u}}_F^{\left({N}_F\right)}\right\} \) and we have \( {\boldsymbol{u}}_F^{(i)}\in {S}^N \). IDF centered on those points can be defined as

$$ h\left(\mathbf{u}\right)=\frac{1}{N_F}\sum \limits_{j=1}^{N_F}N\left({\mathbf{u}}_F^{(j)},1\right) $$
(20)

A number of samples are generated according to h(u) and the samples will populate all the failure regions that mainly contribute to failure probability. Then we continually execute the active learning process stated above by treating the IS samples as candidate points. Finally, the ALK model can accurately estimate the low failure probability.

3.3 Summary of ALK-CRA-IS

The flowchart of the proposed algorithm is given in Fig. 2. The basic procedure is summarized as follows.

  1. (1)

    Transform the input variables into the standard normal space. For non-Gaussian random variables, Rosenblatt’s transformation or Rackwitz-Fiessler transformation (Luo et al. 2009) should be utilized to fulfill this task.

  2. (2)

    Define the initial DoE. The number of training points is 12 which is the same as AK-MCS. Latin Hypercube Sampling (LHS) is utilized to generate the points and the lower and upper bounds are chosen as [−5 5].

  3. (3)

    Define the initial ring by (10) and (11).

  4. (4)

    Generate a large number of samples located in the current ring by MCMC. They are treated as candidate points. The number is chosen as 104 × n with n the dimension of input random variables.

  5. (5)

    Pick out the optimal point \( {\mathbf{u}}^{\left({}^{\ast}\right)} \) by (13) from the current set of candidate points and update the Kriging model.

  6. (6)

    Repeat Step (5) until the stopping condition in (17) is satisfied.

  7. (7)

    Judge whether failure regions arise in the ring. If the number of failure points (located in SN) is very small, i.e. NF ≤ 100, we deem failure region does not exist. Expand the ring by (18)–(19) and return to Step (4).

  8. (8)

    Configure the IDF by (20) and generate a large number of important samples as candidate points. Repeat Steps (5)–(6) until the stopping condition in (17) is satisfied. Estimate the failure probability by

Fig. 2
figure 2

Flowchart of ALK-CRA-IS

Full size image
$$ {\hat{P}}_f^{IS}=\frac{1}{N_{IS}}\sum \limits_{i=1}^{N_{IS}}I\left[{\mu}_G\left({\boldsymbol{u}}^{(i)}\right)<0\right]\frac{f\left({\mathbf{u}}^{(i)}\right)}{h\left({\mathbf{u}}^{(i)}\right)} $$
(21)

4 Numerical examples

4.1 A highly nonlinear example

The first example is taken from Ref. (Echard et al. 2013) and the performance function is defined as

$$ G\left(\mathbf{u}\right)=0.5{\left({u}_1-2\right)}^2-1.5{\left({u}_2-5\right)}^3-3 $$
(22)

where u1 and u2 are two independent standard Gaussian random variables.

The initial ring and the points uniformly covering the ring is shown in Fig. 3. It can be seen that no failure points exist in this ring. The points are used as candidate points and 12 training points are used to build an initial Kriging model. Because all the candidate points are far away from the limit state, no new training points are added into the DoE and the ALK model is precise enough to predict the sign of points in Ring 1. ALK model successfully predicts no failure points exist and thus the ring is expanded. Until Ring 3, failure points firstly emerge. Treat the points in Ring 3 as candidate points and continually refine the ALK model. Only two new training points very close to the limit state are added into the DoE, the ALK model is precise enough to predict the sign of points in Ring 3. From Fig. 3, it can be seen that ALK model rightly identifies the failure points and the MPFR is rightly recognized. With the failure points located in the MPFR, Stage (2) of ALK-CRA-IS is triggered. The instrumental density function is configured and IS samples are generated, as shown in Fig. 3. With the training points in Stage (1) as initial training points and those IS samples as candidate points, ALK model is refined again. Two new training points are added into the DoE in this stage and the ALK model is competent to predict the sign of performance function at the IS samples.

Fig. 3
figure 3

Executing process of ALK-CRA-IS for example 4.1

Full size image

As shown in Table 1, ALK-CRA-IS provides a precise estimation for failure probability at a smaller expense than other methods. Note that, for AK-IS, 19 function evaluations are cost to obtain the MPP. Although the 19 points are used to build the Kriging model, they have little contribution to improving the sign prediction of Kriging model. Therefore, 7 more function evaluations are still needed in Stage (2). All the added training points are chosen for maximally improving the sign prediction of Kriging model. That is the main advantage of ALK-CRA-IS over AK-IS.

Table 1 Results of example 4.1 with different methods
Full size table

4.2 2D example with four failure regions

The second example is a performance function with four MPFRs which is defined as (Echard et al. 2011; Schueremans and Van Gemert 2005)

$$ G\left(\boldsymbol{u}\right)=\min \left\{\begin{array}{l}{k}_1+\frac{{\left({u}_1-{u}_2\right)}^2}{10}-\frac{\left({u}_1-{u}_2\right)}{\sqrt{2}}\\ {}{k}_1+\frac{{\left({u}_1-{u}_2\right)}^2}{10}+\frac{\left({u}_1-{u}_2\right)}{\sqrt{2}}\\ {}\left({u}_1-{u}_2\right)+\frac{k_2}{\sqrt{2}}\\ {}-\left({u}_1-{u}_2\right)+\frac{k_2}{\sqrt{2}}\end{array}\right\} $$
(23)

where u1 and u2 are two independent standard Gaussian random variables; k1, k2 are two constants. Two cases are considered in this example, i.e. k1 = 3, k2 = 7 and k1 = 5, k2 = 10. The results of different methods are listed in Table 2.

Table 2 Results of example 4.2 with different methods
Full size table

4.2.1 Case 1

As shown in Fig. 4, the proposed method successfully recognizes the four MPFRs with two iterations. The failure region contained in Ring 1 is very small. After 10 training points are added into the initial DoE, ALK model is capable to predict the sign of points located in Ring 1. Only about 27 failure points are predicted and thus one more iteration is executed. Ring 2 contains all the MPFRs. 22 training points located in Ring 2 and in the vicinity of the contour G(u) = 0 are added into the DoE. More than 1000 failure points are identified and thus we deem the MPFRs are large enough. In Stage (2), 104 important samples surrounding the four MPFRs are generated and ALK model is continually updated. The training points in Stage (1) have been deployed close to the limit state intersected by the four MPFRs. Therefore, in Stage (2), there is no need to add more training points in such regions. As shown in Fig. 4, most of the training points in Stage (2) get rid of such regions. That means all the training points in Stage (1) are made full use in ALK-CRA-IS method.

Fig. 4
figure 4

Executing process of ALK-CRA-IS for example 4.2(case 1)

Full size image

From Table 2, it can be seen that ALK-CRA-IS accurately predicts the failure probability with a remarkably fewer function evaluations than other methods. Note that AK-IS is not applicable to this example because multiple failure regions exist. Obtaining only one MPP cannot favor the IS samples to populate all the main failure regions and biased estimation will be obtained. For MetaAK-IS2, the training points in Stage (1) are not necessary the optimal points to improve the sign prediction of Kriging model. Therefore, a large number of training points are still required in Stage (2). Achieving satisfactory estimations with similar coefficients of variation, ALK-CRA-IS costs 68 fewer function evaluations than MetaAK-IS2.

4.2.2 Case 2

The “true” failure probability is 8.95 × 10−7 which is obtained by MCS with 6 × 108 simulations. The active learning process of the proposed method is illustrated in Fig. 5. It can be seen that ALK-CRA-IS manages to identify the four failure regions by sequentially expanding the ring five times. After all the MPFRs are obtained, importance samples surrounding them are generated and IS method can be efficiently executed. Only 104 importance samples are enough to obtain an unbiased estimation with a Cov about 2.5%. By treating them as candidate samples, ALK model can be efficiently established. That is why the method combining ALK model with IS method is researched in this paper.

Fig. 5
figure 5

Executing process of ALK-CRA-IS for example 4.2(case 2)

Full size image

From Fig. 5, it also can be seen that most of the training points for identifying the MPFRs are located in the vicinity of limit state surface. They have largely improved the sign prediction of an ALK model. On the other hand, the training points of Meta-IS2 in Stage (1) are not necessarily located near the limit state surface, as shown in Fig. 6. Although similar number of training points are required in Stage (1), much fewer training points are required in Stage (2) for the proposed method. That is the main reason why ALK-CRA-IS saves 32 training points in total compared with MetaAK-IS2.

Fig. 6
figure 6

Executing process of Meta-IS2 for example 4.2(case 2)

Full size image

4.2.3 Performances of different learning functions

Note that except for learning function U, various learning functions are applicable to ALK-CRA-IS. The performances of some representative ones, such as ERF, EFF, and FPF, when they are applied to ALK-CRA-IS are compared in the subsection. The results are given in Table 2. Note that the initial training points, the stopping conditions, the candidate points in each ring and candidate points of importance samples are kept the same for different learning functions during this comparison. It can be seen that U, ERF and EFF, which focus on rightly predicting the sign of performance function, have similar performance for both cases. While, all of them behave better than FPF. That is because FPF tends to choose points located in the failure region and points with large predicted error, even if a point has little contribution to improving the sign prediction of a Kriging model. This feature makes it waste some extent of training points when it is applied into ALK-CRA-IS. Figure 7 gives the iterative process in the fifth ring with different learning functions. It can be seen that, with different learning functions, the proposed strategy smoothly converges to the stopping condition of (17). That reflects the robustness of the proposed method.

Fig. 7
figure 7

Iterative process in the fifth ring of ALK-CRA-IS with different learning functions (example 4.2.2)

Full size image

4.3 A non-linear oscillator

A non-linear oscillator with a moderate dimensionality of inputs is investigated here (Echard et al. 2013). As shown in Fig. 8, the oscillator is subject to a rectangular pulse load. The performance function is defined as

$$ G\left({c}_1,{c}_2,m,r,{t}_1,{F}_1\right)=3r-\left|\frac{2{F}_1}{m{\omega}_0^2}\sin \left(\frac{\omega_0{t}_1}{2}\right)\right| $$
(24)

where \( {\omega}_0=\sqrt{\left({c}_1+{c}_2\right)/m} \). The six random variables are given in Table 3. Two cases are studied in this example. It is worth emphasizing that both cases have very low failure probability. The benchmark solutions are obtained by MCS with 1.8 × 108 and 9 × 1010 samples respectively.

Fig. 8
figure 8

A non-linear oscillator

Full size image
Table 3 Random variables of the non-linear oscillator
Full size table

Results obtained by different methods are listed in Table 4. Again, it can be seen that ALK-CRA-IS shows remarkable advantages in terms of accuracy and efficiency. Only a single MPP exists in the performance function. Therefore, AK-IS behaves very well in accuracy. In efficiency, although 29 points are evaluated to search for the MPP in Stage (1), they produce little benefit on improving the sign prediction of Kriging model. Therefore, 38 new training points are still required in Stage (2). However, the points for identifying the MPFR are made full use and they do a large favor on improving the sign prediction of Kriging model. Therefore, only a little number of training points are required in Stage (2). That is why ALK-CRA-IS can be more efficient than AK-IS.

Table 4 Results of example 4.4 with different methods
Full size table

4.4 Vehicle side impact problem

This problem comes from Refs. (Wang and Wang 2016; Youn et al. 2004). The performance function is defined as

$$ G\left(\mathbf{x}\right)=0.489{x}_1{x}_4+0.843{x}_2{x}_3\hbox{-} 0.0432{x}_5{x}_6+0.0556{x}_5{x}_7+0.000786{x}_7^2-0.75 $$
(25)

where x = [x1, ⋯, x7] are random variables, details about them can be seen in Table 5. G(x) represents whether the side impact of a car satisfies the regulated requirement with known uncertainties.

Table 5 Random variables of the vehicle side impact problem
Full size table

The results obtained by each method are listed in Table 6. It can be seen that the performance of the proposed method outperforms other methods in terms of Ncalls for obtaining satisfactory estimation with a similar Cov. From the last column, it can also be seen that several learning functions can be applied into ALK-CRA-IS and the learning functions which focus on improving the sign prediction of Kriging model are more appropriate than the one which focuses on approximating the failure region.

Table 6 Results of example 4.4 with different methods
Full size table

5 Conclusion

Reliability methods based on ALK model are competent to accurately estimate the failure probability with as few function evaluations as possible. However, the estimation of low failure probability remains an issue in this field. Several strategies have been proposed to fuse ALK model with IS methods. This paper proposes a brand-new methodology, i.e. ALK-CRA-IS, in this context. The key of the proposed method is the identification of all the MPFRs. The basic idea is the formation of serial concentric rings in the standard normal space. In a small ring, active learning process is executed to build a Kriging model rightly predicting the sign of performance function. And then the ALK model is utilized to judge whether failure region arises in the current ring. If not, the ring is expanded and Kriging model is updated in the new ring. By expanding the ring step by step, all the MPFRs can be approached by our method. And then IS samples populating all the MPFRs can be generated and active learning process is executed by treating the IS samples as candidate points.

Four cases are researched to demonstrate the accuracy and efficiency of the proposed method. Compared with AK-IS, ALK-CRA-IS is capable of identifying all the MPFRs and obtaining unbiased estimation for performance functions with multiple failure regions. Compared with AK-IS and MetaAK-IS2, ALK-CRA-IS is more efficient because all the points evaluated in Stage (1) are made full use to improve the sign prediction of Kriging model and thus much fewer training points are needed in Stage (2). In one word, the proposed method is more efficient than other ALK-model-based IS methods.

However, we should admit that ALK-CRA-IS is not applicable to high dimensional problems. In Stage (1) of ALK-CRA-IS, a population of points is required to fill the ring. However, the circular band of a ring can intensively expand as the increase of the dimensionality. For high dimensional problems, a very large number of points are needed so that a ring can be totally covered. And then purely building an ALK model will be very time-consuming like AK-MCS. Another strategy which can alleviate the dimension problem is under research by the authors.