Reliability and global sensitivity analysis based on importance directional sampling and adaptive Kriging model

Abstract

This paper adopts importance directional sampling (IDS) and adaptive Kriging model for reliability and global sensitivity analysis. IDS is the combination of importance sampling (IS) and directional sampling (DS) by establishing directional vector in the importance region, which has the advantages of both IS and DS. A novel stopping criterion which tries to minimize the difference between the real failure region and fitted failure region is proposed based on the idea of auxiliary region to increase the efficiency of active learning. An improved active learning strategy is proposed based on the combination of optimization and learning function to synchronize the calculation process of design point and Kriging model updating, so as to ensure the accuracy of both Kriging model and importance directional density function. Different learning functions are adopted to select the most suitable active learning function of IDS. The global sensitivity index is calculated through failure probability and Bayes theorem based on Gaussian mixture model (GMM). The results show that: Through the proposed auxiliary region-based stopping criterion, the efficiency of active learning in IDS can be improved. The proposed active learning strategy can obtain high accuracy importance directional density function and failure probability with lower required function calls. Considering the accuracy and robustness of failure probability and global sensitivity index, U and EFF functions should be adopted on IDS.

1 Introduction

Reliability and global sensitivity analysis theory is a very important research content, which has been widely used in many engineering problems (Rachedi et al. 2021; Hwang et al. 2021; Pan et al. 2021; Su et al. 2020; Mansour et al. 2020). Presently, reliability methods mainly include numerical simulation methods and moment estimation methods. Numerical simulation methods usually require a large number of random samples, and the efficiency is quite low. Moment estimation methods use the Taylor expansion of the limit state function, and the accuracy will be low for high nonlinearity problems. Global sensitivity analysis methods mainly include variance-based method (Zhang et al. 2017), moment independent-based method (Liu and Homma 2010) and failure probability-based method (Lu et al. 2008). The global sensitivity based on failure probability can more comprehensively measure the average impact of the input variables on the failure probability when the input variables are changed in the entire distribution region (Lemaitre et al. 2015). Through the global sensitivity analysis, the uncertain factors which significantly affect the failure probability can be obtained. Specially, by introducing Bayes theorem into failure probability-based global sensitivity analysis, the computational cost can be significantly reduced (Wang et al. 2019). Since the Bayes method requires the conditional probability density function of input variable in the failure region, it is usually combined with numerical simulation methods for global sensitivity analysis (Guo et al. 2021).

In order to increase the efficiency of numerical simulation methods, most researchers use surrogate model to reduce the required function calls. The most widely used surrogate model is adaptive Kriging model (Zhang et al. 2020; Wang et al. 2021; Xiao et al. 2020a, b; Cadini et al. 2020), as it can provide the variance information of the predicted values and select the most informative samples through learning function. Notably, AK-MCS (Echard et al. 2011) is a milestone in the development of Kriging-based methods, as AK-MCS combines the U learning function and Monte Carlo (MC) method. Based on the idea of AK-MCS, different learning functions (Bichon et al. 2008; Zhang et al. 2019; Yang 2015; Lv et al. 2015; Shi et al. 2020; Meng et al. 2020; Zhou and Li 2023) and stopping criterions (Wang and Shafieezadeh 2019a, b) are also proposed. Researchers also used MC-based failure probability for global sensitivity analysis (Guo et al. 2021). However, a large population of candidate samples are required for MC-based active learning. At least $10^{M + 2} ,\,M = 1,2, \cdot \cdot \cdot$ samples are required for the failure probability with $10^{ - M}$ (Lelièvre et al. 2018), where $M$ is the order of magnitude of failure probability. For small failure probability problems, MC cannot obtain failure samples effectively, which may completely fill the computer memory and lead to computing crash.

In order to solve the shortcomings of MC, researchers often combine other numerical methods with Kriging model, such as importance sampling (IS) (Zhao et al. 2015; Wang et al. 2022; Zhou et al. 2015), subset simulation (SS) (Chen et al. 2021; Tian et al. 2021), line sampling (LS) (Song et al. 2021; Papaioannou and Straub 2021), and directional sampling (DS) (Grooteman 2011). This paper mainly focus on IS and DS methods. Presently, IS might be the most widely used method to improve efficiency. Reference (Echard et al. 2013) proposed the famous AK-IS method, in which sampling center was transplanted to the design point and Kriging model was built through U learning function. Reference (Dubourg et al. 2013) proposed a metamodel-based IS method to approximate the optimal IS density function. Reference (Zhu et al. 2020) proposed a Meta-IS-AK method combining AK-IS and Meta-IS. Reference (Xiao et al. 2020a, b) proposed combined meta-model and stratified IS for reliability analysis. Reference (Zhang et al. 2020) proposed an improved IS method with multiple sampling centers defined by the U learning function. Reference (Yun et al. 2020) proposed a radial-based IS method to increase the efficiency of AK-MCS, and the U learning function was adopted. Reference (Chen et al. 2022) proposed a parallel active learning strategy based on K-medoids clustering and IS.

Compared with IS, DS can reduce the dimension of variable space. Sample points are generated based on the directional vector, and the required candidate samples can be significantly reduced. Reference (Zhang et al. 2021) proposed the AK-DS method, which combined DS and adaptive Kriging through U function. The results show that the required computational cost and computer memory of DS are much lower than those of IS. Specially, importance directional sampling (IDS) is the combination of DS and IS by establishing the directional vector in the importance region. Based on DS, IDS can obtain the failure samples more effectively, and the computational efficiency could be highly improved (Zhang et al. 2022). Reference (Guo et al. 2020) used the design point-based IDS and adaptive Kriging model for reliability analysis. However, in previous studies, U learning function is often adopted for IS- and DS-based Kriging methods. Recent study (Yun et al. 2021) has shown that the stopping criterion of U function is too conservative, which may lead to many redundant training samples. Moreover, in the design point-based IDS method, in addition to the number of IDS samples, the main factor that affects the accuracy is whether the importance directional density function can represent the location of failure region accurately. The accuracy of design point will inevitably affect the accuracy of the method. Reference (Guo et al. 2020) used the approximate design point to establish importance directional density function. However, the approximate degree is not specified, and the calculation of design point is before the establishment of Kriging model through learning function. The model accuracy is quite low at this time, and the precision of the fitted limit state boundary may be poor. This may lead to low accuracy of approximate design point, which may lead to improper importance directional density function. Some researchers suggest that to ensure the accuracy of design point, the condition ${{\left\| {{\mathbf{y}}_{i}^{*} - {\mathbf{y}}_{i - 1}^{*} } \right\|} \mathord{\left/ {\vphantom {{\left\| {{\mathbf{y}}_{i}^{*} - {\mathbf{y}}_{i - 1}^{*} } \right\|} {\left\| {{\mathbf{y}}_{i - 1}^{*} } \right\|}}} \right. \kern-0pt} {\left\| {{\mathbf{y}}_{i - 1}^{*} } \right\|}} < \delta$, where ${\mathbf{y}}_{i}^{*}$ is the design point in the $i$-th iteration and $\delta$ is a small positive constant in standard normal space, should be met (Jia and Wu 2022). As IDS method also needs to update Kriging model in the sample space defined by importance direction density function, using this strategy will inevitably generate many redundant training samples around the real design point, thus significantly increasing the required function calls.

This paper proposes a novel active learning strategy for IDS and adaptive Kriging model for reliability and failure probability-based global sensitivity analysis to solve the above problems, which is called Adaptive Kriging-Importance Directional Sampling-Reliability and Global Sensitivity (AK-IDS-RGS) method. First, an improved stopping criterion is proposed based on the idea of auxiliary region (Katafygiotis et al. 2007) to solve the problem that the stopping criterion of U function is too conservative. Then, an improved active learning strategy is proposed through the combination of optimization calculation and learning function, which realizes the synchronous updating of importance directional density function and Kriging model for the design point-based IDS, so as to ensure the accuracy of both Kriging model and importance directional density function with higher efficiency and avoid the problem of only using approximate design point. Finally, the failure probability and failure samples obtained by IDS are adopted for variable global sensitivity analysis.

2 Importance directional sampling

DS is a uniform sampling strategy in the whole sample space. If the directional vector is only established in the importance region, DS will change into IDS. When the input random variables are converted to standard normal variables ${\mathbf{Y}} = \left( {Y_{1} ,Y_{2} , \cdot \cdot \cdot ,Y_{n} } \right)$, the failure probability is calculated by:

$$p_{f} = \int_{{\mathbf{B}}} {\frac{{\left[ {1 - F_{{\chi^{2} }} \left( {r_{b}^{2} } \right)} \right]f_{{\mathbf{A}}} \left( {\mathbf{b}} \right)}}{{p_{{\mathbf{B}}} \left( {\mathbf{b}} \right)}}p_{{\mathbf{B}}} \left( {\mathbf{b}} \right){\text{d}}{\mathbf{b}}}$$

(1)

where ${\mathbf{B}}$ is the importance direction of ${\mathbf{Y}}$. $p_{{\mathbf{B}}} \left( {\mathbf{b}} \right)$ is the importance directional density function. $F_{{\chi^{2} }} \left( {\mathbf{ \cdot }} \right)$ is the cumulative distribution function of Chi-square distribution. $r_{b}$ is the module of IDS sample point ${\mathbf{b}}$.$f_{{\mathbf{A}}} \left( {\mathbf{b}} \right)$ is the uniform directional density function, which is expressed as:

$$f_{{\mathbf{A}}} \left( {\mathbf{b}} \right) = {{\Gamma \left( {{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0pt} 2}} \right)} \mathord{\left/ {\vphantom {{\Gamma \left( {{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0pt} 2}} \right)} {\left( {2\pi^{{{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0pt} 2}}} } \right)}}} \right. \kern-0pt} {\left( {2\pi^{{{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0pt} 2}}} } \right)}}$$

(2)

The IDS point ${\mathbf{b}}_{i} \left( {i = 1,2, \cdot \cdot \cdot ,N_{IDS} } \right)$ can be generated through $p_{{\mathbf{B}}} \left( {\mathbf{b}} \right)$. Then Eq. (1) is estimated by:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} = \frac{1}{{N_{IDS} }}\sum\limits_{i = 1}^{{N_{IDS} }} {I\left( { - r_{{{\mathbf{b}}i}} } \right)\left[ {1 - F_{{\chi^{2} }} \left( {r_{{{\mathbf{b}}i}}^{2} } \right)} \right]\frac{{f_{{\mathbf{A}}} \left( {{\mathbf{b}}_{i} } \right)}}{{p_{{\mathbf{B}}} \left( {{\mathbf{b}}_{i} } \right)}}}$$

(3)

where $I\left( \cdot \right)$ is the indicator function of $r_{{{\mathbf{b}}i}}$. If $r_{{{\mathbf{b}}i}} > 0$, $I\left( { - r_{{{\mathbf{b}}i}} } \right) = 1$, otherwise $I\left( { - r_{{{\mathbf{b}}i}} } \right) = 0$. $I\left( { - r_{{{\mathbf{b}}i}} } \right)$ is introduced here considering that there is no intersection at the limit state boundary along the direction of ${\mathbf{b}}_{i}$ under the case of $r_{{{\mathbf{b}}i}} < 0$. The variance of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}$ can be obtained by calculating the variance at both ends of Eq. (3), which is estimated by:

$$\begin{gathered} {\text{Var}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} } \right) = {\text{Var}}\left[ {\frac{1}{{N_{IDS} }}\sum\limits_{i = 1}^{{N_{IDS} }} {I\left( { - r_{{{\mathbf{b}}i}} } \right)\left[ {1 - F_{{\chi^{2} }} \left( {r_{{{\mathbf{b}}i}}^{2} } \right)} \right]\frac{{f_{{\mathbf{A}}} \left( {{\mathbf{b}}_{i} } \right)}}{{p_{{\mathbf{B}}} \left( {{\mathbf{b}}_{i} } \right)}}} } \right] = \frac{1}{{N_{IDS}^{2} }}\sum\limits_{i = 1}^{{N_{IDS} }} {{\text{Var}}} \left[ {I\left( { - r_{{{\mathbf{b}}i}} } \right)\left[ {1 - F_{{\chi^{2} }} \left( {r_{{{\mathbf{b}}i}}^{2} } \right)} \right]\frac{{f_{{\mathbf{A}}} \left( {{\mathbf{b}}_{i} } \right)}}{{p_{{\mathbf{B}}} \left( {{\mathbf{b}}_{i} } \right)}}} \right] \hfill \\ \, = \frac{1}{{N_{IDS} }}{\text{Var}}\left[ {I\left( { - r_{{{\mathbf{b}}i}} } \right)\left[ {1 - F_{{\chi^{2} }} \left( {r_{{{\mathbf{b}}i}}^{2} } \right)} \right]\frac{{f_{{\mathbf{A}}} \left( {{\mathbf{b}}_{i} } \right)}}{{p_{{\mathbf{B}}} \left( {{\mathbf{b}}_{i} } \right)}}} \right] = \frac{1}{{N_{IDS} }}{\text{Var}}\left[ {I\left( { - r_{{\mathbf{b}}} } \right)\left[ {1 - F_{{\chi^{2} }} \left( {r_{{\mathbf{b}}}^{2} } \right)} \right]\frac{{f_{{\mathbf{A}}} \left( {\mathbf{b}} \right)}}{{p_{{\mathbf{B}}} \left( {\mathbf{b}} \right)}}} \right] \hfill \\ \, \approx \frac{1}{{N_{IDS} - 1}}\left\{ {\frac{1}{{N_{IDS} }}\sum\limits_{i = 1}^{{N_{IDS} }} {\left[ {I\left( { - r_{{{\mathbf{b}}i}} } \right)\left[ {1 - F_{{\chi^{2} }} \left( {r_{{{\mathbf{b}}i}}^{2} } \right)} \right]\frac{{f_{{\mathbf{A}}} \left( {{\mathbf{b}}_{i} } \right)}}{{p_{{\mathbf{B}}} \left( {{\mathbf{b}}_{i} } \right)}}} \right]^{2} - \left[ {\frac{1}{{N_{IDS} }}\sum\limits_{i = 1}^{{N_{IDS} }} {I\left( { - r_{{{\mathbf{b}}i}} } \right)\left[ {1 - F_{{\chi^{2} }} \left( {r_{{{\mathbf{b}}i}}^{2} } \right)} \right]\frac{{f_{{\mathbf{A}}} \left( {{\mathbf{b}}_{i} } \right)}}{{p_{{\mathbf{B}}} \left( {{\mathbf{b}}_{i} } \right)}}} } \right]^{2} } } \right\} \hfill \\ \, = \frac{1}{{N_{IDS} - 1}}\left\{ {\frac{1}{{N_{IDS} }}\sum\limits_{i = 1}^{N} {\left[ {I\left( { - r_{{{\mathbf{b}}i}} } \right)\left[ {1 - F_{{\chi^{2} }} \left( {r_{{{\mathbf{b}}i}}^{2} } \right)} \right]^{2} \frac{{f_{{\mathbf{A}}} \left( {{\mathbf{b}}_{i} } \right)^{2} }}{{p_{{\mathbf{B}}} \left( {{\mathbf{b}}_{i} } \right)^{2} }}} \right] - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{2} } } \right\} \hfill \\ \end{gathered}$$

(4)

The COV of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}$ can be calculated by ${\text{Cov}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} } \right) = {{\sqrt {{\text{Var}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} } \right)} } \mathord{\left/ {\vphantom {{\sqrt {{\text{Var}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} } \right)} } {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} }}} \right. \kern-0pt} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} }}$.

In order to determine $p_{{\mathbf{B}}} \left( {\mathbf{b}} \right)$, the following methodology based on the design point could be adopted. In standard normal space, the tangent plane $Z_{L}$ of the limit state boundary $Z = g_{{\mathbf{Y}}} \left( {\mathbf{Y}} \right) = 0$ at the design point ${\mathbf{y}}^{{\mathbf{*}}}$ is expressed as:

$$Z_{L} = \left\| {\nabla g_{{\mathbf{Y}}} \left( {{\mathbf{y}}^{{\mathbf{*}}} } \right)} \right\|\left( {\beta - R{{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{B}}} \right) = 0$$

(5)

where ${{\varvec{\upalpha}}}_{{\mathbf{Y}}}$ is the directional vector at the design point, that is, ${{\varvec{\upalpha}}}_{{\mathbf{Y}}} = - {{\nabla g_{{\mathbf{Y}}} \left( {{\mathbf{y}}^{{\mathbf{*}}} } \right)} \mathord{\left/ {\vphantom {{\nabla g_{{\mathbf{Y}}} \left( {{\mathbf{y}}^{{\mathbf{*}}} } \right)} {\left\| {\nabla g_{{\mathbf{Y}}} \left( {{\mathbf{y}}^{{\mathbf{*}}} } \right)} \right\|}}} \right. \kern-0pt} {\left\| {\nabla g_{{\mathbf{Y}}} \left( {{\mathbf{y}}^{{\mathbf{*}}} } \right)} \right\|}}$. $\beta$ is the reliability index. $\left\| {\mathbf{ \cdot }} \right\|$ is the norm of vector. For Eq. (5), in order to make $Z_{L} < 0$, $R{{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{B}} > \beta$ is required. That is, the directional vector which satisfies the condition ${{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{B}} > 0$ can direct to the importance region. If $\beta$ is obtained, $p_{f}$ can be approximately calculated by $p_{f} \approx \Phi \left( { - \beta } \right)$, where $\Phi \left( \cdot \right)$ is the cumulative distribution function of standard normal distribution. If only the importance region with ${{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{B}} > 0$ is considered, submit $\Phi \left( { - \beta } \right)$ into Eq. (1), the following integral can be obtained based on Eq. (1):

$$\int_{{{{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{B}} > 0}} {\frac{1}{{\Phi \left( { - \beta } \right)}}\left\{ {1 - F_{{\chi^{2} }} \left[ {{{\beta^{2} } \mathord{\left/ {\vphantom {{\beta^{2} } {\left( {{{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{b}}} \right)^{2} }}} \right. \kern-0pt} {\left( {{{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{b}}} \right)^{2} }}} \right]} \right\}} f_{{\mathbf{A}}} \left( {\mathbf{b}} \right){\text{d}}{\mathbf{b}} \approx 1$$

(6)

Based on Eq. (6), $p_{{\mathbf{B}}} \left( {\mathbf{b}} \right)$ can be selected as:

$$p_{{\mathbf{B}}} \left( {\mathbf{b}} \right) = \frac{1}{{\Phi \left( { - \beta } \right)}}\left\{ {1 - F_{{\chi^{2} }} \left[ {{{\beta^{2} } \mathord{\left/ {\vphantom {{\beta^{2} } {\left( {{{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{b}}} \right)^{2} }}} \right. \kern-0pt} {\left( {{{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{b}}} \right)^{2} }}} \right]} \right\}f_{{\mathbf{A}}} \left( {\mathbf{b}} \right)$$

(7)

When the directional vector meets the condition ${{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{B}} > 0$, the generated IDS samples ${\mathbf{b}}$ are all located in the region $Z_{L} < 0$. If the nonlinearity degree of $Z$ is low, $Z$ can be approximated by $Z_{L}$ around the design point, and Eq. (7) can completely cover the importance region. If the nonlinearity degree of $Z$ at the design point is high, $Z$ cannot be approximated by $Z_{L}$. The region $Z < 0$ is not completely included in $Z_{L} < 0$, and the direction ${{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{B}} < 0$ should also be considered. In order to ensure that the samples fall into the region $Z_{L} \ge 0 \cap Z < 0$, a combination coefficient $p$ could be adopted to combine Eqs. (7) and (2), as shown in Eq. (8):

$$p_{{\mathbf{B}}} \left( {\mathbf{b}} \right) = \left\{ {p + \frac{1 - p}{{\Phi \left( { - \beta } \right)}}\left\{ {1 - F_{{\chi^{2} }} \left[ {{{\beta^{2} } \mathord{\left/ {\vphantom {{\beta^{2} } {\left( {{{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{b}}} \right)^{2} }}} \right. \kern-0pt} {\left( {{{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{b}}} \right)^{2} }}} \right]} \right\}f_{{\mathbf{A}}} \left( {\mathbf{b}} \right)} \right\}$$

(8)

by defining $p$, the application scope of Eq. (7) can be expanded, which makes it more suitable for the limit state function with high nonlinearity. $p$ is generally a small constant, which is usually assumed in the interval $\left[ {0,0.2} \right]$. If the nonlinearity degree of limit state function is high, $p$ can be appropriately increased. Specially, if $p = 0$, all samples are located in the region $Z_{L} < 0$.

In order to generate samples based on Eq. (8), a following distribution is defined:

$$F_{V} \left( v \right) = \left\{ {\begin{array}{ll} {p\Phi \left( v \right)} & {v \le \beta } \\ {p\Phi \left( v \right) + \left( {1 - p} \right)\left[ {1 - \frac{{\Phi \left( { - v} \right)}}{{\Phi \left( { - \beta } \right)}}} \right]} & {v > \beta } \\ \end{array} } \right.$$

(9)

If random samples are generated for variable $V$, the directional vector ${\mathbf{Y}} + \left( {V - {{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{Y}}} \right){{\varvec{\upalpha}}}_{{\mathbf{Y}}}$ is distributed on both sides of $Z_{L} = 0$. In order to generate random sample $v$, random samples $u$ could be generated firstly based on standard uniform distribution, and $v$ could be calculated by:

$$v = \left\{ {\begin{array}{ll} {\Phi ^{{ - 1}} \left( {{u \mathord{\left/ {\vphantom {u p}} \right. \kern-\nulldelimiterspace} p}} \right)} & {u \le p,\Phi ^{{ - 1}} \left( {{u \mathord{\left/ {\vphantom {u p}} \right. \kern-\nulldelimiterspace} p}} \right) \le \beta } \\ { - \Phi ^{{ - 1}} \left[ {\frac{{\Phi \left( { - \beta } \right)\left( {1 - u} \right)}}{{1 - p + p\Phi \left( { - \beta } \right)}}} \right]} & {{\text{else}}} \\ \end{array} } \right.$$

(10)

Once $v$ are obtained, the corresponding IDS sample ${\mathbf{b}}$ could be obtained, that is:

$${\mathbf{b}} = {{\left[ {{\mathbf{y}} + \left( {v - {{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{y}}} \right){{\varvec{\upalpha}}}_{{\mathbf{Y}}} } \right]} \mathord{\left/ {\vphantom {{\left[ {{\mathbf{y}} + \left( {v - {{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{y}}} \right){{\varvec{\upalpha}}}_{{\mathbf{Y}}} } \right]} {\left\| {{\mathbf{y}} + \left( {v - {{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{y}}} \right){{\varvec{\upalpha}}}_{{\mathbf{Y}}} } \right\|}}} \right. \kern-0pt} {\left\| {{\mathbf{y}} + \left( {v - {{\varvec{\upalpha}}}_{{\mathbf{Y}}}^{{\mathbf{T}}} {\mathbf{y}}} \right){{\varvec{\upalpha}}}_{{\mathbf{Y}}} } \right\|}}$$

(11)

Then the failure probability could be calculated by Eq. (3).

3 Global sensitivity analysis based on failure probability and Bayes theorem

Based on failure probability, the impact of $i{\text{th}}$ variable $Y_{i}$ is measured by:

$$s\left( {y_{i} } \right) = \left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} - p_{f} \left( {F|y_{i} } \right)} \right|$$

(12)

where $p_{f} \left( {F|y_{i} } \right)$ is the conditional failure probability, which is defined as:

$$p_{f} \left( {F|y_{i} } \right) = P\left\{ {g\left( {\mathbf{Y}} \right) \le 0|y_{i} } \right\}$$

(13)

Based on Bayes theorem, $p_{f} \left( {F|y_{i} } \right)$ is rewritten as:

$$p_{f} \left( {F|y_{i} } \right) = {{\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} f_{{Y_{i} }} \left( {y_{i} |F} \right)} \right)} \mathord{\left/ {\vphantom {{\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} f_{{Y_{i} }} \left( {y_{i} |F} \right)} \right)} {f_{{Y_{i} }} \left( {y_{i} } \right)}}} \right. \kern-0pt} {f_{{Y_{i} }} \left( {y_{i} } \right)}}$$

(14)

where $f_{{Y_{i} }} \left( {y_{i} |F} \right)$ is conditional probability density function of $Y_{i}$ in the failure region. Then the global sensitivity index could be calculated by:

$$\eta_{i} = \frac{1}{2}\int_{{Y_{i} }} {\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} - p_{f} \left( {F|y_{i} } \right)} \right|f_{{Y_{i} }} \left( {y_{i} } \right){\text{d}}y_{i} } = \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} }}{2}\int_{{Y_{i} }} {\left| {f_{{Y_{i} }} \left( {y_{i} } \right) - f_{{Y_{i} }} \left( {y_{i} |F} \right)} \right|{\text{d}}y_{i} }$$

(15)

where $f_{{Y_{i} }} \left( {y_{i} |F} \right)$ is the conditional probability density function of $Y_{i}$. Equation (15) could be calculated by discreting $f_{{Y_{i} }} \left( {y_{i} } \right)$ and $f_{{Y_{i} }} \left( {y_{i} |F} \right)$ in the entire distribution region of $Y_{i}$, that is:

$$\eta_{i} = \frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} }}{2}\sum\limits_{j = 1}^{{N_{dis} }} {\left| {f_{{Y_{ij} }} \left( {y_{ij} } \right) - f_{{Y_{ij} }} \left( {y_{ij} |F} \right)} \right|\Delta \left( f \right)}$$

(16)

where $\Delta \left( f \right)$ is the width of discrete interval of $Y_{i}$. $N_{dis}$ is the number of discrete points. $f_{{Y_{ij} }} \left( {y_{ij} } \right)$ and $f_{{Y_{ij} }} \left( {y_{ij} |F} \right)$ are the probability density function and the conditional probability density function values of $Y_{i}$ at the $j{\text{ - th}}$ discrete point. In standard normal space, the distribution region of random variables could be defined in the interval of [− 5,5] (Zhang et al. 2019). In Refs. (Wang et al. 2019; Guo et al. 2021; Lei et al. 2022), kernel density estimation is adopted to build $f_{{Y_{i} }} \left( {y_{i} |F} \right)$. However, it has some limitations, such as the bandwidth has a great impact on the estimation results, and the fitting of edge data is easy to make mistakes. In this paper, Gaussian mixture model (GMM) (Lu et al. 2017), which has stronger applicability than KDE, is used to fit $f_{{Y_{i} }} \left( {y_{i} |F} \right)$. The expression of GMM is:

$$f\left( {{\mathbf{y}}_{i} } \right) = \sum\limits_{k = 1}^{M} {\pi_{k} N\left( {{\mathbf{y}}_{i} |{{\varvec{\upmu}}}_{k} ,{{\varvec{\updelta}}}_{k} } \right)}$$

(17)

where $N\left( \cdot \right)$ is the probability density function of normal distribution.$M$ is the number of Gaussian distributions. $\pi_{k}$ is the weight, and $\sum\limits_{k = 1}^{M} {\pi_{k} = 1}$. ${{\varvec{\upmu}}}_{k} ,{{\varvec{\updelta}}}_{k}$ are the mean and covariance matrix of the $k{\text{th}}$ Gaussian distribution, respectively. In order to estimate ${{\varvec{\upmu}}}_{k} ,{{\varvec{\updelta}}}_{k}$ and $\pi_{k}$, expectation maximization (EM) method is often adopted, as shown in Eqs. (18)–(21).

$$\tau_{ij}^{k} = {{\left[ {\pi_{j} N\left( {{\mathbf{y}}_{i} |{{\varvec{\upmu}}}_{j} ,{{\varvec{\updelta}}}_{j} } \right)} \right]} \mathord{\left/ {\vphantom {{\left[ {\pi_{j} N\left( {{\mathbf{y}}_{i} |{{\varvec{\upmu}}}_{j} ,{{\varvec{\updelta}}}_{j} } \right)} \right]} {\left[ {\sum\limits_{k = 1}^{M} {\left( {{\mathbf{y}}_{i} |{{\varvec{\upmu}}}_{k} ,{{\varvec{\updelta}}}_{k} } \right)} } \right]}}} \right. \kern-0pt} {\left[ {\sum\limits_{k = 1}^{M} {\left( {{\mathbf{y}}_{i} |{{\varvec{\upmu}}}_{k} ,{{\varvec{\updelta}}}_{k} } \right)} } \right]}}$$

(18)

$$\pi_{i}^{k + 1} = \frac{1}{{n_{d} }}\sum\limits_{j = 1}^{{n_{d} }} {\tau_{ij}^{k} }$$

(19)

$$\mu_{i}^{k + 1} = {{\left[ {\sum\limits_{j = 1}^{{n_{d} }} {\left( {\tau_{ij}^{k} {\mathbf{y}}_{j} } \right)} } \right]} \mathord{\left/ {\vphantom {{\left[ {\sum\limits_{j = 1}^{{n_{d} }} {\left( {\tau_{ij}^{k} {\mathbf{y}}_{j} } \right)} } \right]} {\left( {\sum\limits_{j = 1}^{{n_{d} }} {\tau_{ij}^{k} } } \right)}}} \right. \kern-0pt} {\left( {\sum\limits_{j = 1}^{{n_{d} }} {\tau_{ij}^{k} } } \right)}}$$

(20)

$$\delta_{i}^{k + 1} = {{\left\{ {\sum\limits_{j = 1}^{{n_{d} }} {\left[ {\tau_{ij}^{k} \left( {{\mathbf{y}}_{j} - {{\varvec{\upmu}}}_{i}^{k} } \right)\left( {{\mathbf{y}}_{j} - {{\varvec{\upmu}}}_{i}^{k} } \right)^{T} } \right]} } \right\}} \mathord{\left/ {\vphantom {{\left\{ {\sum\limits_{j = 1}^{{n_{d} }} {\left[ {\tau_{ij}^{k} \left( {{\mathbf{y}}_{j} - {{\varvec{\upmu}}}_{i}^{k} } \right)\left( {{\mathbf{y}}_{j} - {{\varvec{\upmu}}}_{i}^{k} } \right)^{T} } \right]} } \right\}} {\left( {\sum\limits_{j = 1}^{{n_{d} }} {\tau_{ij}^{k} } } \right)}}} \right. \kern-0pt} {\left( {\sum\limits_{j = 1}^{{n_{d} }} {\tau_{ij}^{k} } } \right)}}$$

(21)

where $n_{d}$ is the number of training samples. Through continuously iterating, the iteration stops when the variation of the likelihood function less than a small constant $eps$. $eps = 1{\text{e}} - 12$ is adopted to ensure the accuracy. The likelihood function is expressed as:

$$L\left( {{\mathbf{x}}|{{\varvec{\updelta}}}} \right) = \sum\limits_{i = 1}^{{n_{d} }} {\ln \left( {\sum\limits_{k = 1}^{K} {\pi_{k} N\left( {{\mathbf{y}}_{k} |{{\varvec{\upmu}}}_{k} ,{{\varvec{\updelta}}}_{k} } \right)} } \right)}$$

(22)

As $\eta$ is derived from $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}$ and random generated failed sample points, the randomness of $\eta$ should also be considered. Suggested by Refs. (Wang et al. 2019; Zhang et al. 2021), 20 independent runs of the method could be adopted to estimate the mean and standard deviation of $\eta$, which are defined as $\mu \left( \eta \right)$ and $\sigma \left( \eta \right)$ respectively. Then ${\text{COV}}\left( \eta \right) = {{\sigma \left( \eta \right)} \mathord{\left/ {\vphantom {{\sigma \left( \eta \right)} {\mu \left( \eta \right)}}} \right. \kern-0pt} {\mu \left( \eta \right)}}$ could be used to measure the randomness.

4 Adaptive Kriging model

4.1 Learning function

This paper adopts the most commonly used adaptive Kriging model as the surrogate model to reduce the required function calls of IDS. The concept of Kriging model has been described in many previous researches, which will not be discussed in this paper. Learning function is the core of active learning. Presently, U and EFF are the most commonly used learning functions for active learning. Besides, Researchers also provided different learning functions, such as REIF (Zhang et al. 2019), ERF (Yang 2015) and H (Lv et al. 2015) functions. The above learning functions are shown in Eqs. (23)–(27). The adding point criterions of the above learning functions are ${\mathbf{x}}^{*} = \arg \min \left( {{\text{U}}\left( {\mathbf{x}} \right)} \right)$,${\mathbf{x}}^{*} = \arg \max \left( {{\text{EFF}}\left( {\mathbf{x}} \right)} \right)$, ${\mathbf{x}}^{*} = \arg \max \left( {{\text{REIF}}\left( {\mathbf{x}} \right)} \right)$, ${\mathbf{x}}^{*} = \arg \max \left( {{\text{ERF}}\left( {\mathbf{x}} \right)} \right)$ and ${\mathbf{x}}^{*} = \arg \max \left( {{\text{H}}\left( {\mathbf{x}} \right)} \right)$ respectively.

$${\text{U}}\left( {\mathbf{x}} \right) = {{\left| {\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)} \right|} \mathord{\left/ {\vphantom {{\left| {\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)} \right|} {\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}} \right. \kern-0pt} {\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}$$

(23)

$$\begin{gathered} {\text{EFF}}\left( {\mathbf{x}} \right) = \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)\left[ {2\Phi \left( {\frac{{ - \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}} \right) - \Phi \left( {\frac{{ - 2\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right) - \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}} \right) - \Phi \left( {\frac{{2\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right) - \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}} \right)} \right] \hfill \\ \, - \sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)\left[ {2\phi \left( {\frac{{ - \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}} \right) - \phi \left( {\frac{{ - 2\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right) - \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}} \right) - \phi \left( {\frac{{2\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right) - \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}} \right)} \right] \hfill \\ \, + 2\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)\left[ {\Phi \left( {\frac{{2\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right) - \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}} \right) - \Phi \left( {\frac{{ - 2\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right) - \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}} \right)} \right] \hfill \\ \end{gathered}$$

(24)

$${\text{REIF}}\left( {\mathbf{x}} \right) = \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)\left[ {1 - 2\Phi \left( {\frac{{\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}} \right)} \right] + \sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)\left[ {2 - \sqrt {\frac{2}{\pi }} \exp \left( { - \frac{1}{2}\frac{{\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)^{2} }}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)^{2} }}} \right)} \right] \,$$

(25)

$${\text{ERF}}\left( {\mathbf{x}} \right) = - {\text{sign}}\left( {\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)} \right)\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)\Phi \left[ { - {\text{sign}}\left( {\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)} \right)\frac{{\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}} \right] + \sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)\varphi \left( {\frac{{\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}} \right) \,$$

(26)

$${\text{H}}\left( {\mathbf{x}} \right) = \left| \begin{gathered} \ln \left( {\sqrt {2\pi } \sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right) + 0.5} \right)\left[ {\Phi \left( {\frac{{2\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right) - \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}} \right) - \Phi \left( {\frac{{ - 2\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right) - \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}} \right)} \right] \hfill \\ - \frac{{2\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right) - \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{2}\phi \left( {\frac{{2\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right) - \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}} \right) + \frac{{2\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right) + \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}\phi \left( {\frac{{ - 2\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right) - \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{x}} \right)}}} \right) \hfill \\ \end{gathered} \right| \,$$

(27)

4.2 Stopping criterion of learning function

In Ref. (Guo et al. 2020), the stopping criterion for U function is used for IDS. However, this criterion is too conservative and will introduce many redundant training samples. Presently, the error-based stopping criterion has been widely used to solve the problems. The size of samples $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{s}$ which are failed predicted by Kriging model but actually reliable is subjected to a normal distribution, that is:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{s} \sim N\left( {\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{s} }} ,\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{s} }} } \right), \, \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{s} }} = \sum\limits_{i = 1}^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{s} }} {\Phi \left( { - \left| {\frac{{\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {{\mathbf{b}}_{i} } \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {{\mathbf{b}}_{i} } \right)}}} \right|} \right),} \, \sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{s} }} = \sqrt {\sum\limits_{i = 1}^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{s} }} {\Phi \left( { - \left| {\frac{{\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {{\mathbf{b}}_{i} } \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {{\mathbf{b}}_{i} } \right)}}} \right|} \right)\left[ {1 - \Phi \left( { - \left| {\frac{{\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {{\mathbf{b}}_{i} } \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {{\mathbf{b}}_{i} } \right)}}} \right|} \right)} \right]} }$$

(28)

where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{s}$ is the size of reliable samples predicted by Kriging model. In addition, the size of samples $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{f}$ which are reliable predicted by Kriging model but actually failed can be approximately represented by normal distribution with mean and standard deviation $\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{f} }}$ and $\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{f} }}$ respectively:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{f} \sim N\left( {\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{f} }} ,\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{f} }} } \right),\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{f} }} = \sum\limits_{i = 1}^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{f} }} {\Phi \left( { - \left| {\frac{{\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {{\mathbf{b}}_{i} } \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {{\mathbf{b}}_{i} } \right)}}} \right|} \right),} \, \sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{f} }} = \sqrt {\sum\limits_{i = 1}^{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{f} }} {\Phi \left( { - \left| {\frac{{\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {{\mathbf{b}}_{i} } \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {{\mathbf{b}}_{i} } \right)}}} \right|} \right)\left[ {1 - \Phi \left( { - \left| {\frac{{\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {{\mathbf{b}}_{i} } \right)}}{{\sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {{\mathbf{b}}_{i} } \right)}}} \right|} \right)} \right]} }$$

(29)

where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{f}$ is the size of failed samples predicted by Kriging model.

In order to ensure the fitting accuracy of Kriging model, the difference between $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{f}$ and $N_{f}$ should be small enough, where $N_{f}$ is the size of samples which are actually failed. The maximum relative error $\kappa$ between $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{f}$ and $N_{f}$ could be calculated by:

$$\kappa = \left| {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{f} }}{{N_{f} }} - 1} \right| \le \max \left( {\left| {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{f} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{f} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{f}^{u} }}} \right| - 1,\left| {\frac{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{f} }}{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{N}_{f} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{s}^{u} }}} \right| - 1} \right) = \kappa_{thr}$$

(30)

where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{f}^{u}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{s}^{u}$ are the upper bounds of $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{f}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{s}$ respectively. When $\kappa_{thr}$ small enough, the Kriging model is sufficient accuracy.

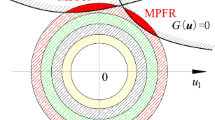
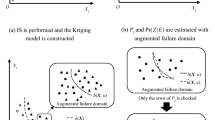
The error-based stopping criterion has been widely used in MC-based Kriging reliability methods. However, there are still some limitations. First, researchers have demonstrated that some additional samples with low contribution to the Kriging model will be introduced (Wang et al. 2022). Second, this criterion requires the distributions of both $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{f}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{f}$. For IDS method, as most of the generated importance directional samples are distributed in the failure region, establishing the distributions of both $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{f}$ and $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{S}_{f}$ considering the number of reliable samples is unnecessary. This paper will propose a more concise stopping criterion, which is established based on the idea of auxiliary region. As shown in Fig. 1, the auxiliary region $\Omega_{A}$ is defined as the failure region fitted by Kriging model, and the real failure region is defined as $\Omega_{R}$. Based on Bayes conditional probability formula, the real failure probability $p_{f} \left( {\Omega_{R} } \right)$ is defined as:

$$p_{f} \left( {\Omega_{R} } \right) = \frac{{p_{f} \left( {\Omega_{A} } \right)p_{f} \left( {\Omega_{R} |\Omega_{A} } \right)}}{{p_{f} \left( {\Omega_{A} |\Omega_{R} } \right)}}$$

(31)

where $p_{f} \left( {\Omega_{A} } \right)$ is the failure probability in $\Omega_{A}$. The conditional failure probabilities $p_{f} \left( {\Omega_{R} |\Omega_{A} } \right)$ and $p_{f} \left( {\Omega_{A} |\Omega_{R} } \right)$ depend on the overlapping degree of $\Omega_{A}$ and $\Omega_{R}$. Actually, the ratio of $\frac{{p_{f} \left( {\Omega_{R} |\Omega_{A} } \right)}}{{p_{f} \left( {\Omega_{A} |\Omega_{R} } \right)}}$ acts as a correction factor of $p_{f} \left( {\Omega_{A} } \right)$ to decrease the difference between $p_{f} \left( {\Omega_{R} } \right)$ and $p_{f} \left( {\Omega_{A} } \right)$. The closer $\frac{{p_{f} \left( {\Omega_{R} |\Omega_{A} } \right)}}{{p_{f} \left( {\Omega_{A} |\Omega_{R} } \right)}}$ to 1 means the lower difference and the higher fitting degree of $\Omega_{R}$ and $\Omega_{A}$. Then, $\frac{{p_{f} \left( {\Omega_{R} |\Omega_{A} } \right)}}{{p_{f} \left( {\Omega_{A} |\Omega_{R} } \right)}}$ could be adopted to define a stopping criterion for Kriging.

Fig. 1

Auxiliary region

Since the introduction of Eq. (31) is to determine whether the failure region can be accurately fitted by Kriging model, it is sufficient to ensure that the symbol of IDS samples can be judged correctly without real failure probability in this step. In regard of this, an estimation method based on the number of failure samples located in the corresponding region and the prediction uncertainty of Kriging model is proposed to estimate $p_{f} \left( {\Omega_{R} |\Omega_{A} } \right)$ and $p_{f} \left( {\Omega_{A} |\Omega_{R} } \right)$. According to Ref. (Yang et al. 2018), the predicted failure region in which the sign of performance function remains uncertain and the region with large probability to be negative are defined as $S_{f}^{u}$ and $S_{f}^{l}$ respectively:

$$S_{f}^{u} = \left\{ {\mu | - \delta \sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{b}} \right) < \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{b}} \right) < {0}} \right\},S_{f}^{l} = \left\{ {\mu |\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{b}} \right) \le - \delta \sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{b}} \right)} \right\}$$

(32)

the predicted reliable region in which the sign of performance function remains uncertain and the region with large probability to be positive are defined as $S_{r}^{u}$ and $S_{r}^{l}$ respectively:

$$S_{r}^{u} = \left\{ {\mu |{0} < \mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{b}} \right) < \delta \sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{b}} \right)} \right\},S_{r}^{l} = \left\{ {\mu |\mu_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{b}} \right) \ge \delta \sigma_{{\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{g} }} \left( {\mathbf{b}} \right)} \right\}$$

(33)

$\delta { = 1}{\text{.96}}$ could be adopted in Eqs. (32) and (33) to select the samples with large probability (larger than 95%) to be negative or positive. Therefore, the predicted failure samples distributed in $S_{f}^{l}$ could be regarded as the real failure samples. Then $p_{f} \left( {\Omega_{R} |\Omega_{A} } \right)$ can be approximately calculated by the ratio of the number of samples falling in the corresponding region to the total number of samples, that is:

$$p_{f} \left( {\Omega_{R} |\Omega_{A} } \right) = {{N_{{S_{f}^{l} }} } \mathord{\left/ {\vphantom {{N_{{S_{f}^{l} }} } {N_{IDS} }}} \right. \kern-0pt} {N_{IDS} }}$$

(34)

where $N_{{S_{f}^{l} }}$ is the number of samples falling in the region $S_{f}^{l}$. For $p_{f} \left( {\Omega_{A} |\Omega_{R} } \right)$, as the number of real failure samples is unknown, based on the prediction uncertainty of Kriging model, the upper bound of the ratio of the number of samples in the real failure region to the total number of IDS samples can be adopted to define $p_{f} \left( {\Omega_{A} |\Omega_{R} } \right)$, that is:

$$p_{f} \left( {\Omega_{A} |\Omega_{R} } \right) \le {{\left( {N_{{S_{f}^{u} }} + N_{{S_{f}^{l} }} + N_{{S_{r}^{u} }} } \right)} \mathord{\left/ {\vphantom {{\left( {N_{{S_{f}^{u} }} + N_{{S_{f}^{l} }} + N_{{S_{r}^{u} }} } \right)} {N_{IDS} }}} \right. \kern-0pt} {N_{IDS} }}$$

(35)

where $N_{{S_{f}^{u} }}$ and $N_{{S_{r}^{u} }}$ are the numbers of samples falling in the regions $S_{f}^{u}$ and $S_{r}^{u}$ respectively. The purpose of introducing $N_{{S_{r}^{u} }}$ is to treat all samples which the sign of performance function is uncertain as failure samples, so as to increase the sample size in the auxiliary region, and the upper bound of $p_{f} \left( {\Omega_{A} |\Omega_{R} } \right)$ could be obtained. Then the auxiliary region-based stopping criterion is defined as:

$$\frac{{p_{f} \left( {\Omega_{R} |\Omega_{A} } \right)}}{{p_{f} \left( {\Omega_{A} |\Omega_{R} } \right)}} \ge {{\left( {\frac{{N_{{S_{f}^{l} }} }}{{N_{IDS} }}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{N_{{S_{f}^{l} }} }}{{N_{IDS} }}} \right)} {\left( {\frac{{N_{{S_{f}^{u} }} + N_{{S_{f}^{l} }} + N_{{S_{r}^{u} }} }}{{N_{IDS} }}} \right)}}} \right. \kern-0pt} {\left( {\frac{{N_{{S_{f}^{u} }} + N_{{S_{f}^{l} }} + N_{{S_{r}^{u} }} }}{{N_{IDS} }}} \right)}} = \frac{{N_{{S_{f}^{l} }} }}{{N_{{S_{f}^{u} }} + N_{{S_{f}^{l} }} + N_{{S_{r}^{u} }} }} \ge \kappa_{af}$$

(36)

$\kappa_{af}$ is a positive constant with the maximum value of 1. The larger $\kappa_{af}$ means the higher coincidence degree of $\Omega_{A}$ and $\Omega_{R}$. The purpose of Eq. (36) is to minimize the proportion of samples which the sign of performance function has large uncertainty in the total failure samples, so as to minimize the difference between $\Omega_{A}$ and $\Omega_{R}$. If ${{N_{{S_{f}^{l} }} } \mathord{\left/ {\vphantom {{N_{{S_{f}^{l} }} } {\left( {N_{{S_{f}^{u} }} + N_{{S_{f}^{l} }} + N_{{S_{r}^{u} }} } \right)}}} \right. \kern-0pt} {\left( {N_{{S_{f}^{u} }} + N_{{S_{f}^{l} }} + N_{{S_{r}^{u} }} } \right)}} = 1$, it means that $N_{{S_{f}^{u} }}$ and $N_{{S_{r}^{u} }}$ are both 0, and $\Omega_{R}$ and $\Omega_{A}$ complete overlap.

4.3 The proposed active learning strategy for IDS

As mentioned in Introduction, the approximate design point-based importance directional density function may be not accurate enough. This paper proposes an improved active learning strategy. Its main idea is to synchronize the calculation process of design points and Kriging model updating, rather than calculating separately.

Suggested by Ref. (Jia and Wu 2022), the essence of calculating design point in standard normal space is to solve the following optimization problems:

$$\left\{ \begin{gathered} {\mathbf{y}}^{*} = \arg \max f\left( {\mathbf{y}} \right) \hfill \\ {\text{s.t.}} \;\hat{g}({\mathbf{y}}) = 0 \hfill \\ \end{gathered} \right.$$

(37)

where $\hat{g}({\mathbf{y}}) = 0$ is the current limit state boundary. $f\left( {\mathbf{y}} \right)$ is the joint probability density function of input variables. Equation (37) could be solved by gradient-based algorithms or other evolutionary algorithms. Based on Eqs. (11) and (37), the proposed active learning strategy is summarized as follows: First, calculate the design point through Eq. (37), and the obtained design point should be added into the current training set of Kriging model. Then, based on this design point, establish the importance directional sampling function through Eq. (8), and the importance directional samples are generated through Eq. (37). Next, take these important directional samples as current candidate sample set, and Kriging model is updated through learning function in the current sample space. The updating process stops when the stopping criterion defined by Eq. (36) is satisfied, and the failure probability could be obtained through Eq. (7). Finally, use Eq. (37) to solve the new design point based on the updated Kriging model. Re-build the importance directional density function and re-generate importance directional candidate sample set. Repeat the above steps and stop calculating when the final stopping criterion is satisfied. The final stopping criterion is defined as:

$${{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i - 1} } \right|} \mathord{\left/ {\vphantom {{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i - 1} } \right|} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i - 1} }}} \right. \kern-0pt} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i - 1} }} < \delta \cap {{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i - 1} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i - 2} } \right|} \mathord{\left/ {\vphantom {{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i - 1} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i - 2} } \right|} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i - 2} }}} \right. \kern-0pt} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i - 2} }} < \delta \cap {{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i - 2} } \right|} \mathord{\left/ {\vphantom {{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i - 2} } \right|} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i - 2} }}} \right. \kern-0pt} {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i - 2} }} < \delta$$

(38)

where $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}^{i}$ is the obtained $i$-th failure probability. The meaning of Eq. (38) is: when the relative error of failure probability for three consecutive times is less than $\delta$, the accuracy is considered to be sufficient, so as to output the final result.

Compared with Ref. (Guo et al. 2020), the major advantage of the proposed active learning strategy is that it realizes the synchronization of Kriging model updating and importance directional density function establishment, rather than only establishing the importance directional density function through the approximate design point, and it will also not put too much computation cost in the process of calculating design point. Since the design point has the largest contribution to failure probability on limit state boundary, adding the obtained design point into the training set is very helpful for the fitting of limit state boundary of Kriging model. Also, the candidate samples generated by the importance directional density function can be used to update Kriging model in the current sample space through learning function, which can not only improve the fitting accuracy of limit state boundary, but also improve the accuracy of design point, thus the update of importance directional density function in the next iteration is achieved. In this way, after satisfying the final stopping criterion, more accurate importance directional density function and failure probability could be obtained at the same time.

5 Summarized of the proposed method

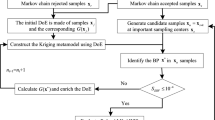
Based on previous sections, the steps of the proposed AK-IDS-RGS method for reliability and global sensitivity analysis are summarized as follows:

Step 1:

Transform the random variables into standard normal space, and establish the initial Kriging model. Suggested by Ref. (Zhang et al. 2019), the samples with the population $N = \max \left( {12,n} \right)$ are generated by Sobol sequence as the initial training set in the interval [− 5,5]. Calculate the real values of limit state function of these samples. Through the initial training set, the initial Kriging model is established.

Step 2:

Calculate design point ${\mathbf{y}}^{{\mathbf{*}}}$ and direction vector ${{\varvec{\upalpha}}}_{{\mathbf{Y}}}$ through the current Kriging model based on Eq. (37).

Step 3:

Generate random samples ${\mathbf{y}}_{i} ,i = 1,2, \cdot \cdot \cdot ,N_{ids}$ and $u_{i} ,i = 1,2, \cdot \cdot \cdot ,N_{ids}$ through standard normal distribution and standard uniform distribution in the interval $\left[ {0,1} \right]$, respectively.

Step 4:

Calculate IDS samples ${\mathbf{b}}_{i} ,i = 1,2, \cdot \cdot \cdot ,N_{ids}$ based on Eq. (11). The sample set containing all IDS samples is defined as the candidate sample set for active learning.

Step 5:

Calculate the value of learning function of all candidate samples. According to the learning function of adaptive Kriging model, the optimal sample point is selected and added to the training set. Calculate the real value of performance function of the optimal point, and update the Kriging model.

Step 6:

Judge the stopping criterion of Kriging model in the current sample space. If the stopping criterion defined by Eq. (36) is satisfied, stop the active learning process and turn to Step 7. Otherwise, return to Step 6 and update the Kriging model. In order to ensure the accuracy, $\kappa_{af} = 0.98$ is adopted.

Step 7:

Calculate $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}$ and ${\text{Var}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} } \right)$ through Eqs. (3) and (4) respectively through the Kriging model.

Step 8:

Return to Step 2 and re-calculate ${\mathbf{y}}^{{\mathbf{*}}}$ and ${{\varvec{\upalpha}}}_{{\mathbf{Y}}}$ through the current Kriging model based on Eq. (37). Repeat Step 2-Step 7 until the final stopping criterion defined by Eq. (38) is satisfied. This paper adopts $\delta = 0.05$. If the final stopping criterion is satisfied, output $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}$ and ${\text{Var}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} } \right)$ in the last iteration as the final result. Otherwise, return to Step 2 and obtain new ${\mathbf{y}}^{{\mathbf{*}}}$ and ${{\varvec{\upalpha}}}_{{\mathbf{Y}}}$.

Step 9:

Judge whether the ${\text{Cov}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} } \right)$ meets the accuracy requirement. This paper selects 5% as the threshold. If ${\text{Cov}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} } \right) < 5\%$, output $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f}$ and ${\text{Cov}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} } \right)$ as the final results. Otherwise, return to Step 3 to expand the candidate sample set.

Step 10:

Select all failure samples. Calculate global sensitivity index $\eta_{i}$ for each input variable through Eq. (15) based on GMM. Based on Eq. (32), the failure samples are distributed in the region $S_{f}^{l}$.

The proposed AK-IDS-RGS is the further development of AK-IDS (Guo et al. 2020). The following major improvements are made: (1) A novel auxiliary region-based stopping criterion is introduced based on the size of failure samples, which can reduce the number of training samples and improve the efficiency of active learning. (2) An improved active learning strategy is proposed based on optimization and active learning function, which realizes the synchronous updating of importance directional density function and Kriging model, instead of only establishing importance directional density function through the approximate design point. The flow chart of the proposed AK-IDS-RGS is presented in Fig. 2.

Fig. 2

Flow chart of AK-IDS-RGS

6 Numerical examples

In this section, five numerical examples are used to illustrate the proposed method. MC method is used as the benchmark, and the relative error is calculated by ${{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} - pf_{mc} } \right|} \mathord{\left/ {\vphantom {{\left| {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{p}_{f} - pf_{mc} } \right|} {pf_{mc} }}} \right. \kern-0pt} {pf_{mc} }}$, where $pf_{mc}$ is the failure probability calculated by crude MC. Several existing methods are used for comparative calculation, including AK-MCS, AK-IS, AK-DIS, AK-MCS-ESC-U, AK-MCS-ESC-EFF and AK-IS-ESC. Each method is independently calculated for 20 times, and the mean values are taken as the final results. In addition, in order to select the optimal active learning strategy, the learning functions in Eqs. (23)–(27) are adopted on the proposed AK-IDS-RGS respectively, and performance of different learning functions will be studied.

6.1 A simple performance function with two random variables

This section studies a bi-dimensional performance function (Zhou et al. 2015), as shown in Eq. (39), where $x_{1}$ and $x_{2}$ are both standard normal variables.

$$g_{1} = \exp \left( {0.2x_{1} + 1.4} \right) - x_{2}$$

(39)

U function is adopted on AK-IDS-RGS firstly. Figure 3 shows the distribution characteristics of candidate samples and the fitting accuracy of limit state boundary of AK-MCS, AK-IS and AK-IDS-RGS. The fitting accuracy of limit state boundary by Kriging models of the three methods are all relatively high. However, a large number of candidate samples are required in AK-MCS. Also, a large number of samples fall outside the failure region, which are very far from the limit state boundary. AK-IS method significantly reduces the number of candidate samples, but there are still about 50% of the points falling outside the failure region. Compared with AK-MCS and AK-IS, the required candidate samples in AK-IDS-RGS-U are much smaller, and most of these samples are located in the failure region. Although a few training points are distributed far from the limit state boundary, the fitting degree of Kriging model is still high, and the total number of training points is less than MC and IS methods. Therefore, AK-IDS-RGS can effectively obtain the failure samples for reliability and sensitivity analysis.

Fig. 3

Sample distribution of different methods

The results of different methods are listed in Table 1. It can be seen that the accuracy of these methods is relatively high, as the relative error and COV are all less than 2%. However, the required computer memory has great differences. The candidate sample size of AK-IDS-RGS is only 2e3, while the required candidate samples of MC- and IS-based Kriging methods are 8e6 and 2e4 respectively. Therefore, the required computation cost of the proposed method is significantly lower than MC and IS.

Table 1 Results of different methods in Example 1

The results of AK-IDS-RGS under different learning functions are shown in Table 2, where “-EFF” means that the EFF learning function is adopted. It can be seen that the relative errors of the four learning functions are all lower that 1.2%, and the required function calls also have little difference. Therefore, all learning functions can obtain high accuracy failure probability based on the proposed AK-IDS-RGS method in this example.

Table 2 Results of AK-IDS-RGS under different learning functions in Example 1

The global sensitivity index is calculated based on failure probability and Bayes theorem through GMM. This paper only discusses the results based on AK-IDS-RGS under different learning functions, and the index based on MC method is used as benchmark. The results are shown in Fig. 4. From Fig. 4a, it can be seen shown that $x_{2}$ is more influential than $x_{1}$ on the failure probability. In AK-IDS-RGS, all learning functions can judge the relative importance of the two variables, and the values of $\mu \left( \eta \right)$ calculated by different learning functions also have little difference. Therefore, AK-IDS-RGS can effectively obtain the failed samples with less candidate samples and computer memory, which is very suitable for failure probability-based global sensitivity analysis. From Fig. 4b, it can be seen that the ${\text{COV}}\left( \eta \right)$ of all learning functions are lower than 3%, which illustrates that the proposed method can obtain high robustness global sensitivity index.

Fig. 4

Results of global sensitivity analysis in Example 1

6.2 An aero-engine turbine disk

The aero-engine turbine disk is studied in this section, as shown in Fig. 5 (Yun et al. 2020). The performance function is defined as:

$$g_{2} = \sigma_{s} A - \frac{{C\left( {2\pi w} \right)^{2} }}{2\pi } + 2\rho \left( {2\pi w} \right)^{2} H_{J}$$

(40)

where $\sigma_{s}$,$\rho$,$C$, $A$,$H_{J}$ and $w$ are the ultimate strength, mass density, coefficient, cross-sectional area, cross section moment of inertia and rotational frequency, respectively. The information of random variables is listed in Table 3, and all variables are independent normal variables. The failure probabilities are listed in Table 4. Comparing AK-IDS-RGS with AK-MCS and AK-IS methods, the number of candidate samples of AK-IDS-RGS is only 2e3, and the number of required function calls is only 63.7. These illustrate that the proposed method has high efficiency with lower computer memory. The required function calls of AK-DIS is 81.3, the efficiency is much lower than the proposed AK-IDS-RGS. The results show that the proposed method can increase the efficiency of active learning of IDS.

Fig. 5

Aero-engine turbine disk

Table 3 Random variables in Example 2

Table 4 Results of different methods in Example 2

The results of AK-IDS-RGS under different learning functions are listed in Table 5. The number of required function calls of EFF is 59.3, which the lowest in the five learning functions. The relative error of H is 3.77%, the accuracy is lower than other functions. The relative errors of REIF and ERF functions are 1.85% and 2.95% respectively, which means that the accuracy of the two functions is also slightly lower than EFF and U functions. The iteration curves of the performance function values of training points and failure probability based on U and EFF learning functions by one calculation are shown in Fig. 6. It can be seen that when the number of added samples is larger than 20, the performance function values of added samples are very close to 0, which means that the proposed active learning strategy can effectively obtain the samples around the limit state boundary. In addition, the numbers of failure probability calculations for the U and EFF functions are 13 and 12 respectively, which means that the number of added design point are 13 and 12 respectively. Therefore, after the design point calculation is completed, the number of samples added based on the current Kriging model is approximately 4–5, and the number of training points based on solving design point is significantly less than the number of training points based on learning function.

Table 5 Results of AK-IDS-RGS under different learning functions in Example 2

Fig. 6

Iteration curves of performance function values of training points and failure probability in Example 2

The global sensitivity indexes calculated by AK-IDS-RGS are shown in Fig. 7 The most influential variable is $w$, while the variable with the least impact is $C$. The learning functions of which the variable sensitivity index order is consistent with MC are U, EFF and H functions, and the ${\text{COV}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\eta } } \right)$ of all variables are all lower than 5%. This illustrates that the proposed AK-IDS-RGS can obtain sensitivity indexes with high robustness. Therefore, combining sensitivity index and failure probability, the suitable learning functions for AK-IDS-RGS should be U, EFF and H functions in this example.

Fig. 7

Results of global sensitivity analysis in Example 2

6.3 A conical structure

A conical structure (Huang et al. 2021) is used in this section, as shown in Fig. 8.

Fig. 8

Conical structure

The performance function of this example is defined as:

$$g_{3} = 1 - \frac{{\sqrt {3\left( {1 - \mu^{2} } \right)} }}{{\pi Et^{2} \cos^{2} \alpha }}\left( {\frac{P}{2\gamma } + \frac{M}{{\lambda r_{1} }}} \right)$$

(41)

the random variables are listed in Table 6. All of them are independent normal variables, and the results are shown in Table 7. The required candidate samples of AK-IDS-RGS are 2e3, which are much lower than MC- and IS-based methods. Therefore, IDS can significantly reduce the candidate sample size in active learning. For MC- and IS-based methods, the required function calls are all larger than 200. In addition, the required function calls of AK-IDS-RGS are only 155.7, which is the lowest in the methods listed in Table 7. The relative error of AK-IDS-RGS is 1.27%, which means that the proposed method also has high accuracy. The required function calls of AK-DIS is 441.9, which is much higher than AK-IDS-RGS. The results show that the proposed active learning strategy is more suitable for IDS.

Table 6 Random variable parameters in Example 3

Table 7 Results of different methods in Example 3

The results of AK-IDS-RGS under different learning functions are shown in Table 8. The relative error of REIF is 6.42%, the accuracy is lower than other learning functions. The required function calls of AK-IDS-RGS under REIF is 151.6, which is the lowest in the five learning functions, but the relative error is 6.42%, the accuracy is the lowest. The relative error of ERF is 2.31%, which is slightly larger than U and EFF. The learning function with the highest accuracy is EFF, as the relative error is only 0.42%. Therefore, U, EFF, H and ERF could be adopted on AK-IDS-RGS in this example. The iteration curves of the performance function values of training points and failure probability based on U and EFF learning functions by one calculation are shown in Fig. 9. The numbers of failure probability calculations are 8 and 9, respectively, which are is significantly less than the total number of training samples. The results show that the active learning method proposed in this paper does not require too much computation cost in design point calculation.

Table 8 Results of AK-IDS-RGS under different learning functions in Example 3

Fig. 9

Iteration curves of performance function values of training points and failure probability in Example 3

The results of global sensitivity index are shown in Fig. 10. $\lambda$ and $t$ have the most significant impact on the failure probability, while $P$ and $\gamma$ have little impact. The sensitivity indexes obtained by U, EFF and H functions are slightly different from those of MC method, while the sensitivity indexes obtained by REIF and ERF functions have big difference comparing with MC. From the ${\text{COV}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\eta } } \right)$, it can be seen that the ${\text{COV}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\eta } } \right)$ of all variables under U, EFF, and H functions are all lower than 5%. Under other learning functions, the ${\text{COV}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\eta } } \right)$ of some variables are larger than 10% or even 15%. Therefore, combining the results of failure probability and global sensitivity index, U, EFF, and H functions are suitable for AK-IDS-RGS in this example.

Fig. 10

Results of global sensitivity analysis in Example 3

6.4 Automobile front axle beam

The reliability of the automobile front axle beam is studied in this section, as shown in Fig. 11. The performance function is written as:

$$\begin{gathered} g_{4} = \sigma_{s} - \sqrt {\sigma^{2} + 3\tau^{2} } \hfill \\ \sigma = {M \mathord{\left/ {\vphantom {M {W_{x} }}} \right. \kern-0pt} {W_{x} }},\tau = {T \mathord{\left/ {\vphantom {T {W_{\rho } }}} \right. \kern-0pt} {W_{\rho } }} \hfill \\ W_{x} = \frac{{a\left( {h - 2t} \right)^{3} }}{6h} + \frac{b}{6h}\left[ {h^{3} - \left( {h - 2t} \right)^{3} } \right] \hfill \\ W_{\rho } = 0.8bt^{2} + 0.4\left[ {{{a^{3} \left( {h - 2t} \right)} \mathord{\left/ {\vphantom {{a^{3} \left( {h - 2t} \right)} t}} \right. \kern-0pt} t}} \right] \hfill \\ \end{gathered}$$

(42)

Fig. 11

Automobile front axle beam

The information of random variables is listed in Table 9. All variables are independent normal random variables. The results of failure probability are shown in Table 10. The required candidate sample size of AK-IDS-RGS is 2e3, and the required function calls and relative error are 37.3 and 1.02% respectively. The number of required function calls of AK-IDS-RGS is the lowest compared with other techniques, and the candidate sample size of IDS is much smaller than MC and IS. The results show that the efficiency of AK-IDS-RGS is much higher than MC- and IS-based Kriging method. Compared with AK-IDS-RGS, the number of required function calls of AK-DIS is 65.8. Once again, the results show that the proposed active learning strategy can effectively reduce the number of training samples in IDS.

Table 9 Random variables parameters in Example 4

Table 10 Results of different methods in Example 4

The results of AK-IDS-RGS under different learning functions are shown in Table 11. The relative error of AK-IDS-RGS under EFF is 1.10%, while the relative errors under REIF, ERF and H functions are both larger than 4%. The required function calls of U and EFF also have little difference, which are all lower than 40, while the required function calls of other three functions are all larger than 40. Therefore, in terms of failure probability, U and EFF functions could be adopted on the proposed method in this example. The iteration curves of the performance function values of training points and failure probability based on U and EFF learning functions by one calculation are shown in Fig. 12.

Table 11 Results of AK-IDS-RGS under different learning functions in Example 4

Fig. 12

Iteration curves of performance function values of training points and failure probability in Example 4

The global sensitivity indexes are shown in Fig. 13. It can be seen that $T$ and $M$ have the most significant impact on the failure probability, while $t$ and $h$ have little impact. The orders of sensitivity indexes under U, EFF, and H functions are same as those of MC. While in other functions, the orders of some variables are miscalculating. For instances, in REIF, the order of $\sigma_{s}$ and $a$ is opposite. In addition, the ${\text{COV}}\left( \eta \right)$ of all variables under U and EFF functions are all lower than 5%. However, the ${\text{COV}}\left( \eta \right)$ of some variables under other learning functions are higher than 10%, even 15%. Therefore, comprehensively considering failure probability and global sensitivity index, the suitable functions should be U and EFF in this example.

Fig. 13

Results of global sensitivity analysis in Example 4

6.5 Latch lock mechanism of hatch

A latch lock mechanism of hatch is studied, as shown in Fig. 14 (Ling and Lu 2021). Table 12 illustrates the information of input variables, which are all independent normal variables.

Fig. 14

Latch lock mechanism of hatch

Table 12 Random variable parameters in Example 5

The limit state function of this example is defined as:

$$g_{5} = r\cos \left( {\alpha_{1} } \right) + \sqrt {L_{1}^{2} - \left( {e - r\sin \left( {\alpha_{1} } \right)} \right)^{2} } + L_{2} - L_{3}$$

(43)

where $L_{3} = 270\;{\text{mm}}$. The results of failure probability are shown in Table 13. It can be seen that the failure probability of this example is very small, which reaches the level of $10^{ - 7}$. 5e9 candidate samples are required in MC to obtain a robust failure probability. The efficiency is very low, and the required computer memory is very large. Therefore, the MC-based Kriging methods are not used for comparison in this example. The relative errors of AK-IS and AK-IS-ESC are 11.14% and 10.50% respectively, the accuracy of these two methods is quite low. Also, the required function calls of IS-based method are all larger than 300, the efficiency is quite low. For the proposed AK-IDS-RGS, the required function calls of AK-IDS-RGS and AK-DIS are 46.6 and 253.2 respectively, and the relative errors are 1.92% and 3.13% respectively. Compared with AK-DIS, AK-IDS-RGS can significantly reduce the number of required function calls without losing accuracy. Therefore, the proposed active learning strategy can effectively reduce the required function calls.

Table 13 Results of different methods in Example 5

The results of AK-IDS-RGS under different learning functions are shown in Table 14. The required function calls of the five learning functions have little difference. However, the relative errors under REIF and ERF functions are 11.20% and 4.15% respectively, the accuracy of the two functions is quite low. If U, EFF and H functions are used, the accuracy of AK-IDS-RGS will be very high, as the relative errors are all lower than 3%. The results show that AK-IDS-RGS is also suitable for the reliability problem with small failure probability. The iteration curves of the performance function values of training points and failure probability based on U and EFF learning functions by one calculation are shown in Fig. 15.

Table 14 Results of AK-IDS-RGS under different learning functions in Example 5

Fig. 15

Iteration curves of performance function values of training points and failure probability in Example 4

The global sensitivity indexes of AK-IDS-RGS are shown in Fig. 16. The orders of sensitivity indexes under different learning functions are all the same as those of MC. The results show that the combination of IDS and failure probability-based global sensitivity analysis can effectively evaluate the relative importance of random variables. The ${\text{COV}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\eta } } \right)$ of all variables under U and EFF functions are all lower than 5%. Therefore, the proposed AK-IDS-RGS can effectively and accurately evaluate the global sensitivity index under U and EFF learning functions.

Fig. 16

Results of global sensitivity analysis in Example 5

6.6 Discussion about the proposed method

6.6.1 The derived variance formula of IDS-based failure probability

The variance of failure probability calculated by the design point-based IDS method is derived in this paper, and it is adopted on the proposed AK-IDS-RGS to calculate COV. In Ref. (Guo et al. 2020), the MC-based COV formula is directly used for AK-DIS. This section will verify the effectiveness of the derived variance formula. Since the formula of failure probability variance is only related to the calculation method, this section will not use Kriging model. The failure probability is directly calculated through the performance function and the design point is calculated by Eq. (37). Based on the candidate sample size defined by the derived variance formula, each performance function is independently calculated by IDS for 20 times, and the COV of failure probability is obtained through statistical analysis. The results of the five examples are 1.49%, 1.85%, 2.43%, 2.48% and 2.58% respectively. It can be seen that the difference between the results of statistical analysis and derived formula is small. In addition, if the MC-based COV formula is adopted for IDS, the candidate sample size should be same as MC, and the results of COV are 1.85%, 2.21%, 2.51%, 2.62% and 2.39% respectively, the difference between the MC-based formula and the derived formula is also quite small. The results show the effectiveness of the derived variance formula of IDS. Therefore, if MC-based COV formula is directly used, it will cause many unnecessary samples.

6.6.2 The auxiliary region-based stopping criterion

This section will compare the performance between the proposed auxiliary region-based and the existed error-based stopping criterions through the optimal U learning function. As the difference between different methods in Example 1 is quite small, only Examples 2–5 are used in this section. Suggested by Refs. (Yun et al. 2021), the maximum relative error is defined as 0.05, and the error-based stopping criterion is adopted in the proposed active learning strategy, Step 7. Each example is also independently calculated 20 times, and the mean results are taken as the final results, as shown in Table 15. It can be seen that the relative errors of the four examples are all lower than 3%, which means that the error-based stopping criterion can also obtain high accuracy failure probability. However, the number of required function calls is much larger than the proposed auxiliary region-based stopping criterion, since the required function calls of auxiliary region are 63.1, 155.7, 37.3 and 46.6 respectively. Especially in Examples 3 and 5, the number of required function calls has increased by nearly 100 times. This illustrates that the convergence of the proposed auxiliary region-based stopping criterion is significantly higher than the existed error-based stopping criterion in IDS.

Table 15 Results of AK-IDS-RGS under error-based stopping criterion

6.6.3 The proposed active learning strategy

Besides the auxiliary region-based stopping criterion, the purpose of the proposed active learning strategy is to realize the synchronization of Kriging model updating and importance directional density function establishment. It is noted that if the condition ${{\left\| {{\mathbf{y}}_{i}^{*} - {\mathbf{y}}_{i - 1}^{*} } \right\|} \mathord{\left/ {\vphantom {{\left\| {{\mathbf{y}}_{i}^{*} - {\mathbf{y}}_{i - 1}^{*} } \right\|} {\left\| {{\mathbf{y}}_{i - 1}^{*} } \right\|}}} \right. \kern-0pt} {\left\| {{\mathbf{y}}_{i - 1}^{*} } \right\|}} < \delta$ is adopted firstly before using learning function to update Kriging model, it will also obtain a precise design point, which can also ensure the accuracy of importance directional density function. The method of ensuring the accuracy of design point firstly and then calculating failure probability is called segmented learning strategy in this paper. This section will compare the performance between the two strategies. $\delta = 0.05$ is adopted to ensure the accuracy of design point, and the auxiliary region-based stopping criterion is adopted in Kriging model updating through U function. The results of segmented learning strategy are shown in Table 16. It can be seen that the relative errors are all lower than 3%, which means that both the two active learning strategies have high accuracy. However, in Examples 3–5, the required function calls of segmented learning strategy are 162.8, 55 and 60.3 respectively, which shows that the segmented learning strategy will increase dozens of function calls compared with the synchronized learning strategy. Therefore, the proposed active learning strategy is more suitable for IDS.

Table 16 Results of AK-IDS-RGS under segmented learning strategy

7 Conclusions

In this paper, an improved active learning Kriging model is proposed for IDS reliability and failure probability-based global sensitivity analysis, which is called AK-IDS-RGS method. A novel auxiliary region-based stopping criterion based on the size of failure samples is introduced for IDS to accelerate the efficiency of active learning, and an improved active learning strategy based on optimization and learning function, which realizes the synchronization of Kriging model updating and importance directional density function establishment is established. Different learning functions are adopted on AK-IDS-RGS respectively to select the most suitable active learning strategy. The failure probability-based global sensitivity index is calculated through Bayes theorem and GMM. Different numerical examples are adopted to verify the efficiency and accuracy. The conclusions are summarized as follows:

• (1) From numerical examples, it can be seen that only 2e3 candidate samples are required in AK-IDS-RGS to obtain a robust failure probability with COV < 3% in Examples 1–4, and Example 5 requires only 4e3 candidate samples. IDS can significantly reduce the candidate sample size and the required function calls, which is very helpful to improve the efficiency of active learning and reduce the required computer memory. For the reliability problem with small failure probability, AK-IDS-RGS can also obtain high accuracy evaluation results.

• (2) The proposed auxiliary region-based stopping criterion is established based on the proportion of failure samples in total samples and the prediction uncertainty of Kriging model. Compared with the existed error-based stopping criterion, the auxiliary region-based stopping doesn’t require the probability distribution model of the size of failure samples, the form is much simpler. From Sect. 6.6.2, it can also be seen that the required function calls of auxiliary region-based stopping criterion is also smaller than the error-based stopping criterion, which means that the proposed criterion is more suitable for IDS.

• (3) Comparing with AK-DIS, the major advantage of the proposed segmented learning strategy is that it realizes the synchronization of Kriging model updating and importance directional density function establishment, rather than only establishing the importance directional density function through the approximate design point. From the numerical examples, it can be seen that the proposed method can obtain high accuracy failure probability with lower required function calls, the efficiency of the proposed method is higher than AK-DIS. In addition, if an accurate design point is obtained through optimization before using learning function to update Kriging model, it will also ensure the accuracy of importance directional density function. However, the required function calls will be much larger than the proposed segmented learning strategy.

• (4) The relative errors of failure probability of AK-IDS-RGS under U and EFF learning functions in the five numerical examples are all lower than 5%, and the required function calls of these two learning functions are also lower than other functions. From the global sensitivity index, the orders of sensitivity indexes under U and EFF functions are the same as those of MC method, and the ${\text{COV}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\eta } } \right)$ of all variables under U and EFF functions are also lower than 5%. Therefore, U and EFF learning functions should be adopted on the proposed AK-IDS-RGS method.