1 Introduction

Design optimization methods for fluid-structure interaction (FSI) problems have become popular as they provide a systematic framework for including sophisticated FSI models in the design process (Sobieszczanski-Sobieski and Haftka 1997; Maute et al. 2003; Martins et al. 2005). Traditionally, FSI problems are optimized by varying the external (wet) shape and/or the shape and dimensions of the internal (dry) structure. Such geometry variations can typically be defined by a small number of optimization variables and accommodated by traditional FSI analysis methods. To enable larger, conceptual design changes, the topology of the dry and/or wet geometry needs to be varied in the optimization process. Topology optimization for FSI problems leads to interesting challenges for both the geometry and analysis model, and is the focus of this study.

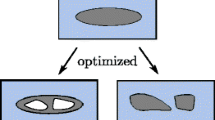
Figure 1 illustrates the differences of shape and topology optimization of FSI problems. Both wet and dry methods of shape variation preserve the nominal topology regardless if the dry or wet geometries are varied. Varying the dry shape of the structure alters the FSI response; see, for example, the studies by Butler et al. (1995), Gern et al. (1999), Guo et al. (2005), Guo (2007), Gasbarri et al. (2009), and Dillinger et al. (2013). Wet shape optimization of FSI problems was considered, for example, by Lund et al. (2001). Varying simultaneously the wet and dry geometries requires a design model that defines both external shape and internal structure as functions of the optimization variables; see, for example, the works of Gumbert et al. (2001), Maute et al. (2001), Martins et al. (2004), Allen and Maute (2005), Martins et al. (2005), and Ghazlane et al. (2011).

Fig. 1
figure 1

Geometrical variations in FSI problems

Full size image

Analogous to shape optimization methods, dry and wet topology optimization approaches exist for FSI problems; see the bottom half of Fig. 1. The most popular method for optimizing FSI problems is dry topology optimization; see, for example, Krog et al. (2002), Krog et al. (2004), Allen and Maute (2004), Maute and Reich (2006), Gomes and Suleman (2008), Stanford (2008), Stanford and Ifju (2009), James and Martins (2010), Brampton et al. (2012), (Stanford and Beran 2013), Dunning et al. (2014), Dunning et al. (2015), Jenkins and Maute (2015), and Munk et al. (2015).

Dry topology optimization is a direct extension of structural topology optimization, as the wet surface where the fluid forces and structural deformations interact is not altered in the optimization process. Therefore, standard FSI models can be easily integrated into the topology optimization framework, irrespective of whether a density approach or a level set method is used. Purely wet topology variation of FSI problems has not been considered yet, due to its limited relevance to solving practical design problems. Varying the wet and dry topology simultaneously is the most comprehensive approach to FSI geometry optimization, and poses interesting challenges in representing geometry changes in the FSI model.

The method of geometry discretization has large implications on the method of FSI interface condition enforcement. The FSI response needs to be predicted to evaluate the performance of a particular fluid-structure configuration in each design iteration. At the FSI interface, no-slip velocity boundary conditions must be enforced, and the fluid traction needs to be applied to the structure. Note that the applied fluid load is dependent on the structural deformation.

An FSI design can be represented by a density method, which approximates material boundaries by a fictitious porous material (Bendsøe 1989; Zhou and Rozvany 1991), or an implicit boundary method, e.g. the Level Set Method (LSM) (Osher and Sethian 1988). The geometry of a design described by a density method is typically mapped onto the mechanical model by a material interpolation scheme, such as the Ersatz material method (Allaire et al. 2004) and the SIMP approach (Zhou and Rozvany 1991). For most physical models it is sufficient to define material properties as functions of the density of the fictitious material. However, enforcing the FSI interface conditions with material interpolation schemes is less intuitive: a Brinkmann penalty approach is often employed to enforce the no-slip condition, and the fluid surface tractions are converted to a volumetric body force to approximate the action of the fluid on the structure.

To date, the only existing works to perform wet and dry topology optimization of FSI problems are by Yoon (2010), Yoon (2014), and, more recently, Picelli et al. (2015). In the studies of Yoon (2010) and Yoon (2014), a density method is used to vary the wet and dry topology. Picelli et al. (2015) vary the design by a smoothed discrete design variable method. All of these works employ a material interpolation approach with a Brinkmann penalization to model the fluid-structure coupling conditions. The solid and fluid governing equations are discretized with a single, deforming mesh to allow the fluid to follow the deformation of the structure. Density methods, however, require a fine mesh resolution to avoid blurred and/or jagged material boundaries. For wet and dry topology optimization of FSI problems in particular, material interpolation schemes may lead to an inaccurate enforcement of the coupling conditions as the fluid-structure interface is smeared over multiple cells or elements.

Alternatively, the LSM defines material boundaries with the zero iso-contour of a scalar function, resulting in a crisp description of the fluid-solid interface for FSI problems. The main advantage of the LSM in the context of wet and dry topology optimization is the increased flexibility in mapping the design onto the FSI model. A material layout described by the LSM can be evaluated either by material interpolation schemes or with immersed boundary methods, such as the Extended Finite Element Method (XFEM). The reader is referred to Jenkins and Maute (2015) for a detailed comparison of density methods and LSMs for dry optimization of FSI problems.

This work presents a LSM for wet and dry topology optimization of FSI problems that resolves well the fluid-structure interface geometry and the FSI model even on rather coarse meshes, compared to those typically needed with density approaches. We combine the LSM with the XFEM that provides a mathematically rigorous framework to enforce both velocity no-slip conditions and traction continuity at the FSI interface. The method presented in this paper builds on our previous work on dry topology optimization of FSI problems (Jenkins and Maute 2015), and expands the LS-XFEM approach onto optimizing the shape and topology of the fluid-structure interface.

An important aspect of numerical FSI models is tracking the deformation of the fluid-structure interface. Figure 2 shows three methods to model a deforming structure within a flow. The most widely used approach is to model the flow in an Arbitrary Eulerian-Lagrangian reference frame on a deforming, body-fitted mesh; see Fig. 2a. Deforming mesh approaches track the interface motion and can be easily combined with standard finite element methods. As they preserve the refinement of the mesh along the fluid-structure interface, these approaches allow enforcing the fluid-structure coupling conditions with high accuracy. However, interface tracking methods require re-meshing of the fluid domain for large structural deformations; otherwise they are limited to small to moderate deformations.

Fig. 2
figure 2

Three types of meshing schemes for FSI problems

Full size image

To overcome the restrictions of deforming mesh approaches, the flow can be modeled in a fixed reference frame, using immersed boundary techniques to describe material deformation; see Fig. 2b. This approach belongs to the class of interface capturing methods, which requires specialized re-initialization schemes and time integration approaches (Kamensky et al. 2015).

Figure 2c illustrates the combination of a deforming mesh scheme and an immersed boundary mesh. This approach is well suited for topology optimization of FSI problems as it allows the accurate tracking of the fluid-structure boundary due to an explicit mesh motion scheme, but it removes the requirement to generate body-fitted fluid and structure meshes. Note that the immersed boundary method used here, i.e. the XFEM, provides the same resolution of the interface geometry as a body-fitted mesh.

In this study, we introduce a formulation for FSI problems where both the structure and the fluid domains are discretized by the XFEM. The structure is immersed into a deforming fluid mesh that follows the structural deformations. The coupling conditions are enforced along the fluid-structure interface which is crisply defined by the LSM. We intend to show in this paper that the proposed LS-XFEM combination is a good compromise in terms of simplicity and attractiveness for wet and dry topology optimization of FSI systems. However, it is limited to moderate structural displacements and is not able to handle large structural deformations and rigid body motion.

A distinct challenge associated with topology optimization of wet FSI geometries is dealing with the emergence of free-floating volumes of solid material and structural features that exhibit extreme local deformations. Figure 3a and b depict designs without and with free-floating volumes of solid material. The free-floating solid may emerge in the course of the optimization process. As it is not connected to an anchor point, the free-floating solid undergoes rigid body motion, see Fig. 3c. Sophisticated, transient FSI models would be needed to describe the motion of free-floating material in the flow. While such models exists, see e.g. Mayer et al. (2010), they significantly increase the algorithmic complexity and computational cost without noticeable benefits for advancing the optimization problem. Although neither Yoon (2010), Yoon (2014), nor Picelli et al. (2015) report observing the emergence of free-floating volumes of solid material in the examples studied in their papers, this issue exists in all wet topology optimization methods, irrespective whether a density approach or a LSM with Ersatz material schemes or immersed boundary models is used.

Fig. 3
figure 3

Emergence of free-floating solid material in wet topology optimization

Full size image

As the XFEM scheme used in this study is not suited to describe rigid body motion of solids, we introduce an approach where free-floating solid volumes are identified and removed from the model before the FSI response is computed. While this approach mitigates issues due to large mesh deformations, the elimination of free-floating solid volumes may introduce a discontinuity in the optimization process. The implications of this technique are studied with numerical examples.

The remainder of this paper is organized as follows: Section 2 summarizes the indicator model to sense free-floating volumes, and the incompressible Navier-Stokes and linear elasticity models that describe the FSI response; Section 3 presents the stabilized and coupled, discretized monolithic system of equations solved at each design iteration; Section 4 details the XFEM enrichment strategy and the formulation of the immersed coupling conditions; Section 5 outlines the wet and dry topology optimization design approach; Section 6 presents three examples to demonstrate the viability and characteristics of the proposed framework for wet and dry topology optimization of FSI problems, and finally the main conclusions of this study are discussed in Section 7.

2 Physical model

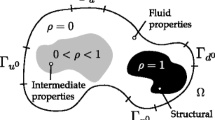
This section summarizes the indicator model for identifying free-floating solid volumes and the monolithic FSI formulation. As depicted in Fig. 4, we consider a two-dimensional computational design domain that is decomposed into non-overlapping fluid and solid domains, Ω f and Ω s , respectively. The intersection between the fluid and solid domains defines the fluid-solid interface: Γ f s i =Γ f ∩Γ s .

Fig. 4
figure 4

Fluid-structure problem domain

Full size image

2.1 Indicator model

To identify free-floating volumes of solid and model them as fluid in the FSI analysis, an indicator field is computed prior to solving the FSI problem for a given design. The indicator field is described by a linear isotropic diffusion model, and requires computing the solution to the associated differential equation presented below. Methods for dealing with free-floating volumes, and similar types of ill-posed design features, using a remeshing approach were presented, for example, by Allaire et al. (2014), Christiansen (2014), and Dapogny (2014). However, in addition to the computational complexity of remeshing methods, they also affect the numerical consistency of the sensitivities of the mechanical response with respect to the design variables; see, for example, Schleupen et al. (2000). The approach outlined in this work is based on a single variational formulation of the problem, and allows for a unified approach to compute the design sensitivities. Recently, Liu et al. (2015) published a similar approach for ensuring manufacturable designs in the topology optimization process.

The indicator field is modeled with both an ambient convective flux and a prescribed boundary flux. The governing equation for the indicator field is:

$$\begin{array}{@{}rcl@{}} \pmb{\nabla}\cdot\pmb{Q} + h_{I}\ \left( \chi - \chi_{0}\right) & = 0. \end{array} $$
(1)

The indicator variable is χ, and the ambient indicator value, χ 0, is a non-zero constant. The convective coefficient is h I , and the internal flux, Q, is defined as:

$$\begin{array}{@{}rcl@{}} \pmb{Q} = \pmb{\kappa}\pmb{\nabla}\chi, \end{array} $$
(2)

where the isotropic diffusivity tensor is κ. A bold symbol represents a vector or tensor.

The indicator field domain is equivalent to the structural domain. As shown in Fig. 4, the indicator boundary flux is applied at the same locations as the structural essential boundary conditions:

$$\begin{array}{@{}rcl@{}} {{\Gamma}^{n}_{I}}={{\Gamma}^{c}_{s}}. \end{array} $$
(3)

The applied indicator boundary flux describes the natural boundary condition for the diffusion model:

$$\begin{array}{@{}rcl@{}} \pmb{Q}\cdot\pmb{n}_{I} = \hat{t}_{I}\qquad \forall \ \pmb{x} \in {{\Gamma}^{n}_{I}}, \end{array} $$
(4)

where \(\hat {t}_{I}\) is the indicator boundary flux. The outward facing normal is n I , and x is the vector of spatial coordinates. An adiabatic condition is imposed at the fluid-structure boundary, and consequently no indicator flux can diffuse through the fluid domain. Note that the ambient convective model ensures that if an isolated solid volume emerges, the diffusion problem remains well posed.

Figure 5 illustrates the effect of the indicator field for two potential FSI designs: one with all solid volume connected (left) and one with a free-floating solid volume (right). The top row shown in Fig. 5 depicts the configurations defined by the optimization variables; the structure is denoted by \(\tilde {\Omega }_{s}\). The middle row shows the result of the indicator field calculation, and the bottom row shows the resulting configuration to be modeled in the FSI analysis, where the structural domain is denoted by Ω s .

Fig. 5
figure 5

Design without (left) and with free-floating solid volume (right)

Full size image

If the design is such that all solid volume is connected to an anchor point (as illustrated in the left column, middle row of Fig. 5), the indicator field solution will be χ>χ 0. This case results in no change to the topology of the design for the FSI analysis. If in the course of the optimization process, the configuration of the right column, top row of Fig. 5 emerges, the indicator field is χ = χ 0 in a subset of the solid domain. Solid material with an indicator value equal to the ambient value, χ 0, is identified as free-floating solid, and thus is considered to be fluid in the subsequent FSI analysis.

2.2 Fluid-structure interaction model

The fluid is modeled by the incompressible Navier-Stokes equations, and the solid is modeled by linear elasticity. The fluid mesh deformation at the interface results from the structural deformation. Within the fluid domain, the fluid mesh displacements are described by linear elasticity to ensure smooth mesh deformations.

The steady state response of the system is governed by the following set of partial differential equations:

$$\begin{array}{@{}rcl@{}} \rho_{f}\ \pmb{v}\cdot\pmb{\nabla}\pmb{v} - \pmb{\nabla}\cdot\pmb{\sigma}_{f} &=& 0, \end{array} $$
(5)
$$\begin{array}{@{}rcl@{}} \pmb{\nabla}\cdot\pmb{v} &=& 0, \end{array} $$
(6)
$$\begin{array}{@{}rcl@{}} \pmb{\nabla}\cdot\pmb{\sigma}_{s} &=& 0, \end{array} $$
(7)
$$\begin{array}{@{}rcl@{}} \pmb{\nabla}\cdot\pmb{\sigma}_{m} &=& 0. \end{array} $$
(8)

The conservation of momentum (5) and mass (6) in the fluid domain govern the fluid velocity v and pressure p, which are defined over the fluid domain Ω f . The structural displacements u are defined over the solid domain Ω s and the fluid mesh displacements, d, over the fluid domain Ω f . The fluid density and the fluid stress tensor are denoted by ρ f and σ f , respectively. The stress tensor of the structural displacement is σ s , and σ m is the fluid mesh displacement stress tensor. The fluid stress tensor is defined assuming a Newtonian fluid:

$$\begin{array}{@{}rcl@{}} \pmb{\sigma}_{f}(\pmb{v},p)=2\mu_{f}\pmb{\epsilon}\left( \pmb{v}\right) - \pmb{1}p. \end{array} $$
(9)

The dynamic viscosity of the fluid is denoted by μ f , and 𝜖 is the strain (rate) tensor:

$$\begin{array}{@{}rcl@{}} \pmb{\epsilon}\left( \pmb{v}\right)=\frac{1}{2}\left( \pmb{\nabla}\pmb{v}+\left( \pmb{\nabla}\pmb{v}\right)^{T}\right). \end{array} $$
(10)

The linear constitutive relations for the solid and fluid mesh are:

$$\begin{array}{@{}rcl@{}} \pmb{\sigma}_{s}=\pmb{C}_{s}\pmb{\epsilon}\left( \pmb{u}\right), &&\hspace{25pt} \pmb{\sigma}_{m}=\pmb{C}_{m}\pmb{\epsilon}\left( \pmb{d}\right). \end{array} $$
(11)

The structural strain tensor is 𝜖(u), and the fluid mesh strain tensor is 𝜖(d). The solid constitutive tensor, C s , is a function of the solid elastic modulus, E s , and Poisson’s ratio, ν s . Likewise, E m and ν m determine the entries in the constitutive tensor, C m , for the fluid mesh.

Essential boundary conditions prescribed on Γc, and are denoted by the hat symbol, \(\left ({\hat {\cdot }}\right )\):

$$\pmb{v}=\hat{\pmb{v}}, ~\pmb{u}=\hat{\pmb{u}}, ~\pmb{d}=\hat{\pmb{d}}~ \forall \ \pmb{x} \in {\Gamma}^{c}. $$

Prescribed boundary tractions, \(\hat {\pmb {t}}\), describe the natural conditions on Γn:

$$\pmb{\sigma}_{f}\cdot{\pmb{n}}_{f}=\hat{\pmb{t}}_{f}, ~\pmb{\sigma}_{s}\cdot{\pmb{n}}_{s}=\hat{\pmb{t}}_{s}, ~\pmb{\sigma}_{m}\cdot{\pmb{n}}_{f}=\hat{\pmb{t}}_{m}~ \forall \ \pmb{x} \in {\Gamma}^{n}. $$

The outward facing normals for the fluid and solid are n f and n s , respectively. The FSI boundary normal is denoted by n s→f , defined as outward for the solid and inward for the fluid.

The fluid load is applied to the solid, resulting in structural deformation. To accommodate the resulting changes of the flow domain, the fluid mesh is deformed by enforcing that the fluid mesh displacements are equal to the structural displacements at the fluid-solid interface. This fluid-structure interaction is enforced by the following interface conditions:

$$\begin{array}{@{}rcl@{}} \pmb{\sigma}_{f}\cdot{\pmb{n}}_{s\rightarrow f} = \pmb{\sigma}_{s}\cdot{\pmb{n}}_{s\rightarrow f} \quad \forall \ \pmb{x} \in {\Gamma}_{fsi}, \end{array} $$
(12)
$$\begin{array}{@{}rcl@{}} \pmb{v} = 0 \quad \forall \ \pmb{x} \in {\Gamma}_{fsi}, \end{array} $$
(13)
$$\begin{array}{@{}rcl@{}} \pmb{u} \models \pmb{d} \quad \forall \ \pmb{x} \in {\Gamma}_{fsi}. \end{array} $$
(14)

The balance of fluid and solid surface tractions is described by (12), and the no-slip condition on Γ f s i is enforced by (13). The continuity of the structural and fluid mesh displacements is imposed by (14), where “ ⊧” symbolizes that the fluid mesh displacement is set to the solid displacement. This one-way coupling ensures that the fluid mesh does not exert a reactive load on the structure.

3 Spatial discretization

In this section we present the finite element discretization of the FSI problem for the two-dimensional case, including the indicator field model. The computational domain, Ω=Ω f ∪Ω s , is discretized by quadrilateral finite elements. Given suitable spaces for trial solutions, \(\mathcal {S}^{h}\), and test functions, \(\mathcal {V}^{h}\), the variational problem is defined as follows:

$$\text{ Find }\hspace*{25pt} \{\pmb{v},p,\pmb{u},\pmb{d},\chi\}\in\mathcal{S}^{h}, \text{such that} $$
$$\begin{array}{@{}rcl@{}} a_{f}(\{\pmb{v},p\},\{\pmb{w},q\})&+& a_{s}(\pmb{u},\pmb{y}) + a_{m}(\pmb{d},\pmb{z}) + a_{I}(\chi,g)\\ &+& a^{fsi}_{V}(\{\pmb{v},p\},\{\pmb{w},q,\pmb{y}\})\\ &+& a^{fsi}_{D}(\{\pmb{u},\pmb{d}\},\{\pmb{y},\pmb{z}\}) = 0, \end{array} $$
$$\hspace*{25pt} \forall~\{\pmb{w},q,\pmb{y},\pmb{z},g\}\in\mathcal{V}^{h}, $$

where a f , a s , a m , and a I are the bi-linear forms of the fluid, solid, fluid mesh, and indicator field governing equations, respectively. The bi-linear forms associated with the interface coupling conditions are \(a^{fsi}_{V}\) and \(a^{fsi}_{D}\). Here, (⋅,⋅) denotes the inner product over the volume Ω=Ω f ∪Ω s , and <⋅,⋅> denotes the inner product along the boundary Γ. The test functions associated with the fluid velocity, fluid pressure, fluid mesh displacement, solid displacement, and indicator value are w, q, z, y, and g, respectively. The weak forms of the governing equations are defined as:

$$\begin{array}{@{}rcl@{}} a_{f} &=& \left( \rho_{f}\ \pmb{v}\cdot\pmb{\nabla}\pmb{v},\pmb{w}\right) + \left( \pmb{\sigma}_{f}(\pmb{v},p), \pmb{\epsilon}\left( \pmb{w}\right)\right) + \left( \pmb{\nabla}\cdot\pmb{v},q\right)\\ &&+ \sum\limits_{{n^{e}_{f}}}\left( \tau^{SUPG}\ \pmb{v}\cdot\pmb{\nabla}\pmb{w}+\tau^{PSPG}\ \pmb{\nabla}\cdot q,\pmb{R}^{v}_{f}\right)\\ &&-\left<\pmb{\sigma}_{f}(\hat{\pmb{v}},\hat{p})\cdot\hat{\pmb{n}}_{f},\pmb{w}\right>_{{\Gamma}_{f}}, \end{array} $$
(15)
$$\begin{array}{@{}rcl@{}} a_{s} &=& \left( \pmb{\sigma}_{s},\pmb{\epsilon}\left( \pmb{y}\right)\right) - \left<\pmb{\sigma}_{s}(\hat{\pmb{u}})\cdot\hat{\pmb{n}}_{s},\pmb{w}\right>_{{\Gamma}_{s}}, \end{array} $$
(16)
$$\begin{array}{@{}rcl@{}} a_{m} &=& \left( \pmb{\sigma}_{m},\pmb{\epsilon}\left( \pmb{z}\right)\right) - \left<\pmb{\sigma}_{m}(\hat{\pmb{d}})\cdot\hat{\pmb{n}}_{m},\pmb{w}\right>_{{\Gamma}_{f}}, \end{array} $$
(17)
$$\begin{array}{@{}rcl@{}} a_{I} &=& \left( \pmb{Q},\pmb{\nabla}g\right)-\left<\pmb{Q}\cdot\hat{\pmb{n}}_{s},g\right>_{{\Gamma}_{s}} - \left( h_{I} \left( \chi - \chi_{0}\right),g\right), \end{array} $$
(18)
$$\begin{array}{@{}rcl@{}} a^{fsi}_{V} &=& \left<\pmb{\sigma}_{f}\left( \pmb{w},q\right)\cdot\hat{\pmb{n}}_{s\rightarrow f},\pmb{v}\right>_{{\Gamma}_{fsi}} + \gamma_{V}\left<\pmb{w}-\pmb{y},\pmb{v}\right>_{{\Gamma}_{fsi}} \\ &&+ \left<\pmb{w}-\pmb{y},\pmb{\sigma}_{f}\left( \pmb{v},p\right)\cdot\hat{\pmb{n}}_{s\rightarrow f}\right>_{{\Gamma}_{fsi}}, \end{array} $$
(19)
$$\begin{array}{@{}rcl@{}} a^{fsi}_{D} &=& \left<\pmb{\sigma}_{m}\left( \pmb{z}\right)\cdot\hat{\pmb{n}}_{s\rightarrow f},\pmb{d}-\pmb{u}\right>_{{\Gamma}_{fsi}} + \gamma_{D}\left<\pmb{z},\pmb{d}-\pmb{u}\right>_{{\Gamma}_{fsi}} \\ &&+ \left<\pmb{z},\pmb{\sigma}_{m}\left( \pmb{d}\right)\cdot\hat{\pmb{n}}_{s\rightarrow f}\right>_{{\Gamma}_{fsi}}. \end{array} $$
(20)

The convective term in (15) introduces an inf-sup instability, and may lead to numerical oscillations. In addition, employing equal order interpolation spaces for both fluid velocity and fluid pressure leads to oscillations in the pressure solution. These numerical instabilities are remedied by the streamline upwind Petrov-Galerkin (SUPG) and pressure stabilizing Petrov-Galerkin (PSPG) stabilization methods. The stabilization term in (15) is the sum of the elemental inner products, where \(\pmb {R}^{v}_{f}\) is the strong form the fluid residual (5), and the total number of fluid elements is \({n^{e}_{f}}\). The stabilization parameters, τ SUPG and τ PSPG are defined in Tezduyar et al. (1992).

The interface conditions (19)–(20) are enforced with Nitsche formulations; the reader is referred to Hansbo et al. (2004) and Bazilevs et al. (2013) for further details of this method for FSI problems. The weak form of the FSI no-slip interface condition leads to the terms collected in \(a^{fsi}_{V}\). Following Hansbo et al. (2004), the traction at the interface is approximated by just the fluid traction. This approach relaxes the strength of FSI coupling, and reduces the magnitude of the spatial gradients near the interface. Imposing the continuity of the structural and fluid mesh displacements leads to the terms collected in \(a^{fsi}_{D}\). The consistency condition in \(a^{fsi}_{D}\) (last term) is only weighted with the test functions of the fluid mesh displacements, and the interface traction is set to the fluid mesh surface traction. This enforces the one-sided structural-fluid mesh displacement coupling condition described in (14). The penalty factors for the no-slip condition and the displacement continuity, γ V and γ D , depend on the discretization scheme and are given in Section 4.

4 Extended finite element enrichment

In this section we present the XFEM framework used to discretize the fluid-structure problem. The XFEM permits modeling physical or material boundaries with a non-body fitted mesh. The state variable interpolation is enriched to account for discontinuities of the variables across interfaces within an element. Here, the geometry of the immersed boundaries is described by the zero iso-contour of the level set field, ϕ, as follows:

$$ \begin{array}{ll} \phi(\pmb{x}) < 0, & \forall \ \pmb{x} \in {\Omega}_{f},\\ \phi(\pmb{x}) > 0, & \forall \ \pmb{x} \in {\Omega}_{s},\\ \phi(\pmb{x}) = 0, & \forall \ \pmb{x} \in {\Gamma}_{fsi}. \end{array} $$
(21)

To allow for discontinuous state variable fields across phase boundaries, we approximate the state variable field within an intersected element as follows:

$$\begin{array}{@{}rcl@{}} \pmb{f}(\pmb{x})=\sum\limits_{m=1}^{M}H(-\phi\left( \pmb{x}\right))\ \delta^{f}_{mi}\ \pmb{N}^{e}\cdot\bar{\pmb{f}}^{m,e}_{f} \\ + \sum\limits_{m=1}^{M}H(\phi\left( \pmb{x}\right))\ \delta^{s}_{mj}\ \pmb{N}^{e}\cdot\bar{\pmb{f}}^{m,e}_{s}, \end{array} $$
(22)

with H being the Heaviside function:

$$ H(\xi) = \left\{ \begin{array}{ll} 1 & \text{if \(\xi > 0\)}\\ 0 & \text{if \(\xi \leq 0\)}\end{array} \right. . $$
(23)

The local shape functions of element e are N e. The elemental vector of nodal degrees of freedom for enrichment level m, in phase k∈[f,s], is \(\bar {\pmb {f}}^{m,e}_{k}\). The maximum number of enrichment levels is M, and takes the value of M=10 for the two dimensional examples presented here. The Heaviside function turns on/off two sets of shape functions associated with the phases “f” and “s”. Note that no more than one degree of freedom per node is used to interpolate the solution at a point in a finite element. The active degrees of freedom are denoted by i for the fluid phase, and j for the solid phase. The Kronecker Delta is denoted by \(\delta ^{b}_{ij}\) with b=[f,s]. For each phase, multiple enrichment levels, i.e. sets of shape functions, are necessary if the degrees of freedom interpolate the solution in multiple, physically disconnected regions of the same phase; see Terada et al. (2003) and Tran et al. (2011). This generalization prevents spurious coupling and load transfer between disconnected regions of the same phase. A detailed explanation of this phenomenon is provided by Makhija and Maute (2014).

Here, we interpolate the level set field bi-linearly on meshes with quadrilateral elements. Therefore, each edge of the quadrilateral element can only be intersected once, which inhibits some geometric configurations. The reader is referred to Villanueva and Maute (2014) and Jenkins and Maute (2015), where this issue is discussed in further detail.

The XFEM framework presented here triangulates intersected quadrilateral elements in order to accurately integrate the weak form of the static equilibrium equations given in Section 3. The elemental interface is \({\Gamma }^{e}_{fsi}\) in an element, Ωe, intersected by the fluid-solid interface. Following the method proposed by Annavarapu et al. (2012), we define the Nitsche penalty parameters as:

$$\begin{array}{@{}rcl@{}} \gamma_{V}= \omega_{V}\mu_{f} \frac{\left|{\Gamma}^{e}_{fsi}\right|}{\left|{\Omega}^{e}\right|}, \end{array} $$
(24)
$$\begin{array}{@{}rcl@{}} \gamma_{D}=\omega_{D}E_{m}\frac{\left|{\Gamma}^{e}_{fsi}\right|}{\left|{\Omega}^{e}\right|}. \end{array} $$
(25)

The choice for weighting parameters, ω D and ω V , is problem dependent; typical values range between 100 and 103.

5 Geometry model

The geometry of the fluid solid interface is described by the zero level set iso-contour. The level set field is discretized by the same mesh as used for the FSI model response calculation. We adopt the explicit LSM of Kreissl and Maute (2011), and define the nodal level set values as explicit functions of the optimization variables. Each node in the finite element mesh is assigned one optimization variable, s i . Explicit LSMs, which have been also studied, for example, by Wang and Wang (2006), Luo et al. (2007), and Pingen et al. (2010), are a deviation from traditional LSMs; see, for example, Allaire et al. (2002), Wang et al. (2003), Allaire et al. (2004), and Burger and Osher (2005). Instead of updating the level set field via the solution of the Hamilton-Jacobi equation, as done in traditional LSMs, explicit LSMs solve the parametrized optimization problem by standard nonlinear programming schemes. Note that, similar to traditional LSMs, the method presented here uses shape sensitivities for computing the gradients of objective and constraints with respect to optimization variables; details of the sensitivity analysis are provided by Coffin and Maute (2015).

We distinguish between two level set fields: \(\tilde {\phi }(\pmb {x})\) and ϕ(x). The field \(\tilde {\phi }(\pmb {x})\) is used to evaluate geometric quantities, such as the volume of the structural domain and the perimeter of the fluid-structure interface, and may contain free-floating volumes of solid material. These free-floating volumes are removed in the construction of the level set field ϕ(x), which is used in the XFEM analysis; see also (21).

The nodal level set values, \(\tilde {\phi }_{i}\), depend explicitly on the optimization variables s i , and are computed via a linear filter:

$$ \tilde{\phi}_{i} = \left( {\sum\limits^{N_{nodes}}_{j=1} \eta_{ij}}\right)^{-1} \ \sum\limits^{N_{nodes}}_{j=1} \eta_{ij} \ s_{j} , $$
(26)

with

$$ \eta_{ij}={max}\left( 0, (r-|\mathbf{x}_{i} - \mathbf{x}_{j}|)\right), $$
(27)

where x i is the location of node i and r is the filter radius. The total number of nodes in the mesh is N n o d e s . The level set field, \(\tilde {\phi }(\pmb {x})\), defines the structural domain, \(\tilde {\Omega }_{s}\), on which the indicator field, χ(x), is computed; see Fig. 5 and (1).

The geometry of the fluid-structure interface used in the XFEM analysis is defined by the level set field, ϕ(x). The nodal level set values, ϕ i , are determined as follows:

$$ \phi_{i} = \left\{ { \begin{array}{rll} \tilde{\phi}_{i} & \forall & \tilde{\phi}_{i} < 0\\ \tilde{\phi}_{i} & \forall & \tilde{\phi}_{i} > 0 \ \wedge \ \chi_{i} > \chi_{o}\\ -\tilde{\phi}_{i} & \forall & \tilde{\phi}_{i} > 0 \ \wedge \ \chi_{i} = \chi_{o} \end{array} } \right. . $$
(28)

Thus, for all nodes within the structural domain, \(\tilde {\Omega }_{s}\), the sign of the level set function, \(\tilde {\phi }_{i}\) is flipped if the indicator function identifies the node belonging to a free-floating volume, i.e. χ i = χ o .

The level set filter (26) widens the zone of influence of the optimization variables on the level set field and thus enhances the convergence of the optimization process. It neither guarantees the convergence of the optimized geometry with mesh refinement nor provides local size control; see, for example, the discussions in van Dijk et al. (2013), Sigmund and Maute (2013), and Villanueva and Maute (2014). To control globally, i.e. in an integral sense, the geometry of the optimized design, we penalize the perimeter of the FSI boundary in the formulation of the LS-XFEM optimization problems studied in Section 6. Numerical experiments suggest that penalizing or constraining the perimeter leads to smooth shapes and impedes the emergence of small features and free-floating material; see, for example, Makhija and Maute (2014).

While the level set field \(\tilde {\phi }(\pmb {x})\) is a smooth function of the optimization variables, the level set field ϕ(x) is not if free-floating volumes of solid material emerge. To reduce the impact of discontinuities in the evolution of ϕ(x), we found through numerical studies that it is beneficial for the convergence of the optimization process to compute geometric quantities based on \(\tilde {\phi }(\pmb {x})\). As penalizing the perimeter gradually removes free-floating volumes described by \(\tilde {\phi }\), the inconsistency in the geometries described by \(\tilde {\phi }(\pmb {x})\) and ϕ(x) vanishes as the design converges.

6 Numerical examples

In this section we study the proposed LS-XFEM with three two-dimensional numerical examples. The first example verifies that the framework discussed in Section 5 senses free-floating volumes of solid material, and converts them into fluid for the FSI analysis. This example also illustrates the evolution of the FSI response as solid disconnects from an anchored volume.

The second example is the design of a bio-prosthetic aortic heart valve. The fluid average maximum shear stress, which is a measure of blood cells suffering blood cell damage, is minimized by manipulating the wet shape of a flexible “leaflet”. This example demonstrates that the LS-XFEM is well suited for shape optimization problems where the objective characterizes the flow solution.

The third example is the design of a support structure for a deflecting beam immersed in a fluid channel. We design the topology of the fluid-solid materials immediately downstream of a beam to minimize compliance, subject to a constraint on solid volume. This example showcases the wet and dry topology optimization capability of the LS-XFEM for FSI problems.

In all examples we discretize the computational domain with 4-node bi-linear quadrilateral elements. The steady-state response of the FSI problem is computed by Newton’s method, equipped with an adaptive under-relaxation strategy. This feature is crucial for handling (intermediate) designs with thin structural members that lead to large, local deformations. In the FSI analysis, such deformations can result in large distortions of the fluid mesh which may cause the fluid solution to diverge.

The design sensitivities of the objective and constraints are determined by the adjoint method. The Jacobian of the state equations and gradients of objective and constraints with respect to the state variables are computed based on analytically derived expressions. The partial derivatives of the residual, objective, and constraints with respect to the optimization variables within the adjoint framework are evaluated by a central finite difference scheme. The reader is referred to Coffin and Maute (2015) for further details on the adjoint framework employed here. The linear sub-problems in the forward and adjoint sensitivity analysis are solved by a direct parallel solver (Amestoy et al. 2000; Sala et al. 2008).

The parameter optimization problems resulting from the proposed LS-XFEM approach are solved by the Globally Convergent Method of Moving Asymptotes of Svanberg (2002). We use an initial adaptation of 0.5, and a value of 0.7 thereafter. Relative step size and penalty values are defined specifically for each example. No inner GCMMA iterations are used in the examples shown here.

Fig. 6
figure 6

Setup of the disconnecting cylinders example

Full size image

6.1 Disconnecting cylinders in flow

This example verifies that the evaluation of the level set function ϕ(x) in (28) converts free-floating solid volume to fluid and illustrates the behavior of the design criteria used in the next two examples as a solid volume becomes disconnected.

The problem setup is illustrated in Fig. 6a, where a structure is immersed in a rectangular flow channel. The geometry of the structure is defined by the union of two initially overlapping cylinders of equal radius, L R . One cylinder is stationary whereas the other one is moved. The structure is supported by constraining the displacements of the nodes within a square region at the center of the stationary cylinder. Figure 6b shows the structural mesh, where black dots denote the location of the structural essential boundary condition and the indicator natural boundary condition, i.e. applied indicator flux.

The FSI response is determined for a sequence of positions for the non-fixed cylinder. The two cylinders start concentric (L c =0), and the non-fixed cylinder is moved away from the fixed cylinder along a straight path inclined by 45.0o with respect to the channel axis in 32 increments of ΔL c . Initially, as the non-fixed cylinder protrudes outward, only the shape of the structure is varied. As the distance, L c , between the cylinder centers exceeds 2 L R , the structural topology changes, and a volume of free-floating material is created. Once this topological change occurs, the indicator field solution causes the sign of the level set value in the disconnected solid region to change. Note that the cylinder does not move in time, but rather the steady-state response is computed for each configuration.

A parabolic inflow velocity profile is imposed at the left edge of the channel, and no slip velocity conditions are prescribed on the top and bottom walls. A constant pressure outlet is enforced (\(\hat {p}=0\)). Using the cylinder diameter for the reference length, the Reynolds number of the flow is 1.0. The remaining problem parameters are given in Table 1.

Table 1 Physical parameters of disconnecting cylinders example
Full size table

The structural compliance, U, and the fluid average maximum shear stress, T, are considered as design criteria, and are computed as:

$$\begin{array}{@{}rcl@{}} U ={\int}_{{\Omega}_{s}}\pmb{\sigma}_{s} \ \pmb{\epsilon}\left( \pmb{u}\right) \ d{\Omega}, \end{array} $$
(29)
$$\begin{array}{@{}rcl@{}} T=\frac{1}{\|{\Omega}_{f}\|} {\int}_{{\Omega}_{f}}\tau^{max}\left( \pmb{\sigma}_{f}\right)d{\Omega}, \end{array} $$
(30)

The local maximum shear stress, τ max, is computed as:

$$\begin{array}{@{}rcl@{}} \tau^{max}\left( \pmb{\sigma}_{f}\right)=\sqrt{\left( \frac{\sigma^{xx}_{f}-\sigma^{yy}_{f}}{2}\right)^{2}+\left( \sigma^{xy}_{f}\right)^{2}} \end{array} $$
(31)

The flow, structure, and indicator fields for different cylinder locations are given in Figs. 7 and 8. The fluid velocity solutions show a constriction in the top of the channel as the second cylinder protrudes further into the upper flow region until L c =0.102 [m], when the two cylinders disconnect. In the last fluid solution in Fig. 7, the non-fixed cylinder is sensed as free-floating and vanishes. After the disconnect, the flow and deformation fields are identical to the initial configuration, where the two cylinders are concentric.

Fig. 7
figure 7

Contours of fluid velocity and fluid mesh displacement magnitudes at various cylinder center separation distances

Full size image
Fig. 8
figure 8

Indicator value and structural displacement magnitude for the disconnecting cylinder example

Full size image

The solid compliance and fluid average maximum shear stress are plotted over the separation distance between the cylinder center points in Fig. 9. As the cylinders disconnect, the FSI response is non-differentiable due to the on/off nature of the indicator field solution. In particular, T is rather sensitive to design changes; the severity of oscillations could be reduced with mesh refinement. The impact of the non-differentiability of topological changes on the convergence of the optimization process is studied subsequently with two design optimization problems.

Fig. 9
figure 9

Evolution of design criteria for various cylinder center separation distances

Full size image

6.2 Bio-prosthetic aortic heart valve design

We study the proposed optimization approach by optimizing the wet shape of a bio-prosthetic aortic heart valve (BAHV), illustrated in Fig. 10.

Fig. 10
figure 10

Illustration of the aortic valve location within a human heart

Full size image

During ventricular systole, the pressure in the left ventricle increases. When the pressure difference between the aorta and the left ventricle is sufficiently high, the leaflet is displaced by the fluid force and blood flows from the left to the right ventricle of the heart. Once the pressure difference is relieved, the leaflet displaces back to its undeformed position. Modeling the BAHV as an FSI system is crucial to predicting sticking or premature opening of the valve.

We aim to minimize the average maximum shear stress (30) in the fluid, which characterizes the amount of blood platelet damage as the blood flows through the valve (Morbiducci et al. 2015). The average maximum shear stress is one of many metrics for blood damage; see, for example, Arora et al. (2004). An equality constraint on the pressure drop across the value is included to guarantee that the leaflet has a sufficient stiffness needed to open and close (Griffith 2012). The design problem is defined as follows:

$$ \begin{array}{llll} & \underset{\pmb{s}}{\text{minimize}} \ & z(\pmb{s}) & = k_{s} \ T + k_{P} {\int}_{{\Gamma}_{fsi}}d{\Gamma}, \\ & \text{subject to} & g\left( \pmb{s}\right) & = k_{\Delta p} \ \left( \frac{\Delta p}{\Delta p^{*}}-1.0\right)^{2} \leq 0, \end{array} $$
(32)

where k s and k P scale the fluid average maximum shear stress and the fluid-solid interface length, respectively.

As GCMMA cannot handle equality constraints, we express the equality constraint on the pressure drop via an equivalent inequality constraint. The inequality constraint in (32) is only satisfied if the pressure drop across the valve, Δp, is equal to the desired value, Δp ∗. We scale the constraint by the parameter k Δp to control the rate the GCMMA satisfies this condition.

A simplified BAHV model is shown in Fig. 11, where the semicircle of radius L R is referred to as the sinus. The leaflet design is initially a rectangle with thickness L t and length L L , which includes a semi-circle of radius L t /2 on the tip. The design domain is a square with side length L R . The upper left corner of the design domain is L d behind and above the corner node that joins the top of the valve body with the sinus to provide some overlap for connecting the leaflet to the arterial wall. Figure 11b shows the design domain offset, and the pin conditions for the leaflet root. Note that the leaflet is not seeded with fluid inclusions because we intend to optimize the bulk profile of the leaflet, and the volume of the leaflet is not relevant.

Fig. 11
figure 11

Setup of the BAHV example

Full size image

The BAHV model employed here is idealized, but is sufficient to demonstrate the advantages of the proposed optimization framework for this class of design problems. The leaflet structural deformation is modeled by linear elasticity, and we assume a Newtonian flow model. In general, blood viscosity is shear rate dependent; however, a rate independent model is a reasonable approximation given the size of the bulk flow of the heart (Vasava et al. 2012). We assume the arterial walls are rigid. This simplifying assumption may affect the accuracy of our model for practical applications (Hsu et al. 2014).

The physical properties of the model are provided in Table 2, where the dimensions and physical parameters are primarily taken from Hart (2002). The approximate Reynolds number of the flow is 10.0, where the length of the leaflet is used as reference length. This Reynolds number indicates that the flow is laminar. A symmetry (slip) condition is imposed at the bottom surface, and a parabolic inflow is prescribed at the left edge of the valve model. A no-slip velocity condition is enforced at the upper arterial walls, including the sinus cavity. A zero-pressure condition is prescribed at the outflow. The pressure drop across the valve in (32) is computed as:

$$\begin{array}{@{}rcl@{}} {\Delta} p={\int}_{{\Gamma}_{in}}p+\frac{1}{2}\pmb{v}^{2}d{\Gamma}-{\int}_{{\Gamma}_{out}}p+\frac{1}{2}\pmb{v}^{2}d{\Gamma}. \end{array} $$
(33)

The structural displacements at the nodes on the arterial wall (upper wall and sinus cavity) are prescribed to be zero. Note that the indicator boundary flux is also applied to these same locations.

Table 2 Parameters for the BAHV example
Full size table

We optimize the problem on two computational grids, a coarse and fine version, in order to gain insight into mesh dependency of the proposed optimization method. The coarse mesh has 17,089 nodes, yielding approximately 225,000 degrees of freedom at the initial design stage. The fine mesh has 32,800 nodes, yielding approximately 410,000 degrees of freedom at the initial design configuration.

The final designs for the coarse and fine meshes are given in Fig. 12, where the black color depicts the deformed solid, and the red line represents the undeformed FSI boundary. The pressure contours with fluid velocity streamlines are plotted in Fig. 13. The evolution of the objective and the constraint value is shown in Fig. 14.

Fig. 12
figure 12

Initial (top), and final designs for coarse (center) and fine (bottom) meshes, with undeformed level set zero-contour shown in red

Full size image
Fig. 13
figure 13

Pressure contours with streamlines of initial design (top), and final designs for coarse (middle) and fine (bottom) meshes

Full size image
Fig. 14
figure 14

BAHV valve objective and constraint evolution

Full size image

Both the coarse and fine mesh lead to designs with similar behavior: the root of the leaflet expands to stiffen the leaflet and to increase the pressure drop such that the constraint is satisfied. To reduce the average maximum shear stress, the bottom of the leaflet is elongated and a thin tip section is formed. This process enables the pressure drop to still be satisfied, but leads to more deformation near the tip which impedes the flow less.

Figure 14 shows that, in the course of the optimization process, the pressure drop constraint is quickly satisfied at the cost of an increase of the average maximum shear stress. The convergence of the coarse mesh suffers from oscillations which are due to fluctuations of the insufficiently resolved fluid stresses near the interface.

Figure 15 illustrates that in both the initial and the optimized configurations the shear stress distribution exhibits large spatial gradients near the fluid-structure interface. This feature leads to ill-conditioning of the interface coupling conditions and oscillatory behavior in Fig. 14, in particular for the coarse mesh.

Fig. 15
figure 15

Initial and optimized fluid shear stress distributions for fine BAHV mesh

Full size image

While the shape of the leaflet changed in the optimization process, the topology remained unchanged. This is to be expected, given new holes cannot be generated with the LSM employed here. For this particular problem the internal topology of the leaflet is not important because the bulk deformation profile of the valve governs the pressure drop and blood shear. The capability of describing topological changes in the optimization process are illustrated in the next example in Section 6.3.

6.3 Beam support design

In this example we study the proposed LS-XFEM for optimization of a beam support structure. We seek to maximize the structural stiffness while constraining the volume of the solid. Figure 16 shows the problem setup along with the initial topology. A beam of thickness L b,t is immersed at a horizontal distance L b,c in the fluid channel. A parabolic velocity profile is prescribed along the left edge of the flow channel. No slip conditions at the upper and lower walls are imposed, and a zero-pressure outflow condition is enforced at the right edge of the channel. The nodes along the bottom structural boundary are clamped, and an indicator flux is applied to them. The design domain begins at the rear edge of the beam, and extends L D,w downstream. The design domain height is L D,H , referenced from the channel bottom boundary. The beam support is seeded with eighteen equispaced holes (three in horizontal direction, six in vertical direction) of fluid with radius r i .

Fig. 16
figure 16

Setup of beam support design example

Full size image

This problem is similar to one of Yoon (2010). Here we consider a Reynolds number, R e=10.0, which results in a laminar, steady-state flow, and we only allow topological changes to the structure just downstream of the nominal beam structure.

The design objective is to minimize the structural compliance, augmented by a perimeter penalty, subject to a constraint on total solid volume. The design problem is as follows:

$$ \begin{array}{llll} & \underset{\pmb{s}}{\text{minimize}} \ & z(\pmb{s}) & = k_{D} \ U + k_{P} {\int}_{{\Gamma}_{fsi}}d{\Gamma}, \\ & \text{subject to} & g\left( \pmb{s}\right) & = k_{V}\left( \frac{1}{V^{*}_{s}} \ {\int}_{{\Omega}_{s}}\ d{\Omega}-1.0\right) \leq 0, \end{array} $$
(34)

where k D scales the compliance and k P scales the perimeter in the objective calculation. The volume constraint scaling is k V , and \(V^{*}_{s}\) is the maximum allowable volume of solid. We linearly ramp up the scaling parameter on the volume constraint, shown in Fig. 17, in order to control the rate at which GCMMA satisfies this condition. If the constraint is satisfied too quickly, too much material is removed early in the optimization process, affecting the performance of the final design. Throttling the constraint ensures that both the objective and the constraint are considered in a balanced fashion. The scaling parameter is linearly increased from k V,o to k V,f over s ∗ iterations.

Fig. 17
figure 17

Increase of volume constraint scaling in the optimization process

Full size image

The XFEM model has approximately 200,000 total degrees of freedom; the exact number depends on the intersection geometry and changes throughout the optimization process. The remaining parameters for the beam support problem are given in Table 3.

Table 3 Parameters for the beam support example
Full size table

The final structural design in the undeformed configuration is given in Fig. 18. The normal, shear, and von Mises stress contours are plotted in the optimal, deformed configuration in Fig. 19. The initial and optimized structural designs in the deformed configuration, with the fluid colored by pressure contours and velocity streamlines, are shown in Fig. 20. The objective and constraint are plotted in the top row of Fig. 21. The bottom left plot of Fig. 21 is the constraint divided by the scaling parameter k V , and the bottom right plot is the evolution of the free-floating volume over the optimization process.

Fig. 18
figure 18

Optimal beam support design in the undeformed state

Full size image
Fig. 19
figure 19

Optimal beam support designs in the deformed state with stress contours

Full size image
Fig. 20
figure 20

Initial and final beam support designs in the deformed state with the fluid colored by pressure contours and velocity streamlines

Full size image
Fig. 21
figure 21

Evolution of objective, constraint, and volume of free-floating solid material in the course of the optimization process for the beam support design example

Full size image

Between the 10th and 50th design iterations free-floating pieces of solid material emerge, are sensed by the indicator field, and converted to fluid prior to the FSI analysis. However, as these solid volumes are described by the level-set field, \(\tilde {\phi }\), their perimeter still contributes to the objective; see Section 5. In the process of minimizing the objective, all of the free-floating solid volumes vanish eventually.

Figure 22 shows the evolution of the objective and free-floating volume together with snapshots of design for distinct iterations. A single snapshot of the FSI response for the 12th design iteration is shown in the bottom of Fig. 22. At this iteration, free-floating solid volumes have been converted to fluid in the FSI analysis, yet thin, hinge-like structural members lead to large local deformations and a sudden increase in the objective. Such discontinuities were observed previously by Jenkins and Maute (2015) for dry topology optimization problems when internal structural members disconnect. Thus, discontinuities in the optimization process are not solely due to eliminating free-floating volumes of solid material, but may emerge whenever the dry or wet topology changes. While Newton’s method in combination with an adaptive under-relaxation scheme was successful in computing an FSI response for the configuration studied here, the emergence of such features may severely impact the robustness of the FSI analysis.

Fig. 22
figure 22

Snapshots of the beam support design along the evolution of the objective and free-floating volume (right), and the FSI response of the 12th iteration (left)

Full size image

Despite oscillations in the design convergence history, caused by both the removal of free-floating solid volume (seen in the two previous examples) and the emergence of thin compliant structural features, the method converged to a well-defined support structure topology. This example shows that the proposed LS-XFEM is well-suited for wet and dry topology optimization of FSI problems that exhibit moderate structural deformations. However, an additional strategy for preventing large local deformations of intermediate designs with thin, flexible structures needs to be developed to take full benefit of the approach.

7 Conclusions

An immersed boundary approach for optimization of FSI problems was presented. The approach combines the level set and extended finite element methods to allow for shape and topological changes of the fluid-structure interface. The proposed FSI analysis scheme integrates an immersed boundary method with a deforming fluid mesh motion technique, which allows for moderate structural deformations. The immersed fluid-structure interface is defined by the zero iso-contour of a level set function which is constructed such that free-floating volumes of solid materials which may undergo rigid body motion are eliminated from the FSI model. In this study the fluid was modeled by the incompressible Navier-Stokes equations and the structure by linear elasticity. The coupling conditions were enforced weakly at the fluid-structure interface.

The main characteristics of the proposed methods were studied with two-dimensional problems at steady-state. It was shown that the conversion of isolated solid volumes to fluid in the FSI analysis may introduce discontinuities in design criteria as the design evolves. These discontinuities may affect the convergence of gradient-based optimization schemes, as used in this study.

The emergence of thin structural members was identified as another issue that may affect the convergence of the optimization process and the robustness of the FSI analysis. As the thickness of structural features drops below some threshold, their deformations may increase significantly, due to the inherent nonlinearity of the fluid-structure coupling. This FSI phenomenon may cause a discontinuity in the evolution of the design criteria and may affect severely the convergence in the FSI analysis. In this study Newton’s method with adaptive under-relaxation was successfully employed to stabilize the FSI analysis.

While discontinuities due to the removal of free-floating solid material and due to large local deformations were observed, the optimization examples studied here demonstrated that the designs still converge to interesting and meaningful solutions. However, improved methods for treating free-floating volumes and for stabilizing the FSI analysis against large local deformations should be investigated in future studies. The approaches and results presented here may provide some guidance for these studies.