Fluid–structure interaction analysis of bioprosthetic heart valves: significance of arterial wall deformation

Abstract

We propose a framework that combines variational immersed-boundary and arbitrary Lagrangian–Eulerian methods for fluid–structure interaction (FSI) simulation of a bioprosthetic heart valve implanted in an artery that is allowed to deform in the model. We find that the variational immersed-boundary method for FSI remains robust and effective for heart valve analysis when the background fluid mesh undergoes deformations corresponding to the expansion and contraction of the elastic artery. Furthermore, the computations presented in this work show that the arterial wall deformation contributes significantly to the realism of the simulation results, leading to flow rates and valve motions that more closely resemble those observed in practice.

1 Introduction

Heart valves are passive structures that ensure the unidirectional blood flow through the heart by opening and closing in response to hemodynamic forcing. Hundreds of thousands of diseased valves are replaced by prosthetics annually [1, 2]. Bioprosthetic heart valves (BHV) are prosthetics composed of thin flexible leaflets that are fabricated from biological materials and mimic the structure of native heart valves to avoid pathological hemodynamics [2]. The principal drawback of this style of prosthetic is its durability, which is limited to 10–15 years [3]. Accurate computational analysis of these devices could provide insights into the mechanical processes that both contribute to and follow from their deterioration, streamlining the design process of new prosthetics.

The biomechanical significance of arterial elasticity was first clearly described by Hales [4] in 1733, after performing a series of pioneering experiments on animals. Hales found that arteries expand elastically to store the systolic output of the heart, then gradually release this blood during diastole. This is now known as the Windkessel effect.¹ Frank [5–7] developed the first mathematical model of the Windkessel effect in 1899. Frank’s model may be intuitively understood through the electronic–hydraulic analogy [8], which substitutes electrical current for volumetric flow and voltage for pressure. In this analogy, Frank’s model—the two-element Windkessel model—consists of a capacitor and resistor in parallel, downstream of the aortic valve, which acts as a pulsatile current source.

The capacitor models the elastic arteries, which accumulate blood to develop pressure, while the resistor models viscous head loss within the circulatory system by analogy to Ohm’s Law. This model allows prediction of the time-dependent aortic pressure based on the history of flow rate through the aortic valve. Many refinements to Frank’s model have been proposed since his initial contribution, including the three- [9], and four- [10] element Windkessel models. Such models are referred to as “lumped-parameter models”. Lumped-parameter models may be coupled with detailed computational fluid dynamics (CFD) simulations of specific arterial sections of interest. The voltage of the lumped-parameter model acts as a pressure boundary condition on the outflow of the CFD domain, and the volumetric flow from the CFD domain acts as a current source for the lumped-parameter model [11]. However, to fully account for the Windkessel effect of arterial elasticity, fluid–structure interaction (FSI) must be incorporated into the detailed model of the section of interest. In this paper, we demonstrate that the elasticity of the section of aorta immediately surrounding an implanted BHV can have profound effects on the dynamics of both the valve itself and the surrounding blood flow.

For the reasons discussed in our earlier work [12], we simulate the BHV leaflets using a non-boundary-fitted (variational immersed-boundary) method, in which the structural discretization is free to move independently through a background fluid mesh. Detailed reviews of non-boundary-fitted methods for FSI can be found in Sotiropoulos and Yang [13], Mittal and Iaccarino [14], and Peskin [15]. These methods are particularly attractive for applications with complex moving boundaries, such as heart valve leaflets [16–21]. However, they have the inherent disadvantage of uncontrolled mesh quality near the fluid–structure interface, and may be unable to resolve important boundary layer features that may globally affect the flow.

More accurate results can be obtained using boundary-fitted approaches by building a fluid mesh that is tailored to the structure and deforms as the structure moves. In such computations, the fluid subproblem may be posed using an arbitrary Lagrangian–Eulerian (ALE) formulation [22–24], or a space–time formulation [25–27], both of which explicitly account for the motion of the fluid mechanics domain and mesh. For the parts of an arterial FSI computation with no contact between solid surfaces,the problem of mesh deformation may be effectively solved using a simple fictitious linear elasticity problem [28–32]. This makes vascular FSI an ideal application for boundary-fitted approaches.

In the analysis of a BHV implanted in a deforming artery, we are faced with the confluence of two problems that suggest different computational methods. We therefore elect to use a hybrid method that leverages the advantages of both ALE and immersed-boundary techniques for FSI. We discretize the valve leaflets separately, and immerse them into a deforming boundary-fitted mesh of the artery volume. The proposed technique falls under the umbrella of the recently proposed Fluid–Solid Interface-Tracking/Interface-Capturing Technique (FSITICT) [33], a method that targets FSI problems in which interfaces that are possible to track are tracked, and those too difficult to track are captured. The FSITICT was introduced as an FSI version of the Mixed Interface-Tracking/Interface-Capturing Technique (MITICT) [34]. The MITICT was successfully tested in 2D computations with solid circles and free surfaces [35, 36] and in 3D computation of ship hydrodynamics [37]. Recently Wick [38, 39] made use of the FSITICT approach, coupling a boundary-fitted and immersed-boundary discretizations in a single computation, to compute several 2D FSI benchmark problems.

Our immersed-boundary approach for FSI was first developed in Kamensky et al. [12] using the variational framework of augmented Lagrangian methods. The augmented Lagrangian approach for FSI was proposed in Bazilevs et al. [40] to handle boundary-fitted computations with non-matching fluid–structure interface discretizations. We found in Kamensky et al. [12] that this augmented Lagrangian framework can be extended to handle non-boundary-fitted CFD and FSI problems, and its efficacy was demonstrated using several computations including the coupling of a BHV and surrounding blood flow at physiological pressure levels.

In this work, we take the augmented Lagrangian framework for FSI as the starting point of our ALE/immersed-boundary hybrid methodology. A single computation combines a boundary-fitted, deforming-mesh treatment of some fluid–structure interfaces with a non-boundary-fitted treatment of others. This approach enables us to simulate the FSI of a BHV implanted in an elastic artery through the entire cardiac cycle, at full scale, under realistic physiological conditions.

The paper is organized as follows. In Sect. 2 we present the details of our hybrid ALE/immersed-boundary method developed for the FSI simulation of a heart valve implanted in a deformable artery. In Sect. 3 we provide the simulation details and report the results of the FSI computations of an actual BHV design. In particular, we compare the results from the rigid- and elastic-wall simulations and find that wall elasticity plays an important role in the overall system response. In Sect. 4 we draw conclusions.

2 FSI modeling using a hybrid ALE/immersed-boundary approach

In this section, we present the computational framework for FSI analysis of a BHV implanted in a deformable artery. The blood flow in a deforming artery is governed by the Navier–Stokes equations of incompressible flow posed on a moving domain. The domain motion is handled using the ALE formulation, which is a widely used approach for vascular blood flow applications [41–46]. The coupling of the BHV leaflet dynamics to the artery is handled through the recently proposed variational immersed-boundary method [12], in which the structural discretization is free to move independently through a background fluid mesh. The hybrid ALE/immersed-boundary method will be presented and applied to the simulation of an aortic BHV coupled to an elastic arterial wall and blood flow over cardiac cycles.

2.1 Augmented Lagrangian framework for FSI

Let $(\varOmega _1)_t$ and $(\varOmega _2)_t \in \mathbb {R}^d, d=\{2,3\}$ represent the time-dependent domains of the fluid and structural mechanics problems, respectively, at time $t$, with $(\varGamma _1)_t$ and $(\varGamma _2)_t$ representing their corresponding boundaries. Let $(\varGamma _{\text {I}})_t \in \mathbb {R}^d$ represent the interface between the fluid and structural domains. Let $\mathbf {u}_1$ and $p$ denote the fluid velocity and pressure, respectively. Let $\mathbf {y}$ denote the displacement of structural material points from their positions in a reference configuration, and define the structure velocity $\mathbf {u}_2$ as the material time derivative of $\mathbf {y}$.We introduce an additional unknown function $\pmb {\lambda }$ defined on $(\varGamma _{\text {I}})_t$, which takes on the interpretation of a Lagrange multiplier. Let $\mathcal {S}_u$, $\mathcal {S}_p$, $\mathcal {S}_d$, and $\mathcal {S}_\ell$ be the function spaces for the fluid velocity, fluid pressure, structural velocity, and Lagrange multiplier solutions, respectively, and $\mathcal {V}_u$, $\mathcal {V}_p$, $\mathcal {V}_d$, and $\mathcal {V}_\ell$ be the corresponding weighting function spaces. The variational problem of the augmented Lagrangian formulation is: find $\mathbf {u}_1\in \mathcal {S}_u$, $p\in \mathcal {S}_p$, $\mathbf {y}\in \mathcal {S}_d$, and $\pmb {\lambda }\in \mathcal {S}_\ell$ such that for all test functions $\mathbf {w}_1\in \mathcal {V}_u$, $q\in \mathcal {V}_p$, $\mathbf {w}_2\in \mathcal {V}_d$, and $\delta \pmb {\lambda }\in \mathcal {V}_\ell$

$$\begin{aligned}&B_1(\{\mathbf {w}_1,q\},\{\mathbf {u}_1,p\};\hat{\mathbf{u }})-F_1(\{\mathbf {w}_1,q\}) \nonumber \\&\quad +\int \limits _{(\varGamma _{\text {I}})_t}\mathbf {w}_1\cdot \pmb {\lambda }~\text {d}\varGamma + \int \limits _{(\varGamma _{\text {I}})_t}\mathbf {w}_1\cdot \beta (\mathbf {u}_1-\mathbf {u}_2)~\text {d}\varGamma = 0,\end{aligned}$$

(1)

$$\begin{aligned}&B_2(\mathbf {w}_2,\mathbf {y})-F_2(\mathbf {w}_2) \nonumber \\&\quad -\int \limits _{(\varGamma _{\text {I}})_t}\mathbf {w}_2\cdot \pmb {\lambda }~\text {d}\varGamma -\int \limits _{(\varGamma _{\text {I}})_t}\mathbf {w}_2\cdot \beta (\mathbf {u}_1-\mathbf {u}_2)~\text {d}\varGamma = 0,\end{aligned}$$

(2)

$$\begin{aligned}&\int \limits _{(\varGamma _{\text {I}})_t}\delta \pmb {\lambda }\cdot (\mathbf {u}_1-\mathbf {u}_2)~\text {d}\varGamma =0. \end{aligned}$$

(3)

In the above, the subscripts 1 and 2 denote the fluid and structural mechanics quantities, and $\beta$ is a penalty parameter, which we leave unspecified for the moment. $B_1, B_2, F_1$, and $F_2$ are the semi-linear forms and linear functionals corresponding to the fluid and structural mechanics problems, respectively, and are given by

$$\begin{aligned}&B_1\left( \{\mathbf {w},q\},\{\mathbf {u},p\};\hat{\mathbf{u }}\right) \! =\! \int \limits _{(\varOmega _1)_t}\mathbf {w}\cdot \rho _1\left( \left. \frac{\partial \mathbf {u}}{\partial t}\right| _{\hat{x}}\!+\!\left( \mathbf {u}-\hat{\mathbf{u }}\right) \cdot \pmb {\nabla } \mathbf {u}\right) \text {d}\varOmega \nonumber \\&\quad +\int \limits _{(\varOmega _1)_t}\pmb {\varepsilon }(\mathbf {w}):\pmb {\sigma }_1~\text {d}\varOmega +\!\int \limits _{(\varOmega _1)_t}q\pmb {\nabla } \cdot \mathbf {u}~\text {d}\varOmega ,\end{aligned}$$

(4)

$$\begin{aligned}&F_1(\{\mathbf {w},q\})=\int \limits _{(\varOmega _1)_t}\mathbf {w}\cdot \rho _1\mathbf {f}_1~\text {d}\varOmega +\!\int \limits _{(\varGamma _{\text {1h}})_t}\mathbf {w}\cdot \mathbf {h}_1~\text {d}\varGamma ,\end{aligned}$$

(5)

$$\begin{aligned}&B_2(\mathbf {w},\mathbf {y})=\int \limits _{(\varOmega _2)_t}\mathbf {w}\cdot \rho _2\left. \frac{\partial ^2\mathbf {y}}{\partial t^2}\right| _{X}\text {d}\varOmega +\int \limits _{(\varOmega _2)_t}\pmb {\varepsilon }(\mathbf {w}):\pmb {\sigma }_2~\text {d}\varOmega ,\end{aligned}$$

(6)

$$\begin{aligned}&F_2(\mathbf {w})=\int \limits _{(\varOmega _2)_t}\mathbf {w}\cdot \rho _2\mathbf {f}_2~\text {d}\varOmega +\!\int \limits _{(\varGamma _{\text {2h}})_t}\mathbf {w}\cdot \mathbf {h}_2~\text {d}\varGamma \end{aligned}$$

(7)

where $\rho _1$ and $\rho _2$ are the densities, $\pmb {\sigma }_1$ and $\pmb {\sigma }_2$ are the Cauchy stresses, $\mathbf {f}_1$ and $\mathbf {f}_2$ are the applied body forces, $\mathbf {h}_1$ and $\mathbf {h}_2$ are the applied surface tractions, $(\varGamma _{\text {1h}})_t$ and $(\varGamma _{\text {2h}})_t$ are the boundaries where the surface tractions are specified, $\pmb {\varepsilon }(\cdot )$ is the symmetric gradient operator given by $\pmb {\varepsilon }(\mathbf {w}) = \frac{1}{2}(\pmb {\nabla } \mathbf {w}+\pmb {\nabla } \mathbf {w}^T)$, ${\hat{{\mathbf {u}}}}$ is the velocity of the fluid domain $(\varOmega _1)_t$, $\left. \tfrac{\partial (\cdot )}{\partial t}\right| _{\hat{x}}$ is the time derivative taken with respect to the fixed spatial coordinate $\hat{\mathbf{x }}$ in the referential domain (which does not follow the motion of the fluid itself), and $\left. \tfrac{\partial (\cdot )}{\partial t}\right| _{X}$ is the time derivative holding the material coordinates $\mathbf {X}$ fixed. The gradient $\pmb {\nabla }$ is taken with respect to the spatial coordinate $\mathbf {x}$ of the current configuration. We assume that the fluid is Newtonian with dynamic viscosity $\mu$ and Cauchy stress $\pmb {\sigma }_1= -p\mathbf {I}+2\mu \pmb {\varepsilon }(\mathbf {u}_1)$.

Bazilevs et al. [40] demonstrate how the Lagrange multiplier, $\pmb {\lambda }$, may be formally eliminated by substituting an expression for the fluid–structure interface traction in terms of the other unknowns. This leads to the following variational formulation for the coupled problem: find $\mathbf {u}_1\in \mathcal {S}_u$, $p\in \mathcal {S}_p$, and $\mathbf {y}\in \mathcal {S}_d$ such that for all $\mathbf {w}_1\in \mathcal {V}_u$, $q\in \mathcal {V}_p$, and $\mathbf {w}_2\in \mathcal {V}_d$

$$\begin{aligned}&B_1(\{\mathbf {w}_1,q\},\{\mathbf {u}_1,p\};\hat{\mathbf{u }}) - F_1(\{\mathbf {w}_1,q\}) + B_2(\mathbf {w}_2,\mathbf {y})-F_2(\mathbf {w}_2)\nonumber \\&\quad -\int \limits _{(\varGamma _{\text {I}})_t} (\mathbf {w}_1 - \mathbf {w}_2) \cdot \pmb {\sigma }_1(\mathbf {u}_1,p)\,\mathbf {n}_1~\text {d}\varGamma \nonumber \\&\quad -\int \limits _{(\varGamma _{\text {I}})_t}\delta \pmb {\sigma }_1(\mathbf {w}_1,q)\,\mathbf {n}_1\cdot (\mathbf {u}_1-\mathbf {u}_2)~\text {d}\varGamma \nonumber \\&\quad +\int \limits _{(\varGamma _{\text {I}})_t}(\mathbf {w}_1-\mathbf {w}_2)\cdot \beta (\mathbf {u}_1-\mathbf {u}_2)~\text {d}\varGamma =0. \end{aligned}$$

(8)

In the above, $\delta \pmb {\sigma }_1(\mathbf {w},q) {\mathbf n_1} = 2 \mu \pmb {\varepsilon }(\mathbf {w}) {\mathbf n_1} + q{\mathbf n_1}$. Equation (8) may be interpreted as an extension of Nitsche’s method [47], which is a consistent, stabilized method for imposing constraints on the boundaries by augmenting the governing equations with additional constraint equations.

This augmented Lagrangian approach for FSI was originally proposed by Bazilevs et al. [40] and further studied in Hsu and Bazilevs [48] to handle boundary-fitted computations with non-matching fluid–structure interface discretizations. In Kamensky et al. [12], we found that this framework can be extended to handle non-boundary-fitted FSI problems and the accuracy and efficiency of the methodology was examined through several computations. In this work, we take the augmented Lagrangian framework for FSI as the starting point of our hybrid ALE/immersed-boundary method. A single computation can combine a boundary-fitted, deforming-mesh treatment of some fluid–structure interfaces with a non-boundary-fitted treatment of others.

Remark 1

In the above developments we assumed that the trial and test function spaces of the fluid and structural subproblems are independent of each other. This approach provides one with the framework that is capable of handling non-matching fluid and structural interface discretizations. If the fluid and structural velocities and the test functions are explicitly assumed to be continuous (i.e. $\mathbf {u}_1 = \mathbf {u}_2$ and $\mathbf {w}_1=\mathbf {w}_2$) at the interface, the FSI formulation given by Eq. (8) reduces to: find $\mathbf {u}_1 \in \mathcal {S}_u, p\in \mathcal {S}_p$, and $\mathbf {y} \in \mathcal {S}_d$ such that for all $\mathbf {w}_1 \in \mathcal {V}_u, q_1 \in \mathcal {V}_p$, and $\mathbf {w}_2 \in \mathcal {V}_d$

$$\begin{aligned} B_1(\{\mathbf {w}_1,q\},\{\mathbf {u}_1,p\};\hat{\mathbf{u }})- F_1(\{\mathbf {w}_1,q\}) + B_2(\mathbf {w}_2,\mathbf {y}) - F_2(\mathbf {w}_2) = 0.\!\!\nonumber \\ \end{aligned}$$

(9)

This form of the FSI problem is suitable for matching fluid–structure interface meshes. Although somewhat limiting, matching interface discretizations were successfully applied to cardiovascular FSI in many earlier works [32, 44, 49–54].

2.2 Semi-discrete fluid formulation with weak boundary conditions

The fluid subproblem may be obtained by setting $\mathbf {w}_2 = {\mathbf 0}$ in Eq. (8). This approach gives a formulation for weak imposition of Dirichlet boundary conditions for the fluid problem, which was first proposed by Bazilevs and Hughes [55] and further refined in Bazilevs et al. [56, 57] to improve the performance of the fluid mechanics formulation in the presence of underresolved boundary layers. This weak imposition of the Dirichlet boundary conditions is also the starting point of the variational immersed-boundary approach [12]. In a non-boundary-fitted method, the elements of the fluid discretization may extend into the interior of an immersed object. Imposing Dirichlet boundary conditions is no longer straightforward given that the basis functions are non-interpolating at the object boundaries. In order to enforce essential boundary conditions, one can either modify the basis functions so they vanish at the interface [58] or augment the governing equations with additional constraint equations. In this work we choose the latter approach.

Consider a collection of disjoint elements $\{\varOmega ^e\}$, $\cup _e\varOmega ^{e}\subset \mathbb {R}^d$, with closures covering the fluid domain: $\varOmega _1\subset \cup _e\overline{\varOmega ^{e}}$. Note that $\varOmega ^{e}$ is not necessarily a subset of $\varOmega _1$. $\{\varOmega ^{e}\}$, $\varOmega _1$, and $\varGamma _{\text {I}}$ remain time-dependent, but we drop the subscript $t$ for notational convenience. The mesh defined by $\{\varOmega ^{e}\}$ deforms with a velocity field $\hat{\mathbf{u }}^h$ and the boundary $\varGamma _{\text {I}}$ moves with velocity $\mathbf {u}_2$. The semi-discrete fluid problem is given by: find $\mathbf {u}_1^h\in \mathcal {S}_u^h$ and $p^h\in \mathcal {S}_p^h$ such that for all $\mathbf {w}_1^h\in \mathcal {V}_u^h$ and $q^h\in \mathcal {V}_p^h$

$$\begin{aligned}&B_1^{\text {VMS}}\left( \{\mathbf {w}_1^h,q^h\},\{\mathbf {u}_1^h,p^h\};\hat{\mathbf{u }}^h\right) -F_1^{\text {VMS}}\left( \{\mathbf {w}_1^h,q^h\}\right) \nonumber \\&\quad -\int \limits _{\varGamma _{\text {I}}}\mathbf {w}_1^h\cdot \left( -p^h\mathbf {n}_1+2\mu \pmb {\varepsilon }(\mathbf {u}_1^h)\mathbf {n}_1\right) \text {d}\varGamma \nonumber \\&\quad -\int \limits _{\varGamma _{\text {I}}}\left( 2\mu \pmb {\varepsilon }(\mathbf {w}_1^h)\mathbf {n}_1+q^h\mathbf {n}_1\right) \cdot \left( \mathbf {u}_1^h - \mathbf {u}_2\right) \text {d}\varGamma \nonumber \\&\quad -\int \limits _{\left( \varGamma _{\text {I}}\right) ^-}\mathbf {w}_1^h\cdot \rho _1\left( \left( \mathbf {u}_1^h-\hat{\mathbf{u }}^h\right) \cdot \mathbf {n}_1\right) \left( \mathbf {u}_1^h-\mathbf {u}_2\right) \text {d}\varGamma \nonumber \\&\quad +\int \limits _{\varGamma _{\text {I}}}\tau ^B_{\text {TAN}}\left( \mathbf {w}_1^h-\left( \mathbf {w}_1^h\cdot \mathbf {n}_1\right) \mathbf {n}_1\right) \cdot \nonumber \\&\qquad \left( \left( \mathbf {u}_1^h - \mathbf {u}_2\right) -\left( \left( \mathbf {u}_1^h - \mathbf {u}_2\right) \cdot \mathbf {n}_1\right) \mathbf {n}_1\right) \text {d}\varGamma \nonumber \\&\quad +\int \limits _{\varGamma _{\text {I}}}\tau ^B_{\text {NOR}}\left( \mathbf {w}_1^h\cdot \mathbf {n}_1\right) \left( \left( \mathbf {u}_1^h - \mathbf {u}_2\right) \cdot \mathbf {n}_1\right) \text {d}\varGamma =0, \end{aligned}$$

(10)

where $(\varGamma _\text {I})^-$ is the “inflow” part of $\varGamma _\text {I}$, on which $(\mathbf {u}_1^h-\hat{\mathbf{u }}^h)\!\cdot \mathbf {n}_1 < 0$, the constants $\tau _{\text {TAN}}^B$ and $\tau _{\text {NOR}}^B$ correspond to a splitting of the penalty term into the tangential and normal directions, respectively, and $\varGamma _{\text {I}}$ may cut through element interiors. The discrete trial function spaces $\mathcal {S}_u^h$ for the velocity and $\mathcal {S}_p^h$ for the pressure, as well as the corresponding test function spaces $\mathcal {V}_u^h$ and $\mathcal {V}_p^h$ are assumed to be equal order, and, in this work, are comprised of isogeometric [59, 60] functions. The forms $B_1^{\text {VMS}}$ and $F_1^{\text {VMS}}$ are the variational multiscale (VMS) discretizations of $B_1$ and $F_1$, respectively, given by

$$\begin{aligned}&B_1^{\text {VMS}}(\{\mathbf {w},q\},\{\mathbf {u},p\};\hat{\mathbf{u }})\nonumber \\&\quad =\int \limits _{(\varOmega _1)_t}\mathbf {w}\cdot \rho _1\left( \left. \frac{\partial \mathbf {u}}{\partial t}\right| _{\hat{x}}+(\mathbf {u}-\hat{\mathbf{u }})\cdot \pmb {\nabla } \mathbf {u}\right) \text {d}\varOmega \nonumber \\&\qquad + \int \limits _{(\varOmega _1)_t}\pmb {\varepsilon }(\mathbf {w}):\pmb {\sigma }_1~\text {d}\varOmega + \int \limits _{(\varOmega _1)_t}q\pmb {\nabla } \cdot \mathbf {u}~\text {d}\varOmega \nonumber \\&\qquad +\sum _e\int \limits _{\varOmega ^{e}\cap \varOmega _1}\left( (\mathbf {u} - \hat{\mathbf{u }})\cdot \pmb {\nabla } \mathbf {w}+\frac{\pmb {\nabla }q}{\rho _1}\right) \cdot \mathbf {u}'~\text {d}\varOmega \nonumber \\&\qquad +\sum _e\int \limits _{\varOmega ^{e}\cap \varOmega _1}\pmb {\nabla } \cdot \mathbf {w}~\rho _1 p'~\text {d}\varOmega \nonumber \\&\qquad -\sum _e\int \limits _{\varOmega ^{e}\cap \varOmega _1}\mathbf {w}\cdot (\mathbf {u}'\cdot \pmb {\nabla } \mathbf {u})~\text {d}\varOmega \nonumber \\&\qquad -\sum _e\int \limits _{\varOmega ^{e}\cap \varOmega _1}\frac{\mathbf {\pmb {\nabla } w}}{\rho _1}:\left( \mathbf {u}'\otimes \mathbf {u}'\right) \text {d}\varOmega \nonumber \\&\qquad +\sum _e\int \limits _{\varOmega ^{e}\cap \varOmega _1}\left( \mathbf {u}'\cdot \pmb {\nabla } \mathbf {w}\right) \overline{\tau }\cdot \left( \mathbf {u}'\cdot \pmb {\nabla } \mathbf {u}\right) \text {d}\varOmega , \end{aligned}$$

(11)

and

$$\begin{aligned} F_1^{\text {VMS}}(\{\mathbf {w},q\}) = F_1(\{\mathbf {w},q\}), \end{aligned}$$

(12)

where

$$\begin{aligned} \mathbf {u}'&= \tau _\text {M}\left( \rho _1\left( \left. \frac{\partial \mathbf {u}}{\partial t}\right| _{\hat{x}}+(\mathbf {u}-\hat{\mathbf{u }})\cdot \pmb {\nabla } \mathbf {u}-\mathbf {f}\right) - \pmb {\nabla } \cdot \pmb {\sigma }_1\right) ,\end{aligned}$$

(13)

$$\begin{aligned} p'&= \tau _\text {C}\pmb {\nabla } \cdot \mathbf {u}. \end{aligned}$$

(14)

Equations (11)–(14) correspond to the ALE–VMS formulation of the Navier–Stokes equations of incompressible flows [61–63]. The additional terms may be interpreted both as stabilization and as a turbulence model [64–72]. The stabilization parameters are

$$\begin{aligned}&\tau _\text {M} = \left( s(\mathbf {x},t)\left( \frac{C_t}{\varDelta t^2} + (\mathbf {u}-\hat{\mathbf{u }})\cdot \mathbf {G}(\mathbf {u}-\hat{\mathbf{u }})+ C_I\nu ^2\mathbf {G}:\mathbf {G}\right) \right) ^{-\frac{1}{2}},\nonumber \\\end{aligned}$$

(15)

$$\begin{aligned}&\tau _\text {C} = \left( \tau _\text {M} \,\text {tr}\,\mathbf {G}\right) ^{-1},\end{aligned}$$

(16)

$$\begin{aligned}&\overline{\tau } = \left( \mathbf {u}'\cdot \mathbf {G}\mathbf {u}'\right) ^{-\frac{1}{2}}, \end{aligned}$$

(17)

where $\varDelta t$ is the time-step size, $\nu =\mu /\rho _1$ is the kinematic viscosity, $C_I$ is a positive constant derived from an appropriate element-wise inverse estimate [73–76], $\mathbf {G}$ is the element metric tensor defined as

$$\begin{aligned} \mathbf {G} = \frac{\partial \pmb {\xi }}{\partial \mathbf {x}}^T\frac{\partial \pmb {\xi }}{\partial \mathbf {x}}, \end{aligned}$$

(18)

where $\partial \pmb {\xi }/\partial \mathbf {x}$ is the inverse Jacobian of the element mapping between the parametric and physical domain, $\text {tr}\,\mathbf {G}$ is the trace of $\mathbf {G}$, and the parameter $C_t$ is typically taken equal to 4 [66, 70, 77]. The scalar function $s(\mathbf {x},t) \ge 1$ in Eq. (15) is a dimensionless scaling factor introduced in Kamensky et al. [12] to improve local mass conservation near concentrated loads. Locally increasing $s$ near thin immersed structures can greatly improve the quality of approximate solutions when the concentrated surface force due to the structure induces a significant pressure discontinuity. In most of the domain, we keep $s=1$, as in the usual VMS formulation, but, in an $\mathcal {O}(h)$ neighborhood around thin immersed structures, we increase it to equal the dimensionless constant ${s^\mathrm{shell}}\ge 1$.

Remark 2

On the fluid mechanics domain interior, the mesh velocity, $\hat{\mathbf{u }}^h$, may be obtained by solving a linear elastostatics problem subject to the displacement boundary conditions coming from the motion of the boundary-fitted fluid–solid interface [28–32]. This method is effective for relatively mild deformations, such as those of the artery. However, for scenarios that involve large translational and/or rotational structural motions, such as heart valve dynamics, the boundary-fitted fluid mesh can become severely distorted. Non-boundary-fitted approaches could be an alternative for these type of problem.

Remark 3

The last term of Eq. (11) provides additional residual-based stabilization and originates from Taylor et al. [78]. The term is consistent and dissipative, and has similarities with discontinuity-capturing methods such as the DCDD [68, 79, 80] and YZ$\beta$ [81–83] techniques.

The terms from the second to the last line of Eq. (10) are responsible for the weak enforcement of kinematic and traction constraints at the non-matching or immersed boundaries. It was shown in earlier works [55–57, 84, 85] that imposing the Dirichlet boundary conditions weakly in fluid dynamics allows the flow to slip on the solid surface when the wall-normal mesh size is relatively large. This effect mimics the thin boundary layer that would otherwise need to be resolved with spatial refinement, allowing more accurate solutions on coarse meshes. In the immersed-boundary method, the fluid mesh is arbitrarily cut by the structural boundary, leaving a boundary layer discretization of inferior quality compared to the body-fitted case. Therefore, in addition to imposing the constraints easily in the context of non-boundary-fitted approach, we may obtain more accurate fluid solutions as an added benefit of using the weak boundary condition formulation (10).

In Eq. (10), the parameters $\tau _{\text {TAN}}^B$ and $\tau _{\text {NOR}}^B$ must be sufficiently large to stabilize the formulation, but not so large as to degenerate Nitsche’s method into a pure penalty method. Based on previous studies of weakly-enforced Dirichlet boundary conditions in fluid mechanics [55–57], we expect these parameters to scale as

$$\begin{aligned} \tau ^B_{(\cdot )} = \frac{C^B_I\mu }{h} \end{aligned}$$

(19)

where $h$ is a measure of the element size at the boundary and $C^B_I$ is a dimensionless constant. However, in the case of an immersed boundary, neither the appropriate definition of $h$ nor the principle for deriving $C^B_I$ is straightforward. As a result, we chose the penalty-parameter values through numerical experiments.

Integrating the fluid formulation (11) over elements that are only partially contained in $\varOmega _1$ typically requires special quadrature techniques, as discussed in Kamensky et al. [12]. In the present work, we do not need these quadrature techniques, because fluid elements only overlap spatially with thin shell structures, which are modeled geometrically as $(d-1)$-dimensional surfaces and therefore have zero Lebesgue measure in $\mathbb {R}^d$. To evaluate the surface integrals of Eq. (10) over immersed boundaries, we define a Gaussian quadrature rule with respect to a parameterization of the immersed surface, then locate the quadrature points of this rule in the parameter space of the background mesh elements to evaluate traces of the fluid test and trial functions.

Unsteady flow computations may sometimes diverge due to flow reversal on outflow boundaries. This is known as backflow divergence and is frequently encountered in cardiovascular simulations. In order to preclude backflow divergence, an outflow stabilization method originally proposed in Bazilevs et al. [50] and further studied in Esmaily-Moghadam et al. [86] is employed in our fluid mechanics formulation.

2.3 Arterial wall modeling

In this section we show the variational formulation of the boundary-fitted solid problem for the arterial wall modeling. The fluid–solid interface discretization is assumed to be conforming. Let $\mathbf {X}$ be the coordinates of the initial or reference configuration and let $\mathbf {y}$ be the displacement with respect to the reference configuration. The coordinates of the current configuration, $\mathbf {x}$, are given by $\mathbf {x} = \mathbf {X} + \mathbf {y}$. The deformation gradient tensor $\mathbf {F}$ is defined as

$$\begin{aligned} \mathbf {F}&= \frac{\partial \mathbf {x}}{\partial \mathbf {X}} = \mathbf {I} + \frac{\partial \mathbf {y}}{\partial \mathbf {X}}, \end{aligned}$$

(20)

where $\mathbf {I}$ is the identity tensor.

Let $\mathcal {S}_d$ and $\mathcal {V}_d$ be the trial solution and weighting function spaces for the solid problem. The arterial wall is modeled as a three-dimensional hyperelastic solid and the variational formulation which represents the balance of linear momentum for the solid is stated as follows: find the displacement $\mathbf {y} \in \mathcal {S}_d$, such that for all weighting functions $\mathbf {w}_2 \in \mathcal {V}_d$

$$\begin{aligned} B_2(\mathbf {w}_2,\mathbf {y})-F_2(\mathbf {w}_2)=0, \end{aligned}$$

(21)

where

$$\begin{aligned}&B_2(\mathbf {w},\mathbf {y})=\int \limits _{(\varOmega _2)_t}\mathbf {w}\cdot \rho _2\left. \frac{\partial ^2\mathbf {y}}{\partial t^2}\right| _{X}\text {d}\varOmega + \int \limits _{(\varOmega _2)_0}\pmb {\nabla }_{X}\mathbf {w}:\mathbf {P}~\text {d}\varOmega ,\end{aligned}$$

(22)

$$\begin{aligned}&F_2(\mathbf {w})=\int \limits _{(\varOmega _2)_t}\mathbf {w}\cdot \rho _2\mathbf {f}_2~\text {d}\varOmega +\int \limits _{(\varGamma _{\text {2h}})_t}\mathbf {w}\cdot \mathbf {h}_2~\text {d}\varGamma \end{aligned}$$

(23)

In the above, $(\varOmega _2)_0$ is the solid domain in the reference configuration, $\pmb {\nabla }_X$ is the gradient operator on $(\varOmega _2)_0$, and $\mathbf {P}=\mathbf {F}\mathbf {S}$ is the first Piola–Kirchhoff stress tensor, where $\mathbf {S}$ is the second Piola–Kirchhoff stress tensor given by

$$\begin{aligned} \mathbf {S} = \mu J^{-2/3} \left( \mathbf {I} - \frac{1}{3} \text {tr}\,\mathbf {C} \, \mathbf {C}^{-1}\right) + \frac{1}{2} \kappa \left( J^2-1\right) \mathbf {C}^{-1}. \end{aligned}$$

(24)

In Eq. (24), $\mu$ and $\kappa$ are interpreted as the blood vessel shear and bulk moduli, respectively, ${J = \det \mathbf {F}}$ is the Jacobian determinant, and ${\mathbf {C} = \mathbf {F}^T \mathbf {F}}$ is the Cauchy–Green deformation tensor. Equation (24) is a generalized neo-Hookean model with dilatational penalty given in Simo and Hughes [87]. Its stress-strain behavior was analytically studied on simple cases of uniaxial strain [32] and pure shear [88]. The model was argued in Bazilevs et al. [44] to be appropriate for arterial wall modeling in FSI simulations. It was shown that the level of elastic strain in arterial FSI problems is sufficiently large to preclude the use of infinitesimal (linear) strains, yet not large enough to be sensitive to the nonlinearity of the particular material model. However, the current model has the advantage of stable behavior for the regime of strong compression and therefore is selected in this work for the modeling of the arterial wall.

2.4 Immersed shell structures

We model the heart valve as a shell structure immersed into a deforming background mesh covering the lumen of the artery. The exact solution for the pressure around a shell structure may be discontinuous at the structure, which presents a conceptual difficulty. The fluid discretization cannot be informed by the structure’s position. This means that our fluid approximation space cannot be selected in such a way that the pressure basis functions are themselves discontinuous at the immersed boundary. This implies an inherent approximation error in the pressure field. This error will converge slowly for polynomial bases [89]. Nonetheless, we believe that solutions of sufficient accuracy for engineering purposes can be obtained in this fashion and we focus on developing a robust method for obtaining these solutions.

2.4.1 Reduction of Nitsche’s method to the penalty method

Consider integrating the boundary terms of Eq. (10) over both sides of a thin immersed shell structure. If the velocity and pressure approximation spaces are continuous through the vanishing thickness of the shell (and the velocity approximation space is continuously differentiable), then the dependence of the consistency and adjoint consistency terms on the normal vector will cause contributions from opposing sides to cancel one another. The only remaining terms will be the penalty and the inflow stabilization. In the case of an immersed shell structure, we may view the inflow term as a velocity-dependent penalty. The Nitsche-type formulation given by Eq. (10) therefore reduces to the following penalty method:

$$\begin{aligned}&B_1^{\text {VMS}}\left( \{\mathbf {w}_1^h,q^h\},\{\mathbf {u}_1^h,p^h\};\hat{\mathbf{u }}^h\right) -F_1^{\text {VMS}}\left( \{\mathbf {w}_1^h,q^h\}\right) \nonumber \\&\quad -\int \limits _{\left( \varGamma _{\text {I}}\right) ^-}\mathbf {w}_1^h\cdot \rho _1\left( \left( \mathbf {u}_1^h-\hat{\mathbf{u }}^h\right) \cdot \mathbf {n}_1\right) \left( \mathbf {u}_1^h-\mathbf {u}_2\right) \text {d}\varGamma \nonumber \\&\quad +\int \limits _{\varGamma _{\text {I}}}\tau ^B_{\text {TAN}}\left( \mathbf {w}_1^h-\left( \mathbf {w}_1^h\cdot \mathbf {n}_1\right) \mathbf {n}_1\right) \cdot \nonumber \\&\qquad \left( \left( \mathbf {u}_1^h-\mathbf {u}_2\right) -\left( \left( \mathbf {u}_1^h-\mathbf {u}_2\right) \cdot \mathbf {n}_1\right) \mathbf {n}_1\right) \text {d}\varGamma \nonumber \\&\quad +\int \limits _{\varGamma _{\text {I}}}\tau ^B_{\text {NOR}}\left( \mathbf {w}_1^h\cdot \mathbf {n}_1\right) \left( \left( \mathbf {u}_1^h-\mathbf {u}_2\right) \cdot \mathbf {n}_1\right) \text {d}\varGamma =0, \end{aligned}$$

(25)

when the approximation spaces $\mathcal {V}_u^h$ and $\mathcal {V}_p^h$ are sufficiently regular around the shell.

To determine the velocity and pressure about an immersed valve in its closed state, a method must be capable of developing nearly hydrostatic solutions in the presence of large pressure gradients. Penalty forces will only exist if there are nonzero violations of kinematic constraints. A pure penalty method rules out the desired hydrostatic solutions: every term that could resist the pressure gradient to satisfy balance of linear momentum depends on velocity. Increasing $\beta$ may diminish leakage through a structure, but it is a well-known disadvantage of penalty methods that extreme values of penalty parameters will adversely affect the numerical solvability of the resulting problem. This motivates us to return to Eqs. (1)–(3) and develop a method that does not formally eliminate the multiplier field.

2.4.2 Reintroducing the multipliers

Since the introduction of constraints tends to make discrete problems more difficult to solve, we will only reintroduce a scalar multiplier field to strengthen enforcement of the no-penetration part of the FSI kinematic constraint, rather than the vector-valued multiplier field of Eqs. (1)–(3). The viscous, tangential component of the constraint will continue to be enforced by only the penalty $\tau _{\text {TAN}}^B$. This may be thought of as a formal elimination of just the tangential component of the multiplier field, which also retains the ability to allow the flow to slip at the boundary, which tends to produce more accurate fluid solutions as discussed in Sect. 2.2. For clarity, we redefine the FSI boundary terms on the mid-surface of the shell structure, $\varGamma _t$, rather than considering the full boundary, $\varGamma _{\text {I}}$. This means that constants in the current formulation may differ from those of Eqs. (1)–(3) by factors of two. We arrive, then, at the formulation

$$\begin{aligned}&B_1(\{\mathbf {w}_1,q\},\{\mathbf {u}_1,p\};\hat{\mathbf{u }})-F_1(\{\mathbf {w}_1,q\}) \nonumber \\&\quad +\int \limits _{\varGamma _t}\mathbf {w}_1\cdot (\lambda _n\mathbf {n}_2)~\text {d}\varGamma + \int \limits _{\varGamma _t}\mathbf {w}_1\cdot \beta (\mathbf {u}_1-\mathbf {u}_2)~\text {d}\varGamma = 0,\end{aligned}$$

(26)

$$\begin{aligned}&B_2(\mathbf {w}_2,\mathbf {y})-F_2(\mathbf {w}_2) \nonumber \\&\quad -\int \limits _{\varGamma _t}\mathbf {w}_2\cdot (\lambda _n\mathbf {n}_2)~\text {d}\varGamma -\int \limits _{\varGamma _t}\mathbf {w}_2\cdot \beta (\mathbf {u}_1-\mathbf {u}_2)~\text {d}\varGamma =0,\end{aligned}$$

(27)

$$\begin{aligned}&\int \limits _{\varGamma _t}\delta \lambda _n \mathbf {n}_2 \cdot (\mathbf {u}_1-\mathbf {u}_2)~\text {d}\varGamma =0, \end{aligned}$$

(28)

where $\lambda _n$ is the new scalar multiplier field and, to emphasize the relation to Eqs. (1)–(3), the penalty force has not been split into normal and tangential components. The consistency and adjoint consistency terms associated with eliminating the tangential component of the multiplier have been omitted under the assumption that they will vanish after integrating over both sides of the thin shell, as discussed in Sect. 2.4.1.

We discretize the multiplier field by collocating kinematic constraints at points of the quadrature rule for integrals over $\varGamma _t$. This entails adding a scalar multiplier unknown at each quadrature point. In discrete evaluations of integrals, these multiplier unknowns are treated like point values of a function defined on $\varGamma _t$. Because the spatial resolution of the discrete multiplier representation is not controlled relative to the background fluid mesh, we must relax the collocated constraints to ensure stability of the numerical scheme. We accomplish this through the time-discrete algorithm given in Sect. 2.5. The algorithmic constraint relaxation is interpreted at the time-continuous level by Kamensky et al. [12], through an analogy to Chorin’s method of artificial compressibility [90], in which the Lagrange multiplier solves an auxiliary differential equation in time.

2.4.3 Treatment of shell structure mechanics

We assume that the structure is a thin shell, represented mathematically by its mid-surface. Further, we assume this surface to be piecewise $C^1$-continuous and apply the Kirchhoff–Love shell formulation and isogeometric discretization studied by Kiendl et al. [91–93]. The spatial coordinates of the shell mid-surface in the reference and current configurations are given by $\mathbf {X}(\xi _1,\xi _2)$ and $\mathbf {x}(\xi _1,\xi _2)$, respectively, parameterized by $\xi _1$ and $\xi _2$. Assuming the range $\{1,2\}$ for Greek letter indices, we define the covariant surface basis vectors

$$\begin{aligned}&\mathbf {g}_\alpha = \frac{\partial \mathbf {x}}{\partial \xi _\alpha },\end{aligned}$$

(29)

$$\begin{aligned}&\mathbf {g}_3 = \frac{\mathbf {g}_1\times \mathbf {g}_2}{||\mathbf {g}_1\times \mathbf {g}_2||}, \end{aligned}$$

(30)

and

$$\begin{aligned}&\mathbf {G}_\alpha = \frac{\partial \mathbf {X}}{\partial \xi _\alpha },\end{aligned}$$

(31)

$$\begin{aligned}&\mathbf {G}_3 = \frac{\mathbf {G}_1\times \mathbf {G}_2}{||\mathbf {G}_1\times \mathbf {G}_2||}, \end{aligned}$$

(32)

in the current and reference configurations, respectively. Using kinematic assumptions and mathematical manipulations given in Kiendl [93], we split the in-plane Green–Lagrange strain $E_{\alpha \beta }$ into membrane and curvature contributions

$$\begin{aligned} E_{\alpha \beta } = \varepsilon _{\alpha \beta } + \xi _3\kappa _{\alpha \beta }, \end{aligned}$$

(33)

where

$$\begin{aligned}&\varepsilon _{\alpha \beta } = \frac{1}{2}\left( \mathbf {g}_\alpha \cdot \mathbf {g}_\beta -\mathbf {G}_\alpha \cdot \mathbf {G}_\beta \right) ,\end{aligned}$$

(34)

$$\begin{aligned}&\kappa _{\alpha \beta } = \frac{\partial \mathbf {G}_\alpha }{\partial \xi _\beta }\cdot \mathbf {G}_3 - \frac{\partial \mathbf {g}_\alpha }{\partial \xi _\beta }\cdot \mathbf {g}_3, \end{aligned}$$

(35)

are the membrane strain and change of curvature tensors, respectively, at the shell mid-surface. In Eq. (33), $\xi _3 \in [-h_\text {th}/2,h_\text {th}/2]$ is the through-thickness coordinate and $h_{\text {th}}$ is the shell thickness. The forms $B_2$ and $F_2$ appearing in the structure subproblem then become, in the case of a thin shell structure,

$$\begin{aligned}&B_2(\mathbf {w},\mathbf {y}) = \int \limits _{\varGamma _t}\mathbf {w}\cdot \rho _2h_{\text {th}}\left. \frac{\partial ^2\mathbf {y}}{\partial t^2}\right| _{X}\text {d}\varGamma + \int \limits _{\varGamma _0}\int \limits _{h_{\text {th}}}\delta \mathbf {E}:\mathbf {S}~\text {d}\xi _3\text {d}\varGamma ,\end{aligned}$$

(36)

$$\begin{aligned}&F_2(\mathbf {w}) = \int \limits _{\varGamma _t}\mathbf {w}\cdot \rho _2h_{\text {th}}\mathbf {f}_{2}~\text {d}\varGamma + \int \limits _{\varGamma _t}\mathbf {w}\cdot \mathbf {h}_{2}^{\text {net}}~\text {d}\varGamma , \end{aligned}$$

(37)

where $\mathbf {S}$ is the second Piola–Kirchhoff stress, $\delta \mathbf {E}$ is the variation of the Green–Lagrange strain, $\varGamma _0$ and $\varGamma _t$ are the shell mid-surface in the reference and deformed configurations, respectively, $\mathbf {h}_{2}^{\text {net}}=\mathbf {h}_{2}(\xi _3=-h_\mathrm{th}/2) + \mathbf {h}_{2}(\xi _3 = h_\mathrm{th}/2)$ sums traction contributions from the two sides of the shell. For the purposes of this paper, we assume a St. Venant–Kirchhoff material, in which $\mathbf {S}$ is computed from a constant elasticity tensor, $\mathbb {C}$, applied to ${\mathbf {E}}$. For isotropic materials, the constitutive material tensor may be derived from a Young’s modulus, $E$, and Poisson ratio, $\nu$, and the integral over $\xi _3$ in Eq. (36). The St. Venant–Kirchhoff material model can become unstable when subjected to strongly compressive stress states [94], but such states are not encountered in the present application, because transverse normal stress is ignored by the thin-shell formulation and in-plane stresses within heart valve leaflets are primarily tensile.

Isogeometric analysis [59, 60] is employed for modeling the shell structure. We use $C^1$-continuous quadratic B-spline functions to represent both the geometry and displacement solution field. The details of this discretization are given in Kiendl et al. [91–93]. A noteworthy aspect of this discretization is the fact that it requires no rotational degrees of freedom. The $C^1$-continuous approximation space (for a single patch) is in $H^2$, so we may directly apply Galerkin’s method to the forms defined in Eqs. (36) and (37).

2.5 Time integration and FSI solution strategy

We complete the discretization of the coupled FSI formulation by using finite differences to approximate the time derivatives appearing therein. In particular, we employ the Generalized-$\alpha$ technique [32, 95, 96], which is a fully-implicit second-order accurate method with control over the dissipation of high-frequency modes. This produces a nonlinear algebraic system of equations relating the unknown coefficients of the fluid, solid structure, mesh-movement, shell structure, and multiplier solutions at time level $t^{n+1}$ to the known solutions from time level $t^n$. An attempt to solve this system with a monolithic approach (e.g., by Newton’s iteration with a consistent tangent) would encounter the following difficulties: (1) The sparsity pattern of the nonlinear residual’s Jacobian matrix would change as the immersed shell structure moves through the background mesh. (2) Fluid, structure, and mesh solvers would become more difficult to interchange. (3) The potential for drastically-different multiplier and fluid resolutions could lead to instability.

To circumvent the third issue, at each time step, we compute the solution using the following two-step procedure:

• 1. Solve for the fluid, solid structure, mesh displacement, and shell structure unknowns, holding $\lambda _n$ fixed. Note that the fluid and shell structure are still coupled in this problem, due to the penalty term.

• 2. Update the multiplier $\lambda _n$, by adding the normal component of penalty forces present in the solution from Step 1.

The solution from Step 1 will not satisfy the kinematic constraints exactly at all quadrature points on $\varGamma _t$. This is a deliberate weakening of the constraints to improve stability, as mentioned in Sect. 2.4.2. The two-step solution procedure may be interpreted as penalization of an implicitly-evaluated time integral of the velocity difference between the fluid and shell structure, as detailed in Kamensky et al. [12], and is conceptually-similar to the method of artificial compressibility [90] for incompressible flow problems. Note that the time integral of the velocity difference is a displacement: we effectively implement spring-like sliding contact elements between the fluid and shell structure. This prevents the steady creeping flow through shell structures that can occur when only the current velocity difference is penalized, as in the penalty approach coming from Nitsche’s method.

To solve the nonlinear coupled problem in Step 1 , we apply a fixed-point iteration based on Newton’s method. The linear system to be solved within each iteration of Newton’s method would have the form

$$\begin{aligned} \begin{pmatrix} \dfrac{\partial \mathbf {R}_{\text {fl}}}{\partial \mathbf {U}_{\text {fl}}}&{}\quad \dfrac{\partial \mathbf {R}_{\text {fl}}}{\partial \mathbf {U}_{\text {so}}}&{}\quad \dfrac{\partial \mathbf {R}_{\text {fl}}}{\partial \mathbf {U}_{\text {me}}}&{}\quad \dfrac{\partial \mathbf {R}_{\text {fl}}}{\partial \mathbf {U}_{\text {sh}}} \\ \dfrac{\partial \mathbf {R}_{\text {so}}}{\partial \mathbf {U}_{\text {fl}}}&{}\quad \dfrac{\partial \mathbf {R}_{\text {so}}}{\partial \mathbf {U}_{\text {so}}}&{}\quad \dfrac{\partial \mathbf {R}_{\text {so}}}{\partial \mathbf {U}_{\text {me}}}&{}\quad \dfrac{\partial \mathbf {R}_{\text {so}}}{\partial \mathbf {U}_{\text {sh}}} \\ \dfrac{\partial \mathbf {R}_{\text {me}}}{\partial \mathbf {U}_{\text {fl}}}&{}\quad \dfrac{\partial \mathbf {R}_{\text {me}}}{\partial \mathbf {U}_{\text {so}}}&{}\quad \dfrac{\partial \mathbf {R}_{\text {me}}}{\partial \mathbf {U}_{\text {me}}}&{}\quad \dfrac{\partial \mathbf {R}_{\text {me}}}{\partial \mathbf {U}_{\text {sh}}} \\ \dfrac{\partial \mathbf {R}_{\text {sh}}}{\partial \mathbf {U}_{\text {fl}}}&{}\quad \dfrac{\partial \mathbf {R}_{\text {sh}}}{\partial \mathbf {U}_{\text {so}}}&{}\quad \dfrac{\partial \mathbf {R}_{\text {sh}}}{\partial \mathbf {U}_{\text {me}}}&{}\quad \dfrac{\partial \mathbf {R}_{\text {sh}}}{\partial \mathbf {U}_{\text {sh}}} \end{pmatrix} \begin{pmatrix} \varDelta \mathbf {U}_{\text {fl}}\\ \varDelta \mathbf {U}_{\text {so}}\\ \varDelta \mathbf {U}_{\text {me}}\\ \varDelta \mathbf {U}_{\text {sh}} \end{pmatrix} \!=\!- \begin{pmatrix} \mathbf {R}_{\text {fl}}\\ \mathbf {R}_{\text {so}}\\ \mathbf {R}_{\text {me}}\\ \mathbf {R}_{\text {sh}} \end{pmatrix}, \end{aligned}$$

(38)

where $\mathbf {R}_{(\cdot )}$ and $\mathbf {U}_{(\cdot )}$ are the nonlinear residuals and discrete unknowns of the fluid (fl), solid structure (so), mesh (me), and shell structure (sh). $\varDelta \mathbf {U}_{(\cdot )}$ are the corresponding solution increments. To avoid the aforementioned disadvantages of assembling the full consistent tangent, we approximate it with the block-diagonal matrix

$$\begin{aligned} \begin{pmatrix} \dfrac{\partial \mathbf {R}_{\text {fl}}}{\partial \mathbf {U}_{\text {fl}}}&{}\quad \dfrac{\partial \mathbf {R}_{\text {fl}}}{\partial \mathbf {U}_{\text {so}}}&{}\quad 0&{}\quad 0\\ \dfrac{\partial \mathbf {R}_{\text {so}}}{\partial \mathbf {U}_{\text {fl}}}&{}\quad \dfrac{\partial \mathbf {R}_{\text {so}}}{\partial \mathbf {U}_{\text {so}}}&{}\quad 0&{}\quad 0\\ 0&{}\quad 0&{}\quad \dfrac{\partial \mathbf {R}_{\text {me}}}{\partial \mathbf {U}_{\text {me}}}&{}\quad 0\\ 0&{}\quad 0&{}\quad 0&{}\quad \dfrac{\partial \mathbf {R}_{\text {sh}}}{\partial \mathbf {U}_{\text {sh}}}\\ \end{pmatrix}, \end{aligned}$$

(39)

then assemble and solve each block of equations in sequence (from top to bottom). We use a number of further approximations within each of the left-hand side blocks, but maintain the original nonlinear residuals, $\mathbf {R}_{(\cdot )}$, of the fully-coupled problem. Converging these residuals to zero solves the original problem, regardless of any approximations used in the tangent matrix. The procedure that we apply at each step of the fixed-point iteration is not equivalent to a linear solve with matrix (39). To accelerate convergence, we use the updated solutions from previous blocks to assemble the equations for subsequent ones. We repeat this fixed-point iteration to converge $\mathbf {R}_{(\cdot )}$ toward zero and obtain a fully-coupled solution of the fluid-solid-mesh-shell system. In practice, we use a fixed number of iterations, chosen to yield typically-satisfactory convergence at the selected time step size. This algorithm combines the quasi-direct and block-iterative FSI coupling approaches outlined in Tezduyar et al. [97–99] and Bazilevs et al. [100].

3 Bioprosthetic heart valve simulations

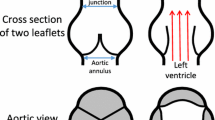
In this section, we use the proposed hybrid ALE/immersed-boundary method to simulate the FSI of an aortic BHV implanted in an elastic artery over cardiac cycles. The aortic valve regulates flow between the left ventricle of the heart and the ascending aorta. Figure 1 provides a schematic depiction of its position in relation to the surrounding anatomy. The valve leaflets are discretized separately and immersed into a deforming boundary-fitted background mesh of the artery lumen.

Fig. 1

A schematic drawing illustrating the position of the aortic valve relative to the left ventricle of the heart and the ascending aorta

3.1 Heart valve model

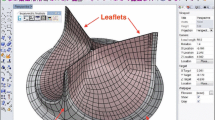
The BHV leaflet geometry used in this study is based on a 23-mm design by Edwards Lifesciences. We model each leaflet using a $C^1$-continuous B-spline patch, which comprises 468 quadratic B-spline elements. The pinned boundary condition is applied to the leaflet attachment edge as shown in Fig. 2. An isotropic St. Venant–Kirchhoff material with $E=10^7$ dyn/cm$^2$ and $\nu =0.45$ is applied to the BHV. The thickness and density of the leaflets are 0.0386 cm and 1.0 g/cm$^3$, respectively. There is no damping applied to the valve dynamics in this study.

Fig. 2

B-spline heart valve mesh comprised of 1,404 quadratic elements. The pinned boundary condition is applied to the leaflet attachment edge

3.2 Leaflet–leaflet contact

Contact between leaflets is an essential feature of a functioning heart valve. BHV leaflets contact one another during the opening, and especially during the closing to block flow. An advantage of immersed-boundary methods for FSI is that pre-existing contact algorithms from structural analysis [101–105] may be incorporated directly into the structural subproblem without affecting the fluid subproblem. We adopt a penalty-based approach for sliding contact and employ contact elements associated with the quadrature points of the shell structure.

As detailed in Kamensky et al. [12], a contact element activates when its associated quadrature point, located on a particular BHV leaflet designated $S_1$, is found to penetrate through another leaflet, designated $S_2$. Penalties are computed using a signed distance, $d$, from $S_2$ to the quadrature point on $S_1$, and their activation is controlled by several geometrical conditions omitted from the current paper for brevity. Opposing concentrated loads are applied at the quadrature points on $S_1$ and their closest points on $S_2$. This notation is illustrated for a pair of contacting points in Fig. 3. The designation of one leaflet as $S_1$ and another as $S_2$ is arbitrary, and to preserve geometrical symmetries, we sum the forces resulting from both choices.

Fig. 3

Illustration of contact notation

3.3 Artery model

The BHV model mentioned earlier is immersed into a pressure-driven incompressible flow through a deformable artery. The fluid density and viscosity are $\rho _1 = 1.0\, \hbox { g/cm}^3$ and $\mu = 3.0\times 10^{-2}$ g/(cm s), respectively, which model the physical properties of human blood.

The artery is modeled as a 16 cm long elastic cylindrical tube with a three-lobed dilation near the BHV, as shown in Fig. 4. This dilation represents the aortic sinus, which is known to play an important role in heart valve dynamics [106]. The cylindrical portion of the artery has an inside diameter of 2.3 cm and a thickness of 0.15 cm. It is comprised of quadratic NURBS patches, allowing us to represent the circular portions exactly. The sinus is generated by displacing control points radially from an initial cylindrical configuration, so the normal thickness of the sinus varies. We use a multi-patch design to avoid including a singularity at the center of the cylindrical sections. Cross-sections of this multi-patch design are shown in Fig. 5. The mesh of this artery, which includes the fluid-filled interior and solid arterial wall, consists of 69,696 quadratic B-spline elements. For analysis purposes, basis functions are made $C^0$-continuous at the fluid–solid interface and the discretization is conforming.

Fig. 4

A view of the arterial wall and lumen into which the valve is immersed

Fig. 5

Cross-sections of the fluid and solid meshes, taken from the cylindrical portion and from the sinus

Mesh refinement is focused near the valve and sinus, as shown in Fig. 4. Figure 5 shows that the mesh is clustered toward the wall to better capture the boundary-layer solution. As shown in Fig. 6, we extend the pinned edges of the valve leaflets with a rigid stent. The stent extends outside of the fluid domain and intersects with the solid region, to properly seal the gap between the pinned edge of the valve and the arterial wall.

Fig. 6

The sinus, magnified and shown in relation to the valve leaflets (pink) and rigid stent (blue). (Color figure online)

The arterial wall is modeled as a hyperelastic material—a neo-Hookean model with dilatational penalty (see Simo and Hughes [87] and Sect. 2.3 of the present paper)—with Young’s modulus and Poisson’s ratio set to 10$^7$ dyn/cm$^2$ and 0.45, respectively. The density of the arterial wall is 1.0 g/cm$^3$. Mass-proportional damping is added to model the interaction of the artery with surrounding tissues and interstitial fluids. In this case the inertial term in Eq. (22) is replaced as follows:

$$\begin{aligned} \rho _2\frac{\partial ^2\mathbf {y}}{\partial t^2} \leftarrow \rho _2\frac{\partial ^2\mathbf {y}}{\partial t^2} + a\rho _2\frac{\partial \mathbf {y}}{\partial t}, \end{aligned}$$

(40)

and the damping coefficient, $a$, is set to $1.0\times 10^{4}$ s$^{-1}$.

3.4 Boundary conditions and parameters of the numerical scheme

The solid wall is subjected to zero traction boundary conditions at the outer surface. The inlet and outlet branches are allowed to slide in their cut planes as well as deform radially in response to the variations in the blood flow forces (see Bazilevs et al. [44] for details). This gives more realistic arterial wall displacement patterns than fixed inlet and outlet cross-sections.

Because the BHV stent is assumed to contain an effectively-rigid metal frame [107], the dynamics of the artery and BHV leaflets are coupled primarily through the fluid rather than the sutures connecting the stent to the artery. We therefore constrain the stent to be stationary, and likewise fix the displacement unknowns of any control point of the solid portion of the artery mesh whose corresponding basis function’s support intersects the stent.

The nominal outflow boundary is 11 cm downstream of the valve, located at the right end of the channel, based on the orientation of Fig. 4. The nominal inflow is located 5 cm upstream at the left end of the channel. The designations of inflow and outflow are based on the prevailing flow direction during systole, when the valve is open and the majority of flow occurs. In general, fluid may move in both directions and there is typically some regurgitation during diastole. A physiologically-realistic left ventricular pressure profile obtained from Yap et al. [108] and shown in Fig. 7 is applied as a traction boundary condition at the inflow. The duration of a single cardiac cycle is 0.86 s.

Fig. 7

Physiological left ventricular (LV) pressure profile applied at the inlet of the fluid domain. The duration of a single cardiac cycle is 0.86 s. The data is obtained from Yap et al. [108]

The traction $-(p_0 + RQ)\mathbf {n}_1$ is applied at the outflow, where $p_0$ is a constant physiological pressure level, $Q$ is the volumetric flow rate through the outflow (with the convention that $Q>0$ indicates flow leaving the domain), $R>0$ is a resistance constant, and $\mathbf {n}_1$ is the outward facing normal of the fluid domain. This resistance boundary condition and its implementation are discussed in Bazilevs et al. [50]. In the present computation, we use $p_0=80$ mmHg and $R=70$ (dyn s)/cm$^5$. These values ensure a realistic transvalvular pressure difference of 80 mmHg in the diastolic steady state (where $Q$ is nearly zero) while permitting a reasonable flow rate during systole. At both inflow and outflow boundaries we apply backflow stabilization with $\gamma =0.5$ (see Esmaily-Moghadam et al. [86] for details).

The time-step size is set to $\varDelta t=1.0\times 10^{-4}$ s and the $\tau _\text {M}$ scaling factor is $s^{\text {shell}}=10^6$. For the immersed heart valve, we find that results are relatively insensitive to the tangential-velocity penalty-parameter values, while conditioning and nonlinear convergence improve when the values are lower. We therefore set a lower value for $\tau _{\text {TAN}}^B = 2.0\times 10^2$ g/(cm$^2$ s) and a higher value for $\tau _{\text {NOR}}^B = 2.0\times 10^3$ g/(cm$^2$ s), also because the no-penetration condition is more critical for accuracy.

3.5 Results and discussion

We compute both the rigid- and elastic-wall cases to study the importance of including arterial wall elasticity in the heart-valve FSI simulations. Starting from homogeneous initial conditions, we compute several cardiac cycles until a time-periodic solution is achieved. Figure 8 shows the volumetric flow rate through the top of the tube throughout the cardiac cycle. The flow rates computed using rigid and elastic arteries differ primarily in the period immediately following valve closure. The rigid-wall results show large oscillation in the flow rate, as well as in the valve movement (see Fig. 9). The oscillation is much smaller when arterial wall elasticity is included.

Fig. 8

Computed volumetric flow rate through the top of the fluid domain, during a full cardiac cycle of 0.86 s, for the rigid and elastic arterial wall cases

Fig. 9

Leaflet oscillation and the highest MIPE during the cardiac cycle for the rigid and elastic arterial wall cases. The strains are evaluated on the aortic side of the leaflets. The maximum MIPE on the plots are 0.766 for the rigid-wall case and 0.483 for the elastic-wall case

In the rigid-wall case, the energy of the fluid hammer striking the closed valve is initially converted to elastic potential in the leaflets, transferred back to kinetic energy as the valve rebounds, converted into potential as the fluid moves through an adverse pressure gradient, then converted once again to kinetic energy as the blood reverses direction, forming a new fluid hammer and restarting a cyclic reverberation. This oscillation is gradually damped by the resistance outflow condition and viscous forces in the fluid being directly modeled.The reverberation of the fluid hammer impact on the closing valve is the source of the S$_2$ heart sound, marking the beginning of diastole [109, 110]. However, the flow rate oscillation that follows from the rigid artery assumption is observed to be much smaller or completely absent in human aortas [111, 112]. This is consistent with our elastic-wall computations, which show that an elastic artery has a compliance effect and can distend to absorb a fluid hammer impact and dissipate the initial kinetic energy to surrounding tissues and interstitial fluids (modeled here through damping). The artery’s absorption of fluid hammer impacts on the valve greatly reduces the maximum strains (and thus stresses) observed in the leaflets, as shown in Fig. 9.

Remark 4

The strains shown in Fig. 9 are the maximum in-plane principal Green–Lagrange strain (MIPE, the largest eigenvalue of $\mathbf {E}$). We choose to plot the strains on the aortic side of the leaflets to include contributions from both stretching and bending. Evaluation of strain at the shell mid-surface, $\xi _3=0$, would only display the membrane contribution.

Remark 5

Note that the effect we demonstrate here is not the full Windkessel effect. Direct simulation of the Windkessel effect would require a much larger network of arteries downstream of the valve, and the final outflow from these arteries should be relatively constant [8]. We instead demonstrate that the elasticity of the arteries directly adjacent to a heart valve can significantly impact its dynamics, especially at the point of valve closure, where maximum strains occur, and should therefore not be neglected in simulations. We recommend combining this technology with a lumped-parameter Windkessel model of arteries further downstream, but we have applied a simple resistance boundary condition in this present work to more clearly highlight the effect of arterial FSI within the directly-simulated domain.

We now examine the details of the fluid and structure solutions obtained from the elastic-artery computation. Figure 10 shows several snapshots of the details of the fluid solution fields and Fig. 11 shows the deformations and strain fields of the leaflets at several points during the cardiac cycle. As the valve opens during systole, we see transition to turbulent flow. We also see that the leaflets remain partially in contact while opening. The snapshot at $t=0.35$ s illustrates the fluid hammer effect that is evident in the flow rate. After 0.62 s, the solution becomes effectively hydrostatic. The strain near the commissure points at $t=0.35$ s is slightly higher than at $t=0.7$ s. This is due to the effect of the fluid hammer striking the valve as it initially closes. This phenomenon is usually neglected by both quasi-static and pressure-driven dynamic computations, as neither accounts for the inertia of the fluid [107, 113]. The FSI solution also shows that the geometrical symmetry of the initial data is not preserved, which is typical for turbulent flow. This result underscores the importance of computing FSI for the entire valve, without symmetry assumptions. In Fig. 12, the models are superposed in the configurations corresponding to the opening ($t=0.24$ s) and closing phases ($t=0.345$ s) for better visualization of the relative arterial wall displacement results.

Fig. 10

Volume rendering of the velocity field at several points during a cardiac cycle. The time $t$ is synchronized with Fig. 7 for the current cycle

Fig. 11

Deformations of the valve from the FSI computation, colored by the MIPE evaluated on the aortic side of the leaflet. Note the different scale for each time

Fig. 12

Relative wall displacement between opening ($t=0.24$ s) and closing ($t=0.345$ s) phases

4 Conclusions

We presented a computational framework for FSI which combines a recently proposed variational immersed-boundary method [12] and the traditional ALE technique. We applied this hybrid ALE/immersed-boundary framework to simulate a BHV implanted in an artery that is allowed to deform in the model. Our computations demonstrate that the variational immersed-boundary method for FSI remains effective for heart valve analysis when the background fluid mesh undergoes relatively mild deformations, corresponding to the expansion and contraction of an elastic artery. Further, we find that arterial wall deformation contributes significantly to the realism of BHV simulation results. It damps out oscillations in the flow rate and valve deformation during the closing phase, leading to flow profiles that more closely resemble those observed in practice [111, 112].

The highest strain on the valve, occurring at the point of valve closure, is much lower when wall elasticity is considered. This difference in peak strain between the rigid-artery and elastic-artery computations suggests a potential future research direction: it indicates that arterial stiffness could be an important variable to consider in computational studies of structural fatigue in BHVs. Atherosclerosis and BHV leaflet deterioration are known to be correlated [114], although the prevailing hypothesis, which we do not purport to refute in this work, is that these phenomena have a shared etiology rather than a cause-and-effect relationship.

One conspicuous shortcoming of our simulations is the relatively simple material model of the valve leaflets. The St. Venant–Kirchhoff material used in this work does not accurately reflect some of the properties of biological materials [94, 115]. In the present application, the largest strains are primarily tensile, avoiding the St. Venant–Kirchhoff material’s most significant pathology: instability under compression. However, its tensile behavior does not exhibit the exponential stiffening characteristic of soft tissues [116, 117]. The introduction of a more realistic soft tissue material model will allow for meaningful comparison of the valve’s deformations with detailed geometrical data collected in the flow loop experiments of Iyengar et al. [118] and Sugimoto et al. [119].