Revisiting density-based topology optimization for fluid-structure-interaction problems

Abstract

This study revisits the application of density-based topology optimization to fluid-structure-interaction problems. The Navier-Cauchy and Navier-Stokes equations are discretized using the finite element method and solved in a unified formulation. The physical modeling is limited to two dimensions, steady state, the influence of the structural deformations on the fluid flow is assumed negligible, and the structural and fluid properties are assumed constant. The optimization is based on adjoint sensitivity analysis and a robust formulation ensuring length-scale control and 0/1 designs. It is shown, that non-physical free-floating islands of solid elements can be removed by combining different objective functions in a weighted multi-objective formulation. The framework is tested for low and moderate Reynolds numbers on problems similar to previous works in the literature and two new flow mechanism problems. The optimized designs are consistent with respect to benchmark examples and the coupling between the fluid flow, the elastic structure and the optimization problem is clearly captured and illustrated in the optimized designs. The study reveals new features of topology optimization of FSI problems and may provide guidance for future research within the field.

1 Introduction

Fluid-structure-interaction (FSI) is a multi-physics problem which concerns the interaction between a moving fluid and an elastic or rigid, movable or constrained structure. FSI is a strongly coupled phenomenon, which means that the structural deformations depend on the fluid flow and the fluid flow may depend on the structural deformations. FSI is an interesting and important phenomenon as it is relevant for a large number of engineering applications and natural phenomena such as airfoils (Dowell and Hall 2001; Farhat et al. 1998), engines (Shangguan and Zhen-Hua 2004), compressors (Wu and Wang 2014), moving containers (Kolaei et al. 2016), the human blood flow system (Gerbeau et al. 2005; Gerbeau and Vidrascu 2003), the human lung system (Tezduyar et al. 2008), among many more.

Over the past decades, a considerable international research effort has been addressing FSI problems; in 2015 alone more than 400 FSI journal papers were published. Despite the large research effort, only a small number of papers has been concerned with structural topology optimization of FSI problems, see e.g. Yoon (2010), Kreissl et al. (2010), Yoon et al. (2014a, b), g. Jenkins and Maute (2015, 2016) and Picelli et al. (2015, 2017). The motivation and aim of the present study is to contribute to the development of the topology optimization approach for FSI problems, which in the future may be used to analyze and optimize industrially relevant problems, such as bridges, turbines or compliant component designs.

The optimization framework presented in this work is based on topology optimization which is a material distribution method for finding optimized structural layouts subjected to some specified design constraints. Topology optimization was originally suggested for elastic problems by Bendsøe and Kikuchi (1988), and the methodology has ever since its introduction been developed and matured within structural elasticity and a large number of multiphysic problems. Topology optimization may have an advantage compared to other optimization approaches, such as sizing or shape optimization as topology optimization allows internal holes to occur in the structure during the optimization process, and a qualified initial guess is generally not required for obtaining well-performing designs.

Topology optimization can be utilized in all problems modeled by partial differential equations, and therefore the methodology has proven its relevance in a large range of multiphysics applications, such as acoustics (Dühring et al. 2008), electrostatics (Yoon and Sigmund 2008), fluid-structure-interaction in poroelasticity (Andreasen and Sigmund 2011), photonics (Jensen and Sigmund 2011), fluid dynamics (Borrvall and Petersson 2003), thermal transport (Andreasen et al. 2009; Alexandersen et al. 2014) among many more. For an extensive introduction to topology optimization, please consult e.g. Sigmund and Maute (2013), Chen (2016), and Bendsøe and Sigmund (2003).

Topology optimization of fluid dynamical problems was pioneered by Borrvall and Petersson (2003). Inspired by lubrication theory, Borvall and Petersson introduced a Brinkman-type penalization term in the Stokes equations, which hereby allowed the amount of dissipated energy in a Stokes flow problem to be minimized using a topology optimization approach. Topology optimization for flow problems was later extended with a similar approach to the Navier-Stokes equations by Gersborg-Hansen et al. (2005). The Brinkman approach has within the last 10-12 years been used in a large sequence of multi-physic fluid flow problems such as transport problems (Andreasen et al. 2009), reactive flows (Okkels and Bruus 2007), transient flows (Deng et al. 2011; Kreissl et al. 2011), flow driven by constant body force (Deng et al. 2013), among many more.

The field of topology optimization of FSI problems was initiated by Yoon (2010), who minimized the structural compliance of an elastic structure subjected to a fluid flow in a channel. Yoon solved the Navier-Stokes equations and the linear Navier-Cauchy equations in a unified formulation. This unified formulation employs that the deformations of the elastic structure and the velocity and pressure fields of the fluid flow are solved simultaneously in the hole modeling domain. The dependency between the structural deformations and the fluid flow (from hereon denoted the deformation dependency) was taken into account in the framework presented in Yoon (2010). The same author presented a topology optimization framework for a passive valve flap optimization problem in Yoon (2014a). The topology of a valve flap was optimized with deformation dependency for two different Reynolds numbers. In the papers by Picelli et al. (2015, 2017), a bi-directional evolutionary (BESO) topology optimization method was used to optimize structural compliance problems under design-dependent pressure loads. In this framework the deformation dependency was neglected. Most recently Jenkins and Maute (2016) demonstrated an optimization framework for an immersed method with explicit boundary representation (IMwEBR) method using the extended finite element method and an explicit level set method. In the works by Yoon (2010) and Jenkins and Maute (2016) the deformation dependency was taken into account, and full-scale topological changes were observed for compliance optimization problems. Furthermore, Jenkins and Maute (2016) studied a heart valve inspired problem where the objective was to minimize the average maximum shear stress in the fluid.

Topology optimization of FSI problems is to some extend related to pressure loaded acoustic problems (Yoon et al. 2007; Vicente et al. 2015) and FSI for porous flow problems (Andreasen and Sigmund 2013), though in structure-acoustic problems the structural forces are imposed by the acoustic pressure.

In this work, the deformation dependency is neglected, which means that the finite element analysis, sensitivity analysis and the optimization problem are carried out in the undeformed structural configuration.

In this study, we devote our primary focus on various design problem formulations. We refine several aspects of the field of density-based topology optimization for FSI problems, which provide new insight and may provide guidance for future research within the field. The study takes basis in the work of Yoon (2010) however the study includes several new features and reveals several new findings in relation to TO of FSI problems. The new findings and features have been summarized in the following list:

• 1. The coupling between the fluid flow, the elastic structure and the optimization problem is clearly captured and demonstrated for six objective functions and three numerical examples. The optimized designs are consistent with respect to benchmark problems and cross-check tables. The presented framework is tested and compared with well-know problems from the literature and two new challenging problems are proposed that procure new insight in the field of topology optimization for FSI problems.

• 2. The derivation of the unified finite element formulation of the fluid-structure-interaction problem is elaborated, and an additional term in the coupling between the fluid and the structure is included in the TO and FSI formulations compared to the equivalent formulations in Yoon (2010).

• 3. A robust optimization formulation is added, which ensures length-scale-controlled well-performing and binary optimized designs, and may make the optimization process less sensitive to the choice of interpolation function parameters, model parameters, and penalization and continuation strategies.

• 4. The importance of choosing a “sufficiently” high structural impermeability is highlighted.

• 5. A methodology to ensure a monotonic relationship between the objective functions and the design variables. A monotonic relationship between the objective functions and the design variables may ensure well-performing designs and smooth and stable optimization processes.

• 6. Non-physical free-floating islands of solid elements (FFIOSE), which also have been encounted in other works, can be removed from the optimized designs by combining different objective functions with different features and weights.

The paper is organized as follows. The governing equations and assumptions are introduced in Section 2, the finite element formulation is introduced in Section 3, the topology optimization problem is introduced in Section 4, the implementation details is covered in Section 5, numerical examples are presented in Section 6, Section 7 contains discussions and Section 8 contains conclusions.

2 Governing equations

2.1 The Navier-Stokes and Navier-Cauchy equations

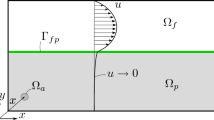
The weak form of the governing equations are defined in domain, Ω. The domain Ω consists of a solid sub-domain Ω_S and a fluid sub-domain Ω_F which initially are clearly segregated and non-overlapping with the interface Γ_SF. The segregated sub-domains fulfill that Ω ∈ Ω_S ∪ Ω_F. The Navier-Cauchy equations are assumed linear elastic, the Navier-Stokes equations are limited to constant and incompressible fluid properties, and the physics are modeled assuming steady state. Shear stresses on the interface between the fluid and the structure are neglected. The strong form of the partial differential equations can be written as (e.g. Cook et al. 1991, Farhat and Roux 2002, White and Corfield 1991)

$$\begin{array}{@{}rcl@{}} \frac{\partial{\sigma^{s}_{ij}}}{\partial{x_{j}}} + f_{i} &=& 0 \quad \text{in} \quad {{\Omega}_{S}} \sigma^{s}_{ij} = C_{ijkl} \epsilon_{kl} \end{array} $$

(1a)

$$\begin{array}{@{}rcl@{}} \epsilon^{s}_{kl} &=& \frac{1}{2} \left( \frac{\partial{d_{k}}}{\partial{x_{l}}} + \frac{\partial{d_{l}}}{\partial{x_{k}}} \right) \\ u_{j} \frac{\partial{u_{i}}}{\partial{x_{j}}} - \frac{\partial{\sigma^{f}_{ij}}}{\partial{x_{j}}} &=& b_{i} \quad \text{in} \quad {{\Omega}_{F}} \sigma^{f}_{ij} = \frac{2}{Re} \dot{\epsilon}^{f}_{ij} - \delta_{ij} p \end{array} $$

(1b)

$$\begin{array}{@{}rcl@{}} \dot{\epsilon}_{ij} &=& \frac{1}{2} \left( \frac{\partial{u_{i}}}{\partial{x_{j}}} + \frac{\partial{u_{j}}}{\partial{x_{i}}} \right)\\ \frac{\partial{u_{j}}}{\partial{x_{j}}} &=& 0 \quad \text{in} \quad {{\Omega}_{F}} \end{array} $$

(1c)

$$\begin{array}{@{}rcl@{}} \sigma^{s}_{ij} n_{j} &=& \sigma^{f}_{ij} n_{j} \quad \text{on} \quad {{\Gamma}_{SF}} \end{array} $$

(1d)

where σ^s is the Cauchy stress tensor, x_j is the spatial variables, f_i is the external applied loads, C_ijkl is the structural stiffness tensor, $\epsilon _{kl}^{s}$ is the structural strains, d_k is the structural displacements, u_i is the fluid velocity, $\sigma ^{f}_{ij}$ is the fluid stress tensor, b_i is the fluid body forces, Re is the Reynolds number, $\dot {\epsilon }^{f}$ is the fluid strain rate, δ_ij is Kronecker’s delta, p is the fluid pressure and n_j is the normal vector to the surface Γ. The tensor indices i, j, k, l have two entries, x and y, which refer to the spatial directions x and y. The Reynolds number is defined as Re = U_maxρ^fL/μ, where U_max is a maximum fluid velocity in the inlet, ρ^f is the fluid density, μ is the fluid viscosity and L is the width in the inlet.

The boundary conditions of the governing equations in (1a–d), are:

$$\begin{array}{@{}rcl@{}} \text{No-slip fluid:}&& \quad u_{i} = {u_{i}^{0}} = 0 \quad \text{on} \quad {{\Gamma}_{u^{0}}} \end{array} $$

(2a)

$$\begin{array}{@{}rcl@{}} \text{Fluid inflow:}& &\quad u_{i} = u_{i}^{*} \quad \text{on} \quad {{\Gamma}_{u^{*}}} \end{array} $$

(2b)

$$\begin{array}{@{}rcl@{}} \text{Fluid outflow:}&& \quad p = p^{0} = 0 \quad \text{on} \quad {{\Gamma}_{p^{0}}} \end{array} $$

(2c)

$$\begin{array}{@{}rcl@{}} \text{Structual displacement:}&& \quad d_{i} = {d_{i}^{0}} = 0 \quad \text{on} \quad {{\Gamma}_{d^{0}}} \end{array} $$

(2d)

where $\square ^{*}$ indicates a boundary condition with a prescribed non-zero magnitude, and $\square ^{0}$ indicates a boundary condition with a prescribed zero magnitude.

3 Finite element formulation

The segregated formulation of the governing equations in (1a–d) is inadequate for density-based topology optimization, so the equations are rewritten to a unified domain formulation, see Fig. 1.

Fig. 1

A schematic of an arbitrary FSI domain Ω relaxed by the design variable field ρ

The unified formulation is obtained by introducing a design variable field, 0 ≤ ρ ≤ 1; adding a Brinkman penalization term, b_i = −α(ρ)u_i, to the Navier-Stokes equations in (1b); and introducing design-dependent material parameters for the structural stiffness E = E(ρ) and the permeability of the Brinkman penalization term, α = α(ρ), see e.g. Borrvall and Petersson (2003) and Yoon (2010) for more details. In the unified formulation, elements with unity design variable, ρ = 1, are mainly governed by the structural equations; elements with zero design variable, ρ = 0, are mainly governed by the fluid equations; and intermediate design variables, 0 < ρ < 1, are in an intermediate state between the fluid and the solid structure.

The finite element discretized equations of the Navier-Cauchy equations are obtained by multiplying the weak form of the equations, (1a), with a suitable test function; integrating over the domain; assuming that the forces on the structure and the fluid are in equilibrium, i.e. $\sigma ^{f}_{ij} n_{j} = \sigma ^{s}_{ij} n_{j}$ (see (1d)); performing integration by parts of higher dimensions on the boundary load terms; and introducing the design dependent pressure-coupling filter function Ψ = Ψ(ρ) on the pressure coupling terms:

$$\begin{array}{@{}rcl@{}} \underset{\text{Structural stiffness}}{{\int}_{{{\Omega}}} \frac{\partial{{w^{h}_{i}}}}{\partial{x_{j}}} \sigma^{s,h}_{ij}(\rho) \text{d} V} = \underset{\text{Pressure coupling 1}}{{\int}_{\Omega} {\Psi}(\rho) {w^{h}_{i}} \frac{\partial{p^{h}}}{\partial{x_{i}}} \text{d} V} \\ + \underset{\text{Pressure coupling 2}}{{\int}_{{{\Omega}}} {\Psi}(\rho) \frac{\partial{{w^{h}_{i}}}}{\partial{x_{i}}} p^{h} \text{d} V} + \underset{\text{External load}}{{\int}_{{{\Omega}}} {w^{h}_{i}} f_{i} \text{d} V} \end{array} $$

(3)

where $\square ^{h}$ denotes that the term has been discretized and ${w_{j}^{h}}$ denotes the basis functions. Details on the derivation of (3) can be found in Appendix A.1. The design dependent pressure-coupling filter function, Ψ, ensures that the unified formulation of the domain-integrals of the pressure load in (3) for 0/1 designs is equal to the segregated formulation of the pressure load in (1d). The pressure load is interpolated in intermediate designs for which reason the pressure load in the unified formulation may differ from the equivalent surface integral in the segregated formulation.

The Pressure-Stabilising Petrov-Galerkin (PSPG) and the Streamline-Upwind Petrov-Galerkin (SUPG) methods are used to suppress oscillations in the pressure and velocity fields due to first order shape functions which are used to descretize the fluid velocity and the fluid pressure field (Hughes et al. 1986; Tezduyar 1991; Brooks and Hughes 1982). The weak form of the momentum equations in (1b) are hereby written as:

$$\begin{array}{@{}rcl@{}} &&{\kern-.6pc}\underset{\text{Convection}}{{\int}_{{{\Omega}}} {w^{h}_{i}} {u^{h}_{j}} \frac{\partial{{u^{h}_{i}}}}{\partial{x_{j}}} \text{d} V} + \underset{\text{Viscocity-diffusion}}{{\int}_{{{\Omega}}} \frac{1}{Re} \frac{\partial{{w^{h}_{i}}}}{\partial{x_{j}}} \left( \frac{\partial{{u^{h}_{i}}}}{\partial{x_{j}}} + \frac{\partial{{u^{h}_{j}}}}{\partial{x_{i}}} \right) \text{d} V} \\ &&{\kern-.8pc}- \underset{\text{Pressure coupling}}{{\int}_{{{\Omega}}} \frac{\partial{{w^{h}_{i}}}}{\partial{x_{j}}} \delta_{ij} p^{h} \text{d} V} + \underset{\text{Brinkman penalization}}{{\int}_{\Omega} \alpha(\rho) {w^{h}_{i}} {u^{h}_{i}} \text{d} V} \\ &&{\kern-.8pc}+ \sum\limits_{e = 1}^{N}{} \underset{\text{SUPG Convection }}{{\int}_{{{\Omega}_{e}}}{} \tau^{SU}{} {u^{h}_{j}} \frac{\partial{{w_{i}^{h}}}}{\partial{x_{j}}}{} {u^{h}_{k}} \frac{\partial{{u^{h}_{i}}}}{\partial{x_{k}}} \text{d} V}{} +\! \sum\limits_{e = 1}^{N}{} \underset{\text{SUPG Pressure coupling}}{{\int}_{{{\Omega}_{e}}}{} \tau^{SU}{\kern-.5pt} {u^{h}_{j}}{\kern-.5pt} \frac{\partial{{w_{i}^{h}}}}{\partial{x_{j}}}{\kern-.5pt} \frac{\partial{p^{h}}}{\partial{x_{i}}} \hspace{1pt}\text{d} V} \\ &&{\kern-.8pc}+ \sum\limits_{e = 1}^{N} \underset{\text{SUPG Brinkman penalization}}{{\int}_{{{\Omega}_{e}}} \tau^{SU} {u^{h}_{j}} \frac{\partial{{w_{i}^{h}}}}{\partial{x_{j}}} \alpha(\rho) u_{i} \hspace{2pt}\text{d} V} = 0 \end{array} $$

(4)

where τ^SU is the SUPG stabilization parameter. The weak form of the unified continuity equations, (1c), is written as:

$$\begin{array}{@{}rcl@{}} &&-\underset{\text{Continuity}}{{\int}_{{{\Omega}}} q^{h} \frac{\partial{{u^{h}_{i}}}}{\partial{x_{i}}} \text{d} V} + \sum\limits_{e = 1}^{N} \underset{\text{PSPG Convection}}{{\int}_{{\Omega}_{e}}} \tau^{PS} \frac{\partial{q^{h}}}{\partial{x_{i}}} {u^{h}_{j}} \frac{\partial{{u^{h}_{i}}}{\partial{x_{j}}} \text{d} V}{} \\ &&+ \sum\limits_{e = 1}^{N} \underset{\text{PSPG Pressure coupling}}{{\int}_{{{\Omega}_{e}}} \tau^{PS} \frac{\partial{q^{h}}}{\partial{x_{i}}} \frac{\partial{p^{h}}}{\partial{x_{i}}} \text{d} V} \\ &&+ \sum\limits_{e = 1}^{N} \underset{\text{PSPG Brinkman penalization}}{{\int}_{{{\Omega}_{e}}} \tau^{PS} \alpha(\rho) \frac{\partial{q^{h}}}{\partial{x_{i}}} u_{i} \text{d} V} = 0 \end{array} $$

(5)

where τ^PS is the PSPG stabilization parameter. For more information on the PSPG and SUPG stabilization parameters see e.g. Alexandersen et al. (2014) and the references therein.

The Brinkman penalization term α, the pressure coupling filter function ψ and the elastic structural stiffness E are interpolated between solid and fluid via the design variables by the following interpolation functions:

$$\begin{array}{@{}rcl@{}} \alpha({\rho}) = \alpha_{\max} + \frac{(\alpha_{\min} - \alpha_{\max})(1 - \rho)(1+p_{\alpha})}{((1-\rho)+p_{\alpha}} \end{array} $$

(6a)

$$\begin{array}{@{}rcl@{}} E(\rho) = E_{\min} + (E_{\max} - E_{\min}) \rho^{p_{E}} \end{array} $$

(6b)

$$\begin{array}{@{}rcl@{}} \psi(\rho) = \psi_{\min} + (\psi_{\max} - \psi_{\min}) \rho^{p_{{\Psi}}} \end{array} $$

(6c)

The symbol $\square _{\min }$ denotes the minimum of the parameter, and $\square _{\max }$ denotes the maximum of a parameter.

4 Topology optimization

4.1 Problem definition

To ensure length-scale-control and robustness with respect to manufacturing errors, the optimization problem is formulated in a min-max form for k = {1,2,...,N^k} projected realizations of the design variable field (Wang et al. 2011b). The optimization problem reads:

$$\begin{array}{@{}rcl@{}} \begin{array}{lllllllllll} \underset{\rho}{\textup{min.}} & \underset{k}{\max} \left( f^{k} \right) & & \\ \textup{s.t.} & \vec{R}^{k} (\vec{\bar{\tilde{\rho}}}^{k},\vec{S}^{k}) = \vec{0}^{k} & & \\ & g(\vec{\bar{\tilde{\rho}}}^{N^{k}}_{i}) = {\sum}_{i}^{N^{e}} \bar{\tilde{\rho}}^{N^{k}}_{i} v_{i}/V \leq V^{f} & \forall \rho_{i} \in {\Omega}_{{D}} & \\ & 0 \leq \rho_{i} \leq 1 & \forall \rho_{i} \in {\Omega}_{{D}} & \end{array} \end{array} $$

(7)

where f^k is the objective function of the k’th realization of the design field (the superscripted k denotes the design realizations); $\vec {R}^{k}$ is the residual equations; $\vec {\bar {\tilde {\rho }}}^{k}$ is the filtered and projected design field realization; $\vec {S}^{k}$ is the state field vectors; g is the volume inequality constraint; N^e is the number of elements in the design domain, Ω_D; v_i is the volume of element i, V is the total volume of the Ω_D and V^f is the volume fraction. The optimization problem in (7) is in the rest of this paper denoted as the robust formulation.

The optimization problem in (7) is solved for three projected realizations of the designs variable field which are denoted the eroded, the nominal and the dilated designs, respectively. Design solutions are throughout this paper plotted for the nominal design realization. The volume fraction for the dilated design is updated every 20 design iteration so the volume of the intermediate design becomes equal a prescribed value, please confer Wang et al. (2011b) for more details.

The robust formulation was suggested by Sigmund (2009) in linear elasticity problems to provide manufacturing tolerant design. Later the methodology was improved and applied to heat problems (Wang et al. 2011b), optical problems (Wang et al. 2011a), acoustics problems (Christiansen et al. 2015), time dependent fluid problems (Nørgaard et al. 2016), elasticity problems with spatially varying manufacturing errors (Schevenels et al. 2011), among many more.

4.2 Adjoint sensitivities

Gradients of the objective function with respect to the design variable field, in this study denoted sensitivities, are required in order to solve the optimization problem in (7). The sensitivities of the k’th design realization, $\hspace {2pt}\text {d} L^{k} / \hspace {2pt}\text {d} \vec {\rho }$, where L is the general Lagrangian functional, are computed by the discrete adjoint approach, see Michaleris and Vidal (1994) and Bendsøe and Sigmund (2003), which reads:

$$ \left( \frac{\partial{\vec{R}^{k}}}{\partial{\vec{S}^{k}}}\right)^{T} \vec{\lambda}^{k} = \left( \frac{\partial{f^{k}}}{\partial{\vec{S}^{k}}}\right)^{T} $$

(8)

where $\vec {\lambda }^{k}$ is the vector of adjoint variables and $\square ^{T}$ denotes the transpose. The sensitivities can now be computed by the following expression:

$$ \frac{\hspace{2pt}\text{d} L^{k}}{\hspace{2pt}\text{d} \vec{\rho}} = \frac{\partial{f^{k}}}{\partial{\vec{\rho}}} - \left[\vec{\lambda}^{k}\right]^{T} \frac{\partial{\vec{R}^{k}}}{\partial{\vec{\rho}}} $$

(9)

where $\frac {\text {d}\square }{\text {d} \square }$ denotes the total derivative and ${\frac {\partial ^{} {\square }}{\partial {\square }^{}}}$ denotes the partial derivative.

4.3 Filters and projection strategy

The physical design variables used in the finite element analysis, $\bar {\tilde {\rho }}_{i}^{k}$, are obtained by imposing the projection filter (10):

$$ \bar{\tilde{\rho}}_{i}^{k} = \frac{\tanh(\beta \eta^{k}) + \tanh(\beta(\tilde{\rho}_{i} - \eta^{k}))}{\tanh(\beta \eta^{k}) + \tanh(\beta (1-\eta^{k}))} $$

(10)

where β is the Heaviside projection parameter, η^k is the projection filter threshold value, k is the design realization, and $\tilde {\rho }_{i}$ is the density filtered design variables. The density filtered design variables $\tilde {\rho }_{i}$ are obtained from the mathematical design variables by the following filter operation:

$$ \tilde{\rho}_{i} = \frac{{\sum}_{j \in \mathbb{N}_{i}} w (\vec{x}_{j}) v_{j} \rho_{j}}{{\sum}_{j \in \mathbb{N}_{i}} w(\vec{x}_{j}) v_{j}} $$

(11)

where v_j is the area of the j th element, $\mathbb {N}_{i}$ is the index set of the design variables which is within the radius R of design variable i, $w(\vec {x})$ is the filter weighting function, ρ_j is the mathematical design variables and $\vec {x}_{j}$ is the spatial location of the element j. The filter weighting function is given by:

$$ w(\vec{x}_{j}) = \left\{\begin{array}{ccccccccc} R - |\vec{x}| & \forall |\vec{x}|\leq R \land \vec{x} \in {\Omega}_{{D}} \\ 0 & \text{otherwise} \end{array}\right. $$

(12)

where R is the filter radius, $|\vec {x}| = x_{i} - x_{j}$ and $w(\vec {x}_{j})$ is a weighting function.

The field sensitivities are obtained by utilizing the chain rule twice:

$$ \frac{\partial{f}}{\partial{\rho_{i}}} = \sum\limits_{j \in {\Omega}_{{D}}} \frac{\partial{f}}{\partial{\bar{\tilde{\rho}}^{k}_{j}}} \frac{\partial{\bar{\tilde{\rho}}_{j}^{k}}}{\partial{\tilde{\rho}_{j}}} \frac{\partial{\tilde{\rho}_{j}}}{\partial{{\rho_{i}^{k}}}} $$

(13)

4.4 Design-dependent loads

If a design problem takes design dependent loads into account, it implies that the interaction between the fluid and the structure depends on the topology of the design. This framework takes design dependent loads into account, as the pressure loads are transfered from the fluid to the structure through the pressure coupling terms in (3). The pressure coupling terms enter the sensitivity analysis in (8)–(9) entailing that the design problem and FSI problem are implicitly related though the sensitivities as L = L(ρ). Design dependent loads are also seen in the work of Yoon (2010, 2014a), Jenkins and Maute (2016), Picelli et al. (2015, 2017).

5 Implementation

The finite element equations and the sensitivities for the TO FSI framework are derived in the mathematical software Maple and implemented in the scripting programming language Matlab. The Matlab framework is parallelized to the extend where multiple processors are used to evaluate the finite element matrices which may constitute a minor speed up for some problems.

5.1 Finite element formulation

The finite element equations are solved using rectangular elements and linear basis functions for the fluid velocity field, the fluid pressure field and the structural displacement field. Each finite element consists of one design variable and four nodes with five degrees of freedom (DOF). The DOF are: Two structural displacements, one fluid pressure and two fluid velocities. The residual equation is written as: $\vec {R}(\vec {S},\vec {\rho }) = \vec {M}(\vec {S},\vec {\rho }) \vec {S} - \vec {F} = \vec {0}$, where $\vec {R}$ is the residual vector, $\vec {F}$ is the force vector, $\vec {M}$ is the system matrix, $\vec {S} = \left \{ \vec {U},\vec {P},\vec {D} \right \}$ is the state variable vector, where $\vec {U}$ is the fluid velocity vector, $\vec {P}$ is the fluid pressure vector, $\vec {D}$ is the structural displacements vector. The residual equation is solved by a combination between the undamped Newton’s method (see e.g. Deuflhard 2014) and Pichard iterations. Newton iterations have relative to Pichard iterations fast convergence for initial guesses close to the solution, where Pichard iterations have relatively to Newton steps fast convergence for initial guesses far away from the solution.

5.2 Optimization parameters

The optimization problem is solved using the method of moving asymptotes (MMA) (Svanberg 2006) with the standard settings and a move limit of 0.1. The Heaviside projection parameter, β, is updated every 100th design iteration following the scheme: β = {4,8,16,32,64}. The optimization algorithm is stopped when the maximum difference between the design variables in iteration i and i − 1 is less than 0.1% and β = 64. The projection filter threshold values η for the eroded, nominal and dilated designs are, unless otherwise stated, η^k = {0.3,0.5,0.7}, respectively. The initial density distributions for all design problems presented in this study are $\vec {\rho }=V^{f}$. The density filter radius R is chosen to be $R = 4/75 {N_{C}^{y}}$ where ${N_{C}^{y}}$ is the number of elements in the Y direction. This density filter radius, combined with the robust formulation, corresponds to a length scale of ≈ 0.05.

5.3 Brinkman penalization

The Brinkman penalization parameter (BPP) for void and solid are {α_min,α_max} = {0,10⁹}, respectively. The BPP is chosen relatively large compared to previous work in the literature (Borrvall and Petersson 2003; Gersborg-Hansen et al. 2005; Yoon 2010, 2014a; Andreasen et al. 2009; Alexandersen et al. 2014), as it turns out that the correctness of the FE modeling of the pressure field and the validity of the optimized designs are conditioned by a large BPP. Designs optimized for e.g. {α_min,α_max} = {0,10⁵} may be unphysical and meaningless, however, design problems with low α_max may be better posed compared to design problems optimized with high α_max. The pressure modeling issue was discovered during numerical studies with the TO FSI framework. It turned out that the optimization algorithm took advantage of the poorly resolved pressure field to provide physically meaningless but well-performing designs (note: well-performing with respect to the poor physical model) for some problems. To avoid a similar pitfall, we suggest researchers always to validate all designs with a body fitted mesh and a segregated solver configuration. This will ensure that the performances of the optimized designs are caused by the features of the optimized designs and not caused by poor physical modeling. Interested readers are referred to Appendix A.4, where a detailed description of the issue and numerical examples can be found.

5.4 Interpolation function parameters

The interpolation function parameters (IFP) in(6a–c) are p_Ψ = 1, p_E = 1 and p_α = {5.25 ⋅ 10⁻⁶,2.75⋅10⁻⁶,1 ⋅ 10⁻⁶,2.5 ⋅ 10⁻⁷,9.2 ⋅ 10⁻⁷} for problems with Re = {1,5,10,40,100}, respectively. The pressure coupling filter function parameters are {Ψ_min,Ψ_max} = {0,1} and the structural stiffness of the void and the solid are {E_min,E_max} = {1 ⋅ 10⁻⁵,1 ⋅ 10⁵}.

The degree of well-posedness of a density-based TO FSI design problem is very dependent of the choice of interpolation functions (IF) and IFP. Numerical studies with the TO FSI framework have suggested that a poor choice of IF and IFP provides ill-posed optimization problems and poorly performing optimized designs. However, a good choice of IF and IFP provides well-posed optimization problems and well-performing optimized designs.

The determinations of the IF and IFP take basis in a systematic comparison between the topology sensitivities and the shape sensitivities for a simple elastic problem and a simple FSI problem. By tuning the IF and IFP, such that the topology gradients resemble of the shape gradients for intermediate design variables, we obtain well-performing and well-posed optimization problems. A detailed description and numerical examples of this approach can be found in Appendix A.3.

5.5 Units of physical parameters

All equations have been derived in non-dimensional form and all physical parameters are given in SI base units, e.g. pressure is given in [Pa], displacements in [m], velocity in [m/s], dissipated energy in the flow in [W/kg], structural compliance in [1/Pa], the BBP in [m²], and so forth. Optimization parameters such as β, η^k, p_Ψ, p_E and p_α are given in non-dimensional form and are mesh independent.

5.6 The assumption of neglecting the shear stress

In Fig. 2, we have sketched what we call the Hungry Horse (HH) problem, which has been used to validate the unified FSI framework. The HH problem is a good benchmark example due to its simple design and many focal FSI relevant features such as internal holes, boundaries with high pressure and low fluid velocity and boundaries with low fluid velocity and high pressures.

Fig. 2

Schematic of the hungry horse problem

The HH problem is subject to the following BCs: A parabolic fluid flow with maximum velocity of unity enters the channel on Γ^W and the fluid exits on Γ^E. No-slip boundary conditions are imposed on Γ^N and Γ^S, and the structural deformations in all DOF are fixed on Γ^S. A prescribed p = 0 is imposed on the Γ^E which models the outflow condition.

The pressure field, the velocity field and the flow streamlines for Re = 1 have been plotted in Fig. 3. The relationship between the pressure and shear stress along the outer boundary (sketched with the red line in Fig. 2) have been plotted in Fig. 4. The integrated absolute pressure and shear stress along the outer boundary of the HH problem are 411.15 N and 29.72 N, respectively. The shear stress is large compared to the pressure near boundaries where the velocity and its gradients are large and the pressure is low, such as in and between points F and G. The ratio between shear stress and pressure depends on the problem. However in detailed computations the shear forces should always be taken into account. Shear forces may be difficult to model with a density-based Brinkman penalization approach as the porous media in the intermediate design variables penalizes the fluid velocity and hereby the fluid shear stresses. Penalization of the fluid flow velocity implies that the shear stress may be poorly resolved during the optimization process when intermediate design variables are present. IMwEBR for FSI problems may be better suited for building frameworks in which effects such as shear stresses are taken into account.

Fig. 3

State fields of the Hungry Horse problem

Fig. 4

The shear stress and pressure along r for the HH problem

6 Numerical examples

6.1 The wall

The first example concerns a well-known problem from the literature, which we call the wall problem. The wall problem was originally suggested by Yoon (2010) and later revisited for slightly different problem layout and flow properties by Picelli et al. (2017), Jenkins and Maute (2015), and Jenkins and Maute (2016). The aim of the wall problem is to minimize the structural compliance of a wall subjected to a fluid flow in a channel.

In this work, the wall problem has, compared to the problem layout presented by Yoon, Picelli and Jenkins, a smaller ratio between the length and the height of the computational domain and a relatively larger design domain. We believe, that the larger design domain yields a higher level of design freedom, a more pronounced fluid-structure-interaction, and hence facilitates a more challenging optimization problem.

To provide guidance for future research within the field of TO of FSI problem and to demonstrate the new features and the stronger approximations of present framework, we have revisited the exact wall problems presented in Yoon (2010), Jenkins and Maute (2016) and Picelli et al. (2017) in Appendix A.2.

The problem layout and the corresponding boundary conditions are as illustrated in Fig. 5 for the wall problem investigated in this work. Ω_D, and the fixed domain, Ω_I, are non-overlapping, and the design variables in Ω_I are all fixed to unity. The sub-domains I and D are non-overlapping for all problems but all sub-domains are part of the computational domain. The domain Ω_I is referred to as the wall.

Fig. 5

Schematic of the wall problem

A parabolic fluid flow with maximum velocity of unity enters the channel on Γ^W and exits on Γ^E. No-slip boundary conditions are imposed on Γ^N and Γ^S of the channel, and the structural deformations in all DOF are fixed on Γ^S. A prescribed p = 0 is imposed on the Γ^E modeling the outflow condition.

The objective of the wall problem is to minimize the structural compliance, f_C, in Ω_D and Ω_I. The compliance function for the wall flow problem is given by:

$$ f_{C} = {\int}_{{\Omega}_{{ID}} }\epsilon_{ij}^{s} {\sigma_{ij}^{s}} \hspace{2pt}\text{d} V $$

(14)

Ω is discretized into $\left \{{N_{C}^{x}},{N_{C}^{y}}\right \}=\left \{ 300,150 \right \}$ elements, where ${N_{C}^{x}}$ and ${N_{C}^{y}}$ refer to the number of elements in the x and y directions in the computational domain, respectively. The domain Ω_D consists of $\left \{{N_{D}^{x}},{N_{D}^{y}}\right \}=\left \{ 210,120 \right \}$ elements, where ${N_{D}^{x}}$ and ${N_{D}^{y}}$ refer to the number of elements in the x and y directions in Ω_D, respectively. The total number of state DOF is 227,255 and the maximum allowed volume fraction is V^f = 0.1.

The problem is investigated for four Reynolds numbers, Re = {1,5,10,40} and the optimized designs and relevant state fields are plotted in Figs. 6, 7, 8 and 9. The pressure coupling forces are the discrete vectors of the pressure coupling terms 1 and 2 in (3) obtained in the finite element discretization and are plotted in Figs. 6a, 7,a 8a and 9a. The blue arrows in the pressure force coupling plot illustrate the direction and the magnitude of the reaction forces of the structure against the fluid pressure. These are plotted in the FE nodes and each arrow has contributions from the neighboring elements for which reason they may appear non-perpendicular to the surfaces of the elements in some instances.

Fig. 6

Optimized designs and the state field plots for Re = 1

Fig. 7

Optimized designs and the state field plots for Re = 5

Fig. 8

Optimized designs and the state field plots for Re = 10

Fig. 9

Optimized designs and the state field plots for Re = 40

The fluid pressure field and the fluid flow streamlines, seeded along Γ^W, have been plotted in Figs. 6b, 7b, 8b and 9b. The normalized fluid flow velocity and the fluid flow streamlines, seeded along Γ^W, have been plotted in Figs. 6c, 7c, 8c and 9c. The scaled deformed and undeformed configuration of the optimized structures have been plotted in Figs. 6d, 7d, 8d and 9d. In plots with the deformed and undeformed configuration of the optimized designs, the deformation of the deformed configurations have been scaled so that the maximum deformation occur with the same magnitude in all plots. However, recall that the deformations of the designs are not taken into account in the optimization process, so the plots of the deformed configurations are only for illustrative purposes. The internal pressures of the holes in the optimized designs in Figs. 6a, 7,a 8a and 9a are physical reasonable, as we assume that the structures are leaking through the finite permeability of the solid regions. The leaking features of the structure allow fluid to enter and pressurize internal holes. Optimized designs and relevant state field plots follow a similar setup as the wall flow presented in Figs. 6–9 in the rest of this paper.

The relationships between the normalized f_D and iteration number, k, for the eroded, the dilated and the nominal designs in the design in Fig. 6 have been plotted in Fig. 10. Snapshots of the design evolution for every 100 iteration have been plotted in Fig. 11.

Fig. 10

Convergence plot for the nominal, the dilated and the eroded design for the wall flow problem with Re = 1

Fig. 11

Design evolution for the Re = 1 wall flow design problem

To determine how much significance one may attribute to the features of the optimized designs, one can consider a cross-check table, which contains the evaluations of the objective function for all combinations of model parameters (the Reynolds number in the present problem) and the optimized designs. A design optimized for one model parameter is required to outperform designs optimized for other model parameters if one shall attribute any significance to the features of the design solutions.

The objective values of the four designs for the four Reynolds numbers have been listed in Table 1. The design optimized for one Reynolds number outperforms the designs optimized for other Reynolds numbers (the lowest objective values are in the diagonal), confirming that the designs indeed have superior performance for the Reynolds number they are optimized for.

Table 1 Cross-check between f_C and Re for the designs optimized for f_C in Figs. 6–9

All objective functions in this work are evaluated for projected binary (0/1) designs using $\tilde {\bar {\rho }}= 0.5$ as threshold value. This sharp thresholding is carried out to ensure that the improved performances of the optimized designs are not governed by nonphysical intermediate design variables that may be present. However, the difference between the thresholded designs and the design which contain intermediate design variables are less than 1% for all cases.

Visual inspection of Fig. 6–9 and analysis of the cross-check table shows that the optimized designs are dependent on the choice of Re and that the coupling between the fluid flow, the elastic structure and the optimization problem is captured. The amount of material placed in the upstream area of the wall and the degree of asymmetry around the axis (x, y) = (x = 1,y) increases as Re increases.

The optimization process is governed by two main, and possibly conflicting, features: (1) Minimization of the drag of the structure and (2) maximization of the stiffness of the structure. To determine which of the features that governs the design process is non-trivial, but an interesting observation is made when evaluating the design solutions in Figs. 6–9 for dissipated energy in the flow, f_E (see (17)). Tables 1 and 2 suggest that f_E for the designs placed in the diagonal is positively correlated with f_C; a small amount of dissipated energy in the fluid is connected to a small structural compliance and vice versa. The drag on the structure is not explicitly stated in f_C, but the correlation between f_C and f_E seems to be an inherent feature of this optimization problem.

Table 2 Cross-check between f_E and Re for the designs optimized for f_C in Figs. 6–9

Jenkins and Maute (2016) reported on FFIOSE during their optimization process. We did not observe such phenomenon in this optimization problem, which may be explained by the continuous relationship between the design variables and the element stiffnesses in the density-based topology optimization approach.

6.2 The flow obstacle

The aim of the second numerical example and optimization problem is to minimize the downstream deformations of the center of a plate in a channel by optimizing the material distribution in the proximity of the plate, see Fig. 12. A prescribed fluid flow with a parabolic velocity profile enters the computational domain at Γ^W and the fluid exits through Γ^E. No-slip boundary conditions are imposed on Γ^N, Γ^S and Γ^E has a prescribed zero pressure condition. The domain Ω_D is placed in the center of the channel (light grey area) and contains a vertical solid domain with prescribed unity design variables, Ω_I, and a square volume, Ω_S, which is encircled by red lines. All structural DOF in Ω_S are supported by linear springs with stiffness k_s = 10⁵ in both x and y directions. The springs in Ω_S constitute the only structural constraints of the problem.

Fig. 12

Schematic of the problem layout and the boundary conditions of the flow obstacle problem

The symmetry around (x, y) = (x,0.5) is exploited in the state and optimization problems, to discretize Ω into $\left \{{N^{x}_{C}},{N^{y}_{C}} \right \} = \left \{400,100 \right \}$ finite elements. The domain Ω_D consists of $\left \{{N^{x}_{D}},{N^{y}_{D}} \right \} = \left \{240,80\right \}$ finite elements. The total amount of state DOF is 202,505, the volume fraction is V^f = 0.3 and the Reynolds number is Re = 1. The volume constraint was chosen so high that it was inactive for all final optimized designs.

In FSI optimization problems, it may be non-trivial to determine which features of a design solution that have been governed by maximizing structural stiffness, minimizing the fluid drag, or exploiting features of the fluid-structure-interaction. With basis in the flow obstacle problem and six different objective functions, we may find a road to a better understanding of the interaction between these possibly conflicting objectives.

6.2.1 Structural displacements in the spring-domain

The overall aim of the plate optimization problem is to minimize the average of the x-directional displacements in Ω_S. The domain Ω_S is non-overlapping with Ω_I and Ω_D, and the displacement objective function, f_D, is given by:

$$ f_{D} = \frac{{\int}_{{\Omega}_{{S}}} d_{x} \hspace{2pt}\text{d} V}{{\int}_{{\Omega}_{S}} \hspace{2pt}\text{d} V} $$

(15)

The optimized designs and the pressure coupling reaction forces, the pressure field and the fluid flow streamlines, and the deformed and undeformed configuration (from now on denoted the relevant state fields) for f_D have been plotted in Fig. 13. The pressure fields of the flow obstacle problem are plotted on the same scale for easier comparison.

Fig. 13

f_D optimized designs and the state field plots

The optimized design for f_D is non-physical due to the FFIOSE. The objective function f_D does not put any requirements on the stiffness of the structure and nothing inherent in the optimization formulation removes the non-physical FFIOSE. The FFIOSE may or may not occur if the dependency of the structural deformations was taken into account. In the simplified model, the FFIOSE exploit several features of the interaction between the fluid and the structure, such as: The pressure difference between the upstream surface and the downstream surface of the Ω_I is reduced; the fluid flow is lead past the Ω_I to reduce the fluid dynamical drag force; and a high fluid pressure is build up in the proximity of the upstream FFIOSE which generates a negative x-directional pressure-force contribution on the structure.

Jenkins and Maute (2016) reported on a similar issue with FFIOSE in similar f_C optimization problems which included the deformation dependency. Jenkins and Maute dealt with the issue of FFIOSE by solving an additional heat transport problem. The FFIOSE were excluded from the finite element analysis based on the heat transport problem and the corresponding temperature field. A similar approach to ensure manufacturable designs in linear elastic topology optimization problems was presented in Liu et al. (2015).

Physically realistic designs are characterized by a connected topology where all solid elements are connected to Ω_S. As an alternative to the indicator models, we investigate several objective functions which put different requirements on the stiffness of the optimized structure. An appropriately chosen objective function may provide inherent features of the optimization process, which avoid FFIOSE, while the design maintains a good performance for f_D.

6.2.2 Structural compliance

The problem in Fig. 12 is now optimized with respect to minimum structural compliance, f_C, in the domain Ω_IDS. The objective function reads:

$$ f_{C} = {\int}_{{\Omega}_{{IDS}} }\epsilon^{s}_{ij} {\sigma^{s}_{ij}} \hspace{2pt}\text{d} V $$

(16)

The optimized design and the state fields of the structural compliance problem are plotted in Fig. 14. This objective results in a connected structure since islands could result in very large strain energies in the void domains between Ω_S and the islands. However, this objective does not provide a satisfactory performance in the original f_D objective.

Fig. 14

f_C-optimized designs and the state field plots

6.2.3 Dissipated energy in the flow

The optimization problem in Fig. 12 is minimized with respect to the amount of dissipated energy in the fluid flow, f_E, in the full domain Ω. The objective function reads:

$$ f_{E} = {\int}_{{\Omega}} \frac{1}{Re} \left( \frac{\partial{u_{i}}}{\partial{x_{j}}} + \frac{\partial{u_{j}}}{\partial{x_{i}}}\right)\hspace{2pt}\text{d} V + {\int}_{{\Omega}} \alpha u_{i} \hspace{2pt}\text{d} V $$

(17)

The f_E-optimized design and the state fields are plotted in Fig. 15. The optimized design corresponds to the minimum surface solution as f_E for highly viscous flows, Re = 1, are positively correlated with the surface area of the structure; a small surface area is connected with a small f_E. The optimized design has the smallest surface area possible for this optimization problem.

Fig. 15

f_E-optimized designs and the state field plots

6.2.4 Structural free body motion

The aim of the fourth optimization problem is to minimize the free-body-motion of the intermediate and solid elements (i.e. ρ > 0) in the x and y-directions in Ω_IDS (from now on denoted the free-body motion objective function). The free body motion objective function, f_F, is given by:

$$ f_{F} = \frac{{\int}_{{\Omega}_{IDS}} \rho d_{i} d_{i} \hspace{2pt}\text{d} V}{{\int}_{{\Omega}_{IDS}} \rho \hspace{2pt}\text{d} V} $$

(18)

The optimized design with respect to f_F and the corresponding state fields are plotted in Fig. 16.

Fig. 16

f_F-optimized designs and the state field plots

The holes in the upstream part of the design have a relatively high internal pressure. The high internal pressure constitutes a negative x-directional pressure-load component which may explain the occurrence of the holes. The design optimized for f_F has, compared to the design optimized for f_C in Fig. 14, a lower drag force and exhibits a smaller pressure loss.

6.2.5 Structural displacement variance

The optimization problem in Fig. 12 is minimized with respect to the variance between the average of the x-directional structural displacements in Ω_S and the x-directional structural displacements of the solid elements in Ω_ID. The objective function is denoted f_V and referred to as the structural displacement variance objective function. Designs optimized for f_V seeks a topology in which all non-zero density elements undergo the same structural displacement with respect to direction and magnitude. This formulation may provide a well performing f_D and a connected topology of the solid elements. The displacement variance function objective function is formulated as:

$$ f_{V} = \frac{{\int}_{{\Omega}_{{ID}}} \rho (d_{x}-\bar{d}_{x})(d_{x}-\bar{d}_{x}) \hspace{2pt}\text{d} V }{{\int}_{{\Omega}_{{ID}}} \rho \hspace{2pt}\text{d} V} $$

(19)

where d_x is the x-directional displacement and $\bar {d}_{x}$ is the average of the x-directional displacements in Ω_S:

$$ \bar{d}_{x} = \frac{{\int}_{{\Omega}_{{S}}} d_{x} \hspace{2pt}\text{d} V}{{\int}_{{\Omega}_{{S}}} \hspace{2pt}\text{d} V} $$

(20)

The optimized design and the state fields are plotted in Fig. 17. The upstream part of the design is a compromise between fluid dynamic properties (low drag force) and structural free-body motion of the solid elements in Ω_D. The fluid dynamical properties of the design (lower drag force) may be improved by increasing the amount of the material in the upstream part of Ω_I and Ω_S. A larger amount of solid in the upstream part of Ω_I and Ω_S may cause a larger pressure drop over the design and hereby cause a larger imposed pressure-coupling force, which decreases the performance of the design.

Fig. 17

f_V-optimized designs and the state field plots

The downstream part of the design is primarily serving fluid dynamical purposes, such as minimizing the drag force.

6.2.6 Multi-objective function

The objective functions in (16)–(18) provide physically meaningful optimized designs, but the introduction of new objective functions does not put any requirements on the performance of f_D. The sixth optimization problem takes basis in a multi-objective function, which combines different objectives with different weights, a₁ and a₂. The multi-objective function may ensure that non-physical features of f_D-optimized designs are avoided, while the design maintains a good performance in f_D. The multi-objective function, f_M, contains a combination of (15) and a general version of (19) and is given by:

$$\begin{array}{@{}rcl@{}} f_{M} &=& \frac{(1-a) {\int}_{{\Omega}_{{S}}} d_{x} \hspace{2pt}\text{d} V}{{\int}_{{\Omega}_{S}} \hspace{2pt}\text{d} V} \\ &&+ \frac{a {\int}_{{\Omega}_{{D}}} \rho \left( (d_{x}-\bar{d}_{x})(d_{x}-\bar{d}_{x}) \right)\hspace{2pt}\text{d} V }{{\int}_{{\Omega}_{{D}}} \rho \hspace{2pt}\text{d} V} \\ &&+ \frac{a {\int}_{{\Omega}_{{D}}} \rho \left( (d_{y}-\bar{d}_{y})(d_{y}-\bar{d}_{y}) \right)\hspace{2pt}\text{d} V }{{\int}_{{\Omega}_{{D}}} \rho \hspace{2pt}\text{d} V} \end{array} $$

(21)

where

$$\begin{array}{@{}rcl@{}} \bar{d}_{x} = \frac{{\int}_{{\Omega}_{{S}}} d_{x} \hspace{2pt}\text{d} V}{{\int}_{{\Omega}_{{S}}} \hspace{2pt}\text{d} V} \quad \text{and} \quad \bar{d}_{y} = \frac{{\int}_{{\Omega}_{{S}}} d_{y} \hspace{2pt}\text{d} V}{{\int}_{{\Omega}_{{S}}} \hspace{2pt}\text{d} V} \end{array} $$

(22)

The optimization problem seeks a design which fulfills two conditions: (1) f_D is minimized and (2) the x and y directional displacements variance are minimized. The f_M-optimized design and the relevant state fields have been plotted in Fig. 18. The optimized design is obtained for the weight of a = 0.01.

Fig. 18

f_M-optimized designs and the state field plots

The x and y directional displacement variance terms in (21) penalize the free-floating island of solid elements in the displacement design in Fig. 13. The design optimized for f_M outperforms all other designs in f_D except the design optimized purely for f_D.

6.2.7 Comparison of the optimized design

The optimized designs for the objective functions in (15)–(21) have been cross-checked in Table 3. The cross-check table reveals that all designs optimized for one objective have superior performance in that objective compared to designs optimized for other objectives. This demonstrates that the coupling between the fluid flow, the elastic structure and the optimization problem indeed is captured. The f_E-optimized design is not defined for the f_V objective due to division by zero as all design variables are equal to zero.

Table 3 Cross-check between the objectives in (15)–(21)

Multi-objective functions can be formulated from arbitrary combinations of (15)-(18). Different sets of multi-objective functions provide different characteristics of the optimized designs. We have tried several combinations of different objective functions, and to our experience, (21), provides the best results.

6.3 The fluid gripper

The aim of the third numerical example is to optimize a gripper mechanism which is capable of converting the pressure load caused by the moving fluid into a structural force in a spring. The design problem is inspired by the linear elastic structural mechanism which was presented by Sigmund (1997), and later extended to include stress constraints (De Leon et al. 2015), manufacturing error tolerances (Schevenels et al. 2011), large structural displacements (Pedersen and Buhl 2001), among others.

The aim of the optimization problem is to maximize the structural y-directional displacement of a spring with spring stiffness k using only the pressure load cased by the fluid flow. The problem layout and the boundary conditions of the optimization problem have been sketched in Fig. 19. The objective function, f_P, reads:

$$ f_{P} = {\int}_{{\Omega}_{P}} d_{y} \hspace{2pt}\text{d} V $$

(23)

Fig. 19

Schematic of the problem layout and the boundary conditions of the fluid gripper

The spring point (a single node) is denoted Ω_P and is placed in the center of a squared domain, Ω_I, which has fixed unity design variables. The objective function is defined in a single node instead of a domain, as we aim on defining a problem which resembles as much as possible of the original gripper problem in Sigmund (1997). The fluid flow boundary conditions of the fluid gripper problem are similar to the boundary conditions presented for the flow obstacle problem in Fig. 12, but fixed structural boundary conditions in all DOF have been imposed along Γ^S and Ω_D has been enlarged so solid elements can connect from Ω_P to Γ^S.

The domain Ω is discretized into $\left \{{N_{C}^{x}},{N_{C}^{y}}\right \}=\left \{ 200,100 \right \}$ elements. The total number of state DOF is 101,505 and the maximum allowed volume fraction is V^f = 0.2. The problem is investigated for Re = {1,100} and for the spring stiffness of k = 10¹³.

The optimized design and the relevant state fields of the fluid gripper optimization problem in (23) have been plotted in Figs. 20 and 21.

Fig. 20

Optimized designs and the state field plots for Re = 1

Fig. 21

Optimized designs and the state field plots for Re = 100

The cross-check table in Table 4 confirms that the design optimized for one Re indeed has superior performance compared to the design optimized for the other Re.

Table 4 Cross-check between f_P and Re

The optimized designs consist of four main parts: A horizontal superjacent bar; a pivot which converts positive y-directional fluid pressure loads working on the superjacent bar into negative y-directional motion in Ω_P; a vertical bar which connects the pivot and the superjacent bar to Ω_P; and a foundation structure which connects the pivot to the structural constraints along Γ^S.

The foundation structures are robust to ensure that the pressure load is converted into a force in Ω_P. Designs optimized for a too low k_s may cause a “fragile” optimized designs with poor conversion of pressure loads into spring forces.

The horizontal superjacent bars have two purposes: (1) the y-directional vertical pressure forces on the horizontal superjacent bars are converted into a clockwise moment around the pivot. The moment around the pivot is transferred to Ω_P through the vertical bar which connects Ω_P and the pivot. (2) the input velocity of the fluid flow is fixed, and the optimization problem does not put any requirements on the maximum allowed pressure drop. A large drag force of the optimized design causes a large pressure drop between the Γ^W and Γ^E and hereby a large pressure load on the superjacent bar. The large pressure load causes a large pivoting moment and hereby a large force on Ω_P.

The vertical superjacent bar of the Re = 1 design is longer than the vertical superjacent bar of the Re = 100 design. The difference in lengths between the superjacent bars may be explained by the difference in the pressure loss between the two optimized designs. Due to the difference in the viscous forces of the fluid, the pressure loss over the vertical superjacent bar of the Re = 1 design is significantly lower than the pressure loss over the vertical superjacent bar of the Re = 100 design. The lower pressure loss of the Re = 1 design makes the downstream part of the superjacent bar efficient, as it contributes to the clockwise moment around the pivot.

The superjacent bar for the Re = 1 design is straight, where as the superjacent bar of the Re = 100 design has a small concave (with respect to an observer on Γ^N) feature in the upstream tip. The concave feature of the tip of the Re = 100 design generates a low pressure in the northern proximity of the superjacent bar which sucks the superjacent bar upwards and hereby contributes to the clockwise moment around the pivot.

The cross-checks in Table 4 indicate that the topology of the optimized designs and the fluid properties are significantly correlated and adequately captured by the optimization algorithm, and that a design optimized for one Re indeed have superior performance compared to designs optimized for the other Re.

To provide guidance for future research within TO of FSI problems, we have plotted the normalized sensitivity fields and the 0/1 contour for the optimized fluid gripper designs in Fig. 22. Negative values of the sensitivities advice a decrease in design variable density and positive values of the sensitivities advice an increase in design variable density. The design evolution is solely driven by the convective response as the shear stresses of the flow are neglected in the physical model. High positive sensitivity values are observed in the pivots for the both Re = 1 and Re = 100 designs. This indicates the urge for thinner and more flexible pivots which, however, is hindered by the minimum length scale strongly imposed by the robust design formulation.

Fig. 22

Normalized sensitivity fields for the optimized fluid gripper designs

7 Discussion

7.1 Interaction between fluid, structure and the optimization problem

The passed cross-checks in Tables 1, 3 and 4 prove that the coupling between the fluid problem, the structural problem and the optimization problem is appropriately and consistently captured. The cross-checks strongly indicate that the various optimized designs are governed by the changes in the model parameters, and not caused by poor local minima.

7.2 The choice of interpolation functions and parameters

The choice of interpolation functions and their parameters is crucial in order to obtain well-posed optimization problems. For a specific set of discretized equations, the choice of interpolation functions and their parameters determine the relationship between the objective function and the design variables. Appendix A.3 demonstrates that a monotonic relationship between the design variables and the objective function may provide a better performing and smoother optimization process.

The density-based topology optimization approach is sensitive to the interactions between various interpolation functions. The introduction of the design field and poorly chosen interpolation functions may cause non-monotonic relationships between the objective function and the design variables and well-performing design consisting of intermediate design variables for standard density methods. A well-performing topology optimization based framework supported by monotonic relationship between the objective function and design variables. Other topology optimization approaches such as explicit boundary controlled methods may not encounter these kinds of issues, as the sensitivities for such methods always point in the correct direction.

7.3 The robust formulation

The robust formulation and the continuation scheme in the projection filter threshold may make the optimization framework, apart from providing manufacturing robustness and length-scale-control, less sensitive to non-monotonic relationships between the objective function and the design variables. The robust formulation uses several realizations of the designs, and the probability for the optimizer to find a non-physical, but well-performing, intermediate state is hereby reduced.

7.4 The choice of Brinkman penalization parameter

A very high Brinkman penalization parameter, e.g. α_max = 10⁹, in the solid elements is crucial in order to model the pressure field correctly. The underlying physical model is incorrect (compared to the segregated approach) for problems in which the Brinkman penalization is too small as the pressure field is incorrectly modeled. Designs optimized for too low Brinkman penalization may perform poorly in segregated models, as the optimized designs may contain features which take advantage of the too permeable structure. The large Brinkman penalization is most important when the objective function or the optimization constraints are directly related to the fluid pressure field, such as in FSI problems.

7.5 Free floating island of solid elements

The multi-objective formulation for the f_D optimization problem in (15) constitutes an alternative to the auxiliary indicator method presented in the work of Jenkins and Maute (2016). The multi-objective approach requires a tuning of an additional parameter as the choice of a₂ is important to obtain an adequate ratio between the influence of the multiple objective functions. The approach has shown promising results in removing FFIOSE from the flow obstacle problem, however comparison between the performance of the indicator method and the multi-objective approach requires more studies.

Jenkins and Maute (2016) reported on FFIOSE for compliance problems; such issues were not observed in compliance problems in this study. The absence of FFIOSE in compliance problems may be explained by the continuous nature of the design variables in the density-based topology optimization approach. Elements disconnected from the main structure are removed continuously during the optimization process as the void elements connected between the FFIOSE and the structural constraints undergo large structural compliance. Void elements with large structural compliance are inefficient for the design performance for which reason the FFIOSE are removed.

7.6 The displacement dependency

The displacement dependency significantly increases the non-linearity of the design problem. A design framework which takes the displacement dependency into account could identify design concepts which may not be encountered when neglecting the displacement dependency. To demonstrate the influence of the deformation dependency, we suggest future research to include a comparison between an optimized design which complements the deformation dependency and an optimized design which neglects the deformation dependency.

7.7 Topology optimization with immersed versus density-based methods

Immersed methods with explicit boundary representation (IMwEBR) have a well defined boundary between the fluid and the structure, which resolves the physics correctly though the entire optimization process. Intermediate design variables in density-based methods rely in interpolation functions, which do not guarantee correct physical modeling during the optimization process unless a complete 0/1 design is present. We showed that adequate choice of interpolation function parameters provided well-posed optimization problems. IMwEBR may generally have an advantages compared to density-based topology optimization approaches for fluid-structure-interaction, as IMwEBR have a well defined boundary between the fluid and the structure whereas density-based methods are prone to a complex interplay between the fluid and the structure in the intermediate design variables.

7.8 Shear stress

In the Hungry Horse problem in Section 5.6, we demonstrated that the shear stress may be significant magnitude compared to the pressure for some problems. Shear stresses should therefore be taken into account in detailed computations. Shear forces may be difficult to model with a density-based Brinkman penalization approach as the porous media in the intermediate design variables penalizes the fluid velocity and hereby the fluid shear stresses. IMwEBR for FSI problems may be better suited for taking such effects into account as IMwEBR always have well-defined boundaries, which avoid issues with non-physical intermediate design variables.

7.9 Future work

Future developments in the field of topology optimization for FSI problems may concern: (1) Taking the deformation dependency in the finite element model and the sensitivity analysis into account to demonstrate the connection between optimized topology and the magnitude of the structural deformations. (2) Investigation of the dependency between the optimized topology of various mechanism problems and the choice of input spring stiffnesses, pressure drop constraints and Reynolds numbers. (3) A three dimensional and time dependent implementation of the framework in a parallel code to optimize for more realistic problems. (4) The influence of the shear stress for low Reynolds number flows.

8 Conclusion

The density-based topology optimization approach is revisited, and the framework is tested for low and moderate Reynolds numbers on benchmark problems, well-know design problems from the literature, and two new challenging design problems. The framework takes basis in the finite element discretization of the Navier-Cauchy and Navier-Stokes equations which are solved in an unified formulation. The physical modeling is limited to two dimensions, steady state, the influence of the structural deformations on the fluid flow is assumed negligible, and the structural and fluid properties are assumed constant.

The derivation of the unified finite element formulation is elaborated, where an additional term in the coupling between the fluid and the structure is included compared to the equivalent formulations in the literature. Critical implementation details concerning the Brinkman penalization parameter and the interpolation functions and parameters are provided.

The framework is built on basis of a robust formulation, which ensures length-scale-controlled well-performing and binary optimized designs and makes the optimization process less sensitive to the choice of interpolation function parameters, model parameters, and penalization and continuation strategies. The coupling between the fluid flow, the elastic structure and the optimization problem is clearly captured and demonstrated with comprehensive numerical studies and cross-check tables.

By combining different objective functions with different features and weights, non-physical free-floating islands of solid elements (FFIOSE) can be removed during the design process.

The study procures new insight in the field of topology optimization for fluid-structure-interaction problems, and may provide guidance for future research within topology optimization for fluid-structure-interaction problems.

Appendix

1.1 A.1 Details on the derivation of (3)

The Navier-Cauchy equations are given by:

$$\begin{array}{@{}rcl@{}} \frac{\partial{\sigma^{s}_{ij}}}{\partial{x_{j}}} + f_{i} &=& 0 \quad \text{in} \quad {{\Omega}_{S}} \\ \sigma^{s}_{ij} &=& C_{ijkl} \epsilon_{kl} \\ \epsilon^{s}_{kl} &= &\frac{1}{2} \left( \frac{\partial{d_{k}}}{\partial{x_{l}}} + \frac{\partial{d_{l}}}{\partial{x_{k}}} \right) \end{array} $$

(24)

The coupling between the fluid and the structure is given by (Farhat and Roux 1991; Yoon 2014a)

$$ \sigma^{s}_{ij} n_{j} = \sigma^{f}_{ij} n_{j} \quad \text{on} \quad {{\Gamma}_{SF}} $$

(25)

The weak form of (24) is given by:

$$ {\int}_{{{\Omega}_{S}}} {w^{h}_{i}} \frac{\partial{\sigma_{ij}^{s}}}{\partial{x_{j}}} \hspace{2pt}\text{d} V + {\int}_{{{\Omega}_{S}}} {w^{h}_{i}} f_{i} \hspace{2pt}\text{d} V = 0 $$

(26)

where ${w^{h}_{i}}$ is a suitable basis function. Integration by parts of higher dimensions on the first term of (26), yields:

$$\begin{array}{@{}rcl@{}} {\int}_{{{\Gamma}_{SF}}} {w^{h}_{i}} \sigma^{s}_{ij} n_{j} \hspace{2pt}\text{d} S - {\int}_{{{\Omega}_{S}}} \frac{\partial{{w^{h}_{i}}}}{\partial{x_{j}}} \sigma_{ij}^{s} \hspace{2pt}\text{d} V \\ + {\int}_{{{\Omega}_{S}}} {w^{h}_{i}} f_{i} \hspace{2pt}\text{d} V = 0 \end{array} $$

(27)

Shear stresses on the interface between the fluid and the structure are neglected for which reason (25) can be written as $\sigma ^{s}_{ij} n_{j} = -p n_{i}$ on ΓSF, where p is the pressure on the interface surface. Equation (27) is now rewritten as:

$$\begin{array}{@{}rcl@{}} {\int}_{{{\Gamma}_{SF}}} {w^{h}_{i}} p^{h} n_{i} \hspace{2pt}\text{d} S - {\int}_{{{\Omega}_{S}}} \frac{\partial{{w^{h}_{i}}}}{\partial{x_{j}}} \sigma_{ij}^{s} \hspace{2pt}\text{d} V \\ + {\int}_{{{\Omega}_{S}}} {w^{h}_{i}} f_{i} \hspace{2pt}\text{d} V = 0 \end{array} $$

(28)

Integration by parts of higher dimensions on the first term of (28), yields:

$$\begin{array}{@{}rcl@{}} {\int}_{{{\Omega}_{S}}} \frac{\partial{{w^{h}_{i}}}}{\partial{x_{i}}} p^{h} \hspace{2pt}\text{d} V + {\int}_{{{\Omega}_{S}}} {w^{h}_{i}} \frac{\partial{p^{h}}}{\partial{x_{i}}} \hspace{2pt}\text{d} V \\ - {\int}_{{{\Omega}_{S}}} \frac{\partial{{w^{h}_{i}}}}{\partial{x_{j}}} \sigma_{ij}^{s} \hspace{2pt}\text{d} V + {\int}_{{{\Omega}_{S}}} {w^{h}_{i}} f_{i} \hspace{2pt}\text{d} V = 0 \end{array} $$

(29)

Equation (29) may now be rewritten from the segregated domains Ω_S to a unified domain Ω, by introducing a design variable field 0 ≤ ρ ≤ 1 and the following interpolation function:

$$ C_{ijkl} = E(\rho) C^{0}_{ijkl} $$

(30)

Correct integration of the fluid pressure on the elastic structure is ensured by introducing the filter function Ψ(ρ):

$$ {\int}_{{\Omega}_{S}} \square \hspace{2pt}\text{d} V = {\int}_{{\Omega}} {\Psi}(\rho) \square \hspace{2pt}\text{d} V $$

(31)

Ψ(ρ) is a function which is unity for ρ = 1 and zero for ρ = 0. Inserting (30) and (31) into (29), we arrive at the following expression for the Navier-Cauchy equation defined in a unified domain Ω:

$$\begin{array}{@{}rcl@{}} {\int}_{{{\Omega}}} {\Psi}(\rho) \left( \frac{\partial{{w^{h}_{i}}}}{\partial{x_{i}}} p^{h} + {w^{h}_{i}} \frac{\partial{p^{h}}}{\partial{x_{i}}} \right) \hspace{2pt}\text{d} V \\ + {\int}_{{{\Omega}}} {w^{h}_{i}} f_{i} \hspace{2pt}\text{d} V = {\int}_{{{\Omega}}} E(\rho) \frac{\partial{{w^{h}_{i}}}}{\partial{x_{j}}} \sigma_{ij}^{s_{0}} \hspace{2pt}\text{d} V \end{array} $$

(32)

1.2 A.2 Benchmark examples

To demonstrate the features of the present framework, we have revisited the wall flow design problems presented in the works of Yoon (2010) and Picelli et al. (2017) and Jenkins and Maute (2016). These, what we call, benchmark designs problems are solved with the same physical parameters as in the respective papers but with our framework. The design solution, obtained with the framework presented in this study, to the design problem presented in Jenkins and Maute (2016) has been plotted in Fig. 23. The design solution shown in Jenkins and Maute (2016) and our design solution in Fig. 23 are by visual comparison quite similar. The small difference in the design solutions suggests that the internal pressure, the displacement dependency and /or the shear stress may have minor effects for this specific optimization problem. However, more studies and other optimization problems are required to fully understand the influence of the different modeling approaches and assumptions.

Fig. 23

Design solution for the wall flow problem in (Jenkins and Maute 2016) with Re = 10

In Figs. 24 and 25, the Yoon (2010) and Picelli et al. (2017) benchmark design problems, solved by our framework, have been plotted for Re = 0.004 and Re = 12. The designs have been optimized for the full pressure coupling formulation in (3). It is unclear whether the design solutions in Yoon (2010) are solved for pressure-coupling term 1 or pressure-coupling term 1 and 2. In Yoon (2010), it is seen that an increased Reynolds number causes the wall support to move to the downstream part of the design domain. This tendency is conflicting with the tendencies observed in Picelli et al. (2017) and in Figs. 24–25. In these design problems, it is observed that an increased Reynolds number causes the wall support to move to the upstream part of the design domain. As far as we are aware there does not exist any crosschecks between the Reynolds number and the optimized designs in the mentioned papers, for which reason it is challenging to assess how much significance we can attribute to the features of the optimized designs in Yoon (2010) and Picelli et al. (2017). However, please notice that our optimized designs in Figs. 24–25 pass a crosscheck.

Fig. 24

Design solutions for the wall flow problem stated in (Yoon 2010; Picelli et al. 2017) with Re = 0.004

Fig. 25

Design solutions for the wall flow problem in Yoon (2010) and Picelli et al. (2017) with Re = 12

1.3 A.3 Details on the determination of interpolation functions

TO for FSI problems are highly non-linear, ill-posed and non-convex. Several model parameters influences the design processes and the design solutions, which require a significant amount of parameter tuning due to the deepness of the design space. Numerical experiments with the framework presented in this work, have suggested that the design process is highly dependent on the choice of interpolation functions, α(ρ),E(ρ) and Ψ(ρ) (abbreviated: H_{{α, E,Ψ}}), and the choice of interpolation function parameters, p_α, p_E and p_Ψ (abbreviated: p_{{α, E,Ψ}}). It is our experience that adequate choices of p_{{α, E,Ψ}} and H_{{α, E,Ψ}} are critical to obtain well-performing and 0/1 design solutions. As p_{{α, E,Ψ}} and H_{{α, E,Ψ}} are key to carry out successful optimization problems, we will in this section present a methodology which can be used to determine adequate p_{{α, E,Ψ}} and H_{{α, E,Ψ}} and hereby formulate well-posed optimization problems.

IMwEBR are based on shape sensitivities which may be better suited for TO for some multi-physics problems. IMwEBR have a well-defined boundary between the different types of physics, which ensures that the physics are resolved correctly throughout the entire design process, as no sub-domains are dependent on the quality of the interpolation functions of the intermediate design variables. In density-based methods the correctness of the physical modeling rely, among many other aspects, on the choice of p_{{α, E,Ψ}} and H_{{α, E,Ψ}}. The hypothesis is that topology sensitivities, ∂f/∂ρ_d, may obtain the same well-behaving features as shape sensitivities, ∂f/∂ρ_s, if some adequateH_{{α, E,Ψ}} and p_{{α, E,Ψ}} are chosen.

To determine adequate sets of H_{{α, E,Ψ}} and p_{{α, E,Ψ}}, we compare ∂f/∂ρ_s and ∂f/∂ρ_d for two different problems: (1) a purely elastic problem and (2) an FSI problem. The problem layouts and the boundary conditions have been sketched in Fig. 26. To carry out the study, we compare four different objective functions, f_E, f_C, f_T and f_P (abbreviated: f_{{E, C, T, P}}):

• 1. Dissipated energy in the flow, f_E, see (17).

• 2. Structural compliance f_C, see (16)

• 3. The y-displacement of the tip of the beam in point {x, y} = {2, 0.45}:

  $$ f_{T} = \frac{1}{{\int}_{{{\Omega}_{T}}} \hspace{2pt}\text{d} V} {\int}_{{{\Omega}_{T}}} d_{y} \hspace{2pt}\text{d} V $$

  (33)

• 4. The pressure induced y-directional force on the beam:

  $$ f_{P} = {\int}_{{\Gamma}_{B}} p n_{j} \hspace{2pt}\text{d} S $$

  (34)

Fig. 26

Problem layouts and boundary conditions used to compare the topology sensitivities and the shape sensitivities

The relationship between f_{{E, C, T, P}}, ρ_S and ρ_D is determined with basis in a simple problem where a beam separates a channel into two regions of the same size. The problem is modeled in the unified framework. The beam separating the channel, Ω_I, has fixed unity design variables and the tip of the beam is loaded with a force f_y. With reference to Fig. 26, we consider two different problems: (a) An elastic problem where $u_{x}^{*}= 0$ and f_y = 10, and (b) an FSI problem where $u_{x}^{*}= 1$ and f_y = 0.

With reference to Fig. 26a, the topology sensitivities of various objective functions are computed by changing the design variables of the lowest line of elements of the vertical beam. With reference to Fig. 26b, the shape gradients of various objective functions are computed by changing the position of the nodes on the lower boundary of the beam. The position of the boundary is varied over the length of one element, entailing that ∂f/∂ρ_d and ∂f/∂ρ_s are comparable in material usage.

The relationship between f_{{C, P}}, f_{{C, P}}, ρ_d and ρ_s for the elastic problem have been compared in Fig. 27. The relationships are different but can be characterized by the following attribute: f_{{C, T}}(ρ_s) and f_{{C, T}}(ρ_d) are strictly monotonic entailing that ∂f_{{C, T}}/∂ρ_s and ∂f_{{C, T}}/∂ρ_d are strictly monotonic. Well-versed and crisp 0/1 designs and smooth optimization processes are obtained for a large number of TO for elastic problems, see e.g. (Bendsøe and Sigmund 2003). The hypothesis in this study is, that the well-posed properties of linear elastic problems are explained by the strictly monotonic features of the ∂f_C/∂ρ_d.

Fig. 27

The relationship between f_C, f_P and ρ_d/ρ_s for various choices of H_{{α, E,Ψ}} and p_{{α, E,Ψ}}

We now point out attention to the FSI problem, where we investigate the monotonicity of f_{{E, C, T, P}}(ρ_s) and f_{{E, C, T, P}}(ρ_d). The relationships have been plotted in Fig. 28, and are characterized by:

• 1. f_{{E, C, T, P}}(ρ_s) are strictly monotonic in all cases, which entail that ∂f_{{E, C, T, P}}/∂ρ_s are strictly monotonic in all cases.

• 2. f_{{E, C, T, P}}(ρ_d) are strictly monotonic for some choices of p_{{α, E,Ψ}} and H_{{α, E,Ψ}}.

• 3. The relationship between f_{{E, C, T, P}}(ρ_d) seem to be very sensitive with respect to the choice of p_α, as a small change in p_α may disrupts the monotonicity for all f_{{E, C, T, P}}.

Fig. 28

The relationship between f_E, f_C, f_P, f_T and ρ_d/ρ_s for various choices of H_{{α, E,Ψ}} and p_{{α, E,Ψ}}

To demonstrate the importance of the monotonicity of f_{{E, C, T, P}}(ρ) we have included a numerical example where we compare two design optimized for two different p_α. In Fig. 29, f_D have been optimized for the flow obstacle problem (see Section 6.2) for p_α = 0.5 ⋅ 10⁻⁶ and p_α = 10⁻⁶. The design optimized with a strictly monotonic f_D perform much better than the design optimized for non-monotonic f_{D}. We notice that a small change in p_α significantly influences the topology and the performance of the design solutions.

Fig. 29

Optimized designs for the flow obstacle problem in Fig. 12 for two different interpolation function parameters

We suggest that the correlation between the monotonicity of the objective functions and the well-posedness of the design problems is likely to generalize to all multiphysics topology optimization problems.

1.4 A.4 Details on the Brinkman penalization parameter

Numerical experiments with the framework suggested that α_max should be chosen high (e.g. α_max = 10⁹) to model the pressure field correctly. A low α_max, e.g. α_max = 10⁵, provides a more well-posed optimization problem, however the pressure field is not modeled correctly. Modeling the pressure field incorrectly may provide unintuitive and physically meaningless optimized designs, as the coupling from the fluid to the structure is transfered through the pressure field. To demonstrate the relationship between the pressure field and the magnitude of α_max, we have plotted the pressure field along the line {x, y} = {x, 0.34} for the design shown in Fig. 30 in Fig. 31. The pressure fields for the COMSOL composite model and the unified model with α_max = 10⁹ is closely correlated. However, for small α_max, a large difference between the composite model and the unified model is observed. As a final remark, the minor difference between the fields is caused by different finite element discretizations of the segregated and unified models.

Fig. 30

Design used to evaluate the pressure

Fig. 31

The pressure as function of x for various α_max

To demonstrate the occurrence of unintuitive optimized topologies for design problems with too low α_max, we consider two different design problems. The design in Fig. 32a has been optimized for α_max = 10⁵ and the design in Fig. 32b has been optimized for α_max = 10⁹. The designs provide superior performance for the model parameters under which the designs were optimized. However, the design optimizd for α_max = 10⁵ does not performing well in a segregated FSI formulation. The too low α_max causes poor resolvement of the pressure field which causes unintuitive optimized designs. For comparison we have plotted the design optimized for α_max = 10⁹ in Fig. 32b. This design performs well in a segregated model.

Fig. 32

Design solutions for the flow obstacle problem in Fig. 12 for various α_max

The coupling between the structure and the fluid is carried out through the pressure field, for which reason adequate modeling of the pressure field is crucial in FSI problems. Previous work on topology optimization for fluid problems has used magnitudes of α_max which do not resolve the pressure field correctly. Non-intuitive designs may not have been observed in these studies because the pressure fields were not directly related to the objective functions or the constraints of the optimization problems.