Abstract
This work develops a framework for SIMP-based topology optimization of a metallic panel structure subjected to design-dependent aerodynamic, inertial, elastic, and thermal loads. Multi-physics eigenvalue-based design metrics such as thermal buckling and dynamic flutter are derived, along with their adjoint-based design derivatives. Locating the flutter point (Hopf-bifurcation) in a precise and efficient manner is a particular challenge, as is outfitting the optimization problem with sufficient constraints such that the critical flutter mode does not switch during the design process. Results are presented for flutter-optimal topologies of an unheated panel, thermal buckling-optimal topologies, and flutter-optimality of a heated panel (where the latter case presents a topological compromise between the former two). The effect of various constraint boundaries, temperature gradients, and (for the flutter of the heated panel) thermal load magnitude are assessed. Off-design flutter and thermal buckling boundaries are given as well.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Panel flutter has received a great deal of attention over the last fifty years within the computational aeroelasticity community. The problem is classically defined by a very thin two-dimensional elastic structure, constrained in some capacity at either edge, and subjected to high supersonic flow over the top surface. For increasing flow speeds, a pair of complex conjugate eigenvalues of the system can cross the imaginary axis via a Hopf-bifurcation, and the subsequent loss of dynamic stability is defined as flutter. This system has received such widespread attention due, in part, to the fact that the aeroelastic system is computationally tractable, yet can display highly-complex coupled unsteady behavior. Furthermore, a wide range of aerospace configurations utilize elastic panels (high-speed aircraft, jet engines, space re-entry vehicles, missiles, etc.), and the need to prevent aeroelastically-induced panel failures can have a substantial impact on the overall design process. Important early papers on this subject are given by Fung (1958), Dugundji (1966) and Dowell (1966), more recent survey papers are given by Dowell (1970), Reed et al. (1987), and Mei et al. (1999).
Beyond the basic problem description given above, many additional factors may be included in the panel flutter analysis (e.g., a static pressure differential, various boundary conditions and support mechanisms, post-flutter nonlinear limit cycle oscillations, acoustic loadings: all of which are covered in the cited review papers), with thermal effects of particular concern for this work. If both ends of the panel are constrained from moving and/or rotating, the application of a temperature field will weaken the panel, and a buckling temperature can be identified, above which the structure is statically unstable to transverse loadings. The heating fundamentally alters the flutter point of the panel as well, which is now defined by a balance of inertial, elastic, aerodynamic, and thermal effects: aerothermoelasticity. Survey papers on this general subject are given by Garrick (1963), Thornton (1992), McNamara et al. (2008), and McNamara and Friedmann (2011). Many papers have been written which specifically detail the buckling and flutter boundaries of heated panels: see Schaeffer and Heard (1965), Yang and Han (1976), Xue and Mei (1993), and Librescu et al. (2004) (prescribed temperature field), Abbas et al. (1993) and Gee and Sipcic (1999) (temperature field obtained via aerodynamic heating), and Thornton and Dechaumphai (1988), Kontinos (1997), Culler and McNamara (2010), and Miller et al. (2011) (temperature field obtained via a balance of aerodynamic heating, thermal radiation, and transient heat transfer throughout the vibrating structure).
As with any aero-structural component, the weight of a panel should be as low as possible, provided that the resulting physical response is acceptable. In the context of the above discussion, this would imply a minimum-mass structure with constraints on buckling and flutter, though vibrations, deflections, stresses, noise, and fatigue life may also be of concern. Many papers exist which consider the minimum mass of a thin panel under a flutter constraint, or vice-versa: maximum flutter speed under a mass constraint. This may be done by parameterizing the thickness distribution throughout the panel (via either discrete or continuous variables), where a change in thickness impacts both the inertial and elastic loads throughout the panel. Early work in this area is given by Weisshaar (1972) and Peirson (1975), and additional papers are found by Weisshaar (1976), Van Keuren and Eastep (1977), Beiner and Librescu (1983), Barboni et al. (1999), and Palaniappan et al. (2006). Panel flutter objectives/constraints have also been handled with planform parameters (Livne and Mineau 1997), optimal placement of piezoelectric actuators and dampers (Nam et al. 1996; Sadri et al. 2002; Tanaka et al. 2005), and stacking sequence design (Hirano and Todoroki 2004; Seresta et al. 2006). Structural optimization of panels for buckling loads is also well-studied (see Manickarajah et al. 2000 and Maalawi 2002 for overviews on the subject), with thermal effects accounted for by Foldager et al. (2001), Chen et al. (2003), and Wang et al. (2004) (among many others). But the work of Seresta et al. (2006) appears to be one of very few that conducts structural optimization of a panel with both flutter and buckling (thermal or otherwise) metrics, providing Pareto trade-offs between the two.
This work is concerned with using a subset of structural optimization, topology optimization, to optimize aerthermoelastic panels for flutter and buckling metrics. Smaller length-to-thickness ratios than might be traditionally considered (\(L/h \sim 100\)) are utilized here (\(L/h=25\)), so that the cross-section of the two-dimensional panel may be discretized into a series of quadrilateral finite elements. Each element is assigned a design variable, which continuously interpolates between 0 (void) and 1 (solid), and the optimal layout of material within the panel may be obtained such that the structure behaves as intended when subjected to thermal and aerodynamic effects. The monograph by Bendsøe and Sigmund (2003) provides a general overview of the method. In the field of dynamics, topology optimization has been used to tailor the response of structures subjected to dynamic loads (Ma et al. 1995; Min et al. 1999; Tcherniak 2002; Jog 2002; Jensen 2007, 2009; Stanford and Beran 2011a, b), and (of more concern to this work) to optimize free vibration eigenvalues (Pedersen 2000; Maeda et al. 2006), frequency gaps (Du and Olhoff 2007), or complete frequency response spectra (Yoon 2010a). The method has also been used for buckling design (Neves et al. 1995; Rahmatalla and Swan 2003), numerous thermoelastic studies (Jog 1996; Li et al. 2000; Sigmund 2001), and convection heat transfer (Bruns 2007), each of which is a field that may be significant to panel design. It is particularly important to note that, given the large number of design variables utilized in topology optimization (in comparison to shape, sizing, or stacking sequence optimization), several papers (Du and Olhoff 2007; Neves et al. 1995) have noted that the large design freedom can lead to eigenvalue-related optimization issues. Specifically, repeated eigenvalues and discontinuous mode-switching must be accounted for.
Aeroelastic applications of topology optimization are rare. Eschenauer and Olhoff (2001) and Krog et al. (2004) both studied the topological design of internal wing ribs, but the aerodynamic loads are prescribed, not design-dependent. Studies which include aerodynamic loading feedback via true fluid-structure coupling are given by Maute and Allen (2004) (topology of an underlying wing structure), Maute and Reich (2006) (compliant airfoil morphing mechanisms), Gomes and Suleman (2008) (wing box design for rolling maneuvers), Stanford and Ifju (2009) (membrane wing design), Yoon (2010b) (monolithic methods for fluid-structure interaction in topology optimization), Kreissl et al. (2010) (microfluiduc devices), and Stanford and Beran (2011a) (compliant flapping mechanisms). Only the latter paper deals with dynamic aeroelasticity, rather than steady fluid-structure interaction. Recently, some researchers have specifically incorporated aeroelastic instability (i.e., flutter) into the topology optimization of cantilevered wing structures: see Stanford and Beran (2011b) and De Leon et al. (2012).
Many topology and (more generally) structural optimization papers cited above study the individual elements important to an aerothermoelastic panel. To the best of the author’s knowledge, none have combined them into a single topology optimization framework, which is the goal of this paper. The development of such a framework is important in the sense that both buckling and flutter are common modes of failure for aerospace panels (Mei et al. 1999), but design trends needed to alleviate them can be at strong odds with one another (Seresta et al. 2006). The specific objectives are as follows:
-
1.
A quasi-static thermoelastic model will be developed: the temperature of the top and bottom panel surfaces is prescribed, and the conduction through the topology of the internal layout is subsequently computed. This model will be used to compute stresses, and the concomitant critical buckling temperatures of the panel.
-
2.
Assuming that the characteristic time of the thermal system is large relative to the vibration of the panel (Culler and McNamara 2010), linear piston theory aerodynamics (Ashley and Zartarian 1956) (a common tool for panel analysis) will be used to compute the flutter speed of the panel for a prescribed top and bottom panel surface temperature.
-
3.
The analytical sensitivities of both the critical buckling temperature and the flutter speed with respect to a large number of topological design variables will be computed, for a given material interpolation scheme between solid and void.
-
4.
Three basic types of topology optimization problems will be solved: maximum thermal buckling load, maximum unheated flutter speed, and maximum heated flutter speed (with a prescribed top and bottom panel surface temperature), where the latter problem should pose a topological compromise between the two former. A set of constraints will be carefully posed such that mode-switching is avoided during the optimization process, as discussed in by Hanoaka and Washizu (1980).
-
5.
The dependence of the optimal panel topology upon various factors will be assessed: constraint boundaries, ratios of the prescribed upper and lower panel surface temperatures, and (for the flutter of the heated panel) magnitude of the thermal load. Furthermore, the off-design performance of the topologies will be examined.
2 Problem description
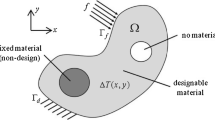
The geometry of a metallic panel structure considered in this work can be seen in Fig. 1. This test case is meant to emulate the aerospace configurations described above: an elastic surface embedded in an otherwise rigid plane (the outer surface of a high-speed aircraft wing, or the side of a re-entry vehicle, for example), exposed to flow over its top surface only. The length and thickness of the two-dimensional panel are \(L\) and \(h\), respectively, the structure is assumed to be infinitely-long in the third dimension, and both the leading edge and the trailing edge are restricted from moving. As noted above, \(L/h\) is fixed as 25: this is smaller than found in typical panel flutter studies (which may utilize thin beam/plate methods), but is required to study the internal topology of the structure in a computationally feasible manner.
The panel cross section will be discretized into a series of bilinear finite elements, and each element assigned a density measure \(x_{e}\) which smoothly varies between 0 (void) and 1 (solid). Portions of the panel are fixed as solid (elements that lie in the upper 10 % or the lower 5 %, as drawn in Fig. 1), the remainder constitutes the design domain. Finite element nodes that lie along the upper and lower surfaces are prescribed spatially-uniform temperatures \(T_{U}\) and \(T_{L}\), respectively, and the upper surface of the panel is subjected to high-speed supersonic flow (flow density \(\rho _{\infty }\), flow velocity \(U_{\infty }\), and Mach number \(M_{\infty }>1\)). Prescribing the upper surface of the panel to always remain solid (\(x_{e}=1\)) circumvents potential ambiguities concerning the transfer of aerodynamic loads to the structure, though strategies are discussed by Yoon (2010b). Prescribing the lower surface of the panel to remain solid as well, though this surface is not exposed to aerodynamic loads, is found to help stabilize the topology optimization process.
3 Aerothermoelastic modeling framework
Linear unsteady finite element solutions are used to ascertain the thermal buckling and flutter boundaries of the panel topologies. The geometry seen in Fig. 1 is discretized into bilinear Q4 finite elements, a common choice for topology optimization (Bendsøe and Sigmund 2003). The remainder of this section details the computational steps needed to compute the relevant metrics.
3.1 Heat conduction modeling
A typical assumption in panel analyses is to assume a set temperature distribution throughout the entirety of the structure (Xue and Mei 1993). This is reasonable in the sense that the Biot number for a thin panel is small enough to warrant a lumped-capacity model (Gee and Sipcic 1999), though the temperature of the panel could be linked to the flow conditions via an aerodynamic heating model (assumption of an adiabatic wall temperature, for example). A compromise between the two approaches is taken for this work, in that the thermal boundary conditions of the panel are prescribed, but the internal conduction is subsequently computed. Presumably, the small value of \(L/h\) and the substantial variations in mechanical properties throughout an optimized topology limit the usefulness of a lumped-capacity assumption. Furthermore, unsteady thermal effects are neglected for this work, assuming that the time scale of the thermal system is large relative to the vibration of the panel (Culler and McNamara 2010).
In addition to the prescribed temperature boundary conditions stated in Fig. 1, adiabatic boundary conditions are applied to the sides of the panel. The conductivity matrix of the panel is assembled over each finite element \((e)\) in the typical manner (Cook et al. 2002):
where \(x_{e}\) is the relative density of each finite element and \(p\) is the penalization power. The solid-void interpolation scheme used here is SIMP (solid isotropic material with penalization), described extensively by Bendsøe and Sigmund (2003) and Gao and Zhang (2010) specifically with regard to thermoelastic problems. \(\boldsymbol {K}_{Te}\) is an elemental conductivity matrix (one temperature degree of freedom per node) for the fully solid material. The assembled matrix \(\boldsymbol {K}_{T}\) is then partitioned into known (\(\boldsymbol {T}_{c}\)) and unknown (\(\boldsymbol {T}_{x}\)) nodal temperatures:
where the prescribed vector \(\boldsymbol {T}_{c}\) is entirely composed of \(T_{U}\) (nodes along the upper surface) and \(T_{L}\) (nodes along the lower surface). For the linear analysis considered here, \(T_{U}\) is set equal to unity. The unknowns are then computed as:
The thermal load vector \(\boldsymbol {R}_{T}\) is defined by \(-\boldsymbol {K}_{T_{xc}} \cdot \boldsymbol {T}_{c}\).
If \(T_{L}\) is set equal to \(T_{U}\) (uniformly heated panel) the conduction problem of (3) becomes trivial, as the temperature at every node is equal to \(T_{U}\), entirely independent of the topology of the structure \(x_{e}\). Only when \(T_{L}\) differs from \(T_{U}\) is thermal conduction activated throughout the panel, and a dependency on \(x_{e}\) is introduced.
3.2 Panel stresses
The temperature is assumed to be spatially uniform within each finite element \((T_{e})\), and is computed by simply averaging the four nodal temperatures found in the vector \(\boldsymbol {T}\). The initial elastic stresses within each element, due to thermal expansion, are then given by:
where \(\alpha \) is the coefficient of thermal expansion, \(\textit {v}\) is the Poisson’s ratio, and \(E\) is the elastic modulus of the structure. A power law interpolation (SIMP) is used here as well, with the penalty \(p\) assumed to be identical to that used for the conduction terms in (1). Furthermore, the thermal expansion coefficient is assumed to be independent of \(x_{e}\): both of these assumptions follow those made by Sigmund (2001). From \(\boldsymbol {\sigma }_{o_e}\), a thermal load vector \(\boldsymbol {F}\) may be computed by assembling contributions from each element. A linear stiffness matrix is given by the following assembly:
where \(\boldsymbol {K}_{e}\) is an elemental stiffness matrix for the fully solid material (as in (1)). This matrix is computed assuming a unit depth of the structure, and is divided by \((1-\textit {v}^{2})\) to account for this very-long third dimension (i.e., a semi-infinite plate). \(x_{\min }\) is a lower bound on the element density (\(0<x_{\min } \le x_{e} \le 1\)). In general, a small positive value of \(x_{\min }\) is utilized to prevent singular stiffness matrices due to void portions of the topology, and also to allow for the reappearance, during the optimization process, of material in elements that were once void (i.e., to prevent design gradients from becoming exactly zero). The specific material interpolation scheme used in (5) is a minor modification of that used for (1), and is taken from Bendsøe and Sigmund (2003). The modified interpolation scheme is aimed at preventing artificial local vibration and buckling modes in low-density elements, as the ratio of mass to stiffness (for vibration problems) or nonlinear stress stiffening to linear stiffness (for buckling problems) is finite for small values of \(x_{e}\). Additional schemes to avoid this problem in eigenvalue-based topology optimization are given by Tcherniak (2002), Pedersen (2000), Du and Olhoff (2007), and Neves et al. (1995). Furthermore, Pedersen (2000) discusses situations where (5) is unable to prevent the development of localized modes, though the method is found to be completely satisfactory for the cases presented here.
Next, a linear system is solved for the thermally-induced deflections of the structure:
The stresses produced by the deflection vector \(\boldsymbol {u}\) are then computed, and superposed upon \(\boldsymbol {\sigma }_{o_e}\) to obtain the total stresses within each element (Cook et al. 2002):
where \(\boldsymbol {B}_{e}\) is a strain-displacement matrix, and \(\boldsymbol {u}_{e}\) are the nodal displacements (two degrees of freedom per node) of each element, taken as a subset of \(\boldsymbol {u}\). It should be noted that a plane-stress formulation is utilized in (5) and (7), which follows from the common methodology found in the panel literature (Dowell 1970; Librescu et al. 2004; Culler and McNamara 2010), and a desire to reproduce well-known panel stability boundaries (Fig. 3). A plane-strain assumption is certainly arguable in light of the very-long third panel dimension (semi-infinite plate), though the boundary conditions in this third dimension are unspecified, both here and in the general literature. Future work may assess the impact of this assumption upon the optimal topology.
3.3 Thermal buckling
A geometric stress stiffness matrix for the structure may be assembled as:
where \(V_{e}\) is the volume of the element, \(\boldsymbol {S}_{e}\) is a matrix re-ordering of the element stress \({\boldsymbol {\sigma }}_{e}\), and \(\boldsymbol {G}_{e}\) is a shape function differentiation matrix; each of which is described by Cook et al. (2002). The buckling eigenproblem is defined as:
where \({\boldsymbol {\Phi }}_{k}\) is the eigenvector associated with the \(k\)th eigenvalue \(T_{k}\), and \(T_{k}\) is a multiplicative factor of the upper panel temperature \(T_{U}\) (Fig. 1), which has been set to unity for (2). Each buckling temperature factor is positive, and ordered such that \(0 < T_{1} \le T_{2} \le \ldots T_{N_{m} -1} \le T_{N_{m}} \cdot N_{m} \) is the number of retained modes (for the purposes of eigenvalue separation constraints, as discussed below), which is much smaller than the total degrees of freedom of the elastic system. The critical buckling temperature of the system is defined as \(T^{\ast }=T_{1}\), which can be nondimensionalized as:
where the bending stiffness of the panel is given by \(D={E\cdot h^3} / {\left ( {12\cdot ({1-\textit {v}^2})}\right )}\). For a solid panel with uniform heating (\(T_{L}=T_{U}=1\)) and clamped boundary conditions (which are assumed for this work, as drawn in Fig. 1), an analytical value of \(R^\ast =4\cdot \pi ^2\) is obtained (Shigley and Mishke 2001). Alternatively, if \(T_{L}\) is set to 0 and \(T_{U}=1\), double this value is expected: \(R^\ast = 8 \cdot \pi ^2\).
Only buckling modes in the plane of the panel structure of Fig. 1 are included in the \(N_{m}\) modes, though buckling (or flutter) modes can certainly develop in the omitted third direction. These may be accounted for within the context of the two-dimensional finite element model used here via a finite strip method, but their inclusion is out-of-scope for the current paper, and may be considered in future efforts.
3.4 Aerodynamic modeling
Linear quasi-steady piston theory relates the aerodynamic pressure \(p_{a}\) at a point along the upper surface of the panel to the instantaneous velocity of that point:
where \(x\) is the freestream direction along the panel in Fig. 1, \(\textit {w}\) is the transverse deflection of the panel, and \(t\) is time. Terms are included in (11) to correct the aerodynamic pressure for low Mach numbers (Dowell 1966); for values of \(M_{\infty }\) much larger than unity, (11) coincides with that originally given by Ashley and Zartarian (1956). Equation (11) has a stiffness-based component (via \(\partial \textit {w} /\partial x\)) and a temporal component (via \(\partial \textit {w}/\partial t\)), and so aerodynamic stiffness and damping matrices may be computed by looping over each finite element edge which lies along the top surface (as only this surface is exposed to the flow), but assembling into matrices which are the same size as \(\boldsymbol {K}\) and \(\boldsymbol {K}_{\sigma }\) above.
The panel deflection at any time due to aerodynamic forces is given by the vector \(\boldsymbol {q}\), which is the same size as the thermal deformation vector \(\boldsymbol {u}\), and has two displacement degrees of freedom at each node. The third and fourth nodes of the bilinear finite element lie along its upper surface, and the third node lies downstream of the fourth (i.e., has a larger value of \(x\)). The aerodynamic pressure applied to each finite element along the top surface can then be given by:
where \(\boldsymbol {q}_{e}\) is the elemental deflection vector, \(\dot {\boldsymbol {q}}_{e}\) is the time derivative of that vector, and \(L_{e}\) is the length of the upper surface of the element. It can be seen that only the transverse degrees of freedom of the top two nodes of the element correspond to an aerodynamic response, in keeping with (11). A work-equivalent aerodynamic force vector for that element is then computed:
where the negative sign is indicative of the fact that positive aerodynamic pressure on the top surface will push the structure downward. As with (11), only transverse forces along the upper surface are produced.
A global aerodynamic force vector \(\boldsymbol {F}_{a}\) may be computed by assembling over the finite elements along the top surface (\(e_{\rm top}\)). Because \(\boldsymbol {F}_{a}\) must be the same size as the stiffness matrices in (9), aerodynamic forces at finite element nodes within the panel are zero. The force vector may be written as a linear combination of \(\boldsymbol {q}\) and \(\dot {\boldsymbol {q}}\):
The aerodynamic stiffness matrix \(\boldsymbol {K}_{a}\) reflects aerodynamic pressures proportional to \(\boldsymbol {q}\) in (12), the aerodynamic damping matrix \(\boldsymbol {C}_{a}\) reflects proportionality to \(\dot {\boldsymbol {q}}\), and the aerodynamic pressure parameter is defined as Dowell (1966):
3.5 Panel dynamics
A mass matrix for the panel may be computed as:
where \(\boldsymbol {M}_{e}\) is a consistent mass matrix for the fully solid material, and elemental mass terms are assumed to be linearly proportional to the element density (Pedersen 2000). A structural damping matrix is computed via Rayleigh damping (Cook et al. 2002):
For dynamic compliance (resonance) problems, Tcherniak (2002) recommends computing an elemental \(\boldsymbol {C}_{e}\) based on proportionality to \(\boldsymbol {M}_{e}\) and \(\boldsymbol {K}_{e}\), and then assembling into global form similarly to (16), with \(x_{e}\) raised to a power less than unity (e.g., \((x_{e})^{1/2}\)). This can help remove intermediate densities from the topology during the optimization process, as these densities will dissipate a relatively large amount of energy, decreasing actuator quality. This strategy has been successfully used by Stanford and Beran (2011a) as well, but for the eigenvalue-based problems considered here the simpler approach of (17) is satisfactory.
Combining information from (5), (8), (14), (16), and (17), the equations of motion for the panel can be written as:
\(T\) is a multiplicative factor of the upper panel temperature (where \(T_{U}\), as above, is set to unity). The applied temperature \(T\) is entirely unrelated to the pre-computed critical temperature \(T^{\ast }\) in (9); values above or below \(T^{\ast }\) may be selected. Furthermore, \(T\) may be nondimensionalized as in (10): \(R={\alpha \cdot E\cdot T\cdot h\cdot L^2}/D\). If both \(T\) and \(\lambda \) are set equal to zero, (18) represents the free vibration of an unheated panel, and a characteristic frequency (the first bending vibration mode) is identified as \(\omega _{o} =({4.73})^2\cdot \sqrt {D / {( {\rho _{m} \cdot h\cdot L^4})}}\), where \(\rho _{m}\) is the density of the panel. If a positive value of \(\lambda \) is selected, (18) provides the aerodynamically-forced vibration of a panel with a mass ratio of: \(\mu ={\rho _{\infty } \cdot L} / {( {\rho _{m} \cdot h} )}\). The inclusion of non-zero values of \(\lambda \) and \(T\) subjects the panel to both aerodynamic and thermal loads, where it is understood that \(\boldsymbol {K}_{\sigma }\) must be computed by first solving for the temperature distribution \(\boldsymbol {T}\) throughout the panel (2), then computing the thermal deformations \(\boldsymbol {u}\) (6), and finally the element stresses \(\boldsymbol {\sigma }_{e}\) (7).
Defining the vector \(\boldsymbol {\eta } =\{\boldsymbol {q}^T\,\, \dot {\boldsymbol {q}}^T\}^T\), (18) may be placed in standard first-order form:
The state vector is assumed to be of the form \(\boldsymbol {\eta } =\boldsymbol {\psi } \cdot e^{\beta \cdot t}\), which leads to the following eigenproblem:
where \({\boldsymbol {\psi }_k^R} \) is the right eigenvector associated with the \(k\)th eigenvalue \(\beta _{k}\), both of which, in general, will be complex-valued. Specifically, \(\beta _{k}\) are complex conjugate pairs, where the imaginary part is indicative of the frequency of vibration, and the real part dictates stability: a positive real part is an unstable mode with unbounded growth in time.
3.6 Flutter computations
Flutter is defined as a loss of dynamic stability of the equations of motion (20) about an equilibrium solution, which for this work is assumed to be the trivial state: \(\boldsymbol {\eta }_{e}=\mathbf {0}\). For an unheated panel with a geometry as drawn in Fig. 1, this is exactly true, as the panel has no curvature (camber) and is not oriented at an angle of attack to the free-stream vector: perturbations to the system state will always settle back to an undeformed state, as long as the flow speed is below the flutter speed. For a heated panel, this is only an assumption (unless both the heating and the topology are uniform), as there will be some static offset deformation associated with the thermal loads \((\boldsymbol {u})\). But the effect should be small, and so this nonlinearity is not included (Hanoaka and Washizu 1980); pre-buckling deformations have been similarly ignored in the thermal buckling eigenproblem of (9).
Flutter occurs at a Hopf-bifurcation point: for increasing values of \(\lambda \), a pair of complex conjugate eigenvalues \(\beta _{k}\) of the system cross the imaginary axis. Defining the aeroelastic damping of each mode as \(g_{k}= \mathit {Re}(\beta _{k})\), the system loses stability (grows exponentially with time) via flutter when \(g_{k}\) of any mode becomes positive (Bisplinghoff et al. 1955). The damping of the composite response, \({G}\), corresponds to the eigenvalue with the largest real part (the most unstable mode): \({G}={\max }(g_{k})\). The flutter point is the point where \({G}=0\), and occurs at \(\lambda =\lambda ^{\ast }\); the imaginary portion of this critical eigenvalue at \(\lambda ^{\ast }\) is the flutter frequency, \(\omega ^{\ast }\). An example of this process is given in Fig. 2. The eigenvalues at \(\lambda =0\) (wind off) are the uncoupled vibration eigenvalues of the system, and \(\mathit {Re}({\beta }_{k})\) is entirely governed by the structural damping \(\boldsymbol {C}\). If both damping parameters (\(\alpha _{c}\) and \(\beta _{c}\)) are set to zero (which is not the case in Fig. 2), \({G}=0\) at this point as well, though \(\lambda =0\) is not a Hopf-bifurcation point. If the applied temperature \(T\) is larger than the critical value of \(T^{\ast }\), the buckled panel will have at least one eigenvalue whose imaginary portion is equal to zero at \(\lambda =0\).
Several methods can be used for locating the flutter point in a direct manner: most require an initial guess for \(\lambda ^{\ast }\), \(\omega ^{\ast }\), and the eigenvector \(\boldsymbol {\psi }^{R\ast }\) (aeroelastic mode) associated with this critical eigenvalue. This can be done by setting \(\lambda =0\), computing the eigenvalues \(\beta _{k}\), and evaluating \(G={\max }({\textit {Re}}({\beta }_{k}))\). If \({G}\) is less than 0, \(\lambda \) is augmented by some \(\Delta \lambda \), and the process is repeated until \({G}\) becomes positive. Provided that \(\Delta \lambda \) is not too large, the value of \(\lambda \) at which this occurs should be a reasonable approximation to \(\lambda ^{\ast }\), and the least-stable mode provides initial guesses for \(\omega ^{\ast }\) and \(\boldsymbol {\psi }^{R\ast }\). The repetitive eigenvalue computations during the search for \(\lambda ^{\ast }\) can be very costly, particularly if \(\Delta \lambda \) is of a small size. In an optimization context, the process may be conducted just once for the initial baseline design: a subsequent design iterate may use the previous design iterate’s flutter point as an initial guess. It will be shown however, that eigenvalue information is needed in the range \(0 \le \lambda \le \lambda ^{\ast }\) to properly stabilize the flutter optimization problem, and so this \(\lambda \)-marching process is conducted for every design iterate.
Once an initial guess has been obtained, the precise location of the flutter point may be computed with a class of techniques that track the position of the least stable eigenmode. Three methods fall within this class: (1) direct eigenanalysis for the most unstable mode, (2) direct analysis of the expanded system of equations for the Hopf-bifurcation point, and (3) an inverse power method with shifting. Only the first will be discussed here due to its inherent simplicity; the interested reader may study the second approach (Griewank and Reddien 1983; Morton and Beran 1999), or the third approach (Timme et al. 2011), which have both been successfully applied to complex aeroelastic problems.
The first approach uses Newton’s recurrence formula to drive \({G}\) to zero:
where \(n\) is the iteration number. Solving the eigenproblem (21) at the current iterate \(\lambda ^{n}\) provides \({G}(\lambda ^{n})\), which is the damping of the least stable mode (if the \(\lambda \)-marching process detailed above is used, \({G}(\lambda ^{0})\) will be positive). The right and left eigenvectors may also be obtained (\({\boldsymbol {\psi }}^{R}\), \({\boldsymbol {\psi }}^{L}\)), and then the slope of the damping with respect to \(\lambda \) is computed as (Murthy and Haftka 1988):
where it can be seen in (20) that \(\boldsymbol {A}\) has no dependence on \(\lambda \) \((\partial \boldsymbol {A}/\partial \lambda ={\textbf 0})\), and the mode number \(k\) in (23) corresponds to the least stable mode. The region of convergence of (22) is wide above the flutter point (\(\lambda ^{n}>\lambda ^{\ast }\), where the unstable mode is clearly distinguished from the others, as seen in Fig. 2), but narrow below \(\lambda ^{\ast }\). As such, an under-relaxation factor \(\overline \omega \) is typically needed to prevent overshoots that may drive the approximation well below the flutter point. This process requires the repeated computation of a right and a left eigenvector, whose cost will depend strongly upon the sparsity of \(\boldsymbol {A}\) and \(\boldsymbol {B}\) (Lehoucq et al. 1998). Upon convergence of (22): \(\lambda \to \lambda ^{\ast }\), \(\omega \to \omega ^{\ast } \), \({\boldsymbol {\psi }}^{R}\to {\boldsymbol {\psi }}^{R\ast }\), and \({\boldsymbol {\psi }}^{L}\to {\boldsymbol {\psi }}^{L\ast }\). Information about higher eigenmodes at the flutter point (\(\beta _k^{\ast }\), \(\boldsymbol {\psi }_k^{R\ast }\), \(\boldsymbol {\psi }_k^{L\ast }\)) are not directly available using this method, but they can be obtained by re-solving (21) at \(\lambda ^{\ast }\).
A verification study is given in Fig. 3, where data from the aeroelastic model formulated above is compared to data from Erickson (1966) and Beloiu et al. (2005). This is done for a solid panel: referencing Fig. 1, each element has a density \(x_{e}\) of unity. Furthermore, the ratio of the mass ratio to the Mach number, \(\mu /M_{\infty }\), is set to 0.1 (a typical value for aeronautical applications (Dowell 1966)), and the structural damping \(\boldsymbol {C}\) is set to zero. Two stability boundaries are shown in Fig. 3. The upper boundary shows the (nearly-linear) decrease in the flutter speed (\(\lambda ^{\ast }\)) as heating is uniformly applied to the structure (i.e., increased \(R\), the normalized value of the multiplicative factor \(T\) in (18)). The edges of the panel are constrained from moving, and so the compressive thermal stresses weaken the structure and thus lower its flutter speed. The lower set of points in the figure details the boundary across which a buckled panel, for a given value of \(R\), is blown flat by the aerodynamic loads. This boundary emanates from \(R=4\cdot \pi ^2\), noted above as being the critical buckling load \(R^{\ast }\) of the panel (Shigley and Mishke 2001). Except for \(R^{\ast }\), this latter boundary is of no interest for the current topological design study, but does present a useful comparison with published data.
All combinations of (\(\lambda \), \(R\)) below the flutter boundary and above the buckling boundary would ultimately result in a flat panel. Data points below the lower boundary result in a static buckled panel, and data points above the upper boundary result in nonlinear limit cycle oscillations (which may or may not be periodic, depending on whether \(R\) is to the left or right of the point at which the two boundaries in Fig. 3 meet) 0, but this behavior is beyond the scope of the current work. Erickson (1966) and Beloiu et al. (2005) use Euler–Bernoulli thin-beam modeling, with clamped boundary conditions at either end, to compute these boundaries, whereas the current work uses a lattice of plane-stress bilinear finite elements. Despite this difference, and despite the fact that \(L/h\) seen in Fig. 1 is clearly too large to be considered a thin beam/panel (much larger values are presumably used in the two references), the current model matches well with the published results. Unheated flutter speeds are given as 636.57 by Erickson (1966), and computed as 633.05 in the current work. The buckling load \(R^{\ast }/\pi ^{2}\) is less accurate, computed as 3.906 for the current work, whereas Beloiu et al. (2005) arrive closer to the analytical solution of 4. Numerical experiments have indicated that this is not due to discretization errors, but rather to the geometrical violation of the thin beam assumption. This same problem leads to a moderate under-prediction of the flutter speed for heated panels.
4 Sensitivity analysis
Topological design studies formulated below utilize the thermal buckling eigenvalues \(T_{k}\), the flutter speed \(\lambda ^{\ast }\), and the dynamic eigenvalues \(\beta _{k}\) for flow speeds in the range \(0 \le \lambda \le \lambda ^{\ast }\), to form various objective functions and constraints. The number of design variables (\(\boldsymbol {x}\), a vector which collects the design density \(x_{e}\) for each finite element) will be very large, and so design derivatives must be computed analytically, as is typically the case for topology optimization.
4.1 Buckling derivatives
Considering the buckling eigenvalue problem of (9), the linear stiffness matrix \(\boldsymbol {K}\) is an explicit function of the element densities \(\boldsymbol {x}\), though the (nonlinear) stress-stiffness matrix \(\boldsymbol {K}_{{\sigma }} \) is an implicit function of the nodal temperatures and element stresses as well, and of course these dependencies must be accounted for. The total derivative of this matrix is:
Explicit \(\boldsymbol {x}\)-dependencies come from both \(\boldsymbol {\boldsymbol {\sigma }}_{o_{e}} \) and the second term in (7). Implicit dependencies via the thermal deformation \(\boldsymbol {u}\) are due to the second term in (7), and dependencies via the unknown nodal temperatures \(\boldsymbol {T}_{x}\) are due to the \(\boldsymbol {\sigma }_{o_{e}} \) computation in (4) (where a linear interpolation from nodal values \(\boldsymbol {T}_{x}\) to elemental values \(T_{e}\) is assumed in the chain rule computation of \(\partial \boldsymbol {K}_{{\sigma }}/\partial \boldsymbol {T}_{x}\)). The derivatives of (3) and (6) are:
Explicit derivatives of the thermal load vector \(\boldsymbol {R}_{T}\) are computed via the matrix \(\boldsymbol {K}_{T_{xc}}\). Derivatives of \(\boldsymbol {F}\) may be computed via the \(\boldsymbol {{\sigma }}_{o_{e}} \) computation of (4).
With this information, the gradients of the buckling eigenvalues \(T_{k}\) are:
The first term in (27) is the well-known derivative of an eigenvalue (Murthy and Haftka 1988) (where \(({\boldsymbol {\Phi }_{k}})^T\cdot \boldsymbol {K}_{{\sigma }} \cdot ({\boldsymbol {\Phi }_{k}})\) is a modal normalization condition), the second two represent the multidisciplinary nature of the problem (Sigmund 2001): \(\boldsymbol {\lambda }_{u}\) and \(\boldsymbol {\lambda }_{T}\) are adjoint vectors, both of which pre-multiply terms which are exactly equal to zero. Collecting terms that pre-multiply \(\partial \boldsymbol {u}/\partial \boldsymbol {x}\) provides a linear system of equations for \(\boldsymbol {\lambda }_{u}\):
Similarly, \(\boldsymbol {\lambda }_{T}\) is computed by collecting terms associated with \(\partial \boldsymbol {T}_{x}/\partial \boldsymbol {x}\):
Having solved these two systems (once per each eigenvalue \(T_{k}\) of interest), (27) can be written in final form:
It should be noted that (30) specifically assumes that none of the eigenvalues \(T_{k}\) are repeated (i.e., bimodal). Gradients of repeated eigenvalues may be computed (Seyranian et al. 1994), but the current work instead forces adjacent eigenvalues to be separated by a certain amount during the optimization process. Additional discussion regarding this point is provided below.
4.2 Flutter derivatives
Gradients of the dynamic eigenvalue problem (21) proceeds in a similar manner to the process given above, though differences arise because the dynamic eigenproblem is complex-valued (i.e., left and right eigenvectors are needed), and also due to dependence on the dynamic pressure parameter \(\lambda \). If eigenvalue derivatives are desired at a given value of \(\lambda \) (less than the flutter speed \(\lambda ^{\ast }\)), these may be computed as Murthy and Haftka (1988):
where \(\boldsymbol {v}_{u}\) and \(\boldsymbol {v}_{T}\) are adjoint vectors. It can be seen that \(\boldsymbol {A}\), which is only composed of the mass matrix, only has an explicit dependence on \(\boldsymbol {x}\), whereas \(\boldsymbol {B}\) depends on the thermoelastic problem as well, due to the inclusion of \(\boldsymbol {K}_{\sigma } \) in this matrix ((19) and (20)). Similar to (28) and (29), the adjoint vectors are given by:
and the final eigenvalue derivatives are:
As above, this formulation assumes that none of the eigenvalues \(\beta _{k}\) are repeated.
If eigenvalue derivatives are desired at the flutter speed \(\lambda ^{\ast }\), then a \(\lambda \)-dependence must be included in the chain rule:
where the partial derivative \({\partial \beta _k^{\ast }} / {\partial \boldsymbol {x}}\) may be computed using (34), with all terms evaluated at \(\lambda ^{\ast }\). The derivative of the eigenvalues with respect to \(\lambda \) has already been given in (23), but will be provided in a more general form here:
The flutter point derivative \(\partial \lambda ^{\ast }/\partial \boldsymbol {x}\) is required because of (35), but also because \(\lambda ^{\ast }\) will be used as a topological objective function. It may be computed by considering the aeroelastic damping at the flutter point, which is by definition zero, regardless of the design vector:
The term \(\partial G/\partial \lambda \) is the real part of (36) (which has already been computed for use in (22) during the flutter point search), and the term \(\partial G^{\ast } /\partial \boldsymbol {x}\) is the real part of (35), with the mode number \(k\) in both equations corresponding to the flutter mode.
5 Optimization strategies
Of the various restriction methods used in topology optimization, a spatial filter of the design gradients is the most popular (Bendsøe and Sigmund 2003). For the heavily-constrained optimization problems developed below, this degradation in gradient accuracy was found to cause difficulties in improving the objective function in a feasible manner. As such, a density filter developed by Bruns and Tortorelli (2001) is used for this work, where the element densities \(\boldsymbol {x}\) are obtained by filtering a vector of design variables \(\tilde {\boldsymbol {x}}\). This is done via a linearly-decaying cone-shape function, generically represented by a filtering matrix: \(\boldsymbol {x}={\boldsymbol {\cal H}}\cdot \tilde {\boldsymbol {x}}\). The gradients may then be altered in an exact fashion via the chain rule. For example:
where the gradients with respect to \(\boldsymbol {x}\) are what is computed in the previous section, but gradients with respect to the actual design variables \(\tilde {\boldsymbol {x}}\) are required by the optimizer. A continuation method is then used: once the optimization problem has converged to within a suitable tolerance, the filtering radius is decreased, and the problem is restarted. As the radius becomes zero, \(\boldsymbol {x}\to \tilde {\boldsymbol {x}}\). This was found to be a suitable strategy for obtaining a final topology largely composed of strictly solid and void elements. The initial radius size is set to 15 % of the panel thickness \(h\).
The first topology optimization problem considered here seeks to maximize the critical buckling temperature:
where the elemental design variables are constrained to lie between \(x_{\min }\) and unity. Because the filter \({\boldsymbol {\cal H}}\) is volume-preserving, the elemental densities \(\boldsymbol {x}\) will also lie within these side constraints. The volume constraint \(V^{\ast } \) is required as an implicit penalty on intermediate densities via the SIMP scheme (Bendsøe and Sigmund 2003), and is written directly in terms of \(\boldsymbol {x}\) rather than \(\tilde {\boldsymbol {x}}\). The final set of constraints in (40) requires that the first \(N_{m}\) eigenvalues be separated by some small tolerance \(\varepsilon _{T}\), in order to prevent discontinuities associated with critical mode switching. For the high aspect ratio of the panel cross section in Fig. 1, this constraint is typically active only for higher mode numbers \(k\) (as opposed to the closely spaced first and second buckling eigenvalues seen during optimization of lower aspect ratios by Neves et al. 1995), and is of only minor importance.
The second topology optimization seeks to maximize the flutter speed \(\lambda ^{\ast }\). As seen in Fig. 2, flutter may occur (as the parameter \(\lambda \) is increased) when the imaginary portions of two distinct eigenvalues coalesce. Shortly after this coalescence, the real part of one of these eigenvalues (mode 1, in the figure) becomes positive, defining \(\lambda ^{\ast }\). Simply maximizing \(\lambda ^{\ast }\) during the optimization process will inevitably cause critical mode switching, where the eigenvalues of two higher modes coalesce, redefining the flutter point. This may happen at a value of \(\lambda \) well below the previous design iterate’s flutter point \(\lambda ^{\ast }\), causing a sharp drop in the objective function (Odaka and Furuya 2005). In order to prevent this, a series of constraints can be formulated such that the imaginary portions of two consecutive eigenvalues, \(\beta _{k-1}\) and \(\beta _{k}\), be separated by some finite amount at every value of \(\lambda \) between 0 (no flow) and \(\lambda ^{\ast }\) (Langthjem and Sugiyama 1999):
where the dynamic eigenvalues have been ordered based upon their imaginary parts. The point of minimum separation between two modes is \(\lambda ^{\Delta \omega _{k}} \), and may coincide with \(\lambda ^{\ast }\). If the \(\lambda \)-marching method described above is used to locate an initial guess for the flutter point, \(\lambda ^{\Delta \omega _{k}} \) and \(\Delta \omega _{k}\) for each mode pair will be available at the end of this process. These will only be approximate values, but provided \(\Delta \lambda \) is of a moderate size, their accuracy will be acceptable for the current purpose, and no direct method to hone in on an exact value of \(\lambda ^{\Delta \omega _{k}} \) is considered here.
The frequency separation \(\Delta \omega _{2}\) is of no consequence (as interactions between modes 1 and 2 will always cause flutter, and \(\lambda ^{\Delta \omega _{2}}\) is always equal to \(\lambda ^{\ast }\)), and so \(k\) starts at 3 in (41). If, for two consecutive eigenvalues, this frequency separation is minimum at the flutter point \(\left ({\lambda ^{\Delta \omega _{k}} =\lambda ^{\ast }} \right )\), then the constraint gradients may be computed with (35). If, on the other hand, the point of minimum separation occurs at any other point \(({\lambda ^{\Delta \omega _{k}} <\lambda ^{\ast }} )\), the second term in the chain rule of (35) becomes zero. This is because (41) is a local minimum: \({\partial ( {\Delta \omega _{k}} )} / {\partial \lambda } =0\). Similar arguments can be made (Greene and Haftka 1991) for critical point constraints in time during a transient analysis.
For variable-thickness aeroelastic plate problems, Odaka and Furuya (2005) show that the frequency-separation constraint becomes more important for larger side-bounds on the thickness of each finite element. Topological design represents an extreme of this process (as elements can become completely void), and so this set of constraints is expected to be very important. If flutter is always characterized by a modal coalescence, then the constraints of (41) are enough to stabilize the optimization problem, as the “nature” of the eigenvalue migration is forced to remain unchanged during the design process (Langthjem and Sugiyama 1999). For the topologically-optimized panels considered here, however, it was found that flutter could occasionally occur without a strong eigenvalue coalescence. For these cases, the enforcement of a series of \(\Delta \omega _{k}\) constraints is not enough to prevent mode switching during the optimization process, as the interaction between modes \(k\) and \(k-1\) may still cause flutter even though \(\Delta \omega _{k} \ge \varepsilon _{\omega }\). Additional constraints are then required to stabilize the process:
where it is required that the aeroelastic damping at the flutter point be more stabilizing (i.e., more negative) than the structural (no flow) damping (similar constraints are considered by Haftka 1975). This constraint is impossible to satisfy for mode 1, as \(g_{1}^{\ast }=0\) is the definition of a flutter point, and so (42) starts with mode 2.
The combination of frequency separation (41) and damping separation (42) was found to prevent mode switching for all of the cases presented in this work. The complete optimization problem is written as:
Both the thermal buckling and the flutter optimization problems are solved with the method of moving asymptotes (Svanberg 1987), a scheme known to be effective for topology problems with large numbers of variables and constraints.
Presumably, it may be expected that an alternative handling of the eigenvalue-switching issues, as opposed to the separation constraints in (40) and (43), could provide superior optimal results (larger values of \(T^{\ast }\) or \(\lambda ^{\ast }\)) by removing limitations on the feasible design space. For the thermal buckling problem of (40), a bound formulation, in conjunction with an eigen-tracking scheme (when the modes inevitably switch) and algorithms to compute bimodal eigenvalue sensitivities (Seyranian et al. 1994) may be a preferred method. As noted above, however (and shown in Fig. 12), switching of the critical thermal buckling mode is never observed for this particular panel geometry, and the separation-based formulation in (40) should give very similar results to a bound formulation.
The separation constraints of the aeroelastic optimization problem in (43), on the other hand, will be shown to be highly active, and unquestionably drive the design process to some extent. However, alternative schemes to those used in (41) and (42) are less obvious, due primarily to the fact that the flutter problem is an eigenvalue migration problem, rather than just computing and optimizing eigenvalues at some fixed point. Mode tracking schemes and repeated eigenvalue sensitivity methods remain viable, but a bound formulation becomes far more complex. Multiple flutter points would be obtained to formulate the series of bound constraints: \(\lambda _1^{\ast } \le \lambda _2^{\ast } \le \ldots \lambda _{N_{m} -1}^{\ast } \le \lambda _{N_{m}} ^{\ast } \). The computational cost of this is large, as the range of the \(\lambda \)-marching method (to obtain initial guesses for each \(\lambda _{k}^{\ast }\)) would need to extend to very high flight speeds, and then the recurrence formula of (22) used to strongly converge to each flutter point. It is also very possible, during the optimization process, for the slope \(\partial G/\partial \lambda \) of a higher mode to become zero at the flutter point, and that mode then cease to flutter at all (a hump mode, Haftka 1975). This would pose difficulties for the bound method, in the sense that the number of flutter points \(N_{m}\) would change.
The separation constraints of the current flutter optimization method are likely to limit the design process to some extent, but only require the computation of a single (lowest) flutter point, and are therefore relatively inexpensive. Clearly, more research is needed in this area to compare these methods, not just for topology optimization, but for any design of fluttering structures that relies upon gradients-based optimization.
6 Results
All results presented here are for a titanium panel (a typical material choice for thermoelastic panel flutter studies, see Librescu et al. 2004 and Culler and McNamara 2010) operating at \(\mu /M_{\infty }=0.1\) and an aspect ratio \(L/h=25\). The damping parameters are set as \(\alpha _{c}=5\) s\(^{-1}\) and \(\beta _{c}=10^{-7}\) s. The penalization factor \(p\) is set to 3, the first 8 eigenmodes (\(N_{m}\)) are considered for the separation constraints in (40) and (43), and \(x_{\min }\) is set to 0.01. Three basic sets of results are given: flutter of an unheated panel, buckling of a heated panel, and flutter of a heated panel, where the latter problem should pose a topological compromise between the two former. For each optimal topology, a logical comparison is to an entirely solid panel with the same mass. This is drawn in Fig. 4 for a given volume fraction \(V^{\ast }\), where finite elements in the upper portion of the panel are set as solid; the remainder are void. The domain thickness \(h\) is still used as a length-scale for normalization in (10) and (15) (rather than \(V^{\ast }\cdot h\)), in order to maintain a consistent comparison with the optimal topologies.
6.1 Flutter of an unheated panel
Results are first obtained for a volume fraction \(V^{\ast }\) of 0.35, and a frequency separation constraint (\(\varepsilon _{\omega }\), normalized by the characteristic frequency \(\omega _{o}\)) of 0.95. The panel is unheated, a situation which is obtained by setting the multiplicative temperature \(T\) to zero in (18). The topology of the panel at selected design iterations of (43) is given in Fig. 5, while the actual objective function and constraint metrics are plotted at every design iteration in Fig. 6. The baseline design in Fig. 5 consists of setting the density \(x_{e}\) of each element in the design domain to a value slightly less than 0.35: accounting for the areas of the panel which are fixed as solid (\(x_{e}=1\) within the top 10 % and bottom 5 % of the panel), the volume fraction of the complete structure \(\boldsymbol {v}^T\cdot \boldsymbol {x}\) is then exactly equal to 0.35. Within the first 30 iterations, material is allocated to the center and the two ends of the panel, where the former is mostly due to inertial considerations, and the latter due to stiffness effects. The structure is entirely symmetric at this point, though the biasing effects of the flow vector (plotted at the top of Fig. 5) provides the optimizer with some incentive to develop asymmetric topologies in order to further increase the flutter point \(\lambda ^{\ast }\). The advent of asymmetry after 30 iterations occurs (not coincidentally) at the same point when two of the frequency separation constraints (\(\Delta \omega _{5}\) and \(\Delta \omega _{6}\)) become active, and convergence becomes much slower as the optimizer must travel along these highly nonlinear constraint boundaries.
Convergence metrics of the topologies in Fig. 5: objective function \(\lambda ^{\ast }\) (top), frequency separation constraints (middle), and damping separation constraints (bottom)
A third frequency separation constraint (\(\Delta \omega _{3}\)) becomes active at iteration 380, by which time the skewed shape of the center mass and the cross-bracing at the leading edge is fully formed. The topology at the trailing edge continues to develop through to iteration 700, at which point the entire process has converged. Constraints \(\Delta \omega _{4}\), \(\Delta \omega _{7}\), and \(\Delta \omega _{8}\) (the latter is very large, and not shown in Fig. 6) remain inactive, as do all of the damping separation constraints (42). For this case, the frequency separation has acted as a more-conservative surrogate for the damping separation in preventing critical mode switching, but for many of the cases presented below, both sets of constraints are active. Though not shown in Fig. 6, the volume constraint is also active beyond iteration 20. After iteration 700, the continuation process described above is utilized, by continually shrinking the radius of the filter \({\boldsymbol {\cal H}}\) and re-running the optimizer to convergence. Only the final design from this process (when the filter radius is zero) is given at the bottom of Fig. 5: the structure has largely converged to a solid-void design by removing the blurred boundaries of the topology, as intended. The flutter speed has been further increased during this process, and the active constraints at iteration 700 remain active. All topologies shown in Fig. 5 are the filtered element densities \(\boldsymbol {x}\), as opposed to the design variables \(\tilde {\boldsymbol {x}}\), which have no physical meaning. For the final design obtained via continuation, the filter radius is zero, and so \(\boldsymbol {x}\) and \(\tilde {\boldsymbol {x}}\) coincide.
Though a relatively large number of design iterations are required for convergence in Fig. 6, the improvements in the flutter speed \(\lambda ^{\ast }\) are substantial. This objective has been increased by a factor of 3 over the baseline, though this may not be a logical comparison, as the baseline is composed of a fictitious material with an intermediate density. The optimal flutter point, 474.08, is lower than the unheated flutter point of the solid panel in Fig. 3 (633.05), though this isn’t a good comparison either, as the structure in Fig. 3 is much heavier (\(V^{\ast }=1\)) than the current case (\(V^{\ast }=0.35\)). The best comparison is with the solid panel drawn in Fig. 4: the dynamic eigenvalues for this case are shown in Fig. 2, with a flutter speed of 40.52. As such, the optimal topology has a flutter speed over ten times higher than the equivalent solid panel with the same mass.
For further comparison with Fig. 2, the eigenvalue migration of the optimal topology is given in Fig. 7. The flutter point of 474.08 is noted, as are the active frequency separation constraints. The critical separation of modes 2 and 3 and modes 5 and 6 occur at the flutter point, the critical separation of modes 4 and 5 occurs just before the flutter point. For the solid panel of Fig. 2, the higher mode eigenvalues experience very little drift as \(\lambda \) increases, the imaginary portion of modes 1 and 2 strongly coalesce, and the damping slope of the flutter mode (\(\partial G/\partial \lambda \)) is very steep. Contrastingly, both the real and the imaginary portions of the optimal eigenvalues in Fig. 7 are strong functions of \(\lambda \). No coalescence of modes 1 and 2 occurs, though the flutter mode (\(\boldsymbol {\psi }^{R\ast }\)) is clearly a combination of these two modes (shown in Fig. 8), where larger vibration amplitudes occur near the three-quarters point of the panel length (Dowell 1966). Furthermore, the damping slope at flutter is very shallow: if the panel were to operate at a flow speed just beyond \(\lambda ^{\ast }\), unacceptable deformations would accumulate throughout the structure relatively slowly (as the system is lightly unstable), which is in stark contrast to most aeronautical structures (Bisplinghoff et al. 1955), including the results of Fig. 2.
Normalized eigenvalue migration for the optimal topology of Fig. 5
First two free-vibration modes and the flutter mode \((\boldsymbol{\psi}^{R\ast})\) for the optimal topology of Fig. 5
It can also be seen in Fig. 7 that a strong coalescence of modes 5 and 6 occurs after \(\lambda ^{\ast }\): mode 5 flutters at a value of 521.12, and similarly, mode 2 flutters at 598.06. These are both “conventional” flutter points in the sense that the damping slope \(\partial G/\partial \lambda \) is very steep, and they occur via a frequency coalescence. Without the presence of the frequency separation constraints in (43), these higher flutter modes would become critical during the optimization process (presumably near iteration 30, which is when the first set of constraints becomes active in Fig. 6), and the resulting design space discontinuity would hinder further improvements in \(\lambda ^{\ast }\) (Odaka and Furuya 2005). This would result in a substantially non-optimal topology, as \(\lambda ^{\ast }\) is increased by over 100 between iteration 30 and the final design.
The presence of these higher mode flutter points beyond \(\lambda ^{\ast }=474.08\) are of no consequence in a deterministic sense, as the flow speeds over aerospace structures are typically ramped up from \(\lambda =0\), and so the lowest instability is encountered first (Bisplinghoff et al. 1955). In a non-deterministic sense however, where the material properties, topology boundaries, flow details, etc., may be inherently uncertain, these higher flutter modes may become critical in certain areas of the random variable space. It is demonstrated by Odaka and Furuya (2005) that more robust designs are obtained with higher values of \(\varepsilon _{\omega }\), via smaller standard deviations in the flutter speed. Though stochastic effects are not considered here, the topological effect of \(\varepsilon _{\omega }\) is demonstrated in Fig. 9, where the topology/eigenvalues at the center of the figure are reproduced from above. Increasing the required separation distance from 0.95 to a normalized value of 1.32 (i.e., making the constraint harder to satisfy) decreases the flutter speed \(\lambda ^{\ast }\) and also forces more of the frequency separation constraints to become active, as expected. The next flutter point, however, is well beyond the marked value of \(\lambda ^{\ast }\), and presumably this design (which removes material from the center mass to increase the cross-bracing at the edges of the panel) is very robust in the presence of uncertainties. Opposite trends are seen for a normalized separation distance of 0.56, which has the highest flutter speed, the fewest number of active constraints, but a modal coalescence (modes 3 and 4) shortly after \(\lambda ^{\ast }\).
Fixing the normalized frequency separation to the original value of 0.95, the effect of the volume fraction \(V^{\ast }\) is now explored. The upper and lower areas of the panel which are fixed as solid account for a volume fraction of 0.15, so the lowest constraint boundary considered in Fig. 10 is 0.20. For this volume the topology is entirely symmetric, with sparse truss-like members at the ends and center of the panel. Increasing the volume constraint has the expected result of increasing the flutter speed, by increasing the thickness of the cross-bracing at either end, as well as the width of the center mass. Topological asymmetries are seen for every panel above \(V^{\ast }=0.20\) (where the design for \(V^{\ast }=0.35\) is repeated from above), but no clear pattern emerges concerning which side of the panel may be allocated more stiffness or mass, as the volume is increased. The final topology in Fig. 10 has a volume of 0.587, but the volume constraint for this case, which was set to 0.60, is inactive. Higher values of \(V^{\ast }\) therefore need not be considered, as the optimizer cannot take advantage of the relaxed constraint. Similar trends are noted in thickness design variables for flutter-optimal panels: areas of low stiffness increase the flutter speed via decreased inertial loads (Weisshaar 1976; Barboni et al. 1999).
This point is reinforced by noting that all topologies above \(V^{\ast }=0.40\) have a higher flutter speed than the fully solid panel of Fig. 3 (\(\lambda ^{\ast }=633.05\)), despite weighing much less. The flutter speeds of solid panels of volume fractions between 0.05 and 1.00 (referencing Fig. 4) are also given on the right of Fig. 10; each of which is non-Pareto-optimal as compared to the optimized topologies. The nonlinear relationship between \(V^{\ast }\) and \(\lambda ^{\ast }\) for solid panels is due to the \(h^{3}\) term in the definition of the bending stiffness \(D\). It should be noted that if the true thickness of the panel \(V^\ast \cdot h\) were used in the definition of \(D\), the flutter speed \(\lambda ^{\ast }\) would not be a function of \(V^{\ast } \), instead everywhere equal to the plotted value at \(V^{\ast }=1.00\) (notwithstanding finite element discretization errors). It can also be seen that the flutter speed at \(V^{\ast }=1.00\) has a slightly different flutter speed than that quoted for Fig. 3. This is due to the fact that the data in Fig. 10 includes structural damping, whereas the verification study in Fig. 3 does not.
The topological boundaries in most of the panel structures in Fig. 10 are well-defined, though “grey stripes” are present in three of the cases: \(V^{\ast }=0.30\), 0.40, and 0.45. These regions of intermediate-density are entirely due to the filter-based continuation process. When the radius of the filter \({\boldsymbol {\cal H}}\) is decreased from one size to a slightly smaller size, a level of non-smooth discreteness is introduced to the problem, as the number of elements which fall within the neighborhood of any central element drops. This effect causes the optimizer, in some cases, to struggle to hold the highly nonlinear frequency separation constraints \(\Delta \omega _{k}\) (many of which are active during the continuation process) directly after the filter radius is decreased, and some grey material is added in response. More sophisticated filters and continuation schemes (which gradually force the topology to entirely black and white designs without changing the filter size, as reviewed by Sigmund 2007) may out-perform the methods used here, particularly with regards to this problem.
6.2 Thermal buckling
Next, results are provided for buckling-optimal topologies designed under (40), where aeroelastic effects are not considered. A topological convergence for a volume fraction \(V^{\ast }\) of 0.35 and an eigenvalue separation \(\varepsilon _{T}\) of 0.5 is seen in Fig. 11. For the initial results in this section, the heating is entirely uniform, obtained by setting \(T_{L}=T_{U}=1\). This effectively turns the conduction problem (3) “off”, as the temperature of each finite element is equal to unity, regardless of its element density. All terms associated with \(\partial T_{x}/\partial x\) in the sensitivity analysis derived above may be disregarded for uniform heating. Comparing Fig. 11 with similar convergence results in Fig. 5, it can be seen that the optimal buckling problem converges much quicker than the optimal flutter problem, as it has fewer constraints. Furthermore, these eigenvalue separation constraints (\(T_{k} - T_{k - 1}\ge \varepsilon _{T}\)) are only active for higher modes, as seen in Fig. 12. It is understood that the normalized buckling eigenvalue for mode 1 defines the normalized objective function \(R^{\ast }\), and at no point during the optimization is any higher mode poised to become critical. Modes 3 and above are all separated by the critical distance \(\varepsilon _{T}\). Numerical experiments (not shown here) indicate that increasing \(\varepsilon _{T}\) by an order of magnitude has no discernible effect upon the topology. This lack of dependence on eigenvalue separation is in stark contrast to the flutter results (e.g., Fig. 9), and is presumably (from a buckling standpoint) due to the high aspect ratio of the geometry considered here (Bendsøe and Sigmund 2003).
Normalized buckling eigenvalues corresponding to the topologies in Fig. 11
The topology in Fig. 11 is fully converged after 300 iterations; the continuation process largely removes the grey transition areas between solid and void, and further increases the normalized objective function \(R^{\ast }\) as well. A relatively high normalized value of \(R^{\ast }/\pi ^{2}=10.21\) is obtained, much higher than the value of 4 quoted above for a fully solid (and much heavier) panel. Objective function improvements over the baseline design are moderate, but as above, this comparison is of limited usefulness due to the use of intermediate-density material. The optimal topology is entirely symmetric (about the mid-chord) as the biasing effect of the flow velocity is not present here, and consists of a series of diagonally-oriented truss-like members. Whereas the flutter-optimal panel of Fig. 5 utilizes a large inertial mass within the center of the structure, static-stress metrics drive the design process in Fig. 11. According to the critical buckling mode shown in Fig. 13, flexural stresses will be relatively small at the panel center, and so material can be removed from the panel center and reallocated to the highly-stressed panel ends. Largely due to this effect, a strong trade-off between buckling- and flutter-optimal topologies is to be expected, and will be demonstrated in the next section. It is also noted that the third buckling mode in Fig. 13, though largely of a global nature, shows some local buckling patterns along the thin members that make up the lower panel surface.
First three buckling modes of the optimal topology in Fig. 11
The relationship between volume fraction and the buckling-optimal topology is seen in Fig. 14, again starting with a \(V^{\ast }\) of 0.20. Like the flutter data of Fig. 10, beyond a certain threshold (0.628 in this case) the volume constraint boundary becomes inactive, and so higher values are of no interest. Indeed, the last topology in Fig. 14, which was designed under \(V^{\ast }=0.65\), is non-Pareto-optimal (in the \(V^{\ast }\), \(R^{\ast }\) space) with respect to the preceding lighter optimal topologies. The remaining topologies are all Pareto-optimal, and highly superior (for a given volume fraction) to the critical buckling temperature of the solid panels, which is also plotted in Fig. 14. As before, metrics for the solid panels are obtained using concepts of Fig. 4. Unlike the flutter data of Fig. 10, the buckling-optimal topology changes in a consistent manner with increases in \(V^{\ast }\), with thickness primarily added to the ends and the center of the panel along with a continual decrease in the length scale of the diagonal truss-like members.
For the remainder of this paper, the volume fraction is fixed at 0.35. Attention is now turned to the effect of a thermal gradient; leaving the upper surface temperature \(T_{U}\) at unity, the buckling topology optimization problem of (40) is solved for various values of the lower surface temperature \(T_{L}\) between zero and one. \(T_{L}\) values above one are probably unrealistic, as aerodynamic/radiated heating will typically flow from the environment into the structure (Thornton 1992) through the top surface, as the bottom surface is not exposed to the flow. It should also be noted here that radiation heat transfer within the panel, a nonlinear effect which may be important at elevated temperatures, has not been included here. Radiation can be systematically included in topology optimization problems with a structure surrounded by a hot environment (a cooling fin, for example) via a nonlinear convective boundary condition (Bruns 2007). The current internal radiation case is far more challenging however, with the role of radiation view factors in the variable-density SIMP approach a particularly interesting complication.
Topologies for \(T_{L}\) values of 0, 0.25, 0.5, 0.75, and 1.0 are given in Fig. 15. The critical value of \(R^{\ast }\) for each design is given as well; this is the critical buckling measured at the design temperature. For different values of \(T_{L}\), \(R^{\ast } \) for a given design will change, as the stresses will have been redistributed (4) and (7). Typically, decreasing \(T_{L}\) will increase the multiplicative buckling temperature \(R^{\ast } \) due to the subsequent decrease in stress throughout the panel. The upper topology in Fig. 15 (\(T_{L}=T_{U}=1\)) is repeated from above, and every finite element has the same temperature. Lower values of \(T_{L}\) bring about minor changes in the topology at the center and the ends of the panel, and the number of thin diagonal truss-like members continually increases.
Given the large aspect ratio of the panel and the spatially-uniform upper and lower surface boundary conditions, the thermal profile for most cases in Fig. 15 is entirely expected: bulk heat transfer from top to bottom, with the orientation of the temperature gradient vector altered to travel along the local axis of individual truss-like members. In light of this, an interesting question is the impact that simply fixing the temperature distribution (a linearly-varying spatial distribution between \(T_{L}\) and \(T_{U}\), for example) would have on the topology optimization. Taking the case of \(T_{L}=0.5\) as a representative example, setting \(\lambda _{T}\) equal to zero in (30) (which essentially removes the relationship between the elemental density and the temperature distribution) will change \(\textit {dT}_{k}/\textit {dx}\) by 7.2 % for the initial baseline design, and 12.3 % for the final optimal design in Fig. 15: a moderate impact. This result is problem-dependent of course, depending somewhat upon the geometry of the design domain, and strongly upon the type of boundary condition (convection heat-flux, e.g.).
For a \(T_{L}\) of zero however (and to a lesser extent, 0.25), the optimizer has developed a topology in which the upper heated surface is entirely disconnected from the remainder of the panel, which thus remains unheated and unstressed. The critical eigenvalue for this case is purportedly very high (\(R^{\ast }/\pi ^{2}=19.22\)), though clearly the buckling eigenvalue for the upper heated layer, considered on its own, should be much lower (i.e., the buckling mode should be entirely localized to the upper layer, but is instead of a global nature). A closer inspection reveals that the upper surface and the remainder of the truss members are separated by a single row of low density (\(x_{e}\)) finite elements. Their density is low enough such that very little thermal energy may pass through, but high enough to structurally reinforce the surface at several locations. Clearly, this topology is of little practical value; the optimizer has taken advantage of the problem description in general and the finite element discretization in particular. Additional constraints may be formulated into (41) to prevent this behavior, but as will be seen in the next section, this structure is highly non-optimal in an aerothermoelastic sense.
6.3 Flutter of a heated panel
Flutter-optimal results are now provided for heated panels, which involves solving the optimization problem of (43) for various value of the multiplicative temperature \(T\). It is repeated here that \(T\) is in no way related to the buckling temperature \(T^{\ast }\) of the panel’s topology (which is not included in the design optimization), but instead is a quantity which is held fixed during the optimization. A series of topologies are given in Fig. 16 for various levels of uniform heating, along with the value of \(R\) used to design the structure, the resulting objective function (flutter speed, \(\lambda ^{\ast }\)), and the resulting critical buckling load \(R^{\ast }\). This latter metric is not utilized by the optimizer, but is provided for completeness. The first topology in Fig. 16 is repeated from Fig. 5, which was developed under zero thermal load. The buckling temperature of this case is \(R^{\ast }/\pi ^{2}=6.03\), which is much lower than the buckling-optimum result’s in Fig. 11. This would confirm the topological trade-off between buckling- and flutter-optimal structures discussed above.
Increasing the value of the applied temperature \(R\) in Fig. 16 has a substantial effect upon the flutter-optimal topology. With increasing \(R\), the inertial mass at the center of the panel becomes less defined (and is completely removed from the hottest structures), and the cross-bracing is increased at the ends of the panel. The maximum attainable flutter speed generally decreases, as higher thermal loads weaken the structure, but the critical buckling load \(R^{\ast }/\pi ^{2}\) is relatively insensitive, between 6.0 and 6.4 for each case. This is surprising in the sense that the topologies optimized for flutter under higher thermal loads clearly are being driven by strategies observed for buckling-optimum structures in the previous section. The third structure of Fig. 16 is an outlier in the sense that its flutter point is larger than the adjacent structures optimized for higher or lower heating levels. This may be indicative of a highly-complex design space, or the fact that the continuation process in this case has not provided a truly solid-void design. The optimizer may be taking advantage of this fictional intermediate-density material (seen in the center of the panel) to obtain a higher flutter speed than would be obtained if every finite element was explicitly forced to its density limits.
Off-design behavior for the five topologies of Fig. 16, the buckling-optimum design in Fig. 11, and a solid panel, are given in Fig. 17. Each panel in this figure has the same volume (\(V^{\ast }=0.35\)), and each is largely composed of solid and void elements. The plot is provided in the same format as the verification study of Fig. 3: the flutter boundary \(\lambda ^{\ast }\) is given has a function of the applied thermal load \(R\), and the boundary across which, for a given value of \(R\), the panel is blown flat, is also shown. This latter boundary emanates from the buckling load \(R^{\ast }\), and eventually merges with the flutter boundary at some larger value of \(R\). The design point in (\(R\), \(\lambda ^{\ast }\)) space is also indicated in the figure. Several interesting observations can be made from Fig. 17. First, many topologies are seemingly out-performed by another topology’s off-design behavior. For example, the unheated panel has a flutter speed of 474.08 at its design point (\(R/\pi ^{2}=0\)), but the panel optimized at \(R/\pi ^{2}=6.11\) has a higher flutter speed (541.93) at this same point. Only the unheated panel is feasible at this point however, as the other topologies violate the frequency separation constraints when their off-design behavior is computed, and as such, cannot be considered as robust.
An indicator of this robustness manifests itself through changes in the critical mode along the flutter boundary. At the design point, the critical flutter mode is always the first mode, as this is stipulated by the frequency and damping separation constraints added to the optimization problem (43). For an off-design point, however, the critical flutter mode could be due to an interaction of higher modes. Again taking the panel designed under unheated conditions as an example: the flutter speed starts at the designed value of 474.08, and decreases in a monotonic fashion with increasing values of \(R\), which is very similar to the behavior seen for a solid panel (Fig. 3). At \(R/\pi ^{2}=3.53\), a coalescence of modes 2 and 3 becomes more critical than the original flutter mode, and \(\lambda ^{\ast }\) drops off at a much faster rate. At \(R/\pi ^{2}=4.91\), the flutter mode changes again (a coalescence of modes 5 and 6), after which the flutter speed actually increases with increased heating. This would indicate a highly complex relationship between the fluttering fifth vibration mode and the stresses accumulated by uniform heating.
At \(R/\pi ^{2}=6.07\), the flutter mode reverts back to the original first mode, and \(\lambda ^{\ast }\) decreases until the flutter boundary merges with the buckling boundary. The end result is a dangerous “flutter dip”, whose presence would go undetected if higher mode effects were not included in the analysis. A discontinuous flutter boundary (namely, a dip) via mode-switching is a commonly-seen behavior in aeroelastic systems undergoing parametric sweeps: see for example Forster and Yang (1998) (via changes in skin thickness) and Beran et al. (2004) (via changes in Mach number), among many others.
In many of the cases in Fig. 17, these areas of low flutter occur only for highly off-design areas of the plot. An alternative aerothermoelastic optimization procedure to the one taken here is to maximize the unheated flutter speed \(\lambda ^{\ast }\) under a series of constraints upon the critical buckling temperature \(R^{\ast }\): in this way, a Pareto front may be formed. The aeroelastic behavior of these designs under (off-design) heated conditions, however, is likely to be very poor, due to the advent of higher flutter modes and their associated dips. The procedure used here, to maximize flutter directly under a heated environment, is superior. The panel optimized at \(R/\pi ^{2}=6.11\), for example (bottom topology of Fig. 16), has a relatively high flutter speed through the entire heating range of Fig. 17, and a very mild dip between 1.21 and 4.37. As expected, the flutter performance of the buckling-optimal design is poor despite having the largest \(R^{\ast }\) in the plot, and both the heated flutter and the buckling characteristics of the solid panel (with a volume fraction of 0.35) are very low.
The qualitative shape of each design’s lower buckling boundary is the same, which would indicate that higher buckling modes do not become active in the same way that is observed along the flutter boundary. To further explore the “blown flat” concept (which occurs across this boundary), eigenvalue migration for the flutter-optimal panel topology designed at \(R/\pi ^{2}=6.11\) are given in Fig. 18. This is done across a range of flow speeds \(\lambda \) for a fixed value of the heating parameter \(R/\pi ^{2}=7.50\), which is greater than the buckling temperature of this design (\(R^{\ast }/\pi ^{2}=6.36\), given in Fig. 16). For low values of \(\lambda \) the panel is buckled: one of the eigenvalues has a positive real part, but its imaginary portion (frequency) is 0, and so this is a static instability. The panel is blown flat at \(\lambda =37.50\), when the imaginary portion becomes positive and the real part negative (stabilizing) This occurs due to the collision of two real-valued eigenvalues, which then become complex conjugates. This same pair loses stability at \(\lambda ^{\ast }=175.68\), which defines the flutter speed.
The \(\lambda \)-marching concept outlined above to locate a good initial guess for the flutter point will fail in the case of Fig. 18. To repeat, \(\lambda \) is increased from a low value (typically 0) until \({G}={\textit {max}}({\textit {Re}}({\beta }_{k}))\) becomes positive. But it can be seen in the figure that \({G}\) is positive at \(\lambda =0\) (due to the static buckling instability), though this clearly is not the desired flutter point. The problem is solved by only considering eigenvalues whose imaginary portions are greater than zero (i.e., dynamic) in the identification of \({G}\). This issue is not encountered for any of the cases given in Fig. 16, as none are operating under a thermal load greater than their buckling load, and so all of their eigenvalues will have a nonzero imaginary part. The exercise of Figs. 16 and 17 is repeated for the case of non-uniform heating. Two of the topologies are subjected to a temperature in the post-buckled regime, and so the modification to the \(\lambda \)-marching process is required. Flutter-optimal topologies under non-uniform heating (specifically, \(T_{L}=0\)) are given in Fig. 19 and off-design behavior is given in Fig. 20.
The first topology in Fig. 19 is repeated from above, designed without a thermal load. The critical buckling temperature is higher than that cited in Fig. 16, as less of the panel is being heated, though of course the flutter speed is the same. As above, increasing the thermal load on the structure leads the optimizer to remove the central mass in favor of additional cross-bracing at the panel ends. For the highest thermal load, the structure is almost entirely symmetric, composed of a series of thin diagonally-oriented members. Despite the fact that flutter speed is the actual objective function, the buckling-sensitive aspects of the problem drive the design process: in (18), the energy associated with the thermal term \(T\cdot \boldsymbol {K}_{\sigma } \) dominates the aerodynamic contribution from \(\lambda \cdot \boldsymbol {K}_{a} \) during the \(\lambda ^{\ast }\) computation. A compromise is forced between flutter-optimal topologies and bucking-optimal topologies, although the latter metric is not explicitly included in the optimization statement.
The lower surface temperature \(T_{L}\) is set to zero for these results, a potentially poor choice given that the buckling optimizer gave questionable results for this value in Fig. 15. It is seen in Fig. 20 that the off-design aerothermoelastic performance of the buckling-optimal design is very poor however, with consistently low flutter speeds. Furthermore, none of the topologies in Fig. 19 mimic the structures seen above, where the heated upper panel was largely disconnected from the remainder of the topology. The off-design flutter boundaries in Fig. 20 are similar to those found for uniformly-heated panels, with strong flutter dips for heating values far less than the design point. It is further noted that data for a solid panel has not been included in Fig. 20: because the lower portion of this panel is fixed as entirely void, the imposition of a thermal gradient from the top to the bottom surface is not a feasible situation.
7 Conclusions
This work has optimized the internal topology of a metallic panel subject to a high supersonic flow over its upper surface, and prescribed temperature boundary conditions along the upper and lower surfaces. The cross-section of the panel is discretized into finite elements, each of which is assigned a density-based design variable which indicates a solid element or a void. The quasi-steady temperature distribution throughout the panel is computed, followed by the thermal stresses and the critical buckling temperatures. Using well-known piston theory aerodynamics, the flutter speed of the structure can be found for a given thermal load, which occurs at a Hopf-bifurcation point. Both eigenvalue-related metrics (buckling temperature and flutter point) are optimized using the SIMP-based topology optimization methodology, though each problem must be outfitted with highly nonlinear eigenvalue-separation constraints to prevent switching of the critical mode (and the associated design space discontinuities) during the optimization process. Following a model verification study, three sets of results are presented: unheated flutter-optimal topologies, thermal buckling-optimal topologies (no aerodynamic loading), and flutter optimal topologies under a thermal load (aerothermoelastic). The following conclusions can be drawn:
-
1.
Unheated flutter-optimal topologies can be obtained by allocating mass to the center of the panel (inertial effects) and cross-bracing at the ends of the panel (elastic effects). Due to the biasing effect of the flow vector, asymmetries develop in the structure later in the optimization process, though the initial iterates are entirely symmetric.
-
2.
Whereas the flutter of a solid panel occurs very rapidly (steep damping slope) after the coalescence of the imaginary portion of two eigenvalues, the flutter of an optimized topology does not involve a strong coalescence, and the damping slope through the Hopf-bifurcation is very moderate.
-
3.
Frequency separation constraints are typically active at values of \(\lambda \) both equal to and less than the flutter point. Increasing the required separation distance drops the optimal flutter value and increases the number of active constraints, but should provide more robust designs in the presence of uncertainties, as higher mode flutter points are forced to reside at much higher \(\lambda \)-values than \(\lambda \)*.
-
4.
The thermal buckling optimization problem converges much faster than the flutter problem, as fewer eigenvalue separation constraints are needed, and are typically only active among the higher buckling modes. These designs involve removing all mass from the center of the panel (where the stresses will be small) in favor of truss-like members. These topologies are entirely symmetric.
-
5.
Accuracy issues are noted in the buckling-optimal topology when designed under a large thermal gradient, as the optimizer obtains a structure where the heated upper panel is entirely disconnected from the lower portion of the panel, which thus remains unheated. This structure is found to be highly non-optimal in a flutter sense.
-
6.
Aerothermoelastic conditions are obtained by optimizing the flutter speed under a specified thermal load. Increasing this load forces a compromise between the flutter-optimal topologies and buckling-optimal topologies, although buckling is not explicitly included as an objective function or a constraint.
-
7.
Off-design flutter behavior for these structures (over a range of heating levels) is characterized by changes in the critical flutter mode, which can cause drastic drops in the flutter speed. Robust panels will clearly need to simultaneously consider several heating conditions during the topology optimization process, a common tactic in aerospace design.
References
Abbas J, Ibrahim R, Gibson R (1993) Nonlinear flutter of orthotropic composite panel under aerodynamic heating. AIAA J 31(8):1478–1488
Ashley H, Zartarian G (1956) Piston theory—a new aerodynamic tool for the aeroelastician. J Aeronaut Sci 23(12):1109–1118
Barboni R, Mannini A, Gaudenzi P (1999) On the use of the P-TFE method for panel flutter optimization. Comput Struct 70(1):109–117
Beiner L, Librescu L (1983)Minimum-weight design of an orthotropic shear panel with fixed flutter speed. AIAA J 21(7):1015–1016
Beloiu D, Ibrahim R, Pettit C (2005) Influence of boundary conditions relaxation on panel flutter with compressive in-plane loads. J Fluid Struct 21(4):743–767
Bendsøe M, Sigmund O (2003) Topology optimization. Springer, Berlin
Beran P, Khot N, Eastep F, Snyder R, Zweber J (2004) Numerical analysis of store-induced limit-cycle oscillation. J Aircr 41(6):1315–1326
Bisplinghoff R, Ashley H, Halfman R (1955) Aeroelasticity. Addison-Wesley, Cambridge
Bruns T (2007) Topology optimization on convection-dominated, steady-state heat transfer problems. Int J Heat Mass Transfer 50(15):2859–2873
Bruns T, Tortorelli D (2001) Topology optimization of non-linear elastic structures and compliant mechanisms. Comput Methods Appl Mech Eng 190(26):3443–3459
Chen B, Gu Y, Zhao G, Lin W, Chang T, Kuang J (2003) Design optimization for structural thermal buckling. J Therm Stress 26(5):479–494
Cook R,Malkus D, PleshaM,Witt R (2002) Concepts and applications of finite element analysis. Wiley, New York
Culler A, McNamara J (2010) Studies on fluid-thermal-structural 48(10):1721–1738
De Leon D, de Souza C, Fonseca J, da Silva R (2012) Aeroelastic tailoring using fiber orientation and topology optimization. Struct Multidisc Optim 46(5):663–677
Dowell E (1966) Nonlinear oscillations of a fluttering plate. AIAA J 4(7):1267–1275
Dowell E (1970) Panel flutter: a review of the aeroelastic stability of plates and shells. AIAA J 8(3):385–399
Du J, Olhoff N (2007) Topological design of freely vibrating continuum structures for maximum values of simple and multiple eigenfrequencies and frequency gaps. Struct Multidisc Optim 34(5):91–110
Dugundji J (1966) Theoretical considerations of panel flutter at high supersonic mach numbers. AIAA J 4(7):1257–1266
Erickson L (1966) Supersonic flutter of flat rectangular orthotropic panels elastically restrained against edge rotation. NASA TN D-3500
Eschenauer H, Olhoff N (2001) Topology optimization of continuum structures: a review. Appl Mech Rev 54(4):331–390
Foldager J, Hansen J, Olhoff N (2001) Optimization of the buckling load for composite structures taking thermal effects into account. Struct Multidisc Optim 21(1):14–31
Forster E, Yang H (1998) Flutter control of wing boxes using peizo-electric actuators. J Aircr 35(6):949–957
Fung Y (1958) On two-dimensional panel flutter. J Aeronaut Sci 25(4):145–160
Gao T, Zhang W (2010) Topology optimization involving thermo-elastic stress loads. Struct Multidisc Optim 42:725–738
Garrick I (1963) A survey of aerothermoelasticity. Aero/Space Eng 22(1):140–147
Gee D, Sipcic S (1999) Coupled thermal model for nonlinear panel flutter. AIAA J 37(5):642–650
Gomes A, Suleman A (2008) Topology optimization of a reinforced wing box for enhanced roll maneuvers. AIAA J 46(3):548–556
Greene W, Haftka R (1991) Computational aspects of sensitivity calculations in linear transient structural analysis. Struct Multidisc Anal 3(3):176–201
Griewank A, Reddien G (1983) The calculation of Hopf points by a direct method. IMA J Numer Anal 3(1):295–303
Haftka R (1975) Parametric constraints with application to optimization for flutter using a continuous flutter constraint. AIAA J 13:471–475
Hanoaka M, Washizu K (1980) Optimum design of Beck’s column. Comput Struct 11(5):473–480
Hirano Y, Todoroki A (2004) Stacking sequence optimizations for composite laminates using fractal branch and bound method: application for supersonic panel flutter problem with buckling load condition. Adv Compos Mater 13(2):89–106
Jensen J (2007) Topology optimization of dynamics problems with padé approximants. Int J Numer Methods Eng 72:1605–1630
Jensen J (2009) Space-time topology optimization for one-dimensional wave propagation. Comput Methods Appl Mech Eng 198(5):705–715
Jog C (1996) Distributed-parameter optimization and topology design for nonlinear thermoelasticity. Comput Methods Appl Mech Eng 132(1):117–134
Jog C (2002) Topology design of structures subjected to periodic loading. J Sound Vib 253(3):687–709
Kontinos D (1997) Coupled thermal analysis methods with application to metallic thermal protection panels. J Thermophys Heat Transf 11(2):173–181
Kreissl S, Pingen G, Evgrafov A, Maute K (2010) Topology optimization of flexible micro-fluidic devices. Struct Multidisc Optim 42(4):495–516
Krog L, Tucker A, Kemp M (2004) Topology optimization of aircraft wing box ribs. In: AIAA/ISSMO multidisciplinary analysis and optimization conference, Albany, NY, 30 August–1 September
Langthjem M, Sugiyama Y (1999) Optimum shape design against flutter of a cantilevered column with an end-mass of finite size subjected to a non-conservative load. J Sound Vib 226(1):1–23
Lehoucq R, Sorensen D, Yang C (1998) ARPACK users’ guide: solution of large-scale eigenvalue problems with implicitly restarted Arnoldi methods. SIAM, Philadelphia
Li Q, Steven G, Querin O, Xie Y (2000) Structural topology design with multiple thermal criteria. Eng Comput 17(6):715–734
Librescu L, Marzocca P, Silva W (2004) Linear/nonlinear supersonic panel flutter in a high-temperature field. J Aircr 41(4):918–924
Livne E, Mineau D (1997) Panel flutter constraints: analytic sensitivities and approximations including planform shape design variables. J Aircr 34(4):558–568
Ma Z, Kikuchi N, Cheng H, Hagiwara I (1995) Topology optimization technique for free vibration problems. J Appl Mech 62:200–207
Maalawi K (2002) Buckling optimization of flexible columns. Int J Solid Struct 39(23):5865–5876
Maeda Y, Nishiwaki S, Izui K, Yoshimura M, Matsui K, Terada K (2006) Structural topology optimization of vibrating structures with specified eigenfrequencies and eigenmode shapes. Int J Numer Methods Eng 67(12):597–628
Manickarajah D, Xie Y, Steven G (2000) Optimisation of columns and frames against buckling. Comput Struct 75(1):45–54
Maute K, Allen M (2004) Conceptual design of aeroelastic structures by topology optimization. Struct Multidisc Optim 27(1):27–42
Maute K, Reich G (2006) Integrated multidisciplinary topology optimization approach to adaptive wing design. J Aircr 43(1):253–263
McNamara J, Friedmann P (2011) Aeroelastic and aerothermoelastic analysis of hypersonic flow: past, present, and future. AIAA J 49(6):1089–1122
McNamara J, Friedmann P, Powell K, Thuruthimattam B, Bartels R (2008) Aeroelastic and aerothermoelastic behavior in hypersonic flow. AIAA J 46(10):2591–2610
Mei C, Abdel-Motagaly K, Chen R (1999) Review of nonlinear panel flutter at supersonic and hypersonic speeds. Appl Mech Rev 52(10):321–332
Miller B, McNamara J, Spottswood S, Culler A (2011) The impact of flow induced loads on snap-through behavior of acoustically excited, thermally buckled panels. J Sound Vib 330(23):5736–5752
Min S, Kikuchi N, Park Y, Kim S, Chang S (1999) Optimal topology design of structures under dynamic loads. Struct Multidisc Optim 17(2):208–218
Morton S, Beran P (1999) Hopf-bifurcation analysis of airfoil flutter at transonic speeds. J Aircr 36(2):421–429
Murthy D, Haftka R (1988) Derivatives of eigenvalues and eigen-vectors of a general complex matrix. Int J Numer Methods Eng 26(2):293–311
Nam C, Kim Y, Weisshaar T (1996) Optimal sizing and placement of piezo-actuators for active flutter suppression. Smart Mater Struct 5(2):216–224
Neves M, Rodriguez H, Guedes J (1995) Generalized topology design of structures with a buckling load criterion. Struct Optim 10(2):71–78
Odaka Y, Furuya H (2005) Robust structural optimization of plate wing corresponding to bifurcation in higher mode flutter. Struct Multidisc Optim 30(2):437–446
Palaniappan K, Beran P, Jameson A (2006) Optimal control of LCOs in aero-structural systems. In: AIAA structures, structural dynamics, and materials conference, Newport, RI, 1–4 May
Pedersen N (2000) Maximization of eigenvalues using topology optimization. Struct Multidisc Optim 20(1):2–11
Peirson B (1975) Panel flutter optimization by gradient projection. Int J Numer Methods Eng 9(2):271–296
Rahmatalla S, Swan C (2003) Continuum topology optimization of buckling-sensitive structures. AIAA J 41(6):1180–1189
Reed W, Hanson P, Alford W (1987) Assessment of flutter model testing related to the national aero-space plane. NASA CN-156, 823
Sadri A,Wright J,Wynne R (2002) LQG control design for panel flutter suppression using piezoelectric actuators. Smart Mater Struct 11(6):834–839
Schaeffer H, Heard W (1965) Flutter of a flat plate exposed to a nonlinear temperature distribution. AIAA J 3(10):1918–1923
Seresta O, Abdalla M, Mulani S, Marzocca P (2006) Stacking sequence design of flat composite panel for flutter and thermal buckling. AIAA J 44(11):2726–2735
Seyranian A, Lund E, Olhoff N (1994) Multiple eigenvalues in structural optimization problems. Struct Optim 8(4):207–227
Shigley J, Mishke C (2001) Mechanical engineering design. McGraw Hill, New York
Sigmund O (2001) Design of multiphysics actuators using topology optimization—part I: one-material structures. Comput Methods Appl Mech Eng 190(49):6577–6604
Sigmund O (2007) Morphology-based black and white filters for topology optimization. Struct Multidisc Optim 33(11):401–424
Stanford B, Ifju P (2009) Aeroelastic topology optimization of membrane structures for micro air vehicles. Struct Multidisc Optim 38(3):301–316
Stanford B, Beran P (2011a) Conceptual design of compliant mechanisms for flapping wings with topology optimization. AIAA J 49(4):855–867
Stanford B, Beran P (2011b) Optimal structural topology of a plate-like wing for subsonic aeroelastic stability. J Aircr 48(4):1193–1203
Svanberg K (1987) The method of moving asymptotes—a new method for structural optimization. Int J Numer Methods Eng 24(2):359–373
Tanaka M, Todoh M, Maetaka A (2005) Optimal allocation of piezo-electric passive dampers for a panel exposed to fluid flow: maximum critical velocity design problem. J Intell Mater Syst Struct 16(11):925–930
Tcherniak D (2002) Topology optimization of resonating structures using SIMP method. Int J NumerMethods Eng 54(11):1605–1622
Thornton E (1992) Thermal structures: four decades of progress. J Aircr 29(3):485–498
Thornton E, Dechaumphai P (1988) Coupled flow, thermal, and structural analysis of aerodynamically heated panels. J Aircr 25(11):1052–1059
Timme S, Marques S, Badcock K (2011) Transonic aeroelastic stability analysis using a kriging-based schur complement formulation. AIAA J 49(6):1202–1213
Van Keuren G, Eastep F (1977) Use of galerkin method for minimum-weight panels with dynamic constraints. J Spacecr 14(7):414–418
Wang X, Hansen J, Oguamanam D (2004) Layout optimization of stiffeners in stiffened composite plates with thermal residual stresses. Finite Elem Anal Des 40(9):1233–1257
Weisshaar T (1972) Aeroelastic optimization for a panel in high mach number supersonic flow. J Aircr 9(9):611–617
Weisshaar T (1976) Panel flutter optimization—a refined finite element approach. Int J Numer Methods Eng 10(1):77–91
Xue D, Mei C (1993) Finite element nonlinear panel flutter with arbitrary temperatures in supersonic flow. AIAA J 31(1):154–162
Yang T, Han A (1976) Flutter of thermally buckled finite element panels. AIAA J 14(7):975–977
Yoon G (2010a) Structural topology optimization for frequency response problem using model reduction schemes. Comput Methods Appl Mech Eng 199:1744–1763
Yoon G (2010b) Topology optimization for stationary fluid-structure interaction problems using a new monolithic formulation. Int J Numer Methods Eng 82(5):591–616
Acknowledgments
This work is sponsored by the Air Force Office of Scientific Research under Laboratory Task 03VA01COR, monitored by Dr. Fariba Fahroo.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Stanford, B., Beran, P. Aerothermoelastic topology optimization with flutter and buckling metrics. Struct Multidisc Optim 48, 149–171 (2013). https://doi.org/10.1007/s00158-013-0885-x
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00158-013-0885-x